Gradient Boosted Trees for Corrective Learning

Abstract

Random forests (RF) have long been a widely popular method in medical image analysis. Meanwhile, the closely related gradient boosted trees (GBT) have not become a mainstream tool in medical imaging despite their attractive performance, perhaps due to their computational cost. In this paper, we leverage the recent availability of an efficient open-source GBT implementation to illustrate the GBT method in a corrective learning framework, in application to the segmentation of the caudate nucleus, putamen and hippocampus. The size and shape of these structures are used to derive important biomarkers in many neurological and psychiatric conditions. However, the large variability in deep gray matter appearance makes their automated segmentation from MRI scans a challenging task. We propose using GBT to improve existing segmentation methods. We begin with an existing ‘host’ segmentation method to create an estimate surface. Based on this estimate, a surface-based sampling scheme is used to construct a set of candidate locations. GBT models are trained on features derived from the candidate locations, including spatial coordinates, image intensity, texture, and gradient magnitude. The classification probabilities from the GBT models are used to calculate a final surface estimate. The method is evaluated on a public dataset, with a 2-fold cross-validation. We use a multi-atlas approach and FreeSurfer as host segmentation methods. The mean reduction in surface distance error metric for FreeSurfer was 0.2 – 0.3 mm, whereas for multi-atlas segmentation, it was 0.1mm for each of caudate, putamen and hippocampus. Importantly, our approach outperformed an RF model trained on the same features (p < 0.05 on all measures). Our method is readily generalizable and can be applied to a wide range of medical image segmentation problems and allows any segmentation method to be used as input.

1 Introduction

Deep gray matter atrophy is an important feature of many neurodegenerative diseases. In particular, the volumes of the caudate nucleus and the putamen are among the strongest predictors of motor disease onset in Huntington’s disease [11]. Hippocampus may also be implicated in Huntington’s and is also highly relevant in other neurodegenerative diseases such as Alzheimer’s [24]. However, the automated segmentation of these structures from MRI scans is challenging due to the large variability in their appearance, especially in the presence of neurodegeneration. Many approaches have been proposed, including probability-atlas approaches [6], Bayesian models of shape and appearance [13], surface-based graph cuts [12], and multi-atlas label fusion [20]. However, none of these methods are perfect, and the errors they make can often be of a systematic nature reflecting the bias of each approach. Wang et al. [19] have proposed a learning-based wrapper method to learn and correct for this systematic segmentation error of ‘host’ segmentation methods, which was further developed by Tustison et al. [17] in the context of hippocampal subfields. We propose a similar approach based on gradient boosted trees in a surface-based sampling setup.

Gradient boosting was first proposed in [7]. GBT models build ensembles of decision trees, and apply the boosting principle to learn a tree structure where each new tree is built to approximate the negative gradient of the empirical loss function in order to correct the errors made by previous trees in the ensemble. These trees are typically weak learners, i.e., the size of the individual trees is typically kept small. Furthermore, in each iteration of the training phase, only a random subsample of the data instances (rows) and features (columns) are used, in order to prevent overfitting [8]. The final prediction is calculated by combining the individual predictions with coefficients learned during the training phase. This is in contrast to random forests (RF), another tree-based ensemble model, where full-grown trees are built and their predictions are combined uniformly.

Novelty

Although GBT models have been studied for over a decade, their use in practice has been limited until recently, mainly due to their computational cost. We use XGBoost¹, which is an efficient and open source implementation of GBT models, first released in 2014. Unlike the popular RF approach, there has only been a few previous studies using GBT in the general medical image analysis field [2,3,21], and even fewer in 3D medical image segmentation. A notable exception is the work of Bakas et al. [1] who use GBT to refine brain tumor segmentation. Here, we show that GBT models outperform RF models trained on identical feature sets. While the current study is focused on corrective learning for deep gray matter structures, our results highlight that GBT models have potential for improving many medical image analysis problems where RF’s are commonly used.

2 Methods

We propose using gradient boosted trees (GBT) to learn the appearance model of the caudate nucleus, putamen and hippocampus from human brain MRI and to improve the accuracy of existing segmentation methods. The automated pipeline begins with T1-weighted MRI images and applies the ‘host’ initial segmentation method to create an initial surface estimate for these subcortical structures. Next, a surface-based sampling process is used to construct a set of candidate locations for the vertices using this estimate as the base mesh. Raw numerical features are extracted at each candidate location, including spatial coordinates, image intensities, gradient magnitudes and texture. GBT classifiers are trained on an augmented set of features, labeling the node closest to the true surface in each column as the positive class. Finally, the classification probabilities from the GBT models are used as weights to calculate a final surface estimate.

2.1 Host Segmentation Methods

We use two different host methods to illustrate our segmentation correction algorithm. (1) Multi-atlas. Each training image was deformably registered² to the target image [23]. The manual segmentations for the training images were warped to the target image using these transformations. A consensus segmentation was achieved using the Joint Label Fusion (JLF) algorithm [20]. (2) FreeSurfer. FreeSurfer formulates subcortical segmentation as a Bayesian parameter estimation problem and leverages a probabilistic atlas to classify each voxel [6]. FreeSurfer v5.3 was used with the default settings and no manual interventions.

2.2 Construction of Candidate Locations

Given the initial segmentation results, a surface model was created using the marching cubes algorithm and smoothed for 25 iterations with a sinc filter. The resulting model was used as the base mesh. Starting with the base mesh, a column was constructed at each surface vertex, with the column consisting of 30 candidate locations (15 inside, 15 outside) at 0.15 mm intervals. The idea is to use the machine learning algorithm to move each surface vertex along the corresponding column to deform the surface into a more accurate configuration, similar to surface-based graphs [12,22] and active shape models [5]. The paths of the columns were determined following the electric lines of field [12,22] and were smoothed using Kochanek splines [10] for better geometric behavior.

2.3 Raw Feature Set

We begin with a series of pre-processing steps to reduce the variability between the image intensities. First, N4 bias correction [18] was used to remove inhomogeneity across the spatial domain, after skull-stripping with BET [15] for increased effectiveness. The WhiteStripe intensity normalization algorithm [14] was applied to the N4 results to normalize intensities across subjects. Finally, a non-local means filter [16] was applied to reduce noise. The intensity normalization (BET+N4+WhiteStripe) and noise filtering (BET+N4+WhiteStripe+NLM) results contributed 2 normalization features at each location.

Classical texture features [4,9] were computed using normalized gray-level co-occurrence matrices (GLCM). Given g(i, j) elements of the GLCM matrix, and their weighted pixel average μ = Σ i · g(i, j) and variance σ = Σ(i − μ)² · g(i, j), 8 texture features were computed: energy (Σ(g(i, j)²), entropy (Σg(i, j)log(g(i, j))), correlation ( $\sum \frac{(i-\mu )(j-\mu )g(i,j)}{{\sigma }^2}$), difference moment ( $\sum \frac{1}{1+{(i-j)}^2}g(i,j)$), inertia, also known as contrast (Σ(i − j)²g(i, j)), cluster shade (Σ((i − μ) + (j − μ))³g(i, j)), cluster prominence (Σ((i − μ) + (j − μ))⁴g(i, j)) and Haralick’s correlation ( $\frac{\sum (i,j)g(i,j)-{\mu }^2}{{\sigma }^2}$). The GLCM was computed in each of 13 possible directions in a 3 × 3 neighborhood, resulting in a total of 8 × 13 = 104 texture features at each graph node location.

The anatomy surrounding deep brain structures is very heterogeneous; thus, the image appearance near the surface can vary for different regions. To encourage the trained model to capture these regional properties, we parcellate each surface into regions of interest (ROIs) and use the ROIs as a feature. We compute the bounding box of each base mesh surface, and divide it into 3 equal sections along the P-A axis and 2 equal sections along the I-S axis. The subdivision along the L-R axis was done based on the orientation of the surface normal vector. Thus, each vertex was assigned to one of 3 × 2 × 2 = 24 ROIs.

The mean μ and standard deviation σ of intensity for each structure were determined from the host segmentation. Then, we use ((I − μ)/σ) at each node as a proxy surface confidence feature.

In addition to the normalization and texture features, 12 raw features were thus extracted for each candidate location. 8 of these are node based (spatial coordinates of the node (3), node height along graph column, image intensity, intensity diff, gradient magnitude, surface confidence), and 4 are shared by all nodes in a given column (surface normal direction (3), ROI).

The features for the training set were created using the same process on the training set. The only difference was that in the multi-atlas experiment, for each training subject, the remaining N-1 training subjects were used as atlases.

2.4 Feature Engineering

For each node, we create 4 vectors in Euclidean space from the node to its 2 neighboring nodes up and down the column. We calculate the length of each vector (4 features), and the angles between each pair of vectors (6 features). Note that the angles encode approximate local curvature. Combined with the original 8 node-based raw features, this produces 18 raw features.

These features, however, may still vary in magnitude despite the normalization steps with WhiteStripe and N4. In order to prevent overfitting to the wrong signal, these features are normalized by min-max scaling, both per subject and per column (36 features). For the 8 original raw features, we also include the difference of the normalized values of the current node with 2 neighboring nodes up and down the column (64 features). The 4 column-based features are included as is, resulting in 104 base features. Thus, we have 104 base features + 2 normalization features + 104 texture features, resulting in a total of 210 features per location. Two nodes at each end of the column do not have enough neighbors; the values for these features are duplicated from the end node.

2.5 Gradient Boosted Trees

For each of the left/right caudate/putamen/hippocampus structures, a GBT model is trained on features described above. For each column in the sample set, the node that is closest to the true surface is labeled as the positive class. All other nodes in the column are labeled as the negative class.

Model parameter tuning is performed separately for each of the 6 structures, optimizing the mean surface distance over inner cross-validation folds; logarithmic loss and area under the receiver operating characteristic curve were also monitored during this phase. In the XGBoost implementation, the following parameters were used for all testing subjects, for all structures: ‘colsample by level’ = 0.05, ‘learning rate’ = 0.6, ‘max depth’ = 4, ‘min child weight’ = 10, ‘n estimators’ = 100, ‘subsample’ = 0.8. All other parameters were left at default values. We note that the number of parameters that need to be tuned is dramatically smaller than more complicated models such as deep learning methods, where number and type of layers as well as nodes per layer, connections between layers, activation functions, etc. need to be fine-tuned.

The final surface is fitted via a surface-based graph cut [12] using the probability output from the GBT model as weights. While this does not strongly affect the quantitative performance, it results in smoother surfaces.

3 Experimental Methods

3.1 Data and Cross-Validation

The method is evaluated on the MICCAI 2012 Multi-Atlas Segmentation Challenge dataset, consisting of T1-w MR images from 35 subjects. For each subject, manual segmentations of various regions, including the left and right caudate nuclei, putamen and hippocampi, were provided as part of the Challenge.

Given the relatively low number of subjects, a simple train/test split could lead to overfitting to the samples in the test set. GBT and other tree-based ensembles (e.g., RFs) are more prone to overfitting than linear models without a proper validation scheme. It has been extensively argued in the machine learning literature that overfit models will produce superficially good results on the test set they were tuned on, but will fail to generalize to new unseen data.

To prevent this, we use a two-fold cross-validation setup. We split the 35 subjects as 15 train/20 test, identical to the original Challenge for comparability with previous methods, and a second fold with the reversed setup (20 train/15 test). The whole automated pipeline is applied to the raw data in each cross-validation fold, to prevent contamination between folds. We tuned our method using cross-validation within the inner folds; after this tuning step within the training set, a single set of parameters was used to generate results on all test subjects (in the outer folds), across all structures (left/right caudate/putamen/hippocampus). Random forests (RF) models have also been trained on the same 210 features for each structure, using similar parameter tuning methods.

3.2 Evaluation Metrics

Mean vertex-to-surface distance between estimated surface and reference manual segmentation (for symmetry, distance from estimated to truth and vice versa are averaged) were used to evaluate the models. In the context of this surface-based analysis framework, we consider this a more appropriate metric than volumetric overlap measures such as Dice.

4 Results

Table 1 presents the surface-to-surface distance for the raw FreeSurfer results, and for corrective learning using GBT and RF. For each structure, for both metrics, both the GBT and the RF corrective learning led to statistically significant improvements (p < 1e⁻⁴) over the raw FS results. Furthermore, the GBT corrective learning results were significantly more accurate than RF corrective learning results in every t-test (p < 1e⁻⁴).

Table 1.

Surface-to-surface error, with FreeSurfer as host. Mean ± std. dev. are shown. Differences between all pairs of methods were statistically significant.

Distance	FreeSurfer (Host)			FreeSurfer + RF Bias Correction			FreeSurfer + GBT Bias Correction
Structure	Fold1	Fold2	Fold1+Fold2	Fold1	Fold2	Fold1+Fold2	Fold1	Fold2	Fold1+Fold2
LCaudate	0.87 ± 0.28	0.70 ± 0.09	0.80 ± 0.24	0.76 ± 0.29	0.59 ± 0.09	0.69 ± 0.24	0.68 ± 0.30	0.50 ± 0.09	0.60 ± 0.25
RCaudate	0.95 ± 0.21	1.07 ± 0.91	1.00 ± 0.61	0.86 ± 0.22	0.96 ± 0.91	0.90 ± 0.61	0.75 ± 0.23	0.84 ± 0.89	0.79 ± 0.60
LPutamen	1.09 ± 0.14	1.11 ± 0.10	1.10 ± 0.12	0.92 ± 0.13	0.94 ± 0.09	0.93 ± 0.11	0.77 ± 0.12	0.76 ± 0.10	0.76 ± 0.11
RPutamen	0.95 ± 0.15	1.14 ± 0.51	1.03 ± 0.36	0.78 ± 0.12	0.98 ± 0.50	0.86 ± 0.35	0.65 ± 0.11	0.81 ± 0.51	0.72 ± 0.35
LHippocampus	0.85 ± 0.18	0.83 ± 0.12	0.84 ± 0.16	0.78 ± 0.17	0.76 ± 0.11	0.77 ± 0.14	0.69 ± 0.16	0.65 ± 0.09	0.67 ± 0.14
RHippocampus	0.80 ± 0.08	1.01 ± 0.77	0.89 ± 0.51	0.73 ± 0.07	0.94 ± 0.78	0.82 ± 0.52	0.65 ± 0.07	0.84 ± 0.78	0.73 ± 0.51

Table 2 presents similar results using joint label fusion (JLF) as host method. Both the GBT and the RF corrective learning led to statistically significant improvements (p < 0.002) over the raw JLF results across the board. Furthermore, the GBT corrective learning results were significantly more accurate than RF corrective learning results in every t-test (p < 0.04).

Table 2.

Surface-to-surface error, with joint label fusion as host. Mean ± std. dev. are shown. Differences between all pairs of methods were statistically significant.

Distance	Joint Label Fusion (Host)			JLF + RF Bias Correction			JLF + GBT Bias Correction
Structure	Fold1	Fold2	Fold1+Fold2	Fold1	Fold2	Fold1+Fold2	Fold1	Fold2	Fold1+Fold2
LCaudate	0.50 ± 0.16	0.42 ± 0.08	0.47 ± 0.13	0.43 ± 0.15	0.34 ± 0.05	0.39 ± 0.13	0.39 ± 0.16	0.30 ± 0.04	0.35 ± 0.13
RCaudate	0.57 ± 0.22	0.40 ± 0.06	0.50 ± 0.19	0.51 ± 0.22	0.33 ± 0.04	0.44 ± 0.19	0.45 ± 0.22	0.29 ± 0.03	0.38 ± 0.19
LPutamen	0.46 ± 0.11	0.42 ± 0.03	0.44 ± 0.09	0.40 ± 0.12	0.36 ± 0.03	0.38 ± 0.09	0.35 ± 0.13	0.29 ± 0.03	0.32 ± 0.10
RPutamen	0.41 ± 0.12	0.35 ± 0.02	0.38 ± 0.10	0.39 ± 0.13	0.33 ± 0.03	0.36 ± 0.10	0.35 ± 0.13	0.29 ± 0.03	0.32 ± 0.10
LHippocampus	0.54 ± 0.14	0.50 ± 0.06	0.52 ± 0.11	0.52 ± 0.13	0.48 ± 0.06	0.50 ± 0.11	0.48 ± 0.12	0.43 ± 0.06	0.46 ± 0.10
RHippocampus	0.52 ± 0.10	0.50 ± 0.06	0.51 ± 0.08	0.50 ± 0.09	0.47 ± 0.06	0.48 ± 0.08	0.47 ± 0.08	0.43 ± 0.06	0.45 ± 0.08

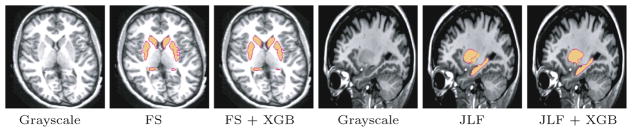
Figure 1 shows qualitative results comparing the raw input segmentations and the GBT corrective learning results for two subjects. For FreeSurfer input, the improvement is especially pronounced for the lateral surface of the putamen, where our approach successfully fixes leakage into the neighboring external capsule white matter. For the JLF input, our method successfully fixes an under-segmentation problem for the putamen.

Fig. 1.

Qualitative bias correction results for FreeSurfer (left) and joint label fusion (right). The reference manual segmentation is shown in solid yellow, whereas the automated segmentations are shown as pink outlines. (Color figure online)

Each GBT model for each left-right pair of structures takes around 15 min in total for both training and predicting the probabilities. The RF run time was about twice longer than the GBT run time.

Note that the JLF+GBT performance is superior to FS+GBT result in the reported metrics. This is presumably due to differences in host methodologies: while JLF uses the training data which has similar characteristics and segmentation protocol, FS uses its own external training data, which may be less compatible with the testing data.

5 Discussion

Our results show the proposed GBT-based corrective learning approach can be successfully applied to learn and correct systematic errors in input ‘host’ segmentation algorithms, leading to a substantial boost in accuracy. Importantly, the results of the GBT-based learning were significantly more accurate than a comparable RF-based learning approach trained on identical features. Given the popularity of the RF model in the medical image analysis community, this data suggests that GBT models may also offer improvements in other machine learning applications in medical image analysis.

We note that while the current experiments focused on the caudate, putamen and hippocampus which are of specific interest in Huntington’s disease studies, the methods we propose are readily generalizable and can be used to learn and correct errors in other structures, given a suitable host segmentation algorithm.

The current ROI choice is based on a coarse heuristic, and a more sophisticated parcellation based on an atlas initialization or clustering of columns based on intensity similarity and spatial proximity may further enhance the performance. Exploring these issues as well as additional feature sets such as SIFT features remains as future work.