Abstract
With this article, we propose using a Bayesian multilevel latent class (BMLC; or mixture) model for the multiple imputation of nested categorical data. Unlike recently developed methods that can only pick up associations between pairs of variables, the multilevel mixture model we propose is flexible enough to automatically deal with complex interactions in the joint distribution of the variables to be estimated. After formally introducing the model and showing how it can be implemented, we carry out a simulation study and a real-data study in order to assess its performance and compare it with the commonly used listwise deletion and an available R-routine. Results indicate that the BMLC model is able to recover unbiased parameter estimates of the analysis models considered in our studies, as well as to correctly reflect the uncertainty due to missing data, outperforming the competing methods.
Keywords: Bayesian mixture models, latent class models, missing data, multilevel analysis, multiple imputation
1. Introduction
Nested or multilevel data are typical in educational, social, and medical sciences. In this context, Level 1 (or lower level) units, such as students, citizens, and patients, are nested within Level 2 (or higher level) units such as schools, cities, and hospitals. When lower level units within the same group are correlated with each other, the nested structure of the data must be taken into account. Although standard single-level analysis assumes independent Level 1 observations, multilevel modeling allows these dependencies to be taken into account. In addition, variables can be collected and observed at both levels of the data set, which is another feature not taken into account by single-level analyses.
Akin to single-level analysis, however, the problem of missing data arises and must be properly handled also with multilevel data. Although multilevel modeling has in general gained a lot of attention in the last decades, issues related to item nonresponses in this context are still open (Van Buuren, 2011). In this respect, Van Buuren (2011) observed that the most common practice followed by analysts is discarding all the units with nonresponses and performing the analysis with the remaining data, a technique known as listwise deletion (LD). Although LD can potentially lead to a large waste of data (for instance, with a missing item for a Level 2 unit, all the Level 1 units belonging to that group are automatically removed), it also introduces bias in the estimates of the analysis model when the missingness is in the predictors. Another missing-data handling technique, maximum likelihood for incomplete data, which is considered one of the major methods for missing data in single-level analysis (Allison, 2009; Schafer & Graham, 2002) under the missing at random (MAR) assumption,1 has certain drawbacks with multilevel data (Allison, 2009; Van Buuren, 2011). First, the variables that rule the missingness mechanism must be included in the analysis model. As a consequence, specifying and interpreting the joint distribution of such data can become a complex task in this case. Furthermore, departures from the true model can lead to biased estimates or incorrect standard errors (Van Buuren, 2011). Second, with multilevel models, the derivation of the maximum likelihood estimates, for instance, through expectation-maximization (EM) algorithm or numerical integration can be computationally troublesome (Goldstein, Carpenter, Kenward, & Levin, 2009).
A more flexible tool present in the literature is multiple imputation (MI; Rubin, 1987). MI substitutes the original incomplete data set with M > 1 completed data sets, in which the missing values have been replaced by means of an imputation model. Good performance of MI is obtained when the imputation model preserves the original relationships present among the variables (reflected in the imputed data), although the imputation model parameters are not of primary interest: The imputation model is only used to draw imputed values from the posterior distribution of the missing data given the observed data. After this step, standard full-data analysis can be performed on each of the M completed data sets. By doing this, uncertainty coming from the sampling stage can be distinguished from uncertainty due to the imputation step in the pooled estimates and their standard errors. One of the major advantages of MI is that, after the imputation stage, any kind of analysis can be performed on the completed data (Allison, 2009). In particular, in this article, we deal with MI of missing Level 1 and Level 2 predictors of the analysis model.
Specification of the imputation model is one of the most delicate steps in MI. Two main imputation modeling techniques are present in the literature: full conditional specification (FCS; Van Buuren, Brand, Groothuis-Oudshoorn, & Rubin, 2006) and joint modeling (JOMO; Schafer, 1997). Although the former is based on a variable-by-variable imputation and requires specification of separate conditional models for each item with missing observations, the latter only needs specification of a joint multivariate model of the items in the data set, from which the imputations are drawn. As a general rule, the imputation model should be at least as complex as the substantive model in order not to miss important relationships between the variables and the observations that are object of study in the final analysis (Schafer & Graham, 2002).
In a multilevel context, this means also that the sampling design must be taken into account. A number of studies have shown the effect of ignoring the double-level structure of the data when imputing with standard single-level models (Andridge, 2011; Carpenter & Kenward, 2013; Drechsler, 2015; Reiter, Raghunathan, & Kinney, 2006; Van Buuren, 2011). Results indicate that including design effects in the imputation model—when they are not actually needed—can lead in the worst case to a loss of efficiency and conservative inferences, while using single-level imputation models when design effects are present in the data can be detrimental for final inferences. The latter case can result in biased final estimates as well as in severe underestimation of the between-groups variation and biased standard errors of the fixed effects (Carpenter & Kenward, 2013). To take the nested structure of the data into account, mixed effects models are better equipped than fixed effects imputation models with dummy variables, since the latter can overestimate the between-groups variance (Andridge, 2011). Furthermore, single-level imputation can yield different values for Level 2 variables within the same group, if these are included in the model. Conversely, multilevel modeling automatically incorporates the nested structure of the data, takes into account Level 1 units correlations within the same Level 2 unit, and imputes the data respecting the exact level of the hierarchy under which the imputations have to be performed.
Survey data often record categorical item responses. Although multilevel MI for continuous data has already been discussed in the literature (Schafer & Yucel, 2002; Van Buuren, 2011; Yucel, 2008), to our knowledge, no ad hoc methods have been proposed in the literature for categorical data and require better coverage (Van Buuren, 2012). Most of the standard software focuses on single-level imputation models (see Andridge, 2011, for a review of software packages wrongly suggested for multilevel studies) or does not allow for the MI of multilevel categorical data, such as the mice package (Van Buuren & Groothuis-Oudshoorn, 2000; Zhao & Schafer, 2016), which bases its imputations on FCS modeling. An MI technique based on multilevel JOMO can be found in the pan R-library (Zhao & Schafer, 2016). However, pan is also not suited for categorical data because it does not work with the original scale type and treats all the variables as continuous. The imputed data are then imputed through rounding, which can introduce bias in the MI estimates (Horton, Lipsitz, & Parzen, 2003). Recently developed FCS approaches for multilevel data are the one-step FCS (Jolani, Debray, Koffijberg, Van Buuren, & Moons, 2015) and the two-step FCS (Resche-Rigon & White, 2016): The former uses a homoscedastic covariance matrix for the Level 1 errors, while the second assumes heteroscedastic matrices. These methods cannot handle more than two categories for each categorical variable and have not been extended yet to the imputation of Level 2 predictors. An R package that allows for the MI of multilevel mixed type of data (categorical and continuous) is the jomo package version 2.1 (Quartagno & Carpenter, 2016), another JOMO approach. For each categorical variable with missingness, JOMO assumes an underlying latent q-variate normal distribution, where q + 1 is the number of categories of each variable at both levels. The joint distribution of the lower and higher level variables is then estimated, and the imputations are based on the normal variable components scores. For more information about the functioning of JOMO, see Carpenter and Kenward (2013). JOMO works under a Bayesian paradigm and uses the Gibbs sampler (Gelfand & Smith, 1990) to perform the imputations. Although representing a further step in the literature, JOMO still has some major limitations. By working with multivariate normal distributions, imputations yielded by JOMO can correctly reflect only pairwise linear relationships in the data, that is, important relationships that may occur between pairs of variables. Possible higher orders of associations, such as interactions and nonlinearities, are disregarded by JOMO, making it less flexible and possibly leading to less optimal imputations if more complex dependencies are present which are of interest in the subsequent analysis of the MI data set. Furthermore, the default prior distributions for the covariance matrices used by JOMO can become very informative in case of small (Level 1) sample sizes, leading to biased parameter estimates and/or standard errors, as observed through a simulation study by Audigier et al. (2017).
Vermunt, Van Ginkel, Van der Ark, and Sijtsma (2008) proposed performing single-level MI of categorical data with frequentist latent class (LC) or mixture models, while Si and Reiter (2013) implemented the same model under a nonparametric Bayesian framework. The attractive part of using LC models for MI is their flexibility, since mixture models can pick up very complex associations in the data at both levels when a large enough number of LCs (or mixture components) are specified (Vermunt, Van Ginkel, Van der Ark, & Sijtsma, 2008). Furthermore, the model works with the original scale type of the data, preventing the risk of rounding bias (Horton et al., 2003). The Bayesian setting allows for an easier and more appealing computation in the presence of multilevel data (Goldstein et al., 2009; Yucel, 2008) through Markov chain Monte Carlo (MCMC) algorithms, and it is viewed as a natural choice in an MI context (Schafer & Graham, 2002), since the posterior distribution of the missing data given the observed data can be directly specified as a part of the model.
Multilevel MI of categorical data with LC models can be performed by estimating single-level LC models separately for each higher level unit, performing in this way the imputations independently for each higher level unit. However, this approach has some disadvantages. First, by focusing on a single higher level unit, it becomes impossible to either use or impute values of higher level variables since these are constants within a higher level unit. Therefore, this method cannot be used when missingness is present also in the higher level variables. Second, this method can be applied only when the number of Level 2 units is small and the number of Level 1 units for each group is large. When this method is run with a large number of higher level units, model estimation (and selection) becomes time-consuming because a larger number of LC models (and, therefore, parameters) must be implemented. Furthermore, small Level 1 sample sizes for (some of the) Level 2 units will make the LC model extremely unstable (Vermunt, 2003), leading to overly uncertain imputations.
With this article, we propose the use of an LC imputation model, which is more naturally tailored for multilevel data: the Bayesian Multilevel Latent Class (BMLC) model. The BMLC imputation model we propose corresponds to the nonparametric version of the multilevel LC model introduced by Vermunt (2003) in a frequentist setting. Unlike the single-level LC model, the BMLC is able to capture heterogeneity in the data at both levels of the data set, by clustering the Level 2 units into Level 2 LCs and, conditioned on these clusters, Level 1 units are classified into Level 1 LCs. With this setting, units at Level 1 of groups within the same Level 2 LC are assumed to be independent from each other. The BMLC model extends the work of Vermunt (2003) to include also Level 2 indicators, allowing for correct imputations at both levels of the data set.
The outline of this article is as follows. In Section 2, the BMLC model is introduced, along with model and prior selection and model estimation issues. In Section 3, a simulation study is performed with two different sample size conditions. Section 4 shows an application to a real-data situation. Finally, Section 5 concludes with final remarks by the authors.
2. The BMLC Model for MI
In MI, imputations are drawn from the distribution of the missing data conditioned on the observed data. With Bayesian imputations, this is the posterior predictive distribution of the missing data given the observed data and the model parameter π, that is , which can be derived from the posterior of the model parameter given the observed data, . This allows for modeling uncertainty about π. Since , we need to specify a data model——and a prior distribution—Pr(π)—in order to obtain the posterior of π. Model estimation, as well as the imputation step, is performed through Gibbs sampling.
2.1. The Data Model
We now introduce the BMLC models as if there were no missing data in the data set (). Let denote a nested data set with J Level 2 units and nj Level 1 units within Level 2 unit j (), with a total sample size of . Suppose, furthermore, that the data set contains T Level 2 categorical items , each with Rt observed categories () and S Level 1 categorical items , each with Us () observed categories.
We denote with the vector of the T Level 2 item scores for Level 2 unit j and with the full vector of the Level 1 observations within the Level 2 unit j, in which is the vector of the S Level 1 item scores for Level 1 unit i within the Level 2 unit j. The data model consists of two parts, one for the Level 2 (or higher level) units and one for the Level 1 (or lower level) units. Let us introduce the Level 2 LCs variable Wj with L classes (Wj can take on values ) and the Level 1 LCs variables —with K classes—within the l th Level 2 LC (with Xji ranging in ).
The higher level data model for unit j can then be expressed by
This model is linked to the lower level data model for the Level 1 unit i within the Level 2 unit j through
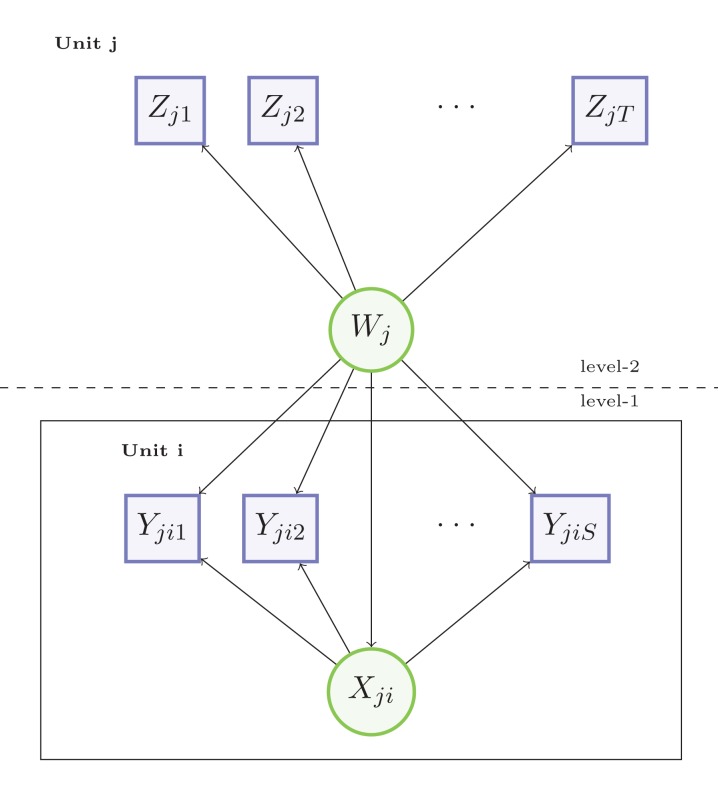
Figure 1 represents the underlying graphical model. From the figure, it is possible to notice both how the number of Level 1 latent variables is allowed to vary with j (because within each Level 2 unit, we have nj Level 1 units and, accordingly, nj latent variables Xji) and how Wj affects Zj, Xji, and Yji simultaneously.
Figure 1.
Graphical representation of the multilevel latent class model with observed items at both levels of the hierarchy.
As in a standard LC analysis, we will assume multinomial distributions for the Level 1 LCs variable X|W and the conditional response distributions . Additionally, we will assume multinomial distributions for the conditional responses at the higher level , and as we are considering the nonparametric2 version of the multilevel LC model, also the Level 2 mixture variable W is assumed to follow a multinomial distribution. Formally,
The parameters denote a vector containing the probabilities of each category of the corresponding multinomial distribution. That is, , , , and . The whole parameter vector is for each l, t, k, s.
Assuming multinomiality for all the (latent and observed) items of the model, we can rewrite the model for as
| 1 |
in which if and 0 otherwise, and . The latter quantity is derived from the lower level data model, given by
| 2 |
where if and 0 otherwise.
The model is capable of capturing between- and within-Level 2 unit variability by first classifying the J groups in one of the L clusters of the mixture variable W and subsequently, given a latent level of W, classifying the Level 1 units within j in one of the K clusters of the mixture variable X|W. In order to capture heterogeneity at both levels, the model makes two important assumptions:
the local independence assumption, according to which items at Level 2 are independent from each other within each LC Wj and items at Level 1 are independent from each other given the Level 2 LC Wj and the Level 1 LC ;
the conditional independence assumption, where Level 1 observations within the Level 2 unit j are independent from each other once conditioned on the Level 2 LC Wj.
By virtue of these assumptions, the mixture variable W is able to pick up both dependencies between the Level 2 variables and dependencies among the Level 1 units belonging to Level 2 unit j, while the mixture variable X is able to capture dependencies among the Level 1 items. Both Equations 1 and 2 incorporate these assumptions through their product terms. Diagnostics have been proposed to test the conditional independence assumption of multilevel LC models by Nagelkerke, Oberski, and Vermunt (2016, 2017).
It is also noteworthy that by excluding the last product (over i) in Equation 1, we obtain the standard LC model for the Level 2 units, while by excluding the product over t in Equation 1 and setting L = 1, we obtain the standard LC model for the Level 1 units.
In Bayesian MI, the quantity tends to dominate the (usually noninformative) prior distribution of the parameter because the primary interest of an imputation model is the estimation of the joint distribution of the observed data, which determines the imputations. Thus, as remarked by Vermunt et al. (2008), we do not need to interpret π but rather obtain a good description of the distribution of the items. Moreover, since an imputation model should be as general as possible (i.e., it should make as few assumptions as possible) in order to be able to describe all the possible relationships between the items needed in the postimputation analysis (Schafer & Graham, 2002), we will work with the unrestricted version of the multilevel LC model proposed by Vermunt (2003). In such a version, both the Level 1 latent proportions and the Level 1 conditional response probabilities are free to vary across the L Level 2 LCs. For a deeper insight into the (frequentist) multilevel LC model, we refer to Vermunt (2003, Vermunt et al., 2008).
2.2. The Prior Distribution
In order to obtain a Bayesian estimation of the model defined by Equations 1 and 2, a prior distribution for π is needed. For the multinomial distribution, a class of conjugate priors widely used in the literature is the Dirichlet distribution. The Dirichlet distribution gives a probability measure in the simplex (where D represents the number of categories of the multinomial distribution) and its parameters represent pseudocount artificially added by the analyst in the model. Thus, for the BMLC model, we assume as priors:
Under this notation, the hyperparameters of the Dirichlet distribution denote vectors, in which each single value is the pseudocount placed on the corresponding category. Thus, αW corresponds to the vector , and similarly , , and . The vector containing all the hyperparameter values will be indicated by .
Because in our MI application we will work with symmetric Dirichlet priors,3 in the remainder of this article, we will use the value of a single pseudocount to denote the value of the whole corresponding vector. For instance, the notation αl = 1 will indicate that the whole vector αW will be a vector of 1s.
In MI, a large number of LCs are usually required when performing the imputations. The probability of empty clusters increases with the number of classes L or K when standard priors (such as the uniform Dirichlet prior) are used (Hoijtink & Notenboom, 2004). This causes the Gibbs sampler (described in Section 2.4) to sample from the prior distributions of the empty components, hence becoming unstable (Fruhwirth-Schnatter, 2006). In turn, this can lead to imputations that produce poor inferences, especially in terms of bias and coverage rate for some of the parameter estimates in the analysis model, as shown in Vidotto, Vermunt, and van Deun (2018). Better inferences can be obtained by setting the hyperparameters of the mixture components in such a way that units are distributed across all the LCs during the Gibbs sampler iterations. This is achievable by increasing the values of αl and αlk (maintaining symmetric Dirichlet distributions) until all the LCs are filled throughout the sampler iterations. Whether the selected values are large enough can easily be assessed with MCMC graphical output.4 With such priors, the Gibbs sampler is able to draw from the equilibrium distribution , and accordingly, it can produce imputations that lead to correct inferences, since the model exploits all the selected classes. Because the imputation model parameter values do not need be interpreted in MI, more informative priors do not represent a problem here.
About the prior distribution of the conditional response probabilities, Vidotto et al. (2018) advocated using hyperparameters that influence the imputations as little as possible. Their results indicated that uniform Dirichlet priors lead to biased parameter estimates of the analysis model, especially interaction terms (when present). However, decreasing the hyperparameter of the items’ conditional distribution probabilities to .01 (or .05) led the imputation model to obtain unbiased terms. Making the prior distribution of the conditional response probabilities as noninformative as possible is effective because it helps to identify the LCs and create imputations that are almost exclusively based on the observed data.
Concerning the BMLC model, little is known about the effect of the choice of prior distributions for Model 1 because the model has not been extensively explored in the literature. Nonetheless, we suspect that behaviors observed for single-level LC imputation models will also hold at the higher level of the hierarchy. In order to assess the effect of different prior specifications for the Level 2 model parameters, we will manipulate αl and αltr in the study of Section 3. For the lower level model (Model 2 in the previous section), we will assume that the findings of Vidotto et al. (2018) hold.5 Therefore, we will set informative values for and noninformative values for .
2.3. Model Selection
In MI, misspecifying a model in the direction of overfitting is less problematic than misspecifying toward underfitting (Carpenter & Kenward, 2013; Vermunt et al., 2008). Although the former case, in fact, might lead to slightly overconservative inferences in the worst scenario, the latter case is likely to introduce bias (and too liberal inferences) since important features of the data are omitted. In mixture modeling, overfitting corresponds to selecting a number of classes larger than what is required by the data.
For the BMLC model in MI applications, model selection can be performed similar to Gelman et al.’s method (Chapter 22). The procedure requires running the Gibbs sampler described in Algorithm 1 (without Step 7) of Section 2.4 with arbitrarily large L* and K* and setting hyperparameters for the LC probabilities that can favor empty superfluous components. Following Gelman, Carlin, Stern, and Rubin’s (2013) guidelines,6 these values could be equal to and . At the end of every iteration of the preliminary Gibbs sampler, we keep track of the number of LCs that are allocated in order to obtain a distribution for L and K when the algorithm terminates. If the posterior maxima L max and K max of such distributions are smaller than the proposed L* and K*, in the next step, the imputations can be performed with L max and K max. However, if either L max or K max (or both of them) equals L* or K*, we rerun the preliminary Gibbs sampler by increasing the corresponding value(s) and repeat the procedure until optimal L and K are found. This method corresponds to the multilevel extension of the model selection proposed by Vidotto et al. (2018) for single-level LC MI. The method for BMLC models will be tested in the simulation study of Section 3 and in the real-data experiment of Section 4.
2.4. Estimation and Imputation
Since we are dealing with unobserved variables ( W and X), model estimation is performed through a Gibbs sampler with data augmentation configuration (Tanner & Wong, 1987). Following the estimation and imputation scheme proposed for single-level LC imputation models by Vermunt et al. (2008), we will perform the estimation only on the observed part of the data set (denoted by {}). In particular, in the first part of Algorithm 1 (see below), the BMLC model is estimated by first assigning the units to the LCs (Steps 1 and 2) through the posterior membership probabilities—the probability for a unit to belong to a certain LC conditioned on the observed data, and —and subsequently by updating the model parameter (Steps 3–6). At the end of the Gibbs sampler (Step 7), after the model has been estimated, we impute the missing data through M draws from .
After fixing K, L, and α, we must establish I, the number of total iterations for the Gibbs sampler. If we denote with b the number of the iterations necessary for the burn-in, we will set I, such that , where I − b is the number of iterations used for the estimation of the equilibrium distribution , from which we will draw the parameter values necessary for the imputations. Of course, b must be large enough to ensure convergence of the chain to its equilibrium (which can be assessed from the output of the Gibbs sampler).
We initialize π (0) through draws from uniform Dirichlet distributions (i.e., Dirichlet distributions with all their parameter values set equal to 1), in order to obtain , , , and . After all these preliminary steps are performed, the Gibbs sampler is run as shown in Algorithm 1.
Algorithm 1:


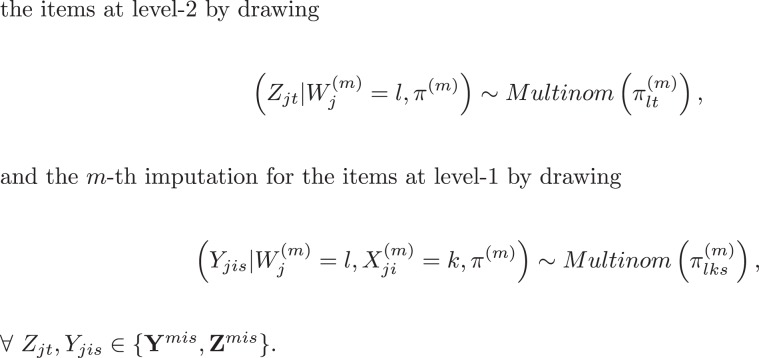
Clearly, the M parameter values obtained in Step 7 should be independent, such that no autocorrelations are present among them. This can be achieved by selecting I large enough and performing M equally spaced draws between iteration b + 1 and iteration I. The Gibbs sampler output can help to assess the convergence of the chain.
3. Study 1: Simulation Study
3.1. Study Setup
In Study 1, we evaluated the performance of the BMLC model and compared it with the performance of the LD and the JOMO methods.
We generated 500 data sets from a population model, created missing data through an MAR mechanism, and then applied the JOMO and BMLC imputation methods, as well as the LD technique, to the incomplete data sets. To assess the performance of the missing data methods bias, stability and coverage rates of the 95% confidence intervals were compared, where the results of the complete data case (i.e., the results obtained if there was no missingness in each data set) were taken as benchmark.
Population model. For each of the 500 data sets, we generated T = 5 binary Level 2 predictors for each higher level unit from the log-linear model:
Within each Level 2 unit j, S = 5 binary Level 1 predictors were generated for each Level 1 unit from the (conditional) log-linear model
where cross-level interactions were inserted to introduce some intraclass correlation between the Level 1 units. Finally, we generated the binary outcome Y 6 from a random intercept logistic model, where
| 3 |
was the Level 1 response model and
| 4 |
was the Level 2 model. Table 1 shows the numerical values of the Level 1 parameters , the Level 2 parameters , and the cross-level interaction γ 35. Table 1 also reports the value of the variance of the random effects, τ 2. Models 3 and 4 was the analysis model of our study, in which the main goal was recovering its parameter estimates after generating missingness.
Sample size conditions. We fixed the total Level 1 sample size to , and generated 500 data sets for two different Level 2 and Level 1 sample size conditions. In the first condition, J = 50 and , while in the second condition, J = 200 and .
Generating missing data. From each data set, we generated missingness according to the following MAR mechanism. For each combination of the variables , observations were made missing in Y 1 with probabilities ; for each combination of the variables , observations were made missing in Y 2 with probabilities ; for each combination of , observations were made missing in Y 5 with probabilities ; for each possible value of the variable Z 2, missingness was generated on Z 1 with probabilities (0.15, 0.4); finally, for each of the values taken on by Z 5, missingness was generated on Z 2 with probabilities (0.1, 0.5). Through such a mechanism, the rate of nonresponses across the 500 data sets was on average 30% for each item with missingness.
Missing data methods. We applied three missing data techniques to the incomplete data sets: LD, JOMO, and BMLC imputation, with the latter setup as follows. We applied Gelman et al.’s (2013) method described in Section 2.3 for model selection by running a preliminary Gibbs sampler (with 1,000 burn-in and 2,000 estimation iterations) and obtaining a posterior distribution for L and K for each incomplete data set. From these distributions, we selected the posterior maxima as the number of components to be used in the imputation stage. This led to an average number of classes equal to L = 8.52 at Level 2 and K = 10.89 at Level 1 when J = 50, nj = 20, and L = 9.68 at Level 2 and K = 10.85 at Level 1 when J = 200 and nj = 5. Hyperparameters of the Level 1 LCs and conditional responses (namely, αlx and ) were set following the guidelines of Section 2.2, that is, with informative prior distributions7 for the parameters πlX and with a noninformative prior distribution for the parameters πlks. In order to assess the performance of the BMLC model under different Level 2 prior specifications, we manipulated the Level 2 hyperparameters αl and αltr. Each possible variant of the BMLC model will be denoted by . In particular, we tested the BMLC model with uniform priors for both the Level 2 LC variable parameters and the Level 2 conditional response parameters—the BMLC(1, 1) model—or with noninformative prior for the conditional responses—the BMLC(1, .01) model. We alternated the same values for the conditional response pseudocounts with a more informative value for the Level 2 mixture variable parameter, the BMLC(*, 1) and the BMLC(*, .01) model. Here, the “*” denotes the hyperparameter choice based on the number of free parameters8 within each class ; since this number could change with K, different values for this hyperparameter were used across the 500 data sets. For each data set, M = 5 imputations were performed and a total of I = 5,000 Gibbs sampler iterations were run, of which b = 2,000 were used for the burn-in and I − b = 3,000 for the imputations.
Table 1.
Parameter Values for Models 3 and 4
| Parameter | β 00 | β 1 | β 2 | β 3 | β 4 | β 5 | β 24 | γ 1 | γ 2 | γ 3 | γ 4 | γ 5 | γ 35 | τ 2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Value | −0.5 | 1.35 | −1 | −0.4 | 0.8 | −0.75 | 0.25 | 0.5 | 0.85 | 0.45 | −0.6 | 0.3 | 0.15 | 1 |
For the JOMO imputation method, which also performs imputation through Gibbs sampling, we specified a joint model for the categorical variables with missingness and used the variables with completely observed data as predictors. We set the number of burn-in iterations equal to and performed the five imputations for each data set across iterations, in order to have a number of iterations for the imputations equal to the Gibbs sampler of the BMLC method. We ran the algorithm with its default noninformative priors and cluster-specific random covariance matrices for the lower level errors.
In order to have a benchmark for results comparison, we also estimated Models 3 and 4 to the complete data before generating the missingness.
Study outcomes. For each parameter of Models 3 and 4, we compared the bias of the estimates, along with their standard deviation (to assess stability) and coverage rate of the 95% confidence intervals. Analyses were performed with R version 3.3.0. JOMO was run from the jomo R-library. For each data set, the analysis Models 3 and 4 was estimated with the lme4 package in R.
3.2. Study Results
Figures 2a and b and 3 show the bias, standard deviations, and coverage rates of the 95% confidence intervals for the 13 fixed effect coefficients of Models 3 and 4, averaged over the 500 data sets. The figures also show point estimates of each coefficient, distinguishing between Level 1, Level 2, and cross-level interaction fixed effects.
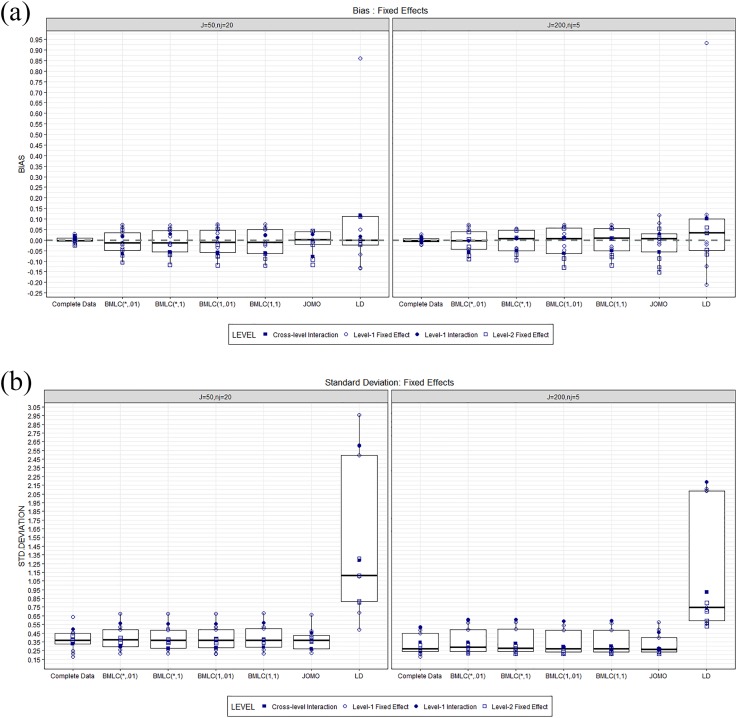
Figure 2.
Bias (a) and standard deviation (b) observed for the 13 fixed multilevel logistic regression Level 1, Level 2, and cross-level coefficients obtained with complete data and the missing data methods BMLC(*, .01), BMLC(*, 1), BMLC(1, .01), BMLC(1, 1), JOMO, and LD. Left: J = 50 and nj = 20. Right: J = 200 and nj = 5. BMLC = Bayesian multilevel latent class. JOMO = joint modeling. LD = listwise deletion.
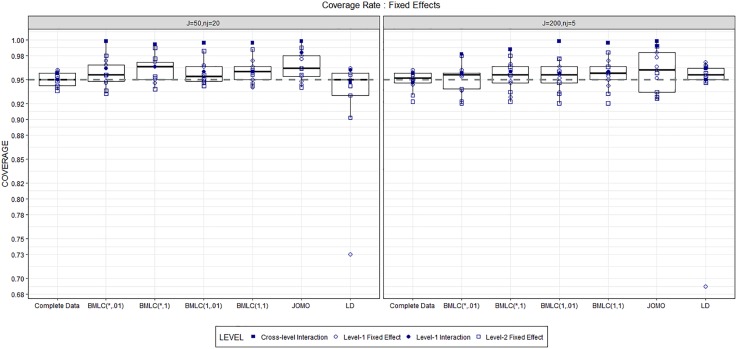
Figure 3.
Coverage rates observed for the confidence intervals of the 13 fixed multilevel logistic regression Level 1, Level 2, and cross-level coefficients obtained with complete data and the missing data methods BMLC(*, .01), BMLC(*, 1), BMLC(1, .01), BMLC(1, 1), JOMO, and LD. Left: J = 50 and nj = 20. Right: J = 200 and nj = 5. BMLC = Bayesian multilevel latent class. JOMO = joint modeling. LD = listwise deletion.
Figure 2a reports the bias of the fixed effects estimates. When J = 50 and nj = 20, the JOMO method is the best performing one in terms of bias of the parameters. The BMLC model also retrieved, in general, parameter estimates close to the true parameter values; however, estimates for some of the Level 1 fixed effects resulted in a larger bias with the BMLC imputation model than with the JOMO method. The choice of the prior distribution for the BMLC model did not seem to affect the final results in terms of bias. The LD method, which was negatively affected by a smaller sample size, yielded the most biased coefficients. In particular, some of the Level 1 and Level 2 fixed effects, as well as the cross-level interaction, appeared heavily biased both down- and upward. In the J = 200 and nj = 5 condition, the specification of the prior distribution seemed to have an effect in the final estimates produced by the BMLC model. In particular, models with priors that favored a full allocation of the Level 2 units across all the L classes, as the BMLC(*, .01) and the BMLC(*, 1), resulted with a slightly smaller bias than models with priors that did not favor full allocation, namely, the BMLC(1, .01) and the BMLC(1, 1). Furthermore, both the BMLC(*, .01) and the BMLC(*, 1) imputation models could reduce the bias observed in the condition with J = 50 groups for some of the Level 2 fixed effects. In the second condition (J = 200 and nj = 5), furthermore, the LD method still yielded the most biased parameter estimates. As far as the JOMO imputation is concerned, no particular improvements were observed in the bias of the estimates from the scenario with J = 50 to the scenario with J = 200. On the contrary, some of the Level 1 fixed effects (), as well as most of the Level 2 fixed effects, resulted in a larger bias than the previous case. This was probably due to the default prior distributions used by the JOMO method to perform the imputations, which can become too influential in case of small Level 1 sample sizes. In addition, in both scenarios, the BMLC imputation model under all prior specifications could retrieve the Level 1 interaction term (with almost no bias) and the least biased cross-level interaction term among all missing data techniques.
Figure 2b shows the stability of the estimates produced by all models, represented by their standard deviations across replications. The BMLC methods were the most similar—in terms of magnitude—to the complete data case, with both J = 50 and J = 200. For such models, the prior distribution did not seem to have an influence on the stability of the estimates. LD technique estimates were the most unstable, as a result of a smaller sample size. The JOMO imputation technique, on the other hand, resulted with the most stable estimates, even more than the complete data case. This was probably due to the fact that the JOMO method, by ignoring complex relationships, was an imputation model simpler than what was required by the data and produced estimates that did not vary as they should.
Figure 3 displays the coverage rates of the 95% confidence intervals obtained with each method. LD produced, overall, coverage rates closed to the ones obtained under the complete data case. However, the coverages of the confidence intervals yielded by the LD method were the result of a large bias and large standard errors of the parameter estimates, which led to too wide intervals. Furthermore, the LD method generated coefficients for one of the parameters (β 3) with a too low coverage (about 0.7). The BMLC imputation method produced more conservative confidence intervals when J = 50 than the J = 200 condition, and their coverage rates strongly depended on the specified prior distribution. In particular, in the case with J = 50 groups, the BMLC(1, .01) model produced the closest confidence intervals to their nominal level. On the other hand, the BMLC(*, .01) imputation model was the best performing one (on average) in terms of coverage rates of the confidence intervals with J = 200 groups, although also BMLC models with different priors, overall, led to confidence intervals rather close to their nominal 95% level. Last, the JOMO method produced in both conditions confidence intervals with coverage rates—on average—larger than the ones produced by the BMLC imputation models.
Table 2 reports the results obtained for the variance of the random effects in terms of bias. All the BMLC models yielded a random effect variance very close to the complete data case under both scenarios, while the JOMO method—which uses continuous random effects for the imputations—led to the least biased estimates for such parameter. Interestingly, in the condition with J = 50 groups, the variance estimated by JOMO was less biased than the complete data estimator. Finally, the LD method produced the most biased variance of the random effects, in particular when the number of Level 2 units was equal to J = 50.
Table 2.
Bias of the Variance of the Random Effect for the Complete Data and the Missing Data Methods BMLC(*, .01), BMLC(*, 1), BMLC(1, .01), BMLC(1, 1), JOMO, and LD
| : Bias | ||
|---|---|---|
| Method | ||
| Complete data | −.11 | −.03 |
| BMLC(*, .01) | −.15 | −.06 |
| BMLC(*, 1) | −.13 | −.04 |
| BMLC(1, .01) | −.15 | −.06 |
| BMLC(1, 1) | −.13 | −.05 |
| JOMO | −.09 | −.03 |
| LD | −.31 | .07 |
Note. Significant bias (with respect to the complete data estimator) is marked in boldface. BMLC = Bayesian multilevel latent class; JOMO= joint modeling; LD = listwise deletion.
4. Study 2: Real-Data Case
The European Social Survey (Norwegian Centre for Research Data [NSD], 2012), or ESS, collects sociological, economical, and behavioral data from European citizens. The survey is performed by the NSD every 2 years and consists of items both at the individual (Level 1) and at the country (Level 2) level. The data are freely available at the website (http://www.europeansocialsurvey.org/). In order to assess the performance of the BMLC model with real data, we carried out an analysis using the ESS data of Round 6, which consists of multilevel data collected in 2012.
After cleaning the data set, we estimated a possible analysis model using one of the items as outcome variable. Subsequently, we introduced missingess according to an MAR mechanism. Finally, the results (bias of the estimates, standard errors, and p values) obtained after BMLC imputation were compared with the results obtained under the complete data case and the LD method. We also made an attempt to perform imputations with the JOMO technique, but the data set was too large for this routine. After 5 days of computation on a normal calculator (Intel Core i7), JOMO had not completed the burn-in iterations yet, and we decided to stop the process. This highlights another issue of the JOMO method (as implemented in the jomo package): When dealing with large data sets, the routine must handle too many multivariate normal variables and random effects and becomes extremely slow. As a comparison, computations with the BMLC model required less than 2 days on the same machine for both the model selection and the imputation stages (see below for details).
4.1. Study Setup
Data preparation
The original data sets consisted of Level 1 respondents within J = 29 countries and 36 variables, of which T = 15 were observed at the country level, S = 20 at the person level and one item was the country indicator. At Level 1, items consisted either of social, political, economical, and behavioral questions, which the respondents were asked to rate (e.g., from 0 to 10) according to their opinion, or of background variables, such as age and education. At Level 2, some economical and political (continuous) indicators related to the countries were reported. Some of the units (at both levels) contained missing or meaningless values (such as “not applicable”), and those units were removed from the data set in order to work with “clean” data. Furthermore, we recoded the qualitative levels of the rating scales and converted them to numbered categories and transformed some continuous variables (such as age or all the Level 2 items) into integer valued categories.9 This enabled us to run the BMLC model on this data set.
After removing Level 1 items related with the study design and least “recent” versions of the items (i.e., all the replicated items across the survey waves, observed before 2010) and discarding units younger than 18 years old and/or not eligible for voting (in the next subparagraph, we will explain the reason of this choice), T = 11 Level 2 and S = 17 Level 1 items were left, observed across Level 1 units within J = 21 countries. These countries were Belgium (), Switzerland (), Czech Republic (), Germany (), Denmark (), Estonia (), Spain (), Finland (), France (), UK (), Hungary (), Ireland (), Iceland (nj = 519), Italy (nj = 623), the Netherlands (), Norway (), Poland (), Portugal (), Sweden (), Slovenia (nj = 706), and Slovakia ().
Analysis model
We looked for a possible model of interest that can be estimated with the data at hand. First, we selected the binary variable “voted in the last elections” (Y 0) as outcome. This is why we deleted the Level 1 units “not eligible for voting” from the data set in the previous step. Second, we looked for possible items that could significantly explain the variability of this item through a multilevel logistic model. Selection of the predictors (and of the random effects) was performed through stepwise forward selection including in the model only the significant predictors (i.e., with p values lower than .05), which led to a drop of the AIC index of the model. The final model for “voted in the last elections” was a multilevel logistic model with random intercept and random slope and was specified as
| 5 |
at Level 1 and
| 6 |
at Level 2. A description of the 11 variables used in the model can be found at the top of Table 3, while the values of the coefficients (both fixed and random) are reported in the second column of Table 4. Furthermore, Columns 5 and 8 of Table 4 show standard errors and p values (for the hypothesis of null coefficients) of the fixed effect parameters, obtained with the original data.
Table 3.
ESS Data Items Used in Study 2
| Item Name | Description | Coding |
|---|---|---|
| Y 0 | Voted in the last elections | 0 = no, 1 = yes |
| Y 1 | TV watching: news and politics | 0 = no time, 7 = >3 hours |
| Y 2 | Trust in politicians | 0 = no trust, 10 = complete trust |
| Y 3 | Placement in the right/left scale | 1 = left, 5 = right |
| Y 4 | Life satisfaction | 0 = dissatisfied, 10 = satisfied |
| Y 5 | Immigration is bad/good for economy | 0 = bad, 10 = good |
| Y 6 | National elections are free and fair | 0 = not important, 10 = extremely important |
| Y 7 | Age (range) | 1 (18/34), 5 (68/103) |
| Y 8 | Marital status | 0 = not married, 1 = married |
| Y 9 | Highest level of education | 1 = <secondary, 7 = >tertiary |
| Z 1 | Social expenditure (country level) | 1 = low, 2 = high |
| Cross-level interaction between Y 1 and Z 1 | — | |
| Other items used to generate missingess | ||
| Item name | Description | |
| Y 10 | Subjective general health | |
| Y 11 | Political parties offer alternatives | |
| Y 12 | Media provide reliable information | |
| Z 2 | Area (country level) | |
| Z 3 | Median age (country level) | |
| Z 4 | Population size (country level) | |
| Z 5 | Unemployment level (country level) | |
| Z 6 | Number of students (primary–secondary education; country level) | |
| Z 7 | Number of students (tertiary education; country level) | |
| Z 8 | Governmental capabilities (country level) | |
| Z 9 | Transparency (country level) | |
| Z 10 | Health Expenditure (country level) | |
Note. ESS = European Social Survey.
Table 4.
Study 2: Estimates, Standard Errors, and p Values Obtained With Complete Data, LD, and BMLC Methods for the Fixed and Random Effects Parameters of Models 5 and 6, Attained After Applying Each Method to the (Fully or Partially) Observed Data
| Parameter | Estimates | Standard Errors | p Values | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Complete Data | LD | BMLC | Complete Data | LD | BMLC | Complete Data | LD | BMLC | |
| β 00 | −3.45 | −2.72 | −3.29 | .33 | .44 | .36 | .00 | .00 | .00 |
| β 1 | 0.15 | 0.07 | 0.16 | .04 | .08 | .04 | .00 | .42 | .00 |
| β 2 | 0.07 | 0.07 | 0.07 | .01 | .02 | .01 | .00 | .00 | .00 |
| β 3 | 0.05 | 0.01 | 0.05 | .02 | .03 | .02 | .00 | .82 | .00 |
| β 4 | 0.06 | 0.07 | 0.06 | .01 | .02 | .01 | .00 | .00 | .00 |
| β 5 | 0.02 | 0.04 | 0.02 | .01 | .01 | .01 | .02 | .01 | .01 |
| β 6 | 0.12 | 0.10 | 0.11 | .01 | .02 | .01 | .00 | .00 | .00 |
| β 70 | 0.34 | 0.35 | 0.33 | .03 | .05 | .03 | .00 | .00 | .00 |
| β 8 | 0.39 | 0.33 | 0.40 | .03 | .07 | .03 | .00 | .00 | .00 |
| β 9 | 0.23 | 0.23 | 0.22 | .01 | .02 | .01 | .00 | .00 | .00 |
| γ 1 | 0.71 | 0.57 | 0.62 | .20 | .24 | .23 | .00 | .03 | .02 |
| γ 11 | −0.06 | −0.01 | −0.07 | .03 | .06 | .03 | .02 | .87 | .03 |
| 0.29 | 0.42 | 0.32 | |||||||
| 0.02 | 0.03 | 0.01 | |||||||
Note. Not significant 5% p values are marked in boldface. BMLC = Bayesian multilevel latent class; LD = listwise deletion.
Entering missingness
Subsequently, we entered MAR missingness in the data set. Missingness was generated on Y 2, Y 4, Y 7, Y 6, and Z 1 through logistic models for the nonresponse indicator. We did not only use the variables in Models 5 and 6 in order to generate the missingness but also other items still present in the data set. The latter are listed in the bottom part of Table 3. Table 5 shows the logistic models used to create missingness. The coefficients of these models were chosen in such a way to ensure between (about) 14% and 25% of missingness for each of the selected items. At the end of the process, only 18 countries and 9,871 Level 1 units (about one third of the data set) were left with fully observed data.
Table 5.
Missingness Generating Mechanism for the Items of the ESS Data Set
| Missingness in | Missingness Generating Model |
|---|---|
| Y 2 | |
| Y 4 | |
| Y 6 | |
| Y 7 | |
| Z 1 |
Note. ESS = European Social Survey.
Missing data methods
We applied LD and BMLC to the sample with nonresponses. The BMLC was run with all the 23 variables listed in Table 3 and was set as follows. We performed model selection using the method exposed in Section 2.3 based on Gelman et al.’s (2013) technique. A preliminary run of the Gibbs sampler with and indicated that running Algorithm 1 with L = 2 (the posterior maximum of L) and K = 26 (the posterior maximum of K) was sufficient to perform the imputations. We set the hyperparameter priors for each , and the prior hyperparameters for the mixture weights which guaranteed full allocation were for each l at Level 2 and for each l, k at Level 1. M = 100 imputations were performed across 25,000 iterations after a burn-in period of iterations, for a total of iterations.
Outcomes
We applied the considered methods (LD and BMLC) and evaluated bias, standard errors, and p values of the final estimates and compared them with the complete data case.
4.2. Study Results
Table 4 shows the results of the experiment. From the table, it is possible to observe how the BMLC method led to final parameter estimates very close to the complete data case. Only two coefficients (β 00 and γ 1) were slightly off the complete data case value. The LD method tended to retrieve slightly more biased estimates (in particular β 00, β 1, and γ 1), but overall the retrieved values with such technique were acceptable. In Columns 5 through 7 of the table, standard errors of the estimates are reported. The standard errors obtained with the LD method were larger than the ones yielded by the BMLC imputation model, as a consequence of a smaller sample size. On the other hand, the BMLC imputation model could exploit the full sample size and retrieved standard errors very close to the complete data case. The effect of the smaller standard errors obtained with the BMLC imputation model can be observed in the last three columns of Table 4, reporting the p values of the fixed effects: The fixed effects estimated through the BMLC imputation were all significant (p < .05), as they were supposed to be. The LD technique, on the other hand, produced some nonsignificant coefficients (β 1, β 3, and γ 11), showing how this method, unlike MI, could lead to loss of power in statistical tests.
With respect to the variance of the random components (reported in the bottom of Table 4), the complete data case and the BMLC imputation method yielded roughly similar values of and . Conversely, the LD method led to an overly large estimate of the random intercept .
5. Discussion
In this article, we proposed the use of BMLC models for the MI of multilevel categorical data. After presenting the model and its configurations in Section 2, we performed two studies in order to assess its performance under different conditions.
In Study 1, a simulation study with two sample size conditions was carried out in which the BMLC imputation method was compared to the LD method (still one of the most applied techniques in the presence of multilevel missing data according to Van Buuren, 2011) and the JOMO technique, one of the few available routines that allow for the MI of multilevel categorical data. The analysis model used was a random intercept logistic model. In Study 2, data coming from the ESS survey were used to investigate the behavior of the BMLC model with real-case data and compared with the LD method. In this second study, the analysis model was a multilevel logistic model with random intercept and slope.
Overall, the BMLC model showed a good performance in terms of bias, stability of the estimates, and coverage rates of the coefficient intervals of the final estimates. Unlike the LD and the JOMO methods, which had limitations either because of a too small sample size used (LD) or because of too influential default prior distributions (JOMO), the BMLC model offers a flexible imputation technique, able to pick up complex orders of associations among the variables of the data set at both levels, returning unbiased and stable parameter estimates of the analysis model. This imputation model can be a useful tool for applied researchers that need to deal with missing multilevel categorical data (e.g., coming from surveys), since it can help to recover potentially valuable information that could be lost if the subjects with missingness were simply discarded, as the results coming from the LD method have shown in both Study 1 and Study 2 of this article.
Despite the proven utility of the BMLC imputation model, some issues still need to be better crystallized by further studies. First, the current article aimed to give a general introduction of the BMLC model as a tool for MI, highlighting some of its strengths. Therefore, the simulation study in Section 3 was carried out under two sample size conditions typical of multilevel analysis (i.e., few large or several small Level 2 units) and a moderately large proportion of missing data (about 30% per item). The performance of the BMLC imputation model may be investigated further with other more extensive simulation studies, in which the model is tested against more extreme missingness rates and sample size conditions (e.g., with few small or several large higher level units). Second, the setting of the prior distribution for the higher level mixture weights must be better examined, especially when the Level 2 sample size is small and the number of classes selected with the method of Section 2.3 is (relatively) large. In these cases, achieving full allocation of the higher level units across all the Level 2 LCs is problematic, no matter how large the value of αl. For instance, in the condition with J = 50 groups in the simulation study of Section 3, in which we selected an average number of Level 2 LCs equal to L = 8.53 and a value for the hyperparameter αl equal to the number of free parameters within each higher level LC, the number of classes filled by the Gibbs sampler was on average roughly equal to L = 5. We tried to rerun the experiment by increasing the value of αl, always obtaining similar results (in terms of classes allocated and MI inferences). It is possible that, because of the small sample size J, the Gibbs sampler reached the maximum possible number of classes that could be filled, and the groups could not be allocated to any new LC. We noticed, however, that the informative values used for αl could help the Gibbs sampler to stabilize the number of occupied classes at that possible maximum. That is, for a maximum number of classes that the sampler could occupy with informative hyperparameter αl, the posterior distribution of the occupied number of classes during the imputation stage was . Therefore, it is possible that in order for the Gibbs sampler to work correctly in the presence of a small number of higher level groups, it is more important to have the Level 2 units allocated to a stable number of classes rather than to reach the full allocation of all the specified LCs. This can be the reason of the good results obtained in the simulation study of Section 3 with J = 50. However, in order to confirm our intuition, a more comprehensive study with different settings for the number of higher level units and LCs, as well as for the value of the Level 2 mixture weights hyperparameter αl, should be carried out in future research.
Finally, the proposed approach can be extended in various meaningful ways. First, the BMLC model can be also applied to longitudinal data, in which multiple observations in time (Level 1 units) are nested within individuals (Level 2 units). If the Level 1 observations within the same subject are independent with each other, but depend on a (discrete) time indicator, it suffices to include the latter in the BMLC model as Level 1 item and perform the imputations. Second, while we dealt with multilevel categorical data, the BMLC model can also be applied to continuous or mixed type of data. This can be achieved, for instance, by assuming mixture of univariate normal (for the continuous data) and multinomial (for the categorical data) distributions. In this case, Gelman et al.’s (2013) method might still be used for the model selection. Third, the model can be easily extended to deal with three or more levels of the hierarchy. This can be the case, for instance, when a sample of students (Level 1) is drawn from a sample of schools (Level 2) which, in turn, is drawn from a sample of countries (Level 3). Fourth, the proposed BMLC imputation model with LCs at two levels can easily be generalized to situations with more levels, where there is no need that the multiple levels are mutually nested. For example, one could deal with children nested within both schools and neighborhoods, where schools and neighborhoods form crossed rather than nested levels. These extensions are straightforward by making sure that the Gibbs sampler gets the LCs at one level conditioning on the sampled LCs for all other levels.
Authors
DAVIDE VIDOTTO is a post-doc researcher at the Department of Methodology and Statistics, Tilburg University, Warandelaan 2, 5037 AB Tilburg, The Netherlands; email: d.vidotto@uvt.nl. He received his PhD in methodology and statistics from Tilburg University (Netherlands) in 2018, with a dissertation focused on missing data imputation. He is currently working on a project concerning sparse principal component analysis.
JEROEN K. VERMUNT received his PhD degree in social sciences research methods from Tilburg University in the Netherlands in 1996, where he is currently a full professor in the Department of Methodology and Statistics, Tilburg University, Warandelaan 2, 5037 AB Tilburg, The Netherlands; email: j.k.vermunt@uvt.nl. In 2005, he received the Leo Goodman early career award from the methodology section of the American Sociological Association. His research interests include latent class and finite mixture models, IRT modeling, longitudinal and event history data analysis, multilevel analysis, and generalized latent variable modeling. He is the codeveloper (with Jay Magidson) of the Latent GOLD software package.
KATRIJN VAN DEUN is an assistant professor in methodology and statistics at Tilburg University, Warandelaan 2, 5037 AB Tilburg, The Netherlands; email: k.vandeun@uvt.nl. She obtained a master in psychology and in statistics and a PhD in psychology. Her main area of expertise is scaling, clustering, and component analysis techniques, which she applies in the fields of psychology, chemometrics, and bioinformatics.
Notes
That is, the distribution of the missing data depends exclusively on other observed data and not on the missing data itself.
Vermunt (2003) denoted with “nonparametric” the version of the multilevel latent class (LC) model that uses a categorical random effect, for which a multinomial distribution is assumed. This is opposed to the “parametric” version of the model, which uses a (normally distributed) continuous random effect.
That is, Dirichlet distributions whose all the pseudocounts are equal to each other.
The value of the pseudocounts for the LC proportions hyperparameter should be at least equal to half times the number of free parameters to be estimated within each LC, in order to cause the sampler to give nonzero weights to the extra components. See Rousseau and Mergensen (2011) for technical details.
This conjecture is justified by noticing that, given a Level 2 LC Wj, the lower level model corresponds to a standard LC model.
Importantly, while Gelman, Carlin, Stern, and Rubin’s (2013) goal was to find a minimum number of interpretable clusters for inference purposes, here, our goal is to find a large enough number of LCs for the imputations. Therefore, Gelman et al. determined the number of classes based on the posterior mode, while we perform model selection based on the posterior maximum. Moreover, Gelman et al.’s method was designed for single-level mixture models. We extend here the mechanism to the Level 2 mixture variable.
We set , that is, the number of free parameters within each Level 1 LC; this value was sufficiently large to ensure units’ allocation across all the Level 1 LCs.
Calculated through .
In particular, percentiles were used to create break points and allocate units into the new categories. The choice of the percentiles depended on the number of categories used for each item.
Footnotes
Declaration of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: The research was supported by the Netherlands Organisation for Scientific Research (NWO), grant project number 406-13-048.
References
- Allison P. D. (2009). Missing data In Millsap R. E., Maydeu-Olivares A. (Eds.), The SAGE handbook of quantitative methods in psychology (pp. 72–89). Thousand Oaks, CA: Sage. [Google Scholar]
- Andridge R. (2011). Quantifying the impact of fixed effects modeling of clusters in multiple imputation for cluster randomized trials. Biometrical Journal, 53, 57–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Audigier V., White I. R., Jolani S., Debray T., Quartagno M., Carpenter J.…Resche-Rigon M. (2017). Multiple imputation for multilevel data with continuous and binary variables. Retrieved from https://arxiv.org/abs/1702.00971
- Carpenter R., Kenward M. (2013). Multiple imputation and its application. New York, NY: Wiley. [Google Scholar]
- Drechsler J. (2015). Multiple imputation of multilevel missing data—Rigor versus simplicity. Journal of Educational and Behavioral Statistics, 40, 69–95. [Google Scholar]
- Fruhwirth-Schnatter S. (2006). Finite mixture and Markov switching models (1st ed). New York, NY: Springer. [Google Scholar]
- Gelfand A. E., Smith A. F. M. (1990). Sampling based approaches to calculating marginal densities. Journal of the American Statistical Association, 85, 398–409. [Google Scholar]
- Gelman A., Carlin J. B., Stern H. S., Rubin D. B. (2013). Bayesian data analysis (3rd ed). London, England: Chapman and Hall. [Google Scholar]
- Goldstein H., Carpenter J. R., Kenward M., Levin K. (2009). Multilevel models with multivariate mixed response types. Statistical Modelling, 9, 173–197. [Google Scholar]
- Hoijtink H., Notenboom A. (2004). Model based clustering of large data sets: Tracing the development of spelling ability. Psychometrika, 69, 481–498. [Google Scholar]
- Horton N. J., Lipsitz S., Parzen M. (2003). A potential for bias when rounding in multiple imputation. The American Statistician, 57, 229–232. [Google Scholar]
- Jolani S., Debray T., Koffijberg H., Van Buuren S., Moons K. (2015). Imputation of systematically missing predictors in an individual participant data meta-analysis: A generalized approach using MICE. Statistics in Medicine, 34, 1841–1863. [DOI] [PubMed] [Google Scholar]
- Nagelkerke E., Oberski D., Vermunt J. (2016). Goodness-of-fit of multilevel latent class models for categorical data. Sociological Methodology, 46, 252–282. [Google Scholar]
- Nagelkerke E., Oberski D., Vermunt J. (2017). Power and type I error of local fit statistics in multilevel latent class analysis. Structural Equation Modeling, 24, 216–229. [Google Scholar]
- Norwegian Centre for Research Data. (2012). ESS Round 6: European Social Survey Round 6 Data. Norway: Data Archive and distributor of ESS data for ESS ERIC; Data file edition 2.2. [Google Scholar]
- Quartagno M., Carpenter J. (2016). JOMO: A package for multilevel joint modelling multiple imputation [Computer software and manual]. Retrieved from https://CRAN.R-project.org/package=jomo
- Reiter P., Raghunathan T. E., Kinney S. (2006). The importance of modeling the survey design in multiple imputation for missing data. Survey Methodology, 32, 143–149. [Google Scholar]
- Resche-Rigon M., White I. (2016). Multiple imputation by chained equations for systematically and sporadically missing multilevel data. Statistical Methods in Medical Research, 1–16. doi:10.1177/0962280216666564 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rousseau J., Mergensen K. (2011). Asymptotic behaviour of the posterior distribution in overfitted mixture models. Journal of the Royal Statistical Society Series B (Statistical Methodology), 73, 689–710. [Google Scholar]
- Rubin D. B. (1987). Multiple imputation for nonresponse in surveys. New York, NY: Wiley. [Google Scholar]
- Schafer J. L. (1997). Analysis of incomplete multivariate data. London, England: Chapman and Hall. [Google Scholar]
- Schafer J. L., Graham J. W. (2002). Missing data: Our view of the state of the art. Psychological Methods, 7, 147–177. [PubMed] [Google Scholar]
- Schafer J. L., Yucel R. M. (2002). Computational strategies for multivariate linear mixed-effects models with missing values. Journal of Computational and Graphical Statistics, 11, 437–457. [Google Scholar]
- Schafer J. L., Zhao J. H. (2014). pan: Multiple imputation for multivariate panel or clustered data (Version 0.9). [Computer software]. Retrieved from http://CRAN.R-project.org/package=pan
- Si Y., Reiter J. P. (2013). Nonparametric Bayesian multiple imputation for incomplete categorical variables in large-scale assessment surveys. Journal of Educational and Behavioral Statistics, 38, 499–521. [Google Scholar]
- Tanner A. M., Wong W. H. (1987). The calculation of posterior distributions by data augmentation. Journal of the American Statistical Association, 82, 528–540. [Google Scholar]
- Van Buuren S. (2011). Multiple imputation of multilevel data In Hox J., Roberts J. K. (eds.), The handbook of advanced multilevel analysis (Vol. 10, pp. 173–196). Milton Park, England: Routledge. [Google Scholar]
- Van Buuren S. (2012). Flexible imputation of missing data. Boca Raton, FL: Chapman and Hall/CRC. [Google Scholar]
- Van Buuren S., Brand J. P. L., Groothuis-Oudshoorn C. G. M., Rubin D. B. (2006). Fully conditional specification in multivariate imputation. Journal of Statistical Computation and Simulation, 76, 1049–1064. [Google Scholar]
- Van Buuren S., Groothuis-Oudshoorn K. (2000). Multivariate imputation by Chained equations: MICE V.1.0 User’s manual. Leiden, the Netherlands: Toegepast Natuurwetenschappelijk Onderzoek (TNO) Report PG/VGZ/00.038. [Google Scholar]
- Vermunt J. K. (2003). Multilevel latent class models. Social Methodology, 33, 213–239. [Google Scholar]
- Vermunt J. K., Van Ginkel J. R., Van der Ark L. A., Sijtsma K. (2008). Multiple imputation of incomplete categorical data using latent class analysis. Sociological Methodology, 38, 369–397. [Google Scholar]
- Vidotto D., Vermunt J. K., van Deun K. (in press, 2018). Bayesian latent class models for the multiple imputation of categorical data. Methodology. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yucel R. (2008). Multiple imputation inference for multivariate multilevel continuous data with ignorable non-response. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 366, 2389–2403. [DOI] [PMC free article] [PubMed] [Google Scholar]