Revised M06 density functional for main-group and transition-metal chemistry

Significance

Kohn–Sham density functional theory (KS-DFT) has been widely utilized for applications in chemistry, condensed-matter physics, and materials science, but the accuracy of KS-DFT depends on the approximations to the exchange–correlation functional, and thus functional development is very important. The M06 and M06-2X functionals, which are hybrid metafunctionals, have been widely used due to their broad applicability. In this study, we present a hybrid metafunctional called revM06 that has broader accuracy than either M06 or M06-2X. As a result, the revM06 functional is well suited for a broad range of applications on main-group chemistry, transition-metal chemistry, and molecular structure prediction. The reoptimization takes advantage of the better databases and of our recently developed strategy for obtaining smoother functionals.

Abstract

We present a hybrid metageneralized-gradient-approximation functional, revM06, which is based on adding Hartree–Fock exchange to the revM06-L functional form. Compared with the original M06 suite of density functionals, the resulting revM06 functional has significantly improved across-the-board accuracy for both main-group and transition-metal chemistry. The revM06 functional improves on the M06-2X functional for main-group and transition-metal bond energies, atomic excitation energies, isomerization energies of large molecules, molecular structures, and both weakly and strongly correlated atomic and molecular data, and it shows a clear improvement over M06 and M06-2X for noncovalent interactions, including smoother potential curves for rare-gas dimers. The revM06 functional also predicts more accurate results than M06 and M06-2X for most of the outside-the-training-set test sets examined in this study. Therefore, the revM06 functional is well-suited for a broad range of chemical applications for both main-group and transition-metal elements.

Kohn–Sham density functional theory (1) (KS-DFT) and its extension (2) to the spin-polarized case are the most widely used quantum mechanical (QM) methods for a wide range of applications, involving large or complex molecules, metals, catalysis, dynamics, and nanotechnology. The success of KS-DFT rests on the accuracy of the approximate exchange–correlation functional, which is often called the density functional. The introduction of functionals based on local gradients [for example, generalized gradient approximations (GGAs) (3–6)], nonlocal orbital-dependent Hartree–Fock exchange (7–9), and local kinetic energy density (10, 11) were turning points in making density functional theory (DFT) a valuable tool in chemistry. Adding Hartree–Fock exchange to a gradient approximation yields what is called a hybrid gradient approximation. Adding dependence on the local orbital-dependent kinetic energy density to gradient approximations or hybrid gradient approximations yields functionals called metafunctionals or hybrid metafunctionals, respectively, and this generally improves the results, with hybrid metafunctionals usually having the best accuracy on broad datasets.

Hybrid density functionals are usually developed in an explicitly semiempirical way and are especially useful for thermochemical energies, reaction barriers, and electronic excitation energies. Key features to be considered in semiempirical development are the functional form, the training databases and their weights, and the optimization strategy. A key strategic decision is whether to develop functionals to treat as broad a range of chemical systems and properties as possible or to try to treat a more restricted set of problems at a higher level of accuracy by sacrificing some broadness. One particularly useful distinction is between weakly correlated systems (i.e., systems that are reasonably well described by a single configuration state function) and strongly correlated systems (i.e., systems with near-degeneracy correlation effects requiring multiple configurations for a good zero-order description); these are often called single-reference and multireference systems, respectively. The M06-L and M06 functionals (12, 13) were developed for the ability to treat both weakly and strongly correlated systems. The M06-2X functional, in contrast, was developed to provide better results for weakly correlated systems, even though that meant it could not be recommended for strongly correlated systems, most notably for transition-metal chemistry. Both M06 and M06-2X were found to be useful for excited-state calculations (14, 15).

More recently, functionals have been optimized with larger and broader databases, providing new challenges not always met as well as possible by the older functionals (15–17). For instance, the mean unsigned errors (MUEs) of M06-2X and M06 for the mainly atomic excitation energy subdatabase (EE18) in Minnesota Database 2017 (16, 17) are 7.27 and 7.96 kcal/mol, respectively, which are larger than the MUEs for the recently developed MN15-L (17) and MN15 (15) functionals. The performances of the M06 functional for chemical reaction barrier heights (database BH76/18) and noncovalent interactions (database NC51) can also be improved. Furthermore, calculations with the M06 suite of functionals are sensitive to the choice of quadrature grid, and this can cause oscillations of the computed potential energy curves (18).

In a recent work (19), we reparametrized the M06-L functional by fitting to a larger database including both chemical and physical data and using smoothness restraints. The new local functional was named revM06-L. Here, in the present work, we report a functional obtained by adding Hartree–Fock exchange to the revM06-L functional form and optimizing the hybrid functional against a larger database (of atomic and molecular energetic data and diatomic bond lengths) than was used for M06 and with smoothness restraints on the fitting parameters. The functional developed in this way is named revM06, and details of the functional form are given in SI Appendix. The main goal of developing revM06 was to improve the performance for molecular bond energies, excitation energies, noncovalent interactions, and isomerization energies. Because revM06 has a constant fraction of nonlocal exchange at all interelectronic distances, it is not well suited for use in calculations with plane-wave basis functions, which are usually used for optimizing lattice constants; therefore, we excluded lattice constants from the functional optimization. Our goal was for the revM06 functional to simultaneously rival the good performance of the M06-2X functional on main-group chemistry and the good performance of the M06 functional for transition-metal chemistry. Moreover, because of the smoothness restraints, the revM06 functional is less sensitive to the size of the quadrature grid and is expected to require fewer self-consistent-field (SCF) iterations.

Databases

The present work involves several databases. Full details are given in SI Appendix, but here we summarize the information needed to understand Results and Discussion. Database 2017 in SI Appendix, Table S1 is an updated subset of the 2015A database used in the revM06-L paper (19). Database 2015A has both molecular and solid-state data, but the present work is concerned only with molecular data. We updated the molecular subset of Database 2015A, and the update is called Database 2017. Database 2017 is divided into two main subdatabases: 418 atomic and molecular energies (database AME418) and 10 molecular structures (database MS10), and AME418 is further subdivided into seven subdatabase groups, each of which is further divided, yielding a total of 25 subdatabases. In addition, we also define Database 2018, which includes Database 2017 plus nine new databases from the work of Goerigk et al. (20). The revM06 functional was optimized on an early version of Database 2017, but all results and tests reported in this work for Databases 2017 and 2018 are for the final versions. We tested 94 functionals, including revM06, on the entire Database 2018. We also tested revM06 and selected other functionals on six additional databases described below.

Results and Discussion

In the present work, we compare the results for the revM06 hybrid metafunctional to two previous M06 hybrid metafunctionals (M06 and M06-2X) (13) and to the newer MN15 (15) and M08-HX (21) hybrid metafunctionals. We also selected some representative functionals of other types from the literature for comparison. These functionals, listed in SI Appendix, Table S4, include GAM (16) and PBE (22) to represent gradient approximations; MN15-L (17), revM06-L (19), M06-L (12), TPSS (23), τ-HCTH (24), VSXC (10), and MGGA_MS2 (25), representing metafunctionals; B97-1 (26), PBE0 (27), and B3LYP (5, 6, 8, 28) representing hybrid gradient approximations; ωB97X-D (29) as an example of a hybrid gradient approximation combined with a molecular mechanics damped dispersion term; and PW6B95-D3(BJ) (30) as an example of a hybrid metafunctional combined with a molecular mechanics damped dispersion term. These 19 functionals are applied to the entire Database 2018 and to a series of additional test cases. Although we consider only 19 functionals in the main text, SI Appendix puts the results in a broader context involving 94 functionals.

Atomic and Molecular Energies.

SI Appendix, Table S4 shows the performance for atomic and molecular energies (AME418) and 10 selected subsets of AME418. These include seven subdatabases: 136 main-group bond energies (MGBE136), 30 transition-metal bond energies (TMBE30), 76 chemical reaction barrier heights (BH76/18), 51 noncovalent interaction energies (NC51), 18 excitation energies (EE18, which has 17 data for p- and d-block atoms plus one datum for Fe₂), 14 main-group isomerization energies (IsoE14), 20 thermochemical data for hydrocarbons (HCTC20), and 73 miscellaneous data (Misc73). SI Appendix, Table S4 also shows results for the 297 single-reference systems (SR297) and the 53 multireference systems (MR53); these subsets are collected from among the various subdatabases.

The table shows that for NC51, revM06 and MN15 give the lowest MUE; for Misc73, revM06 is the best; and for SR297, MGBE136, and HCTC20, revM06 is the second best. For IsoE14, EE18, and BH76/18, revM06 is the third best, and for MR53 it is the sixth best. The highest average ranks on the 10 subsets (8 subdatabases and 2 collections) are MN15 (3.3), revM06 (3.8), MN15-L (4.6), M06 (6.9), M08-HX (7.2), M06-2X (7.3), and PW6B95-D3(BJ) (7.7).

Overall, the revM06 functional gives the second lowest MUE of 2.24 kcal/mol for AME418, which is slightly larger than that given by the recently developed hybrid meta MN15 functional. The performance of revM06 is especially striking if we leave out data involving bonds in transition-metal dimers, in particular if we exclude TMD-BE7. This is shown in Table 1, where we see that revM06 has the best performance of all functionals considered, both in average rank and in MUE.

Table 1.

MUEs for the 411 energetic data remaining in AME418 after the TMD-BE7 subdatabase is removed and average rank on 10 subdatabases of AME418 as listed in SI Appendix, Table S4, except that TMBE30 is replaced by TML-BE23^*

Functional	MUE, kcal/mol	AR
revM06	1.91	3.1
MN15	2.00	3.4
MN15-L	2.16	4.7
M06-2X	2.36	7.3
M06	2.48	6.4
M08-HX	2.57	7.1
ωB97X-D	2.89	7.9
revM06-L	2.90	9.6
B97-1	3.03	8.4
M06-L	3.49	10.3
GAM	4.43	12.8
B3LYP	4.60	13.9
PBE0	4.79	11.8
τ-HCTH	5.21	16.0
TPSS	5.24	14.3
MGGA_MS2	5.46	15.6
VSXC	5.93	14.9
PW6B95-D3 (BJ)	6.51	7.4
PBE	7.29	15.1

^*The TMBE30 subdatabase is divided into TMD-BE7 and TML-BE23 subdatabases. The TML-BE23 subdatabase of transition-metal bond energies consists of SR-TML-BE11 and MR-TML-BE12. AR devotes average rank.

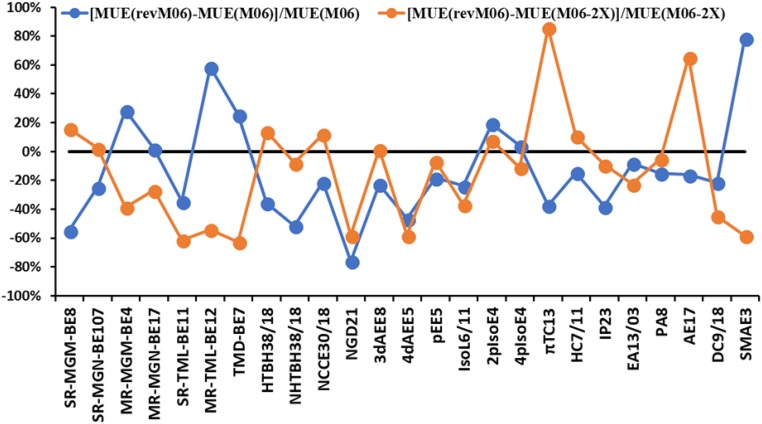
Broadening the discussion beyond the subsets in SI Appendix, Table S4, we show in Fig. 1 the percentage change of MUE for revM06 on each of the full set of 25 subdatabases with reference to M06 and M06-2X. The revM06 functional gives better results for 18 and 16 subdatabases of the 25 subdatabases compared with M06 and M06-2X, respectively. The revM06 functional gives significantly better results for 4dAEE5 and NGD21 databases than both M06 and M06-2X, where the MUEs of revM06 are reduced by more than or close to a factor of two compared with M06 and M06-2X. The performance of the revM06 functional on transition-metal bond energies (SR-TML-BE11, MR-TML-BE12, and TMD-BE7) is substantially better than the M06-2X functional, with MUEs decreased by >50%. Moreover, the performance of revM06 on main-group chemistry, such as chemical reaction barrier heights (HTBH38/18), noncovalent complexation energies (NCCE30/18), and thermochemistry of π systems (πTC13), is much better than M06, but not improved compared with M06-2X. On the other hand, the accuracies of revM06 on multireference main-group and transition-metal bond energies (MR-MGM-BE4, MR-MGN-BE17, and MR-TML-BE12) are better than M06-2X, but not superior to M06.

Fig. 1.

The percentage change of MUEs for revM06 on all 25 subdatabases of AME418 with reference to M06 and M06-2X.

Molecular Structure Databases.

SI Appendix, Fig. S1 shows the MUEs of 19 representative functionals (the same as those in SI Appendix, Table S4) on the molecular structures (MS10), including six diatomic bond lengths of light-atom molecules (DGL6) and four diatomic bond lengths of heavy-atom molecules (DGH4). The revM06 functional gives the eighth best results for MS10 with an MUE of 0.012 Å. The MUEs given by M06 and M06-2X are 0.012 and 0.022 Å, respectively. The varying performances among these three functionals are dominated by the deviations on the DGH4 subdatabase, where the MUEs are, respectively, 0.018, 0.022, and 0.048 Å for the revM06, M06, and M06-2X functionals (SI Appendix, Table S7).

Performance of revM06 on Nontraining Test Sets.

The performance of revM06 and the other 18 selected functionals was also evaluated on 15 databases not used for training, and the results for nine of these (AL2X6, BHDIV10, BHPERI26, BHROT27, DIPCS10, HEAVYSB11, PX13, SIE4x4, and YBDE18) are given in SI Appendix, Table S8. The revM06 functional gives the second lowest overall MUE for these nine new databases, trailing only the M08-HX functional.

As discussed above, revM06 shows the third best result for BH76/18 in the training set. M08-HX gives the best results for both BH76/18 and BH152. Four of the nine new databases we have just considered—in particular, BHDIV10, BHPERI26, BHROT27, and PX13—are for barrier heights of a variety of reactions. We collected these together in a database called NewBH76, and the combination of the original BH76/18 and NewBH76 is called BH152; the performance for these barrier height databases is shown in SI Appendix, Table S9. The revM06 functional gives the fifth best average results for NewBH76, better than both the M06 and M06-2X functionals.

Alkyl bond dissociation energies have historically been a difficult test for DFT (31), probably due to significant contribution from noncovalent interactions, and the 10th nontraining database has 13 alkyl bond dissociation energies (15) (ABDE13; SI Appendix, Fig. S2). The MUE of the revM06 functional is 1.32 kcal/mol, which is the second best result and is close to the MUE of 1.50 kcal/mol for the MGBE136 database in the training set. This shows that the good performance of revM06 on the main-group bond energies is transferable from the training set to the extra tests. The M08-HX functional gives the best result for ABDE13 with an MUE of 1.27 kcal/mol. The MUEs of the M06-2X and M06 functionals for ABDE13 are 1.38 and 2.29 kcal/mol, respectively, showing that the revM06 functional gives better results on main-group bond energies than the M06 and M06-2X functionals for both training and nontraining databases.

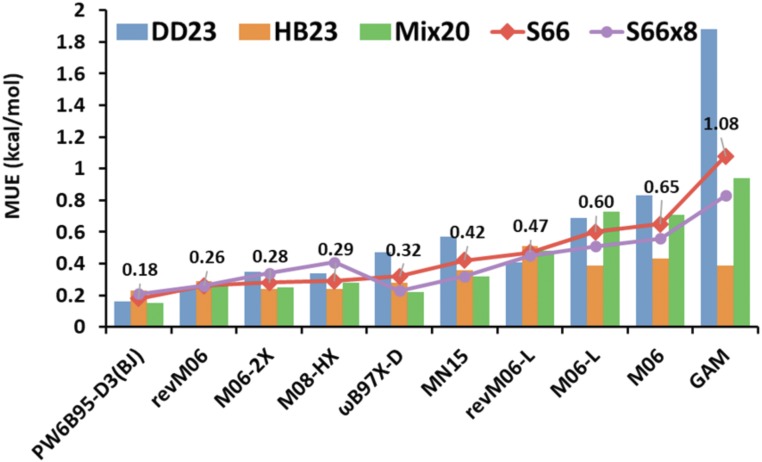
The 11th nontraining database is S66x8. A subdatabase of S66x8 is the S66 database (32), which has 66 benchmark interaction energies of diverse noncovalent binding complexes at their equilibrium van der Waals distances and is a widely used dataset for testing the performance of QM methods on describing intermolecular weak interactions. The S66 dataset can be divided into three subdatabases: 23 dispersion-dominated complexes (DD23), 23 hydrogen-bonded complexes (HB23), and 20 complexes bound by a mix of dispersion and electrostatic interactions (Mix20). The S66x8 database (15, 32, 33) not only includes the S66 dataset, it also contains accurate interaction energies of these 66 complexes at seven other interaction distances between 0.9 and 2.0 times the equilibrium distance. Hence, the S66x8 database has 528 interaction energies. SI Appendix, Table S11 shows the results of 19 selected functionals for the S66 and S66x8 databases and the subdatabases of S66. Fig. 2 shows the results of the top 10 functionals of the 19 functionals for S66. As can be seen from Fig. 2, the revM06, MN15, and M06-2X functionals are among the top five functionals (out of 19, or top 3 out of 17 that do not have molecular mechanics terms to improve noncovalent interactions) for the S66x8 test set. These three functionals are also ranked the top three for NC51 in the training set, again showing some correlation between performance on training and nontraining datasets. Among the functionals without molecular mechanics terms, the revM06 functional gives the best performance for the S66x8 database with an MUE of 0.26 kcal/mol, and this error is only 0.03–0.05 kcal/mol larger than that for the dispersion-corrected PW6B95-D3(BJ) and ωB97X-D functionals. The MN15 and M06-2X functionals have MUEs of 0.32 and 0.34 kcal/mol, respectively. Both revM06 and M06-2X give better results for the 66 interaction energies of binding complexes at the equilibrium distances (S66) than the ωB97X-D and MN15 functionals. Therefore, the revM06 functional shows good performance for noncovalent interactions in both training and test sets; it is much improved from the M06 functional, and it is close to the performance of the M06-2X functional.

Fig. 2.

The MUEs (in kilocalories per mole) for the S66 and S66X8 databases and subdatabases of S66; DD23 is the dispersion-dominated subdatabase; HB23 is the hydrogen-bonding subdatabase; and Mix20 is the mixed subdatabase. The labels are the MUEs for the S66 database. Only the 10 best-performing functionals (of 19 considered) are shown.

The 12th nontraining database is EE69 (14, 34), which includes results from linear response time-dependent DFT calculations of valence and Rydberg excitation energies of 11 organic molecules. SI Appendix, Fig. S3 shows that the revM06 functional gives the fourth best results for EE69 among the 19 density functionals considered in the present discussion. The MUE of revM06 is 0.37 eV, only slightly larger than 0.30 eV given by the M06-2X and ωB97X-D functionals. Note that both the M06-2X and ωB97X-D functionals give the MUEs close to or above the average value (7.30 kcal/mol) of the 19 selected functionals (listed in SI Appendix, Table S4) for EE18 in the training set. To understand this, we note that the EE18 subdatabase mainly consists of transition-metal atomic excitation energies, and our experience is that—in general—atomic excitation energies and transition-metal excitation energies present different kinds of challenges than do organic-molecule excitation energies. The MN15 functional gives the best result for EE69 in the test set (MUE = 0.26 eV). Therefore, the MN15 and revM06 functionals are capable of providing accurate prediction on excitation energies for both organic molecule excitation energies and transition-metal excitation energies. The revM06 functional also gives much better results for excitation energies than the M06 functional. As shown in SI Appendix, Table S6, for pAEE5 and 3dEE8, the differences of MUEs between revM06 and M06-2X functionals are relatively small, but for 4dAEE5, the revM06 functional gives much better result than M06-2X.

The 13th nontraining database is the TMBH22 database (35–37), which has barrier heights for transition metal reactions involving Mo, W, Zr, and Re, none of which are represented in any way in our training set. The revM06 functional gives better-than-average performance on the TMBH22 subdatabase as shown in SI Appendix, Fig. S4 and Table S13. Because the revM06 functional gives the third best results for BH76/18 and the fifth best results for NewBH76 (SI Appendix, Table S9), we conclude that the revM06 functional provides balanced performance for both main group and transition-metal reaction barrier heights.

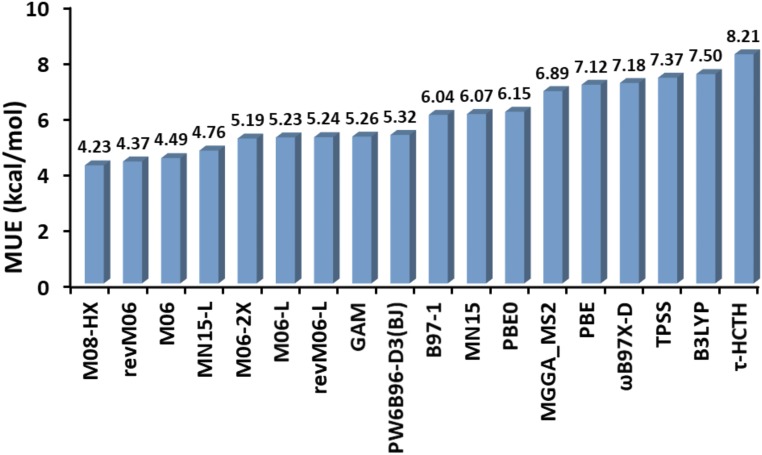
The 14th nontraining database is WCCR9 (38, 39), with ligand dissociation energies of large cationic transition-metal complexes. [In this case, we consider only 18 functionals because we were unable to converge SCF iterations for the VSXC for a few of these systems. Furthermore, reaction 4 of the original WCCR10 (38, 39) database was excluded due to SCF convergence problems for several functionals.] The reference data used here are taken from ref. 39. As shown in Fig. 3 and SI Appendix, Table S14, the revM06 functional gives the second lowest MUE, in particular, 4.4 kcal/mol for WCCR9, followed by the M06, MN15-L, and M06-2X functionals, with MUEs of 4.5, 4.8, and 5.2 kcal/mol, respectively. The M08-HX functional gives the best result for WCCR9, with MUE = 4.2 kcal/mol. Although the performance of revM06 on TMBH22 is not as good as the M06 functional, revM06 gives a better result on the WCCR9 subdatabase than does M06. Therefore, the revM06 functional has comparable performance to M06 for transition-metal energies.

Fig. 3.

The MUEs (kilocalories per mole) for ligand dissociation energies of large cationic transition-metal complexes (WCCR9). VSXC was excluded due to SCF convergence problems for a few systems.

The 15th nontraining database has equilibrium bond lengths of homonuclear transition-metal dimers (40) (TMDBL7). SI Appendix, Fig. S5 shows the MUEs of the 19 functionals under consideration here. Local functionals usually give more accurate equilibrium bond lengths than do hybrid functionals for transition-metal dimers (19). Among the 10 hybrid functionals in SI Appendix, Table S15, the revM06 functional gives the fourth best results for TMDBL7, in particular, MUE = 0.044 Å, with the three better hybrid functionals being only slightly better with MUEs in the range 0.040–0.041 Å. The performances of the M06 and M06-2X functionals are both worse than revM06, with MUEs of 0.048 and 0.066 Å, respectively. In comparison with the results for TMDBL7, for MS10, the revM06 functional also trails only three functionals among the hybrid functionals (the same three; SI Appendix, Fig. S1 and Table S7), and it gives better results than both M06 and M06-2X functionals.

Potential Energy Curves for Rare-Gas Dimers.

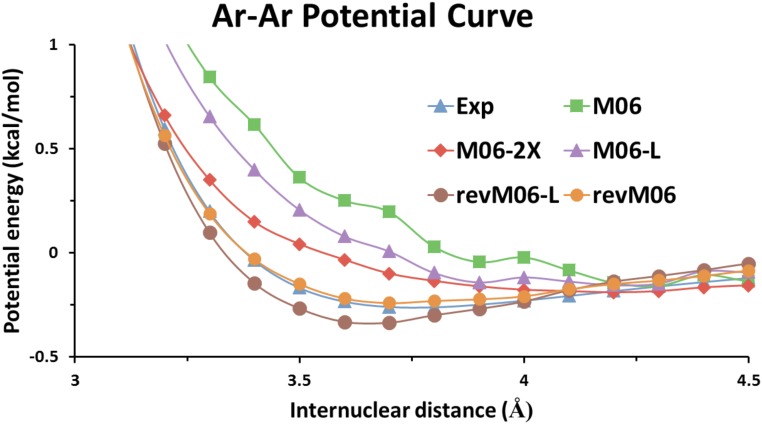
Fig. 4 and SI Appendix, Fig. S6 show the potential curves calculated for rare-gas dimers Ar₂ and Kr₂ using revM06, M06, M06-2X, revM06-L, and M06-L with the aug-cc-pVQZ basis set and a pruned grid of 99 radial shells and 590 angular points per shell for each atom [“(99, 590) grid” is used in the following discussion]. The two figures show that both the equilibrium distances and the binding energies calculated by revM06 are very close to the experimental data. In contrast, the binding energies of both dimers at the equilibrium distances calculated by M06 and M06-2X functionals are all notably higher than the experimental results. The equilibrium distances of Ar₂ and Kr₂ are also significantly overestimated by the M06 and M06-2X functionals. Furthermore, the potential curves of M06 and M06-2X are also not as smooth as the results given by revM06. Thus, the equilibrium distances of rare-gas dimers are sometimes difficult to locate for M06 and M06-2X with the (99, 590) grid, but the potential curves calculated by revM06 are already smooth with the (99, 590) grid. Similar to previous work (19), we attribute the improvement to the smoothness restraints on the fitting parameters and the removal in the parameterization of revM06-L and revM06 of some large electronic integral terms (see SI Appendix for more details).

Fig. 4.

Ar–Ar potential curve calculated by revM06-L, M06-L, revM06, M06, and M06-2X with the (99, 590) grid and the aug-cc-pVQZ basis set compared with the experimental curve. The basis set superposition errors were corrected for all calculations.

Conclusions

This work presents a hybrid meta-GGA functional, named revM06, for improved across-the-board accuracy of both main-group and transition-metal chemistry. The revM06 functional was optimized against 418 atomic and molecular energies and 10 molecular structures of the Minnesota Database 2017 with smoothness restraints. The performance of revM06 was further assessed on 15 nontraining datasets.

The overall performance of the revM06 functional on the AME418 database is significantly improved compared with the original M06 suite of functionals. In particular, the revM06 functional gives better results than M06 for all of the subdatabase groups of AME418, except for TMBE30 (SI Appendix, Table S4), and it performs better than M06-2X for MGBE136, TMBE30, NC51, EE18, IsoE14, and Misc73.

For the nine new nontraining databases in Minnesota Database 2018, the revM06 functional gives the second best result for the overall 137 data. The revM06 functional gives better results than M06 for eight of the nine databases, except for database HEAVYSB11. The revM06 functional performs better than M06-2X for DIPCS10, HEAVYSB11, and PX13, and the overall MUE of revM06 for the nine databases is lower than M06-2X.

For the six additional nontraining sets beyond Database 2018, the revM06 functional predicts better results than M06 for ABDE13, S66x8, EE69, WCCR9, and TMDBL7, although the M06 functional shows better performance than revM06 on TMBH22. The revM06 functional gives better results than M06-2X for ABDE13, S66x8, TMBH22, WCCR9, and TMDBL7, and the performance of the revM06 functional on EE69 is very close to the result given by M06-2X.

The revM06 functional also gives smoother potential curves for rare-gas dimers, which reduces the grid errors and improves the numerical stability.

In summary, the revM06 functional gives much better performance than M06 for main-group chemistry, and it provides almost equivalent results as M06 for transition metals; in addition, the revM06 functional predicts much more accurate results than M06-2X for systems containing transition metals, and it offers comparably good results for main-group chemistry, including thermochemistry, excitation energies, barrier heights, and noncovalent interaction energies, when compared with M06-2X. Furthermore, the revM06 functional provides better equilibrium geometries for molecular structures involving both main-group and transition-metal elements than do M06 and M06-2X. This good performance combined with the improved smoothness means that the revM06 functional is well suited for a broad range of applications on main-group chemistry, transition-metal chemistry, and molecular structure prediction.