Energy-dependent quenching adjusts the excitation diffusion length to regulate photosynthetic light harvesting

Significance

Plants’ photosynthetic mechanism adjusts to fluctuations in light intensity. Intermittent bright sunlight can damage light-harvesting proteins; to preempt this, plants dissipate excess absorbed excitation energy as heat. Energy-dependent quenching (qE) of excitations occurs on the seconds to minutes timescale through conformational changes in antenna proteins. Using a multiscale model of photosystem II, we show that changes in light harvesting due to qE can be explained using a single parameter, the excitation diffusion length, which decreases as qE activates. These findings have implications for the interpretation of pulse amplitude-modulated fluorescence, a common noninvasive measurement of photosynthetic activity in leaves.

Abstract

An important determinant of crop yields is the regulation of photosystem II (PSII) light harvesting by energy-dependent quenching (qE). However, the molecular details of excitation quenching have not been quantitatively connected to the fraction of excitations converted to chemical energy by PSII reaction centers (PSII yield), which determines flux to downstream metabolism. Here, we incorporate excitation dissipation by qE into a pigment-scale model of excitation transfer and trapping for a 200 $\times$ 200-nm patch of the grana membrane. We show that excitation transport can be rigorously coarse grained to a 2D random walk with an excitation diffusion length determined by the extent of quenching. We present an alternative method for analyzing pulse amplitude-modulated chlorophyll fluorescence measurements that incorporates the effects of a variable excitation diffusion length during qE activation.

Plants fix $\sim$60 Pg of carbon every year (1) and are an essential food source. Roughly two-thirds of harvested global crop calories come from four crops (2), and optimizing yields to feed the growing population is an important goal. Predicting how photosynthetic metabolism and crop yield change in response to genetic and environmental perturbations constitutes a grand challenge for science. Although much has been learned about the molecular mechanisms of light harvesting and charge separation, using this knowledge to create a tractable but rigorously defined multiscale model consistent with data from the pigment and the membrane levels remains a complex challenge. In this paper, we create such a model of the rapidly reversible portion of plants’ response to excess light in a 200- $\times$ 200-nm patch of the grana membrane. In doing so, we are able to identify a single variable, the excitation diffusion length, that controls the response of plant photosystem II (PSII) to rapid changes in light level. This regulatory system is important for plant fitness (3) and crop yield (4, 5).

Nonphotochemical quenching (NPQ) regulates PSII light harvesting by dissipating excess absorbed sunlight in the pigment–protein complexes that serve as antenna. In dim sunlight, a photon absorbed by an antenna complex results in a nascent excitation that is efficiently delivered to a reaction center (RC), where charge separation converts the excitation energy to chemical energy. Approximately 83% of excitations result in productive charge separation [photochemical yield (${\mathrm{\Phi }}_{\mathrm{P}\mathrm{C}}$)] in optimal conditions (6). A brief period of intense light, or sunfleck (7), results in a transient increase in the flux of photochemistry at the RCs. Consequently, the pH gradient across the thylakoid membrane increases, and there is a decrease in the fraction of RCs available for performing charge separation (open RCs). In response to the increased pH gradient, the largest rapidly reversible component of NPQ, energy-dependent quenching (qE), activates, and specific pigment sites dissipate excitation energy in the antenna. By decreasing the flux of excitation that reaches the RCs, qE increases the fraction of open RCs and decreases the fraction of excitations that damage closed RCs momentarily occupied with charge separation (3, 8). In this fashion, qE is thought to optimize the balance between the energetic benefit of photochemistry and the metabolic cost of RC damage, while meeting the demands of downstream reactions, such as ${\mathrm{C}\mathrm{O}}_2$ fixation (9, 10). Quantifying the net metabolic benefit of qE thus requires an accurate description of how it influences the photochemical yield.

The key challenge to establishing a quantitative relationship between qE and the photochemical yield (${\mathrm{\Phi }}_{\mathrm{P}\mathrm{C}}$) is reconciling events occurring and data taken on the pigment and membrane scales. While qE acts on the pigment scale, the photochemical yield is the result of all productive charge separation events occurring at open RCs across the thylakoid membrane. Looking from the nanoscale up, several different pigment sites and photophysical mechanisms of quenching in the antenna complexes have been proposed (11), and it remains unclear how these details influence the photochemical yield. From the top down, the photochemical yield is determined by applying phenomenological (“lake” and “puddle”) models (12) to the chlorophyll (Chl) fluorescence yield measured on leaves exposed to fluctuating light (6, 13). However, it remains unclear how well these models describe the interaction between qE and PSII light harvesting because they neglect any of the molecular details of quenching as well as the excitation transport that occurs across tens of nanometers in the thylakoid membrane (14, 15). Thus, a multiscale model is required to explicitly calculate the photochemical yield from the light-harvesting dynamics of a PSII membrane containing $\sim$30,000 pigments in the presence of qE. Such a model could reveal simplifying principles at the membrane scale that accurately connect qE to the photochemical yield without the need of the full simulation.

In this paper, using a pigment-scale model of excitation energy transfer and quenching, we show that the excitation diffusion length is the key degree of freedom connecting the molecular mechanism of qE quenching to PSII yields. We find that qE simply modulates the extent of 2D diffusion via the excitation diffusion length to control the flux of excitations to the RCs. We delineate the main effects of a variable excitation diffusion length on light harvesting when RCs are open. We incorporate the influence of a variable excitation diffusion into the interpretation of pulse amplitude-modulated (PAM) fluorescence measurements on leaves. We believe that this multiscale approach to PSII light harvesting will prove useful for quantitatively connecting the molecular mechanisms of individual complexes to their functional role in photosynthetic metabolism and growth.

Results

Emergence of 2D Diffusive Excitation Transport from a Multiscale Model of PSII Light Harvesting.

While there are currently no spectroscopic techniques for characterizing excitation transport in PSII on the 100-nm length scale, we have previously combined structural, spectroscopic, and biochemical data to build a multiscale model of PSII light harvesting (14, 15). For clarity, in this section, we describe the multiscale model and the physical picture of light harvesting that arose from it.

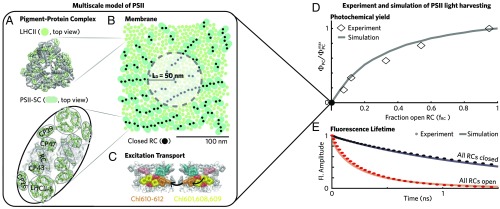
In vivo, a nascent excitation transfers across the PSII-enriched portion of the thylakoid (PSII) membrane (Fig. 1B) through a dense network of protein-bound Chls predominately associated with the major light-harvesting complex II trimers (LHCIIs) (Fig. 1A) and photosystem II supercomplexes (PSII-SCs) (Fig. 1A) until it reaches an RC, where charge separation takes place. The model treats excitation transport between domains of approximately three to four tightly coupled Chls using generalized Förster theory (14, 24, 25) (domains are indicated by colors in Fig. 1C), with Hamiltonian parameters extracted from spectroscopic measurements of isolated pigment–protein complexes and the interaction of pigments in different proteins treated as dipole–dipole coupling. Generalized Förster theory provides the most coarse-grained model of energy transfer that correctly reproduces the dynamics from more quantum-mechanically exact simulations (26, 27). With a simple kinetic model for charge separation parametrized on data of isolated PSII-SCs with variously sized antenna (14) and a method to get positions for LHCIIs and PSII-SCs in a 200- $\times$ 200-nm patch of the PSII membrane (28), we simulated data taken on an intact membrane. Our model reproduces (15), in the absence of free parameters, (i) the photochemical yield of dark-acclimated leaves as measured by Chl fluorescence yield, (ii) the Chl fluorescence lifetime measured on intact membranes when all RCs are open (Fig. 1E, red), and (iii) the hyperbolic shape of oxygen evolution as a function of the fraction of open RCs ($f_{\mathrm{R}\mathrm{C}}$) as measured originally by Joliot and Joliot (20) in 1964 and reproduced in ref. 21 (Fig. 1D).

Fig. 1.

A multiscale model of PSII light harvesting reproduces experimental data on dark-acclimated leaves. (A) PSII is composed of two types of pigment–protein complexes: the LHCIIs and PSII-SCs. The multiscale model represents these complexes using their crystal structures (16, 17). The PSII-SC is a dimer, with each monomer containing one RC, a pair of core antenna proteins (CP43 and CP47), a pair of minor LHCs (CP26 and CP29) replaced by LHCII monomers, and a strongly bound LHCII. The pigments are indicated in light green, and the surrounding protein scaffold is in gray. (B) PSII harvests sunlight across the mesoscopic (approximately hundreds of nanometers) thylakoid membrane. The model arranges the crystal structures of LHCII (indicated by circles in the membrane image) and PSII-SCs (pills) into a mixed configuration. The membrane image indicates the organization of LHCII and PSII-SCs used for all simulations in this work and omits the pigment-level detail for visual clarity. The filled black circles indicate closed RCs. The radius of the shaded circle is equal to the excitation diffusion length ($L_{\mathrm{D}}$ = 50 nm), indicating the spatial extent of transport for an initial excitation at the center of the circle. (C) Energy transfer (black arrows) is described using generalized Förster theory between domains of approximately three to four tightly coupled Chls (colored pigments). This approach reproduces spectroscopic data taken on isolated LHCII and PSII-SCs (14, 18, 19). (D) The multiscale simulation of PSII light harvesting (solid gray line) reproduces the hyperbolic dependence of the photochemical yield (diamonds) on the fraction of open RCs ($f_{\mathrm{R}\mathrm{C}}$) as measured by Joliot and Joliot (20) and reproduced in ref. 21. The model for charge separation at open and closed RCs is described in SI Appendix, SI Materials and Methods. (E) Simulation (solid lines) of fluorescence lifetime measurements (dotted lines) taken on intact membranes or leaves in different states. Red indicates a state of open RCs with no qE (“all RCs open”), and black indicates closed RCs with no qE (“all RCs closed”). Open RC data are from ref. 22, and closed RC data are from ref. 23.

The following picture emerges for how PSII light harvesting occurs in dim light when all RCs are open. A photon of sunlight excites PSII, and that excitation rapidly localizes to a domain of approximately three to four Chls somewhere in the membrane. That excitation is transferred to a neighboring domain with a probability given by the ratio of the rate of that transfer over all possible transfer rates out of the domain. While PSII is composed of a complex network of transport rates between clusters of Chl, we find overall that excitations undergo an effective 2D random walk until they reach an open RC, which serves as a strong trap from which the excitation is unlikely to escape. Our previous conclusion of an effective 2D diffusion is consistent with contemporaneous work that fit fluorescence data from an intact thylakoid membrane assuming a random walk on a fractional dimensional ($d$) Chl network and found a value of approximately two (29).

The 2D spread of excitation can be characterized using a single parameter, the excitation diffusion length ($L_{\mathrm{D}}$). To determine how far an excitation can travel to locate an open RC, we calculate the excitation diffusion length when all RCs are closed (filled black circles in Fig. 1B). As the excitation spreads outward, its amplitude decreases due to the loss of excitation by relaxation back to the ground state via intrinsic decay pathways, such as fluorescence, internal conversion, and intersystem crossing. The latter two processes are grouped together into a single phenomenological nonradiative loss rate in our model. The excitation diffusion length ($L_{\mathrm{D}}$) is the radius of excitation population distribution sampled from a classical ensemble of separate excitation events, at which 1/$e$ (37%) of the initial excitations remains when all RCs are closed. The $L_{\mathrm{D}}$ in the antenna is 50 nm, which is indicated by the radius of the shaded circle in Fig. 1B. The area of the circle represents the portion of the membrane that a single excitation starting in the center can sample while attempting to locate an open RC. Thus, we find that the functional role of antenna proteins in delivering excitations to RCs only emerges on the length scale of the intact thylakoid membrane ($\sim$100 nm).

The large number of RCs contained in a 50-nm radius circle of the membrane explains the nonlinear shape of the photochemical yield as a function of the fraction of open RCs (Fig. 1D). If an excitation reaches an initial RC and it is closed, then it has a high probability of reaching another RC before being quenched. Thus, the connectivity between RCs means that, when 50% of RCs are open, the photochemical yield is more than 50% of the value when 100% of the RCs are open.

This physical picture for PSII light harvesting is incomplete, as it only pertains to PSII in leaves acclimated to darkness. In nature, a leaf responds to rapid fluctuations in sunlight (3) via NPQ mechanisms, such as qE. Thus, PSII is predominantly in a state with some fraction of RCs open and qE present. Here, we construct a more biologically relevant picture of PSII light harvesting by incorporating qE.

qE Controls the Excitation Diffusion Length.

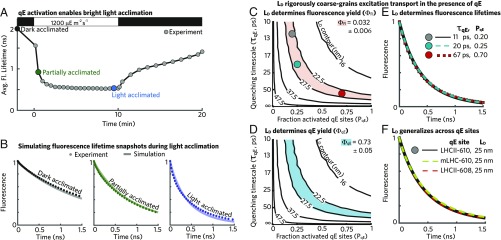
As an Arabidopsis thaliana leaf acclimates to a sudden exposure to bright light (Fig. 2A, 1,200 $\mathrm{\mu }$mol photons ${\text{m}}^{-2}$ ${\text{s}}^{-1}$), the average Chl fluorescence lifetime when all RCs are closed decreases from $\sim$2,000 ps to a steady state of $\sim$550 ps over the course of 10 min. To decrease the fluorescence lifetime without open RCs, additional quenching must arise at sites across the membrane, a process that is collectively known as qE. We note that other components of NPQ, such as the zeaxanthin (Zea)-dependent quenching (30), may also have begun appearing within 10 min, but we will refer to the collective effect of short time acclimation as qE for simplicity. Whether the excitation diffusion length ($L_{\mathrm{D}}$) remains the key degree of freedom for describing transport depends on whether the 2D diffusional picture remains accurate even when excitations land on domains with an additional timescale of quenching.

Fig. 2.

The excitation diffusion length defines transport in the presence of a homogeneous distribution of weak qE quenchers. (A) The average fluorescence lifetime when all RCs are closed of a wild-type A. thaliana leaf exposed to a dark–light–dark sequence (data from ref. 23). The black, dark-green, and blue dots represent the correspondingly colored fluorescence lifetime decays (dotted lines) in B. (B) Simulation (solid line) of fluorescence lifetime measurements (dotted lines) taken on leaves with all RCs closed in different states of acclimation to bright light. Black (Left) indicates leaves in the “dark-acclimated” state, dark green (Center) indicates the “partially acclimated” state, and blue indicates (Right) the “light-acclimated” state. The simulation lines use the following values for the timescale of quenching (${\tau }_{\mathrm{q}\mathrm{E}}$) and the fraction of activated qE sites ($P_{\mathrm{q}\mathrm{E}}$): ${\tau }_{\mathrm{q}\mathrm{E}}=\infty$, $P_{\mathrm{q}\mathrm{E}}$ = 0; ${\tau }_{\mathrm{q}\mathrm{E}}=30$ ps, $P_{\mathrm{q}\mathrm{E}}$ = 0.1; and ${\tau }_{\mathrm{q}\mathrm{E}}=40$ ps, $P_{\mathrm{q}\mathrm{E}}$ = 0.45 for the dark-acclimated, partially acclimated, and light-acclimated curves, respectively. (C) Contour plot (black lines) of excitation diffusion length ($L_{\mathrm{D}}$) as a function of ${\tau }_{\mathrm{q}\mathrm{E}}$ and $P_{\mathrm{q}\mathrm{E}}$. The red area indicates a Chl fluorescence yield (${\mathrm{\Phi }}_{\mathrm{F}\mathrm{l}}$) of 0.032 $\pm 0.006$, consistent with the best-fit Chl fluorescence lifetime for the light-acclimated state (blue line; B, Right). The colored circles correspond to the matched fluorescence lifetimes in E. (D) The contour plot (black lines) of excitation diffusion length ($L_{\mathrm{D}}$) as a function of ${\tau }_{\mathrm{q}\mathrm{E}}$ and $P_{\mathrm{q}\mathrm{E}}$. The cyan area indicates a fraction of excitation quenched by qE [qE yield (${\mathrm{\Phi }}_{\mathrm{q}\mathrm{E}}$)] equal to 0.73 $\pm 0.05$. (E) Three fluorescence lifetimes are plotted corresponding to (${\tau }_{\mathrm{q}\mathrm{E}},P_{\mathrm{q}\mathrm{E}}$) combinations with an excitation diffusion length of 25 nm—the matched points are shown in C. (F) Three fluorescence lifetimes are plotted corresponding to different sites of qE with combinations of (${\tau }_{\mathrm{q}\mathrm{E}},P_{\mathrm{q}\mathrm{E}}$) that give an excitation diffusion length of 25 nm. The black line corresponds to an LHCII-610 quenching site, which was used to generate simulation data for B–E. Simulation results using an mLHC-610 (dashed green line; ${\tau }_{\mathrm{q}\mathrm{E}}=20$ ps, $P_{\mathrm{q}\mathrm{E}}$ = 1) and LHCII-608 (dashed red line; ${\tau }_{\mathrm{q}\mathrm{E}}=10$ ps, $P_{\mathrm{q}\mathrm{E}}$ = 1) quenching site are also shown.

The validity of the diffusional picture depends on the relative timescales of qE quenching and excitation transport out of a qE site. In the “strong quenching” limit, the timescale of quenching is much less than the “dwell time” or the inverse of the sum of all other rates out of the qE site. In this scenario, the excitation density is locally depleted, and the overall process of transport can no longer be completely described by 2D diffusion. In the opposite “weak quenching” limit, the timescale of quenching is much greater than the dwell time, and local excitation densities are unperturbed. In other words, excitations make multiple visits to a weak quenching site on average before dissipation. We can explore which regime qE inhabits by comparing the intrinsic timescales of potential quenching processes along with the dwell times for excitation on a proposed site of quenching.

A range of photophysical mechanisms has been suggested to underlie qE (11): (i) energy transfer from excited Chl to carotenoid (Car) S1 states with lifetimes of $\sim$10 ps (31), (ii) energy transfer to mixed Chl–Car states that undergo charge transfer and subsequent recombination to the neutral ground states (32), and (iii) some form of conformation change-induced “concentration quenching,” which may involve symmetry-breaking charge transfer between two Chl molecules (33, 34). The first two mechanisms have rates consistent with weak quenching. The lack of spectroscopic signatures associated with mechanism iii makes it difficult to quantify its timescale, but no evidence for subpicosecond lifetimes has been reported for isolated light-harvesting complexes. Thus, we assume that the intrinsic rate of quenching is of the order of 10 ps or higher for all mechanisms.

To simulate Chl fluorescence in the presence of qE, we incorporated additional sites of quenching into our multiscale model. A quenching site has a probability ($P_{\mathrm{q}\mathrm{E}}$) of activating an additional decay pathway with a timescale of ${\tau }_{\mathrm{q}\mathrm{E}}$. The lowest-energy chlorophyll 610–612 domain of light-harvesting complex II (LHCII-610) (31, 35) has been proposed to be a site of qE quenching. We find the median dwell time for excitation in an LHCII-610 site within our multiscale model to be $\sim$3 ps, which would be consistent with weak quenching as long as the qE timescale is longer than 10 ps. In what follows, we scan $P_{\mathrm{q}\mathrm{E}}$ between zero and one and ${\tau }_{\mathrm{q}\mathrm{E}}$ between 10 and 100 ps for an LHCII-610 quenching site and simulate fluorescence decays. We find that, by varying the two qE parameters (${\tau }_{\mathrm{q}\mathrm{E}}$, $P_{\mathrm{q}\mathrm{E}}$), our simulations (lines in Fig. 2B) reproduce the Chl fluorescence decays measured (dots in Fig. 2B) during light acclimation. Indeed, there is a wide range of (${\tau }_{\mathrm{q}\mathrm{E}}$, ${\mathrm{P}}_{\mathrm{q}\mathrm{E}}$) combinations that result in simulated fluorescence decays that are consistent with experimental measurement (SI Appendix, Fig. S1A).

The degeneracy of fits to the fluorescence lifetime snapshots combined with the expectation of weak quenching suggests that further simplification might be possible by considering the excitation diffusion length ($L_{\mathrm{D}}$). A broad range of quenching timescales (${\tau }_{\mathrm{q}\mathrm{E}}$) and fractions of activated quenching sites ($P_{\mathrm{q}\mathrm{E}}$) reproduces the Chl fluorescence yield (${\mathrm{\Phi }}_{\mathrm{F}\mathrm{l}}=0.032\pm 0.006$) that is consistent with the measured lifetime in light-acclimated leaves (red area in Fig. 2C). All of these (${\tau }_{\mathrm{q}\mathrm{E}}$, $P_{\mathrm{q}\mathrm{E}}$) combinations, moreover, have an excitation diffusion length of $25\pm 2.5$ nm (black contours in Fig. 2C). We find that an excitation diffusion length of 25 nm also reproduces a consistent fraction of excitations quenched by qE [qE yield (${\mathrm{\Phi }}_{\mathrm{q}\mathrm{E}}=0.73\pm 0.05$)], as shown by the blue area in Fig. 2D. Because the model contains only one other loss mechanism due to nonradiative decay (and the sum of all yields must be one), we find that the excitation diffusion length determines the simulated yields. Fig. 2E shows Chl fluorescence decays simulated for three ${\tau }_{\mathrm{q}\mathrm{E}}$, $P_{\mathrm{q}\mathrm{E}}$ combinations with the same excitation diffusion length of 25 nm (colored circles in Fig. 2C). The equivalency of the plotted curves shows that the excitation diffusion length also determines the transport dynamics underlying the Chl fluorescence lifetime. In summary, excitation transport in the presence of qE can be rigorously coarse grained to an effective 2D random walk with a reduced excitation diffusion length.

Other sites of qE quenching have been proposed, including the lowest-energy 610–612 domain of the minor light-harvesting complexes CP26 and CP29 (mLHC-610) (36, 37) and the chlorophyll 601,608,609 domain in light-harvesting complex II (LHCII-608) (38). To what extent does the particular site of quenching change the results presented here? We calculated the median dwell time for each proposed site and found that they are all consistent with weak quenching as long as the timescale of qE quenching is longer than 10 ps (SI Appendix, Table S1). Furthermore, the Chl fluorescence lifetimes simulated with our multiscale model are consistent between different sites of quenching (SI Appendix, Fig. S1A) with different combinations of the quenching timescales (${\tau }_{\mathrm{q}\mathrm{E}}$) and fraction of activated quenching sites ($P_{\mathrm{q}\mathrm{E}}$) as long as the resulting excitation diffusion length is the same (Fig. 2F). Thus, the excitation diffusion length acts as general parameter to describe excitation transport underlying Chl fluorescence in the presence of qE without depending on the specifics of the molecular mechanism.

To summarize, current evidence suggests that qE occurs in the weak quenching regime, and the 2D diffusive picture holds. A homogeneous distribution of weak qE sites simply reduces the excitation diffusion length ($L_{\mathrm{D}}$). When reaction centers are closed, the decreased excitation diffusion length completely characterizes the fractions of excitation emitted from Chls as fluorescence, lost by nonradiative decay, and dissipated by activated quenching sites (Fig. 2 C–F). This dimensionality reduction holds regardless of the proposed site (or combination of sites) and mechanism of quenching as long as the mechanism has an intrinsic timescale of quenching ${\tau }_{\mathrm{q}\mathrm{E}}>10$ ps.

Light Harvesting in the Presence of qE.

We have established that qE modifies the excitation diffusion length in the PSII membrane and that this control parameter is invariant to the precise site of quenching. How does the change in the excitation diffusion length ($L_{\mathrm{D}}$) influence the trapping of excitation at open RCs? We note that, unlike qE quenching sites, open RCs are strong quenchers that locally deplete excitation. Therefore, excitation transport is no longer spatially homogeneous in the membrane. As a result, the net process of light harvesting depends on the excitation diffusion length, the fraction of open RCs ($f_{\mathrm{R}\mathrm{C}}$), and the spatial distribution of open RCs.

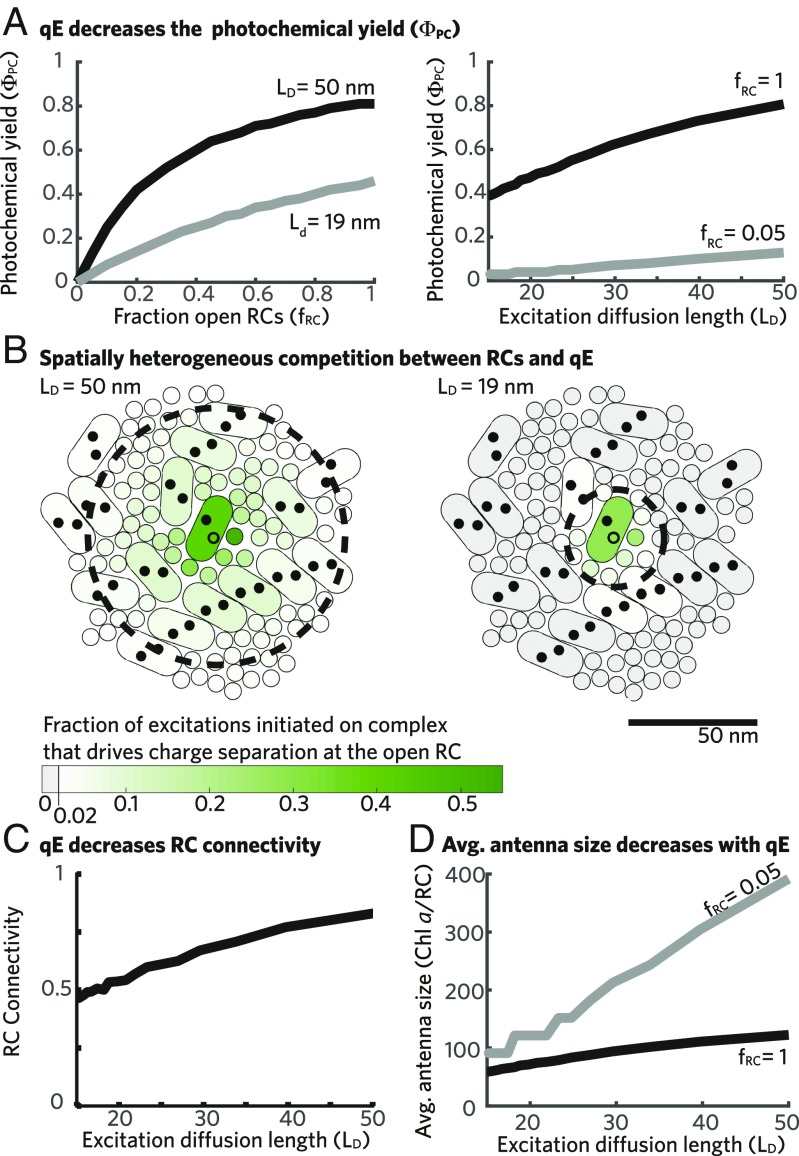
Activating qE, and thereby decreasing the excitation diffusion length, decreases the fraction of excitations that drive productive charge separation at open RCs [photochemical yield (${\mathrm{\Phi }}_{\mathrm{P}\mathrm{C}}$)] as shown in Fig. 3A, Right for two different fractions of open RCs ($f_{\mathrm{R}\mathrm{C}}$). We explore the mechanism underlying the decrease in photochemical yield as a function of the excitation diffusion length by considering the case where open RCs do not compete for excitations, here simulated as one open RC in the membrane. In the absence of qE, a single open RC (open circles in Fig. 3B) captures $\sim 50$% of excitations initiated in its PSII-SC but captures some excitation ($>2$%; darker green shading indicates larger percentages) initiated on antenna complexes within approximately one excitation diffusion length (dashed black lines in Fig. 3B). As qE activates and the excitation diffusion length shrinks, the single open RC captures a smaller fraction of excitation (lighter green in Fig. 3B, Right) initiated on antenna proteins that are within the decreased excitation diffusion length ($L_{\mathrm{D}}$). In addition, the open RC is unable to capture excitations from many antenna proteins that previously contributed in the absence of qE (gray proteins in Fig. 3B, Right). Thus, two different effects cause a decrease in photochemical yield. First, for excitations started on antenna complexes within one excitation diffusion length of an open RC, qE will compete for those excitations and, thereby, reduce the probability that they drive productive charge separation. Second, for excitations starting on antenna complexes more than one excitation diffusion length ($L_{\mathrm{D}}$) away from any open RC, the probability of being quenched is nearly unity, and charge separation has no opportunity to compete for these excitations. This second effect can be thought of as a decrease in the pool of excitation available to open RCs as qE activates. The combination of these effects allows qE to act as a tap that controls the flux of excitations to open RCs.

Fig. 3.

Light harvesting in the presence of qE. (A) The photochemical yield (${\mathrm{\Phi }}_{\mathrm{P}\mathrm{C}}$) is plotted as a function of the fraction of open RCs ($f_{\mathrm{R}\mathrm{C}}$; Left) and the excitation diffusion length ($L_{\mathrm{D}}$; Right). (B) The spatial extent of the RC antenna for a single open RC in the membrane (open black circles) is visualized by plotting the fraction of excitations started in each complex that drive productive charge separation at the open RC when $L_{\mathrm{D}}=50$ nm (Left) and 19 nm (Right). The fraction of excitations initiated on a complex that drive productive charge separation at the single open RC is represented by the green shading (color bar)—the darker green complexes contribute a larger fraction. Only complexes that contribute $>$2% of initial excitations to the open RC when $L_{\mathrm{D}}=50$ nm are shown. Complexes that contribute $<$2% of initial excitations to charge separation when $L_{\mathrm{D}}=19$ nm are shown in gray (Right). A circle with radius equal to the $L_{\mathrm{D}}$ is shown plotted with a dashed black line. (C) The fraction of excitations starting at a closed RC that reach another RC before being quenched (RC connectivity) is plotted as a function of the $L_{\mathrm{D}}$. (D) The average RC antenna size as measured by the number of Chl a equivalents that contribute excitation to the average open RC is plotted as a function of the $L_{\mathrm{D}}$ for two values of $f_{\mathrm{R}\mathrm{C}}$.

Activating qE also decreases the curvature of the photochemical yield (${\mathrm{\Phi }}_{\mathrm{P}\mathrm{C}}$) as a function of the fraction of open RCs ($f_{\mathrm{R}\mathrm{C}}$) as seen in Fig. 3A, Left for two values of the excitation diffusion length. The hyperbolic (i.e., nonlinear) shape of the photochemical yield as a function of the fraction of open RCs in the absence of qE occurs because an excitation that arrives at a closed RC has a high probability of subsequently visiting another RC (which might be open) before being quenched by a loss pathway, which we refer to as the RC connectivity parameter (Fig. 3C). The presence of qE decreases the RC connectivity parameter, consistent with the smaller number of RCs that are found in a circle of the membrane with radius equal to one excitation diffusion length (black dashed lines in Fig. 3B).

Finally, we note the difference between the spatial extent over which an open RC can capture excitations and the effective number of Chl that contributes to charge separation. In keeping with our physical intuition, the long excitation diffusion length of PSII leads to a spatially extended (plotted antenna in Fig. 3B) set of Chls that contribute to charge separation at an open RC, which we call the RC antenna. We characterize the size (summed magnitude, not spatial extent) of the average antenna for an open RC (${\sigma }_{\mathrm{P}\mathrm{C}}$; units of Chl a per RC) as the effective number of Chl that contributes to productive charge separation at an open RC, which can be calculated as

$${\sigma }_{\mathrm{P}\mathrm{C}}\left(L_{\mathrm{D}},f_{\mathrm{R}\mathrm{C}}\right)=\frac{{\mathrm{\Phi }}_{\mathrm{P}\mathrm{C}}\left(L_{\mathrm{D}},f_{\mathrm{R}\mathrm{C}}\right)\cdot {\mathrm{N}}_{\mathrm{C}\mathrm{h}\mathrm{l}a}}{{\mathrm{N}}_{\mathrm{R}\mathrm{C}}\cdot f_{\mathrm{R}\mathrm{C}}},$$ [1]

where ${\mathrm{N}}_{\mathrm{R}\mathrm{C}}$ and ${\mathrm{N}}_{\mathrm{C}\mathrm{h}\mathrm{l}a}$ are the numbers of RCs and Chl a in the membrane, respectively; ${\mathrm{\Phi }}_{\mathrm{P}\mathrm{C}}$ is the photochemical yield; and $f_{\mathrm{R}\mathrm{C}}$ is the fraction of open RCs. When 5% of RCs are open ($f_{\mathrm{R}\mathrm{C}}=0.05$), the effective number of Chl a that contributes to charge separation at the average open RC decreases from $\sim$400 to $\sim$100 as the excitation diffusion length ($L_{\mathrm{D}}$) goes from 50 to 19 nm (gray line in Fig. 3D). If we compare these values with the number of Chl contained in the PSII-SC, we find that, when $L_{\mathrm{D}}=19$ nm, the average RC antenna size is smaller than that expected for an RC in an isolated PSII-SC in the absence of qE ($\sim$140), although the spatial extent of the antenna is greater than one supercomplex. In the absence of qE, when $L_{\mathrm{D}}=50$ nm, the same effect is present—the average RC antenna size is substantially smaller than the total number of Chls contained in the pigment–protein complexes that contribute to the RC antenna (Fig. 3B, Left). The disjoint between the spatial extent and average size of an open RC antenna (${\sigma }_{\mathrm{P}\mathrm{C}}$) points to the critical role of entropy arising from the random walk of each excitation: while the isolated PSII-SC contains many fewer pigments than a 19-nm radius on the membrane, in the membrane, many excitations will wander away from the open RC rather than lingering close, which they must in an isolated PSII-SC.

To summarize, qE quenchers and open RCs have a spatially heterogeneous competition that results in the photochemical yield having a complex dependence on the excitation diffusion length and the fraction of open RCs. Our simulations suggest that the influence of qE on PSII light harvesting arises from three effects: (i) it competes for excitations close to open RCs, (ii) it creates a fraction of excitations that are inaccessible to any open RC by shrinking the excitation diffusion length, and (iii) it decreases the probability that an excitation on a closed RC reaches another (possibly open) RC before quenching—the RC connectivity. We once again find that the excitation diffusion length generalizes between different sites of quenching and, therefore, provides a useful tool for understanding the influence of qE without depending on the specifics of the molecular mechanism (SI Appendix, Fig. S1B).

Implications for Interpreting PAM Fluorescence Data.

In the previous two sections, we established that the effect of qE quenchers on excitation transport can be rigorously coarse grained to a reduction in the excitation diffusion length ($L_{\mathrm{D}}$). A variable excitation diffusion length, in turn, influences the relationship between the fraction of open RCs ($f_{\mathrm{R}\mathrm{C}}$) with the photochemical yield (${\mathrm{\Phi }}_{\mathrm{P}\mathrm{C}}$). Here, we incorporate this understanding into the interpretation of PAM Chl fluorescence measurements, which are used extensively as a noninvasive method to characterize PSII light harvesting when plants are genetically altered or exposed to different environmental conditions (6, 39–41). PAM fluorescence reports indirectly on PSII light harvesting, and as a result, models are needed to extract the key parameters from the fluorescence data. The accuracy of extracted PAM parameters depends on the extent to which models correctly capture the underlying excitation transport dynamics.

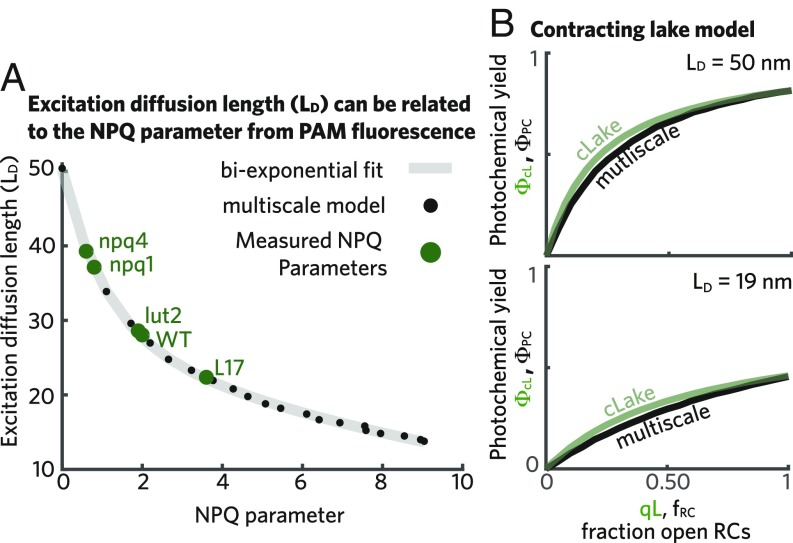
Given the importance of the excitation diffusion length ($L_{\mathrm{D}}$) and the absence of any direct measurement, we explored the possibility of estimating this length scale using PAM fluorescence. The excitation diffusion length ($L_{\mathrm{D}}$) characterizes the distance that an excitation will travel when all RCs are closed. During a PAM measurement, brief ($<$1 s) pulses of saturating light transiently close all RCs. The NPQ parameter (SI Appendix, SI Materials and Methods) depends on both the Chl fluorescence yield measured during a saturating light pulse when qE is not active and the fluorescence yield during a saturating pulse when qE is active, thereby providing a measure for how many excitations qE quenches in the absence of open RCs. We find that the NPQ parameter has a one-to-one relationship with the excitation diffusion length in our multiscale simulations (black dots in Fig. 4A). In particular, the relationship between increasing NPQ and decreasing excitation diffusion length can be fit to a biexponential function (gray line in Fig. 4A). This relationship suggests that the excitation diffusion length can be characterized using the NPQ parameter, which is a ubiquitous measurement in studies of qE activation.

Fig. 4.

Interpreting PAM Chl fluorescence in the presence of a variable excitation diffusion length. (A) The excitation diffusion length is plotted as a function of the NPQ parameter extracted from Chl fluorescence simulations (black dots). A biexponential fit to these data given by $L_{\mathrm{D}}=21.44\cdot e^{-NPQ/1.07}+28.76\cdot e^{-NPQ/12.15}$ is shown as a gray line. The green dots indicate the measured steady-state values of the NPQ parameter of several qE mutants at 1,200 $\mathrm{\mu }$mol photons ${\text{m}}^{-2}$ ${\text{s}}^{-1}$: L17, a PsbS overexpressor (8), as well as npq1, lut2, and npq4, which are lacking Zea, lutein, and PsbS, respectively (42). The wild-type measurement is also taken from ref. 42. (B) The photochemical yield as a function of the fraction of open RCs is plotted for both the contracting lake model (cLake; green line) and the multiscale model (black line) when $L_{\mathrm{D}}=50$ nm (Upper) and when $L_{\mathrm{D}}=19$ nm (Lower). For the case of the cLake, the x axis corresponds to the qL parameter extracted from PAM measurements.

The ability to translate the NPQ parameter to an excitation diffusion length ($L_{\mathrm{D}}$) provides a physical picture for interpreting variations between PAM measurements. The NPQ parameter has been used to assess the extent of qE in mutants and in different environmental conditions. However, the interpretability of the NPQ parameter has been limited by the inability to connect it to the physical processes of excitation transport and quenching (41). The connection of NPQ to excitation diffusion length that we report here provides insight into the change in excitation transport due to qE activation and thus, on the (${\tau }_{\mathrm{q}\mathrm{E}}$, $P_{\mathrm{q}\mathrm{E}}$) combinations that are consistent with a PAM measurement. For instance, we can now see that different changes in NPQ, say from 0 to 0.5 and from 2 to 4.2, reduce the excitation diffusion length by an equivalent amount—10 nm. Using this relationship, we can compare the excitation diffusion length measured in a range of qE mutants (labels in Fig. 4A), for which the mechanism of their deviation from the wild-type NPQ level remains unknown. Of course, these assignments assume that the PSII membrane in the mutant has the same arrangement and antenna to RC ratio as the wild type that we have simulated here.

We next considered how to obtain correct estimates of the fraction of open RCs and the photochemical yield given a variable excitation diffusion length. The two dominant models used to extract these quantities from PAM data are the lake and puddle models (4, 12, 13). The lake model assumes simple kinetic competition between photochemistry, qE, and intrinsic decay pathways, such as fluorescence and intersystem crossing for a single pool of Chl excitations. The puddle model, however, assumes that this kinetic competition occurs separately for each RC and its associated antenna. While the lake and puddle models both predict the same photochemical yield (the ${\mathrm{\Phi }}_{\mathrm{I}\mathrm{I}}$ parameter) given the same PAM data, they predict a different fraction of open RCs (known as the qL and qP parameters in the literature where L and P refer to the lake and puddle models, respectively) (SI Appendix, SI Materials and Methods) (13). We calculated the ${\mathrm{\Phi }}_{\mathrm{I}\mathrm{I}}$, qL, and qP parameters using fluorescence yields simulated with our multiscale model, which accounts for a variable excitation diffusion length, and assessed how well the lake/puddle models reproduce the interaction between Chl fluorescence, qE activation, and open RCs (a complete discussion of the lake and puddle models is in SI Appendix, Figs. S2 and S3A). As qE activates, the ${\mathrm{\Phi }}_{\mathrm{I}\mathrm{I}}$ parameter consistently overestimates the photochemical yield from the multiscale model (SI Appendix, Fig. S3A). However, unlike the puddle model, the lake model provided a reasonable estimate of the fraction of open RCs across the range of qE activation (SI Appendix, Fig. S2B).

We observed previously that qE reduces the photochemical yield by competing for excitation near open RCs and reducing the excitation accessible to open RCs. As the lake/puddle models account for competition but not a changing excitation diffusion length, we reasoned that accounting for excitations that are inaccessible to open RCs could better reproduce the multiscale simulations. A linear relationship (SI Appendix, Fig. S3A) exists between the photochemical yield predicted by the lake/puddle models (${\mathrm{\Phi }}_{\mathrm{I}\mathrm{I}}$ parameter) and the multiscale model [${\mathrm{\Phi }}_{\mathrm{P}\mathrm{C}}\approx m\left(L_{\mathrm{D}}\right)\cdot {\mathrm{\Phi }}_{\mathrm{I}\mathrm{I}}$]. The excitation diffusion length-dependent slope [$m\left(L_{\mathrm{D}}\right)$] represents the fraction of excitations that remain available to RCs as the activation of qE decreases the excitation diffusion length. Furthermore, the slope [$m\left(L_{\mathrm{D}}\right)$] has a simple monoexponential form (SI Appendix and SI Appendix, Fig. S3B) as a function of $L_{\mathrm{D}}$ going from 1 (when $L_{\mathrm{D}}=50$ nm) to 0.65 (when $L_{\mathrm{D}}=19$ nm). Incorporating this effect simply requires scaling the lake/puddle models’ prediction of photochemical yield by $m\left(L_{\mathrm{D}}\right)$. The resulting “contracting lake” model provides a good estimate of the photochemical yield during qE activation [green line of ${\mathrm{\Phi }}_{\mathrm{c}\mathrm{L}}=m\left(L_{\mathrm{D}}\right)\cdot {\mathrm{\Phi }}_{\mathrm{I}\mathrm{I}}$ in Fig. 4B].

Taken together, we have the following method for extracting the excitation diffusion length, the fraction of open RCs, and the photochemical yield from PAM data. First, $L_{\mathrm{D}}$ can be determined from the NPQ parameter. This $L_{\mathrm{D}}$ is used to determine the fraction of accessible excitation [$m\left(L_{\mathrm{D}}\right)$] and generate the contracting lake model prediction for the photochemical yield (${\mathrm{\Phi }}_{\mathrm{c}\mathrm{L}}$). Second, the fraction of open RCs is computed using the lake model without any adjustment (the qL parameter) (13). The relationship between these three parameters so calculated reproduces their relationship as simulated by the multiscale model. We note that we arrived at these parameters using a purely phenomenological approach based on our multiscale model. This method should work well for the fast response NPQ modeled here, but we do not take into account slower acclimation processes. Thus, some caution should be used before applying this method to evaluating PAM data.

Discussion

The key finding of this paper is that the efficacy of NPQ in the PSII antenna on the seconds to minutes timescale (or qE) can be related to a single quantity—the excitation diffusion length ($L_{\mathrm{D}}$). In other words, qE works by reducing the number of Chl molecules that can excite a given RC via the decrease in excitation diffusion length. The origin of the reduction in the excitation diffusion length is, of course, the generation of quenching sites with a probability $P_{\mathrm{q}\mathrm{E}}$, which quench singlet excitons with a rate 1/${\tau }_{\mathrm{q}\mathrm{E}}$. Correctly capturing the competition between qE and charge separation at open RCs requires modeling a region of the membrane with a diameter significantly larger than the excitation diffusion length. Such a model enables an empirical connection to be made between the value of excitation diffusion length and the conventional NPQ parameter for a series of mutants, thereby providing a bridge between measurements on molecular length scales and those on leaf or even field length scales.

On what assumptions does the picture described above rest? Provided that our model of the membrane morphology is reasonably accurate, the key question is what the actual values of the $P_{\mathrm{q}\mathrm{E}}$ and ${\tau }_{\mathrm{q}\mathrm{E}}$ are in specific NPQ conditions. We showed that different combinations of $P_{\mathrm{q}\mathrm{E}}$ and ${\tau }_{\mathrm{q}\mathrm{E}}$, which result in identical fluorescence decays, have identical $L_{\mathrm{D}}$ values. We find that the median dwell time on any of the proposed qE sites is $<3$ ps, and therefore, any ${\tau }_{\mathrm{q}\mathrm{E}}$ values much longer than a few picoseconds place the process in the weak quenching regime. For example, if ${\tau }_{\mathrm{q}\mathrm{E}}$ = 10 ps, the excitation visits about five quenching sites before dissipation. As long as the quenching is in the weak limit and there is no large scale restructuring or composition change of the membrane, our conclusions are not strongly dependent on the specific quenching mechanism or ${\tau }_{\mathrm{q}\mathrm{E}}$.

Whether qE occurs in the weak quenching regime depends on the rate of dissipation, which arises from the photophysical mechanism at play. Although the mechanisms of NPQ are still debated, a number of possibilities can be delineated. It is clear that the xanthophyll cycle Car Zea is a key component (43), although whether as a direct quencher or as an allosteric effector (or both) is not settled. Evidence for the formation of a Zea radical cation formed by electron transfer from Chl has been presented and debated. Evidence for electronic energy transfer from Chl a to Zea S1 has recently been described. It is likely that both processes would give ${\tau }_{\mathrm{q}\mathrm{E}}$ values $\gg 5$ ps. Enhanced internal conversion in closely spaced dimers, either of Chl a or of Chl a and Zea via symmetry-breaking charge transfer, may not produce clear spectroscopic observables as has been the case for concentration quenching in solution (33, 34).

While ultrafast spectroscopic measurements hold promise for directly measuring the quenching process, the recent development of single-molecule fluorescence lifetime measurements of photosynthetic complexes has raised the possibility of measuring the intrinsic timescale of quenching (${\tau }_{\mathrm{q}\mathrm{E}}$) only on activated complexes provided that a model for energy transport and quenching is available. Using our structure-based model of energy transfer in PSII-SCs (14), we could estimate the timescale of quenching that is consistent with single-molecule measurements of PSII-SCs by Gruber et al. (44) (SI Appendix, SI Text). Assuming that the quenching site is the lowest-energy LHCII-610 (31, 35), we estimate the underlying timescale of quenching (${\tau }_{\mathrm{q}\mathrm{E}}$) to be 20 ps, consistent with weak quenching (SI Appendix). The same conclusion is reached when assuming either of the other proposed qE quenching sites, mLHC-610 and LHCII-608 (SI Appendix, Table S1). The fluorescence lifetimes measured on single quenched LHCII complexes are also consistent with a weak quenching regime and suggest that ${\tau }_{\mathrm{q}\mathrm{E}}>100$ ps (38). Taken together, single-molecule evidence supports a weak quenching model of qE. However, these measurements are still being developed, and as a result, establishing their physiological relevance is an active area of research.

The connection established here from a nanoscale description of excitation dissipation by qE (${\tau }_{\mathrm{q}\mathrm{E}}$, $P_{\mathrm{q}\mathrm{E}}$, site) to a mesoscale description of excitation dynamics ($L_{\mathrm{D}}$) to an in-field assessment of photoprotective capacity (NPQ parameter) enables a physical connection between in vitro measurements on isolated complexes with in vivo measurements on intact leaves. As a proof of concept, consider a model of qE parameterized on single-molecule measurements. We can estimate the maximum possible probability for a qE quenching site to be active ($P_{\mathrm{q}\mathrm{E}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$) from single-molecule data of LHCII in conditions mimicking qE of 0.3 (SI Appendix, SI Text) (35). Similarly, single-molecule measurements of PSII-SCs suggest a timescale of quenching (${\tau }_{\mathrm{q}\mathrm{E}}$) of $\sim$20 ps (SI Appendix, SI Text), consistent with semiempirical electronic structure calculations for the LHCII-610 site (45). This combination of a ${\tau }_{\mathrm{q}\mathrm{E}}$ and $P_{\mathrm{q}\mathrm{E}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ results in an excitation diffusion length of 24 nm in our multiscale simulation. Mapping this $L_{\mathrm{D}}$ value to an NPQ parameter (using Fig. 4A) gives 2.95 as the maximum value consistent with this qE model parameterized on single-molecule measurements. The level of quenching observed in a mutant in which PsbS is overexpressed (L17) is 3.6 and seems inconsistent with the in vitro bound, which suggests that some aspect of the in vitro picture must change—perhaps by adding another qE site—to get agreement with in vivo data on leaves. Thus, the connection between measurements on different length scales facilitated by the excitation diffusion length offers quick feedback on proposed models of quenching and may help generate new mechanistic insight.

Concluding Remarks

We have rigorously reduced the complexity of excitation transport in PSII in the presence of weak quenching, a process composed of thousands of rate constants, down to a single parameter: the excitation diffusion length in the antenna ($L_{\mathrm{D}}$). We find that, in response to fluctuating light intensity, qE acts as a “tap” that adjusts the flux of excitation to open RCs via the excitation diffusion length. We show that the interaction between qE and open RCs results in spatially heterogeneous competition. Despite this complexity, we were able to construct a phenomenological “contracting” lake model, which is capable of describing the influence of excitation diffusion length on the relationship between the photochemical yield and the fraction of open RCs. Elucidating the mechanisms that connect excitation transport and quenching in proteins to Chl fluorescence and PSII light harvesting, as done here, will become particularly valuable as spatial measurements of excitation dynamics (46, 47) become feasible in intact membranes. Looking forward, we expect the overall framework established here to offer a fertile avenue for resolving the qE mechanism and parameterizing higher-scale models of plant photosynthetic metabolism.

Materials and Methods

Multiscale Model.

A model for PSII light harvesting that includes qE quenching requires several components: (i) a membrane structure with pigment resolution, (ii) a model for energy transfer, (iii) a model for electron transfer in the RCs, and (iv) a model for quenching. Combining these components results in a rate matrix that contains all of the rates of transport and loss in the membrane (41). We described i–iii in detail in previous work (14, 15), and we provide a brief description in SI Appendix, SI Materials and Methods.

We modeled qE by adding a first-order rate of quenching at a qE site (domain) in activated antenna complexes. Each protein housing a qE site can occupy two conformational states, one inactive and one active, and it occupies the active state with probability $P_{\mathrm{q}\mathrm{E}}$. This simple two-state switch is a simplification of the multiple states observed in single-molecule data (35, 38). In the active state, there is a timescale of excitation dissipation, ${\tau }_{\mathrm{q}\mathrm{E}}=1/k_{\mathrm{q}\mathrm{E}}$, from the qE site. This effectively coarse grains the photophysical mechanism of quenching, of which several have been postulated (31, 32, 48), into a single first-order rate constant. With qE sites located on LHCII, we only allowed unbound LHCII (circles in Fig. 1B) to quench excitation. However, the overall effect of weak quenching—that excitation visits, on average, several active qE sites before being quenched (see below)—means that the main results would not be altered if bound LHCII was also allowed to quench excitation.

Running Simulations.

The result of the model building in the previous section is an $\sim$11,000 × 11,000 rate matrix ($K$) that describes the total kinetic network of PSII light harvesting. Thus, the effects of changing the fraction of open RCs, the timescale of quenching, or the probability of quenching are entirely accounted for by changing $K$ accordingly. In a master equation formalism, the time dependence of excitation population [$P\left(t\right)$] is determined entirely by $K$:

$$\dot{P}\left(t\right)=KP\left(t\right).$$ [2]

We used two numerical methods for calculating $P\left(t\right)$. First, we used a finite difference calculation of population dynamics to simulate fluorescence lifetime curves. A time step of 10 fs was found to be well-converged. Second, we used kinetic Monte Carlo to calculate yields for the different decay pathways and the excitation diffusion length scale. For simulations that involved the presence of qE sites or fractionally open RCs, we averaged between 10 and 50 different configurations of qE quenchers and open RCs on the membrane, where in each simulation, the probability of a given quencher being active is $P_{\mathrm{q}\mathrm{E}}$ and the probability of a given RC being open is $f_{\mathrm{R}\mathrm{C}}$. In theory, the influence of closing one RC modifies the probability that an adjacent RC is closed. We have simulated this previously but found the effect to be small enough that it is neglected here. Details of the kinetic Monte Carlo simulations are in SI Appendix, SI Materials and Methods.

$P\left(0\right)$ was proportional to the number of Chl a in the domain and initiated across the membrane in all but two cases. In Fig. 3B, we localized the initial excitation to a single complex (either LHCII or a PSII-SC) and calculated the photochemical yield at a single open RC in the membrane. In Fig. 3C, to calculate the excitonic connectivity, excitation was started on a closed RC. Using the kinetic Monte Carlo method, excitation was sampled until it reached another RC or was quenched by fluorescence, dumping, or qE. The connectivity was the fraction of excitation that reached another RC.

Fluorescence Lifetime Snapshot Data Analysis.

The fluorescence decays shown in Fig. 2 A and B were the extracted as the PSII component from fluorescence lifetime snapshot data from dark-adapted wild-type leaves of A. thaliana exposed to a dark–light–dark actinic light sequence (23). We describe the extraction of the fluorescence decays and the calculation of an amplitude-weighted error to compare simulated decays with the data in SI Appendix, SI Materials and Methods.

Chl Fluorescence Parameters.

The relative changes in ${\mathrm{\Phi }}_{\mathrm{F}\mathrm{l}}$ are typically measured using PAM fluorescence. PAM fluorescence consists of three light sources: a dim light for measuring Chl fluorescence without perturbing PSII function, an actinic light that mimics changes in natural sunlight intensity and can (de-)activate qE, and brief ($<$1 s) high light pulses that close (saturate) all of the RCs. Prediction of various PSII outputs in the context of the lake or puddle models follows from arranging Chl fluorescence responses to the actinic light and the saturating flashes into equations. A full discussion of PAM fluorescence and how it is used to monitor PSII function is in refs. 6 and 13. In SI Appendix, SI Materials and Methods, we list the main Chl fluorescence parameters and equate them with the state of PSII that they correspond to in the multiscale model.