3D deep learning for detecting pulmonary nodules in CT scans

Abstract

Objective

To demonstrate and test the validity of a novel deep-learning-based system for the automated detection of pulmonary nodules.

Materials and Methods

The proposed system uses 2 3D deep learning models, 1 for each of the essential tasks of computer-aided nodule detection: candidate generation and false positive reduction. A total of 888 scans from the LIDC-IDRI dataset were used for training and evaluation.

Results

Results for candidate generation on the test data indicated a detection rate of 94.77% with 30.39 false positives per scan, while the test results for false positive reduction exhibited a sensitivity of 94.21% with 1.789 false positives per scan. The overall system detection rate on the test data was 89.29% with 1.789 false positives per scan.

Discussion

An extensive and rigorous validation was conducted to assess the performance of the proposed system. The system demonstrated a novel combination of 3D deep neural network architectures and demonstrates the use of deep learning for both candidate generation and false positive reduction to be evaluated with a substantial test dataset. The results strongly support the ability of deep learning pulmonary nodule detection systems to generalize to unseen data. The source code and trained model weights have been made available.

Conclusion

A novel deep-neural-network-based pulmonary nodule detection system is demonstrated and validated. The results provide comparison of the proposed deep-learning-based system over other similar systems based on performance.

BACKGROUND

Lung cancer is the leading cause of cancer mortality throughout the world.¹ Regular screening of high-risk individuals using low-dose computed tomography (CT) has been shown to reduce mortality in lung cancer patients.² Errors in cancer diagnosis are the most costly and detrimental type of diagnosis errors³ with type II errors being particularly common in lung cancer diagnosis.⁴ Subject to errors in both reading and interpretation, lung cancer diagnosis is highly error prone; however, many errors from diagnosis based on CT imagery can be reduced with a second reader.⁵ Due to the large number of individuals at high risk of lung cancer, regular screening with or without the assistance from a second reader could impose significant workflow and workload challenges for radiologists and clinical staff. Instead, computer-aided detection (CAD) systems have the potential to aid radiologists in lung cancer screening by reducing reading times or acting as a second reader.

CAD systems for pulmonary nodule detection consist of 2 essential tasks: candidate generation (CG) and false positive reduction (FPR).⁶ Various methods have been proposed for CG, including thresholding-based methods,^7–9 shape-based methods,^10,11 rule-based methods,¹² and filtering-based methods.¹³ The best results for this task have been demonstrated using a 2D multiscale enhancement filter.^14–16 Methods for FPR are also varied, and include methods similar to those used for CG.^17–19 Neural networks were first used for FPR of nodule candidates over 20 years ago^20,21 and have been accepted as a leading method for FPR in radiographs for over a decade.^22,23

In recent years, deep neural networks (DNNs) have been responsible for significant improvements in a variety of complex tasks. The potential of DNNs for such improvements was first demonstrated at the 2012 ImageNet general image classification competition by Krizhevsky et al.²⁴ Krizhevsky’s team used the first DNN in the competition’s history, winning by such a large margin that each of the top 10 teams in the following year’s competition were also using DNNs. In the years since, deep learning has been applied to a variety of medical imaging tasks,^25,26 many of which involve segmentation.^27–30 For some medical imaging tasks, deep learning methods have been demonstrated performing at or above the level of licensed experts.^31,32 DNNs have also been applied for FPR,^33–37 and just recently for pulmonary nodule segmentation.^38,39

Since the 2012 ImageNet competition, substantial progress has been made developing increasingly complex DNNs that have surpassed human-level performance in general image classification tasks.⁴⁰ In 2014, Szegedy et al⁴¹ demonstrated an accuracy of 93.33% using an extensive DNN comprised of 22 layers. A key feature of this network, dubbed GoogLeNet, was the inclusion of new components called inception modules that enabled the use of multiple convolutions in each layer of the network. In 2015, He et al⁴² demonstrated an architecture for deep residual learning using a DNN comprised of 152 layers to achieve an accuracy of 96.43%. This architecture, dubbed a residual network, employed a new feature for learning residual functions with reference to layer inputs.

Recent studies on nodule detection that utilize machine learning approaches, such as neural networks^6,34,39 and support vector machines (SVMs),^12,15,43,44 have several deficiencies. For example, several prior studies^37,39,43,44 exclude high resolution scans, several studies^37,39 use 20-year-old deep learning architectures,⁴⁵ and several^34,37,39 exclude small nodules and non-nodules from system evaluation. To address these deficiencies, we present a complete CAD system that uses novel, 3D adaptations of recent deep learning research,^46–48 achieves performance comparable to the best existing systems, and exceeds the performance of all previous deep learning systems.

MATERIALS AND METHODS

Dataset

The Lung Image Database Consortium (LIDC) and Image Database Resource Initiative (IDRI) compiled a repository of CT scans specifically for the development of CAD systems for lung cancer.^49,50 These data are made available by the National Cancer Institute’s Cancer Imaging Archive under the Creative Commons Attribution 3.0 Unported License.⁵⁰ The LIDC-IDRI repository is comprised of 1018 openly available CT scans collected from 5 participating institutions with each of the scans including annotations by 4 radiologists. Lesions identified by radiologists were labeled as large nodule (≥ 3mm), small nodule (< 3mm), or non-nodule. A total of 2669 lesions were marked as a large nodule by at least 1 radiologist, with 928 lesions being marked as large nodule by all 4 radiologists.

Although a large number of CAD systems have been demonstrated,^{12,34,43,44,51–53} comparing their relative performance has been challenging due to the lack of an objective evaluation framework. The LUNA16 dataset⁶ was created in part to address this issue. It is a collection of 888 thin-slice CT scans (ie, slice thickness ≤ 3mm) of consistent slice spacing from the LIDC-IDRI dataset.⁵⁴ These scans were randomly divided into 10 bins for cross-validation purposes, and these bins were used in this study to enable reproducibility and aid in objective comparative evaluation. The small and non-nodule objects, typically ignored by other systems, are included as part of the testing set for this system, resulting in the inclusion of 30 513 items for evaluation, and the detection of these objects is considered a false positive.

Method

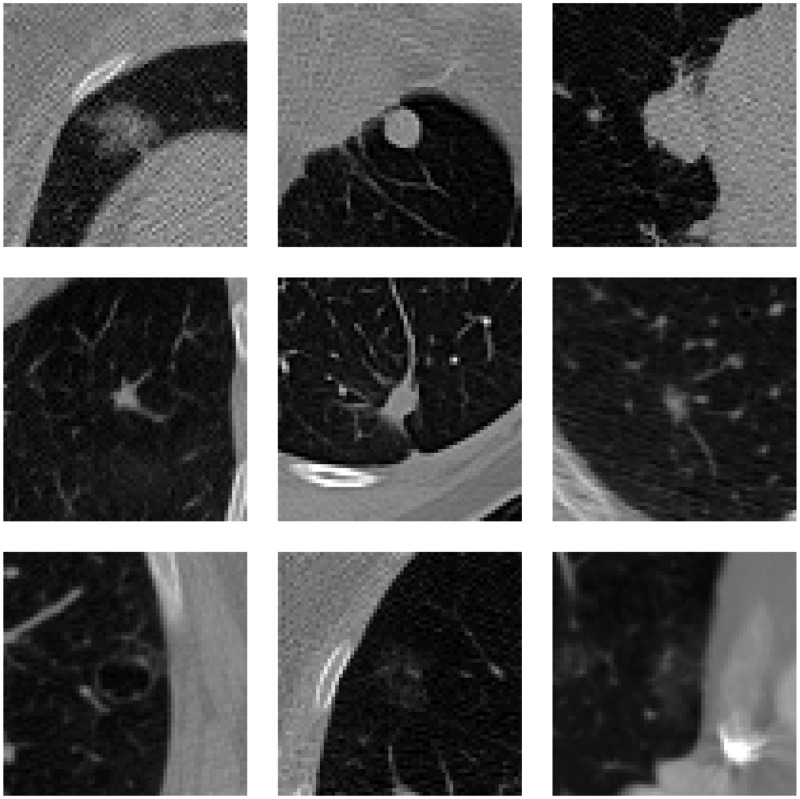
As depicted in Figure 1, pulmonary nodules can vary greatly in density, shape, size, etc. A typical pulmonary nodule exists as an isolated lesion¹ in the parenchyma of the lung. Pulmonary nodules are frequently found attached to the pleural wall or vascular structures. Such juxtapleural and juxtavascular nodules, depicted in the first and second rows of Figure 1, respectively, can complicate automated nodule detection. Other nodules that can be challenging for CAD systems to detect are low-density nodules, as seen in the third row of Figure 1. Due to the variety and unique challenges, CAD systems have had difficulty achieving high performance for all varieties

Figure 1.

Different types of pulmonary nodules: juxtapleural (top row), juxtavascular (middle row), and low-density (bottom row).

Deep learning offers unique advantages over traditional methods for nodule detection. Rather than relying on mathematical techniques or hand-crafted features, deep learning enables learning internal feature representations directly from the input data.^55,56 The multiple processing layers in DNNs allow for learning these internal representations of the input data with multiple levels of abstraction.⁵⁷ These characteristics enable DNNs to learn feature representations for a large variety of features hierarchically, ie, at different scales, and combine them for learning more complex features (eg, nodules). This capability is well suited for the unique challenges posed by nodule variety in pulmonary nodule detection.

We use DNNs for each of the 2 essential tasks of computer-aided pulmonary nodule detection. The first DNN is used for volume-to-volume prediction of nodules, ie, segmentation, to identify potential pulmonary nodules within the input CT scan. These potential nodules that are generated are considered candidate nodules. This segmentation generates a large number of candidate nodules, many of which are false positives. The second DNN is used for reducing false positives among these nodule candidates through a binary classification of nodules and non-nodules. Figure 2 describes the system including the 2 primary tasks and the associated subtasks for each DNN.

Figure 2.

a) Process diagram of the proposed detection system. b) Segmented volume of the lungs.

The CT scans from the LUNA16 dataset range from 0.461 mm to 0.977 mm in pixel size and from 0.6 mm to 3.0 mm in slice thickness. Thus, the features depicted in the raw CT scans represent a scaled version of the actual features corresponding to the specifications of the imaging equipment used. To ensure uniformity of the data processed by the system, we begin with an isotropic resampling of the images, using third-order spline interpolation to resize all voxels to a uniform size of 1 mm³. As lung cancer screening is concerned solely with the lungs, a large portion of thoracic CT scans is irrelevant to lung cancer detection. To reduce computational expense, we next segment the lung region using a threshold-based segmentation technique² that isolates the lung and allows us to ignore the extraneous regions of the original scan. Figure 2b depicts the lungs following segmentation. A bounding box is created circumscribing the lung, and this region of interest is input into the CG DNN.

To date, only 1 study has demonstrated the use of DNNs for the segmentation of pulmonary nodules,³⁸ and DNNs have not been previously used in CG. The U-Net architecture⁵⁸ is a DNN architecture used for generating high-quality segmentations of medical imagery from small training datasets using heavy augmentation. The U-Net architecture has also been extended to 3D imaging applications successfully.⁴⁶ In this study, we adapt and apply this 3D U-Net architecture specifically for the segmentation of relatively small volumes in CT scans such as pulmonary nodules. The architecture, depicted in Figure 3a, comprises 135.6 million trainable parameters.

Figure 3.

⁴ . a) Modified 3D U-Net architecture used for the CG segmentation. b) 3D residual network architecture used for FPR.

The U-Net-inspired DNN architecture that we use for CG acts as a volume-to-volume prediction (ie, segmentation) network that takes an input volume of 64x64x64 and outputs a volume of 32x32x32. CT scans and the regions of interest generated from the lung segmentation are much larger than 64x64x64. As the output is 32x32x32, a 16-unit buffer was created on all sides of the region of interest in order to generate an output volume corresponding with every voxel in the region of interest. A sliding window technique was used with a step size of 32 for each axis to iteratively progress through the region of interest, extracting 64x64x64 volumes for input to the DNN. This required the application of the DNN nearly a thousand times in generating candidate nodules for a single scan. The output volume was an array of probabilities. A threshold was applied setting all values less than 0.1³ to zero. The remaining probabilities were converted to a binary array, and labels were generated for the adjacent voxels, yielding an array of numbered volumes. Centroids were computed from these labeled volumes for evaluation and for generating output candidate nodules. During this process, a variety of features were also extracted from nodules, including the volume in voxels of each nodule candidate.

The features extracted during the centroid computation for each of the candidate nodules were used as a threshold as an initial FPR technique. The only feature selected for use in this step was nodule volume due to its strength in discriminating among positive and false positive nodules. The optimal threshold value was determined empirically to be 8 mm³. Nodule candidates smaller in volume than 8 mm³ were deemed false positives. Examples are shown in Figure 4. Following the features-based FPR step, remaining candidate nodules were processed with the DNN FPR module. The DNN model used here involved a complex DNN architecture for the simple task of binary classification. The architecture was based on the work by Szegedy et al⁵⁹ in combining the inception network architecture⁴¹ with residual learning elements.⁴² The architecture used in our proposed model is adapted from the Inception-ResNet architectures proposed by Szegedy et al, albeit adapted to 3D images. Rather than using leaky rectified linear units as activation functions, scaled exponential linear units, recently demonstrated as better than standard rectified linear units for very deep networks,⁴⁷ were used, as initial testing indicated performance improvements. Consequently, Gaussian initialization and alpha dropout were used to improve convergence and performance.

Figure 4.

Top: actual nodules. Bottom: corresponding segmented volumes of generated candidates for diameter sizes 6 mm, 12 mm, and 20 mm.

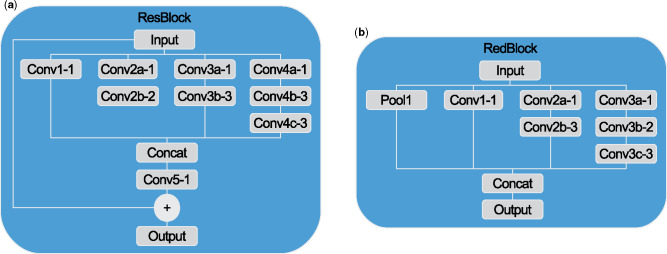
The reduction and residual blocks (Figures 5a and b) provide further details on the architecture of the network (Figure 3b). The reduction block in Figure 5a was adapted from the wider “Reduction-B” block from Inception-ResNet-v1, 1 of 3 Inception-ResNet architectures proposed by Szegedy et al.⁴⁸ The residual block was adapted from the “Inception-ResNet-A” block of Inception-ResNet-v1 with an extra convolution layer similar to the residual inception blocks of Inception-ResNet-v4. Unlike Inception-ResNet-v1, the entire architecture of our proposed model was built from only 2 of these reduction blocks and 4 of these residual blocks. Each of the convolution layers depicted in the overall architecture applies 1x1x1 convolutions. These are included between concurrent residual blocks to maintain a constant number of features. A smaller input size of 32x32x32 was used to speed up training, as it did not affect the results. The entire architecture was comprised of 1.28 million trainable parameters.

Figure 5.

Architectures for a) 3D reduction blocks and b) 3D residual blocks. Convolutions were uniform in 3 dimensions of size denoted by the hyphenated number in the diagrams.

Training⁵,⁶,⁷

We used 10-fold cross-validation consistent with the cross-validation experimental design used by Setio et al.³⁷ For each of the 10 folds of the cross-validation, 9-fold cross-validation was conducted, and the 10th bin was held out as test data. The best performing model from the 9-fold cross-validation was evaluated on the test data. This enabled the use of all 888 scans as test data.

Training for the CG network was conducted with all available positive nodules⁸ for each of the 9-fold cross-validations conducted. The nodule candidates generated for each of the validation bins during each cross-validation were used to train the FPR network. Over 1000 positive examples were used for each of the 10 9-fold cross-validations.

A 3D array of training labels was required, as the CG network was a volume-to-volume prediction network. Approximate binary labels for each nodule were generated as spheres based on the diameter of each nodule. Heavy data augmentation was employed during training, involving random translation up to 14 units along each axis, random rotation about each axis up to 90°, and random flipping about each axis. Implementation of this augmentation required the application of the same random transformations to both the input image and its associated labeled array.

The Sorensen-Dice coefficient,^60,61 or simply the Dice coefficient (DC), was used to measure the spatial overlap between the predicted volume and the ground truth for the purposes of optimization. It is defined as:

$$DC\left(G,P\right)=\frac{2\left|G\cap P\right|}{\left|G\right|+\left|P\right|}$$

where P is the set of prediction results, and G is the set of ground truth. It ranges in value from 0 to 1, with 1 indicating perfect prediction accuracy. In order to optimize the network architecture, the objective function, J(θ), was defined as:

$$J\left(\theta \right)=1-DC(G,\mathrm{}\mathrm{P})$$

The Adam optimizer,⁶² with an initial learning rate of 1e⁻⁵, was used for minimizing J(θ). In order to minimize overfitting, the dropout technique⁶³ and batch normalization⁶⁴ were used for regularization. As noted, the CG architecture included over 100 million trainable parameters. This effectively restricted the batch size to 2, significantly slowing training.⁹ Due to this, each epoch required training 400 minibatches. Models were trained for 210 epochs. Upon completion of the training, the models exhibiting lowest $J\left(\theta \right)$ values were evaluated systematically in order to identify the best models at a minimal computational expense. Results were recorded, and the process was repeated until performance gains plateaued.

The FPR network was trained as a binary classifier with the candidates generated from the best performing models of each validation bin during cross-validation. These candidate nodules were labeled as either nodule or non-nodule.¹⁰ Data augmentation was used involving random translation along each axis up to 2 units, random rotation of up to 15° about each axis, and random flipping about each axis. Data were centered by subtracting the image mean and normalized by the image standard deviation.

Categorical cross-entropy was used as an objective function and was minimized using the AdaDelta optimizer.⁶⁵ Again, to minimize overfitting, dropout⁶³ and batch normalization⁶⁴ were used. With the architecture including over a million trainable parameters, a batch size of 64 was trained per epoch. During training, only positive examples were included in the validation dataset in order to prioritize sensitivity. Consequently, a large number of well performing models were saved, and specificity was assessed among these.

RESULTS

By conducting 10 9-fold cross-validations, each scan and nodule in the dataset could be evaluated as test data. To evaluate test data, scans were first evaluated with the CG module. The resulting candidate nodules were determined to be a direct hit, a near hit, or a miss. A candidate nodule was classified a “direct hit” when the center of the true nodule was within the segmented volume of the candidate nodule. A nodule was treated as “near hit” when the center of the candidate nodule was within 0.75D of the true nodule.¹⁵ Direct hits and near hits were taken as positive candidates. All candidate nodules generated were then evaluated with the FPR module.

The results from the cross-validation and the test data are reported in Table 1. This table reports only mean values of sensitivity, false positives per scan (FPPS), and receiver operating characteristic area under the curve (ROC AUC). The full test results for each of the 10 cross-validations are reported in Supplementary Appendix A in Table 3. The cross-validation results are depicted for comparison only and, unless otherwise noted, all references to results in the paper refer to the test results. The full cross-validation results for the 8 values reported in Table 1 are presented in Tables 4 through 9 in Supplementary Appendix A, which also reports the cross-validation results for each of the 90 cross-validation systems.

Table 1.

Results

Task	Dataset	Sensitivity	FPPS	ROC AUC
CG	Cross-validation	0.9516	30.68	–
	Test	0.9477	30.39	–
FPR	Cross-validation	0.9594	1.815	0.9849
	Test	0.9421	1.789	0.9835
Complete system	Cross-validation	0.9129	1.815	0.9372
	Test	0.8929	1.789	0.9324

The free-response ROC curve (FROC) is commonly used in lieu of the traditional ROC curve for cases such as pulmonary nodule detection in which 1 or more abnormalities may be present for each evaluated case.^66,67Figure 6 depicts an FROC curve for the system plotted on a logarithmic scale. Recent work on pulmonary nodule CAD systems^6,33,37 has featured a metric referred to as the “competition performance metric” (CPM), which is based on the FROC curve for evaluating CAD systems.⁶⁸ This metric is computed by taking the mean sensitivity value for each of the 7 labeled positions on the x axis in Figure 6. The CPM for the system was 0.8135.

Figure 6.

FROC curve for the complete system and depicted on a logarithmic scale¹¹ of base 2 from 0.125 to 8.0.

DISCUSSION

A comparison of the features and performance of pulmonary nodule CAD systems is reported in Table 2. In this table, a range of values for the proposed system’s sensitivity is reported in order to enable comparisons with the various systems. The middle value is the raw result of the FPR module. The top and bottom values are sensitivities taken from the FROC curve for 1.0 and 4.0 FPPS, respectively. This table includes no studies that exclusively use the LUNA16 Challenge evaluation framework due to its limitations. Detailed explanation for this is provided in Supplementary Appendix B. Results reported by Setio et al³⁷ and van Ginneken et al³⁴ for CAD systems employing deep learning for FPR presented sensitivities based on false positive rates from FROC curves. Table 2 demonstrates the improvements in the performance of the proposed systems over these 2 systems. Setio et al³⁷ reported a CPM of 0.722 and was the only one of the studies listed in Table 2 to report this metric. As reported earlier, the CPM in this study is 0.8135. Shaukat et al¹⁵ demonstrated excellent performance for their complete system, which was heavily influenced by the strong performance of their FPR module, and is discussed further in Supplementary Appendix C. These results suggest that future work could explore the combination of deep learning systems for feature extraction and SVMs for classification. As reported in Table 2, among the studies included for comparison, only Setio et al³⁷ and Jacobs et al⁵² used the complete number of scans for test data. While Setio et al³⁷ used existing CG systems, Jacobs et al⁵² simply evaluated existing systems. Shaukat et al¹⁵ did, however, use 30% of their total dataset for test, which is substantial. Of the other studies involving a large number of scans, Hamidian et al³⁹ used 25 scans for test while Firmino et al¹² and van Ginneken et al³⁴ strictly reported cross-validation results. We are not aware of another novel system in the literature to have been evaluated as rigorously. A complete comparison and discussion of results for each of the tasks can be found in Supplementary Appendix C.

Table 2.

Comparison of pulmonary nodule CAD systems

	# Scans	Sensitivity	FPPS	CG	FPR	Thickness	Small/non-nodules
Proposed system	888	0.8446	1.00	3D DNN	3D DNN	<=3.0mm	Yes
		0.8929	1.79
		0.9273	4.00
Shaukat et al15	850	0.9269	1.91	Filter-based segmentation	Specified features w/ SVM classifier	1.0-3.0 mm	Yes
Hamidian et al39	509	0.8000	15.28	3D CNN	3D CNN	1.5-3.0 mm	Yes
Firminio et al12	420	0.9440	7.04	Segmentation and rule-based	HOG features and SVM classifier	<=3.0mm	No
Jacobs et a.52	888	0.8200	3.10	Comparison of 3 systems (commercial and academic)		<=3.0mm	Yes
Setio et al37	888	0.7820	1.00	Ensemble of existing systems	Multi-view CNN	<=3.0mm	Yes
		0.8790	4.00
Van Ginneken et al34	865	0.7300	1.00	Existing system	Comparison of 3 existing DNNs	<=2.5mm	No
		0.7600	4.00
Choi and Choi44	84	0.9545	6.76	Dot-enhancement filter	AHSN features and SVM classifier	1.0-3.0 mm	Yes
Choi and Choi43	58	0.9276	2.27	Block segmentation	Specified features w/ SVM classifier	1.0-3.0 mm	Yes

Strengths and limitations

Strengths of the study include the robust experimental design, the large test dataset, and the methodology. Particularly, retaining 30 513 false positive items to evaluate the system strongly distinguishes this study from a large number of current deep learning studies for nodule detection. A further strength of the study is the open availability of the source code and the trained weights for the 180 different models for which results are reported in Supplementary Appendix A.

Despite the use of a substantial amount of test data, the lack of evaluation on an external dataset remains a significant limitation. Further limitations of the dataset are described by Armato et al⁴⁹ and include the lack of clinical information and the fact that scans were not all scored by the same radiologists. Other limitations concern limited analysis of segmentation quality due to the focus on the CAD system and limited computational capacity due to the high computational costs.

CONCLUSION

We present a novel, fully automated system for the detection of pulmonary nodules that was extensively validated using each scan in the dataset for both training and test. As described earlier, the CG and FPR modules each independently demonstrated results that outperform other reported or known systems for their respective tasks. Overall, the results indicate that the system is comparable with the best existing systems.

The proposed CAD system is designed for detecting pulmonary nodules. Extending it to quantify malignancy and offer diagnostic predictions is an important research direction for future work. Such a system could be evaluated rigorously with a large external dataset—a significant limitation of this study—using data from the National Lung Screening Trial.^2,69

FUNDING

Support for this work was provided by Auburn University. This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

CONTRIBUTORS

RG developed the model and did coding for the model under supervision of AG. RG and AG developed the manuscript and performed revisions. DP edited the manuscript and provided feedback.

Conflict of interest statement. None declared.