Mechanistic machine learning: how data assimilation leverages physiologic knowledge using Bayesian inference to forecast the future, infer the present, and phenotype

Abstract

We introduce data assimilation as a computational method that uses machine learning to combine data with human knowledge in the form of mechanistic models in order to forecast future states, to impute missing data from the past by smoothing, and to infer measurable and unmeasurable quantities that represent clinically and scientifically important phenotypes. We demonstrate the advantages it affords in the context of type 2 diabetes by showing how data assimilation can be used to forecast future glucose values, to impute previously missing glucose values, and to infer type 2 diabetes phenotypes. At the heart of data assimilation is the mechanistic model, here an endocrine model. Such models can vary in complexity, contain testable hypotheses about important mechanics that govern the system (eg, nutrition’s effect on glucose), and, as such, constrain the model space, allowing for accurate estimation using very little data.

INTRODUCTION

Prediction is fundamental to medical practice, both to select treatment and to gauge prognosis. Despite centuries of amassing biomedical knowledge and decades of increasing reliance on computing and information technologies, predictions in medicine remain imprecise and generic. For example, knowledge of endocrine physiology and detailed glucose measurements have not led to precise (ie, quantitative patient-level) predictions in type 2 diabetes. We would like precise predictions regarding the impact of nutrition on glycemic control, but instead nutritional therapy in diabetes relies on findings generated by population-wide studies and consultation with clinical experts.¹ Our physiologic knowledge is sometimes quantitatively encoded in mathematical models,² but the models are approximate, vary significantly by patient, and are not personalized unless entrained with previous and incoming data. Techniques such as deep learning³ promise to predict the future without mechanistic knowledge, learning the structure directly from the data, but they are limited in settings with sparse, irregular, inaccurate data, and they do not bring much understanding about the patient or the disease beyond their predictions.

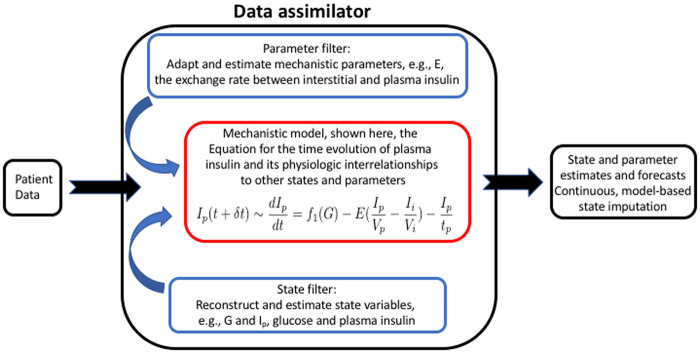
Data assimilation (DA),^4–6 known also as state space models, point processors,^7–10 Kalman filters,¹¹ and linear dynamical systems, is a regression method meant to solve inverse problems (estimating model parameters),^12,13 often in the context of solving a forward problem (issuing a forecast) and was initially developed in contexts of space travel by Kalman and Brownian motion by Thiele.¹⁴ Conceptually, DA (Figure 1) takes a model believed to represent a system being studied and synchronizes the model with data by estimating states and parameters of the system. In this way, DA provides a bridge between physiology and empirical data, such that imperfect models and sparse data can be co-leveraged to overcome each other’s failings. The physiology constrains the learning process, minimizing the data required, while the data tailor the model to the patient and synchronize it with the patient. Furthermore, DA can be integrated with control algorithms,¹⁷ so that instead of predicting the future under current conditions, it predicts what changes need to be made today to reach a desired outcome in the future. At its essence, DA is a family of regression methods that project data onto a physiologically meaningful mechanistic model the way linear regression projects data onto simpler linear models and the way deep learning projects data onto more flexible but data-hungry neural networks. DA has advanced over the decades from its original formulation as a linear, stochastic method to more recently developed nonlinear approaches.

Figure 1.

Schematic diagram of how data assimilation synchronizes a model with data by estimating parameters and states. The model equation is drawn from the ultradian glucose model.^15,16

The purpose of this perspective is to introduce, or re-introduce, biomedical informatics to the long-standing approach to prediction—using mechanistic modeling to make data-driven predictions—because we believe it has application well beyond its current use in biomedical informatics. There are recent advances in DA, such as the development of nonlinear filters that allow DA to be used on problems biomedical informatics focuses on in particular, including prediction and furthering biological and medical science using data collected over the process of giving care. Forecasting, at its foundation, is about helping people make better decisions, ie, decision support, and DA has the potential to be able to make predictions with data collected over the course of current clinical care, eg, with far less data than are needed for many other techniques. But DA also requires integration with an informatics pipeline to be made useful. The raw output of a DA is not useful because it is generally too complex in its raw from and must be translated to a user in a way users can understand and use in their decision workflow. This makes the application of DA an interdisciplinary informatics problem. But biomedical informatics is not limited to clinical care alone because it lives at an interface between basic science and clinical applications. When DA is used in the inverse problems,^13,18 its smoothing context, DA addresses another key goal of biomedical informatics, using clinical data to drive basic science. The goal of smoothing is to fill in the past and to infer features and physiology we cannot directly measure. In atmospheric science, reanalysis data,¹⁹ or the DA output of the past that includes the entire physics of the atmosphere well beyond what can be measured, is used to train new models, including non-mechanistic machine learning type models, to study the physical system. It is easy to imagine inverse problems approaches to physiology following a similar path in translational bioinformatics. Our goal is to inform informatics that new machinery exists to apply DA to these informatics applications.

Because of the intuitively fundamental nature of DA, there have been many formulations of the same basic idea. For example, a traditional Bayesian machine is Dempster–Shafer,^20–23 a belief function for reasoning given uncertainty that is used to fuse empirical sources of information. The continuous version of Dempster–Shafer can be formulated as a linear Kalman filter,²⁴ where the DA state space and the Dempster–Shafer frame of discernment are equivalent. Thus, the methods in this paper can be framed as a nonlinear, continuous belief network.

DA has transformed fields such as space travel, weather forecasting, flight, and manufacturing. It has seen some use in biomedicine for decades, usually in data-rich settings and usually in its linear formulation. Early examples of connecting mathematical physiologic models to data include Hodgkin and Huxley,²⁵ who proposed a model of neurons, and Mackey and Glass,¹⁷ who proposed a model of physiologic control systems. DA has been used in biomedicine in several settings: algorithms in implantable defibrillators and pacemakers to cope with irregular heartbeats,^26–29 model construction and fitting for prostate cancer treatment,^30,31 the artificial pancreas for type 1 diabetes,^32–38 pharmacodynamics,^39–42 female reproductive endocrinology,⁴³ sleep modeling,⁴⁴ ICU glucose forecasting,^38,45–47 many uses in epidemiology,⁴⁸ viral modeling,⁴⁹ and inverse physiologic problems in general.^13,18

The inavailability of data and previously limited methods for integrating data with nonlinear physiologic models may have restricted the degree to which DA has permeated biomedicine. This situation may be improving. For example, we have recently shown that we can use sparse, inaccurate data collected in the course of care paired with a simple glucose-insulin model to produce accurate postprandial glucose and hemoglobin A1c predictions.¹⁵ This worked despite the relatively complex physiology of type 2 diabetes. This example demonstrates that recent and continuous development of nonlinear methods together with the availability of clinical data, self-monitoring data, etc., provide room for substantial advancement and associated challenges.

The mechanistic model aspect of DA allows it to bear several novel results. It can produce optimal predictions given the measured data under the constraints of the physiological model, such as for post-meal glucose. It can recommend actions needed to produce desired outcomes, such as what meal must I eat to keep my peak glucose below some threshold? The unmeasured but estimated model parameters may represent useful patient phenotypes, such as decreased or changing kidney function and liver function, insulin secretion rates, stress response, etc. The model can produce smoothed versions of the sparse data, such as interpolating the glucose between measurements and then using that output to infer an aggregate measurement such as hemoglobin A1c. And the DA can test a mechanistic physiologic hypothesis by estimating how parameters change when circumstances change, or by comparing models with differing physiology.

To understand the power of DA methodologically, consider what Al Roker, an NBC weatherman, was able to discuss on October 3, 2016, when reporting the path of Hurricane Matthew. In a short two-minute video segment, Roker showed the size and path of the hurricane, forecast seven days into the future, using three different model-driven DAs. By doing this, the audience was shown not only a believable, actionable weather forecast, but also how and why the forecast was uncertain intuitively. One can imagine how such technology could transform medicine.

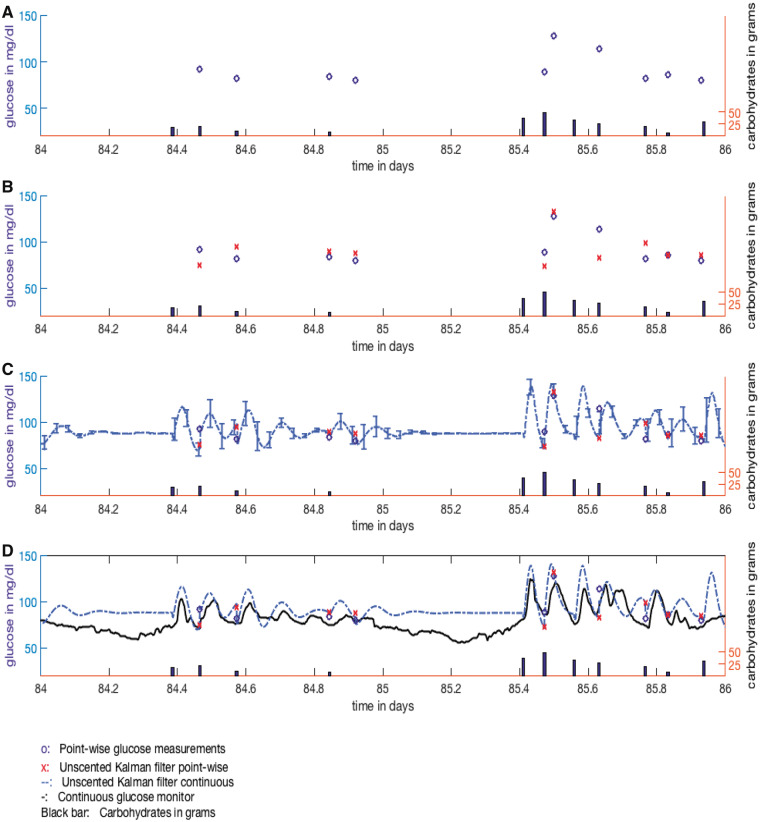
We illustrate DA with real data from a type 2 diabetes patient in Figure 2. Figure 2A has a two-day sample of sparse finger-prick glucose measurements and meal data; Figure 2B adds the point-wise DA glucose forecasts for the patient using an ultradian glucose model.⁵⁰Figure 2C has the DA’s continuous glucose predictions and continuous uncertainty estimates, which appear to be over fit. Figure 2D, however, shows the underlying continuous glucose monitor, whose data were withheld from the DA. The match is uncanny, yet the oscillations in the glucose level could never have been learned from the sparse finger-prick data alone. Only by using physiological knowledge implicit in the ultradian model could those oscillations have been predicted. Moreover, the second bump in glucose at 85.6 days, which appeared to have been missed by the DA (Figure 2B), was actually just a several-minute miscalculation (Figure 2D).

Figure 2.

(A) Finger-prick glucose measurements and meal carbohydrates serve as the training data (one segment shown) with a goal to predict glucose in the future. (B) DA’s point-wise forecasts seem reasonable but not perfect, predicting one spike but missing another. (C) Underlying continuous DA forecast with uncertainty quantification (which the point-wise forecasts are based on) appears to overfit the data with large glucose swings. (D) Continuous glucose monitoring, which was hidden from the DA, reveals striking overlap between the continuous DA predictions and the actual glucose levels. Despite insufficient information in the training set, the DA tracked glucose well based on the combination of its glucose metabolism constraints and the sparse measurements.

Data assimilation inference

There are several ways to frame DA; here we use Bayesian inference.¹² Bayesian inference can be summarized with Bayes formula:

$$p\left(\theta ||y\right)\propto L\left(\theta ||y\right)p\left(\theta \right)$$

where $y$ are the data, $\theta$ are the parameters, $p\left(\theta \right|y)$ is the posterior distribution or the model predictions given data, and $L$ is the likelihood function. The goal of Bayesian inference and prediction is to characterize the posterior distribution. It is determined by our prior knowledge and the likelihood function. The likelihood contains our understanding of mechanisms and determines how current data, initial conditions, and parameters are mapped to future states and parameters. The predictive model determining the likelihood, eg, a glucose-insulin model, generates forecasts, smooths data, and quantifies uncertainty.

In the simplest situation, the predictive model determining the likelihood is linear. The linear case formulated by Kalman in the 1960s¹¹ has been applied often with great success, and is the “optimal” linear filter. Nevertheless, many situations are not, and cannot be made, linear. When the predictive model determining the likelihood is nonlinear, meaning the current states are a complex function of the past, estimating the likelihood is substantially more difficult. A primary goal of machine learning and related fields is to infer the nonlinear likelihood using data alone. While DA can be cast within this framework, it can also incorporate mechanistic knowledge of the likelihood function using mechanistic equations that constrain, limit, and probabilistically determine the values the states can take. Many methods for this computation exist, including iterative methods, such as dual unscented Kalman filters^51,52 and extended Kalman filters,^53,54 and Markov chain Monte Carlo-based methods,^55–57 such as ensemble Kalman filters^58,59 and particle filters.⁹ Here we use 2 methods, a dual unscented Kalman filter we previously developed¹⁵ and a Metropolis–Hastings-within-Gibbs Markov chain Monte Carlo method, explained in detail⁵⁵ and demonstrated in.⁶⁰

If the system generating the data—an individual’s endocrine system—changes in time, then the parameters must adapt in time also. Continuous parameter estimation can be done online or offline. Online means the parameters are computed in real time as data arrive. Offline means the parameters are computed on the whole data set in retrospect. Filters such as the dual unscented Kalman filter can continuously adapt parameters in time because they are computationally cheap, whereas computationally intensive techniques, such as those based on Markov chain Monte Carlo, are usually used offline. It is also possible to treat parameters as unknown functions that evolve in time.⁵⁵

Mechanistic models

At the core of DA lies a mechanistic (physiological) model that encodes our knowledge about a given system. The model depends on the domain area and the goal. We use the ultradian endocrine model^2,50 as an example for the rest of the paper; we summarize it here and note the full description of the model can be found in.^15,61,62 The differential equations for the three state variables are:

$$\begin{array}{c}\frac{d{I}_p}{dt}=f_1\left(G\right)-E\left(\frac{I_p}{V_p}-\frac{I_i}{V_i}\right)-\frac{I_p}{t_p}\\ \frac{d{I}_i}{dt}=E\left(\frac{I_p}{V_p}-\frac{I_i}{V_i}\right)-\frac{I_i}{t_i}\\ \frac{dG}{dt}=f_4\left(h_3\right)+I_G\left(t\right)-f_2\left(G\right)-f_3\left(I_i\right)G\end{array}$$

where, eg, I_p is plasma insulin, I_i is remote (non-plasma) insulin, and G is glucose. Our physiologic understanding is encoded in these equations. For example, the first equation describes how plasma insulin changes in time as a function of other state variables, parameters, and parameterized physiologic processes. The time rate of change of plasma insulin is dependent on the rate of insulin production minus the rate of exchange between remote and plasma insulin times the concentration of plasma insulin minus the remote insulin, all minus the amount of plasma insulin divided by rate at which plasma insulin degrades. The DA estimates parameters, eg, the exchange rate between remote and plasma insulin, E, and estimates, forecasts and tracks the time evolution of the state variables, eg, I_i as far into the future as is desired, being corrected whenever new data are encountered. Every model represents a computable hypothesis of how a physiologic system functions and how important variables interact to represent the system.

Model error, identifiability, and uncertainty quantification

Model error—the difference between the model and the physical system—represents both parameter errors and the functional difference between the model, fit perfectly, and the physiologic system it is designed to represent. Identifiability¹⁸ is the theoretical property of a model’s ability to have its parameters estimated given ideal data. Models can have completely, partially, or un-identifiable parameter sets. Uncertainty quantification^63,64 is the identification, quantification, and reduction of all error types.

Depending on the application, model error, identifiability, and uncertainty quantification must be addressed to differing degrees. When biological fidelity is required, estimated parameters should have detailed uncertainty estimates and their identifiability properties must be explained. Figure 2C shows very coarse uncertainty quantification at forecast points, which can be sharpened considerably with more advanced techniques. Quantified model error is the primary focus when developing new models, averaging models, or comparing several models as hypotheses.^65–67 When an accurate clinical forecast is important, uncertainty quantification is essential for putting trustworthy bounds on forecast reliability.

Forecasting the future

To forecast glucose in real time we use a dual unscented Kalman filter. In previous work we have used that filter to forecast glucose for people with type 2 diabetes mellitus¹⁵ using only sparse, irregular finger-prick data. In Figure 2, discussed in the introduction, we use finger-prick glucose and carbohydrate data to estimate continuous glucose using the dual unscented Kalman filter and compare this forecast with the output of a continuous glucose monitor.

Completing the past

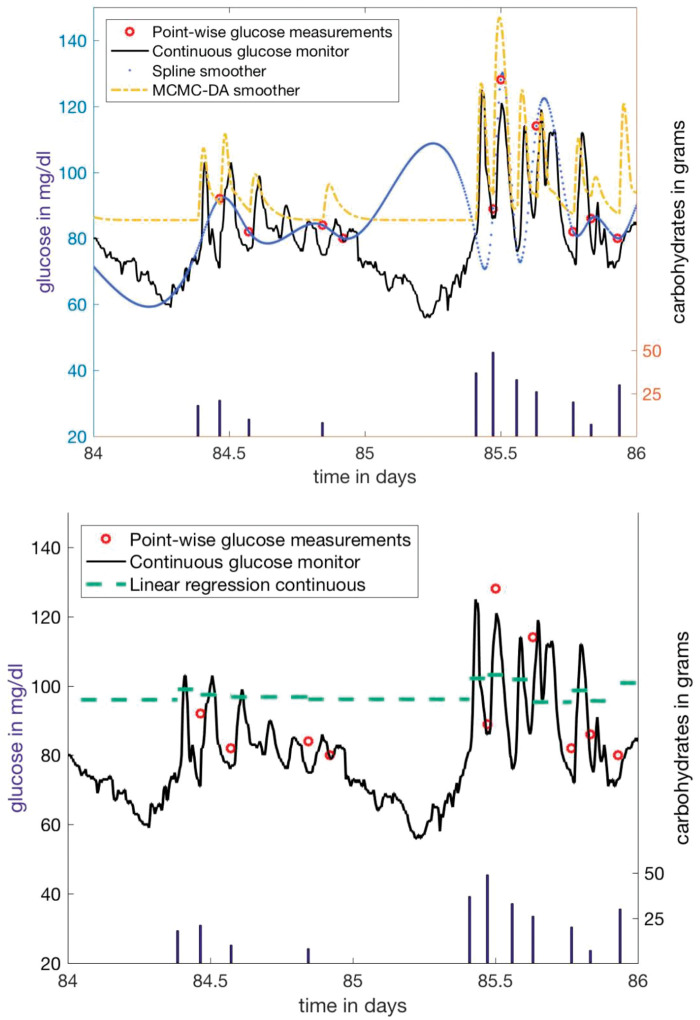
Sometimes it is important to impute missing data or parameters using sparse past measurements influenced by noisy external factors—the essential task of smoothing. Figure 3 compares continuous glucose measurements and continuous glucose estimates from both a Metropolis-within-Gibbs DA using the ultradian model and a cubic spline smoother.^68,69 Both smoothing techniques use only finger-prick data to estimate the most probable curve that generated the finger-prick data from the set of all possible curves available to the model class. The DA, constrained by physiology, matches the glucose oscillations well. The spline smoother, free to select any curve that minimizes the error, is unconstrained by physiology and selects a curve that minimizes error but has non-physical off-data oscillations. Contrasting the DA with the spline estimates shows the consequences of physiologic constraints: the root mean squared errors between the continuous glucose data and the continuous DA and spline glucose estimates were 16 mg/dl and 110 mg/dl, respectively. The knowledge-based physiologic constraints decrease model flexibility in a way that increases accuracy.

Figure 3.

Continuous glucose monitor data, finger-prick glucose measurements, Markov chain Monte Carlo-based DA smoothing using finger-prick data, and spline smoothing using only finger-prick data. The spline, with no physiologic constraints, can deviate wildly from the real glucose measurements, while the physiologically constrained DA glucose inferences closely resemble the continuous glucose monitor data. The spline does not have enough data to infer the physiology necessary to constrain its inferences. In contrast, the DA, leveraging physiologic knowledge, is able to infer glucose dynamics that are impossible to infer according to the sampling theorem, because of the hardcoded physiologic knowledge with very little data.

We use a spline here not because it is the best smoother, although splines are very able smoothers designed to balance goodness of fit against smoothness based on derivatives, but rather to demonstrate the problem machine learning faces when not anchored to a mechanical model: choosing the most probable curve to represent the data according to a cost function sans physiologic constraints with sparse, irregular data may not accurately represent the underlying system. While compressed sensing^70,71offers some hope of coping with inference using sparse data, the sampling theorem^72,73 still poses a fundamental limitation of machine learning with sparse data.

Comparing DA to many other regression methods is complex because DAs often involve iterative estimation of parameters that can start close to or far from optimality. Moreover, DA carries a continuous simulation of the system, while other methods generally do not. But comparisons can still be informative. We compare DA in a next-step prediction task with linear regression and a non-model-based nonlinear regression, Gaussian process regression. These methods iterate through the data set estimating model parameters using the previous N preprandial glucose and carbohydrates to predict postprandial glucose measurements; they then use that model to predict the (N + 1)^th postprandial glucose measurement.

The bottom plot in Figure 3 shows DA compared with linear regression forecasts. The linear regression represents the mean glucose well, but does not capture any oscillatory glycemic behavior, implicating the subtleties of model evaluation. The mean squared error for linear regression is approximately bounded by σ/2, while for DA it can be greater than 2σ, because linear regression approximates the mean response and DA approximates the oscillating trajectory. Because of this, evaluation metrics can have different meanings for different prediction tasks and methods. Table 1 shows forecast errors for the next-step task for linear and Gaussian process regression for different training window lengths, N. While DA outperforms linear regression and Gaussian processes⁷⁷ for this participant, this is not always the case.¹⁵ Moreover, the table shows both mean and root mean squared errors, forecast validation metrics that emphasize different forecast features in their evaluation. The MSE places a greater emphasis on outlier errors, while RMSE places a greater emphasis on approximating the mean. Forecast verification metrics heavily influence forecast machinery evaluation and must be selected based on the goal of the forecasting task;^74,75 it is common and recommended in evaluation analyses to use several verification metrics.

Table 1.

Mean squared error and root mean squared error of next measured glucose for DA, linear regression, and Gaussian process modeling vs. training set size. Comparing the MSE with the RMSE highlights the impacts of selecting different forecast validation metrics.^74,75.The MSE places more weight on outlier or excursion error, whereas the RMSE places more weight on errors associated with estimating the mean, an interpretation that can be seen by comparing the formulas of RMSE and MSE. The DA used here was the unscented Kalman filter without optimizing or carefully selecting parameters estimated; it adjusted the model as new data arrive so the concept of a training set for the DA is not equivalent to the training set of the other two regressions. While the DA is the best forecasting engine for this person, this is not always the case.¹⁵ Moreover, DA forecasting errors can be further reduced by at least 20% if the parameters estimated are more carefully chosen⁷⁶

	N = 5	N = 10	N = 15	N = 20	N = 25
Mean Squared Error
DA	340	340	340	340	340
Linear regression	555	425	380	385	380
Gaussian process	505	405	410	480	490
Root MSE
DA	18	18	18	18	18
Linear regression	24	21	19	20	19
Gaussian process	22	20	20	22	22

Phenotyping the present

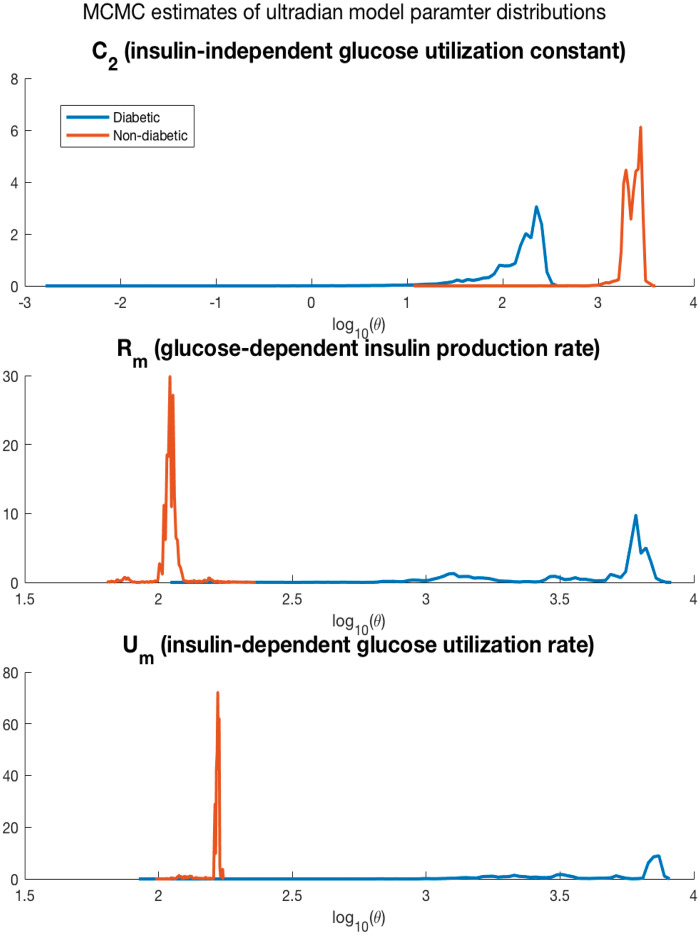
DA can potentially be used for mechanism-based phenotyping, estimating phenotypes composed of features that govern, determine, and directly correspond to patient physiology. In Figure 4, we see the posterior probability densities of the Markov Chain Monte Carlo parameter estimates for the ultradian model for two people, one with type 2 diabetes and one with normal endocrine function. Both Markov chains converge to distinctly different parameter values, or phenotypes relative to the presence of diabetes. The densities in Figure 4 reveal that parameters affecting insulin secretion and insulin-dependent glucose utilization are distinctly different for the diabetic and non-diabetic participant. Uncertainty quantification for parameter estimates can be derived from the parameter estimate densities; eg, the mean and variance of the 2 phenotypes do not overlap. This example, showing only 2 people, is meant only to demonstrate how to use DA to construct higher fidelity phenotypes⁷⁸ rooted in physiologic mechanics.

Figure 4.

Markov chain Monte Carlo-based mechanistic model parameter estimates the Markov chains that minimized the mean square error for a normal person and a person with type 2 diabetes mellitus. The plot shows the distributions of 3 parameters, C₂, an exponential term affecting insulin-independent glucose utilization, R_m, a linear constant affecting insulin secretion, and U_m, a linear constant affecting insulin-dependent glucose utilization. The converged parameters take distinctly different values for each individual, revealing the type 2 diabetes phenotype as mechanistically different with parameters that are difficult to measure. While a full external validation of these phenotypic parameter estimates, the parameters are internally validated by minimizing the mean squared error. This plot shows the potential for DA to produce higher-fidelity, mechanistic-physiology anchored phenotypes.

The foundational ideas of DA are not new—regression, Kalman filters, etc.—but DA has gone mostly unused in biomedical informatics. There are several potential reasons for this, and some reasons that this should change. DA, especially integrated with mechanisms, is not really in the mainstream intellectual lineage of informatics. Similarly, in its linear form—the Kalman filter or linear dynamical system—while extremely powerful, cf. its use for the artificial pancreas or in pacemakers, is also relatively limited and has data requirements that informatics researchers almost never have. When DA is used in medicine, it is often used with the goal of circumventing clinicians and patients with a closed-loop formulation, an approach that is more akin to bioengineering than bioinformatics; again cf. the artificial pancreas or pacemakers. These applications, developed and applied in data-rich environments, did not easily translate to data-poor environment informatics inhabits that include data collected in the course of maintaining health.

Underuse of data assimilation

Similarly, the linear form of DA also lacks the capability to utilize more realistic modeling, a severe limitation, as most physiologic systems and models are nonlinear. This lack of realism also reduced the amount of knowledge incorporated into the system, simultaneously decreasing the functional flexibility and the functional restrictions of the models that often restricted their usefulness. The chief innovation that circumvents these problems, the development of nonlinear filtering techniques, was developed largely away from biomedicine, and certainly away from informatics, within data-rich environments such as robotics. The advent of nonlinear filtering opens the door to methodological innovation, clinical decision innovation, and basic scientific innovation using clinical data. This innovation does not mean that all DA methodology problems are solved; they are not, but DA is in a place now where it can be developed in the informatics context with clinically collected data that were previously believed to be inadequate, noisy, and generally not useful in the DA context. Moreover, to identify and then overcome DA innovations, the interdisciplinary pipeline from bench to machine to bedside is critical. And here the informatics perspective is special—informatics methodological innovations are driven by needs identified while integrating and assembling computational machinery for use in clinical and basic science contexts. It is this sociologic reason, this lack of siloed research approaches, that necessitates informatics adoption of DA.

Limiting factors and next steps

DA’s use of mechanistic models brings limitations as well as advantages. As a regression, DA’s task is to select the most probable curve from those restricted by what is mechanically possible rather than from the set of linear functions or neural networks. If the mechanistic model is too wrong—if the human knowledge or insight is wrong—then the model error will prevent accurate approximation. Furthermore, because the model is created to represent physiology rather than the data scenario, it can have non-identifiable parameters and fail to have a unique set of optimal parameters. And finally, the initial state and parameters matter for DA performance and affect the data requirements—if the starting point of the states or parameters is very wrong, the model will make a poor forecast. In contrast, more flexible methods such as deep learning can approximate nearly any distribution.^79,80 This universal approximator flexibility comes at a cost of substantially greater data requirements, an inability to cope with nonstationary systems, and interpretation difficulties; deep learning also shares some of DA’s identifiability challenges. These approaches are not mutually exclusive and can complement each other.

DA can better serve biomedicine if there are advancements in several areas. Methodological advancements include incorporating clinically meaningful constraints and improving initial parameter seeding, which give DA greater forecasting skill with particularly small data sets. DA can benefit from integrating with machine learning to manage external factors with model errors, such as parameter selection, forecast correction, and model averaging.^15,66,67 Physiological models require development, selection, and refinement, and they may benefit from tailoring to the real-world clinical care data that are available, and they must be created or adapted to meet practical intervention needs. And finally, we must advance our understanding of how to best integrate DA output into scientific, clinical, and self-management workflows. For example, it is not enough to produce a glucose and nutrition-based glucose forecast; the forecast must be made in a way that enables behavioral adaptation. All of these advancements are needed to unlock the potential of DA in a biomedical context.

CONCLUSION

DA is an established way to combine mechanistic knowledge with empirical data. It constrains the search space so that machine learning can proceed in the setting of limited data; eg, using 5 to 20 randomly sampled data points to resolve continuous-time physiology. This is important in medicine because sources of data, such as electronic health records, are often sparse. It allows us to generate predictions, recommendations, smoothed measurements, and otherwise unmeasurable phenotypes. While most mechanistic models may be imperfect, by anchoring them to empirical data, DA adjusts them and keeps them tied to the actual state. In this way, relatively simple models can be highly effective. The ultradian glucose model is very simple but produces accurate forecasts¹⁵ when used within DA.

We present DA here both because it is relatively underused in biomedicine and to encourage further research. While some forms of DA may be mature, more research is needed for using DA in the context of biomedicine in order to handle sparse, potentially biased data and to deliver forecasts and recommendations within clinical settings.

FUNDING

This work was funded by grants from the National Institutes of Health R01 LM006910 “Discovering and applying knowledge in clinical databases,” U01 HG008680 “Columbia GENIE (GENomic Integration with EHR),” and “Mechanistic machine learning,” LM012734.

Conflict of interest statement. None.

CONTRIBUTORS

All authors made substantial contributions to the conception and design of the work; DJA wrote the original draft and all authors revised it critically for important intellectual content; had final approval of the version to be published; and agreed to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.