Biased Inference of Selection Due to GC-Biased Gene Conversion and the Rate of Protein Evolution in Flycatchers When Accounting for It

Abstract

The rate of recombination impacts on rates of protein evolution for at least two reasons: it affects the efficacy of selection due to linkage and influences sequence evolution through the process of GC-biased gene conversion (gBGC). We studied how recombination, via gBGC, affects inferences of selection in gene sequences using comparative genomic and population genomic data from the collared flycatcher (Ficedula albicollis). We separately analyzed different mutation categories (“strong”-to-“weak,” “weak-to-strong,” and GC-conservative changes) and found that gBGC impacts on the distribution of fitness effects of new mutations, and leads to that the rate of adaptive evolution and the proportion of adaptive mutations among nonsynonymous substitutions are underestimated by 22–33%. It also biases inferences of demographic history based on the site frequency spectrum. In light of this impact, we suggest that inferences of selection (and demography) in lineages with pronounced gBGC should be based on GC-conservative changes only. Doing so, we estimate that 10% of nonsynonymous mutations are effectively neutral and that 27% of nonsynonymous substitutions have been fixed by positive selection in the flycatcher lineage. We also find that gene expression level, sex-bias in expression, and the number of protein–protein interactions, but not Hill–Robertson interference (HRI), are strong determinants of selective constraint and rate of adaptation of collared flycatcher genes. This study therefore illustrates the importance of disentangling the effects of different evolutionary forces and genetic factors in interpretation of sequence data, and from that infer the role of natural selection in DNA sequence evolution.

Introduction

The relative role of different evolutionary forces and genetic factors that determine rates and patterns of sequence evolution is a long-standing question in molecular evolution (Gillespie 1984; Kimura 1991; Nei 2005). One important factor is the mutation rate (μ), which is the rate at which new genetic variants enter a population. The fitness effect of a particular mutation governs the direction and strength of natural selection acting on it, and is represented by the relative selection coefficient (s). The effective population size (N_e) determines the strength of genetic drift, where small populations will experience stronger drift than larger populations (Wright 1931). Together, N_e and s affect the fate of new mutations and, consequently, variation in any of those factors leads to variation in the rate of sequence evolution (Charlesworth 2009). In addition, the environment and temporal fluctuations in the environment determine the shape and stability of the fitness landscape of a population and hence the distribution of fitness effects (DFE) of new mutations. There is a higher probability that any new mutation is advantageous if a population is far away from its fitness optimum. Conversely, if a population is close to its fitness optimum, the probability that a mutation is advantageous is very low (Fisher 1930; Orr 2005; Lourenco et al. 2013).

In addition to variation among populations, any regional variation in μ, N_e, and s in the genome will lead to variation in evolutionary rates among genes (Eyre-Walker and Keightley 2007). One important factor associated with this variation is the local recombination rate. Variation in recombination rate along the genome influences the rate of protein evolution through two distinct processes: GC-biased gene conversion (gBGC) (Duret and Galtier 2009; Mugal et al. 2015) and Hill–Robertson interference (HRI) (Hill and Robertson 2007). gBGC is a process that takes place during meiotic recombination, at sites heterozygous for one “weak” (W) and one “strong” (S) allele, and increases the probably of fixation of S over W alleles (strong or weak in the sense of the number of hydrogen bonds between the two nucleotides within base pairs, i.e., three between G and C and two between A and T). As a consequence, the W-to-S substitution rate is elevated in high-recombination regions (since gene conversion is a form of recombination) at the same time as the S-to-W substitution rate is reduced. HRI occurs when different targets of selection are genetically linked, making natural selection less efficient and leading to an increase in the fixation rate of slightly deleterious alleles and a decrease in the fixation rate of advantageous alleles. Recombination breaks up physical linkage between selected sites and counteracts HRI, and thereby increases the efficacy of both negative and positive selection. The effect of HRI is thus most pronounced in genomic regions with low recombination.

The strength and direction of selection on protein evolution are further influenced by patterns of gene expression and individual properties of proteins (Pal et al. 2006; Zhang and Yang 2015). For example, a correlation between gene expression level and the strength of purifying selection has been reported in diverse taxa (Pal et al. 2001; Krylov et al. 2003; Rocha and Danchin 2004; Drummond and Wilke 2008). Proteins have been found to evolve under strong selective constraint if the level of pleiotropy is high (Krylov et al. 2003; Zhang and Li 2004; He and Zhang 2006). In line with this, genes that are broadly expressed or whose gene products are involved in a high number of protein–protein interactions (PPI) are under stronger negative selection than other genes (Pal et al. 2006; Drummond and Wilke 2008; Zhang and Yang 2015). In addition, elevated rates of protein evolution have been reported for genes that show sex-biased expression (reviewed in Ellegren and Parsch 2007), potentially as a result of sexual selection (Grath et al. 2009; Ávila et al. 2015). Nevertheless, the relative importance of the genomic location and individual protein properties on protein sequence evolution remains an open question. A better understanding of how these factors interact can ultimately help us to understand how populations respond to environmental changes.

Rates of protein evolution are frequently measured by the d_N/d_S ratio (commonly denoted as ω), which quantifies the strength of selection in protein-coding genes as judged from sequence divergence between two or more lineages (Goldman and Yang 1994; Muse and Gaut 1994). The incorporation of information on the frequency of synonymous and nonsynonymous polymorphisms within a population in a McDonald–Kreitman test (MK-test) framework allows to compute an expected value of ω (McDonald and Kreitman 1991). Some methods derived from the MK-test use this information to estimate the DFE of new mutations (Eyre-Walker et al. 2006; Eyre-Walker and Keightley 2007; Keightley and Eyre-Walker 2007; Eyre-Walker and Keightley 2009). Under the assumption that advantageous mutations reach fixation so fast that they are rarely observed as polymorphisms, the DFE provides an expected value of ω for nonadaptive substitutions (ω_na) (Keightley and Eyre-Walker 2007). The difference between ω and ω_na can then be attributed to the rate of adaptive substitutions (ω_a). Further, based on ω_na and ω_a, the proportion of adaptive substitutions (α) can be derived (Eyre-Walker 2006; Eyre-Walker and Keightley 2009).

It should be noted that α must not be interpreted as the rate of adaptation, as it depends on both ω_a and ω_na. Low α can simply reflect fast accumulation of effectively neutral nonsynonymous substitutions (Lourenco et al. 2013; Williamson et al. 2014; Galtier 2016). Since N_e determines the efficacy of selection, we expect a negative relationship between N_e and ω_na, which should lead to a correlation between N_e and α irrespective of if the rate of adaptation increases with N_e. Therefore, ω_a may be a better measure of the strength of positive selection than α (Lourenco et al. 2013). If the DFE is independent of N_e, we expect to see a correlation between N_e and ω_a. This means that populations with larger N_e should have higher rates of adaptation, which is supported by some studies (Gossmann et al. 2010; Strasburg et al. 2011). However, in large comparisons of animal (Galtier 2016) and plant taxa (Gossmann et al. 2010), no evidence was found to support the idea that adaptive substitutions would accumulate faster in larger populations. Further analyses are needed to clarify these conflicting results and to help elucidating the relative impact of genomic features of genes and of individual protein properties in determining rates of adaptive and nonadaptive protein evolution (Pal et al. 2006; Charlesworth and Campos 2014).

In this study, we investigate the relative importance of negative and positive selection on protein evolution in an avian lineage, the lineage leading to collared flycatcher (Ficedula albicollis) since its split from the zebra finch (Taeniopygia guttata) lineage ∼21 Ma (Moyle et al. 2016). The collared flycatcher is a small bird of the order Passeriformes (the most species-rich clade of birds) that mainly breeds in deciduous forests in southeastern Europe and winters in sub-Saharan Africa. Recent findings indicate that recombination rate variation, through the process of linked selection, strongly affects patterns of genetic diversity and differentiation in the flycatcher genome (Burri et al. 2015; Dutoit et al. 2017; Kawakami et al. 2017). There is also evidence that recombination rate variation via gBGC has a strong impact on protein coding sequence evolution in the collared flycatcher (Bolívar et al. 2016), in agreement with studies of other birds (Mugal et al. 2013). More specifically, divergence data showed that both synonymous and nonsynonymous W-to-S substitution rates were positively correlated with recombination rate, while S-to-W rates were negatively correlated. GC content varies considerably along the flycatcher genome and is strongly associated with recombination rate. The current GC content is not at its equilibrium and appears to be increasing at nonsynonymous and, even more so, at synonymous sites. As a consequence, gBGC has a higher impact on synonymous than on nonsynonymous sites, leading to a negative association between d_N/d_S and recombination rate (Bolívar et al. 2016). Analyses of polymorphism data showed an excess of high frequency derived alleles for W-to-S polymorphisms but an opposite trend for S-to-W polymorphisms. Moreover, polymorphism data were dominated by S-to-W polymorphisms, and divergence data by W-to-S substitutions.

While there is clear evidence that signatures of gBGC are pronounced in the collared flycatcher genome, it is still unclear how gBGC interacts with the direction and efficacy of selection acting on protein-coding sequences, and which other factors may play a role in protein evolution. To address these questions we aimed to dissect the interplay between selection and gBGC in more detail and to investigate the relationship between the efficacy of natural selection in protein-coding genes and several genomic factors after accounting for gBGC. These analyses show that gene expression level, sex-bias in expression and the number of protein–protein interactions, but not HRI, are strong determinants of both the rate of protein evolution and the rate of adaptation in this avian lineage.

Results

Using branch-specific estimates of divergence based on a three-species-alignment with zebra finch and chicken, and polymorphism data from resequencing of a population sample of 20 collared flycatchers, we obtained multiple measures of selection in the flycatcher lineage. Genome-wide estimates, based on all mutations, of the ratio of nonsynonymous to synonymous diversity (π_N/π_S) and ω were 0.160 (99% confidence interval, CI, 0.159–0.162) and 0.144 (0.143–0.144), respectively, where the larger value of π_N/π_S than of ω indicates a prevalence of slightly deleterious mutations. We computed the site frequency spectrum (SFS) for synonymous and nonsynonymous polymorphisms in order to estimate the DFE for nonsynonymous mutations and found that 77.8% (77.7–78.0) mutations were strongly deleterious (N_es > 10), 8.9% (8.7–9.0) were deleterious (1 < N_es < 10) and 13.3% (13.0–13.6) were slightly deleterious or effectively neutral (N_es <1). By contrasting the estimates of the DFE and ω, we obtained an estimate of ω_a of 0.025 (0.023–0.027) and found that 18% (16.4–18.8) of nonsynonymous substitutions have been fixed in the flycatcher lineage due to positive selection (α). A major question in this study was now if these estimates of selection may be biased by gBGC.

gBGC Impacts Inferences of Selection of Protein Coding Sequences in the Collared Flycatcher

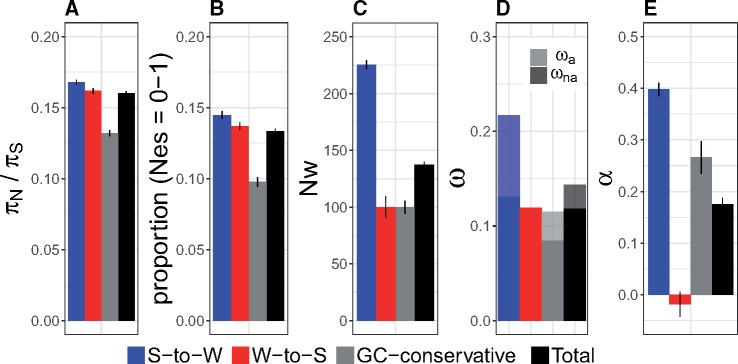
The substitution rate at synonymous sites is more strongly affected by gBGC than the rate at nonsynonymous sites in the flycatcher lineage (Bolívar et al. 2016). As a consequence, ω is not only given by selection and drift but also by gBGC. Therefore, it cannot be excluded that gBGC similarly influences other measures of selection and could lead to biased conclusions. In order to assess the impact of gBGC on the inference of selection, we separately estimated π_N/π_S, the DFE, ω, ω_a, and α for the three mutation categories S-to-W, W-to-S, and GC-conservative changes. Figure 1 illustrates that all measures of selection were strongly influenced by gBGC, and this was most clear at the time scale of fixed differences (ω, ω_a, and α exhibited more pronounced differences between mutation categories than π_N/π_S or the proportion of effectively neutral mutations). Using results from GC-conservative changes as a reference, ω was higher by 27% when estimated using all changes (0.144 vs. 0.113), α was 33% lower (0.180 vs. 0.270), and ω_a was 22% lower (0.025 vs. 0.032). In other words, gBGC had the effect of leading to a significant underestimation of the amount of adaptive evolution.

Fig. 1.

Estimates of six different test statistics and 99% confidence intervals for different mutation categories: S-to-W (blue), W-to-S (red), GC-conservative (gray), and all sites (“Total”; black). (A) π_N/π_S, (B) proportion (N_es = 0–1), that is, the proportion of nonsynonymous mutations for which N_es < 1, (C) N_w: the weighted change in N_e relative to 100, (D) ω, with the proportion of ω represented by ω_na and ω_a shown in bold and light color, respectively, and (E) α.

The effect of gBGC on segregating polymorphisms mirrored the effect of demographic changes. This had the consequence that different demographic scenarios were inferred for different mutation categories despite them obviously sharing the same evolutionary history (fig. 1C; note that N_w is the weighted change in N_e relative to 100). Specifically, the best-fit demographic model for the S-to-W mutation category was a population expansion, which is characterized by a relative increase of low frequency variants (a left skew of the SFS). Although the best-fit model for the W-to-S mutation category was a constant population size, the one-step model inferred a population contraction (data not shown), characterized by a relative increase of intermediate and high frequency alleles (a right skew of the SFS). Furthermore, the demographic effect was stronger in high recombination regions for both S-to-W and W-to-S categories than in low recombination region. The demographic model for GC-conservative polymorphisms fell between the demographic model for S-to-W and W-to-S mutations, with either no or only a modest change in population size (supplementary table S1, Supplementary Material online). These observations can be explained by that gBGC decreases the fixation probability of S-to-W while increases it for W-to-S polymorphisms, and that the effect increases with recombination rate.

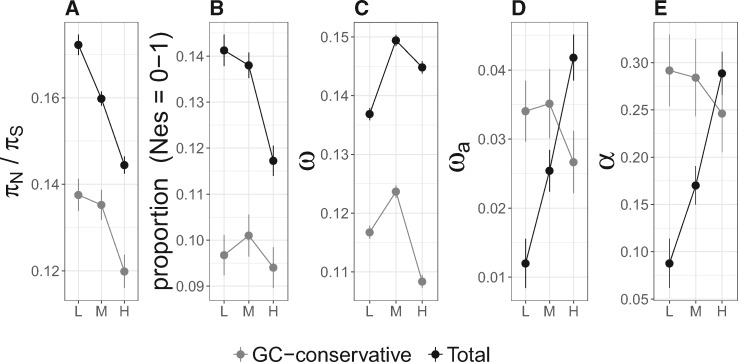
In light of the above, the interpretation of measures of selection needs careful consideration in the presence of gBGC. To overcome the effects of gBGC, a safe alternative should be to base inferences on data from the GC-conservative mutation category only. We illustrate this by comparing the outcome of analyses based on GC-conservative changes with analyses based on all changes in genomic regions with low, medium, and high recombination rate, respectively. HRI would predict that selection is more efficient in high recombination regions. Using GC-conservative changes, we observed a weak negative relationship between recombination rate and π_N/π_S, and no relationship between recombination rate and the proportion of effectively neutral mutations. In contrast, distinct relationships were seen when analyzing all changes (fig. 2A and B). The relationships between either of ω, ω_a, or α, and recombination rate showed no clear trend for GC-conservative changes (fig. 2C–E). In contrast, we observed a positive relationship between all these selection parameters and recombination rate for all changes. Hence, a “conventional” analysis using all changes would suggest that the efficacy of positive selection increases with increasing recombination rate in this avian lineage, following HRI predictions. However, this seems entirely due to the effect of gBGC (fig. 2D and E). Our results therefore indicate that the rate of adaptive evolution is not correlated with local variation in N_e, as this can be approximated by the recombination rate.

Fig. 2.

Estimates of five different test statistics and 99% confidence intervals for genes in low (L), mid (M), and high (H) recombination environments for different mutation categories: GC-conservative (gray) and all sites (“Total”; black). (A) π_N/π_S, (B) proportion (N_es = 0–1), that is, the proportion of nonsynonymous mutations for which N_es < 1, (C) ω, (D) ω_a, and (E) α.

Identification of Determinants of the Rate of Protein Sequence Evolution in the Collared Flycatcher

In order to further understand which factors influence estimates of selection in the collared flycatcher, we investigated the relationship between ω and different genomic factors and protein properties in a multiple linear regression (MLR) analysis. In these gene-by-gene analyses, we estimated ω using all mutation categories due to an otherwise low signal-to-noise ratio. First, we assessed the relationship between ω and the level of gene expression in eight different organs. We observed a significant negative correlation in all organs except of testis (supplementary table S2, Supplementary Material online), with the strongest correlation seen for gene expression in the brain. As expression level between organs was highly correlated (data not shown), we focused on brain in all further analyses. We fitted a MLR model including expression level in brain, expression breadth, sex-bias in expression, the number of PPI (an indicator of network centrality), and recombination rate as candidate explanatory variables. The MLR analysis indicated that expression level, the number of PPI and sex-bias in expression were the most important determinants of ω. The effect of recombination rate was only marginally significant and expression breadth was not significant (table 1).

Table 1.

Results from a Multiple Linear Regression Analysis between ω and Different Explanatory Variables.

Variable	Estimate	P value
Expression level in brain	−4.07×10−4	<2.2×10−16***
Protein–protein interactions	−3.76×10−5	3.37×10−4***
Female-biased expression	−2.01×10−2	5.18×10−5***
Male-biased expression	2.11×10−2	1.94×10−4***
Recombination rate	−1.00×10−3	0.08
Expression breadth	1.41×10−2	0.27
Adjusted R-squared	0.053	<2.2×10−16 ***

^***Statistical significance at P < 0.001 level.

To account for gBGC, we investigated the relationship between several measures of selection and the factors that showed significant effect on ω in the MLR analysis for GC-conservative changes only. To do this and at the same time obtain a reasonable signal-to-noise ratio, we categorized genes into a small number of bins based on each explanatory variable (two or three bins per analysis, supplementary table S3, Supplementary Material online). Expression level showed a strong negative relationship with π_N/π_S (supplementary fig. S1A, Supplementary Material online) and also with the proportion of sites with N_es = 0–1 (supplementary fig. S1B, Supplementary Material online), indicative of an increase of selective constraint with level of gene expression. In addition, the strength of positive selection (ω_a and α) showed a strong positive relationship with level of gene expression (supplementary fig. S1C and D, Supplementary Material online). We observed similar trends for groups of genes binned with respect to the number of PPI (supplementary fig. S2, Supplementary Material online). Furthermore, we explored the relationship between measures of selection and sex-bias in gene expression, using data from gonads (supplementary fig. S3, Supplementary Material online). Male-biased genes, but not female-biased genes, showed larger π_N/π_S than unbiased genes, a larger proportion of sites with N_es = 0–1, and higher estimates of ω. Both female- and male-biased genes showed higher ω_a and α compared with unbiased genes, which indicates that sex-biased genes have a higher rate of adaptation and a larger fraction of adaptive substitutions than unbiased genes. Overall, these results are in good agreement with the MLR analysis and support the hypothesis that expression level, PPI, and sex-bias in gene expression influence protein evolution in the collared flycatcher, both in terms of constraint and the rate of adaptation.

Detection of Positively Selected Genes

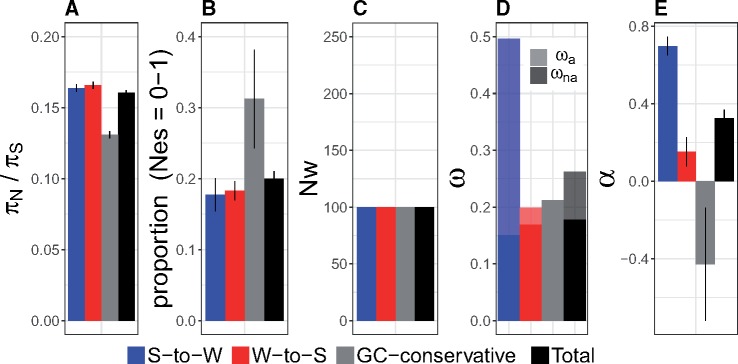
Branch-site tests for genes evolving under positive selection in the flycatcher lineage were performed on a set of 4,855 genes based on a 10-species alignment of different bird species (see Materials and Methods). Based on a FDR of 5%, 79 candidate genes were identified. This test does not distinguish between substitutions of different mutation categories. Since, to our knowledge, branch-site tests that specifically analyze GC-conservative changes are not available, we supplemented the analysis by a comparison of measures of selection based on GC-conservative changes in the candidate genes (fig. 3) with the genome-wide average (fig. 1). As expected, estimates of ω were on average higher for genes identified as positively selected using branch-site tests than the genome-wide average. However, these candidate genes also had higher estimates of π_N/π_S and a higher proportion of sites with N_eS = 0–1, indicative of relaxed selective constraint. Figure 3 shows that putatively positively selected genes had lower estimates of ω_a and α for GC-conservative changes than for all mutations together. This seems to be a result of particularly high estimates of ω_a and α for S-to-W changes in candidate genes. This indicates that putatively positively selected genes evolve under relaxed selective constraint, and might actually represent false positives due to biases induced by gBGC. Evidence for false positives due to gBGC has also been observed in primates, where the prevalence of W-to-S substitutions (and not S-to-W substitutions) at lineage-specific accelerated loci has been identified as a potential problem (Berglund et al. 2009; Galtier et al. 2009). In light of our findings, we therefore raise caution that gBGC can bias inferences of selection in complex ways, and that many inferred positively selected genes may represent false positives from which misleading interpretations can be made.

Fig. 3.

Estimates of six different test statistics and 99% confidence intervals for different mutation categories for genes identified as positively selected: S-to-W (blue), W-to-S (red), GC-conservative (gray), and all sites (“Total”; black). (A) π_N/π_S, (B) proportion (N_es = 0–1), that is, the proportion of nonsynonymous mutations for which N_es < 1, (C) N_w: the weighted change in N_e relative to 100, (D) ω, with the proportion of ω represented by ω_na and ω_a shown in bold and light color, respectively, and (E) α.

Discussion

gBGC Biases Inferences of the Direction and Strength of Selection

Our results based on diversity and divergence data in an avian lineage add to a growing body of evidence that gBGC impacts rates of protein evolution and may bias inferences of the direction and efficacy of natural selection (Galtier et al. 2009; Ratnakumar et al. 2010; Lartillot 2013; Bolívar et al. 2016; Corcoran et al. 2017). For example, our study illustrates that the proportion of nearly neutral mutations inferred from polymorphic data differ for different mutation categories. The same was true for measures of the strength of selection that rely on estimates of sequence divergence, such as ω, ω_a, and α. In general, the observed differences can be explained by gBGC, but the effect is complex. The underlying model assumption of the different test statistics for selection that rely on the comparison between nonsynonymous and synonymous sites, such as the DFE, ω, ω_a, and α, is that synonymous mutations evolve neutrally. Prevalence of selection on codon usage (SCU) could therefore further bias inferences of selection.

Shifts in the synonymous SFS for different mutation categories mirrored the effect of demographic changes, with opposite effects for W-to-S and S-to-W categories. The demographic model for GC-conservative polymorphisms was intermediate to the demographic model for S-to-W and W-to-S polymorphisms, without strong evidence for change in population size. A stronger effect was observed in high than in low recombination regions (both with and without filtering of CpG-prone sites). These observations are consistent with gBGC. Moreover, similar shifts were observed for nonsynonymous mutations (Bolívar et al. 2016), which provides evidence that shifts in the SFS are not caused by SCU, but by a mechanism operating to increase GC content at synonymous and nonsynonymous positions, such as gBGC. Therefore, if there is SCU, it is masked by a more conspicuous effect of gBGC as observed in other species (Galtier et al. 2018).

With gBGC, nonsynonymous W-to-S mutations should show the highest proportion of slightly deleterious alleles, as these mutations will be “favored” by gBGC. On the contrary, nonsynonymous S-to-W mutations should show the lowest proportion of slightly deleterious alleles segregating as gBGC decreases the probability of fixation of this category of mutations. Accordingly, GC-conservative changes should show intermediate values. However, given that inferences of the proportion of slightly deleterious alleles are based on the contrast between nonsynonymous and synonymous mutation, the mentioned predictions are only valid under the assumption that synonymous mutations are not affected by gBGC (within each mutation category and bin). This assumption is not met in the collared flycatcher (Bolívar et al. 2016). On the contrary, synonymous sites seem to be more strongly affected by gBGC, as the current GC is farther away from its equilibrium value. Since synonymous and nonsynonymous sites are differently affected by gBGC, the demographic correction either underestimates (in the case of S-to-W) or overestimates (in the case of W-to-S) the efficacy of selection. Therefore, the respective DFE for S-to-W and W-to-S mutations, as well as for all mutations, are biased partly because of a real effect of gBGC on nonsynonymous mutations and partly because of an overcorrection due to a stronger effect of gBGC on synonymous mutations. Tearing these two aspects apart is not trivial. Similarly, we show that estimates of ω, ω_a, and α are higher for S-to-W mutations, whereas they are lower for W-to-S mutations, although the latter effect is more modest. Estimates of ω are higher, and those of ω_a and α are lower, based on all mutations compared with estimates based on GC-conservative changes only. In our study species, ω_a and α are thus likely to be underestimated in conventional analyses using all sequence data. It is reasonable to expect that similar biases would occur in other organisms where gBGC is prevalent.

As GC-conservative changes are not affected by gBGC, they should represent the most appropriate category of substitutions to use in analyses of selection and, for example, the relationship between selection and recombination. The negative relationship between ω and recombination rate seen when implementing a regular codon branch-specific model in PAML (Bolívar et al. 2016) was less evident when based on the L95 model implemented in bio++, which allows for nonstationary base composition. This highlights the importance of the applied models; allowing for nonequilibrium conditions alleviates biases in evolutionary rate estimation (Kaehler 2017; Guéguen and Duret 2018) and enables more accurate assessment of the impact of gBGC. Moreover, the increased efficacy of positive selection with increased recombination rate indicated in this study using all sequence data is probably not correct, as the relationship was not detected with GC-conservative changes only. Furthermore, genes falling into the high-recombination bin showed on an average lower estimates of α for GC-conservative changes than for all mutations together. It thus seems that while α on an average is larger based on GC-conservative changes, not all genes follow this trend. Our analysis suggests that the relative contribution of S-to-W versus W-to-S changes to estimates of α is responsible for the observed difference. The W-to-S contribution can explain the lower α when analyzing all mutations compared with GC-conservative changes only (fig. 1). On the other hand, the genes identified as positively selected using branch-site tests (fig. 3) showed lower estimates of α for GC-conservative changes than for all mutations together due to a strong contribution of S-to-W changes to estimates of α.

High Degree of Selective Constraint and Low Proportion of Adaptive Substitutions in Protein Coding Genes in the Collared Flycatcher

Our results indicate a prevalent role of purifying selection, that is, a high degree of selective constraint, in gene sequence evolution in the flycatcher lineage. Only 10% of segregating nonsynonymous mutations were estimated to be effectively neutral (based on GC-conservative changes; 13% based on all mutations). Compared with some well-studied animal model organisms, this estimate lies in between that observed in D. melanogaster (5–6%) and humans (21–34%) (Keightley and Eyre-Walker 2007; Halligan et al. 2010), which is consistent with long-term N_e of collared flycatchers (∼4 × 10⁵ in the study population) (Nadachowska-Brzyska et al. 2016) being larger than in humans (∼10⁴), but smaller compared with Drosophila (∼10⁶) (Charlesworth 2009; Halligan et al. 2010). The fraction of effectively neutral mutations in flycatcher is similar to that estimated for mice (Mus musculus) (10–17%), which also has similar N_e (∼6 × 10⁵) (Halligan et al. 2010; Kousathanas and Keightley 2013).

Our estimate of α indicates that a rather low proportion of nonsynonymous substitutions have been fixed by positive selection (α = 0.27 based on GC-conservative changes, 0.18 based on all mutations). This value is comparable or lower to what has previously been estimated for other birds and reptiles (Axelsson and Ellegren 2009; Galtier 2016). It is in the same range as reported for humans (0.13–0.31), but lower than for Drosophila (> 0.5) and mice (0.29–0.57) (Halligan et al. 2010, 2013; Kousathanas and Keightley 2013). It is important to remember that α is a relative measure and it is therefore problematic to use it for comparisons of the strength of positive selection in different lineages. It strongly depends on ω_na, which may often differ between species. However, also the estimate of ω_a of 0.03 for the collared flycatcher (based on GC-conservative changes; 0.025 based on all mutations) is smaller than estimates observed for several other species of birds and reptiles, which are all >0.08 (Galtier 2016). Since estimates specifically based on GC-conservative changes are rarely available, we cannot make broad-scale comparisons with other species. Variation in the strength of gBGC and in the temporal stability of the recombination landscape between species might bias comparisons. Conclusions on how the rate of adaptive evolution varies among species might thus need careful reconsideration. However, recently reported estimates of selection based on GC-conservative changes in another passerine bird, the great tit (Parus major), indicate similar efficacy of selection as in flycatchers (Corcoran et al. 2017). Estimates of the proportion of effectively neutral mutations (∼10%), ω_a (∼0.03), and α (∼0.22) in the great tit are similar to the collared flycatcher estimates, consistent with similar N_e of the two species (Laine et al. 2016).

There are obviously biological factors other than differences in N_e that may result in differences in the DFE, α, and ω_a among species. For example, differences in the shape of the fitness landscape may cause the DFE to differ between species even if they have similar N_e. The distance of the population to the fitness optimum will determine the average selection coefficient of new mutations, affecting the DFE and therefore also α and ω_a (Lourenco et al. 2013; Huber et al. 2017).

Expression Level, the Number of PPI and Sex-Bias in Expression, but Not HRI, Modulate the Efficacy of Selection

We found no clear relationship between recombination rate and either ω, ω_a, or α, when analyzing GC-conservative changes only. This suggests that HRI plays a minor role in determining genome-wide rates of protein evolution and that variation in local N_e does not drive intragenomic variation in ω_a or α in Ficedula flycatchers. Alternatively, given a lower mutation rate for GC-conservative than for other changes (supplementary table S4, Supplementary Material online), our power to detect these relationships may not have been sufficient. Moreover, our binning approach only considered three recombination categories, where the average recombination rate of the low recombination regions was 0.77 cM/Mb. It is therefore possible that HRI occurs in regions with lower recombination rate, but is not detected by this binning approach. Our results therefore do not exclude the presence of HRI, but suggest that gBGC has a stronger impact on genome-wide patterns of divergence and diversity in flycatchers. Nonetheless, the absence of a strong HRI signal is an unexpected observation. In contrast to many other organisms, the recombination landscape of avian lineages has been shown to be stable across millions of years (Singhal et al. 2015). An evolutionary stable recombination landscape allows for signatures of gBGC to accumulate over time. Similar, signatures of HRI may be more evident in evolutionary stable low-recombining regions. Interestingly, and in contrast to our findings in the collared flycatcher, it was suggested that recombination rate is a key factor that modulates the efficacy of selection in another passerine bird, the great tit (Gossmann, Santure, et al. 2014). Evidence for HRI was still observed after accounting for gBGC (Corcoran et al. 2017). These conflicting results suggest that the impact of recombination on the efficacy of selection varies between species (e.g., related to changes in N_e through time), and that generalizations among taxa might not be justified.

Our results indicated strong relationships between all estimated measures of selection and gene expression level as well as the number of PPI. A correlation between functional constraint and protein properties has been reported for several taxa (reviewed in Pal et al. 2006; Zhang and Yang 2015); genes that are highly expressed or part of several protein complexes or metabolic pathways accumulate fewer slightly deleterious alleles compared with other genes. Similar results have been reported in other passerine bird species (Gossmann, Santure, et al. 2014). Besides, we observed that gene expression level and PPI were positively correlated with ω_a and α, which suggests that highly expressed genes and genes part of several protein complexes have a higher rate of adaptation and a larger fraction of adaptive substitutions. Alternatively, this may indicate that particularly pronounced SCU leads to an overestimation of positive selection (ω_a and α) in these genes. If SCU is strong in these genes, it could explain lower estimates of d_S in highly expressed genes (supplementary fig. S4B, Supplementary Material online), and higher values of d_N/d_S could falsely be interpreted as stronger signature for adaptive evolution (Matsumoto et al. 2016). Similar to previous reports across different taxa (Gossmann, Schmid, et al. 2014; Lipinska et al. 2015; Yang et al. 2016) we also found that both female- and male-biased genes have higher rates of adaptation (higher estimates of ω_a) compared with unbiased genes. Male-biased genes seemed to evolve under weaker selective constraint compared with female-biased and unbiased genes (lower π_N/π_S). Since sexual selection is typically more pronounced in males than in females (Clutton-Brock 2007; Harrison et al. 2015), this could lead to stronger signatures of sexually antagonistic selection on male-biased than on female biased genes (Harrison et al. 2015). This might explain the observed differences in π_N/π_S between female- and male-biased genes.

In summary, we have investigated which factors determine rates of protein evolution in the temporally stable recombination environment of the collared flycatcher genome. There is evidence that rates, and evolutionary conclusions based on these rates, are strongly impacted by gBGC. Specifically, we observed that the strength of selection was underestimated when all sequence data were used and that a more unbiased picture was given when only analyzing GC-conservative changes, which are not affected by gBGC. Our study therefore highlights the importance of taking gBGC into account when analyzing genome-wide patterns of selection, especially for making comparison between taxa where the strength of gBGC may vary. We further show that individual protein properties—gene expression level, the number of PPI and sex-biased gene expression—are important determinants of both the strength of negative and positive selection in the collared flycatcher.

Materials and Methods

Coding Sequence Divergence

Alignments of one-to-one orthologous sequences between collared flycatcher, zebra finch, and chicken (Gallus gallus) were retrieved from Bolívar et al. (2016). Briefly, Ensembl version 73 (Flicek et al. 2014) sequences were aligned with PRANK v.140603 (options: +F, translate) (Loytynoja and Goldman 2005) and filtered using the GUIDANCE/HOT algorithm (codon model, column cutoff =0.99) (Landan and Graur 2007; Penn et al. 2010). Gene-by-gene estimates of ω were obtained by fitting a free-ratio model in PAML v.4.6 (Yang 1997). In addition, estimates of the number of nonsynonymous and synonymous substitutions for different mutation categories (S-to-W, W-to-S, GC-conservative, as well as all changes) were based on concatenated alignments (i.e., bins of genes) using the L95 model (Lobry 1995) implemented in the package BppML in the Bio++ suite of programs (Dutheil and Boussau 2008). In this case, we used 0- and 4-fold degenerated sites as proxies for nonsynonymous and synonymous sites, respectively. We excluded all genes with a coding sequence length shorter than 200 base-pairs, genes with unknown genomic location, sex-linked genes, and genes in microchromosomes with <5 Mb of assembled sequence (chromosomes LGE22, 25, and Fal35) according to the FicAlb1.5 assembly version of the collared flycatcher genome (Kawakami et al. 2014). This resulted in a set of 7,919 genes. In order to compute the number of divergent sites and the number of sites per mutation category, we first computed the total number of G + C and, A + T sites, as well as the total number of 0- and 4-fold degenerated sites in the collared flycatcher. The number of S-to-W, W-to-S, and GC-conservative sites is equal to the number of G + C, A + T, and total number of nucleotides, respectively. This is because the number of possible S-to-W and W-to-S changes is determined by the GC and AT content, respectively. The number of divergent sites of each mutation category was then calculated by multiplying the number of sites of the respective category by the respective substitution rate estimated by BppML. The number of divergent sites in each mutation category is provided in supplementary table S4, Supplementary Material online.

Coding Sequence Diversity

We obtained single-nucleotide polymorphisms (SNP) from these 7,919 genes based on whole-genome resequencing data from 20 unrelated individuals of an Italian collared flycatcher population; information regarding data collection and processing is described in detail in (Burri et al. 2015). Briefly, whole-genome Illumina reads were mapped to the collared flycatcher genome assembly (version FicAlb1.5) using BurrowsWheeler Aligner 0.7.4 (bwa-mem) (Li and Durbin 2009). The Genome Analysis Toolkit (GATK) 2.8-1 (McKenna et al. 2010) was used for variant calling. Base Quality Score Recalibration and variant quality score recalibration were applied. In addition to the variant calling and filtering criteria described in Burri et al. (2015), we removed sites with a mean mapping quality <20 or variant quality <15, sites from overlapping transcripts, and sites that showed more than two alleles. We discarded genotypes with lower coverage than 5× per individual and sites for which we had <12 genotypes (i.e., 24 allele copies) sampled. To estimate the site frequency spectra (SFS) and π_N/π_S, we randomly sampled 24 alleles at every site to make sample size equal among sites. We restricted our analysis to over 2.6 million 0-fold and 0.4 million 4-fold degenerated sites as representatives for nonsynonymous and synonymous sites, respectively. This resulted in a set of 9,528 SNPs, that is, an average of 1.2 SNPs per gene.

The number of SNPs in each mutation category is provided in supplementary table S4, Supplementary Material online. For polarization of W-to-S and S-to-W polymorphisms we used available genotype information from two outgroup flycatcher species, Ficedula parva and F. hyperythra (Burri et al. 2015). Following Bolívar et al. (2016), we defined the ancestral state as the allele shared by at least two out of the three species, discarding sites where more than one species was polymorphic. The number of 0- and 4-fold degenerate sites of each mutation category was calculated from the ancestral Ficedula sequence. Specifically, the number of S-to-W, W-to-S, and GC-conservative sites is equal to the number of G + C, A + T, and total number of 0- and 4-fold degenerate sites, respectively.

We excluded 22,212 CpG and CpG-prone sites (i.e., CA, TG, and CG, as well as potential CpG sites such as NG and CN) from the ancestral sequence in order to avoid problematic polarization and inferences based of sites affected by CpG-hypermutability (Hernandez et al. 2007); the impact of CpG filtering is illustrated in supplementary figure S5 and table S1, Supplementary Material online. Moreover, signatures of negative selection on synonymous and/or nonsynonymous CpG-prone sites could be confounded with the signature of gBGC on S-to-W changes, making the interpretation of the results more difficult. Since we were interested in the relative impact of gBGC between different mutation categories, it was therefore reasonable to exclude CpG-prone sites. Furthermore, selective constraint on CpG sites may also affect GC-conservative mutations. Note that the relative proportion of CpG sites overlapping with synonymous and nonsynonymous sites may differ and may vary among genes (Suzuki et al. 2009; Ying and Huttley 2011), which could lead to biases in the selection statistics that are based on the comparison between the two site classes.

Estimation of the Distribution of Fitness Effects, ω_a, and α

The DFE was estimated using the DFE-alpha software v2.16 (with default parameters) (Keightley and Eyre-Walker 2007; Eyre-Walker and Keightley 2009), which is based on a maximum likelihood framework to model the DFE of nonsynonymous mutations assuming a gamma distribution of fitness effects on the negative real line. The program estimates the DFE by comparing the folded SFS of mutations that are neutrally evolving to mutations that are under selection. The SFS of neutrally evolving mutations is used to estimate the population mutation rate (N_eμ) allowing for simple demographic scenarios that may equally influence the neutral and the selected SFS. The null model assumes a constant N_e (constant model) through time, while the alternative model allows for a one-step change in N_e (one-step change model). We compared the two models using a LRT with a 0.01 significance level and show the results for the best-fit model for every mutation category and bin. The parameters of the demographic model for each mutation category and recombination rate bin were estimated using only synonymous sites of that respective category and bin. Hence, the “selected” SFS was normalized by the “neutral” SFS of the same genomic region and mutation category, a normalization procedure that corrects for variation in mutation rate along the genome. Importantly, it also accounts for variation in the degree of linkage between sites and hence the strength of background selection and genetic draft in different genomic regions (Messer and Petrov 2013; Huber et al. 2017). To assess the goodness of fit statistically, we estimated r² between the observed and expected SFS for each mutation category (Keightley and Eyre-Walker 2007); the fit is shown in supplementary figure S6 and table S5, Supplementary Material online.

The estimation of ω_a and α was performed with the DFE-alpha software v2.16 (Keightley and Eyre-Walker 2007; Eyre-Walker and Keightley 2009), and based on the total number of nonsynonymous and synonymous substitutions retrieved for the different mutation categories using the L95 model in the bio++ suite (as described earlier) and the respective DFE. As the L95 model corrects for multiple substitutions, the Jukes–Cantor correction made by DFE-alpha was not applied, neither a correction for ancestral polymorphisms.

Estimates of Recombination Rate

Estimates of recombination rate in cM/Mb for nonoverlapping 200-kb windows of the collared flycatcher genome were retrieved from Kawakami et al. (2014). Rates were assigned to each gene according to the window they were located in. When a gene covered two or more windows, we calculated a weighted average of the recombination rates in the corresponding windows. We ranked genes and created bins of low, medium, and high recombination rate, where each bin contained the same number of genes.

RNAseq Data and Expression Patterns

The collection and early processing stages of transcriptome data from eight different organs (brain, kidney, liver, lung, muscle, skin, ovary, and testis) of four male and four female collared flycatchers have been described in previous work (Uebbing et al. 2013, 2016). For downstream processing of the data we first used FastQC to check the quality of RNA-seq reads. All duplicated reads were marked and reduced to a single copy using Picard v 2.0.1. We mapped untrimmed reads from each sample to a repeat-masked assembly version using default parameters in STAR v.2.5.1b (Dobin et al. 2013). Only uniquely mapped reads were used for further analyses.

We estimated the normalized gene expression level in transcripts per million (TPM) for every annotated gene and separately for every organ using RSEM (Li and Dewey 2011). We discarded the 5% of genes with the highest coefficient of variation in TPM values within males and within females, respectively. Genes expressed in less than four individuals across both sexes and genes with an average TPM <1 were removed in order to avoid genes with a low signal-to-noise ratio within and between sexes. Based on ranking we generated bins of low, medium, and high expression level for each organ separately. Finally, expression breadth was measured based on all eight organs as the tissue specificity index (τ) (Yanai et al. 2005) that ranges from 0 (even expression across all tissues) to 1 (tissue-specific). Ranking was also made based on τ and bins were generated as above.

To assess sex-bias in gene expression we first applied HTseq v0.6.1 (Love et al. 2014; Anders et al. 2015) to uniquely mapped reads and computed transcript abundance. We restricted the read counting to reads with a mapping quality of at least 30, and set the HTseq model to “union” and “reverse stranded.” Then we used the DESeq2 package (Love et al. 2014) to estimate the fold-change in expression between male and female gonads, which is the organ with the highest proportion of sex-biased genes. DESeq2 estimates differential expression between two groups while accounting for overdispersion. HTseq was used for quantification instead of RSEM, as it is not recommended to use DESeq2 in combination with RSEM (Love et al. 2014). Genes were subsequently grouped into three categories based on their fold-change between sexes: genes with a male-to-female expression ratio (log₂male−log₂female) < −1 were assigned as female-biased and genes with a ratio >1 were assigned as male-biased, while the remaining genes were considered unbiased.

Protein–Protein Interactions

The number of protein–protein interactions for chicken genes was retrieved from FunCoup v.3.0 (Schmitt et al. 2014) and limited to 1:1 flycatcher-chicken orthologs. In FunCoup different evidence types for protein–protein interactions result in a probabilistic confidence score (pfc) that ranges from 0 to 1, reflecting the amount of evidence for the interaction, for which we chose a threshold of 0.5. We ranked genes and created bins of low, medium, and high number of PPI as above.

Concatenation of Genes and Estimation of Confidence Intervals

For binning we only included genes for which we had both divergence and diversity data. CIs were obtained by independently estimating parameters for 100 bootstrap replicates by sampling genes with replacement within each bin. Note that resampling of genes instead of sites resulted in larger CIs since sites within genes might be dependent on each other due to the effect of linkage. The standard error of the mean (SE) for each test statistic was estimated as the standard deviation of the resampling distribution divided by 10. CIs were defined as the product of the SE and the 0.5th and 99.5th percentiles of the Student’s t-distribution.

Branch-Site Test for Positive Selection

Orthologous sequences of zebra finch, chicken, budgerigar (Melopsittacus undulates), crested ibis (Nipponia nippon), little egret (Egretta garzetta), emperor penguin (Aptenodytes forsteri), turkey (Meleagris gallopavo), duck (Anas platyrhynchos), and ostrich (Struthio camelus) were retrieved from the Avian Phylogenomic Project Database (Zhang et al. 2014). Collared flycatcher sequences were retrieved from the Ensembl database and added based on 1:1 orthology with chicken (Yates et al. 2016). In case of splicing isoforms, the longest transcript was kept. The species were chosen following three main criteria: i) to include a sufficient number of species in the tree to have power to detect positive selection using branch-site tests (McBee et al. 2015), ii) the topology of the tree needed to be well supported (Jarvis et al. 2014), and iii) species with the lowest proportion of gaps in a 48-avian species alignment from the avian phylogenomics project (Jarvis et al. 2014); a large fraction of gaps could indicate assembly problems. Sequences were aligned with PRANK v.140603 and filtered using the GUIDANCE/HOT algorithm as above. The alignments were further filtered using GBLOCKS (Castresana 2000) with stringent parameters (minimum number of sequences for a conserved position = 7, minimum number of sequences for a flanking position = 9, maximum number of contiguous nonconserved positions = 6, minimum length of block = 10). In total, data for 4,855 orthologs were available.

We conducted branch-site tests for signatures of positive selection using the codeml program in the PAML4.7 package on a gene-by-gene basis, where the flycatcher branch was specified as the only foreground branch in the tree. We used a likelihood ratio test with a 0.05 significance level between two nested models: the nearly neutral model (M1a), and a model for positive selection (M2a). P values from the tests were Bonferroni–Holm corrected. Genes significant after Bonferroni–Holm correction were considered positively selected, whereas remaining genes were classified as other genes.