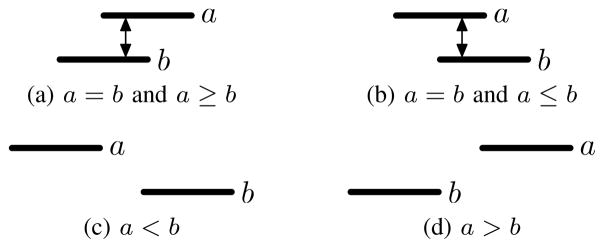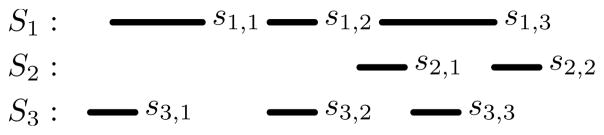A parallel algorithm for N-way interval set intersection

Abstract

The comparison of sets of genome intervals (e.g., genes, repeats, ChIP-seq peaks) is essential to genome research, especially as modern sequencing technologies enable ever larger and more complex experiments. Relationships between genomic features are commonly identified by their intersection: that is, if feature sets contain overlapping intervals then it is inferred that they share a common biological function or origin. Using this technique, researchers identify genomic regions that are common among multiple (or unique to individual) datasets. While there have been recent advances in algorithms for pairwise intersections between two sets of genomic intervals, few advances have been made to the intersection of many sets of genomic intervals. Identifying intersections among many interval sets is particularly important when attempting to distill biological insights from the massive, multi-dimensional datasets that are common to modern genome research. For such analyses, speed and efficiency are crucial given the size and sheer number of datasets involved. To solve this problem, we present a novel “slice-then-sweep” algorithm that, given N interval sets, efficiently reveals the subset of intervals that are common to all N sets. We demonstrate that our algorithm is more efficient in the sequential case and has a vastly higher capacity for parallelization with a 19x speedup over the existing algorithm.

I. Introduction

A Genomic interval is a continuous stretch of chromosomal base pairs between a start and an end nucleotide, and is a natural representation for genomic features. Genome assemblies provide a map of the relative location of a particular DNA sequence within a species’s genome, which allows genomic features (e.g., genes, fragile sites, repeat sequences, etc.) to be represented by a genomic interval. For example, the BRCA1 gene exists on chromosome 17 at the interval from 41,196,312 to 41,277,500 in build 37 of the human genome. Since the completion of first human genome assembly, the genomics community has labored to annotate it by identifying the chromosomal intervals that harbor, for example, genes associated with disease, significant conservation across diverse species, or the many functional elements that modulate gene expression. Each such annotation is itself a distinct set of genome intervals, and the majority of discovery in genomics research involves, in some way, comparing the relationships between sets of genomic features. Such comparisons involve screens for interval intersection: that is, if feature sets contain intervals that overlap one another, then an underlying biological relationship can often be inferred. As such, an efficient intersection algorithm provides researchers with the ability to identify genomic regions that are common among multiple (or unique to an individual) datasets, and place their experimental results in a broader context.

Algorithms that find the intersection between two genomic interval sets have received considerable attention [1], [2], [3], [4], [5], [6], but the ability of these algorithms to consider many interval sets is limited. Identifying intersections common to many sets, the N-way intersection, is particularly important when attempting to distill biological insights from large, multi-dimensional datasets such as those produced by the ENCODE [7] or Roadmap Epigenomics [8] projects. These projects endeavor to catalog the spectrum of functional elements in the human genome, and in so doing, they have thus far produced thousands of distinct sets of genomic features (intervals) among many different cell types. Understanding the biological relationships of the these functional elements requires a higher-level analysis that considers many sets at once. For example, novel gene enhancers can be discovered by finding genomic intervals that are common across relevant histone modification and transcription factor binding sites.

In this manuscript, we introduce a “slice-then-sweep” algorithm as a novel and efficient solution to the N-way intersection problem. While any algorithm that can identify intersection between pairs of interval sets can be extended to find N-way intersections by iterative pair-wise set comparisons, such approaches require a significant amount of overhead to create intermediate results and track intersection provenance. One widely-used algorithm, the linear sweep, has been directly extended to find N-way intersections [5], but may lead to over-processing and has little opportunities for parallelization. In contrast, the “slice-then-sweep” algorithm we present attempts to minimize wasted computation and increase the amount of parallelism by creating independent slices of the data. The slice step identifies and discards regions that cannot possibly contain an N-way intersection. The resulting subsets of the data are completely independent and can therefore be efficiently processed by linear sweeps in parallel. While the speedup provided by slicing depends on the number of intervals that can be excluded, we demonstrate that, even in the worst case, the “slice-then-sweep” strategy performs as well as a linear sweep. Moreover, by enabling parallelization, we show that it provides significant speedups for the analysis of typical large-scale genomics datasets.

II. Interval Sets and Intersections

An interval a = 〈a.start, a.end〉 is a continuous set of values between start and end locations (e.g., a gene), and an interval set A = {a₁, …, a_N} is a collection of intervals (e.g., all known genes). Two intervals a and b intersect when a.start ≤ b.end and a.end ≥ b.start. For convenience, we let a = b if a and b intersect (Figure 1a, 1b), a < b if a ends before b starts (a.end < b.start) (Figure 1c), a > b if a starts after b ends (a.start > b.end) (Figure 1d), a ≤ b if a intersects b and starts before b (Figure 1b), and a ≥ b if a intersect b and ends after b (Figure 1a). We emphasize that this notation is for convenience, and that some properties associated with these relations do not necessarily hold. In particular the transitive property does not hold for interval intersection (i.e., if a, b, and c are intervals, then a = b and b = c does not imply that a = c).

Fig. 1.

Interval equality and inequality relationships.

Within a set, it is possible for an interval a_i to both start before and end after another interval a_j (a_i ≤ a_j and a_i ≥ a_j), in which case we say a_i contains a_j (Figure 2). Let a ≡ b only if a and b refer to the same interval in the same set.

Fig. 2.

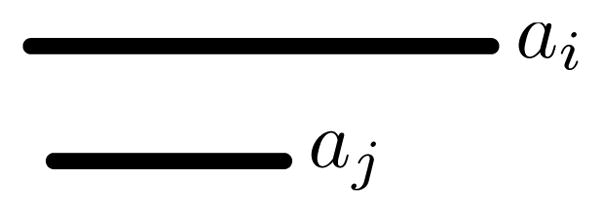
Interval a_i contains interval a_j.

Interval sets are assumed to be free of contained intervals. While in general interval sets can contain contained intervals, this assumption is reasonable for two reasons. First, from a practical perspective, the experimental methods that are used to generate the genomic functional element interval sets (e.g., ChIP-Seq [9], DNase-Seq [10], and RNA-seq [11]) that are most relevant to an N-way intersection do not produce contained intervals. Second, from a conceptual standpoint, since the N-way intersection identifies regions that are involved in N different sets, any set with m contained intervals could contain up to m nearly identical intersections. This would likely over represent the actual biological relationship between the sets. In cases where this assumption does not hold, interval sets can easily be flattened so that any contained interval is absorbed into the larger interval. This operation can be performed with a single linear scan of the intervals within each set, which does not affect the asymptotic complexity of the algorithm.

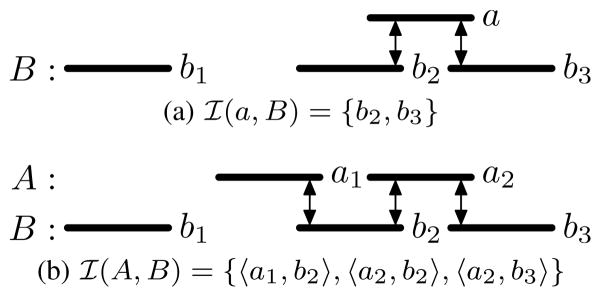
The intersection of an interval a and interval set B is the set of intervals: ℐ(a, B) = {b_i|b_i ∈ B, a = b_i} (Figure 3a), and the intersection of two interval sets A and B is the set of interval pairs: ℐ(A, B) = {a_i × ℐ(a_i, B)|a_i ∈ A} (Figure 3b).

Fig. 3.

Intersections between intervals and intervals sets.

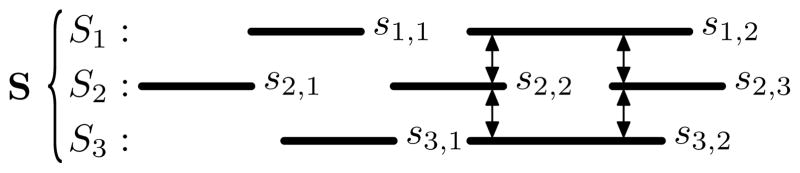
The intersection among a set of intervals sets S = {S₁, …, S_N}, where S_i = {s_i,1, …, s_i,|Si|}, (the N-way intersection, Figure 4) is a set of interval sets where each set contains exactly one interval from each S_i ∈ S, and all of the intervals within a set intersect:

$$\mathcal{I}(\mathbf{S})=\left\{s_{1,j},\dots ,s_{N,l}|\begin{array}{l}{s}_{a,b}\in S_a,\hfill \\ s_{a,b}=s_{c,d}\forall s_{a,b},s_{c,d}\in \{s_{1,j},\dots ,s_{N,l}\}\hfill \end{array}\right\}$$

Fig. 4.

The N-way intersection ℐ(S) = {{s_1,2, s_2,2, s_3,2}, {s_1,2, s_2,3, s_3,2}}

III. Related work

Interval intersection has many applications in genomics, and several algorithms have been developed that, in general, are either based on trees [2], [1], or linear sweeps of pre-sorted intervals [4]. The UCSC genome browser introduced a widely-used scheme based on R-trees. This approach partitions intervals from one dataset into hierarchical “bins.” Intervals from a second dataset are then compared to matching bins (not the entire dataset) to narrow the search to a focused regions of the genome. Although this approach is used by the UCSC Genome Browser, BEDTools [5], and SAMTOOLS [12], the algorithm is inefficient for counting intersections since all intervals in each candidate bin must be enumerated in order to count the intersections. Since the number of intersections is at most quadratic, any algorithm that requires enumeration is O(N²). As an alternative strategy, recent versions of BEDTools and BEDOPS [3] conduct a linear “sweep” through pre-sorted datasets while maintaining an auxiliary data structure to track intersections as they are encountered.

Moreover, both tree-based and linear sweep algorithms are poor candidates for parallelization. In the case of tree-based algorithms, thread divergence can be a significant problem if intervals are not uniformly distributed (e.g., exome sequencing or RNA-seq), since a small number of bins will often contain many intervals while most other bins are empty. Consequently, threads searching full bins will take substantially longer than threads searching empty (or nearly empty) bins. While the complexity of linear sweep algorithms is theoretically optimal, the potential for parallelism is also limited and some overhead is required to guarantee correctness. Any linear sweep algorithm must maintain the “sweep invariant” [13], which states that all segment starts, ends, and intersections behind the sweep must be known. A parallel sweep algorithm must therefore either partition the input space such that each section can be swept in parallel without violating the invariant, or threads must communicate about intervals that span partitions. In the first case parallelism is limited to the number of partitions that can be created, and threads can diverge when the number of intervals in each partition is unbalanced. In the second case, the communication overhead between threads prevents work efficiency and can have significant performance implications.

These barriers to parallelism were the primary motivation for our recently described Binary Interval Search (BITS) algorithm [6]. Unlike previous methods, BITS directly counts intersections without the need for enumerating intersecting intervals; therefore, the underlying interval distribution does not impact the relative workload of each thread. Unfortunately, the BITS algorithm is specifically designed to count intersection between pairs of interval sets and as such, its parallelism strategy is ill-intersection problem. However, the key insight from BITS is that an interval set can be efficiently partitioned into subsets of intervals that begin before and after a particular interval; this approach is used here as the basis for creating independent interval slices.

IV. N-way intersection algorithms

It is clear that any pair-wise interval intersection algorithm can be extended to the N-way problem by considering pairs of sets iteratively; however, the overhead associated with this method limits its practical use. Given a set S = {S₁, …, S_N}, the result of ℐ(S₁, S₂) = R_1,2 can be input into an intersection with S₃ by mapping the set of pairs in R_1,2 to a set of intervals that contain the regions common to each pair. That result is then paired with with S₄, and so on. Once all interval sets have been considered, the final set contains intervals that are common to each N-way intersection. From those common intervals, the full N-way intersection can be constructed by either tracking back through each intersection, or using a secondary data structure to maintain a list of intervals common to each result. This extra bookkeeping, the effort required to create the N − 1 intermediate results, and the fact that regions are being reconsidered many times, adds a considerable amount of overhead.

The linear sweep, which is used by a number of current methods [5], [3], can be efficiently extended to consider N sets. The sweep scans the intervals across the sets to determine if any are in-context at the same time. In many data sets the number of N-way intersections is much smaller than the number of intervals, and a considerable amount of processing time can be saved by skipping regions of the input space that cannot possibly contain an intersection. Since the sweep algorithm must track each interval as it starts and ends, it is not able to skip over these regions. Furthermore, this type of serial processing has limited opportunities for parallel execution.

We propose the “slice-then-sweep” strategy, a novel algorithm that can improve performance by both skipping regions that clearly lack N-way intersections, and exposing a significant amount of fine-grain parallelism. Our algorithm first efficiently slices the interval sets into independent regions so that only slices lacking empty regions are considered. Since the regions are inherently independent, they can also be easily processed in parallel. While the extent of the performance gain in the sequential case depends on the number of intervals that are excluded, the “slice-then-sweep” strategy performs as well as a linear sweep even in the worst case where none of the intervals may be excluded. Furthermore, the number of excluded intervals does not affect the level of parallelism that is achieved by slicing.

A. Sweep

The generalized sweep algorithm proposed by Bentley and Ottmann [14] is the basis for several pair-wise genomic interval intersection solutions [5], [3]. The two sorted interval sets are treated as stacks, and at each step the minimum interval between the sets (the current interval) is popped and added to an ordering data structure that maintains the set of intervals that are in-context. Intervals that end before the current interval starts are no longer in-context and are thus removed from the ordering. Intervals that intersect will be present in the ordering at the same time. The pair-wise sweep algorithm has been extended to solve the N-way intersection problem by adding an ordering for each of the interval sets and a priority queue to manage the removal of in-context intervals [5]. When all N orderings are not empty, the Cartesian product of the orderings gives a set of N-way intersections.

At each iteration, the N-way sweep (Algorithm 1) considers the interval with the next smallest start position across the ordered sets in S. This process is similar to a merge operation and is managed by a priority queue Q where the minimum element in the queue has the highest priority. Each queue element q ∈ Q is associated with an interval x ∈ S_i, and is assigned a priority (q.p) equal to the interval start position (q.p = x.start) and a value (q.v) equal to the index of the contributing set (q.v = i). Initially, the queue contains the first element in each set. As the sweep progresses, the next interval to be considered is determined by popping the highest priority element q₀ from Q. To replace this element with another that corresponds to the next element from the same set, an interval is popped from S_q0._v, and a new element q_n is added to the queue where q_n.p = x.start and q_n.v = q₀.value. Using a priority queue with O(log N) inserts and removes, the time required to sweep N sets is proportional to O(M log N), were M is the total number of intervals among the sets.

Algorithm 1.

The N-way sweep algorithm.

Within the sweep, N ordering data structures o₁ … o_N maintain the set of intervals that are in-context. Since the sets in S are free of contained intervals, each ordering data structure can be represented by the pair of indices o_i = 〈o_i.start, o_i.end〉 that specify the range of intervals in S_i that are in-context. For example, if o₁ = 〈3, 4〉 then s_1,3 and s_1,4 are in-context. If o_i.start > o_i.end, then none of the intervals in S_i are in-context. Each ordering is initialized to be empty (o_i = 〈0, −1〉 for i = 1 … N) and intervals are added by incrementing o_i.end and removed by incrementing o_i.start.

When q₀ is popped from Q, any interval that is in-context and ends before q₀.p (the start position of the interval associated with q₀) must be removed from context. Instead of scanning the orderings, which would require O(N) time, another priority queue C is used to determine which orderings need to be updated in time O(log N) for each interval that is removed from context. Similar to Q, the minimum element in C has the highest priority, and the value of each element is the index of the contributing set. But unlike Q, the priority of the elements in C are interval end positions. To update the orderings, elements are popped from C until the top element has a priority greater than or equal to q₀.p. For every popped element c, the ordering o_c.v is updated (o_c.v += 1). An element associated the current interval is then added to C.

With the out-of-context intervals removed from the orderings, the interval corresponding to q₀ is placed in-context (o_q0v += 1). If none of the orderings are empty (tracked by the number_empty variable), then an N-way intersection has been found. Each ordering represents the sequences of interval indices that are in-context. The Cartesian product of sequences defined by o₁ … o_N yields a set of N-way intersections. For example, if the orderings equal 〈1, 1〉〈3, 4〉〈2, 2〉, then the product gives a set of N-way intersections {(1, 3, 2), (1, 4, 2)}. In Algorithm 1, the sequence function is used in to convert an ordering from two endpoints to the full sequence (e.g. sequence(1, 4) = 〈1, 2, 3, 4〉).

1) Complexity

Within the scan each interval is added to and removed from the priority C exactly once, and the time required to scan a set of N interval sets with M total intervals is O(M log M). Since N ≤ M, total time required to sweep a set the set is O(M log M + M log N + WN) = O(M log M + WN) where W is the number of N-way intersections, and each intersection contains N intervals.

B. Basic Slicing

While the sweep algorithm is an efficient, general solution, it must consider all of the intervals in S. As a result, when the number of intersections is much smaller than the number of intervals (as is common in in the case of typical genomics datasets), a significant amount of time is spent sweeping regions of S that do not contain intersections. We propose a new algorithm that attempts to minimize this type of over-processing by creating slices of S. Any slice that cannot possibly contain an N-way intersection is discarded so that processing can focus on more promising regions. Slicing also creates independent subsets of S that can be processed in parallel.

Slices are composite sets that contain a subset of consecutive intervals from each set in S. Since the intervals in each subset are consecutive, a slice T = t₁ … t_N can be represented by a set of start and end pairs t_j = 〈t_j.start, t_j.end〉, where t_j.start denotes the index of the first interval of the slice from S_j and t_j.end denotes the last. A subset is empty when t_j.start > t_j.end.

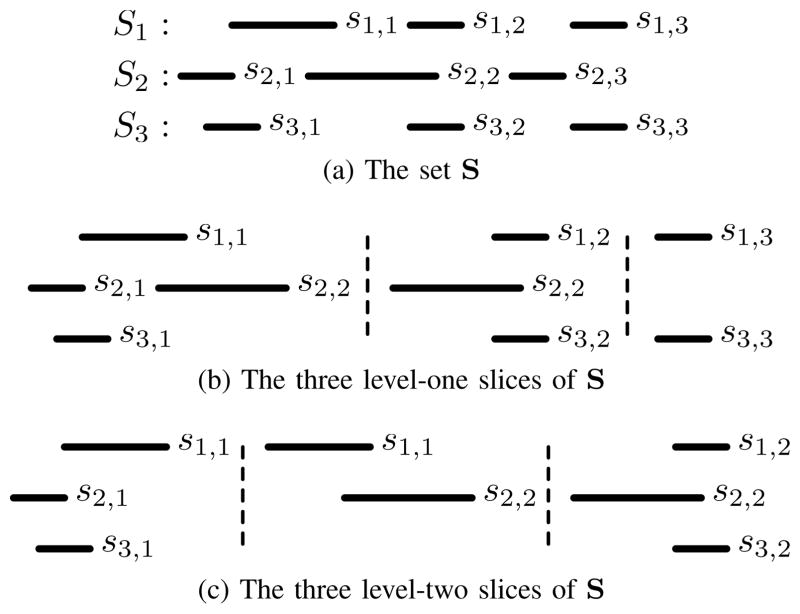
A slice is at level λ when the intervals in t_λ+1 … t_N intersect all of the intervals in t₁ … t_λ, and all of the intervals in t₁ … t_λ intersect each other. For example, the subsets in Figure 5b are level-one slices of the set in Figure 5a (which itself is considered a level-zero slice), and the subsets in Figure 5c are level-two slices. A slice at a particular level may contain an empty subset (such as the third slice in Figure 5b and the second slice in Figure 5c) if there are no intersecting intervals in the corresponding set. An interval may exist in multiple slices (such as interval s_2,2 in the first two level-one slices) if it intersects more than one interval in a higher level, and an interval may be excluded from any slice (such as interval s_2,3) if it doesn’t intersect any higher-level intervals. A level-N slice with exactly one interval per subset is equivalent to an N-way intersection.

Fig. 5.

An example set of intervals sets S, and level-one and - two slices of S. Interval s_2,2 is in two level-one slices because it intersects both s_1,1 and s_1,2, and s_2,3 is not in any slice because it does not intersect any interval in S₁.

Considering that none of the sets in S have fully-contained intervals, a single level-one slice can be found with two binary searches per set for the start and end coordinates of a top-level interval s_1,i (Algorithm 2). The first binary search ( binarySearchEnds) finds the insert position of s_1,i.start among the list of end coordinates in S_j, giving the index of the last interval in S_j to end before s_1,i starts. The second binary search ( binarySearchStarts) finds the insert position of s_1,i.end among the list of start coordinates in S_j, giving the index of the first interval in S_j to start after s_1,i ends. The range between these two positions gives the intervals in S_j that intersect s_1,i, and the values to t_i. If that range is empty, then the start position will be greater than the end position.

Algorithm 2.

The basic N-way slice operation.

1) Complexity

The time required to compute all level-one slices for each interval in S₁ is O(|S₁|log(NM)), where |S_i| is the number of intervals in S_i, N is the number of interval sets in S, and M is the number of intervals in S. The creation of each subset of each slice takes time O(log(|S_i|)), and the time to create a full slice is O(Σlog(|S_i|)) = O(log(Π|S_i|)) = O(log(NM)) (given that ${\prod }_{i=1}^N\mid S_i\mid \le NM$). There are |S₁| level-one slices, making total time O(|S₁| log(NM)).

C. Pivot Slicing

While the basic slicing process is reasonably efficient, when level-one slices are created in a particular order, information about the distribution of intervals can be utilized by future slicing operations to both reduce the search space and possibly prevent some slices from being created. For example, consider the set in Figure 6. In the basic process, three level-one slices are created ({{s_1,1}, {}, {s_3,1}}, {{s_1,2}, {}, {s_3,2}}, and {{s_1,3}, {s_2,1, s_2,2}, {s_3,2}}). Two of the these slices contain an empty subset (the two based on intervals s_1,1 and s_1,2), and thus they cannot possibly be part of an N-way intersection. If the process instead started by creating the slice centered on s_1,2, then it could have been inferred that the slice on s_1,1 would contain an empty subset (since s_1,1 ≤ s_1,2 and s_2,i > s_1,2 for i = 1, …, |S₂|), and that it did not need to be created since it could not possibly lead to an N-way intersection.

Fig. 6.

If the sliced based on s_1,2 is created first, then it can be inferred that s_1,1 is not part of an N-way intersection and a slice based on it does not need to be created.

The “emptiness” of future slices can be inferred by systematically creating slices based on a pivot interval s_1,p ∈ S₁ (Algorithm 3). The algorithm is similar to the previous slicing method, requires less work, and in some instances results in fewer slices. With respect to the pivot (e.g., the middle interval), the sets in S are partitioned into left, center, and right slices. The left slice includes intervals that are less than or equal to s_1,p, the center slice includes intervals that intersect s_1,p, and the right slice includes intervals that are greater than or equal to s_1,p. Any slice containing an empty subset is discarded. Non-empty left and right slices are recursively re-sliced in a breadth-first search style algorithm (Algorithm 4), and the center slices make up the set of level-one slices. To find the N-way intersections, level-one slices can be similarly re-sliced into left, center, and right slices, and the center slices are then level-two slices. The center slices of level-two slices are level-three slices and are re-sliced into level-four slices, and so on until level-N. After level-N, all non-empty center slices give the N-way intersections.

Algorithm 3.

The left, center, and right N-way slice operation.

Algorithm 4.

The pivot slice algorithm.

To allow for re-slicing, LCR_SLICE is defined in terms of a slice T and a pivot in the first subset of T. The binary searches are also modified to operate only within the bounds of the current slice. This reduces the amount of work required to find all slices since only the first round of slicing considers all intervals in S (t_i.start = 1 and t_i.end = |S_i| for i = 1 … N), and subsequent rounds consider increasingly smaller subsets of S. At each iteration slices are roughly divided in half by setting the pivot interval to the medoid interval in t₁.

D. Slice and Sweep

N-way intersections can be found by re-slicing each level-one slice into level-two slices, then level-three slices, and so on. Following this procedure, level-N slices will contain exactly one interval per subset, and all the intervals will intersect each other. However, as with the sweep operation, re-slicing level-one slices may result in over-processing.

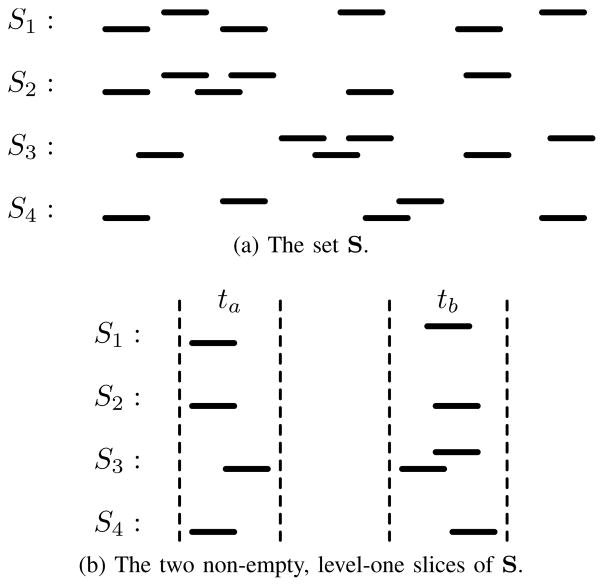
The slice operation is best suited for cases where the proportion of intervals involved in an N-way intersection is much smaller than the total number of intervals. While this property exists in many real-world data sets, it may not continue to exist in the level-one slices of the data. Consider the full set and the level-one slices in Figure 7. The nonempty, level-one slices contain less than half the number of intervals that are in the full set. If these two slices were then re-sliced, the resulting level-two slices would contain the exact same number of intervals as the level-one slices and only one additional interval would have been added to the possible N-way intersections. To obtain the final result, such wasted processing would continue through the remaining sets with a runtime total runtime of O(WN log(NM)), where W is the total number of N-way intersections.

Fig. 7.

The non-empty level-one slices comprise less than half of the full set.

Considering that over-processing occurs in the sweep when the proportion of intervals in N-way intersections to the total number of intervals is low, and in the slice when the proportion is high, it follows that the most efficient algorithm is a hybrid that intelligently switches from slicing to sweeping. Conceptually, slicing should stop before the amount of work required to slice is greater than the amount of work required to sweep the intervals that would have been excluded by the slice. Since determining exactly when this transition will occur requires a priori knowledge of the final result (i.e., the total number of the N-way intersections in the slice), a heuristic must be used.

1) Complexity

While the number of intervals that would be removed by performing an additional level of slicing is unknown, it is obviously bound by the total number of intervals in the slice. To account for the varying number of sets, the decision to slice or sweep can be based on the ratio of the number of intervals in the slice to the number of sets. As the ratio approaches one, the potential for the slicing algorithm to remove intervals decreases. Outside of pathological cases (very long intervals or very dense collections of intervals), the ratio drops to near one after the first level of slicing. Based on this observation, the slice and sweep algorithms presented here switch to sweeping after one level of slicing. If the ratio for a slice is exactly one (there is only one interval per subset) then a sweep in not needed, and the intervals in each slice are simply tested to see if they form an N-way intersection. The runtime of this algorithm is equal to the time required to create the level-one slices plus the time required to sweep those slices, which is O(|S₁| log(NM) + M′ log(M′) + W), where M′ is the number of intervals that were not excluded by the slice.

2) Parallel slice and sweep

Beyond reducing the over-processing in the sweep algorithm, slicing also creates inherently independent sections of S that can be processed in parallel. While pivot slicing reduces the amount of work required to create a set of level-one slices, the basic slicing algorithm is a better candidate for parallelization since each slice is completely independent (pivot slicing creates new slices at each step, creating a dependency between slices) and there are no shared resources (pivot slicing has a queue that must be locked on push and pop). In the parallel slice and sweep algorithm, each thread creates one level-one slice. Then, any non-empty level-one slice is swept. Each thread maintains a private list of N-way intersections that are merged in the final step of the algorithm.

V. Results

To assess the performance of these algorithms, the sweep (sweep), pivot-slice (pslice), pivot slice then sweep (pslice-sweep), and parallel slice then sweep that is based on the basic slice operation (Pbslice-sweep) algorithms were implemented as stand-alone C utilities using the Pthreads library for parallel thread manipulation. The sweep algorithm is based on the a widely-used technique [5], [3] that has been improved and adapted here to consider N sets. As we point out in the previous section, the relative performance of each algorithm depends on the distribution of the data. As the proportion of intervals involved in an N-way intersection increases, the opportunities for the split algorithm to reduce the amount of data that must be considered diminishes. To identify where slicing no longer provides improvement over sweeping, we tested the performance of the algorithms against simulated data sets with a varying numbers of sets and varying proportion of N-way intersections. We also tested each algorithm using previously published data from a large-scale DNase I hypersensitive site study [15], and CTCF transcription factor sites from the ENCODE project [16].

All tests were performed on an Intel Xeon(R) CPU with eight 2.6 GHz cores (16 threads), and 20 MB of cache. The system was running Red Hat Linux version version 2.6.32-358.6.1.el6.x86_64, with gcc version 4.4.7-3. Unless otherwise noted, the results do not include disk read or write time. The software tested here is freely available at https://github.com/ryanlayer/nway.

A. Performance with simulated interval sets

To test the extent to which the slice algorithms can improve performance over the sweep algorithm, each was tested against uniformly distributed random data sets with varying numbers of sets and varying proportions of N-way intersections. Each set within the test contained 10,000 intervals, each interval was 100 base pairs long, and all intervals were placed within the genome. The number of sets ranged from 10 to 200, and the proportion of N-way intersections ranged from 1% to 100%.

In each test, the sites of the intersections were randomly generated. Then for each set and for each site, an interval was generated to contain the site at a random point within the interval. The remaining non-intersecting intervals were then added at random locations within the range. Each test was executed three times and the mean runtime in microseconds is given in Figure 8.

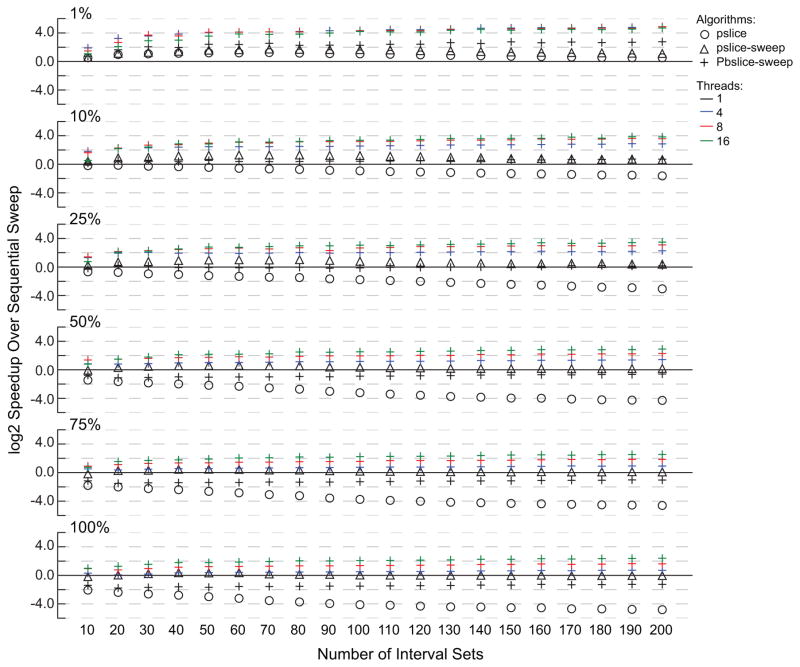
Fig. 8.

The log 2 speedup over sequential sweep of N-way intersection problems on simulated data. The proportion of intervals in an intersection increases from 1% to 100% from top to bottom, and the number of data sets increases from left to right.

As expected, the benefit of slicing is highest when the proportion of intervals in an N-way intersection is low. At 1%, all of the slice-based algorithms outperform the sweep, including the slice-only algorithm which is known to over process. The pivot slice-sweep algorithm is up to three times faster than sweep, and the sequential slice-then-sweep is nearly seven times faster. The parallel slice-then-sweep has a dramatic improvement with a 25 to 30 fold speedup over the sequential sweep.

When the proportion of intersections increases, the opportunities for slicing to reduce the amount of work decreases. As a result, when the density of intersections increases, the improvement of the slice algorithms decreases. However, the sequential slice-then-sweep algorithm performs as well as or better than the sweep in every case, and the parallel slice-then-sweep is up to 7.5 times faster when 50% of the intervals are in N-way intersections, and up to 5 times faster when all intervals N-way intersect.

B. Performance with published genomic interval sets

In an attempt to understand the function of specific regions of the human genome, large-scale studies are continuously publishing interval sets that describe the locations of particular genomic features and cellular functions across many different cell types. The experiments used to find these sites can have a significant amount of noise and each experiment can result in hundreds of thousands of sites. By comparing results among many experiments, researchers can narrow the search space to the most promising regions and develop new hypotheses and future experiments that focus on these regions.

Maurano et al. [15] published sites of DNase I hypersensitivity observed among more than 200 fetal tissue samples (e.g., lung, heart, kidney). These sites mark regions of the genome that are accessible to cellular processes such as DNA binding proteins and are thought to be active regions of the genome. The interval sets have on average 200,000 intervals per set, intervals have a mean length of 500, and there are 15,340 N-way intersections across the 200 datasets (7.5% of intervals in an intersection).

The ENCODE project has published thousands of interval sets [16], including CTCF binding sites from over 100 different cell lines (e.g., the myelogenous leukemia line K562, and the cervical cancer line Hela). CTCF is a transcription faction that has been shown to have a role in repressing cellular activity. The interval sets have on average 180,000 intervals per set, intervals have a mean length of 215, and there are 17,071 N-way intersections across the 100 datasets (9.5% of intervals in an intersection).

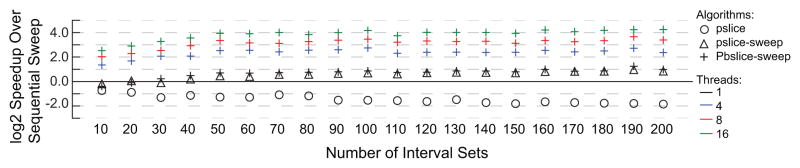
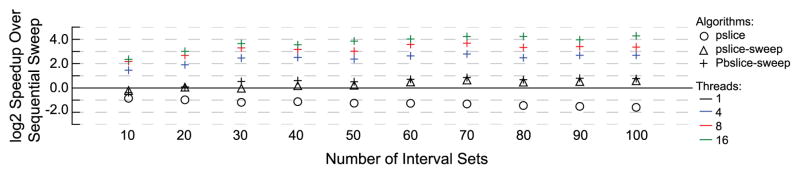
Considering the data set sizes and the proportion of intersecting intervals in these data sets, the runtime improvements of the slice algorithms over the sweep algorithm are consistent with the results from the simulated data. In the DNase I hypersensitive sites data set, the slice-then-sweep algorithm is nearly twice as fast as sweep, and the parallel versions of slice-then-sweep are 5x, 10x and 19x faster for four, eight, and 16 threads, respectively (Figure 9). While the CTCF data does not have as many data sets (100 vs. 200 for DNase I and the simulations) the speedup trends are still consistent, with the slice-then-sweep being 1.5x faster and the parallel slice-then-sweep being 6x, 10x, and 19x faster with four, eight, and 16 threads, respectively (Figure 10). Both data sets also demonstrate the issues with wasted processing in the slice algorithm.

Fig. 9.

The log 2 speedup over sequential sweep of N-way intersection problems on DNase I hypersensitive sites. The proportion of intervals in an intersection increases from 1% to 100% from top to bottom, and the number of data sets increases from left to right.

Fig. 10.

The log 2 speedup over sequential sweep of N-way intersection problems on CTCF binding sites. The proportion of intervals in an intersection increases from 1% to 100% from top to bottom, and the number of data sets increases from left to right.

VI. Discussion and future work

In order to improve upon the efficiency of linear sweep approaches to interval intersection, the presented “slice-then-sweep” algorithm employs a hybrid strategy that is designed to find intersections across all N data sets. Given its inherent potential for parallelism by partitioning interval sets into independent subsets, it provides an approach that scales to the size and complexity of modern genomics datasets. As such, we anticipate that the software implementation of the “slice-then-sweep“ algorithm will be broadly useful to researchers facing the now common task of comparing and exploring many diverse genomic datasets.

An important generalization of the N-way intersection problem is to find intersections occurring among at least k of N interval sets. While the algorithm we describe does not solve the “k of N” problem, we anticipate that future modifications to the sweep algorithm can be made to solve “k of N”, but we recognize that such solutions may require too many interval comparisons to allow parallelism to yield substantial performance gains beyond that of a straightforward linear sweep. That said, it is also possible that the slice algorithm could be generalized to the “k of N” intersection problem by creating and merging level-one slices for each of the N sets. The outstanding issue with this solution would be to prevent an exponential number of comparisons between slices.

Another important consideration for future research is to minimize the memory footprint of the algorithm in order to enable scaling to thousands of genomic interval sets. Recent advances such as Tabix [17] allow random access into overlapping intervals within compressed genomic interval files. Modifications to this format such as Grabix [18] allow random access to arbitrary records in such files and therefore permit slicing interval sets without loading them into memory. Extending our algorithm to leverage such functionality in the interest of greater scalability with be the focus of future research.

Biographies

Ryan M. Layer received B.S and Masters degrees in computer science from Texas A&M University, College Station, US, in 2003 and 2005, and a Ph.D. in computer science from the University of Virginia, Charlottesville, US, in 2014. He is now a Postdoctoral Researcher at the University of Utah, Salt Lake City, US, and develops algorithms for analyzing large-scale genetic data sets.

Aaron R. Quinlan received his B.S. degree in Computer Science from The College of William and Mary in 1997 and a Ph.D. in Biology from Boston College in 2008. He is now an Associate Professor of Human Genetics and Biomedical Informatics at the University of Utah. His research in computational biology focuses on the development of new methods for understanding the biology of the genome and the genetic basis of inherited and somatic disease.