Using double pulsed-field gradient MRI to study tissue microstructure in traumatic brain injury (TBI)

Abstract

Double pulsed-field gradient (dPFG) MRI is proposed as a new sensitive tool to detect and characterize tissue microstructure following diffuse axonal injury. In this study dPFG MRI was used to estimate apparent mean axon diameter in a diffuse axonal injury animal model and in healthy fixed mouse brain. Histological analysis was used to verify the presence of the injury detected by MRI.

Graphical abstract

1. Introduction

Traumatic brain injury (TBI) is a major cause of disability and death worldwide, accounting for about 30% of all injuries related deaths in the USA [1]. One of the most common pathologies which is present in about 40%–50% of cases of traumatic brain injury (TBI) cases is diffuse axonal injury (DAI) [2], resulting in preferential damage to white matter [3]. DAI ranges from mild to severe, and is accompanied by tissue microstructural alterations including axonal abnormalities such as varicosities and axonal loss, as well as gliosis and microglia cell infiltration [4, 5]. While clinical MRI is routinely used to detect gross anatomical and vascular abnormalities, the subtle white matter changes associated with DAI are challenging to diagnose and characterize using conventional MRI methods. Often DAI can only be detected at autopsy [2]. Diffusion MRI methods such as diffusion tensor imaging (DTI) [6] show promise for probing subtle changes in brain microstructure [7–9], however, the resulting metrics such as fractional anisotropy (FA), and mean diffusivity (MD) lack sufficient specificity to suggest the biophysical origin of these changes. Diffusion correlation methods such as double pulsed-field gradient (dPFG) [10, 11], illustrated in Figure 1, in which the MRI signal is sensitized to displacement correlations rather than the mean-squared net displacements, may improve both sensitivity and specificity in detecting brain abnormalities following injury. In the central nervous system (CNS), dPFG data may be used to characterize features of a cylindrical pack of axons that constitute white matter fascicles. By using a dPFG variant with vanishing mixing time between the two diffusion encoding blocks (i.e., τ_m = 0) average axon diameter (AAD) [12–15] or axon mean diameter (AMD) and axon diameter distribution [16, 17] can be estimated.

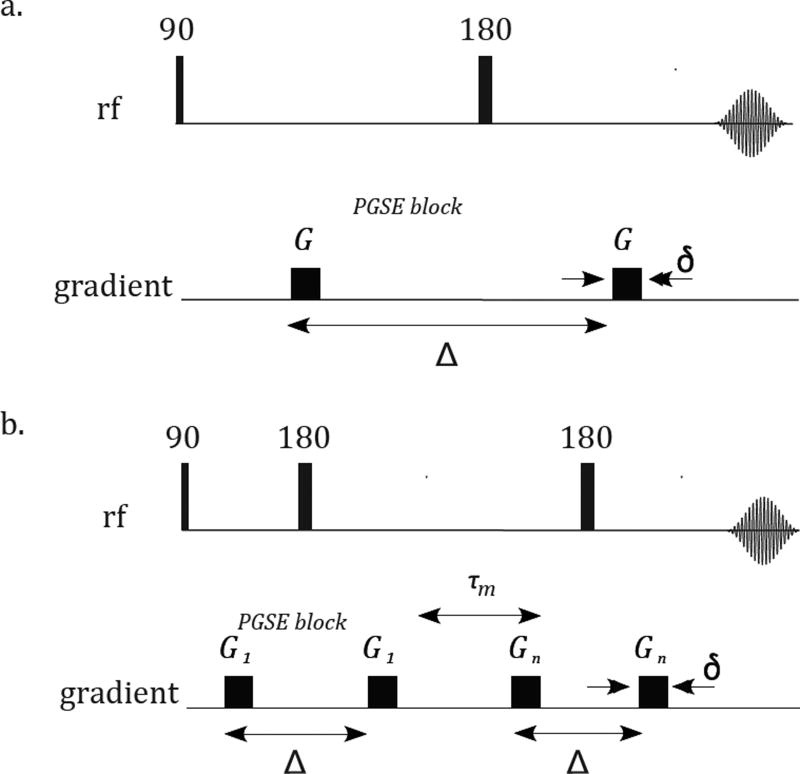
Figure 1.

Pulse sequences of a. Pulsed-field gradient [18], encoding net displacements; b. Double pulsed-field gradient, encoding diffusion correlation.

The objective of this study was to apply a 3D implementation of the dPFG acquisition and modeling of axon diameters to a recently developed closed-head impact model of engineered rotation acceleration (CHIMERA) that induces DAI in the mouse brain in select white matter tracts, including the optic tract [5]. We present pilot results in using the dPFG method to detect cellular alterations in the CHIMERA injury model by comparison of the more conventional FA metric computed from DTI with the AMD metric in the optic tract.

2. Materials and Methods

All animals were housed and treated according the national animal care guidelines and institutional oversight by the NIH/NIAAA IACUC. Brain specimens were obtained from two mice (C57BL/6N, males), one following CHIMERA injury and one with a sham injury (i.e., placed in device, but without impact). The CHIMERA [5] involves delivering an impact of a defined energy to a mouse head. During impact head motion is not constrained. The injury is caused by shear force developing within the brain following impact. Note, this injury model affects predominantly white matter while the skull remains intact. The injury was induced with 0.5J impact energy and repeated three times with 24 hour interval between injuries. One week after the third injury, mice underwent transcardial perfusion with cold 4% formaldehyde in PBS and the fixed brains were removed from the skull. Following a 24 hour post-fixation period in 4°C, brains were rehydrated and stored in PBS with % sodium azide prior to MRI scanning.

All experiments were performed on a 7 T Bruker vertical wide-bore magnet with an AVANCE III MRI spectrometer equipped with a Micro2.5 microimaging probe and three GREAT60 gradient amplifiers, which have a nominal peak current of 60 A per channel. This configuration can produce a maximum nominal gradient strength of 24.65 mT m⁻¹ A⁻¹ along each of the three orthogonal directions. The ambient temperature of the magnet bore was 16.8°C.

Diffusion tensor imaging (DTI) MRI data were acquired using a 3D EPI MRI sequence with the following MRI parameters: echo time (TE)/ repetition time (TR)=23/700 ms, 8 segments, and voxel resolution of 100 100 100 µ_m³; DTI parameters were: gradient pulse duration, δ, of 3 ms, diffusion time, Δ, of 20 ms, and the b-value (b = γ²δ²G²[Δ δ/3], where γ is the gyromagnetic ratio and G is the diffusion gradient amplitude) of 400 and 2000 s mm⁻¹. DPFG imaging parameters were acquired with the same imaging parameters as the DTI. The dPFG filter parameters were τ_m = 0, δ 3 ms, and Δ = 20 ms. To define the diffusion gradient orientations in space, a spherical coordinate system was used. The angle between the two pulsed-field gradient (PFG) blocks, φ, was applied twice −0° and 180° for each orientation [14]. The diffusion data were acquired on three shells, representing different diffusion amplitudes, with q values (q = γ Gδ/2π) of 84.8, 71.6, and 56.6 mm⁻¹, each with 37, 16, and 7 uniformly distributed orientations on a hemisphere, respectively. The directions along each shell are independent of the other shells, providing additional spatial and directional information due to more homogeneous sampling of the space. A comprehensive description, including the pulse sequence scheme and gradient orientations, is provided elsewhere [14].

High resolution T2-weighted images were acquired to serve as anatomical templates for registration of the DTI and dPFG data during correction for image distortions/artifacts due to the EPI acquisition. A 3D spin echo sequence was used with TE/TR = 40/2000 ms, voxel resolution of 100 100 100 µm³. First, the Diffusion-weighted data were registered to the T₂-weighted structural image and processed using the TORTOISE software package [19]. Non-linear fitting was used to calculate the DTI metrics such as the eigenvectors, FA maps, mean and axial diffusivities, and the amplitude image with no diffusion sensitization (A_b=0). Manual segmentation was performed on A_b=0 of the injured and sham brains to define the optic tract region of interest (ROI), resulting in left and right optic tracts ROIs (total of four) later to be used to calculate the mean FA and AMD. To perform a voxelwise estimation of the AMD, the optic tract axons were modelled as a pack of impermeable parallel cylinders of infinite length with a known orientation. The dPFG signal attenuation from the restricted compartment (i.e., axons) was computed using the multiple correlation function (MCF) method [20–22]. In addition to diffusion within the axons, the extra-axonal diffusion was modeled as Gaussian [23]. DTI-derived metrics were used to reduce the complexity of the AMD estimation model. In each voxel, the tensor’s main eigenvector was assumed to indicate the orientation of the par-allel cylinders [14]. In addition, the DTI-derived mean and axial diffusivities were assumed to be the intra-and extra-axonal diffusivities in the AMD estimation, respectively. All data processing was performed with in-house code written in MATLAB (The Mathworks, Natick, MA).

Immunohistochemistry for axonal neurofilament protein was performed in slices from each brain containing the optic tract to detect the presence of axonal varicosities in this location. After a cryoprotection by a series of sucrose solutions, brains were frozen and cryosectioned with 20 µm slice thickness. Floating sections in which the optic tract was evident were selected for IHC using the primary antibody rabbit anti-NF light chain (Cell Signaling #2837, Danvers, MA, 1:200) and secondary an-tibody Alexa Fluor 488 (Thermo Fisher, Waltham, MA, 1:500). Stained sections were imaged using a Zeiss 700 laser scanning confocal microscope with FITC filters and a 63x** oil immersion objective. Images were acquired for the left and right optic tract of each brain.

3. Results and Discussion

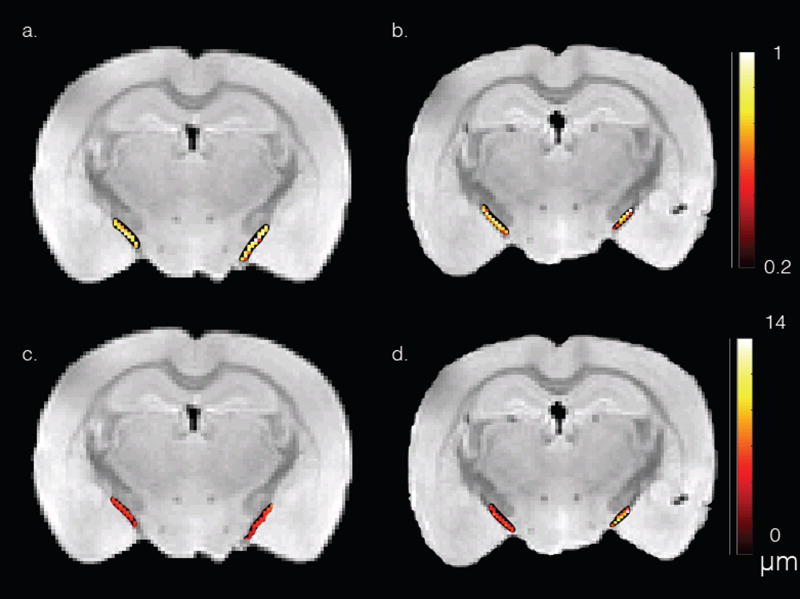
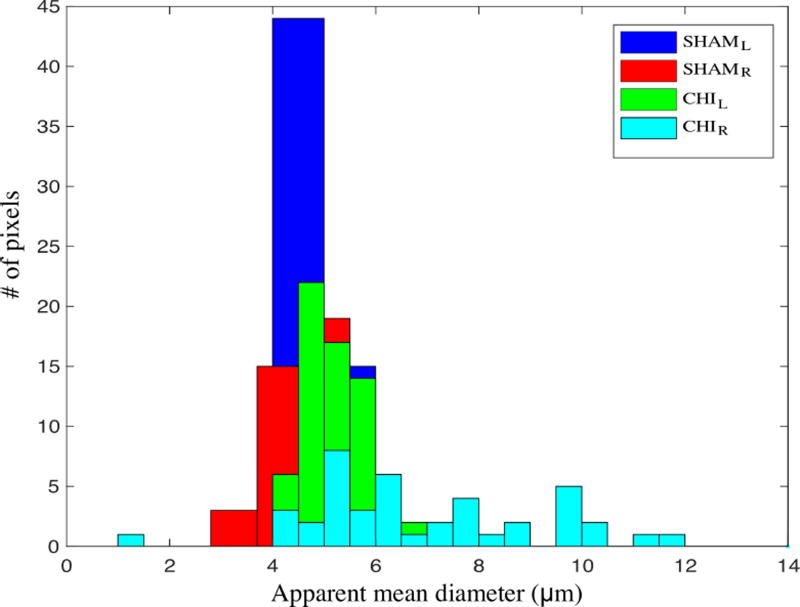
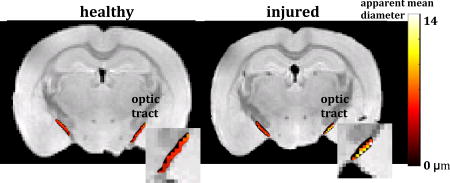
Figure 2 shows the DTI fractional anisotropic (FA) (a–b) and dPFG AMD (c–d) maps of the optic tract overlay a structural image of the sham (a, c) and CHIMERA (b, d) mouse brains. ROIs comprising the optic tract show mean FA of 0.66 and 0.75 for the right and left optic tract of the CHIMERA, and 0.79 and 0.78 for the right and left optic tract of the sham, respectively. The lower FA value of the right CHIMERA optic tract vs. the sham is consistent with injury at this location [24]. ROI analysis of the dPFG data shows AMD of 8.6 µm and 5.4 µm for the right and left optic tracts of the CHIMERA and 4.8 µm and 5.2 µm of the right and left optic tract of the sham, respectively. The estimated AMD of the right CHIMERA brain is noticeably larger compared with than that of the sham mouse. Figure 3 shows a histogram of the AMDs within the optic tracts. Note the tight distribution of diameters in the sham and left optic tract of the CHIMERA while the right optic tract shows a broader distribution of diameters. Both the AMD map and the histogram of the right CHIMERA brain points to an axonal damage at the same site detected by DTI, indicating alteration in the tissue microstructure are likely due to axonal varicosities and axonal loss. The left optic tract of the CHIMERA shows no significant decrease of FA, nor increase of AMD, suggesting an asymmetrical degree of severity of the injury that commonly occurs in DAI.

Figure 2.

DTI FA (a–b) and dPFG AMD (c–d) maps of the optic tract overlay a structural image of the sham (a, c) and CHIMERA (b, d) mouse brains.

Figure 3.

Histogram of AMDs within the CHIMERA and sham optic tracts.

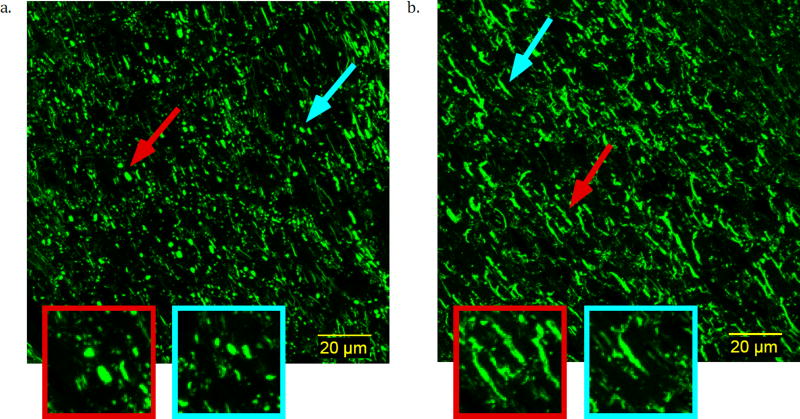
The presence of axonal varicosities (Figure 4a), which is a characteristic pathology of mild TBI, in the CHIMERA injured brain, but not the sham brain (Figure 4b) was demonstrated by neurofiliament immunohistochemistry. Axonal morphology appeared to be normal in the optic tract of the sham brain with linear shape and consistent spatial dimensions across axons. In the optic tract of the injured brains, features were found that are consistent with axonal varicosities. While this suggests that changes in axonal morphology may contribute to the detected abnormalities in dPFG and FA values, it is important to note that other cellular alterations (e.g. reactive gliosis or myelin abnormalities), which were not investigated in this study are likely also present in addition to the observed axon varicosities.

Figure 4.

Confocal microscopy images of immunohistochemistry for axonal neurofilament protein in the optic tract of a. CHIMERA and b. sham mouse brains. Examples for axonal varicosities (a) and normal shaped axon (b) are magnified.

4. Conclusion

dPFG MRI shows promise in detecting cellular and microstructural alterations between DAI injured and healthy brains. Efforts are underway to explore developing this method into a new quantitative imaging tool to detect TBI.

• A double-pulsed field gradient (dPFG) MRI sequence was proposed to detect diffuse axonal injury.

• Apparent mean axon diameters were estimated using dPFG MRI in injured and healthy fixed mouse brain tissue.

• Significantly different mean diameters were measured in injured and healthy tissues.