Abstract
In COPII mediated vesicle formation, Sec13/Sec31 heterotetramers play a role in organizing the membranes into a spherical vesicle. There they oligomerize into a cage that interacts with the other COPII proteins to direct vesicle formation and concentrate cargo into a bud. In this role they must be flexible to accommodate different sizes and shapes of cargo, but also have elements that provide rigidity to help deform the membrane. Here we characterize the influence the C-terminal disordered region of Sec31 has on cage flexibility and rigidity. After deleting this region (residues 820–1220), we characterized Sec13/Sec31ΔC heterotetramers biophysically and structurally through cryo-EM. Our results show that Sec13/31ΔC self-assembles into canonical cuboctahedral cages in vitro at buffer conditions similar to wild type. The distribution of cage sizes indicated that unlike the wild type, Sec13/31ΔC cages have a more homogeneous geometry. However, the structure of cuboctahedrons exhibited more conformational heterogeneity than wild type. Through localized reconstruction of cage vertices and molecular dynamics flexible fitting we found a new hinge for the flexing of Sec31 β-propeller domain and more flexibility of the previously known hinge. Together, these results show that the C-terminal region of Sec31 regulates the flexing of other domains such that flexibility and rigidity are not compromised during transport of large and/or asymmetric cargo.
Keywords: Vesicle trafficking, Cryo-EM, Subparticle refinement, Coat protein complex, Membrane remodeling
Introduction
Transport of cargo in the early secretory pathway from the endoplasmic reticulum (ER) to the cis-Golgi apparatus is mediated by coat complex II (COPII) proteins. It has been estimated that up to one-third of proteins translated from the eukaryotic genome are transported through this pathway (Ghaemmaghami et al., 2003). The COPII coat assembles on the ER membrane at socalled ER exit sites (ERES) and forms vesicles or tubules that ultimately bud off to be delivered and fused with the Golgi cisternae (Barlowe, 1994; Rothman and Wieland, 1996; Schekman and Orci, 1996). The minimal components required for vesicle formation in vitro are five cytosolic proteins that are sequentially recruited to the ER membrane forming an inner coat made of Sar1, a middle coat made of Sec23/24, and an outer coat made of Sec13/31 (Matsuoka et al., 1998; 2001). The GTPase Sar1 in its GTP-bound state, inserts an amphipathic helix into the ER bilayer to increase its flexibility (Bi et al., 2007; Huang et al., 2001; Nakano and Muramatsu, 1989). Sec23, the GTPase activating protein (GAP) of Sar1 (Yoshihisa et al., 1993), forms a bow-tie shaped complex with Sec24 which is an adaptor for cargo recruitment (Bi et al., 2002). The outer coat consists of Sec13/31 heterotetramers or so-called edges that form a lattice to provide structural support for vesicle/tubule formation (Fath et al., 2007; Noble et al., 2012; Stagg et al., 2006). Together, the proteins impose curvature on ER membrane leading to its complete budding while maintaining the structural integrity of the coat complex. Sec13/31 edges alone can self-assemble into cuboctahedron or icosidodecahedron structures in vitro depending on pH, salt concentration, and protein concentration (Stagg et al., 2008).
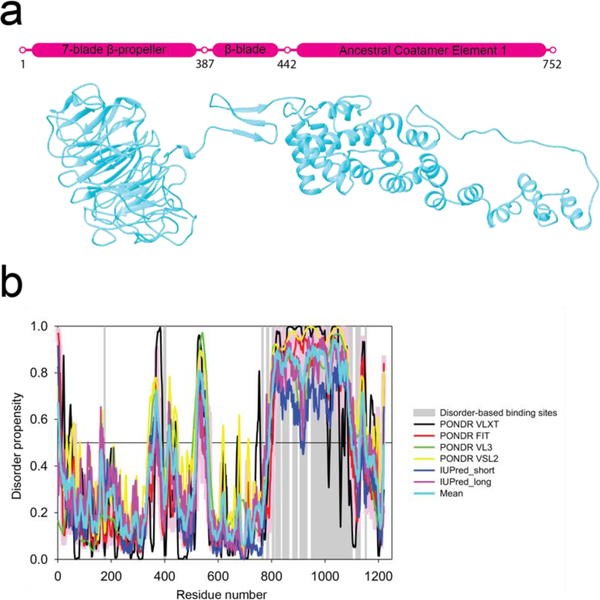
Sec31 is a relatively large ~139 kDa protein made up of several domains with an N-terminal 7-bladed β-propeller domain that is connected via a coil region to a smaller region made up of three β-strands (β-blade) that form the interface for binding Sec13 (Fig. 1a). This in-turn connects via another coil region or the so-called hinge (Copic et al., 2012a; Noble et al., 2012) to an ancestral coatamer element 1 (ACE1) domain made up of a series of α-solenoids followed by a C-terminal proline-rich disordered region which ends in a small α-helical domain (Brohawn et al., 2008). Sec13 is comprised of a 6-bladed β-propeller domain and binds with Sec31 by incorporating Sec31’s three free β-strands into its open region to form a 7-bladed β-propeller that sits between Sec31’s β-propeller and ACE1 domains (Fath et al., 2007). Sec13/Sec31 dimer then homodimerizes by a domain swap of two Sec31 ACE1 domains to form a complete Sec13/31 heterotetramer. The Sec13/31 heterotetramer is the assembly unit for the COPII cage where it oligomerizes to form a geometric lattice. The Sec13/31 heterotetramers form the edges of the lattice, and their assembly is mediated by interactions between the β-propeller domains at either end of the edges (Fath et al., 2007; Noble et al., 2012).
Figure 1.
Sequence analysis of Sec31. a) Schematic diagram and flexibly fitted model from crystal structures of Sec31 domains (ΔC half-edge model derived from wt map) (Noble et al., 2012). Marked residues 387–442 contain the Sec13 binding β-sheet and the two coil regions connecting it to the N-terminal β-propeller domain and the C-terminal ACE1 domain. The latter coil region is also known as the hinge which enables the flexing of the ACE1 domain (Fig 5e). Residues 752–1273 (not shown) are known to constitute a disordered region for which there is no crystal structure or electron-microscopy map which is followed by a small α-helical domain. b) Intrinsic disorder propensity analysis of human Sec31A sequence by a set of commonly used disorder predictors, PONDR® VLXT, PONDR® VL3, PONDR® VSL2, IUPred_long and IUPred_short. Mean disorder propensity represent averaged disorder scores per residue from six individual predictors (indicated in the figure legend). All the scores consistently indicate a high disorder propensity (above 0.5) for the C-terminal region except for the small α-helical domain. Positions of potential disorder-based binding sites found by ANCHOR are shown by gray shaded areas.
In vitro, Sec13/31 can self-assemble into cages with different geometries (Stagg et al., 2008). In the absence of any other proteins, the most common geometry is a cuboctahedron, where 24 Sec13/31 heterotetramers form the edges of the cuboctahedron. In this structure, there are 12 X-shaped vertices with 2-fold symmetry that are formed by the intersection of four different edges. The structure of the Sec13/31 cuboctahedron has been determined by cryo-EM (Noble et al., 2012; Stagg et al., 2008; 2006; Zanetti et al., 2013; Zeuschner et al., 2006), and atomic models of the complete cages can be determined by flexibly fitting the crystal structures of domains of Sec13 and Sec31 into the EM density map (Fath et al., 2007; Noble et al., 2012). This revealed that the assembly of cages is mediated by the interactions of Sec31 β-propeller domains at the center of the cage vertices. The only regions of Sec13/31 that have been resolved structurally are the β-propeller and αsolenoid domains that comprise Sec13 and 2/3 of the sequence of Sec31. However, the Cterminal 1/3 of Sec31 has remained structurally elusive. In the crystal structure of yeast Sec13/31 (PDB ID: 2PM6), the C-terminal region (residues 764–1273) was removed from the expression construct. The cryo-EM structures were determined from full-length human Sec13/31 proteins, but the C-terminal regions were completely unresolved, suggesting that that region is disordered (Gürkan et al., 2006). In order to establish a common terminology in this manuscript, it should be noted that there are two crystal structures of Sec13/31: 1) 2PM9 is the crystal structure of Sec13 and the B-propeller domain of Sec31, and 2) 2PM6 is the crystal structure of Sec13 and the ACE1 domain of Sec31 which we refer to as “ΔC crystal structure” because it lacks the C-terminal region. By aligning these two crystal structures with respect to Sec13, one can get an edge/heterotetramer model which we refer to as “ΔC edge model”. Building on this terminology, we refer to the ΔC edge model flexibly fitted to the cryo-EM map of full-length Sec13/31 as “ΔC edge model derived from wt (wild-type) EM map, or wt map for brevity”.
Despite being unresolved structurally, the C-terminal region is important functionally. It is the region that contains the Sec23/24 binding site (Bi et al., 2007), which is crucial to couple cage formation with the binding of cargo proteins and membrane, and it also contains a peptide that has been shown to promote Sar1’s GTPase activity (residues 899–947) (Bi et al., 2007). Additionally, there is some evidence indicating that it could have a structural role. Hydrogen/deuterium exchange experiments on edges vs. cages (Noble et al., 2012) showed that a small region in between residues 1,000 and 1,100 shows a significantly lower H/D exchange rate after edges are assembled into cages (>40% difference). These data indicate that this region might make contact with other domains after cage assembly. Another piece of evidence that points to a possible role for the C terminal residues is the observation that the central angle of the α-solenoid region of the Sec13/31 heterotetramer changes from 165° in the ΔC crystal structure to 135° in the wt map and subsequently the ΔC edge model derived from that wt map. This difference in the central angle might be attributed to the presence of the C terminus in the full-length Sec13/31 used for cryo-EM images and its absence in the ΔC crystal structure.
We hypothesized that by removing the C terminal disordered residues we can investigate whether or not this region is involved in cage assembly and flexibility. Here, we show that Sec13/31ΔC heterotetramers are able to form cages in vitro at the same pH and salt concentration at which the wt Sec13/31 edges self-assemble to cages but that there is a concomitant increase in the heterogeneity of the conformation of heterotetramers that comprise the Sec13/31 cages. Altogether, our data suggest that the C-terminal disordered region plays a role in regulating flexibility of the COPII cage.
Methods
Computational analyses of intrinsic disorder predisposition of human Sec31 proteins
Intrinsic disorder propensity of human Sec31A protein (UniProt ID: O94979) was analyzed using several established per-residue disorder predictors, each having a unique strength, including PONDR® VLXT (Romero et al., 2001), PONDR® VSL2B (Obradovic et al., 2005), PONDR® VL3 (Obradovic et al., 2003), IUPred (Dosztányi et al., 2009), and PONDR® FIT (Xue et al., 2010). PONDR® VLXT has high sensitivity to local sequence peculiarities and can be used for identifying disorder-based interaction sites (Dunker et al., 2001). PONDR® VSL2B is an accurate, stand-alone disorder predictor (K. Peng et al., 2005; Z. Peng and Kurgan, 2012; Uversky et al., 2000) whereas PONDR® VL3 is characterized by high accuracy for predicting long intrinsically disordered regions (Obradovic et al., 2003). IUPred was designed to recognize intrinsically disordered protein regions from the amino acid sequence alone based on the estimated pairwise energy content (Dosztányi et al., 2005a; 2005b). As a metapredictor, PONDR-FIT is moderately more accurate than each of the component predictors.
For each test, scores above 0.5 correspond to the disordered residues/regions. We also calculated the mean disorder propensity by averaging disorder profiles of individual predictors because empirical observations report that use of consensus for evaluating intrinsic disorder can increase the predictive performance over the use of a single predictor (Walsh et al., 2015).
Since disordered regions of many proteins are known to contain specific disorder-based protein-protein interaction sites, we utilized the ANCHOR computational tool (Dosztányi et al., 2005b; Mészáros et al., 2009) to look for predictable sites that undergo disorder-to-order transitions when interacting with specific partners. This approach relies on the pairwise energy estimation approach developed for the general disorder prediction method IUPred (Dosztányi et al., 2005b; 2005a), being based on the hypothesis that long regions of disorder contain localized potential binding sites that cannot form enough favorable intrachain interactions to fold on their own, but are likely to gain stabilizing energy by interacting with a globular protein partner (Dosztányi et al., 2009; Mészáros et al., 2009).
Sample preparation for cryo-EM
Sec13/31ΔC heterotetramers were prepared similarly to Stagg et al. (Stagg et al., 2006). Briefly, wt Sec13/31 protein are co-expressed using baculovirus infected insect cells, using the pFastBAC dual expression system (ThermoFisher). For the Sec13/31ΔC construct, the Sec31 gene was truncated to the first 820 amino acids of the full 1205 residue sequence. Proteins were expressed in baculovirus infected Sf9 cells. Sec13 has an N-terminal 6× His tag, and Sec13 pulls down Sec31 during purification. Sf9 extracts were purified by immobilized metal affinity chromatography followed by anion exchange and size exclusion. The purified proteins were assembled into cages by dialysis into cage buffer consisting of 20 mM Tris–Cl, pH 7.5, 700 mM KOAc, 1 mM MgOAc, 10 mM DTT. Following assembly, cages were prepared for cryo-EM by placing 3 μL onto a Quantifoil R2/2 400 mesh holey carbon grid that had been plasma cleaned for 12 s using a Gatan SOLARIS model 950 advanced plasma cleaner and blotting using a Vitrobot Mark IV (FEI).
Cryo-EM image collection and processing
Approximately 4000 images were collected on a Titan Krios at 300 kV voltage, spherical aberration of 2.7 mm, nominal defocus range of 2–4 μm, and with a DE20 camera with a pixel size of 2.03 Å/pixel and a box size of 448 pixels for the picked particles. 13000 particles were selected. These particles were sorted into 5 classes using RELION (Scheres, 2012), using an initial model from a previously refined wt Sec13/31 cage structure low-pass filtered to 60 Å. Particles from four of these classes were used for further refinement, with the same initial model settings. The Euler angles from this refinement and octahedral symmetry operations were used for subparticle extraction by localized reconstruction script with unit vector’s coordinates of 0.707, 0.707, 0 for xyz, respectively, and a vector length of 250 Å (Fig. S1). The extracted image size was set to 200 pixels. A new stack of 150k subparticle images was created and used for further processing. An initial reconstruction of all of the subparticle images created after their extraction and based on computed Euler angles was used as a checkpoint for the quality and success of the procedure. These images of vertices were then sorted into 5 classes using RELION and treated just as single particles. The initial model used for this classification was a vertex extracted from the density map of the refined cage structure from the same dataset; the same vertex density map was used to make a custom mask. For this classification, the oversampling parameter of relion_refine was set to zero, and the healpix_order parameter was set to 3, as opposed to classification of cages where these parameters were set to 1 and 2, respectively. Two of these classes from iteration 11 (out of 13) which are reported here were chosen for further analysis. Classification with a higher number of classes did not result in an improvement in the resolution of the vertices. Another procedure for classifying vertices was also carried out in which the extracted vertex images were classified without alignment and then each class was individually refined. The refined vertices were similar to those of the above procedure. Other software packages for refining cages were also tested which due to heterogeneity in the dataset were not able to improve the resolution.
Molecular dynamics flexible fitting
The ΔC edge model derived from wt map was initially rigidly fitted into the four edges of each of the two classes of vertices, making sure that they follow the plus and minus-end pattern. These models of vertices and their density maps were then used for molecular dynamics flexible fitting. The fitting was carried out with the constraints that preserve hydrogen bonds, dihedral angles, chirality, and cis/trans configuration of peptide bonds in order to preserve all secondary structures. The simulation time was set to 2.5 ns and the gscale to 0.3 for both cases.
Analytical ultracentrifugation
Sedimentation velocity analytical ultracentrifugation experiments were performed in a Beckman XL-I centrifuge (Beckman Coulter, Inc.) using absorbance optics and measuring intensity scans at 280 nm. The experiments were performed at 20°C in two-channel Epon centerpieces with an AN60 Ti rotor at 12.5k rpm and using 6 μM of Sec13/31ΔC and 12 μM of wt Sec13/31, equilibrated in cage buffer (20 mM Tris–Cl, pH 7.5, 700 mM KOAc, 1 mM MgOAc, 10 mM DTT). Data were analyzed using the UltraScan II version 9.9 software suite (Demeler, 2007; Schuck and Demeler, 1999). All computations were performed on the TIGRE cluster at the University of Texas Health Science Center at San Antonio and the Texas Advanced Computing Center at the University of Texas in Austin. All data were first analyzed by two-dimensional spectrum analysis (Brookes et al., 2009) with simultaneous removal of time-invariant noise, and then by genetic algorithm refinement (Brookes and Demeler, 2007), followed by Monte Carlo analysis (Demeler and Brookes, 2007). The partial specific volumes at 20°C of Sec13/31 (0.7309 cm3∕g) proteins were estimated from peptide sequence as described by Durchschlag (Durchschlag, 1987).
Dynamic light scattering
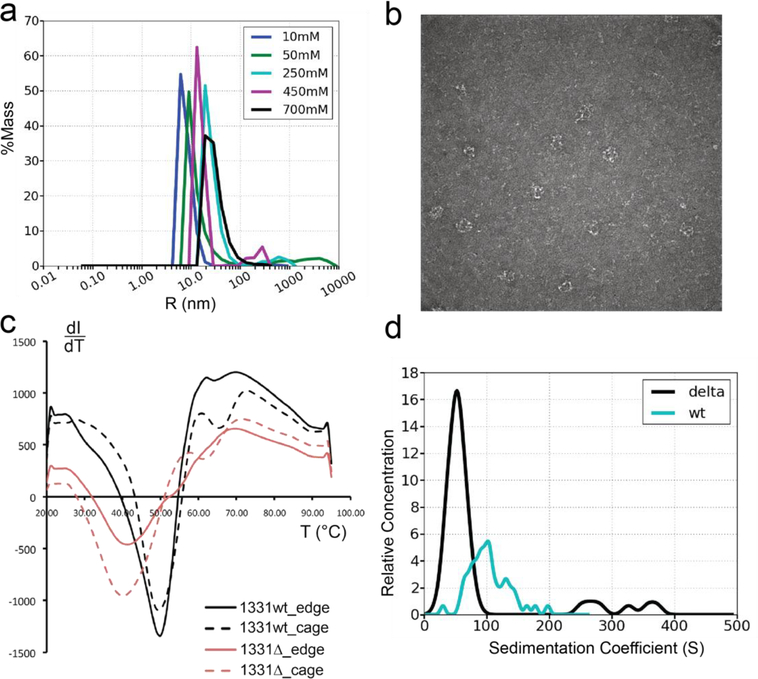
DLS data were acquired at 20°C using Wyatt DynaPro DLS system with Dynamics® V7 and analysis was carried out using Dynamics® V7.0.0.95. The intensity autocorrelation function provides a direct indicator of the size distribution of the sample. The poly-dispersity index provides a direct measure of the heterogeneity of the molecular species in sample. A total of 10 measurements were performed for each sample, Sec13/31ΔC at pH 7.5 contains larger species than at any other pH value, which was indicated by the longer rate of decay in the autocorrelation function. The histogram from the regularization fit of the autocorrelation function graph in figure 2a shows the size distribution of Sec13/31ΔC at different salt concentrations (10 mM, 50 mM, 250 mM, 450 mM, 700 mM) with a constant pH of 7.5, while the histogram from the regularization fit of the autocorrelation function graph in supplementary figure 2c shows the size distribution of Sec13/31ΔC at different pH (pH 5.5, pH 6.5, pH 7.5, pH 8.5) with a constant salt concentration of 700 mM KOAc.
Figure 2.
Biophysical characterization of Sec13/31ΔC compared to wt Sec13/31. a) Distributions of hydrodynamic radii obtained from dynamic light scattering on Sec13/31ΔC heterotetramers in buffers with 10mM, 50mM, 250mM, 450mM, and 700mM concentrations of KOAc. wt Sec13/31 heterotetramers form cages with a diameter of 60nm at 700mM concentration of KOAc. As the graph indicates, the peak of the hydrodynamic radii distribution shifts to a bigger radius as the salt concentration reaches 700mM. The peak of the curve corresponding to 700mM actually happens at 33.7nm which is smaller than the expected value of 60nm. This is in part due to the high ionic concentration medium which reduces the measured hydrodynamic radius indirectly. b) Exemplar negative-staining image of COPII cages made of Sec13/31ΔC and formed in 700mM KOAC buffer. c) Assessing the thermodynamic stability of edges and cages made of wt Sec13/31 and Sec13/31ΔC. Edges and cages are represented by solid lines and dashed lines, respectively, and the wt and the construct are represented by black and red curves, respectively. The cages have an additional minimum in the curve compared to the edges at a temperature of 65 °C for the wt and 62 °C for the ΔC construct. This difference between the melting behavior of cages and edges is attributed to the structural difference between the two structures, namely, the β-propeller contacts that are essential for cage assembly. Although the difference between the wt and the construct for this minimum is small, the difference between the two for the first minimum is around 10 °C. This minimum is attributed to the edge domains that are not involved in the β-propeller contacts at the center of the vertices such as the flexible ACE1 domain. d) Distribution of particle sizes for wt Sec13/31 and Sec13/31ΔC in cage-assembly buffer. According to literature, the sedimentation coefficient of cuboctahedrons is around 60 S. Both histograms show an abundance of particles at that size, but the ΔC construct is more constrained and homogenous in terms of particle size.
Differential scanning fluoremetry
Samples were 5 μM with a total volume of 48 μl. 2ul SYPRO Orange was added to each. Samples were prepared in triplicate and loaded on PCR plates. For cages, buffer used was 700mM KOAc and for edges the buffer used was 50 mM KOAc. Data were collected on BIO-RAD C1000 Thermal cycle. Cycle was set to hold for 30 seconds at 20°C and then scanning started from 20°C to 95°C with an increment of 1°C. Scan mode was set to FRET. Data was also collected for buffer and SYPRO orange (control) in triplicate from which the average was calculated and subtracted from the protein sample signal.
Map deposition in EMDB
The two subvolume reconstructions class 1 and class 2 were deposited in the EMDB under accession number EMD7527 with class 1 as the primary and class 2 as the accompanying maps.
Results
We first analyzed the Sec31 sequence to assess the likelihood that the C terminal residues were intrinsically disordered. This computational analysis was performed on the human Sec31A sequence (UniProt ID: O94979). The disorder propensity scoring per residue using was assessed using a set of commonly used disorder predictors, such as PONDR® VLXT (Romero et al., 2001), PONDR® VSL2B (Obradovic et al., 2005), PONDR® VL3 (Obradovic et al., 2003), IUPred (Dosztányi et al., 2009), and PONDR® FIT (Xue et al., 2010) (Fig 1b). The mean disorder propensity was also calculated by averaging disorder profiles of individual predictors, because empirical observations report that use of consensus for evaluating intrinsic disorder can increase the predictive performance over the use of a single predictor (Z. Peng and Kurgan, 2012; Walsh et al., 2015). In this analysis, disorder propensity score lies between 0 and 1, with scores above 0.5 indicating a high disorder propensity. This analysis consistently indicated a high disorder propensity for the C-terminal region of human Sec31A (Fig. 1b).
It is known that many intrinsically disordered proteins and regions are involved in promiscuous protein-protein interactions (Dunker et al., 2001; 2002a; 2002b; Dunker and Uversky, 2008; Oldfield et al., 2005; Radivojac et al., 2007; Tompa, 2002; Uversky, 2013; 2012; 2011; Uversky and Dunker, 2010; Uversky et al., 2005) and can undergo at least partial folding (disorder-to-order transition) upon binding to their specific biological partners (Dunker et al., 2001; Dyson and Wright, 2005; 2002; Mohan et al., 2006; Oldfield et al., 2005; Uversky, 2013; Uversky et al., 2000; Vacic et al., 2007; Wright and Dyson, 1999). These potential disorder-based binding sites are characterized by specific sequence patterns, and therefore they can be identified by several specialized computational tools, such the ANCHOR algorithm (Dosztányi et al., 2009; Mészáros et al., 2009). Of note, this analysis identified several disorder-based binding regions in human Sec31A that are preferentially concentrated within the C-terminal domain (residues 173 – 178, 396 – 405, 763 – 769, 781 – 790, 802 – 810, 815 – 833, 841 – 865, 879 – 896, 906 – 933, 948 – 1102, 1115 – 1132, and 1150 – 1155). Fig. 1b shows that of 12 such disorder-based binding regions found in Sec31A, 10 are located within the highly disordered C-terminal tail. Curiously, this analysis shows that almost entire C-terminal region (residues 750–1220) can serve as a disorder-based binding platform, since 295 of 470 residues in this region can be engaged in disorder-based protein-protein interactions. Importantly, one of these predicted binding regions (residues 948–1102) includes the aforementioned 1,000–1,100 region that shows a noticeable decrease in the H/D exchange rate due to the assembly of edges into cages (Noble et al., 2012). Also, a region shown to promote Sar1’s GTPase activity (residues 899–947) (Bi et al., 2007) includes another predicted disorder-based binding region (residues 906–933). Finally, predicted binding site located between residues 841 and 865 includes ALG-2-binding site motif-2 (residues 842–848) (Takahashi et al., 2015). Therefore, this computational analysis provides strong evidence that the C-terminal tail of human Sec31A protein, despite being highly disordered, is functionally important, housing a number of disorder-based binding regions.
Characterization of Sec13/31ΔC cage formation activity
Given the observation that the C-terminal region is largely unstructured, we deleted it in order to characterize the effect the truncation would have on the structure of Sec13/31 cages. The C-terminal residues 820–1220 were deleted from our human Sec31 construct, and this truncated Sec31 variant was expressed together with Sec13 and purified as Sec13/31ΔC heterotetramers. Then, their biophysical properties were investigated and compared against the wt Sec13/31. First, the buffer conditions that are conducive to self-assembly of cages were examined and compared to literature values. It has been shown that wt Sec13/31 heterotetramers with a length of 20nm self-assemble to cages with a diameter of 60nm at a pH of 7.5 and a salt (KOAc) concentration of 700mM (Noble et al., 2012; Stagg et al., 2006). We used dynamic light scattering to look for such a transition in size while titrating salt or pH. In the salt titration assay, five different KOAc concentrations were probed: 10mM, 50mM, 250mM, 450mM, and 700mM. As the concentration of KOAc reached 700mM, the peak of the hydrodynamic radii distribution shifted to larger values indicating that the diameters of the particles in the buffer increased to sizes consistent with cuboctahedral COPII cages (Fig. 2a and Fig. S2a). The presence of cages was further confirmed by negative-staining imaging of the five different buffer conditions. While the lower concentration conditions were dominated by edges and vertices, the 700mM condition was dominated by cages (Fig. 2b).
Next, pH was changed at four different conditions: pH 5.5, 6.5, 7.5, and 8.5, and cage formation assessed by DLS (Fig. S2c). This showed that the optimal pH for cage formation for Sec13/31ΔC is 7.5, similarly to the wt. The salt titration and pH titration assays combined with DLS and negative-staining imaging demonstrated that Sec13/31ΔC can form cages in vitro at the same buffer conditions that support wt Sec13/31 cage assembly.
Next, the thermodynamic stability of Sec13/31ΔC assemblies was compared to wt Sec13/31 using differential scanning fluorimetry. Cages were formed for both Sec13/31ΔC and wt Sec13/31 by dialyzing the proteins into 700 mM KOAc. The thermal stability of both unassembled edges and assembled cages was assessed by collecting fluorescence intensity profiles for SYPRO Orange and the different proteins as a function of temperature. SYPRO Orange serves as an indicator for protein unfolding as its fluorescence intensity increases in the presence of hydrophobic residues (Boivin et al., 2013; Chari et al., 2015). The intensity derivative (with respect to temperature) vs. temperature curve of the melting of wt Sec13/31 edges indicates a single-transition melting behavior with a Tm of about 50 °C (Fig. 2c). Similarly, the melting curve of wt Sec13/31 cages indicates a Tm of 50 °C (Fig. 2c). However, there was also an additional transition point at a temperature of 65 °C in the melting curve of wt cages. The single-transition and double-transition behavior also holds for the edges and cages made of Sec13/31ΔC, respectively, where the first Tm shifted to 40 °C (20% decrease) and the second Tm has shifted to 62 °C (4.6% decrease). The emergence of the second transition point at ~65°C in the melting curve of the cages suggested that this transition represents the β-propeller contacts which mediate cage vertex assembly. The fact that the second transition point for Sec13/31ΔC cages occurred at a slightly lower temperature compared to wt suggests that the Sec13/31ΔC vertices are destabilized in some way. An even bigger difference between the wt and ΔC was observed in the temperature of the first transition point where the Sec13/31ΔC was at a 20% lower temperature than wt. This suggests that deleting the C-terminal region of Sec31 also destabilized regions of the protein not directly involved in cage formation, namely, Sec13 or Sec31’s ACE1 domain.
Given that wt and Sec13/31ΔC both readily form cages but have substantially different thermodynamic characteristics, we carried out analytical ultracentrifugation (AUC) in order to characterize the distribution of sizes of higher order assemblies that the proteins can form (Fig. 2d and Fig. S2b). We analyzed the sedimentation velocity of Sec13/31 wt and Sec13/31ΔC cages and determined the distribution of sedimentation coefficients of the different assemblies in those solutions. The wt sample had a broad size distribution centered between 60S and 150S. Previous studies have shown that cuboctahedral Sec13/31 cages have sedimentation coefficients of approximately 60S (O’Donnell et al., 2011). The broad distribution observed here demonstrates the range of sizes of assemblies that wt Sec13/31 can form including, concatenated cages (O’Donnell et al., 2011) where adjacent cages form an interlocking chain, cuboctahedrons (Stagg et al., 2006), and icosidodecahedrons (Stagg et al., 2008). The presence of some of concatenated cages in this sample was confirmed by negative staining (Fig. S2B). In contrast to the wt, the Sec13/31ΔC cages had a narrower distribution of sizes centered around 50S. This size is consistent with the formation of cuboctahedral cages, and the slightly smaller sedimentation coefficient for the cages is consistent with the loss of mass due to the deletion of the C-terminal residues. The observation that the distribution of sedimentation coefficients of the ΔC cages is reduced relative to the wild type suggests that it forms a more restricted range of sizes of cages and does not form concatenated cages.
Taken together, the biophysical analysis of Sec13/31ΔC results suggested that it can readily self-assemble into cuboctahedral cages but that the cages were perturbed in a way that doesn’t affect cage assembly. This suggested that the presence of the C terminal disordered region is not required for cage assembly but can affect the conformation of the edges. To characterize the contribution of the C-terminal region on the structure of cages, we carried out cryo-EM single particle analysis on Sec13/31ΔC cages.
Structural characterization of Sec13/31ΔC cages.
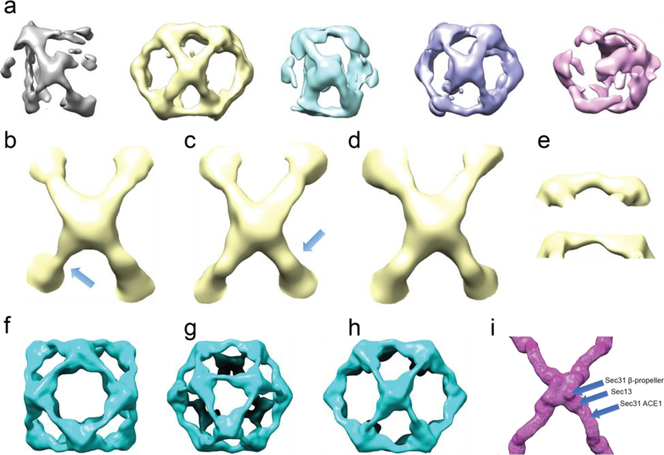
Cryo-EM images were collected for single particle analysis of Sec13/31ΔC cages (Fig. S3). ~13k particles were selected for refinement after picking, CTF estimation, and particle sorting. These particles were then sorted into five 3D classes using Relion (Scheres, 2012) without imposing symmetry (Fig. 3a). This showed that the particles refined with the same topology as a cuboctahedron, but all the structures were distorted, and none showed the octahedral symmetry expected for a cuboctahedron. Furthermore, only two of the classes showed well-defined density for all 12 cuboctahedral vertices (vertices of the yellow map in Fig. 3a (Fig. 3a, maps in yellow and purple). A close look at the -e) revealed heterogeneity among the edges and vertices that constitute the cage. One prominent difference was the curvature of the α-solenoid region of the edges (Fig. 3e). Visualization of the edges of the different cage structures revealed very broad contours consistent with the 40 Å resolution of the structures. Nonetheless, comparing different edges revealed that they have different curvatures, however, at that resolution it was not possible to fit a model into the densities to measure the underlying differences. Furthermore, the broad contours and low resolution also indicate even more heterogeneity between the particle images contributing to each class.
Figure 3.
Heterogeneous structures present in Sec13/31ΔC cages. a) 3D classification and alignment of particle images without imposing symmetry. All classes represented with different colors. The classes in yellow and purple show the most structural integrity of a Sec13/31 cage. b-d) Three different vertices from the cage class represented in yellow in a. The edges shown in e are pointed to with arrows in b and c. f-h) Symmetrically refined structure from the second and fourth classes shown in a. Panels f-h show views along the fourfold, threefold, and twofold symmetry axes, respectively. Due to symmetry, all the vertices look the same, and they represent an average of all the different conformations of vertices with a huge contour for the central density of the vertices which leaves a lot of room for different models to fit inside. i) Structure of a wt vertex for comparison. The positions of the three different domains that make up the whole vertex are marked. The density contours of Sec13 and Sec31 β-propeller domains in panels f-h are broader than that of the wt shown in i.
Neither the good classes, nor any combination of classes could be refined to higher resolution. Further refinement of the cage classes using RELION with imposed octahedral symmetry did not improve the resolution significantly, as can be seen in (Fig. 3f-h), because of the trade-off between the number of particles and homogeneity.
Localized reconstruction delineates vertex heterogeneity
Since the cage vertices are large enough to be treated as single particles for image processing (1,000 kDa), we employed the strategy of classifying and refining vertices individually in order to overcome cage heterogeneity (Fig. S1). The localized reconstruction method (Ilca et al., 2015) was used to extract and then classify/refine the individual vertices from all particles in all cages show1 represented in Figure 4a and class 2 represented in Figure 4b, with resolutions of 22 and 21 Å n in Figure 3a. Two prominent classes were identified, which we hereafter refer to as class (according to FSC0.143 without masking, Fig. S4), respectively. A comparison between each class and the vertex from the refined cage indicated that the two classes had better-defined density contours which in turn indicated that heterogeneity was partially eliminated.
Figure 4.
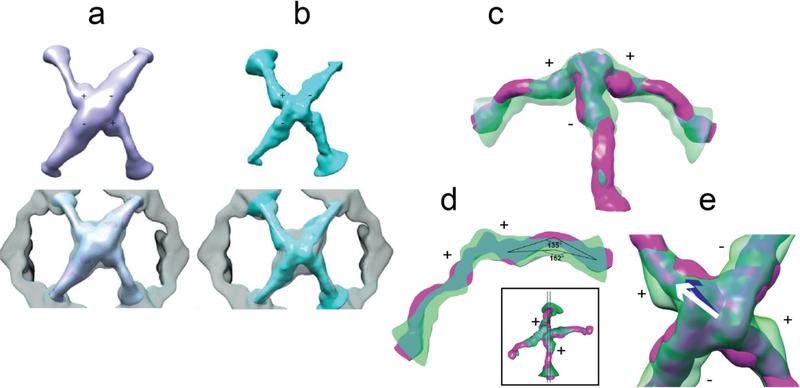
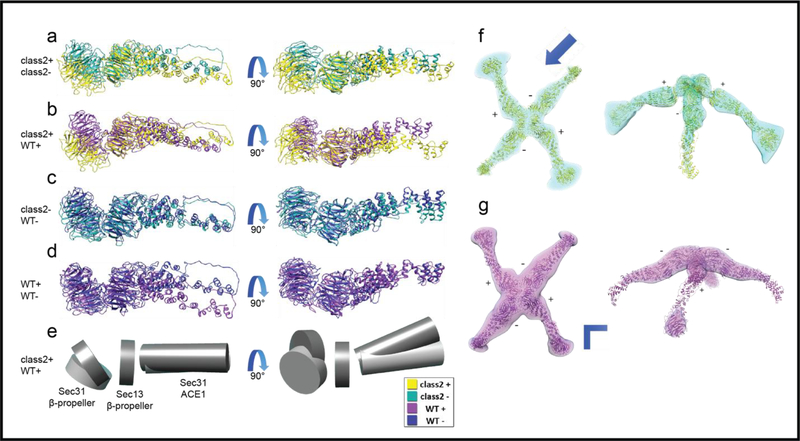
Two vertex classes from localized reconstruction and their comparison to Sec13/31ΔC and wt Sec13/31 vertices. a) Top: the top view of refined vertex class 1; bottom: comparison of density contours of the refined vertex versus an averaged vertex from the refined cage which is represented as the transparent density. The central density region of the refined vertex shows relatively better-defined contours which is an indicator of less heterogeneity. b) Same representation as in a for refined vertex class 2. c) Side view of class 2 (transparent green density), with its plus-ends lying in the plane of the page, and rigidly fitted to the wt vertex (magenta). The smaller curvature of ACE1 domain of plus ends of class 2 are easily noticeable as well as the shift of Sec13. d) A thin slice through the plus ends as shown in the small inset. The centers of Sec13 and ACE1 domain are used to measure the angles. Class 2 exhibits a less acute curvature (162°) than wt vertex (135°). e) A close look at the center of the vertex along the 2-fold symmetry axis. The center of wt Sec13 (blue arrow), the center of Sec13 of class 2 (white arrow), and the point on the 2-fold symmetry axis (the shared end of the arrows) lie in a plane perpendicular to the symmetry axis (the arrows are elevated for representation purposes). In that plane, the center of Sec13 shifts ~11 Å between class 2 and wt vertex.
Conformational differences between the two classes and the native structure.
Comparing the densities of the two subparticle classes to the previously published wt vertex density (Noble et al., 2012) revealed conformational deviations in conformations of both the edges and the vertices. Specifically, Class 2 exhibited two noticeable deviations (Fig. 4c-e). First, the curvature of the ACE1 domain of the plus-ends of class 2 were less acute (162°) than that of the wt (135°, Fig. 4d). Another prominent difference was the position of Sec13 in the plus-ends. The center of mass of Sec13 in the plus-ends of wt vertex moved about 11 Å to a new position in the flexed vertex (Fig. 4e), in a plane perpendicular to the 2-fold symmetry axis. Although the minus-end edges of class 2 exhibited less dramatic differences to wt vertex than its plus-end edges do, they also demonstrate shifts of Sec13 and Sec31.
A similar pattern was seen for the vertices contributing to class 1. The plus ends of class 1 have less acute curvature (148°) than that of the wt, while they are more curved than that of class 2 (not shown). Also, the Sec13 of plus ends of class 1 are shifted with respect to that of wt approximately 10 Å towards the center of the vertex in a plane perpendicular to the 2-fold symmetry axis. In order to better understand the conformational changes from wt to C-terminally truncated vertices, molecular dynamics flexible fitting (MDFF) was carried out to generate an atomic model of the flexed vertices (Trabuco et al., 2008).
Modeling the flexed vertices
When the ΔC edge model derived from wt map (Noble et al., 2012) was fit as a rigid body into the Sec13/31ΔC density, there were regions that were clearly outside of the Sec13/31ΔC contours (Fig. S5a). Thus, the structure was flexibly fitted into class 1 and 2 densities. The Sec31 β-propeller domains at the peripheral minus-ends and both of the Sec13/31 β-propeller domains at the peripheral plus-ends were trimmed off because their corresponding densities are averaged out in the two classes. The flexible fitting converged to new structures with an RMSD value of ~11 Å for class 1 and an RMSD value of ~12 Å for class 2, both with respect to the initial structures (Fig. 5f and 5g). We refer to these models as “ΔC models derived from ΔC maps”. We confirmed visually and also by calculating cross-correlation values that the flexible fitting of the ΔC model into the ΔC maps is an improvement over rigid-body fitting of ΔC models into ΔC maps (Fig. S5b). However, it is clear, given the modest resolution of the reconstructions that there is still a good deal of conformational flexibility that remains unresolved.
Figure 5.
Flexible fitting of ΔC edge models derived from wt map into ΔC maps. a) Left: superimposition of the plus end dimer (yellow) and the minus end dimer (green) of class 2, with the plane of the figure being the same as the plane which is normal to the four-fold axis of the cage, this view will be called the top view. Right: superimposition of the same dimers with a view perpendicular to the top view, this view will be called the side view. b) Left: superimposition of the plus end of class 2 and the plus end of the wt (purple), top view. Right: superimposition of the same dimers, side view. c) Left: superimposition of the minus end of class 2 and the minus end of wild type (blue), top view. Right: superimposition of the same dimers, side view. d) Left: superimposition of the plus end and the minus end of wild type, top view. Right: superimposition of the same dimers, side view. e) Schematic diagram of the domain shifts that illustrate a new hinge motion between the two β-propeller domains and a new mode of flexibility for the ACE1 domain. The plus-end of class 2 and wt are represented in light grey and dark grey, respectively, with a top view on the left-hand side and a side view on the right-hand side. f) Left: class 2 density and the flexibly fitted ΔC edge model. Right: side view along the arrow’s direction at a lower isosurface threshold. g) Left: class 1 density and the flexibly fitted ΔC edge model. Right: side view along the arrowhead’s direction at a lower isosurface threshold.
Conformational differences in Sec31 between the different classes and the wild type edges were identified by superimposing the ΔC models derived from ΔC maps”. We confirmed visually and also by calculating cross-correlation values that the flexible fitting of the ΔC model into the ΔC maps is an improvement over rigid-body C models derived from ΔC models derived from ΔC maps”. We confirmed visually and also by calculating cross-correlation values that the flexible fitting of the ΔC model into the ΔC maps is an improvement over rigid-body C maps on each other with respect to Sec13. In case of class 2, the superposition revealed a hinge motion between Sec13 and the Sec31 ACE1 domain that was previously observed for the wt vertex (Fig. 5a and 5d). This shift occurs in a plane normal to the four-fold axis of the cage. In addition to that motion, we identified another hinge motion perpendicular to the direction of the original hinge (Fig. 5a, right panel) that does not occur in the wt vertex (Fig. 5d, right panel). This suggested that in the absence of the C terminal residues, the hinge region gained additional flexibility compared to wt. Another difference with wt vertices was seen in the β-propeller domain in the Sec13/31ΔC structures. There the truncated Sec31 exhibited a shift between the relative positions of the Sec13 and Sec31 β-propellers respectively for the plus and minus ends of class 2, (Fig. 5a). This suggested the presence of a previously unobserved hinge (somewhere in between residues 335–391) that enabled the β-propeller domains of Sec13 and Sec31 to move relative to each other (Fig. 4e). The plus and minus ends of the flexed vertex were also compared to their wt counterparts. In the case of the plus end, the Sec31 β-propeller and ACE1 domains similarly underwent shifts between the two that were enabled by the same hinge regions (Fig. 5b). The minus end exhibits the same shifts in both domains in terms of directionality, only with the magnitude of the shift being smaller, (Fig. 5c). It is worth mentioning that the shifts in the domains of the plus end of class 2 effectively increase the length of the dimer. Together, these observations reveal more flexibility in the previously known hinge region, a new hinge region that can shift the β-propeller domain of Sec31, and a new effect which is the increased length of the dimer due to Sec31 domain shifts.
The same analysis was carried out for class 1. Similar to class 2, the ACE1 domain of class 1 exhibited the same shifts in terms of directionality between the plus and minus ends, (Fig. S6a and S6b). However, the shift in the β-propeller domain of Sec31 in class 1 was less substantial than that of class 2 and in this case the length of the minus end was effectively decreased, (Fig. S6b and S6f), which is opposed to the increased length of the plus end of class 2 (Fig. S7). Altogether, the structural analysis of the Sec13/31 dimer models generated from the two cryo-EM classes show that the deletion of the C-terminal region of Sec31 led to changes in the structure of the dimer which are mediated through the flexing of the well-known hinge region and a new hinge region that enables the movement of Sec31 β-propeller domain.
Discussion
In this study, we have investigated the structural role of the C-terminal disordered region of Sec31 (residues 820–1220). First, we set out to examine the effects of the deletion of the Sec31 C-terminal region on the biophysical characteristics of the Sec13/31ΔC heterotetramer. Salt and pH titration assays on Sec13/31ΔC followed by dynamic light scattering demonstrated a change in particle size distribution as the salt concentration and pH values approached 700mM and pH 7.5, respectively, conditions at which wt Sec13/31 self-assembles to cages. This observation along with visual inspection through negative-staining electron microscopy and sedimentation velocity AUC indicated that the deletion of the C-terminal region of Sec31 did not interfere with the ability of Sec13/31ΔC to form cages in vitro. Moreover, the AUC analysis showed that the Sec13/31ΔC cages showed less size heterogeneity than wt cages.
Cages made from Sec13/31ΔC were then prepared for cryo-EM to investigate the disordered region’s involvement in COPII cage structure. To our surprise, the resolution of the reconstructions of Sec13/31ΔC cages was significantly poorer than all the previously reported Sec13/31 cages despite being more homogeneous in size. This was explained by observing reconstructions without octahedral symmetry imposed on the cuboctahedral cages. The resulting reconstructions showed substantial asymmetry; they all showed edge topology consistent with cuboctahedrons, but they were all distorted relative to canonical cuboctahedrons (Fig. 3b-e). The distortions were not just at one vertex but instead propagated to all edges and vertices. By treating individual vertices as single particles using the localized reconstruction method (Ilca et al., 2015) we were able to characterize the conformational changes in Sec13/31ΔC that gave rise to these distortions. Two classes of well-defined vertices were obtained that showed significant improvement in resolution, which further demonstrates that we were able to successfully sort out some of the vertex heterogeneity. Additionally, the two classes show deviations from the wt vertex structure and also the initial model that was used to align/classify them which gives us confidence in the results.
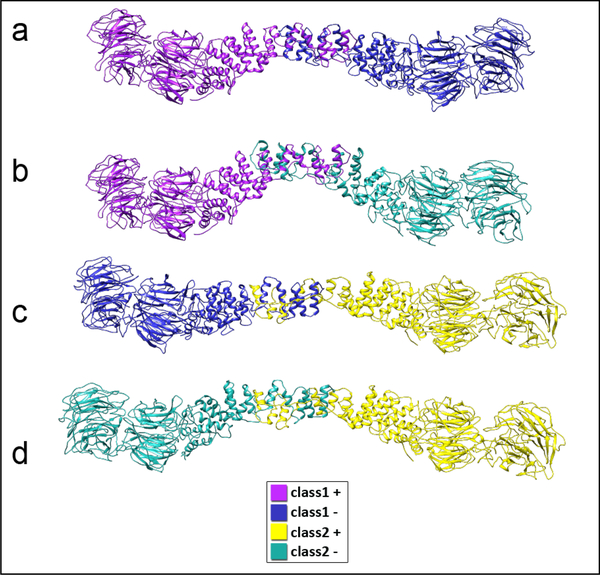
The conformational changes in Sec13/31ΔC that gave rise to the flexed vertices were characterized by flexibly fitting the Sec13/31ΔC edge model derived from wt map into the densities of the two classes of Sec13/31ΔC vertices. In a previous study, flexible fitting was carried out with the density map of an edge. Since the current study focused on vertices instead of edges, we were able to combine all the different observed conformations of Sec13/31ΔC to recapitulate the multiple edge conformations that arise from the flexed cages. Due to the twofold symmetry of the vertices, each vertex contains one unique plus end and one unique minus end. Since we reconstructed two classes of vertices, this resulted in four unique Sec13/31ΔC conformations which we used to reproduce four different asymmetric heterotetramer structures each containing both the plus and minus end conformations as they would appear in cages (Fig. 6). Although MDFF was carried out independently for the two classes, we observed that their flexibly fitted structures exhibit complementary features such that the ACE1 domain of the plus end of class 2 is longer than its wt counterpart, (Fig. 5b, right panel), whereas the ACE1 domain of the minus end of class 1 is shorter than its wt counterpart, (Fig. S6f). The significant difference in curvature of the recapitulated ACE1 domains (Fig. 6) is in accordance with the different edges shown in Figure 3e. Moreover, these conformations capture only a fraction of the possible conformations of Sec13/31ΔC dimers. It is likely that Sec13/31ΔC cages are continuously flexible, and this is evident in the relatively low resolution of our reconstructions despite classifying some of the conformational heterogeneity. Indeed, there are likely additional modes of flexibility that we have not characterized due to the high degree of conformational heterogeneity in the Sec13/31 ΔC sample. Additionally, we have captured edge conformations (Fig. 6c and Fig. 4d) that are similar to the yeast ΔC crystal structure of Sec31 (Fath et al., 2007) in terms of the central edge angle or curvature. Rigid-body fitting of the ΔC crystal structure and ΔC edge model derived from wt map into the reconstituted ΔC edge maps further confirms existence of conformations with varying central edge angle (Fig. S5c and S5d). Considering that all of these conformations lack the C-terminal region of Sec31, it can be concluded that the specific curvature of the ΔC crystal structure of Sec31 may be due to the absence of Sec31’s C-terminal region rather than a crystallization artifact.
Figure 6.
Reconstitution of possible heterotetramer conformations using the central dimers of flexibly fitted vertex structures. All dimers in this panel are color-coded according to their origin (refer to the legend). These conformational variations lend more support to the hypothesis that the C-terminal region of Sec31 has a structure regulation role beside the previously introduced biochemical roles.
The structures obtained by cryo-EM help rationalize our observations from thermofluor and AUC analysis. We hypothesized that deleting the C-terminal region of Sec31 introduced new conformations in ACE1 and Sec13 domains such that the β angle and hence the cage size was not affected. This was clearly seen in both of the vertex classes where the edges form the usual cuboctahedron alpha and beta angles at 60° and 90°, respectively, while the curvature of the ACE1 domain and the orientation of all the β-propeller domains have changed with respect to the wt vertex. Although the ACE1 domain has been shown to flex in a plane normal to the fourfold axis of the cage to give rise to plus and minus ends and ultimately different β angles, we demonstrate here for the first time that the ACE1 domain in a cage structure flexes in a direction perpendicular to that, while the β-propeller domain of Sec31 also flexes using a hitherto unknown hinge located between the β-propeller domain and the β-blade. This is in accordance with another study by Čopič et al. (Copic et al., 2012b) where they examined the rigidity of yeast Sec31p in the absence of Sec13p by either deleting the β-blade and the previously known hinge or deleting the whole loop that connects the β-propeller domain to the ACE1 domain. They found out that in the latter case, Sec31p exhibits more rigidity which is also what our model predicts. Čopič et al. showed that Sec13p rigidifies and thus enables Sec31p to overcome the opposing curvature that asymmetric cargo may induce on the ER membrane. In our study, we show that in the absence of the C-terminal region of Sec31, Sec13 can shift and rotate in directions that enables new modes of flexibility for Sec31. Therefore, we propose a more complete picture in which the C-terminal region, through its interaction with either or both of the β-propeller domains, locks their orientation so that the only degree of freedom is that of the β angle as the published structures indicate; whereas, the absence of the C-terminal region transfers that degree of freedom to the re-orientation of β-propeller domains and thus the β angle becomes less flexible.
Altogether, our data suggest a model for the COPII cage where the C-terminal region regulates cage flexibility. Deletion of the C-terminal disordered region results in additional modes of flexibility, and in in vivo COPII coated vesicles this could relate to the modulation of cage flexibility in response to cargo binding. Sec13/31 binds to Sec23/24 through residues 899–947 in the C-terminus. Sec23/24 in turn binds cargo proteins. Thus, binding of cargo necessarily sequesters Sec31 C-termini and could, in turn, mediate increased flexibility of the Sec13/31 edges. This presents an attractive model where cargo binding directs increases in Sec13/31 flexibility. In this way, the cage structure has a built-in mechanism for responding to the needs for flexibility and structural adaptability in response to cargo binding. Future high-resolution structural studies will help to test this hypothesis.
Supplementary Material
Acknowledgements
The research was supported by NIH R01 GM086892 and R01GM108753. CryoEM data were collected on instruments at the Biological Science Imaging Resource supported by Florida State University and NIH grants S10 RR025080 and S10 OD018142. The authors thank Dr. Claudius Mundoma for help with data collection and analysis for the DLS and AUC experiments and Dr. Joan Hare for help with protein expression.
Footnotes
Declarations of Interest: none.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Barlowe C, 1994. COPII: A membrane coat formed by Sec proteins that drive vesicle budding from the endoplasmic reticulum. Cell 77, 895–907. doi: 10.1016/0092-8674(94)90138-4 [DOI] [PubMed] [Google Scholar]
- Bi X, Corpina RA, Goldberg J, 2002. Structure of the Sec23/24–Sar1 pre-budding complex of the COPII vesicle coat. Nature 419, 271–277. doi: 10.1038/nature01040 [DOI] [PubMed] [Google Scholar]
- Bi X, Mancias JD, Goldberg J, 2007. Insights into COPII Coat Nucleation from the Structure of Sec23•Sar1 Complexed with the Active Fragment of Sec31. Developmental Cell 13, 635–645. doi: 10.1016/j.devcel.2007.10.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boivin S, Kozak S, Meijers R, 2013. Optimization of protein purification and characterization using Thermofluor screens. Protein Expression and Purification 91, 192–206. doi: 10.1016/j.pep.2013.08.002 [DOI] [PubMed] [Google Scholar]
- Brohawn SG, Leksa NC, Spear ED, Rajashankar KR, Schwartz TU, 2008. Structural evidence for common ancestry of the nuclear pore complex and vesicle coats. Science 322, 1369–1373. doi: 10.1126/science.1165886 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brookes E, Cao W, Demeler B, 2009. A two-dimensional spectrum analysis for sedimentation velocity experiments of mixtures with heterogeneity in molecular weight and shape. European Biophysics Journal 39, 405–414. doi: 10.1007/s00249-009-0413-5 [DOI] [PubMed] [Google Scholar]
- Brookes EH, Demeler B, 2007. Parsimonious regularization using genetic algorithms applied to the analysis of analytical ultracentrifugation experiments, in:. Presented at the the 9th annual conference, ACM Press, New York, New York, USA, pp. 361–368. doi:10.1145/1276958.1277035 [Google Scholar]
- Chari A, Haselbach D, Kirves J-M, Ohmer J, Paknia E, Fischer N, Ganichkin O, Möller V, Frye JJ, Petzold G, Jarvis M, Tietzel M, Grimm C, Peters JM, Schulman BA, Tittmann K, Markl J, Fischer U, Stark H, 2015. ProteoPlex: stability optimization of macromolecular complexes by sparse-matrix screening of chemical space. Nat Methods 12, 859–865. doi: 10.1038/nmeth.3493 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Copic A, Latham CF, Horlbeck MA, D’Arcangelo JG, Miller EA, 2012. a. ER cargo properties specify a requirement for COPII coat rigidity mediated by Sec13p. Science 335, 1359–1362. doi: 10.1126/science.1215909 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Copic A, Latham CF, Horlbeck MA, D’Arcangelo JG, Miller EA, 2012. b. ER cargo properties specify a requirement for COPII coat rigidity mediated by Sec13p. Science 335, 1359–1362. doi: 10.1126/science.1215909 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Demeler B, Brookes E, 2007. Monte Carlo analysis of sedimentation experiments. Colloid \& Polymer Science 286, 129–137. doi: 10.1007/s00396-007-1699-4 [DOI] [Google Scholar]
- Demeler DJ, 2007. UltraScan - A Comprehensive Data Analysis Software Package for Analytical Ultracentrifugation Experiments, in: Demeler DJ, Harding SE, Rowe AJ (Eds.), Analytical Ultracentrifugation, Techniques and Methods. Royal Society of Chemistry, Cambridge, pp. 210–230. doi: 10.1039/9781847552617-00210 [DOI] [Google Scholar]
- Dosztányi Z, Csizmok V, Tompa P, Simon I, 2005a. IUPred: web server for the prediction of intrinsically unstructured regions of proteins based on estimated energy content. Bioinformatics 21, 3433–3434. doi: 10.1093/bioinformatics/bti541 [DOI] [PubMed] [Google Scholar]
- Dosztányi Z, Csizmok V, Tompa P, Simon I, 2005b. The pairwise energy content estimated from amino acid composition discriminates between folded and intrinsically unstructured proteins. J Mol Biol 347, 827–839. doi: 10.1016/j.jmb.2005.01.071 [DOI] [PubMed] [Google Scholar]
- Dosztányi Z, Mészáros B, Simon I, 2009. ANCHOR: web server for predicting protein binding regions in disordered proteins. Bioinformatics 25, 2745–2746. doi: 10.1093/bioinformatics/btp518 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunker AK, Brown CJ, Lawson JD, Iakoucheva LM, Obradovic Z, 2002a. Intrinsic disorder and protein function. Biochemistry 41, 6573–6582. [DOI] [PubMed] [Google Scholar]
- Dunker AK, Brown CJ, Obradovic Z, 2002b. Identification and functions of usefully disordered proteins. Adv. Protein Chem 62, 25–49. [DOI] [PubMed] [Google Scholar]
- Dunker AK, Lawson JD, Brown CJ, Williams RM, Romero P, Oh JS, Oldfield CJ, Campen AM, Ratliff CM, Hipps KW, Ausio J, Nissen MS, Reeves R, Kang C, Kissinger CR, Bailey RW, Griswold MD, Chiu W, Garner EC, Obradovic Z, 2001. Intrinsically disordered protein. J. Mol. Graph. Model 19, 26–59. [DOI] [PubMed] [Google Scholar]
- Dunker AK, Uversky VN, 2008. Signal transduction via unstructured protein conduits. Nature Chemical Biology 4, 229–230. doi: 10.1038/nchembio0408-229 [DOI] [PubMed] [Google Scholar]
- Durchschlag H, 1987. Thermodynamic data for biochemistry and biotechnology. Comparative Biochemistry and Physiology Part A: Physiology 87, 823. doi: 10.1016/0300-9629(87)90410-5 [DOI] [Google Scholar]
- Dyson HJ, Wright PE, 2005. Intrinsically unstructured proteins and their functions. Nat Rev Mol Cell Biol 6, 197–208. doi: 10.1038/nrm1589 [DOI] [PubMed] [Google Scholar]
- Dyson HJ, Wright PE, 2002. Coupling of folding and binding for unstructured proteins. Curr Opin Struct Biol 12, 54–60. [DOI] [PubMed] [Google Scholar]
- Fath S, Mancias JD, Bi X, Goldberg J, 2007. Structure and Organization of Coat Proteins in the COPII Cage. Cell 129, 1325–1336. doi: 10.1016/j.cell.2007.05.036 [DOI] [PubMed] [Google Scholar]
- Ghaemmaghami S, Huh W-K, Bower K, Howson RW, Belle A, Dephoure N, O’Shea EK, Weissman JS, 2003. Global analysis of protein expression in yeast. Nature 425, 737–741. doi: 10.1038/nature02046 [DOI] [PubMed] [Google Scholar]
- Gürkan C, Stagg SM, LaPointe P, Balch WE, 2006. The COPII cage: unifying principles of vesicle coat assembly. Nat Rev Mol Cell Biol 7, 727–738. doi: 10.1038/nrm2025 [DOI] [PubMed] [Google Scholar]
- Huang M, Weissman JT, Béraud-Dufour S, Luan P, Wang C, Chen W, Aridor M, Wilson IA, Balch WE, 2001. Crystal structure of Sar1-GDP at 1.7 Å resolution and the role of the NH 2terminus in ER export. J Cell Biol 155, 937–948. doi: 10.1083/jcb.200106039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ilca SL, Kotecha A, Sun X, Poranen MM, Stuart DI, Huiskonen JT, 2015. Localized reconstruction of subunits from electron cryomicroscopy images of macromolecular complexes. Nat Commun 6, 8843. doi: 10.1038/ncomms9843 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuoka K, Orci L, Amherdt M, Bednarek SY, Hamamoto S, Schekman R, Yeung T, 1998. COPII-Coated Vesicle Formation Reconstituted with Purified Coat Proteins and Chemically Defined Liposomes. Cell 93, 263–275. doi: 10.1016/S0092-8674(00)81577-9 [DOI] [PubMed] [Google Scholar]
- Matsuoka K, Schekman R, Orci L, Heuser JE, 2001. Surface structure of the COPII-coated vesicle. Proceedings Of The National Academy Of Sciences Of The United States Of America 98, 13705–13709. doi: 10.1073/pnas.241522198 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mészáros B, Simon I, Dosztányi Z, 2009. Prediction of protein binding regions in disordered proteins. PLoS Comput Biol 5, e1000376. doi: 10.1371/journal.pcbi.1000376 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mohan A, Oldfield CJ, Radivojac P, Vacic V, Cortese MS, Dunker AK, Uversky VN, 2006. Analysis of molecular recognition features (MoRFs). J Mol Biol 362, 1043–1059. doi: 10.1016/j.jmb.2006.07.087 [DOI] [PubMed] [Google Scholar]
- Nakano A, Muramatsu M, 1989. A novel GTP-binding protein, Sar1p, is involved in transport from the endoplasmic reticulum to the Golgi apparatus. J Cell Biol 109, 2677–2691. doi: 10.1083/jcb.109.6.2677 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noble AJ, Zhang Q, O’Donnell J, Hariri H, Bhattacharya N, Marshall AG, Stagg SM, 2012. A pseudoatomic model of the COPII cage obtained from cryo-electron microscopy and mass spectrometry. Nat Struct Mol Biol 20, 167–173. doi: 10.1038/nsmb.2467 [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Donnell J, Maddox K, Stagg S, 2011. The structure of a COPII tubule. J Struct Biol 173, 358–364. doi: 10.1016/j.jsb.2010.09.002 [DOI] [PubMed] [Google Scholar]
- Obradovic Z, Peng K, Vucetic S, Radivojac P, Brown CJ, Dunker AK, 2003. Predicting intrinsic disorder from amino acid sequence. Proteins 53 Suppl 6, 566–572. doi: 10.1002/prot.10532 [DOI] [PubMed] [Google Scholar]
- Obradovic Z, Peng K, Vucetic S, Radivojac P, Dunker AK, 2005. Exploiting heterogeneous sequence properties improves prediction of protein disorder. Proteins 61 Suppl 7, 176–182. doi: 10.1002/prot.20735 [DOI] [PubMed] [Google Scholar]
- Oldfield CJ, Cheng Y, Cortese MS, Romero P, Uversky VN, Dunker AK, 2005. Coupled folding and binding with alpha-helix-forming molecular recognition elements. Biochemistry 44, 12454–12470. doi: 10.1021/bi050736e [DOI] [PubMed] [Google Scholar]
- Peng K, Vucetic S, Radivojac P, Brown CJ, Dunker AK, Obradovic Z, 2005. Optimizing long intrinsic disorder predictors with protein evolutionary information. J Bioinform Comput Biol 3, 35–60. [DOI] [PubMed] [Google Scholar]
- Peng Z, Kurgan L, 2012. On the complementarity of the consensus-based disorder prediction. Pac Symp Biocomput 176–187. doi: 10.1142/9789814366496_0017 [DOI] [PubMed] [Google Scholar]
- Radivojac P, Iakoucheva LM, Oldfield CJ, Obradovic Z, Uversky VN, Dunker AK, 2007. Intrinsic disorder and functional proteomics. Biophys J 92, 1439–1456. doi: 10.1529/biophysj.106.094045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romero P, Obradovic Z, Li X, Garner EC, Brown CJ, Dunker AK, 2001. Sequence complexity of disordered protein. Proteins 42, 38–48. [DOI] [PubMed] [Google Scholar]
- Rothman JE, Wieland FT, 1996. Protein sorting by transport vesicles. Science 272, 227–234. doi: 10.1126/science.272.5259.227 [DOI] [PubMed] [Google Scholar]
- Schekman R, Orci L, 1996. Coat Proteins and Vesicle Budding. Science 271, 1526–1533. doi: 10.1126/science.271.5255.1526 [DOI] [PubMed] [Google Scholar]
- Scheres SHW, 2012. RELION: Implementation of a Bayesian approach to cryo-EM structure determination. Journal of Structural Biology 180, 519–530. doi: 10.1016/j.jsb.2012.09.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuck P, Demeler B, 1999. Direct Sedimentation Analysis of Interference Optical Data in Analytical Ultracentrifugation. Biophysical Journal 76, 2288–2296. doi: 10.1016/S0006-3495(99)77384-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stagg SM, Gürkan C, Fowler DM, LaPointe P, Foss TR, Potter CS, Carragher B, Balch WE, 2006. Structure of the Sec13/31 COPII coat cage. Nature 439, 234–238. doi: 10.1038/nature04339 [DOI] [PubMed] [Google Scholar]
- Stagg SM, LaPointe P, Razvi A, Gürkan C, Potter CS, Carragher B, Balch WE, 2008. Structural Basis for Cargo Regulation of COPII Coat Assembly. Cell 134, 474–484. doi: 10.1016/j.cell.2008.06.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahashi T, Kojima K, Zhang W, Sasaki K, Ito M, Suzuki H, Kawasaki M, Wakatsuki S, Takahara T, Shibata H, Maki M, 2015. Structural analysis of the complex between penta-EF-hand ALG-2 protein and Sec31A peptide reveals a novel target recognition mechanism of ALG-2. Int J Mol Sci 16, 3677–3699. doi: 10.3390/ijms16023677 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tompa P, 2002. Intrinsically unstructured proteins. Trends in Biochemical Sciences 27, 527–533. [DOI] [PubMed] [Google Scholar]
- Trabuco LG, Villa E, Mitra K, Frank J, Schulten K, 2008. Flexible Fitting of Atomic Structures into Electron Microscopy Maps Using Molecular Dynamics. Structure 16, 673–683. doi: 10.1016/j.str.2008.03.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uversky VN, 2013. Intrinsic disorder-based protein interactions and their modulators. Curr. Pharm. Des 19, 4191–4213. [DOI] [PubMed] [Google Scholar]
- Uversky VN, 2012. Disordered competitive recruiter: fast and foldable. J Mol Biol 418, 267–268. doi: 10.1016/j.jmb.2012.02.034 [DOI] [PubMed] [Google Scholar]
- Uversky VN, 2011. Multitude of binding modes attainable by intrinsically disordered proteins: a portrait gallery of disorder-based complexes. Chem Soc Rev 40, 1623–1634. doi: 10.1039/c0cs00057d [DOI] [PubMed] [Google Scholar]
- Uversky VN, Dunker AK, 2010. Understanding protein non-folding. Biochim Biophys Acta 1804, 1231–1264. doi: 10.1016/j.bbapap.2010.01.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uversky VN, Gillespie JR, Fink AL, 2000. Why are “natively unfolded” proteins unstructured under physiologic conditions? Proteins 41, 415–427. [DOI] [PubMed] [Google Scholar]
- Uversky VN, Oldfield CJ, Dunker AK, 2005. Showing your ID: intrinsic disorder as an ID for recognition, regulation and cell signaling. J. Mol. Recognit. 18, 343–384. doi: 10.1002/jmr.747 [DOI] [PubMed] [Google Scholar]
- Vacic V, Oldfield CJ, Mohan A, Radivojac P, Cortese MS, Uversky VN, Dunker AK, 2007. Characterization of molecular recognition features, MoRFs, and their binding partners. J. Proteome Res. 6, 2351–2366. doi: 10.1021/pr0701411 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walsh I, Giollo M, Di Domenico T, Ferrari C, Zimmermann O, Tosatto SCE, 2015. Comprehensive large-scale assessment of intrinsic protein disorder. Bioinformatics 31, 201–208. doi: 10.1093/bioinformatics/btu625 [DOI] [PubMed] [Google Scholar]
- Wright PE, Dyson HJ, 1999. Intrinsically unstructured proteins: re-assessing the protein structure-function paradigm. J Mol Biol 293, 321–331. doi: 10.1006/jmbi.1999.3110 [DOI] [PubMed] [Google Scholar]
- Xue B, Dunbrack RL, Williams RW, Dunker AK, Uversky VN, 2010. PONDR-FIT: a meta-predictor of intrinsically disordered amino acids. Biochim Biophys Acta 1804, 996–1010. doi: 10.1016/j.bbapap.2010.01.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshihisa T, Barlowe C, Schekman R, 1993. Requirement for a GTPase-activating protein in vesicle budding from the endoplasmic reticulum. Science 259, 1466–1468. doi: 10.1126/science.8451644 [DOI] [PubMed] [Google Scholar]
- Zanetti G, Prinz S, Daum S, Meister A, Schekman R, Bacia K, Briggs JAG, 2013. The structure of the COPII transport-vesicle coat assembled on membranes. Elife 2, e00951. doi: 10.7554/eLife.00951 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeuschner D, Geerts WJC, van Donselaar E, Humbel BM, Slot JW, Koster AJ, Klumperman J, 2006. Immuno-electron tomography of ER exit sites reveals the existence of free COPII-coated transport carriers. Nat Cell Biol 8, 377–383. doi: 10.1038/ncb1371 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.