An approach to estimate bidirectional mediation effects with application to body mass index and fasting glucose

Summary

Obesity and type 2 diabetes are major public health issues with known interdependence. Genetic variants have been associated with obesity, type 2 diabetes, or both; thus, we hypothesize that some single nucleotide polymorphisms (SNPs) associated with both conditions may be mediated through obesity to affect type 2 diabetes or vice versa. We propose a framework for bidirectional mediation analyses. Simulations show that this approach accurately estimates the parameters, whether the mediation is unidirectional or bidirectional. In many scenarios, when the mediator is regressed on the initial variable and the outcome is regressed on the mediator and the initial variable, the resulting residuals are correlated because of other unmeasured covariates not in the model. We show that the proposed model provides accurate estimates in this scenario, too. We applied the proposed approach to investigate the mediating effects of SNPs associated with type 2 diabetes and obesity using genetic data from the Multi-Ethnic Study of Atherosclerosis cohort. Specifically, we used body mass index as a measure for obesity and fasting glucose as a measure for type 2 diabetes. We evaluated the top 6 SNPs associated with both body mass index and fasting glucose. Two SNPs (rs3752355 and rs6087982) had indirect effects on body mass index mediated through fasting glucose (0.2677; 95% confidence interval (CI) [0.0007, 0.6548] and 0.3301; 95% CI [0.0881, 0.8544], respectively). The remaining four SNPs (rs7969190, rs4869710, rs10201400 and rs12421620) directly affect body mass index and fasting glucose without mediating effects.

INTRODUCTION

The prevalence of obesity is increasing, and recent statistics show that nearly 38% of Americans are obese (Flegal et al., 2016). Obese individuals have higher risk of developing chronic diseases that reduce their lifespan (Kitahara et al., 2014). About 9.4% of the US population has diabetes and about 33.9% of US adults have prediabetes. Diabetes is the 7^th leading cause of death in the United States (National Diabetes Statistics Report) and accounts for total costs of $245 billion per year (American Diabetes, 2013). Type 2 diabetes, which accounts for 90% to 95% of all diabetes cases, is much more prevalent than type 1 diabetes. Environmental (e.g., exposure to chemical pollution), lifestyle (e.g., low physical activity levels) and dietary factors (e.g., unhealthy food consumption) are known to be associated with both obesity and type 2 diabetes (Maier et al., 2013; Park et al., 2003; Rathmann et al., 2013). Many studies have described the relationship between type 2 diabetes and obesity (Bays et al., 2007; Chan et al., 1994; Mokdad et al., 2003). These conditions are interrelated, and each is a known risk factor for the other. However, the true nature of the relationship is unclear. Understanding the nature of this relationship is critical for uncovering the pathophysiological process that leads to type 2 diabetes or obesity. Studies generally report the common clinical observation that individuals with higher body mass index (BMI) are at higher risk of developing type 2 diabetes (Bays et al., 2007; Chan et al., 1994; Mokdad et al., 2003). However, the converse is also true: that a majority of the patients with type 2 diabetes are obese (Bays et al., 2007). This shows that there is much to understand about the pathophysiology of both conditions (Bays, 2005; Grundy et al., 2005; Kahn et al., 2005).

Recent advances in genetics have identified several genes associated with obesity, type 2 diabetes, and related endophenotypes (e.g., hemoglobin A1C, fasting glucose serum levels). Recent genome-wide association studies (GWAS) have identified 146 single nucleotide polymorphisms (SNPs) that are associated with obesity and 234 SNPs that are associated with type 2 diabetes (Welter et al., 2014; Zhao et al., 2017; Locke et al., 2015). Interestingly, FTO, M4CR and QPCTL/GIPR genes are associated with both obesity and type 2 diabetes (Grarup et al., 2014). Because of the interdependence between obesity and type 2 diabetes, we hypothesize that some of the SNPs may be mediated through obesity to affect type 2 diabetes or mediated though type 2 diabetes to affect obesity or both. Typically, categorized BMI and fasting glucose are used to define obesity and type 2 diabetes. In this study, we used BMI and fasting glucose as continuous variables.

Causal mediation analysis was traditionally performed using the standard regression approach proposed by Baron and Kenny (1986). Later, counterfactual notions were introduced by Robins and Greenland (1992) so that the mediation effects could be defined in a general framework. VanderWeele and Vansteelandt (2009) showed that the direct and indirect effects described in the counterfactual framework can be estimated using regression analysis under appropriate identifiability conditions. Mediation analysis has been used in various scenarios to uncover the causal relationships in genetics (Pierce et al., 2014; VanderWeele et al., 2012; Wang et al., 2010; Wang et al., 2012). Those methods were developed in scenarios in which there is a cause and effect relationship between a mediator and an outcome, i.e., unidirectional mediation models. In contrast, in the present study we investigate mediation analyses in which two outcomes act as mediators for each other. For example, type 2 diabetes acts as a mediator when we investigate the association between SNPs and obesity, and obesity acts as a mediator when we investigate the association between the same SNPs and type 2 diabetes. One can naively perform analyses using two unidirectional mediation models by interchanging the mediator and the outcome in the two models. For example, Thakkinstian et al., 2015, used such an approach to identify association between the GC gene and uric acid mediated through the 25-hydroxy vitamin D. In this manuscript, we show that such strategy leads to biased estimates of the direct and indirect effects, and we propose an approach for performing bidirectional mediation analyses that leads to accurate estimation of the model parameters.

We perform simulations to characterize the properties of the proposed bidirectional mediation model and show that using two unidirectional mediation analyses leads to biased estimates when there is a bidirectional effect; whereas our proposed bidirectional mediation model provides accurate estimates. Importantly, we also show that when a true relationship is only unidirectional, our bidirectional mediation model still provides accurate estimation. Furthermore, when the mediator is regressed on the initial variable (e.g., the SNP) and the outcome is regressed on the mediator and the initial variable, the resulting residuals can be correlated because of other unmeasured predictors not in the model. Such correlated residuals lead to biased estimates in the standard unidirectional mediation models (Imai et al., 2010). We show that the proposed bidirectional mediation model provides accurate parameter estimation in this scenario, too.

We apply the proposed mediation model to the genetic data from the Multi-Ethnic Study of Atherosclerosis (MESA) cohort to investigate the direct and indirect effects of SNPs that are associated with BMI and fasting glucose. Specifically, we investigate the mediation effects of the top 6 SNPs that are associated with both BMI and fasting glucose.

MATERIALS AND METHODS

Consider a bidirectional mediation model as shown in Figure 1. Let Y₁ and Y₂ denote the BMI and fasting glucose, respectively, and let X₁ denote a SNP that is associated with both BMI and fasting glucose. In this model, Y₂(fasting glucose) mediates the relationship between Y₁(BMI) and X₁(SNP), and simultaneously Y₁(BMI) mediates the relationship between Y₂(fasting glucose) and X₁(SNP). This bidirectional mediation model can be represented by the following system of joint equations:

$$\left[\begin{array}{l}{\mathrm{Y}}_1={\mathrm{\beta }}_{21}{\mathrm{Y}}_2+{\mathrm{\gamma }}_{11}{\mathrm{X}}_1+{\mathrm{\epsilon }}_1\hfill \\ {\mathrm{Y}}_2={\mathrm{\beta }}_{12}{\mathrm{Y}}_1+{\mathrm{\gamma }}_{12}{\mathrm{X}}_1+{\mathrm{\epsilon }}_2\hfill \end{array}\right]$$

Figure 1.

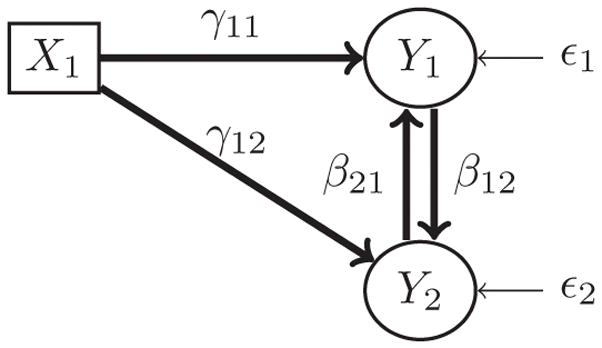
Bidirectional mediation model without instrumental variables; the model is not identifiable.

A model needs to be identifiable before the parameters of the model can be estimated. However, the underlying parameters of the above bidirectional mediation model are not identifiable and therefore cannot be estimated (see the Appendix for proof that the mediation model in Figure 1 is not identifiable). To ensure identifiability and estimate the bidirectional mediation model parameters, we introduce instrumental variables that are related to one of the responses but not the other. For example, let X₂ be associated with only Y₁ (BMI), but not Y₂ (fasting glucose), and X₃ be associated with only Y₂ (fasting glucose), but not Y₁ (BMI). The covariates X₂ and X₃ are called instrumental variables. SNPs or other covariates (e.g., serum cholesterol level, blood pressure, race, smoking status) can be used as instrumental variables. The model with the addition of the two instrumental variables is shown in Figure 2 (see the Appendix for proof of bidirectional mediation model identifiability). The joint system of equations representing the bidirectional mediation model in Figure 2 is

Figure 2.

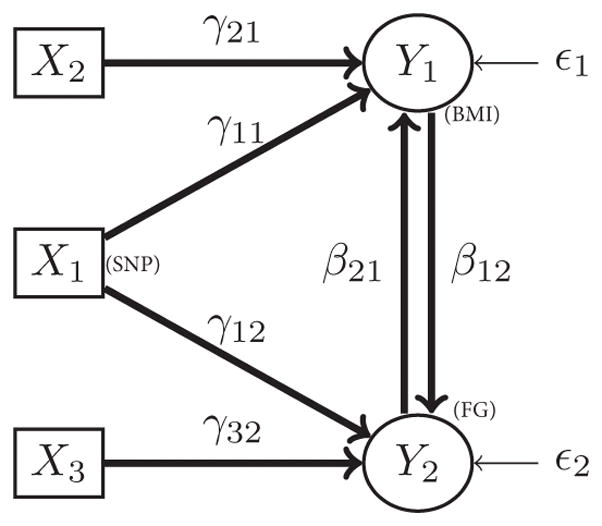
Bidirectional mediation model with instrumental variables; the model is identifiable.

$$\left[\begin{array}{l}{\mathrm{Y}}_1={\mathrm{\beta }}_{21}{\mathrm{Y}}_2+{\mathrm{\gamma }}_{11}{\mathrm{X}}_1+{\mathrm{\gamma }}_{21}{\mathrm{X}}_2+{\mathrm{\epsilon }}_1\hfill \\ {\mathrm{Y}}_2={\mathrm{\beta }}_{12}{\mathrm{Y}}_1+{\mathrm{\gamma }}_{12}{\mathrm{X}}_1+{\mathrm{\gamma }}_{32}{\mathrm{X}}_3+{\mathrm{\epsilon }}_2\hfill \end{array}\right]$$

Even though the model is now identifiable, the parameters in the above equations cannot be estimated using ordinary least squares regression (OLS) because the errors are correlated with the responses because of the bidirectionality. However, the reduced form of the equations can be estimated using OLS (Paxton et al., 2011). The reduced form of the equations for the model shown in Figure 2 can be written as

$$\begin{gathered} {\mathrm{Y}}_1=\frac{1}{1-{\mathrm{\beta }}_{21}{\mathrm{\beta }}_{12}}({\mathrm{\beta }}_{21}{\mathrm{\gamma }}_{12}{\mathrm{X}}_1+{\mathrm{\beta }}_{21}{\mathrm{\gamma }}_{32}{\mathrm{X}}_3+{\mathrm{\gamma }}_{11}{\mathrm{X}}_1+{\mathrm{\gamma }}_{21}{\mathrm{X}}_2+{\mathrm{\epsilon }}_1+{\mathrm{\beta }}_{21}{\mathrm{\epsilon }}_2) \\ {\mathrm{Y}}_2=\frac{1}{1-{\mathrm{\beta }}_{21}{\mathrm{\beta }}_{12}}({\mathrm{\beta }}_{12}{\mathrm{\gamma }}_{11}{\mathrm{X}}_1+{\mathrm{\beta }}_{12}{\mathrm{\gamma }}_{21}{\mathrm{X}}_2+{\mathrm{\gamma }}_{12}{\mathrm{X}}_1+{\mathrm{\gamma }}_{32}{\mathrm{X}}_3+{\mathrm{\epsilon }}_2+{\mathrm{\beta }}_{12}{\mathrm{\epsilon }}_1). \end{gathered}$$

The parameters of the model can be estimated by solving the reduced form of the equations even when the measurement errors of Y₁(obesity) and Y₂ (diabetes) are correlated.

Estimation of total direct and indirect effects

In bidirectional mediation models, we have to define the total, direct and indirect effects differently than in standard mediation models.

For the scenario in which X₁ is the initial variable, Y₁is the mediator and Y₂ is the response, the total effect of X₁ on Y₂ is the coefficient of X₁in the reduced form of the equation of Y₂.

$$\text{Total}\text{Effect}=\frac{1}{1-{\mathrm{\beta }}_{21}{\mathrm{\beta }}_{12}}({\mathrm{\beta }}_{12}{\mathrm{\gamma }}_{11}+{\mathrm{\gamma }}_{12}).$$

The direct effect and indirect effect of X₁ on Y₂ can be computed from the following equation:

$${\mathrm{Y}}_2={\mathrm{\beta }}_{12}{\mathrm{Y}}_1+{\mathrm{\gamma }}_{12}{\mathrm{X}}_1+{\mathrm{\gamma }}_{32}{\mathrm{X}}_3+{\mathrm{\epsilon }}_2.$$

Here, γ₁₂ is the direct effect of X₁ on Y₂. But, X₁ also affects Y₂ though the term β₁₂Y₁. This is the indirect effect of X₁on Y₂ through Y₁, which can be computed as the coefficient of X₁ in the term β₁₂Y₁, which can be written as

$${\mathrm{\beta }}_{12}{\mathrm{Y}}_1={\mathrm{\beta }}_{12}({\mathrm{\beta }}_{21}{\mathrm{Y}}_2+{\mathrm{\gamma }}_{11}{\mathrm{X}}_1).$$

This is a recursive equation that results in an infinite sum, which is a geometric series (see the Appendix). The series converges to $(\frac{{\mathrm{\beta }}_{12}{\mathrm{\gamma }}_{11}}{1-{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}}+\frac{{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}{\mathrm{\gamma }}_{12}}{1-{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}})X_1$. Therefore, the indirect effect of X₁on Y₂ through Y₁ is

$$\text{Indirect}\text{Effect}=\frac{{\mathrm{\beta }}_{12}{\mathrm{\gamma }}_{11}+{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}{\mathrm{\gamma }}_{12}}{1-{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}}.$$

In this formulation, as expected, the indirect effects are equal to the difference between the total and the direct effects. Similarly, one can derive the total, direct and indirect effects for the other scenario in which X₁ is the initial variable, Y₂ is the mediator and Y₁ is the response.

Simulations

We performed simulations to demonstrate the performance of the bidirectional mediation model compared to that of the standard unidirectional mediation model. We simulated data under three different scenarios.

Simulation Scenario1 – the standard unidirectional mediation model

We simulated data with β₂₁ = 0, for the model in Figure 2. This is equivalent to the standard unidirectional mediation model in which Y₁ is the mediator for the association between X₁ and Y₂. The SNP X₁ was simulated with a minor allele frequency of 0.3 and assuming Hardy-Weinberg equilibrium. The residuals ε₁ and ε₂ were simulated from a standard normal distribution, and Y₁ and Y₂ were simulated using the reduced form of the equations. The purpose of this simulation scenario is to show that parameter estimation using the bidirectional mediation model is accurate even when the simulated mediation model is unidirectional.

Simulation Scenario 2 – the bidirectional mediation model

We simulated data with both β₁₂ ≠ 0 and β₂₁ ≠ 0, for the model in Figure 2. We analyzed the data using three approaches: (a) the proposed bidirectional mediation model, (b) the standard unidirectional mediation model with Y₁ as the mediator, referred to as Uni-M-Y1, and (c) the standard unidirectional mediation model with Y₂ as the mediator, referred to as Uni-M-Y2. We also evaluated the magnitude of the bias of the standard unidirectional mediation model by simulating a range of positive and negative values for β₂₁.

Simulation Scenario 3 – the standard unidirectional mediation model with correlated residuals

As remarked above, when the mediator is regressed on the initial variable and the outcome is regressed on the mediator and the initial variable, the resulting residuals can be correlated. For such a scenario, we simulated residuals ε₁ and ε₂ from a bivariate normal distribution with a correlation coefficient ρ. The simulating model for this scenario is a standard unidirectional mediation model with β₂₁ = 0, Y₁ as the mediator, and Y₂ as the response. The purpose of this simulation scenario is to show that the proposed bidirectional mediation model provides accurate parameter estimation in these scenarios too.

RESULTS

We present the results for the simulation scenarios and the application of the proposed bidirectional mediation model to evaluate the direct and indirect effects of SNPs that are associated with BMI and the fasting glucose utilizing the MESA cohort.

Simulation Scenario 1

In this scenario, 1000 replicates of the data for 1000 individuals were simulated from a standard unidirectional mediation model with Y₁ as the mediator and Y₂ as the response. The results of this simulation are presented in Table 1, which lists the true simulated values (column labeled True Value) and the estimated parameter values using the bidirectional mediation model and the standard unidirectional mediation model, respectively reported in the next two columns. These results show that the bidirectional mediation modeling approach leads to accurate estimation of parameters even when the simulation model is the standard unidirectional mediation model. For example, compared to the true value of 0.75, the estimated direct effect of X₁on Y₂ using the bidirectional and the standard unidirectional mediation models is 0.75 and 0.75, respectively, with associated 95% coverage of 94.40% and 92.60%, respectively. Also, the estimated indirect effect of X₁ on Y₂ through Y₁using both approaches was 0.38, which is the same as the simulated value of 0.38, with associated 95% coverage of 95.10% and 93.80%, respectively. Importantly, the estimated indirect effect of X₁on Y₁ through Y₂ using the bidirectional mediation model was −0.03, which is very close to zero, with a coverage percentage of 96.70%.

Table 1. Simulation Scenario 1 — The simulation model is the standard unidirectional mediation model.

The parameter estimates and the coverage percentages are based on 1000 replicates using the bidirectional and unidirectional mediation models.

Parameter	True Value	Bidirectional Mediation Model	Uni-M-Y1
β12	0.75	0.76 (94.30%)	0.75 (94.20%)
β21	0.00	−0.01 (95.40%)	0.00 (100%)a
γ21	−0.25	−0.25 (95.90%)	−0.25 (94.90%)
γ32	−0.25	−0.25 (95.80%)	−0.25 (95.50%)
Direct Effect of X1 on Y2	0.75	0.75 (94.40%)	0.75 (92.60%)
Direct Effect of X1 on Y1	0.50	0.51 (96.10%)	0.50 (95.60%)
Indirect Effect of X1 on Y2 through Y1	0.38	0.38 (95.10%)	0.38 (93.80%)
Indirect Effect of X1 on Y1 through Y2	0.00	−0.03 (96.70%)	0.00 (100%)a

Uni-M-Y1 is the univariate mediation model: X₁ is the initial variable, Y₁ is the mediator, and Y₂ is the outcome.

^aThe parameters β₂₁ and indirect effect of X₁ on Y₁ through Y₂ are not modeled in the standard unidirectional model, Uni-M-Y1; therefore, these parameters are assumed to be zero.

Simulation Scenario 2

For this scenario, 1000 replicates of the data for 1000 individuals were simulated from the bidirectional mediation model presented in Figure 2. The results of this simulation are presented in Table 2, where the true simulated values of the parameters are reported (column labeled True Value), as well as the estimated parameter values using the bidirectional mediation model (under that column heading) and the results for the unidirectional mediation models in which Y₁ is the mediator (Uni-M-Y1; under that column heading) and Y₂ is the mediator (Uni-M-Y2; under that column heading). The results show that using either unidirectional mediation model leads to biased estimates; whereas the bidirectional mediation modeling approach leads to accurate estimation of the model parameters. For example, when the true direct effect of X₁ on Y₂ is 0.75, the bidirectional mediation model estimated this effect to be 0.75, with associated 95% coverage of 94.70%; whereas the standard unidirectional mediation models (Uni-M-Y1 and Uni-M-Y2) estimated the effect to be 0.60 and 1.38, with 95% coverage of 14.00% and 0.00%, respectively. Similarly, when the true indirect effect of X₁ on Y₂ through Y₁ is 0.63, the bidirectional mediation model estimated it to be 0.63, with associated 95% coverage of 94.30%; whereas the standard unidirectional mediation model Uni-M-Y1 estimated the effect to be 0.79, with associated 95% coverage of 24.40%. This indirect effect was not modeled in the unidirectional mediation model Uni-M-Y2 and is therefore assumed to be zero.

Table 2. Simulation Scenario 2 –The simulation model is the bidirectional mediation model.

The parameter estimates and the coverage percentages are based on 1000 replicates using the bidirectional mediation model and both unidirectional mediation models.

Parameter	True Value	Bidirectional Mediation model	Uni-M-Y1	Uni-M-Y2
β12	0.75	0.75 (94.40%)	0.93 (0.00%)	0.00 (0%) b
β21	0.25	0.24 (94.60%)	0.00 (0%) a	0.63 (0.00%)
γ21	−0.25	−0.25 (95.20%)	−0.31 (67.90%)	−0.16 (8.90%)
γ32	−0.25	−0.25 (95.70%)	−0.24 (92.80%)	−0.31 (78.00%)
Direct Effect of X1 on Y2	0.75	0.75 (94.70%)	0.60 (14.00%)	1.38 (0.00%)
Direct Effect of X1 on Y1	0.50	0.51 (94.50%)	0.85 (0.00%)	−0.02 (0.00%)
Indirect Effect of X1 on Y2 through Y1	0.63	0.63 (94.30%)	0.79 (24.40%)	0.00 (0%) b
Indirect Effect of X1 on Y1 through Y2	0.27	0.24 (94.00%)	0.00 (0%) a	0.87 (0.00%)

Uni-M-Y1 is the univariate mediation model: X₁ is the initial variable, Y₁ is the mediator, and Y₂ is the outcome.

Uni-M-Y2 is the univariate mediation model: X₁ is the initial variable, Y₂ is the mediator, and Y₁ is the outcome.

^aThe parameters β₂₁ and indirect effect of X₁ on Y₁ through Y₂ are not modeled in the unidirectional model Uni-M-Y1; therefore, these parameters are assumed to be zero.

^bThe parameters β₁₂ and indirect effect of X₁ on Y₂ through Y₁ are not modeled in the unidirectional model Uni-M-Y2; therefore, these parameters are assumed to be zero.

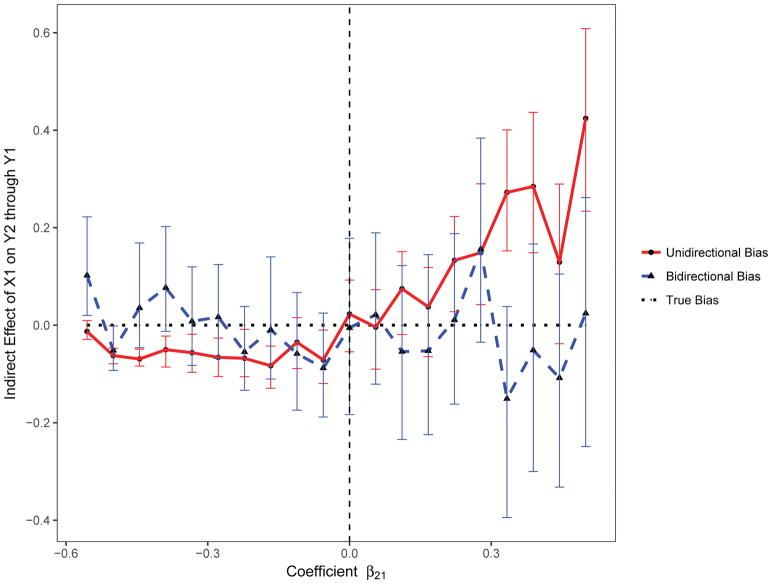
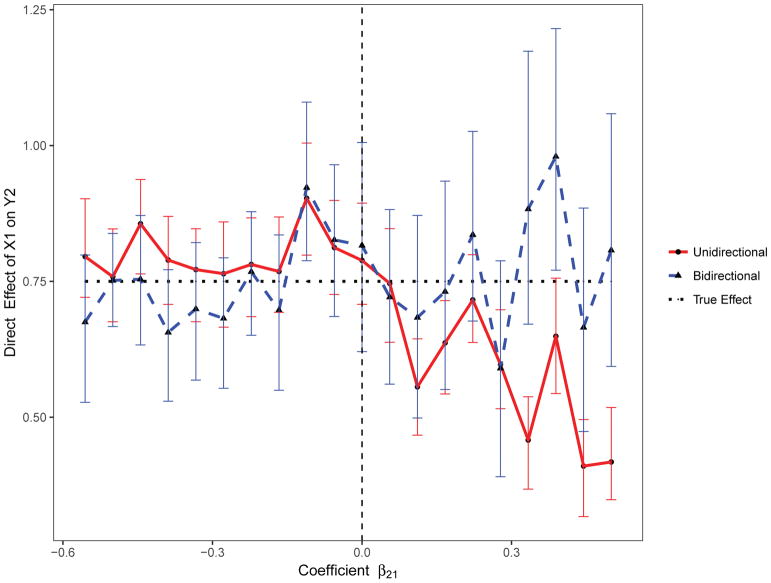
We also assessed the magnitude of the bias in the estimation of the indirect and for varying values of the coefficient β₂₁ using the standard unidirectional model (Uni-M-Y1) and the proposed bidirectional mediation model. On average, the indirect effect of X₁ on Y₂ through Y₁was overestimated for positive values of the β₂₁ coefficient, and underestimated for negative values (Figure 3). In contrast, on average, the direct effect of X₁ on Y₂ was underestimated for positive values of β₂₁and overestimated for negative values (Figure 4).

Figure 3.

The bias in estimation of the indirect effect with varying effect size using the proposed bidirectional and the standard unidirectional mediation models.

Figure 4.

The estimated direct effect with varying effect size using the proposed bidirectional and the standard unidirectional mediation models.

Simulation Scenario 3

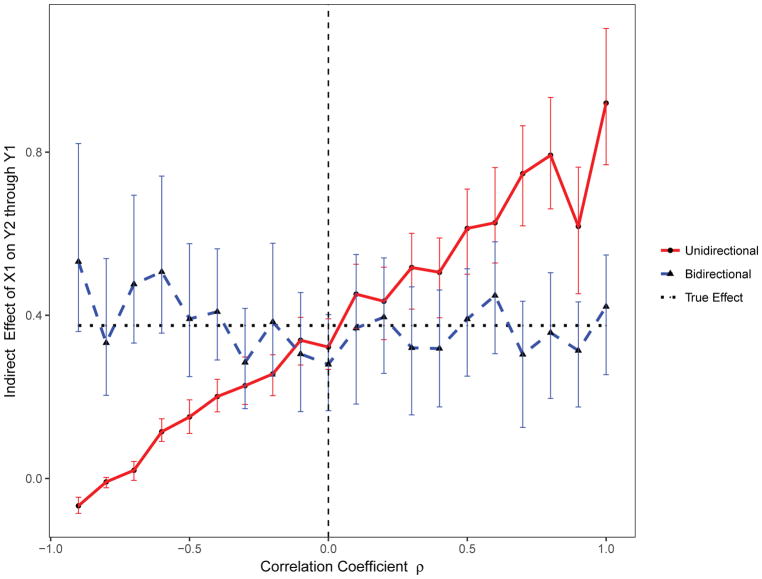
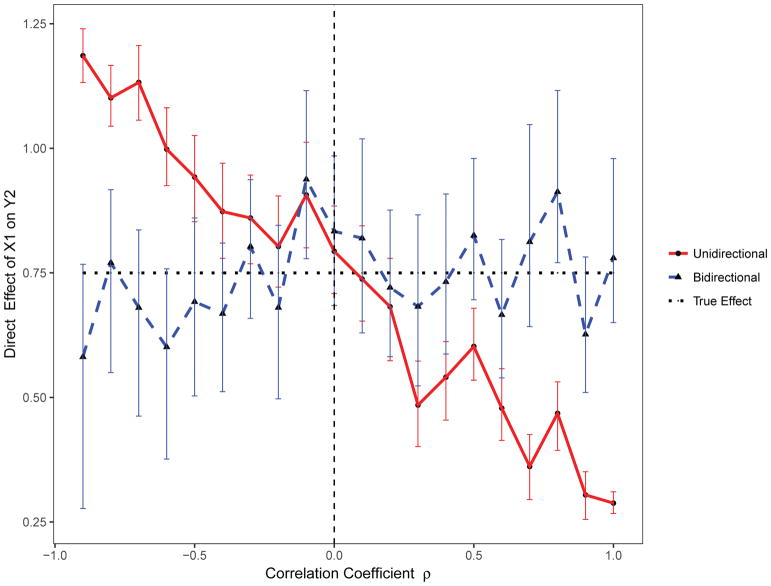
For this scenario, 1000 replicates of the data for 1000 individuals were simulated from a standard unidirectional mediation model (β₂₁ = 0). Using the standard unidirectional mediation model, when the residual errors are negatively correlated, the indirect effect of X₁ on Y₂ through Y₁ is underestimated; it is overestimated when the residual errors are positively correlated (Figure 5). In contrast, the direct effect of X₁ on Y₂ is overestimated when the residual errors are negatively correlated and underestimated when the residual errors are positively correlated (Figure 6). Importantly, the proposed bidirectional mediation model accurately estimated both the direct and indirect effects even when residual errors are either positively or negatively correlated (Figures 5 and 6).

Figure 5.

The estimated indirect effect with varying correlated residuals using the proposed bidirectional and the standard unidirectional mediation models.

Figure 6.

The estimated direct effect with varying correlated residuals using the proposed bidirectional and the standard unidirectional mediation models.

Results of the analysis of the relationship between BMI and fasting glucose using data from the MESA cohort

We applied the proposed bidirectional mediation model to investigate the direct and indirect effects of SNPs that are associated with both BMI and fasting glucose using the MESA cohort, which contained data on 47,871 SNPs from 5764 individuals. We performed genetic association analysis and evaluated the top 6 SNPS (rs3752355, rs6087982, rs7969190, rs4869710, rs10201400 and rs12421620) that were associated with both BMI and fasting glucose.

We also identified 739 SNPs that were significantly associated with BMI but not associated with fasting glucose. One such SNP, rs671, was used as an instrumental variable for BMI (BMI association p-value = 9.06E-35 and FG association p-value 0.245). Similarly, we identified 42 SNPs that were significantly associated with fasting glucose but not associated with BMI. One such SNP, rs2227692, was used as an instrumental variable for fasting glucose (BMI association p-value = 0.504 and FG association p-value = 4.77E-09). The effect sizes and associated p-values for the top 6 SNPs associated with both BMI and fasting glucose and the 2 SNPs selected as instrumental variables for BMI and fasting glucose are presented in Supplementary Table 1. The results for the bidirectional mediation models for each of the 6 SNPs are shown in Table 3. Our analyses identified two SNPs with a significant indirect effect on BMI. The SNP rs3752355 had a significant indirect effect on BMI (0.2677; 95% CI [0.0007, 0.6548]), which was mediated through the fasting glucose. Similarly, SNP rs6087982 had an indirect effect on BMI (0.3301; 95% CI [0.0881, 0.8544]) which was also mediated though the fasting glucose. The remaining four SNPs (rs7969190, rs4869710, rs10201400 and rs12421620) did not have significant indirect effects on BMI through fasting glucose or on fasting glucose through BMI.

Table 3.

Parameter estimates of the bidirectional mediation model for MESA data for the top 6 SNPs that are associated with both body mass index (BMI) and fasting glucose (FG).

	rs3752355		rs6087982		rs7969190		rs4869710		rs10201400		rs7969190
Parameter	Estimate	95% CI	Estimate	95% CI	Estimate	95% CI	Estimate	95% CI	Estimate	95% CI	Estimate	95% CI
β12	0.3105	(−0.9152,1.2712)	0.4110	(−0.8017,1.4555)	−0.2571	(−1.4368,0.7594)	−0.3349	(−1.4678,0.5980)	−0.1338	(−1.1333,0.7415)	−0.3403	(−1.6510,0.6286)
β21	0.0852	(0.0003,0.2017)	0.1092	(0.0317,0.2788)	0.0293	(−0.0521,0.1149)	0.0433	(−0.0306,0.1385)	0.0259	(−0.0525,0.1164)	0.0240	(−0.0706,0.1296)
γ21	−3.6570	(−4.2307,−3.0794)	−3.3989	(−4.0550,−2.7352)	−3.8062	(−4.3703,−3.3601)	−3.8608	(−4.4230,−3.3480)	−3.9280	(−4.4642,−3.4261)	−3.8268	(−4.4044,−3.2743)
γ32	3.9374	(1.9293,5.8691)	3.9138	(1.6875,6.1633)	4.2872	(2.2578,6.6812)	4.2555	(2.1759,6.1995)	4.1479	(2.0819,6.0586)	3.7808	(1.7564,5.8762)
Direct effect on FG	3.2726	(1.6517,4.8562)	3.2726	(1.4547,5.1697)	3.7594	(1.9131,5.4783)	6.4888	(2.8083,9.7904)	4.7779	(2.1729,7.6237)	6.5147	(3.2478,9.9851)
Direct effect on BMI	−0.6936	(−1.1639,−0.3007)	−0.9351	(−1.5171,−0.5291)	0.9433	(0.5188,1.3748)	0.7480	(−0.0662,1.5404)	1.1267	(0.4634,1.7511)	0.9017	(0.0630,1.7100)
Indirect effect on FG through BMI	−0.1323	(−0.6878,0.4542)	−0.2487	(−0.9128,0.4409)	−0.2688	(−1.5250,0.7740)	−0.3396	(−1.6703,0.6406)	−0.1667	(−1.4502,0.9533)	−0.3571	(−1.7400,0.6233)
Indirect effect on BMI through FG	0.2677	(0.0007,0.6548)	0.3301	(0.0881,0.8544)	0.1024	(−0.1639,0.4262)	0.2660	(−0.1802,0.8491)	0.1192	(−0.2469,0.6473)	0.1475	(−0.4677,0.8210)

DISCUSSION

In GWAS, the association between SNPs and outcomes is investigated without regard to the presence of possible mediators. The effect sizes obtained through such analyses are the total effects and include the direct effects of SNPs on the outcome as well as the indirect effects mediated through other factors. Subsequently, standard mediation analysis can be performed to accurately estimate the direct and indirect effects of the SNPs on the outcome. However, standard mediation models provide accurate estimation only when there is a cause and effect relationship between a mediator and an outcome, i.e., unidirectional mediation models. In this manuscript, we proposed an approach to estimate the direct and indirect effects when performing mediation analyses in which two outcomes acts as mediators for each other. Also, even in the unidirectional mediation models, because of unmeasured confounders, when the mediator is regressed on the initial variable and the outcome is regressed on the mediator and the initial variable, the resulting residuals can be correlated. Our bidirectional mediation model provides accurate estimates even in such scenarios. We conducted simulation studies in three scenarios to assess the performance of the proposed bidirectional mediation model in estimating the direct and indirect effects. We showed that the proposed bidirectional mediation model provides accurate estimates even when the true underlying mediation model is unidirectional. We also showed that the standard unidirectional mediation model leads to biased estimates when the true underlying model is bidirectional, and that the proposed bidirectional mediation model provides accurate estimation of all parameters, including direct effects and mediating indirect effects. Our simulations also showed that even when the residual errors are correlated, the proposed bidirectional mediation model provided accurate estimates whereas the standard unidirectional mediation models provided biased estimates.

The selection of proper instrumental variables is vital for the performance of the proposed method. The instrumental variables need to be selected such that they are significantly associated with one outcome but not the other. In studies with small sample sizes, selecting instrumental variables on the basis of being associated with one outcome but not the other may lead to poor instrumental variables. For example, a significantly associated factor may actually appear to be statistically non-significant due to low power. Although any covariate (e.g., SNP, gene expression, age, and gender) can be used as an instrumental variable, SNPs have been generally preferred (Smith et al., 2014; Burgess et al., 2017; Bennett et al., 2017). Through simulations, we showed that improperly selected instrumental variables can lead to biased estimation of the direct and indirect effects (see Supplementary Figure 1).

It is important to note that we utilized the instrumental variables differently than their use in the Mendelian randomization method, a method to estimate causal association between a risk factor and outcome in the presence of confounders. In Mendelian randomization, genotypes are used as instrumental variables to establish such causal relationship, assuming that the genotypes only affect the outcome through the risk factor under investigation. In the proposed method, the instrumental variables are used only to establish identifiability of the bidirectional mediation model and as long as they are chosen appropriately, the direct and indirect effects are accurately estimated. Also, in the proposed method, the SNP of interest is associated with both outcomes that act as mediators for each other which is not the conceptual framework assumed in the Mendelian randomization method.

In the proposed method, the instrumental variables are used only to establish identifiability of the bidirectional mediation model and as long as they are chosen appropriately, the direct and indirect effects are accurately estimated.

We applied the proposed bidirectional mediation model to estimate the direct and indirect effects of SNPs that were associated with both BMI and fasting glucose. The proposed model is particularly relevant in this context because of the interdependence between obesity and type 2 diabetes. We hypothesized that variations in BMI associated with SNPs could be at least partially mediated through the fasting glucose. Similarly, variations in fasting glucose associated with SNPs could also be at least partially mediated through BMI. In such a scenario, the observed effect sizes from GWAS include both direct and indirect effects. The proposed model can delineate these direct and indirect effect and provide the true contribution of SNPs to the relevant phenotype.

Using the proposed bidirectional mediation framework, we investigated the direct and indirect roles of the top 6 SNPs that are associated with BMI and fasting glucose. We found that the fasting glucose partially mediates the effects of SNPs rs3752355 and rs6087982 on BMI; whereas SNPs rs7969190, rs4869710, rs10201400 and rs12421620 do not have significant indirect effects on BMI through fasting glucose nor on fasting glucose through BMI.

The proposed method has some limitations. It is not suitable for investigating causal relationships between a mediator and outcomes. Its purpose is to delineate the direct and indirect effects of the SNP on the outcome and evaluate the true contribution of the SNP on the outcome. Also, the proposed method only works for a single-sample–based approach and further research needs to be performed to extend it to a two-sample setting that combines GWAS results from different studies.

In summary, the proposed method accurately estimates the direct and indirect effects when performing mediation analyses in which two outcomes act as mediators for each other. Our analyses of the MESA data provide novel insights into the genetics of the relationship between BMI and fasting glucose.

Appendix

Identifiability of Models

The rank condition is a necessary and sufficient condition for the identifiability of a model. All equations in the model need to be identifiable for model identifiability. If there are p equations in the model with p responses/mediators, an equation satisfies the rank condition if and only if a matrix of the order (p − 1) × (p − 1) with a non-zero determinant can be constructed from the coefficients of the variables excluded from that equation but included in other equations (Gujarati, 1995).

Identifiability of Model 1 (Figure 1)

The equations for model 1 can be written equivalently in matrix form as

$$\begin{gathered} \mathrm{Y}=\text{BY}+\text{GX}+\mathrm{\epsilon } \\ \left[\begin{array}{l}{\mathrm{Y}}_1\hfill \\ {\mathrm{Y}}_2\hfill \end{array}\right]=\left[\begin{array}{cc}0& {\mathrm{\beta }}_{21}\\ {\mathrm{\beta }}_{12}& 0\end{array}\right]\left[\begin{array}{c}{\mathrm{Y}}_1\\ {\mathrm{Y}}_2\end{array}\right]+\left[\begin{array}{cc}{\mathrm{\gamma }}_{11}& 0\\ {\mathrm{\gamma }}_{12}& 0\end{array}\right]\left[\begin{array}{c}{\mathrm{X}}_1\\ 0\end{array}\right]+\left[\begin{array}{c}{\mathrm{\epsilon }}_1\\ {\mathrm{\epsilon }}_2\end{array}\right] \end{gathered}$$

The rank condition of a model can be evaluated using the matrix M = [I − B| − G]. For the above model, $\mathrm{M}=\left[\begin{array}{cccc}1& -{\mathrm{\beta }}_{21}& -{\mathrm{\gamma }}_{11}& 0\\ -{\mathrm{\beta }}_{12}& 1& -{\mathrm{\gamma }}_{12}& 0\end{array}\right]$. None of the rows can be identified, so this is an unidentifiable model.

Identifiability of Model 2 (Figure 2)

The equations for model 2 can be written equivalently in matrix form as

$$\begin{gathered} \mathrm{Y}=\text{BY}+\text{GX}+\mathrm{\epsilon } \\ \left[\begin{array}{l}{\mathrm{Y}}_1\hfill \\ {\mathrm{Y}}_2\hfill \end{array}\right]=\left[\begin{array}{cc}0& {\mathrm{\beta }}_{21}\\ {\mathrm{\beta }}_{12}& 0\end{array}\right]\left[\begin{array}{c}{\mathrm{Y}}_1\\ {\mathrm{Y}}_2\end{array}\right]+\left[\begin{array}{ccc}{\mathrm{\gamma }}_{11}& {\mathrm{\gamma }}_{21}& 0\\ {\mathrm{\gamma }}_{12}& 0& {\mathrm{\gamma }}_{32}\end{array}\right]\left[\begin{array}{c}{\mathrm{X}}_1\\ {\mathrm{X}}_2\\ {\mathrm{X}}_3\end{array}\right]+\left[\begin{array}{c}{\mathrm{\epsilon }}_1\\ {\mathrm{\epsilon }}_2\end{array}\right] \end{gathered}$$

The rank condition for these equations can be tested using the matrix M:

$$\mathrm{M}=\left[\begin{array}{ccccc}1& -{\mathrm{\beta }}_{21}& -{\mathrm{\gamma }}_{11}& -{\mathrm{\gamma }}_{21}& 0\\ -{\mathrm{\beta }}_{12}& 1& -{\mathrm{\gamma }}_{12}& 0& -{\mathrm{\gamma }}_{32}\end{array}\right]$$

All the equations are identifiable, as a 1×1 nonzero determinant can be obtained for each equation.

Estimation of total direct and indirect effects

The total effect (TE) of X₁ on Y₂ can be obtained from the reduced form equation of Y₂, which is

$$TE=\frac{1}{1-{\mathrm{\beta }}_{21}{\mathrm{\beta }}_{12}}({\mathrm{\beta }}_{12}{\mathrm{\gamma }}_{11}+{\mathrm{\gamma }}_{12}).$$

The direct effect (DE) and indirect effect (IE) of X₁ on Y₂ can be computed using the equation

$${\mathrm{Y}}_2={\mathrm{\beta }}_{12}{\mathrm{Y}}_1+{\mathrm{\gamma }}_{12}{\mathrm{X}}_1+{\mathrm{\gamma }}_{32}{\mathrm{X}}_3+{\mathrm{\epsilon }}_2.$$

Here, γ₁₂ is the DE of X₁ on Y₂. The IE can be computed as the coefficient of X₁ in the term β₁₂Y₁, which can be written as

$$\begin{gathered} {\mathrm{\beta }}_{12}{\mathrm{Y}}_1={\mathrm{\beta }}_{12}({\mathrm{\beta }}_{21}{\mathrm{Y}}_2+{\mathrm{\gamma }}_{11}{\mathrm{X}}_1) \\ ={\mathrm{\beta }}_{12}({\mathrm{\beta }}_{21}\text{(}{\mathrm{\beta }}_{12}{\mathrm{Y}}_1+{\mathrm{\gamma }}_{12}{\mathrm{X}}_1))+{\mathrm{\beta }}_{12}{\mathrm{\gamma }}_{11}{\mathrm{X}}_1 \\ ={\mathrm{\beta }}_{12}({\mathrm{\beta }}_{21}\text{(}{\mathrm{\beta }}_{12}\text{(}{\mathrm{\beta }}_{21}{\mathrm{Y}}_2+{\mathrm{\gamma }}_{11}{\mathrm{X}}_1))+{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}{\mathrm{\gamma }}_{12}{\mathrm{X}}_1+{\mathrm{\beta }}_{12}{\mathrm{\gamma }}_{11}{\mathrm{X}}_1 \\ ={\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}\text{(}{\mathrm{\beta }}_{12}{\mathrm{Y}}_1+{\mathrm{\gamma }}_{12}{\mathrm{X}}_1)+{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}{\mathrm{\beta }}_{12}{\mathrm{\gamma }}_{11}{\mathrm{X}}_1+{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}{\mathrm{\gamma }}_{12}{\mathrm{X}}_1+{\mathrm{\beta }}_{12}{\mathrm{\gamma }}_{11}{\mathrm{X}}_1 \\ ={\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}{\mathrm{\beta }}_{12}{\mathrm{Y}}_1+{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}{\mathrm{\gamma }}_{12}{\mathrm{X}}_1+{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}{\mathrm{\beta }}_{12}{\mathrm{\gamma }}_{11}{\mathrm{X}}_1+{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}{\mathrm{\gamma }}_{12}{\mathrm{X}}_1+{\mathrm{\beta }}_{12}{\mathrm{\gamma }}_{11}{\mathrm{X}}_1 \end{gathered}$$

This is an infinite series that can be written as the summation of two series,

$$={\mathrm{\beta }}_{12}{\mathrm{\gamma }}_{11}{\mathrm{X}}_1+\text{(}{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}\text{)}{\mathrm{\beta }}_{12}{\mathrm{\gamma }}_{11}{\mathrm{X}}_1+{({\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21})}^2{\mathrm{\beta }}_{12}{\mathrm{\gamma }}_{11}{\mathrm{X}}_1,\dots +{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}{\mathrm{\gamma }}_{12}{\mathrm{X}}_1+{({\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21})}^2{\mathrm{\gamma }}_{12}{\mathrm{X}}_1+\cdots$$

Both of these are infinite geometric series that converge only when |β₁₂β₂₁| < 1.

The first series converges to

$${\mathrm{\beta }}_{12}{\mathrm{\gamma }}_{11}{\mathrm{X}}_1+\text{(}{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}\text{)}{\mathrm{\beta }}_{12}{\mathrm{\gamma }}_{11}{\mathrm{X}}_1+{({\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21})}^2{\mathrm{\beta }}_{12}{\mathrm{\gamma }}_{11}{\mathrm{X}}_1,\dots =\frac{{\mathrm{\beta }}_{12}{\mathrm{\gamma }}_{11}{\mathrm{X}}_1}{1-{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}}$$

and the second series converges to

$${\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}{\mathrm{\gamma }}_{12}{\mathrm{X}}_1+{\text{(}{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}\text{)}}^2{\mathrm{\gamma }}_{12}{\mathrm{X}}_1+\cdots =\frac{{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}{\mathrm{\gamma }}_{12}{\mathrm{X}}_1}{1-{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}}$$

Therefore, the IE is the coefficient of X₁ in β₁₂Y₁, which is

$$\text{IE}=\frac{{\mathrm{\beta }}_{12}{\mathrm{\gamma }}_{11}}{1-{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}}+\frac{{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}{\mathrm{\gamma }}_{12}}{1-{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}}$$

This is equal to the difference in the total effect and direct effect (TE − DE):

$$\begin{gathered} \text{TE}-\text{DE}=\frac{{\mathrm{\beta }}_{12}{\mathrm{\gamma }}_{11}+{\mathrm{\gamma }}_{12}}{1-{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}}-{\mathrm{\gamma }}_{12} \\ \text{TE}-\text{DE}=\frac{{\mathrm{\beta }}_{12}{\mathrm{\gamma }}_{11}+{\mathrm{\gamma }}_{12}-(1-{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}){\mathrm{\gamma }}_{12}}{1-{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}} \\ \text{TE}-\text{DE}=\frac{{\mathrm{\beta }}_{12}{\mathrm{\gamma }}_{11}+{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}{\mathrm{\gamma }}_{12}}{1-{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}}=\frac{{\mathrm{\beta }}_{12}{\mathrm{\gamma }}_{11}}{1-{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}}+\frac{{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}{\mathrm{\gamma }}_{12}}{1-{\mathrm{\beta }}_{12}{\mathrm{\beta }}_{21}}=\text{IE} \end{gathered}$$