Shock attenuation, spatio-temporal and physiological parameter comparisons between land treadmill and water treadmill running

Abstract

Purpose

The purpose of this study was to compare shock attenuation, spatio-temporal and physiological parameters during water immersed (depth: anterior superior iliac spine) aquatic treadmill (ATM) running and land based treadmill (LTM) running matched for speed.

Methods

Six participants completed 15 min running under 2 conditions (LTM and ATM) in a randomised and balanced order, matched for speed. Synchronised tri-axial accelerometers placed at the distal tibia, lumbar region, and forehead were used to identify running dynamics and measure acceleration on impact and its attenuation. Expired respiratory gases and heart rate were sampled on a breath-by-breath basis for physiological variable collection throughout each trial.

Results

Participants experienced reduced accelerations on impact at the distal tibia (p < 0.0001) but not the lower back (p = 0.1363) or forehead (p = 0.0551) during ATM compared to LTM. Consequently, large reductions in shock attenuation occurred during the ATM compared to LTM (p = 0.0001). Stride frequency was greater (p < 0.0001) and stride length was shorter (p = 0.0341) as a result of reduced swing time (p = 0.0201) for LTM, whilst ATM running increased physiological demand for both heart rate (p < 0.0001) and O₂ (p < 0.0001) compared to LTM.

Conclusion

These findings show ATM reduces impact stress on the passive structures of the lower limbs whilst increasing physiological demand when running at matched speeds.

1. Introduction

Land based, body supported exercise such as running is associated with repetitive strain and stress injuries to the lower extremities.1, 2 It is hypothesised that these injuries are due, at least in part, to the shockwave of energy transmitted throughout the body on impact with the ground.² At impact, vertical ground reaction forces of 2–5 times greater than body weight with rate of force development of 113 BW/s are observed.³ Accompanying the large ground reaction forces, a shockwave of energy is transmitted through the body which must be attenuated to enable proper function of the vestibular and visual systems.⁴ Typically, shock attenuation from the distal tibia to the head is reported as ~60% during running with increases of ~20% per m/s speed increment.⁵ Whilst anatomical structures provide the greatest potential to attenuate shock via active eccentric muscle action, passive mechanisms such as the elasticity of bone, cartilage, synovial fluid, and soft tissue⁶ have an increasing role as muscle fatigue develops.⁷ Additionally, footwear choices,⁸ surface characteristics such as running over uneven ground⁹ or downhill,¹⁰ and technique (incorporating proprioception, joint position, and muscle tone) can be manipulated to alter individual shock attenuation profiles. However, the repetitive nature and load of such impacts, particularly during the support phase, means endurance runners are always going to be susceptible to injury of the lower extremities.⁴

Unloading forces, expressed in the scientific literature as effects on total accelerations experienced at the lower limb,⁶ through the hydrostatic pressure of water immersion (Archimedes principle) have been seized upon by the sport and health industry. The reduced impact produced by hydrostatic unloading provides positive adherence to exercise programmes because it can lessen the pain or discomfort experienced⁴ during running and subsequently reduce injury risk. Equally important is the finding that similar cardiovascular fitness gains can be obtained from aquatic exercise compared to land based activity providing physiological intensity is matched.¹¹

Previously, deep water running has only been used as a means of cross-training or as a rehabilitation process.¹² However more recently, the benefits of water treadmill exercise, supplementary to normal land based training, have become apparent,4, 11 particularly, the emphasis on decreased mechanical load on the lower limbs and the diminished risk of injury. However, there are no published data quantifying the level of shock attenuation aquatic treadmill (ATM) running provides when compared to normal land based treadmill (LTM) running; or whether such training affects normal land based running spatio-temporal parameters. Understanding such an influence would provide useful information to trainers so that they might confidently prescribe supplementary ATM training without incurring additional injury risks.

Therefore, the purpose of this study was to compare shock attenuation, spatio-temporal and physiological parameters during ATM and LTM at a matched speed. We hypothesised that the hydrostatic pressure and resistance to movement during ATM would diminish the required shock attenuation between the tibia and head. This would appear as decreased acceleration magnitude and rate of acceleration development at the anterolateral aspect of the lower leg but not the forehead. Additionally, we hypothesised that stride length (swing time) would increase due to increased buoyancy effect but greater resistance at toe-off due to increased hydrostatic resistance would result in greater ground contact time.

2. Methods

2.1. Subjects

Six nationally competitive middle and long distance runners (age: 29.8 ± 13.0 years, height: 169.3 ± 7.0 cm, LTM body weight: 54.6 ± 5.5 kg, BMI: 18.84 ± 0.73 kg/m², ATM body weight: 23.2 ± 4.9 kg; mean ± SD), free from injury, experienced at both LTM and ATM participated in this study. The research was approved by the Institutional Review Board of Massey University Human Ethics Committee: Southern A (Application 14/93). All participants provided written inform consent in accordance with the University Human Ethics Committee approval.

2.2. Procedures and measurements

The experimental protocol consisted of 2 conditions, each performed within 1 session on the same day in a counter balanced order to prevent any sequence effect on the dependent variables of interest. Both conditions involved running for 15 min on an LTM (TechnoGym, Cesena, Italy) and ATM (O'Leary Engineering, Palmerston North, New Zealand). Each treadmill was calibrated to the same speed (Eq. (1)) by using a magnetic switch that was triggered with each belt revolution. The depth of the LTM was set to anterior superior iliac spine level. This offered the least disturbance to arm swing whilst running and has previously been shown to balance the effects of increased resistance with increased buoyancy in terms of work done comparable to LTM.¹³ Water temperature was 21°C in order to alleviate effects of thermal stress.¹⁴

$$\begin{array}{l}\text{Treadmill speed}\left(\text{km/h}\right)\\ =\left(\left(\text{Treadmill belt length}\left(\mathrm{m}\right)\times \text{revs}/\min \right)\times 60\right)/1000\end{array}$$ Eq. (1)

On arrival at the laboratory, participants were measured in order to determine the water depth for ATM (height from floor to anterior superior iliac spine (cm)) and weighed using hanging scales (PCE Instruments, Southampton, UK). For the water immersed body weight participants were suspended from the scales and immersed to the anterior superior iliac spine.

Following this, participants were fitted with the wireless, tri-axial accelerometers (Emerald; APDM, Portland, OR, USA). These were used to measure accelerations (reported accuracy 0.0012 m/s²/√Hz)¹⁵ of the distal anterolateral aspect of the right tibia, lower back (lumbar) and frontal bone of the head (forehead) at 128 Hz (Fig. 1). Specific sites were selected to minimise soft tissue oscillations during impact⁶ and not interfere with gait patterns during ATM running. The accelerometers were packed tightly into a waterproof sport armband housing (H₂O Audio, San Diego, CA, USA) and secured tightly. Additionally, participants were connected to a calibrated¹⁶ automated portable gas analyser (K42b; COSMED, Rome, Italy) that sampled expired air on a breath-by-breath basis, and were also fitted with a heart rate monitor strap (Polar Electro, Kempele, Finland).

Fig. 1.

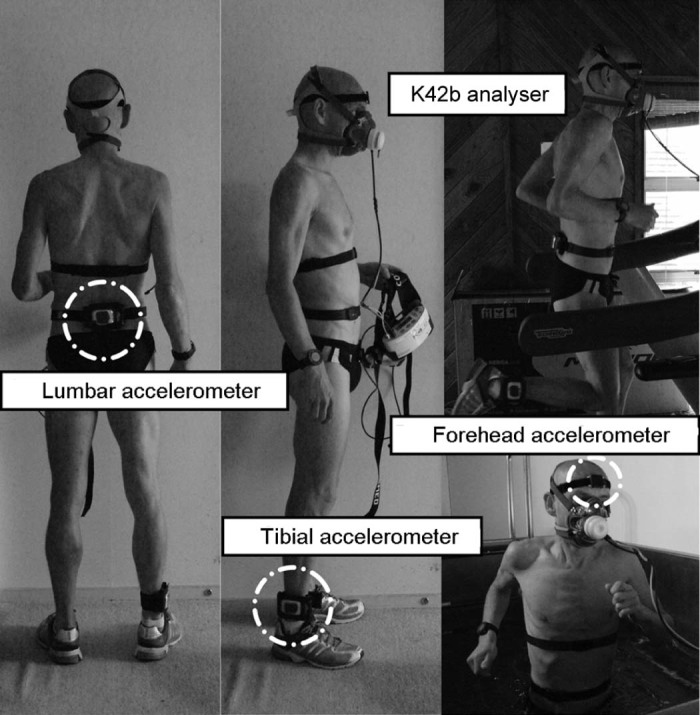
Photographs depicting accelerometer locations and equipment used during the experimental protocol.

All participants completed both tests in shod conditions wearing their normal running shoes. Where the ATM condition was performed first, participants used an identical (dry) model of running shoe for the LTM trial. Prior to each data collection period a familiarisation period at speeds below 2.78 m/s for 5 min was performed. Following this and immediately preceding the main trial participants ran at 2.83 m/s for 2 min. This would eliminate any differences between oxygen kinetics that may occur at the onset of exercise due to water immersion.¹⁷ The main trials consisted of participants running at 2.83 m/s over a 15 min period, and separated by 15 min recovery.

2.3. Outcome measures

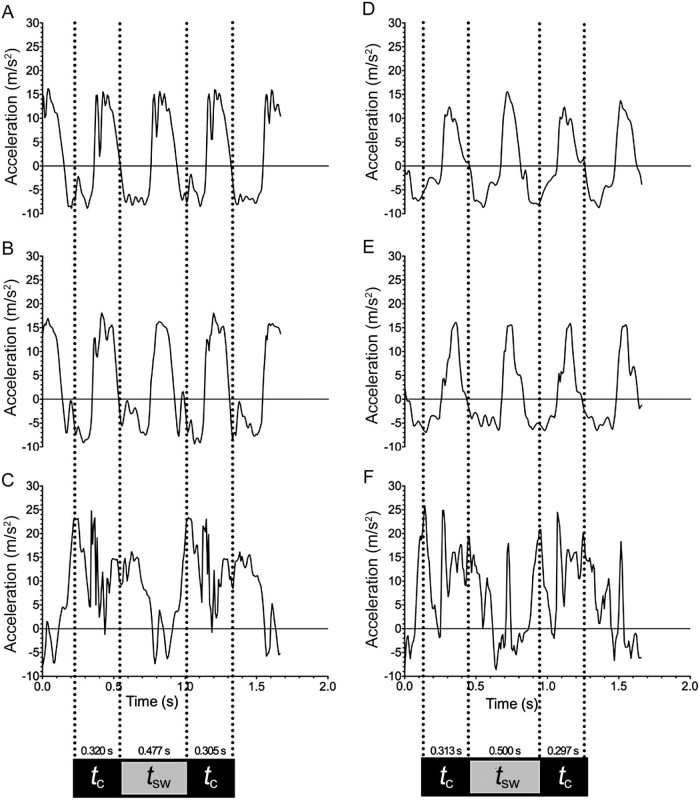
Synchronised accelerometry data were processed using MATLAB R2014a (Mathworks Inc., Natick, MA, USA), analyzed for total (XYZ) accelerations (m/s) allowing identification of the precise times of foot contact, peak impact and toe-off for each stride (Fig. 2), verified via high-speed video footage (Exilim Pro EX-F1; Casio, Tokyo, Japan). Algorithms, developed in MATLAB for identifying the peak impact and toe-off accelerations for the leg, and the peak acceleration for the head per gait cycle are explained in the following paragraphs. The algorithms were adjusted until the algorithm matched the visually identified peaks shown in Fig. 2.

Fig. 2.

Accelerometer output for total accelerations (XYZ-planes) versus time for Subject 5. (A) LTM head; (B) LTM lumbar; (C) LTM ankle; (D) ATM head; (E) ATM lumbar; (F) ATM ankle. Ground contact (t_c) and swing time (t_sw) are highlighted along with peak impact and peak toe-off. ATM = aquatic treadmill; LTM = land treadmill.

The leg total (XYZ) acceleration was analyzed to find the peak impact and peak toe-off accelerations. For each condition, a threshold of 60% of the maximum acceleration during that condition was used, and the first point in each gait cycle that exceeded that threshold was identified. For the standard treadmill, the peak impact was found by looking for the maximum acceleration in the 10 data points (0.0781 s) following the crossing of the acceleration threshold, and the toe-off peak was found by looking between 8 and 20 points following the crossing of the threshold (0.0625 s and 0.1563 s, respectively).

A different pattern was observed in the water treadmill, with lower peak impacts, requiring a different algorithm. Here the threshold was set at 40% of the maximum acceleration for that condition. The peak impact was identified as the largest acceleration found between 30 and 4 data points before the crossing of the threshold (0.2344 s and 0.0313 s respectively before the threshold was reached). The peak toe-off was the largest acceleration in the 30 data points (0.2344 s) following the threshold being crossed.

For finding the peak acceleration in the head, the time (taken from the lower leg accelerometer) of the thresholds being crossed for each gait was used. The head peak acceleration was the largest value between 8 points prior to the threshold being crossed for the leg acceleration and 30 points after the threshold was crossed (0.0625 s before and 0.2344 s after, respectively).

Based on the calculated foot strike and toe-off as described above, the following variables were calculated from the accelerometer data:

• (1)
  Transfer function. During the stance phase, whilst the right foot was on the ground, the total acceleration was analyzed in the frequency domain. A fast Fourier transform (FFT) was applied to the total acceleration signal for the head and ankle, giving a power spectral density (PSD). To compare different strides at the same frequencies, the PSD was resampled to 0–32 Hz in 2 Hz increments. The resampled FFT of the head and ankle was then used to calculate the transfer function (Eq. (2)):⁴

  $$\text{Transfer function}=10{\log }_{10}\left({\text{PSD}}_{\text{head}}{/\text{PSD}}_{\text{ankle}}\right)$$ Eq. (2)
• (2)Ground contact time (t_c), defined as the time (s) from initial foot contact to the point of toe-off.¹⁸
• (3)Swing time (t_sw) defined as the time (s) from toe-off to initial ground contact of consecutive footfalls of the same foot.¹⁸
• (4)Stride duration defined as the time (s) taken for consecutive peak impacts of the same foot.
• (5)Stride frequency (Hz), defined as the number of strides taken per second.
• (6)Stride length (m), calculated by dividing treadmill speed (m/s) by stride frequency (Hz).
• (7)
  Vertical oscillation (cm), calculated from the lumbar accelerometer for each stride between peak impacts. The acceleration was integrated twice to get vertical position y(t). This gives the equation:

  $$y\left(t\right)={\displaystyle \int dt}{\displaystyle {\int }_{\mathrm{o}}^{t}a\left(t\right)dt}+ct$$ Eq. (3)

where a(t) is the acceleration signal with the time set to 0 at each peak impact.

To correct for drift in integration and to account for the unknown initial velocity it was assumed that the vertical height at each impact peak was identical, and arbitrarily set to 0. This implies that:

$$y\left(0\right)=y\left(T\right)=0$$ Eq. (4)

where T is the time between peak impacts.

Solving Eq. (3) for position to find c yields

$$y\left(t\right)={\displaystyle \int dt}{\displaystyle {\int }_{\mathrm{o}}^{t}a\left(t\right)dt}-\frac{{\displaystyle \int dt}{\displaystyle {\int }_{\mathrm{o}}^{T}a\left(t\right)dt}}{T}t$$ Eq. (5)

Simpson's rule was applied for the calculation of integrals and vertical oscillation was defined as the range (maximum–minimum) for y(t) during each gait cycle.

• (8)
  Peak impact shock attenuation, calculated (Eq. (6)) from the leg (LgPk) and head (HgPk) peak impact accelerations:19, 20

  $$\text{Shock attenuation}=\left[1-\left(\text{HgPk}/\text{LgPk}\right)\right]\times 100\%$$ Eq. (6)

where LgPk and HgPk are the peak leg and head accelerations at impact, respectively.

• (9)Acceleration loading rate of the leg in relation to the maximum rate of acceleration21, 22 was taken as the maximum derivative of the leg acceleration in the 20 data points prior to the peak impact.
• (10)Maximum slope at toe-off is assumed to relate indirectly to the combined effects of force development including elastic recoil.²² This is taken as the maximum derivative of the leg acceleration in the 12 data points prior to the maximum acceleration for each foot strike.

Additionally, physiological analysis of expired respiratory gases collected breath-by-breath (K42b) enabled the calculation (CPET suite, Version 10.0e; COSMED) of the body's rate of oxygen utilisation (VO₂, expressed mL/kg/min); the ratio of the carbon dioxide produced to oxygen used (respiratory exchange ratio, RER); the amount of air expired from the lungs during a minute (minute ventilation (V_E, L/min)); breathing frequency (Rf, breaths/min); and total energy expenditure (Σ_EE, kcal). Heart rate was collected and synchronised with the breath-by-breath data and logged for analysis as per respiratory gases.

Spatio-temporal and physiological data were analyzed collectively as a means to determine the efficiency of the 2 conditions via the oxygen consumed per stride (O₂ per stride, mL).¹

2.4. Data analysis

Descriptive data (mean ± SD) were calculated for all dependent variables collected continuously throughout the complete 15 min period. Further analysis of all continuous data over 5 min epochs was used to assess for drift amongst variables using two-way analysis of variance (ANOVA, condition × time). Accelerometer data comparisons were made via three-way ANOVA (condition × accelerometer location × time).

Where an overall significant difference was found for the two-way and three-way ANOVAs, post hoc analysis of the main effect was performed using Sidak's multiple comparison test. All statistical analyses were performed using SPSS Statistics Version 20.0 (IBM Corp., Armonk, NY, USA), significance was set at p < 0.05.

3. Results

Participants completed each 15 min of running with no (p < 0.01) within-condition differences in any of the outcome measures for 5 min epochs indicating there were no technical or physiological changes as a result of either condition. As such the following analyses assess the overall effect of condition (LTM vs. ATM) on performance, and that the data reported below are for the entire 15 min sessions.

3.1. Accelerometry and shock attenuation

Peak accelerations (Fig. 3A) experienced at impact revealed significant interactions between condition × location (F(2, 11) = 202.851, p < 0.0001) along with main effect differences for condition (F(1, 17) = 273.876, p < 0.0001) and between accelerometer locations (F(2, 17) = 358.811, p < 0.0001). Post hoc analysis identified differences for the distal anterolateral aspect of the right tibia (LTM 75.89 ± 10.22 m/s², ATM 23.53 ± 4.15 m/s², p < 0.0001) but not the lower back (LTM 21.01 ± 6.84 m/s², ATM 17.39 ± 2.70 m/s², p = 0.1363) or forehead (LTM 15.20 ± 2.86 m/s², ATM 12.96 ± 2.74 m/s², p = 0.0551). Importantly, the rate of acceleration development at the distal anterolateral aspect of the right tibia was significantly greater on impact (LTM 1649 ± 601, ATM 758 ± 350; t₍₅₎ = 3.70, p = 0.0208) and during toe-off (LTM 1871 ± 905, ATM 1513 ± 613; t₍₅₎ = 3.70, p = 0.0208) during the LTM compared to ATM.

Fig. 3.

(A) Acceleration at impact for the 3 different accelerometer locations; and (B) transfer function for ground contact time averaged over 10 strides from each participant, for each condition (mean ± SD). *p < 0.05, **p < 0.0001, signifies post hoc differences between conditions at specific time points. ATM = aquatic treadmill; LTM = land based treadmill; PSD = power spectral density.

The difference in peak acceleration reported for the lower leg but not the head produced overall significant differences in shock attenuation (LTM 79.62% ± 4.57%, ATM 42.92% ± 6.52%; t₍₆₎ = 14.83, p = 0.0001). Two-way ANOVA of time domain analysis data (transfer function) for the stance phase showed a significant interaction (F(32, 330) = 1.914, p = 0.0022) between condition × frequency, with main effect differences for condition (F(1, 330) = 127.5, p < 0.0001) and frequency (F(32, 330) = 1.651, p = 0.0170). Post hoc analysis identified differences between LTM and ATM only at the high frequency range (>20 Hz) typically associated with impact (Fig. 3B).

3.2. Spatio-temporal parameters

There was a significant difference for the main effect of condition (LTM vs. ATM) for stride frequency (LTM 1.377 ± 0.033 Hz, ATM 1.163 ± 0.081 Hz; F(1, 12) = 38.67, p < 0.0001) and consequently stride length (LTM 2.058 ± 0.050 m, ATM 2.445 ± 0.158 m; F(1, 12) = 5.716, p = 0.0341). LTM had a smaller t_sw than ATM (520.8 ± 35.0 ms vs. 632.3 ± 55.3 ms; t₍₅₎ = 3.327, p = 0.0201), but no differences were seen for either t_c (207.2 ± 38.4 ms vs. 234.1 ± 43.9 ms; t₍₅₎ = 1.137, p = 0.3072) or vertical oscillation (0.128 ± 0.025 m vs. 0.119 ± 0.020 m, t₍₅₎ = 0.7074, p = 0.5109).

3.3. Physiological variables

Two-way ANOVA showed no interaction (p > 0.05) between time × condition for all physiological variables and no main effect of time. However, there were significant main effects of condition for all variables except breathing frequency (Table 1).

Table 1.

Statistical outputs for two-way ANOVA main effect comparison of condition for physiological variables (mean ± SD).

	Land based treadmill	Water treadmill	p value
VO2 (mL/min/kg)	37.37 ± 6.83	52.61 ± 8.79	<0.0001
VE (L/min)	51.24 ± 6.02	75.72 ± 13.03	<0.0001
VE: VO2	28.09 ± 2.00	30.26 ± 2.21	<0.0001
Rf (breaths/min)	44 ± 9	44 ± 5	0.7364
Tidal volume (L)	1.198 ± 0.170	1.720 ± 0.357	<0.0001
RER	0.89 ± 0.03	0.96 ± 0.03	<0.0001
HR (bpm)	125 ± 19	149 ± 20	<0.0001
O2 per stride (mL)	0.452 ± 0.080	0.752 ± 0.084	<0.0001
∑ EE (kcal)	139.7 ± 17.4	194.7 ± 29.2	0.0002

Abbreviations: ANOVA = analysis of variance; HR = heart rate; RER = respiratory exchange ratio; Rf = breathing frequency; V_E = minute ventilation; Σ_EE = total energy expenditure; VO₂ = oxygen consumption.

4. Discussion

The aim of this study was to compare shock attenuation, spatio-temporal and physiological parameters during LTM and ATM running at the same speed. The main findings were: (a) shock attenuation was considerably lower during ATM running, particularly at higher frequencies; (b) accelerations were significantly greater at the anterolateral aspect of the tibia compared with those located at the lower back and head during LTM, but not ATM; (c) stride frequency was significantly slower, whilst stride length was significantly longer during ATM due to a greater swing time; and (d) ATM running increased physiological demand compared to LTM.

All of the variables studied were constant over time, with no significant main effects of time or interactions with time. This suggested running technique was not altered during the course of the experiment. This is important, as any differences obtained within the ATM condition will reflect stability following long-term application in regard to efficacy as a rehabilitative or supplementary training process.

During ATM there was a decrease in both peak acceleration (Fig. 3A) and the rate of acceleration development at the distal tibia. As the impact accelerations were so greatly diminished, less shock had to be attenuated between the tibia and head (36.7% ± 5.5%) during ATM when compared to LTM. This is important from the perspective of injury prevention, particularly for athletes participating in high volume training in a non-body weight supported mode. In these activities the magnitude of impact is associated with overuse of soft tissue structures⁵ as the shockwave of energy must be attenuated prior to reaching the central nervous system and brain.⁴ This attenuation occurs at high frequencies during LTM running and is associated with ground impact.6, 23 As such the reduction of accelerations shown during ATM (Fig. 3A) means that attenuation was considerably reduced at high frequencies associated with impact (Fig. 3B). This unequivocally confirms the benefit of ATM as a mode of weight-bearing exercise, minimising impact related stress through increased buoyancy, and the hydrodynamic resistance to movement.

The theory of body weight reduction following water immersion has long been understood. According to Archimedes principle, the upward net force of the body (buoyancy), partially or fully submerged, is equal to the weight of the water that the body displaces, whilst the downward force is simply body weight. As such, the net downward force is reduced during the ATM trial due to increased buoyancy.

Similar body weight changes as those presented in this study have previously²⁴ shown much smaller changes in ground reaction forces. However, the data presented in Fig. 3A highlight significant differences between LTM and ATM for accelerations at impact, reflecting considerable increases in drag forces, thus supporting the importance of the velocity of the foot at impact, on ground reaction force exposure levels previously observed in land based research.⁵

The decreased acceleration at impact and therefore limb movement velocity is reflected by decreased stride frequency and increased stride length. As such, the addition of hydrodynamic resistance to movement during ATM running caused participants to alter spatio-temporal parameters. These adaptations are indicative of positive and negative changes to normal land based running speed.⁶ However, the ATM speed was kept constant and such changes (decreased stride frequency and increased stride length) are major contributors towards lower impact acceleration and consequently decreased attenuation.

The observed increase in stride duration as a result of greater swing time for the ATM condition is unusual. Typically, under LTM conditions, any stride length increase is associated with increases in force development and ground contact time. In the ATM condition this would likely result in greater vertical oscillation, distance travelled per stride, and increased utilisation of stretch-shortening energy conservation such as in the case of a more “loping” running style. However, the rate of acceleration development at toe-off during ATM was significantly less than LTM. This intimates that the artificial alteration to stride length (0.387 ± 0.151 m) during the ATM centres around the buoyancy effects of water immersion and the z-forces exerted to oppose gravity during ground contact which normally equals body weight.²⁵ In this respect, less force application would suggest that the metabolic cost of running in the ATM would be less than LTM.¹⁸ Our findings disagree on both fronts as the non-significant difference (−9 ± 3 mm) for vertical oscillation during ATM and an overall decrease in running economy during ATM suggest that reductions in work done to overcome gravity as a result of increased buoyancy do not offset that required to overcome hydrodynamic resistance to limb movement (Table 1).

Mechanically, such results mean ATM could lessen the strain on anatomical structures via decreased eccentric loading across the hip, knee, and ankle joints typical of peak impact phases during LTM running.6, 7 The result of this probable loss of energy conservation during stretch-shortening (normally ~65% on land²⁶) means decreased economy of gait. The latter is supported through combining spatio-temporal with physiological data. Specifically, O₂ per stride and Σ_EE (Table 1) confirm significant decreases in economy during ATM. However, the ground reaction time which was not different suggests that elastic energy was not dissipated in the tissues, but perhaps in the surrounding environment (water). Nevertheless, the reduction of energy conservation means an increased demand on the muscles involved in the propulsive phase²⁷ prior to toe-off, and knee extension during the swing phase in order to overcome the resistive forces of the water.²⁸ Interestingly, the rate of acceleration development at toe-off was not different amongst our participants for the 2 conditions. Considering the extra resistance encountered during ATM, this indicates greater muscle unit recruitment during this (concentric) phase of gait in this mode. Therefore, the added-mass effect due to hydrodynamic resistance is more plausible for both the increase in HR and O₂. The O₂ results for the LTM (3.66 mL/kg⋅km/h) agree with traditional metabolic calculations²⁹ associated with LTM running at 10.2 km/h, whilst the ATM values were 141% greater (5.16 mL/kg⋅km/h). This (ATM) value equates to an estimated LTM running speed of ~14.2 km/h,²⁹ and suggests that athletes using ATM as training method should use HR combined with speeds ~72% of LTM training.

5. Conclusion

The results of the present study confirm our hypothesis that water immersed ATM running significantly reduces shock attenuation compared to LTM running at the same speed. Importantly, this was shown to be a direct result of reductions in accelerations experienced at the lower limb, typically associated with a multitude of overuse running injuries. In addition, spatio-temporal parameters for ATM highlight significantly lower stride frequency, greater swing time per stride as a result of both hydrostatic resistance and increased buoyancy. The balance between these 2 factors resulted in an increase in physiological demand which combined with the shock attenuation data implies ATM is a valuable training mode for runners.

Authors' contributions

PWM conceived of the study, carried out data collection and data analysis, and drafted the manuscript; PWF assisted in data analysis and helped to draft the manuscript; SRS helped to draft the manuscript. All authors have read and approved the final version of the manuscript, and agree with the order of presentation of the authors.

Competing interests

The authors declare that they have no competing interests.