Why are muscles strong, and why do they require little energy in eccentric action?

Highlights

• •Muscles are stronger in eccentric contractions than in isometric and concentric contractions.
• •Following eccentric action, muscle force is increased—a phenomenon referred to as residual force enhancement (RFE).
• •RFE remains unexplained but is associated with an increase in passive force originating from structural proteins in sarcomeres.
• •Titin was identified as one of the structural proteins whose force is increased in eccentric muscle action but not in passive muscle stretching.
• •A new model of muscle contraction is proposed that explains the increased force in eccentric muscle action, the decreased metabolic energy, and the RFE.

Abstract

It is well acknowledged that muscles that are elongated while activated (i.e., eccentric muscle action) are stronger and require less energy (per unit of force) than muscles that are shortening (i.e., concentric contraction) or that remain at a constant length (i.e., isometric contraction). Although the cross-bridge theory of muscle contraction provides a good explanation for the increase in force in active muscle lengthening, it does not explain the residual increase in force following active lengthening (residual force enhancement), or except with additional assumptions, the reduced metabolic requirement of muscle during and following active stretch. Aside from the cross-bridge theory, 2 other primary explanations for the mechanical properties of actively stretched muscles have emerged: (1) the so-called sarcomere length nonuniformity theory and (2) the engagement of a passive structural element theory. In this article, these theories are discussed, and it is shown that the last of these—the engagement of a passive structural element in eccentric muscle action—offers a simple and complete explanation for many hitherto unexplained observations in actively lengthening muscle. Although by no means fully proven, the theory has great appeal for its simplicity and beauty, and even if over time it is shown to be wrong, it nevertheless forms a useful framework for direct hypothesis testing.

1. Introduction

When a muscle is lengthening while activated (i.e., eccentric muscle action), it produces significantly more force and requires less energy than a muscle contracting isometrically (i.e., constant muscle length) or concentrically (i.e., active shortening).1, 2 These observations, made as early as a century ago, have been repeated hundreds of times and are now considered to be general properties of skeletal muscle contraction. Nevertheless, the reason eccentric muscle action produces more force and requires less energy remains a partial mystery, particularly because the original cross-bridge theory vastly overestimated the eccentric force and energy requirements.² A. F. Huxley, the first to formulate the cross-bridge theory in a precise mathematical framework, was aware of the shortcomings of his theory for eccentric muscle action2, 3 and suggested a variety of ways how the discrepancy between the cross-bridge theory and experimental observations could be explained.

Regarding the reduced energy cost for eccentric muscle action compared with isometric and concentric muscle action, Huxley² suggested that cross bridges were not necessarily tied to the hydrolysis of 1 adenosine triphosphate (ATP) per cross-bridge cycle (as is typically assumed for isometric and concentric contractions), but that there might be multiple cross-bridge cycles per 1 ATP hydrolyzed in eccentric contractions. He also suggested that perhaps there were additional structures yet to be discovered that would explain the extra force and reduced energy cost for eccentric muscle actions as opposed to that found with isometric and concentric muscle actions.³ Others have suggested that the extra force following eccentric muscle action might arise from the development of nonuniformities in sarcomere length during stretch and that these nonuniformities might potentially increase the force during active muscle stretching.⁴

Here, the ideas surrounding the increased force and reduced metabolic energy cost of eccentric muscle action compared with isometric and concentric muscle actions are reviewed briefly. This will be done by (1) reviewing the predictions of the cross-bridge theory, (2) reflecting on the sarcomere length nonuniformity idea, and (3) exploring the possibility of an “additional structural element” in muscle that might cause the increased force and reduced energy cost in eccentric muscle action. Selected aspects of these ideas have been presented previously in recent reviews, and the reader is referred to these reviews for greater detail.5, 6, 7, 8

2. Eccentric muscle action and the cross-bridge theory

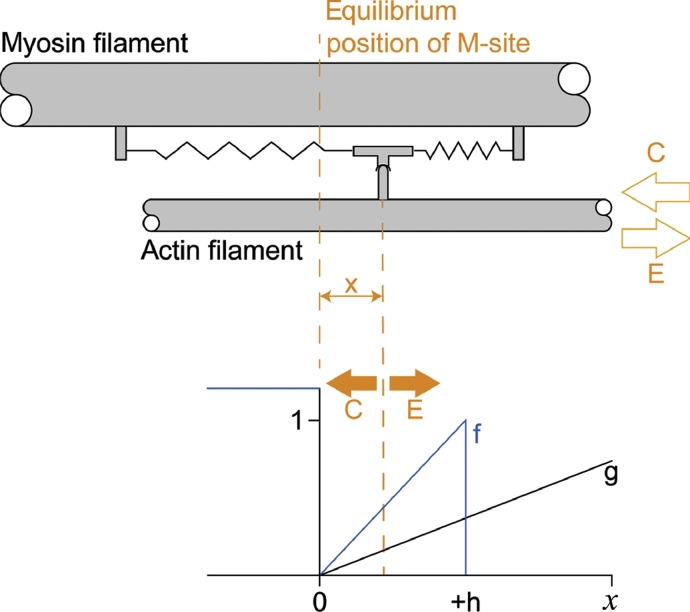
The original cross-bridge theory² and more recent derivatives9, 10, 11, 12 are based on the idea that there are cross bridges emanating from the myosin filaments that interact in a cyclic manner with specific attachment sites on the actin filaments. These interactions are driven by the hydrolysis of 1 ATP per cross-bridge cycle, and they produce force and muscle contraction. Basic assumptions underlying the cross-bridge theory are that (1) all cross bridges have the same force potential, (2) they are aligned uniformly along the myosin filament, (3) the actin attachment sites are uniformly spaced, (4) cross bridges act independently of each other, (5) cross bridges are attached via a linear elastic spring to the myosin backbone (therefore, extension of the cross bridge from its equilibrium position dictates its instantaneous force: F_CB = ke, where F_CB is the force in a cross bridge, k is the spring constant for the elastic element that attaches the cross bridge head to the myosin backbone, and e is the distance of the cross bridge from its equilibrium position), and (6) cross bridges attach and detach from actin stochastically (i.e., based on rate functions that are exclusively determined by the distance from a cross bridge's equilibrium position to its nearest eligible attachment site, referred to as the x-distance in Huxley's original work²) (Fig. 1).

Fig. 1.

Original cross-bridge model developed by A. F. Huxley (1957).² Top panel: The cross-bridge head (M) is attached to the myosin filament via linearly elastic springs with its equilibrium position at 0. The cross bridge can attach to its nearest binding site on actin (A), and x designates the distance of the cross bridge's equilibrium position to the nearest eligible binding site. Bottom panel: Rate functions of attachment (f) and detachment (g) of cross-bridges from actin; +h designates the maximal range of possible cross-bridge attachments to actin. Note that the attachment and detachment functions depend on x exclusively. Adapted from Huxley² with permission.

The rate functions of attachment and detachment defined by Huxley² in his original derivation of the cross-bridge theory were chosen because they satisfied the well-known force-velocity properties of skeletal muscle contraction derived by Hill¹ 19 years prior. This required an asymmetry of the rate functions about the equilibrium position, a definition of the attachment rate function only on one side of the cross-bridge equilibrium position, and a definition of the detachment rate functions that reached beyond the lower and upper end of the region defined for the attachment rate function (Fig. 1). Because the force–velocity relationship provides a much greater force for eccentric than isometric or concentric muscle actions, we can use the cross-bridge theory in its original formulation and derive mathematically why eccentric force is greater than isometric and concentric forces. However, even without solving Huxley's equations mathematically (as he2, 10 and many others13, 14 have done), we can show on intuitive grounds why eccentric muscle force is greater than isometric or concentric force.

For our intuitive argument, we use eccentric vs. concentric muscle force and remind ourselves that according to the cross-bridge theory, the force in a muscle is given by the number of attached cross bridges multiplied by the average force per cross bridge (which depends exclusively on the distance of the cross bridge from its equilibrium position—Huxley's x-distance, Fig. 1). Imagine a cross bridge attaching to actin at some random x-distance from its equilibrium position (Fig. 2). In a concentric contraction, the x-distance (distance of the cross bridge from its equilibrium position) will become smaller, and thus the force in the cross bridge decreases. In contrast, in an eccentric muscle action, the x-distance of the cross bridge will increase, and so will its force. Therefore, the average x-distance, and thus the average cross-bridge force, in eccentric muscle action is greater than in concentric contractions¹⁵ (Fig. 3). Furthermore, because of the high rate constant of detachment on the negative x-distance side (Fig. 1), the number of cross bridges attached at any given time is smaller in a concentric muscle action than in an eccentric muscle action at comparable speeds of shortening or stretching (Fig. 3). Therefore, we can explain the greater force in eccentric action as opposed to that in concentric action (and a similar argument can be made for isometric contractions) exclusively with the cross-bridge theory. In other words, for a given speed of stretching or shortening, the number of attached cross bridges and the average force per cross bridge is predicted to be greater for the eccentric muscle action compared with that for the concentric muscle action.

Fig. 2.

Imagine a cross bridge attached at an actin binding site as shown in the top panel of the figure. Its force is given by the force in the linear elastic spring that attaches the cross bridge to the myosin filament, which depends exclusively on how far the cross bridge is from its equilibrium position, given by x. If the cross-bridge attachment occurs during a concentric contraction (C), the muscle is shortening and the actin filament will move to the left relative to the myosin filament, thereby decreasing the cross-bridge x-distance and thus the force exerted by the cross bridge on actin. In contrast, if the cross-bridge attachment occurs during an eccentric action (E), the actin filament will move to the right relative to the myosin filament, thereby increasing the cross bridge's x-distance and thus its force. f = rate function of attachment; g = rate function of detachment; +h = the maximal range of possible cross-bridge attachments to actin; M = the myosin cross bridge.

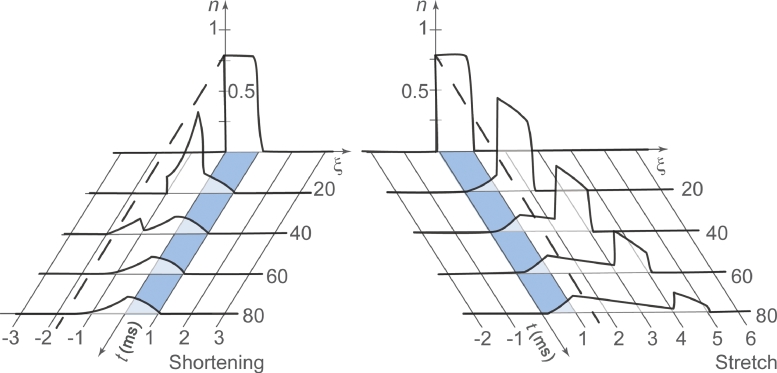
Fig. 3.

Depiction of the cross-bridge attachment distribution function (n) in a concentric (shortening, left panel) and an eccentric (stretch, right panel) contraction of equal speed as a function of time. The speed of shortening or stretch corresponds to the maximal speed of shortening of the muscle. The exact solution is predicted by Huxley's equation.² Note how in the shortening contraction the x-distances decrease as a function of time, whereas in the stretch contraction they increase. Note also that for any given instant in time, the proportion of attached cross bridges (the areas under the attachment distribution curves) is greater for the eccentric than for the concentric conditions. Integers on the x-axis correspond to multiples of the allowable attachment rate function; that is, 1 corresponds to the distance over which a cross bridge can reach and attach to actin. Adapted from Zahalak and Ma¹⁵ with permission.

The cross-bridge theory, as stated originally,² dramatically overestimated the energy consumption in eccentric muscle action and thus cannot be used to readily explain the reduced metabolic cost for eccentric compared with isometric and concentric muscle actions. As mentioned, Huxley² realized that his cross-bridge theory was not good at predicting the energetics of eccentric muscle action, and he therefore suggested that multiple cross-bridge attachment cycles per 1 ATP were possible in eccentric but not in isometric or concentric muscle action. This explanation, of course, could account for the reduced metabolic cost of eccentric action, but it was a post hoc interpretation of his theory with no direct supporting experimental evidence (at that time).

3. Eccentric muscle action and sarcomere length nonuniformity

The steady-state, isometric, force–length relationship of skeletal muscle has an ascending portion, a plateau, and a descending portion16, 17, 18 (Fig. 4). The slope of the static force–length relationship has often been interpreted as the instantaneous stiffness of muscle. Specifically, the negative slope between force and length on the descending portion of the force–length relationship has been thought to be unstable because of its presumed negative stiffness.16, 19^,20 This instability has been thought to cause sarcomere length nonuniformities during active muscle lengthening on the descending limb of the force–length relationship, which causes an increase in force during and following eccentric muscle action.4, 21 The increase in force following active muscle stretching has been referred to as residual force enhancement (RFE).22, 23 In the sarcomere length nonuniformity theory, it is implicitly assumed that isometric contractions of muscles occur with essentially uniform sarcomere lengths, whereas sarcomere lengths become nonuniform during stretching, allowing for an increased force compared with that of a purely isometric contraction with uniform sarcomeres.

Fig. 4.

Sarcomere force–length relationship for a frog skeletal muscle. The blue sarcomeres indicate schematically an isometric contraction with all sarcomeres at essentially the same length; thus, they have the same force. The brown sarcomeres indicate schematically an isometric contraction following an eccentric muscle action with sarcomeres becoming nonuniform in length. Some of the sarcomeres remain shorter than the sarcomeres for the purely isometric contraction, whereas others are pulled beyond actin-myosin filament overlap (they “pop”) and are rescued by the passive force of the sarcomere. Note that the average sarcomere length for the blue and brown sarcomeres is the same, and thus the muscle, fiber, and myofibril length is also the same. Once in force equilibrium, the nonuniform sarcomeres are higher up on the descending limb of the force–length relationship and are presumed to be stronger than the uniform sarcomeres of the purely isometric contraction. This sarcomere length nonuniformity has been thought (erroneously) to be the major (if not the exclusive) mechanism producing the so-called RFE property of skeletal muscle. RFE = residual force enhancement. Adapted from Gordon et al.¹⁶ with permission.

Imagine an isometric contraction on the descending limb with uniform sarcomeres (Fig. 4, blue sarcomeres). The isometric force is then proportional to the sarcomere length or, equivalently, to the average overlap between actin and myosin filaments, and thus the proportion of cross bridges that can be formed between these contractile filaments2, 16 (Fig. 4, blue dot). If the muscle is now stretched from a short length to the length at which the isometric contraction was performed (on the descending limb of the force–length relationship), sarcomeres are assumed to become nonuniform (Fig. 4, brown sarcomeres). Most of the sarcomeres are assumed to remain close to the initial length prior to stretch (or even shorten a bit), whereas a few sarcomeres are believed to be stretched beyond actin-myosin filament overlap (they are said to “pop”⁴), and they are caught by the passive structural elements of the sarcomere (Fig. 4, brown dots). These short (active force) and long (passive force) sarcomeres are then assumed to be in force equilibrium, and because the short sarcomeres are higher up on the (active) force–length relationship than for the isometric contraction, they are implicated in producing the increased active force during and after active lengthening of muscle,4, 21^,24 or RFE (Fig. 4).

However, this theory has serious flaws. First, it has been shown that force after active stretching is greater than the corresponding force for isometric contractions at the corresponding length in single-sarcomere preparations, where sarcomere length nonuniformities (by definition) cannot occur²⁵ (Fig. 5). However, not only was the isometric steady-state force after stretch greater than the corresponding isometric force, but it was also greater (by 38% on average) than the isometric force obtained at the plateau of the isometric force–length relationship (Fig. 5). Although it has been argued that half-sarcomere length nonuniformities might explain this result,²⁶ this argument obviously does not hold because 1 of the 2 half-sarcomeres would have to be in the actin-myosin overlap zone and would have to produce force greater than its maximal active isometric force at the plateau of the force–length relationship. Such an increase in force would be impossible to explain based on sarcomere or half-sarcomere length nonuniformity.

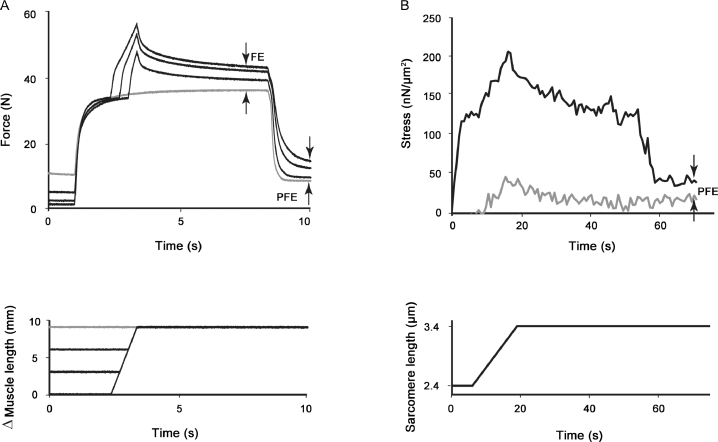
Fig. 5.

Stress (force per cross-sectional area) time plot (A) and sarcomere length–time plot (B) for a single sarcomere stretched from an initial length of 2.4 µm to a final length of 3.4 µm. FE indicates the difference between the isometric steady-state force for a purely isometric contraction (grey line) and the corresponding isometric steady-state force following active stretching of this single sarcomere. Note that the isometric steady-state force following active stretching is about 3 times greater than the corresponding purely isometric force and is also about 25% greater than the isometric steady-state force at the plateau of the force–length relationship (OFE). Because single sarcomeres can have substantial FE and can exceed the purely isometric reference forces at the optimal sarcomere length (the length where the sarcomere is strongest), this result cannot be explained with sarcomere length nonuniformity. FE = force enhancement; OFE = force enhancement above the optimal force at the plateau of the force–length relationship.

Another assumption of the sarcomere length nonuniformity theory is that sarcomeres are essentially uniform in isometric contractions and become nonuniform when stretched on the descending limb of the force–length relationship. However, they are not. Sarcomeres in passive and active isometric muscles are nonuniform.27, 28 These sarcomere length nonuniformities are vast, easily reaching a range of 1.0 µm,28, 29, 30 and they have been shown to increase with activation.³⁰ Detailed studies of sarcomere and half-sarcomere length nonuniformities in single myofibril preparations suggest that sarcomere length nonuniformities are about the same or greater for purely isometric contractions than for isometric contractions following active muscle stretching.30, 31, 32, 33 Therefore, it appears that sarcomere length nonuniformity is a normal occurrence for isometric, concentric, and eccentric contractions, and thus the notion that sarcomeres become nonuniform during active lengthening is a myth not supported by scientific evidence.

There are a series of other predictions that can be made based on the sarcomere length nonuniformity theory for explaining the RFE property following active lengthening. These include the following: (1) RFE should not occur on the ascending limb and the plateau region of the force–length relationship, (2) RFE can only occur in the presence of “popped” sarcomeres, and (3) RFE is associated with 2 distinct groups of sarcomere length in single myofibril preparations. However, all of these predictions have been rejected by experimental evidence.4, 20^,21, 25^,30,34, 35, 36, 37 Therefore, it appears that sarcomere length nonuniformities are merely a normal accompaniment of muscle contraction rather than a specific emerging property that is reserved for active muscle lengthening causing an increase in force.

4. Eccentric muscle action and an additional structural element

Ever since the emergence of the cross-bridge theory,² the increased force in actively lengthening muscle has been explained with an increase in the proportion of attached cross-bridges and an increase in the average force per cross bridge. However, the corresponding decrease in energetic cost associated with eccentric contractions compared with that of isometric or concentric contractions always needed an additional assumption (e.g., an increase in the number of cross-bridge cycles per ATP hydrolyzed).2, 38 Furthermore, the experimentally observed increase in peak force with stretches of increasing magnitudes³⁹ and the increased steady-state isometric force following active muscle lengthening compared with the corresponding isometric reference force cannot be accommodated within the traditional cross-bridge theory.¹² Therefore, it always appeared that there was a missing link—something unexplained—in the cross-bridge theory, particularly for eccentric muscle action. Huxley, in his book Reflections on Muscle,³ remarked on the insufficiency of the cross-bridge theory for lengthening muscle. He wrote: “I imagine that special features have been evolved which allow elongation (of muscles) to take place.” Furthermore, he explained: “I suspect that many of the unexplained phenomena, such as those I have just described (all related to eccentric muscle action) are related to these special features, and have little relation to the processes that take place during shortening.”

When studying the RFE in skeletal muscles, 2 basic properties have always persisted and are unanimously accepted: (1) RFE increases with increasing stretch magnitude,^22,40, 41, 42, 43 and (2) RFE is independent of the stretch speed.²² These properties could easily be explained if there was an elastic structural element in skeletal muscle that somehow became engaged upon activation and produced the extra force observed during and after stretch. This idea had early supporters,24, 44^,45 and it not only explains the increased force in actively stretched muscle but also explains the fact that this additional force is generated at no (or little) energetic cost.2, 46 However, for a long time, there was no experimental evidence in support of the engagement of a structural element.

In 2002, we performed experiments on actively stretched cat soleus muscles and observed that the force following active stretching and after deactivation of the muscle (the passive force) was much greater than the passive force following an isometric contraction at that same length, and it was also much greater than the passive force of a passively stretched muscle⁴² (Fig. 6A). We termed this observation passive force enhancement and demonstrated that there was a structural passive element that engaged when a muscle was actively stretched, and that this additional passive force persisted for minutes following deactivation but was abolished instantaneously if the muscle was quickly shortened to its prestretched length and then stretched back to its final length.⁴² We then demonstrated that this passive force enhancement also existed in single myofibrils but was lost when the structural protein titin was eliminated from sarcomeres47, 48, 49 (Fig. 6B). Therefore, we concluded that the passive force enhancement, and possibly much of the increase in force after stretching and some of the force during stretching, might arise from the “engagement” of titin during active muscle lengthening.

Fig. 6.

(A) Force-time trace of the cat soleus muscle (at 37°C) stretched by different amounts. Note the increased FE and increased PFE with increasing stretch magnitude. The gray line represents the isometric reference contraction, whereas the black lines represent the corresponding active stretch contractions. (B) Force-time trace of a single, isolated myofibril from rabbit psoas muscle showing PFE following active stretching of the myofibril. The gray line represents a passive muscle stretch, whereas the black line represents the active stretch contraction and subsequent deactivation. FE = force enhancement; PFE = passive force enhancement.

We proposed that titin “engagement” could occur in one of two ways: (1) titin could increase its inherent stiffness upon activation and stretch by binding calcium upon activation, and (2) titin could shorten its active spring length, thereby becoming stiffer, for example, by binding proximally to actin (Fig. 7). Research in our lab and by others verified that titin has calcium-binding sites and that once calcium is bound to selected segments (PEVK (region of titin rich in proline, glutamate, valine, and lysine) segment,⁵⁰ immunoglobulin domains⁵¹) of titin, it indeed changes its mechanical properties and becomes stiffer, thus producing more force when stretched in the presence of calcium (i.e., in the activated compared with the passive state; Fig. 8). However, this increase in force was merely about 10%–20% of that observed experimentally.⁴⁷ Titin binding to actin could explain theoretically the remainder of the experimentally observed force increase during and after eccentric muscle action.⁵² Using selected titin antibodies conjugated with a fluorescent label, we measured the elongations of the proximal and distal segments of titin in actively and passively stretched myofibrils.⁵³ We observed that for passive stretching, both the proximal and distal segments were elongating, as expected. However, for active stretching, the proximal titin segment elongated initially but then stopped elongating, and all of the length changes of titin were accommodated by the distal segment exclusively (Fig. 9). We interpreted this result as titin binding to actin, thereby shortening its spring length, becoming stiffer, and increasing the force during active as opposed to passive muscle stretching (Fig. 9).

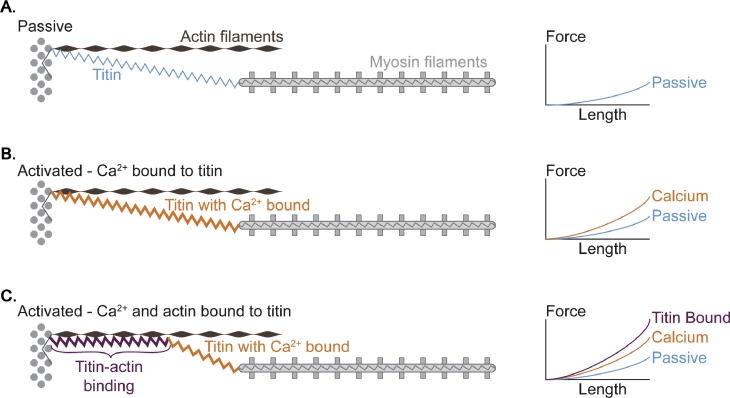
Fig. 7.

Schematic illustration of titin mechanics in passive (A) and active (B, C) sarcomeres. (A) Passive stretching is associated with elongation of the entire I-band region of titin in accordance with the mechanical properties of the individual titin subfragments. (B) Upon activation (increase in calcium in the contractile space), calcium binds to titin and increases titin's stiffness; thus, when sarcomeres are stretched in the active compared to the passive state, titin force is greater. (C) Upon activation and stretching, titin is thought to bind to actin, thereby reducing its free spring length, and only the segments distal to the titin binding site can be used for elongation. This mechanism has the potential to vary titin stiffness differentially, depending on the length of the sarcomere where activation and stretching occurs.

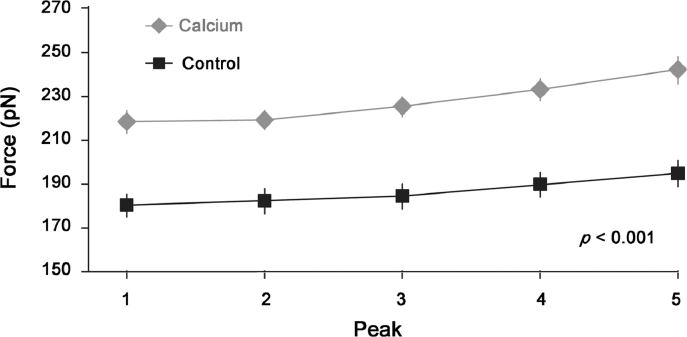
Fig. 8.

Unfolding force of titin immunoglobulin domains (cardiac I27 domains) in the absence (Control) and the presence of physiologically relevant concentrations of calcium (Calcium). Note that unfolding of the immunoglobulin domains requires substantially more force in the Calcium (activated) compared to the Control (passive) condition. Means ± SE are shown. In some of the symbols, the standard error cannot be seen because it is smaller than the dimension of the symbol. Adapted from Duvall et al.⁵¹ with permission.

Fig. 9.

Titin segmental elongations for passive (A) and active (B) stretching of sarcomeres. (A) For passive stretches, the proximal segment of titin (diamond symbols) for both myofibrils shown here elongates with sarcomere elongation up to a sarcomere length of 4.0 µm, as shown for myofibril 1. (B) For active stretches, the proximal segment of titin (diamond symbols) elongates for part of sarcomere stretching but then stops elongating and remains at a constant length for the remainder of the sarcomere stretch. We interpret these data as shown in the schematic figures to the right of the raw data figures; that is, titin somehow binds to actin during active sarcomere or muscle stretching, and its proximal segments cannot elongate any farther because they are fixed on the “rigid” backbone of actin. PEVK = region of titin rich in proline, glutamate, valine, and lysine. M-line indicates the middle of the sarcomere and Z-line indicates the end of the sarcomere.

Titin stiffening upon activation and active muscle stretching is an appealing theory because it can explain beautifully and simply many unresolved observations in eccentric muscle action. It can explain the RFE following active stretching and its dependence on stretch magnitude, the passive force enhancement, and the reduction in metabolic cost of eccentric compared with isometric and concentric contractions. In fact, we recently showed that force in the enhanced state requires much less metabolic energy (ATP) per unit of force than force in the regular isometric state.⁴⁶ Moreover, titin as a variable stiffness spring can also explain why sarcomeres are stable on the descending limb of the force–length relationship33, 54 and why myosin filaments remain aligned in the center of sarcomeres⁵⁵ when the cross-bridge theory is unable to provide this stability.

Needless to say, there are many more experiments that need to be performed to identify the detailed molecular functions of titin in muscle contraction. However, independent of the outcome of this work, the idea that titin is an adaptable molecular spring in sarcomeres (e.g., as illustrated in Fig. 10) is an appealing, simple, and beautiful solution to many problems that have plagued the muscle mechanics and physiology communities ever since the emergence of the cross-bridge theory more than 60 years ago,² particularly the inability of the cross-bridge theory to explain the mechanics of eccentric muscle action properly.

Fig. 10.

Possible model of muscle contraction incorporating titin as the third force-regulating filament other than actin and myosin. (A) Electron micrograph of a single myofibril (top panel) with a sarcomere isolated (middle panel) and a schematic illustration of the three-filament sarcomere that includes actin, myosin, and titin (bottom panel). (B) Schematic proposal of muscle contraction including titin as a force-regulating protein. In the top panel, we have 2 (half) sarcomeres with a short (left) and a long (right) initial length. If passively stretched from these 2 initial configurations, the passive force at the stretched length is the same (middle panel, passive stretch). If, however, the sarcomeres are activated first at the short and long lengths, respectively (top panel), titin will bind to actin at a more proximal (short initial length) or a more distal (long initial length) site, thus experiencing more stretch for the remnant-free spring when the initial sarcomere length is short rather than when it is long. Simultaneously, calcium binds to specific sites on titin upon activation, providing an additional increase in stiffness to the remnant-free spring, thereby adding even more titin-based force when sarcomeres are stretched actively compared with when they are stretched passively. (C) Active and passive sarcomere force–length relationships. Note that in this model, the passive (titin-based) force increases upon activation because of the calcium binding to titin and the reduction of titin's free-spring length. The shift of the passive force curve upon activation depends crucially on the initial sarcomere length at which activation occurs, because that will determine where titin binds to actin. The black-filled circle shows the expected force of an isometric contraction at the initial (prestretch) length, the open diamond represents the expected force of an isometric contractions at the final (end-stretch) length, and the orange diamond represents the FE following active stretching of a muscle from the initial to the final length. This FE is associated exclusively with the increase in titin-based passive force upon muscle activation and active stretching. FE = force enhancement. A indicates the A-band of the sarcomere, I indicates the I-band of the sarcomere, M indicates the M-line, and Z indicates the Z-line. Adapted from Herzog⁸ with permission.

5. Final remarks

The idea of a link between actin and myosin that engages upon activation, as proposed for titin in skeletal muscles, has a precedent in muscles of molluscs.56, 57, 58, 59 Molluscan smooth muscles have a titin analogue protein called twitchin. Molluscan muscle can enter a so-called catch-state where the muscle produces great tension and great resistance to stretch at little (or no) energy cost at resting calcium concentrations.⁶⁰ This catch-state is thought to be brought about by twitchin links that are formed between the actin and myosin filaments. The regulation of these twitchin links are thought to occur by phosphorylation, with the catch-state occurring in the dephosphorylated state. The idea of recruiting twitchin for force production in the passive (resting calcium levels) muscle is intriguing and bears great resemblance to the passive force enhancement observed in vertebrate skeletal muscle.48, 49^,61, 62, 63 The actions of twitchin also bear more than a casual resemblance to the proposed titin links between actin and myosin filaments in vertebrate skeletal muscles and can be used to explain the RFE property.5, 6, 7, 8^,23, 63