Crustal evolution and mantle dynamics through Earth history

Abstract

Resolving the modes of mantle convection through Earth history, i.e. when plate tectonics started and what kind of mantle dynamics reigned before, is essential to the understanding of the evolution of the whole Earth system, because plate tectonics influences almost all aspects of modern geological processes. This is a challenging problem because plate tectonics continuously rejuvenates Earth's surface on a time scale of about 100 Myr, destroying evidence for its past operation. It thus becomes essential to exploit indirect evidence preserved in the buoyant continental crust, part of which has survived over billions of years. This contribution starts with an in-depth review of existing models for continental growth. Growth models proposed so far can be categorized into three types: crust-based, mantle-based and other less direct inferences, and the first two types are particularly important as their difference reflects the extent of crustal recycling, which can be related to subduction. Then, a theoretical basis for a change in the mode of mantle convection in the Precambrian is reviewed, along with a critical appraisal of some popular notions for early Earth dynamics. By combining available geological and geochemical observations with geodynamical considerations, a tentative hypothesis is presented for the evolution of mantle dynamics and its relation to surface environment; the early onset of plate tectonics and gradual mantle hydration are responsible not only for the formation of continental crust but also for its preservation as well as its emergence above sea level. Our current understanding of various material properties and elementary processes is still too premature to build a testable, quantitative model for this hypothesis, but such modelling efforts could potentially transform the nature of the data-starved early Earth research by quantifying the extent of preservation bias.

This article is part of a discussion meeting issue ‘Earth dynamics and the development of plate tectonics’.

1. Introduction

Plate tectonics, a special class of mantle convection so far observed only on the Earth [1], is responsible for a vast array of geological processes, from the generation of continental crust [2] to the modulation of atmospheric composition [3]. Given its central role in the Earth system, it is natural that considerable interests in its evolutionary path have emerged in the past decade or so (e.g. [4–10]), i.e. when plate tectonics began on the Earth, and how it has evolved through time. Deciphering the history of plate tectonics is intrinsically difficult, as plate tectonics keeps erasing evidence for its past operation by subduction. We thus need to look for its traces left on continents, but even such secondary evidence is not available in abundance for deep time. The interpretation of relevant geological records preserved in continental rocks often suffers from non-uniqueness, the degree of which is only compounded by the increasing scarcity of such records in deeper time. This fragmentary nature of ancient geological records places a certain limit on the efficacy of a purely empirical approach, and developing a theoretical framework appears to be essential. Ideally, such a framework not only helps to interpret existing data in a unifying fashion, but also produces testable predictions that will motivate further field-based studies. We may be able to build a quantitative theory of the Earth by repeating theoretical development and observational testing, and such a theory could potentially be applied to terrestrial planets at large.

The purpose of this paper is to review the existing literature on crustal evolution and mantle dynamics, with a particular emphasis on the history of plate tectonics, and to propose a plausible working hypothesis that is capable of satisfying both observational and theoretical constraints. We are still far from the quantitative theory of the Earth, and what will be attempted in this paper is to present a qualitative but reasonably comprehensive scenario for the evolution of the Earth system. The first part of the paper will focus on chemical and isotope records preserved in continental crust. Whereas some recent studies suggest that crustal evolution reflects the onset of plate tectonics [11,12], the growth of continents has long been controversial, warranting a careful assessment of various growth models. The second part will review a theoretical basis for the possibility of having a different mode of mantle convection in the early Earth. Even though the sufficient and necessary conditions for plate tectonics are still widely debated, plate tectonics is certainly taking place on the present-day Earth, and it may be possible to tell whether it is less likely or not in the distant past on the basis of secular trends in more recent times. An emerging picture for the coupled ocean–crust–mantle evolution will then be presented as the synthesis of available geological data and theoretical considerations. The paper will finish with some future directions to explore.

2. Models of continental growth

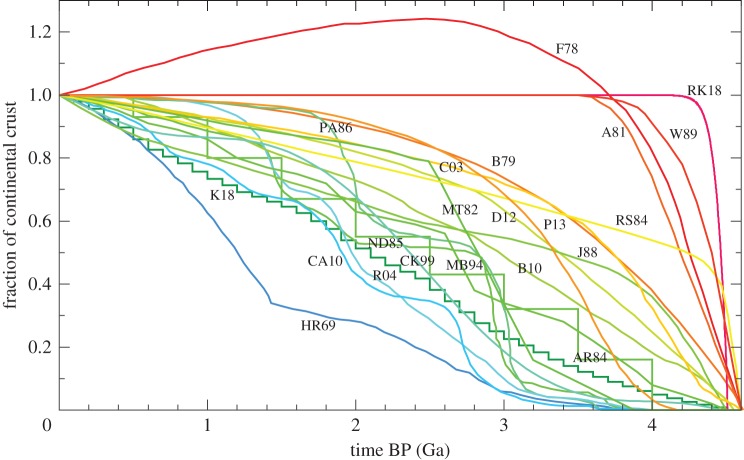
Numerous papers have been written on the evolution of continental crust [13–21], and crustal growth models proposed so far exhibit a considerable diversity (figure 1). Though it is customary to compare these models in one plot (as done in figure 1), such comparison could be misleading. For the purpose of discussion, it may be useful to classify existing models into the following three categories: (i) crust-based, (ii) mantle-based, and (iii) others. The first category provides only the lower bound on net crustal growth, whereas the second and third categories aim at estimating net crustal growth itself. Crust- and mantle-based models can thus be different from each other, and if we wish to infer the history of plate tectonics from crustal evolution, the difference between these two categories of models becomes equally important as growth models themselves. Also, by the very nature of how each model is constructed, some models are subject to greater uncertainties than others. In this section, these different categories are reviewed in turn. It will be seen that some aspects of crustal evolution have been relatively secured, though there remains a substantial amount of future work to fully exploit available observational constraints.

Figure 1.

Various published models for the growth of continental crust: HR67 [13], F78 [22], B79 [23], A81 [24], MT82 [25], RS84 [26], AR84 [16], ND85 [27], PA86 [28], J88 [29], W89 [30], CK99 [31], C03 [32], R04 [33], CA10 [34], B10 [35], D12 [11], K18 [36] and RK18 [37]. The volume or mass of the continental crust is normalized by the present-day value. Line colours are assigned to produce gradations from blue to red across the models; each model retains its line colour in figures 2, 3 and 6.

In this paper, the term ‘crust’ usually means the continental crust. Reference to protocrust and oceanic crust also appears in the text, and care has been taken to minimize potential confusion. Also, the term ‘crustal recycling’ is used exclusively to mean the loss of continental crust to the mantle by subduction or delamination, whereas ‘crustal reworking’ is to mean the remobilization of preexisting crust by partial melting or erosion and sedimentation, all taking place within the continental crust. Crustal reworking can disturb the isotopic compositions of continental rock and reset its apparent age. This terminology appears to be standard in the recent literature (e.g. [20]), and it is usually straightforward to correlate it with different terminologies used in older studies; for example, Veizer & Jansen [38,39] called crustal reworking and crustal recycling as ‘recycling’ and ‘crust–mantle exchange’, respectively, and McLennan [40] called them as ‘intracrustal recycling’ and ‘crust–mantle recycling’, respectively.

(a). Crust-based models

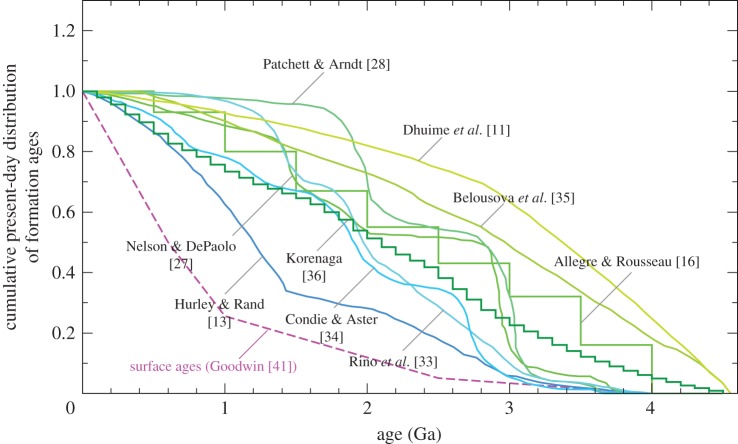
Crust-based models are estimates on the present-day distribution of original crust formation ages. Whereas it is common to show these models as if they represent the evolution of crustal mass (figure 1), it is more appropriate to describe them as the cumulative distribution of formation ages at the present day (figure 2). Also shown in figure 2 for comparison is the present-day distribution of surface ages [41]. The surface ages of continental rocks can be reset by the most recent tectonic events, and crust-based models try to estimate when they were originally created from the mantle. The difference between the surface age distribution and crust-based models reflects the extent of crustal reworking. The present-day distribution of formation ages does not contain any information on the crust that has been lost to the mantle, so crust-based models are best seen as the lower bound on net crustal growth.

Figure 2.

Crust-based ‘growth’ models discussed in §2a. As indicated here, these models aim to estimate on the present-day distribution of formation ages, so they serve as the lower bound on net crustal growth. The cumulative distribution is normalized by the present-day continental mass or area. Also shown in dashed line is the surface age distribution according to Goodwin [41].

There are two tasks for a crust-based model to accomplish: to estimate the formation age of a given continental sample, and to do it globally. The history of crust-based models has witnessed continuous efforts to improve on previous attempts in either of these tasks (or occasionally both). Hurley & Rand [13] was the first attempt to compile the formation age information of continental crust globally (excluding the former Soviet Union and China due to the lack of accessible data) based on K-Ar and Rb-Sr ages. In the 1970s, the acquisition of high-precision Sm-Nd isotope data became possible, and the notion of Nd model age was developed, first with the evolution of the chondritic uniform reservoir (CHUR) as the reference [42], and then with the evolution of the depleted mantle [43]. The latter reference is deemed more appropriate given the complementary nature of the continental crust and the depleted mantle [44]. In the simplest situation, the depleted mantle model age may be equated with the formation age, but in a more likely situation in which the preexisting crust is reworked with new mantle-derived melt, it may be thought as the weighted average of multiple formation ages [28,45]. Nelson & DePaolo [27] proposed the crustal growth curve based on Nd-depleted mantle model ages for North American igneous samples, and Patchett & Arndt [28] revised their growth curve by adding more data from Europe and Greenland and also by correcting for the likely effect of crustal mixing on the model age. Around the same time, Allègre & Rousseau [16] proposed a method to estimate a growth curve from the Nd model ages of sedimentary rocks, by assuming some erosion law to undo the averaging effect of sediment formation. A mathematical framework for this approach was developed further by Jacobsen [46]. Starting from the late 1990s, the use of global databases of detrital zircon has become popular [11,33–35,47]; each zircon grain provides its own age information, eliminating the need to undo averaging associated with sediment formation. In early applications, U-Pb crystallization ages were directly used [33,34,47]. Then, Belousova et al. [35] proposed a combined use of U-Pb crystallization ages and Hf-depleted mantle model ages, and Dhuime et al. [11] added data screening with oxygen isotope data. More recently, Korenaga [36] suggested a new method of estimating the formation ages from U-Pb crystallization ages and Hf model ages, by taking into account the covariation of these two different ages.

However, the period from 2010 to 2017, i.e. after the publication of Belousova et al. [35] and before that of Korenaga [36], was singularly confusing, and it deserves some detailed account. First of all, as demonstrated by Korenaga [36], the method proposed by Belousova et al. [35] does not produce an estimate on formation age distribution. There is no logical connection between the formation age distribution and the mathematical operation conducted in their method, and any ‘growth-curve-looking’ result from their method is better regarded as a procedural artefact. This fact was already hinted by one of the two synthetic tests conducted by Belousova et al. [35] themselves (see section 5.2 of [36]) and was also alluded by Payne et al. [48]. Dhuime et al. [11] incorporated oxygen isotope screening, but the core of the method remained the same in their application. They also introduced an additional layer of confusion; they regarded their ‘growth curve’ as an estimate on net crustal growth, not on the formation age distribution. That is, they seemed to think that they could correct not only for crustal reworking but also for crustal recycling. This fact may not be very obvious in their paper; in their fig. 2, they denote their growth curve as ‘crustal reworking corrected’ (a tag appropriate for the formation age distribution), but in the main text, they use this curve to discuss ‘net rates of continental growth’. A series of review papers written subsequently by the same authors [20,21,49,50] has made it clear that they do believe that the method of Belousova et al. [35] provides an estimate on net crustal growth. For example, Cawood et al. [20] state: ‘Dhuime et al. [11] argued that some ∼65% of the current-day crustal volume was present by the end Archean, yet compilations of present age distributions equate to less than 5% of the current volume at that time [41]. The striking implication is that much of the crust that was generated in the Archean, and since then, has been destroyed and recycled back into the mantle’. It is rather puzzling that the methods of Belousova et al. [35] and Dhuime et al. [11], which cannot even correct for crustal reworking, were (and probably still are) widely believed to be able to correct also for crustal recycling, although there has been no demonstration, using some synthetic datasets with simulated crustal reworking and recycling, that their methods can yield an estimate on net crustal growth. The reader is referred to Korenaga [36] for some illustrative examples with synthetic data, in which their methods fail spectacularly to recover the assumed distribution of crustal formation ages (see fig. 2). Whereas his demonstration is regarding only the effect of crustal reworking, it can also be taken as the limit of no crustal recycling; it thus suffices as counterexamples for the claim that their methods can estimate net crustal growth.

It is important to distinguish between uncertainties and misunderstandings. Uncertainties can be improved, but misunderstandings should be corrected. For example, how to estimate the formation age distribution from zircon ages is still subject to a number of uncertainties [36,48,51,52], including but not limited to the uncertainty of U-Pb crystallization ages due to ancient Pb loss, the uncertainty of Lu/Hf that affects the accuracy of Hf model ages, the screening criteria when using oxygen isotope data, the different interpretations of Hf model ages, the weighting of different datasets and the assumption of each grain representing the same amount of continental crust. With some further efforts, these uncertainties may be reduced in future. By contrast, the problem with the method of Belousova et al. [35] is not a matter of scientific uncertainty or geological interpretation. It is simply a logical error. Claiming that the method can estimate net crustal growth [11] has made the matter even worse. Without acknowledging these mistakes, it would be difficult to make meaningful progress. As will be seen later (§2c), a proper understanding of what crust-based models can offer is essential to discuss the evolution of continental crust in a sensible manner.

(b). Mantle-based models

Mantle-based models of crustal growth aim at net crustal growth. This is based on the notion that the extraction of continental crust from the mantle leaves the mantle correspondingly depleted for the kind of elements that are enriched in the crust such as Rb, Pb, U, Th, K and light rare-earth elements (REEs) [53]; the generation of continental crust involves not only mantle melting but also other processes such as intracrustal differentiation and crustal delamination, all of which tend to enhance its trace element budget. Thus, if the mantle at three billion years ago was only half as depleted as the present-day mantle, for example, the continental crust at that time would be only half as massive as the present-day crust, assuming that the crust was similarly enriched in the past. This can potentially be a very efficient approach, bypassing all the complexities involved in the evolution of continental crust itself. Unlike the crust-based approach, the mantle-based approach automatically takes into account the crust that has been recycled back to the mantle and provides the total mass of continental crust as a function of time.

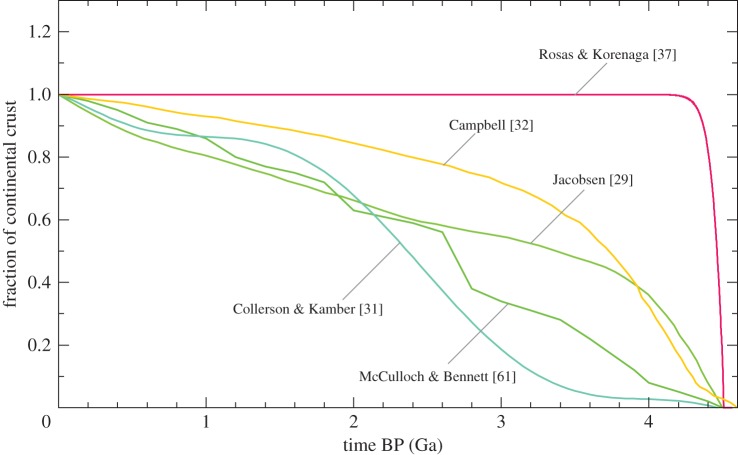
One drawback of this approach is that we have to deal with the complexity of mantle evolution, which is not trivial. There are two different kinds of issues. The first issue is that the present-day mantle is known to be chemically and isotopically heterogeneous [54,55]. Thus, how to quantify the history of mantle-average chemical depletion, which is required to estimate the coexisting crustal mass, becomes challenging. The second issue is that the information on the ancient state of mantle depletion has to be gleaned from the so-called ‘mantle-derived’ igneous rocks found within the continental crust. One of the important criteria used to identify such rocks is that ϵ¹⁴³Nd (deviation of the measured¹⁴³Nd/¹⁴⁴Nd ratio from the CHUR evolution) is sufficiently high, but by doing so, it limits ourselves to the depleted end-member component of the mantle (commonly referred to as the depleted MORB-source mantle, where MORB stands for mid-ocean-ridge basalts [54]). Given this practical difficulty to estimate the degree of whole-mantle depletion in the past, it has been common to divide the mantle into two parts, the depleted mantle and the primitive mantle (or something similar), and relate the extraction of continental crust to the former. Such simple treatment of the mantle cannot capture the diversity of isotopic heterogeneities inferred for the present-day mantle, but it is probably a good compromise to characterize some gross features of mantle evolution from highly sparse rock records (figure 3).

Figure 3.

Mantle-based models of net crustal growth discussed in §2b.

An effort to understand the coupled crust–mantle evolution using geochemical box modelling has a long history [14,29,56–66]. It is a history of exploring the model space and improving the quantity and quality of observational constraints. Based on box modelling with time-independent crustal recycling, for example, DePaolo [59] suggested that the Nd isotope evolution of the depleted mantle preferred gradual continental growth over instantaneous growth, but Armstrong [67] pointed out that instantaneous growth would be consistent with the Nd evolution if crustal recycling had declined with time. Also, the rapid growth of continental crust in the early Earth was once suggested on the basis of highly positive ϵ¹⁴³Nd of Archean rocks [68–70], but the reliability of these data have been questioned [71], and they have been revised since then [72–74]. A similar debate exists for the Hf isotope data [75,76]. A modelling philosophy has changed through time as well. In the 1980s, an inverse approach was popular, motivated by the development of a general inverse theory by Tarantola & Vallette [77,78]. The inversion of Allègre et al. [60,79] indicated that then available data were not accurate enough to draw definite conclusions. Jacobsen [29] inverted the Nd isotope evolution of the depleted mantle as well as the continental crust to determine the continental growth. After this, no more inversion-based model followed. McCulloch & Bennett [61] employed a forward modelling approach to test their preferred model of crustal growth against a number of different isotope systems, trace element abundances and trace element ratios. Kramers & Tolstikhin [62] conducted forward modelling of U-Th-Pb evolution with an elaborate box model containing four different reservoirs for the continental crust. As U, Th and Pb are more enriched in continental crust than light REEs, the modelling of these elements has greater sensitivity to crustal growth than the modelling of the Sm-Nd system, but at the same time, the former is known to require more complex box models. Also, U has an active biological cycle unlike REE. As the complexity of box modelling increases, it becomes increasingly difficult to fully constrain it with available observations. Forward modelling does not prove the uniqueness of a preferred solution nor quantify its uncertainty, but it still provides some quantitative basis for discussion.

More recent mantle-based models of crustal growth are not based on geochemical box modelling; they are based simply on trace element ratios. The approach with trace element ratios has the advantage of being very simple (no calculus involved), but unlike box modelling, it does not provide an estimate on crustal recycling. Collerson & Kamber [31] used Nb/Th, whereas Campbell [32] used Nb/U. In fact, Collerson & Kamber [31] tried Nb/U as well, but they discounted the corresponding growth curve because it indicated greater continental mass in the past. After the net growth model of Campbell [32], an interest in creating a new growth model with the mantle-based approach seems to have faded away. Instead, the evolution of continental crust has been studied mostly through the crust-based approach using the global databases of detrital zircon. This shift from the mantle-based approach to the crust-based one is partly because of the aforementioned misconception that the crust-based approach can constrain net crustal growth (§2a), and partly because of the intrinsic difficulty of the mantle-based approach. Estimating the degree of mantle depletion in ancient times from ancient igneous rocks, which do not exist in abundance, is obviously challenging.

Nevertheless, the mantle-based approach can in principle constrain net crustal growth in the most direct fashion, and it is important to make headway with this approach. To this end, Rosas & Korenaga [37] recently revisited the Sm-Nd isotope evolution of the depleted mantle component with geochemical box modelling. In contrast to earlier inversion-based studies [29,60], which are based on the linearized version of the general nonlinear theory [78], their study employed the Monte Carlo sampling of the model parameter space to implement the fully nonlinear inverse theory of Tarantola & Vallette [77]. The pair of these two elements provides a unique probe for the history of crust–mantle differentiation, because of two isotope systems with very different decay constants:¹⁴⁷Sm and¹⁴⁶Sm decay into¹⁴³Nd and¹⁴²Nd, respectively, with the corresponding half-lives of approximately 106 Gyr and approximately 103 Myr. They found that the evolution of¹⁴²Nd/¹⁴⁴Nd was consistent with rapid crustal growth as well as efficient recycling in the Hadean, whereas the evolution of¹⁴³Nd/¹⁴⁴Nd indicated the declining efficiency of crustal recycling through time. This gradual decline in recycling is essentially the same as what Armstrong [57,67] suggested many years ago, but here it naturally emerges as a result of satisfying both¹⁴³Nd and¹⁴²Nd isotope data. It should be noted, however, that their interpretation of the Nd isotope evolution is not unique. In particular, the¹⁴²Nd evolution can be explained without calling for the evolution of continental crust [73,74,80]. Even if we assume that the¹⁴²Nd evolution is solely caused by the extraction of the continental crust, different combinations of crustal growth and recycling would be consistent with the same isotope constraints by modifying the formulation of geochemical box modelling. The number of relevant data for early Earth evolution is still limited, and their interpretation is usually far from being straightforward as one has to deconvolve various intracrustal and infracrustal processes [81–83]. At the moment, therefore, it appears premature to derive any definitive conclusion on net crustal growth with the mantle-based approach. As will be discussed later (§5), there remain a number of tasks to be done if we wish to pursue this approach further. Regardless how we will proceed, it will always be important to distinguish between crust-based models and mantle-based models and understand their relation. This is the subject of the next section.

(c). On the difference between crust- and mantle-based models

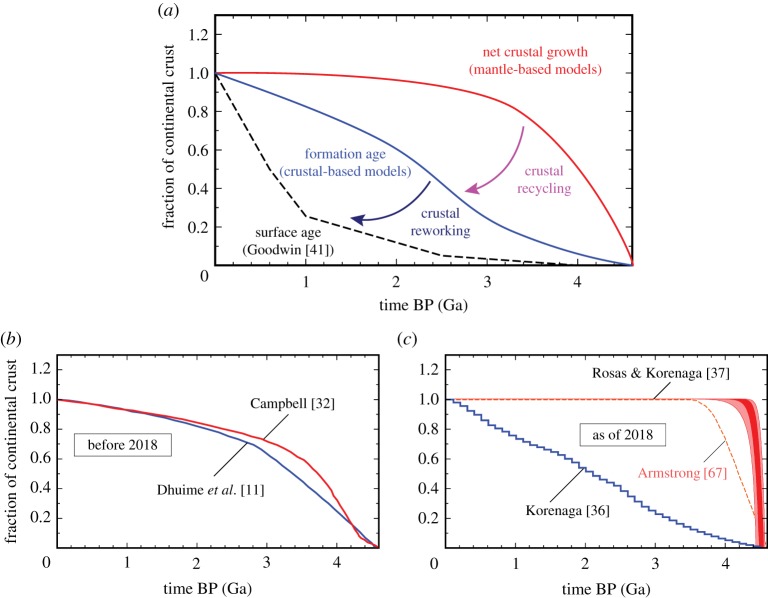
The crust-based approach constrains the present-day distribution of formation ages, whose deviation from the surface age distribution indicates the effect of crustal reworking. The mantle-based approach estimates the history of net crustal growth, and the difference between net crustal growth and the formation age distribution represents the extent of crustal recycling (figure 4a). As crustal recycling is commonly associated with subduction and thus plate tectonics, the difference between crust- and mantle-based models would be as important as net crustal growth, when inferring the style of mantle convection from the evolution of continental crust.

Figure 4.

(a) Schematic diagram to illustrate the relation among net crustal growth (from mantle-based models), the formation age distribution (from crust-based models), the surface age distribution, crustal recycling and crustal reworking. In particular, the difference between crust- and mantle-based models reflects the extent of crustal recycling, thus the operation of plate tectonics. (b) Before 2018, the difference between the latest crust- and mantle-based models was remarkably small. Note that the model of Dhuime et al. [11] cannot be a model for net crustal growth because of the nature of their data. (c) The latest crust-based model [36] and the latest mantle-based model [37] as of 2018. Rosas & Korenaga [37] employed Monte Carlo sampling, and dark and light shades denote the 50% and 90% confidence limits, respectively, of the successful Monte Carlo ensemble. The Armstrong model [24] is also shown for comparison.

From this perspective, the situation prior to year 2018 (figure 4b) presented a considerable challenge. The then latest mantle-based model of Campbell [32] and the then latest crust-based model of Dhuime et al. [11] are very similar to each other, leaving little room for crustal recycling. The apparent convergence of the two approaches is difficult to reconcile with the continuous operation of plate tectonics at least for the last one billion years or so [6]. This problem was largely unnoticed because, as noted earlier, the model of Dhuime et al. [11] was repeatedly advertised as a model for net crustal growth. However, the method of Belousova et al. [35], on which their study is based, has nothing to do with net crustal growth. The method just happens to generate a ‘growth-curve-looking’ result [36], and it is a remarkable coincidence that such an artefact resembles closely the net growth model of Campbell [32]. Just for the record, the global database of detrital zircon does contain the information on mantle depletion, which could be used to constrain net crustal growth. The age distribution of the Hf isotope data of zircon is bounded from the above by the evolution of the depleted mantle [84], which can be related to the growth of continental crust using the mantle-based approach. In the method of Belousova et al. [35], however, the use of the depleted mantle evolution is limited to defining depleted mantle model ages, which are related to crustal formation ages. From the nature of input data used, therefore, the models of Belousova et al. [35] and Dhuime et al. [11] can only belong to the category of crust-based models.

A radically different role of crustal recycling is implied from the crust-based model of Korenaga [36] and the mantle-based model of Rosas & Korenaga [37] (figure 4c). As discussed in detail later (§5), both models should be regarded as a tentative solution subject to future revisions, but they can still provide an illuminating example for how to compare different ‘growth’ models. The net growth model of Rosas & Korenaga [37] is similar to the instantaneous growth model of Armstrong [24], which is usually regarded as an unlikely end-member. On the other hand, the crust-based model of Korenaga [36] is similar to what is normally referred to as gradual growth. It is of vital importance to understand that the difference between these two models does not necessarily indicate any inconsistency between them. A crust-based model is an estimate on the formation age distribution, so it is merely the lower bound on net crustal growth. As long as such lower bound does not exceed the net crustal growth of a mantle-based model, these crust- and mantle-based models remain mutually consistent.

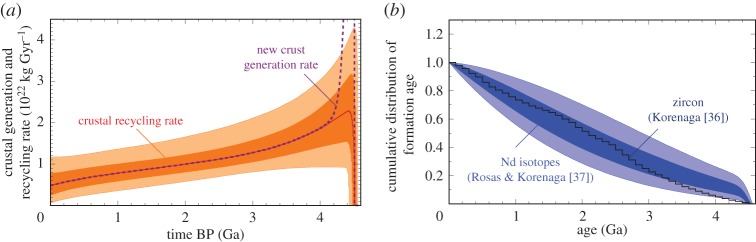
If a mantle-based growth model is derived from geochemical box modelling, it is possible to evaluate its consistency with a crust-based model in greater depth (figure 5). This is because geochemical box modelling provides estimates of crustal growth as well as crustal recycling, and by combining them, one can compute the corresponding distribution of formation ages at the present-day [37,46,87]. As shown in figure 5b, the present-day distribution of formation ages predicted from the mantle-based model of Rosas & Korenaga [37] is in good agreement with that of Korenaga [36]. This agreement is notable because these two estimates on the formation age distribution are based on completely independent kinds of data (the Nd isotopes of igneous rocks [37] and the U-Pb crystallization ages and Hf model ages of detrital zircon [36]), and on entirely different methods (mantle-based and crust-based). Given the provisional nature of these models, such agreement could still be a mere coincidence, and it certainly does not prove the uniqueness of the growth model of Rosas & Korenaga [37]. Nevertheless, the model of Rosas & Korenaga [37] appears promising because the evolution of crustal recycling in their model successfully encompasses the present-day recycling rate inferred from sediment subduction [85,86] (figure 5a), without being forced to do so in the box modelling. In addition, the secular evolution of continental basalt chemistry over the past ∼3.8 Gyr [88], which points to a nearly constant degree of depletion in the source mantle, is also consistent with this new growth model.

Figure 5.

(a) Crustal recycling rate (orange shades) corresponding to the net crustal growth model of Rosas & Korenaga [37]. The meaning of dark and light shades is the same as in figure 4c. For comparison, the present-day recycling rate based on sediment subduction is 0.7–0.9 × 10²² kg Gyr⁻¹ [85,86]. The rate of new crustal generation is shown in purple dashed line. For the sake of clarity, only the median solution is shown for the crustal generation rate. (b) The present-day formation age distribution predicted from the box modelling of the Nd isotope evolution [37] (blue shades) is compared with that estimated from the global database of detrital zircon [36] (dark blue line).

A few general lessons can be learned from this exercise of comparing these models through the calculation of formation age distribution. First, vastly different-looking models can be consistent if they belong to different categories of ‘growth’ models. Second, a mantle-based net growth model cannot be compared with a crust-based model without information on crustal recycling. When different ‘growth’ models are compared (figure 1), no distinction between crust- and mantle-based models is usually made, and mantle-based models are almost always shown without corresponding information on crustal recycling. It is hard to learn anything useful from such comparison. Third, the history of crustal recycling cannot be read off simply from the difference between crust- and mantle-based models, as such difference represents the time-integrated effect of crustal recycling. Finally, it would be virtually impossible to infer the magnitude of crustal growth and recycling from crust-based models alone. The preservation of the Hadean crust to the present day, for example, does not demand inefficient crustal recycling or stagnant lid convection in the early Earth. The present-day distribution of formation ages is the net outcome of the competing processes of crust generation and destruction, and without the complementary information from the mantle-based approach, crustal evolution becomes a hopelessly under-determined problem. These considerations underscore the importance of pursuing geochemical box modelling, as it can constrain directly both crustal growth and recycling.

(d). Other types of models

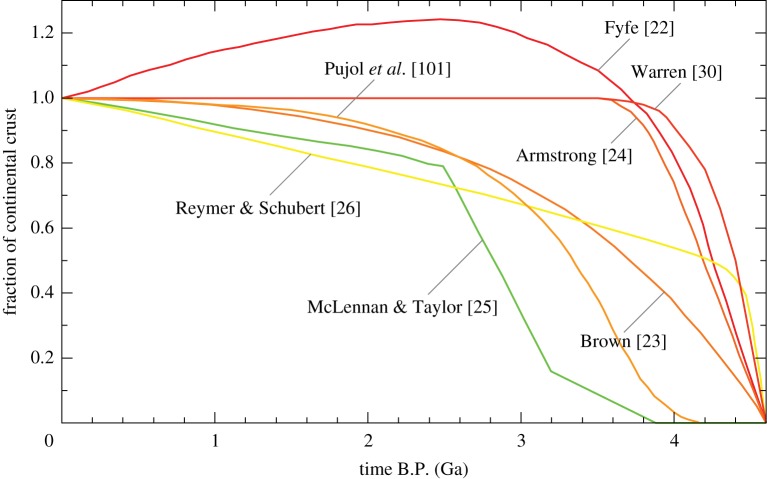
The third kind of ‘growth’ models (figure 6) are neither crust-based nor mantle-based, but they aim at net crustal growth. Some of these models are largely speculative. Others employ some quantitative constraints such as the secular evolution of upper crustal composition, but arriving at net crustal growth from such constraints is less direct than the mantle-based approach, so these models are subject to considerable uncertainties.

Figure 6.

Crustal growth models in the third category (i.e. neither crust-based nor mantle-based) discussed in §2d.

Perhaps the most famous model in this category is that of Armstrong [17,24,57]. As he extensively explored its consistency with mantle geochemistry, it might also qualify as mantle-based, but it is still fair to list it here because his stance was to start with an assumption and then test its predictions against observations. His belief is that large terrestrial planets must have experienced early planetary-scale differentiation, which resulted in the rapid formation of a metallic core, a silicate mantle, an enriched crust and a hydrosphere. Whereas such differentiation is probably inevitable in the highly energetic phase of the very early Earth, the resulting crustal layer does not have to be continental crust; it could be just oceanic crust, which can be formed by a single-stage melting of the mantle. Though the Armstrong model has been remarkably unpopular, his 1991 valedictory paper argued against many of the criticisms, and his model still merits serious consideration [89], especially in light of the recent mantle-based model of Rosas & Korenaga [37]. The model of Warren [30] was proposed in a manner similar to the Armstrong model. The model of Fyfe [22] is based on the speculation that crustal recycling could have exceeded crustal addition during some time of Earth history. The model of Brown [23] is another speculation-based model with some qualitative arguments.

McLennan & Taylor [25] built their growth model based on the notion that the Archean upper crust was probably more mafic than the post-Archean upper crust. Their principal reasoning is that the change in sediment chemistry between Archean and later times requires a major episode of continental growth around the Archean–Proterozoic boundary. The other parts of their model were adjusted so that little crust was present before 3.8 Ga and crustal growth was slow and gradual after 2.5 Ga. Armstrong [17] once commented on their model as follows: ‘I have never been able to figure out the logical connection between sediment chemistry and crustal volume. Crustal chemistry could change, as tectonic styles evolve and stable cratons enter the picture, without any necessary change in volume’. Despite this caveat, the approach taken by McLennan & Taylor [25] is still popular today [12,90]. It is noted that the lower part of continental crust remains poorly understood, even for its present state, owing to the paucity of direct samples; estimates for the lower crustal composition exhibit an order of magnitude differences in terms of trace elements [91]. The continental lower crust does not have to be depleted in trace elements, because some of them (e.g. U and Th) are concentrated in accessory minerals such as zircon, which could survive through intracrustal differentiation [92].

The model of Reymer & Schubert [26] is based on two independent considerations. They first estimated the Phanerozoic net crustal growth by estimating the crustal addition rate from the volume of magmatic arc and subtracting the sediment subduction rate. Then, they corroborated this estimate by the modelling of continental freeboard. It is now understood that the agreement of these two considerations was fortuitous. The rate of sediment subduction has been found to be more substantial [85,86] than estimated by Reymer & Schubert [26]. Also, their freeboard modelling is based on the classical type of thermal evolution modelling [93,94], which has been shown to be at odds with a range of geological and geochemical observations [95–100]. In general, freeboard modelling involves quite a few moving parts [100], the most important of which is the history of ocean volume, and it cannot be used to distinguish between different growth models.

The most recent model in this category was put forward by Pujol et al. [101], who used the secular evolution of atmospheric argon isotopic composition. However, the relationship between crustal growth and the argon isotope data is tenuous, because the generation of continental crust is not the primary mechanism for argon degassing from the mantle. For comparison, the present-day rate of oceanic crust production is approximately 7 × 10²² kg Gyr⁻¹ [102], which is several times higher than the rate of continental crust production according to the model of Rosas & Korenaga [37] (figure 5a), so mid-ocean-ridge magmatism is expected to have contributed predominantly to the evolution of atmospheric argon. Also, the degassing modelling of Pujol et al. [101] does not acknowledge the uncertainty of potassium budget in the Earth [95,103] nor the debate over the thermal evolution of the Earth [104–107], so their modelling result suffers from far greater uncertainties than claimed.

Thus, in terms of reliability, the models in this third category are not comparable with those in other two categories. In fact, it would not be appropriate to expect that even those with some quantitative constraints (e.g. [25,101]) could supersede mantle-based models, because the connection between such constraints and net crustal growth is rather remote. At the same time, the secular evolution of upper crustal composition or atmospheric composition does provide additional insights into the evolution of continental crust, and any successful holistic model of crustal evolution must be able to satisfy such observations. Crustal growth is a complex process, which involves not only the continental crust but also other major components of the Earth systems such as the mantle, the oceanic crust, the oceans and the atmosphere. To build a scientific framework that can assimilate diverse observations in a coherent manner, it will be essential to clarify what data constrains which aspect of crustal growth and to quantify how well it does so.

3. Modes of mantle convection in the Precambrian

Given the paucity of geological records pertinent to the early Earth, it is understandable to seek some theoretical hints in the study of mantle dynamics. Though our understanding of mantle dynamics may be too incomplete to meet such expectations, recognizing the current limitations of our knowledge should still facilitate interaction between geologists and geophysicists. As high-performance computing has become increasingly accessible in recent years, the numerical simulation studies of mantle convection have proliferated, with a vast range of quality. Without a good understanding of fluid dynamics and rock mechanics, it would be difficult to appraise any theoretical study on mantle dynamics, but one can still cultivate a critical eye by familiarizing with some important peculiarities of mantle convection.

In this section, therefore, the basics of mantle convection that are directly relevant to early Earth dynamics are summarized first, to prepare the reader for subsequent discussion. Then, a few prevailing notions regarding the early Earth, such as vigorous convective mixing, thin lithosphere and stagnant lid convection, are examined for their current theoretical footing. This section closes with the discussion of some first-order observations and their implications for mantle dynamics in the Precambrian.

(a). Preliminaries

The advent of plate tectonics theory in the 1960s prompted the modern study of mantle convection, initially with the simplest system with constant material properties [108,109]. In the following few decades, our modelling capability has gradually expanded to incorporate realistic complexities [110], such as strongly temperature-dependent viscosity, phase transitions, spherical-shell geometry and various weakening mechanisms. At the same time, the number of model parameters has also increased, making it difficult to explore the model space extensively and gain a thorough understanding of the effects of different model parameters. There exists an elegant theory for stagnant lid convection [111], which accurately captures the physics of thermal convection with strongly temperature-dependent viscosity. This theory involves only two parameters: the internal Rayleigh number (a measure of convective potential) and the Frank–Kamenetskii parameter (a measure of the temperature dependence of viscosity), and is applicable only to the case of purely internal heating. Extending this type of scaling theory to cover more general situations is difficult, and as such, the theoretical study of mantle dynamics is often conducted in an exploratory fashion with a limited number of numerical simulations or laboratory experiments. Such exploratory studies naturally focus on the implications of their new findings to mantle dynamics, but the connection between simulated results and the actual Earth could be substantially weaker than advertised. When examining a study of mantle convection aiming at early Earth dynamics or long-term mantle evolution, it is always worth paying attention to the following details: (i) assumed weakening mechanisms, (ii) the degree of temperature dependence of viscosity, and (iii) the heating mode of convection. In what follows, these issues will be discussed in turn.

Mantle rheology is the most important factor in mantle dynamics. Ironically, it is the least understood factor as well. For the mode of mantle convection in the early Earth, the central question is how the oceanic lithosphere, or the top thermal boundary layer of mantle convection, behaves through time. In plate tectonics on the present-day Earth, the top boundary layer is broken into a dozen or so plates, and many plates return to the mantle by subduction. With the strongly temperature-dependent viscosity of silicate rocks [112], however, the top boundary layer is expected to form a single rigid shell covering the entire planet [113]; this style of convection is known as stagnant lid convection. For plate tectonics to take place, therefore, some weakening mechanisms have to exist to compensate for the temperature-dependent viscosity. There are a few candidate mechanisms such as grain-size reduction [114,115] and thermal cracking [116], but their efficacy is still debated. Given this uncertainty, how to parametrize mantle rheology to simulate plate tectonics (or lack thereof) is currently arbitrary. The only constraint is that a model has to exhibit plate tectonics under the present-day conditions, and the key question is usually whether or not such a model switches to a different mode of convection under early Earth conditions. In many simulation studies, the strength of oceanic lithosphere is limited by some constant yield strength, but this common approach neglects the possibility that the efficiency of the weakening mechanism that results in the assumed yield strength could vary with time. The details of how any weakening mechanism works are still subject to future research, so it is difficult to predict its efficiency in the past when the mantle was hotter and thus the nature of oceanic lithosphere (such as the thickness of oceanic crust) was likely to be different from the present [117].

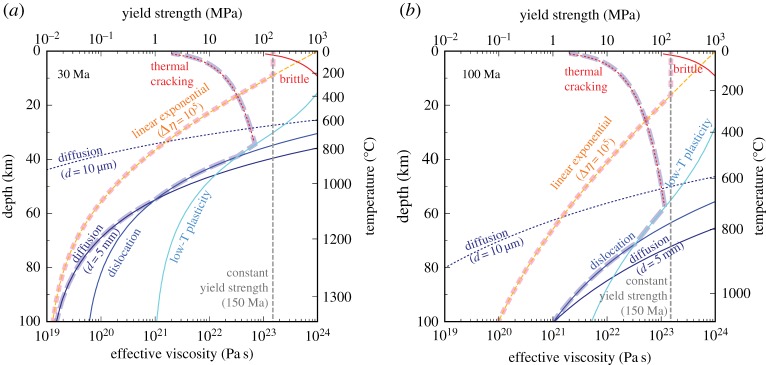
This ambiguity with weakening mechanisms is further compounded by different implementations of temperature-dependent viscosity. As noted above, the viscosity of silicate rocks is strongly temperature-dependent, but many simulation studies employ only mildly temperature-dependent viscosity [118–120]. The activation energy, which controls the temperature dependence, of diffusion creep in olivine aggregates is approximately 300 kJ mol⁻¹ [112,121], and such activation energy corresponds to a viscosity contrast of approximately 10⁴⁷ for the total temperature drop across the oceanic lithosphere, from 1300°C to 0°C. This extreme viscosity contrast is, however, not relevant to the strength of oceanic lithosphere because other deformation mechanisms, such as brittle failure and low-temperature plasticity, likely limit the yield strength below approximately 1 GPa [122], which corresponds to the effective viscosity of approximately 10²⁴ Pa s with the geological strain rate of 10⁻¹⁵ s⁻¹ (figure 7). If the viscosity of the asthenosphere is 10¹⁹ Pa s, then, the viscosity contrast across the lithosphere would be limited to just 10⁵. An often overlooked fact is that this small viscosity contrast results from the combined effect of multiple deformation mechanisms, and using mildly temperature-dependent viscosity does not reproduce the realistic strength profile of oceanic lithosphere (figure 7, compare cases A and B). The viscosity contrast of 10⁵ is sufficient to produce stagnant lid convection [113], so even with this mild temperature dependence, one can simulate a transition from stagnant lid convection to plate tectonics by turning on some weakening mechanism, or more commonly, just by imposing a constant yield strength. In such an exercise, a system is already situated close to the boundary of different convection regimes, thereby being primed to exhibit a change in the mode of convection by small perturbations in model parameters. Also, weaker temperature-dependence facilitates the delamination of lithosphere [127,128] and enhances the efficiency of convective mixing. Thus, the apparently innocuous approximation for temperature-dependent viscosity could affect the various aspects of numerical simulation. A similar comment can be made on laboratory experiments because the rheology of analogue materials used for such experiments [129,130] can be only qualitatively similar to that of silicate rocks.

Figure 7.

Hypothetical yield strength profiles for present-day oceanic lithosphere at the seafloor age of (a) 30 Ma and (b) 100 Ma. Only the top 100 km is shown, and the assumed thermal structure, based on half-space cooling with the initial temperature of 1350°C, is indicated on the right axis. Yield strength is calculated assuming the geological strain rate of 10⁻¹⁵ s⁻¹, so the yield strength of 1 GPa corresponding to the effective viscosity of 10²⁴ Pa s. The effect of thin crustal layer is ignored, and deformation mechanisms considered here include: (1) diffusion creep with the activation energy of 300 kJ mol⁻¹ and the grain size exponent of 2, with the reference viscosity of 10¹⁹ Pa s at 1350°C and the grain size of 5 mm, (2) dislocation creep with the activation energy of 600 kJ mol⁻¹ and the stress exponent of 3, with the reference viscosity of 10¹⁹ Pa s at 1350°C and the deviatoric stress of 0.1 MPa, (3) low-temperature plasticity based on the reanalysis of the experimental data of Mei et al. [123] by Jain et al. [124], with the exponents of p = 1 and q = 2, (4) linear exponential viscosity with the total viscosity contrast of 10⁵, (5) brittle strength with the friction coefficient of 0.8 and with optimal thrust faulting [125] and (6) brittle strength with the effective friction coefficient of 0.03 to emulate the effect of thermal cracking [126]. Shown for comparison is the constant yield strength of 150 MPa, which is a typical value used in numerical simulation studies. Diffusion creep with the grain size of 10 mm is shown to illustrate the efficacy of grain-size reduction; this weakening mechanism is not effective in the cold part of lithosphere. Thick dashed lines trace two contrasting cases: case A (pink, short-dashed) for the combination of linear exponential viscosity with constant yield strength, and case B (blue, long-dashed) for the combination of more realistic ductile deformation mechanisms and thermal cracking. These cases are different by up to two orders of magnitudes over the bulk of lithosphere.

Finally, mantle convection is heated both from below and within, and this mode of heating is called mixed heating. Heating from below represents core heat flow, and heating from within originates from the decay of radioactive isotopes. Because both types of heating change with time, the heating mode of mantle convection is fundamentally transient. There are two ways to handle this transient mixed heating. One is to simulate a time-dependent system directly (e.g. [120,131]), but such simulation would depend on the particular choice of initial conditions. The other is to translate transient mixed heating to equivalent steady-state mixed heating, by emulating the effect of secular cooling with fictitious internal heating [132,133], and run a model until it reaches some steady state; such a steady-state solution is usually independent of initial conditions. This steady-state approach has been popular because it is easier to characterize steady-state solutions and thus understand the underlying physics better. However, the effect of secular cooling is sometimes not properly incorporated, and in that case, simulation results may not find their application to the dynamics of the Earth's mantle [134]. If only radiogenic heat production is used in a steady-state simulation, i.e. the effect of secular cooling is entirely neglected, a resulting solution would be characterized by too strong upwelling from the bottom (corresponding to unrealistically high core heat flow). This is because, in a steady-state convection model, the top heat flow must be equal to the sum of internal heating and the bottom heat flow, so if fictitious internal heating is not provided to emulate secular cooling, the bottom heat flow has to increase accordingly.

(b). Some remarks on popular notions

By the very nature of radioactive decay, the amount of radiogenic heat production must have been higher in the past. It is commonly assumed that higher heat production results in more vigorous convection, but the amount of heat production and the vigour of convection are not directly related. They are connected through the notion of self-regulation, which was originally suggested by Urey [135] and then popularized by Tozer [136]. The self-regulation of mantle convection would work just like homeostasis. If the surface heat flow of the Earth is higher than its internal heat production, the Earth cools down, lowering the vigour of convection and thus surface heat flow. If heat flow is lower than heat production, on the other hand, the Earth heats up to increase the vigour of convection until surface heat flow reaches internal heat production. For this idea to work, surface heat flow and mantle temperature have to be positively correlated, but such a relation is unlikely to hold if we consider the effect of melting on mantle convection whether in the regime of plate tectonics [137,138] or stagnant lid convection [139]. Recently, Korenaga [140] introduced the Tozer number to evaluate the likelihood of self-regulating mantle convection, and the Tozer number for the Earth's mantle turned out to be too low to achieve self-regulation.

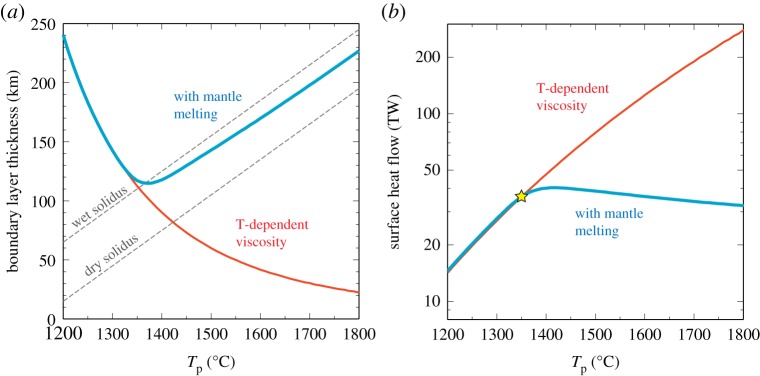
The positive correlation between surface heat flow and mantle temperature, i.e. more vigorous convection for a hotter mantle, has long been taken for granted, so it may be beneficial to explain in some detail why it may be incorrect. In thermal convection, whether plate tectonics or stagnant lid, surface heat flow is controlled by the thickness of the top thermal boundary layer. A thinner boundary layer is equivalent to higher heat flow. If mantle viscosity is purely temperature-dependent, a hotter mantle means lower viscosity, which reduces the thickness of the boundary layer (figure 8a). In general, the thickness of the thermal boundary layer is limited by its convective instability [141], and low viscosity acts to prevent the growth of the boundary layer. There are two important realistic complications that must be added to this simple picture. First, mantle viscosity is very sensitive to not only temperature but also the water content [112,121]. Second, the convecting mantle in the present-day Earth is known to contain a trace amount of water [142,143], and during the decompressional melting of the mantle, this water is mostly partitioned to the melt phase, leaving the solid mantle residue very dry [144]. Because a hotter mantle starts to melt at greater depth [145,146], the melting of a hotter mantle results in thicker depleted mantle lithosphere, which, being dry and stiff, could sustain the growth of the boundary layer [137,147] (figure 8a). Thus, mantle melting, in the presence of water in the convecting mantle, can counteract the effect of temperature-dependent viscosity, making surface heat flow insensitive to the internal state for some range of mantle temperature [138,139] (figure 8b). The Earth's mantle was certainly hotter in the past than present, at least back to approximately 3 Ga [97], but a hotter mantle does not necessarily imply higher surface heat flow, or, equivalently, more vigorous convection. Also, given this sensitivity of viscosity to water, we need to specify the evolution of mantle temperature as well as the water content in the mantle, when extrapolating to early Earth conditions. Considering only the temperature dependence of mantle viscosity is equivalent to assuming that the water content of the mantle has been constant, but this assumption is difficult to justify from the perspective of global water cycle (§3c).

Figure 8.

(a) The thickness of top thermal boundary layer as a function of mantle potential temperature [117]. For the calculation of convective instability, the reference viscosity of 10¹⁹ Pa s at 1350°C and the activation energy of 300 kJ mol⁻¹ are used. The case of purely temperature-dependent viscosity is shown in red, and the case with the effect of mantle melting (on viscosity as well as density) in blue. Assumed dry and wet solidi are also shown. (b) Surface heat flow as a function of mantle potential temperature [117], based on the scaling of boundary layer thickness shown in (a), and assuming the operation of plate tectonics. Star denotes the present-day condition. Both scaling laws were originally derived from a simple boundary layer theory, but their first-order features are also supported by fully dynamic convection models [126,138].

Because a hotter mantle may not convect faster, convective mixing does not have to be more efficient in the past. We also have to be aware that the efficiency of mantle mixing is not well understood even for present-day plate tectonics. Numerical simulations of mantle mixing [148–150] depend on assumed rheology, and rheological details matter for mantle mixing [151,152]. Unfortunately, our knowledge of rheology is still subject to large uncertainty even for that of olivine [124,153,154], although it is among the most extensively studied minerals. Thus, theoretical considerations cannot be conclusive, but geochemical observations may provide some useful (albeit crude) hints. The existence of distinct isotopic heterogeneities in the present-day mantle, as mentioned in §2b, already indicates the limited efficiency of convective mixing. Indeed, with the present-day mantle processing rate by mid-ocean-ridge magmatism, it would take as long as approximately 5 Gyr to process the entire mantle [117]. So, if the vigour of mantle convection does not change much with time, it would not be unreasonable to expect that various memories of mantle differentiation over Earth history are still preserved. This conjecture seems to be supported by the survival of ancient (approx. 4.5 Ga) isotopic signatures in the convecting mantle [155,156]. Also, based on the preservation of the positive¹⁴²Nd anomaly in the convecting mantle through the Archean, Debaille et al. [80] once suggested the possibility of stagnant lid convection in the early Earth, but such preservation may simply reflect that mixing by plate tectonics was not more efficient in the past.

Stagnant lid convection, or something other than plate tectonics, has been discussed as a possible regime of mantle convection in the early Earth. For example, by calculating the net buoyancy of oceanic lithosphere, Davies [157] suggested that the operation of plate tectonics may have been unlikely before approximately 1 Ga. He argued that a hotter mantle in the past must have produced thicker oceanic crust, making oceanic lithosphere too buoyant to subduct. This argument, however, relies on the notion of a thinner thermal boundary layer for a hotter mantle. If we consider the effect of mantle melting on not only buoyancy but also viscosity, a thermal boundary layer can be thicker for a hotter mantle (figure 8a), and oceanic lithosphere can become dense enough to subduct even under early Earth conditions [117]. Note that there was some confusion regarding the buoyancy of oceanic lithosphere, with some authors suggesting that oceanic lithosphere is not negatively buoyant even at present [158–160], but it has since been shown that this claim originates from the misunderstanding of the physics of compressible media [161]. In the recent literature, the possibility of stagnant lid convection in the early Earth has been entertained on the basis of numerical simulations that explore different convection regimes [119,162,163]. These simulations were, however, conducted with only mildly temperature-dependent viscosity (10⁴–10⁵), so it is difficult to judge whether a change in the mode of convection seen in these studies is because their models are set up to facilitate such a change (§3a) or it has some real connections to early Earth dynamics. Also, these simulations are steady-state runs, yet they consider only radiogenic heat production. As noted earlier (§3a), this failure to treat the transient heating mode of mantle convection obscures the relationship between these simulation results and planetary evolution. At the moment, it is difficult to find a sound theoretical argument for the operation of stagnant lid convection, or the lack of plate tectonics, in the early Earth.

(c). Key observational constraints on long-term mantle evolution

Mantle convection is driven by planetary-scale cooling, i.e. the need to dissipate internal heat into space. The thermal evolution of the Earth thus provides a global perspective to the issue of the style of mantle convection in the early Earth. A reasonably coherent picture is now available for the thermal evolution from approximately 3 Ga to the present, a good understanding of which is indispensable when probing deeper in time.

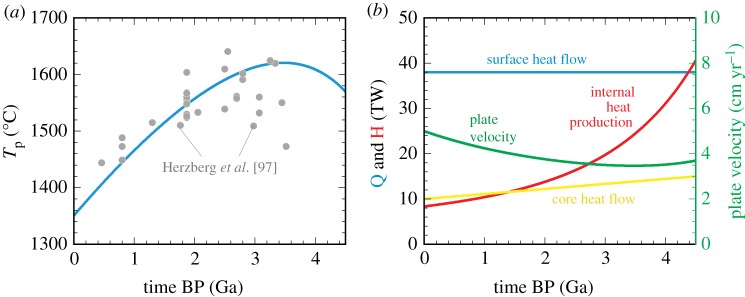
The present-day thermal budget of mantle convection indicates that the mantle is considerably out of thermal equilibrium [106]; whereas surface heat flow from the convecting mantle is estimated to be approximately 37 TW, geochemical data suggest that radiogenic heat production in the mantle is only approximately 9 TW. With the core heat flow of approximately 10 TW [164] and the mantle heat capacity of approximately 5 × 10²⁷ J K⁻¹ [165], this imbalance between surface heat loss and internal heat generation indicates that the mantle is cooling down with the rate of approximately 110 K Gyr⁻¹. Traditionally, this imbalance was deemed problematic because, when combined with the popular notion of higher heat flux for a hotter mantle, it predicts an unrealistically hot mantle in the past (e.g. greater than 1000 K hotter at 1.5 Ga) [93,94,166]. Two common resolutions were (i) to assume higher internal heat production than indicated by geochemical data [93,94,167] and (ii) to assume lower (long-term) surface heat flow [168–170]. The first option is well beyond the uncertainty of available geochemical constraints [95,103], and the second option is inconsistent with sea-level data [171]. The remaining possibility is to abandon the notion of higher heat flux (and faster convection) for a hotter mantle [166], and indeed, the effect of mantle melting on the growth of thermal boundary layer (figure 8) supports this possibility.

The speed of mantle convection, or the tempo of plate tectonics, has long been believed to be faster in the hotter past, so rejecting this notion requires more than a theoretical possibility. Fortunately, this possibility can be tested against a variety of observations, because the evolution of the mantle is connected to all other components of the Earth system; the mantle generates the crust by partial melting, controls the cooling of the core and modulates the evolution of atmosphere and oceans through degassing and regassing. For example, the melting of a hotter mantle results in a thicker crust with different chemical composition, so it is possible to track the cooling history of the ambient mantle from the chemistry of igneous rocks erupted at different ages [97] (figure 9a). Such reconstruction of past mantle temperatures indicates the modern cooling rate of approximately 100 K Gyr⁻¹, in good agreement with the geochemistry-based thermal budget. This agreement forms strong evidence against the notion of self-regulating mantle convection, and it would be most straightforward to explain the petrology-based cooling history if convective heat flow is relatively insensitive to mantle temperature (figures 8b and 9b). Incidentally, this cooling history is at variance with the kind of intermittent plate tectonics proposed by Silver & Behn [174], regardless of assumed heat flow scaling [175]. The cooling rate of approximately 100 K Gyr⁻¹ is also consistent with the secular decrease in oceanic crust thickness [176] and seems necessary to explain the observed rate of seafloor subsidence [161].

Figure 9.

(a) Petrological estimates on the past potential temperature of the ambient mantle (grey circles) [97], and the predicted thermal history (blue curve) using the constant surface heat flow with the present-day Urey ratio of 0.22 [134]. The core heat flow is assumed to vary linearly from 15 TW at 4.5 Ga to 10 TW at present [172]. (b) Surface heat flow (blue), core heat flow (yellow) and radiogenic heat production in the mantle (red) used for the thermal history shown in (a). Also shown is corresponding plate velocity (green), with the present-day average velocity of 5 cm yr⁻¹ [173].

In contrast to the long-held belief in faster convection for a hotter mantle, supporting geological records have been lacking for decades [177–179]. As a matter of fact, recent studies suggest that plate motion may have been even slightly slower in the past, based on the lifespan of passive margins [96] and continental reconstruction [98,99]. Such slower plate motion in the past is consistent with a constant surface heat flux through time (figure 9b); plate velocity, U and surface heat flux, Q, are related as 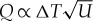, where ΔT is the temperature contrast between surface and the interior [180], so when Q is constant, U should decrease as ΔT increases. It has also been suggested that faster convection in the past cannot explain the xenon isotopic composition of the present-day atmosphere [107] as well as the inferred chemistry of Archean seawater [100]. Finally, using core-related observations, such as the evolution of the geomagnetic field, to discriminate between different scenarios of mantle evolution is difficult, partly because the quality of such observations is under intense debate [181–184] and partly because our understanding of core dynamics is in a state of flux [185–187]. Whereas it is possible to construct a coupled core-mantle evolution model with the kind of heat flow scaling shown in figure 8b [172], such modelling exercise is still of exploratory nature.

As mantle viscosity is sensitive to temperature as well as water content, the history of mantle cooling needs to be supplemented with the secular evolution of mantle water content, if we wish to understand how the viscosity of the ambient mantle has changed with time. A direct geochemical constraint on the average water content of the ancient mantle is yet to come. Whereas the possibility of hydrous source mantle for Archean komatiites has long been debated [188–193], the field occurrence of komatiites is limited, typically less than 10% of the total volume of volcanic rocks in most greenstone belts [194]; thus, the water content of a ‘typical’ Archean mantle could have been different from that of the komatiite source mantle. Though indirect, a complementary approach through the history of ocean volume may be more promising. Hydrogen escape into space is trivial after the rise of atmospheric oxygen at approximately 2.4 Ga [195,196], and the chemical interaction between the mantle and the core is likely to be diffusion-limited. Thus, any change in the mantle water content would be reflected in the history of ocean volume at least since the end of the Archean. Estimating the past ocean volume is still challenging but is not intractable. To this end, the most important constraint is the constancy of continental freeboard [197]: the relative height of the mean continental landmasses has been close to the sea level. Owing to abundant sedimentary records on the continents, the constancy of freeboard during the Phanerozoic is well established, and a recent compilation of spatially expansive (greater than 30 000 km²) exposure horizons through the Precambrian suggests that freeboard had been roughly constant since the Paleoproterozoic [100]. The history of ocean volume can be estimated by combining this freeboard constraint with how the relative buoyancy between continental and oceanic lithosphere changes with time. Such an attempt yields positive net water influx from the surface to the mantle, at the rate of 3–4.5 × 10¹⁴ g yr⁻¹ on the time scale of billion years [100]. This estimate is broadly comparable with other independent estimates. Based on an imbalance between water input by magmatism and water output by subduction, Ito et al. [198] estimated the net water flux into the mantle as 1.2–11 × 10¹⁴ g yr⁻¹ at the present-day. A more recent compilation by Jarrard [199] arrived at a similar conclusion. Using the numerical simulation of slab dehydration, Magni et al. [200] estimated the net water influx to be 7 × 10¹⁴ g yr⁻¹ at present and 0.5–3.7 × 10¹⁴ g yr⁻¹ in the Archean.

Interestingly, the non-zero net water influx, i.e. the possibility of a greater ocean volume in the past, has been unfavoured in the literature. Ito et al. [198], for example, argued that the upper end of their estimate quoted above would correspond to a geologically unrealistic change in the global sea level and suggested that the rate of 1–3 × 10¹⁴ g yr⁻¹ might be acceptable, if it lasted only for periods of 100 Myr or so. More recently, Parai & Mukhopadhyay [201] repeated the same argument to limit the net water influx below 1 × 10¹⁴ g yr⁻¹. An implicit assumption in these studies is that the hypsometric curve of the Earth is time-independent, but the assumption is probably too simplistic. The tempo of plate tectonics affects the storage capacity of ocean basins [171,202], and seafloor subsidence is greater for a hotter mantle [180]. Also, the average depth of mid-ocean-ridge axes is presently at approximately 2.5 km, but it is likely to have been deeper in the past owing to the secular evolution of the relative buoyancy of continental lithosphere with respect to oceanic lithosphere [100].

If the net water influx of 3–4.5 × 10¹⁴ g yr⁻¹ had been sustained over the duration of 4.5 Gyr, it could have brought approximately 1–1.5 ocean water into the mantle, which happens to be similar to some estimates on the present-day water content in the mantle [100,203]. Thus, it becomes plausible, though not necessary, for Earth history to start with a very dry mantle overlain by abundant surface water, and such an initial condition is indeed ideal for the onset of plate tectonics in the early Earth and its continuous operation through Earth history [126]. The viscosity of a dry and hot mantle can be similar to that of a wetter and colder mantle, because of the competing effects of temperature and water content, so mantle convection in the early Earth can exert sufficiently high convective stress to break the top boundary layer and initiate plate tectonics. Abundant surface water also facilitates the onset of plate tectonics as it can guarantee lithospheric weakening by thermal cracking. Admittedly, however, this is a very speculative idea. The long-term net water influx estimated by Korenaga et al. [100] is reasonably robust back to approximately 2.5 Ga, for which we have the decent freeboard constraint, but extrapolating it by another 2 Gyr is precarious at the best. In general, we are very much in the dark about how deep water cycle is coupled with long-term mantle evolution, as tracking the fate of water through the solid Earth and the hydrosphere is challenging both theoretically and observationally. For example, even the amount of water contained in the subducting slab is under active debate [204–206]. Our progress on this issue will likely be slow, but having an overarching working hypothesis may stimulate interaction between different disciplines and accelerate feedback among theories, observations and experiments. The next section is dedicated for this purpose.

4. An emerging picture of ocean–crust–mantle coevolution

As reviewed in §2, the crust-based models of continental growth provide the lower bound on net crustal growth, whereas the mantle-based models directly constrain net crustal growth. The other kind of growth models do not have comparable reliability. A recent crust-based model suggested by Korenaga [36], if taken literally, indicates nearly linear crustal growth (figure 4c), but it is just the lower bound on net crustal growth. Estimating the history of crustal mass from a crust-based model, i.e. what has been preserved to the present, by correcting for crustal recycling is difficult; our estimate on the magnitude of crustal recycling comes from the present-day sediment subduction, and there is virtually no geological record that can directly constrain the efficiency of crustal recycling in the past. We thus need to turn to mantle-based net growth models, and a recent model based on the coupled¹⁴⁷Sm-¹⁴³Nd and¹⁴⁶Sm-¹⁴²Nd evolution [37] indicates a rapid growth model (figure 4c), reminiscent of the Armstrong model [24], with efficient crustal recycling in the early Earth (figure 5a). In this growth model, there is no change in crustal mass after the Hadean, but this does not mean no generation of new continental crust in the last four billion years. On the contrary, to maintain a constant crustal mass with non-zero crustal recycling, new crust must be generated at the same rate of recycling (figure 5a). The crustal growth model of Rosas & Korenaga [37] thus indicates the continuous generation and destruction of continental crust throughout Earth history, and its consequence is remarkably consistent with the present-day distribution of formation ages (figure 5b).

The simplest interpretation of such continuous crustal processes would be to assume the onset of plate tectonics in the very early Earth, perhaps soon after the solidification of the putative magma ocean. As seen in §3b, there is no compelling theoretical support for the absence of plate tectonics in the early Earth, and the history of ocean volume does point to the possibility of a dry mantle and abundant surface water in the Hadean, both of which facilitate the operation of plate tectonics (§3c). The extremely rapid crustal growth in the early Hadean does not necessarily mean that the continental crust like today already existed at that time; it could correspond to the formation of the protocrust during the solidification of the magma ocean. Subsequent subsolidus mantle convection, however, must have been able to steadily produce the continental crust at the rate of approximately 2 × 10²² kg Gyr⁻¹ and then destroy it at a similar rate. The gradual decline in the crustal generation rate (figure 5a) may reflect the secular cooling of the mantle (figure 9a).

The rate of crustal recycling also declines with time (figure 5a), and this may be puzzling for those who are familiar with the thermal evolution of the Earth (figure 9); one might expect that slower plate motion in the past corresponds to less efficient crustal recycling. This expectation, however, assumes that the thickness of subducting sediment layer does not vary with time, but the volume of terrigenous sediments may have been greater in the past. In fact, the likely secular evolution of mantle water content alludes to this possibility. A decline in the efficiency of crustal recycling is equivalent to an increase in the preservation potential of continental crust, and because the continental crust is protected from below by thick lithospheric mantle [207], it may also be linked to the gradual strengthening of lithospheric support. Such evolution of lithospheric support is anticipated from the positive net water flux in the mantle. At the present day, the continental mantle lithosphere is more viscous than the convecting mantle, primarily because the former is drier than the latter [208–212]. In the early Earth when the convecting mantle is estimated to have been dry as well, however, such intrinsic viscosity contrast would have been absent or much reduced. The continental mantle lithosphere could then have been easily deformed by convecting currents, facilitating crustal deformation, erosion, and eventually crustal recycling. This connection between deep water cycle and the preservation potential of continental crust was originally suggested to explain the Archean–Proterozoic boundary [6], and it could be applied to the gradual decline in crustal recycling as well. Note that the gradual stabilization of continental crust via cratonization [20,50] is conceptually similar to the evolution of lithospheric support discussed here.

A likely transition in mantle dynamics and surface environment through Earth history is illustrated in figure 10. From the Hadean to the Archean, the oceans were deep, and the convecting mantle was dry. The mantle was also hot, which resulted in voluminous crustal production. Because the convecting mantle was as dry as the continental mantle lithosphere, the lithosphere was easily eroded by convecting currents and the absence of strong lithospheric support led to efficient crustal recycling. Over time, the oceans become gradually shallower as subduction hydrates the mantle. The mantle cools down, and crustal generation dwindled. The continental mantle lithosphere is still dry. The dryness of the mantle lithosphere does not change much with time. It could be rewetted by hydrogen diffusion from the adjacent convecting mantle, but the diffusion of hydrogen in olivine is rather slow under lithospheric conditions; the diffusion length at 1100°C is only approximately 8 km for 4 Gyr [217]. As the convecting mantle becomes wetter, therefore, the continental mantle lithosphere becomes relatively stronger, making crustal recycling less efficient than before. This increasing preservation potential of continental crust, resulting from gradual mantle hydration by plate tectonics, could naturally explain the Hadean to Archean as well as the Archean to Proterozoic transitions, as these geological eons are defined by relative abundances of preserved continental rocks.

Figure 10.

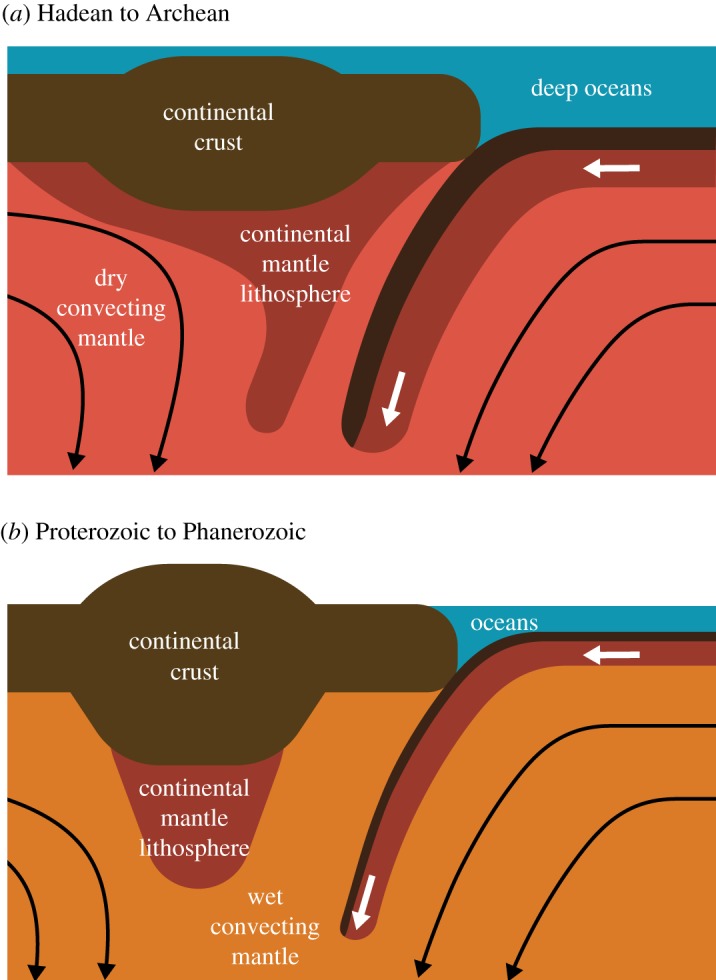
Schematic for the working hypothesis on the coupled ocean–crust–mantle evolution. The illustrations are not drawn to scale in every possible detail, though certain details are intentional. The topography of continental crust was probably more reduced in the past because of hotter geotherm [213]. Continental mantle lithosphere could have been thicker in the past if we take into account the effect of convective erosion [208,214]. No significant difference in plate velocity is expected (figure 9b), but the structure of oceanic lithosphere is very different because of the secular cooling of the mantle (figures 8a and 9a). The average thickness of continental crust is likely to have been stable since around 3 Ga [215]. Continental crust could have been largely submarine during the Archean, as suggested by the abundance of submarine continental flood basalts [216] and also implied by freeboard modelling [100].

What is shown in figure 10 is not sheer speculation. It is based on the collective assessment of a large number of diverse geological observations and theoretical considerations (§§2 and 3), and it will be worthwhile to develop this working hypothesis into a physics-based theory. Such effort will produce an array of testable predictions and help to revise or correct any aspect of the hypothesis. It will also allow us to evaluate the issue of preservation bias in a quantitative manner. Though often downplayed in the community, preservation bias presents a serious problem to our inquiry to the history of plate tectonics. The primary function of plate tectonics may be described as destroying geological records by subduction, so the absence of evidence is clearly not the evidence of absence. Also, what has been preserved to the present may not be representative of what has been lost by subduction; the very fact of being preserved, despite the destructive nature of plate tectonics, may require some special conditions [6]. In spite of these obvious concerns, arguments based on preservation bias are usually discouraged because they are hard (if not impossible) to test. However, if we can build a physics-based theory for the coupled ocean–crust–mantle evolution, such a theory could also quantify the preservation likelihood of a certain geological record, providing a statistical basis for the discussion of its rarity. For example, Shirey & Richardson [218] suggested the onset of global plate tectonics at 3 Ga based on the absence of eclogitic diamonds, which are thought to have originated from subducted oceanic crust, in the continental mantle lithosphere prior to 3 Ga, but this observation may also be explained by preservation bias. At any given time, the amount of subducted oceanic crust trapped in the continental mantle lithosphere is likely to be small [219], and the likelihood of its trace being preserved to the recent geological times is low when the lithosphere was easily destroyed by convecting currents (figure 10a). Geodynamic modelling stemming from the working hypothesis proposed here can potentially measure the plausibility of this alternative explanation, and it would be ideal if such modelling could also suggest some novel ways of exploring geological data.

5. Discussion and outlook

The state of the early Earth remains elusive, but there are also quite a few promising observational clues and theoretical possibilities to be probed deeper. In this paper, the various aspects of crustal evolution and mantle dynamics have been reviewed so far, with numerous comments and caveats dispersed throughout. This section summarizes such remarks with an emphasis on possible future directions.

The present-day distribution of formation ages, as estimated by crust-based ‘growth’ models, will continue to be an important boundary condition for the evolution of continental crust. The model of Korenaga [36] represents major methodological advances in the use of zircon age data, but it could be further improved in several ways. The model is based on the global compilation of Roberts & Spencer [51], which contains approximately 42 000 U-Pb-Hf isotope data collected from over 160 publications. Though these data were treated equally, a careful evaluation of individual datasets, together with the geological and geochemical information of likely host rocks, would lead to a more judicious use of published data. Different datasets would probably have to be weighted differently to reflect corresponding areal extents properly (e.g. [220]). Also, how new mantle-derived melt mixes with the preexisting crust varies spatially as well as temporally [221], and depending on the temperature and composition of parental magma, different zircon grains can represent different volumes of continental crust [222,223]. The new method devised by Korenaga [36] is flexible enough to accommodate all of these realistic complications. The first-order feature of the current estimate on the formation age distribution (figure 4c) is unlikely to change with such revisions; a similar distribution was obtained [36] even when approximately 55% of zircon data were discarded by the oxygen isotope screening as parametrized by Dhuime et al. [11]. A careful treatment of global database, however, will allow us to exploit the details of the formation age distribution.

Constraining net crustal growth is much more difficult, and it is hoped that the recent work of Rosas & Korenaga [37] will revitalize interest in the mantle-based approach for crustal growth. As the number of Early Archean localities is limited, data interpretation will continue to suffer from ambiguity. In the geochemistry literature, it is common to supplement this shortage of data with geodynamical arguments such as more efficient mixing in a hotter mantle, but because our understanding of early Earth dynamics is far from being established (§3b), it would be more prudent to isolate data from speculation, at least in the initial phase of data interpretation. Importance sampling such as the Markov chain Monte Carlo method [224] may help exploring a wide range of possibility efficiently. The non-uniqueness of geochemical box modelling can be reduced if the isotope evolution of continental crust is also available, though such information is difficult to obtain [29]. The method of Korenaga [36] can be adapted to estimate the Hf isotope evolution of the extant crust (though not the entire crust), and even such partial information may be useful. Combining constraints from different chemical and isotope systems could also help to tighten our inference, though care must be taken to consider that each system has its own sensitivity to crustal growth and recycling and that some systems are affected more strongly by processes unrelated to crustal evolution.

The meaning of net crustal growth from the mantle-based approach is not always clear, especially in the early Earth stage. The solidification of the putative magma ocean must have formed some kind of crustal layer, but the nature of such protocrust, including its eventual fate, is yet to be resolved [76,225,226]. How the magma ocean solidified is a challenging theoretical issue by itself [227], and the fate of protocrust is even harder as it depends on the mode of mantle convection in the Hadean. Physical mechanisms for crustal recycling are also the subject that demands further investigation. In addition to subduction, crustal recycling could take place by delamination as well [228,229], but the likelihood of crustal delamination hinges on crustal rheology and the magnitude of ambient tectonic stress [230].

Regarding the modes of mantle convection in the Precambrian, robust theoretical constraints are currently unavailable. It will be important to design geodynamical modelling that properly honours the transient nature of mixed heating as well as the uncertainty of lithospheric weakening mechanisms. As recent studies demonstrate [162,163,231], the modes of mantle convection is a difficult problem to tackle, involving complex mantle rheology, the sensitivity to initial conditions and time-varying boundary conditions, most of which are still poorly understood. Given such a multitude of controlling factors, it is desirable to have a clear understanding of elementary processes, as it will help us to better interpret the outcome of complex models. While it is important to develop sophisticated numerical models that can incorporate as many realistic complexities as possible, it would be most effective if such efforts are combined with insights gained from simple, well-understood systems. At the moment, we do not even know how the style of thermal convection depends on the following four basic parameters: the Rayleigh number, the temperature dependence of viscosity, the type of weakening mechanisms and the heating mode of convection.

The existing uncertainty of mantle rheology is an obvious concern. It has long been known that the deformation of silicate rocks depends on a number of factors, including temperature, pressure, stress, grain size, water content, melt fraction and oxygen fugacity [112,121,232], and it has become increasingly common to incorporate such reality of rock mechanics in geodynamical modelling [233–239]. It does not seem to be widely appreciated, however, that the mantle rheology assumed in these studies are subject considerable uncertainties. Rock deformation under laboratory conditions usually involves the simultaneous operation of multiple deformation mechanisms [121,210], and analysing such deformation data in a statistically satisfactory manner has become possible only recently [153,240], the results of which are rather unsettling [124,154]. Future experimental efforts, combined with rigorous statistical analysis, will be essential to improve the status quo. There is also a possibility to reduce the uncertainty of the upper mantle rheology through ‘probabilistic’ geodynamical modelling [154].

Developing a geodynamical model for the stabilization of continental crust, either by the relative strengthening of continental mantle lithosphere (figure 10) or by the emergence of the mantle lithosphere itself [20,50], will be a challenging but rewarding endeavour, as it may also help us to transform the issue of preservation bias into scientific inquiry. Preservation bias is a real possibility, and its implications can become only more severe for deeper time. For example, East Pilbara Terrane in Western Australia, being the oldest and best-preserved remnant of the Archean crust, has been extensively studied [241–244]. Whereas findings from this particular locality are often generalized, the areal extent of this craton is approximately 200 × 200 km², i.e. only 0.02% of the surface area of the present-day continental crust. Being a geological rarity is a double-edged sword; it can provide a precious constraint, but its generality is hard to prove. This is ironic because, in this context, the true value of such a constraint depends on its generality. How to estimate global situations from highly localized observations is a fundamental difficulty in early Earth research, and any attempt to quantify preservation bias will be laudable.

This data-starved nature of the early Earth could be the ultimate bottleneck for future research. One possible solution is to develop stronger connections to currently observable processes, for which there are abundant data. As the nature of basic physics and chemistry is time-invariant, the onset of plate tectonics in the early Earth may be addressed by a more complete understanding of contemporary plate tectonics. Whereas the initiation of subduction is usually difficult to reconstruct [96,245], the modern evolution of divergent plate boundaries is well preserved in seafloor, often exhibiting bewildering kinematics such as ridge jump, ridge propagation and microplate formation [246–250]. Through geodynamical modelling, useful constraints on the rheology of oceanic lithosphere may be extracted from such fine details of marine tectonics. When doing so, a multiscale approach may be important to model regional dynamics within a global framework (cf. [251]). Also, a need for a more comprehensive theory for planetary evolution, in particular, the evolution of Earth-like habitable planets, is strong in exoplanetary science [252–254]. Such a demand can serve as an impetus for seeking theoretical underpinning for our empirical knowledge of geological processes. The progress of early Earth research and its well-being may be contingent on how we can leverage these data-rich fields.

Data accessibility

This article has no additional data.

Competing interests

I declare I have no competing interests.

Funding

This material is based upon work supported in part by the US National Aeronautics and Space Administration through the NASA Astrobiology Institute under Cooperative Agreement No. NNA15BB03A issued through the Science Mission Directorate and by the US National Science Foundation under grant no. EAR-1753916.