Test of the Transferability of the Specific Reaction Parameter Functional for H₂ + Cu(111) to D₂ + Ag(111)

Abstract

The accurate description of the dissociative chemisorption of a molecule on a metal surface requires a chemically accurate description of the molecule–surface interaction. Previously, it was shown that the specific reaction parameter approach to density functional theory (SRP–DFT) enables accurate descriptions of the reaction of dihydrogen with metal surfaces in, for instance, H₂ + Pt(111), H₂ + Cu(111), and H₂ + Cu(100). SRP–DFT likewise allowed a chemically accurate description of dissociation of methane on Ni(111) and Pt(111), and the SRP functional for CH₄ + Ni(111) was transferable to CH₄ + Pt(111), where Ni and Pt belong to the same group. Here, we investigate whether the SRP density functional derived for H₂ + Cu(111) also gives chemically accurate results for H₂ + Ag(111), where Ag belongs to the same group as Cu. To do this, we have performed quasi-classical trajectory calculations using the six-dimensional potential energy surface of H₂ + Ag(111) within the Born–Oppenheimer static surface approximation. The computed reaction probabilities are compared with both state-resolved associative desorption and molecular beam sticking experiments. Our results do not yet show transferability, as the computed sticking probabilities and initial-state selected reaction probabilities are shifted relative to experiment to higher energies by about 2–3 kcal/mol. The lack of transferability may be due to the different character of the SRP functionals for H₂ + Cu and CH₄ + group 10 metals, the latter containing a van der Waals correlation functional and the former not.

1. Introduction

The benchmark system of H₂ interaction with a metal surface is very important to understand and accurately model elementary reactions on metal surfaces. This is relevant to heterogeneous catalysis, which is employed in the majority of reactive processes in the chemical industry.¹ Breaking heterogeneously catalyzed processes into elementary steps is one way to describe them. Dissociative chemisorption, in which a bond in the molecule impacting on a surface is broken and two new chemical bonds are formed by the fragments to the surface, is an elementary and often the rate-limiting step,^2,3 for example in ammonia synthesis.⁴

It is essential to have an accurate potential energy surface (PES) and obtain an accurate barrier for the reaction to accurately perform calculations on dissociation of a molecule on a surface. Although there is no direct way to measure barrier heights experimentally, a close comparison of molecular beam experiments and dynamics calculations reproducing the reaction probabilities may enable this determination to be within chemical accuracy (1 kcal/mol).^5,6

The most efficient electronic structure method to compute the interaction of a molecule with a metal surface is density functional theory (DFT). However, there are limitations to the accuracy of the exchange-correlation (XC) functional, where the XC functional is usually taken at the generalized gradient approximation (GGA)⁶ level. For barriers of gas-phase reactions, it has been shown that mean absolute errors (MAE) of GGA functionals are greater than 3 kcal/mol.⁷ To address the problem of the accuracy with DFT, an implementation of the specific reaction parameter approach to DFT (SRP–DFT) was proposed.⁵ Fitting of a single adjustable parameter of this semiempirical version of the XC functional to a set of experimental data for a molecule interacting with a surface may allow the production of an accurate PES.⁶ The quality of the derived XC functional is tested by checking that this XC functional is also able to reproduce other experiments on the same system, to which it was not fitted.^5,6 The SRP–DFT methodology has provided the possibility to develop a database of chemically accurate barriers for molecules reacting on metal surfaces. Results are now available for H₂ + Cu(111),^5,6 H₂ + Cu(100),^6,8 H₂ + Pt(111),⁹ CH₄ + Ni(111),¹⁰ CH₄ + Pt(111), and CH₄ + Pt(211).¹¹ However, this effort is at an early stage and demands more efforts to extend the database.

In a previous study, it was shown that the SRP–DFT XC functional can be transferable among systems in which one molecule interacts with metals from the same group in the periodic table. Nattino et al.¹⁰ demonstrated the accurate description of dissociation of methane on Ni(111) with an SRP functional. Migliorini et al.¹¹ showed the transferability of the derived SRP functional for this system to the methane + Pt(111) system.

The goal of this article is to check the transferability of the SRP48 functional¹² for H₂ + Cu(111) to a system in which H₂ interacts with a (111) surface of another group 11 element. The SRP48 functional was selected to investigate whether it would allow a chemically accurate description of the dissociative adsorption of D₂ on the (111) surface of silver, as it yields a chemically accurate description of a range of experiments on H₂/D₂ + Cu(111).¹² A previous study using the SRP48 functional computed initial-state selected reaction probabilities for H₂ + Au(111) using quasi-classical dynamics.¹³ Subsequent associative desorption experiments measured initial-state selected reaction probabilities that were shifted to substantially lower translational energies.¹⁴ These results suggest that the SRP48 functional is not transferable from H₂ + Cu(111) to H₂ + Au(111). The experimentalists also suggested that the dissociation of H₂ on Au(111) should be affected by electron–hole (e–h) pair excitation. However, molecular beam sticking experiments are not yet available for the H₂ + Au(111) system.

Here, quasi-classical trajectory (QCT)¹⁵ calculations are performed using a H₂ + Ag(111) PES based on density functional theory (DFT) calculations with the SRP48 functional. Comparison is made with available molecular beam experiments and associative desorption experiments to evaluate the accuracy of the SRP DF extracted for H₂ + Cu(111) for the H₂ + Ag(111) system. Our calculations used the Born–Oppenheimer static surface (BOSS) model, in which nonadiabatic effects, i.e., electron–hole (e–h) pair excitations, and phonon inelastic scattering were neglected. The recent theoretical study of the H₂–Ag(111) system by Maurer et al.¹⁶ has provided evidence for a strong mode dependence of nonadiabatic energy loss, with loss especially occurring along the H₂ bond stretch coordinate. However, the effect on the dissociation probability curve could not yet be quantified. Moreover, for a variety of chemical reactions on surfaces, chemicurrents have been observed due to the nonadiabaticity in the recombination reaction, leading to transfer of energy to the substrate electronic degrees of freedom.¹⁷⁻¹⁹

Despite the experimental and the latest theoretical evidence, most of the theoretical works based on purely adiabatic approximation can accurately describe the reactive and nonreactive scattering of H₂ from metal surfaces and dissociation on surfaces such as Cu(111)⁵ and Ru(0001).²⁰ Furthermore, a study on H₂/Pt(111) using a single PES has shown that employing the Born–Oppenheimer (BO) approximation, i.e., neglecting e–h pair excitations, could describe both reaction and diffractive scattering.²¹ On the basis of these studies, it has been suggested that the BO approximation is reliable enough to accurately describe H₂ reaction on and scattering of metal surfaces. This expectation is borne out by theoretical studies that have directly addressed the effect of e–h pair excitation on the reaction of H₂ on metal surfaces using electron friction and have without exception found the effect to be small.²²⁻²⁶

The validity of the static surface approximation and the neglect of surface motion and surface temperature have been discussed elsewhere (see for instance ref (27)). Due to the large mass mismatch between H₂ and the surface atoms and because molecular beam experiments are typically performed for low surface temperatures, the static surface approximation usually yields good results for activated sticking.^9,12,28 For associative desorption experiments, which tend to use high surface temperatures, the width of the reaction probability curve may be underestimated with the static surface approximation, but the curve should be centered on the correct effective reaction barrier height.^5,28

There have been a few studies on H₂ + Ag(111). The studies showed that the dissociative chemisorption of H₂ on silver is highly activated and does not proceed at room temperature.²⁹⁻³¹ The observation of dissociative chemisorption of molecular D₂ on Ag(111) was reported for the first time by Hodgson and co-workers, using molecular beam scattering at translational energies above 220 meV and nozzle temperatures above 940 K.^32,33 They reported that the sticking coefficient of D₂ to Ag(111) at low incidence energy is very small. These experimental studies also suggested that the dissociative chemisorption of H₂/D₂ on the Ag(111) surface is an endothermic activated process. Furthermore, the sticking probability is sensitive to the internal temperature, or state distribution, of the D₂ beam. Specifically, the population of highly vibrationally excited states enhances the dissociative chemisorption probability. The molecular beam experiments were able to measure sticking probabilities up to 0.02 for average incidence energies up to about 0.48 eV using a pure D₂ beam. Achieving higher incidence energies (up to 0.8 eV) was possible, by seeding the D₂ beam in H₂ and using the King and Wells technique for detection,³⁴ but the experimentalists reported that the reaction could not be observed with this technique,^32,33 indicating a D₂ sticking probability <0.05 for energies up to 0.8 eV. Thus, the activation barrier for D₂(ν = 0) dissociation was reported to be >0.8 eV.³²

Due to the large activation barrier height for dissociation of D₂ on the Ag(111) surface, the adsorption process is not so accessible to the experiment. In this situation, recombinative desorption provides a useful method to investigate the adsorption dynamics by employing the principle of detailed balance.³⁵⁻³⁷ Hodgson and co-workers measured the energy release into translational motion for D₂ recombinative desorption from Ag(111) for specific rovibrational D₂ states and various surface temperatures. They found that surface temperature can affect the form of the translational energy distribution and thereby the sticking probability curve, where it is derived by applying detailed balance. At higher surface temperature, the energy distribution in recombinative desorption broadens. Therefore, the initial-state selected sticking probability broadens with increasing surface temperature. At a surface temperature of 570 K, the translational energy distribution for H₂/D₂(ν = 0)^36,37 becomes bimodal and shows a peak at high translational energy. The large energy release in recombination is due to the large activation barrier to the reverse process, i.e., direct activated dissociation. At higher surface temperature and at low translational energy, the sticking probability increases rapidly with surface temperature and shows an energy-independent behavior.³⁷ The sticking probability curves can be reproduced using an error function at higher translational energies. However, this model cannot reproduce the low-energy tail of the sticking probability curve and describe the bimodal energy distribution. In this article, the focus will be on the high-energy tail of the reaction probability.

Jiang and Guo³⁸ examined the reactivity in the H₂–Ag(111) system. They showed that the reactivity in this system is controlled not only by the height of the reaction barrier but also by the topography of the PES in the strongly interacting region. They reported a reaction barrier height of 1.15 eV for H₂ dissociation on Ag(111) using the PBE functional.³⁹ Although they compared computed initial-state selected reaction probabilities with results of associative desorption experiments, no comparison was made with the molecular beam experiments of Hodgson and co-workers.^32,33 For the associative desorption experiments, good agreement was reported with the PBE theory at higher incidence energies.

This article is organized as follows. Section 2.1 describes the dynamical model, and Section 2.2 describes the construction of the PES. The dynamics methods that are used here to study H₂ + Ag(111) are explained in Section 2.3. Section 2.4 describes how we calculate the observables. Section 2.5 provides computational details. In Section 3, the results of the calculations are shown and discussed. Section 3.1 describes the computed PES, and Sections 3.2.1–3.2.3 provide results on vibrationally inelastic scattering, initial vibrational state selected reaction, and sticking in molecular beam experiments. Conclusions are provided in Section 4.

2. Method

2.1. Dynamical Model

In our calculations, the Born–Oppenheimer static surface (BOSS) model⁵ is used. There are two approximations in this model. In the Born–Oppenheimer approximation, it is considered that the reaction occurs on the ground-state PES and that electron–hole pair excitation does not affect the reaction probability. The second approximation is that the surface atoms are static and occupy their ideal, relaxed 0 K lattice configuration positions at the (111) surface of the face-centered cubic (fcc) structure of the metal. As a result, motion in the six molecular degrees of freedom is taken into account in our dynamical model. Figure 1a shows the coordinate system used for our study, and Figure 1b shows the surface unit cell for the Ag(111) surface and the symmetric sites relative to the coordinates used for H₂.

Figure 1.

(a) Coordinate system used to describe the H₂ molecule relative to the static Ag(111) surface. (b) Top view of the surface unit cell and the sites considered for the Ag(111) surface. The center-of-mass (of H₂) coordinate system is centered on a top site (a surface atom). The hexagonal close-packed site corresponds to a second-layer atom and the fcc site to a third-layer atom.

2.2. Construction of Potential Energy Surface

A full six-dimensional (6D) PES was constructed using DFT with the SRP48 functional being a weighted average of two functionals¹² (0.48 × RPBE⁴⁰ + 0.52 × PBE³⁹). The DFT procedure and the way the data are interpolated are almost entirely the same as those used before for H₂ + Au(111).¹³ Here, we describe only the most important aspects and provide a few details on which the present procedure differs from that used earlier.

For the interpolation of the 6D PES, in total 28 configurations were used, spread over the 6 different sites on the surface unit cell indicated in Figure 1b. The accurate corrugation reducing procedure (CRP)⁴¹ was used to interpolate DFT data, which were computed on grids of points. All our calculations were carried out for interatomic distances r in the range 0.3–2.3 Å. The low starting value of r was needed because high initial vibrational states were involved in the Boltzmann sampling of the molecular beam simulations. We extended the H–H distance to a lower bound than that used for H₂ + Au(111)¹³ to guarantee the accurate calculation of higher vibrationally excited states (see below). In all other aspects, the procedure followed to produce the DFT data on grids of points and to interpolate the points with the CRP is entirely analogous to that used earlier for H₂ + Au(111). For more detailed information, the reader is referred to refs (13) and (20). In the interpolation procedure to obtain the PES from DFT data on the six sites in Figure 1b, the p3ml plane group symmetry⁴² is used. Tests to confirm the accuracy of the interpolation for additional DFT data not included in the interpolation data set were carried out and confirmed the quality of the procedure. As a check on the accuracy of the PES, we compare two different DFT data sets, which were not used in the construction of the PES, with the corresponding CRP-interpolated values. In method 1300 geometries of H₂ + Ag(111) were selected completely at random, with the only restrictions being 0.3 Å ≤ r ≤ 2.3 Å and 0.25 Å ≤ Z ≤ 4.0 Å. In method 2, only dynamically relevant points in the barrier region were selected: 300 randomly selected points were taken from QCT calculations, from 10⁴ trajectories, a further restriction being 0.7 Å ≤ r ≤ 2.3 Å and 0.9 Å ≤ Z ≤ 3.5 Å. (For more details, we refer the reader to ref (43).)

2.3. Dynamics Methods

2.3.1. Quasi-Classical Dynamics

The QCT method¹⁵ was used to compute dynamical observables so that the initial zero-point energy of H₂ is taken into account. To calculate the initial-state-resolved reaction probabilities, the molecule is initially placed at Z = 7 Å with a velocity normal toward the surface that corresponds to the specific initial incidence energy. To obtain accurate results, for each computed point on the reaction probability curves, at least 10⁴ trajectories were calculated; more trajectories were computed to obtain a sufficiently small error bar for low sticking probabilities. In all cases, the maximum propagation time was 2 ps. The method of Stoer and Bulirsh⁴⁴ was used to propagate the equations of motion.

The Fourier grid Hamiltonian method⁴⁵ was used to determine the bound state rotational–vibrational eigenvalues and eigenstates of gas-phase H₂ by solving the time-independent Schrödinger equation. This method was used to compute the rovibrational levels of the hydrogen molecule in the gas phase. Other initial conditions are randomly chosen. The orientation of the molecule, θ and ϕ, is chosen also based on the selection of the initial rotational state. The magnitude of the classical initial angular momentum is fixed by 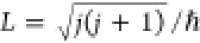, and its orientation, while constrained by 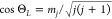, is otherwise randomly chosen as described in.^13,20 Here, j is the rotational quantum number, m_j is the magnetic rotational quantum number, and Θ_L is the angle between the angular momentum vector and the surface normal. The impact sites are chosen at random. The amount of vibrational energy corresponding to a particular vibrational and rotational level is initially given to the H₂ molecule. The bond distance and the vibrational velocity of the molecule are randomly sampled from a one-dimensional quasi-classical dynamics calculation of a vibrating H₂ molecule for the corresponding vibrational energy.¹³

2.3.2. Quantum Dynamics (QD)

For quantum dynamics (QD) calculations, the time-dependent wave packet method was used.^46,47 To represent the wave packet in Z, r, X, and Y, a discrete variable representation⁴⁸ was used. To represent the angular wave function, a finite base representation was employed.^49,50 To propagate the wave packet according to the time-dependent Schrödinger equation, the split operator method⁵¹ was used (see ref (47) for more details).

The wave packet is initially located far away from the surface. The initial wave packet is written as a product of a Gaussian wave packet describing the motion of the molecule toward the surface, a plane wave for motion parallel to the surface, and a rovibrational wave function to describe the initial vibrational and rotational states of the molecule. At Z = Z_∞, analysis of the reflected wave packet is done using the scattering amplitude formalism,⁵²⁻⁵⁴Z_∞ being a value of Z where the molecule and surface no longer interact. S matrix elements for state-to-state scattering are obtained in this way and used to compute scattering probabilities. An optical potential is used to absorb the reacted (r) or scattered (Z) wave packet for large values of r and Z.⁵⁵ Full details of the method are presented in ref (47).

2.4. Computation of the Observables

2.4.1. Degeneracy-Averaged Reaction Probabilities

In the QCT calculations of the reaction probabilities, the molecule is considered dissociated when its interatomic distance becomes greater than 2.5 Å. The reaction probability is computed from P_r = N_r/N_total, in which N_r is the number of reactive trajectories and N_total is the total number of trajectories. For a particular initial vibrational state ν and rotational state j, the degeneracy-averaged reaction probability can be computed by

1

where P_r is the fully initial-state-resolved reaction probability. In the quantum dynamics, the fully initial-state-resolved reaction probability is defined as

2

In this equation, P_scat(E_i; ν, j, m_j → ν′, j′, m_j′, n, m) are the state-to-state scattering probabilities. Initial (final) vibrational, rotational, and magnetic rotational quantum numbers are denoted ν (ν′), j (j′), and m_j (m_j′), respectively. n and m are the quantum numbers for diffraction. Vibrationally inelastic scattering probabilities can be obtained from

3

2.4.2. Vibrational Efficacy

The vibrational efficacy Θ_ν=0→1(P) is another interesting quantity in our study. The vibrational efficacy describes how efficiently the vibrational energy can be used to promote the reaction relative to translational energy.^28,56 It is typically computed by

4

where E_vib(ν, j) is the vibrational energy corresponding to a particular state of the gas-phase molecule and E_i^ν, j(P) is the incidence energy at which the initial-state-resolved reaction probability becomes equal to P for H₂ (D₂) initially in its (ν, j) state. In evaluating eq 4, j is typically taken as 0.

2.4.3. Molecular Beam Sticking Probabilities

In the molecular beam, the population of the rovibrational levels depends on the nozzle temperature. The rovibrational levels of the hydrogen molecule approaching the surface are assumed populated according to a Boltzmann distribution at the nozzle temperature used in the experiment. The monoenergetic reaction probabilities R_mono(E_i; T_n) are computed via Boltzmann averaging over all rovibrational states populated in the molecular beam with a nozzle temperature T_n at a collision energy E_i(27)

5

Here, F_B(ν, j; T_n) is the Boltzmann weight of each (ν, j) state. The factor F_B(ν, j; T_n) is described by

6

in which

7

In this equation, E_vib and E_rot are the vibrational and rotational energies, respectively, and K_B is the Boltzmann constant. The factor W(J) describes the nuclear spin statistics of H₂ and D₂. With even j, W(J) is 1 (2) for H₂ (D₂), and with odd values, it is 3 (1) for H₂ (D₂). The vibrational temperature of the molecule is assumed to be equal to the nozzle temperature (T_vib = T_n). However, in the molecular beam simulation, it is assumed that the rotational temperature of the molecule in the beam is lower than the nozzle temperature (T_rot = 0.8T_n).⁵⁷

The experimentalists showed that vibrational excitation promotes dissociation of D₂ on Ag(111)³² and suggested that sticking is dominated by higher vibrational states.³³ In the theoretical simulation of the molecular beam, we have to consider the Boltzmann factor of the populated vibrational states. To ensure a proper contribution of the higher rotational and vibrational states in the QCT calculations, the highest-populated vibrational state is allowed to be up to 5 and the highest rotational state to be up to 25. The threshold of the Boltzmann weight for an initial rovibrational state to be considered is 4 × 10^–6. The convergence of the sticking probability with respect to this threshold was checked.

To extract the sticking probability from the theoretical model, in principle, flux-weighted incidence energy distributions should be used. Subsequently, the reaction probability on sticking probability is computed via averaging over the incident velocity distribution of the experimental molecular beam, according to the expression⁵⁸

8

where f(v_i; T_n) is the flux-weighted velocity distribution given by⁵⁹

9

Here, C is a constant, v_i is the velocity of the molecule (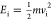), v_s is the stream velocity, and α is a parameter that describes the width of the velocity distribution.

According to the experimentalists, the mean translational energies obtained from time-of-flight distributions for the pure D₂ beam were related to the nozzle temperature by ⟨E_i⟩ = 2.7kT_n. This indicates a slight rotational cooling of the incident molecular beam (T_rot ≈ 0.8T_n). However, they could not detect any relaxation of the incident vibrational state distributions. To simulate the molecular beam with our dynamical model, we use energy distributions, which have been fitted by the experimentalists [Hodgson, private communication] with the exponentially modified Gaussian function of the form

10

Here, σ is defined as

11

and the nozzle temperature T_n (in K) is related to ⟨E⟩ by

12

Hereafter, we refer to these energy distributions, eq 10, as G(E). While we will use the G(E) provided by the experimentalist, we note that these do not correspond to the usual asymmetry flux-weighted distributions defined in terms of the stream velocity v_s and the width parameter α given by eq 9. Using the energy distribution G(E), the reaction probability is then described by

13

The experimentally measured reaction probabilities and the corresponding average translational energies for D₂ + Ag(111) are listed in Table 1, which also presents the values of T_n and σ. Figure 2 shows the experimental incident energy distributions for different average incidence energies.

Table 1. Average Energies and Experimental Sticking Coefficient S₀^a.

average energy (eV)	σ (meV)	S0	Tn (K)
0.221	1.26	7.6 × 10–8	969
0.274	1.53	3.9 × 10–6	1177
0.304	1.68	8.6 × 10–6	1295
0.336	1.85	8.6 × 10–5	1421
0.376	2.05	3.9 × 10–4	1579
0.424	2.30	3.1 × 10–3	1768
0.452	2.44	9.2 × 10–3	1878
0.486	2.62	2.0 × 10–2	2012

^aT_n shows the nozzle temperatures. The data were obtained from Hodgson (private communication).

Figure 2.

Incident energy distributions G_H-dis(E) for different values of T_n data from Hodgson [private communication].

To obtain statistically reliable QCT results, we performed convergence tests on the number of trajectories for each set of incidence conditions. To simulate molecular beam experiments, at least 10⁶ trajectories were computed for each incidence condition. To simulate the molecular beam experiments, we also used the beam parameters presented in Table 9 of the supporting material of ref (5), which describe the D₂ pure beams produced in experiments of Auerbach and co-workers⁵⁶ in terms of the flux-weighted velocity distributions (eq 9).

2.5. Computational Details

The DFT calculations were performed with the Vienna ab initio simulation package (VASP) software package (version 5.2.12). Standard VASP ultrasoft pseudopotentials were used, as done originally for H₂ + Cu(111).⁵ First, the bulk fcc lattice constant was computed in the same manner as used previously for H₂ + Au(111),¹³ using a 20 × 20 × 20 Γ-centered grid of k points. The distance between the nearest-neighbor Ag atoms in the top layer was obtained as a = a_3D/√2 = 2.97 Å with the SRP48 functional, where a_3D is the bulk lattice constant. With the SRP48 functional, a bulk lattice constant a_3D of 4.20 Å was computed. It is in reasonable agreement with the computed value of 4.16 Å of the PBE functional.³⁸ Compared with the experimental value (4.08 Å),^60,61 the SRP48 functional overestimates the lattice constant by about 3%.

A (2 × 2) surface unit cell has been used to model the H₂/Ag(111) system. The slab consisted of four layers. A relaxed four-layer slab was generated again in the same manner as used before for H₂ + Au(111),¹³ using 20 × 20 × 1 Γ-centered grid of k points. The interlayer distances computed with the SRP48 functional were d₁₂ = 2.41 Å and d₂₃ = 2.40 Å, and d₃₄ was taken as the SRP48 bulk interlayer spacing (2.41 Å).

After having obtained the relaxed slab, the single-point calculations for the PES were carried out using a 11 × 11 × 1 Γ-centered grid of k points and a plane wave cutoff of 400 eV. In the supercell approach, a 13 Å vacuum length between the periodic Ag(111) slabs was used. Other details of the calculations were the same as in ref (27). With the computational setup used, we estimate that the molecule–surface interaction energy is converged to within 30 meV.¹³

For quantum dynamics calculations on the reaction, wave packets were propagated to obtain results for the energy range of 0.5–1.0 eV. Table 2 lists the parameters that were used. Figure 3a shows convergence tests for using different numbers of grid points on the surface unit cell for quantum dynamics calculations on D₂(ν = 2, j = 0). Taking the number of grid points in X and Y equal to n_X = n_Y = 28, the results of quantum dynamics calculations are in good agreement with quantum dynamics results with n_X = n_Y = 32. Convergence could thus be achieved with n_X = n_Y = 28 (see Figure 3a). By repetition of the same procedure, we found that the numbers of X and Y grid points n_X = n_Y = 20 and n_X = n_Y = 32 are sufficient to obtain converged quantum dynamics results for D₂(ν = 1, j = 0) and D₂(ν = 3, j = 0), respectively. We also checked convergence with the highest rotational level j_max and m_jmax for the angular part of the wave packet (see Figure 3b). As can be seen, convergence is achieved with j_max = 24 and m_jmax = 16.

Table 2. Input Parameters for the Quantum Dynamical Calculations of D₂(ν = 2, j = 0) Dissociating on Ag(111)^a.

parameter	description	energy range (0.5–1.0) (eV)
nX = nY	no. of grid points in X and Y	24 (20, 32)
nZ	no. of grid points in Z	154
nZ(sp)	no. of specular grid points	256
ΔZ	spacing of Z grid points	0.1
Zmin	minimum value of Z	–1.0
nr	no. of grid points in r	42
Δr	spacing of r grid points	0.15
rmin	minimum value of r	0.4
jmax	maximum j value in basis set	24
mjmax	maximum mj value in basis set	16
Δt	time step	2
Z0	center of initial wave packet	15.8
Zinf	location of analysis line	12.5
Zstartopt	start of optical potential in Z	12.5
Zendopt	end of optical potential in Z	14.3
PZ	optical potential in Z	0.4
rstartopt	start of optical potential in r	4.15
rendopt	end of optical potential in r	6.55
Pr	optical potential in r	0.3
Z(sp)startopt	start of optical potential in Z(sp)	20.0
Z(sp)endopt	end of optical potential in Z(sp)	24.5
PZ(sp)	optical potential in Z(sp)	0.3
T	total propagation time	20 000

^aFor different vibrational states, the same input parameters could be used, aside from the number of grid points in X and Y. They are listed in parentheses for ν = 1 and ν = 3, respectively. All values are given in atomic units (except for the parameters P for the quadratic optical potentials, which are given in eV).

Figure 3.

Convergence test for the reaction of D₂(ν = 2, j = 0) on Ag(111) for the (a) number of grid points in the X and Y coordinates and (b) highest j_max and m_jmax in the basis sets.

3. Results and Discussion

3.1. Potential Energy Surface

Figure 4 shows elbow plots of the PES computed with the SRP48 functional for different configurations. Table 3 shows the geometries and heights of the barrier to dissociation found for impact on the top, bridge, fcc hollow, and t2f sites. In all cases, H₂ is positioned parallel to the Ag(111) surface. The minimum barrier height (1.38 eV) is found for bridge-to-hollow dissociation (see Figure 4b), similar to that for H₂ + Cu(111).⁵ Comparing the reaction paths in the two-dimensional (2D) elbow plots, we suggest that the impact on the fcc site is most likely relevant for vibrationally inelastic scattering and for the dissociation of vibrationally excited H₂. The 2D elbow plot for this site displays a large curvature of the reaction path. The minimum barrier position for that site also shows a large intermolecular distance r, i.e., a later barrier. It is known that these two characteristics promote vibrationally inelastic scattering and vibrationally enhanced dissociation.^62,63 The lowest curvature of the reaction path in front of the barrier was found for the bridge site. Due to the lower reaction barrier height for the bridge site, we predict that the reaction occurs mostly above this site for ν = 0 H₂.

Figure 4.

Elbow plots (i.e., E(Z, r)) of the H₂ + Ag(111) PES computed with the SRP48 functional and interpolated with the CRP method for four high-symmetry configurations with the molecular axis parallel to the surface (θ = 90°) as depicted by the insets, for (a) the top site and ϕ = 0°, (b) the bridge site and ϕ = 90°, (c) the fcc site and ϕ = 0°, and (d) the t2f site and ϕ = 240°. Barrier geometries are indicated with white circles, and corresponding barrier heights and geometries are given in Table 3.

Table 3. Barrier Heights (E_b) and Positions (Z_b, r_b) for Dissociative Chemisorption of H₂ on Ag(111) Above Different Sites in Which H₂ is Parallel to the Surface (θ = 90°)^a.

configuration	ϕ°	Zb (Å)	rb (Å)	Eb (eV)
top	0	1.51	1.57	1.69
bridge	90	1.10	1.27	1.38
t2f	240	1.34	1.45	1.58
fcc	0	1.34	1.67	1.70

^aThe results are provided for the SRP48 PES.

To carefully check the accuracy of the interpolation method (the CRP), additional electronic structure single-point calculations have been performed using VASP, for molecular configurations centered on a symmetric site bridge (X = 0.5a, Y = 0.0, where a is the lattice constant). Figure 5 presents the results of a comparison between DFT results not included in the input database for the interpolation and the CRP-interpolated PES along θ on this site, with ϕ = 90° and r = 1.27 Å. The black curve and symbols (r = 1.27 Å and Z = 1.2 Å) represent the θ-variation of the PES around a point near the minimum barrier position. The curves show that H₂ prefers to change its orientation from perpendicular to parallel when it approaches the surface. The interpolated PES faithfully reproduces the DFT results. The same finding was obtained for interpolation in X (see Figure 6). Hence, the accuracy in the interpolation of the PES guarantees that the comparison of our dynamical results with experiments should reflect the accuracy of the electronic structure results and the computational model.

Figure 5.

θ-Dependence of the H₂ + Ag(111) SRP48 PES is shown for molecular configurations centered on a bridge site (X = 1/2a; Y = 0), ϕ = 90° and r_b = 1.27 Å, where a is the surface lattice constant. Full lines: interpolated PES; symbols: DFT results. The values of Z corresponding to different curves and sets of symbols are provided with matching color.

Figure 6.

X-dependence of the H₂ + Ag(111) SRP48 PES is shown for molecular configurations including the top site (X = 0.0; Y = 0.0), for ϕ = 0°, θ = 90°, and r_b = 1.57 Å. Full lines: interpolated PES; symbols: DFT results. The values of Z corresponding to different curves and sets of symbols are provided with matching color.

As described in Section 2.2, we also evaluate the accuracy of the CRP-interpolated PES using two additional methods. We evaluate interpolation errors by comparing DFT data points with corresponding CRP values and computing the root-mean-square error (RMSE), mean absolute error (MAE), and mean signed error (MSE, obtained by subtracting DFT energies from CRP energies). To test the accuracy of the PES in more detail, we chose three different energy ranges: (1) 0–0.69 eV (less than 1/2 times the minimum barrier height), (2) 0.69–1.38 eV (between half times the minimum barrier height and the minimum barrier height), and (3) 1.38–2.07 eV (larger than the minimum barrier height but smaller than 1.5 times the barrier height). The corresponding values for both data sets ((1) data selected in a completely random way and (2) data from QCT calculations) are listed in Table 4. Importantly, the errors for the dynamically selected data set are in all cases less than 1 kcal/mol.

Table 4. Accuracy of the 6D PES in Comparison with DFT Calculations^a.

energy	N	RMSE (1)	RMSE (2)	MAE (1)	MAE (2)	MSE (1)	MSE (2)
(0.0–0.69)	100	0.024	0.009	0.012	0.007	0.006	0.007
(0.69–1.38)	100	0.086	0.021	0.044	0.020	0.008	0.020
(1.38–2.07)	100	0.132	0.036	0.069	0.031	0.015	0.031

^aAll energies are in eV, with the zero of energy taken as the gas-phase-H₂ minimum energy. N is the number of data points. The number in brackets behind the error refers to the method used to evaluate the error in Section 2.2.

3.2. Dynamics

3.2.1. Scattering

In Figure 7, vibrationally elastic and inelastic excitation probabilities P (ν = 2, j = 0 → ν = ν′) are presented as a function of the initial normal incidence energy. At an incidence energy of 0.5 eV, the probability for vibrationally elastic scattering is about 1. At higher incidence energies, the sizeable P values (ν = 2, j = 0 → ν ≠ ν′) indicate a substantial competition between vibrationally elastic and inelastic scattering probabilities on the one hand and reaction on the other hand for all energies shown. This behavior can result from a PES that describes reaction paths with especially late barriers with a high degree of curvature in r and Z (see Section 3.1),^62,63 leading to a coupling between molecular vibration and motion toward the surface. This explains why we see reaction probabilities no larger than about 0.8 for the highest incidence energy E_i we employed.

Figure 7.

Vibrationally elastic and inelastic scattering probabilities are shown as a function of the normal incidence energy for scattering of D₂(ν = 2, j = 0) from Ag(111) using the SRP48 PES.

3.2.2. Initial-State-Resolved Reaction

The comparison between the calculated and measured results for H₂ (ν = 0, j = 3), D₂(ν = 0, j = 2), and D₂(ν = 1, j = 2) is shown in Figures 8 and 9. The theoretical results were obtained by degeneracy averaging the fully initial-state-resolved reaction probabilities. The experimental results were extracted from associative desorption experiments.^36,37 In the figure, the symbols show the experimental data and the solid curves show the theoretical results based on a PES computed with the PBE functional by Jiang et al.³⁸ The dotted lines show our theoretical results obtained with the SRP48 functional. One thing to keep in mind is that our calculated reaction probabilities saturate at high E_i at about 0.8. In contrast, fits made by the experimentalists assumed the reaction probability to saturate at 1 (this condition was not imposed on the data shown). The agreement of theory and experiment is good at high translational energies for the results of the Jiang et al. group. However, the initial-state-resolved reaction probabilities obtained with the SRP48 functional underestimate the experimental reaction probabilities. Jiang et al. obtained the minimum barrier height of 1.16 eV with the PBE functional, while we computed a value of 1.38 eV with the SRP48 functional. The comparison suggests that the SRP48 functional overestimates the reaction barrier height so that the computed reaction probabilities are too low.

Figure 8.

Comparison of experimental and computed reaction probabilities as a function of incidence energy E_i for H₂ in the (ν = 0, j = 3) state, dissociating on Ag(111). The experimental data were reported in ref (36). The quantum dynamics results obtained for the PBE functional were reported in ref (38).

Figure 9.

Comparison of experimental and computed reaction probabilities as a function of incidence energy E_i for D₂ in the (ν = 0–1, j = 2) states, dissociating on Ag(111). The experimental data were reported in ref (37). The quantum dynamics results obtained for the PBE functional were reported in ref (38).

Other initial-state (ν, j)-resolved reaction probabilities for several vibrational states and j = 0 of H₂ and D₂ have also been computed for the SRP48 PES using QCT. They are presented as a function of incidence energy E_i in Figure 10a for H₂ (ν = 0, 1, 2, 3, 4, and 5, j = 0 states). Figure 10b shows the results for D₂.

Figure 10.

Reaction probabilities as a function of incidence energy E_i for H₂ (a) and D₂ (b) in the (ν = 0–5, j = 0) states. Horizontal arrows and the number above these indicate the energy spacing between the reaction probability curves for the (ν = 0–2, j = 0) states for a reaction probability equal to 0.24.

The theoretical vibrational efficacy computed from our results for H₂(D₂) (ν = 0, j = 0) and H₂(D₂) (ν = 1, j = 0) is greater than 1. For example, at a reaction probability of 0.24, the calculated shift between the ν = 0 and ν = 1 reaction probability curves is about 0.504 eV, while the vibrational excitation energy is 0.37 eV for D₂(ν = 0 → 1), yielding a vibrational efficacy of 1.37.

Vibrational promotion of reaction with vibrational efficacies up to 1 may be explained conceptually through a picture in which the molecule moves along the reaction path in a potential elbow in the two dimensions r and Z. Analyzing the effect based on the vibration perpendicular to the reaction path, the reaction may be promoted by increasing ν if the frequency of motion perpendicular to the path is decreased. This can be done through a mass effect (leading to larger vibrational efficacies for later barriers,^64,65 the Polanyi rules⁶⁶) or by a decrease of the force constant for this motion,^67,68 when the molecule moves toward the barrier (vibrationally elastic enhancement). It is also possible that the vibration discussed is de-excited before the molecule gets to the barrier,⁶³ possibly leading to a vibrational efficacy as high as 1.0 (vibrationally inelastic enhancement). However, vibrational efficacies greater than 1.0, as found here, can only be explained if the assumption is made that for low ν (and high incident energy) the molecule cannot follow the minimum-energy path and slides off it^69,70 (this has also been called a bobsled effect in the past⁷¹).

A comparison between the reaction threshold energy of D₂(ν = 0, j = 0) and H₂ (ν = 0, j = 0) shows that this energy for D₂ is at a somewhat higher incidence energy than for H₂. This is known as a zero-point energy effect,⁷² where H₂ has more energy in zero-point vibrational motion so that more of this energy can be converted to energy along the reaction coordinate (via softening of the H–H bond).

Figure 10a also shows an interesting effect: at the highest ν, the reaction probability curve takes on the shape of a curve affected by trapping-mediated dissociation at low incident energies, i.e., the reaction becomes nonactivated for the highest ν for H₂. The same effect was observed by Laurent et al.,⁷³ who investigated the reaction in five different H₂ metal systems and found that for high-enough ν the reaction probability curve takes on this shape, with the value of ν at which this effect occurs depending on how activated the dissociation is. They attributed the nonmonotonic dependence on incidence energy to an increased ability of the highly vibrationally excited molecule to reorient itself to a favorable orientation for reaction.

The experimentalists³³ used a model to fit the molecular beam sticking data, assuming that dissociation is independent of molecular rotation, with the sum of contributions from dissociation of the molecule in different initial vibrational states ν being described by a sticking function

14

Here, E₀ is the translational energy required for the sticking probability to reach half of its maximum value, w is the width of the function, and A is the saturation parameter. In this model, the molecular sticking probability is assumed to be a function of the incidence energy and the vibrational state. All parameters are assumed to be dependent on the initial vibrational state as well. E_i is the normal incidence energy. We use this model to check whether we reproduce the deconvoluted initial vibrational state-resolved sticking probability for D₂ on Ag(111). The experimentally determined parameters can be found in ref (33).

The comparison between the experimentally fitted results and our computed initial-state-resolved reaction probabilities for D₂(ν = 1–4, j = 0) is presented in Figure 11a. Figure 11b also shows the computed sticking probability as a function of collision energy, in which Boltzmann averaging is performed over all rotational states for each specific vibrational state and specific incidence energy of D₂. This figure shows that also considering higher rotationally excited states (>j = 0) in our calculations may considerably enhance the vibrational-state-resolved reaction probabilities. In particular, it is clear that the sticking probability for the j = 0 rotational level is smaller than the sticking probability obtained by averaging over the rotational distribution of the molecular beam at T_n = 2012 K. Also, as a result of this rotational state averaging effect, our computed vibrational-state-resolved reaction probabilities have a much larger width w than the experimentally extracted data. The QCT results indicate that the saturation value of the reaction probability is approximately equal to 0.8 and not 1 as was assumed in extracting w from experimental data using eq 14.

Figure 11.

(a) Deconvoluted sticking function S₀(E_i, ν) for D₂ at Ag(111) (lines)³³ and the computed initial-state-resolved reaction probabilities for the (ν = 1–4, j = 0) states (symbols with matching color). (b) Same functions S₀(E_i, ν) resulting from the experimental analyses³³ are compared with the computed initial vibrational-state selected reaction probabilities with Boltzmann averaging over the rotational states using T_n = 2012 K. Comparison between the computed initial-state-resolved reaction probabilities and initial vibrational-state-resolved reaction probabilities is also shown for the ν = 4 state.

To check the accuracy of the QCT results and to investigate the possible quantum effects in the dissociation of a small and light molecule on the surface, quantum dynamics calculations were performed. In Figure 12, the initial-state-resolved reaction probability for D₂ dissociating on Ag(111) obtained from QCT calculations is compared to QD calculations for the initial (ν = 1–3, j = 0) states. We found an excellent agreement between these two dynamical methods (QCT and QD), giving us enough confidence to use the QCT results for the molecular beam sticking simulations. The results for ν = 1 suggest that the comparison with experiment in Figure 9 should be accurate for the ν = 1, j = 2 state of D₂, at least for probabilities larger than 0.01. The comparison between QCT and QD results for (ν = 0, j = 0) H₂ + Ag(111) presented in Figure 6 of ref (74) on the other hand would suggest that using QD would move the computed reaction probability curve to higher energies by a few tens of meV for ν = 0, which would slightly worsen the agreement between the present theory and experiment for ν = 0 in Figure 9.

Figure 12.

Comparison between the initial-state-resolved reaction probabilities calculated with QD and QCT calculations for (ν = 1–3, j = 0) D₂ dissociating on Ag(111).

3.2.3. Molecular Beam Sticking

In Figure 13, the computed sticking probabilities are shown as a function of the average collision energy for D₂ dissociation on Ag(111). A comparison is made with available experimental results of Cottrell et al.³³ Calculations were performed for two sets of beam parameters corresponding to different velocity distributions.

Figure 13.

(a) Reaction probability for molecular beams of D₂ dissociating on Ag(111) computed with the SRP48 functional. For comparison, experimental results³³ are plotted. Horizontal arrows and the number above these indicate the energy spacing between the theoretical reaction probability results and the interpolated experimental curve. (b) Energy distributions for two different sets of beam parameters. The red curve shows the energy distribution (G_H-disE_av = 0.486 eV, σ = 2.61 × 10^–3 eV) at the nozzle temperature 2012 K, and the blue curve presents the flux-weighted velocity distributions G_A-dis, for E_av = 0.449 eV, at the nozzle temperature 1975 K.

The experimentalists claimed that the sticking of all vibrational levels ν < 4 may be significant and must be included in modeling the experimental data.³³ Our calculations show that the contributions of the initial vibrational states in the D₂ molecule dissociating on the surface are 3% for ν = 1, 8% for ν = 2, 52% for ν = 3, 31% for ν = 4, and 5% for ν = 5, when the average incidence energy of the beam is 0.486 eV and T_n = 2012 K. This theoretical result is in agreement with the experimental expectation.

The sticking probabilities are plotted as a function of average incidence energy in Figure 13a. Here, the black symbols show the experimental data measured by Cottrell et al.³³ The dotted line represents the interpolation of the experimental data. The red symbols are our computed beam simulation results, averaging over translational energy distributions according to the formula provided by the experimentalists and described above and Boltzmann averaging over the initial rovibrational states of the D₂ molecule in the beam according to the nozzle temperatures given in Table 1. The energy differences between the computed data and the spline-interpolated experimental curve are in the range of 87–100 meV (2–2.3 kcal/mol). Therefore, our theoretical results do not agree with the experimental results to within chemical accuracy (1 kcal/mol ≈ 43 meV). The discrepancy should not be due to the use of the QCT method instead of quantum dynamics. As discussed above, at even the largest average collision energy in the experiment, the dominant contributions to the QCT reaction probabilities come from ν ≥ 3. These probabilities are not expected to exhibit large errors due to zero-point energy violation (see Figure 12). The QCT reaction probabilities for lower ν (especially for ν = 0) may exhibit larger zero-point energy violation errors (see for instance Figure 6 of ref (74) for ν = 0 H₂ + Ag(111)), but in any case, their contribution should be small at all energies. Furthermore, their contribution would lead to (small) overestimates by the computed reaction probabilities rather than underestimates, as zero-point energy violation tends to increase the reaction probability (see again Figure 6 of ref (74)). Therefore, correcting for zero-point energy violation errors should not improve the agreement with experiment and would only lead to small changes.

The discrepancy between the molecular beam sticking probabilities and the QCT results is also not due to the neglect of nonadiabatic effects (e–h pair excitation). Earlier work on the reaction of H₂ on copper surfaces (refs (22−24) and (26)) and on H₂ + Ag(111)⁷⁵ suggests that including these effects would lead to a minor reduction of the reaction probability, increasing the disagreement with experiment further. Inclusion of phonon effects, however, could somewhat increase the reaction probability at the low-energy sides of the reaction probability curves for specific ν contributing to the sticking probability if there is a mechanical coupling with the surface phonons (if the barrier position moves with a phonon coordinate),⁷⁶ as in the surface oscillator model.⁷⁷ Additionally, the sticking probability could be increased somewhat if there is an electronic (or energetic) coupling with the surface phonons (if the barrier height changes with the phonon displacement coordinate).⁷⁶ However, these effects are expected to be small, as there is a large mass mismatch between H₂ and Ag, and the surface temperature in the molecular beam experiments was very low (100 K).³³ Also, the mechanical and electronic couplings for H₂–metal surface interactions tend to be small⁷⁸ compared to those for the case of methane interacting with transition metal surfaces, for which the effects may be large.⁷⁶ Future research could show how large these effects are, but we note that including both effects is not likely to increase the agreement between the molecular beam experiment and calculations using the SRP48 functional.

The comparison of computed initial-state selected reaction probabilities and probabilities extracted from associative desorption experiments in Figures 8 and 9 suggests that using the PBE functional might lead to better agreement with the molecular beam experiments than that obtained with the SRP48 functional. Thus, the PBE functional (or a PBE/RPBE mixture with a much lower RPBE weight than that presently used (0.48)) might be a good starting point for the development of an SRP functional for H₂ + Ag(111).

The lack of agreement found between the present calculations and the molecular beam sticking probabilities is at odds with the finding of transferability between CHD₃ + Ni(111) and Pt(111).¹¹ A possible reason for the lack of transferability found is that the SRP48 functional is not based on a van der Waals correlation functional,⁷⁹ as was the case for CHD₃ + Ni(111) and Pt(111).¹¹ The only case¹¹ for which transferability has been established among systems in which one specific molecule interacts with surfaces of different transition metals belonging to the same group so far involved a SRP functional incorporating a van der Waals correlation functional. For H₂ + Cu(111), such an SRP functional has already been identified,²⁷ which gave a somewhat better overall description of experiments than the SRP48 functional, although the minimum barrier height obtained with the new functional exceeded that of the SRP48 functional by 76 meV.²⁷

The blue symbols in Figure 13a show the computed results based on energy distributions and nozzle temperatures of pure D₂ beams from the experiments on D₂ + Cu(111) reported by Auerbach et al.⁵ We call these energy distributions (i.e., the flux-weighted velocity distribution) G_A-dis. The energy differences between these computed results and the interpolated experimental curve are in the range of 64–79 meV (1.5–1.8 kcal/mol). The theoretical sticking probabilities are therefore in somewhat better agreement with experiment if the more asymmetric incidence energy distributions of Auerbach and co-workers are used.

In Figure 13b, the energy distribution G_A-dis is wider and shows a longer tail toward high energies than G_H-dis. As a result, more molecules should be able to overcome the reaction barrier. As the G_A-dis curves should be more realistic, a better comparison between theory and experiment would be possible if we acquire more information on the experimental translational energy distributions and, in particular, regarding their high-energy tails.

Our finding that the initial-state-resolved reaction probabilities computed with the SRP48 functional are shifted to somewhat higher energies (by about 0.1 eV for D₂, see Figure 9) is consistent with our comparison for the molecular beam sticking measurements.

4. Conclusions

To investigate whether the SRP functional derived for the H₂ + Cu(111) system is transferable to the H₂ + Ag(111) system, where Ag is the same group as Cu, we have performed calculations on the dissociative chemisorption of H₂/D₂ on Ag(111).

The raw DFT data have been computed by the VASP software package, and an accurate fitting method (the CRP) has been used to map out the 6D PES based on the SRP48 functional. The minimum barrier heights and geometries have been reported.

We have discussed the dynamics methods within the BOSS model. The QCT method has been used to compute the initial-state-resolved reaction probabilities for several rovibrational states of D₂ and H₂. The reliability of the QCT method, to accurately calculate the reaction probabilities for D₂ + Ag(111), has been tested by a comparison with quantum dynamics calculations for the ν = 1–3, j = 0 states of D₂. It was found that QCT reproduces the QD results very well.

Results for vibrationally (in)elastic scattering, i.e., probabilities P (ν = 2, j = 0 → ν = ν′) as function of incidence energy, have been presented and discussed. These calculations serve for better understanding of why we see reaction probabilities no larger than about 0.8 for the highest incidence energy. A clear competition was shown between vibrational inelastic scattering and reaction at higher incidence energies, resulting in reaction probabilities saturating at 0.8 instead of what was assumed to be 1.0 in the fitting procedures of the experimental data.³³

A comparison of our computed initial-state-resolved reaction probabilities with the computed state-specific reaction probabilities of the Jiang et al. group³⁸ and with the experimental associative desorption results of Hodgson and co-workers,^36,37 extracted by application of the detailed balance principle, has been presented. The comparison suggests that the barrier heights in the SRP48 PES are too high. Also, a nonmonotonic dependence on incidence energy has been observed in our results for H₂ dissociation at the highest ν (ν = 5). A vibrational efficacy Θ_ν=0→1(P) greater than 1 has been reported for H₂(D₂)(ν = 0, j = 0) and also for H₂(D₂)(ν = 1, j = 0). Such a high vibrational enhancement suggests that for low ν (and high incidence energy) the molecule is not able to stay on the minimum-energy path for reaction.

The computed reaction probabilities for several D₂ vibrational states and j = 0 have been compared with data used to analyze the molecular beam experiments and reaction probabilities that were Boltzmann-averaged over j. The comparison suggests that the rotational state averaging effect contributes to a larger width w in our computed vibrational-state-resolved reaction probabilities than found for the experimentally extracted reaction probability curves for specific ν.

Finally, using the obtained QCT results, we have also simulated molecular beam sticking probabilities and compared with the experimental results of Cottrell et al.³³ We have reported the energy differences between the computed data and the spline-interpolated experimental curve to be in the range of 2–2.3 kcal/mol. Thus, no chemical accuracy was achieved in our theoretical results. Theoretical calculations using flux-weighted velocity distributions with the beam parameters taken from the D₂ + Cu(111) experiment⁵ have also been shown. We have found that these calculations are in somewhat better agreement with the experiment and energy differences between the computed results and interpolated experimental curve shrink to 1.5–1.8 kcal/mol. It has been suggested that the asymmetric incidence energy distributions should be more realistic and a better comparison between theory and experiment might result if more information about the experimental energy distributions of the beam would become available. The present comparison suggests that the PBE functional (or a PBE/RPBE mixture with a much lower RPBE weight than presently used (0.48)) might be a better starting point for the development of an SRP functional for H₂ + Ag(111) than the SRP48 functional.

Our finding of a vibrational efficacy greater than 1 suggests that a trial-and-error procedure involving dynamics calculations will be required to obtain a new SRP functional for H₂ + Ag(111), as the H₂ molecule is apparently unable to follow the minimum-energy path. This would seem to disqualify a procedure based solely on static energy profiles. Ultimately, our results for the reaction based on the SRP48 functional systematically underestimate the available experimental results. Therefore, it is concluded that a chemically accurate description of the dissociative chemisorption of D₂ on Ag(111) is not yet obtained with the SRP48 DFT functional. Despite the chemically accurate description of dissociative chemisorption of H₂ on Cu(111) with the SRP48 functional, it is not transferable to the H₂ + Ag(111) system, although Cu and Ag belong to the same group.

The authors declare no competing financial interest.