Numerical analysis of flow distribution behavior in a proton exchange membrane fuel cell

BH Lim; EH Majlan; WRW Daud; MI Rosli; T Husaini

doi:10.1016/j.heliyon.2018.e00845

. 2018 Oct 10;4(10):e00845. doi: 10.1016/j.heliyon.2018.e00845

Numerical analysis of flow distribution behavior in a proton exchange membrane fuel cell

BH Lim ^a, EH Majlan ^a,^∗, WRW Daud ^a,^b, MI Rosli ^a,^b, T Husaini ^a

PMCID: PMC6190529 PMID: 30338304

Abstract

The flow distribution of a proton exchange membrane fuel cell within a manifold plays an important role on its performance. This study presents a numerical analysis of the flow distribution behavior within different manifold configurations. A two-dimensional model with 75 cells was employed to study the flow behavior. The variation in the stoichiometry and number of cells was also studied. Three different flow configurations were considered with different numbers of flow inlets and outlets. The flow characteristics, such as the pressure and velocity variations in the manifold and cells, were measured to determine the effects of the different flow configurations. The results indicated that the double inlet/outlet configuration had the best flow distribution when using 75 cells. Moreover, increasing the stoichiometry resulted in a better flow distribution to the cells in a stack.

Keyword: Energy

1. Introduction

Fuel cells that directly convert chemical energy to electrical energy are promising alternative energy converters for building a future carbon-free environment [1]. Among the multiple types of fuel cells, proton exchange membrane fuel cells (PEMFCs) have received major attention due to their low operating temperature, easy scale up, low pollution and high power density [2]. In PEMFCs, hydrogen in the anode is oxidized into protons and electrons, and oxygen or air in the cathode is reduced to form water. The proton ions that are oxidized in the anode will flow thru an external circuit to the cathode and this produces the electrical energy. The electrochemical reactions that occur in the PEMFC only generate heat and water as waste, which makes PEMFCs suitable for automotive applications. However, PEMFCs have not been commercialized because the fuel cell performance is not stable during the scale-up process [3, 4]. Studies have reported on the success of smaller scale PEMFC stacks [5], and issues that usually occur during scale up are due to the reactant distribution, which causes localized hotspots and flooding or drying [6, 7, 8].

Many studies have focused on optimizing the flow field distribution by creating multiple flow field designs [9, 10, 11, 12, 13, 14, 15, 16, 17, 18]. However, the first stage of the reactant distribution in a fuel cell stack occurs in the manifold area. Manifolds provide the channels in a fuel cell stack in which the reactants flow from the inlet to each channel cell and vice versa. Uniformly distributing the reactants from the manifold to the cells could improve the overall stack performance because it was known that the performance of a fuel cell is determined by the cell that produces the lowest power. Thus, uniformly distributing the reactants within the manifold could stabilize the power generated by each cell.

The common flow distributor in a fuel cell stack is a consecutive configuration with a U or Z structure [19]. Consecutive designs are known for their maldistribution, but they have a simple design and low pressure drop. Several numerical studies have been carried out using U-configurations and Z-configurations [20, 21]. These studies reported that the Z-configuration has a better flow distribution compared to the U-configuration, but the distribution depends on the operating conditions. Z-configurations have a high pressure drop because the flow accumulates at the outlet manifold, which helps to direct the flow towards the end of the cell, creating a uniform distribution among the cells. For U-configurations, the flow tends to follow the shortest path length, so the cells located near the inlet and outlet have more flow compared to the cells that are located further away [22]. The number of cells allocated in a PEMFC stack affects the flow distribution. As the number of cells increases, both configurations exhibit severe maldistributions among the cell [23]. However, it was reported that a judicially selected stack design could balance the effects of the pressure drop and maldistribution in U- and Z-configurations to attain an optimal stack performance [24]. Numerical and experimental studies have been carried out to improve both configurations of flow distributions [25, 26, 27]. These studies mentioned that increasing the manifold width for both configurations could enhance the flow distribution. The flows within the manifold became uniformly distributed by using larger cross sections that could reduce the total pressure drop in the stack [28]. Studies was also carried out on different tapered designs of Z-configuration [29, 30]. It was concluded that the tapered manifold would increase the flow uniformity. However, this design is not feasible for PEMFC stack manifold because of the complex alignment between each cell of a stack. Uniform flow distributions in the manifold can also be achieved by employing bifurcation structures in which the flow is distributed in stages with different cross sections. Liu and Li [31] experimentally studied the effects of cascade bifurcation and tee-channel flow distributions on a fuel cell stack. They concluded that the cascaded bifurcation flow distributor caused nearly uniform performance in each cell, and it also produced a higher voltage and power output compared to the tee-channel distributor. Still, this structure is not commonly used for PEMFCs due to turning losses that cause a high pressure drop, and the designs are complex and costly [32]. Increase of flow uniformity in the manifold can also be achieved by having baffle at the entrance of each cell. Wei et al., Luo et. al. and Pistorese et. al. [33, 34, 35] numerically investigated the flow uniformity by introducing baffle in the inlet manifold area and they concluded that addition of baffle could produce relatively uniform distribution. Even so, addition of baffle would increase the cost and complexity of the PEMFC stack design. Hence, the purpose of the present work is to enhance the flow uniformity in a PEMFC stack by using Z-configuration PEMFC stack manifold design with a higher number of cells in a stack. This paper will study on the effects of using consecutive configurations at multiple inlets and outlets on the manifold flow distribution. The main objective of this study is to produce a simple and compact design of manifold distribution for a PEMFC stack.

2. Design

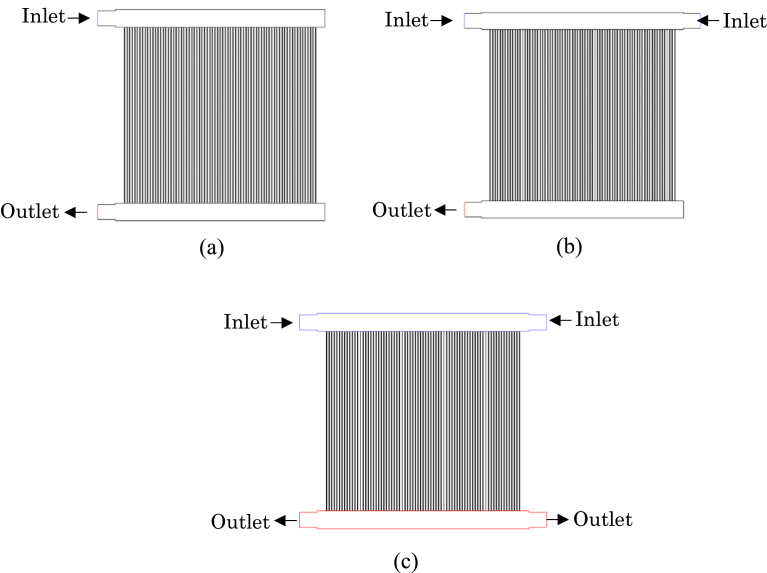
A manifold configuration with multiple inlets and outlets was studied in this paper. As shown in Fig. 1, three different configurations were considered; single inlet/outlet, double inlet/single outlet and double inlet/outlet. The flow entered from the top manifold and exited from the bottom manifold. Fig. 1a shows the single inlet/outlet manifold configuration. This is the common configuration for PEMFC stacks, but researchers have reported that the single inlet/outlet manifold configuration has an uneven flow distribution when the number of cells increases [36].

In this study, different numbers of inlet and outlets were investigated to evaluate their flow distributions. Table 1 shows the parameters and properties used for the simulations. The number of cells in a stack influenced the flow distribution because it would elongate the manifold as the number of cell increased, and it would affect the overall stack pressure drop. To understand the effects of the number of cells on the flow distribution, different manifold widths with different numbers of cells were studied.

Table 1.

Properties and parameters.

Properties and parameters	Value
Number of cells	50, 75, 100
Cell distance	3.6 mm
Width (inlet/outlet)	25.4 mm
Manifold width	30 mm
Air stoichiometry	2 and 5
Air viscosity	1.846 × 10⁻⁵ kg/m·s
Air density	1.1614 kg/m³

Open in a new tab

3. Model

A two-dimensional steady-state stack model was used while considering turbulent flow for all simulations. The k-ɛ model was employed to solve the governing equations. Gas diffusion layer, water formation and heat transfer analysis were neglected in this study. The cells in the model were filled with porous media, which created flow resistance during the simulation, to represent the flow field in a bipolar plate. The governing incompressible Navier-Stokes equations shown in Eqs. (1), (2), (3), and (4) were used:

Continuity:

\frac{\partial u_{i}}{\partial x_{i}} = 0,

(1)

Momentum:

ρ u_{j} \frac{\partial u_{i}}{\partial x_{i}} = - \frac{\partial p}{\partial x_{i}} + \frac{\partial}{\partial x_{j}} [μ_{t} (\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}})],

(2)

Turbulent kinetic energy:

ρ u_{j} \frac{\partial k}{\partial x_{i}} = \frac{\partial}{\partial x_{j}} [(μ + \frac{μ_{t}}{σ_{k}}) \frac{\partial k}{\partial x_{j}}] + μ_{t} (\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}}) \frac{\partial u_{i}}{\partial x_{j}} - ρ ε,

(3)

Turbulent dissipation:

ρ u_{j} \frac{\partial ε}{\partial x_{i}} = \frac{\partial}{\partial x_{j}} [(μ + \frac{μ_{t}}{σ_{ε}}) \frac{\partial ε}{\partial x_{j}}] + C_{1} μ_{t} \frac{ε}{k} (\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}}) \frac{\partial u_{i}}{\partial x_{j}} - C_{2} ρ \frac{ε^{2}}{k},

(4)

where $ρ$ is the density, $μ$ is the kinematic viscosity, k is the turbulent kinetic energy, ε is the turbulent dissipation and $u_{i}$ is the i^th component of the velocity field (i = 1, 2).

ANSYS Fluent R15.0 commercial software with the Semi-Implicit Method for Pressure Linked Equation Consistent (SIMPLEC) algorithm was employed to solve the governing equations, and the convergence criterion was 10⁻⁵ for all equations. A grid independence test (GIT) was carried out using the single inlet/outlet manifold configuration to ensure the optimal number of elements and computational time was used. Different element sizes were considered in the GIT, and the results are shown in Table 2. Decreasing the element size increased the total pressure drop in the stack. The percentage difference in the pressure drop between the refined and course element sizes was calculated. We determined the optimum element size for the simulation when the percentage difference was less than 0.1%. The minimal iteration time and maximum simulation accuracy were achieved using an element size of 0.25 mm because the average percentage difference in the total pressure drop between element sizes 0.25 mm and 0.2 mm was 0.03%. In a nutshell, an element size of 0.25 mm was used for all the models in this study.

Table 2.

GIT study.

Element size (mm)	No. of elements	Total pressure drop (Pa)	Avg. percentage difference (%) $\frac{R e f i n e d - C o u r s e}{R e f i n e} \times 100 %$
1	46934	2980	0.34
0.5	187148	2990	0.33
0.25	739456	3000	0.03
0.2	1023052	3001	-

Open in a new tab

4. Results & discussion

4.1. Manifold configuration flow distribution

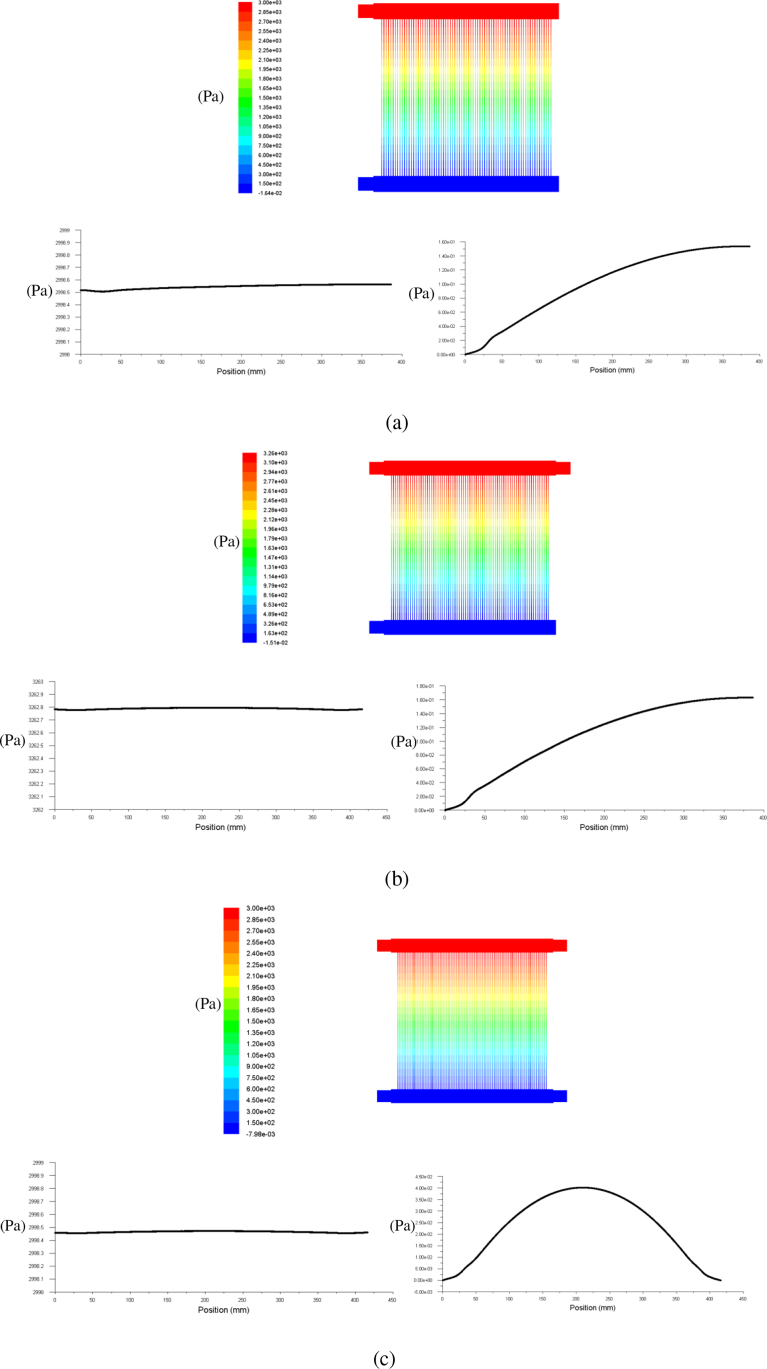
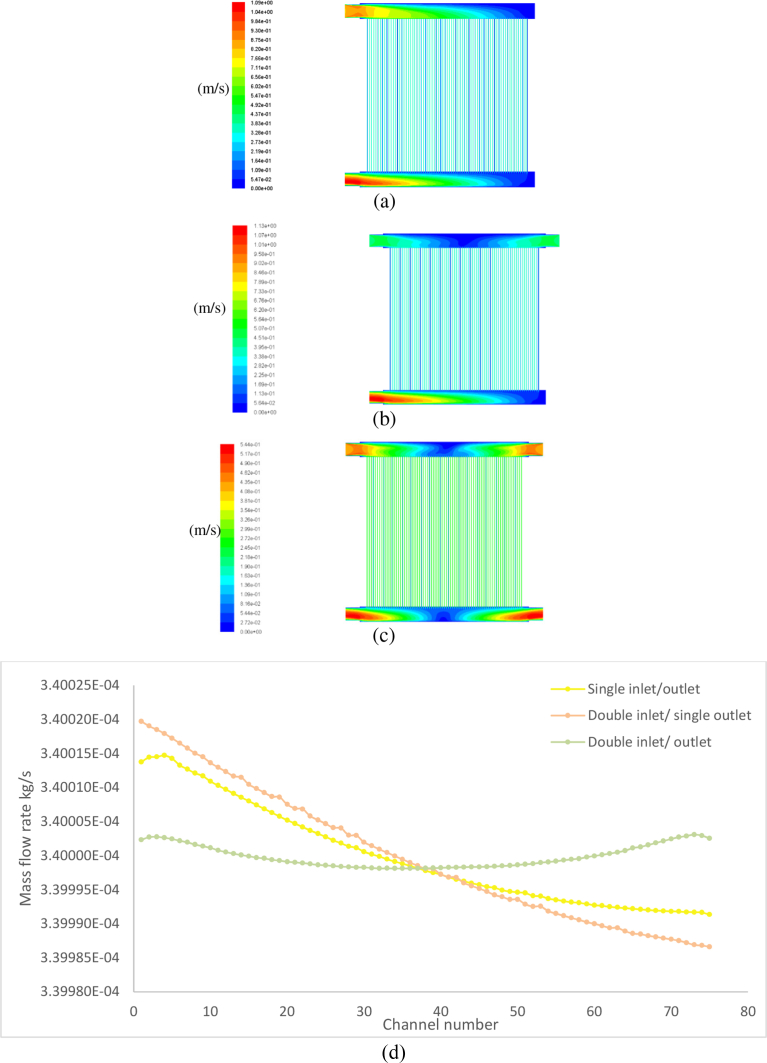
Three different manifold configurations were studied to determine their effects on the flow distribution in a PEMFC stack. The pressure distributions contour of the flow in the three manifold configurations (single inlet/outlet, double inlet/single outlet and double inlet/outlet) are shown in Fig. 2. The pressure was distributed evenly from the inlet to the outlet in all three manifold configurations. The highest pressure was recorded in the inlet manifold, and the pressure gradually decreased from the inlet manifold to the outlet manifold along the cell area. This result matches with Chen et al. [26] although the manifold width used in current study was wider to enhance flow uniformity. From the pressure contour plots, each cell in the manifold configuration exhibited a similar pressure decreasing trend in each stack.

Fig. 2 — Pressure distributions contour and plot of the manifold configurations: (a) single inlet/outlet; (b) double inlet/single outlet; and (c) double inlet/outlet.

To further determine the effects of the pressure drop among the three manifold configurations, the pressure variations in center line of the inlet and outlet manifolds (Fig. 1) were plotted and is shown in Fig. 2. The single inlet/outlet and double inlet/outlet manifolds exhibited similar total pressure drop values in the stack (approximately 3000 Pa). However, the pressure drop of the double inlet/outlet manifold was higher in the center of the stack compared to the single inlet/outlet configuration. For the outlet manifold pressure variation in Fig. 2c, a comparison between both manifold configurations in the pressure outlet plots shows that the peak pressure value (0.04 Pa) in the double inlet/outlet configuration was much lower compared to the peak value (0.16 Pa) in the single inlet/outlet configuration. For the double inlet/single outlet configuration, the outlet manifold pressure plot was similar to that of the single inlet/outlet configuration. Moreover, the manifold with the double inlet/single outlet configuration had a higher pressure drop (3260 Pa) compared to the other 2 configurations. Therefore, among the three manifold configurations, the double inlet/single outlet had the highest total pressure drop followed by the double inlet/outlet and, finally, the single inlet/outlet configuration. These results show that increasing the number of inlets can increase the total pressure drop in a stack.

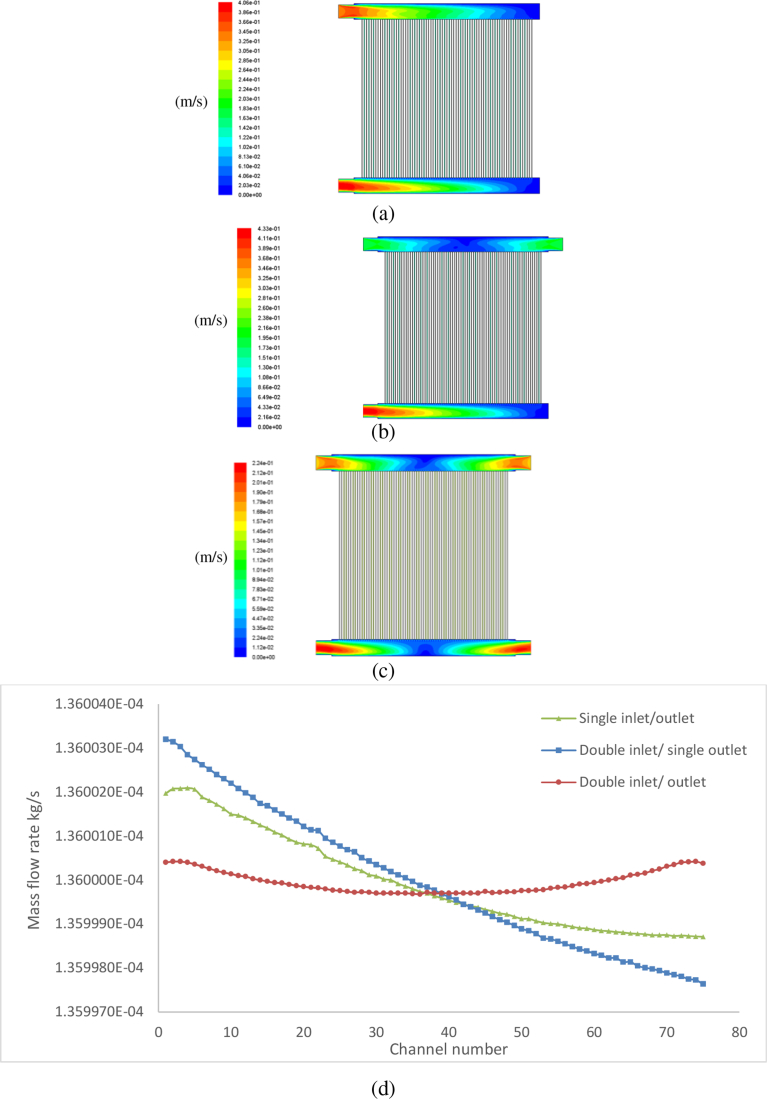
Velocity plots of the three manifold configurations are shown in Fig. 3a–c. The highest velocity occurred in the outlet area for all configurations. The lowest velocity occurred in the dead-end area and center area for the double inlet/outlet configuration. In the double inlet/single outlet configuration, the area in the dead-end outlet had the lowest velocity, which was nearly a stagnant flow area. Hence, an additional inlet does not enhance the flow entering the channel with a lower pressure difference. In comparison, Fig. 3c shows that with the double inlet/outlet, the pressure differences from the inlet to outlet for each cell were similar. Thus, this configuration promoted a uniform flow distribution among the cells.

It was difficult to determine the optimum configuration to achieve an even flow distribution in a stack using the pressure and velocity. Thus, the flow distribution in each stack was determined, and the distribution results are plotted in Fig. 3d. The single inlet/outlet configuration shows that the cell mass flow rate decreased further from the inlet, which matches the results from the study by Mustata et al. [20]. The double inlet/outlet configuration exhibited the best flow distribution among the cells compared to the other two configurations. By using double inlets and outlets the maldistribution among the cells decreased further from the inlet. As a result, an even flow distribution was achieved among the cells, and the lowest flow rates in the cells shifted from the end to the center of the stack. Moreover, the overall average flow rate distribution in the double inlet/outlet configuration was higher than that of the single inlet/outlet and double inlet/single outlet configurations.

A comparison between the single inlet/outlet and double inlet/single outlet configurations shows that the single inlet/outlet configuration exhibited a better uniformity because the flow rates in the first cell from both sides of the inlet in the double inlet/single outlet configuration exhibited a larger difference compared to the single inlet/outlet configuration. Even though there were two inlets, the flow distribution was not uniform due to the single outlet configuration. The flow tended to increase near the outlet because the area near the outlet had a larger pressure drop compared to the dead-end area.

4.2. Effects of the mass flow rate

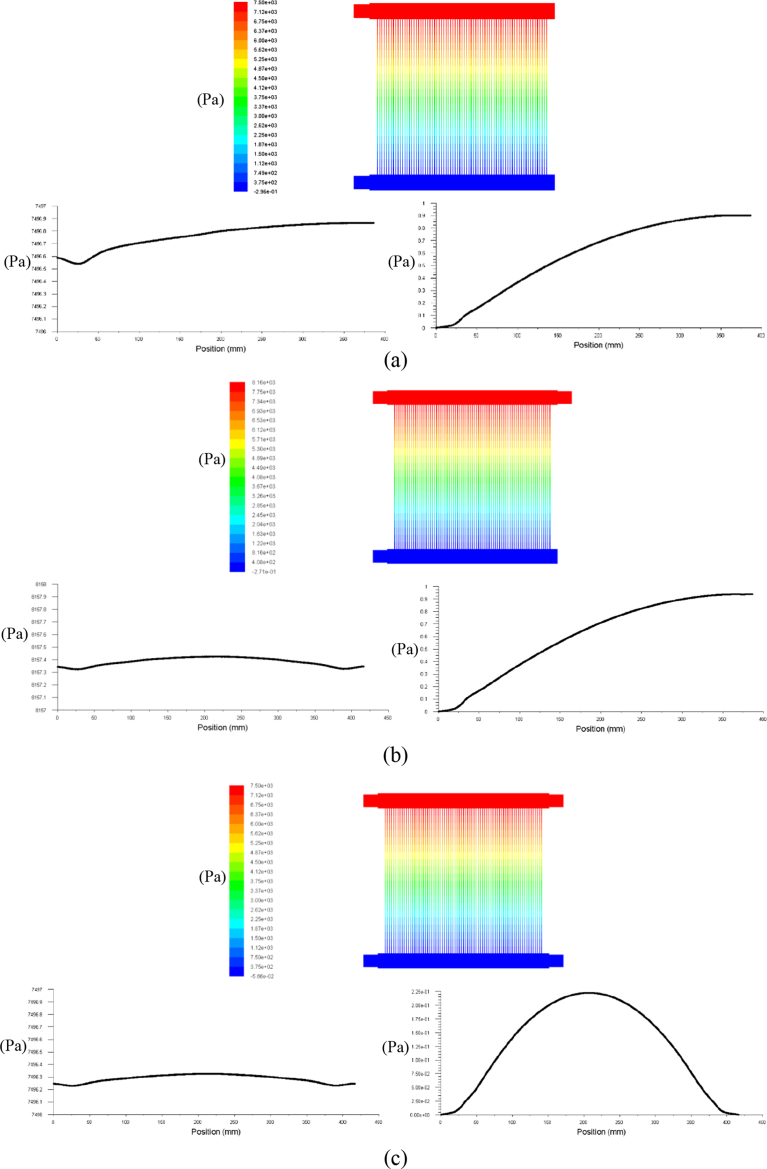
The mass flow rate affects the power generated from a PEMFC stack. A higher mass flow rate supplied to a PEMFC stack can increase the generated power. Thus, we conducted a study to determine the effect of using an excessive flow rate in the PEMFC stack. A stoichiometry value of 5 was used to supply the excess air with a mass flow rate 0.0255 kg/s. The same model, configuration and operating conditions were used in this study; only the mass flow rate was changed. The pressure variations in the three configurations (single inlet/outlet, double inlet/single outlet and double inlet/outlet) with the increased mass flow rate are shown in Fig. 4. A similar trend in the pressure drop was seen for all three configurations with a stoichiometry value of 2 for the mass flow rate, in which the pressure gradually decreased from the inlet to the outlet manifold.

Fig. 4 also shows the pressure variations plot in the three different configurations along the centre line of inlet and outlet manifold (Fig. 1). The highest overall pressure drop among the three configurations occurred in the double inlet/single outlet configuration, followed by the double inlet/outlet and single inlet/outlet configurations. Table 3 shows the changes in the pressure drop for a stoichiometry of 2 and 5 in the three different manifold configurations. The double inlet/single outlet exhibited the highest overall pressure drop using both stoichiometries. Higher pressure drops were observed for all three manifold configurations using a higher stoichiometry value because the manifold resistance increased at a higher stoichiometry value due to the increased mass flow rate, causing the pressure in the inlet manifold to increase. For both stoichiometries, the single inlet/outlet and double inlet/outlet configurations exhibited the same overall pressure drop in the stack. Hence, the double inlet/outlet configuration does not affect the overall pressure drop in a stack, and it also reduces the maldistribution conditions in a stack, as mentioned in the above study.

Table 3.

Total pressure drops in the stack for stoichiometry values of 2 and 5 for three different configurations.

Configuration/Stoichiometry	2	5
Single inlet/outlet	3000 Pa	7500 Pa
Double inlet/single outlet	3260 Pa	8160 Pa
Double inlet/outlet	3000 Pa	7500 Pa

Open in a new tab

Fig. 5a–c shows the velocity distribution of the air flow in the stack for the three different configurations. The velocity gradually decreased in the single inlet/outlet configuration along the inlet manifold, and the opposite trend occurred in the outlet manifold, where the velocity gradually increased from the dead-end area to the outlet area. Different phenomena were observed for the velocity distribution in the double inlet configuration, in which the center of the inlet manifold exhibited a lower velocity compared to the single inlet configuration. The changes in the pressure and velocity distributions in the manifold were dissimilar; the velocity decreased in the manifold, while the pressure increased for all three manifold configurations. In Fig. 5d, the distributions of the mass flow rates in each cell are plotted for a stoichiometry of 5. A comparison between Figs. 3d and 5d shows that similar flow distribution trend was seen for both stoichiometry 2 and 5. Since the parameters and properties in the model remained constant, the trends of the flow distributions are similar to those in Fig. 3d, in which the double inlet/outlet configuration exhibited a better flow uniformity compared to the other two configurations.

4.3. Effects of the number of cells in a stack

The study above used stoichiometry values of 2 and 5 with 75 cells in a stack to determine the flow uniformity. To understand the effects of changing the number of cells in a stack on the flow uniformity, we conducted a study using 50 and 100 cells in a stack. The single inlet/outlet manifold configuration was used to carried out this study with a stoichiometry of 2 with the flow rate. Then, 50 and 100 cell stacks were considered. By using a constant flow rate, the study could determine the effect of using an excess flow rate on the flow distribution for a 50 cell stack and the effect of using a minimum flow rate in the stack for a 100 cell stack. Thus, the study was conducted by altering the number of cells with the same flow rate supply. Other than the number of cells in the stack, the parameters and simulation conditions used for this study were the same as those used in the study above.

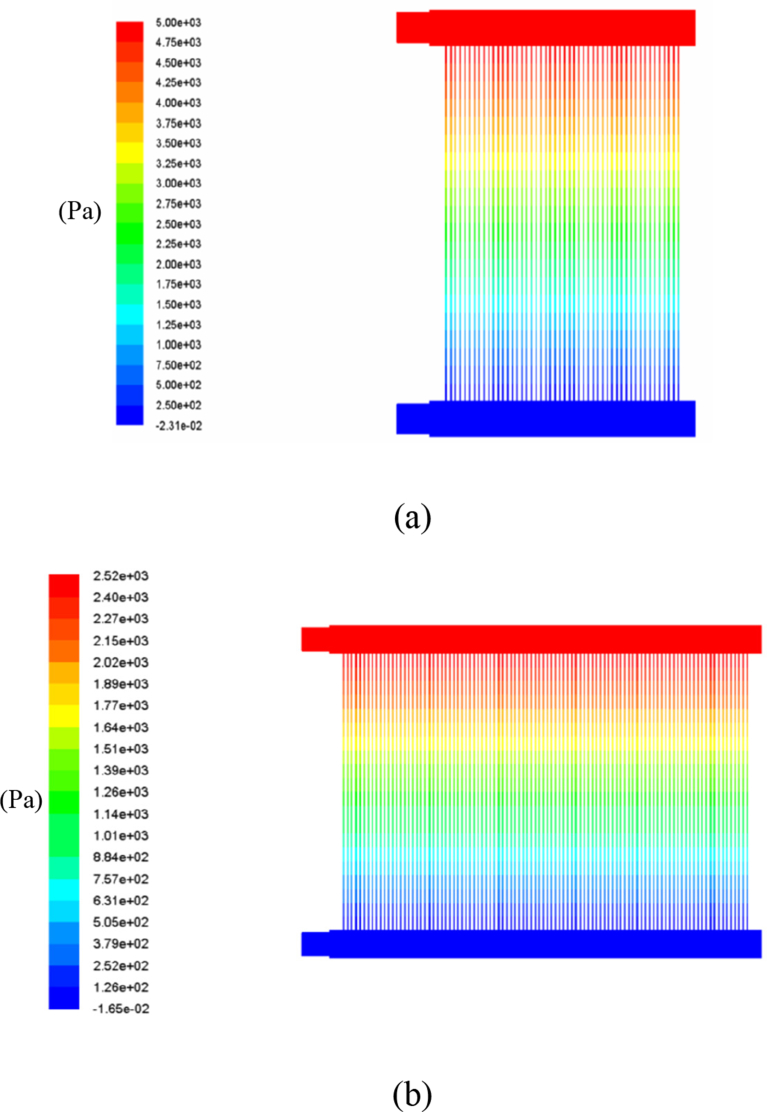
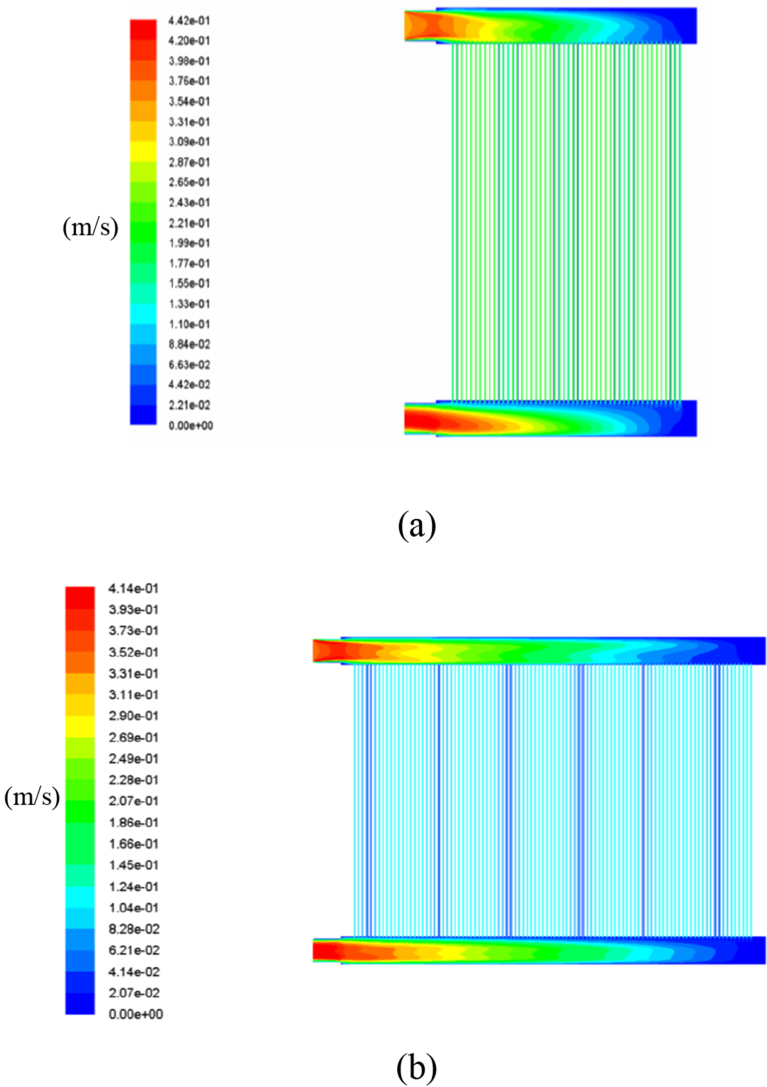
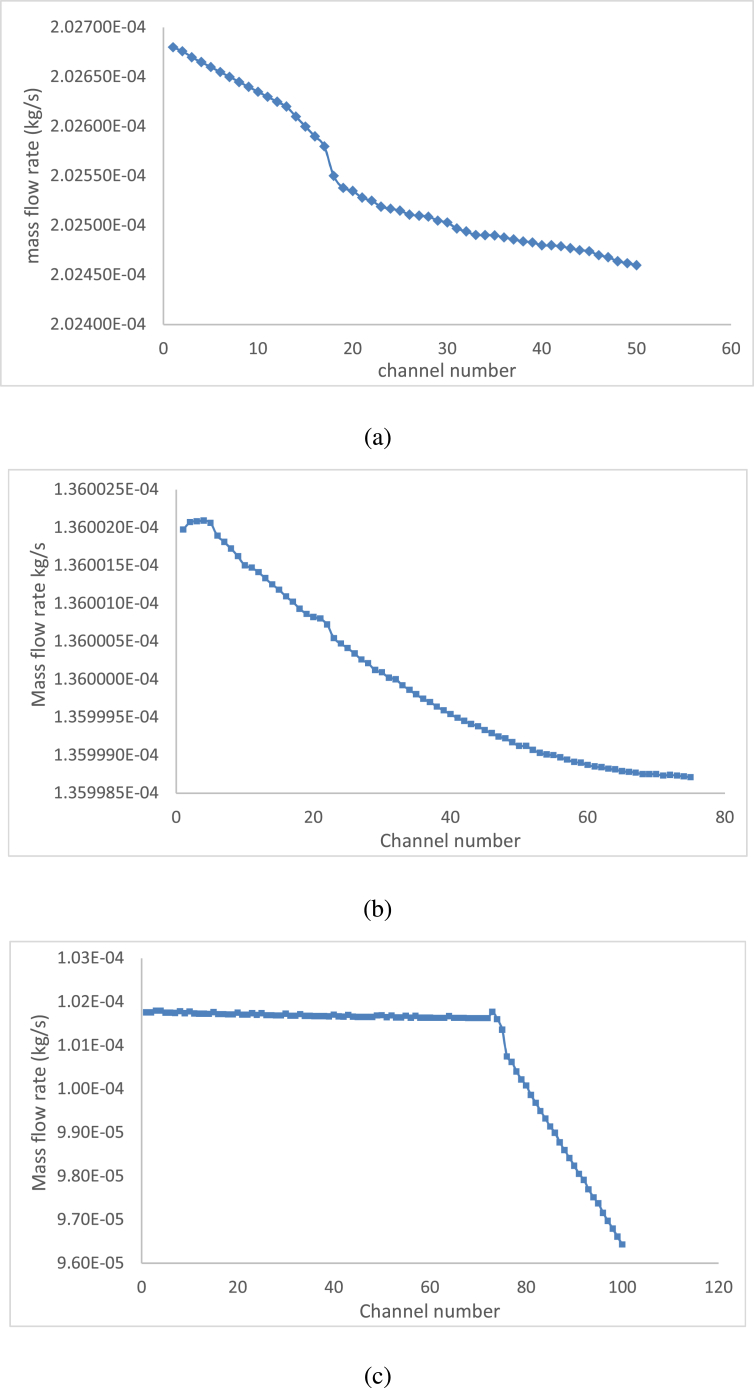
Fig. 6 shows the pressure distributions of the stacks with 50 and 100 cells. It was shown that the 50 cell stacks had a higher pressure drop (5000 Pa) compared to the 100 cell stacks (2520 Pa), and the 75 cell stack that was considered in the first part of the paper had a total pressure drop in between that of the 50 and 100 cell stacks. Thus, as the number of cells in the stack increased, the overall pressure drop decreased. Fig. 7 shows the velocity distributions of both the 50 and 100 cell stacks, the dead end-areas of both the inlet and outlet manifolds in the 100 cell stack had larger areas with a stagnant velocity. To determine the uniformity of the flow distribution to each cell for the 50, 75 and 100 cell stacks, the mass flow rate in each cell was measured and is shown in Fig. 8. For the same stoichiometry, the 75 cell stack exhibited better flow uniformity compared to the 50 cell stack. It can be seen that supplying excess mass flow rate would enhance the uneven flow distribution among the cells as it would increase the pressure drop in the stack as reported by Chen et al. [26]. As the number of cells further increased to 100 cells, as shown in Fig. 8c, the distribution of the flow rates into the cells near the dead-end inlet manifold decreased drastically. Therefore, this study indicates that an excess flow rate in a cell stack with fewer cells promotes maldistribution, and the maldistribution becomes more severe using stacks with more cells.

Fig. 7 — Velocity distribution using different numbers of cells in the stack: (a) 50 cells and (b) 100 cells.

Fig. 8 — Flow rate distribution: (a) 50 cell stack; (b) 75 cell stack; and (c) 100 cell stack.

5. Conclusion

A flow uniformity study was carried out using a numerical model for three different manifold configurations: single inlet/outlet, double inlet/single outlet and double inlet/outlet. The pressure and velocity distributions were studied to determine the effects of different manifold configurations. The results indicated that the total pressure drop of the double inlet/outlet configuration was identical to that of the single inlet/outlet manifold configuration. However, the double inlet/outlet manifold configuration was shown to have a better flow distribution among the cells. Even though the double inlet/single outlet manifold configuration had a higher overall pressure drop than the single inlet/outlet and double inlet/outlet manifold configurations, the flow distribution graphs indicated that the distribution of the flow rates was uneven, and lower flow rates in the cells were located near the dead-end outlet manifold. A study was also carried out to determine the effect of increasing the stoichiometry on the three manifold configurations. Similar flow distribution trends were captured among the cells for the different manifold configurations. The overall pressure drops increased when the stoichiometry increased. Still, this study has shown that there was no significant difference of flow uniformity as the stoichiometry increased from 2 to 5. Theoretically, increasing the pressure drop in the stack could increase the performance and water purging in the PEMFC stack, but it would also incur higher costs for the system. Lastly, a study was also carried out using different numbers of cells in the stacks, using the same stoichiometry for each stack. The results showed that using an excessive flow rate in a stack with fewer cells would lead to maldistribution. Thus, the present study showed that double inlet/outlet has shown better flow distribution as compared to others configuration. Further analyzing the flow uniformity of different configuration of inlet/outlet with 3D model will be recommended for future work.

Declarations

Author contribution statement

Bee Huah Lim: Performed the experiments; Wrote the paper.

Edy H. Majlan: Conceived and designed the experiments; Contributed reagents, materials, analysis tools or data.

Wan R. W. Daud: Contributed reagents, materials, analysis tools or data.

Masli Rosli: Conceived and designed the experiments; Analyzed and interpreted the data.

Husaini Teuku: Analyzed and interpreted the data.

Funding statement

This work was supported by the Ministry of Education (LRGS/2013/UKM-UKM/TP-01) and Universiti Kebangsaan Malaysia (GUP-2016-044).

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.

References

1.Brouwer J. On the role of fuel cells and hydrogen in a more sustainable and renewable energy future. Curr. Appl. Phys. 2010;10:S9–S17. [Google Scholar]
2.Sharaf O.Z., Orhan M.F. An overview of fuel cell technology: fundamentals and applications. Renew. Sustain. Energy Rev. 2014;32:810–853. [Google Scholar]
3.Karthikeyan P., Velmurugan P., George A.J., Ram Kumar R., Vasanth R.J. Experimental investigation on scaling and stacking up of proton exchange membrane fuel cells. Int. J. Hydrogen Energy. 2014;39:11186–11195. [Google Scholar]
4.Miller M., Bazylak A. A review of polymer electrolyte membrane fuel cell stack testing. J. Power Sources. 2010;196:601–613. [Google Scholar]
5.Vargas J.V.C., Ordonez J.C., Bejan A. Constructal PEM fuel cell stack design. Int. J. Heat Mass Tran. 2005;48:4410–4427. [Google Scholar]
6.Lee D., Bae J. Visualization of flooding in a single cell and stacks by using a newly-designed transparent PEMFC. Int. J. Hydrogen Energy. 2012;37:422–435. [Google Scholar]
7.Le A.D., Zhou B. A numerical investigation on multi-phase transport phenomena in a proton exchange membrane fuel cell stack. J. Power Sources. 2010;195:5278–5291. [Google Scholar]
8.Jahnke T., Futter G., Latz A., Malkow T., Papakonstantinou G., Tsotridis G. Performance and degradation of proton exchange membrane fuel cells: state of the art in modeling from atomistic to system scale. J. Power Sources. 2016;304:207–233. [Google Scholar]
9.Wang J. Pressure drop and flow distribution in parallel-channel configurations of fuel cells: U-type arrangement. Int. J. Hydrogen Energy. 2008;33:6339–6350. [Google Scholar]
10.Daniels F.A., Attingre C., Kucernak A.R., Brett D.J.L. Current collector design for closed-plenum polymer electrolyte membrane fuel cells. J. Power Sources. 2014;249:247–262. [Google Scholar]
11.Bao C., Bessler W.G. Two-dimensional modeling of a polymer electrolyte membrane fuel cell with long fl ow channel. Part II. Physics-based electrochemical impedance analysis. J. Power Sources. 2015;278:675–682. [Google Scholar]
12.Kee R.J., Zhu H. Distribution of incompressible flow within interdigitated channels and porous electrodes. J. Power Sources. 2015;299:509–518. [Google Scholar]
13.Maharudrayya S., Jayanti S., Deshpande A.P. Pressure drop and flow distribution in multiple parallel-channel configurations used in proton-exchange membrane fuel cell stacks. J. Power Sources. 2006;157:358–367. [Google Scholar]
14.Bahiraei M., Heshmatian S. Optimizing energy efficiency of a specific liquid block operated with nanofluids for utilization in electronics cooling: a decision-making based approach. Energy Convers. Manag. 2017;154:180–190. [Google Scholar]
15.Bahiraei M., Heshmatian S. Thermal performance and second law characteristics of two new microchannel heat sinks operated with hybrid nanofluid containing graphene–silver nanoparticles. Energy Convers. Manag. 2018;168:357–370. [Google Scholar]
16.Bahiraei M., Heshmatian S. Efficacy of a novel liquid block working with a nanofluid containing graphene nanoplatelets decorated with silver nanoparticles compared with conventional CPU coolers. Appl. Therm. Eng. 2017;127:1233–1245. [Google Scholar]
17.Bahiraei M., Heshmatian S. Application of a novel biological nanofluid in a liquid block heat sink for cooling of an electronic processor: thermal performance and irreversibility considerations. Energy Convers. Manag. 2017;149:155–167. [Google Scholar]
18.Dabiri S., Hashemi M., Rahimi M., Bahiraei M., Khodabandeh E. Design of an innovative distributor to improve flow uniformity using cylindrical obstacles in header of a fuel cell. Energy. 2018;152:719–731. [Google Scholar]
19.Friedl a., Fraser S.D., Baumgartner W.R., Hacker V. Experimental analysis of internal gas flow configurations for a polymer electrolyte membrane fuel cell stack. J. Power Sources. 2008;185:248–260. [Google Scholar]
20.Mustata R., Valiño L., Barreras F., Gil M.I., Lozano A. Study of the distribution of air flow in a proton exchange membrane fuel cell stack. J. Power Sources. 2009;192:185–189. [Google Scholar]
21.Chang P.A.C., St-Pierre J., Stumper J., Wetton B. Flow distribution in proton exchange membrane fuel cell stacks. J. Power Sources. 2006;162:340–355. [Google Scholar]
22.Lebæk J., Bang M., Kær S.K. Flow and pressure distribution in fuel cell manifolds. J. Fuel Cell Sci. Technol. 2010;7:61001. [Google Scholar]
23.Zhang W., Hu P., Lai X., Peng L. Analysis and optimization of flow distribution in parallel-channel configurations for proton exchange membrane fuel cells. J. Power Sources. 2009;194:931–940. [Google Scholar]
24.Park J., Li X. Effect of flow and temperature distribution on the performance of a PEM fuel cell stack. J. Power Sources. 2006;162:444–459. [Google Scholar]
25.Pandiyan S., Elayaperumal A., Rajalakshmi N., Dhathathreyan K.S., Venkateshwaran N. Design and analysis of a proton exchange membrane fuel cells (PEMFC) Renew. Energy. 2013;49:161–165. [Google Scholar]
26.Chen C.-H., Jung S.-P., Yen S.-C. Flow distribution in the manifold of PEM fuel cell stack. J. Power Sources. 2007;173:249–263. [Google Scholar]
27.Dheeraj N.A., Rao S., Vas R.S., Rathnakar M. Fuel cell stack manifold optimization through modelling and simulation. Energy Power. 2016;6:15–21. [Google Scholar]
28.Imbrioscia G.M., Fasoli H.J. Simulation and study of proposed modifications over straight-parallel flow field design. Int. J. Hydrogen Energy. 2014;39:8861–8867. [Google Scholar]
29.Pistoresi C., Fan Y., Luo L. Numerical study on the improvement of flow distribution uniformity among parallel mini-channels. Chem Eng Process Process Intensif. 2015;95:63–71. [Google Scholar]
30.Tong J.C.K., Sparrow E.M., Abraham J.P. Geometric strategies for attainment of identical outflows through all of the exit ports of a distribution manifold in a manifold system. Appl. Therm. Eng. 2009;29:3552–3560. [Google Scholar]
31.Liu H., Li P. Maintaining equal operating conditions for all cells in a fuel cell stack using an external flow distributor. Int. J. Hydrogen Energy. 2013;38:3757–3766. [Google Scholar]
32.Wang J. Theory of flow distribution in manifolds. Chem. Eng. J. 2011;168:1331–1345. [Google Scholar]
33.Wei M., Fan Y., Luo L., Flamant G. CFD-based evolutionary algorithm for the realization of target fluid flow distribution among parallel channels. Chem. Eng. Res. Des. 2015;100:341–352. [Google Scholar]
34.Luo L., Wei M., Fan Y., Flamant G. Heuristic shape optimization of baffled fluid distributor for uniform flow distribution. Chem. Eng. Sci. 2015;123:542–556. [Google Scholar]
35.Pistoresi C., Fan Y., Aubril J., Luo L. Fluid flow characteristics of a multi-scale fluidic network. Chem Eng Process Process Intensif. 2018;123:67–81. [Google Scholar]
36.Palaniappan K., Govindarasu R., Parthiban R. Investigation of flow mal-distribution in proton exchange membrane fuel cell stack. Int. J. Renew. Energy Resour. 2012;2:4–8. [Google Scholar]

[bib1] 1.Brouwer J. On the role of fuel cells and hydrogen in a more sustainable and renewable energy future. Curr. Appl. Phys. 2010;10:S9–S17. [Google Scholar]

[bib2] 2.Sharaf O.Z., Orhan M.F. An overview of fuel cell technology: fundamentals and applications. Renew. Sustain. Energy Rev. 2014;32:810–853. [Google Scholar]

[bib3] 3.Karthikeyan P., Velmurugan P., George A.J., Ram Kumar R., Vasanth R.J. Experimental investigation on scaling and stacking up of proton exchange membrane fuel cells. Int. J. Hydrogen Energy. 2014;39:11186–11195. [Google Scholar]

[bib4] 4.Miller M., Bazylak A. A review of polymer electrolyte membrane fuel cell stack testing. J. Power Sources. 2010;196:601–613. [Google Scholar]

[bib5] 5.Vargas J.V.C., Ordonez J.C., Bejan A. Constructal PEM fuel cell stack design. Int. J. Heat Mass Tran. 2005;48:4410–4427. [Google Scholar]

[bib6] 6.Lee D., Bae J. Visualization of flooding in a single cell and stacks by using a newly-designed transparent PEMFC. Int. J. Hydrogen Energy. 2012;37:422–435. [Google Scholar]

[bib7] 7.Le A.D., Zhou B. A numerical investigation on multi-phase transport phenomena in a proton exchange membrane fuel cell stack. J. Power Sources. 2010;195:5278–5291. [Google Scholar]

[bib8] 8.Jahnke T., Futter G., Latz A., Malkow T., Papakonstantinou G., Tsotridis G. Performance and degradation of proton exchange membrane fuel cells: state of the art in modeling from atomistic to system scale. J. Power Sources. 2016;304:207–233. [Google Scholar]

[bib9] 9.Wang J. Pressure drop and flow distribution in parallel-channel configurations of fuel cells: U-type arrangement. Int. J. Hydrogen Energy. 2008;33:6339–6350. [Google Scholar]

[bib10] 10.Daniels F.A., Attingre C., Kucernak A.R., Brett D.J.L. Current collector design for closed-plenum polymer electrolyte membrane fuel cells. J. Power Sources. 2014;249:247–262. [Google Scholar]

[bib11] 11.Bao C., Bessler W.G. Two-dimensional modeling of a polymer electrolyte membrane fuel cell with long fl ow channel. Part II. Physics-based electrochemical impedance analysis. J. Power Sources. 2015;278:675–682. [Google Scholar]

[bib12] 12.Kee R.J., Zhu H. Distribution of incompressible flow within interdigitated channels and porous electrodes. J. Power Sources. 2015;299:509–518. [Google Scholar]

[bib13] 13.Maharudrayya S., Jayanti S., Deshpande A.P. Pressure drop and flow distribution in multiple parallel-channel configurations used in proton-exchange membrane fuel cell stacks. J. Power Sources. 2006;157:358–367. [Google Scholar]

[bib14] 14.Bahiraei M., Heshmatian S. Optimizing energy efficiency of a specific liquid block operated with nanofluids for utilization in electronics cooling: a decision-making based approach. Energy Convers. Manag. 2017;154:180–190. [Google Scholar]

[bib15] 15.Bahiraei M., Heshmatian S. Thermal performance and second law characteristics of two new microchannel heat sinks operated with hybrid nanofluid containing graphene–silver nanoparticles. Energy Convers. Manag. 2018;168:357–370. [Google Scholar]

[bib16] 16.Bahiraei M., Heshmatian S. Efficacy of a novel liquid block working with a nanofluid containing graphene nanoplatelets decorated with silver nanoparticles compared with conventional CPU coolers. Appl. Therm. Eng. 2017;127:1233–1245. [Google Scholar]

[bib17] 17.Bahiraei M., Heshmatian S. Application of a novel biological nanofluid in a liquid block heat sink for cooling of an electronic processor: thermal performance and irreversibility considerations. Energy Convers. Manag. 2017;149:155–167. [Google Scholar]

[bib18] 18.Dabiri S., Hashemi M., Rahimi M., Bahiraei M., Khodabandeh E. Design of an innovative distributor to improve flow uniformity using cylindrical obstacles in header of a fuel cell. Energy. 2018;152:719–731. [Google Scholar]

[bib19] 19.Friedl a., Fraser S.D., Baumgartner W.R., Hacker V. Experimental analysis of internal gas flow configurations for a polymer electrolyte membrane fuel cell stack. J. Power Sources. 2008;185:248–260. [Google Scholar]

[bib20] 20.Mustata R., Valiño L., Barreras F., Gil M.I., Lozano A. Study of the distribution of air flow in a proton exchange membrane fuel cell stack. J. Power Sources. 2009;192:185–189. [Google Scholar]

[bib21] 21.Chang P.A.C., St-Pierre J., Stumper J., Wetton B. Flow distribution in proton exchange membrane fuel cell stacks. J. Power Sources. 2006;162:340–355. [Google Scholar]

[bib22] 22.Lebæk J., Bang M., Kær S.K. Flow and pressure distribution in fuel cell manifolds. J. Fuel Cell Sci. Technol. 2010;7:61001. [Google Scholar]

[bib23] 23.Zhang W., Hu P., Lai X., Peng L. Analysis and optimization of flow distribution in parallel-channel configurations for proton exchange membrane fuel cells. J. Power Sources. 2009;194:931–940. [Google Scholar]

[bib24] 24.Park J., Li X. Effect of flow and temperature distribution on the performance of a PEM fuel cell stack. J. Power Sources. 2006;162:444–459. [Google Scholar]

[bib25] 25.Pandiyan S., Elayaperumal A., Rajalakshmi N., Dhathathreyan K.S., Venkateshwaran N. Design and analysis of a proton exchange membrane fuel cells (PEMFC) Renew. Energy. 2013;49:161–165. [Google Scholar]

[bib26] 26.Chen C.-H., Jung S.-P., Yen S.-C. Flow distribution in the manifold of PEM fuel cell stack. J. Power Sources. 2007;173:249–263. [Google Scholar]

[bib27] 27.Dheeraj N.A., Rao S., Vas R.S., Rathnakar M. Fuel cell stack manifold optimization through modelling and simulation. Energy Power. 2016;6:15–21. [Google Scholar]

[bib28] 28.Imbrioscia G.M., Fasoli H.J. Simulation and study of proposed modifications over straight-parallel flow field design. Int. J. Hydrogen Energy. 2014;39:8861–8867. [Google Scholar]

[bib29] 29.Pistoresi C., Fan Y., Luo L. Numerical study on the improvement of flow distribution uniformity among parallel mini-channels. Chem Eng Process Process Intensif. 2015;95:63–71. [Google Scholar]

[bib30] 30.Tong J.C.K., Sparrow E.M., Abraham J.P. Geometric strategies for attainment of identical outflows through all of the exit ports of a distribution manifold in a manifold system. Appl. Therm. Eng. 2009;29:3552–3560. [Google Scholar]

[bib31] 31.Liu H., Li P. Maintaining equal operating conditions for all cells in a fuel cell stack using an external flow distributor. Int. J. Hydrogen Energy. 2013;38:3757–3766. [Google Scholar]

[bib32] 32.Wang J. Theory of flow distribution in manifolds. Chem. Eng. J. 2011;168:1331–1345. [Google Scholar]

[bib33] 33.Wei M., Fan Y., Luo L., Flamant G. CFD-based evolutionary algorithm for the realization of target fluid flow distribution among parallel channels. Chem. Eng. Res. Des. 2015;100:341–352. [Google Scholar]

[bib34] 34.Luo L., Wei M., Fan Y., Flamant G. Heuristic shape optimization of baffled fluid distributor for uniform flow distribution. Chem. Eng. Sci. 2015;123:542–556. [Google Scholar]

[bib35] 35.Pistoresi C., Fan Y., Aubril J., Luo L. Fluid flow characteristics of a multi-scale fluidic network. Chem Eng Process Process Intensif. 2018;123:67–81. [Google Scholar]

[bib36] 36.Palaniappan K., Govindarasu R., Parthiban R. Investigation of flow mal-distribution in proton exchange membrane fuel cell stack. Int. J. Renew. Energy Resour. 2012;2:4–8. [Google Scholar]

PERMALINK

Numerical analysis of flow distribution behavior in a proton exchange membrane fuel cell

BH Lim

EH Majlan

WRW Daud

MI Rosli

T Husaini

Abstract

1. Introduction

2. Design