Abstract
This paper estimates returns to education using a dynamic model of educational choice that synthesizes approaches in the structural dynamic discrete choice literature with approaches used in the reduced form treatment effect literature. It is an empirically robust middle ground between the two approaches which estimates economically interpretable and policy-relevant dynamic treatment effects that account for heterogeneity in cognitive and non-cognitive skills and the continuation values of educational choices. Graduating college is not a wise choice for all. Ability bias is a major component of observed educational differentials. For some, there are substantial causal effects of education at all stages of schooling.
Keywords: education, earnings, health, rates of return, causal effects of education, cognitive skills, non-cognitive skills
1 Introduction
In his pioneering analysis of human capital, Gary Becker (1962; 1964) emphasized the importance of the rate of return for evaluating the effectiveness of human capital investments. He launched an active industry estimating returns to schooling.1
At the time Becker crafted his analysis, modern economic dynamics was in its infancy, as was research on the economics of uncertainty in dynamic sequential models. In an early contribution, Burton Weisbrod (1962) noted that each year of schooling attained opened up options for additional schooling and training and provided opportunities for learning about personal abilities and life opportunities.2
A parallel development in empirical economics was the growing awareness of heterogeneity and diversity among individual cognitive and non-cognitive abilities.3 Agents differ in their returns to schooling. Failure to account for this heterogeneity leads to confusion in interpreting estimated effects of schooling.
Becker’s early work focused on internal rates of return that equated ex post discounted values of earnings streams net of monetary and psychic costs at different levels of education. He noted that the full return to schooling includes non-market benefits and non-pecuniary costs. In modern parlance, individuals should continue their schooling as long as their ex ante marginal return exceeds their ex ante marginal opportunity cost of funds.
Formidable empirical challenges arise in estimating ex post internal rates of return: lifetime earnings profiles are required; observed earnings profiles are subject to the selection bias that arises from the fact that earnings are observed only at schooling levels selected by agents; and quantifying non-market benefits and non-pecuniary costs is a difficult task. For estimating ex ante returns, information on how agents forecast future events is also required.
In a neglected paper, Becker and Chiswick (1966) developed a tractable framework for measuring ex post returns to schooling that utilizes cross-section synthetic cohort data on earnings to approximate life cycle earnings data.4 Mincer (1974) improved on this model by adding work experience. The “Mincer Equation” has become the workhorse of the empirical literature on estimating ex post rates of return:
| (1) |
where Y(Si, Xi) is the earnings of individual i with Si years of schooling and a vector of other determinants Xi.
This equation is interpreted as a causal relationship generated by hypothetical variations of each of γi, ρi, and ϕ(Xi), holding other components on the right-hand side of (1) fixed.5 γi is what person i would earn independent of any influence of schooling Xi. Correlation between γi and Si is the source of “ability bias” (Griliches, 1977). Strictly speaking, γi may or may not be related to ability. It is a determinant of earnings that may also be correlated with Si. ρi is the “return to a unit of schooling” for person i and is allowed to vary among individuals. It is a causal parameter realized by acquiring one more unit of schooling. There are both ex ante and ex post definitions of γi and ρi. The early literature and most of the empirical literature today focuses on estimating ex post returns.
This paper examines the economic foundations of Equation (1) and its generalizations accounting for the dynamics of educational decision-making and multidimensional heterogeneity in abilities among agents. We develop and estimate an empirically robust dynamic discrete choice model that allows for agent fallibility arising from imperfect information and learning, as well as time inconsistency. We allow agents to make schooling decisions based on expected future values. We test and reject strong forms of forward-looking behavior, but nonetheless find that agents sort on ex post gains.
We develop and estimate a variety of economically motivated and policy-relevant treatment effects. For most of the outcomes studied in this paper, we find strong evidence of ability bias at all levels of education, where ability includes both cognitive and non-cognitive skills, but only find sorting on gains (a relationship between ρi and Si) at higher levels of schooling.
1.1 Interpreting Returns to Education
The Becker-Chiswick-Mincer Equation (1), and variants of it, have become the standard framework for estimating ex post returns to schooling for a variety of outcomes.6 While ρi is not, in general, an internal rate of return for individual i, it is the ex post causal effect of increasing final schooling by exactly one year from any base state of schooling, holding γi and Xi fixed.7 It is the slope of an hedonic wage function—the derivative of the aggregate production function evaluated at S = s for a fixed γi and Xi.
ρi ignores the continuation values arising from the dynamic sequential nature of the schooling decision where information is updated and schooling at one stage opens up options for schooling at later stages. More generally, for a person at s − 1, the perceived ex ante gain in log earnings of moving to schooling level s is the anticipated direct effect ρi and the (undiscounted) perceived continuation value of schooling for person i:
| (2) |
Under an ex ante interpretation, Ps,l,i is the agent’s perceived probability of attaining (at least) schooling level S = l for a person starting at schooling level s, including any relevant discounting of future benefits; s̄ is the highest attainable value of S. Rs,i captures Weisbrod’s notion of valuing the future options that attaining schooling level s opens up.8 It is the individual causal effect of an extra year of schooling inclusive of continuation values. As long as ρi ≠ 0, it is distinct from Rs,i. One can define different versions of Rs,i depending on how Ps,l,i and ρi are specified.
Determining (2) poses major empirical challenges. There are multiple sources of heterogeneity in Rs,i. Individuals may differ in their values of ρi. Even if all people have the same ρi, they may differ in their expected anticipated probabilities of attaining schooling level s′ (Ps,s′,i, s′ > s).9
The causal effects ρi and Rs,i are formulated at the individual level. The modern treatment effect literature defines versions of these parameters for different groups and typically estimates ex post effects.10 Thus, one can define the mean causal effect for the whole population E(ρ).11 Another possible causal effect is E(Rs) defined for schooling level s for the entire population. One could also define the direct return to schooling for those who choose to be at a given level of schooling E(ρ|S = s). This is the causal effect of one more unit of schooling for those who stop at S = s. One can define causal parameters for samples defined by other choices (e.g., for those indifferent between s and s′; for those who would stop at s − 1; etc.), and for different notions of returns, e.g., E(R|S = s).
E(γ|S = s) is the population mean γ arising solely from statistical dependence between γ and S. It has no causal basis and is the source of ability bias. Since dependence between γ and S may arise from multiple sources, we refer to “ability bias” as selection bias throughout much of this paper.
The early literature adopted a simple approach to identifying returns. It assumed that ρi is identical for persons with the same observed characteristics. In this case, the only source of bias in estimating (1) is the statistical dependence between γi and Si (selection bias). The recent literature recognizes heterogeneity in both γi and ρi. Both may be statistically dependent on Si, giving rise to both selection bias and sorting on gains. The latter arises because the causal effect of S may be moderated by other variables. Whether or not sorting gains are a source of bias depends on the question being addressed.
To illustrate the importance of accounting for continuation values, consider a compulsory schooling policy that forces all persons to take a minimum level of schooling (S ≥ s). What causal effect is identified by this “natural experiment?” Abstracting from general equilibrium effects, any estimated treatment effect is defined conditional on the set of people who change their schooling from below s to at or above s. However, there is no presumption that such agents will stop at s if they are forced to attain it. They may learn things about themselves and their possibilities, so they continue beyond s and thereby generate continuation values.12 Thus, an experiment that evaluates the effects of this policy does not, in general, estimate E(ρ) or even E(ρ|S = s). It does not, in general, estimate the marginal effect of a change in S on the log marginal price of schooling.
The analysis just presented can be generalized to incorporate non-linear structural (causal) returns to schooling by allowing the ρi to depend on the origin and destination schooling states (ρs,s′,i) for s′ > s. Non-linearities associated with sheepskin effects associated with graduation are a potentially important source of continuation values.
1.2 Approaches to Identifying Causal Effects and Causal Rates of Return
Two general approaches have been developed to estimate returns to schooling in the general case. They are: (i) structural models that jointly analyze outcomes and schooling choices; and (ii) treatment effect models that use instrumental variables methods (including randomization and regression discontinuities as instruments) as well as matching on observed variables to identify causal parameters.13
The structural approach explicitly models agent decision rules that generate Ps,l,i and the dependence between ρi and Si. The modern version explicitly models agent expectations and distinguishes ex ante from ex post returns.14 It uses a variety of sources of identification, including exclusion restrictions (instrumental variables), conditional independence assumptions about unobservables, and functional form assumptions (see, e.g., Blevins, 2014). Among other features, the structural approach identifies causal effects at well-defined margins of choice and can evaluate the impacts of different policies never previously implemented.15
The treatment effect approach is typically agnostic about agent decision rules and relies on exclusion restrictions to identify its estimands. It rarely distinguishes ex ante from ex post returns.16 This approach is more transparent in securing identification than the structural approach.17 However, the economic interpretation of its estimated parameters is often quite obscure. In a model with multiple levels of schooling, LATE typically does not identify returns at the various margins of choice that generate outcomes or the sub-populations (defined in terms of observables and unobservables) affected by the instruments used.18 Its estimands do not identify a variety of well-posed policy questions except when the variation induced by the instruments corresponds closely to the variations induced by the policies of interest.19
We build on the analyses of Heckman and Vytlacil (1999, 2005, 2007a,b), Carneiro et al. (2010, 2011), and Eisenhauer et al. (2015b), who introduce choice theory into the modern analysis of instrumental variables. They focus on binary choice models but also analyze ordered and unordered choice models with multiple outcomes to estimate economically interpretable treatment effects. Expanding on that body of research, we consider multiple sources of identification besides instrumental variables. We do not rely on continuous instruments. In addition, we link our analysis to the dynamic discrete choice literature.
1.3 Our Approach
This paper develops a methodological middle ground between the reduced form treatment approach and the fully structural dynamic discrete choice approach. As in the structural literature, we estimate causal effects at clearly identified margins of choice. Our methodology identifies which agents are affected by instruments as well as which persons would be affected by alternative policies not previously implemented. As in the treatment effect literature, we are agnostic about the precise rules used by agents to make decisions. Unlike that literature, we recognize the possibility that people make decisions and account for the consequences of their choices. We approximate agent decision rules and do not impose the cross-equation restrictions that are the hallmark of the structural approach, nor do we explicitly model agent expectations about costs and returns.20
Using a generalized Roy framework, we estimate a multistage sequential model of educational choices and their consequences. An important feature of our model is that educational choices at one stage open up educational options at later stages. Each educational decision is characterized using a flexible discrete choice model. The anticipated consequences of future choices and their costs can be assessed in a variety of ways by individuals in deciding whether or not to continue their schooling. Our model approximates a dynamic discrete choice model without taking a stance on exactly what agents are maximizing or their information sets.
Like structural models, our model is identified though multiple sources of variation. Drawing from the matching literature, we identify the causal effects of schooling at different stages of the life cycle by using a rich set of observed variables and by proxying unobserved endowments. Unlike previous work on matching, we correct the match variables for measurement error and the bias introduced into the measurements by family background. We also use exclusion restrictions to identify our model as in the IV and control function literatures. Unlike many structural papers, we provide explicit proofs of model identification.21
Our framework allows agents to make ex ante valuations as in dynamic discrete choice models but does not explicitly identify them.22 However, we estimate a variety of ex post returns to schooling, and model how they depend on both observed and unobserved variables. We decompose ex post treatment effects into (i) the direct benefits of going from one level of schooling to the next;23 and (ii) continuation values arising from access to additional education beyond the next step.
Estimating our model on NLSY79 data, we investigate foundational issues in human capital theory. We report the following findings.
There are substantial returns/causal effects of education on wages, the present value of wages, health, and smoking.24
The continuation values arising from sequential choices are empirically important components of returns to education. Low-ability individuals gain mostly from graduating high school and stopping there. High-ability individuals have substantial post-high school continuation values.
Estimated returns (causal effects) differ by schooling level and depend on observed and unobserved characteristics of individuals. Graduating high school benefits all—and especially low-ability persons. Only high-ability individuals receive substantial benefits from college graduation. There is positive sorting on gains only at higher educational levels.
People sort on ex post gains, especially more able people at higher schooling levels, confirming a core tenet of human capital theory. Yet, at the same time, people do not know or act on publicly available information when making decisions about high school graduation.
This paper contributes to an emerging literature on the importance of both cognitive and non-cognitive abilities in shaping life outcomes.25 Consistent with the recent literature, we find that both types of abilities are important predictors of educational attainment. Within schooling levels, cognitive and non-cognitive abilities have impacts on most outcomes.26
Selection bias arising from both observed and unobserved variables accounts for a substantial portion (typically over one half) of the observed differences in wage outcomes classified by education. This finding runs counter to a common interpretation in the literature based on comparing IV and OLS estimates of Equation (1).27
Using our estimated model, we conduct two policy experiments. In the first, we examine the impact of a tuition subsidy on college enrollment. We identify who is affected by the policy, how their decisions change, and how much they benefit. Those induced to enroll benefit from the policy, and many go on to graduate from college. In a second experiment, we analyze a policy that improves the ability endowments of those at the bottom of the distribution to see how this impacts educational choices and outcomes. Such improvements are produced by early intervention programs.28 Increasing cognitive endowments positively impacts all outcomes, while increasing non-cognitive endowments mostly impacts smoking and health outcomes.
Our paper proceeds in the following way. Section 2 presents our model. Section 3 presents economically interpretable treatment effects (rates of return) that can be derived from it. Section 4 discusses identification. Section 5 discusses the data analyzed and presents unadjusted associations and regression-adjusted associations between different levels of education and the outcomes analyzed in this paper. Section 6 reports our estimated treatment effects and interprets them. Section 7 uses the estimated model to address two policy-relevant questions. Section 8 tests a key identifying assumption. Section 9 compares our estimates to those derived from alternative methodological approaches such as OLS and matching. Section 10 concludes.
2 Model
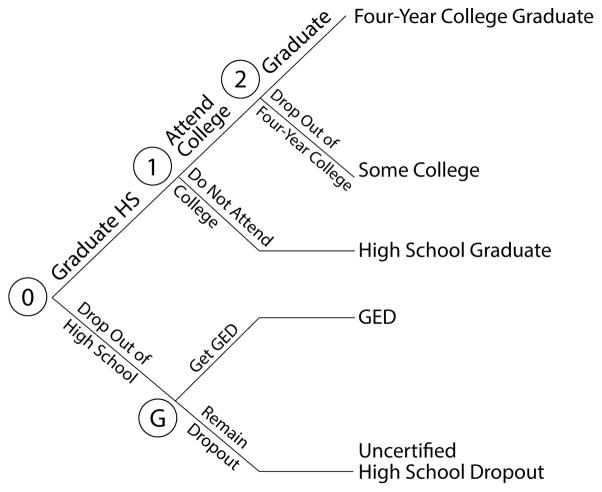
This paper estimates a multistage sequential model of educational choices with transitions and decision nodes shown in Figure 1. Let 𝒥 denote a set of possible terminal states. At each node there are only two possible choices: remain at j or transit to the next node (j + 1 if j ∈ {1, …, s̄ − 1}). Dj = 0 if a person at j does not stop there and goes on to the next node. Dj = 1 if the person stops at j for j ≠ 0. D0 = 1 opens an additional branch of the decision tree. A person may remain a dropout or get the GED.29 For D0 = 1, we define the attainable set as {0, G}. Thus, in the lower branch (D0 = 1), agents can terminate as a dropout (D0 = 1, DG = 1) or as a dropout who gets a GED certificate (D0 = 1, DG = 0). Dj ∈ 𝒟 is the set of possible transition decisions that can be taken by the individual over the decision horizon. Let 𝒮 = {G, 0, …, s̄} denote the set of stopping states with S = s if the agent stops at s ∈ 𝒮(Ds = 1 for s ∈ 𝒮\{0, G}). Define s̄ as the highest attainable element in 𝒮 in the ordered subset {0, …, s̄}. We assume that the environment is time-stationary and decisions are irreversible.30
Figure 1.
A Multistage Dynamic Decision Model
Qj = 1 indicates that an agent gets to decision node j and acquires at least the education associated with j. Qj = 0 if the person never gets there. QG = 1 if the agent drops out of high school and faces the GED option. The history of nodes visited by an agent can be described by the collection of the Qj such that Qj = 1. Observe that Ds = 1 is equivalent to S = s for s ∈ {1, …, s̄} and Ds̄ = 1 if Dj = 0, ∀j ∈ 𝒮\{s̄}.31 Finally, D0 = 1 and DG = 0 is equivalent to S = G.
2.1 A Sequential Decision Model
The decision process at each node is assumed to be characterized by an index threshold-crossing property:
| (3) |
where Ij is the agent’s perceived value at node j of going on to the next node. The requirement Qj = 1 ensures that agents are able to make the transition at j by conditioning on the population eligible to make the transition.
Associated with each final state s ∈ 𝒮 is a set of Ks potential outcomes for each agent with indices k ∈ 𝒦s. We define the as latent variables that map into potential outcomes :
| (4) |
The outcome variables may be in levels, logs, or other transformations. Using the switching regression framework of Quandt (1958, 1972), the observed outcome Yk for a k common across all decision nodes is
| (5) |
2.2 Parameterizations of the Decision Rules and Potential Outcomes for Final States
Following a well-established tradition in the treatment effect and structural literatures, we approximate Ij using a separable model:
| (6) |
where Z is a vector of variables observed by the analyst, components of which determine the transition decisions of the agent at different stages, and ηj is unobserved by the analyst. A separable representation of the choice rule is an essential feature of LATE (Vytlacil, 2002) and is often invoked in dynamic discrete choice models (Blevins, 2014).
This specification of agent decision-making is quite agnostic. It does not impose forward-looking behavior. Agents may be myopic or time-inconsistent and may be confronted by surprises. Because we do not impose particular expectation formation assumptions, we are not tied to a particular set of assumptions about agent rationality. A drawback of this approach is that we cannot identify ex ante versions of the economic parameters we estimate.
Outcomes are also assumed to be separable:
| (7) |
where X is a vector of observed determinants of outcomes and is unobserved by the analyst.32 Separability of the unobserved variables in the outcome equations is often invoked in the structural literature but is not strictly required in the structural or discrete choice literatures.33
2.3 Assumptions about the Unobservables
Central to our main empirical strategy is the existence of a finite dimensional vector θ of unobserved (by the economist) endowments that generate all of the dependence across the ηj and the . We assume that
| (8) |
and
| (9) |
where νj is an idiosyncratic error term for transition j. represents an idiosyncratic error term for outcome k in state s.
Conditional on θ, X, Z, choices and outcomes are statistically independent. Controlling for this set of variables eliminates selection effects. If the analyst knew θ, X, Z, he/she could use matching to identify the model.34
The standard “random effects” approach in the structural literature treats θ as a nuisance variable and does not interpret it.35 Our approach is to proxy θ using multiple interpretable measurements of it. We correct for errors in the proxy variables. The measurements facilitate the interpretation of θ. We develop this intuition further in Section 4, after presenting the rest of our model.
We array the νj, j ∈ 𝒥 into a vector ν = (νG, ν0, ν1, …, νs̄−1), and the ηj into η = (ηG, η0, …, ηs̄−1). Array the into a vector . Array the into vector , and array the Us into U = (UG, U0, …, Us̄).
Letting “⫫” denote statistical independence, we assume that, conditional on X
| (A-1a) |
| (A-1b) |
| (A-1c) |
| (A-1d) |
| (A-1e) |
Assumption (A-1a) maintains independence of the shocks affecting transitions; (A-1b) assumes independence of shocks across all states; (A-1c) assumes independence of the shocks to transitions and the outcomes; (A-1d) assumes independence of θ with respect to the observables; and (A-1e) assumes independence of the shocks with the factors θ and Z. Versions of assumptions (A-1d) and (A-1e) play fundamental roles in the structural dynamic discrete choice literature.36 Any dependence postulated across the ω and ν can be captured by introducing factors in θ.
2.4 Measurement System for Unobserved Factors θ
We allow for the possibility that θ cannot be measured precisely, but that it can be proxied with multiple measurements. We correct for the effects of measurement error in the proxy. We link θ to measurements, and adjoin measurement equations to choice and outcome equations, making θ interpretable.
Let M be a vector of NM measurements on θ. They may consist of lagged or future values of the outcome variables or additional measurements.37 The system of equations determining M is
| (10) |
where X are observed variables, θ are the factors, and
where we array the ej into e = (e1, …, eNM). We assume, in addition to the previous assumptions that, conditional on X,
| (A-1f) |
| (A-1g) |
For the purpose of identifying treatment effects, we do not need to identify each equation of system (10). We just need to identify the span of θ that preserves the information on θ in (10). That is sufficient to produce conditional independence between choices and outcomes.38 However, in this paper we estimate equation system (10) to enhance interpretability.
3 Defining Returns/Causal Effects of Education
A variety of ex post counterfactual outcomes and associated treatment effects can be generated from our model. There is no single “causal effect” of education. The causal effects we analyze can be used to predict the effects of changing education levels through different policies for people of different backgrounds and abilities. They allow us to improve on the “effects” reported in the literature on instrumental variables to understand the effectiveness of policies for different identifiable segments of the population, and the benefits to people at different margins of choice. These effects are defined for different conditioning sets and thought experiments. Our dynamic model suggests a new range of treatment parameters that do not arise in models with binary treatments. This section makes precise the notions of returns to education discussed in Section 1.
In principle, we could define and estimate a variety of causal effects, many of which are not plausible. For example, many empirical economists would not find estimates of the effect of fixing (manipulating) Dj = 0 if Qj = 0 to be credible (i.e., the person for whom we fix Dj = 0 is not at the decision node to take the transition).39 In the spirit of credible econometrics, we define such treatment effects conditional on Qj = 1. This approach blends structural and treatment effect approaches. Our causal parameters recognize agent heterogeneity and are allowed to differ across different subsets of the population.
The person-specific treatment effect for outcome k for an individual selected from the population Qj = 1 with characteristics X = x, Z = z, θ = θ̄, making a decision at node j between going on to the next node or stopping at j, is the difference between the individual’s outcomes under the two actions:
| (11) |
The random variable (Yk|X = x, Z = z, θ = θ̄, Qj = 1, Fix Dj = 0) is the outcome at node j for a person with characteristics X = x, Z = z, θ = θ̄ from the population that attains node j (or higher), Qj = 1, and for whom we fix Dj = 0 so they go on to the next node. They may choose to go even further. Random variable (Yk|X = x, Z = z, θ = θ̄, Qj = 1, Fix Dj = 1) is defined for the same population but forces persons with those characteristics not to transit to the next node.
We present population-level treatment effects based on (11). We focus our discussion on means, but we also discuss distributional counterparts for all of the treatment effects considered in this paper.
3.1 Direct Effects and Continuation Values
A principal contribution of this paper is the definition and estimation of treatment effects that take into account the direct effect of moving to the next node of a decision tree, plus the benefits associated with the further schooling that such movement opens up. The associated mean treatment effect is the difference in expected outcomes arising from changing a single educational decision in a sequential schooling model and tracing through its consequences, accounting for the dynamic sequential nature of schooling.
Person-specific treatment effects at node j can be decomposed into two components. The first component is the direct effect of going from j to , the effect often featured in the literature on the returns to schooling when comparing schooling levels j + 1 and j (Becker, 1964). The second component is the continuation value of going beyond j + 1 for persons with D0 = 0 (the upper branch of Figure 1), which is
| 40 |
The continuation value for the lower branch of Figure 1 (D0 = 1) is defined for the attainable set {0, G}. G is the only option available to a high school dropout in that branch. In the following, we analyze the upper branch of Figure 1. The analysis for the lower branch is similar.
At the individual level, the total effect of fixing Dj = 0 on Yk is decomposed into
| (12) |
The associated population level average treatment effect at node j inclusive of continuation values, conditional on Qj = 1, is
| (13) |
which can be decomposed into direct and continuation value components.
Integrating over the X, Z, θ, conditioning on Qj = 1, the component of (13) due to the population continuation value at j + 1 is
| (14) |
where Qs̄ = 1 if S = s̄.
We can also define conditional (on X, Z, θ) population distributions of total effects as in Heckman et al. (1997):41
| (15) |
and the population counterpart, integrating over X, Z, θ, which can be further decomposed into the distributions of direct effects and of continuation values.42
Because we do not specify or attempt to identify choice-node-specific agent information sets, we can only identify ex post treatment effects. Hence, we can identify continuation values associated with choices, but cannot identify option values. A benefit of this more agnostic approach is that it does not impose specific decision rules or assumptions about agent expectations. Our model allows for irrationality, regret, and mistakes in agent decision-making associated with maturation and information acquisition and allows us to test the validity of certain assumptions commonly made about agent expectations.
3.2 Average Marginal Treatment Effects
In order to understand the economic returns to an additional unit of schooling for persons at the margin of indifference at each node of the decision tree of Figure 1, we estimate the Average Marginal Treatment Effect (AMTE).43 It is the average effect of transiting to the next node for individuals at or near the margin of indifference between the two nodes:
| (16) |
where ε is an arbitrarily small neighborhood around the margin of indifference.44 These effects are inclusive of all consequences of taking the transition at j, including the possibility of attaining final schooling levels well beyond j.45 AMTE defines causal effects at well-defined and empirically identified margins of choice. It is the proper measure of the ex post marginal gross benefit for evaluating the gains from moving from one stage of the decision tree to the next for those at that margin of choice. In general, it is distinct from LATE, which is not defined for any specific margin of choice, and generally does not estimate E(ρ) or E(ρ|S = s), and includes the effects on outcomes for transitions induced by instruments beyond any schooling level at which the instrument operates.46 Since we identify the distribution of Ij, we can identify the characteristics of agents in the indifference set, something not possible using LATE.47
The population distribution counterpart of AMTE is defined over the set of agents for whom |Ij| ≤ ε, which can be generated from our model: . Distributional versions can be defined for all of the treatment effects considered in this section.
3.3 Policy-Relevant Treatment Effects
The policy-relevant treatment effect (PRTE) is the average treatment effect for those induced to change their choices in response to a particular policy intervention. Let Yk(p) be the aggregate outcome under policy p for outcome k. Let S(p) be the final state selected by an agent under policy p. The policy-relevant treatment effect from implementing policy p compared to policy p′ for outcome k is:
| (17) |
where S(p) ≠ S(p′) denotes the set of the characteristics of people for whom attained states differ under the two policies. In general, it is different from AMTE because the agents affected by a policy can be at multiple margins of choice. PRTE is often confused with LATE. In general, they are different unless the proposed policy change coincides with the instrument used to define LATE.48
3.4 Differences Across Final Schooling Levels
Becker’s original approach to estimating returns to schooling (1964) focused on the upper branch of Figure 1 and reported estimates from pairwise comparisons of returns at final schooling levels. He defines returns to education as the gains from choosing between a terminal base state and a terminal final schooling level, implicitly assuming that the probabilities of all intervening transitions in Equation (2) are 1. Following Becker, but controlling for θ, Z, and X, the mean gain for the subset of the population that completes one of the two adjacent schooling level S ∈ {s, s′} is:
| (18) |
Unlike (13), this parameter ignores continuation values.
Conditioning in this fashion recognizes that the characteristics of people not making either final choice could be far away from the population making one of those two choices, and hence, might be far away from having any empirical or policy relevance.49 One can also compute parameters of ATEs,s′ for other conditioning sets, such as S = s′ (treatment on the treated). We report estimates of different versions of these treatment effects in the Web Appendix A.14.1.
3.5 Decomposing Observed Differences in Outcomes into Selection Bias, Sorting Gains, and Average Treatment Effects
Using our model, we interpret “ability bias” (really selection bias) and sorting on gains using the traditional Becker-Chiswick-Mincer model (1) and its extensions as a benchmark. To simplify the exposition, we focus on the upper branch of Figure 1 (D0 = 0) and analyze continuous outcomes.50
There are two basic models used in the empirical literature estimating returns to schooling. One version studies outcomes and selection bias in terms of pairwise final schooling levels (s0, s) attained by agents (Ds0 + Ds = 1), s0 ≠ s. It is defined for the population at one of these two terminal schooling states. It does not include terminal values beyond s. Another version studies gains and ability bias in terms of benefits associated with attaining (and possibly exceeding) given schooling levels (Qj = 1). This includes continuation values. In the text, we develop both widely-used versions.
The effect of additional schooling starting at s0 and stopping at s is captured by .51 This is the direct gain of going from s0 to s. It does not include any gains from transitions beyond s:
In this notation we may write the outcome Yk relative to base state as
| (19) |
This is a version of (1) where schooling is discretized at final schooling attainment levels: S = s if Ds = 1. is one version of the returns to schooling compared to benchmark s0 defined for the entire population.
Except for knife-edge cases, if λs ≠ 0, dependence between Ds and is generated if either , or , or both.52 Sorting on gains (correlation between and Ds) may not appear in empirical estimates if agents are sorting on gains beyond s and not on direct effects (i.e., sorting on components of Rs,i as defined in (2)). Only in the case where there is no continuation value can we conclude from empirical estimates that absence of sorting effects defined in this fashion implies absence of sorting on potential future gains.
The traditional Griliches (1977) analysis of returns to schooling ignores sorting on gains and only considers ability bias. Assuming analysts condition on X (in levels and in interactions with Ds), sorting gains arise only if and λs ≠ 0. Even if , as long as , ability bias will arise in estimating the mean of the gains in (19), provided λs ≠ 0.53
Note that the choice of a base state matters for estimating sorting gains in the general case where the magnitude of changes depending on the base state selected. Some representations may generate sorting gains that are absent from other representations with different base states.54
Within this framework, there are several meaningful ways to decompose the observed difference in outcomes between those at j who go on to S = j + 1. The observed difference can be decomposed as follows:
| 55 | (20) |
Note that the ATE parameter depends on the distributions of characteristics of X and θ for persons at node j, as do the sorting on gains and selection bias parameters. These components can be further decomposed into selection on observed variables and selection on unobserved ability components θ, and the ability components can be further decomposed into cognitive and non-cognitive components.
These decompositions focus on gains up to final schooling states. They compare observed differences across pairs of final schooling levels. The empirical literature on the returns to schooling also compares the observed differences in outcomes between persons at a given node (Qj = 1) who make a particular schooling transition with those who do not make that transition.
Thus, we can decompose the observed gain from going to j + 1 from j for those at j (Qj = 1) into a gain for those who take the transition (Dj = 0) and a selection bias term (the difference in the mean outcomes between those who would have gone on (Dj = 0), but are stopped at j (Fix Dj = 1), and those who chose not to go on). We can further decompose the treatment on the treated parameter into a node-specific ATE (the mean difference between those for whom Qj = 1 where we fix Dj = 0 and we fix Dj = 1, respectively), and a “sorting gains” term which is the difference between the node-specific treatment on the treated term and the node-specific ATE.
In Web Appendix A.15.3, we decompose the values of being at j into components associated with stopping at j and continuing beyond j where, for the upper branch of Figure 1 (D0 = 0),
| (21) |
where . The expected future gain for a person at j (≥ 1) is
where the conditioning D0 = 0 is kept implicit.56
Analogous to decomposition (20), we can decompose the observed difference between those with Dj = 0 and those with Dj = 1, i.e., the observed difference between those that do and do not make a particular transition conditional on making that transition. is the expected incremental gain of proceeding to the next stage. For the upper branch (D0 = 0), we may write for the kth outcome at node j:
| (22) |
The node-specific ATE is defined for the population at Qj = 1 and considers either forcing population members to stay at j, or moving the entire group from j to j + 1 (i.e, Fix Dj = 1 and Fix Dj = 0, respectively). The sorting gain is the average net gain beyond ATE to those who actually take the transition (Dj = 0).
4 Identification and Model Likelihood
The treatment effects defined in Section 3 can be identified using alternative empirical approaches. The main approach used in this paper exploits the fact that, conditional on θ, X, Z, outcomes and choices are statistically independent where X and Z are observed and θ is not. If θ were observed, one could condition on θ, X, Z and identify the model of Equations (3)–(9) and the treatment effects that can be generated from it. We use factor model (10) to proxy θ using measurements M.
Under the conditions presented in Heckman et al. (2016), we can non-parametrically identify the model of Equations (3)–(7) including the distribution of θ, as well as the Φ functions and the distribution of e (which can be interpreted as measurement errors). Effectively, we match on proxies for θ and correct for the effects of measurement error (e) in creating the proxies. Such corrections are possible because with multiple measures on θ we can identify the distribution of e.57 We can identify treatment effects even though we do not isolate individual factors. We only need that the factors θ are spanned by M, not that Equations (10) are separately identified.58
Another approach to identification uses instrumental variables which, if available, under the conditions presented in Heckman et al. (2016) can be used to identify the structural model (3)–(9) without invoking the factor structure (8) and (9) or the postulated conditional independence assumptions.
The precise parameterization and the likelihood function for the model we estimate is presented in Web Appendix A.4. While, in principle, it is possible to identify the model non-parametrically, in this paper we make parametric assumptions in order facilitate computation. We subject the estimated model to rigorous goodness-of-fit tests which the model passes.59
5 Our Data, A Benchmark OLS Analysis of the Outcomes We Study, and Our Exclusion Restrictions
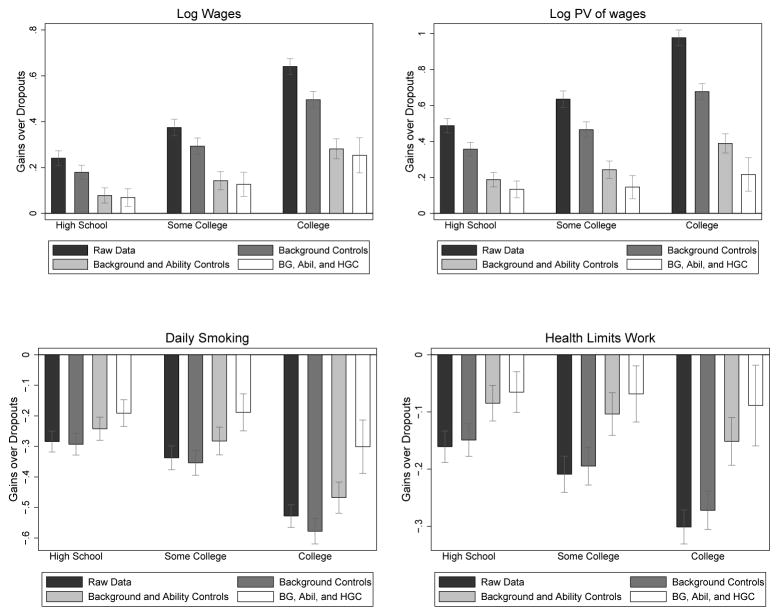
We estimate our model on a sample of males extracted from the widely-used National Longitudinal Sample of Youth (NLSY 79).60 Before discussing estimates from our model, it is informative to set the stage for what follows and present adjusted and unadjusted associations between the outcomes we study and schooling. Figure 2 presents estimated linear regression relationships between different levels of schooling relative to high school dropouts and the four outcomes analyzed in this paper: wages, log present value of wages (or PV of wages), health limitations, and smoking.61 These are least squares regressions using the regressors indicated at the base of the figure, including our proxies for ability. They do not separate out the roles of X and θ in contributing to the causal and selection bias components of the observed differences. Least squares estimates of this form are commonly reported in the literature that investigates the effects of schooling controlling for X, Z, θ.
Figure 2.
Observed and Adjusted Benefits from Education
Notes: The bars represent the coefficients from a regression of the designated outcome on dummy variables for educational attainment, where the omitted category is high school dropout. Regressions are run adding successive controls for background and proxies for ability. Background controls include race, age in 1979, region of residence in 1979, urban status in 1979, broken home status, number of siblings, mother’s education, father’s education, and family income in 1979. Proxies for ability are average score on the Armed Services Vocational Aptitude Battery (ASVAB) tests and ninth grade GPA in core subjects (language, math, science, and social science). See the discussion surrounding Table 1 (below) and Web Appendix A.2 for additional details. “Some College” includes anyone who enrolled in college, but did not receive a four-year college degree. The white bars additionally control for highest grade completed (HGC). Source: NLSY79 data.
The black bars in each panel show the unadjusted mean differences in outcomes for persons at the indicated levels of educational attainment compared to those for high school dropouts. Higher ability is associated with higher earnings and more schooling. However, as shown by the grey bars in Figure 2, adjusting for family background and adolescent measures of ability attenuates, but does not eliminate, the estimated least squares estimates of the effects of education.
Figure 2 shows that controlling for proxied ability substantially reduces the observed differences in earnings across educational groups. These regression estimates suggest, but do not identify, substantial causal effects which we report below.
Entering θ as a regressor is a traditional way to control for ability bias. It eliminates the ability bias emphasized by Griliches (1977). If there is sorting on gains that depend on X and θ, this approach over-controls for those variables that are components of the causal effect of treatment on the treated as defined in (20).62 Figure 2 reports traditional measures of regression-adjusted causal effects of schooling. At the same time, such regressions do not discriminate among the components of (20) which have different causal interpretations. In Web Appendix A.17.2, we compare the OLS pairwise causal effects implicit in the estimates reported in Figure 2 with the estimates from our version of a structural model discussed below.63
It is sometimes claimed that a linear-in-years-of-schooling model fits the data well.64 The white bar in Figure 2 displays the OLS-adjusted effect of schooling controlling for years of completed schooling as in Equation (1).65 The white bars in all figures show that, even after controlling for years of schooling, the educational indicators still play an important role. OLS estimates of Mincer specification (1) do not precisely describe the data. There are effects of schooling beyond those captured by a linear years-of-schooling specification.66
5.1 Control Variables and Exclusion Restrictions
As previously noted, identification of our model and the associated treatment effects does not depend exclusively on conditional independence assumptions associated with our factor model.67 Node-specific instruments can non-parametrically identify treatment effects without invoking the full set of conditional independence assumptions.68 We have a variety of exclusion restrictions that affect choices but not outcomes. Table 1 documents the control variables (X) and the exclusion restrictions (components of Z not in X) used in this paper. Our instruments are traditional in the literature that estimates the causal effects of education.69
Table 1.
Control Variables and Instruments Used in the Analysis
| Control Variables | Measurement Equations | Choice | Outcomes |
|---|---|---|---|
| Race | x | x | x |
| Broken Home | x | x | x |
| Number of Siblings | x | x | x |
| Parents’ Education | x | x | x |
| Family Income (1979) | x | x | x |
| Region of Residencea | x | x | x |
| Urban Statusa | x | x | x |
| Ageb | x | x | x |
| Local Unemploymentc | x | ||
| Local Long-Run Unemployment | x | ||
|
| |||
| Instruments (Exclusion Restrictions) | |||
|
| |||
| Local Unemployment at Age 17d | x | ||
| Local Unemployment at Age 22e | x | ||
| College Present in County 1977f | x | ||
| Local College Tuition at Age 17g | x | ||
| Local College Tuition at Age 22h | x | ||
Notes:
Region and urban dummies are specific to the age that the measurement, educational choice, or outcome occurred.
Age in 1979 is included as a cohort control. We also included individual cohort dummies which did not change the results.
For economic outcomes, local unemployment at the time the outcome is measured.
This is an instrument for choices at nodes 0 and 1. It represents opportunity costs at the time schooling decisions are made.
This is an instrument for the choice at node 2.
Presence of a four-year college in the county in 1977 is constructed from Kling (2001) and enters the choice to enroll and the choice to graduate from college.
Local college tuition at age 17 only enters the college enrollment graduation decisions.
Local college tuition at age 22 only enters the college completion equation. The measurement system includes the arithmetic reasoning, coding speed, paragraph comprehension, word knowledge, mathematical knowledge, and numerical operations sub-tests of the ASVAB, 9th grade GPA in math, English, science, and social studies, and early risky and reckless behavior. We assume ASVAB only loads on the cognitive factor. See Web Appendix Section A.2 for details.
6 Estimated Causal Effects
In this section of the paper, we move beyond OLS analyses of causal effects of schooling and present the estimated causal effects of schooling from our model. Since the model is non-linear and multidimensional, in the main body of the paper we only report the treatment effects derived from it.70 We randomly draw sets of regressors from our sample and a vector of factors from the estimated factor distribution to simulate the reported treatment effects.71
Section 6.1 presents estimated treatment effects across final schooling levels. These are based on Equation (18) and extend Becker (1964) by controlling for observed and proxied unobserved variables. Section 6.2 presents the main empirical analysis of this paper. We estimate dynamic treatment effects, inclusive of continuation values. We analyze the contribution of continuation values, sorting on gains, and selection bias to measured differences in education across levels. Section 6.3 analyzes the effects of cognitive and non-cognitive endowments on estimated treatment effects. Section 6.4 presents estimates of distributions of treatment effects. Section 6.5 examines the implications of our analysis for the validity of the Becker-Chiswick-Mincer model. Section 6.6 summarizes our analysis. In the text of our paper, we focus on the transitions in the upper branch of Figure 1, although our model is estimated over both branches.
6.1 The Estimated Average Causal Effect of Educational Choices by Pairwise Final Schooling Levels
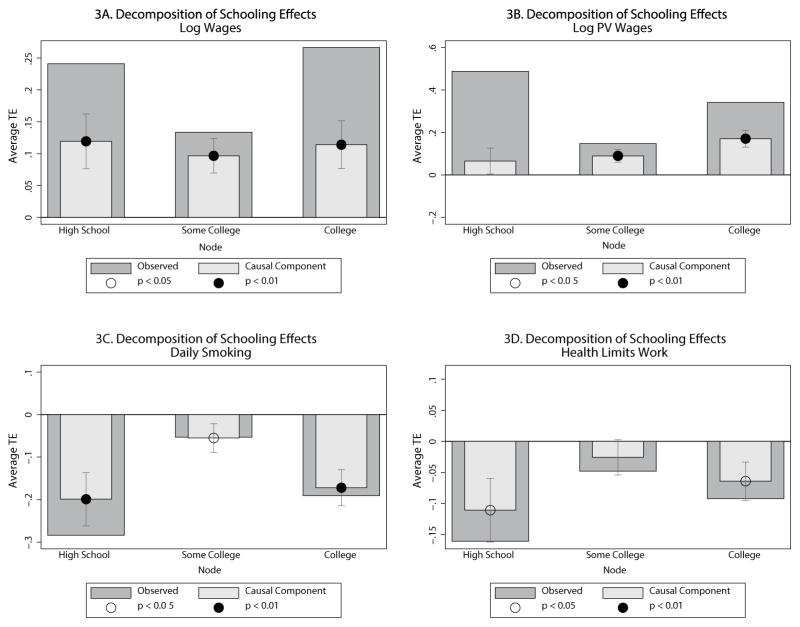
We first present estimates of average treatment effects ATEs−1,s (18) for the four outcomes studied in this paper at final schooling level s compared to final schooling level s−1.72 They ignore continuation values.
The shaded regions labeled “Observed” in Figure 3 are the raw differences found in our data. The estimated average causal effects (displayed in the light blocks) are large and statistically significant for all outcomes except for the log PV wages for graduating high school (compared to dropping out).73 For example, the leftmost bar in panel 3a can be interpreted as follows: while high school graduates make on average 24 log points higher wages than high school dropouts, we find that the average causal effect of graduating high school is on average 12 log points for the same population.
Figure 3.
Causal Versus Observed Differences by Final Schooling Level (compared to next lowest level)
Notes: These figures report pairwise treatment effect (18) for the indicated schooling nodes. Each bar compares the mean outcomes from a particular schooling level j and the next lowest level j−1 defined for the set of persons who complete schooling at j−1 or j. The “Observed” bar displays the observed differences in the data. The “Causal Component” bar displays the estimated average treatment effect to those who get treated (ATE) for the indicated group. The difference between the observed and causal treatment effect is attributed to the effect of selection and ability. Selection includes sorting on gains. The error bars and significance levels for the estimated ATE are calculated using 200 bootstrap samples. Error bars show one standard deviation and correspond to the 15.87th and 84.13th percentiles of the bootstrapped estimates, allowing for asymmetry. Significance at the 5% and 1% levels is shown by open and filled circles on the plots, respectively.
Web Appendix A.14.1 reports traditional treatment effects (treatment on the treated, treatment on the untreated, as well as the ATEs displayed in Figure 3). Web Appendix A.15.2 presents estimates of decomposition (20) for all four outcomes. The decompositions show substantial gains for high-ability persons who graduate college. A large component of the observed difference is properly attributed to selection bias for most outcomes.74
6.2 Dynamic Treatment Effects
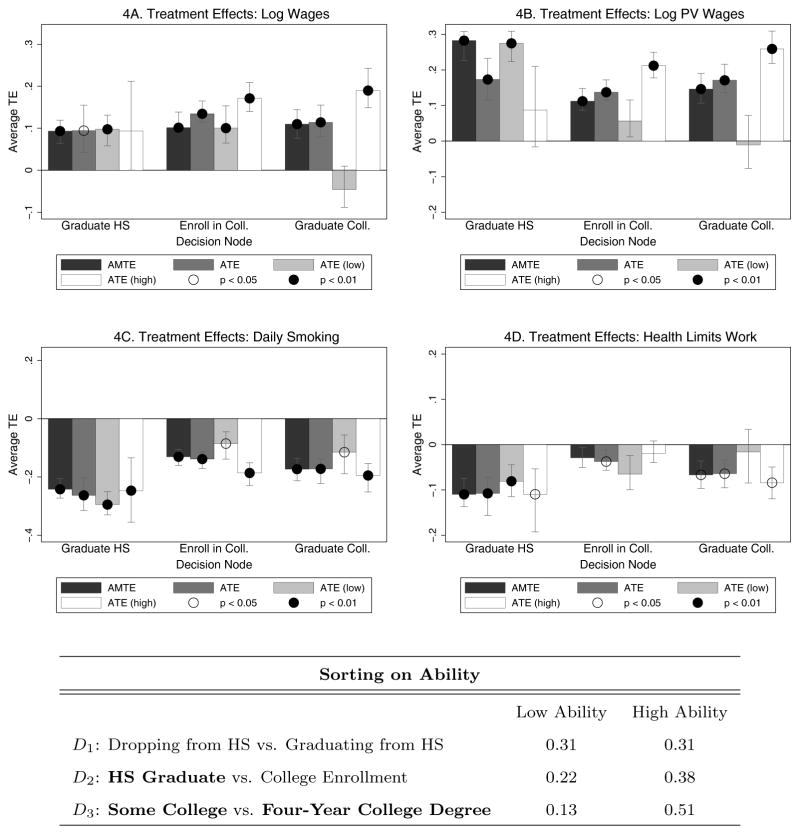
A major contribution of this paper is the estimation of dynamic treatment effects that include continuation values. These are defined for populations that achieve a node (Qj = 1) which includes people who might go beyond j and even j + 1. Specifically, we calculate the average gains to fixing Dj = 0 (and possibly going beyond j + 1) compared to those at j (Qj = 1) who stop at j (Dj = 1). See Equation (11) for the precise expression. Figure 4 plots these treatment effects by the level of educational decision faced by the agent. These treatment effects are also broken down into those for low-ability and high-ability populations using the ability categories defined at the base of the figure. The figure also reports AMTE for individuals at the margin of indifference at each transition.75
Figure 4.
Treatment Effects of Outcomes by Decision Node
E(Yk|Fix Dj = 0, Qj = 1) − E(Yk|Fix Dj = 1, Qj = 1)
Notes: The nodes in the table correspond to the next stage of the transition analyzed. Thus, “Graduate HS” refers to the decision node of whether or not the agent will graduate high school, and refers to the base state of not graduating high school. The error bars and significance levels for the estimated ATE Equation (13) are calculated using 200 bootstrap samples. Error bars show one standard deviation and correspond to the 15.87th and 84.13th percentiles of the bootstrapped estimates, allowing for asymmetry. Significance at the 5% and 1% level are shown by hollow and black circles on the plots, respectively. The figure reports various treatment effects for those who reach the decision node, including the estimated ATE conditional on endowment levels. The high- (low-) ability group is defined as those individuals with cognitive and socio-emotional endowments above (below) the median in the overall population. These categories are not mutually exclusive, as some people may be high-ability in one dimension but low-ability in another. The table below the figure shows the proportion of individuals at each decision (Qj = 1) that are high- and low-ability. The larger proportion of the individuals are high-ability and a smaller proportion are low-ability in later educational decisions. In this table, final schooling levels are highlighted using bold letters.
There are large and statistically significant average causal effects of education for all wage outcomes.76 Disaggregating by ability, the effects are strong for high-ability people who enroll in college. They are especially strong for those who graduate college. We find little to no evidence of any benefit of graduating college for low-ability individuals.77 In fact, the point estimates are negative, albeit imprecisely estimated. Although there are wage rate benefits to low-ability people for enrolling in college (Figure 4A), the benefits in terms of the log present value of wages are minimal. For these people, the wage benefits of attending college barely offset the lost work experience and earnings from attending school.
At all levels of education, the estimated AMTE is substantial: there are marginal benefits to additional education at every transition node for individuals at or near the margin of indifference for that transition. The marginal benefits are close to (but generally somewhat below) the average benefits. This is consistent with diminishing benefits of educational expansion.78 For people at all margins, there are benefits to taking the next transition that are especially pronounced for high school graduation. There are unrealized potential gains in the current system.
We probe more deeply in the Web Appendices. In A.14.2, we present a variety of treatment effects, including treatment on the treated (TT), treatment on the untreated (TUT), and the average treatment effect defined for the entire population, and not just for those at a particular node in our decision tree. This enables us to examine the extent of sorting on gains. In A.15.3, we go further and decompose observed differences in the data into average treatment effects, sorting gains, and selection bias (Equation (22)).
Broadly speaking, for wage outcomes we find sorting on gains for college graduation. This arises primarily from the gains to high-ability people documented in Figure 4. We find the reverse pattern for high school graduation: negative sorting for graduating high school that is especially pronounced for log present value of our earnings.79 Consistent with our analysis of AMTE, there are unrealized gains available in the system for a policy of promoting high school graduation for low-ability individuals. For all wage outcomes, there are substantial selection effects, ranging from 50–70% of the observed differences.
The story is different for the estimated educational causal effects on non-market outcomes. We first discuss smoking. There are strong average causal effects on reducing smoking. They are particularly strong for graduating high school for low-ability individuals. Nonetheless, there are substantial negative average causal effects from education on smoking for all nodes. There is little evidence of sorting on gains. Unlike the evidence for wages, there is substantially less evidence of selection bias at any transition.
The evidence for “Health Limits Work” indicates strongly beneficial causal effects for high school graduation, and weak—but generally precisely determined—causal effects for college graduation, which essentially vanish for low-ability persons. There is little evidence of causal effects of attending some college. There is no evidence of sorting on gains. Selection bias is a strong component of observed differences.
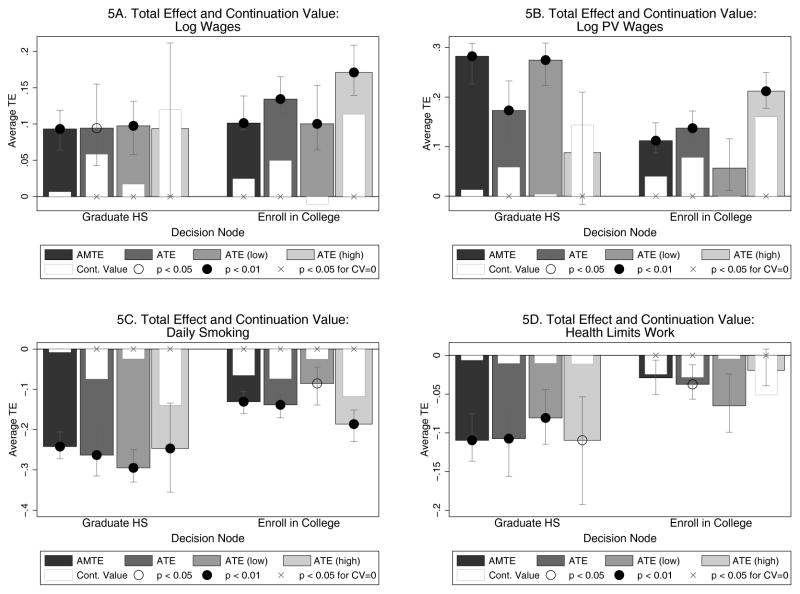
6.2.1 Continuation Values
We next decompose the node-specific average treatment effects, just discussed, into continuation value components. Figure 5 presents (in the white bars) the estimated continuation value components, while the bars behind the white boxes are the full treatment effects from Figure 4. We only display continuation values for nodes where these are possible.
Figure 5.
Dynamic Treatment Effects:
Continuation Values and Total Treatment Effects by Node
Notes: High-ability individuals are those in the top 50% of the distributions of both cognitive and socio-emotional endowments. Low-ability individuals are those in the bottom 50% of the distributions of both cognitive and socio-emotional endowments. The error bars and significance levels for the estimated ATE are calculated using 200 bootstrap samples. Error bars show one standard deviation and correspond to the 15.87th and 84.13th percentiles of the bootstrapped estimates, allowing for asymmetry. Significance at the 5% and 1% level are shown by hollow and black circles on the plots, respectively. Statistical significance for continuation values at the 5% level are shown by “x.” Section 3 provides details on how the continuation values and treatment effects are defined.
For all outcomes except “Health Limits Work,” there are large continuation values for high-ability individuals. While returns to high school are roughly the same across ability levels, the mechanisms producing these effects are different. The benefits for low-ability persons come through direct values. The benefits for high-ability persons come through continuation values. For most nodes and treatment effects, the continuation values are statistically significant as indicated by the “x” in Figure 5.80
6.3 The Effects on Cognitive and Non-Cognitive Endowments on Treatment Effects
Disaggregating the treatment effects for “high-” and “low-” endowment θ individuals in Figure 4 is a coarse approach. A byproduct of our analysis is that we can determine the contribution of cognitive and non-cognitive endowments (θ) to the explanation of estimated treatment effects. We can decompose the overall effects of θ into their contribution to the causal effects at each node and the contribution of endowments to attaining that node. We find substantial contributions of θ to each component at each node.
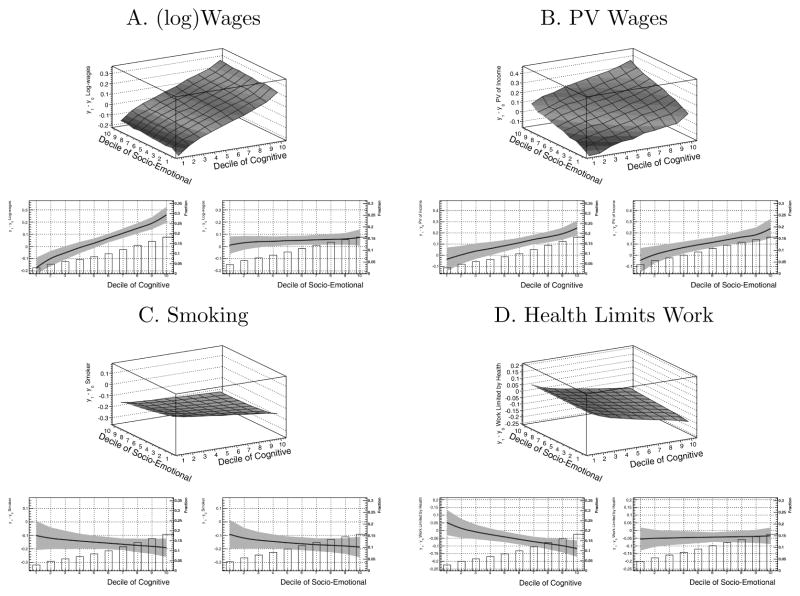
To illustrate, the panels in Figure 6 display the estimated average treatment effect of getting a four-year degree (compared to stopping with some college) for each decile pair of cognitive and non-cognitive endowments.81,82 Treatment effects, in general, depend on both measures of ability. Moreover, different outcomes depend on the two dimensions of ability in different ways. For example, the treatment effect of graduating college is increasing in both dimensions for the present values of wages, but the reductions in health limitations with education depend mostly on cognitive endowments.
Figure 6.
Average Treatment Effect of Graduating from a Four-Year College by Outcome
Notes: Each panel in this figure studies the average effects of graduating with a four-year college degree on the outcome of interest. The effect is defined as the differences in the outcome between those with a four-year college degree and those with some college. For each panel, let Ysome college and Yfour-year degree denote the outcomes associated with attaining some college and graduating with a four-year degree, respectively. For each outcome, the first figure (top) presents E(Yfour-year degree − Ysome college|dC, dSE) where dC and dSE denote the cognitive and socio-emotional deciles computed from the marginal distributions of cognitive and socio-emotional endowments. The second figure (bottom left) presents E(Yfour-year degree − Ysome college|dC) so that the socio-emotional factor is integrated out. The bars in this figure display, for a given decile of cognitive endowment, the fraction of individuals visiting the node leading to the educational decision involving graduating from a four-year college. The last figure (bottom right) presents E(Yfour-year degree − Ysome college|dSE) and the fraction of individuals visiting the node leading to the educational decision involving graduating from a four-year college for a given decile of socio-emotional endowment.
6.4 Distributions of Treatment Effects
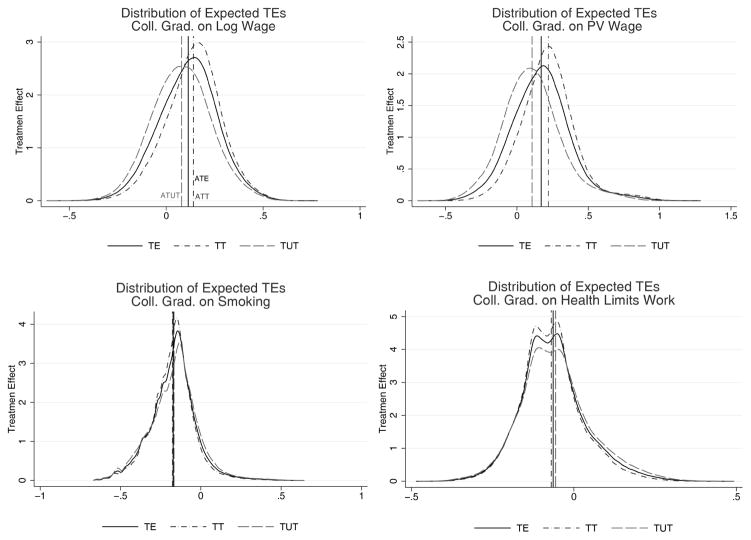
One benefit of our approach over the standard IV approach is that we can identify the distributions of expected treatment effects—a feature missing from the standard treatment effect literature. Figure 7 plots the distribution of gains for persons who graduate from college (compared to attending college but not attaining a four-year degree) along with the mean treatment effects.83
Figure 7.
Distributions of Expected Treatment Effects: College Graduation
Notes: Distributions of treatment effects including continuation values for those who reach the educational choice. The vertical lines represent the average treatment effects (ATE, ATT, and ATUT) for each of the distributions.
The graphs provide a nice summary of our main findings for all dynamic treatment effects for college graduation. There are strong causal effects for all outcomes. There is also substantial heterogeneity among persons. Sorting on gains is pronounced for wage outcomes but less so for health and smoking. This is consistent with the analysis in Appendix A.15.3, where we report estimates of sorting on gains.
A byproduct of our analysis is that we can test the rank-invariance of counterfactual outcomes across states. The assumption of rank invariance is the basis for the numerous analyses based on quantile treatment effects.85 It implies that the Spearman correlations are 1 across any pair of counterfactual states. In our simulations, we find that the Spearman correlations are large but are also not 1. They are between 0.70 and 0.85 for log wages, 0.60 and 0.90 for present value of wages, and notably smaller for smoking and health limitations.86 Rank invariance is an especially poor assumption for those outcomes.
6.5 Taking Stock of the Becker-Chiswick-Mincer Model
We have tested many features of the widely-used model of Equation (1) to determine its robustness. Some features of Mincer model (1) are broadly consistent with our estimated structural model. While OLS-regression-adjusted versions are not linear in years of schooling (see the evidence in Web Appendix A.8), our estimated ATEs are roughly consistent with linearity for most outcomes.
The correlation between ρi and Si is a centerpiece of the modern IV literature.87 It varies across transitions (see Web Appendix A.13). However, ρi turns out to be node-specific (ρs,s′,i) and not the same across transitions.
Sorting on gains, measured either for specification as in (19) (COV (ρs,s′, Ds) ≠ 0), or for specification as in (21) (COV (ρj−1,j, Qj) ≠ 0), reveals that there is positive sorting on wage gains only at the higher levels of education. Our estimated correlation patterns are consistent with our evidence on sorting gains presented in Web Appendix A.15.
6.6 Summarizing Our Analysis of Causal Effects of Education
In this section and in our Web Appendix, we have analyzed a variety of economically interpretable treatment effects. We reach the following broad conclusions.
There are substantial causal benefits for all outcomes analyzed from education, except for GED certification.
Continuation values are an important component of causal effects for most outcomes except health limits work.
There are substantial benefits from graduating high school that are especially strong for the less able, many of whom currently do not graduate. This suggests strong gains from programs promoting high school graduation.
For the wage outcomes we study, there is evidence on sorting on gains from graduating college for high-ability persons.88 There are no causal effects of college graduation for low-ability persons. College graduation is not for all.
There are strong benefits of education for those at the margin of indifference at all nodes. These are largely direct effects with little contribution from continuation values.
We estimate strong causal effects for the non-monetary outcomes studied. They are particularly strong for high school graduation. There is little evidence of sorting on gains in either non-monetary outcome examined. Continuation values are largely absent for our measure of health. For smoking, continuation values are most pronounced among higher-ability persons. Selection bias is less empirically important for smoking, but is substantial for health limits work.
7 Policy Simulations from Our Model
Using our model, it is possible to conduct a variety of counterfactual policy simulations, a feature not shared by standard treatment effect models. We achieve these results without imposing strong assumptions on the choice model. We consider two policy experiments: (i) a tuition subsidy; and (ii) an increase in the cognitive and non-cognitive endowments of those at the bottom of the endowment distribution. The first policy experiment is similar to what is estimated by LATE only in the special case where the instrument in LATE corresponds to the exact policy experiment. The second policy experiment is of interest because early childhood programs boost these endowments (Heckman et al., 2013a). Neither set of counterfactuals generated can be estimated from instrumental variable estimands. We ignore general equilibrium effects in these simulations.
7.1 Policy-Relevant Treatment Effects
Unless the instruments correspond to policies, IV does not identify policy-relevant treatment effects. The PRTE allows us to identify who would be induced to change educational choices under specific policy changes, and how these individuals would benefit on average. As an example of the power of our methodology, we simulate the response to a policy intervention that provides a one standard deviation subsidy to early college tuition (approximately $850 dollars per year of college). Column 1 of Table 2 presents the average treatment effect (including continuation values) in our estimated model for those who are induced to change education levels by the tuition subsidy. Since we do not find evidence that college tuition affects high school graduation rates, the subsidy only induces high school graduates to change their college enrollment decisions and does not affect high school graduation decisions. Those induced to enroll may then go on to graduate with a four-year degree.89 Columns 2 and 3 of Table 2 decompose the PRTE into the average gains for those induced to enroll and then go on to earn four-year degrees and the average gains for those who do not. For the most part, the PRTE is larger for those who go on to earn four-year degrees.
Table 2.
PRTE: Standard Deviation Decrease in Tuition
| PRTE | Four-Year Degree | No Four-Year Degree | |
|---|---|---|---|
| Log Wages | 0.125 (0.023) | 0.143 (0.027) | 0.114 (0.027) |
| PV Log Wages | 0.129 (0.03) | 0.138 (0.033) | 0.123 (0.028) |
| Health Limits Work | −0.036 (0.022) | −0.025 (0.021) | −0.043 (0.023) |
| Smoking | −0.131 (0.029) | −0.166 (0.030) | −0.108 (0.030) |
Notes: The table shows the policy-relevant treatment effect (PRTE) of reducing tuition for the first two years of college by a standard deviation (approx. $850 per annum). The PRTE is the average treatment effect of those induced to change educational choices as a result of the policy: . Column 1 shows the overall PRTE. Column 2 shows the PRTE for those induced to enroll by the policy who then go on to complete four-year college degrees. Column 3 shows the PRTE for individuals induced to enroll but who do not complete four-year degrees.
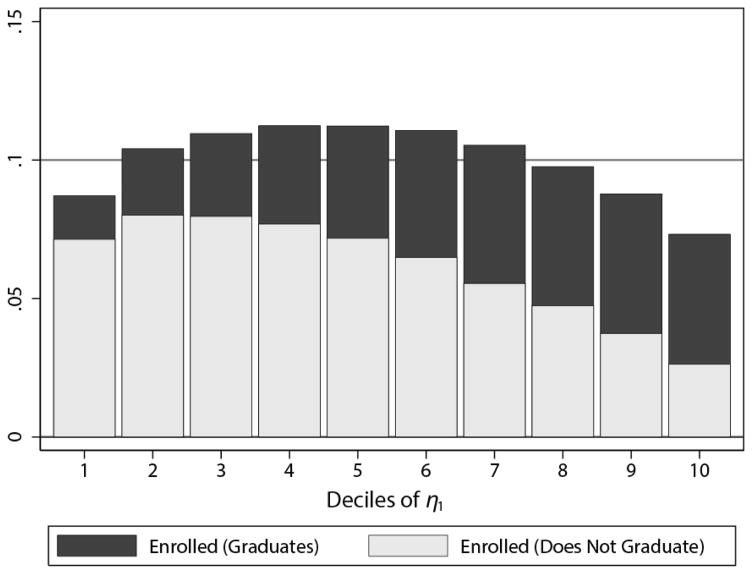
Figure 8 shows which individuals are induced to enroll in college within the deciles of the distribution of the unobservable in the choice equation for node 2,90 conditional on Q2 = 1 (the node determining college enrollment). These are the unobserved components of heterogeneity acted upon by the agent but unobserved by the economist.
Figure 8.
PRTE: Who Is Induced to Switch?
Notes: The figure plots the proportion of individuals induced to switch from the policy that lay in each decile of η2, where η1 = −(θ′λ1−ν1). η1 is the unobserved component of the educational choice model. The deciles are conditional on Q1 = 1, so η2 for individuals who reach the college enrollment decision. The bars are further decomposed into those that are induced to switch that then go on to earn four-year degrees and those that are induced to switch but do not go on to graduate.
The policy induces some individuals at every decile to switch, but places more weight on those in the middle deciles of the distribution. The figure decomposes the effect of those induced to switch into effects for those who go on to graduate with four-year degrees and effects for those who do not. Those induced to switch in the top deciles are more likely to go on to graduate with a four-year college degree.
The $850 subsidy induces 12.8% of high school graduates who previously did not attend college to enroll in college. Of those induced to enroll, more than a third go on to graduate with a four-year degree. For outcomes such as smoking, the benefits are larger for those who graduate with a four-year degree. The large gains for marginal individuals induced to enroll is consistent with the empirical literature, that finds large psychic costs are necessary to justify college schooling choices, and the failure of agents to respond to strong monetary incentives.
Using the estimated benefits, we can determine if the monetary gains in the present value of wages at age 18 is greater than the $850 subsidy.91 Given a PRTE of 0.13 for log present value of wage income, the average gains for those induced to enroll is $36,401 in year 2000 dollars. If the subsidy is given for the first two years of college, then the policy clearly leads to monetary gains for those induced to enroll. If the subsidy is also offered to those already enrolled, the overall monetary costs of the subsidy is much larger because it is given to more than 8 students previously enrolled for each new student induced to enroll (dead weight).
7.2 Boosting Cognitive and Non-Cognitive Endowments
Using simulation methods, it is possible to construct counterfactual policy simulations unrelated to any particular set of instruments. For example, some early childhood programs have been shown to have lasting impacts on the cognitive and non-cognitive endowments of low-ability children (see Heckman et al., 2013a). We simulate two policy experiments: (i) increasing the cognitive endowment of those in the lowest decile; and (ii) increasing the non-cognitive endowment of those in the lowest decile.92
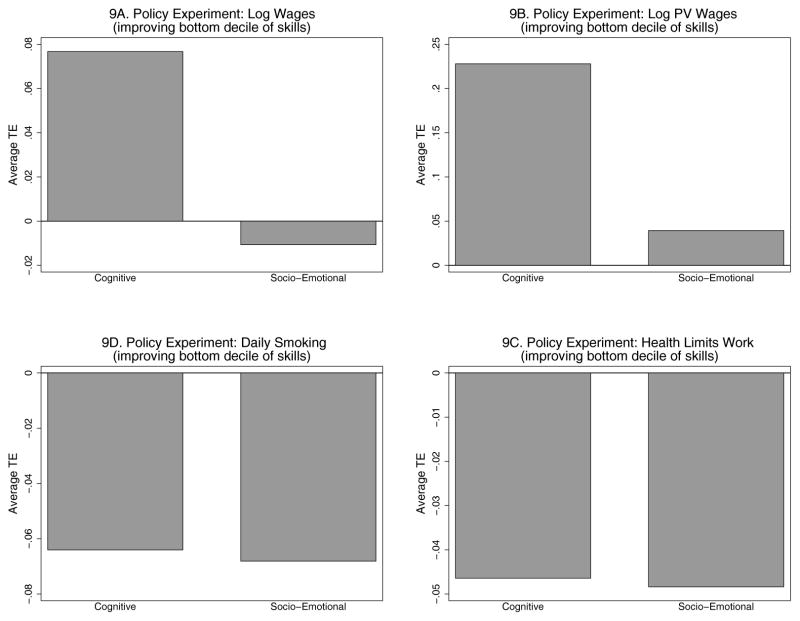
The panels of Figure 9 show the average gains for increasing the cognitive or non-cognitive endowments of those in the lowest decile of each ability. Increased cognition helps individuals across the board. Increasing socio-emotional endowments has a smaller effect on labor market outcomes but has substantial effects on health.93
Figure 9.
Policy Experiments
Notes: This plot shows the average gains for those in the bottom deciles of cognitive ability (left) and socio-emotional ability (right), from an increase in the endowment.
8 Testing the Two-Factor Assumption
Throughout this paper, we have assumed that selection of outcomes occurs on the basis of a two-component vector θ, where the components can be proxied by our measures of cognitive and non-cognitive endowments. An obvious objection to this approach is that there may be unproxied endowments that affect both choices and outcomes that we do not measure. For example, one could imagine that a component of the idiosyncratic error terms in the educational choices (νj) represent taste for schooling. This could generate correlations between the unobservables in the different educational choices and bias our results.
In order to test for the presence of a third factor that influences both choices and outcomes, we test whether the simulated model fits the sample covariances between Yk and Dj, j = 1, …, s̄, k = 1, …, 4. If an important third factor common to both outcome and choice equations has been omitted, the sample fit should be poor. In fact, we find a good fit.
Cunha and Heckman (2016) estimate a related model using the same data source. They find that a three-factor model explains wages and present value of wages. Two of their factors correspond to the factors used in this paper. Their third factor improves the fit of the wage outcome data but does not enter agent decision equations or affect selection or sorting bias. Our evidence is consistent with their findings.
9 Comparisons with Simple Treatment Effect Estimators
In this paper, we have exploited the assumption of conditional independence of outcomes and choices given X, Z, θ. This raises the question of how similar our results would be if we had used simple matching and regression methods.
Table 3 presents two sets of estimates for the models discussed in detail at the base of the table. The first four columns of numbers are node-specific linear-regression estimators of Equation (11), using as regressors the background variables reported in Table 1 but not the “exclusion restriction” variables. The first column of estimates come from a model without any control for θ. The estimates for the other three models control for θ in various ways as noted at the base of Table 3.
Table 3.
Average Treatment Effects - Comparison of Estimates from Our Model to Those from Simpler Methods
| HS Grad. | Linear Regression |
Matching |
Model |
|||||
|---|---|---|---|---|---|---|---|---|
| OLS | OLS-P | OLS-F | OLS-FI | NNM(3)-F | PSM-F | * | ||
| Wages | 0.205 | 0.073 | 0.155 | 0.159 | 0.098 | 0.132 | 0.094 | |
| SE | (0.025) | (0.026) | (0.025) | (0.035) | (0.037) | (0.051) | (0.056) | |
| PV-Wage | 0.380 | 0.213 | 0.318 | 0.277 | 0.196 | 0.226 | 0.173 | |
| SE | (0.030) | (0.031) | (0.030) | (0.041) | (0.053) | (0.058) | (0.059) | |
| Smoking | −0.327 | −0.246 | −0.281 | −0.301 | −0.260 | −0.271 | −0.263 | |
| SE | (0.028) | (0.029) | 0.028 | 0.041 | (0.058) | (0.060) | (0.056) | |
| Health-Limits-Work | −0.178 | −0.115 | −0.151 | −0.150 | −0.048 | −0.095 | −0.108 | |
| SE | (0.022) | (0.024) | (0.023) | (0.033) | (0.029) | (0.036) | (0.042) | |
|
| ||||||||
| Coll. Enroll | OLS | OLS-P | OLS-F | OLS-FI | NNM(3)-F | PSM-F |
|
|
|
| ||||||||
| Wages | 0.223 | 0.121 | 0.186 | 0.190 | 0.177 | 0.207 | 0.134 | |
| SE | (0.023) | (0.024) | (0.024) | (0.023) | (0.029) | (0.031) | (0.025) | |
| PV-Wage | 0.221 | 0.109 | 0.176 | 0.171 | 0.188 | 0.226 | 0.137 | |
| SE | (0.027) | (0.029) | (0.028) | (0.027) | (0.030) | (0.032) | (0.029) | |
| Smoking | −0.177 | −0.138 | −0.165 | −0.170 | −0.129 | −0.144 | −0.139 | |
| SE | (0.026) | (0.028) | (0.027) | (0.028) | (0.029) | (0.058) | (0.028) | |
| Health-Limits-Work | −0.085 | −0.037 | −0.066 | −0.057 | −0.029 | −0.042 | −0.037 | |
| SE | (0.020) | (0.022) | (0.021) | (0.021) | (0.022) | (0.029) | (0.022) | |
|
| ||||||||
| Coll. Grad | OLS | OLS-P | OLS-F | OLS-FI | NNM(3)-F | PSM-F |
|
|
|
| ||||||||
| Wages | 0.210 | 0.146 | 0.184 | 0.185 | 0.173 | 0.143 | 0.114 | |
| SE | (0.032) | (0.034) | (0.033) | (0.035) | (0.041) | (0.051) | (0.037) | |
| PV-Wage | 0.243 | 0.163 | 0.208 | 0.228 | 0.191 | 0.269 | 0.171 | |
| SE | (0.037) | (0.040) | (0.038) | (0.037) | (0.039) | (0.042) | (0.040) | |
| Smoking | −0.209 | −0.171 | −0.195 | −0.192 | −0.132 | −0.161 | −0.172 | |
| SE | (0.032) | (0.035) | (0.033) | (0.035) | (0.039) | (0.039) | (0.043) | |
| Health-Limits-Work | −0.085 | −0.069 | −0.078 | −0.077 | −0.048 | −0.051 | −0.064 | |
| SE | (0.024) | (0.026) | (0.025) | (0.026) | (0.026) | (0.027) | (0.031) | |
Notes: We estimate the ATE inclusive of continuation values for each outcome and and educational choice using a variety of methods. All models are estimated for populations that reach the node being analyzed (Qj = 1), inclusive of those who go on to further schooling in order to make them comparable to the ATE from our model that includes continuation values (Equation (21)). All OLS models use the full set of controls listed in Table 1. “OLS” estimates a linear model using a schooling dummy (Qj+1), and controls (Y = Qj+1bj + X′β + ε). “OLS-P” estimates a linear model using a schooling dummy, a vector of controls, and three measures of abilities arrayed in a vector A: summed ASVAB scores, GPA, and an indicator of risky behavior (Y = Qj+1bj + X′β + A′α + ε). All models ending in “-F” are estimated using Bartlett factor scores (Bartlett, 1937, 1938) estimated using our measurement system, but using the built-in routine for estimating factor models in STATA via maximum likelihood, not accounting for schooling at the time of the test. “OLS-F” estimates the model Y = Qj+1bj + X′β + θ̂′α+ ε where θ̂ are the Bartlett factor scores described above. “OLS-FI” is similar to “OLS-F” except that Qj+1 is interacted with the X and θ̂ allowing the coefficients on the controls and abilities to vary by education level. “NNM(3)-F” is the estimated treatment effect from nearest-neighbor matching with 3 neighbors. Neighbors are matched on their Bartlett cognitive factor, Bartlett non-cognitive factor, and an index constructed from their observed characteristics (Z) generating choices as described in Web Appendix A.18. “PSM-F” presents the estimated average treatment effect from propensity score matching where propensity scores are estimated using Bartlett cognitive factors, Bartlett non-cognitive factors, the full set of control variables, and the full set of node-specific instruments. “ ” presents the estimated average treatment effect from the model presented in this paper (inclusive of continuation value), corresponding to Equation (13).
We use two versions of nearest-neighbor matching estimators based on the full set of control variables listed in Table 1. Details of the matching procedures are given at the base of Table 3 and in Web Appendix A.18.
The OLS estimates differ greatly from model estimates when there is no adjustment for ability. Controlling for ability has substantial effects on the estimated average treatment effects. Across schooling nodes, all of the estimates that control for θ are “within the ball park” of the estimates produced from our model, although some discrepancies are substantial. This is good news for applied economists mainly interested in using simple methods to estimate node-specific average treatment effects. However, these simple methods do not estimate decision rules, do not enable analysts to estimate AMTE and PRTE, or address many of the other questions addressed in this paper.94
10 Summary and Conclusion
Gary Becker’s pioneering research on human capital launched a large and active industry estimating causal effects and returns to schooling. Multiple methodological approaches have been used to secure these estimates ranging from reduced-form treatment effect methods to fully structural methods. Each methodology has its benefits and limitations.
The early literature on human capital ignored the dynamics of schooling choices. This paper develops and estimates a robust dynamic model of schooling and its causal consequences for earnings, health, and smoking. Our model recognizes the sequential dynamic nature of educational decisions. We borrow features from both the reduced-form treatment effect literature and the structural literature. Our estimated model passes a variety of goodness-of-fit and model specification tests.
We allow agents to be irrational and myopic in making schooling decisions. Hence, we can use our model to test some of the rationality and information processing assumptions maintained in the dynamic discrete choice literature on education.
We use our dynamic choice model to estimate causal effects arising from multiple levels of schooling rather than just the binary comparisons typically featured in the literature on treatment effects and in many structural papers.95 By estimating a sequential model of schooling in a unified framework, we are able to analyze the ex post returns to education for people at different margins of choice and analyze a variety of economically interesting policy counterfactuals. We are able to characterize who benefits from education for a variety of market and non-market outcomes.
We decompose the benefits of schooling at different levels into direct components and indirect components arising from continuation values. We estimate substantial continuation value components of graduating high school and completing college for high-ability individuals. For them, schooling opens up valuable options for future schooling. Standard estimates of the benefits of education based only on direct components of dynamic treatment effects underestimate the full benefits of education. For low-ability individuals, there are substantial direct effects of graduating high school, but little continuation value.
Without imposing rationality, we nonetheless find evidence consistent with it. We find positive sorting into schooling based on gains, especially for higher schooling levels. Schooling has strong causal effects on earnings, health, and healthy behaviors. Both cognitive and non-cognitive endowments affect schooling choices and outcomes at each level of schooling.
We link the structural and matching literatures using conditional independence assumptions. We investigate how simple methods used in the treatment effect literature perform in estimating average treatment effects.96 They roughly approximate our model estimates of average treatment effects, provided we condition on endowments of cognitive and non-cognitive skills. However, these simple methods do not identify the treatment effects for persons at the margins of different choices (the average marginal treatment effects).97 We test the empirical foundations of the Mincer model and find it wanting. A richer specification of the schooling earnings decision is warranted to generate empirically supported estimates of causal effects.
We use our estimated model to conduct two policy experiments. We determine the groups that benefit from a tuition reduction policy and what those benefits are. We also examine how the impact of boosts in cognitive and non-cognitive skills affects educational choices and outcomes.
Our analysis enriches the pioneering analysis of Becker (1964). The early research on human capital was casual about agent heterogeneity. It ignored selection bias and sorting gains from schooling. Later work by Griliches (1977) focused on selection bias (“ability bias”), but ignored sorting gains. In this paper, we quantify both components of outcome equations. We find evidence of selection bias at all levels of schooling for all outcomes and sorting gains at higher levels of schooling for wage outcomes.
Our findings thus support the basic insights of Becker (1964). Schooling has strong causal effects on market and non-market outcomes. Both cognitive and non-cognitive endowments affect schooling choices and outcomes. People sort into schooling based on realized incremental gains.
Supplementary Material
Acknowledgments
We thank Chris Taber for insightful comments on an early draft. We also thank Ariel Pakes and other participants at a Harvard Labor Economics Workshop in April, 2014, for helpful comments on a previous draft. We thank Eleanor Dillon and Matthew Wiswall for comments received at a seminar at Arizona State University, February, 2015. We thank the special editor, Ed Lazear, and an anonymous referee for helpful comments. We also thank Jessica Yu Kyung Koh, Joshua Shea, Jennifer Pachon, and Anna Ziff for comments on this draft.
Footnotes
This research was supported in part by: the American Bar Foundation; the Pritzker Children’s Initiative; the Buffett Early Childhood Fund; NIH grants NICHD R37HD065072, NICHD R01HD054702, and NIA R24AG048081; an anonymous funder; Successful Pathways from School to Work, an initiative of the University of Chicago’s Committee on Education funded by the Hymen Milgrom Supporting Organization; and the Human Capital and Economic Opportunity Global Working Group, an initiative of the Center for the Economics of Human Development, affiliated with the Becker Friedman Institute for Research in Economics, and funded by the Institute for New Economic Thinking. Humphries acknowledges the support of a National Science Foundation Graduate Research Fellowship. The views expressed in this paper are solely those of the authors and do not necessarily represent those of the funders or the official views of the National Institutes of Health.
Becker (1964) also estimated rates of return. For surveys of this literature, see, e.g., Card (1999, 2001); Heckman et al. (2006a); Oreopoulos and Salvanes (2011); McMahon (2009); Oreopoulos and Petronijevic (2013).
Weisbrod’s paper stimulated research on the option value of schooling. See, e.g., Comay et al. (1973); Dothan and Williams (1981); Bamberger (1987); Altonji (1993); Cameron and Heckman (1993); Keane and Wolpin (1997); Arcidiacono and Miller (2011); Heckman et al. (2008); Stange (2012); Eisenhauer et al. (2015a).
See Heckman (2001).
It is based on the assumption that the earnings of a person age a in a given cross section when that person turns a′(> a) is well-approximated by the earnings of agents a′ in that same cross section. This synthetic cohort assumption is standard in the literature.
See Heckman (2008) and Heckman and Pinto (2015) for a discussion of causality and the role of fixing.
See, e.g., Cutler and Lleras-Muney (2010) who apply model (1) to estimate the causal effect of education on health.
The stringent conditions under which ρi is an internal rate of return, and evidence that they are not satisfied in many commonly used samples, are presented in Heckman et al. (2006a).
Note, however, that the continuation value is different from the option value. See, e.g., Stange (2012) and Eisenhauer et al. (2015a).
Rational expectations models assume that objectively measured probabilities are subjective probabilities. We do not impose this assumption in our analysis. For a survey of the expectation elicitation literature, see, e.g., Manski (2004).
See Heckman (2008).
See, e.g., Card (1999; 2001).
This is recognized in the LATE literature. See Angrist and Imbens (1995). What is not recognized in that literature is that LATE estimates the returns expected by agents only under a rational expectations assumption.
See, e.g., Angrist and Imbens (1995) and Angrist and Pischke (2009) for IV, and Heckman et al. (1998) for matching.
See, e.g., Keane and Wolpin (1997); Eisenhauer et al. (2015a).
See Heckman (2010) and Heckman and Urzúa (2010).
Eisenhauer et al. (2015b) distinguish and estimate ex ante and ex post returns in an instrumental variable model.
The modern instrumental variables case requires assumptions about the validity of the instruments. If there are heterogeneous treatment effects, additional assumptions such as “monotonicity” (better termed uniformity) are required to interpret IV estimates. See Imbens and Angrist (1994); Heckman and Vytlacil (2005); Angrist and Pischke (2009) for details.
See Heckman et al. (2006c) and Heckman et al. (2016) for a discussion.
See Heckman (2010).
Such approximations are discussed in Heckman (1981), Eckstein and Wolpin (1989), Cameron and Heckman (2001), and Geweke and Keane (2001).
Heckman and Navarro (2007) and Blevins (2014) also proof identifiability of structural models.
See, e.g., Eisenhauer et al. (2015a).
The human capital literature traditionally focused on the direct causal benefits of one final schooling level compared to another, but makes sequential comparisons from the lowest levels of schooling to the highest (Becker, 1964).
There is a small, but growing literature on the effects of education on health and healthy behaviors. See Grossman (2000); McMahon (2000); Lochner (2011); Oreopoulos and Salvanes (2011); Cutler and Lleras-Muney (2010). For a review of this literature see Web Appendix A.1.
See, e.g., Borghans et al. (2008); Heckman et al. (2006b); Almlund et al. (2011).
Our estimates of the causal effects of education do not require that we separately isolate the effects of individual cognitive and non-cognitive endowments on outcomes, just that we control for them as a set.
See, e.g., Griliches (1977) and Card (1999, 2001).
The GED is a test high school dropouts can take to earn state-issued high school equivalency credentials. For strong evidence on the nonequivalence of GEDs to high school dropouts, see Heckman et al. (2014).
Versions of this model are also analyzed in Cunha et al. (2007), Heckman and Navarro (2007), and Heckman et al. (2016).
For notational convenience, we assign Dj = 0 for all j > s.
In our model, X and Z can vary by decision or outcome depending on the specification of functions and ϕj(Z). See Table 1 for details.
Moreover, we can condition on observable covariates X.
See, e.g., Keane and Wolpin (1997); Rust (1994); Adda and Cooper (2003); Blevins (2014).
For example, the widely-used “types” assumption of Keane and Wolpin (1997) postulates conditional independence between choices and outcomes conditional on types (θ) that operate through the initial conditions of their model.
See, e.g., Abbring and Heckman (2007); Schennach et al. (2012).
See, e.g., Heckman et al. (2013b).
The distinction between fixing and conditioning traces back to Haavelmo (1943). White and Chalak (2009) use the terminology “setting” for the same notion. For a recent analysis of this crucial distinction, see Heckman and Pinto (2015).
The relationship between this notion of continuation values and the definition used in the dynamic discrete choice literature is explored in Web Appendix A.3.
See Abbring and Heckman (2007) for a review of the literature.
The modifications for the unordered case require that we define these terms over the admissible options available for D0 = 1 or D0 = 0.
See Carneiro et al. (2010, 2011).
Note that the limit of (16) as ε → 0 is not well-defined without further assumptions. This is the so-called “Borel paradox” discussed in this context in Carneiro et al. (2010). We avoid this problem by assuming a functional form for the distribution of ε.
One might also define a version of this treatment effect for two adjacent states ignoring continuation values.
aSee Heckman and Vytlacil (2007a) and Carneiro et al. (2010). The LATE can correspond to people at multiple margins. See Angrist and Imbens (1995) and Heckman et al. (2016).
Note that the indifference set may contain multiple margins, as in Heckman and Vytlacil (2007b) and Heckman and Urzúa (2010).
See Carneiro et al. (2011) for an empirical example. The differences between the two parameters can be substantial as we show in Heckman et al. (2016).
The estimated differences in treatment effects for the conditional and total populations are not large for outcomes associated with the decision to enroll in college, but are substantial for the choice to graduate from college. See Web Appendix A.14.2.
The analysis for discrete outcomes is straightforward.
Note that can be log outcomes as in (1). We can also formulate the outcomes in terms of latent variables.
Notice that even if there is no such dependence, some agents may still choose to go beyond s because of later gains in outcomes.
For a given level of s, selection bias is defined as , the mean difference in baseline outcomes for persons who stop at S = s compared to those who stop at S = s0.
The extension of this analysis to more general model (5) with the GED is straightforward.
Appendix A.15.1 gives the exact decomposition for our specific functional forms.
The more general expression incorporating D0 is presented as Equation (A.10) in the Web Appendix.
Under linear specifications for (10), we can directly estimate the θ and use factor regression methods. See, e.g., Heckman et al. (2013a), Heckman et al. (2016), and the references cited therein.
As noted in Heckman et al. (2011b), we do not need to solve classical identification problems associated with estimating equation system (10) in order to extract measure-preserving transformations of θ on which we can condition in order to identify treatment effects. In the linear factor analysis literature these are the classical rotation and normalization problems.
See Web Appendix A.5.
Web Appendix A.2 presents a detailed discussion of the data we analyze and our exclusion restrictions.
Adjustments are made through linear regression. This decomposition uses high school dropout as the base category (s0).
See also the decompositions in (A.7).
The OLS estimates do not identify treatment on the treated parameters. They are in rough agreement with ATEs except for the log present value of earnings.
See, e.g., Card (1999, 2001). Heckman et al. (2006a) dispute this claim.
Mis-measurement of schooling is less of a concern in our data, as the survey asks numerous educational questions every year which we use to determine an individual’s final schooling state.
Using our estimated model, we find, however, that population ATEs are well described by a linear-in-schooling specification. See Web Appendix A.8.
For example, presence of a nearby college or distance to college is used by Cameron and Taber (2004), Kling (2001), Carneiro et al. (2013), Cawley et al. (1997), Heckman et al. (2011a), and Eisenhauer et al. (2015b). Local tuition at two- or four-year colleges is used as an instrument by Kane and Rouse (1993), Heckman et al. (2011a), Eisenhauer et al. (2015b), and Cameron and Taber (2004). Local labor market shocks are used by Heckman et al. (2011a) and Eisenhauer et al. (2015b).
Parameter estimates for individual equations are reported in Web Appendix A.6.
We randomly draw an individual and use their full set of regressors.
This is Expression (18) for the case s′ = s + 1.
For that group, the delay in receiving high school wage rates is not sufficiently compensated by higher wage rates.
For a comparison of the treatment effects implicit in Figure 2 with those implicit in Figure 3, see Web Appendix A.17.2, Tables A71–A74. For most outcomes, the agreement is rather close, except for the ln PV of wages.
We define the margin of indifference to be ||Ij/σj|| ≤ 0.01, where σj is the standard deviation of Ij.
Across all outcomes, the GED has no benefit.
These estimates are imprecisely determined, in part, because there are few low-ability persons in this category.
A notable exception is for the AMTE for log PV of wages for high school graduation, for which the marginal benefits greatly exceed the average benefits.
TUT > ATE > TT.
Note that if direct effects are negative, continuation values may be larger than treatment effects.
Web Appendix A.7 reports a full set of results across all nodes.
These figures show average benefits by decile over the full population, rather than for the population that reaches each node.
Web Appendix A.9 reports a full set of distributions of treatment effects for all outcomes. Expectations are computed over the idiosyncratic error terms ( ).
Variation in the expected treatment effect comes from the variation in observed variables (X) and the unobserved endowments (θ).
See, e.g., Bitler et al. (2006).
This is the correlated random coefficient model. See Heckman and Vytlacil (1998).
Part of the relationship between ability and returns to college could operate through college quality. For example, Dillon and Smith (2015) show that ability is an important determinant of college quality and that college quality improves wages even after controlling for ability.
Models were estimated that include tuition as a determinant of the high school graduation decision. However, the estimated effects of tuition on high school graduation are small and statistically insignificant. We do not impose the requirement that future values of costs affect current educational choices. This highlights the benefits of our more robust approach. We do not impose the requirement that agents know and act on publicly available information.
The unobservable is the bundle η1 = −(θ′λ1−ν1).
However, a limitation of our model is that we can only estimate the monetary costs and do not estimate psychic costs.
The details of how these simulations were conducted are presented in Web Appendix A.11. Our model does not address general equilibrium effects of such a change in the endowment distribution.
We present additional policy simulations in Web Appendix A.11.
Table A70 of the Web Appendix compares OLS estimates of dynamic treatment effects and continuation values with our model estimates. The OLS estimates are “within ballpark” for smoking and health limits work, but they are wide off the mark for wages and PV wages.
See, e.g., Willis and Rosen (1979).
IV estimates are very different from our model estimates. See Heckman et al. (2016).
We can roughly approximate continuation values using simple methods. See Table A70 in the Web Appendix.
This paper was presented at the Becker Friedman Institute conference in honor of Gary Becker, October 30, 2014. It was also presented as the Sandmo Lecture at the Norwegian School of Economics, January 13, 2015.
The Web Appendix for this paper is https://heckman.uchicago.edu/eff-ed-earn-health.
JEL codes: C32, C38, I12, I14, I21
Contributor Information
James J. Heckman, University of Chicago and the American Bar Foundation
John Eric Humphries, University of Chicago.
Gregory Veramendi, Arizona State University.
References
- Abbring Jaap H, Heckman James J. Econometric Evaluation of Social Programs, Part III: Distributional Treatment Effects, Dynamic Treatment Effects, Dynamic Discrete Choice, and General Equilibrium Policy Evaluation. In: Heckman James J, Leamer Edward E., editors. Handbook of Econometrics. 6B. Amsterdam: Elsevier Science B. V; 2007. pp. 5145–5303. chap. 72. [Google Scholar]
- Adda Jéerôme, Cooper Russell W. Dynamic Economics: Quantitative Methods and Applications. Cambridge, MA: The MIT Press; 2003. [Google Scholar]
- Almlund Mathilde, Duckworth Angela, Heckman James J, Kautz Tim. Personality Psychology and Economics. In: Hanushek Eric A, Machin Stephen, Wößmann Ludger., editors. Handbook of the Economics of Education. Vol. 4. Amsterdam: Elsevier; 2011. pp. 1–181. chap. 1. [Google Scholar]
- Altonji Joseph G. The Demand for and Return to Education When Education Outcomes Are Uncertain. Journal of Labor Economics. 1993;11(1):48–83. [Google Scholar]
- Angrist Joshua D, Imbens Guido W. Two-Stage Least Squares Estimation of Average Causal Effects in Models with Variable Treatment Intensity. Journal of the American Statistical Association. 1995;90(430):431–442. [Google Scholar]
- Angrist Joshua D, Pischke Jörn-Steffan. Mostly Harmless Econometrics: An Empiricist’s Companion. Princeton, NJ: Princeton University Press; 2009. [Google Scholar]
- Arcidiacono Peter, Miller Robert A. Conditional Choice Probability Estimation of Dynamic Discrete Choice Models with Unobserved Heterogeneity. Econometrica. 2011;7(6):1823–1868. [Google Scholar]
- Bamberger Gustavo. PhD thesis. University of Chicago, Graduate School of Business; 1987. Occupational Choice: the Role of Undergraduate Education. [Google Scholar]
- Bartlett Maurice S. The Statistical Conception of Mental Factors. British Journal of Psychology. 1937;28(1):97–104. [Google Scholar]
- Bartlett Maurice S. Methods of Estimating Mental Factors. Nature. 1938;141:609–610. [Google Scholar]
- Becker Gary S. Investment in Human Capital: A Theoretical Analysis. Journal of Political Economy. 1962;70(5 Part 2):9–49. [Google Scholar]
- Becker Gary S. Human Capital: A Theoretical and Empirical Analysis, with Special Reference to Education. 1 Chicago: University of Chicago Press for the National Bureau of Economic Research; 1964. [Google Scholar]
- Becker Gary S, Chiswick Barry R. Education and the Distribution of Earnings. American Economic Review. 1966;56(1/2):358–369. [Google Scholar]
- Bitler Marianne P, Gelbach Jonah B, Hoynes Hilary W. What Mean Impacts Miss: Distributional Effects of Welfare Reform Experiments. American Economic Review. 2006;96(4):988–1012. [Google Scholar]
- Blevins Jason R. Nonparametric Identification of Dynamic Decision Processes with Discrete and Continuous Choices. Quantitative Economics. 2014;5(3):531–554. [Google Scholar]
- Borghans Lex, Duckworth Angela L, Heckman James J, ter Weel Bas. The Economics and Psychology of Personality Traits. Journal of Human Resources. 2008;43(4):972– 1059. [Google Scholar]
- Cameron Stephen V, Heckman James J. The Nonequivalence of High School Equivalents. Journal of Labor Economics. 1993;11(1 Part 1):1–47. [Google Scholar]
- Cameron Stephen V. The Dynamics of Educational Attainment for Black, Hispanic, and White Males. Journal of Political Economy. 2001;109(3):455–499. [Google Scholar]
- Cameron Stephen V, Taber Christopher. Estimation of Educational Borrowing Constraints Using Returns to Schooling. Journal of Political Economy. 2004;112(1):132–182. [Google Scholar]
- Card David. The Causal Effect of Education on Earnings. In: Ashenfelter Orley C, Card David., editors. Handbook of Labor Economics. 3A. Amsterdam: Elsevier Science B.V; 1999. pp. 1801–1863. chap. 30. [Google Scholar]
- Card David. Estimating the Return to Schooling: Progress on Some Persistent Econometric Problems. Econometrica. 2001;69(5):1127–1160. [Google Scholar]
- Carneiro Pedro, Hansen Karsten, Heckman James J. Estimating Distributions of Treatment Effects with an Application to the Returns to Schooling and Measurement of the Effects of Uncertainty on College Choice. International Economic Review. 2003;44(2):361–422. [Google Scholar]
- Carneiro Pedro, Heckman James J, Vytlacil Edward J. Evaluating Marginal Policy Changes and the Average Effect of Treatment for Individuals at the Margin. Econometrica. 2010;78(1):377–394. doi: 10.3982/ECTA7089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carneiro Pedro, James J. Estimating Marginal Returns to Education. American Economic Review. 2011;101(6):2754–2781. doi: 10.1257/aer.101.6.2754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carneiro Pedro, Meghir Costas, Parey Matthias. Maternal Education, Home Environments, and the Development of Children and Adolescents. Journal of the European Economic Association. 2013;11(S1):123–160. [Google Scholar]
- Cawley John, Conneely Karen, Heckman James J, Vytlacil Edward J. Cognitive Ability, Wages, and Meritocracy. In: Devlin Bernie, Fienberg Stephen E, Resnick Daniel P, Roeder Kathryn., editors. Intelligence, Genes, and Success: Scientists Respond to The Bell Curve. chap. 8. New York: Springer Verlag; 1997. pp. 179–192. [Google Scholar]
- Comay Yochanan, Melnik Arie, Pollatschek Moshe A. The Option Value of Education and the Optimal Path for Investment in Human Capital. International Economic Review. 1973;14(2):421–435. [Google Scholar]
- Cunha Flávio, Heckman James J. Decomposing Trends in Inequality in Earnings into Forcastable and Uncertain Components. Journal of Labor Economics. 2016 doi: 10.1086/684121. Forthcoming. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cunha Flávio, Heckman James J, Navarro Salvador. The Identification and Economic Content of Ordered Choice Models with Stochastic Cutoffs. International Economic Review. 2007;48(4):1273–1309. [Google Scholar]
- Cutler David M, Lleras-Muney Adriana. Understanding Differences in Health Behaviors by Education. Journal of Health Economics. 2010;29(1):1–28. doi: 10.1016/j.jhealeco.2009.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dillon Eleanor Wiske, Smith Jeffrey Andrew. IZA Discussion Paper 9080. Institute for the Study of Labor; Bonn: 2015. The Consequences of Academic Match between Students and Colleges. [Google Scholar]
- Dothan Uri, Williams Joseph. Education as an Option. The Journal of Business. 1981;54(1):117–139. [Google Scholar]
- Eckstein Zvi, Wolpin Kenneth I. The Specification and Estimation of Dynamic Stochastic Discrete Choice Models: A Survey. Journal of Human Resources. 1989;24(4):562–598. [Google Scholar]
- Eisenhauer Philipp, Heckman James J, Mosso Stefano. Estimation of Dynamic Discrete Choice Models by Maximum Likelihood and the Simulated Method of Moments. International Economic Review. 2015a;56(2):331–357. doi: 10.1111/iere.12107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eisenhauer Philipp, Heckman James J, Vytlacil Edward J. Generalized Roy Model and Cost-Benefit Analysis of Social Programs. Journal of Political Economy. 2015b;123(2):413–433. doi: 10.1086/679498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geweke John, Keane Michael. Computationally Intensive Methods for Integration in Econometrics. In: Heckman James J, Leamer Edward E., editors. Handbook of Econometrics. Vol. 5. Amsterdam: Elsevier Science B. V; 2001. pp. 3463–3568. chap. 56. [Google Scholar]
- Griliches Zvi. Estimating the Returns to Schooling: Some Econometric Problems. Econometrica. 1977;45(1):1–22. [Google Scholar]
- Grossman Michael. The Human Capital Model. In: Culyer Anthony J, Newhouse Joseph P., editors. Handbook of Health Economics. Vol. 1. Amsterdam: Elsevier Science B. V; 2000. pp. 347–408. chap. 7. [Google Scholar]
- Haavelmo Trygve. The Statistical Implications of a System of Simultaneous Equations. Econometrica. 1943;11(1):1–12. [Google Scholar]
- Heckman James J. Unpublished manuscript. University of Chicago, Department of Economics; 1981. The Empirical Content of Alternative Models of Labor Earnings. [Google Scholar]
- Heckman James J. Micro Data, Heterogeneity, and the Evaluation of Public Policy: Nobel Lecture. Journal of Political Economy. 2001;109(4):673–748. [Google Scholar]
- Heckman James J. Econometric Causality. International Statistical Review. 2008;76(1):1–27. [Google Scholar]
- Heckman James J. Building Bridges Between Structural and Program Evaluation Approaches to Evaluating Policy. Journal of Economic Literature. 2010;48(2):356–398. doi: 10.1257/jel.48.2.356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckman James J, Carneiro Pedro, Vytlacil Edward. Estimating Marginal Returns to Education. American Economic Review. 2011a;101(6):2754–2871. doi: 10.1257/aer.101.6.2754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckman James J, Humphries John Eric, Kautz Tim., editors. The Myth of Achievement Tests: The GED and the Role of Character in American Life. Chicago: University of Chicago Press; 2014. [Google Scholar]
- Heckman James J, Humphries John Eric, Veramendi Gregory. Dynamic Treatment Effects. Journal of Econometrics. 2016;191(2):276–292. doi: 10.1016/j.jeconom.2015.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckman James J, Ichimura Hidehiko, Todd Petra E. Matching as an Econometric Evaluation Estimator. Review of Economic Studies. 1998;65(2):261–294. [Google Scholar]
- Heckman James J, Lochner Lance J, Todd Petra E. Earnings Functions, Rates of Return and Treatment Effects: The Mincer Equation and Beyond. In: Hanushek Eric A, Welch Frank., editors. Handbook of the Economics of Education. Vol. 1. Amsterdam: Elsevier; 2006a. pp. 307–458. chap. 7. [Google Scholar]
- Heckman James J. Earnings Functions and Rates of Return. Journal of Human Capital. 2008;2(1):1–31. [Google Scholar]
- Heckman James J, Navarro Salvador. Dynamic Discrete Choice and Dynamic Treatment Effects. Journal of Econometrics. 2007;136(2):341–396. [Google Scholar]
- Heckman James J, Pinto Rodrigo. Causal Analysis after Haavelmo. Econometric Theory. 2015;31(1):115–151. doi: 10.1017/S026646661400022X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckman James J, Pinto Rodrigo, Savelyev Peter A. Understanding the Mechanisms Through Which an Influential Early Childhood Program Boosted Adult Outcomes. American Economic Review. 2013a;103(6):2052–2086. doi: 10.1257/aer.103.6.2052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckman James J, Schennach Susanne M, Williams Benjamin. Unpublished manuscript. University of Chicago, Department of Economics; 2011b. Matching with Error-Laden Covariates. [Google Scholar]
- Heckman James J. Unpublished Manuscript. University of Chicago, Department of Economics; 2013b. Matching on Proxy Variables. [Google Scholar]
- Heckman James J, Smith Jeffrey A, Clements Nancy. Making the Most Out Of Programme Evaluations and Social Experiments: Accounting for Heterogeneity in Programme Impacts. Review of Economic Studies. 1997;64(4):487–535. [Google Scholar]
- Heckman James J, Stixrud Jora, Urzúa Sergio. The Effects of Cognitive and Noncognitive Abilities on Labor Market Outcomes and Social Behavior. Journal of Labor Economics. 2006b;24(3):411–482. [Google Scholar]
- Heckman James J, Urzúa Sergio. Comparing IV With Structural Models: What Simple IV Can and Cannot Identify. Journal of Econometrics. 2010;156(1):27–37. doi: 10.1016/j.jeconom.2009.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckman James J, Urzúa Sergio, Vytlacil Edward J. Understanding Instrumental Variables in Models with Essential Heterogeneity. Review of Economics and Statistics. 2006c;88(3):389–432. [Google Scholar]
- Heckman James J, Vytlacil Edward J. Instrumental Variables Methods for the Correlated Random Coefficient Model: Estimating the Average Rate of Return to Schooling When the Return Is Correlated with Schooling. Journal of Human Resources. 1998;33(4):974–987. [Google Scholar]
- Heckman James J. Local Instrumental Variables and Latent Variable Models for Identifying and Bounding Treatment Effects. Proceedings of the National Academy of Sciences. 1999;96(8):4730–4734. doi: 10.1073/pnas.96.8.4730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckman James J. Structural Equations, Treatment Effects and Econometric Policy Evaluation. Econometrica. 2005;73(3):669–738. [Google Scholar]
- Heckman James J. Econometric Evaluation of Social Programs, Part I: Causal Models, Structural Models and Econometric Policy Evaluation. In: Heckman James J, Leamer Edward E., editors. Handbook of Econometrics. 6B. chap. 70. Amsterdam: Elsevier Science B. V; 2007a. pp. 4779–4874. [Google Scholar]
- Heckman James J. Econometric Evaluation of Social Programs, Part II: Using the Marginal Treatment Effect to Organize Alternative Economic Estimators to Evaluate Social Programs and to Forecast Their Effects in New Environments. In: Heckman James J, Leamer Edward E., editors. Handbook of Econometrics. 6B. Amsterdam: Elsevier Science B. V; 2007b. pp. 4875–5143. chap. 71. [Google Scholar]
- Imbens Guido W, Angrist Joshua D. Identification and Estimation of Local Average Treatment Effects. Econometrica. 1994;62(2):467–475. [Google Scholar]
- Kane Thomas J, Rouse Cecilia E. Working Paper 4268. National Bureau of Economic Research; 1993. Labor Market Returns to Two- and Four-Year Colleges: Is a Credit a Credit and Do Degrees Matter? [Google Scholar]
- Keane Michael P, Wolpin Kenneth I. The Career Decisions of Young Men. Journal of Political Economy. 1997;105(3):473–522. [Google Scholar]
- Kling Jeffrey R. Interpreting Instrumental Variables Estimates of the Returns to Schooling. Journal of Business and Economic Statistics. 2001;19(3):358–364. [Google Scholar]
- Lochner Lance. Working Paper 16722. National Bureau of Economic Research; 2011. Non-Production Benefits of Education: Crime, Health, and Good Citizenship. [Google Scholar]
- Manski Charles F. Measuring Expectations. Econometrica. 2004;72(5):1329–1376. [Google Scholar]
- McMahon Walter W. The Appraisal of Investments in Educational Facilities. Paris: European Investment Bank/OECD; 2000. Externalities, Non-Market Effects, and Trends in Returns to Educational Investments; pp. 51–83. [Google Scholar]
- McMahon Walter W. Higher Learning, Greater Good. Baltimore, MD: Johns Hopkins University Press; 2009. [Google Scholar]
- Mincer Jacob. Schooling, Experience, and Earnings. New York: Columbia University Press for National Bureau of Economic Research; 1974. [Google Scholar]
- Oreopoulos Philip, Petronijevic Uros. Working Paper 19053. National Bureau of Economic Research; 2013. Making College Worth It: A Review of Research on the Returns to Higher Education. [DOI] [PubMed] [Google Scholar]
- Oreopoulos Philip, Salvanes Kjell G. Priceless: The Nonpecuniary Benefits of Schooling. Journal of Economic Perspectives. 2011;25(1):159–184. [Google Scholar]
- Quandt Richard E. The Estimation of the Parameters of a Linear Regression System Obeying Two Separate Regimes. Journal of the American Statistical Association. 1958;53(284):873–880. [Google Scholar]
- Quandt Richard E. A New Approach to Estimating Switching Regressions. Journal of the American Statistical Association. 1972;67(338):306–310. [Google Scholar]
- Rust John. Structural Estimation of Markov Decision Processes. In: Engle Robert F, McFadden Daniel L., editors. Handbook of Econometrics. Vol. 4. New York, NY: North-Holland; 1994. pp. 3081–3143. chap. 51. [Google Scholar]
- Schennach Susanne M, White Halbert, Chalak Karim. Local Indirect Least Squares and Average Marginal Effects in Nonseparable Structural Systems. Journal of Econometrics. 2012;166(2):282–302. [Google Scholar]
- Stange Kevin M. An Empirical Investigation of the Option Value of College Enrollment. American Economic Journal: Applied Economics. 2012;4(1):49–84. [Google Scholar]
- Vytlacil Edward J. Independence, Monotonicity, and Latent Index Models: An Equivalence Result. Econometrica. 2002;70(1):331–341. [Google Scholar]
- Weisbrod Burton A. Education and Investment in Human Capital. Journal of Political Economy. 1962;70(5 Part 2):106–123. Investment in Human Beings. [Google Scholar]
- White Halbert, Chalak Karim. Settable Systems: An Extension of Pearl’s Causal Model with Optimization, Equilibrium, and Learning. Journal of Machine Learning Research. 2009;10:1759–1799. [Google Scholar]
- Willis Robert J, Rosen Sherwin. Education and Self-Selection. Journal of Political Economy. 1979;87(5 Part 2):S7–S36. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.