Ethane diffusion in mixed linker zeolitic imidazolate framework-7-8 by pulsed field gradient NMR in combination with single crystal IR microscopy

Abstract

Pulsed field gradient (PFG) NMR was used in combination with single crystal IR microscopy (IRM) to study diffusion of ethane inside crystals of a mixed linker zeolitic imidazolate framework (ZIF) of the type ZIF-7–8 under comparable experimental conditions. These crystals contain 2-methylimidazolate (ZIF-8 linker) and benzimidazolate (ZIF-7 linker). It was observed that the PFG NMR attenuation curves measured for ethane in ZIF-7–8 exhibit deviations from the monoexponential behaviour, thereby indicating that the ethane self-diffusivity in different crystals of a crystal bed can be different. Measurements of the ethane uptake curves performed by IRM under the same conditions in different ZIF-7–8 crystals of the bed yield different transport diffusivities thus confirming that the rate of ethane diffusion is different in different ZIF-7–8 crystals. The IRM observation that the fractions of ZIF-8 and ZIF-7 linkers are different in different ZIF-7–8 crystals allowed attributing the observed heterogeneity in diffusivities to the heterogeneity in the linker fraction. The quantitative comparison of the average ethane self-diffusivities measured by PFG NMR in ZIF-7–8 with the corresponding data on corrected diffusivities from IRM measurements revealed a good agreement between the results obtained by the two techniques. In agreement with the expectation of smaller aperture sizes in ZIF-7–8 than in ZIF-8, the average ethane self-diffusivities in ZIF-7–8 were found to be significantly lower than the corresponding self-diffusivities in ZIF-8.

Graphical Abstract

1. Introduction

Zeolitic imidazolate frameworks (ZIFs) represent a type of metal organic framework (MOF) that are structurally and topologically similar to zeolites.^1–3 ZIFs are also similar to zeolites with respect to their ability to serve as promising molecular sieves in gas separations.^{4, 5} While a large variety of ZIF structures can be synthesized, ZIF-8 has become a popular choice for research due to its potential to separate small molecules and act as a catalyst support.^{4, 6–8} A number of experimental studies utilizing both microscopic techniques such as pulsed field gradient (PFG) NMR^9–12 and macroscopic permeation and uptake measurements^13–15 have examined the transport properties of various sorbates in ZIF-8. These studies were motivated by the observation of competitive separation performance of ZIF-8 membranes.^{4, 13, 14, 16–19} In addition to experimental studies, molecular-level simulations have been used to investigate diffusion behaviour, selective adsorption, and framework flexibility in ZIF-8.^{15, 20–22}

Recently, significant interest has been generated around mixed linker ZIFs and MOFs owing to the potential of fine-tuning material properties by mixing different linkers in the same material.^23–27 By using different amounts of two imidazolate linkers in the ZIF synthesis, ZIF crystals can be formed with different proportions of linkers.^{24, 26} Several studies have been performed on various aspects of mixed linker ZIFs and MOFs, however they generally focus on their structural properties. One example is the use of solid-state nuclear magnetic resonance (NMR) measurements in combination with molecular modelling to study the spatial distribution of functional groups of mixed linkers in MTV-MOF-5.²⁸ In general, this technique can be applied to any mixed linker ZIF or MOF to determine the degree of clustering and order of linkers within the framework.²⁹ This approach of solid-state NMR characterization in combination with computer modelling was used to determine structural details of ZIF-8–90.³⁰ Further examples of studies of properties of mixed-linker MOFs include investigation of light-stimulated structural changes and probing for catalytic tuning.^{31, 32}

However, in order to understand the mixed linker ZIF’s applicability for broader use, the transport properties of these materials are critical to evaluate. PFG NMR and gravimetric uptake measurements of liquid sorbate diffusion have been recently reported for mixed linker ZIF-8–90.²⁶ Another recent example of a mixed linker ZIF is ZIF-7–8, which is composed of Zn⁺² ions tetrahedrally coordinated to 2-methylimidazolate (mIm, ZIF-8 linker) and benzimidazolate (blm, ZIF-7 linker). It has been shown that the varying proportions of linkers results in intermediate diffusive transport properties of ZIF-7–8 to the parent materials (ZIF-7 and ZIF-8) by comparing pure gas permeabilities through the ZIF membrane with different linker compositions.²³

Here we present the first study of microscopic diffusion of a gas in a mixed linker ZIF or MOF of any type. ZIF-7–8 was chosen for this study because the potential usefulness of ZIF-7–8 has generated interest in detailed understanding of its transport properties to enable further optimization of this material for possible applications in separations and catalysis. Ethane was selected as an initial probe gas as it is highly industrially relevant, and future studies can evaluate challenging separations, including ethane/ethylene separation, using ZIF-7–8. Another reason for selecting ethane is that it can be used as a guest molecule in diffusion studies in ZIF-7–8 by PFG NMR and single crystal infrared microscopy (IRM) at similar conditions. Multinuclear (¹³C and ¹H) PFG NMR diffusion studies of ethane reported here were performed at high magnetic fields (14 and 17.6 T) and large magnetic field gradients up to 25 T/m. The self-diffusivities measured by PFG NMR and transport diffusivities measured by IRM were analysed together to evaluate congruence of results between the measurement techniques, and develop detailed fundamental understanding of the main factors influencing diffusion process in ZIF-7–8.

2. Materials and methods

2.1. Materials

Zinc nitrate hexahydrate (Zn(NO₃)₂•6H₂O, 98%, Sigma-Aldrich) was used as a metal source. 2-methylimidazole (C₄H₅N₂, 97%, Sigma-Aldrich) and benzimidazole (C₇H₆N₂, 98%, Sigma-Aldrich) were used as linker sources. Methanol (99.8%, Alfa Aesar) and dimethylformamide (99.8%, Alfa Aesar) were used as solvents. Sodium formate (HCOONa, 99%, Sigma-Aldrich) was used as a modulator. All materials were used as purchased without further purification.

2.2. ZIF synthesis and standard characterisation

ZIF-7, ZIF-8, mixed linker ZIF-7–8 crystals were synthesized through conventional solvothermal synthesis route. For ZIF-7, a growth solution was prepared by mixing 0.446 g of zinc nitrate hexahydrate and 0.234 g of benzimidazole dissolved in 30 mL of dimethylformamide. The solution was then transferred to a 45 mL Teflon-lined steel autoclave and placed in an oven at 100 °C for 72 h. For ZIF-8, 0.335 g of zinc nitrate hexahydrate and 0.083 g of 2-methylimidazole were dissolved in 40 mL of methanol. Once the solution is dissolved, it is transferred to a Teflon-lined steel autoclave and placed in an oven at 50 °C for 24 h. For mixed linker ZIF-7–8, a metal solution was prepared by dissolving 0.994 g of zinc nitrate hexahydrate in 20 mL of dimethylformamide. For a mixed linker solution, 0.383 g of 2-methylimidazole, 0.0414 g of benzimidazole, and 0.113 g of sodium formate were dissolved in 20 mL of methanol. The metal solution was then poured into the linker solution and allowed to mix for 1 min. The solution was then transferred to a 45 mL Teflon-lined steel autoclave and placed in an oven at 95 °C for 2 h. For all samples, the autoclaves were then removed from the oven and allowed to cool naturally at room temperature for 2 h. The solutions were then centrifuged at 8000 RPM for 10 min, followed by washing in 30 mL of methanol. The washing cycle was repeated three times to ensure solvent replacement by methanol and removal of unreacted reagent. The resulting ZIF-7, ZIF-8, and ZIF-7–8 crystals were then dried in an oven at 120 °C for 2 days prior to characterization. X-ray diffraction (XRD) (Fig. S1) was performed at room temperature on a Rigaku Miniflex II powder X-ray diffractometer using Cu-Kα radiation (λ = 1.5406 Å) which was scanned with a step size of 0.02°. Scanning electron micrographs (Fig. S2) were collected using a JEOL JSM-7500F operating at 5 keV acceleration voltage and 15 mm working distance. The average crystal sizes were obtained by measuring and averaging the width of 10 crystals observed with SEM. The isotherms for ethane and ethylene (Fig. S3) were obtained using ASAP 2010 (Micromeritics).

2.3. Preparation of NMR samples

NMR tubes (Wilmad-Labglass) with 5 mm outside diameter were loaded with 50–85 mg of a ZIF powder and attached to a custom-built vacuum system. The samples were activated overnight at around 0.08 mbar and 383 K for at least 10 hours in order to ensure any sorbates were removed from the ZIF crystals. A desired quantity of single-labelled ¹³C-enriched (99%) ethane (Sigma-Aldrich) was cryogenically loaded into the tube through the vacuum chamber using liquid nitrogen. After loading, the tubes were flame sealed and left to equilibrate at room temperature for at least 12 hours. To determine the loading pressure above the ZIF bed, a single pulse NMR sequence was performed on the sample in which only the gas region of the NMR tube with ZIF powder was within the radiofrequency (RF) coil. The area under the NMR spectrum of ethane is proportional to the total number of the corresponding (¹³C or ¹H) nuclei of ethane in the measured tube volume.

The proportionality coefficient was determined by comparing this NMR signal to that in the NMR tube containing only ethane gas at a known pressure (no porous material added). To determine concentration of ethane in ZIFs at pressures below 1 bar, measured adsorption isotherms (see Fig. S3) were used. For ethane in ZIF-8 above 1 bar, previously published isotherms³³ were used to calculate intracrystalline concentrations. For ethane in ZIF-7–8 with a loading pressure greater than 1 bar, a mole balance was performed using the known total amount of ethane in the sealed NMR tube. The intracrystalline concentration was determined from the mole balance by assuming that around 70% of the ZIF bed volume consists of the gaps (gas phase) between ZIF crystals with the same ethane density as that measured above the bed. The intracrystalline concentrations for ZIF-7–8 and ZIF-8 are shown in Table 1.

Table 1.

Ethane loading pressure and the corresponding ethane intracrystalline concentrations, which are obtained using the adsorption isotherm data (*) or the NMR data and mole balance (†)

Material	Loading Pressure (bar)	Concentration (mmol/g)
ZIF-7-8	7.9 ± 0.8	4.4 ± 1.1†
ZIF-7-8	2.7 ± 0.3	2.9 ± 0.6†
ZIF-7-8	0.78 ± 0.08	1.2 ± 0.2*
ZIF-7-8	0.28 ± 0.03	0.7 ± 0.1*
ZIF-8	7.9 ± 0.8	4.3 ± 0.6*
ZIF-8	2.7 ± 0.3	3.4 ± 0.5*
ZIF-8	0.89 ± 0.09	2.1 ± 0.3*
ZIF-8	0.34 ± 0.03	0.80 ± 0.12*

2.4. PFG NMR measurements

PFG NMR self-diffusion measurements were performed on a narrow-bore Avance III 14 T spectrometer and a wide-bore Avance III HD 17.6 T spectrometer (Bruker Biospin). Only selected measurements were performed at 17.6 T in order to verify the reproducibility of the results at 14 T and the absence of any measurement artefacts under our experimental conditions. Most of the measurements were performed using ¹³C PFG NMR, while additional ¹H PFG NMR measurements were carried out under selected conditions matching those of ¹³C PFG NMR studies to confirm the absence of any measurements artefacts. ¹³C PFG NMR was chosen over more traditional ¹H PFG NMR due to longer T₂ NMR relaxation times for ¹³C, as has been observed in our previous study of ZIFs loaded with gaseous sorbates.³⁴ In this work, for the selected sample studied using both nuclei (viz. ZIF-7–8 equilibrated with 2.7 bar of ethane), T₁ and T₂ times for ¹³C were found to be 3.0 ± 0.3 s and 29 ± 3 ms, respectively, which are around 5 times as long as those of ¹H. ¹³C measurements were performed at resonance frequencies of 150.1 and 188.6 MHz for the 14 and 17.6 T field strengths, respectively. Proton resonance frequencies were 600 and 750 MHz at the 14 and 17.6 T, respectively. The adsorbed ethane exhibited a single line with a chemical shift around 7 ppm for ¹³C and around 2 ppm for ¹H. Magnetic field gradients of up to around 18 T/m and 25 T/m were generated using a Diff30 and Diff50 diffusion probe at 14 T and 17.6 T, respectively.

A 13-interval PFG NMR sequence with bipolar gradients and a 6 ms longitudinal eddy current delay was used for all diffusion measurements.^35–37 Sinusoidal shaped gradient pulses with effective durations around 1.4 ms were used. The interval between the first and second π/2 pulses was ~7 ms. There are two of these intervals (~14 ms total) in the sequence during which signal is reduced by T₂ relaxation. For normal 3-dimensional diffusion PFG NMR, signal attenuation (Ψ), as measured by the magnitude of the signal, i.e. the area under the NMR spectrum (S), as a function of the gradient strength (g) is:

$$\mathrm{\Psi }=\frac{S(g)}{S(g\approx 0)}=\text{exp}(-\frac{<r^2(t)>q^2}{6})=\text{exp}(-q^2\mathit{Dt}),$$ (1)

where q=2γgδ, γ is the gyromagnetic ratio, δ is the effective gradient pulse length, t is the diffusion time, D is self-diffusion coefficient, and <r²(t)> denotes the mean square displacements (MSD). For normal 3-dimensional diffusion, MSD is related to D and t through the Einstein relation <r²(t)>=6Dt. Experimental uncertainty of self-diffusivities was determined based on the reproducibility of PFG NMR data measured with the identically prepared, but different NMR samples, as well as based on the reproducibility of the data measured with the same samples at different field (17.6 and 14 T) and/or using different types of NMR active nuclei (¹H and ¹³C).

Longitudinal (T₁) NMR relaxation measurements were performed using a standard inversion recovery sequence.³⁸ Transverse (T₂) NMR relaxation measurements were done using the 13-interval PFG NMR sequence by changing the time intervals during which the T₂ NMR relaxation takes place and keeping all other intervals constant as done in previous studies.³⁴ In all samples, there was no observed distribution of T₁ or T₂ relaxation times for adsorbed ethane molecules. T₁ and T₂ relaxation times are shown in Tables S1 and S2. All NMR measurements reported in this work were performed at 296 ± 1 K.

2.5. IRM Measurements

For the IR microscopy (IRM) measurements, several dozens of ZIF-7–8 crystals were filled into a cylindrical vacuum cell with IR quartz glass windows (Starna GmbH). The cell was connected to the gas dosing system and mounted onto the heatable sample holder under the IR microscope (Hyperion 3000 with Vertex 80v, Bruker Optics). The crystals were activated under vacuum (< 10⁻⁵ mbar) at 383 K overnight for at least 15 h.

IRM is based on following the intensity of characteristic IR bands, e.g. of guest molecules like ethane. According to the Beer-Lambert law, the intensity of IR bands is proportional to the concentration of the molecules absorbing the IR light. More details on the method and experimental procedure can be found elsewhere.^{39, 40}

Using the visual mode of the IR microscope, a number of different individual ZIF-7–8 crystals were selected for (i) spectroscopic analysis and (ii) uptake experiments at 298 ± 1 K. This temperature is the same, within uncertainty, as that used in the PFG NMR studies. For (i), IR spectra from about 20 different freshly activated crystals were recorded and the intensity of IR signals related to mIm and bIm linkers compared. For (ii), the crystals were exposed to step-changes in the surrounding gas phase concentration and time-dependence of the IR signal of ethane was recorded. These “uptake curves” were fitted by an appropriate solution of Fick’s 2^nd law to extract transport diffusivities D_T.³⁹ The major part of the IRM diffusion measurements was done at low loadings (pressure step 0 – 0.2 bar) to evidence differences in the intracrystalline diffusivities in different ZIF-7–8 crystals. In addition, loading-dependent measurements were performed with selected crystals in the range 0 – 1 bar to compare the IRM transport and corrected diffusivities with the self-diffusivities obtained by PFG NMR.

Transport diffusivities obtained from repeated identical IRM measurements of uptake curves in several selected crystals of the same sample are usually found to scatter by up to 25%. This scatter in the diffusivities determines experimental uncertainty. The major contributions to this uncertainty are the noise from the initial part of the uptake curve and the exact determination of crystal sizes. For corrected diffusivities, uncertainty is found to increase by 5–10% due to the need to determine a thermodynamic factor from measured adsorption isotherms, which have their own uncertainty.

3. Results and Discussion

ZIF-7, ZIF-8, and ZIF-7–8 crystals were determined to be phase-pure and highly crystalline based on powder X-ray diffraction (PXRD) patterns as presented in Fig. S1. The average sizes of ZIF-7, ZIF-8, and ZIF-7–8 crystals were found to be approximately 9, 18, and 13 μm, respectively (see Fig. S2).

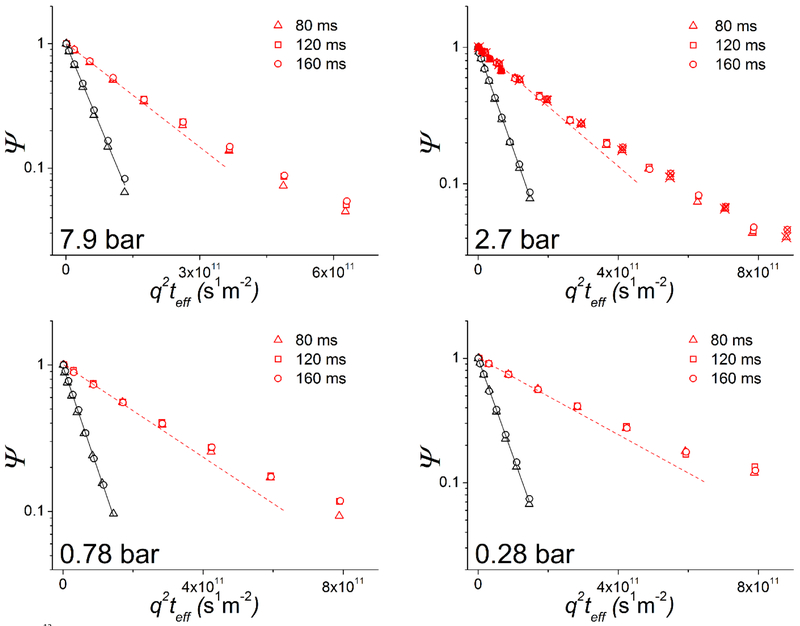
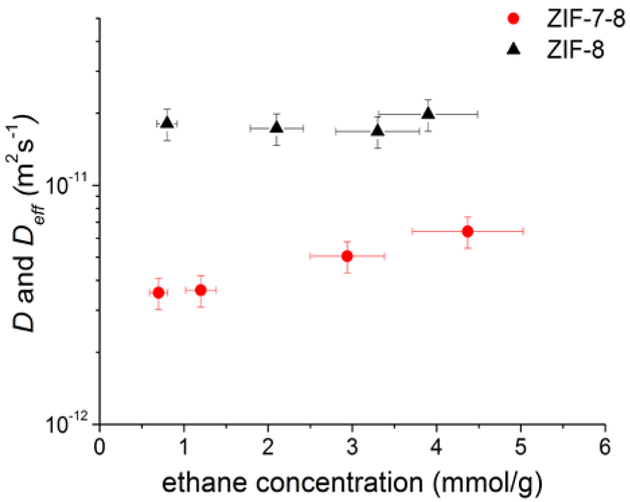
Fig. 1 shows examples of the measured PFG NMR attenuation curves for ethane in ZIF-7–8 at the four ethane loading pressures used in this work. For reference, the corresponding attenuation curves for ZIF-8 are also shown for the same temperature and ethane loading pressures. It was found that for ZIF-7, likely due to very short T₂ NMR relaxation times caused by the small pore and aperture sizes,^{1, 23} no PFG NMR signal could be acquired for ethane under our measurement conditions. The full width at half maximum (FWHM) of the ¹³C NMR line of adsorbed ethane, which is proportional to (T₂)⁻¹, was used to estimate the ¹³C T₂ NMR relaxation time of ethane in ZIF-7. The estimated T₂ value was around 4 ms, which is at least 6 times smaller than that for ethane in ZIF-7–8. This T₂ value was consistent with the absence of any easily measurable ¹³C NMR signal of ethane adsorbed in ZIF-7 using the 13-interval PFG NMR sequence with the sequence parameters used for the measurements of ethane diffusion in ZIF-7–8. These parameters are reported in the Experimental section and result in the combined time of 14 ms during which the signal decays with the T₂ time constant. All PFG NMR measurements for ZIF-7–8 and ZIF-8 were performed at different diffusion times (Fig. 1). The absence of any measurement artefacts under our measurement conditions was confirmed by the coincidence, within uncertainty, of the PFG NMR data measured for the loading pressure of 2.7 bar at 17.6 T and 14 T and when using ¹³C and ¹H PFG NMR (Fig. 1, upper right figure). To obtain ethane self-diffusivities, Eq. 1 was fit to the data using a least squares regression for both ZIF-7–8 and ZIF-8. For ZIF-8, the attenuation curves exhibit a monoexponential decay in agreement with Eq. 1 (i.e. linear in the semilogarithmic presentation of Fig. 1). The best fit lines yielding ethane self-diffusivity, D, for ZIF-8 are shown as black lines in Fig. 1. For ZIF-7–8, all attenuation curves show deviations from the monoexponential behaviour (Fig. 1). In this case, Eq. 1 was fit to the data corresponding to the initial 30% of the signal attenuation (i.e. Ψ ≥ 0.7) in order to obtain an effective (average) self-diffusion coefficient of ethane, D_eff, in the same way as in the previously reported PFG NMR studies.^{38, 41, 42} Monoexponential decays corresponding to the values of D_eff are shown as dashed red lines in Fig. 1. The resulting values of D_eff and D for ethane diffusion in ZIF-7–8 and ZIF-8, respectively, are presented as a function of the intracrystalline concentration of ethane in Fig. 2 and Table S2. These data show that for ZIF-8 the ethane self-diffusivity does not have any dependence, within uncertainty, on the ethane concentration. This observation as well as the absolute values of the ethane self-diffusivities in ZIF-8 (Fig. 2 and Table S2) are in agreement with the previously reported measurements of ethane self-diffusion in ZIF-8 by ¹H MAS PFG NMR and ¹³C PFG NMR under comparable conditions.^{12, 41, 43} At the same time, the results in Fig. 2 and Table S2 show that the effective self-diffusivity of ethane in ZIF-7–8 increases with increasing concentration. Such behaviour was previously reported for self-diffusion of methane and carbon dioxide in ZIF-8.⁹ In complete analogy with the latter study it can be assumed that the diffusion process in ZIF-7–8 is influenced by the framework flexibility.

Figure 1.

¹³C PFG NMR attenuation curves for ethane diffusion in ZIF-7–8 (hollow red symbols) and ZIF-8 (hollow black symbols) at four different ethane loading pressures and at different diffusion times shown in the figure legends. Also shown for comparison is the initial part of the corresponding ¹H PFG NMR attenuation curve for ZIF-7–8 at the loading pressure of 2.7 bar (filled red triangles in the upper right figure). The solid black lines represent a monoexponential fit of the ZIF-8 data using Eq. 1, while the dashed red line is the monoexponential fit using Eq. 1 of the initial 30% of the signal attenuation in ZIF-7–8. Crossed symbols for the loading pressure of 2.7 bar correspond to the measurements at 17.6 T. Symbols without crosses correspond to the measurements at 14 T.

Figure 2.

Effective self-diffusion coefficients (D_eff) in ZIF-7–8 (red circles) and self-diffusion coefficients (D) in ZIF-8 (black triangles) for ethane measured by PFG NMR at 296 K as a function of the ethane concentration in the ZIF crystals.

It is seen in Fig. 1 that the PFG NMR attenuation curves for ethane diffusion coincide in the presentation of the figure over the studied range of diffusion times, thereby yielding the time-independent, within uncertainty, values of D_eff for ZIF-7–8 and D for ZIF-8. This provides a strong indication that any diffusion effects at the external crystal surface do not perturb the measured attenuation curves. Comparison of the root MSD of 2.7 ± 0.3 µm, which was obtained for the largest diffusion time and D_eff in ZIF-7–8 (Fig. 2 and Table S2) using the Einstein relation, with the average size of ZIF-7–8 crystals (~13 μm) shows that molecular displacements remain significantly smaller than the crystal size under our measurement conditions. Hence, the crystal boundary effects are not expected to introduce any appreciable changes in the attenuation curves measured for ZIF-7–8. The same conclusion was also made for ZIF-8 based on the comparison of the root MSD values in Table S1 and the mean size of ZIF-8 crystals (~18 μm). Furthermore, the coincidence of the PFG NMR attenuation curves across multiple diffusion times in the presentation of Fig. 1 is consistent with the absence of any heterogeneity over transport properties in each individual ZIF-7–8 crystal. These data suggest that the structural properties, including linker fractions, are uniform for each ZIF-7–8 crystal. Excluding the crystal boundary effects as the possible reason for the observed deviations of the measured attenuation curves for ZIF-7–8 from the monoexponential behaviour and noting that diffusion anisotropy is not expected for ZIF-7–8, we hypothesize that these deviations are due to differences in ethane self-diffusivities in different crystals of the studied ZIF-7–8 powder.

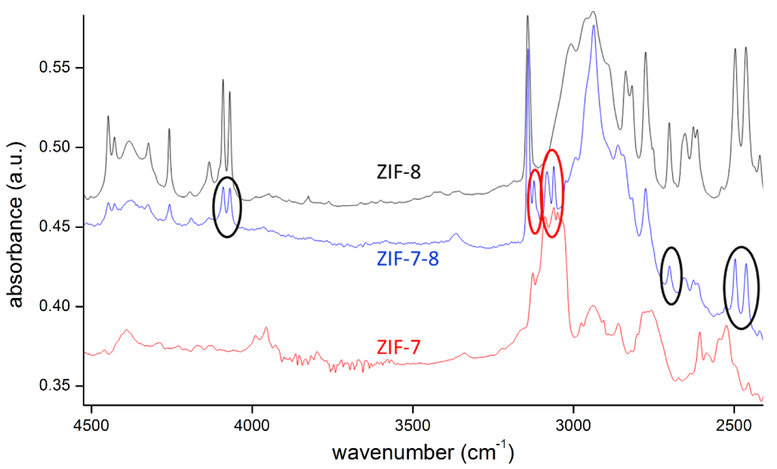
One possible explanation for the existence of multiple diffusivities is that there may exist a different fraction of mIm and bIm linkers in each ZIF-7–8 crystal. This would yield a heterogeneous distribution of diffusivities governed by the mIm and bIm linker fraction in each crystal. In order to investigate this possibility, single crystal infrared microscopy measurements were performed to compare the relative strength of the IR bands corresponding to mIm and bIm linkers in different crystals of the studied ZIF-7–8 sample. When comparing IR spectra of ZIF-7 and ZIF-8 with that of ZIF-7–8, different IR bands are found which can be assigned to one of the “parent materials” (Fig. 3). The IR bands at 4100, 2700 and 2475 cm⁻¹ are only found in ZIF-8, while the bands at 3115 and 3060 cm⁻¹ are typical for ZIF-7, only. It can be assumed that the origin of the different bands is related to the different linkers (mIm and bIm) in the framework. All ZIF-7–8 crystals studied by IRM exhibit some mIm- and bIm-assigned IR bands thus showing an intermediate linker composition to either pure ZIF-8 or ZIF-7.

Figure 3.

Comparison of IR spectra of a ZIF-7, ZIF-8 and ZIF-7–8 crystal. In ZIF-7–8, the IR bands at 4100, 2700 and 2475 cm⁻¹ are related to ZIF-8 (mIm), while the signals at 3115 and 3060 cm⁻¹ are ascribed to ZIF-7 (bIm).

For about 20 individual crystals, the intensities within both classes of bands were analysed. For comparing mIm and bIm-related band intensities, further calibration is needed as the extinction coefficient of both band types might be different and usually depends on the wavenumber. In other words, the same concentration of molecules may cause IR bands of different intensity. Although qualitative differences are already evidenced in the primary data (Fig. 3 and Table S3), quantitative analysis requires calibration or correlation of both signal classes. As a first order approximation, the molar mIm:bIm ratio of 87:13 in the synthesis solution was chosen as a reference. In fact, our solution NMR measurements confirmed a similar averaged concentration of the linkers in the ZIF-7–8 crystals. Using this correlation we find a variation of the bIm-fraction between 9 and 18 % among the different crystals (see Table S3).

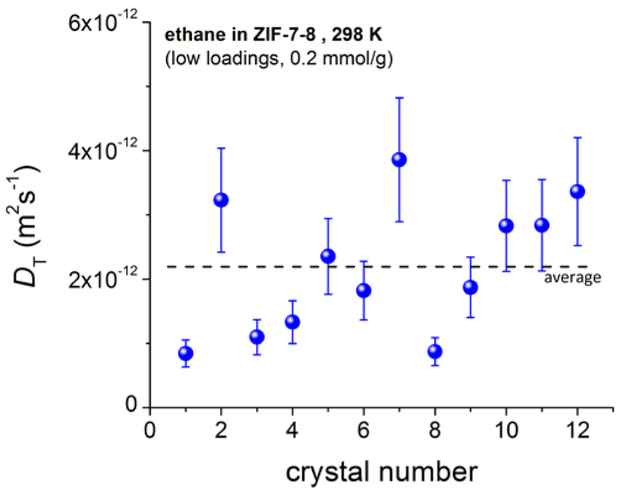
To quantify possible differences in the intracrystalline diffusivity, IRM was used to measure the uptake curves for ethane in individual ZIF-7–8 crystals. Given the well-defined geometry of each chosen crystal, the ZIF-7–8 uptake curves could be used to calculate a transport diffusivity. For more than 10 crystals, diffusivities were measured at low loadings (pressure step 0 – 0.2 bar, corresponding to about 0 – 0.4 mmol/g) and were found to differ by a factor of up to 4.4 with an average of 2.4 × 10^-12 m² s⁻¹ (Fig. 4). The transport diffusivities in individual crystals are found to increase with that crystal’s calculated mIm:bIm ratio. As expected, a larger fraction of mIm linkers results in larger pore apertures thereby leading to an increased diffusivity. The ratio of the mean values of the diffusivities above and below this average diffusivity shown by a dashed line in Fig. 4 was found to be equal to 2.1. The short uptake times allow IRM uptake studies at high loadings only for larger crystals found in the sample. Therefore, it was not possible to repeat the analysis shown in Fig. 4 (done at small loadings) for higher loadings similar to those used in PFG NMR measurements.

Figure 4.

Transport diffusivities, D_T, of ethane in ZIF-7–8 at 298 K measured for different individual crystals at low loadings. The diffusivities were found to scatter by a factor of up to 4.4.

When comparing the data of IRM and PFG NMR, one has to keep in mind that, respectively, transport and self-diffusivities are directly measured by these two techniques. In the limiting case of low loadings for which there are no mutual interactions between guest molecules, both diffusivities are expected to coincide while at high loadings they can differ by several orders of magnitude.³⁸ Although transport diffusivities are inherently different from self-diffusivities, they can be used to calculate a corrected diffusivity (D₀) which is “corrected” by removing thermodynamic effects encompassed by the transport diffusivity.^{38, 44} Corrected diffusivities were calculated from the IRM transport diffusivities using the thermodynamic factor (Γ) estimated from the adsorption isotherms c(p) following the so-called “Darken equation” ^{38, 44}

$$D_T=D_0\frac{d\text{ln}p}{d\text{ln}c}=D_0\mathrm{\Gamma }.$$ (2)

For pore structures consisting of large cavities framed by narrow windows, the corrected diffusivity is expected to coincide with the self-diffusivity over a wide loading range, as has been observed in ZIF-8^{39, 45} and DDR zeolite.⁴⁶ This is also expected to hold for ZIF-7–8 which exhibits the same pore characteristics. To compare IRM and PFG NMR data, loading dependent uptake curves were measured for two different crystals, and the dependencies of the transport diffusivity of ethane on the ethane loading were obtained for these crystals (Fig. 5). As already found in ZIF-8⁴⁵, the transport diffusivities increase strongly with increasing loading.

Figure 5.

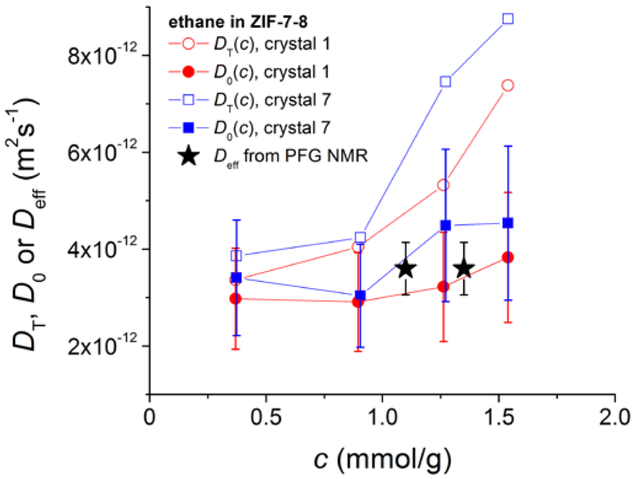
Comparison of corrected diffusivities, D₀, from IRM with the effective self-diffusivities, D_eff, from PFG NMR of ethane in ZIF-7–8. D₀ was calculated from the transport diffusivities, D_T, which are also shown in the figure, using the thermodynamic factor obtained from the adsorption isotherm.

The data in Fig. 5 show that there is a good agreement between the corrected diffusivities obtained by IRM and the corresponding effective self-diffusivities measured by PFG NMR. This agreement confirms that under the conditions of the uptake curve measurements performed by IRM the intracrystalline diffusion of ethane is the rate-limiting process.

For a detailed comparison of the IRM data on the ethane diffusivities in the ZIF-7–8 sample with the corresponding PFG NMR data, it would be desirable to obtain a distribution over ethane self-diffusivities in ZIF-7–8 from the measured PFG NMR attenuation curves. It is well known that approaches based on inverse Laplace transform can be used to extract such a distribution from the measured PFG NMR curves.^{47, 48} However, this problem is ill-defined and under the conditions of non-ideal signal-to-noise ratios (like in the case of the studies reported here for gaseous sorbate) yield an infinite number of distributions that can be quite different but, at the same time, fit the data equally well, within uncertainty. Hence, we decided to use a simpler approach to estimate the characteristic width of the distribution. It was done by assuming the existence of only two self-diffusion coefficients when fitting the measured PFG NMR attenuation curves and using the ratio of these two diffusivities as an estimate of the distribution width. Even though the studied sample of ZIF-7–8 crystals is not expected to exhibit only two modes of diffusion, the measured attenuation curves nonetheless can be fit statistically well using a biexponential relation corresponding to the existence of only two diffusivities (Eq. S1).

An example of such fit is shown in Fig. S4 with the best fit data shown in Table S4. The ratios of high and low diffusivities (D₁/D₂) generated by such fits for different ethane loadings in ZIF-7–8 are shown in Table 2. It is seen from the table that the ratio D₁/D₂ is around 3.0 for all studied loadings. This value can be compared with the ratio of the mean transport diffusivities above and below the average transport diffusivity (Fig. 4) obtained by IRM. As reported above, this ratio is around 2, which is in a good agreement with the corresponding PFG NMR data in Table 2.

Table 2.

Ratio of high (D₁) and low (D₂) biexponential diffusivities calculated for ethane in ZIF-7-8

Ethane pressure above sample bed (bar)	D1/D2
7.9 ± 0.8	2.7 ± 0.5
2.7 ± 0.3	2.7 ± 0.5
0.78 ± 0.08	3.1 ± 0.6
0.28 ± 0.03	3.3 ± 0.7

4. Conclusions

High field PFG NMR in combination with IRM were applied to study microscopic diffusion of ethane in a mixed-linker ZIF of the type ZIF-7–8. The reported PFG NMR data provide evidence for a distribution over ethane self-diffusivities in the studied ZIF-7–8 sample, i.e. ethane self-diffusivities are different in different ZIF-7–8 crystals of the sample. These data were confirmed by IRM measurements of transport diffusivities of ethane in different single crystals of ZIF-7–8. The average ethane self-diffusivities obtained by PFG NMR were found to be in a good agreement with the corresponding corrected diffusivities calculated based on the IRM data. Furthermore, the estimates of the distribution width of the ethane diffusivities measured by PFG NMR and IRM yield data that are in a good agreement. Average ethane self-diffusivities in ZIF-7–8 were compared with the corresponding ethane self-diffusivities measured by PFG NMR in ZIF-8, and found to be lower in ZIF-7–8 than in ZIF-8. This result is in agreement with the expectation that the average aperture size is lower in the former than in the latter ZIF. The reported distribution over ethane diffusivities in ZIF-7–8 is attributed to a difference in the fraction of ZIF-8 and ZIF-7 linkers observed by IRM in different single crystals of ZIF-7–8. An existence of a diffusivity distribution, which is reported in this work for the first time in the case of a mixed-linker ZIF, can be an inherent feature of mixed-linker ZIFs.