Effect of Model Thrombus Volume and Elastic Modulus on Magnetomotive Ultrasound Signal under Pulsatile Flow

Abstract

Direct ultrasonic imaging of arterial and venous thrombi could aid in diagnosis and treatment planning by providing rapid and cost-effective measurements of thrombus volume and elastic modulus. Toward this end, it was demonstrated that open-air magnetomotive ultrasound (MMUS) provides specific contrast to superparamagnetic iron oxide (SPIO)-labelled model thrombi embedded in gelatin-based blood vessel-mimicking flow phantoms. MMUS was performed on model thrombi in the presence of pulsatile flow that mimics cardiac-induced motion found in real vasculature. The MMUS signal and contrast to noise ratio (CNR) was measured across a range of physiologically relevant thrombus volumes and elastic moduli. Model thrombus volumes as small as 0.5 ml were shown to be detectable (CNR > 1) over the entire range of elastic moduli tested (3.5 – 40 kPa). It was also found that MMUS signal and CNR increased with increasing thrombus volume (r = 0.99), and decreasing elastic modulus (r = −0.81), while variations in pulsatile flow rate had little effect. These findings demonstrate that MMUS has promise as a direct in vivo thrombosis imaging modality for quantifying thrombus volume and stiffness.

I. Introduction

Venous and arterial thrombosis, which can lead to serious conditions such as pulmonary embolism, myocardial infarction, and stroke, necessitate imaging techniques that allow for rapid diagnosis and treatment monitoring. Ultrasound has become a standard of care for many types of thrombosis imaging [1], [2], in addition to X-ray angiography and emerging CT and MRI-based modalities [3], [4]. Ultrasound is favorable in many cases due to its low cost, portability, ability to characterize motion within the human body, and absence of ionizing radiation. While ultrasound cannot directly contrast thrombi against a dark-field (bright thrombi on a dark background), duplex ultrasound and, in veins, compression ultrasound are used to infer the presence of thrombi [2]. Doppler ultrasound quantifies blood flow, which may be disrupted by a thrombus, and compression ultrasound detects acute thrombi by virtue of their incompressibility. In comparison, emerging methods such as magnetomotive ultrasound (MMUS) [5], or other contrast-enhanced ultrasound methods [6] can potentially provide dark-field contrast of thrombi via targeted contrast agents.

Thrombus volume is an important marker, which may be predictive of outcomes and is otherwise clinically relevant in a variety of thromboembolic diseases. For example, in patients with abdominal aortic aneurisms (AAA), larger thrombus volumes were shown to be associated with an increased risk for subsequent cardiovascular events such as myocardial infarction, stroke, and death [7]. For deep vein thrombosis (DVT), thrombus volume measurements taken before and after treatment have been proposed as a method to objectively evaluate the effectiveness of those treatments [8], [9]. Furthermore, in prosthetic valve thrombosis (PVT) where transesophageal echocardiography is used for diagnosis, thrombus volume has been shown to be a predictor of clinical outcomes, with larger volumes corresponding to a higher risk of complication [10]. PVT volume may already be used to determine whether to perform surgery or medical therapy in certain cases [11]. Though compression and Doppler ultrasound may be used to diagnose these thromboembolic diseases, an inexpensive imaging technique providing more accurate volumetric data could further improve the quality of care [9].

Similarly, thrombus elastic modulus is of clinical significance, especially in the case of DVT. After a DVT diagnosis, it is important to determine whether the thrombus is acute or chronic, as indicated treatments differ in each case, but compression sonography is a subjective, often inconclusive measure, susceptible to biases, and can be highly painful for patients, while venography is frequently prohibitively costly and invasive [12]–[14]. Thrombus aging is associated with hardening, as the platelet-dominated thrombus transitions to being largely composed of fibrin, and fibroelastic organization occurs [13], [15]. A minimally-invasive elastography modality that could aid in the diagnosis of chronic DVT, where current ultrasound techniques are limited, could decrease the need for venography procedures, and expedite treatment [12], [13].

Ultrasound-based contrast of thrombosis lias previously been proposed. McCarty et al. demonstrated that microbubbles targeted to activated von Willebrand Factor could be used to image both endothelial injury in ex vivo murine aorta, and advanced atherosclerosis in live mice [6]. In comparison to microbubbles, MMUS provides dark-field contrast to magnetic micro- or nanoparticles, which offers additional flexibility for targeting thrombosis. The magnetomotive imaging technique was first developed for use with optical coherence tomography (OCT) in 2005 by Oldenburg et al. [16], and for use with ultrasound in 2006 by Oh et al. [17]. In both magnetomotive OCT and MMUS, axial lines (A-lines) are collected while an applied magnetic field gradient is temporally modulated at a known frequency. Imaging regions containing magnetic particles that are elastically bound to optically- or acoustically-scattering tissues exhibit phase shifts in the OCT or ultrasound signal, respectively, at the magnet modulation frequency. The phase-tracked motion is digitally bandpass filtered at the magnet frequency (“frequency locking”) in order to contrast regions containing magnetic particles [18], [19]. Additional specificity is obtained by further comparing the phase of the magnetomotion with the driving phase of the magnetic waveform, as proposed for OCT [20] and developed for MMUS as a “frequency- and phase-locking” method [19].

MMUS technology development is of increasing interest for a variety of applications. In 2011, Mehrmohammadi et al. demonstrated pulsed MMUS, which is designed to work around the need for the high power magnets found on traditional systems [21]–[23]. Their apparatus was later used to image magnetically-labeled xenograft tumors in live mice [24]. In 2013, Pope et al. demonstrated the first open-air MMUS system suitable for imaging arbitrarily large samples [5], which is the system employed in this paper. Pope then explored magnetic particle-labelled platelets as MMUS contrast agents for thrombosis imaging, due to their clot-targeting abilities as previously demonstrated in magnetomotive OCT [25], [26]. Evertsson (fonnerly Holst) et al. imaged rat sentinel lymph nodes in vivo using MMUS [27]. Meanwhile, Bruno et al. developed a technique for MMUS-based elastography for colorectal cancer screening [28], and Fink et al. demonstrated the use of chirped magnetic field modulation to further avoid potential biological noise [29]. Recently, Hossain et al. proposed the use of a blind source separation algorithm for MMUS image processing to decrease data collection time [30].

To further the application of MMUS for thrombus-specific imaging, in this study frequency- and phase-locked MMUS is investigated for the first time under controlled pulsatile flow conditions. This allowed for the study of how motion arising from blood flow could confound MMUS, which is fundamentally a motion-based imaging technique. For this purpose, blood vessel flow phantoms composed of tissue-mimicking gelatin were created with SPIO-labeled model thrombi for MMUS contrast. The blood vessel mimics each had a 6 mm lumen diameter, which matches larger human and canine veins [31]–[33], and an elastic modulus similar to that of the canine jugular vein [32]–[34]. These phantoms allowed for thrombus detectability testing under a variety of pulsatile flow conditions. For a range of thrombus volumes and elastic moduli, flow rates were varied up to 275 ml/min, which is on the same order of magnitude as flow rates in many human veins and arteries [35], [36].

II. Materials and Methods

A. Open-Air Magnetomotive Ultrasound System Hardware

The open-air MMUS system first described by Pope et al. was used in this work [5]. The apparatus included an Ultrasonix SonixTouch scanner and an L14-5/38 linear array transducer (Analogic Corporation, Peabody, MA) operating with a 10 MHz center frequency, a 17.5 mm focal depth, transmit and receive f-numbers of 1.2 and 1.8 respectively, and 70% bandwidth. Beamformed RF data was collected at a frame rate of 61.667 frames per second (fps), and the sampling frequency was 40 MHz. Image processing was carried out in slow time on a separate PC using Matlab (Mathworks Inc, Natick, MA). The grain-oriented steel core solenoid electromagnets used were the same as in the previous study, but the magnetic gradient in the center of the imaging region was increased to 0.02 T²/m by positioning the cores 10.5 cm apart, and tilting them 10° from the vertical. As shown in Fig. 1a, the open-air design was such that the magnets flanked the transducer allowing an arbitrarily large sample to be imaged. Two Kepco ATE-75-15M, 1000 W power supplies (Kepco Inc, Flushing, NY) signaled by an arbitrary waveform generator powered the electromagnets, and the magnets were water-cooled to prevent overheating. This system provided the 3 cm imaging depths needed for this study.

Fig. 1.

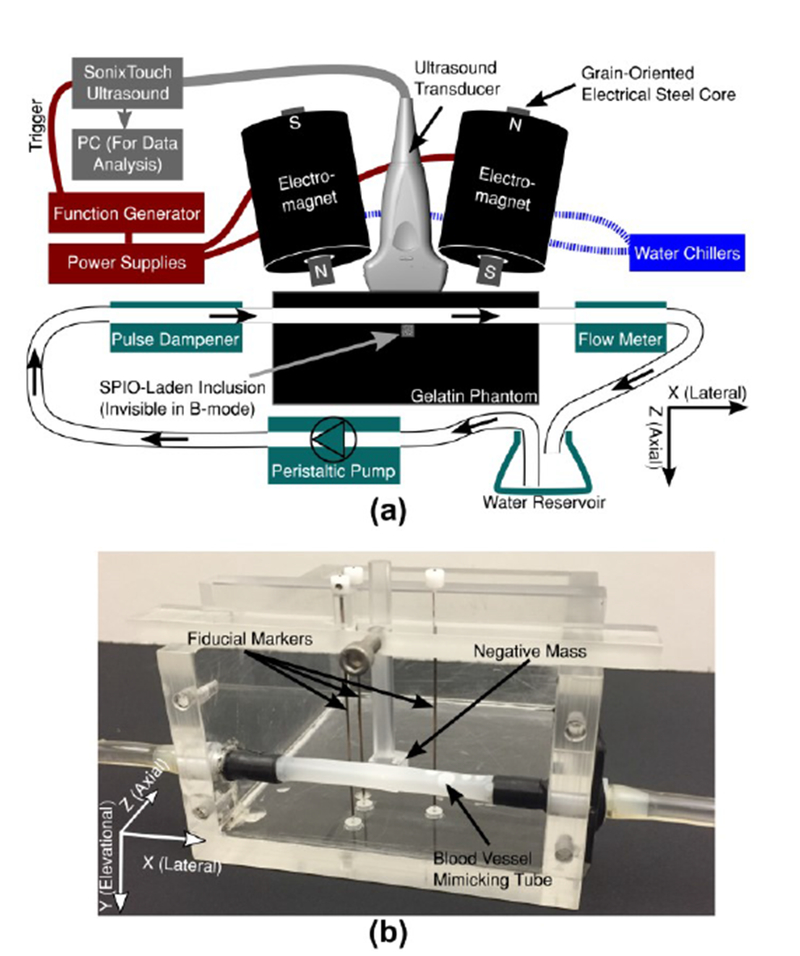
(a) Diagram of the open-air Magnetomotive Ultrasound (MMUS) system, and (b) photograph of the acrylic blood vessel phantom mold.

In order to mimic cardiovascular motion, a flow system was designed to create pulsatile water flow with adjustable flow rate through a gelatin tissue phantom. A Masterflex L/S variable speed drive pump with an Easy-Load II peristaltic pump head (Cole-Panner, Vernon Hills, IL) was used to pump tap water from an Erlemneyer flask, which acted as a reservoir, and through Masterflex L/S 16 Phar-Med BPT tubing, which was used throughout the system. The pump allowed for the frequency of the peristaltic head to be set arbitrarily, which enabled adjustment of the flow rate. Before arriving at the phantom, the water passed through a Cole-Panner pulse dampener (which served to decrease somewhat the forceful vibrations from the un-damped pump), then through the phantom mold described in the following section. The water finally traveled through a Cole-Panner 150 mm correlated flowmeter used to determine flow rate through the phantom.

B. Phantom Mold

As shown in Fig. 1b, a rectangular, acrylic phantom mold with a horizontally-embedded tube was constructed to house the gelatin tissue-mimicking blood vessel phantoms. The phantoms consisted of solid gelatin background material with a Pebax 35, 20% BaSO₄ tube (Apollo Medical Extrusion Technologies Inc, Sandy, UT) passing through the mold to mimic a blood vessel. The tubing had outer and inner diameters of 6.05 mm and 5.94 mm, respectively. A small cube of gelatin, which we will refer to as an inclusion, contained SPIO nanoparticles and was embedded immediately below the tube in the axial direction to serve as a model thrombus. This approach was chosen as a more technically feasible alternative to embedding the thrombus within the tube.

The interior of the mold measured 10 cm axially, 8 cm laterally, and 5 cm elevationally for a total volume of 400 ml, and was enclosed on five sides. The sixth side – the XZ plane at the top of Fig. 1b – was left open to allow gelatin to be poured into the mold. To facilitate ultrasound imaging, one of the five enclosed sides – the XY plane at the front of Fig. 1b – was removable. The panel is shown removed in the figure. This method of pouring gelatin into the mold in one direction and imaging from a perpendicular direction avoided strong echo artifacts from boundaries between gelatin layers. During phantom fabrication, a small acrylic removable cube was suspended from above the phantom mold such that it was in contact with the tube. This cube acted as a negative inclusion mask to create a cubical void within the background gelatin; the void was then filled with SPIO-laden gelatin to create the inclusion. The phantom mold also contained three fiducial markers designed to serve as references for axial and lateral positions within the B-mode image. In order to avoid interference with the magnetic field, 0.64 mm diameter alloy-510 Phosphor Bronze wire, which has a low magnetic susceptibility, was chosen for the markers. The fiducial markers were oriented in the elevational direction, such that they each created one bright point in the B-mode image, as shown in Fig. 2a. Since the locations of and separations between the markers and the negative mask were known, the fiducial markers were used to determine the exact inclusion location, despite the fact that the inclusion was invisible in B-mode. The geometry of the inclusion was chosen to be cubical to provide a uniform cross-section across all elevational planes.

Fig. 2.

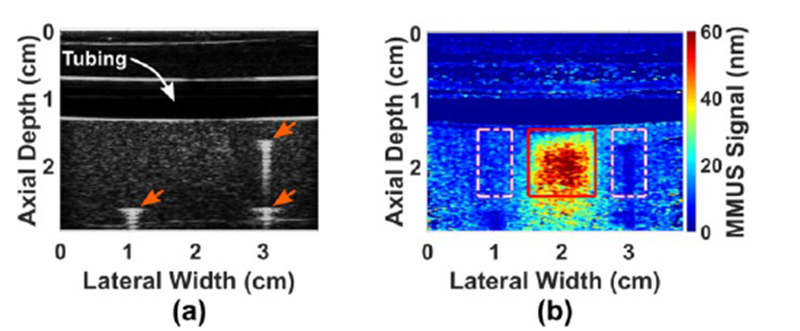
Images of a gelatin blood vessel-mimicking phantom: (a) Ultrasound B-mode image showing the locations of the 3 fiducial markers (3 arrows) used to locate the SPIO-laden inclusion, and the hypoechoic region occupied by the water within the blood vessel-mimicking tubing. The inclusion is tailored to be isoechoic with the background gelatin, and thus invisible, (b) Corresponding MMUS image showing a displacement map of the same phantom. The known location of the inclusion is boxed, and the sidebands, used for CNR, are dashed.

C. Gelatin Tissue-Mimicking Phantom Preparation

A modified version of a procedure first described by Madsen el al. was employed to create gelatin tissue-mimicking phantoms with physiologically-relevant acoustic attenuation and speed of sound values [37]. A total of thirteen phantoms were created with inclusion volumes ranging from 0.25 ml – 1 ml and inclusion Young’s moduli (which will be referred to as elastic moduli throughout) ranging from 3.5 kPa – 40 kPa. The background material, however, was made to be identical for all phantoms. In order to prepare 200 ml of the 5 kPa elastic modulus background material, 182 ml of water was heated to 50°C on one hot plate, and then removed and placed on a second hot plate set to stir vigorously with the heat turned off. Gelatin from porcine skin, gel strength 300 bloom. Type A (Sigma-Aldrich, St. Louis, MO) was then added at a concentration of 3.2 wt%, and allowed to dissolve in the stirring, cooling water. This concentration was shown to produce the desired gelatin stiffness by Hall et al. [38], and measurements performed with a TA.XT Plus texture analyzer (Texture Technologies Corp., Hamilton MA) verified agreement between nominal and actual elastic moduli at 5 and 10 kPa. To obtain an acoustic attenuation of 0.3 dB/cm/MHz and a speed of sound of 1540 m/s, 4.4 wt% synthetic graphite nanopowder (Sigma-Aldrich, St. Louis, MO), and 3.0 wt% 1-propanol were added respectively. The graphite was added about 2 minutes after the gelatin, and the mixture was allowed to stir for approximately 5 more minutes until it was homogeneous. The beaker was then placed on ice to increase the rate of cooling, and vigorous stirring continued. At intervals throughout the rapid cooling process, half of the 1-propanol was added to the solution in 1 ml increments to prevent bubble formation. When the solution reached 27°C, the beaker was removed from the ice, and the remaining 1-propanol was added. The mixture was slowly stirred for 1 minute, and then poured into the phantom mold (with a negative inclusion mask of the appropriate volume inserted). The phantom mold was then placed on ice in a closed Styrofoam cooler, and allowed to gel in the refrigerator for about 30 minutes.

The inclusion gelatin material was prepared in a manner similar to that used for the background material, but with the addition of an SPIO mixture. Graphite and 1-propanol were used in the same concentrations as in the background material so that the inclusion would be isoechoic with the rest of the phantom. Nine of the thirteen phantoms were loaded with SPIOs at a final concentration of 2.2 mg Fe/ml, while the other four were controls, and as such the SPIOs were omitted from their recipes. To create the inclusion material, an aqueous solution was created in a 50 ml conical centrifuge tube with 3.0 mg/ml of lauric acid, > 98% assay (Sigma Aldrich, St. Louis, MO), Iron (II,III) Oxide nanopowder (Sigma Aldrich, St. Louis, MO), and 15 μl/ml ammonium hydroxide 28-30 wt% (Thermo Fisher Scientific, Pittsburgh, PA). The tube was vortexed to suspend the nanoparticles, then warmed to 50°C in a water bath. Next, gelatin and graphite were added, and mixed intermittently for 10 minutes. As prescribed in Hall el al.. gelatin concentrations of 2.8, 3.2, 4.5, 6.3, and 8.8 wt% were used in order to obtain elastic moduli of 3.5, 5.0, 10, 20, and 40 kPa respectively [38]. Ice was added to the water bath, and the mixture was allowed to cool. Meanwhile, 1-propanol was added in 0.2 ml increments to prevent bubbles. The phantom mold was removed from the refrigerator, and the negative inclusion mass was extracted to reveal a cubical void. Once the inclusion mixture reached 27°C, the conical tube was removed from the water bath, mixed again, and the SPIO-laden gelatin was pipetted into the void. The phantom was then refrigerated for 30 additional minutes. To complete the phantom, another layer of background material was prepared and added to the top. Once gelation had completed, the phantom was sealed in plastic wrap to prevent evaporation, and refrigerated for 16 – 22 hours. Prior to imaging, phantoms were removed from refrigeration and allowed to sit at room temperature for two hours.

Two series of blood vessel phantoms were created. In the first series, inclusion volumes were prepared at 0.25, 0.50, 0.75, and 1.00 ± 0.03 ml while keeping the elastic modulus constant at 5.0kPa. In the second series, the inclusion elastic modulus was prepared at 3.5, 5.0, 10, 20, and 40 kPa (± 3%) while keeping the volume constant at 1 ml. Four control phantoms were also created. One of these contained no inclusion at all, while the other three contained sham inclusions without SPIO nanoparticles. These three phantoms had inclusion volumes of 1.00, 0.25, and 1.00 ± 0.03 ml, paired with elastic moduli of 5.0, 5.0, and 40 kPa (± 3%) respectively.

D. Data Collection and Analysis

The data collection procedure detailed in Pope et al. was used with minor modifications [5]. In brief, two 7.5 s sets of beamformed ultrasound RF data were collected at a sampling frequency of 61.667 fps. The first set was taken for background-subtraction purposes with the magnets switched off (B-off), while the second set was taken with the magnets modulated at 1.9891 Hz (B-on). This value was used in order to minimize errors associated with the frequency- and phase-locking scheme by ensuring that the discrete frequency index output by Fourier analysis was within 0.7% of the magnet modulation frequency. The function generator was triggered from the ultrasound such that the modulated magnetic field started with the same phase in the first frame of all RF datasets. Our previously-published signal processing algorithm was then used to isolate motion at the magnet frequency and to suppress noise from motion that was out of phase with the magnetic force [5]. Next, pixels with intensities less than approximately 40% of the average B-mode intensity were rejected. Because low intensity pixels exhibit high phase noise, the threshold was chosen to eliminate displacement noise over an order of magnitude larger than expected magnetically-induced vibration amplitudes. Finally, a custom median filter with a box size of nominally 2/3 the resolution was used to smooth the image. The custom filter excluded zero-valued (rejected) pixels from its median calculation so that low-intensity regions in the B-mode image would not contribute to the signal, since MMUS requires sufficient intensity to track the acoustic phase. The result, a map of magnetically-induced vibration amplitudes in units of nanometers, which will be referred to as the “MMUS signal,” is displayed in Fig. 2b. Note that in Fig. 2a, a standard ultrasound B-mode image, the inclusion, situated beneath the simulated blood vessel, is not visible, while in the MMUS image, the SPIO-laden inclusion is easily distinguishable.

The same data collection procedure was followed for all phantoms. A random number generator was used to select one of the following ten flow rates: 0, 52, 78, 103, 122, 150, 178, 191, 230, and 275 ml/min. The pump was set to an rpm value corresponding to the selected flow rate, and subsequently B-off and B-on data were collected. The process was repeated until four data sets for each of the ten flow rates had been collected, for a total of 40 MMUS images per phantom. While these flow rates were initially chosen in order to avoid peristaltic pump frequencies that matched the harmonics of the magnet modulation frequency, this proved to be an unnecessary precaution, as described in section IV-C.

In order to assess the detectability of inclusions by MMUS, the true location of the inclusion needed to be known precisely for each image. To achieve this, the positions of the fiducial markers were selected in the B-mode image, and their known distances from the inclusion were used to infer the inclusion location. The result is the solid-line square shown in Fig. 2b. The first metric of MMUS performance was an average MMUS signal over all the pixels within the box. MMUS signal, however, is not a measure of detectability, so a second metric, contrast-to-noise ratio (CNR), was used to estimate the ease with which an observer could determine the true location of the inclusion based only on the MMUS image. CNR compares the signal within the inclusion region to a similar exterior region of equal area. For the exterior region, rectangles on either side of the inclusion, called sidebands, were drawn. The sidebands were each the same axial height as the inclusion, half the width laterally, and offset by 1/4^th the width of the inclusion on either side. CNR was computed according to

$$CNR=\frac{{\mu }_{inclusion}-{\mu }_{sidebands}}{{\sigma }_{sidebands}},$$ (1)

Where μ_inclusion and μ_sidebands represent the average MMUS signal in the inclusion and sideband regions respectively, while σ_sidebands represents the standard deviation of the signal in the sidebands. Importantly, in order to ensure that the CNR values were not skewed by any potential differences in B-mode intensity between the inclusion and background, rejected pixels were excluded from this calculation. Any pixels that exhibited negative MMUS signal values were deemed noise, and as such set to zero, before being included in the calculation.

III. Results

A. MMUS Signal with Varying Inclusion Volume

Fig. 3a shows a representative series of MMUS images for blood vessel flow phantoms with 5 kPa elastic modulus inclusions. Inclusion volumes range from 1 ml to 0.25 ml, and a “0 ml” control phantom with no inclusion is also shown. All phantoms had background material with 5 kPa elastic modulus. From these images, it is apparent that the position of the MMUS signal matches that of the known inclusion location, as the majority of the pixels with high MMUS signals occur within the red boxes. Furthermore, the images show that MMUS signal in the inclusion region increases with volume. To quantify this relationship, the mean signal for each of the four repeated MMUS images at each flow rate was averaged. Fig. 3b displays this average MMUS signal plotted as a function of flow rate for every inclusion size. Fig. 3d shows a similar plot for CNR. In both cases, no overall trend is apparent for any phantom as a function of flow rate, as evidenced by the weak correlation (r = −0.21) between inclusion volume-averaged MMUS signal and flow rate. To isolate the dependence of the MMUS signal and detectability (CNR) on volume, these quantities were then averaged across all flow rates, and plotted as a function of inclusion volume in Fig. 3c, and Fig. 3e respectively. The resulting plots exhibit monotonic increases in both metrics as a function of volume, with resulting correlation coefficients of 0.997 and 0.986 respectively.

Fig. 3.

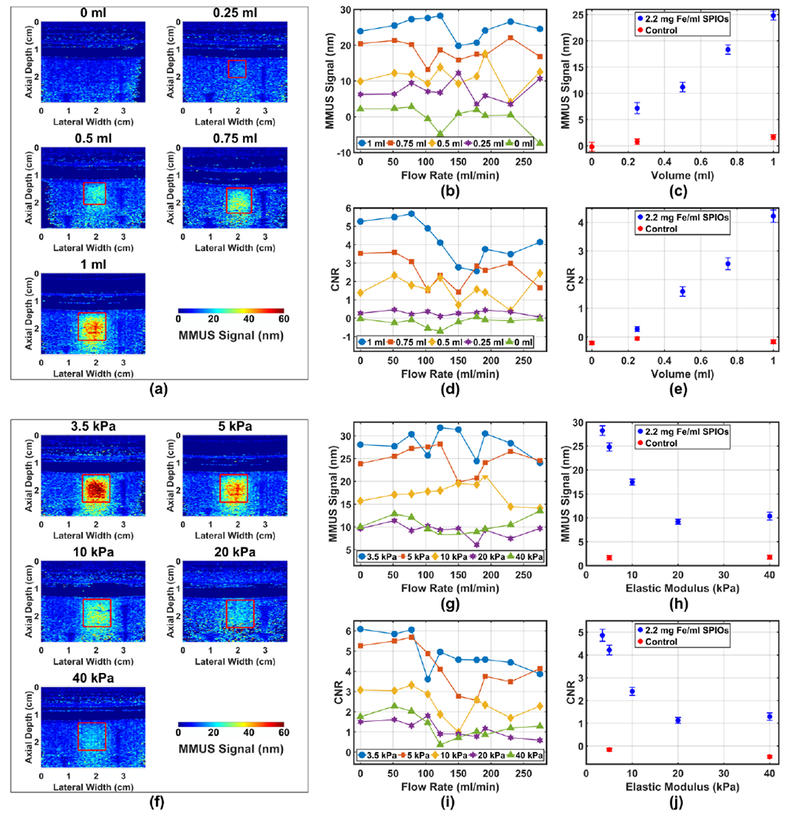
MMUS signals (i.e., magnetically-induced vibration amplitudes) from blood vessel phantoms as a function of SPIO-laden inclusion volume, inclusion elastic (Young’s) modulus, and flow rate. Panels (a)-(e) display MMUS signal with varying volume, while panels (f)-(j) display MMUS signal with varying inclusion elastic modulus, (a) Representative MMUS images at each inclusion volume with 78 ml/min flow; (b) and (c) display average MMUS signal in the inclusion as a function of flow rate, and averaged over all flow rates, respectively; (d) and (e) display CNR as a function of flow rate, and averaged over all flow rates, respectively; (f) Representative MMUS images at each inclusion elastic modulus with 78 ml/min flow; (g) and (h) display average MMUS signal in the inclusion as a function of flow rate, and averaged over all flow rates, respectively; (i) and (j) display CNR as a function of flow rate, and averaged over all flow rates, respectively. Controls containing no SPIOs in the inclusion are included for reference in (c), (e), (h), and (j). Vertical error bars represent the standard error, while uncertainties in volume and elastic modulus are smaller than the size of the plot markers.

B. MMUS Signal with Varying Inclusion Elastic Modulus

The images in Fig. 3f were obtained from 1 ml inclusion phantoms with 5 kPa elastic modulus background material. It can be seen that the MMUS signal decreases as the inclusion elastic modulus increases from 3.5 to 40 kPa, and as with the previous data, the MMUS signal appears to be well localized within the known inclusion region. Figs. 3g and 3i display MMUS signal and CNR respectively, and indicate no large trend as a function of flow rate. The correlation between elastic modulus-averaged MMUS signal and flow rate is −0.37. Upon averaging over all flow rates, it can be seen that MMUS signal (Fig. 3h) and CNR (Fig. 3j) initially fall off rapidly with increasing elastic modulus, before becoming approximately constant for the 20 and 40 kPa inclusions. MMUS signal and CNR correlation coefficients were −0.820 and −0.803 respectively.

IV. Discussion and Future Work

A. MMUS Sensitivity to Model Thrombus Volume

The results indicate that increased inclusion volume is strongly correlated with increased MMUS signal. This is expected behavior because larger inclusions contain higher volumes of SPIOs, and Equation (5) of Oldenburg el al. [18] shows that magnetomotive force on nanoparticles in the imaging region is proportional to the total volume of iron oxide. A higher force, then, would lead to a larger vibration amplitude. Furthermore, the CNR plots indicate that the minimum detectable inclusion size (the smallest inclusion volume with CNR > 1) is between 0.25 ml and 0.5 ml. In acute DVT, for example, mean thrombus volume was found to be 1.1±1.6 ml [9], or larger [39] indicating that the range of detectability may be clinically relevant.

Note that the magnetically induced vibration amplitudes necessary for detection are significantly smaller than those reported by other groups. Peak MMUS signals within the inclusion region, which contained an iron concentration of 2.2 mg Fe/ml, reached ~60 nm (representing 120 nm of peak-to-peak displacement), while average signals within the inclusion region as low ~11 nm exhibited CNR > 1. The peak magnetic field 5 mm below the core of each magnet was 0.13 T, while the average magnetic field in the inclusion region (using both magnets) measured 0.03 T. In comparison, Holst el al. reported average vibration amplitudes in the 3 – 7 μm range for SPIO concentrations of 0.14 – 0.36 mg Fe/ml embedded in PVA phantoms [19]. The maximum magnetic field was 0.18 T near the tip of the magnet. Using pulsed MMUS, Mehrmohammadi el al. obtained average displacement values in PVA phantom inclusions labeled with 1.9 mg Fe/ml Feridex particles to be above 300 μm, with an 0.6 T magnetic field in the inclusion region [21]. In each case, the magnet was positioned directly below the imaging region at least five times closer to the sample than in the system reported on here. The results of this work show that, despite the decrease in vibration amplitude associated with the open-air magnetic field delivery design, for which the magnets must be placed further from the imaging region, the MMUS system continues to provide contrast enhancement.

Detection of thrombi with MMUS in vivo would also depend on the ability to label thrombi with a sufficient concentration of SPIOs. An iron concentration of 2.2 mg Fe/ml (3.0 mg Fe₃O₄/ml) was utilized in this work. Previous work in our lab demonstrated a platelet iron loading of 140 fg Fe/platelet [5], which corresponds to an iron concentration of 2.2 mg Fe/ml when standard parameters, such as platelet number density within thrombi [40], and volume [41], are accounted for, and approximately 27% of platelets are SPIO-labeled.

B. MMUS Sensitivity to Model Thrombus Elastic Modulus

An increased MMUS signal is observed with decreasing elastic modulus. This behavior is as expected because SPIO nanoparticles within inclusions of lower elastic modulus would exhibit greater strain under the same magnetically-induced stress, leading to larger amplitudes of vibration for a given magnetic gradient force. The results also show that inclusions with elastic moduli ranging from 3.5 kPa to 40 kPa could be detected (average CNR > 1). Although thrombus elastic modulus values vary greatly in humans, the range in which detectability was demonstrated here reasonably matches what is found clinically. A study of samples from AAA patients reported an average elastic modulus of ~38 kPa with a range of ~13 – 60 kPa through compression testing [42]. In a similar study, a range of 11 – 22 kPa was later found [43]. The majority of these values fall within the experimental range studied here, while the trend evident in Fig. 3j suggests that values as high as 60 kPa are also detectable.

The ability of the MMUS system to differentiate between different inclusion elastic moduli opens the door for potential elastography in a future iteration of the system. Before full elastic modulus quantification is possible, it will be necessary to develop techniques to account for potentially confounding parameters such as variations in particle loading and distribution, and heterogeneity in magnetic gradient force and background elastic modulus. Fortunately, heterogeneity in the magnetic force field is readily characterized (as shown in Pope et al. [5]), and the volume-, modulus-, and flow-dependent data collected here constitutes a starting point for future work.

C. Dependence on Flow Rate and Pulse Frequencies

MMUS inclusion detection beneath a tube undergoing pulsatile flow at rates up to 275 ml/min was demonstrated. Interestingly, no trend as a function of flow rate was observed, despite the fact that the pulsatile flow-induced vibration amplitude in the phantom was up to two orders of magnitude larger than the magnetically-induced vibration amplitude (see Supplement I). Supplement I also presents a follow-up study in which it was shown that CNR and pulsatile flow-induced vibration amplitude were not correlated. This suggests that the phase and frequency locking method employed by MMUS is effective at rejecting background motion. In humans, flow rates vary widely as a function of blood vessel size, patient age, and health. In the male carotid artery, rates have been measured to vary between 96 and 510 ml/min. For 61+ year-olds, the average flow rate was around 400 ml/min [35]. Higher flow rates are characteristic of the human portal vein, where averages of 1202 ml/min have been observed [36]. Although human blood vessel flow rates can be much higher than the maximum tested flow rate of 275 ml/min, it is important to point out that it was not the MMUS imaging system, but the pumping apparatus that dictated this experimental upper limit. High flow rates required rapid peristaltic pulse frequencies, which lead to unrealistically violent motion in the tubing. In an in vivo scenario, this would not be an issue.

Of notable interest is our choice of ten flow rates to test. Data was collected with water pumping through the phantom at 0, 52, 78, 103, 122, 150, 178, 191, 230, and 275 ml/min, corresponding to peristaltic pump pulse frequencies of 0, 4.2, 6.27, 8.33, 10.4, 12.53, 14.6, 16.67, 20.8, and 25 Hz. These flow rates were selected both to effectively span the flow rate parameter space at relatively regular intervals, and to avoid pulse frequencies at harmonics of 2 Hz, which was feared might conflict with the ~2 Hz frequency of magnetically-induced vibration, leading to noisy images. A follow up study demonstrated this to be an unnecessary precaution. Investigations were performed into whether pump frequencies at 4, 8, and 16 Hz, corresponding to harmonics of the magnetically induced vibration, were associated with lower MMUS signals; no discemable difference was found (see Supplement II). While one limitation of this study is that water, rather than blood was used in the flow system, we note that the high flow-induced vibration amplitude of the nearby tissue-mimicking gelatin did not pose a problem, suggesting that results in blood may be similarly favorable. Our findings suggest that the experimental flow rate choices were inconsequential, and that the frequency- and phase-locking algorithm is sufficiently robust to pulsatile flow noise to be capable of handling a wide range of cardiac pulse frequencies in vivo.

D. Future Work

One of the current limitations of this MMUS system is the required image acquisition time of ~15 s (including B-on and B-off images), and subsequent computation time of ~1 min to produce each MMUS image. Development of real-time MMUS may be possible by increasing the magnetic modulation frequency somewhat, until viscous drag that damps and delays the tissue vibration becomes a limitation. It may also be possible to employ blind source separation (BSS) to decrease the ensemble length necessary to produce an MMUS image, and eliminate the need to collect B-off data [30]. Image processing times can also be improved by GPU-based acceleration. Another limitation of this study was the use of water, which exhibits lower acoustic scattering and attenuation than does blood. Future efforts using blood or blood-mimicking fluid can establish whether the additional scattering and attenuation impact the MMUS signal. A third area of future work involves imaging depth. MMUS signal exhibits roll-off due to an approximately linear 0.0014 T/cm decrease in magnetic field strength with depth. In this work, signals were observed up to 3 cm below the magnet cores, but future studies could test the limits of imaging depth. Finally, in order to accurately determine the total volume of SPIO-laden regions, two improvements could be made. One could develop an algorithm to account for the “halo” of MMUS signal that occurs around the edges of inclusions due to mechanical coupling between the inclusion and the background material. Also, 3D ultrasound could be used to collect data in the elevational dimension.

Translation of MMUS for targeted thrombosis imaging can be envisioned in future efforts by employing SPIOs with specificity for forming clots. One approach is the use of SPIO-labelled platelets which target and magnetically label thrombi [25], [26]. Rehydrated lyophilized (RL) platelets, which have the potential for years of shelf life before use, have been shown to retain their hemostatic properties in dogs [44], suggesting that SPIO-RL platelets could be used as a targeted, on-demand SPIO delivery method for contrasting thrombi. Another option is the use of particles conjugated with antibodies [45] or peptides [6], [46] with specificity to platelets, fibrin, or factors expressed in growing thrombi.

V. Conclusion

The results of this study indicate the potential for MMUS to provide detection and sizing of SPIO-labeled thrombosis in the presence of cardiac-induced blood and vessel wall motion. A blood vessel-mimicking phantom was constructed with simulated blood flow for study with MMUS for the first time. Results show direct (dark-field) detection of model thrombi as small as 0.5 ml, with elastic moduli ranging from 3.5 – 40 kPa, in the presence of flow rates as high as 275 ml/min, and flow-induced vibration amplitudes larger than that of the magnetically-induced vibrations. MMUS signal was demonstrated to increase monotonically with increasing volume and with decreasing elastic modulus, and there was no major trend as a function of flow rate. These findings suggest that MMUS is a promising, emerging technology for thrombosis imaging in vivo in environments that exhibit pulsatile flow.

Biographies

Benjamin E. Levy received his B.A. degree in Physics and Astronomy from Carleton College, Northfield, MN, USA, in 2015. He is currently pursuing his Ph.D. degree in the Department of Physics and Astronomy at The University of North Carolina at Chapel Hill, USA. His interests include magnetomotive imaging, medical ultrasound research, and physics education.

Md Murad Hossain earned his B.Sc and M. Sc degree in electrical engineering from the Islamic University of Technology, Bangladesh and George Mason University, USA in 2009 and 2014, respectively. He is currently pursuing a Ph.D. degree in the joint Department of Biomedical Engineering at the University of North Carolina – Chapel Hill and North Carolina State University. His research interests include acoustic radiation force imaging and medical signal processing.

Justin M. Sierchio earned BS, MS, and PhD degrees in Optical Sciences from the University of Arizona in 2006, 2008, and 2014 respectively. He then performed postdoctoral work at the University of North Carolina at Chapel Hill in magnetomotive ultrasound and imaging research. He currently works as a commercialization engineer at NASA Goddard Space Flight Center in Greenbelt, MD, USA, evaluating technology disclosures for patentability and commercial potential, as well as marketing new technologies to prospective agency partners and licensees. He also serves as an engineering consultant in the Department of Physics at Georgetown University in Washington, DC, USA, assisting in the development of self-assembling nanowire structures for more energy-efficient consumer electronics.

Diwash Thapa received his B.S. in Physics from the University of North Carolina at Chapel Hill in 2016. He is currently working as a clinical support technician in the Intermediate Coronary Care Unit of UNC Hospitals in Chapel Hill. His research interests include magnetomotive ultrasound imaging.

Caterina M. Gallippi earned a B.S.E. degree in electrical engineering and a certificate in engineering biology from Princeton University in 1998. She completed her Ph.D. degree in biomedical engineering at Duke University in 2003 with a focus on ultrasonic imaging. She is currently an associate professor in the joint Department of Biomedical Engineering at the University of North Carolina - Chapel Hill and North Carolina State University. Her research interests include radiation force imaging, adaptive signal filtering, multidimensional motion tracking, and magnetomotive ultrasound.

Amy L. Oldenburg received the B.S. degree in applied physics from the California Institute of Technology in 1995 and the Ph.D. degree in physics from the University of Illinois at Urbana-Champaign in 2001.

Dr. Oldenburg performed postdoctoral work at the Beckman Institute at the University of Illinois at Urbana-Champaign where she invented magnetomotive OCT. In 2008 she founded the Coherence Imaging Laboratory at the University of North Carolina at Chapel Hill, where she is currently an Associate Professor of Physics and Astronomy.

Dr. Oldenburg was a recipient of the NSF CAREER award in 2014. Dr. Oldenburg became a Senior Member of OSA in 2013, and a Senior Member of SPIE in 2011, and serves on the editorial board of the Journal of Biomedical Optics.