Economic Incentives for Managing Filterable Biological Pollution Risks from Trade

Abstract

Infectious livestock disease problems are “biological pollution” problems. Prior work on biological pollution problems generally examines the efficient allocation of prevention and control efforts, but does not identify the specific externalities underpinning the design of efficiency-enhancing policy instruments. Prior analyses also focus on problems where those being damaged do not contribute to externalities. We examine a problem where the initial biological introduction harms the importer and then others are harmed by spread from this importer. Here, the externality is the spread of infection beyond the initial importer. This externality is influenced by the importer’s private risk management choices, which provide impure public goods that reduce disease spillovers to others—making disease spread a “filterable externality.” We derive efficient policy incentives to internalize filterable disease externalities given uncertainties about introduction and spread. We find efficiency requires incentivizing an importer’s trade choices along with self-protection and abatement efforts, in contrast to prior work that targets trade alone. Perhaps surprisingly, we find these incentives increase with importers’ private risk management incentives and with their ability to directly protect others. In cases where importers can spread infection to each other, we find filterable externalities may lead to multiple Nash equilibria.

Introduction

Live animal movement is a key driver behind the spread of infectious livestock diseases (Perry et al. 2011), which are a form of “biological pollution” akin to invasive species (Daszak et al. 2000; Horan et al. 2002). The economic impact of infectious disease is staggering. For example, the costs of the 2001 foot-and-mouth disease outbreak in the United Kingdom—which was initially spread throughout Great Britain via animal movements—totaled over $4 billion (Thompson et al. 2002). Mechanisms to mitigate the externalities associated with live animal movements have thus gained considerable attention.

Efficient biological pollution management generally involves some combination of prevention efforts to limit new introductions and control efforts to limit spread after introduction (Leung et al. 2002; Finnoff et al. 2007; Mehta et al. 2007; Ranjan et al. 2008; Kim et al. 2006; Olson and Roy 2005). This prior economic work on prevention and control examines the efficient allocation of efforts but stops short of identifying the specific externalities that underpin the need for and the design of efficiency-enhancing public policies that jointly address prevention and control issues. Rather, studies that do look at policy design tend to focus either on prevention (e.g., Paarlberg and Lee 1998; McAusland and Costello 2004; Mérel and Carter 2008; Horan and Lupi 2005a,b; Knowler and Barbier 2005) or control (Horan et al. 2011; Fenichel et al. 2010) but not both. Moreover, prior analyses of biological pollution policy design largely focus on problems where those being damaged do not contribute to externalities.

We examine a problem where the initial biological introduction harms the importer and then others are harmed by spread from this importer. The example we focus on is infectious livestock diseases, although other examples also fall into this class of problems (e.g., plant nurseries at risk of importing plants contaminated with pests or disease). Within this setting, the externality is not the biological introduction into the region, but rather the spread of the biological pollutant beyond the initial importer of the pollutant. This externality is therefore influenced by an individual importer’s private risk management choices, which provide impure public goods that filter or reduce disease externalities to neighboring producers—making disease spread a “filterable externality” (Shogren and Crocker 1991). For example, a livestock producer who quarantines newly-imported animals (a type of prevention) for self-protection also reduces disease risks to neighboring susceptible herds. A producer can also protect others directly via risk-abatement measures such as properly disinfecting shared equipment before it leaves his farm (a type of control), although he may not have private incentives to do this.

We examine how filterable externalities affect socially- and privately- optimal decisions, and also the implications for efficient incentive design, for trade-driven disease problems. We explore two cases: (i) unilateral externalities, in which individual importers can introduce a pathogen into a disease-free region but are not themselves at risk of infection from others, and (ii) multilateral externalities, in which individual importers can introduce the pathogen and are also at risk of infection from others. The unilateral case does not involve strategic behavior, whereas the multilateral case does.

For the unilateral case, we find the joint impact of the importer’s prevention and control actions on the externality blurs the distinction between prevention and control. The result is that efficiently-designed incentives must target importers’ behaviors. This contrasts with prior work focused on prevention, which generally considers trade-based policies directed at exporters dealing in potentially contaminated goods (Paarlberg and Lee 1998; McAusland and Costello 2004; Mérel and Carter 2008), or transportation-based policies directed at vessels that inadvertently transport hitchhiking biological pollutants (Horan and Lupi 2005a,b). We also show, perhaps surprisingly, that the magnitude of the efficient incentives for reducing externalities increase when producers have greater private risk management incentives and a greater ability to directly protect others.

The multilateral case explores how things change when strategic behavior is introduced. Some prior work on livestock disease problems has considered strategic behavior when producers can invest in a single risk management activity that protects themselves and others (e.g., Reeling and Horan 2015; Wang and Hennessy 2015). The externalities in these analyses are inherently filterable, but the role of filterability on optimal incentive design or on the potential for multiple Nash equilibria is not explored formally. We find the impact of filterability on incentive design does not change in the multilateral case, although filterability may lead to the existence of multiple equilibria. When multiple equilibria do arise, incentives alone may not be sufficient to achieve efficiency; additional command-and-control policies (e.g., regulations) may also be needed (Anderson and Francois 1997).

A secondary contribution of our analysis is to examine the appropriate basis for economic incentives given multiple types of biological pollution uncertainties, including uncertain movement of pollution-contaminated goods (uncertain pollution generation), and uncertainty about which imports are contaminated and ultimately contribute to transmission beyond the importer’s herd (uncertain observations). These uncertainties imply biological pollution due to trade is stochastic and unobservable unless surveillance costs are incurred—and even then this pollution may only be imperfectly observable. This means the regulatory problem is somewhat analogous to nonpoint source pollution problems (Horan et al. 2002). In particular, it is infeasible to base policy instruments on biological emissions, and instead instruments must be based on specific choices that contribute to the stochastic emissions process or on emissions proxies that are functions of these choices (Horan and Lupi 2005a,b; Griffin and Bromley 1982). In their analysis of invasive species introductions, Horan and Lupi (2005a) construct a biological emissions proxy based on probabilistic relations. We find an analogous proxy works even in the context of filterable externalities and strategic interactions.

Trade and Infection Risks under Unilateral Externalities

We derive a static, one-shot model (c.f. Hennessy 2008; Reeling and Horan 2015) of livestock disease risks and management within an importing region. Livestock importers are at risk of obtaining an animal with a particular infectious disease, causing damage to their herd and then possibly spreading off the farm. We begin by assuming externalities are unilateral in that importers are only at risk of infection from importing and not from spread that originates from other importers. For instance, importers may be situated spatially such that transmission between importers is unlikely, but each importer could infect a wildlife herd that can become infected from—but not spread infection to—livestock.¹ The unilateral externality assumption allows us to avoid the issue of strategic behavior for now while generating insights that will be useful when we later explore strategic interactions arising in the multilateral case.

Consider a region containing N livestock importers, each of whom are price takers operating in competitive input and output markets. We assume N is fixed in what follows, and the region is a sufficiently small part of the industry that importers do not have a collective influence on input or output prices. We further assume importers are homogenous in terms of their production costs and benefits, as well as in their private disease risks, but that they may differ in their generation of external risks (e.g., due to locational differences in relation to other producers or wildlife). Importers are indexed by i ∈ {1,...,N} to indicate these heterogeneous external risks. Focusing only on heterogeneous external risks simplifies the notation without affecting the key results.

Each importer purchases a fixed quantity of live animals, X, from another region to raise on his farm and later sell to a slaughterhouse. We scale the model such that X = 1. These animals generate B in net revenue, not accounting for any disease-related costs (including surveillance costs and biosecurity or abatement costs incurred to protect others) and the purchase price of animal imports. The purchase price varies by supplier in response to the risks posed by the supplier’s animals. In principle, there could be many suppliers, with each posing different levels of risk to the importer. We simplify matters and assume two types of suppliers: a risky supplier (or source) and a risk-free source. The risk-free source is assumed devoid of infected animals. For instance, this source might be certified as disease-free by OIE (the Office International des Epizooties, also known as the World Organization for Animal Health). Certification may not mean no risk, but generally the risk from a certified area is so small as to be negligible. The risky source has animals that carry the infectious disease with a known probability.² This source may be identified by its lack of disease-free certification, with disease prevalence levels known due to sampling efforts (e.g., to foster disease management, to acquire certification, or to satisfy trading partners).³ The importing region and the two exporting regions may be different (small) countries or different areas within the same country: our only assumption is that the disease is novel to the importing region.

Denote the share of the animals purchased from the risk-free source as x_i ∈ [0,1], with a per-unit purchase price of v. The per-unit price of animals from the risky source is w < v. The probability the importer purchases an infected animal is denoted P^I(x_i), where ∂P^I(x_i)/∂x_i < 0, ∂²P^I(x_i)/∂x_i² > 0, ∂P^I(x_i)/∂x_i → − ∞ as x_i → 0, ∂P^I(x_i)/∂x_i → 0 as x_i → 1, and P^I(1) = 0. This probability relation is not importer-specific, and so importers face homogeneous risks for any choice of x.⁴ We simplify matters by assuming that if any imported animal is infected, then the total number of infected animals being imported is ς(1 − x_i), where ς is a fixed proportion.

The importer can inspect and quarantine animals purchased from the risky source prior to introducing them into his herd.⁵ Denote z_i ∈ [0,1] as importer i’s inspection effort. This effort effectively increases import costs from the risky source, so that these costs are w(1 − x_i)h(z_i), where h(·) ≥ 1 is an inspection cost multiplier (with h(0) = 1, h′(0) = 0, h′, h″ > 0 for x_i > 0, and h(1) > v/w). The probability that infected animals are caught via inspection is P^C(z_i), with ∂P^C(z_i)/∂z_i > 0, ∂²P^C(z_i)/(∂z_i)² < 0, P^C(0) = 0, and P^C(1) < 1. If an infection is detected, then all ς(1 − x_i) infected imported animals from the risky source are assumed to be identified and culled (and not replaced). Per-unit losses to the importer, including culling and clean-up costs and foregone net revenues from selling the animals, are denoted ζ. Then the import losses arising from detection are (1 − x_i)δ, where is δ = ςζ interpreted as the per unit loss associated with imports. Conditional on importing an infected animal, the ex ante expected costs of detection are P^C(z_i) (1 − x_i)δ.

Infected animals that are not caught via inspection are assumed to infect additional animals within the importer’s herd, with the number of infected animals within the herd equilibrating at the proportion ς. These animals may be detected on the farm (e.g., by a veterinarian) just before being sold to the slaughterhouse or upon being processed at a slaughterhouse, resulting in additional testing costs for the entire herd and reduced sales value for all infected animals.⁶ The expected per unit losses are denoted λ, with λ > δ due to the testing costs and since the producer has already invested in animal production and foregoes gross (rather than net) revenues. Conditional on importing an infected animal, the expected post-import losses are [1 − P^C(z_i)] λ. Considering both types of losses, as well as the probability of importing an infected animal, importer i’s expected losses from disease are given by

$$\mathrm{\Lambda }(x_i,z_i)=P^I(x_i)\left[P^C(z_i)(1-x_i)\delta +\left(1-P^C(z_i)\right)\lambda \right],$$

where ∂Λ(x_i, z_i)/∂x_i < 0 for x_i < 1, ∂Λ(1, z_i)/∂x_i = 0, and ∂Λ(x_i, z_i)/∂z_i < 0.

Given the specification above and assuming importers are risk-neutral, importer i’s private net benefits are given by the expected profit function⁷

$$\pi (x_i,z_i,a_i)=B-c(x_i,z_i,a_i)-\mathrm{\Lambda }(x_i,z_i).$$ (1)

The second right-hand-side (RHS) term, c(x_i, z_i, a_i) = w(1 − x_i)h(z_i) + vx_i + f(a_i), represents the importer’s costs unrelated to infection. The function f(a_i) is the cost of abatement, where a_i ∈ [0,1] is abatement effort to reduce the probability the disease will spread off an infected importer’s farm via local transmission (which does not include trade of the importer’s animals) to non-importers or wildlife. Abatement may include sanitizing equipment and workers’ clothing before allowing them to leave one’s farm (potentially taking infectious pathogens with them), and reducing contact between potentially infected livestock and susceptible wildlife. In contrast to the risk management actions x_i and z_i, which protect importer i as well as those affected by potential subsequent spread off the importer’s farm, abatement only protects others. We assume increasing, convex abatement costs (f′, f″ > 0, with f(0) = f′(0) = 0), implying c is linear in x_i and increasing and convex in z_i and a_i, with ∂c(x_i, z_i, 0)/∂a_i = ∂²c(x_i, z_i, a_i)/∂a_i∂z_i = ∂²c(x_i, z_i, a_i)/∂a_i∂x_i = 0. In what follows, we focus on c(·) rather than its individual components.

The expected profit function indicates that imports are the only source of risk to importers; an importer is not at risk from the spread of infection from other importers (i.e., externalities within the region are unilateral, as defined earlier). Specifically, an infected animal that goes undetected in importer i’s herd may only transmit the disease to susceptible agents that do not include other importers, such as non-importing local farms or a wildlife reservoir. Examples of externalities involving wildlife include bovine tuberculosis (bTB) introduced from Australian and New Zealand cattle to feral deer and possum populations (Tweddle and Livingstone 1994). Exposure to bTB, e.g., via hunting and field-dressing infected deer, can result in tuberculosis in humans (Wilkins et al. 2003).⁸

The conditional probability the disease spreads from an infected importer’s farm is given by $P_i^S(a_i)$, with $\partial P_i^S(a_i)/\partial a_i<0,{\partial }^2{P}_i^S(a_i)/{(\partial a_i)}^2>0$, and $\partial P_i^S(a_i)/\partial a_i\to 0^{-}$ as a_i → 1. Note that relation $P_i^S(a_i)$ is importer-specific because site-specific factors, the proximity of an importer’s herd to other susceptible agents, and even random events like weather that could affect animal behavior or environmental conditions affecting disease transmission might influence whether the disease spreads off a farm. Once we also account for the probability that importer i’s herd becomes infected, the probability that importer i becomes infected and then spreads the infection—or the (unconditional) probability importer i spreads the infection—is

$$e_i(x_i,z_i,a_i)=P^I(x_i)[1-P^C(z_i)]P_i^S(a_i),$$ (2)

where ∂e_i(x_i, z_i, a_i)/∂v_i < 0 and ∂²e_i (x_i, z_i, a_i)/(∂v_i)² > 0 for v ∈ {x ≠ 1, z, a} and e_i(1, z_i, a_i) = ∂e_i(1, z_i, a_i)/∂x_i = 0. Once off an importer’s farm, the disease is assumed to spread quickly to cause the same external economic damages, Θ, regardless of the source of the externality. These external damages may include disease-related reductions in non-importing farms’ profits as well as non-market damages from spread to a wildlife reservoir.⁹ Moreover, it only takes a single infection to cause these damages; any additional infections are superfluous. This final simplifying assumption means mitigating spread is a weakest-link public good (Perrings et al. 2002; Hirshleifer 1983), such that the probability that damages occur is the same as the probability that at least one importer spreads the disease to non-importers, which is

$$P^D(\mathbf{e})=1-{\prod }_i[1-e_i(x_i,z_i,a_i)],$$ (3)

where e = [e₁...e_N]. Expected social damages from disease spread are D(P^D(e)) = ΘP^D(e), which is linearly increasing in P^D(·) and thereby in e_i.

Expected social net benefits, V, are the sum of importers’ profits less expected social damages: $V={\sum }_{i=1}^N{\pi }_i(x_i,z_i,a_i)-D(P^D(\mathbf{e}))$. The specification of π_i(x_i, z_i, a_i) and of P^D(e) suggests that, while all risk management activities reduce externalities, importers will only have private incentives to invest in the prevention efforts x_i and z_i;a_i only decreases expected profits. This means x_i and z_i provide impure public goods that filter the disease externalities in the unilateral case, whereas a_i is a pure public good.¹⁰

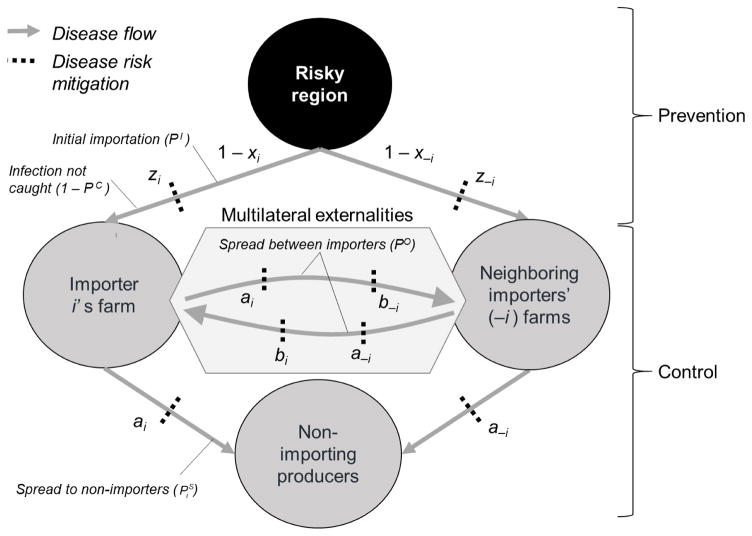
The disease pathways and the role of the various choices in these pathways are illustrated by Figure 1. For our current discussion of unilateral externalities, we ignore the multilateral externality pathways illustrated in the hexagon (these are explored later). The importer’s choices have been placed into one of two categories depending on which disease transmission process the choices primarily affect: (i) prevention (x_i and z_i), which affects the introduction of infected animals into the region; and (ii) control (a_i [and b_i in the case of multilateral externalities]), which affects disease spread within the region.¹¹

Figure 1.

Biological pollution pathways

The Efficient and Privately-Optimal Outcomes under Unilateral Externalities

We now compare the efficient and privately-optimal outcomes to identify the externality, to examine the role of private risk management activities in filtering this externality, and to consider the design of efficient incentives.

The ex ante efficiency conditions are derived by choosing x_i, z_i, and a_i to maximize V, whereas a producer’s privately optimal strategy involves choosing these same variables to maximize π(·). We begin by considering the first order conditions (FOCs) for the prevention choices in the private optimum:

$$\frac{\partial \pi }{\partial v_i}=0\Rightarrow \frac{\partial c}{\partial v_i}+\frac{\partial \mathrm{\Lambda }}{\partial v_i}=0,v\in \{x,z\}$$ (4)

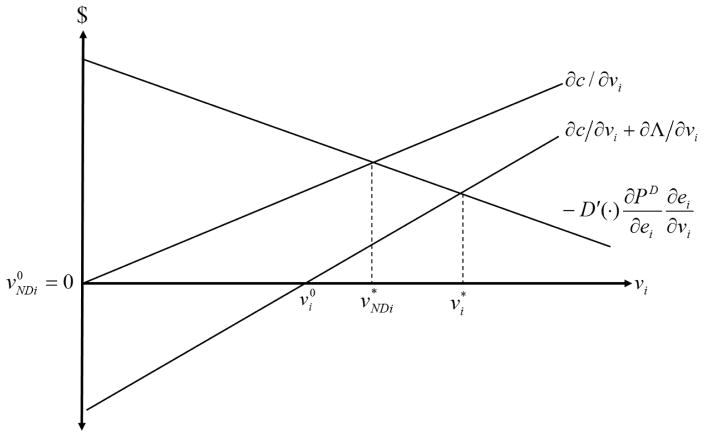
The properties of the relations in (4) ensure that an interior solution arises for x_i and z_i (see Proposition 1 in the Appendix). Condition (4) requires the marginal cost of each choice v_i, ∂c/∂v_i, to equal the marginal private benefit of this choice, −∂Λ/∂v_i, where the marginal private benefits involve the reduced economic risks conferred to producer i through the prevention activity v (i.e., importing more from the safe region to avoid disease risks, x_i, or testing more to prevent infected imports from spreading within the herd, z_i). The term −∂Λ/∂v_i measures the extent to which the choice v will be chosen to filter the externality, with a greater value indicating more filtration will occur. The economic tradeoffs inherent in the FOCs are depicted in Figure 2 via the marginal private net cost curve, ∂c/∂v_i + ∂Λ/∂v_i. The private optimum arises at point $v_i^0$ where marginal private net costs vanish. For the special case where Λ = 0 (i.e., the producer faces no private disease risks), the optimality condition is ∂c/∂v_i = 0 ∀v, which occurs at the origin. We denote the privately optimal value of v_i in this no-private-damage case as $v_{\mathit{NDi}}^0=0\forall v$.

Figure 2.

Privately- and socially-optimal risk management choices

(Note: ∂Λ/∂x_i, ∂Λ/∂z_i < 0; ∂Λ/∂a_i = 0)

The private optimum exhibits a corner (or, more accurately, a weakly interior) solution for the abatement control choice such that $a_i^0=0$. This is because the marginal private benefit of abatement is zero as abatement conveys no protection to importer i’s herd. That is, producers have no private incentive to invest in abatement that only controls spread since there are no private benefits to doing so, and so abatement does not filter the externality.

Now consider the ex ante efficient outcome, or social optimum. The FOCs for both prevention and control choices in the efficient outcome are

$$\frac{\partial V}{\partial v_i}=0\Rightarrow \frac{\partial c}{\partial v_i}+\frac{\partial \mathrm{\Lambda }}{\partial v_i}=-D^{\prime }(·)\frac{\partial P^D}{\partial e_i}\frac{\partial e_i}{\partial v_i},v\in \{x,z,a\}\text{and}\forall i.$$ (5)

The properties of the relations in (5) ensure that an interior solution arises for each choice v_i (see Proposition 2 in the Appendix), such that the first-best outcome generally involves some combination of prevention and control (consistent with Finnoff et al. 2007 and Leung et al. 2002). Condition (5) requires the marginal private net cost of each choice v_i, ∂c/∂v_i + ∂Λ/∂v_i, equal the marginal external benefit of this choice, $-D^{\prime }(·)\frac{\partial P^D}{\partial e_i}\frac{\partial e_i}{\partial v_i}=-\mathrm{\Theta }\frac{\partial P^D}{\partial e_i}\frac{\partial e_i}{\partial v_i}$, which is the expected marginal avoided social damages due to risk management. It is readily verified that the marginal private net cost curve is upward sloping and the marginal external benefit is downward sloping, as illustrated in Figure 2. As $-\mathrm{\Theta }\frac{\partial P^D}{\partial e_i}\frac{\partial e_i}{\partial v_i}>0$, the marginal private net cost of each choice must also be positive, suggesting the social optimum occurs at a point $v_i^{\ast }>v_i^0$ as depicted in Figure 2: the first-best value exceeds the privately-optimal value, which does not account for the expected marginal external benefits of v_i. This is only a partial result. More generally, the private externality, $e_i^0$, exceeds the first-best externality, $e_i^{\ast }$, when the restricted profit function π_i(e_i) = B − c(e_i) − Λ(e_i) = max_xi,zi,ai{B − c(x_i, z_i, a_i) − Λ(x_i, z_i)|e_i(x_i, z_i, a_i) ≤ e_i} is concave in e_i (see Proposition 3 in the Appendix).

Figure 2 suggests two results pertaining to the filterability of producer i’s externality. First, filterability encourages more private disease management efforts as $v_i^0>v_{\mathit{NDi}}^0$. Second, filterability reduces deviations between the privately- and socially-optimal decisions, i.e., $v_i^{\ast }-v_i^0<v_{\mathit{NDi}}^{\ast }=v_{\mathit{NDi}}^{\ast }-v_{\mathit{NDi}}^0$. The partial analysis of Figure 2 makes it difficult to verify that these results hold for each individual choice. However, by focusing on e_i rather than the individual choices, we can determine sufficient conditions under which these results hold. Specifically, the filterability of producer i’s externality, other things equal, reduces

1. both the privately-produced externality and the efficient externality of producer i when π_i(e_i) is concave in e_i and Λ(e_i) is increasing e_i, and

2. the difference between the privately-optimal and socially-optimal externality generated by producer i if, additionally, π_i(e_i) is reasonably approximated by a quadratic relation (so that ∂²π_i(e_i)/(∂e_i)² is essentially constant) and Λ(e_i) is convex in e_i (see Proposition 4 in the Appendix).

Incentives for Efficient Disease Control

We now consider how economic incentives might be designed and implemented to eliminate the externalities described above. Incentives for managing disease transmission would ideally be based on the actual emissions of biological pollutants, but this approach is generally infeasible because disease transmission is stochastic and the actual spread of infection to others is unobservable (at least, without considerable cost to trace the source of infection; Elbakidze 2007).

Disease control incentives must be based on an alternative construct in the face of stochastic and unobservable emissions. Griffin and Bromley (1982), who examine nonpoint source pollution, suggest two alternatives. The first is to base policies on a nonpoint pollution production function that links a firm’s choices to emissions, thereby acting as a performance proxy. The analogous construct for biological pollution is the probability of disease spread, e_i(·). Such a measure can be thought of as a risk-based performance proxy. The second approach is to target the individual choices or inputs that contribute to external infection risks through the use of input-based incentives. Both approaches have been analyzed and applied for the case of invasive species (Horan and Lupi 2005a; Horan and Lupi 2005b), but not for the case of filterable externalities involving both prevention and control activities.

Consider a risk-based incentive in which a tax t_i is levied on the probability of disease transmission, e_i, as calculated from a predictive model based on observations of the importer’s decisions.¹² The importer’s expected profits in this case are π(x_i, z_i, a_i) − t_ie_i(x_i, z_i, a_i), where t_i is the tax rate. Comparison of the FOCs for this problem,

$$\begin{array}{l}\frac{\partial V}{\partial v_i}=\frac{\partial {\mathrm{\pi }}_i}{\partial v_i}-D^{\prime }\frac{\partial e_i}{\partial v_i}=0\\ \Rightarrow \frac{\partial c_i}{\partial v_i}+\frac{\partial {\mathrm{\Lambda }}_i}{\partial v_i}=-D^{\prime }\frac{\partial e_i}{\partial v_i}\forall i;v\in \{x,z,a\}.\end{array}$$ (6)

$$\frac{\partial c}{\partial v_i}+\frac{\partial \mathrm{\Lambda }}{\partial v_i}=-t_i\frac{\partial e_i}{\partial v_i},v\in \{x,z,a\},$$ (7)

with the efficient FOCs (6) shows the first-best risk-based tax rate applied to importer i is

$$t_i^{\ast }=D^{\prime }\left(P^D({\mathbf{e}}^{\ast })\right)\frac{\partial P^D({\mathbf{e}}^{\ast })}{\partial e_i}=\mathrm{\Theta }{\prod }_{j\ne i}\left[1-e_j^{\ast }\right]\forall i,$$ (8)

where $e_j^{\ast }=e_j\left(x_j^{\ast },z_j^{\ast },a_j^{\ast }\right)$. The efficient tax rate in (8) equals damages, Θ, times the marginal impact of e_i on the overall probability of spread, P^D(·), evaluated at the first-best outcome. Due to the weakest-link public good nature of disease spread, the marginal impact depends on the risks posed by other importers—specifically, the probability that none of the other importers spreads the disease—rather than on the risks generated by importer i. This result has three implications, the first two of which have arisen in prior work on biological externalities (Horan and Lupi 2005a). First, the efficient tax rate is importer-specific due to the location-specific risks posed by other importers. Second, the efficient tax will be smaller the greater the likelihood that other importers cause a disease outbreak, all else equal.

The third implication, which is novel, is that the filterable nature of importer i’s externalities do not directly influence importer i’s efficient tax rate.¹³ Rather, others’ filterable externalities directly affect $t_i^{\ast }$ via their influence on the $e_j^{\ast }$ terms. We have already shown that $e_j^{\ast }$ is smaller when externalities are filterable, which means $t_i^{\ast }$ is larger when externalities are filterable. This result indicates filterable externalities increase the required public incentives for risk management, at least when utilizing a risk-based tax. This may seem surprising since our earlier results indicate that, other things equal, the presence of filterable externalities by producer i reduces the difference between the privately-optimal and socially-optimal externalities generated by producer i. However, this is only a partial result and says nothing about the effects of filterable externalities by other producers.

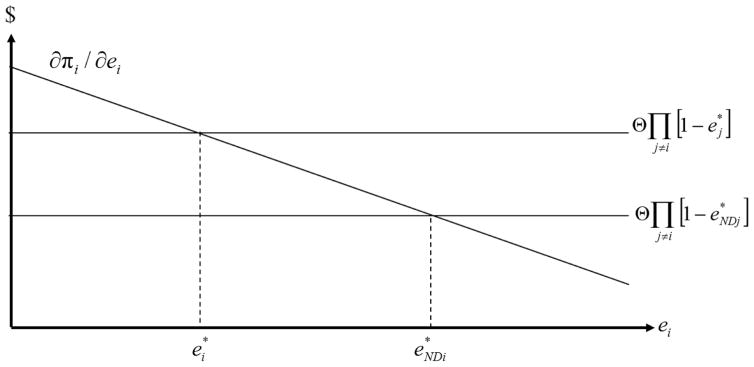
The marginal benefits of e_i, ∂π_i/∂e_i, and the expected marginal damages associated with e_i, $\mathrm{\Theta }{\prod }_{j\ne i}\left[1-e_j^{\ast }\right]$, are illustrated in Figure 3. The expected marginal damage curve, which equals the optimal tax rate $t_i^{\ast }$, is horizontal since this relation is independent of e_i. However, this curve does depend on the e_j terms. The lower marginal damage curve, $\mathrm{\Theta }{\prod }_{j\ne i}\left[1-e_{\mathit{NDj}}^{\ast }\right]$, represents expected marginal damages when the externalities are not filterable. The expected marginal damage curve shifts up to $\mathrm{\Theta }{\prod }_{j\ne i}\left[1-e_j^{\ast }\right]$ when the externalities produced by others are filterable so that others benefit from investing more in risk management ( $e_j^{\ast }<e_{\mathit{NDj}}^{\ast }$). When others invest more, the expected marginal social benefits of investments by importer i also increase due to the weakest-link nature of the problem, and the equilibrium value of e_i falls ( $e_i^{\ast }<e_{\mathit{NDi}}^{\ast }$).

Figure 3.

Filterable externalities reduce efficient emissions from $e_{\mathit{NDi}}^{\ast }$ to $e_i^{\ast }$

Now consider the use of input-based incentives whereby importer i is charged a tariff, τ_i, on all animals purchased from the risky source and receives per-unit subsidies ∂_zi and ∂_ai for each unit of inspection effort and abatement effort he undertakes on his farm, respectively.¹⁴ The importer’s expected profits in this case are π(x_i, z_i, a_i) − τ_i(1 − x_i) + σ_ziz_i + σ_aia_i. Comparing the FOCs for this problem (not shown for conciseness) with the efficient FOCs implies the following first-best input-based incentives

$${\tau }_i^{\ast }=-D^{\prime }\left(P^D({\mathbf{e}}^{\ast })\right)\frac{\partial P^D({\mathbf{e}}^{\ast })}{\partial e_i}\frac{\partial e_i^{\ast }}{\partial x_i}=t_i^{\ast }\left|\frac{\partial e_i^{\ast }}{\partial x_i}\right|\forall i,$$ (9)

$${\sigma }_{vi}^{\ast }=-D^{\prime }\left(P^D({\mathbf{e}}^{\ast })\right)\frac{\partial P^D({\mathbf{e}}^{\ast })}{\partial e_i}\frac{\partial e_i^{\ast }}{\partial v_i}=t_i^{\ast }\left|\frac{\partial e_i^{\ast }}{\partial v_i}z\right|\forall i;v\in \{z,a\},$$ (10)

The first-best incentive rate for each input v_i ∈ {x_i, z_i, a_i} is the efficient risk-based tax times the absolute marginal effect of v_i on the probability the importer spreads the infection.

Two results immediately arise from (9) and (10): to be first-best, incentives should be applied to each input contributing to e_i, and these rates should be importer-specific due to the importer-specific risk-based tax as well as the importer-specific marginal impacts on e_i. Both results are consistent with Horan and Lupi’s (2005) analysis of input-based incentives to prevent species invasions, but they may be obscured in some prior work (e.g., McAusland and Costello 2004; Mérel and Carter 2008; Paarlberg and Lee 1998) that models a single, representative importer that only makes trade decisions. In such models, uniform incentives applied to only trade-related decisions would seem to be optimal. However, when non-trade decisions such as a_i affect social risks, then inefficiencies arise by focusing only on trade-based incentives. Similarly, the use of uniform incentives will generally create efficiency losses as importers with a small effect on expected social damages will receive incentives that are too large, and vice versa (Shortle et al. 1998).

Relations (9) and (10) also provide insights into the role of filterable externalities, which have not been explored in prior work. Specifically, we find that filterable externalities have two impacts on each incentive rate. First, they increase $t_i^{\ast }$ to encourage greater incentive rates. This effect impacts each incentive rate. Second, filterable externalities affect | $\partial e_i^{\ast }/\partial v_i$| in an ambiguous manner. The overall impact of filterable externalities could be to increase or decrease the incentive rates, depending on which effect dominates. However, our prior results on externality-based incentives suggests that filterable externalities will lead to an increase in the overall level of protection, even if investments in one or two risk-protection choices declines.

Trade and Infection Risks under Multilateral Externalities

We now extend the model to consider the case in which disease externalities are multilateral in the sense that an importing producer’s herd is also at risk of becoming infected via spread from other importers. Here, an importer’s payoffs depend on both their own risk mitigation decisions and their neighbors’ (via neighbors’ emissions) so that strategic interactions arise in a one-shot Cournot game. This is in contrast to the unilateral externalities case, where importers’ payoffs are independent of their neighbors’ choices.

Suppose importer i’s herd can be infected via spread from any of the N – 1 neighboring importers’ herds, should they become infected (see the portion of Figure 1 labeled “Multilateral Externalities”). Importer i can protect his own herd from this spread of infection by investing in biosecurity effort b_i ∈ [0,1].¹⁵ We can then write the probability importer i’s herd becomes infected from any of the N − 1 neighboring importers (i.e., the probability of multilateral spread) as

$$P_i^O(b_i;{\mathbf{e}}_{-i})=P^E(b_i)\left(1-{\prod }_{j\ne i}[1-e_j(x_j,z_j,a_j)]\right),$$ (11)

where e_−i = [e_i … e_{i −1} e_i+1 … e_N] and P^E(b_i) is the probability the disease becomes established in importer i’s herd, conditional on spread from at least one of his neighbors. We assume ∂P^E(b_i)/∂b_i < 0, so $P_i^O$ is decreasing in each argument. Importer i’s expected disease losses are $\mathrm{\Lambda }+P_i^O(b_i;{\mathit{e}}_{-i}){\mathrm{\Omega }}_i(x_i,z_i)$, where

$${\mathrm{\Omega }}_i(x_i,z_i)=[1-P^I(x_i)]\lambda +P^I(x_i)P^C(z_i)[x_i+(1-x_i)(1-\varsigma )]\lambda$$ (12)

is the expected losses arising in cases where multilateral transmission occurs. Assuming a currently-infected herd cannot be infected again, there are two scenarios under which multilateral transmission may occur and damage importer i. The first scenario is when producer i’s herd is not infected from imports of risky animals, but is infected via multilateral transmission. The expected losses in this scenario are given by the first RHS term in (12). The second scenario is when surveillance detects infection in producer i’s imports (and the infected animals are subsequently removed), and then the remaining x_i + (1 − x_i)(1 − ς) healthy animals are infected via multilateral transmission. The expected losses in this scenario are given by the second RHS term in (12). We continue to assume importers can spread the disease to other, non-importing producers, causing expected damages D(P^D(e)) in addition to the damages to neighboring importers (i.e., the Ω_i terms).

Given the expected costs of multilateral transmission, importer i’s expected profits are

$${\pi }_i(x_i,z_i,a_i,b_i;{\mathbf{e}}_{-i})=B-c(x_i,z_i,a_i,b_i)-\mathrm{\Lambda }(x_i,z_i)-P_i^O(b_i;{\mathbf{e}}_{-i}){\mathrm{\Omega }}_i(x_i,z_i),$$ (13)

where c(·) takes the same form as in (4) except that it now also includes biosecurity costs, denoted g(b_i), with ∂g/∂b_i > 0.

We simplify the remaining analysis by rewriting (13) as a restricted profit function in b_i and e_i,

$$\begin{array}{l}{\pi }_i(e_i,b_i;{\mathbf{e}}_{-i})=B-c(e_i,b_i;{\mathbf{e}}_{-i})-\mathrm{\Lambda }(e_i;{\mathbf{e}}_{-i})-P_i^O(b_i;{\mathbf{e}}_{-i})\mathrm{\Omega }(e_i;{\mathbf{e}}_{-i})\\ =\underset{e_i,b_i}{max}\{{\pi }_i(e_i,b_i;{\mathbf{e}}_{-i})\mid e_i\le e_i(x_i,z_i,a_i)\},\end{array}$$

and focusing on this relation. This means e_i is treated as a choice in what follows, as is common in pollution problems (e.g., Tietenberg 1985). Note that $\partial {\pi }_i(e_i,b_i;{\mathbf{e}}_{-i})/\partial e_j=[\partial P_i^O(b_i;{\mathbf{e}}_{-i})/\partial e_j]{\mathrm{\Omega }}_i(x_i,z_i)$ by applying the envelope theorem to (13).

The Efficient and Privately-Optimal Outcomes under Multilateral Externalities

We examine a Nash-Cournot game in which importer i’s private problem is to maximize his expected profits, taking e_−i as given: max_ei,bi π_i(e_i, b_i; e_−i). The first order conditions for an interior, private optimum are

$$\frac{\partial {\pi }_i(e_i,b_i;{\mathbf{e}}_{-i})}{\partial b_i}=0;\frac{\partial {\pi }_i(e_i,b_i;{\mathbf{e}}_{-i})}{\partial e_i}=0.$$ (14)

The conditions in (14) imply the familiar result that marginal expected net benefits from self-protection (b_i) and emitting biological pollution, respectively, are zero. Note that the marginal incentives associated with each choice ( $\frac{\partial {\pi }_i(e_i,b_i;{\mathbf{e}}_{-i})}{\partial b_i},\frac{\partial {\pi }_i(e_i,b_i;{\mathbf{e}}_{-i})}{\partial e_i}$) depend on the choices of others, e_−i. In particular, $\frac{{\partial }^2{\pi }_i(e_i,b_i;{\mathbf{e}}_{-i})}{\partial e_i\partial e_j}=-\left(P^E(b_i){\prod }_{k\ne j,i}[1-e_k]\right)\frac{\partial {\mathrm{\Omega }}_i(e_i)}{\partial e_i}$, which is of the opposite sign of ∂Ω_i(e_i)/∂e_i. If ∂Ω_i(e_i)/∂e_i < 0, which is likely since a larger e_i increases the likelihood importer i is damaged by his or her own actions rather than other importers, then $\frac{{\partial }^2{\pi }_i(e_i,b_i;{\mathbf{e}}_{-i})}{\partial e_i\partial e_j}>0$ (producer i’s marginal incentives for e_i are increasing in e_j, and vice versa) so that e_i and e_j are strategic complements (Vives 2005).¹⁶ Multiple equilibria can arise in the presence of strategic complementarities. We discuss the potential implications of multiple equilibria in a later section. For now, suppose a unique Nash equilibrium arises as an interior solution, with the privately-optimal choices that solve (14) being $b_i^0$ and $e_i^0$.¹⁷

Consider next the social planner’s problem, which is to choose b_i and e_i ∀i to maximize aggregate importer profits less damages to non-importers. Formally, the social planner’s problem is max_{ei, bi ∀i} Σ_i π_i(e_i, b_i; e_−i) − D(P^D(e)). Assuming an interior solution, the first-best choices, $b_i^{\ast }$ and $e_i^{\ast }$, solve the necessary conditions

$$\frac{\partial {\pi }_i(e_i,b_i;{\mathbf{e}}_{-i})}{\partial b_i}=0$$ (15)

$$\frac{\partial {\pi }_i(e_i,b_i;{\mathbf{e}}_{-i})}{\partial e_i}-{\sum }_{j\ne i}\frac{\partial P_j^O(b_j;{\mathbf{e}}_{-j})}{\partial e_i}{\mathrm{\Omega }}_j(e_j)-D^{\prime }\left(P^D(\mathbf{e})\right)\frac{\partial P^D(\mathbf{e})}{\partial e_i}=0\forall i.$$ (16)

where the summation term in (16) reflects expected marginal losses to neighboring importers due to spread from importer i’s herd. Comparing (15) and (16) with (14) shows that—as with the externality to non-importers—the externality to importers arises from e_i. In contrast, importers will choose $b_i^0$ at the first-best level whenever policies are implemented to ensure $e_i^0=e_i^{\ast }$. The reason is that b_i does not affect the production of biological pollution, and hence no externalities arise from its under-provision. However, $b_i^0$ will be inefficiently large when $e_i^0>e_i^{\ast }$.

Incentives for Efficient Disease Control with Multilateral Externalities

Consider how economic incentives might be designed and implemented to eliminate the multilateral externalities described above. Efficiency can be attained through either risk- or input-based incentives, as in the unilateral case. For conciseness, we derive only the optimal risk-based tax; deriving the optimal input-based incentives provides little additional insight beyond that discussed for the unilateral case.

Suppose importer i is charged a risk-based tax of t_ie_i, where t_i is a tax rate. Importer i’s after-tax profits are π_i(e_i, e_i; e_−i) − t_ie_i. Only the importer’s first order condition with respect to e_i is influenced by the tax, becoming

$$\frac{\partial {\pi }_i(e_i,b_i;{\mathbf{e}}_{-i})}{\partial e_i}-t_i=0.$$ (17)

Comparing (17) to (16) shows that the first-best tax rate is

$$t_i^{\ast }=\mathrm{\Theta }{\prod }_{j\ne i}\left[1-e_j^{\ast }\right]+{\sum }_{j\ne i}{P}^E\left(b_j^{\ast }\right){\mathrm{\Omega }}_j(e_j^{\ast }){\prod }_{k\ne j,i}[1-e_k^{\ast }]\forall i.$$ (18)

This tax rate is similar to the first-best rate identified in (10), except that the rate in (18) is larger to reflect the external marginal damages to neighboring importers. Moreover, the previously-described effect of filterable externalities on first-best tax rates is strengthened: the tax rates are further increased as neighbors have greater private incentives to reduce their externalities, $e_k^{\ast }$.

Efficient Incentives in the Presence of Multiple Equilibria

The foregoing assumes the decentralized Nash equilibrium is unique. This need not be the case, as prior work suggests strategic interactions between importers’ trade-related choices (e.g., import and surveillance decisions) may result in multiple Nash equilibria under multilateral externalities (Hennessy 2008; Reeling and Horan 2015). Multiple Nash equilibria arise from non-convexities brought on by strategic complementarities between producers’ self-protection choices.¹⁸ As discussed above, strategic complementarities between e_i and e_−i may exist both before and after implementation of the efficient risk-based tax.

The existence of multiple equilibria complicates incentive design, as the equilibrium outcome that arises depends on importers’ expectations regarding their neighbors’ choices. If enough importers believe their neighbors will make choices consistent with the Pareto dominant outcome, which is the efficient equilibrium in the case of an efficient tax (Milgrom and Roberts 1990; Vives 2005), then the system will converge to this outcome. Coordination failure arises when an insufficient number of importers’ expect neighbors will make efficient choices, so that the system instead equilibrates at a Pareto-dominated equilibrium exhibiting lower risk mitigation levels.

The problem of coordination failure is formalized as follows. Suppose there are multiple roots to the importer’s necessary conditions in (17), resulting in an efficient, Pareto-dominant Nash equilibrium, denoted $({\mathbf{b}}^{\ast },{\mathbf{e}}^{\ast })=\left((b_1^{\ast },e_1^{\ast }),\dots ,(b_N^{\ast },e_N^{\ast })\right)$, and K > 1 Pareto-dominated Nash equilibria, $\left({\mathbf{b}}_k^{\#},{\mathbf{e}}_k\right)=\left((b_{1k}^{\#},e_{1k}^{\#}),\dots ,(b_{Nk}^{\#},e_{Nk}^{\#})\right)>({\mathbf{b}}^{\ast },{\mathbf{e}}^{\ast })$ for k ∈ {1, …, K}. Prices alone cannot generally ensure the system converges to the efficient equilibrium in the presence of multiple equilibria and coordination failure risks (Dasgupta and Mäler 2003), which means importers may instead arrive at one of the Paretodominated outcomes.

Following Anderson and Francois (1997), the efficient outcome can be ensured through a combination of the efficient risk-based tax in (18) and command-and-control regulations on e_i. Specifically, suppose a regulatory authority can set and enforce a maximum allowable e_i, say, ${\overline{e}}_i>e_i^{\ast }$.¹⁹ Efficiency can then be attained by setting ē_i sufficiently close to $e_i^{\ast }$, with ${\overline{e}}_i<e_{ik}^{\#}$ for $e_{ik}^{\#}\le e_{i{k}^{\prime }}^{\#}$ ∀k′ = 1, …, K. Importers will then expect their neighbors to make efficient decisions. In other words, this regulation eliminates importers’ expectations that can lead to coordination failure: all Pareto-dominated equilibria are precluded such that the only remaining equilibrium coincides with the efficient outcome. Note also that the regulation ē_i is non-binding in the sense that importers will have private incentives to reduce e_i beyond this level. The need for such a regulation is in contrast to much of the prior literature on trade-related biological pollution externalities (e.g., McAusland and Costello 2004; Mérel and Carter 2008; Paarlberg and Lee 1998; Horan and Lupi 2005), as well as much of the more general pollution literature, due to the fact that multilateral externalities do not arise in these models.

Discussion and Conclusion

Trade-related livestock disease problems are biological pollution problems whose efficient management generally requires that importers adopt both prevention efforts (e.g., import and surveillance choices) limiting introduction and control efforts (e.g., abatement and biosecurity decisions) limiting spread. These disease problems also involve two features not shared by other biological pollution problems, such as invasive species: an importer’s importation decisions create risks to his own herd and to the herds of other local importers. The risks to one’s own herd means that any externalities from an importer are filterable. The risks to other importers’ herds means the externalities are multilateral, introducing a strategic element into the problem. Prior work on pollution problems— including biological pollutants and more traditional nonpoint source pollutants—has not explored the implications of filterability for policy design, largely because many pollution problems do not harm the polluter directly.

Our analysis has examined the design of first-best pollution management incentives when externalities are filterable. When externalities are unilateral, efficiency can be attained via importer-specific incentives on either (i) the probability disease spreads from one’s farm (risk-based incentives) or (ii) on all choices that contribute to the probability of spread (input-based incentives). This is in contrast to prior work in the international trade literature, which generally focuses only on trade-related decisions (e.g., McAusland and Costello 2004; Mérel and Carter 2008). While it is correct to properly incentivize trade-based choices, such policies alone do not fully internalize the biological pollution externality. Perhaps surprisingly, optimal risk-based incentives are greater when importers have greater private incentives for risk mitigation. This result stems from the weakest-link nature of disease externalities: when other importers’ self-protection efforts reduce social risks, then an individual importer becomes a relatively weaker link whose risk management efforts produce greater marginal social benefits.

The marginal incentives for disease management are further increased in the multilateral externality case. We also find that some risk management efforts may be strategic complements in the multilateral case, possibly creating multiple Nash equilibria that may involve coordination failure. Additional command-and-control policies (e.g., regulations) may be needed alongside incentives to avoid coordination failure and suboptimal disease outcomes.

Our analysis has been simplified in two ways that facilitate analytical results but have minimal bearing on the qualitative results. First, we have assumed all importers have identical profit relations, with the only heterogeneity being the probabilistic impacts to others. This assumption is made to highlight that this one source of heterogeneity makes the efficient incentives for disease management importer-specific, and adding additional heterogeneities will not change this result.

Our second simplification was to make the model static, so that the introduction and initial spread of the disease occur within a single period. The model could be easily extended to incorporate two time intervals: (i) a pre-invasion interval that also includes the immediate impact of infection and (ii) a post-invasion interval that includes longerterm impacts (e.g., Berry et al. 2015). But this more complex setting does not affect the impure public good nature of an importer’s actions to reduce his own risks (i.e., externalities remain filterable), either through prevention or control efforts. A dynamic setting also does not eliminate the strategic nature of these externalities in the multilateral case; a differential game simply replaces our one-shot game. Accordingly, there is no reason to suspect that a dynamic approach would affect our qualitative results that efficient incentives are importer-specific and influenced by the filterability of externalities, and that strategic behavior could produce multiple equilibria.

Appendix

This appendix contains proofs of the major results stated in the main article text.

Proposition 1

The private optimum involves interior solutions when Λ_i > 0.

We have already shown that $a_i^0=0$ in the private optimum, and so we focus on the remaining choices. The marginal expected profits from z_i and x_i, respectively, are:

$$\frac{\partial {\pi }_i}{\partial z_i}=-w(1-x_i)h_z(z_i)+P^I(x_i)\frac{\partial P^C(z_i)}{\partial z_i}[\lambda -\delta (1-x_i)]$$ (A1)

$$\frac{\partial {\pi }_i}{\partial x_i}=(wh(z_i)-v)-\frac{\partial P^I(x_i)}{\partial x_i}[P^C(z_i)(1-x_i)\delta +(1-P^C(z_i))\lambda ]+P^I(x_i)P^C(z_i)\delta$$ (A2)

The relations in (A1) and (A2) involve both variables. Suppose x_i → 1. Then (A1) implies ∂π_i /∂z_i → 0 ∀z_i, which means z_i → 0 as there is no economic reason to set z_i > 0. However, if z_i → 0, then (A2) implies ∂π_i/∂x_i < 0 as x_i → 1. These contradictory results imply that $x_i^0<1$. Moreover, our assumptions about P^I(x_i) ensure that $x_i^0>0$: hence $x_i^0\in (0,1)$.

Next, suppose z_i ≥ z̄, where z̄< 1 is defined such that wh(z̄) = v. Then (A2) implies ∂π_i/∂x_i > 0, so that x_i → 1. But we have already shown that x_i → 1 implies z_i → 0, resulting in a contradiction of our premise that x_i ≥ z̄. Further, given x_i < 1, (A1) implies that ∂π_i/∂x_i > 0 when x_i → 0. These last two results imply an interior solution for $z_i:z_i^0\in (0,\overline{z})$.

Proposition 2

The efficient outcome involves interior solutions.

The marginal expected net social values of z_i, x_i, and a_i, respectively, are:

$$\frac{\partial V}{\partial z_i}=\frac{\partial {\pi }_i}{\partial z_i}+\mathrm{\Theta }{P}^I(x_i)\frac{\partial P^C(z_i)}{\partial z_i}{P}_i^S(a_i)$$ (A3)

$$\frac{\partial V}{\partial x_i}=\frac{\partial {\pi }_i}{\partial x_i}-\mathrm{\Theta }\frac{\partial P^D}{\partial e_i}\frac{\partial P^I(x_i)}{\partial x_i}[1-P^C(z_i)]P_i^S(a_i)$$ (A4)

$$\frac{\partial V}{\partial a_i}=-f^{\prime }(a_i)-\mathrm{\Theta }\frac{\partial P^D}{\partial e_i}{P}^I(x_i)[1-P^C(z_i)]\frac{\partial P_i^S(a_i)}{\partial a_i}$$ (A5)

Essentially the same arguments made above for expressions (A1) and (A2) can be applied to expressions (A3) and (A4) to show that $x_i^{\ast }\in (0,1)$ and $z_i^{\ast }\in (0,\overline{z})$. We therefore focus here on expression (A5). When a_i = 0, then $\frac{\partial V}{\partial a_i}=-\mathrm{\Theta }\frac{\partial P^D}{\partial e_i}{P}^I(x_i)[1-P^C(z_i)]\frac{\partial P_i^S(a_i)}{\partial a_i}>0$, whereas ∂V/∂a_i = −f′(a_i) < 0 when a_i = 1. Hence, $a_i^{\ast }\in (0,1)$.

Proposition 3

The private externality, $e_i^0$, exceeds the first-best externality, $e_i^{\ast }$, when the restricted profit function π_i(e_i) = B − c(e_i) − Λ(e_i)= max_xi,zi,ai {B − c(x_i, z_i, a_i) − Λ(x_i, z_i) | e_i(x_i, z_i, a_i) ≤ e_i} is concave in e_i.

Define the generalized restricted profit function

$$\begin{array}{l}{\pi }_i(e_i,{\varphi }_i)=B-c(e_i,{\varphi }_i)-{\varphi }_i\mathrm{\Lambda }(e_i,{\varphi }_i)\\ ={max}_{x_i,z_i,z_i}\{B-c(x_i,z_i,a_i)-{\varphi }_i\mathrm{\Lambda }(x_i,z_i)\mid e_i(x_i,z_i,a_i)\le e_i\},\end{array}$$ (A6)

where ϕ_i ∈ [0,1] is a parameter representing the degree of filterability so that a larger ϕ_i implies more filterability. (Note that ϕ_i only plays a role in proving Proposition 4 below; we introduce it here to avoid re-deriving the restricted profit function.) The privately optimal level of e_i, denoted $e_i^0({\varphi }_i)$, solves

$$\frac{\partial {\pi }_i}{\partial e_i}=0.$$ (A7)

Given (A6), we can rewrite expected social net benefits as

$$V(\mathbf{e},\mathbf{\varphi })={\sum }_{i=1}^N{\pi }_i(e_i,{\varphi }_i)-D(P^D(\mathbf{e},\mathbf{\varphi })),$$ (A8)

where ϕ is a vector with ith element ϕ_i. The first-best externality, $e_i^{\ast }({\varphi }_i)$, solves

$$\frac{\partial {\pi }_i}{\partial e_i}=\mathrm{\Theta }\frac{\partial P^D}{\partial e_i}.$$ (A9)

Upon comparing (A9) and (A7), concavity of π_i(e_i,ϕ_i) in e_i implies that $e_i^0({\varphi }_i)>e_i^{\ast }({\varphi }_i)$.

Proposition 4

Other things equal, the filterability of producer i’s externality reduces (i) both the privately-produced externality and the efficient externality of producer i when π_i(e_i) is concave in e_i and Λ(e_i) is increasing e_i, and (ii) the difference $e_i^0-e_i^{\ast }$ if, additionally, π_i(e_i) is reasonably approximated by a quadratic relation (so that ∂²π_i(e_i)/(∂e_i)² is essentially constant) and Λ(e_i) is convex in e_i.

(i). Assume $\frac{{\partial }^2{\pi }_i}{{(\partial e_i)}^2}<0$ and $\frac{\partial {\mathrm{\Lambda }}_i}{\partial e_i}>0$. Substitute $e_i^0({\varphi }_i)$ into (A7) to create an identity, and then differentiate this identity with respect to ϕ_i to obtain

$$\frac{d{e}_i^0}{d{\varphi }_i}=-\frac{{\partial }^2{\pi }_i^0/(\partial e_i\partial {\varphi }_i)}{{\partial }^2{\pi }_i^0/{(\partial e_i)}^2}=\frac{\partial {\mathrm{\Lambda }}_i^0/\partial e_i}{{\partial }^2{\pi }_i^0/{(\partial e_i)}^2}<0,$$ (A10)

where the second equality in (A10) is due to the envelope theorem: ∂π(e_i,ϕ_i)/∂ϕ_i = −Λ(e_i,ϕ_i). Expression (A10) indicates that greater filterability reduces the privately optimal externality.

Now consider the efficient level of the externality. Recall that the RHS of (A9) is independent of e_i, as P^D is linear in e_i. Substitute $e_i^{\ast }({\varphi }_i)$ into (A9) to create an identity, and then differentiate this identity with respect to ϕ_i to obtain

$$\frac{d{e}_i^{\ast }}{d{\varphi }_i}=-\frac{{\partial }^2{\pi }_i^{\ast }/(\partial e_i\partial {\varphi }_i)}{{\partial }^2{\pi }_i^{\ast }/{(\partial e_i)}^2}=\frac{\partial {\mathrm{\Lambda }}_i^{\ast }/\partial e_i}{{\partial }^2{\pi }_i^{\ast }/{(\partial e_i)}^2}<0.$$ (A11)

Expression (A11) indicates greater filterability reduces the efficient value of the externality.

(ii). We extend the assumptions for part (i) by taking $\frac{{\partial }^2{\pi }_i}{{(\partial e_i)}^2}$ to be essentially constant and $\frac{{\partial }^2{\mathrm{\Lambda }}_i}{{(\partial e_i)}^2}>0$. We want to show that the difference $e_i^0({\varphi }_i)-e_i^{\ast }({\varphi }_i)$ is decreasing in ϕ_i. We therefore derive

$$\frac{\partial (e_i^0({\varphi }_i)-e_i^{\ast }({\varphi }_i))}{\partial {\varphi }_i}=\frac{\partial {\mathrm{\Lambda }}_i^0/\partial e_i}{{\partial }^2{\pi }_i/{(\partial e_i)}^2}-\frac{\partial {\mathrm{\Lambda }}_i^{\ast }/\partial e_i}{{\partial }^2{\pi }_i/{(\partial e_i)}^2}=\frac{\partial {\mathrm{\Lambda }}_i^0/\partial e_i-\partial {\mathrm{\Lambda }}_i^{\ast }/\partial e_i}{{\partial }^2{\pi }_i/{(\partial e_i)}^2},$$ (A12)

where the second equality stems from our assumption that ${\partial }^2{\pi }_i/\partial e_i^2$ is constant (independent of e_i). Given our result in part (i) that $e_i^0({\varphi }_i)>e_i^{\ast }({\varphi }_i)$, combined with convexity of Λ_i, implies the numerator of the RHS of (A12) is positive. As the denominator of the RHS of (A12) is negative due to concavity of π_i, this means (A12) is negative.