Coupled molecular dynamics and continuum electrostatic method to compute the ionization pKa’s of proteins as a function of pH. Test on a large set of proteins.

Abstract

A computational method, to predict the pKa values of the ionizable residues Asp, Glu, His, Tyr and Lys of proteins, is presented here. Calculation of the electrostatic free-energy of the proteins is based on an efficient version of a continuum dielectric electrostatic model. The conformational flexibility of the protein is taken into account by carrying out molecular dynamics simulations of 10 ns in implicit water. The accuracy of the proposed method of calculation of pKa values is estimated from a test set of experimental pKa data for 297 ionizable residues from 34 proteins. The pKa-prediction test shows that, on average, 57%, 86% and 95% of all predictions have an error lower than 0.5, 1.0 and 1.5 pKa units, respectively. This work contributes to our general understanding of the importance of protein flexibility for an accurate computation of pKa, providing critical insight about the significance of the multiple neutral states of acid and histidine residues for pKa-prediction, and may spur significant progess in our effort to develop a fast and accurate electrostatic-based method for pKa-predictions of proteins as a function of pH.

Introduction

Biological properties such as protein folding, protein stability and protein-protein interactions, are greatly influenced by temperature and local pH of the cell environment. A review of the advantages and weaknesses of existing methods to predict pKa’s of ionizable residues in proteins, as a function of pH, is beyond the scope of this work, although recent very good reviews of progress in this field deserve our attention (Nielsen, Gunner, Garcia-Moreno, 2011; Alexov, et al., 2011). Indeed, from a consideration of the specific issue of the journal in which these reviews were published, it appears that almost all the effort to calculate pK_a’s of ionizable residues in proteins is focused on the accuracies of the predictions of the pK_a’s. However, among the several developed methods to predict pK_a’s of ionizable residues in proteins accurately (Bashford, et al., 1993; Alexov, Gunner, 1997; Rabenstein, Knapp, 2001; Soares, Baptista, 2005; Davies, et al., 2006; Khandogin, Brooks, 2006; Khandogin, Brooks, 2006; Stanton, Houk, 2008; Machuqueiro, Baptista, 2009; Song, Mao, Gunner, 2009; Machuqueiro, Baptista, 2011; Wihtam, 2011; Anandakrishn, Aguilar, Onufriev, 2012), the MCCE2 method (Song, Mao, Gunner, 2009) and the ROSETTA-pH method (Kilambi, Gray, 2012) should be highlighted because these methods take multiple conformers and tautomeric states into account to treat neutral acid and His residues for calculations of the pK_a’s in proteins. However, despite the progress in the field, a detailed analysis of the results shows that an accurate treatment of protein ionization is a hard problem and, hence, a perfect solution is not yet available (Song, Mao, Gunner, 2009; Kilambi, Gray, 2012).

As a contribution to the solution of this long-standing problem, we present a method here to compute the pKa’s of ionizable residues of proteins, based on a general theory of the protein binding/release equilibria developed by Machuqueiro & Baptista (2011). However, a proper consideration of the protein dynamics is crucial for an accurate pKa prediction and, hence, the protein flexibility problem is tackled here by carrying out a molecular dynamics simulation in implicit water. Nonetheless, consideration of the protein dynamics entails a fast and accurate evaluation of the solvent effects. For this reason, an efficient Generalized Born model approximation (Vorobjev 2012) is used here.

This paper is organized as follows. In the Materials and Methods section we provide a theoretical background of the approximate and a rigorous method for calculating ionization equilibria in proteins. In the Results and Discussion section, we discuss, among other topics, the following: (i) a general method for calculating pKa’s of residues in proteins using an approximate Monte Carlo (MC) simulation in the ionization phase space; (ii) a test of a convergence of this MC approximate method, i.e., by comparing results obtained on lysozyme with those obtained by using a rigorous ionization partition function method; (iii) a test of the predicted pKa values, by using the approximate MC method, was carried out by comparing predicted against the observed pKa values from 34 proteins wi 297 ionizable residues.

1. Materials and Methods

1.1. The free energy, G(x,z), of the protein molecule

The protonation state z of a protein with ξ sites capable of binding protons is represented as a vector z = (z₁, Z₂,…,Zξ), with z_i denoting the protonation state of site i. It should be noted that the neutral state of some site i is not unique, due to proton tautomerism (Nozaki, Tanford, 1967; Tanford,1970; Schellman, 1975; Machuqueiro, Baptista, 2011). For example, for His, the three states can be defined as 0 for the protonated (His⁺) and 1 for N^δ1-H and 2 for the N^ϵ2-H tautomers, respectively. In general, Z_i = 0 (charged) or 1,..,τ_i, where τ_i is the number of neutral-state tautomers, instead of one state for a site without tautomerism. Hence, the total number of ionization microstates in a molecule is:${\mathrm{N}}_{\mathrm{Z}}=\underset{i}{\overset{\xi }{\mathrm{\Pi }}}(1+{\tau }_{\mathrm{i}})$

The free energy of dissociation of hydrogen ions, ΔG^P, from an amino acid side chains S_i of the protein can be defined by considering the following thermodynamic cycle (Bashford, Karplus, 1990; Beroza, et al., 1991; Beroza, et al., 1993; Yang, Honig, 1993; Vorobjev, Almagro, Hermans, 1998; Vorobjev, Hermans, 1999; Baptista, Soares, 2001; Vorobjev, Vila, Scheraga, 2008) [see cartoon in Figure 1]:

$$\begin{array}{cc}\hfill \underset{i}{\Sigma }& S_i(0)+n(\mathbf{z})H^{+}\stackrel{\Delta G^S(\mathbf{z})}{\to }\underset{i}{\Sigma }{S}_i(z_i)\hfill \\ \hfill & {\downarrow }_{\Delta \mathrm{G}(\mathbf{x},0)}{\downarrow }_{\Delta \mathrm{G}(\mathbf{x},\mathbf{z})}\hfill \\ \hfill P& (\mathbf{x},0)+n(\mathbf{z})H^{+}\stackrel{\Delta G^P(\mathbf{x},\mathbf{z})}{\to }P(\mathbf{x},\mathbf{z})\hfill \end{array}$$ (1)

where P(x,0) and P(x,z) are the protein in conformation x with initial ionized state z = 0, and in conformation x with ionization state z, respectively; S_i(Z_i) is the model compound site i in ionized state Z_i; ΔG^s(z) is the difference in free energy between $\sum _i{S}_i(z_i)$ with n(z) protons and $\sum _i{S}_i(0)$ ionized states, i.e., $\Delta {\mathrm{G}}^{\mathrm{s}}(\mathbf{z})=\sum _{\mathit{i}}{G}_{\mathit{i}}^S(z_{\mathit{i}})-\sum _{\mathit{i}}{\mathit{G}}_{\mathit{i}}^{\mathit{S}}(0);\Delta G^P(\mathbf{x},\mathbf{z})$ is the difference in free energy between P(x,0) and P(x,z) states, i.e., ΔG^P(x,z) = G(x,z) − G(x,0); ΔG(x,0) is the free energy difference between the protein and the model compound in the deprotonated state, i.e., $\Delta G(\mathbf{x},0)=G(\mathbf{x},0)-\sum _i{G}_i^S(0)$ and ΔG(x,z) is the free energy difference between the protein P(x,z) and the set of model compounds$\sum _i{S}_i(z_i)$ and is given by:

$$\Delta G(\mathbf{x},\mathbf{z})=G(\mathbf{x},\mathbf{z})-\underset{i}{\Sigma }{G}_i^S(z_i)$$ (2)

FIGURE 1.

Cartoon for the thermodynamic cycle defining the solvation free energy (see equation 1 for details).

For a protein in a polar solvent, it is a common practice (Honig, Nichollos, 1995; Vorobjev, Vila, Scheraga, 2008; Machuqueiro, Baptista, 2011) to use a continuum dielectric model to calculate the free energy difference in a thermodynamic cycle, i.e., by using eq. (1) and eq. (2), under the assumption that the quantum contributions to the energy in a protein and in a model compound are identical.

The free energy, G(x,z), of the protein molecule in a solvent at fixed ionization state z at a particular conformation x is given by the following expression (Vorobjev, Almagro, Hermans, 1998):

$$G(\mathbf{x},\mathbf{z})=U_m(\mathbf{x},\mathbf{z})+W_{\mathit{solv}}(\mathbf{x},\mathbf{z})$$ (3)

where U_m is the molecular internal potential energy in vacuum, and W_solv (x,z) is the solvation free energy in the microscopic conformation-ionization state (x,z).

Details about how to compute the energies of ionization microstates are provided in the next section.

1.2. Energies of ionization microstates

From the thermodynamic cycle of eq. (1), main text, one can write:

$$\Delta G^P(\mathbf{x},\mathbf{z})=\Delta G^S(\mathbf{z})+\Delta G(\mathbf{x},\mathbf{z})-\Delta G(\mathbf{x},0)$$ (4)

A model compound in solution contributes independently to the free energy ΔG^s(z), according to Machuqueiro & Baptista (2011), of eq.(5):

$$\Delta G^S(\mathbf{z})=2.303\mathit{kT}\sum _i^{\xi }\underset{z_i=0}{\overset{{\tau }_i}{\Sigma }}{\theta }_i[{\mathit{pK}}_i^S(z_i)-\mathit{pH}]$$ (5)

where, θ_i = −1, 1, 0 if the ionizable site i is an acid, base or a neutral tautomer, respectively; pK^S_i(z_i) is the pK_a value of the deprotonation (protonation) reaction involving the neutral tautomeric form S_i(z_i). The values of pK^S_i(z_i) are related to their macroscopic experimental $p{K}_i^S$ and the fraction f_i(z_i) of the tautomer z_i in the mixture of all tautomeric forms of the free model compound i in solvent by the following equation

$${\mathit{pK}}_i^S(z_i)={\mathit{pK}}_i^S-{\theta }_i\log f_i(z_i)$$ (6)

where the last term of eq. (6) describes the correction to the protonation (deprotonation) from the particular tautomer i, due to the entropy of the neutral forms with many tautomeric states. For the isolated neutral histidine residue, the ratio of the N^ε2-H to the N^δ1-H tautomers was assumed to be 70:30 (Machuqueiro, Baptista 2011).

The modern practice is to consider the thermodynamic cycle of eq.(1) of the main text, assuming the following approximations: (a) the protein is frozen in a particular conformational microstate x; (b) the protein is considered as a set of ξ+1 non-overlapping fragments of amino-acid residues capable of binding protons and the remaining background of amino-acid residues that cannot bind protons, and (c) the total protein free energy, eq.(3) in the main text, is approximated by free energy, G(x,z) of the protein in solution in conformation-ionization microstate x,z. The electrostatic free energy is calculated with the linear Poisson-Boltzmann equation in the continuum dielectric model (Machuqueiro, Baptista 2011):

$$G(\mathbf{x},\mathbf{z})=U_{\mathit{el}}(\mathbf{x},\mathbf{z})=U_{\mathit{coul}}(\mathbf{x},\mathbf{z})+G_{\mathit{pol}}(\mathbf{x},\mathbf{z})$$ (7)

where U_el is the microscopic electrostatic free energy, U_Coul is the coulomb electrostatic energy in vacuum, and G_pol is the free energy of solvent polarization. The linearity of the Poisson-Boltzmann equation implies that the superposition principle holds for the set of ξ+1 non-overlapping fragments of amino acids capable of binding protons and the remaining background (B) of amino acids that cannot bind protons, giving:

$$U^P(\mathbf{x},\mathbf{z})=U_B^P(\mathbf{x})+\underset{i}{\overset{\xi }{\Sigma }}{U}_{\mathit{iB}}^P(\mathbf{x},z_i)+\underset{i}{\overset{\xi }{\Sigma }}{U}_{\mathit{ii}}^P(\mathbf{x},z_i)+\underset{i>j}{\overset{\xi }{\Sigma }}{U}_{\mathit{ij}}^P(\mathbf{x},z_i,z_j)$$ (8)

for the free energy U^P of the protein, $U_B^P(\mathbf{x})$ is the free energy of fragment $B,U_{iB}^P(\mathbf{x},z_i)$ is the interaction energy between ionizable and non-ionizable residues, $U_{ii}^P(\mathbf{x},z_i)$ is the free energy of fragment i, and $U_{ij}^P(\mathbf{x},z_i,z_j)$ is the free energy of interaction between fragments i and j in ionization states z_iand z_j, respectively, all in conformational microstate x.

Finally, the microscopic free energy G(x,z,pH) for protonation of the protein in microstate z at a given pH [eq.(9) below] is obtained from (eqs.4-6), with the first and the last two terms of eq. (4) taken from eq.(8).

$$\begin{array}{cc}\hfill & G(\mathbf{x},\mathbf{z},\mathit{pH})=2.303\mathit{kT}\underset{i}{\overset{\xi }{\Sigma }}\underset{z_i}{\overset{{\tau }_i}{\Sigma }}\delta (z_i,\mathbf{z})\left\{{\theta }_i\right[\mathit{pH}-{\mathit{pK}}_i^S]-\log f_i(z_i)\}\hfill \\ \hfill & +\underset{i}{\overset{\xi }{\Sigma }}\underset{z_i}{\overset{{\tau }_i}{\Sigma }}\delta ({\mathbf{z}}_i,\mathbf{z})[(U_{\mathit{iB}}^P(\mathbf{x},z_i)+[U_{\mathit{ii}}^P(\mathbf{x},z_i)-U_{\mathit{ii}}^S(\mathbf{x},z_i)]]+U_B(\mathbf{x})\hfill \\ \hfill & +\underset{i>j}{\overset{\xi }{\Sigma }}\underset{z_i,z_j}{\overset{{\tau }_i,{\tau }_j}{\Sigma }}\delta (z_i,\mathbf{z})\delta (z_j,\mathbf{z})U_{\mathit{ij}}^P(\mathbf{x},z_i,z_j)\hfill \end{array}$$ (9)

where δ(z_i, z) = 0 or 1 is the occupation number of state z_i of site i in the ionization microstate z, in a conformational microstate x at a given pH. The first sum of eq.(9) is the free energy of protonation of the model compounds corrected for the entropy factor, eq.(6), due to the neutral tautomer fraction f_i(Z_i); the second sum is the effect of the protein environment on ionizable site i in state z_i; the third sum is the free energy of interaction of ionizable sites i,j in the isomeric states Z_i,Z_j. Eq. (9) represents an alternative expression to Eq. (7) of (Machuqueiro, Baptista, 2011) for the calculation of the free energy of ionized states with multiple neutral states.

1.3. Calculation of ionization equilibria

The probability p(x,z,pH) to find the protein in microscopic conformation x in microscopic ionization state z at a given pH is defined by the Boltzmann factor:

$$p(\mathbf{x},\mathbf{z},\mathit{pH})=\text{exp}[-G(\mathbf{x},\mathbf{z},\mathit{pH})∕\mathit{kT}]∕Z_{\mathit{inz}}(\mathbf{x},\mathit{pH})$$ (10)

where Z_inz(x,pH) is the ionization partition function for protein conformation x,

$$Z_{\mathit{inz}}(\mathbf{x},\mathit{pH})=\underset{k=1}{\overset{N_z}{\Sigma }}\text{exp}[-G(\mathbf{x},{\mathbf{z}}_k,\mathit{pH})∕\mathit{kT}]$$ (11)

The partition function, eq. (11), can be calculated in reasonable CPU time for a small protein if the number of microstates N_z does not exceed ~10⁹ or ~16 ionizable groups. The microscopic free energy of ionization equilibrium, G_niz(x,pH), is given by the standard relation

$$G_{\mathit{inz}}(\mathbf{x},\mathit{pH})=-\mathit{kT}\text{ln}{Z}_{\mathit{inz}}(\mathbf{x},\mathit{pH})$$ (12)

and the average occupation number <δ(z_i)(x,pH)> of the microscopic ionization state, is

$$<\delta (z_i)(\mathbf{x},\mathit{pH})>=\frac{1}{Z_{\mathit{inz}}}\underset{{\mathbf{z}}_k}{\overset{N_z}{\Sigma }}\delta (z_i,{\mathbf{z}}_k)(\mathbf{x},\mathit{pH})\text{exp}[-G(\mathbf{x},{\mathbf{z}}_k,\mathit{pH})∕\mathit{kT}]$$ (13)

The average occupation numbers, given by eq. (13), and the average ionization energy <G(x,z,pH)> given by eq.(9), can be calculated on the fly with the partition function Z_inz(x, pH). The approximate average occupation numbers <δ(z_i)(x,pH)> and the average ionization free energy <G(x,z,pH)> for a large protein are calculated by the Monte Carlo method (Yang, Honig, 1993; Khandogin, Chen, Brooks, 2006). A random walk in the ionization phase space consists of a random change of ionization state z defined for acid, base and tautomer, and from the set of several combined moves (interchange between states for two base, two acids, or two tautomer states or a proton transfer between two states). The following is an effective way to generate an equilibrium distribution of ionization states: (i) start the calculations from a high pH, when all base groups are neutral, b⁰, while acid sites are negatively charged, a⁻, i.e., the initial ionization state is equal to z = (a⁰b⁺) [for low pH, by similar arguments, the initial ionization state is equal to z = (a⁰b⁺)]; (ii) the MC simulation (see section 1.7 below) proceeds by a small step ~ 0.25 pH units over a wide pH range, e.g. (−10, 20) (Vorobjev et al., 2008). The pK_a’s of titratable residues are defined from a titration curve, eq. (13), at the value of pH_1/2, which is the solution of eq.14),

$$<\delta ({\mathrm{z}}_{\mathrm{i}})(\mathbf{x},{\text{pH}}_{1∕2})>={}^1∕_2,$$ (14)

or by fitting the titration curve <δ(z_i)(x,pH)> to the Henderson-Hasselbalch equation.

By using the Tanford-Schellman integral (Vorobjev et al., 2008)

$$\begin{array}{cc}\hfill & \Delta G_{\mathit{inz}}(\mathbf{x},\mathit{pH})-\Delta G_{\mathit{inz}}(\mathbf{x},\infty )=\hfill \\ \hfill & 2.303\mathit{kT}\underset{i=1}{\overset{\xi }{\Sigma }}{\theta }_i\underset{\infty }{\overset{\mathit{pH}}{\int }}[{\langle \delta ({\mathbf{z}}_i)(\mathbf{x},\mathit{pH})\rangle }_{\mathbf{z}}-\langle {\delta }^{S_i}({\mathbf{z}}_i)(\mathit{pH})\rangle ]\mathit{dpH},\hfill \end{array}$$ (15)

the free energy of ionization equilibrium ΔG_inz(x,pH) is:

$$\Delta G_{\mathit{inz}}(\mathbf{x},\mathit{pH})=G_{\mathit{inz}}(\mathbf{x},\mathit{pH})-G_{\mathit{inz}}^S(\mathbf{x},\mathit{pH})$$ (16)

with the functions <δ(z_i)(x,pH)> and <δ^s_i(z_i)(pH)> representing the average occupation of state z_i at site i in the protein in conformational microstate x, and in the isolated model compound S_i, respectively. In eq.(16), the free energy term $G_{\text{inz}}^S(\mathbf{x},pH)$ for the sum of all isolated ionizable residues is given by:

$$G_{\mathit{inz}}^S(\mathbf{x},\mathit{pH})=-\mathit{kT}\underset{i=1}{\overset{\xi }{\Sigma }}\text{ln}\{1+\text{exp}[-2.303{\theta }_i(\mathit{pH}-{\mathit{pK}}_i^S)\left]\right\}$$ (17)

For pH → ∞, there is only one populated ionization state, namely z^b = (a⁻,b⁰), i.e., when all acidic residues, are negatively charged, a⁻, while all the basic residues are neutral, b⁰. For histidine, the neutral state b⁰ consists of a set of neutral tautomeric microstates. Nevertheless, it was found that choice of initial ionization state (a⁰b⁺) at low pH → −∞, is practically more convenient, (see end of section 1.7), because both tautomers have a comparable probability for most acid groups (93%) from a test set of 34 proteins (see Table S1).

1.4. Calculation of the free energy of ionization microstates

For a protein embedded in a polar (water) solvent, it is common practice (Yang, Honig, 1993; Davies, et al., 2006; Vorobjev, Vila, Scheraga, 2008) to use a continuum dielectric model to calculate the free energy of solvation, i.e. the free energy of solvent polarization, by solving the Poisson equation either by the finite difference method (Alexov, Gunner, 1997; Stanton, Houk, 2008; Song, Mao, Gunner, 2009; Machuqueiro, Baptista, 2011) or by the Fast Adaptive Multi-grid Boundary Element (FAMBE) method (Vorobjev, Scheraga, 1997; Vorobjev, Hermans, 1997; Vorobjev, Almagro, Hermans, 1998; Vorobjev, Vila, Scheraga, 2008; Vorobjev, 2011; Vorobjev, 2012). Recently, an accurate version of the MSR6c Generalized Born model (GB-MSR6c) (Vorobjev, 2012), has been developed. The computation of the polarization free energy with the GB-MSR6c model shows similar accuracy as that computed by using FAMBE, i.e., with an average absolute deviation of ~2.5% (Aguilar, Schardarch, Onufriev, 2010; Vorobjev, 2012). However, the GB-MSR6c model is about two orders of magnitude faster than FAMBE (Vorobjev, 2012), which on the other hand, is fast and accurate as a finite-difference method (Vorobjev, Scheraga, 1997). Consequently, the GB-MSR6c model (Vorobjev, 2012), rather than FAMBE or a finite-difference method, will be used here for all the calculations of electrostatic energy of proteins in this work.

There is evidence (Loffler, Schreiber, Steinhauser, 1997; Vorobjev, Vila, Scheraga, 2008) indicating that a calculation of ionization equilibria by using a large value of D_I = 12.0 −16.0, for a fixed protein conformation x, accounts for solvent structure mobility and reorganization due to nonstructural responses, such as the charge redistribution. A consistent set of atomic charges for protein residues in neutral and ionized states was computed (Arnautova, et al., 2009) by fitting the electrostatic potential of the atomic charges to the reference electrostatic potential which was calculated by a high-quality quantum mechanical method.

Details about the corrected Generalized Born approximation GB-MSR6c method are provided bellow.

1.5. Corrected Generalized Born approximation GB-MSR6c

Here, we briefly highlight the major details of the GB-MSR6c model that replaces the linear Poisson-Boltzmann equation. The total free energy of solvent polarization of the GB method $G_{pol}^{GB}(\mathbf{x})$, is a sum of atomic self-polarization energies, $g_i^{GB}$, and the energy of pair interactions, $w_{ij}^{GB}$, of a pair of atoms i,j as (Aguilar et al., 2010):

$$\begin{array}{cc}\hfill G_{\mathit{pol}}^{\mathit{GB}}(x)& =(\frac{1}{D_0}-\frac{1}{D_I})\sum _i\frac{q_i^2}{2B_i}+\frac{1}{2}\sum _{i\ne j}\frac{q_i{q}_j}{f_{\mathit{GB}}(r_{\mathit{ij}},B_i,B_j)}(\frac{1}{D_0}-\frac{1}{D_I})\hfill \\ \hfill & =\sum _i{\mathrm{g}}_{\mathrm{i}}^{\text{GB}}+\frac{1}{2}\sum _{i\ne j}{w}_{\mathit{ij}}^{\mathit{GB}}\hfill \end{array}$$ (18)

where q_i is the charge of atom i, r_i,j is the distance between atoms i and j,B_i is the atomic Born radius of atom i, D₀ and D_I are dielectric constants of the outer solvent volume and the internal protein volume; the f_GB function (Aguilar et al., 2010) is:

$$f_{\mathit{GB}}(r_{\mathit{ij}},B_i,B_j)={[r_{\mathit{ij}}^2+B_i{B}_j\text{exp}(-r_{\mathit{ij}}^2∕4B_i{B}_j)]}^{1∕2}$$ (19)

By definition, the GB method with Poisson-ideal BoRN atomic radii accurately reproduces the values of atomic self-polarization energies $g_i^{\mathit{FAMBE}}$ calculated by the FAMBE method and approximates the FAMBE solvent polarization pair PMFs $w_{ij}^{\mathit{FAMBE}}$ with an average error of 1.5% (Vorobjev 2012). The GB-MSR6c approximation (Vorobjev 2012). The GB-MSR6c approximation (Vorobjev 2012) allows one to compute the atomic Born radius B_i(MSR6) of a protein atom at position r_i with good precision relative to the FAMBE-ideal Born radii by the integral over the protein Molecular Surface (MS) (Vorobjev, Hermans 1997):

$$B_i^{-1}={\left(\frac{1}{4\pi }\underset{S}{\int }\frac{(\mathbf{s}-{\mathbf{r}}_i)\mathbf{n}(\mathbf{s})\mathit{ds}}{{\mid \mathbf{s}-{\mathbf{r}}_i\mid }^6}\right)}^{1∕3}$$ (20)

where n(s) is a normal vector to the MS, S, at the point s. The fast and accurate method for calculation of the surface integral in eq. (20) is based on the FAMBE adaptive tessellation of the protein MS by multi-sized boundary elements, which reduces the numerical complexity of the calculation of the atomic Born radii to the order of O(NlogN). The B_i(MSR6c) Born radii are related to the B_i(MSR6) radii by the linear regression equation (Vorobjev 2012):

$$B_i(\mathit{MSR}6c)\approx 0.9129B_i(\mathit{MSR}6)+0.0969$$ (21)

where B_i(MSR6) are the Born radii in (Å) defined by eq. (20) over the protein MS calculated by the Smooth Invariant Molecular Surface (SIMS) method (Vorobjev, Hermans 1997) with a solvent probe radius of 2.0 Å, which was found to be optimal for approximation of dielectric surface interface (Vorobjev 2012).

1.6. Molecular dynamics simulations

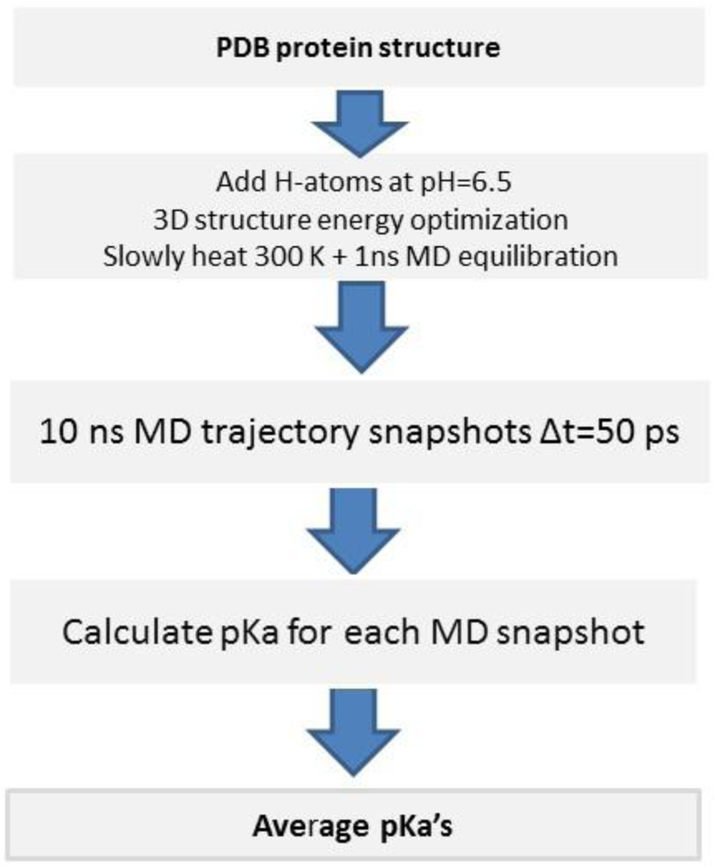
Protein dynamics in water was taken into account by MD simulations with implicit solvent, namely by using the Lazaridis-Karplus solvent model (Lazaridis, Karplus, 1999) with the BioPASED program (Popov, Vorobjev, 2010). For the MD simulation, the following three step protocol was used (see Figure 2). Step 1: construction of an equilibrium protein structure at temperature 300K and pH=6.5. Achievement of this goal requires: (i) building a full atomic protein structure, i.e. with all hydrogen atoms added; this means, for example, that each His residue needs to be built up in the most probable form, i.e. in the ionized His+ form or in the most probable neutral tautomer, N^δ1-H and N^ϵ2-H; (ii) the crystal structure with all the assigned hydrogen atoms and His forms was energy optimized in implicit solvent by using a conjugate gradient method; (iii) the system is heated slowly from 1K to 300K during 150 ps; and (iv) a final equilibration at 300K, during 0.5 – 1 ns was carried out. Step 2: generation of a representative set of 3D protein structures. For this purpose, the collection of the equilibrium MD trajectories of the protein dynamics, during 10 ns as snapshots, were taken every 50 ps time-interval. Step 3: for each snapshot, we calculate the pKa of all ionizable residues, as well as the fractions of the tautomers of His and the acid residues, by carrying out an MC calculation with GB-MSR6c as a solvent model. Finally, we calculate an average pKa for each ionizable residue of the protein.

Figure 2.

Flowchart for the MD simulation and pKa calculation for all ionizable residues of a protein.

1.7. Analysis of the accuracy of Monte Carlo method of pKa prediction

Analysis of the accuracy of our method to predict pKa is focused on a reduced model system, which can be treated analytically via a rigorous calculation of the ionization partition function. A Model system consists of all thirteen acids (Glu3, Asp18, Tyr20, Tyr23, Glu35, Asp48, Asp52, Tyr53, Asp66, Asp87, Asp101, Asp119, plus the C-terminus) and two bases (N-terminus and His15) for the ionizable residues of Hen Egg White Lysozyme (HEWL), PDB code 2LZT, with both base residues Lys and Arg kept in ionized states as Lys+ and Arg+. This approximation is accurate for pH lower than pH ~ 9, because the pK^o of Lys and Arg are 10.5 and 12.5, respectively (Demchuk, Wade, 1996).

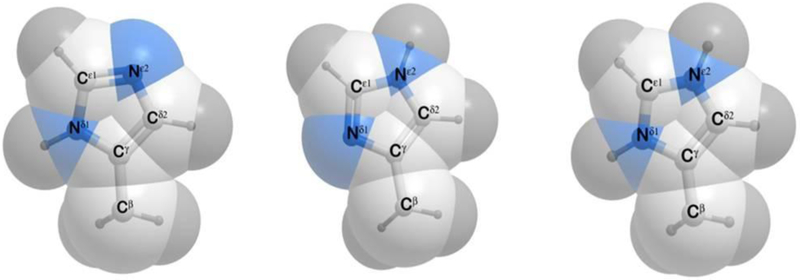
The neutral form COOH of the acid group COO⁻, has two isomers with a hydrogen atom attached to the Oδ1(Oε1) or Oδ2(Oε2) groups for Asp and Glu, respectively. For the COOH group, we adopt the syn rather than anti conformation because the ratio syn/anti conformations are 94.5:5.5 for acid groups (Machuqueiro, Baptista, 2011). A neutral form of a His residue has two isomers with hydrogen atoms attached to N^δ1 or to N^ϵ2, respectively (see Figure 3). For isolated neutral histidine, the ratio of the N_ϵ2-H to the Nδ1-H tautomers was assumed to be 70:30 (Machuqueiro & Baptista 2011). The electrostatic energy of pair interactions of charged residues was calculated, with a dielectric constant D_I = 16.0, for the internal protein volume, and a water dielectric constant D_o = 80.0, for the outside volume (Vorobjev, Vila, Scheraga, 2008).

Figure 3.

(a) Structure of the N^δ1-H form of the His residue; (b) same as (a) for the N^ε2-H form; and (c) same as (a) for the ionized H⁺ form.

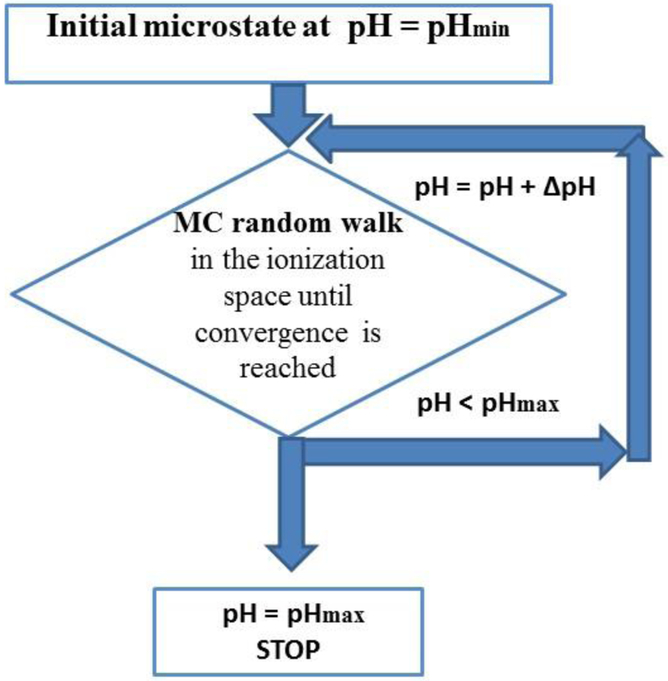
The standard method for calculation of average ionization degrees of residues, which can also be applied to large proteins, is the MC method (Beroza, et al., 1993; Yang, Honig, 1993; Vorobjev, Vila, Scheraga, 2008). Our implementation of the MC method makes use of the following assumptions (i) His and acid groups have three forms, namely two neutral tautomers and one charged state; (ii) the non-protonated Arg is represented by a single neutral form with an average charge distribution, i.e., computed over four structures of the neutral guanidinium group (NH-C-NH₂); (iii) the ionization degrees of all ionizable residues are calculated for a large pH interval (−5, 15) with a step of ΔpH = 0.25 pH units; and (iv) the initial ionization microstate of protein residues at low pH (≈ − 5) has been chosen as the state in which all acid residues are neutral (with both tautomers equally probable) while all His and base residues are considered as being positively charged states. Overall, our MC calculation of the pKa’s for a given structure is organized (see flowchart on Figure 4) as follows:

Figure 4.

Flowchart for the algorithm for the calculation of the pKa values of proteins (see section 1.7 for details).

• (1)Initial ionization microstate assignment (at pH = pH_min): The MC calculations start at the pH_min (≈ −5) with an initial ionization microstate with all base residues (His, Lys, Arg) positively charged and all acid residues are neutral in one of the two tautomers, namely Oδ1-H (or Oδ2-H), for ASP, and Oϵ1-H (or Oϵ2-H), for GLU, chosen randomly with probability 1/2;
• (2)Ionization microstate at a given pH: For each of the MC runs at higher pH, than pH_min, we carry out a random walk in the ionization space of all ionizable residues, until convergence of the average ionization degrees is reached; the most probable ionization state, z, is kept.
• (3)Increasing the pH: If the pH is ≤ pH_max (~15) step (2) is repeated, otherwise we stop the calculations.

The algorithm has a reasonable convergency rate for an MC clculation with ΔpH steps of 0.25 and ~2 ×10⁶ trials.

2. Results and discussion

2.1. Validation of the MC method

Validation of the proposed approximate MC method to compute the pK_a’s of ionization and an ionized and neutral tautomer fractions of His and acid residues was carried out for Hen Egg White Lysozyme (HEWL) protein, PDB code 2LZT, by carrying out a direct comparison between the MC calculations versus the results obtained from a rigorous calculation of the partition function on a reduced model system. This comparison illustrates the convergence and accuracy of each MC approach (see Table 1). In particular, analysis of Table 1 (in terms of the absolute errors, footnote e) indicates that the convergence of the MC calculations approaches the results obtained from a rigorous calculation of the partition function and can be reached only by using a large enough Markov chain length during the MC simulations. Indeed, convergence, during the calculation of the pKa by the MC method is reached if the average absolute errors (<Δ>) do not exceed 0.03 pK units (see footnote g in Table 1). These results suggest that, for a proteins with ~300 residues, the convergence for each pH value, with steps of 0.25 unit, will be reached after ~2 ×l0⁶ trials.

Table 1.

pK_a values calculated for protein 2LZT (Lysozyme) with different MC runs^a in comparison with the results obtained by a rigorous calculation of a partition function over all possible ionization micro states given by Eq.(11) - Eq.(13).

residue	(pKo)b	pKac	pK_Zd	pK_MC5Ke	pK_MC20Ke	pK_MC80Ke	pK_MC320Ke	pKMC1Me
N-end	7.5	7.9	7.44	7.38 (0.04)	7.43 (0.01)	7.40 (0.04)	7.39 (0.05)	7.38 (0.06)
Glu7	4.4	2.8	3.49	3.54 (0.05)	3. 50 (0.06)	3.54 (0.05)	3.56 (0.07)	3.55 (0.06)
His 15	6.6	5.5	7.15	7.16 (0.01)	7.20 (0.07)	7.18 (0.03)	7.18 (0.03)	7.17 (0.02)
Asp 18	4.0	2.7	2.87	2.84 (0.03)	2.82 (0.05)	2.84 (0.03)	2.84 (0.03)	2.86 (0.03)
Tyr20	9.6	10.3	9.74	9.49 (0.15)	9.65 (0.05)	9.78 (0.04)	9.77 (0.03)	9.73 (0.01)
Tyr23	9.6	9.8	9.01	9.10 (0.09)	9.04 (0.03)	8.97 (0.04)	8.98 (0.03)	8.98 (0.02)
Glu35	4.4	6.2	3.85	3.69 (0.16)	3.86 (0.04)	3.86 (0.01)	3.84 (0.01)	3.87 (0.01)
Asp48	4.0	1.6	3.37	3.35 (0.02)	3.36 (0.01)	3.36 (0.01)	3.36 (0.01)	3.36 (0.01)
Asp 52	4.0	3.7	3.29	3.21 (0.08)	3.30 (0.05)	3.30 (0.01)	3.27 (0.02)	3.28 (0.01)
Tyr53	9.6	12.1	11.13	11.33 (0.20)	11.18(0.04)	11.19 (0.06)	11.20 (0.06)	11.20 (0.06)
Asp66	4.0	0.9	3.44	3.43 (0.01)	3.46 (0.02)	3.42 (0.02)	3.47 (0.03)	3.45 (0.01)
Asp 87	4.0	2.1	2.95	3.00 (0.07)	2.93 (0.03)	2.97 (0.02)	2.94 (0.01)	2.93 (0.02)
Asp101	4.0	4.1	3.25	3.31 (0.06)	3.18 (0.07)	3.23 (0.02)	3.24 (0.01)	3.26 (0.01)
Asp119	4.0	3.2	2.84	2.85 (0.01)	2.84 (0.01)	2.82 (0.02)	2.82 (0.02)	2.82 (0.02)
C-end	3.8	2.8	2.73	2.78 (0.05)	2.68 (0.05)	2.74 (0.01)	2.75 (0.02)	2.75 (0.02)
< Δ >			0.96f	0.08 g	0.05g	0.03g	0.03g	0.02g
Δmax			2.54f	0.20 g	0.07g	0.06g	0.07g	0.06g

^aall calculations were carried out with D_I =16.0 and D₀ = 80.0.

^bexperimental pK^o values in 0.15 M NaCl at T= 300 K (Demchuk, Wade, 1996);

^cexperimental values of pK_a for residues in 0.15 M NaCl at T = 300 K (Song, Mao, Gunner, 2009; Kilambi, Gray, 2012);

^dpK_ZS are the pK values obtained by a rigorous computation of the ionization partition function and the average degree of ionization;

^epK_MC5K, MC20K, MC80K, MC320K and MC1M, are the pK_a values obtained by using different numbers of MC trials for the Markov chains, namely (0.005, 0.02, 0.08, 0.32 and 1.2) × 10⁶ steps, respectively, for each pH during the calculation of the ionization equilibria, with a step of 0.25; in parentheses, Δ, the average absolute error (deviation) from the result listed in column 4, i.e., pK_Z obtained by rigorous computation of the ionization partition function;

^faverage (<Δ>) and maximal (Δ_max) absolute deviations between observed pKa (column 3) and computed from pK_Z (column 4) values; the larger Δ_max deviation (2.3 and 2.5) pertains to Glu35 and Asp66, respectively;

^gaverage (<Δ>) and maximal (Δ_max) absolute pKa deviations from pK_Z (column 4) values.

2.2. Dependence of the computed pKa on the adopted D_I value

An analysis of the dependence of the pKa’s of the ionizable residues of lysozyme, as a function of the chosen value for D_i, namely 20.0, 16.0, 12.0, 8.0 and 4.0, was also carried out, and the results are shown in Table 2. Certainly, the best approximation to the observed pKa values of proteins (Demchuk, Wade 1996) was obtained by using a large, rather than a small, D_I, namely, ~ 16.0, in line with existing evidence (Loffler, Schreiber, Steinhauser, 1997; Vorobjev, Vila, Scheraga, 2008).

Table 2.

pKa values^a for protein 2LZT (Lysozyme) calculated for different values of D_I.

Residues	(pKo)b	pKac	DI=20.0a	DI=16.0a	DI=12.0a	DI=8.0a	DI=4.0a
NEND	7.5	7.9	7.4	7.4	7.5	7.3	7.1
GLU7	4.4	2.8	3.8	3.5	3.6	3.5	3.6
HIS15	6.6	5.4 – 5.6d	6.7	6.8	7.1	7.3	8.5
ASP18	4.0	2.7	2.9	2.8	2.4	2.6	2.2
TYR20	9.6	10.3	9.5	9.5	9.9	10.1	> 14e
TYR23	9.6	9.8	9.2	9.1	8.9	8.7	> 14e
GLU35	4.4	6.2	4.7	4.9	4.7	4.1	4.7
ASP48	4.0	1.6	3.7	3.4	3.5	3.7	4.6
ASP52	4.0	3.7	3.5	3.4	3.3	3.1	2.9
TYR53	9.6	12.1	11.0	11.4	11.1	13.3	>14e
ASP66	4.0	0.9	2.2	1.7	2.1	3.1	6.2
ASP87	4.0	2.1	3.2	2.7	2.9	2.9	2.6
ASP101	4.0	4.1	3.8	3.5	3.3	3.3	3.5
ASP119	4.0	3.2	3.1	2.8	2.8	2.7	2.4
CEND	3.8	2.8	2.9	2.7	2.6	2.2	1.4
< Δ > f			0.8	0.7	0.8	1.1	-
Δmax g			2.1	1.8	1.9	2.2	-

^aAverage pKa calculated for equilibrium MD trajectory of 10 ns with different D_I of protein internal dielectric constant;

^bexperimental pK^ovalues in 0.15 M NaCl at T = 300 K (Demchuk, Wade, 1996);

^cexperimental values of pKa for residues in 0.15 M NaCl at T= 300 K (Song, Mao, Gunner, 2009; Kilambi, Gray, 2012);

^drange of variation of the observed pKa values from two different sources (Song, Mao, Gunner, 2009; Kilambi, Gray, 2012);

^efor the purpose of computing Δ (see below, item f) a pKa = 14.01, was adopted.

^f<Δ> is the average absolute difference, in pKa units, between the computed pKa (at each D_I) and the observed pKa value (column 3);

^gΔ_max is the maximum difference in pKa unit.

It is worth noting that there is a “balance” between the chosen values for the internal dielectric constant Di and the length of the MD trajectory, viz., to obtain convergence on the computed average ionization degrees. Indeed, the minimal length of the MD trajectory is determined by the rate of convergence of the computed ionization degree of each ionizable residue. In other words, the length of the MD trajectory depends on the chosen internal Di. If the Di value is large, compared to the gas-phase value, then the influence of fluctuation of the protein structure on the ionization degrees must decrease and, hence, in the limit of a very large Di it goes to pK^o because the inter-residue electrostatic interactions are too weak, i.e., shielded. Therefore, for a large Di a convergence will be faster and, hence, the length of the MD trajectory shorter.

2.3. Test of the GB-MSR6c-pK method

The accuracy of our version of the Generalized Born method for the calculation of pKa’s and ionization curves as a function of pH, i.e., by using the GB-MSR6c method (Aguilar, Schardarch, Onufriev, 2010; Vorobjev, 2012) was estimated by computing the pKa values of a large set of 297 ionizable residues from 34 proteins, for which observed pKa values are known (see Table S1 of the Supporting Material and Tables 3, 4, 5 of the main text). It is worth noting that a similar set of proteins was also used to test the MCCE2 (Song, Mao, Gunner, 2009) and the Rosetta-pH (Kilambi, Gray, 2012) methods, respectively.

Table 3.

Accuracy of the pKa predictions for a set of 297 ionizable groups from 34 proteins ^a

Accuracy (pKa units)	ASP	GLU	HIS	TYR	LYS
< 0.5	53 (61%)	48 (56%)	23 (42%)	12 (43%)	26 (63%)
< 1.0	81 (92%)	76 (88%)	43 (78%)	14 (53%)	38 (93%)
< 1.5	84 (96%)	84 (96%)	52 (94%)	23 (85%)	39 (94%)
< 2.0	86 (98%)	85 (98%)	54 (98%)	25 (93%)	41 (100%)
< 2.5	88 (100%)	86 (100%)	55 (100%)	27 (100%)	41 (100%)

^aData from Table S1 (of SM). In each row we listed the total number of residues and, in parenthesis, the percentage over all same-type of residue with an accuracy (of the pKa prediction) given by the first column (data from Table S1 of SM).

Table 4.

List of largest pKa errors (ΔpKa > 2.0) among the 34 tested proteins^a

Protein	Residue	Observed	GB-MSR6c-pK		ROSETTApHd	MCCI2e
			X-rayb	MDc
2LZT	ASP 66	0.9	3.4	1.7	n/a	1.0
2RN2	ASP 10	6.1	3.8	3.5	5.1	8.2
2RN2	HIS 114	5.0	6.2	6.6	3.2	−0.1
3RN3	ASP 83	3.3	2.9	2.8	1.4	5.3
2CPL	HIS 54	4.2	6.2	6.4	n/a	1.4
2CPL	HIS 92	4.2	5.2	6.0	n/a	−2.8
1RGG	ASP 79	7.4	4.9	5.0	3.3	7.4
3SSI	HIS 43	3.2	5.3	5.5	1.4	n/a
135L	GLU 35	6.1	3.9	3.9	3.5	n/a
1XNB	GLU 172	6.4	3.7	3.6	3.5	n/a
1GYM	HIS 227	6.8	7.2	7.1	2.7	n/a

^athe poorest prediction, among the three methods, is underlined;

^bcalculated for the X-ray structure deposited at the PDB;

^caverage over equilibrium MD trajectories of 10 ns;

^dsee Kilmbi, Gray, 2012;

^esee Song, Mao, Gunner, 2009.

Table 5.

Computed versus NMR-determined pKa values for protein 1YGW

Res	pka	<pK>b	<pK>c	rmsdd	pKe	pKf
ASP 3	3.5	3.6	4.1	0.17 - 0.11	3.1	-
ASP 15	3.5	3.4	3.4	0.31 - 0.15	2.9	4.2
ASP 29	4.3	3.7	3.8	0.15 - 0.19	4.0	5.5
ASP 49	4.2	3.7	3.9	0.07 - 0.09	3.9	5.0
ASP 66	3.9	3.5	3.2	0.11 - 0.10	3.3	4.6
GLU 28	5.6	4.6	3.9	0.17 - 0.20	4.8	6.1
GLU 31	5.4	4.0	4.3	0.11 - 0.12	4.7	46
GLU 46	3.6	4.3	4.3	0.18 - 0.15	4.5	4.0
GLU 58	4.0	4.1	4.2	0.18 - 0.20	3.4	2.5
GLU 82	3.3	3.4	3.4	0.31 - 0.15	4.0	2.8
GLU 102	5.3	4.2	4.4	0.27 - 0.17	4.2	5.3
HIS 27	7.0	7.2	6.7	0.20 - 0.12	6.8	8.4
HIS 40	7.5	7.4	7.6	0.25 - 0.23	6.9	8.5
HIS 93	7.3	6.6	7.6	0.50 - 0.34	5.4	6.1

^aobserved pKa’s for each ionizable residue of protein 1YGM (Kilmbi, Gray, 2012);

^baveraged pK’s value (over 34 NMR-determined structures of 1YGW) computed by using the GB-MSR6c-pK model;

^caveraged pK’s value computed over 10 ns molecular dynamic trajectory for each of the 34 NMR-determined conformations); underlined we highlight pKa errors > 1.0 pK unit;

^dRMSD of pKa fluctuations computed from the: (i) set of 34 NMR-derived models deposited at the PDB (id 1YGW); and (ii) the MD trajectory of 10 ns of length for each of the 34 NMR-derived conformations of 1YGW;

^eaveraged pKa values obtained by using ROSETTA-pH method (Kilmbi, Gray, 2012);

^faveraged pKa values obtained by using MCCI2 method (Song, Mao, Gunner, 2009).

Accuracy of the pKa predictions

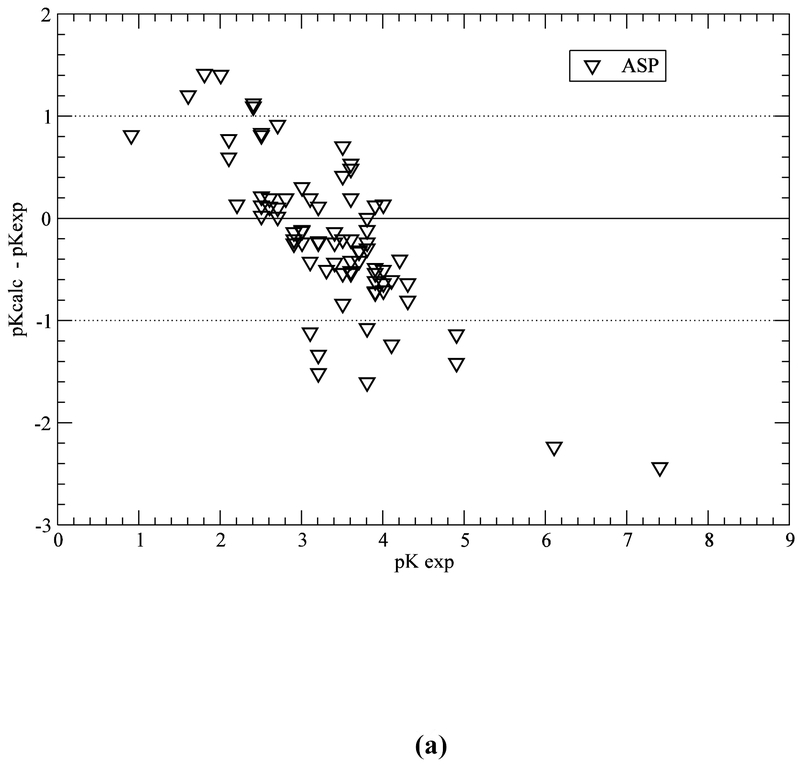
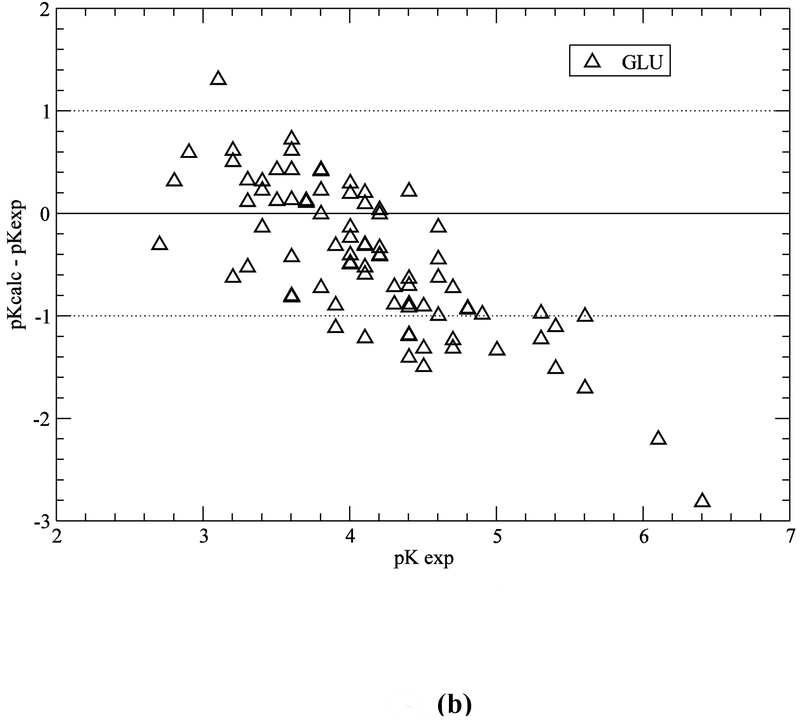
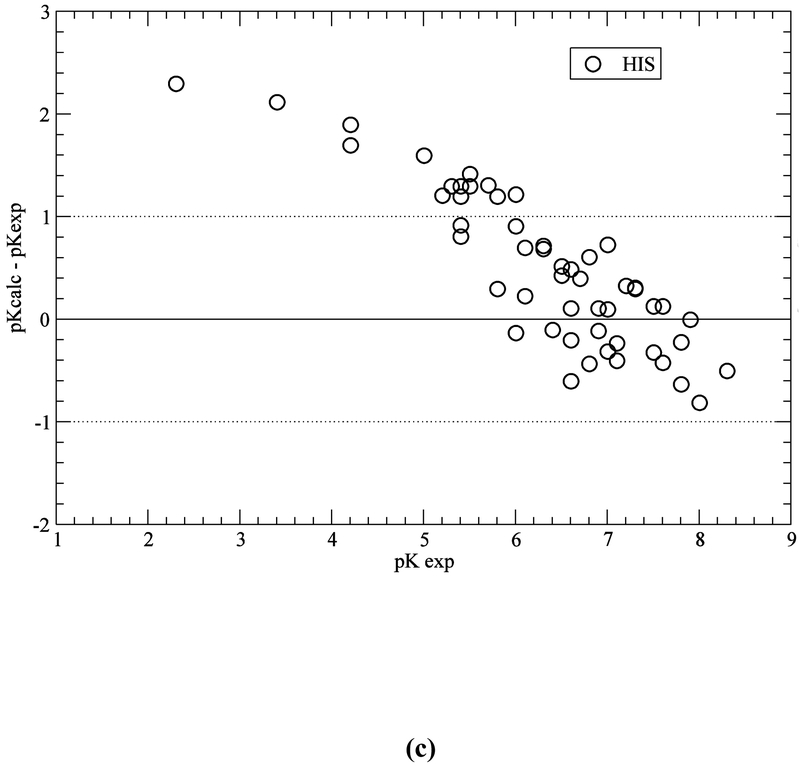
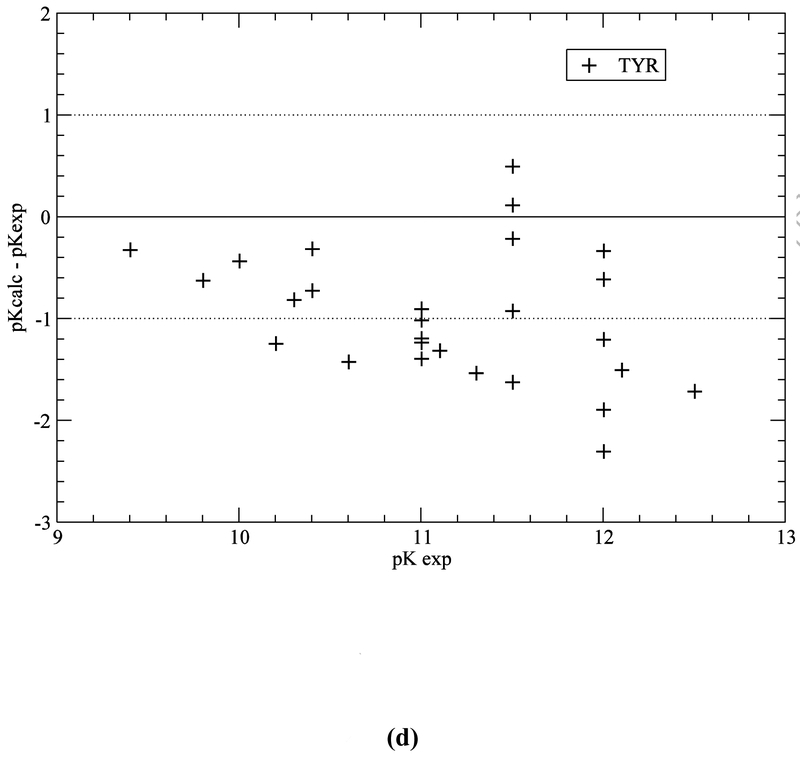
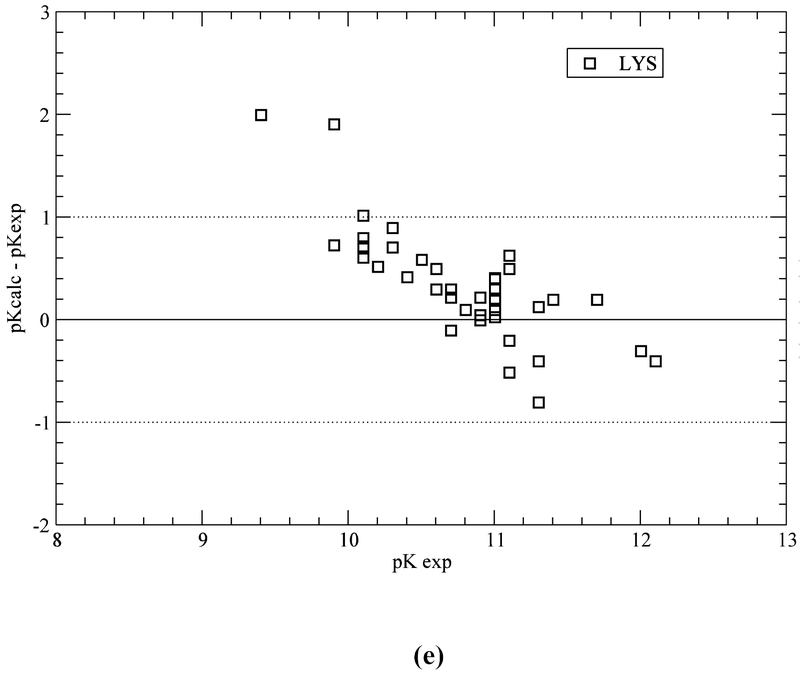
Computation with the GB-MSR6c-pK method, of the pKa value on the test set of proteins is shown in Table 3. The best accuracy of the predictions is achieved for acid Asp, Glu and base Lys residues (see Figure 5a,b,e). The accuracy of the prediction for Tyr and His is lower (see Table 3 and Figure 5c,d). The functionally important His residues are predicted, among the 34 proteins, with an accuracy better than 0.5 (42%), 1.0 (78%) and 1.5 (94%) pK units, respectively (see Table 3 and Figure 5c). These results are similar to the ones obtained by using the ROSETTA-pH method (Kilambi, Gray 2012), namely 50%, 70%, 92% (see Table S3 of Kilambi, Gray 2012), and the MCCI2 method (Song, Mao, Gunner, 2009), namely 41%, 75%, 93%.

Figure 5.

(a) Accuracy of the pKa predictions for all the ASP residues of the test set of 34 proteins (Table S1 of SM); (b) same as (a) for GLU residues; (c) same as (a) for HIS residues; (d) same as (a) for TYR residues; and (e) same as (a) for LYS residues.

On the other hand, for acid (ASP, GLU) and base (LYS) residues, the accuracy of the pKa predictions, with the GB-MSR6c-pK method, shows improvement over other methods (see Table 3 and Figure 5a,b,e). In particular, for ASP, GLU and LYS the pKa predictions with the GB-MSR6c-pK method are slightly better than the ones obtained by the ROSETTA-pH method (see Table S3 in Kilambi, Gray, 2012) or by the MCCI2 method (see Table 2 in Song, Mao, Gunner, 2009). On the contrary, the pKa predictions with the GB-MSR6c-pK method for TYR were slightly worse than for the other two methods; Indeed, the GB-MSR6c-pK method gives 42%, 54% and 85% for all pKa predictions with an accuracy < 0.5, < 1.0 and < 1.5 pK units, respectively (see Table 3), while the ROSETTApH method (Kilambi, Gray, 2012) gives 53%, 76% and 94% and the MCCI2 method gives 28%, 71% and 98% of all predictions (Song, Mao, Gunner, 2009).

It should be noted that both the MCCI2 and the Rosetta-pK methods approximate the protein flexibility by a Monte Carlo sampling of the backbone (φ,ψ) and side chain (χ’s) torsional angles. As a result, the conformers generated by these protocols provide an ensemble of structures with an RMSD < 1Å (Kilambi, Gray 2012), in other words, providing a tight set of conformations. On the other hand, use of our protocol, namely with conformations from snapshots along 10 ns of the MD trajectory, led to an ensemble of conformations with an RMSD of 1.3 Å – 1.6 Å, in other words, a broader set of conformations.

Analysis of the larger pKa errors.

In Table 4, with underlining, we highlight the worst pKa predictions obtained by using the GB-MSR6c-pK, the ROSETTApH and the MCCI2 methods, respectively. In general, the percentages of predictions with error larger than 2.0 pK units is quite small (~4%) for all three methods. However, there is a larger difference among all three methods regarding the maximal absolute error of the pKa predictions. Indeed, maximal errors of 2.6, 4.1 and 7.0 pK units (see Table 4) were obtained by using the GB-MSR6c-pK, ROSETA-pH and MCCI2 methods, respectively. In addition, the percentage of underlined values in Table 4, i.e., those representing the largest wrong prediction for each protein among the three methods, is 57%, 50% and 27% of the 11 listed proteins in Table 4, for MCCI2 and ROSETA-pH, respectively, and lower for GB-MSR6c-pK.

Influence of protein dynamics on the accuracy of the pKa prediction.

To study the influence of the dynamics of the protein on the computation of the pKa, we focus our attention, among all 34 proteins (see Table S1 of SM), on an NMR-determined protein structure for which 34 conformations are deposited in the PDB, namely for ribonuclease T1 (PDB id 1YGW), a four α-helical bundle protein with 104 residues. Analysis of this protein is particularly important because the ensemble of 34 conformations, representing the dynamics of the protein in solution, enable us to define the range of fluctuation of the computed pKa values (~ ± 0.2 to ~ ±0.5 pK unit as shown in Table 3 and Table S1 of SM), as well as to compare it to the observed values (shown in Table 4) and the MD simulated range of fluctuations (Table S1 of SM).

Table 5 lists the results of the computed pKa for protein 1YGW. The NMR-determined structure of this protein is represented by an ensemble of 34 structures, which reflect the protein conformational dynamics in solution. We computed the pKa of each ionizable residue, for each of 34 NMR-determined structures, thereby obtaining an average pKa value (see Table 5, column 3) and the corresponding range of fluctuations of the computed average pKa values (see footnote d in Table 5). Overall, there is good agreement between the observed and the average computed pKa values (see columns 2 and 3 of Table 5) for a set of 34 NMR structures i.e., with average error of only 0.54 pK units. In particular, the average error between observed and computed pKa’s from a set of MD structures determined over 10 ns trajectory (see footnote c in Table 5) is found to be very similar, namely 0.56 pK. Certainly, the good agreement with the observed data indicates that the structural dynamics of the protein in a solvent is realistically reproduced by the molecular dynamics simulation method used (Popov, Vorobjev 2010). At this point it is worth noting that, for the set of conformations obtained from the MD trajectory, only two residues have a pKa error larger than 1.0 pKa unit, namely for GLU 28 and GLU 31 with errors of 1.7 and 1.1 pKa units, respectively (see underlined values at column 4 of Table 5). The same analysis for the computed error from the set of 34 conformations shows only one residue, namely GLU 31 (see underlined value in column 3 of Table 5), with an error (1.4) larger than 1.0 pK unit. Taken as a whole, the accuracy of the pKa predictions, by using the GB-MSR6c-pK method, is within 0.5, 0.75 and 1.0 pKa units for 57%, 78% and 86% of the residues Table 5.

Overall, the larger pKa errors obtained with each of the three tested methods, shown in Table 5, are very similar, namely 1.5, 1.7 and 1.9 pKa units for the MCCI2, the GB-MSR6c-pK and the Rosetta-pH methods, respectively. In addition, we have also been able to show (see a comparison of the values from columns 5 and 6 on Table S1 of SM) that the use of molecular dynamics simulations, to account for the protein dynamics, leads to more accurate pKa predictions of the ionizable groups of proteins.

The CPU-time for a 10 ns MD simulation, for a computation of the pKa’s, and for the titration curves for all ionizable residues, for each of the 34 proteins listed in Table S1 (SM), are given in Table S2 (SM).

2.4. About the multiple neutral states of acid and histidine residues

Analysis of the tautomer distributions of His residues (from Table S1 of SM), among all the 34 proteins containing His, indicates that a strong preference for one tautomer is not commonly seen. Indeed, there are only 7 out of 55 His residues showing a large preference for one of the tautomers, namely: (1) HIS 127 (0.07, 0.43) on 2RN2; (2) HIS 119 (0.05, 0.45) on 3RN3; (3) HIS 92 (0.48, 0.02) on 2CPL; (4) HIS 32 (0.43, 0.07) on 1GYM; (5) HIS 43 (0.02, 0.48) on 3SSI; (6) HIS 167 (0.08, 0.42) on 6GST; and (7) HIS 149 (0.03, 0.47) on 1XNB; where in parenthesis we indicate the fractions of the N^δ1-H and N^ε2-H tautomers for each of these 7 His.

Overall, for only those 7 His residues, i.e., ~13% of a total of 55 His residues of the test set of 34 proteins, the preference (by ~1 kcal/mole) of one tautomer over the other is ≥ 4:1. These results support existing evidence indicating that the tautomeric preference of His residues in proteins is determined, mainly, by their local environment (Vila, et al., 2011). In other words, His in proteins does not behave like free His for which the N^ε2-H tautomer is favored over the N^δ1-H tautomer in a ratio of 4:1 (Reynolds et al., 1973).

An analysis of the acid groups indicates that a large preference of one position of hydrogen atom H over two possible ones for the neutral acid COOH group, as for residues ASP and GLU, is quite rare (~7%). Indeed, it occurs for only 12 out of 167 acid groups (listed in Table S1). Notably, such preferences occur for acid residues involved in hydrogen-bond interactions with His residues. Overall, the low probability of preference of the hydrogen atom in acid groups is a consequence of the fact that most of these residues are on the protein molecular surface and, hence, exposed to solvent.

3. Conclusions

Calculation of the fractions of ionized His⁺ and neutral tautomers N^δ1-H and N^ε2-H of His residues, acid residues and base residues in proteins is a challenging task, because it needs an accurate estimation of relative free energies of protein ionization states within a fraction of 1.0 kcal/mol. Hence, a state of the art method for estimation of the free energy of a protein in a given ionization state is presented here. The method was tested on a large set of 297 ionizable residues from 34 proteins and the results demonstrate good accuracy for the computation of the pKa values, namely, 57%, 86% and 95% of all predictions have an error lower than 0.5, 1.0 and 1.5 pKa units, respectively. Even more important, in a comparison with the other two tested methods, our method shows the lowest percentage of the largest wrong predictions, i.e., prediction with an error, ΔpKa, > 2.0 pK units, among the tested set of 34 proteins.

Moreover, our method enables one to estimate the neutral fractions of both the tautomeric forms of the imidazole ring of His, namely N^δ1-H and N^ε2-H, and similarly for the neutral acidic residues. In agreement with existing evidence, we also show that the fractions of His tautomers are far less different than those observed for isolated histidine in solution, mainly because the tautomer preferences are determined by the protein environment. However, not all the pKa values are predicted with the same accuracy and one of the main reasons relates to the implicit inaccuracy of the continuum dielectric model used for electrostatic calculations. For example, a His residue makes H-bonds with water molecules, i.e. restricting the water mobility/flexibility, and consequently affecting the dielectric properties of water solvent in its vicinity. The fact that His has two different neutral tautomers only exacerbates the problem. In this regard, we can assume that the accuracy of the calculations should be increased by improving the accuracy of the continuum dielectric model, for example by using a mixed implicit/explicit solvent model. Such “mixed solvent model” should take into account explicitly some water molecules while a continuum electrostatic model can be used for the remainder of the protein. However, such “mixed solvent model” will be very CPU time consuming. Consequently, the challenge is to make a “mix solvent model” sufficiently efficient such that the gain in accuracy is not out-weighted by the loss in speed relative to a classic uniform continuum dielectric model.