Augmented outcome-weighted learning for estimating optimal dynamic treatment regimens

Abstract

Dynamic treatment regimens (DTRs) are sequential treatment decisions tailored by patient’s evolving features and intermediate outcomes at each treatment stage. Patient heterogeneity and the complexity and chronicity of many diseases call for learning optimal DTRs that can best tailor treatment according to each individual’s time-varying characteristics (eg, intermediate response over time). In this paper, we propose a robust and efficient approach referred to as Augmented Outcome-weighted Learning (AOL) to identify optimal DTRs from sequential multiple assignment randomized trials. We improve previously proposed outcome-weighted learning to allow for negative weights. Furthermore, to reduce the variability of weights for numeric stability and improve estimation accuracy, in AOL, we propose a robust augmentation to the weights by making use of predicted pseudooutcomes from regression models for Q-functions. We show that AOL still yields Fisher-consistent DTRs even if the regression models are misspecified and that an appropriate choice of the augmentation guarantees smaller stochastic errors in value function estimation for AOL than the previous outcome-weighted learning. Finally, we establish the convergence rates for AOL. The comparative advantage of AOL over existing methods is demonstrated through extensive simulation studies and an application to a sequential multiple assignment randomized trial for major depressive disorder.

1 |. INTRODUCTION

Technology advances are revolutionizing medical research by collecting rich data from individual patient (eg, clinical assessments, genomic data, and electronic health records) for clinical researchers to meet the promise of individualized treatment and health care. The availability of comprehensive data sources provides new opportunities to deeply tailor treatment in the presence of patient heterogeneity and the complexity and chronicity of many diseases. Dynamic treatment regimens (DTRs),¹ also known as adaptive treatment strategies,¹ multistage treatment strategies,² or treatment policies,³ are a sequence of treatment decisions adapted to the time-varying clinical status of a patient. Moreover, DTRs are necessary to treat complex chronic disorders such as major depressive disorder (MDD) when some patients fail to achieve remission with a first-line treatment.⁴

Sequential multiple assignment randomized trials (SMARTs), in which randomization is implemented at each treatment stage, have been advocated⁵ to evaluate any DTR with causal interpretation. Using data collected from SMARTs, numerous methods have recently been developed to estimate optimal DTRs.^6–13 See also the works of Chakraborty and Moodie¹⁴ and Kosorok and Moodie¹⁵ for a detailed review of the current literature. Of all the methods, machine learning methods have received attention because of their robustness and computational advantages. For example, Q-learning¹⁶ was used to analyze SMART data by Zhao et al⁹ and Murphy et al.¹⁷ In this learning algorithm, the optimal treatment at each stage is derived from a backward induction by maximizing the so-called Q-function (“Q” stands for “quality of action”), which is estimated via a regression model. To avoid model misspecification in Q-learning, Zhao et al¹⁰ proposed outcome-weighted learning (OWL) to estimate the optimal treatment rules by directly optimizing the expected clinical outcome in a single-stage trial. They demonstrated in numerical studies that OWL outperforms Q-learning in small sample-size settings with many tailoring variables. Later, Zhao et al¹⁸ generalized OWL to estimating optimal DTRs in a multiple-stage trial and demonstrated the superior performance to existing methods. However, in the aforementioned work,¹⁸ since the weights at each stage of the estimation must be the optimal outcome increment in the future stages, only patients whose later treatments are optimal can be used for estimation. Consequently, a proportion of data have to be discarded from one stage to another in their backward learning algorithm, resulting in significant information loss and thus large variability of the estimated DTRs.

In this paper, we propose a hybrid approach, namely Augmented Outcome-weighted Learning (AOL), to integrate OWL and regression models for Q-functions for estimating the optimal DTRs. Similar to OWL, the proposed method relies on weighted machine learning algorithms in a backward induction. However, the weights used in AOL are constructed by augmenting optimal outcomes for all patients, including those whose later stage treatments are nonoptimal. The augmentation is obtained using prediction from the regression models for Q-functions. Thus, AOL performs augmented outcome-weighted learning using the regression models for Q-functions as augmentation.

There are several novel contributions in this work as compared with previous works.^10,18 First, for single-stage randomized trials, AOL generalizes OWL to allow for negative outcome values instead of adding an arbitrarily large constant, which may lead to numeric instability. Second, by using weights based on residuals after removing prognostic effects that are obtained from the observed outcomes, AOL reduces the variability of weights in OWL to achieve less variable DTR estimation. Third, AOL simultaneously takes advantage of the robustness of nonparametric OWL and makes use of model-based approaches to utilize data from all subjects. Fourth, AOL is theoretically shown to yield the same asymptotic bias as OWL but smaller stochastic variability because of a better weighting scheme and thus guarantees efficiency gain. Moreover, AOL is proved to yield the correct optimal DTRs even if the regression models assumed in the augmentation are incorrect and thus maintains the robustness of OWL.

The rest of this paper is organized as follows. In Section 2, we review some concepts for DTR, Q-learning, and OWL and introduce AOL for single-stage and multiple-stage studies. The last part of Section 2 presents theoretical properties of AOL. In particular, we provide stochastic error bounds for AOL and demonstrate its smaller stochastic variability when compared with OWL; we further derive a fast convergence rate for AOL. Section 3 shows the results of extensive simulation studies to examine the performance of AOL compared with Q-learning and OWL. In Section 4, we present real data analysis results from the Sequenced Treatment Alternatives to Relieve Depression (STAR*D) trial⁴ for MDD. Lastly, we conclude with a few remarks in Section 5.

2 |. METHODOLOGIES

2.1 |. Dynamic treatment regimes and outcome weighted learning

We start by introducing notation for a K-stage DTR. For k = 1, 2, … , K, denote X_k as the observed subject-specific tailoring variables collected just prior to the treatment assignment at stage k. Denote A_k as the treatment assignment taking values in { −1, 1}, and R_k as the clinical outcome (also known as the “reward”) post the kth-stage treatment. Larger rewards may correspond to better functioning or fewer symptoms depending on the clinical setting. A DTR is a sequence of decision functions, $\mathcal{D}=\left({\mathcal{D}}_1,{\mathcal{D}}_2,\dots ,{\mathcal{D}}_K\right)$, where ${\mathcal{D}}_K$ maps the domain of patient health history information, H_k = (X₁, A₁, R₁, … , A_k−1, R_k−1, X_k), to the treatment choices in {−1, 1}. Corresponding to each $\mathcal{D}$, a value function, denoted by $\mathcal{V}\left(\mathcal{D}\right)$, is defined as the expected reward given that the treatment assignments follow regimen $\mathcal{D}$.¹² Mathematically, $\mathcal{V}\left(\mathcal{D}\right)=E_{\mathcal{D}}\left[{\displaystyle {\sum }_{k=1}^K{R}_k}\right]={\displaystyle \int {\displaystyle {\sum }_{k=1}^K{R}_{k}d{P}_{\mathcal{D}}}}$, where ${\mathcal{P}}_{\mathcal{D}}$ is the probability measure generated by random variables (X₁, A₁, R₁, … , X_K,A_K, R_K) given that $A_k={\mathcal{D}}_k\left(H_k\right)$ and $E_{\mathcal{D}}$ is the expectation with respect to this measure. Hence, the goal of personalized DTRs is to find the optimal DTRs that maximize the value function.

To evaluate the value function of a DTR in a SMART, a potential outcome framework in causal inference literature is used. The potential outcome in our context is defined as the outcome of a subject had he or she followed a particular treatment regimen, possibly different from the observed regimen in the actual trial. Several assumptions are required to infer the value function of a DTR, including the standard stable unit treatment value assumption and the no unmeasured confounders assumption.^6,19 In a SMART, the no unmeasured confounders assumption is automatically satisfied because of the virtue of sequential randomization. Furthermore, we need the following positivity assumption: let 𝜋_k(a, h) denote the treatment assignment probability, P(A_k = a|H_k = h), which is given by design so known to investigators in a SMART. We assume that, for k = 1, … , K and any a ∈ {−1, 1} and h_k in the support of H_k, 𝜋_k(a, h_k) = P(A_k = a|H_k = h_k) ∈ [c,c̃], where 0 < c ≤ c̃ < 1 are two constants. That is, the positivity assumption requires that each DTR has a positive chance of being observed.

Under these assumptions, if we let P denote the probability measure generated by (X_k,A_k, R_k) for k = 1, … , K, then according to the work of Qian and Murphy,¹² it can be shown that $P_{\mathcal{D}}$ is dominated by P and

$$\mathcal{V}\left(\mathcal{D}\right)=E\left[\frac{{\displaystyle {\prod }_{k=1}^{K}I\left(A_k={\mathcal{D}}_k\left(H_k\right)\right)\left({\displaystyle \sum _{k=1}^K{R}_k}\right)}}{{\displaystyle \prod _{k=1}^K{\pi }_k\left(A_k,H_k\right)}}\right].$$ (1)

Consequently, the goal is to find the optimal treatment rule ${\mathcal{D}}^{\ast }=\left({\mathcal{D}}_1^{\ast },\dots ,{\mathcal{D}}_K^{\ast }\right)$ that maximizes the above expectation. Note that ${\mathcal{D}}_k$ is usually given as the sign of some decision function f_k. Without confusion, we sometimes express the value function as $\mathcal{V}\left(f_1,\dots ,f_K\right)$ to emphasize its dependence on the decision functions.

Denote data collected from n i.i.d. subjects in a SMART at stage k as (A_ik, H_ik, R_ik) for i = 1, … , n, k = 1, … , K. Recently, outcome-weighted learning (Zhao et al), abbreviated as OWL, was proposed to estimate the optimal treatment regimes. Specifically, Zhao et al proposed a backward induction to implement OWL, where at stage k, they used only the subjects who followed the estimated optimal treatment regimens after stage k in the optimization algorithm. That is, the optimal rule ${\mathcal{D}}_k\left(H_k\right)=\text{\hspace{0.17em}sign}\left(f_k\left(H_k\right)\right)$ solves a weighted support vector machine problem

$$\underset{f\in \mathcal{H}}{\min }\frac{1}{n}{\displaystyle \sum _{i=1}^n\varphi \left(A_{ik}{f}_k\left(H_{ik}\right)\right)}\frac{{\displaystyle {\sum }_{j=k}^K{R}_{ij}}}{{\pi }_{ik}}\frac{I\left(A_{i,k+1}={\widehat{\mathcal{D}}}_{k+1}\left(H_{i,k+1}\right),\dots ,A_{iK}={\widehat{\mathcal{D}}}_K\left(H_{iK}\right)\right)}{{\displaystyle {\prod }_{j>k}{\pi }_{ij}}}+{\lambda }_n\parallel f_k{\parallel }^2,$$ (2)

where Ø(x) = max(0, 1 − x) is the hinge loss ${\pi }_{ij}={\pi }_j\left(A_{ij},H_{ij}\right),{\widehat{\mathcal{D}}}_j\left(H_{ij}\right)$ is the estimated optimal rule at stage j from the backward learning algorithm, and ∥f∥ is some norm defined in a given metric space, $\mathcal{H}$, usually a reproducing kernel Hilbert space (RKHS), for f. However, as discussed before, the use of only those subjects who followed the optimal regimen in future stages may result in information loss, especially when K is not small. Furthermore, the work of Zhao et al¹⁰ suggests to subtract a constant from R_ik to ensure a positive weight in the optimization algorithm, where the choice of constant is arbitrary and can be numerically influential in the above optimization.

2.2 |. AOL with K = 1 stage

We first describe the proposed method, namely AOL, under the single-stage randomized trial setting (K = 1). The main idea of AOL is to improve OWL by replacing R₁ in (1) by some surrogate variable, which should give the same optimal decision rule but with less variability in the empirical estimation of (2).

Note that, for any integrable function s(H₁) and for $\mathcal{D}\left(H_1\right)=\text{sign}\left(f_k\left(H_k\right)\right)$, it holds that

$$\begin{gathered} \mathcal{V}\left(\mathcal{D}\right)=E\left[\frac{I\left(A_{1}f\left(H_1\right)>0\right)R_1}{{\pi }_1\left(A_1,H_1\right)}\right] \\ =E\left[\frac{I\left(A_{1}f\left(H_1\right)>0\right)\left(R_1-s\left(H_1\right)\right)}{{\pi }_1\left(A_1,H_1\right)}\right]+E\left[s\left(H_1\right)\right] \\ =E\left[\frac{\left|R_1-s\left(H_1\right)\right|}{{\pi }_1\left(A_1,H_1\right)}I\left(A_1\text{sign}\left(R_1-s\left(H_1\right)\right)f\left(H_1\right)>0\right)\right]+E\left[s\left(H_1\right)\right]-E\left[\frac{{\left(R_1-s\left(H_1\right)\right)}^{-}}{{\pi }_1\left(A_1,H_1\right)}\right], \end{gathered}$$

where x⁻ = −min(0, x). Therefore, maximizing V(D) is equivalent to maximizing

$$E\left[\frac{\left|R_1-s\left(H_1\right)\right|}{{\pi }_1\left(A_1,H_1\right)}I\left(A_1\text{sign}\left(R_1-s\left(H_1\right)\right)f\left(H_1\right)>0\right)\right].$$

This suggests that, if we choose a surrogate variable, ${\tilde{R}}_1=R_1-s\left(H_1\right)$, to replace R₁ and solve a similar problem to (2), where the weights are changed to $\left|{\tilde{R}}_{i1}\right|/{\pi }_{i1}$ and the class labels become $A_{i1}\text{sign}\left({\tilde{R}}_{i1}\right)$, then we expect to still obtain a consistent estimator of the optimal DTR.

Specifically, the proposed AOL for the K = 1 stage consists of the following two steps.

Step 1. Use data (R_i1,H_i1) to obtain an estimator $\widehat{s}\left(H_1\right)={\widehat{\gamma }}_0+{\widehat{\gamma }}_1^T{H}_1$ by fitting a least squares regression or a penalized least squares regression if H_i1 is high dimensional.

Step 2. Obtain ${\tilde{R}}_{i1}=R_{i1}-\widehat{s}\left(H_{i1}\right)$ for each subject and fit a weighted support vector machine (SVM) to estimate the decision function f₁, where the weights are $\left|{\tilde{R}}_{i1}\right|/{\pi }_{i1}$ and the class labels are $A_{i1}\text{sign}\left({\tilde{R}}_{i1}\right)$. That is, the estimated decision function, denoted by ${\widehat{f}}_1$, minimizes

$$n^{-1}{\displaystyle \sum _{i=1}^n\frac{\left|{\tilde{R}}_{i1}\right|}{{\pi }_{i1}}}\varphi (A_{i1}\text{sign}({\tilde{R}}_{i1})f_1(H_{i1}))+{\lambda }_n\parallel f_1\parallel .$$

The function class for f₁ is from an RKHS with either a linear kernel or a Gaussian kernel, which are the most popular choices in practice, although the proposed method can be applied with any kernels. Computationally, this minimization can be carried out using quadratic programming.²⁰ Finally, the optimal DTR, ${\mathcal{D}}_1^{\ast }$, is estimated as ${\widehat{\mathcal{D}}}_1\left(H_1\right)=\text{\hspace{0.17em}sign}\left({\widehat{f}}_1\left(H_1\right)\right)$.

Remark 1. A heuristic interpretation of AOL is the following: first, learning DTR is essential to learn the qualitative interaction between A₁ and H₁, so the removal of any main effects s(H₁) from R₁ has no influence; second, for a subject with large observed value of |R₁ − s(H₁)|, the above maximization implies that the optimal treatment assignment should be likely to remain the same as the actual treatment he/she is observed to receive in a trial if R₁ − s(H₁) is positive but should be the opposite if negative. Furthermore, there are intuitive advantages to use ${\tilde{R}}_1$ to replace R₁ and use $\left|{\tilde{R}}_1\right|/{\pi }_1\left(A_1,H_1\right)$ as the new weight. When s(H₁) is chosen appropriately, the resulting ${\tilde{R}}_1$ is less variable, so we expect that it may lead to a less variable DTR estimator using empirical observations. Moreover, since the proposed new weights are nonnegative, this guarantees a convex optimization problem when solving (2). In contrast, in the original OWL, when the weights in (2) are negative, they suggested subtracting an arbitrarily small constant from the weights to make it positive. This shifting of negative weights has been demonstrated to be unstable in numerical studies.

2.3 |. AOL with K = 2 stages

Next, we consider K = 2. Because DTRs aim to maximize the expected cumulative rewards across all stages, the optimal treatment decision rule at the current stage must depend on subsequent decision rules and future clinical outcomes or rewards under those rules. This observation motivates us to use a backward procedure similar to the backward induction in Q-learning and OWL in the work of Zhao et al.¹⁸ To estimate the optimal treatment rule at stage 2, AOL has the same two steps as in Section 2.2.

Step 2–1. Use data (R_i2, H_i2) to obtain an estimator ${\widehat{s}}_2\left(H_2\right)={\widehat{\gamma }}_0+{\widehat{\gamma }}_1^T{H}_2$ by fitting a least squares regression or a penalized least squares regression if H_i2 is high dimensional.

Step 2–2. Obtain ${\tilde{R}}_{i2}=R_{i2}-{\widehat{s}}_2\left(H_{i2}\right)$ for each subject and fit a weighted SVM to estimate the decision function f₂, where the weights are $\left|{\tilde{R}}_{i2}\right|/{\pi }_{i2}$, and the class labels are $A_{i2}\text{sign}\left({\tilde{R}}_{i2}\right)$. That is, the estimated function, denoted by ${\widehat{f}}_2$, minimizes

$$n^{-1}{\displaystyle \sum _{i=1}^n\frac{\left|{\tilde{R}}_{i2}\right|}{{\pi }_{i2}}}\varphi (A_{i2}\text{sign}({\tilde{R}}_{i2})f(H_{i2}))+{\lambda }_n\parallel f\parallel .$$

Thus, the estimated optimal DTR at stage 2 is given by ${\widehat{\mathcal{D}}}_2\left(H_2\right)=\text{\hspace{0.17em}sign}\left({\widehat{f}}_2\left(H_2\right)\right)$.

Now, we consider the estimation of the optimal stage 1 treatment rule. For this purpose, a key outcome variable is the so-called Q-function, denoted by Q₂, which is the future reward increment at future stages if a subject is assigned to the optimal treatment in those stages. If Q₂ were observed for each subject, then the optimal treatment rule at stage 1 would be estimated using OWL with R₁ + Q₂ as the outcome part of the weight. For the subjects whose treatment assignments at stage 2 are the same as the optimal treatment rule ${\mathcal{D}}_2^{\ast }$, it is clear that Q₂ = R₂, and thus, their weights are observed; however, for subjects whose treatment assignments at stage 2 are not optimal (ie, not the same as ${\mathcal{D}}_2^{\ast }$), Q₂ is not observed. Moreover, OWL uses only those subjects whose Q₂’s are observed and multiplies by the inverse probability of treatment assignment.

However, if we treat missing Q₂ as a missing data problem, it is well known that the use of only complete data for estimation may not be the most efficient method; instead, one can use auxiliary information prior to stage 2, namely H₂, to predict Q₂ through augmentation for those subjects with missing Q₂ (ie, for those subjects whose treatment assignments at stage 2 are not the same as the optimal treatment rule ${\mathcal{D}}_2^{\ast }$). Define m₂₂(H₂) as an approximation to the optimal reward increment for subjects who receive nonoptimal treatment at stage 2. Following the missing data literature,²¹ such an augmented Q₂ can be defined as

$$\frac{I\left(A_2={\mathcal{D}}_2^{\ast }\left(H_2\right)\right)}{{\pi }_2\left(A_2,H_2\right)}{R}_2-\left\{\frac{I\left(A_2={\mathcal{D}}_2^{\ast }\left(H_2\right)\right)}{{\pi }_2\left(A_2,H_2\right)}-1\right\}{m}_{22}\left(H_2\right).$$

Ideally, we want to choose m₂₂(H₂) as close as possible to E[Q₂|H₂]; however, in practice, because the latter is unknown, and H₂ can be high dimensional, we will estimate m₂₂(H₂) as a linear function of H₂ using a weighed least squares regression for subjects who are treated optimally in stage 2 as described below. To estimate the optimal stage 1 treatment rule, AOL has the following steps.

Step 1–1. Recall ${\widehat{\mathcal{D}}}_2\left(H_2\right)=\text{\hspace{0.17em}sign}\left({\widehat{f}}_2\left(H_2\right)\right)$. Estimate m₂₂(H₂) = β₀ + β^TH₂ by a weighted least squares regression minimizing

$$n^{-1}{\displaystyle \sum _{i=1}^n\frac{I\left(A_{i2}={\widehat{\mathcal{D}}}_2\left(H_{i2}\right)\right)}{{\pi }_{i2}}}\frac{1-{\pi }_{i2}}{{\pi }_{i2}}{\left(R_{i2}-m_{22}\left(H_{i2}\right)\right)}^2,$$

and denote the resulting estimator as ${\widehat{m}}_{22}$.

Step 1–2. For subject i, compute

$${\widehat{Q}}_{i2}=\frac{I\left(A_{i2}={\widehat{D}}_2\left(H_{i2}\right)\right)}{{\pi }_{i2}}{R}_{i2}-\left\{\frac{I(A_{i2}={\widehat{D}}_2\left(H_{i2}\right)}{{\pi }_{i2}}-1\right\}{\widehat{m}}_{22}\left(H_{i2}\right).$$

Step 1–3. Obtain an estimator ${\widehat{s}}_1\left(H_1\right)$ for s₁(H₁) = α₀+α^TH₁ using a least squares regression that minimizes

$${\displaystyle \sum _{i=1}^n{\left(R_{i1}+{\widehat{Q}}_{i2}-s_1\left(H_{i1}\right)\right)}^2}$$

and denote ${\tilde{R}}_{i1}=R_{i1}+{\widehat{Q}}_{i2}-{\widehat{s}}_1\left(H_{i1}\right)$.

Step 1–4. Finally, obtain ${\widehat{f}}_1$ by fitting a weighted SVM with weights $\left|{\tilde{R}}_{i1}\right|/{\pi }_{i1}$ and class labels $A_{i1}\text{sign}\left({\tilde{R}}_{i1}\right)$. The optimal DTR at stage 1 is then ${\widehat{\mathcal{D}}}_1\left(H_1\right)=\text{\hspace{0.17em}sign}\left({\widehat{f}}_1\left(H_1\right)\right)$.

Note that the last two steps (Steps 1–3 and 1–4) essentially repeat the same procedure as in the K = 1 stage except that the outcome is the augmented outcome variable $R_{i1}+{\widehat{Q}}_{i2}$ As a remark, when H_i2 or H_i1 is of high dimension, we recommend that a penalized least squares regression such as Lasso be used in Step 1–1 or Step 1–3 in practice.

Remark 2. The key idea of our proposed approach for two-stage problem is to use prediction models for the Q-function at stage 2 to “impute” the future reward increments for the subjects whose actual treatments received in the second stage are not the optimal because their the observed outcomes cannot be used to estimate the optimal future reward increments. The missingness mechanism is due to the randomization of the treatments in stage 2; thus, it is completely known. The proposed augmented weights in stage 1 are guaranteed to yield the correct optimal treatment rules. Furthermore, if the “imputation” is sufficiently close to the underlying true model, we expect to obtain better accuracy in finding the optimal rule because of using more observations.

2.4 |. Generalization to more than 2 stages

When there are more than two stages, the same backward learning as in K = 2 can be applied, but the augmentation for those subjects with missing future optimal reward increments becomes more complex. First, to estimate the optimal treatment rule at stage K, we perform the same stage 2 steps as AOL with K = 2 (ie, Steps 2–1 and 2–2 in Section 2.3) but with (R₂, A₂, H₂) replaced by (R_K, A_K, H_K). Denote the resulting estimated decision function at this stage as ${\widehat{f}}_K\left(H_K\right)$ and denote the corresponding treatment rule as ${\widehat{\mathcal{D}}}_K\left(H_K\right)=\text{\hspace{0.17em}sign}\left({\widehat{f}}_K\left(H_K\right)\right)$.

We then continue to estimate the optimal treatment rules at stage K − 1, K − 2, … in turn. Specifically, to estimate the optimal (k − 1)th-stage treatment rule, we let $M_{i,k}^{k-1}=1$, and for $j\ge k$, let $M_{ik}^j=I\left(A_{ik}={\mathcal{D}}_k^{*}\left(H_{ik}\right),\dots ,A_{ij}={\mathcal{D}}_j^{*}\left(H_{ij}\right)\right)$ denote whether subject i follows the optimal treatment regimens from stage k to j. From the theory of Robins⁸, also seen in Tsiatis²¹ and Zhang et al²², Q_ik, the optimal reward increment for patient i if she/he follows the estimated optimal rule from stage k to K, has the following expression:

$$Q_{ik}=\frac{M_{ik}^K\left(R_{ik}+\dots +R_{iK}\right)}{{\displaystyle {\prod }_{l=k}^K{\pi }_{il}}}-{\displaystyle \sum _{j=k}^K\left\{\frac{M_{ik}^{j-1}}{{\displaystyle {\prod }_{l=k}^{j-1}{\pi }_{il}}}\left\{\frac{I\left(A_{ij}={\mathcal{D}}_j^{\ast }\left(H_{ij}\right)\right)}{{\pi }_{ij}}-1\right\}{m}_{kj}\left(H_{ij}\right)\right\}},$$

where m_kj(H_ij) is the optimal reward increment for subjects who receive optimal treatments up to stage (j − 1), ie, $E\left(Q_{ik}|H_{ij},M_{ik}^{j-1}=1\right)$.

To implement AOL, at stage k − 1, assume that we have already obtained the estimated optimal rules after this stage, denoted by ${\widehat{\mathcal{D}}}_k,\dots {\widehat{\mathcal{D}}}_K$. Define

$${\widehat{M}}_{ik}^j=I\left(A_{ik}={\widehat{\mathcal{D}}}_k\left(H_{ik}\right),\dots ,A_{ij}={\widehat{\mathcal{D}}}_j\left(H_{ij}\right)\right).$$

Then, the augmentation term for Q_ik is estimated by

$$\frac{{\widehat{M}}_{ik}^K\left(R_{ik}+\dots +R_{iK}\right)}{{\displaystyle {\prod }_{l=k}^K{\pi }_{il}}}-{\displaystyle \sum _{j=k}^K\left\{\frac{{\widehat{M}}_{ik}^{j-1}}{{\displaystyle {\prod }_{l=k}^{j-1}{\pi }_{il}}}\left\{\frac{I\left\{A_{ij}={\widehat{\mathcal{D}}}_j\left(H_{ij}\right)\right\}}{{\pi }_{ij}}-1\right\}{\widehat{m}}_{kj}\left(H_{ij}\right)\right\}},$$ (3)

where ${\widehat{m}}_{kj}\left(H_j\right)$ is estimated as a linear function of H_j by the weighted least squares

$$n^{-1}{\displaystyle \sum _{i=1}^n\frac{{\widehat{M}}_{ik}^K}{{\displaystyle {\prod }_{l=k}^K{\pi }_{ik}}}}\frac{1-{\pi }_{ij}}{{\displaystyle {\prod }_{k\le l\le j}{\pi }_{il}}}{\left({\displaystyle \sum _{l=k}^K{R}_{il}-}{m}_{kj}\left(H_{ij}\right)\right)}^2.$$

We define ${\tilde{R}}_{i,k-1}=R_{i,k-1}+{\widehat{Q}}_{i,k}-{\widehat{s}}_{k-1}\left(H_{k-1}\right)$, where ${\widehat{s}}_{k-1}\left(H_{k-1}\right)$ is estimated via a least squares regression that minimizes ${{\displaystyle {\sum }_{i=1}^n\left\{R_{i,k-1}+{\widehat{Q}}_{ik}-s_{k-1}\left(H_{i,k-1}\right)\right\}}}^2$ for $s_{k-1}\left(H_{k-1}\right)={\alpha }_0+{\alpha }^T{H}_{k-1}$. Then, we will estimate ${\widehat{f}}_{k-1}$. by fitng a weighted SVM with weights $\left|{\tilde{R}}_{i,k-1}\right|/{\pi }_{i,k-1}$ and class labels $A_{i,k-1}\text{sign}\left({\tilde{R}}_{i,k-1}\right)$, ie, ${\widehat{f}}_{k-1}$ minimizes

$$n^{-1}{\displaystyle \sum _{i=1}^n\frac{\left|{\tilde{R}}_{i,k-1}\right|}{{\pi }_{i,k-1}}}\varphi (A_{i,k-1}\text{sign}({\tilde{R}}_{i,k-1})f_{k-1}(H_{i,k-1}))+{\lambda }_n\parallel f_{k-1}\parallel .$$

One important fact for AOL is that the estimated treatment rules are invariant even if we shift R_k by any constant c_k for k = 1, … , K. This is because under constant translation, m_kj will be shifted by ${\displaystyle {\sum }_{l=k}^K{c}_l}$ so ${\widehat{Q}}_{ik}$ becomes ${\widehat{Q}}_{ik}+{\displaystyle {\sum }_{l=k}^K{c}_l}$. Therefore, ${\tilde{R}}_{i,k-1}$ which is the residual after regressing $R_{i,k-1}+c_{k-1}+{\widehat{Q}}_{ik}$ on 1 and H_i,k−1, remains unchanged, so the estimated treatment rule is the same as before. Finally, when H_j’s dimension is large, a penalized least square regression such as Lasso is recommended in the above procedure to obtain ${\widehat{m}}_{kj}\left(H_j\right)$.

2.5 |. Software

We provide an R-package “DTRlearn” https://cran.r-project.org/web/packages/DTRlearn/index.html on CRAN for the single- and multiple-stage implementation of our proposed method (AOL) and Q-learning and O-learning as compared in the following simulation results and real data implementation.

2.6 |. Summary of theoretical results

In the supplementary material, we provide theoretical justification for the proposed methods. Theorem A.1 provides an error bound for single stage AOL. We formally prove that using this new surrogate weight on the basis of the residuals of R₁, the value loss due to using the estimated treatment rule ${\widehat{f}}_1$ has the same deterministic error bound as using the original R₁; however, the error bound due to data randomness is smaller. In this sense, the value function for AOL has the same approximation bias as OWL but a smaller stochastic error asymptotically. Thus, AOL requires fewer observations than OWL to achieve a similar performance.

Theorem A.2 in the supplementary material provides the improved risk bound for multiple stage AOL. We formally show that the above data augmentation method using a surrogate function m₂₂(H₂) for subjects with missing Q₂ values will not increase the approximation bias of the value function estimation based on ${\widehat{f}}_1$; furthermore, we show that compared with OWL, the estimation of m₂₂(H₂) from a weighted least squares in Step 1–1 always leads to a smaller stochastic error bound of the value function estimation. Finally, Theorem A.3 gives a fast convergence rate of AOL under some regularity conditions.

The key idea behind the proofs is to decompose the value function associated with the estimated DTR into two parts: one is the bias due to considering the decision functions f_k at each stage from an RKHS; the other part is the stochastic error due to both the empirical approximation of the value function in terms of the augmented weights in the optimization. The former can be characterized in terms of the richness of the Hilbert space, whereas the latter depends on both the complexity of the function classes in the Hilbert space and, more importantly, the variability of the weights used in our proposed weighted SVM methods. The less variable the weights are, the smaller the stochastic error is. Therefore, the proposed method, which relies on the augmentation, tends to bring more information to reduce the variability in the weights.

3 |. SIMULATION STUDIES

We conducted extensive simulation studies to compare AOL with existing approaches using the value function (reward) of the estimated optimal treatment rules. We compared three methods: (i) Q-learning based on linear regression models with a Lasso penalty; (ii) OWL as in the works of Zhao et al^10,18; (iii) AOL as described in Section 2.

3.1 |. Simulation settings

We simulated single-stage, two-stage, and four-stage randomized trials. In this section, we present the results of four-stage settings. In the supplementary material, we provide additional results of the single-stage (Section B.1) and two-stage (Section B.2) settings.

In the first four-stage scenario, we simulated a vector of baseline feature variables of dimension 20, X₁ = (X_1,1, … , X_1,20), from a multivariate normal distribution, where the first 10 variables had a pairwise correlation of 0.2, the remaining 10 variables were uncorrelated among one another and were also independent of the first 10 X’s, and the variance for X_1,j was 1 for j = 1, … , 20. The reward functions were generated as follows:

$$\begin{gathered} R_1=X_{1,1}{A}_1+\mathcal{N}\left(0,1\right);R_2=\left(R_1+X_{1,2}^2+X_{1,3}^2-0.8\right)A_2+\mathcal{N}\left(0,1\right); \\ {R}_3=2\left(R_2+X_{1,4}\right)A_3+X_{1,5}^2+X_{1,6}+\mathcal{N}\left(0,1\right);R_4=\left(R_3-0.5\right)A_4+\mathcal{N}\left(0,1\right). \end{gathered}$$

The randomization probabilities of treatment assignment at each stage were allowed to depend on the feature variables through

$$P\left(A_1=1|H_1\right)=\frac{1}{1+\exp \left(-0.5X_{1,1}\right)};P\left(A_2=1|H_2\right)=\frac{1}{1+\exp \left(0.1R_1\right)};P\left(A_3=1|H_3\right)=\frac{1}{1+\exp \left(0.2X_{1,3}\right)};P\left(A_4=1|H_4\right)=\frac{1}{1+\exp \left(0.2X_{1,4}\right)}.$$

Patient’s health history information matrix at stage k, H_k, was defined recursively by (H_k−1, A_k−1, A_k−1H_k−1, R_k−1), and at the first stage, it only contains the baseline feature variables, ie, H₁ = X₁. Therefore, there were p = 20 features for OWL and AOL in the first stage, 2p + 2 for the second stage, and 8p + 14 variables for the fourth stage. To handle high dimensionality of the feature space, especially when k increases, weighted least squares with a Lasso penalty was used to estimate ${\widehat{m}}_{kj}$, and ordinary least squares with Lasso penalty was used to estimate ŝ_k. When estimating conditional expectations in Q-learning, (H_k, A_k) was included in the linear regression models (the number of predictors approximately doubles compared to OWL and AOL), and a Lasso penalty was imposed for better fitting.

In the second four-stage scenario, we imitated a real-world scenario of treating chronic mental disorders,⁴ where the patient population consisted of several subgroups that respond to DTRs differently. However, because of unknown and complex treatment mechanisms, instead of directly observing subgroup memberships, only group-informative feature variables (such as clinical symptomatology measures or neuroimaging biomarkers) were observed. Specifically, we created 10 subgroups of equal size and let G = 1, … , 10 denote group. For group G = l, the optimal DTRs across 4 stages were

$$\begin{array}{cc}{A}_{jl}^{*}=2\left(\left[l/\left(2j-1\right)\right]\mathrm{mod}2\right)-1,& j=1,2,3,4.\end{array}$$

To simulate data from a SMART, we randomly generated their treatment assignments with equal probabilities at each stage, and for a subject in group G = l, we generated their reward outcomes as R₁ = R₂ = R₃ = 0 and $R_4={\displaystyle \sum }_{j=1}^4{A}_j{A}_{jl}^{*}+N\left(0,1\right)$. Furthermore, we generated potentially group-informative baseline feature variables, X₁ = (X_1,1, … , X_1,30), from a multivariate normal distribution with means depending on group membership: for patients in group G = l, the center of X_1,1, … , X_1,10 had a group-specific mean value μ_l, which was generated from μ_l ~ N(0, 5), while the means of the remaining feature variables, X_1,11, … , X_1,30, were all zero. The first 10 features had a pairwise correlation of 0.2, and the remaining 20 variables were uncorrelated. Therefore, only X_1,1, … , X_1,10 were informative of the patient subgroup (and thus the optimal DTRs), and the remaining variables were noise. Since the group membership was not observed, the available data for our analysis consisted of (X₁, A₁, A₂, A₃, A₄, R₄). For each data set, we applied Q-learning, OWL, and AOL to estimate the optimal rule. For OWL, we implemented the same algorithm as in the work of Zhao et al,¹⁸ and the minimal value of the reward outcome was subtracted from the outcome to ensure the weights to be positive. In this setting, the clusters and optimal decision boundaries are fixed for each replication but different across replications. Thus, the results do not depend on the specific cluster arrangements. The decision boundaries are not explicitly determined by the observed predictors, but they are determined by the underlying latent classes, which confer information from the observed predictors.

At each stage k, H_k contained baseline feature variables X₁, previous stage treatment assignments, and products between X₁ and previous stage treatments. We varied sample sizes in the simulations. Cross-validation was used to choose the tuning parameter in Lasso regressions and was used to choose the tuning parameter of the SVM (from a grid of 2⁻¹⁵ to 2¹⁵). The linear kernel was used for OWL and AOL. To compare all the methods, we calculated the value function of the corresponding estimated optimal rule using expression (1) as the empirical average of a large independent test data set with a sample size of 20 000.

3.2 |. Simulation results

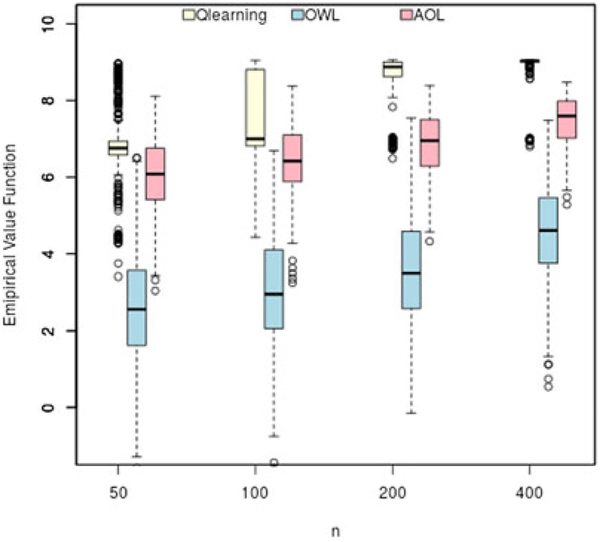
The results from 500 replicates are presented in Figures 1 and 2 and Table 1. In both simulation settings and for all sample sizes, AOL shows a significant advantage over OWL in terms of a higher value function because of augmentation and other improvements highlighted in previous sections. In the first setting, we observe that Q-learning has a higher value function than AOL but also a higher variability with a smaller sample size (n = 50, n = 100, and n = 200). With a large sample size (n = 400), Q-learning has an empirical standard deviation smaller than AOL. The value function for both Q-learning and AOL increases with the sample size, where the former increases at a faster rate. In this setting, the linear regression model is a good approximation for the Q-function since the rewards were generated from a linear model. Therefore, Q-learning may achieve the theoretical optimal value faster than AOL when n increases. Comparing with OWL, AOL achieves a much larger value and a smaller standard deviation for all sample sizes. In the second simulation setting, the optimal treatment boundaries were more complicated and highly nonlinear; therefore, Q-learning performed the worst among the three method at all sample sizes. For example, it only achieves a median value of 0.717 when n = 400 compared with the true optimal value of 4. For a proportion of the 500 replications, no treatment by covariate interaction terms were selected by Lasso regression in at least one step of Q-learning. In this case, the optimal treatment was selected randomly to compute the value function using the test data. Moreover, AOL outperforms OWL and Q-learning in all cases and achieves a median value of 3.211 with a sample size of 400.

FIGURE 1.

Simulation setting 1 with four-stage design (optimal value = 10.1). AOL, Augmented Outcome-weighted Learning. OWL, outcome-weighted learning [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 2.

Simulation setting 2 with four-stage design (optimal value = 4.0). AOL, Augmented Outcome-weighted Learning; OWL, outcome-weighted learning [Colour figure can be viewed at wileyonlinelibrary.com]

TABLE 1.

Mean and median of the empirical value function for two simulation scenarios evaluated with an independent test data set

n	Simulation Setting 1 (Optimal Value 10.1)
	Q-learning		OWL		AOL
	Mean (SD)	Median	Mean (SD)	Median	Mean (SD)	Median
50	6.786(1.119)	6.753	2.604(1.502)	2.561	6.042(0.951)	6.078
100	7.711(1.016)	6.996	3.049(1.448)	2.957	6.436(0.859)	6.415
200	8.475(0.843)	8.874	3.593(1.461)	3.486	6.865(0.756)	6.949
400	8.934(0.398)	9.034	4.566(1.265)	4.603	7.467(0.632)	7.593

n	Simulation Setting 2 (Optimal Value 4)
	Q-learning		OWL		AOL
	Mean (SD)	Median	Mean (SD)	Median	Mean (SD)	Median
50	0.042(0.182)	0.003	0.764(0.522)	0.773	1.105(0.522)	1.097
100	0.103(0.281)	0.011	0.966(0.484)	0.944	1.696(0.595)	1.698
200	0.291(0.404)	0.062	1.281(0.492)	1.284	2.519(0.518)	2.568
400	0.635(0.355)	0.717	1.638(0.446)	1.626	3.177(0.421)	3.211

Abbreviations: AOL, Augmented Outcome-weighted Learning; OWL, outcome-weighted learning.

For the previous two simulation scenarios, we also implemented AOL with Gaussian kernel with four-fold cross validation to choose the bandwidth and compared with OWL with Gaussian kernel. Moreover, AOL with Gaussian kernel performed similarly with linear kernel for AOL in the second scenario, which achieved a median of 0.851, 1.453, 2.427, 3.400 and for the sample size of 50, 100, 200, and 400, respectively. For the first scenario, AOL with Gaussian kernel has a slightly worse performance than linear kernel, with a median value function of 4.965, 5.496, 6.295, 6.905 for sample sizes ranging from 50 to 400. Comparatively, OWL with Gaussian kernel has the median values of 2.529, 2.952, 3.459, 4.288 in the first scenario and 0.804, 1.043, 1.356, 1.743 in the second scenario, so AOL is still superior to OWL. Since the computational burden for the Gaussian kernel is heavier, we conclude that using a linear kernel for AOL is sufficient in these simulation settings. Additional simulations of the single-stage and two-stage settings are reported in the supplementary material (Section B). Similar comparative performances are observed.

In summary, in simulation scenario 1, the data were generated such that a linear function is an adequate approximation for the true cumulative rewards. Thus, Q-learning outperformed OWL and AOL. In simulation scenario 2, the data were generated such that the cumulative rewards cannot be approximated adequately by the linear models. Thus, OWL and AOL outperformed the value-based learning method Q-learning. Nevertheless, in all the presented simulation scenarios, AOL outperformed OWL, which demonstrates that the proposed AOL improves OWL.

4 |. REAL DATA APPLICATION

We applied the proposed method to data from the STAR*D trial,⁴ which was a phase-IV multisite, prospective, multistage, randomized clinical trial to compare various treatment regimes for patients with nonpsychotic MDD.⁴ The detail of the study design is given in the supplementary. The aim of STAR∗D was to find the best subsequent treatment for subjects who failed to achieve adequate response to an initial antidepressant treatment (citalopram). The primary outcome was measured by the Quick Inventory of Depressive Symptomatology (QIDS) score ranging from 0 to 26 in the sample. Participants with a total clinician-rated QIDS score under 5 were considered as having a clinically meaningful response to the treatment and therefore in remission. Remitted patients were not eligible for any future treatments and entered a follow-up phase.

Following the works of Chakraborty and Moodie¹⁴ and Pineau et al,²³ we focused on a two-stage decision-making problem by combining study levels 2 and 2A as the first stage and treating study level 3 as the second stage. Additionally, different drugs were combined as one class of drugs involving selective serotonin reuptake inhibitors (SSRI) and the other class of drugs without SSRI. Thus, at each stage, treatment (A_k), reward outcome (R_k), and feature variables (H_k) were defined as follows:

• A₁: 1 if SSRI drugs are used and −1 SSRI drugs are not used at level 2 and 2A (stage 1);

• A₂: 1 if SSRI drugs are used and −1 SSRI drugs are not used at at level 3 (stage 2);

• R₁: -QIDS score at the end of first stage if remission was achieved, −½ QIDS score at the end of first stage if remission was not achieved;

• R₂: −½ QIDS score at the end of second stage;

• H₁: baseline QIDS score (at the beginning of the trial), the rate of change of QIDS score from baseline to stage 1 randomization (level 1 to level 2), participant preference (taking values −1, 0, or 1), and QIDS at the beginning of stage 1 randomization;

• H₂: H₁, the rate of change of QIDS score during stage 1, participant preference at stage 2 randomization, A₁, and its interactions with the previous variables.

There were 1381 participants with complete feature variables for the first stage analysis, among whom 516 achieved remission at the end of the first stage. Among 865 nonremitted participants, 364 of them had entered the second stage and have complete information on the feature variables and outcomes. In the analysis, the patients who had remission in stage 1 were treated as if they would have received the optimal treatments at stage 2; thus, we only analyzed patients who had entered stage 2 in order to estimate the optimal rule at stage 2.

To implement AOL, we followed the steps in Section 2.3, where the first-stage randomization probability π₁ was calculated as the frequency of SSRI and non-SSRI given patient preference at stage 1 and the second stage randomization probability π₂ was computed as the similar frequency and further multiplied by the nondropout proportions to account for missingness in this stage. More specifically, Lasso regression was implemented in Step 2–1, and a weighted Lasso was used for Step 2–1. For comparison, we also implemented Q-learning and OWL, where Lasso was used in the regression in each stage of Q-learning; the same π₁ and π₂ were used. Both gaussian and linear kernels were implemented for AOL and OWL. Comparison of all the methods were based on 1000 repetitions of two-fold cross-validation: for each cross-validation, one-half data were used for training, and the other half were used to compute the value functions for the estimated DTRs. For each replication, the testing value function was computed as the empirical estimation following Equation (1), which is the weighted average of the cumulative rewards for all patients whose observed treatments agree with the estimated optimal treatments in all stages.

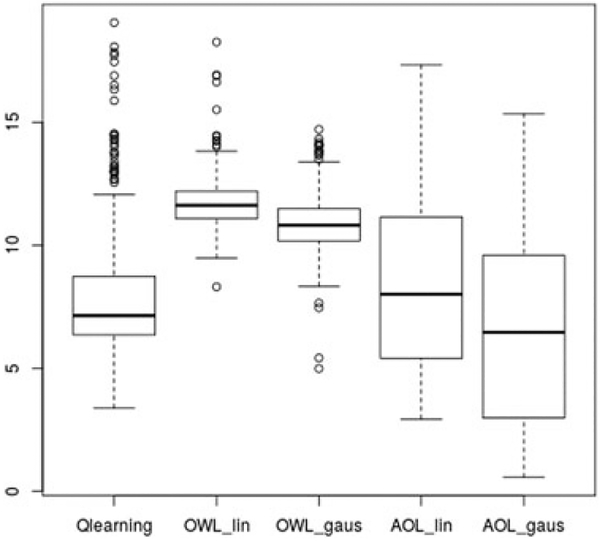
Q-learning, OWL, and AOL were compared in Figure 3. The mean baseline clinician-rated QIDS score in the sample was 16.71, and the mean QIDS at the start of stage 1 randomization was 12.37. The average testing QIDS score for the optimal DTR obtained by AOL with Gaussian kernel was 6.733 points (sd=4.08), which outperformed Q-learning (7.93, sd=2.38) and OWL with Gaussian kernel (10.85, sd=1.11). Gaussian kernel yielded better testing value than linear kernel for both AOL and OWL; AOL with linear kernel had an average testing value of 8.38 (sd=3.10), which was still better than OWL with linear kernel (10.85, sd=0.99). Moreover, AOL-estimated rule also outperformed the one-size-fits-all rules (eg, all subjects receive SSRI in both stages, all subjects received SSRI in the first stage and non-SSRI in the second and so on).

FIGURE 3.

Mean and standard error of the value function (depression symptom score, Quick Inventory of Depressive Symptomatology) based on 1000 repetitions of two-fold cross validation for Sequenced Treatment Alternatives to Relieve Depression data (lower score desirable)

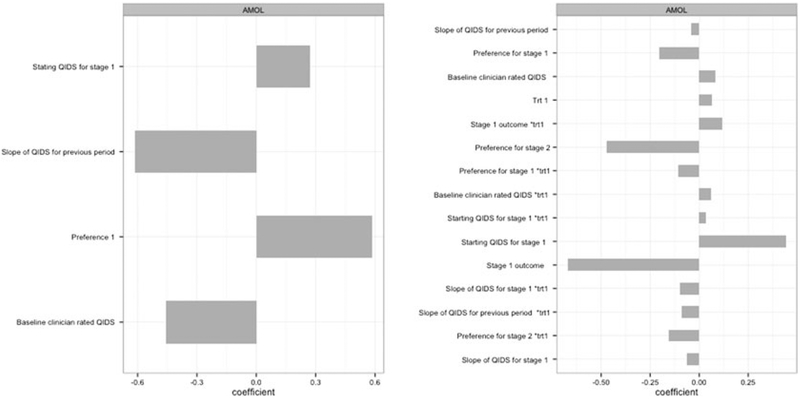
Furthermore, we examine the coefficients of AOL fitted by a linear kernel using the standardized feature variables. We present the normalized effects for the optimal DTR obtained by AOL in Figure 4. We normalized the effect of each tailoring variable through dividing by the L₂ norm of all coefficients of the decision rule. The baseline variables at first stage with strongest effects were baseline QIDS score, rate of change of QIDS in the previous period, and patient preference. The strongest second-stage tailoring variables were intermediate outcome after stage 1 treatment, starting QIDS at stage 1, and patient preference for the second-stage treatment.

FIGURE 4.

Normalized coefficients of the stage 1 tailoring variables (left panel) and stage 2 tailoring variables (right panel) obtained by Augmented Outcome-weighted Learning. QIDS, Quick Inventory of Depressive Symptomatology

In conclusion, the STAR∗D example demonstrates that AOL outperforms the alternative methods in maximizing the clinical benefits, and it also yields some insights on combining tailoring variables for deep tailoring and forming new treatment rules.

5 |. DISCUSSION

In this work, we propose a new machine learning method, AOL, to estimate optimal DTRs through robust and efficient augmentation to OWL. We theoretically prove that AOL guarantees efficiency improvement over OWL for both K = 1 and K > 1 stages. The theoretical results show that AOL has the same approximation bias but a smaller stochastic error. Moreover, AOL achieves efficiency gain by properly constructing surrogate outcomes with smaller second moments. In an earlier version of this paper (https://arxiv.org/abs/1611.02314), we provided an additional application to a SMART of children affected by attention deficit and hyperactive disorder. A recent publication by Zhang and Zhang²⁴ considered similar augmented outcomes as weights in multiple-stage estimation but used genetic algorithm for estimating optimal treatments. In comparison, our proposed method used computationally more stable large margin loss, and we rigorously justified the advantage of the proposed method in terms of the risk bound for the value function.

In real-world studies, it may be difficult to identify a priori which variables may serve as tailoring variables for treatment response. In our simulation studies, AOL has shown to be superior in such settings with non-treatment-differentiating noise variables and unknown treatment mechanisms. In addition, using a more sophisticated prediction method (eg, random forest) to incorporate nonlinear interactions between health history variables H_k to predict s_k(H_k) in the step of taking residuals may be beneficial, although theoretically, a linear model will guarantee improved efficiency of AOL over OWL.

Clinicians may be interested in ranking the most important variables to predict patient heterogeneity to treatment. Biomarkers that could signal patients’ heterogeneous responses to various interventions are especially useful as tailoring variables. This information can be used to design new intervention arms in future confirmatory trials and facilitate discovering new knowledge in medical research. Variable selection may help construct a less noisy rule and avoid over-fitting. Although AOL leads to a sparse DTR in the STAR∗D example, a future research topic is to investigate methods that perform automatic variable selection in the outcome-weighted learning framework. Additionally, our current framework can easily handle nonlinear decision functions by using nonlinear kernels, which may improve performance for high-dimensional correlated tailoring variables. It is also of interest to consider other kinds of decision functions such as decision trees to construct DTRs that are highly interpretable.