System for on- and off-axis volumetric OCT imaging and ray tracing aberrometry of the crystalline lens

Abstract

We present a new in vitro instrument for measuring shape and wavefront aberrations of the primate crystalline lens, both on- and off-axis, while simulating accommodation with a motorized lens stretching system. The instrument merges spectral domain optical coherence tomography (SD-OCT) imaging and ray tracing aberrometry using an approach that senses wavefront aberrations of the lens with the OCT probing beam. Accuracy and repeatability of aberration measurements were quantified. Preliminary experiments on two human and four cynomolgus monkey lenses demonstrate the ability of the system to measure the lens shape, spherical aberration and peripheral defocus, and their changes during simulated accommodation.

1. Introduction

The shape and refractive index gradient of the primate crystalline lens change throughout life [1–4]. These changes influence refractive development [5–10], vision correction outcomes [11], and retinal image quality [12–14]. Both on-axis (central field) and off-axis (peripheral field) properties of the lens are of great interest, given their potential contribution to the peripheral optical performance of the eye [15–17].

Optical and anatomical properties of the crystalline lens can be measured in vivo or in vitro. Both approaches present their own limitations. In vivo, lens thickness measurements and surface topography have been obtained using magnetic resonance imaging (MRI), ultrasonography, and optical techniques [18–20], including optical coherence tomography (OCT) [21]. Only optical biometry provides sufficient spatial resolution to accurately measure lens shape [3, 4, 21–25]. A key limitation of in vivo optical lens biometry is that the iris limits the zone through which optical measurements can be performed to the central region of the lens. Obtaining accurate topography of the posterior lens surface in vivo is also challenging as it requires three-dimensional reconstruction of the lens gradient refractive index (GRIN) distribution with no direct access to the tissue [21]. Indirect estimation of lens aberrations can be obtained in vivo either by measuring the aberration of the eye after canceling the power of the anterior corneal surface or by subtracting the anterior corneal surface aberrations from whole-eye aberrations [14, 26–29]. Both methods provide the internal aberrations of the eye, which are only approximately equal to the aberrations of the lens.

In vitro optical biometry of the lens overcomes most of the limitations of in vivo approaches. Measurements in vitro are performed on crystalline lenses that have been extracted from donor eyes. The lens may be isolated from adjacent tissues or maintained in its accommodative framework while mounted in a lens-stretching system to simulate accommodation [2, 30–32]. Proper care of the post mortem tissue and short measurement times are crucial to avoid alteration of the lens internal structure that could bias optical measurements [33]. Several optical techniques have been used to measure the shape, power or optical aberrations of the in vitro crystalline lens and their changes with age and simulated accommodation [2, 25, 30, 31, 34–44]. In a recent study [45], we described a method based on optical ray tracing to estimate peripheral defocus along one meridian of the monkey crystalline lens.

In this paper, we describe a new instrument to measure dimensions, shape, and on- and off-axis 2D wavefront aberrations maps of the lens in vitro. The instrument merges three-dimensional OCT imaging and ray tracing aberrometry (RTA), and enables experiments to be performed during simulated accommodation using a motorized lens stretching system. The system is fully automated.

2. System for combined OCT imaging and ray tracing aberrometry

2.1 General description

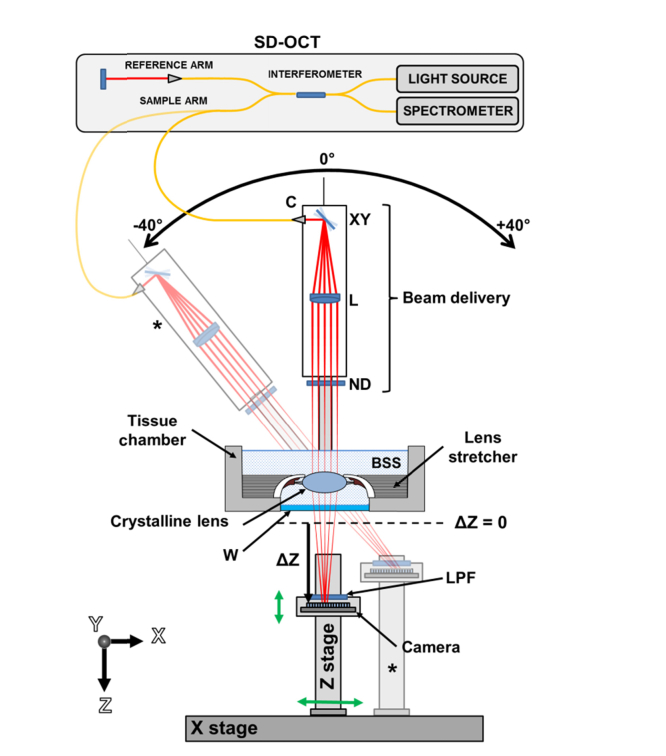
Figure 1 illustrates the experimental setup of the system using a conceptual schematic. The system consists of four sub-units: a tissue chamber, a spectral domain (SD) OCT imaging platform, a ray tracing aberrometer, and an off-axis positioning system. During experiments, the lens is mounted on a lens stretcher, and the unit submerged in a chamber filled with balanced salt solution. The ray tracing aberrometer shares the light source and the beam delivery unit of the OCT system to sequentially deliver a pattern of equally-spaced parallel light rays through the lens. During ray-tracing aberrometry, the light beam is transmitted through the crystalline lens and an optical window at each position of the scanning pattern. A 2D image sensor mounted under the tissue chamber records an image of the spot generated by each sequential ray exiting the optical window. The camera is mounted on a vertical motorized stage (Z stage) positioned under the tissue chamber to record the spots at different axial positions (ΔZ). A rotatory system enables acquisition of OCT images and spot patterns at delivery angles varying between −40° and + 40° with respect to the lens optical axis. The off-axis system consists of a rotation stage that pivots the delivery probe around the center of the lens and a horizontal translation stage (X stage) that is used to position the image sensor at the center of the off-axis spot pattern. Spot patterns acquired with the camera at different axial positions are processed to calculate the slope of each transmitted ray. The ray slopes are used to calculate a wavefront aberration map using standard methods [46]. Lens shape and dimensions are obtained from OCT images using a custom-made segmentation algorithm.

Fig. 1.

Conceptual schematic of the system for combined OCT imaging and RTA of the crystalline lens. The OCT system with interferometer, light source, spectrometer, reference arm and sample arm is shown. The optical components of the beam delivery unit are labelled: XY, dual axis scanning mirrors; L, objective lens; ND, neutral density filter. Sampling beams are shown in red. The beam delivery unit is mounted on a rotation stage. The tissue chamber housing the crystalline lens is shown. The lens is mounted on a motorized lens stretcher and immersed in balanced salt solution. The bottom of the tissue chamber integrates an optical window (W). A long-pass filter (LPF) is positioned in front of the camera to reject the ambient light. The black dashed line indicates the minimum distance of the camera sensor from the bottom of the optical window (ΔZ = 0). The axial position of the camera sensor is indicated (ΔZ). The motorized linear stages of the off-axis positioning system are labeled: Z-stage and X-stage. The camera sensor moves along the X and Z directions (green arrows). The semi-transparent diagram (*) shows the configuration of the positioning system for a delivery angle of −40°.

2.2 Implementation and experiment setup

SD-OCT system and beam delivery probe:

A commercial SD-OCT system (ENVISU R4400, Bioptigen Inc., NC) is used as the imaging platform (Fig. 2(A)). The OCT system is equipped with a super-luminescent light emitting diode (SLD) operating at a center wavelength of 880 nm and FWHM (full width half maximum) bandwidth of 40 nm. The optical axial resolution of the system is 8.5 μm in air. The spectrometer enables imaging at a speed of 32,000 A-lines/s over an axial range of 15.18 mm in air and with a digital axial resolution of 7.4 μm/pixel. The Bioptigen OCT system was modified by replacing the standard delivery probe with a custom-made delivery probe in the sample arm.

Fig. 2.

Photographs of the system. (A) SD-OCT imaging platform (right) and custom-made delivery system (left). (B) OCT and ray tracing aberrometry delivery system. (C) Side of the system showing the Z-stage and the camera. (D) Tissue chamber with motorized lens stretching system.

The probe consists of an aspheric lens collimator (C220TME-B, f = 11 mm, Thorlabs, USA) followed by a set of X-Y transversal galvanometer scanners (6210H, Cambridge Technology, Inc., USA) and a near-infrared (NIR) achromatic lens (AC254-100-B, f = 100 mm, Thorlabs, USA) configured to produce a partially-telecentric scan with flat field along the X direction within the aperture of the system (12 mm in diameter). The simulated (Zemax) focal spot size of the OCT beam is 53 µm at the beam waist and the depth of focus (two times the Rayleigh range) is 5.1 mm in air. In previous studies [34, 47], these parameters were found to provide satisfactory trade-off between lateral resolution and imaging depth for imaging of the crystalline lens in vitro. To generate high-contrast images of the lens, the focal plane of the OCT scanning beam is positioned near the center of the lens and the reference arm is adjusted with the zero delay near the lens anterior surface. Power of the beam delivered to the tissue is 700 µW. A motorized rotation stage (T-RS60A, Zaber Technologies, Vancouver, BC) pivots the delivery system around the lens center (Fig. 1 and 2(B)) to enable off-axis OCT imaging and aberration measurements at angles varying between −40° and + 40° (Fig. 1).

Ray tracing aberrometer:

The ray tracing aberrometer (Fig. 2(A)-2(C)) shares the SLD light source and the beam delivery unit of the SD-OCT system. A complementary metal-oxide-semiconductor (CMOS) board-level image sensor (DCC1545M-GL, Thorlabs, NJ) mounted beneath the tissue chamber is used to record spot images produced on the sensor by rays exiting the tissue chamber as the beam is sequentially scanned across the crystalline lens. The CMOS sensor has an active area of 6.66 mm (X) × 5.32 mm (Y), a resolution of 1.3 Megapixels (1280 × 1024 pixels), a pixel size of 5.20 µm × 5.20 µm and operates at a maximum rate of 25 frames per second (fps). A long-pass filter (FGL850, Thorlabs, NJ) is mounted in front of the camera to filter out ambient light and attenuate the incident beam (~14% transmittance at 880 nm). The image sensor is mounted on a vertical motorized stage (T-LSR075B, Zaber Technologies, BC) (Z-stage – Fig. 1, 2(B)-2(C)) to enable the recording of spot positions at different axial positions. The minimum distance from the image sensor to the posterior surface of the window of the tissue chamber is 7.5 mm (ΔZ = 0, Fig. 1). The total vertical travel range is 67.5 mm (ΔZ, Fig. 1). The vertical stage holding the imaging sensor is mounted on a horizontal motorized translation stage with 150 mm travel range (T-LSR150B, Zaber Technologies, BC) (X stage – Fig. 1 and 2(B)) to enable centering of the imaging sensor during off-axis measurements.

Tissue chamber and lens stretcher:

A tissue chamber (Fig. 2(B) and 2(D)) was fabricated to house a motorized lens stretching system for simulating accommodation. The lens stretching system consists of a manual lens stretcher (STR-MS-B, Bioniko Consulting LLC, FL) that was combined with a geared micro servo motor to allow for motorized stretching of the lens (Fig. 2(D)). The tissue sample is a section of the globe with the anterior and posterior parts removed to leave the lens, zonules, ciliary body and surrounding sclera intact. The outer sclera is bonded to PMMA attachments that are connected to the lens stretcher. The lens stretcher applies or relieves a radial stretching force to the sclera to simulate disaccommodation or accommodation, respectively. The lens stretcher can be programmed to displace the sclera radially in a step-wise fashion with 0.125 mm increments up to 2.625 mm, corresponding to a 5.25 mm increase in outer scleral diameter. The lens stretcher can be flipped to enable stretching experiments to be performed with either the anterior or the posterior lens surface facing the incident beam. A 1 mm thick optical window (45-568, Edmund Optics Inc., NJ) serves as the bottom of the tissue chamber. The tissue chamber is positioned on a custom-built mount that allows the image sensor to move below the chamber. The mount is connected to a three-axis manual positioning system to enable accurate centering of the lens within the imaging field.

Data acquisition:

The software package provided with the SD-OCT system (InVivoVue, Bioptigen Inc., NC) was used for the crystalline lens data acquisition and image display. The position of the lens stretcher and rotation stage during OCT experiments was controlled with custom software (LabVIEW, National Instruments, Inc.). Custom software was also developed in LabVIEW to automatically control acquisition of laser ray-tracing data. The user interface enables the operator to select the input scanning protocol including stretching positions, off-axis beam delivery angles, axial positions of the camera and beam scanning pattern. The camera and the X-Y galvanometer scanner are synchronized so that an image is acquired for each individual ray of the scanning pattern delivered through the lens. Typical scanning protocols for OCT and RTA data acquisitions are described in sections 3.3 to 3.6.

Data processing:

A segmentation algorithm based on edge-detection was developed in MATLAB (The MathWorks, Inc., Natick, MA) to detect the anterior and posterior surfaces of the lens from the OCT volumetric data sets. An algorithm was also developed in MATLAB to calculate lens aberrations for each stretching state and angular positions from the spot patterns acquired with the camera at different axial positions. The program first analyzes the spot images and calculates their centroids. Linear fits of the X and Y spot coordinates as a function of the axial position (Z) of the camera are used to reconstruct the ray path and calculate the slopes of the wavefront for each entrance ray position. The slopes of the wavefront are then used to calculate the Zernike wavefront coefficients up to the 6th order using a least squares curve fitting algorithm [46].

General experimental procedure:

At the start of an experiment, the lens is mounted in the stretcher and positioned in the tissue chamber. The chamber is then filled with saline solution to keep the lens hydrated during the experiment. Real-time OCT images along a meridian of the lens are displayed while filling the chamber. This procedure ensures that the lens is fully submersed and that the fluid level is the same for all experiments, which was set at an optical distance of 15 mm from the bottom of the chamber. A procedure is then performed to ensure correct alignment of the lens with respect to the off-axis delivery system, which takes place when the chief rays for the varying delivery angles intersect at the lens center, or equivalently, when the lens is centered with the pivot point of the rotating stage. The alignment procedure consists of two steps:

• 1) Transverse (X and Y) alignment: Real-time OCT images along the horizontal (X) and vertical (Y) meridians of the lens are displayed on-axis. The position of the tissue chamber is adjusted until the lens is in the center of both OCT images.
• 2) Axial (Z) alignment: Real-time OCT images along the horizontal (X) meridian of the lens are displayed while rotating the delivery system. The axial position of the tissue chamber is adjusted until the lens is displayed at the center of the OCT image for all delivery angles.

Once the lens is correctly aligned, OCT and aberrometry data are acquired on- and off-axis and processed.

3. Experiments

A series of experiments were performed to: 1) estimate the effect of distortion introduced by the scanning system to the OCT images, 2) validate the aberration measurements on a set of plano-convex (PCX) glass and human crystalline lenses and 3) test the capability of the system to acquire OCT and aberration data on- and off-axis on the crystalline lens.

3.1 Scanner induced OCT image distortions

Purpose:

The OCT scanning configuration (Fig. 1) introduces distortions due to aberrations of the scanning lens and the lack of telecentricity of the scanning mirrors [24, 48–50]. The purpose of this experiment was to quantify lateral and axial errors in the OCT image introduced by the delivery system.

Methods:

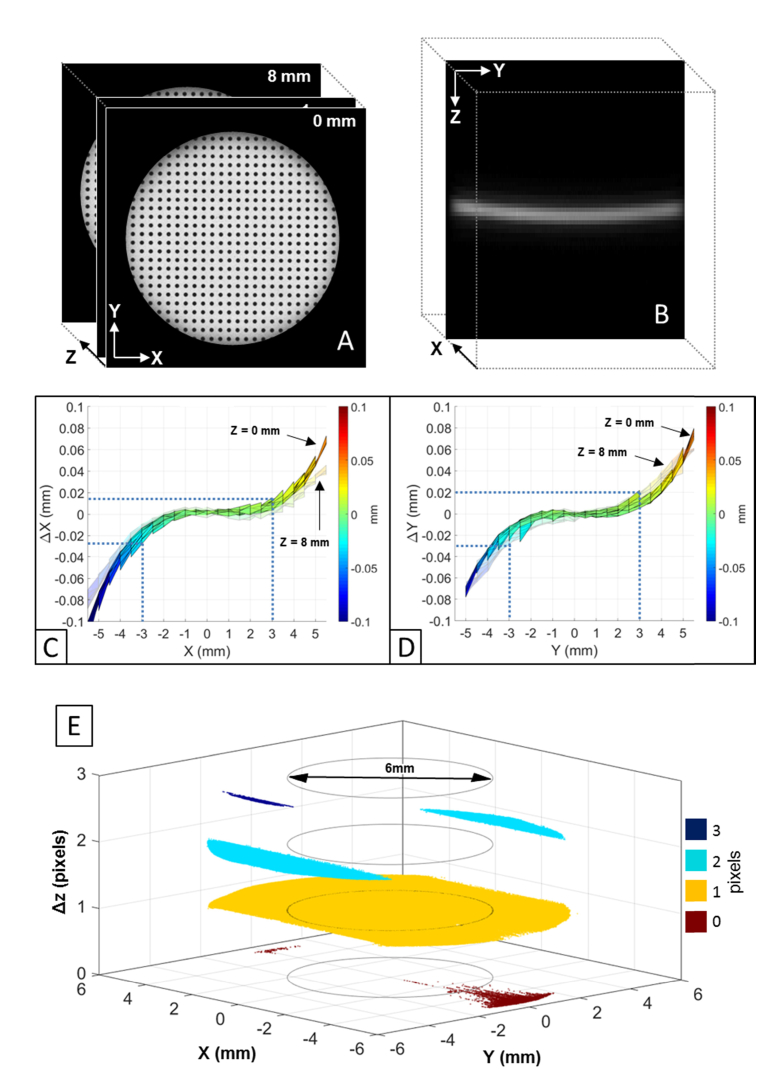
To estimate lateral errors, a low reflection distortion target (#62-951, Edmund Optics Inc., NJ) was mounted on a vertical linear stage and imaged with OCT at different axial positions [24, 48, 49]. The target consists of a grid of dots separated by 0.5 mm. Volumetric OCT data sets were acquired with the target positioned at nine different axial heights spaced 1 mm apart within the effective axial range of the OCT system (8 mm in air). Volumetric Intensity Projection (VIP) images of the target were generated from the volumetric OCT data sets (Fig. 3(A)). Transverse distortion of the VIP images was quantified for each height of the target as the deviation of the X and Y coordinates of the dot centroids in the OCT image from their actual positions. Axial distortion was estimated by acquiring a volumetric OCT image of an optical window (#48-447, Edmund Optics Inc., NJ) [24, 48, 49]. The OCT image of the optically deformed window surface (Fig. 3(B)) was segmented with an algorithm based on edge detection. Axial error was quantified as the elevation of the deformed surface across the transversal scanning field.

Fig. 3.

(A) Volumetric intensity projection images of the distortion target generated from the volumetric OCT data sets acquired at 1-mm spaced heights within the effective OCT axial range (8mm). (B) Magnified OCT image of the deformed optical flat surface. Projection of the X (C) and Y (D) lateral error maps along, respectively, the Y and the X directions. Error maps are calculated across a central optical zone of 12 mm in diameter. Error maps for axial positions of the target equal to 0 mm (solid plot) and 8 mm (semi-transparent plot) are reported. Error maps for intermediate axial positions are not displayed for clarity as the error trends are comparable to the displayed ones. Blue dotted lines show the lateral errors for a central optical zone of 6 mm in diameter. (E) Elevation map of the optical flat surface across an optical zone of 12 mm in diameter. The axial error is displayed in digital pixels. Black circles indicate a central optical zone of 6 mm in diameter.

Results:

Figs. 3(C) and 3(D) show a projection of, respectively, the X and Y lateral error surface maps measured across the entire aperture of the system (12 mm in diameter). Transverse image magnification is positive and increases non-linearly with the distance from the optical axis (X = 0 mm, Y = 0 mm). The maximum lateral error is about 100 µm at the edge of the aperture and when the target is positioned at a height of 0 mm (Fig. 3(C)). Figure 3(E) shows the elevation map of the optical flat surface across the entire aperture. The peak-to-valley height (i.e. axial error) is 1 pixel (7.4 µm) along the X direction and 3 pixels (22.4 µm) along the Y direction. Within a central zone of approximately 6 mm in diameter, the axial error is equal to zero pixels (Fig. 3(E) – black circles) and the maximum absolute lateral errors along X (26 µm) and Y (29 µm) are negligible since they are respectively smaller than the transverse optical resolution (53 µm) (Fig. 3(C) and 3(D) – blue dotted lines) of the OCT beam. For larger optical zones, OCT image distortions induced by the scanning optics (Fig. 3(C), 3(D) and 3(E)) must be corrected to obtain accurate lens shape measurements.

3.2 Testing and validation of aberration measurements on glass lenses

Purpose:

To verify accuracy and repeatability of aberration measurements using glass lenses

Methods:

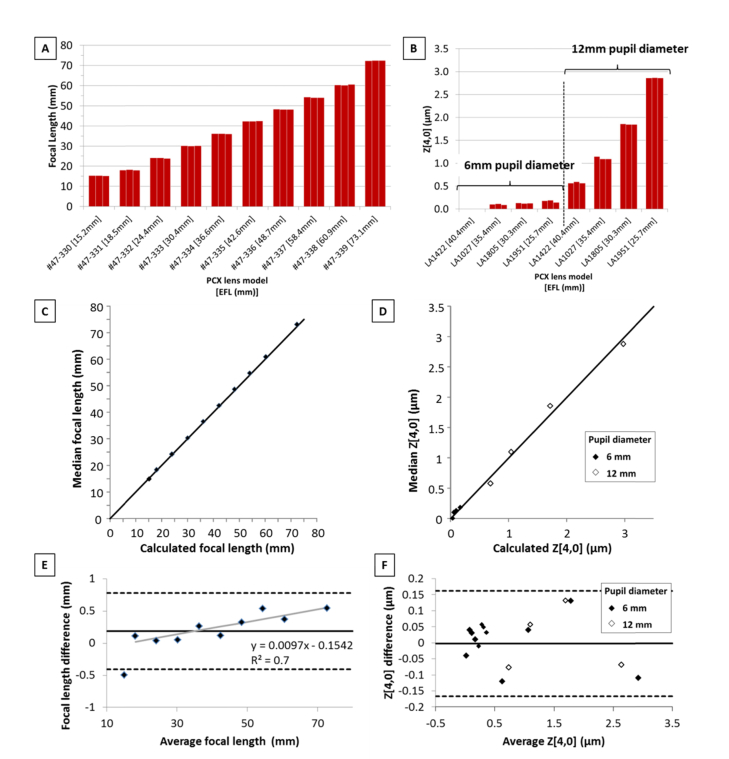
Accuracy and precision of focal length and spherical aberration measurements were estimated on two sets of commercially available plano-convex lenses with focal lengths covering the range expected from primate crystalline lenses. Measurements were performed with the lens mounted in lens tubes and positioned in the empty chamber with the convex surface facing the scanning beam. OCT imaging enabled centering of the lens with respect to the beam delivery optics. Repeatability was assessed by scanning the lens three times. The lens was repositioned in the chamber prior to each scan. Lens power measurements were performed on a set of ten lenses with 12 mm diameter and effective focal length ranging from 15.2 to 73.1 mm (Fig. 4(A)). The ray tracing system was programmed to deliver a matrix of 13 × 13 rays spaced 0.5 mm apart across the horizontal and vertical directions. Zernike coefficients were calculated over a pupil diameter of 6 mm using the method described in section 2.2. Focal length was estimated from the defocus term Z[2,0] [51]. A different set of lenses with larger diameters (25.4 mm) were used to produce spherical aberration on the same scale as the crystalline lens aberration. The paraxial effective focal length of the lenses ranged from 24.6 to 40.0 mm. For each lens, Zernike coefficients were calculated over optical zones of 6 mm and 12mm in diameter by respectively delivering matrices of 13 × 13 and 25 × 25 rays with a spacing of 0.5 mm through the lens. The 4^th order Zernike coefficient Z[4,0] was used to quantify primary spherical aberration. Bland-Altman analysis was used to compare experimental values of focal length and Z[4,0] with those obtained using a ray tracing program (Radiant ZEMAX, Redmond, WA).

Fig. 4.

(A) Experimental focal length values of ten commercially available PCX lenses (Edmund Optics Inc., NJ). Measurements were repeated three times. (B) Experimental spherical aberrations (Z[4,0]) values of four commercially available PCX lenses (Edmund Optics Inc., NJ). Measurements were repeated three times. Spherical aberration was analyzed over optical zones of 6 mm and 12 mm in diameter. Correlation between measured and simulated focal length (C) and Z[4,0] coefficient (D). The graphs show the median value of three consecutive measurements (vertical axis) versus the simulated value (horizontal axis). The diagonal is the 1:1 line (perfect correlation). (E) Bland-Altman analysis of the agreement between the median and simulated focal length. Simulated focal lengths were calculated with ZEMAX as the image plane for the smallest RMS spot size with a pupil diameter of 6 mm at a wavelength of 880 nm. Linear fit of the data samples (gray line). The data point exceeding the lower limit of agreement (average focal length = 15.0 mm) was excluded from the fit as it is likely to be an outlier. Linear fit equation and R² coefficient are displayed. (F) Bland-Altman analysis of the agreement between the median and simulated (ZEMAX) Z[4,0] coefficient.

Results:

Fig. 4(A) shows a bar graph comparing the experimental focal lengths. For all focal lengths, repeated measurements were within ± 0.22 mm from the median value, or, equivalently, within ± 0.6 D from the median focal power. A similar analysis for the Zernike Z[4,0] coefficients (Fig. 4(B)) shows that repeated measurements were all within approximately ± 0.06 µm from the median values. Experimental variability limits the precision of refractive power and spherical aberration measurements to approximately 0.6 D and 0.06 µm, respectively, which provides enough resolution to determine physiological changes in aberrations of the primate lens with age and simulated accommodation [38, 52]. The graphs displayed in Fig. 4(C) and 4(D) show the correlation between measured and simulated focal length and Z[4,0], respectively. Bland-Altman analysis (Fig. 4(E) and 4(F)) shows a mean difference ( ± 95% C.I.) between the median and simulated values of 0.19 ± 0.59 mm, for focal length, and 0.003 ± 0.164 µm, for spherical aberration. A distinct slope in the error in focal length can be observed in Fig. 4E. This slope is likely to arise from a scaling error in the Zemax model of the lenses, which can be corrected so that the mean difference ( ± 95% C.I.) between median and simulated focal length may be closer to ± 0.32 mm.

3.3 Testing and validation of aberration measurements on the crystalline lens

Purpose:

To verify repeatability of aberration measurements on the crystalline lens.

Methods:

Two postmortem human eyes from 35 and 57 year-old donors were obtained from the Ramayamma International Eye Bank at L V Prasad Eye Institute (Hyderabad, India). The tissue preparation is based on a protocol that was designed to preserve hydration of the lens and avoid swelling [53]. In particular, tissue dissection was performed with the sample immersed in saline solution to minimize exposure of the tissue to air. Aberration measurements were obtained from two experiments. In one experiment, the outer sclera of the 57 year-old lens was bonded to the PMMA attachments connected to the lens stretcher. The anterior and posterior parts of the globe were removed and full-thickness incisions were made in the sclera to produce eight radial segments for stretching. After the dissection was completed, the stretcher was immediately lowered in the well of the tissue chamber filled with saline solution.

The stretcher was programmed to maintain the lens unstretched during the experiment. In another experiment, the 35 year-old lens was isolated from the donor globe and immediately placed on a rubber O-ring within the tissue chamber filled with saline solution. In both experiments, the lens was oriented with the anterior surface facing the scanning beam. Off-axis RTA experiments were performed on both human lenses three times to assess measurement repeatability. The tissue chamber was repositioned prior to each scan. OCT imaging enabled centering of the lens with respect to the beam delivery optics prior each measurement. During off-axis RTA, the delivery angle was varied in 5° increments from −25° to + 25°. For each angle, the system was programmed to deliver a matrix of 13 × 13 rays equally-spaced over a 6 × 6 mm transverse zone through the lens while spot images were recorded with the camera positioned at 9 vertical heights equally-spaced from 0 mm to 8 mm. Lens power was calculated using the Zernike defocus coefficient [51] and assuming a group refractive index for the saline environment equal to 1.341 at 880 nm [47]. The 4th order Zernike coefficient was used to quantify primary spherical aberration on-axis.

Results:

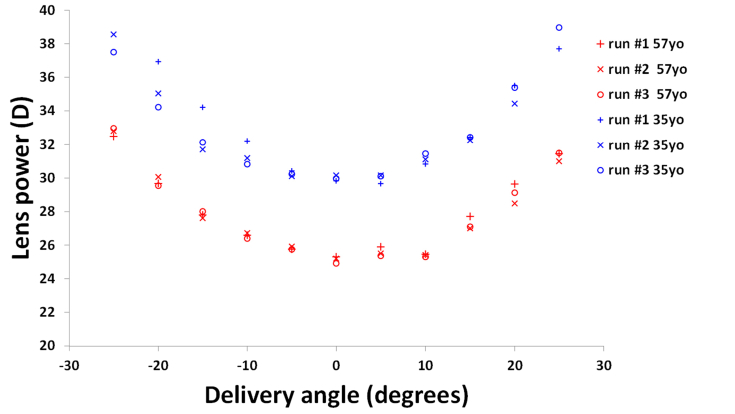
Fig. 5 shows the repeated lens power measurements for the 35 and the 57 year-old lenses as a function of the delivery angle. In all runs, peripheral lens power increases with larger delivery angles. Mean values of on-axis power were 25.1D and 30.0D for the 35 and 57 year-old lens, respectively. These values are within the range of refractive power previously measured on human lenses [30]. For both lenses and all delivery angles, the mean maximum difference in refractive power across the three measurements was 0.78 ± 0.69 D (range ± 2.7 D). Repeated on-axis power measurements were all within ± 0.4 D, which is within the variability we found on-axis on glass lenses ( ± 0.6 D). The repeated Z[4,0] coefficients measured on-axis were 0.01 µm, 0.08 µm and 0.12 µm, for the 57 year-old lens, and −0.05 µm, −0.22 µm and −0.38 µm, for the 35 year-old lens. Repeated spherical aberration measurements were all within ± 0.15 µm from the median values, which is slightly larger than the variability we found on glass lenses ( ± 0.06 µm). The human crystalline lenses used in this experiment present a relatively small amount of spherical aberration, similar to that obtained by indirect estimation in vivo [14]. This repeatability study on biological tissue confirms that the system provides enough resolution to determine physiological changes in aberrations of the primate lens.

Fig. 5.

Repeated power measurements performed on a 35 year-old isolated lens (blue) and a 57 year-old unstretched lens (red) as a function of the delivery angle. Lens power increases with larger delivery angles in all runs.

3.4 On-axis aberrations of the crystalline lens during simulated accommodation

Purpose:

To demonstrate the ability of the system to measure lenticular aberrations changes during simulated accommodation in vitro.

Methods:

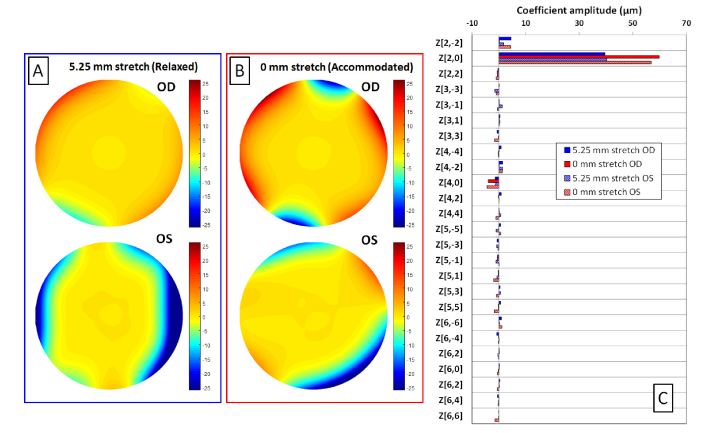
Experiments were performed postmortem on the crystalline lenses of a 4 year-old cynomolgus monkey. The experiments adhered to the Association for Research in Vision and Ophthalmology Statement for the Use of Animals in Ophthalmic and Visual Research. The eyes were obtained from the Division of Veterinary Resources at the University of Miami as part of a tissue-sharing protocol and were used in accordance with Institutional Animal Care and Use Committee Guidelines. The animal was not euthanized for the sole purpose of this study. The crystalline lenses were mounted on the lens stretcher using the same protocol described in section 3.3 and then lowered in the tissue chamber filled with saline solution. Aberration measurements were performed with the delivery probe oriented on-axis. The ray tracing aberrometer was programmed to sequentially deliver a matrix of 13 × 13 rays through the unstretched (0 mm) and fully stretched (5.25 mm) lens. Rays were spaced 0.5 mm apart. The camera was programmed to acquire spot patterns at 9 vertical heights equally-spaced between 0 mm and 8 mm. Aberration data was acquired in the unstretched and in the fully stretched states. Figure 6 shows the reconstructed wavefront aberrations maps for higher order terms of the fully stretched (Fig. 6(A)) and unstretched (Fig. 6(B)) lens and the Zernike terms calculated over a 6 mm pupil diameter (Fig. 6(C)). Lens power (P) is calculated using the Zernike defocus coefficient Z[2,0] [51] assuming a group refractive index of the saline environment equal to 1.341 at 880 nm [47].

Fig. 6.

On-axis aberrations of the left (OS) and right (OD) crystalline lenses of a 4 year-old cynomolgus monkey. Reconstructed higher order wavefront aberration maps for the stretched (A) and unstretched (B) lenses. The scale is in microns. Zernike coefficients calculated over a 6 mm pupil diameter for the left and the right lenses, in the stretched (blue) and unstretched (red) states (C).

Results:

The Zernike defocus terms for the stretched and unstretched lens are, respectively, 39.61 and 59.83 µm, which correspond to lens powers of, respectively, 40.9 D and 61.8 D, for the right eye, and 40.28 and 56.83 µm, which correspond to lens powers of, respectively, 41.6 D and 58.7 D, for the left eye. The Zernike Z[4,0] coefficients for the stretched and unstretched lens are, respectively, −1.33 µm and −3.95 µm for the right eye, and −1.32 µm and −4.44 µm, for the left eye. Refractive power and spherical aberration between the two lenses are similar, as expected. For both lenses, refractive power increases with simulated accommodation (unstretched state), as expected. Spherical aberration is negative and becomes more negative with simulated accommodation. Wavefront analysis shows that higher-order aberrations are primarily dominated by fourth-order spherical aberrations. The results are in agreement with what was found using other ray tracing techniques on the cynomolgus monkey lens [38, 52].

3.5 Peripheral (off-axis) crystalline lens power during simulated accommodation

Purpose:

To evaluate the ability of the system to measure the changes in crystalline lens peripheral power during simulated accommodation.

Methods:

Off-axis RTA experiments were performed on the right cynomolgus monkey lens used in section 3.4 in the unstretched (0 mm), a partially stretched (3.5 mm) and the fully stretched (5.25 mm) states. The delivery angle of the probe was varied in 5° increments from −25° to + 25°. For each angle, the system was programmed to deliver a matrix of 13 × 13 rays equally-spaced over a 6 × 6 mm transverse zone through the lens while spot images were recorded with the camera positioned at 9 vertical heights equally-spaced from 0 mm to 8 mm. Defocus Zernike coefficients were calculated for all angles and used to determine the on- and off-axis lens power. The peripheral lens power was fit with the following second-order polynomial function:

$$P\left(\alpha \right)=P_0+B{\left(\alpha -{\alpha }_0\right)}^2,$$ (1)

where P(α)[DD] is lens power at angle α, P₀ [D] is the lens power on-axis, B [D/degrees²] is a coefficient describing the angular dependence of the power and α₀ [degrees] is an offset that accounts for lens tilt.

Results:

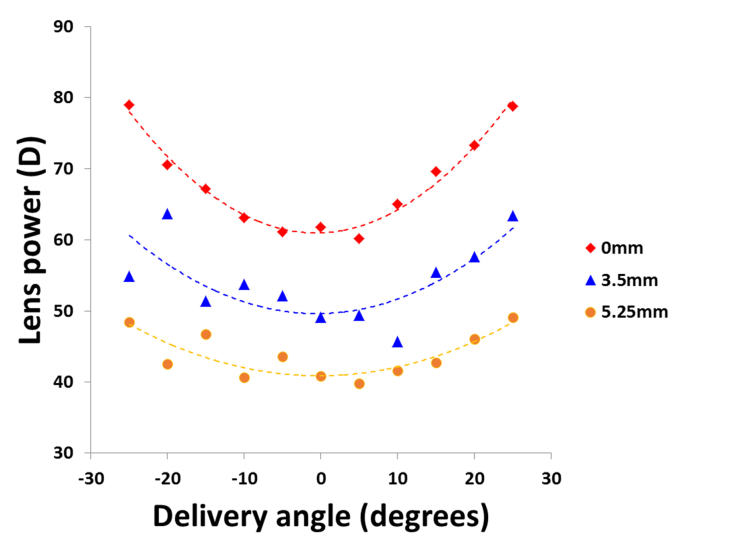
Fig. 7 shows the peripheral lens power for the unstretched and stretched states. Peripheral lens power increases with larger delivery angle for all lens states. However, the defocus effect seems to decrease progressively from the unstretched to the fully stretch state (B = 0.029 D/degrees² at 0 mm, B = 0.018 D/ degrees² at 3.5 mm and B = 0.012 D/ degrees²). Automatic acquisition of the ray tracing data necessary to produce the results displayed in Fig. 6 and 7 took ~30 minutes. A movie showing the automated operation of the ray tracing system during data acquisition is displayed at twice the original speed in Visualization 1 ^{(4.6MB, mpg)} . The on- and off-axis change in power with simulated accommodation is similar to the peripheral defocus that was found using 2D ray tracing on cynomolgus monkey lenses [45, 54].

Fig. 7.

Change in power of the cynomolgus monkey lens (Age: 4 years) in function of the delivery angle and the stretching state (0 mm, 3.5 mm and 5.25 mm). For each stretching state, data points were fit with Eq. (1), where P₀ = 61.0 D, B = 0.029 D/degrees² and α₀ = −0.64 degrees for the 0 mm stretch, P₀ = 49.6.0 D, B = 0.018 D/degrees² and α₀ = −0.56 degrees for the 3.5 mm stretch, and P₀ = 40.9 D, B = 0.012 D/degrees² and α₀ = −0.25 degrees for the 5.25 mm. The R² values were 0.97, 0.56 and 0.71for the 0, 3.5 and 5.25 mm stretches, respectively.

3.6 3D-OCT imaging and biometry

Purpose:

To assess the ability of the system to perform off-axis volumetric OCT imaging of the lens and provide preliminary lens shape measurements.

Methods:

Volumetric OCT data sets of three cynomolgus monkey lenses (age = 3.8, 4.0 and 5.8 years) were acquired on-axis at four different stretching conditions (0, 1.5, 3.5 and 5.25 mm). A series of 17 OCT volume data sets of the unstretched lens (0 mm) were also acquired off-axis with the delivery system positioned at delivery angles ranging from −40° to + 40° in 5° increments. Each OCT volumetric data set consists of 100 OCT images with 600 A-lines acquired along the fast scanning axis (X) covering a zone of 12 mm in diameter. On-axis images were segmented to obtain the profile of the anterior and posterior lens surfaces. The anterior surface of the lens was corrected for distortion caused by the increased optical path in saline solution assuming a group refractive index for the saline solution of 1.341 at 880 nm. In this preliminary study, the posterior surface of the lens was corrected for distortions due to refraction at the anterior lens surface by assuming a uniform refractive index of 1.414 [34, 47]. The surface profiles were then fit with a conic function over a central 6-mm zone to calculate the radius of curvature and asphericity, and lens thickness. Previous studies [34] show that correcting the distortions in the posterior lens surface assuming a uniform index produces reliable values of the central radius of curvature, but not asphericity. The gradient must be taken into account to provide accurate values of asphericity. The values of the posterior surface asphericity provided in this study are therefore approximate values.

Results:

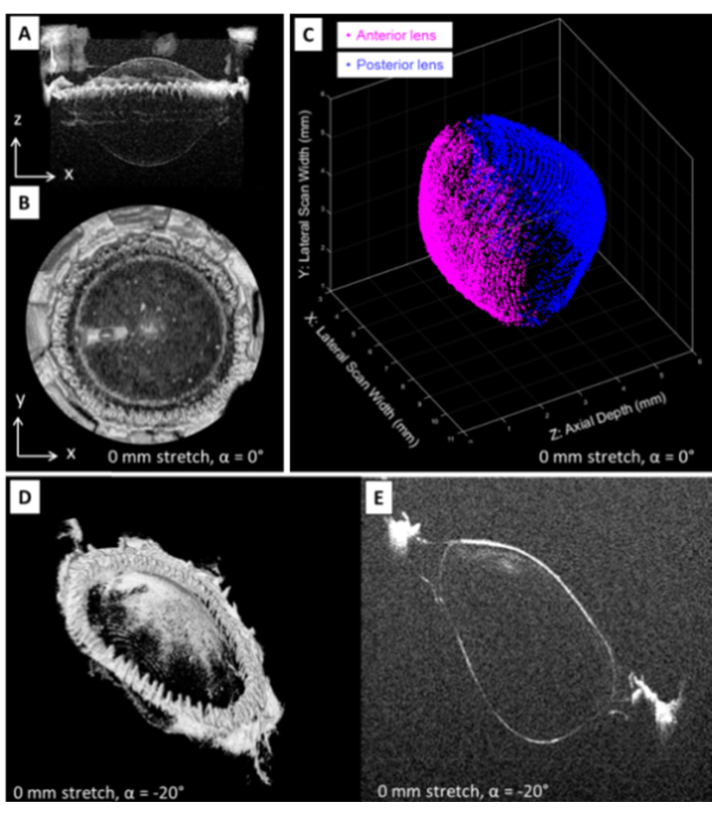
Figs. 8 (A) and (B) show two on-axis OCT volume intensity projections of the unstretched 4 year-old cynomolgus lens along the Y and Z axis, respectively.

Fig. 8.

On-axis OCT volume renderings obtained along directions Y (A) and Z (B) during simulated accommodation on a 4 year-old cynomolgus lens (see Visualization 2 ^{(212.1KB, mp4)} ). Anterior and posterior lens surface segmentation applied to the central 6 mm × 6 mm zone of the volumetric OCT image of the unstretched lens (C) and during maximal stretching of the lens (see Visualization 3 ^{(248.9KB, mp4)} ). Off-axis OCT volume rendering (D) and 2D OCT image (E) acquired at the horizontal (X) meridional plane of the lens with the delivery probe set at −20°. The same images for delivery angles ranging between −40° and + 40° in 5° increments are displayed in Visualization 4 ^{(1.1MB, mp4)} .

OCT volume intensity projections acquired at four different stretching states (0, 1.5, 3.5 and 5.25 mm) are sequentially shown in Visualization 2 ^{(212.1KB, mp4)} . Figure 8(C) reports an example of anterior and posterior lens surface segmentation over a central 6-mm zone obtained from the volumetric OCT data set acquired on-axis (Fig. 8(A) and (B)). OCT image segmentation allows for detection of changes in anterior and posterior lens shape during simulated accommodation (Visualization 3 ^{(248.9KB, mp4)} ). Table 1 reports the lens thickness and the radii of curvature and conic constants of the anterior and posterior surfaces, in the unstretched and in the fully stretched state. The R² values for the conic fits were all above 0.991. Figures 8 (D) and (E) respectively show off-axis (−20°) volume renderings and 2D OCT images acquired at the horizontal (X) meridional plane of the unstretched 4 year-old cynomolgus lens. Visualization 4 ^{(1.1MB, mp4)} shows OCT volume renderings and 2D OCT images acquired with the delivery system position at delivery angles ranging from −40° to + 40° in 5° increments. Acquisition of the volumetric OCT data displayed in Fig. 8 took approximately 10 minutes. The system is capable of acquiring on- and off-axis volumetric OCT data on the lens. On-axis OCT biometry during simulated accommodation shows a decrease in radius of curvature of the anterior and posterior lens surfaces, as expected. The anterior and posterior radii of curvature values are in agreement with those previously measured using 2D OCT and shadowgraph images acquired on cynomolgus monkey lenses during simulated accommodation [55–57]. Conic constants of the anterior lens are also within the range of values previously found using 2D imaging techniques [55, 57]. The distortion introduced by the OCT scanning system to the lens surfaces was negligible within the 6-mm optical zone (Fig. 3C, 3D and 3E). Distortion of the posterior lens was corrected using a uniform refractive index to provide curvature values. Alternately, direct OCT imaging and biometry of the undistorted posterior lens can be obtained by flipping the lens stretcher, as described in Section 2.2 and in previous studies [34, 58].

Table 1. On-axis biometry of the cynomolgus monkey lens ^a.

Age (years)	3.8			4.0			5.7
	Stretch (mm)			Stretch (mm)			Stretch (mm)
	0	5.25		0	5.25		0	5.25
LT (mm)	4.41	3.56		4.28	3.54		4.19	3.53
RA (mm)	2.29	3.94		4.30	9.41		2.07	4.46
QA	−0.80	−0.71		−1.36	−1.54		−1.83	−0.92
RP (mm)	1.43	2.15		2.72	3.88		1.56	2.21
QP	−1.19	−1.27		−1.41	−1.79		−1.25	−1.26

^aLens thickness (LT), radius of curvature (R_A) and conic constant (Q_A) of the lens anterior surface, and radius of curvature (R_P) and conic constant (Q_P) of the posterior surface, in the unstretched (0 mm) and fully stretched (5.25mm) states.

4. Discussion

We have developed a stand-alone instrument for in vitro measurement of dimensions, shape, power and higher-order aberrations of primate lenses on- and off-axis that are either isolated or placed in a lens stretching system for simulated accommodation. The system combines a modified commercial SD-OCT imaging platform and a custom-made ray tracing aberrometer. We have also developed a galvanometer-based beam scanning system for the SD-OCT imaging platform specifically designed to produce high-contrast volumetric images of the lens immersed in fluid. The design of the aberrometer relies on a novel approach that uses the same scanning beam used for OCT imaging to perform three-dimensional ray tracing across the crystalline lens. An image sensor was motorized along the lens optical axis to acquire the spots produced by each refracted ray at different distances from the lens. The ray slopes were calculated by interpolating the spot centroids recorded at different axial distances and used to reconstruct the wavefront. To study the peripheral optics of the lens, we implemented a positioning system that pivots the beam delivery system around the lens center to produce 3D OCT imaging and ray tracing at different delivery angles.

Common approaches for measuring aberrometry of the crystalline lens in vitro include laser ray tracing and Shack-Hartman wavefront sensing [36–41]. Advantages of ray tracing over Shack-Hartmann wavefront sensing have been previously discussed [37, 38, 59]. Briefly, the laser ray tracing method is more reliable against the presence of large aberrations and scattering. Although the sequential nature of ray tracing makes it slower, measurement speed is not critical for in vitro applications where the tissue sample is still. There are several key differences between the proposed in vitro ray tracing technique and those reported earlier [36–41]. In general, other ray tracing systems use slow mechanical scanners to deliver a parallel laser beam sequentially across a meridian of the crystalline lens immersed in saline solution. A single camera positioned laterally with respect to the lens optical axis (referred to as the lateral camera) is used to record the path of the refracted rays. Intersection of the refracted rays with the entrance rays and with the lens optical axis enabled measurement of the lens focal length and spherical aberration [39]. One limitation of this approach is that wavefront measurements can only be performed across a meridional plane of the lens. Moreover, the method is subject to high measurement uncertainty due to the difficulty in quantifying the path of the rays in the paraxial region [39]. In a later study [38], the technique was improved by using two lateral cameras to detect the ray slopes across the lens in three-dimensions. The refined system enabled 2D wavefront sensing from the ray slopes, which is more accurate than detecting the intersection of the rays along the lens optical axis. Detection of the ray path with lateral cameras also requires the addition of a scattering agent (e.g. powdered milk, white paint, ink) to the saline environment to enable detection of the laser beam from a side view. In our setup, no scattering agent is needed. The imaging sensor is transversally oriented with respect to the lens optical axis. The scanning beam is focused on the lens to optimize the OCT image quality. The beam reaching the sensor is defocused and generates spots that are detectable over a relatively wide range of axial positions. Compared to beam detection with lateral cameras, the main drawback of the proposed approach is the need for multiple transverse images to reconstruct the slope of each ray, which in turn increases data size and acquisition time. However, the operation of the motorized stages, lens stretcher and image sensor are fully synchronized and automated to reduce the overall acquisition time of aberration data and manual burden. The system acquires comprehensive biometric data on a single crystalline lens (Fig. 6-8) in a relatively short time (~40 minutes) making the instrument suitable for large-scale studies of the optical properties of the crystalline lens in vitro. More recently, Birkenfeld et al [43, 44] measured focal length and spherical aberration of human and porcine lenses using a custom laser ray tracing system integrating a transverse imaging sensor. The system projects rings of light of different diameters through the crystalline lens and acquires a series of through-focus images around the lens focal plane by moving the transverse imaging sensor at different position behind the lens. This method enables direct calculation of the focal length with a precision of 0.8 mm and estimation of the 4th order Zernike spherical aberration. Our system is different in that it measures ray slopes in 3D to build complete wavefront maps of the lens in two-dimensions.

Accuracy of aberration measurements in our system was verified by measuring a series of plano-convex glasses lenses of known optical characteristics. Power and spherical aberration measurements compared well to those provided by the lens manufacturer. Repeatability was also assessed by comparing repeated measurements on glass and human lenses by repositioning the lens prior to each scan. The instrument demonstrates sufficient accuracy and precision for evaluating aberrations of primate lenses in vitro.

We implemented a segmentation algorithm to detect the anterior and posterior lens surfaces from volumetric OCT data sets. Volumetric OCT imaging of the undistorted and distorted lens surfaces can be used to reconstruct the index gradient in 3D [25, 34]. Additionally, the system provides off-axis ray slopes that can be used for 3D gradient reconstruction using tomographic techniques based on optical ray tracing [42, 60].

Preliminary results obtained on a cynomolgus monkey lens suggest that peripheral lens defocus increases with field angle and simulated accommodation. These results are consistent with previous findings [45, 54]. Peripheral lens defocus was measured with respect to a circular entrance pupil at all field angles, where field angles were defined in air. In the future, optical models must be created to incorporate the peripheral lens aberrations measured with our method to peripheral optics models of the eye and study of the peripheral retinal image quality. In particular, eye models will be needed to establish how the peripheral lens aberrations measured with our system translate to an actual eye with all its components and where shape and position of the entrance pupil undergo distortions with viewing angle [61].

The system is currently being used with human lenses to determine the relative contribution of lens shape and refractive index gradient to lens power and aberrations and their changes with age [62, 63]. Ultimately, the data will help form an understanding of the role of age-related changes in the properties of the crystalline lens in the development of refractive error.

Funding

National Eye Institute (R01EY021834; 1F30-EY027162; F31EY021444); Ruth L. Kirschstein National Research Service Award Individual Pre-doctoral Fellowship; BMH; P30EY14801 (Center Core Grant); the Florida Lions Eye Bank and Beauty of Sight Foundation; the Henri and Flore Lesieur Foundation (JMP); Drs. Raksha Urs and Aaron Furtado; Karl R. Olsen, MD and Martha E. Hildebrandt, PhD; an unrestricted grant from Research to Prevent Blindness; Australian Federal Government Cooperative Research Centre Scheme through the Vision Cooperative Research Centre.

Disclosures

The authors declare that there are no conflicts of interest related to this article.