Abstract
Automatic skin layer segmentation in optical coherence tomography (OCT) images is important for a topographic assessment of skin or skin disease detection. However, existing methods cannot deal with the problem of shadowing in OCT images due to the presence of hair, scales, etc. In this work, we propose a method to segment the topmost layer of the skin (or the skin surface) using 3D graphs with a novel cost function to deal with shadowing in OCT images. 3D graph cuts use context information across B-scans when segmenting the skin surface, which improves the segmentation as compared to segmenting each B-scan separately. The proposed method reduces the segmentation error by more than 20% as compared to the best performing related work. The method has been applied to roughness estimation and shows a high correlation with a manual assessment. Promising results demonstrate the usefulness of the proposed method for skin layer segmentation and roughness estimation in both normal OCT images and OCT images with shadowing.
OCIS codes: (100.2000) Digital image processing, (100.2960) Image analysis, (100.6890) Three-dimensional image processing, (110.4500) Optical coherence tomography, (170.1870) Dermatology
1. Introduction
Skin is the outer covering of the body and is composed of two major layers, namely the epidermis and the dermis. Diagnosis of many skin diseases can be performed by detecting abnormalities in these two layers. The gold standard for detecting abnormalities has been a histological analysis which involves biopsy [1]. Due to the invasive nature of biopsy, researchers are looking into non-invasive methods for skin analysis. A suitable non-invasive method relies on an imaging modality with the optimum resolution and penetration depth. Ultrasound is an imaging modality which has a high penetration depth of approximately 15mm but a resolution of only around 30 μm [2]. This precludes its use in the vast majority of skin conditions as the pathological features cannot be visualised at this low resolution. Confocal microscopy has a high resolution of 0.5 μm–1 μm but it can penetrate only up to 0.2mm [3]. On the other hand, optical coherence tomography (OCT) has a resolution up to 1 μm and penetration depth of around 1mm which is adequate for the analysis of most skin conditions [4].
OCT imaging is performed by correlation of a reference light beam with the light beam backscattered from the sample tissue [5]. Resultant signals constitute an A-scan. Multiple A-scans combine laterally to form a B-scan which is a 2D image. A 3D-OCT volume is captured as a series of B-scans corresponding to adjoining locations. With the development of OCT technology, it has found applications in dermatological applications such as detecting tumors and inflammations. Moreover, being non-invasive, the same site can be imaged repeatably allowing quantification of skin changes and effectiveness of treatments [3]. In spite of these benefits of OCT, its utility has been limited by manual analysis which is prone to be subjective and labor intensive (since there are typically more than 100 B-scans in one 3D-scan). As an example, consider epidermal thickness (ET) measurement for assessing skin health, aging, and photodamage [6]. To determine ET from a 3D-OCT volume, typically dermatologists select the best quality B-scan from the entire volume. On this B-scan, they measure ET at a predefined number of locations using a software tool which has a ‘ruler’ [7]. An average of ET over these locations gives the mean ET. Such manual estimation of ET may be less accurate due to use of a single representative B-scan and can be highly subjective.
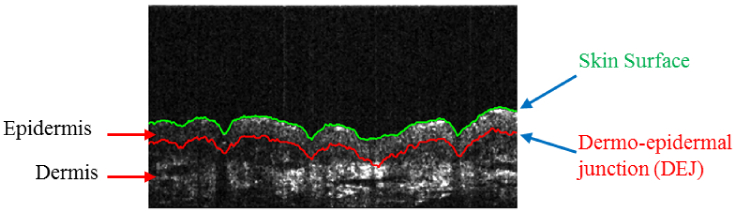
Computerized analysis, on the other hand, can overcome these limitations of manual analysis and broaden the usability of OCT systems. One of the important components in the computerized analysis of skin OCT volumes is automatic skin layer segmentation. This is important since there are certain skin conditions which are observed in specific layers. The major layers of the skin are the epidermis and the dermis (Fig. 1).
Fig. 1.
(Best viewed in color) Epidermis and dermis are two of the major layers of the skin. In the figure, epidermis is bounded by the skin surface (green line) from above and dermo-epidermal junction (DEJ, red line) from below.
There have been fewer works on skin layer segmentation but layer segmentation has been researched fairly well for retina with many works using graph theory. Graph-based methods are either 2D (segmenting each B-scan separately) [8] or 3D (segmenting the whole volume at once) [9, 10]. The 2D methods for retinal layer segmentation mainly used gray level intensity gradients [11] for the task. However, these 2D methods could not utilize the context information available from the adjacent B-scans thereby leading to 3D graph-based methods.
3D graph-based methods especially became popular after the work of K. Li et al. [12] who proposed a general 3D graph-based surface segmentation method. Their method was applied by many works on retinal layer segmentation [13–15]. However, these works used only the gradient information which may be affected by speckle noise. To deal with this limitation, [16] introduced texture information into the segmentation process and improved the performance. Further development of 3D-graph-based methods led to retinal layer segmentation for diseased cases also [17, 18]. These methods cannot be directly applied to skin OCT images because of a difference in image quality. Skin OCT images are usually of inferior quality as compared to retinal OCT images due to various factors such as speckle noise [19], scattering, opacity and limited light penetration. These factors make it difficult to locate layer boundaries.
There have not been many works on skin layer segmentation. Skin layer segmentation may involve segmenting the skin surface and the DEJ (Fig. 1). In order to segment the DEJ, segmenting the skin surface first may be helpful in providing a constraint for DEJ segmentation. In this work, we deal with skin surface segmentation only and show its application for skin roughness measurement. Among the few works on skin surface segmentation, Weissman et al. [6] used shapelets to segment the skin surface. Shapelets analysis correlates an image with a kernel which is in the form of basic image shapes. Shapelets used in [6] were damped Gaussian-like shapelets applied at different scales. Hori et al. [20] used intensity values for skin surface segmentation. To detect the skin surface, intensity peaks were computed for all the A-scans. These peaks formed a surface which was further smoothened to yield the skin surface. A. Li et al. [21] employed a graph-based method for skin surface segmentation. They used vertical intensity gradients to formulate the cost function for their method. This cost function was used with a graph-search algorithm to segment out the skin surface in a B-scan. Yow et al. [22] used a graph-based method for skin surface segmentation in a B-scan. They also used vertical image gradients to define costs for each pixel. Then the path with the lowest cost was searched and it corresponded to the skin surface. They used their skin surface segmentation method for surface roughness estimation.
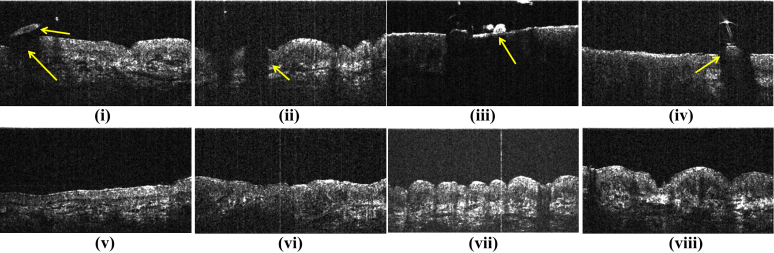
The existing works on skin surface segmentation may work well for good quality images where there is a strong image gradient at the skin surface. However, if the imaged site contains structures such as hair or scales, these structures can be mistaken as the surface itself. Moreover, these structures block the incident light from reaching the skin beneath them and causes shadows in the OCT images (Fig. 2). We refer to these problems as ‘shadowing’ in the text to follow.
Fig. 2.
Upper row shows example of cases where skin layer segmentation is difficult. Such cases constitute the dataset SD2 (Section 4.1) (i) Upper arrow shows hair while lower arrow shows the dark region below hair. (ii)–(iv) also show similar cases of shadowing. (v)–(viii) show examples of B-scans from SD1 which do not suffer from shadowing (Section 4.1)
1.1. Our contribution
In this paper, we propose a 3D graph-based method for skin surface segmentation in high definition (HD)-OCT images. Our main contributions are as follows:
To deal with shadowing in OCT images and to use the existing graph-based methods for skin layer segmentation, we propose a novel cost function to be used with the segmentation algorithm. The cost function uses both the intensity gradients (edge-based cost) and uniformity of the regions surrounding the surface (region-based cost). The proposed method is different from the retinal layer segmentation methods which cannot be directly applied to skin OCT images since skin OCT images are of inferior quality as compared to retinal OCT images (Section 1).
We use a 3D method instead of existing 2D methods for skin surface segmentation. A 3D method uses the context information across the neighboring B-scans which the 2D methods cannot utilize. Using this context information helps in improving the segmentation performance (Section 4).
We apply the proposed method to skin roughness measurement. Based on the surface segmentation, we compute two parameters related to skin’s roughness, namely the furrow depth and the furrow density. The values of these parameters correlate well with the manual ground truth. Measuring skin roughness is useful in dermatological practice to monitor the effectiveness of skin treatments such as scar management therapies [23] and application of moisturizing agents [24]. Skin roughness has also been found to be associated with skin aging [25]. The proposed method will help dermatologists by giving them a faster and more reliable alternative to manual analysis of the skin.
2. Skin surface segmentation
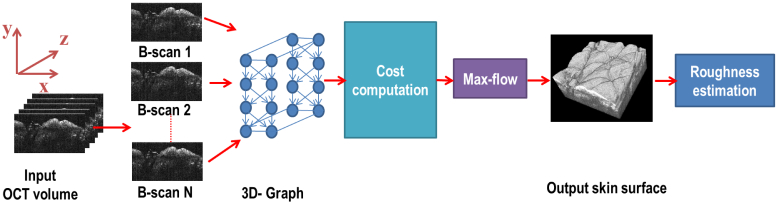
The flowchart of the proposed approach is given in Fig. 3. Given an HD-OCT volume, a 3D node-weighted directed graph was formed representing the HD-OCT volume. The skin surface corresponded to a surface in this graph. Before computing the cost of each node in the graph, each B-scan in the volume was preprocessed to improve the visibility of the layers. After preprocessing, the cost of each node in the graph was computed. The cost functions were designed in such a way that the surface corresponding to the actual skin surface should have the minimum cost. Segmenting out this surface was modeled as a problem of finding the minimum cost closed set in the graph [12]. This problem was solved using the standard max-flow/min-cut algorithm [26]. Once the skin surface was segmented out, the OCT volume was analyzed to determine the roughness of the skin surface.
Fig. 3.
A flowchart of the proposed approach for skin surface segmentation and roughness estimation.
2.1. Notations and definitions
Let each B-scan be along the x–y plane and the successive B-scans in a volume stack in the z-direction (Figure 3, input). Following are the major notations and terms used in the text henceforth. Other notations will be defined as required.
Nx and Ny: Size of a B-scan along x and y directions respectively.
Nz: Number of B-scans in the OCT volume.
I(x, y, z): 3D image representing the OCT volume with I(x, y, z) being the intensity at a voxel (x, y, z). Here x ∈ x = {0, 1, 2, ...., Nx}, represents the voxel indices along the x-axis. Similarly, y and z are defined.
G = (V, E): 3D graph representing the HD-OCT volume. V denotes the nodes while E denotes the edges of the graph.
V(x, y, z): Node in G corresponding to the voxel (x, y, z).
Column: Set of nodes with same (x, z) values. In the context of a B-scan, a column refers to all pixels with the same value of x.
Base layer: Set of all nodes corresponding to y = 0.
C: A closed set C is the set of all those nodes such that the successors of each node in C are also contained in C.
Δy, Δz: Parameters determining smoothness of the layer along y (within a B-scan) and z (across adjacent B-scans) directions respectively.
c(x, y, z): Cost function for a voxel (x, y, z). cZ (x, y) is the cost function for a B-scan located at z =Z.
w(x, y, z): Weight assigned to the node V(x, y, z).
2.2. Graph formation
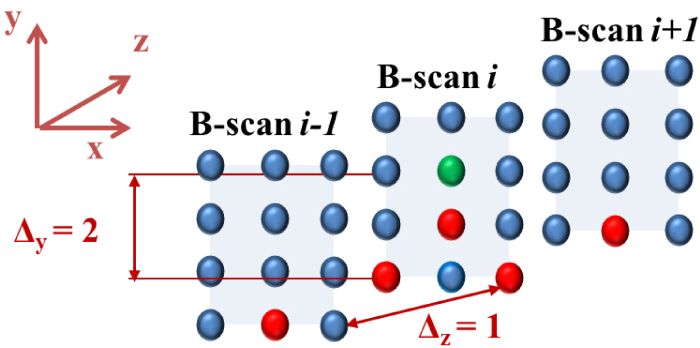
The OCT volume was represented as a 3D graph with each node corresponding to a voxel in the volume. This means there were Nx × Ny × Nz nodes in the graph. Each node was connected to its neighboring nodes through edges. In this work, the node V(x, y, z) was connected to V(x − 1, y − Δy, z), V(x + 1, y − Δy, z), V(x, y − Δy, z − Δz) and V(x, y − Δy, z + Δz). Here, Δy and Δz are the smoothness parameters explained in the next section. In addition, each node (except those in the base layer) was also connected to the node just below it i.e. V(x, y, z) is connected to V(x, y − 1, z). The neighborhood can be understood from Fig. 4 where the neighbors of the green voxel are shown in red. These edges connecting the neighbors enforced smoothness constraints. This means that for a voxel (x, y, z) on a surface, its neighboring voxels along x-direction, (x +1, y′, z) and (x −1, y″, z) were no lower than the voxel (x, max(0, y −Δy), z). Similar smoothness constraint along z-direction (controlled by Δz) enabled the graph cut algorithm to maintain smoothness of the surface across different B-scans and ignore sudden loss of signal or a bump due to hair or scales. Lack of this smoothness in 2D approaches makes the algorithm sensitive to sudden changes in the surface.
Fig. 4.
(Best viewed in color) The neighborhood used in forming the 3D graph is illustrated for the case when Δy = 2 and Δz = 1. The spheres represent the voxels of the graph. Neighbors for the voxel in green are shown in red. Note that in order to avoid clutter, the edges are not drawn.
Once the graph was constructed, the weight of a node V(x, y, z) in G was defined as w(x, y, z) = c(x, y − 1, z) − c(x, y, z) (for y > 0). When the weights were computed at the nodes of the graph G, the graph became a node-weighted graph. The costs c(x, y, z) were computed as explained in the next section.
2.3. Cost computation and segmentation
The raw OCT volume had weak signal at the periphery so we cropped out a region of interest (ROI) from the volume (Fig. 5). Each B-scan of the ROI was extracted as a 16-bit grayscale image as shown in Fig. 6(i). The 16-bit image was converted to 8-bit to improve the contrast at the skin surface (Figure 6(ii)). Thereafter, the contrast of each B-scan was further enhanced using contrast stretching (using imadjust in Matlab with default parameters). Final image after preprocessing is shown in Fig. 6(iii). This pre-processing was performed to improve the contrast between the skin surface and the region above it. After preprocessing, a graph-based method was used to segment out the skin surface.
Fig. 5.
The raw OCT volume was cropped out to remove regions with weak signal.
Fig. 6.
Preprocessing steps shown using a sample B-scan (Section 2.3). (i) Raw B-scan, (ii) The B-scan in (i) after conversion to 8-bit. (iii) Final output of preprocessing after contrast stretching of the 8-bit image. This output was used for cost computation.
In a graph-based segmentation method, the 3D volume to be segmented is represented as a graph which has nodes and the neighboring nodes are connected through edges. Each node has a cost associated to it and the cost of a surface in the graph is equal to the sum of the costs of the nodes comprising the surface. The segmentation algorithm searches for the surface in the graph whose cost is the minimum. In the proposed method, since each node corresponds to a pixel in the B-scan, the cost for each pixel in a B-scan was computed and assigned as the cost of the corresponding node in the graph. Since our objective was to find the surface with the minimum cost, the cost was designed such that the desired surface had lower cost as compared to other regions in the B-scan.
The skin surface is characterized by a strong edge, so an edge-based cost function was used. However, there are other layers below the skin surface which often have strong edges near their boundaries. To avoid false detection of these other layers, a region-based term was also added to the cost function. The cost function cZ (x, y) for a B-scan (along the xy plane) can be defined as:
| (1) |
Here and are the edge-based and region-based terms, respectively and ρ controls the weight given to them. The edge-based term was given by:
| (2) |
The edge-based term consisted of a negated orientation penalty p(ϕZ (x, y)) [12] which was chosen in view of a dark to bright transition observed at the skin surface. Dark to bright transition means the image is darker above the skin surface and brighter below it. Mathematically, p(ϕZ (x, y)) is a function of the gradient orientation ϕZ (x, y) and is defined as
| (3) |
p(ϕZ (x, y)) assigned a lower cost to any dark to bright transition. Its value was −1 only for the desired gradient orientation (0° to 180°) and 0 for undesired orientation (270°). For all other orientations, this value was between −1 and 0 and was determined by linear interpolation. Gradient orientation was defined as the angle between the x and y components of the image gradient. Mathematically, the gradient orientation at a pixel (x,y) is given as:
| (4) |
where Gx and Gy are the x and y components of the image gradient. First and second order image gradients were computed using Gaussian blurring followed by convolution with the Scharr operator which is found to perform better than the standard Sobel operator [27].
In addition to the orientation penalty, for pixels with low intensity gradients (both first and second order derivatives below certain thresholds), while for all other pixels where the gradient was high this value was negative. The threshold for first (second) order derivative was computed such that 95% of the pixels in the B-scan had absolute value of first (second) image derivative less than the threshold.
The region-based cost, for a pixel consisted of two terms and is mathematically given as:
| (5) |
Here, bZ (x, y) was the number of bright pixels above the current pixel.
| (6) |
where,
| (7) |
A bright pixel was defined as any pixel with intensity greater than a threshold θ (empirically chosen as 200). This term will have a lower value for the skin surface as compared to the layers below it. In addition, the sum of intensity variance of the pixels above and below the current pixel [12] (rZ (x, y)) was also added to the region-based cost term.
| (8) |
Here a1 and a2 are constants which can be approximated with â1(x′, y′, Z) and â2(x′, y′, Z) defined for each pixel in the B-scan (at z = Z) as [12]:
| (9) |
| (10) |
where y1 ≡ {y|y ≤ max(0, y′ − |x − x′|Δy)} and y2 ≡ {y|y′ + |x − x′|Δy < y < Ny}.
Once the costs were computed, surface segmentation was performed using the standard max-flow/min-cut algorithm [26]. In this algorithm, in addition to the nodes of the graph corresponding to voxels, two more ‘terminal’ nodes are added which are called ‘source’ and ‘sink’. Each node in the graph is assigned to either ‘source’ of ‘sink’ in such a way that the cost of the surface which separates all the source nodes from the sink nodes is minimized. This surface with the minimum cost corresponds to the desired boundary (or the skin surface). After segmenting the skin surface, the intensities of the pixels above the surface were put to zero which in effect removes the non-zero intensities due to the optical gel applied prior to imaging. Resulting B-scans could be visualized in 3D using the 3D-viewer plugin in ImageJ [28].
Difference from the cost function used in [12]:
The proposed cost function is inspired from [12] but it has been modified to deal specifically with skin surface segmentation. Major differences between the two cost functions are:
-
1.
We have combined edge based and non-edge based cost functions while only an edge based function was used in [12]. Using only the edge based cost function of [12] a false segmentation of other layers below the skin surface was possible. To avoid this issue, we have added a region-based term in the cost function.
-
2.
for pixels with low intensity gradients. This was not used in [12].
-
3.
bZ (x, y) is a newly defined term in the cost function which helped to overcome false segmentation at lower layers.
2.4. Choosing smoothness parameters
The smoothness parameters Δy and Δz control the smoothness of the segmented surface. Δy and Δz are related to intra-B-scan (within a B-scan) and inter-B-scan (across the B-scans) smoothness respectively. The meaning of Δy can be understood further from Fig. 7. Figure 7 shows the effect of varying Δy on the smoothness of the segmented surface for a sample B-scan. A lower value of Δy leads to a smoother surface while a higher value reduces this smoothness. If the surface is expected to be smooth along the x-axis, a lower value of Δy is desirable.
Fig. 7.
(Best viewed in color) Effect of varying Δy. Green curve is the result of the proposed algorithm. Lower Δy (Δy = 1) in (i) leads to a smoother curve but such curve does not fit well to the rugged surface shown. Instead Δy = 2 in (ii) fits better. Δz = 3 for both cases.
Similarly, Δz maintains smoothness between successive B-scans, a lower value leading to a smoother segmentation. In a way, this amounts to using the context information across the slices. Using this information ignores sudden loss of signal or a bump due to hair or scales when going from one B-scan to the next. Since there is no such context information used in 2D approaches, they might be sensitive to such problems as would be shown in the experiments (Section 4.2).
3. Skin roughness estimation
To estimate skin’s roughness, we propose two parameters namely furrow density and furrow depth. These parameters were chosen based on the German Deutsche Industrie Norm (DIN) norms which categorize roughness parameters into amplitude parameters (furrow depth) and spacing parameters (furrow density) [29].
To compute these parameters, a depth map of the skin surface was produced based on the segmented surface (Figure 8(ii)). The depth map was in the form of an image where the intensity at a location corresponded to the detected depth. A darker region meant the surface was deeper. The depth map contained furrows which corresponded to the actual furrows on the skin surface. These furrows were detected using Frangi filters [30] which were originally designed to detect blood vessels in retinal fundus images. Frangi filters when applied on the depth map produced a response which was high on furrows and low elsewhere (Figure 8(iii)).
Fig. 8.
Process of furrow extraction. (i) Segmented skin surface, (ii) Depth map, and (iii) furrows extracted using Frangi filters (Section 3).
From the Frangi filter response, furrow density was computed which is defined as the fraction of the skin surface occupied by furrows, Fdensity and is given by [22]:
| (11) |
where Nfurrows is the number of pixels corresponding to the furrows and Nskin is the total number of pixels in the depth map.
The second parameter was computed from the depth map. This parameter is a variation of the mean furrow depth, Fdepth defined in [22] as the average depth at the furrow pixels and computed using the following equation:
| (12) |
where Df is the depth in pixels at fth furrow pixel and μs is the reference surface level estimated by averaging the depths in the entire depth map. The furrow pixels were detected from the Frangi filter response.
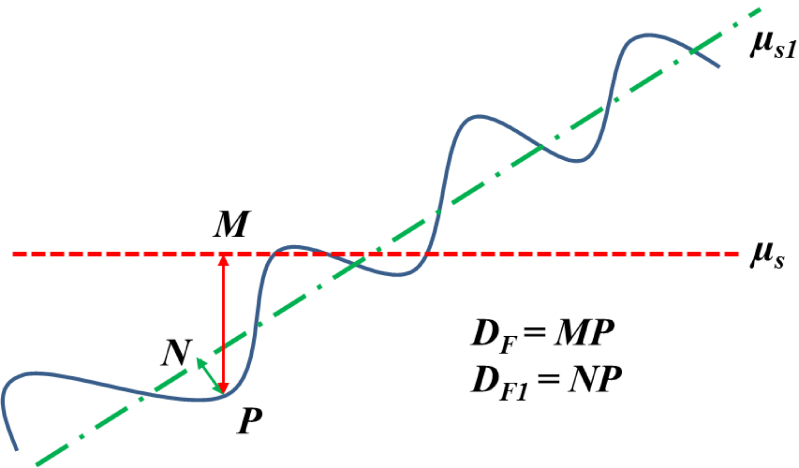
This formula works well for volumes where the skin surface is almost parallel to the x-axis. However, the formula may not be precise enough for surfaces slanted at a significant angle from the x-axis. This is demonstrated in Fig. 9. The reference surface level should be μs1 instead of μs. Consequently we propose to replace μs by μs1 in equation 12. To calculate μs1, we applied principal component analysis (PCA) to the points on the segmented surface. Let the skin surface be represented by a point cloud in 3D, S(x, y, z) or just S for the sake of simplicity. Let the mean of S be given by M = [mx, my, mz]. PCA transforms S into S1 such that:
| (13) |
where W is the 3×3 matrix containing the eigenvectors of the covariance matrix of S corresponding to the three eigenvalues. Mathematically,
| (14) |
Fig. 9.
Computing furrow depth to account for tilted surfaces. The blue curve represents the tilted surface. μs is the reference surface level estimated by averaging the depths in the entire depth map while μs1 is the reference surface level along the tilted surface. For a furrow located at point P, the actual depth is NP instead of MP. Note that we have explained in 2D for ease of understanding however, the actual surface is in 3D.
Note that S lies in a three dimensional space so there will be three eigenvectors resulting from PCA namely w1, w2 and w3. These three eigen-vectors are perpendicular to each other and can form three axes analogous to the x,y and z axes in the original data (before application of PCA). When the points are projected into the new axes formed by these eigenvectors, it is equivalent to a rotation of the surface to make it parallel to the new x-axis. After rotation, the point cloud is given by S1 (Equation 13). Details on eigenvectors, eigenvalues and PCA can be found in [31]. Once the data is rotated, the depth map was computed again followed by furrow extraction as mentioned previously. If M1 = [m1x, m1y, m1z] is the mean of S1, μs1 = m1y and the new equation for Fdepth is:
| (15) |
The new parameters with subscripts ending with 1 are those with reference to the new axes. In addition, | · | denotes the absolute value function.
4. Results and discussions
4.1. Dataset
The data used for experiments were captured using Skintell HD-OCT system [32]. Skintell uses an infrared light source of wavelength 1300nm and achieves a penetration depth of up to 1mm. The captured volumes were of size 640 × 200 × 512 pixels and as per the resolution of Skintell, each pixel is approximately equal to 3 μm in axial and transverse directions. For the captured volumes, the signal at the periphery was weak due to which the volumes were cropped to 360 × 200 × 360 pixels (Figure 5). This meant there were 360 B-scans in one volume, each of size 360 × 200 pixels. Three datasets were used in this work out of which two were used for skin surface segmentation evaluation while the third dataset was used for evaluating roughness estimation. The three datasets are:
-
1.
SD1: The first dataset (Skin dataset 1 or SD1) consisted of 5 HD-OCT volumes captured from anterior and posterior forearms of healthy subjects.
-
2.
SD2: In addition to SD1, for skin surface segmentation a dataset of 26 HD-OCT volumes (from healthy subjects) with shadowing effects was used. These volumes were captured from anterior and posterior forearms and face and contained B-scans with shadowing effects as shown in Fig. 2(i)–(iv).
-
3.
SD3: The third dataset was formed to evaluate roughness estimation using the proposed method. This dataset contained 6 volumes from anterior and posterior forearms and faces of healthy subjects.
The ground truth for the skin surface segmentation was manually marked by an expert in dermatology for all the B-scans in SD1 and SD2. The expert used ImageJ [28] to mark the coordinates of the surface in the image.
Evaluation metric for a B-scan is the unsigned mean vertical error (in pixels) given as:
| (16) |
Here and are the predicted and actual y coordinates for the xth column, respectively and Nx is the number of columns. In addition, the mean signed vertical error, Es, is also reported which uses the signed difference instead of absolute difference in Eq. 16. A positive value of Es indicates that the predicted surface lies above the actual while negative value indicates otherwise. Es is specially relevant in the presence of hair or scales. If these structures were mistaken as skin surface, the predicted surface would lie well above the actual, resulting in a high value for Es. So, Es reflects position of the predicted surface rather than actual performance. Eu and Es give the error for one B-scan. Averaging these errors for all the B-scans in a given volume results in the error for the volume.
For establishing the ground truth for SD3, the 6 volumes were divided into two groups (Figure 10) and the volumes in each group were ranked by 5 clinicians in the order of their furrow density (1 being the least dense and 3 the most dense) and furrow depth (1 being shallowest and 3 deepest). This meant that each clinician gave two rankings for each group abased on visual assessment. The ground truth rankings for furrow density and furrow depth are shown in tables 1 and 2, respectively. From Table 1, it can be observed that all the clinicians agreed in their rankings for both groups. However this agreement was not observed in ranking the furrow depth (Table 2), especially for group 1.
Fig. 10.
The six volumes in SD3 as shown to the clinicians for ranking in order of furrow density and furrow depth (Section 4.1).
Table 1.
Clinicians’ grading for furrow density. 1 denotes the surface with the least dense furrows while 3 is the surface with the densest furrows. Ci refers to the ith clinician while Vi refers to the ith volume.
| Grader ID | Group 1 | Group 2 | ||||
|---|---|---|---|---|---|---|
| V1 | V2 | V3 | V4 | V5 | V6 | |
| C1 | 2 | 1 | 3 | 1 | 3 | 2 |
| C2 | 2 | 1 | 3 | 1 | 3 | 2 |
| C3 | 2 | 1 | 3 | 1 | 3 | 2 |
| C4 | 2 | 1 | 3 | 1 | 3 | 2 |
| C5 | 2 | 1 | 3 | 1 | 3 | 2 |
| Mean | 2.0 | 1.0 | 3.0 | 1.0 | 3.0 | 2.0 |
Table 2.
Clinicians’ grading for furrow depth. 1 denotes the surface with the shallowest furrows while 3 is the surface with the deepest furrows.
| Grader ID | Group 1 | Group 2 | ||||
|---|---|---|---|---|---|---|
| V1 | V2 | V3 | V4 | V5 | V6 | |
| C1 | 1 | 3 | 2 | 2 | 1 | 3 |
| C2 | 3 | 2 | 1 | 1 | 2 | 3 |
| C3 | 3 | 2 | 1 | 1 | 2 | 3 |
| C4 | 2 | 3 | 1 | 1 | 2 | 3 |
| C5 | 2 | 3 | 1 | 1 | 2 | 3 |
| Mean | 2.2 | 2.6 | 1.2 | 1.2 | 1.8 | 3.0 |
4.2. Skin surface segmentation
For skin surface segmentation, values of parameters Δy, Δz and ρ were empirically chosen as 2, 3 and 0.1 respectively. After segmentation, the intersection of the segmented surface with each B-scan is a curve. We performed a B-scan based evaluation of the accuracy of the proposed approach. The predicted curve for a B-scan was compared with the ground truth using equation 16.
Results averaged over all the volumes in SD1 for skin surface segmentation are reported in Table 3(i) and compared against the related works. For SD2, the experiments were run on the full 26 volumes but evaluation was performed on 252 B-scans only and average over these B-scans is reported. This was to assess the performance of the proposed work on the B-scans with shadowing effect. These 252 B-scans were selected through visual inspection of the 26 volumes.
Table 3.
Results of skin surface segmentation on SD1 and SD2. The proposed approach is compared with other related works. Best results are highlighted in bold. Δy = 2 and Δz = 1 for all the experiments. Errors are in pixels and 1 pixel ≃ 3 μm.
We have compared the proposed approach with the following works: 1) A. Li et al. [21]: This is the only work which evaluates the performance of their skin segmentation algorithm. Their method is in 2D and does not consider the presence of hair. 2) K. Li et al. [12]: This work proposed a generic 3D graph-based surface segmentation approach. A comparison was performed with this work to show the importance of the proposed cost function. For comparison, these works were implemented and run on the same datasets as the proposed work.
From Table 3, it can be seen that for skin surface segmentation on SD1 the performance (as per Eu) of the proposed method is better than other works but the improvement in performance is more prominent for SD2. This is because context information (used in the proposed 3D approach) across B-scans is more important for data with shadowing effect (SD2). Lack of using the context information across the B-scans in the 2D approach [21] makes it sensitive to sudden changes in the surface.
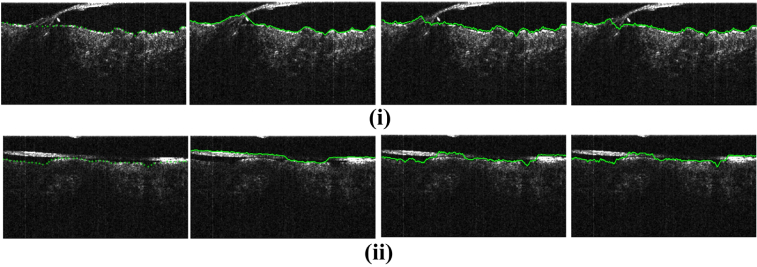
Figure 11(i) and (ii) present sample skin surface segmentation results and for both cases the proposed method outperformed other works. However, for cases where hair touched the skin surface for a higher number of B-scans, the proposed method experienced errors in segmentation as well. Figure 11(ii) shows one such case where all the methods failed to accurately segment the skin surface. Figure 12 compares the 3D visualization of the surface as segmented using the proposed algorithm and the algorithm in [21]. The method in [21] incorrectly segmented strands of hair as surface. As observed, the proposed method produces better results being robust to the presence of hair since it uses the context information as mentioned in sections 1.1 and 2.4.
Fig. 11.
(Best viewed in color) Results for skin surface segmentation for the proposed approach as compared with related works. From left to right are ground truth and the results of A. Li et al. [21], K. Li et al. [12] and the proposed method, respectively. The unsigned mean vertical errors for each sample (from left to right respectively) are (i) 3.24, 3.46 and 2.38 pixels (ii) 11.45, 4.61 and 3.67 pixels.
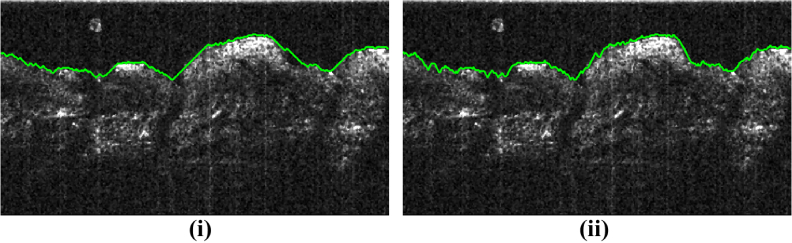
Fig. 12.
A comparison of segmentation obtained using (i) 2D segmentation method of A. Li et al. [21] and (ii) the proposed method. The encircled regions show strands of hair incorrectly segmented by [21] as the skin surface. The proposed method, on the other hand, is more robust to the presence of hair.
4.3. Roughness estimation
The results of surface roughness estimation are presented in this section. Results in Table 4 show the values of Fdensity and Fdepth for all the six volumes. The depth maps generated for each volume are shown in Fig. 13. Results are compared to another related work [22]. If we compare the depth maps produced using the proposed method and [22], the ones produced using [22] have more artifacts. This is because [22] uses 2D segmentation method which cannot achieve continuity between the successive B-scans. Since the proposed method uses 3D segmentation, such artifacts are absent in the resulting depth maps.
Table 4.
Results of roughness estimation on the six volumes (see the depth maps in Fig. 13) using the proposed method and a related work [22]. The values of the two parameters relating to the furrow density and furrow depth are reported.
| Proposed | Yow et al. [22] | |||
|---|---|---|---|---|
| Volume name | Fdensity | F depth1 | Fdensity | Fdepth |
| Group 1 | ||||
| V1 | 0.18 | 3.95 | 0.37 | 8.67 |
| V2 | 0.13 | 3.78 | 0.30 | 10.47 |
| V3 | 0.34 | 1.04 | 0.38 | 7.90 |
| Group 2 | ||||
| V4 | 0.02 | 1.14 | 0.31 | 14.93 |
| V5 | 0.29 | 1.48 | 0.39 | 7.63 |
| V6 | 0.16 | 4.06 | 0.31 | 9.83 |
Fig. 13.
Depth maps generated using the proposed approach (Top row) and the method in [22] (Bottom row) for the six volumes used for roughness estimation. The depth maps generated using the proposed method has fewer artifacts as compared to the depth maps produced by [22].
The parameter Fdensity essentially computes what fraction of the skin surface (as shown in the depth map) is occupied by furrows. The values computed using the proposed method are very different from those computed using [22] since [22] uses a different method to extract furrows. In some cases, it can be seen that values of Fdensity computed using the proposed method is closer to the expected value. One such case is V4 where hardly any furrow is seen (Figure 13) which is reflected in Fdensity = 0.02 meaning that only 2% of the surface has furrows. While the same value computed using [22] is 31% which does not seem to be accurate. In some cases, it is possible that the artifacts were taken to be furrows by [22] such as V5 and V3, however proposed method is robust to such errors. If we compare values of Fdepth, there is a large difference in the values computed using the proposed method and [22]. This is essentially due to different equations used for Fdepth in both the methods (Eqs. 12 and 15). Moreover, difference in furrow extraction method also affects the computation of furrow depth.
Based on the computed values of the roughness parameters, the six volumes were ranked. For ranking based on the furrow density, 1 is the least dense while 3 is the densest. Similarly, for rankings based on the furrow depth, 1 is the shallowest while 3 is the deepest. The rankings made by the proposed system were correlated with the ground truth which was the mean rankings of the clinicians. Results of these rankings are presented in Table 5 along with a comparison with the rankings based on [22]. To quantify the correlation, we computed the Pearson’s correlation coefficients (ρ) between the roughness parameters and the respective ground truth rankings. The correlation of Fdensity with its ground truth is higher in both groups (0.96 and 0.99) for the proposed method as compared to [22] (0.92 and 0.87). For Fdepth1 the correlation coefficients are 0.95 and 0.97 for group 1 and group 2, respectively while these values for [22] are 0.89 and −0.53, respectively. These high correlations of the proposed roughness parameters with the manual rankings show their usefulness in the assessment of skin roughness. Moreover, as compared to [22], the proposed method shows better results.
Table 5.
Ranking of the volumes based on the roughness parameters computed using the proposed method and [22] (Refer to Table 4 for the values of the parameters). The ground truth (GT) is the mean ranking by the clinicians. Pearson’s correlation coefficients (ρ) show the degree of correlation between computed parameters and the ground truth (Section 4.3). For ground truth marking of furrow density, 1 is the least dense while 3 is the densest. For furrow depth, 1 is the shallowest while 3 is the deepest. Best results are highlighted in bold. NA: Not Applicable.
In this work, we have used the roughness parameters to rank the roughness of the OCT volumes taken from different individuals. However, in actual application, the proposed parameters will be used to rank the same location of the body over different visits. This will help in monitoring the effect of treatments on the skin.
5. Conclusion
This paper presented a 3D graph-based approach for skin layer segmentation with a novel cost function which can deal with shadowing effects in OCT images. The proposed method utilized context information across B-scans which was neglected by previous works on skin layer segmentation which used a B-scan-by-B-scan (2D) segmentation approach. For skin surface segmentation, the proposed method outperformed existing related works. Experimental results on OCT images with shadowing effect showed a reduction in error by more than 20% as compared to the best performing related work in skin surface segmentation [21]. The proposed method was used for skin roughness estimation. Roughness estimation is important for cosmeceutical applications. We proposed to use furrow density and furrow depth to measure surface roughness. Experimental results showed that the depth maps produced by the proposed method had fewer artifacts as compared to [22]. Accurately generated depth maps also led to a more accurate computation of the roughness parameter. The roughness rankings made based on the computed parameters correlated well with the ground truth and outperformed the related work [22]. However, in cases of complex curvatures of the skin, our approximation using PCA needs to be tested.
One of the limitations of the proposed method is that when hair touched the skin surface consecutively for many B-scans, segmentation of skin surface was not accurate. Future work will attempt to deal with these problems. Although the evaluation was performed on B-scans with hair, the work can be extended to structures in the skin blocking light, which create shadows such as hair inside the hair follicles and thick scales on the skin surface. The proposed approach for layer segmentation is also applicable to similar problems such as retinal layer segmentation.
As for skin roughness estimation, the proposed method can be very useful owing to robustness to shadowing which can affect roughness estimation. The parameters proposed in this work assess the furrow density and depth on the skin surface. We will be studying ways to combine these two parameters to give one roughness parameter. This can be used to rank skin roughness as a single parameter, rather than using furrow density and depth parameters individually.
Funding
A*STAR-NHG-NTU Skin Research Grant (SRG) (SRG/14010).
Disclosures
The authors declare that there are no conflicts of interest related to this article.
References and links
- 1.Sandby-Moller J., Poulsen T., Wulf H. C., “Epidermal thickness at different body sites: relationship to age, gender, pigmentation, blood content, skin type and smoking habits,” Acta Derm-Venereol 83, 410–413 (2003). 10.1080/00015550310015419 [DOI] [PubMed] [Google Scholar]
- 2.Crisan M., Crisan D., Sannino G., Lupsor M., Badea R., Amzica F., “Ultrasonographic staging of cutaneous malignant tumors: an ultrasonographic depth index,” Arch. Dermatol. Res. 305, 305–313 (2013). 10.1007/s00403-013-1321-1 [DOI] [PubMed] [Google Scholar]
- 3.Sattler E., Kästle R., Welzel J., “Optical coherence tomography in dermatology,” J. Biomed. Opt. 18, 061224 (2013). 10.1117/1.JBO.18.6.061224 [DOI] [PubMed] [Google Scholar]
- 4.Mamalis A., Ho D., Jagdeo J., “Optical coherence tomography imaging of normal, chronologically aged, photoaged and photodamaged skin: A systematic review,” Dermatol. Surg. 41, 993–1005 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gambichler T., Jaedicke V., Terras S., “Optical coherence tomography in dermatology: technical and clinical aspects,” Arch. Dermatol. Res. 303, 457–473 (2011). 10.1007/s00403-011-1152-x [DOI] [PubMed] [Google Scholar]
- 6.Weissman J., Hancewicz T., Kaplan P., “Optical coherence tomography of skin for measurement of epidermal thickness by shapelet-based image analysis,” Opt. Express 12, 5760–5769 (2004). 10.1364/OPEX.12.005760 [DOI] [PubMed] [Google Scholar]
- 7.Gambichler T., Matip R., Moussa G., Altmeyer P., Hoffmann K., “In vivo data of epidermal thickness evaluated by optical coherence tomography: effects of age, gender, skin type, and anatomic site,” J. Dermatol. Sci. 44, 145–152 (2006). 10.1016/j.jdermsci.2006.09.008 [DOI] [PubMed] [Google Scholar]
- 8.Kaba D., Wang Y., Wang C., Liu X., Zhu H., Salazar-Gonzalez A., Li Y., “Retina layer segmentation using kernel graph cuts and continuous max-flow,” Opt. Express 23, 7366–7384 (2015). 10.1364/OE.23.007366 [DOI] [PubMed] [Google Scholar]
- 9.Song Q., Bai J., Garvin M. K., Sonka M., Buatti J. M., Wu X., “Optimal multiple surface segmentation with shape and context priors,” IEEE T. Med. Imaging 32, 376–386 (2013). 10.1109/TMI.2012.2227120 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lee K., Zhang L., Abramoff M. D., Sonka M., “Fast and memory-efficient LOGISMOS graph search for intraretinal layer segmentation of 3D macular OCT scans,” in “SPIE Med. Imaging,” (International Society for Optics and Photonics, 2015), pp. 94133X. [Google Scholar]
- 11.Chiu S. J., Li X. T., Nicholas P., Toth C. A., Izatt J. A., Farsiu S., “Automatic segmentation of seven retinal layers in SDOCT images congruent with expert manual segmentation,” Opt. Express 18, 19413–19428 (2010). 10.1364/OE.18.019413 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Li K., Wu X., Chen D. Z., Sonka M., “Optimal surface segmentation in volumetric images-a graph-theoretic approach,” IEEE T. Pattern Anal. 28, 119–134 (2006). 10.1109/TPAMI.2006.19 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Haeker M., Sonka M., Kardon R., Shah V. A., Wu X., Abràmoff M. D., “Automated segmentation of intraretinal layers from macular optical coherence tomography images,” in “Med. Imaging,” (International Society for Optics and Photonics, 2007), pp. 651214. [Google Scholar]
- 14.Garvin M. K., Abràmoff M. D., Kardon R., Russell S. R., Wu X., Sonka M., “Intraretinal layer segmentation of macular optical coherence tomography images using optimal 3-d graph search,” IEEE T. Med. Imaging 27, 1495–1505 (2008). 10.1109/TMI.2008.923966 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Garvin M. K., Abràmoff M. D., Wu X., Russell S. R., Burns T. L., Sonka M., “Automated 3-D intraretinal layer segmentation of macular spectral-domain optical coherence tomography images,” IEEE T. Med. Imaging 28, 1436–1447 (2009). 10.1109/TMI.2009.2016958 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Antony B. J., Abràmoff M. D., Sonka M., Kwon Y. H., Garvin M. K., “Incorporation of texture-based features in optimal graph-theoretic approach with application to the 3D segmentation of intraretinal surfaces in SD-OCT volumes,” in “SPIE Med. Imaging,” (International Society for Optics and Photonics, 2012), pp. 83141G. [Google Scholar]
- 17.Shi F., Chen X., Zhao H., Zhu W., Xiang D., Gao E., Sonka M., Chen H., “Automated 3-D retinal layer segmentation of macular optical coherence tomography images with serous pigment epithelial detachments,” IEEE T. Med. Imaging 34, 441–452 (2015). 10.1109/TMI.2014.2359980 [DOI] [PubMed] [Google Scholar]
- 18.Chen X., Niemeijer M., Zhang L., Lee K., Abràmoff M. D., Sonka M., “Three-dimensional segmentation of fluid-associated abnormalities in retinal OCT: probability constrained graph-search-graph-cut,” IEEE T. Med. Imaging 31, 1521–1531 (2012). 10.1109/TMI.2012.2191302 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mcheik A., Tauber C., Batatia H., George J., Lagarde J.-M., “Speckle modelization in OCT images for skin layers segmentation,” in “VISAPP, volume 1 (2008), pp. 347–350. [Google Scholar]
- 20.Hori Y., Yasuno Y., Sakai S., Matsumoto M., Sugawara T., Madjarova V., Yamanari M., Makita S., Yasui T., Araki T., Itoh M., “Automatic characterization and segmentation of human skin using three-dimensional optical coherence tomography,” Opt. Express 14, 1862–1877 (2006). 10.1364/OE.14.001862 [DOI] [PubMed] [Google Scholar]
- 21.Li A., Cheng J., Yow A. P., Wall C., Wong D., Tey H., Liu J., “Epidermal segmentation in high-definition optical coherence tomography,” Conf. Proc. IEEE Eng. Med. Biol. Soc., 2015, 3045(2015). [DOI] [PubMed] [Google Scholar]
- 22.Yow A. P., Cheng J., Li A., Srivastava R., Liu J., Wong D. W. K., Tey H. L., “Automated in vivo 3D high-definition optical coherence tomography skin analysis system,” Conf. Proc. IEEE Eng. Med. Biol. Soc. 2016, 3895–3898 (2016). [DOI] [PubMed] [Google Scholar]
- 23.Bloemen M. C., van Gerven M. S., van der Wal M. B., Verhaegen P. D., Middelkoop E., “An objective device for measuring surface roughness of skin and scars,” J. Am. Acad. Dermatol. 64, 706–715 (2011). 10.1016/j.jaad.2010.03.006 [DOI] [PubMed] [Google Scholar]
- 24.Fischer T. W., Wigger-Alberti W., Elsner P., “Assessment of ‘dry skin’: Current bioengineering methods and test designs,” Skin Pharmacol. Physi. 14, 183–195 (2001). 10.1159/000056346 [DOI] [PubMed] [Google Scholar]
- 25.Trojahn C., Dobos G., Richter C., Blume-Peytavi U., Kottner J., “Measuring skin aging using optical coherence tomography in vivo: a validation study,” J. Biomed. Opt. 20, 045003 (2015). 10.1117/1.JBO.20.4.045003 [DOI] [PubMed] [Google Scholar]
- 26.Boykov Y., Kolmogorov V., “An experimental comparison of min-cut/max-flow algorithms for energy minimization in vision,” IEEE T. Pattern Anal. 26, 1124–1137 (2004). 10.1109/TPAMI.2004.60 [DOI] [PubMed] [Google Scholar]
- 27.Scharr H., “Optimal operators in digital image processing,” Ph.D. thesis (2000). [Google Scholar]
- 28.Schneider C. A., Rasband W. S., Eliceiri K. W., “NIH Image to ImageJ: 25 years of image analysis,” Nat. Methods 9, 671–675 (2012). 10.1038/nmeth.2089 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wilhelm K.-P., Elsner P., Berardesca E., Maibach H. I., “Bioengineering of the skin: skin imaging & analysis,” (2006).
- 30.Frangi A. F., Niessen W. J., Vincken K. L., Viergever M. A., “Multiscale vessel enhancement filtering,” MICCAI,” (1998). [Google Scholar]
- 31.Smith L. I., “A tutorial on principal components analysis,” (2002).
- 32.“Agfa-healthcare,” Last accessed 08/09/17.