Full video pulse extraction

Abstract

This paper introduces a new method to automate heart-rate detection using remote photoplethysmography (rPPG). The method replaces the commonly used region of interest (RoI) detection and tracking, and does not require initialization. Instead, it combines a number of candidate pulse-signals computed in the parallel, each biased towards differently colored objects in the scene. The method is based on the observation that the temporally averaged colors of video objects (skin and background) are usually quite stable over time in typical application-driven scenarios, such as the monitoring of a subject sleeping in bed, or an infant in an incubator. The resulting system, called full video pulse extraction (FVP), allows the direct use of raw video streams for pulse extraction. Our benchmark set of diverse videos shows that FVP enables long-term sleep monitoring in visible light and in infrared, and works for adults and neonates. Although we only demonstrate the concept for heart-rate monitoring, we foresee the adaptation to a range of vital signs, thus benefiting the larger video health monitoring field.

1. Introduction

Remote photoplethysmography (rPPG) enables contactless monitoring of human cardiac activities by detecting the pulse-induced subtle color changes on human skin surface using a regular RGB camera [1–3]. In recent years, the core rPPG algorithms that extract the pulse from color-signals have matured rapidly, but the additionally required means for full automation are much less developed, especially for the long-term monitoring.

There are two traditional ways to automate an rPPG system. The first one (most commonly used) uses face detection, face tracking and skin selection [4–6]. The second one uses dense video segmentation with local pulse estimation to find living-skin pixels to initialize the measurement [7–10]. However, neither is designed for the long-term monitoring in real clinical applications such as sleep monitoring and neonatal monitoring. For instance, the first approach is ipso facto not applicable to general body-parts (e.g., palm) or newborns. Furthermore, face detection may fail when the subject changes posture during sleep, when the camera registers the face under an unfavorable angle, or when part of the face is covered by the blanket. Also, long-term object tracking is already a challenging research topic in itself [11], and has to be correctly initialized. For example, when the subject leaves the bed during the night (e.g., drink water or go to toilet (Nocturia)), he/she needs to be registered in the tracking system again when returning to sleep, which relies on accurate face detection. The second approach needs spatio-temporally coherent local segmentation to create long-term time-tubes for pulse extraction and living-skin detection. This method is sensitive to local motion and computationally expensive. Essentially, living-skin detection and pulse extraction depend on each other, leading to a “chicken-or-the-egg” causality dilemma.

The commonality of aforementioned two approaches is that both include the Region of Interest (RoI) identification as an essential step prior to the pulse extraction. However, in a vital signs monitoring system, we only require the extracted target-signal (e.g., pulse) as the output and are not interested in the specifics of the RoI location. If we have means to treat the whole camera as a single PPG-sensor, we may directly extract the pulse from the full video, eliminating the intermediate step of RoI localization.

By restricting the considered scenario, we feel that much simpler systems can be created to achieve a fully functional rPPG system that is directly operable on raw video streams. In a specific fixed environment (e.g., bed or incubator), we argue that the measured subject may move his/her body or change the position/posture, but that the DC-colors of skin and background are usually quite stable over time. Here the “DC-colors” refers to the temporally averaged colors of video objects, which are calculated by taking the mean of the pixels of the objects over a time interval. In an individual image, the spatial location of the subject (the pixel-coordinates) may vary, as the subject can be anywhere in an image, but the DC-colors of surfaces in the scene (including skin and background) can hardly change much. Therefore, we propose to use the DC-color as a feature to automate the pulse extraction, rather than the RoI location. The proposal builds on the hypothesis that the background color and light source color remain stable in the relatively short interval used for pulse extraction. We consider this hypothesis to be valid in restricted applications (e.g., clinical setup), where the illumination of hospital beds/incubators can be managed to have a short-term stable emission spectrum.

Therefore, in this paper, we exploit the DC-color as a spatial feature to differentiate objects in an image for pulse extraction, ignoring their locations or motions. This leads to a novel yet simple rPPG monitoring system, consisting of three steps: (i) exploiting pixel colors in each video frame to create different weighting masks to weight the entire frame, such that the objects having (even subtle) color contrast are biased differently in different weighted images; (ii) deriving from the weighted image a feature per color channel (a statistical value such as the mean or variance) and concatenating it over time as color-signals; and (iii) extracting an rPPG-signal per mask and combining them into a final output. Another attractive property of this approach is that the pixels with similar color are grouped together for pulse extraction, which reduces the number of color variations/distortions in a single rPPG-extraction. The proposed method is called Full Video Pulse extraction (FVP). Our evaluation shows that FVP can achieve a similar accuracy in the heart-rate measurement as the earlier proposed methods in conditions where existing algorithms can detect and track the RoI correctly. Moreover, FVP shows good results even in applications where earlier methods fail, such as long-term monitoring during sleep using an RGB or Near-infrared (NIR) camera, or in neonatal care.

The remainder of this paper is structured as follows. In Section II, we introduce the full video pulse extraction method. In Section V and VI, we use a benchmark with diverse videos to verify its performance. Finally in Section V, we draw our conclusions.

2. Method

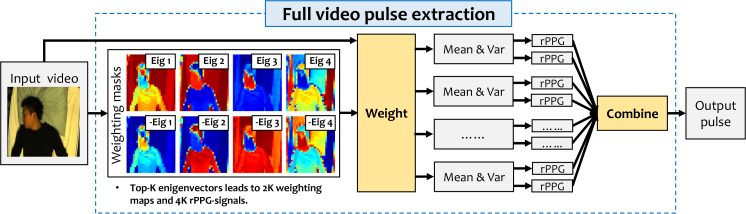
The overview of the proposed full video pulse extraction method is shown in Fig. 1, which will be introduced in detail in the following subsections. Unless stated otherwise, vectors, matrices and operators are denoted as boldface characters throughout this paper.

Fig. 1.

Flowchart of the proposed full video pulse extraction method. The essential step is creating different weighting masks to bias different colored objects prior to pulse extraction. Two different ways are used to combine weighted image pixels: mean and variance (var).

2.1. Weighting masks

Given a video sequence registered by an RGB camera viewing a scene that includes a living-skin, we use I(x, c, t) to denote the intensity of a pixel at the location index x of an image, in the channel c, recorded at time t. In a typical setup, we have c = 1, 2, 3 corresponding to the R-G-B channels of a standard RGB camera. The pixel x is created from a down-sampled version of the image to reduce both the quantization noise and the computational complexity, i.e., 20 × 20 patches from 640 × 480 pixels by default. To reduce the quantization noise, the image is down-sampled by a box filter (e.g., spatial averaging), instead of, for example, the nearest-neighbor interpolation. The time t denotes the frame index with a typical recording rate at 20 frames per second (fps).

Since we aim to combine the patches (or down-sampled pixels) with similar skin-chromaticity features for pulse extraction (through a set of weighting masks), the color features must be independent of the light intensity. So we first eliminate the intensity of each patch by local intensity normalization:

$$I_n(x,c,t)=\frac{I(x,c,t)}{{\sum }_{c=1}^{3}I(x,c,t)},$$ (1)

where I_n(x, c, t) denotes the intensity-normalized color values.

Next, we use I_n(x, t) (i.e., I_n(x, t) = I_n(x, ·, t), which denotes a pixel across all channels) to generate multiple weighting masks where the patches sharing similar normalized color values are assigned a similar weight. To this end, we use the Spectral Clustering [12] to build a fully connected affinity/similarity graph for all the patches using I_n(x, t) and decompose it into uncorrelated subspaces, where each subspace can be used as an independent weighting mask to discriminate the patches with different colors.

In line with [12], the affinity matrix for all patches in the t-th frame is built as:

$${\mathbf{A}}_{\mathbf{x},\mathbf{y}}(t)={\Vert {\mathbf{I}}_{\mathbf{n}}(x,t)-{\mathbf{I}}_{\mathbf{n}}(y,t)\Vert }_2,$$ (2)

where ‖ · ‖₂ denotes the L2-norm (e.g., Euclidean distance); A_x,y(t) denotes the (x, y) element from matrix A(t). Then we decompose A into orthogonal (uncorrelated) subspaces using Singular Value Decomposition (SVD):

$$\mathbf{A}(t)=\mathbf{U}(t)\cdot \mathbf{S}(t)\cdot {\mathbf{U}}^{\top }(t),$$ (3)

where U(t) and S(t) denote the eigenvectors and eigenvalues, respectively. Since each eigenvector describes a group of patches having a similar color feature, we use a number of K top-ranked eigenvectors to create the weighting masks, where K can be defined either automatically (using S(t)) or manually. To fully exploit the eigenvectors, we use both the U(t) and −U(t) (i.e., the opposite direction) to create the weighting vectors:

$$\mathbf{W}(t)=\left[\mathbf{u}(1,t),\dots ,\mathbf{u}(K,t)-\mathbf{u}(1,t),\dots ,-\mathbf{u}(K,t)\right],$$ (4)

where u(i, t) denotes the i-th column eigenvector of U(t) and each column of W(t) represents an image weighting vector. A number of 2K weighting vectors are created by using the top-K eigenvectors. Since the weights in w(i, t) (i.e., i-th column weighting vector of W(t)) must be non-negative and its total sum must be temporally consistent, w(i, t) is first shifted by:

$$\hat{\mathbf{w}}(i,t)=\mathbf{w}(i,t)-\mathbf{min}\left(\mathbf{w}(i,t)\right),$$ (5)

where min(·) denotes the minimum operator, and then normalized by:

$$\overline{\mathbf{w}}(i,t)=\frac{\hat{\mathbf{w}}(i,t)}{\mathbf{sum}\left(\hat{\mathbf{w}}(i,t)\right)},$$ (6)

where sum(·) denotes the summation over all the elements in a vector or a matrix. This step is essential, as it guarantees that the total weight for each frame is identical. We use w̄_i(t) to weight each channel of the image as:

$$\mathbf{J}(i,c,t)=\overline{\mathbf{w}}(i,t)\odot \mathbf{I}(c,t),$$ (7)

where I(c, t) denotes a channel across all pixels at time t; J(i, c, t) is a vector containing the intensities of all pixels, at time t and in the channel c, weighted by the i-th mask. In the next step, we will condense each weighted image into spatial color representations and concatenate these over time for pulse extraction.

Figure 2 exemplifies the RGB and Near-Infrared (NIR) images at time t, and their corresponding weighting masks (based on the top-4 eigenvectors). From the RGB images, we infer that both the visible light source color and background color influence the weighting mask. Also, the intensity-normalized pixel values of skin can be very different in different lighting conditions, which can be difficult to model (or learned off-line). For the NIR images (obtained at 675 nm, 800 nm and 905 nm), the visible light color does not influence the weighting mask. The skin has more or less equal reflections in the used NIR wavelengths, as opposed to the RGB wavelengths. This is also the case for typical bedding materials. However, a difference between the skin reflection and bed reflection starts to occur at around 905 nm, which is due to the water absorption of the skin that is typically absent in the bedding. Thus, even in the challenging background with a white pillow (i.e., the color of the white pillow is very similar to that of skin in NIR), the weighting masks may still be possible to be used to discriminate skin and pillow due to the water absorption contrast at 905 nm.

Fig. 2.

Illustration of images, intensity-normalized images, and generated weighting masks for RGB (left column) and NIR (right column) conditions. The yellow and white numbers, in the intensity-normalized images, denote the normalized color vectors of skin and background, respectively.

Based on the reasoning and tests, we recognize that the weighting masks may not always distinguish skin and non-skin when they have very similar colors. This problem will be particularly discussed and addressed in the next step/subsection. Figure 3 shows the weighting masks generated at different frames in a video. We observe that the sequence of masks slowly and consistently evolves over time in agreement with the hypothesized steady background.

Fig. 3.

Sequence of images and generated weighting mask sequences based on the top-4 eigenvectors. Regardless of the posture and position of the subject, the weighting mask sequences are consistently biasing the image by attenuating similar parts of the scene. Its validity is based on the assumption that the DC-colors of skin and background remain stable over the (short) time interval used for pulse extraction.

2.2. Spatial pixel combination

The conventional way of combining image pixel values into a single spatial color representation is the spatial averaging. However, it only works for the weighted RGB image where the skin-pixels are highlighted (similar to a smoothed binary skin-mask). As a complementary to those where the skin-pixels are suppressed, we propose to use the variance (or the standard deviation) as an additional way to combine the weighted pixel values. We mention that in this subsection the “pixel” refers to the down-sampled image pixels, i.e., the patches.

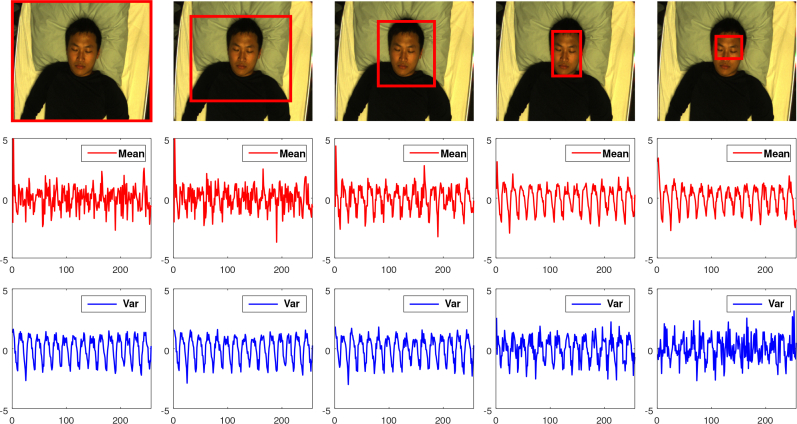
The rationale of using the variance is the following. When the non-skin pixels dominate the weighted image, they dominate the mean. Subtracting the mean and measuring the additional variations reduces the impact of the non-skin pixels. The rationale of using both the mean and variance for spatial pixel combination is underpinned in Appendix A. Based on understanding, we recognize that the variance will be less effective when the skin and non-skin pixels have similar DC-color. In a known and fixed application scenario such as sleep or neonatal monitoring, this problem can be solved by using a bed sheet which provides sufficient contrast with the subject’s skin. Nevertheless, it is an alternative/backup for the mean, especially in the case of imperfect weighting masks, where both the skin and non-skin regions are emphasized. Figure 4 shows that mean and variance have complementary strengths when combining pixels from different RoIs in a video. Therefore, our spatial pixel combination consists of:

$$\{\begin{array}{ll}T(2i-1,c,t)\hfill & =\mathbf{mean}\left(\mathbf{J}(i,c,t)\right)\hfill \\ T(2i,c,t)\hfill & =\mathbf{var}\left(\mathbf{J}(i,c,t)\right)\hfill \end{array},$$ (8)

where T(i, c, t) denotes a statistical value; mean(·) denotes the averaging operator; var(·) denotes the variance operator. Since we use two different ways to combine the pixels in (13), the number of the temporal traces is double of the number of weighting masks (implying 4K traces in total). In the next step, we shall use the core rPPG algorithms to extract the candidate pulse-signals from each statistical color-trace and determine the final output.

Fig. 4.

Comparison of using the mean and variance (var) to combine pixel values in an image. The mean-signal (red) and var-signal (blue) are generated by mean(R/G) and var(R/G) respectively, where R and G are color planes from different RoIs (e.g., red bounding-box). Note that for the visualization purpose, both the mean-signal and var-signal have the low frequency component (< 40 bpm) removed, mean subtracted and standard deviation normalized. Given different RoIs, the mean-signal and var-signal show complementary strength, i.e., when non-skin pixels dominate the RoI, var-signal is better; when skin-pixels dominate the RoI, mean-signal is better.

2.3. Pulse extraction

To extract the pulse-signals from statistical color traces, we can apply the existing core rPPG algorithms, such as G [1], G-R 13], HUE [14], PCA 15], ICA [16], CHROM 17], PBV [18], and POS [19], to name a few. A thorough benchmark on various core rPPG algorithms can be found in [19]. In principle, all of them can be used for the pulse extraction task here.

The extraction of rPPG-signal from T(i, c, t) can be generally expressed as:

$$P(i,t)=\mathbf{rPPG}\left(T(i,c,t)\right),$$ (9)

where rPPG(·) denotes the core rPPG function. Since the focus of this work is not on the core rPPG algorithm, we do not elaborate on it but choose the state-of-the-art POS [19] demonstrated in RGB conditions for (9), although other alternatives would also be possible.

The next step is to determine the final output (i.e., the most likely pulse-signal) from the candidate pulse-signals P(i, t). Due to the use of both the mean and variance for the spatial pixel combination, multiple T(i, c, t) (and thus P(i, t)) may contain useful pulsatile content. Therefore, we treat it as a problem of candidate combination rather than candidate selection. This allows us to profit from all possible extractions. More specifically, since we are only interested in the pulsatile frequency components in P(i, t), our combination is therefore a process of combining frequency components from different signals, instead of directly combining the complete signals.

To arrive at a clean output, we need to give higher weights to the components that are more likely to be pulse-related during the combination. However, we cannot directly use the spectral amplitude to determine the weights or select the components, because the large amplitude may not be due to pulse but to motion changes. Triggered by the relationship of the pulsatile energy and motion energy described in [19], we propose to estimate the intensity-signal of each T(i, c, t) and use the energy ratios between the pulsatile components and intensity components as the weights. The rationale is: if a frequency component in P(i, t) is caused by the blood pulse, it should have larger pulsatile energy w.r.t. the total intensity energy. If a component has balanced pulsatile and intensity energies, its “pulsatile energy” is more likely to be noise/motion induced. We mention that the use of intensity-signal here is mainly for suppressing the background components, although it may suppress the motion artifacts as well.

The extraction of the intensity-signal from each T(i, c, t) can be expressed as:

$$Z(i,t)=\sum _{c=1}^{3}T(i,c,t),$$ (10)

which is basically the summation of the R, G and B feature signals. Since we use the local spectral energy contrast between the frequency components in P(i) (P(i) = P(i, ·)) and Z(i) (Z(i) = Z(i, ·)) to derive their combining weights, we first normalize their total energy (i.e., standard deviation) and then transform them into the frequency domain using the Discrete Fourier Transform (DFT):

$$\{\begin{array}{l}\mathbf{Fp}(i)=\mathbf{DFT}\left(\frac{\mathbf{P}(i)-\mu (\mathbf{P}(i))}{\sigma (\mathbf{P}(i))}\right)\\ \mathbf{Fz}(i)=\mathbf{DFT}\left(\frac{\mathbf{Z}(i)-\mu (\mathbf{Z}(i))}{\sigma \left(\mathbf{Z}(i)\right)}\right)\end{array},$$ (11)

where DFT(·) denotes the DFT operator. The weight for b-th frequency component in Fp(i) is derived by:

$$W(i,b)=\{\begin{array}{ll}\frac{\mathbf{abs}\left(Fp(i,b)\right)}{1+\mathbf{abs}\left(Fz(i,b)\right)},\hfill & \text{if}b\in \mathbf{B}=[b_1,b_2],\hfill \\ 0,\hfill & \text{elsewhere},\hfill \end{array}$$ (12)

where abs(·) takes the absolute value (i.e., amplitude) of a complex value; B denotes the heart-rate band that eliminates the clearly non-pulsatile components, which is defined as [40, 240] beats per minute (bpm) according to the resolution of Fp(i); the denominator 1 prevents the boosting of noise when diving a very small value, i.e., the total energy is 1 after the normalization in (11). Afterwards, we use the weighting vector W(i) = [W(i, 1), W(i, 2), ..., W(i, n)] to weight and combine Fp(i) as:

$$\mathbf{Fh}=\sum _{i=1}^{4K}\mathbf{W}(i)\odot \mathbf{Fp}(i).$$ (13)

The combined frequency spectrum Fh is further transformed back to the time domain using the Inverse Discrete Fourier Transform (IDFT):

$$\mathbf{h}=\mathbf{IDFT}(\mathbf{Fh}),$$ (14)

where IDFT(·) denotes the IDFT operator. Consequently, we derive a long-term pulse-signal H by overlap-adding h (after removing its mean and normalizing its standard deviation) estimated in each short video interval using a sliding window (with one time-sample shift similar to [19]), and output H as the final pulse-signal.

The novelty of our method is using multiple weighting masks to replace the RoI detection and tracking in the existing rPPG systems, as a method to automate the measurement. In a DC-color stable environment (i.e., this assumption is valid in the use-cases where the video background does not constantly change the color in a short time-interval, such as the bed or incubator), we expect that the proposed method can continuously create relevant input signals for the rPPG extraction in a broader range of conditions than RoI detection and tracking can handle. Especially, we are thinking of common real-life situations as frontal/side face changes and associated loss of face features. We kept the algorithm as clean and simple as possible to highlight the essence of our idea and to facilitate the replication, although we recognize there are many ways to improve it, such as using better spectral clustering techniques, more advanced signal filtering methods, or multi-scale image processing techniques.

We also mention that the proposed system, in its current design/form, is particularly aimed at frequency-based pulse-rate measurement. The reason is that in the step of selecting the target-signal from parallel measurements (e.g., multiple skin-masks), we used the “spectral component selection” that selects a (or a few) component(s) showing strong pulsatile information in the frequency domain, which will attenuate the higher-harmonic information in the signal. This particular way of performing target selection is not suitable for instantaneous pulse-rate measurement (i.e., beat-per-beat or inter-beat interval manner). To support the beat-per-beat pulse-rate measurement, we suggest other alternatives for the step of target-signal selection, such as using Blind Source Separation based methods (PCA or ICA), which can preserve the details of the selected target-signal (e.g., pulse-rate variability, dicrotic notch, harmonics, etc.). Since the full-video pulse extraction is a generic concept for fully automatic monitoring, its sub-steps can be substituted by different options to fulfill specific needs in certain applications.

3. Experimental setup

This section presents the experimental setup for the benchmark. First, we introduce the benchmark dataset. Next, we present the evaluation metrics. Finally, we discuss the two rPPG frameworks used in the benchmark, i.e., one is the commonly used “face Detection - face Tracking - skin Classification” (DTC) and the other is the proposed FVP.

3.1. Benchmark dataset

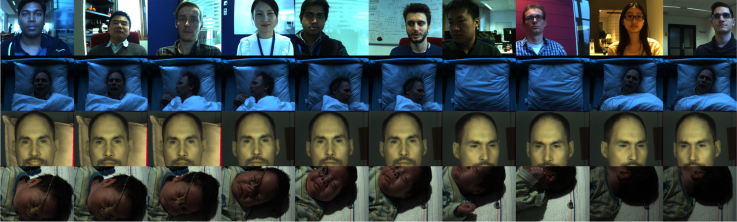
We create a benchmark dataset containing a total of 40 videos recorded in four different scenarios: sitting, sleeping, infrared and Neonate Intensive Cares Unit (NICU). Two camera setups are used for recordings: one is the regular RGB camera (Global shutter RGB CCD camera USB UI-2230SE-C from IDS, with 640 × 480 pixels, 8 bit depth, and 20 frames per second (fps)), and the other is the Near-Infrared (NIR) camera (Manta G-283 of Allied Vision Technologies GmbH, with 968 × 728 pixels, 8 bit depth, and 15 fps). All videos are recorded in an uncompressed bitmap format and constant frame-rate. The ground-truth for the sitting, sleeping and infrared experiments is the PPG-signal sampled by a finger-based transmissive pulse oximetry (Model CMS50E from ContecMedical), for the NICU experiment it is the ECG heart-rate. The ground-truth is synchronized with the video acquisition. A total of 22 subjects, with different skin-tones categorized from type-I to type-V according to the Fitzpatrick scale, participate in recordings. This study has been approved by the Internal Committee Biomedical Experiments of Philips Research, and informed consent has been obtained from each subject (or parents of infants). Below we introduce the four experimenting setups.

• Sitting setup The sitting experiment validates whether FVP can achieve an accuracy similar to DTC, assuming that this condition guarantees a perfectly functional DTC. The sitting experiment is not performed in the fixed lab environment as [19, 20], but randomly selected locations in an office building with uncontrolled illuminations and unpredictable backgrounds. The camera is placed around 1 m in front of the subject, which, with the used focal length, results in around 15 − 20% skin-area in a video frame. 10 subjects with different skin-types are recorded. Each subject sits relaxed in front of the camera without instructions to perform specific body motions, but he/she may have unintentional body motions such as the ballistocardiographic motion, respiration, cough, facial expression, etc. The illumination is a mixture of the ambient daylight and office ceiling light (fluorescent), without the frontal and homogeneous fluorescent illumination that is typical in a lab setup [19, 20]. The video background contains different static/moving colored objects (e.g., walking persons), depending on the (randomly) selected recording place. Figure 5 (top row) exemplifies the snapshots of recordings in the sitting experiment.

• Sleeping setup The sleeping experiment investigates the feasibility of using FVP for sleeping monitoring, i.e., a situation that DTC cannot cope with. The camera is positioned right above the pillow with a full view to the upper part of the bed. With the used focal length, the percentage of the skin-area in each video frame is around 10 − 25%. 12 subjects with different skin-types are recorded. The sleeping experiment is conducted in three scenarios with different illumination sources and bed sheet colors. In the first two scenarios, 6 subjects sleep in a (hospital) ceiling light condition and the other 6 subjects sleep in a daylight condition. In the third scenario, 1 subject sleeps on a bed with 6 different colored sheets (in the ceiling light condition), i.e., the hospital style, white, red, green, blue, and skin-similar colors. This is to verify whether FVP (i.e., weighting masks) is sensitive to different colored backgrounds. During the recording, each subject is instructed to (i) sleep with the frontal face to the camera for 1 minute, (ii) turn the body to sleep with the left-side face to the camera for 1 minute, (iii) turn the body again to sleep with the right-side face to the camera for 1 minute, (iv) exit the bed for 30 seconds, and (v) return back to sleep with a randomly selected posture for 1 minute (see the snapshots exemplified from a sleeping video sequence in the second row of Fig. 5.

• Infrared setup Since sleep monitoring is usually carried out at night, it is also important to investigate FVP in infrared. To this end, we perform recordings on 6 subjects with different skin-types using three separate Near-Infrared (NIR) cameras centered at 675 nm, 800 nm and 905 nm (i.e., the monochrome cameras with selected passband filters). To reduce the parallax between cameras (i.e., the displacement in the apparent position of an object viewed along different optical paths), the NIR cameras are placed around 4 m in front of the subject, which, with the used focal length, results in approximately 50 − 60% skin-area in a video frame. The illumination sources are two incandescent lamps that provide sufficient energy for the NIR-sensing range. Since the skin pulsatility in infrared is much lower than that in RGB (especially compared to the G-channel), the rPPG-signal measured in infrared is more vulnerable to motions. Also, the DC-color contrast between the skin and non-skin (especially the white pillow) is much lower in infrared than that in RGB, which may lead to less discriminative weighting masks for FVP. Thus our recordings include the challenges from the background and motion. During the recording, each subject is instructed to (i) lean the back of his/her head on a white pillow for 1 minute, (ii) sit still without the white pillow but with the dark background for 1 minute, and (iii) periodically rotate the head for 1 minute and 30 seconds. Figure 5 (third row) exemplifies the snapshots from an infrared video sequence, including the changed background and head rotation.

• NICU setup The neonatal monitoring is another interesting application scenario for FVP, as it can replace the skin-contact sensors that cause skin irritations and sleep disruptions to newborns. We use the videos recorded in the Neonate Intensive Cares Unit (NICU) (in Maxima Meidcal Center (MMC), Veldhoven, The Netherlands) to analyze FVP. One infant (with skin-type III) has been recorded by the RGB camera for multiple times with different settings, including different camera positions/view-angles (top-view or side-view), lighting conditions (ambient daylight or incandescent light), and infant sleeping postures. The infant has a gestational age of 32 ± 4 weeks and a postnatal age of 31 ± 23 days. The infant has uncontrolled body motions (e.g., screaming and scratching) and can even move out of the view of the camera during the recording (see the snapshots exemplified from a NICU recording in the bottom row of Fig. 5).

Fig. 5.

Snapshots of some recordings in the benchmark dataset, which show different challenges simulated in four setups.

3.2. Evaluation metric

We perform the quantitative statistical comparison between DTC and FVP in the sitting experiment, and the qualitative comparison between the ground-truth (PPG or ECG) and FVP in the other cases. The metrics used for the quantitative comparison are introduced below.

• Root-Mean-Square Error We use the Root-Mean-Square Error (RMSE) to measure the difference between the reference PPG-rate and the measured rPPG-rate per method per video. Both the PPG-rate and rPPG-rate are obtained in the frequency domain, using the index of the maximum frequency peak within the heart-rate band (e.g., [40, 240] bpm). Since the subject’s heart-rate is time-varying, we use a sliding window to measure the PPG-rate/rPPG-rate from short time-intervals (e.g., 256 frames (12.8 seconds)), and concatenate them into long PPG-rate/rPPG-rate traces for RMSE analysis. RMSE represents the sample standard deviation of the absolute difference between reference and measurement, i.e., larger RMSE suggests that the measurement is less accurate.

• Success-rate The “success-rate” refers to the percentage of video frames where the absolute difference between the reference PPG-rate and measured rPPG-rate is bound within a tolerance range (T). Similar to RMSE, the success-rate is analyzed on the PPG-rate/rPPG-rate traces. To enable the statistical analysis, we estimate a success-rate curve by varying T ∈ [0, 10] (i.e., T = 0 means completely match and T = 3 means allowing 3 bpm difference), and use the Area Under Curve (AUC) as the quality indicator, i.e., larger AUC suggests that the measurement is more accurate. Note that the AUC is normalized by 10 (the total area) and thus varies in [0, 1]. The AUC of success-rate is estimated per method per video.

• ANOVA The Analysis of Variance (ANOVA) is applied to the metric outputs of RMSE and success-rate (AUC) for DTC and FVP over all videos, which analyzes whether the difference between the two methods is significant. In ANOVA, the p-value is used as the indicator and a common threshold 0.05 is specified to determine whether the difference is significant, i.e., if p-value > 0.05, the difference is not significant. We expect DTC to perform well in the sitting experiment where RoI can always be detected and tracked. We do not expect FVP to outperform DTC in the sitting experiment. If their difference is insignificant, we may consider FVP as an adequate replacement for DTC.

In sleeping, infrared and NICU experiments that DTC cannot cope with, we use the spectrograms of PPG-signal and rPPG-signal or the ECG heart-rate signal for the qualitative comparison.

3.3. Compared methods

The FVP method proposed in this paper is an rPPG monitoring framework, which is compared to the commonly used framework of “face Detection [21] - face Tracking [22] - skin classification (by One-Class SVM) [6]” (DTC). In both frameworks, the core rPPG algorithm used for pulse extraction is selected as POS [19]. We mention that for fair comparison, the POS algorithm used in DTC is adapted to include the step of using the intensity-signal to suppress distortions in the rPPG-signal as is done in FVP. Both methods have been implemented in MATLAB and run on a laptop with an Intel Core i7 processor (2.70 GHz) and 8 GB RAM.

Since the window length used for suppressing intensity distortions influences the results of DTC and FVP, we define five groups of parameters to compare both methods in the sitting experiment: (i) L = 32 (1.6 s), B = [3, 6], (ii) L = 64 (3.2 s), B = [4, 12], (iii) L = 128 (6.4 s), B = [6, 24], (iv) L = 256 (12.8 s), B = [10, 50], and (v) L = 512 (25.6 s), B = [18, 100]. Note that the parameter is defined based on the consideration of a 20 fps video camera. For the sleeping, infrared and NICU experiments, we use the L = 128 (6.4 s) and B = [6, 24] by default setting, which we consider as a practical compromise between the robustness and latency.

We mention that the different time window lengths we used to verify the robustness of the proposed system is for pulse-signal generation, not for pulse-rate calculation. The frequency-based pulse-rates are all calculated from the final output pulse-signal H, using the fixed window length of 256 frames.

4. Results and discussion

This section presents the experimental results of the benchmarked methods. Tables 1–2 summarize the RMSE and success-rate (AUC) of DTC and FVP in the sitting experiment. Table 3 lists the ANOVA (p-value) of the values in Tables 1–2. Figures. 6–8 illustrate the qualitative comparison between the reference and FVP in the sleeping, infrared and NICU experiments.

Table 1.

Root Means Square Error (RMSE) of pulse-rate per method per video, as well as average and standard deviation (std) per method across all videos.

Video	L = 32		L = 64		L = 128		L = 256		L = 512
	DTC	FVP	DTC	FVP	DTC	FVP	DTC	FVP	DTC	FVP
1	0.46	2.59	0.49	0.86	0.53	1.84	0.65	0.92	0.98	1.19
2	0.89	1.17	1.22	1.21	1.69	1.35	1.71	1.04	2.13	2.16
3	0.33	7.82	0.33	0.50	0.44	0.50	0.46	0.55	0.60	0.62
4	3.10	23.08	3.09	6.18	3.08	3.39	3.08	3.09	3.24	3.19
5	0.55	14.37	0.56	2.54	0.64	2.37	0.82	0.90	0.86	0.86
6	2.24	2.55	0.97	0.89	1.81	1.58	1.51	1.02	1.19	1.17
7	0.45	0.63	0.50	0.62	0.69	0.73	0.68	0.66	1.04	1.02
8	0.41	0.65	0.60	0.71	0.58	0.72	0.73	0.80	1.03	0.99
9	0.32	2.01	0.43	1.44	0.58	0.83	0.67	0.66	0.84	0.87
10	0.44	0.52	0.42	0.51	0.47	0.49	0.62	0.59	0.72	0.72
Average	0.92	5.54	0.86	1.55	1.05	1.38	1.09	1.02	1.26	1.28
Std	0.91	7.16	0.79	1.65	0.83	0.90	0.77	0.71	0.77	0.75

* Smaller RMSE suggests better measurement.

Table 2.

Success-rate (AUC) of pulse-rate per method per video, as well as average and standard deviation (std) per method across all videos.

Video	L = 32		L = 64		L = 128		L = 256		L = 512
	DTC	FVP	DTC	FVP	DTC	FVP	DTC	FVP	DTC	FVP
1	0.99	0.91	0.99	0.97	0.99	0.93	0.98	0.97	0.96	0.95
2	0.98	0.98	0.97	0.97	0.96	0.97	0.94	0.97	0.92	0.92
3	0.99	0.97	0.99	0.99	0.99	0.99	0.99	0.99	0.98	0.98
4	0.91	0.59	0.92	0.85	0.92	0.86	0.92	0.88	0.91	0.90
5	0.99	0.80	0.98	0.94	0.98	0.95	0.97	0.96	0.97	0.97
6	0.96	0.94	0.99	0.98	0.97	0.97	0.96	0.97	0.95	0.95
7	0.99	0.98	0.99	0.98	0.98	0.97	0.98	0.98	0.96	0.96
8	0.99	0.98	0.98	0.98	0.98	0.97	0.98	0.97	0.96	0.96
9	0.99	0.95	0.99	0.96	0.98	0.97	0.98	0.98	0.97	0.97
10	0.99	0.99	0.99	0.99	0.99	0.99	0.98	0.98	0.98	0.98
Average	0.98	0.91	0.98	0.96	0.97	0.96	0.97	0.96	0.95	0.95
Std	0.02	0.12	0.02	0.04	0.02	0.04	0.02	0.03	0.02	0.02

*Lager AUC of success-rate suggests better measurement.

Table 3.

ANOVA test (p-value) between DTC and FVP over all videos per parameter setting.

Evaluation metric	L = 32	L = 64	L = 128	L = 256	L = 512
	DTC & FVP	DTC & FVP	DTC & FVP	DTC & FVP	DTC & FVP
RMSE	0.07	0.28	0.43	0.84	0.97
Success-rate (AUC)	0.09	0.22	0.27	0.74	0.86

*Larger p-value suggests less significant difference between DTC and FVP. If p-value > 0.05, the difference between DTC and FVP is considered to be insignificant.

Fig. 6.

The spectrograms obtained by the PPG reference and FVP in the sleeping experiment. This experiment includes three different sleeping scenarios. The white dash lines in the spectrograms of the sleeping scenario 1–2 indicate the time-slot of bed exit. The X- and Y- axes of the spectrogram denote the time (video frame index) and frequency (bpm).

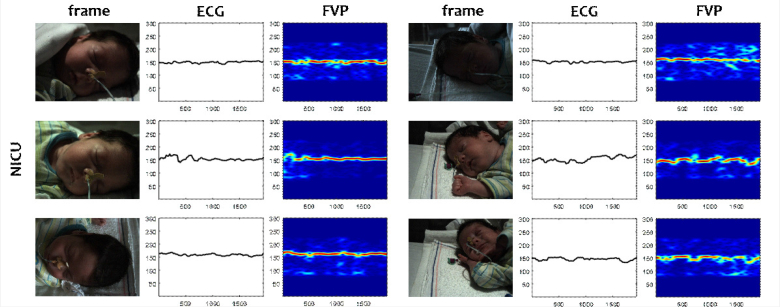
Fig. 8.

The ECG heart-rate traces and spectrograms of FVP in the NICU experiment. The X- and Y- axes of the spectrogram denote the time (video frame index) and frequency (bpm).

Tables 1–2 show that on average the performance of FVP tends to be worse than DTC for the short window analysis, but about equal at larger sizes. The DTC performance is almost independent of size, roughly speaking having an RMS of about 1 bpm. FVP is more sensitive to the size: its optimal performance (over the considered sizes) is at 256 where it also attains an average RMS of 1 bpm. It is also obvious that there is a considerable spread in performance over videos within each method. The ANOVA test suggests that DTC and FVP are almost significantly different at the smallest analysis size, but not at all at larger sizes. Looking at the results obtained by FVP at shorter L, we notice that it is particularly the videos 4 and 5 which affect the accuracy. These two videos are characterized by rather low pulse-rates (around 48 − 52 bpm) and this may merit more attention in future improvement of the FVP.

Figure 6 shows that FVP can continuously measure the heart-rate of a subject during the sleep, even in case that the subject changes sleeping posture or leaves the bed for a while. This application scenario is unsuited for DTC since it relies on the RoI localization and this may fail when the pre-trained (frontal) face is invisible in a sleeping posture, or the RoI tracking may drift when the subject leaves the bed and returns back to sleep. Figure 6 also shows that FVP works with different illumination conditions such as the fluorescent ceiling light and ambient daylight. The reason for this observed insensitivity to illumination stems from two aspects: weighting mask generation and pulse extraction. Due to the use of both the mean and variance for spatial pixel combination, the requirements for the weighting masks are less critical, i.e., the weighting masks do not need to be very discriminative in skin/non-skin separation. Their main function is providing a robust way to concatenate the spatial values for temporal pulse extraction. This is further confirmed by the experiments with different colored bed sheets, especially the skin-similar bed sheet.

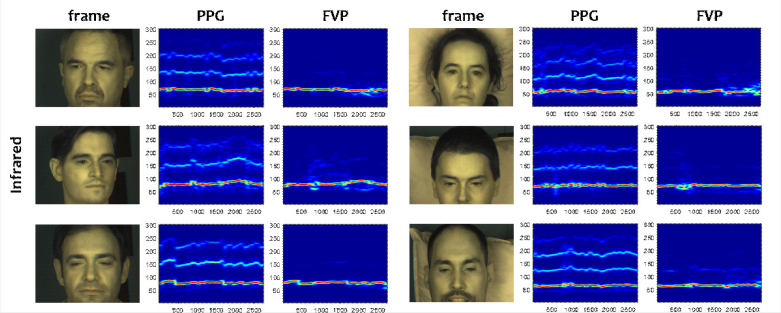
Figure 7 shows that FVP can be used in infrared as well. It measures a heart-rate trace that is very close to the reference, even with different backgrounds or head motions. From the exemplified snapshots, we see that the color of the used white pillow is very similar to that of the skin in infrared, although it would still be possible for FVP to use the water absorption contrast at 905 nm to differentiate skin and pillow (see Fig. 2). Also, as mentioned earlier, FVP is more tolerant to the color contrast due to the use of both the mean and variance for spatial pixel combination. We observe that during the episode (at around 800 frame) that the background is completely changed (i.e., removal of the white pillow), FVP suffers from distortions. This is to be expected since the hypothesis in the design is the background stability. We note, however, that the experimentally introduced background change is intentionally large, and thus atypical for real sleep monitoring situations. During the episode of head rotation (after 1800 frame), FVP continues to measure a reasonably clean heart-rate trace, except for the top-right displayed subject whose motion is severe at the end of the recording.

Fig. 7.

The spectrograms obtained by the PPG reference and FVP in the infrared experiment. The X- and Y- axes of the spectrogram denote the time (video frame index) and frequency (bpm).

Figure 8 shows that FVP is also feasible for neonatal monitoring, although it is more challenging than adult monitoring. The main challenge is that newborns have much lower skin pulsatility than adults, which could be related to the small/underdeveloped cardiac systems or soft blood vessels. Besides, neonates have more abrupt and uncontrolled body-motions like crying, which further degrades the accuracy of FVP. Nevertheless, the examples show that the pulse-rate can be monitored most of the time during sleep, having a relatively stable performance in different lighting conditions, sleeping postures and camera views.

5. Conclusion

We have introduced a new method to automate the heart-rate monitoring using remote photoplethysmography (rPPG). The method replaces Region of Interest (RoI) detection and tracking and does not require initialization. Instead it produces a set of masks that weight the video images in various manners, and extracts and combines candidate pulse-signals from different weighted images to derive the heart-rate. The method is based on the observation that the DC-colors of skin and background are usually quite stable over time in typical application-scenarios, such as monitoring of a subject sleeping in bed, or an infant in an incubator. The resulting system, called Full Video Pulse extraction (FVP), is compatible with all existing core rPPG algorithms and allows the direct use of raw video streams for pulse extraction, eliminating the steps of RoI initialization, detection and tracking from earlier systems. Our benchmark set of diverse videos shows the feasibility of using FVP for sleep monitoring in visible light and in infrared, for adults and neonates. Although we only demonstrated the concept for heart-rate monitoring, we foresee that it can be adapted to detect alternative vital signs, which will benefit the larger video health monitoring field.

Appendix

Dependence of mean and variance on the blood perfusion

In practical situations, it is virtually impossible to make a clear cut distinction between skin and non-skin parts in the image. Typically, setting a high specificity results in loss of many pixels or areas that could have provided valuable information, while setting a high sensitivity for skin typically results in many non-skin area thereby diluting the information of interest. This incapability of striking a correct balance is the underlying notion in the mask generation as it simply refutes the idea of hard boundaries. The consequence is that the further processing needs to handle both the relatively clean RoIs (or proper weighting masks) and rather polluted situations. This ability is attained by using both the mean and variance as statistical values of the RoI or weighted images, i.e., the common approaches use the mean as a source of information only.

We will show that mean and variance have complementary strengths as input signal to a core rPPG algorithm. To simplify the illustration, we prove this for the single channel case. But the conclusions carry over to multi-channel situations.

Consider the task of pulse extraction that each pixel in an image can be described as either skin or non-skin. Thus we have skin and non-skin distributions in an image. Assume further two statistical models for either case with Probability Density Function (PDF) p_o(x), and associated mean μ_o and standard deviation σ_o where x denotes the signal strength (color intensity) and o is either skin s or background b. Suppose furthermore that the full image has a fraction f_o of either pixels (implying f_s + f_b = 1). The composite image pixel PDF p(x) can be written as:

$$p(x)=f_s\cdot p_s(x)+f_b\cdot p_b(x).$$ (15)

The mean of x is:

$$\mu =𝔼(x)=f_s\cdot 𝔼[x_s]+f_b\cdot 𝔼[x_b]=f_s\cdot {\mu }_s+f_b+{\mu }_b,$$ (16)

where 𝔼[·] denotes the expectation. The variance of x is:

$${\sigma }^2=𝔼[x^2]-{\left(𝔼[x]\right)}^2=f_s\cdot 𝔼[x_s^2]+f_b\cdot 𝔼[x_b^2]-{\left(f_s\cdot {\mu }_s+f_b\cdot {\mu }_b\right)}^2.$$ (17)

We know that for x_o (including the skin and non-skin), 𝔼[x_o] = μ_o and $𝔼[{(x_o-{\mu }_o)}^2]={\sigma }_o^2$. Thus $𝔼\left[x_o^2\right]$ can be expressed as:

$$𝔼[x_o^2]=𝔼{[(x_o-{\mu }_o+{\mu }_o)]}^2=𝔼[{(x_o-{\mu }_o)}^2]+2{\mu }_o\cdot 𝔼[x_o-{\mu }_o]+𝔼[{\mu }_o^2]={\sigma }_o^2+{\mu }_o^2.$$ (18)

Therefore, we can rewrite (17) as:

$$\begin{array}{ll}{\sigma }^2\hfill & =f_s\cdot \left({\sigma }_s^2+{\mu }_s^2\right)+f_b\cdot \left({\sigma }_b^2+{\mu }_b^2\right)-{\left(f_s\cdot {\mu }_s+f_b\cdot {\mu }_b\right)}^2\hfill \\ \hfill & =f_s\cdot {\sigma }_s^2+f_b\cdot {\sigma }_b^2+f_s\cdot {\mu }_s^2+f_b\cdot {\mu }_b^2-{\left(f_s\cdot {\mu }_s+f_b\cdot {\mu }_b\right)}^2\hfill \\ \hfill & =f_s\cdot {\sigma }_b^2+f_b\cdot {\sigma }_b^2+f_s\cdot f_b\cdot {\left({\mu }_s-{\mu }_b\right)}^2.\hfill \end{array}$$ (19)

Now we assume that the mean skin-level is modulated by the blood perfusion. μ_s is expressed as the combination of a steady DC-component and a time-dependent AC-component:

$${\mu }_s={\overline{\mu }}_s+\tilde{\mu }(t),$$ (20)

where ${\overline{\mu }}_s$ is the steady DC component and μ̃ is the time-varying AC component. We furthermore assume that the background statistics are constant (i.e., we have means such as a weighting mask to attenuate the background) and we neglect all modulations in the variance of the skin.

Therefore, the full image mean in (16) can be rewritten as:

$$\mu =f_s\cdot \left({\overline{\mu }}_s+\tilde{\mu }(t)\right)+f_b\cdot {\mu }_b=f_s\cdot {\overline{\mu }}_s+f_b\cdot {\mu }_b+f_s\cdot \tilde{\mu }(t),$$ (21)

and the full image variance in (19) can be rewritten as:

$$\begin{array}{ll}{\sigma }^2\hfill & =f_s\cdot {\sigma }_s^2+f_b\cdot {\sigma }_b^2+f_s\cdot f_b\cdot {({\overline{\mu }}_s+\tilde{\mu }(t)-{\mu }_b)}^2=f_s\cdot {\sigma }_s^2+f_b\cdot {\sigma }_b^2+\hfill \\ \hfill & f_s\cdot f_b\cdot ({({\overline{\mu }}_s+{\mu }_b)}^2+2({\overline{\mu }}_s-{\mu }_b)\cdot \tilde{\mu }(t)+{\tilde{\mu }}^2(t))\hfill \\ \hfill & \approx f_s\cdot {\sigma }_s^2+f_b\cdot {\sigma }_b^2+f_s\cdot f_b\cdot {({\overline{\mu }}_s-{\mu }_b)}^2+2f_s\cdot f_b\cdot ({\overline{\mu }}_s-{\mu }_b)\cdot \tilde{\mu }(t),\hfill \end{array}$$ (22)

where μ̃² can be ignored in the approximation, as the squared pulsatile changes are orders of magnitude smaller than other DC-related components.

Consequently, we find that the pulsatile components in the full image mean and full image variance are:

$$\{\begin{array}{l}\hat{\mu }=f_s\cdot \tilde{\mu }(t),\\ {\hat{\sigma }}^2=2f_s\cdot (1-f_s)\cdot ({\overline{\mu }}_s-{\mu }_b)\cdot \tilde{\mu }(t).\end{array}$$ (23)

As expected, if f_s = 0 (no skin), there is no pulsatile component in either statistical variable. We further observe that the pulse-contribution to the mean is a linearly decreasing function of f_s, i.e., the fraction of skin-pixels. In other words, with less skin-pixels also less pulsatile amplitude contained in the mean. The variance shows another behavior as the function of the skin fraction. It contains no pulsatile component in both extreme cases (all skin or all background) but peaks in the middle assuming at least some contrast between skin and background: ${\overline{\mu }}_s$ − μ_b ≠ 0. The previous indicates that dependent on the fraction f_s and contrast, there may be more pulsatile information in the variance than in the mean. This is actually the underlying explanation of the experimental findings illustrated in Fig. 4. When the RoI is dominated by skin-pixels, the mean-signal reflects the blood volume changes in a better way (i.e., the signal is less noisy). When the RoI contains certain amount of non-skin pixels, the variance-signal shows much clear pulsatile variations. Therefore, the use of the variance next to the mean as an input to an rPPG algorithm is valuable in all cases, since it cannot be assumed that the RoI contains only skin.

Funding

The Philips Research and Eindhoven University of Technology (10017352).

Disclosures

The authors declare that there are no conflicts of interest related to this article.