Visible-light optical coherence tomography oximetry based on circumpapillary scan and graph-search segmentation

Abstract

Visible-light optical coherence tomography (vis-OCT) enables retinal oximetry by measuring the oxygen saturation of hemoglobin (sO₂) from within individual retinal blood vessels. The sO₂ calculation requires reliable estimation of the true spectrum of backscattered light from the posterior vessel wall. Unfortunately, subject motion and image noise make averaging from multiple A-lines at the same depth position challenging, and lead to inaccurate sO₂ estimation. In this study, we developed an algorithm to reliably extract the backscattered light’s spectrum. We used circumpapillary scanning to sample the vessels repeatedly at the same location. A combination of cross-correlation and graph-search based segmentation extracted the posterior wall locations. Using measurements from 100 B-scans as a gold standard, we demonstrated that our method achieved highly accurate measures of sO₂ with minimal bias. In addition, we also investigated how the number of repeated measurements affects the accuracy of sO₂ measurement. Our method sets the stage for large-scale studies of retinal oxygenation in animals and humans.

1. Introduction

Visible-light optical coherence tomography (vis-OCT) adds functional information to OCT, such as providing oxygenation measurements in the living retina [1, 2]. Vis-OCT measures the oxygen saturation of hemoglobin (sO₂) – the percentage of oxygen-bound hemoglobin binding sites – from within individual blood vessels. Dysfunctions in oxygen supply and demand have been hypothesized as key contributors to a number of retinal diseases, including diabetic retinopathy, retinopathy of prematurity, retinal vascular occlusions, and glaucoma [3]. In animal model studies of these diseases, vis-OCT can potentially help to elucidate key time-points and pathogenic mechanisms of disease models [4, 5]. In human studies and patient imaging [6, 7], vis-OCT may eventually identify oxygenation related biomarkers that correlate with progression of disease or a response to treatment.

Retinal oximetry with vis-OCT is based upon spectroscopic OCT [8, 9]. In spectroscopic OCT, the spectral interferogram is divided into sub-bands, which are individually processed to produce a set of reduced axial-resolution images. In comparison, conventional OCT uses the entire band of the spectral interferogram to form a single, high axial-resolution image. Although the axial-resolution is sacrificed in spectroscopic OCT, each image corresponds to a different wavelength band, giving the spectrum of the backscattered light that conventional OCT does not provide. The spectrum of the backscattered light can be used to calculate sO₂ by fitting it against a model of light attenuation [10].

A visible-light source is necessary for measuring sO₂ with spectroscopic OCT. Previous studies have typically used supercontinuum light sources with a spectral range between 500 nm and 650 nm. Using visible-light is more advantageous than near-infrared light for three major reasons [2]. First, the shapes of the absorption spectra of oxygenated and deoxygenated hemoglobin (HbO₂ and DeHb) are more distinctive in the visible region, as there are more isosbestic points in the visible regime than in the NIR. Second, the absorption coefficient of Hb in the visible spectral range is ~2 orders of magnitude higher than that in the NIR spectral range. Third, the absorption coefficients in the visible region are around two times higher than the reduced scattering coefficients. Comparisons between visible and NIR oximetry measurements with OCT have been performed in silico, with Monte Carlo simulations [11], and in vivo, with a dual-band (visible and NIR) OCT system [12]. Both studies found superior performance for oxygenation measurements in the visible regime.

Reliable estimation of the backscattered light’s true spectrum often requires averaging the OCT signal from the same depth location across multiple A-lines. Averaging is necessary for two major of reasons. First, from a hardware perspective, supercontinuum light sources suffer from increased relative intensity noise (RIN) compared to superluminescent diodes [13]. Second, from an experimental perspective, breathing motion distorts the OCT volume. In human imaging, saccades and eye movement can also contribute to motion. These noise sources increase the variance of the OCT signal, making the true estimation of the backscattered light spectrum challenging with a small sample of A-lines. Averaging schemes vary in the literature. Previously, Yi et al. and Chen et al. averaged the spectra from A-lines within the entire vessel [10, 14]. Pi et al. recently also used a similar approach [15]. Depending on the scanning density and the size of the vessel, this results in averages using hundreds of A-lines. A downside of this approach is that different locations within a vessel may not have the same sO₂, especially in diseased eyes. Another scanning method is to repeat B-scans at each location to obtain several A-lines for averaging. For example, Chong et al. used 100 B-scans for cerebral sO₂ measurements in rodents [16]. Unfortunately, this method adds time to the experimental process and is not feasibly for clinical retinal imaging.

Here, we present a retinal oximetry algorithm using vis-OCT, which solves the averaging problem using graph-search segmentation of the vessel wall. Graph-search algorithms have been used to solve a multitude of image processing problems in OCT, including retinal layer segmentation [17–19], lumen segmentation [19], and photoreceptor segmentation [20]. We show that graph-search segmentation can be used to simultaneously help with two key tasks: (1) locating the vessel wall to extract the backscattered spectrum and (2) increasing the accuracy of the OCT signal when there is axial motion. Instead of performing retinal raster scans to calculate sO₂, we focused this study on extracting sO₂ from circumpapillary scans [21]. This scanning technique repeatedly scans vessels at the same location on the retina, which reduces error and bias that may arise when averaging OCT signals along the length of a vessel. After presenting an overview of our algorithm, we define each step in detail. Finally, we address the question of how much averaging is required to obtain accurate results, by taking samples of our data set and analyzing the accuracy, precision, and bias of our measurements for different sample sizes.

2. Materials and methods

2.1 Animal preparation

All experimental procedures were approved by the Northwestern University IACUC and conformed to the Association for Research in Vision and Ophthalmology (ARVO) Statement on Animal Research. Our anesthesia protocol had two steps. First, we temporarily anesthetized adult Brown Norway rats (n = 2) with 3% isoflurane for 3 minutes, which enabled them to be easily and safely handled. Second, we took them off isoflurane and administered an intramuscular injection of a ketamine and xylazine cocktail (ketamine: 0.37 mg/kg; xylazine: 0.07 mg/kg). The rat was then placed on a custom-made animal holder for imaging. A pulse oximeter was attached to the right rear paw to monitor peripheral arterial sO₂ and heart rate. The body temperature was maintained with a heat lamp. We applied a drop of 1% tropicamide hydrochloride ophthalmic solution to dilate the pupil. To prevent corneal dehydration, we applied commercial artificial tears after taking each image.

2.2 Algorithm overview

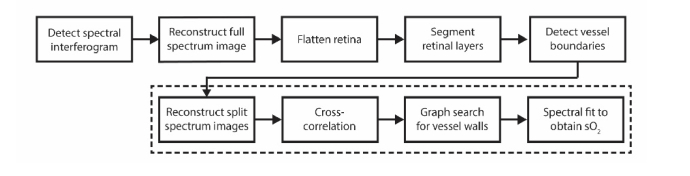
Figure 1 shows a flowchart of the automatic retinal oximetry algorithm. Spectral interferograms were first processed by full-spectrum reconstruction. We flattened the retina, segmented the major layers of interest, and automatically detected the vessels. We then performed split-spectrum reconstruction for each segmented vessel. We aligned the A-lines in each vessel’s B-scan using cross-correlation. To segment the boundaries of the vessel wall, we used a directional graph-search. Finally, to obtain the sO₂ in a vessel, we fit the average spectrum from the vessel wall to a previously described modified Beer’s law model [10]. All data processing was implemented in MATLAB (MathWorks, Inc., version 2017b)

Fig. 1.

Overview of the retinal oximetry algorithm. The dashed box indicates steps of the algorithm that were performed for each vessel.

2.3 OCT data acquisition

We acquired images with a dual-band vis-OCT system, which was reported previously [12]. We made two minor modifications to the system. First, we changed the 50/50 cube beam splitter to a 30/70 (sample/reference arm) cube beam splitter for increased sample arm collection efficiency. Second, to increase our field-of-view, the Keplerian telescope was modified to a 6:1 magnification (previously 5:1), using a pair of 150 mm and 25 mm achromatic lenses. In addition to the larger magnification, these lenses had a 1-inch diameter (previous 0.5 inch), enabling a larger scanning angle from the galvanometers to be used without image distortion from the lens edges. We kept all the other components, including the light source, custom-built spectrometer, and polarization controller, from the previously reported design. Illumination power at the pupil was ~1 mW.

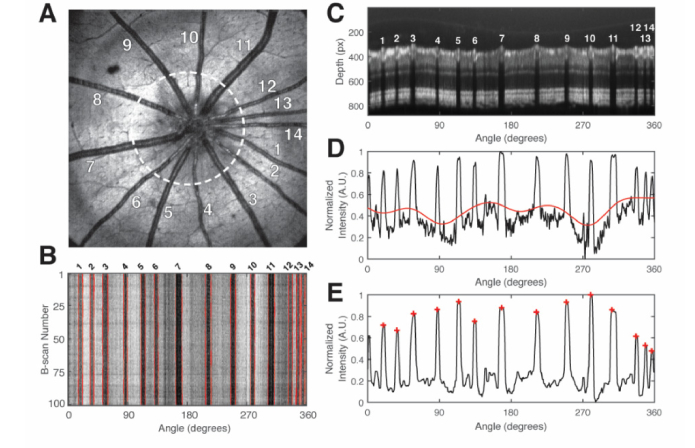
We acquired raster scans solely for visualizing the optic nerve head and positioning the animal. We performed circumpapillary scans for our retinal oximetry measurements. Because circumpapillary scans sample the vessel at the same location, any biases or errors from sampling sO₂ at different vessel locations were reduced. Figure 2(A) shows the en face of an example raster scan. The white dashed circle indicates the clockwise circular path of the circumpapillary scan on the retina. The white numbers indicate the vessel identification number. The circumpapillary scan diameter on the retina was approximately ~1.5 mm, assuming a rat eyeball length of ~6.3 mm.

Fig. 2.

Vessel detection procedure. (A) En face raster scan of an adult rat retina. The white dashed circle indicates the approximate path of the circumpapillary scan on the retina. Numbers 1-14 identify the fourteen vessels; (B) En face of the circumpapillary scan OCT volume. Numbers 1-14 correspond to the vessels in A; (C) Average vis-OCT B-scan of the flattened circular scan volume. Numbers 1-14 correspond the numbers in A and B. Depth pixel size: 0.55 μm; (D) Black line indicates the two-dimensional shadowgram, calculated from C. Red line indicates the baseline, after low pass filtering; (E) Black line indicates the shadowgram after baseline subtraction and median filtering. Each red-cross indicates a peak corresponding to a vessel.

Raster scans consisted of 512 B-scans with 512 A-lines per B-scan, covering an area of ~4.1 mm by 4.1 mm on the retina. The spectrometer integration time per A-line was 37 μs, which corresponded to an A-line rate of 25 kHz. Total imaging time was ~10.5 seconds. Circumpapillary scans consisted of 100 B-scans with 8192 A-lines per B-scan. The spectrometer integration time per A-line was 17 μs, which corresponded to an A-line rate of 50 kHz. Total imaging time was ~16 seconds. Here, the higher A-line rate will eventually allow the calculation of blood flow using Doppler OCT in future work. Henceforth, a circumpapillary scan and B-scan may be used interchangeably, as we will only be referring to B-scans as scans from circumpapillary data sets.

2.4 Full spectrum reconstruction

For full-spectrum reconstruction, we performed standard OCT signal processing for a spectrometer-based OCT system, which included background subtraction, reference arm normalization, numerical dispersion compensation, and k-space resampling. Data processing was performed on a graphics processing unit (NVIDIA, GTX 980).

2.5 Retinal flattening

The retina in circumpapillary scans can often appear S-shaped due to the alignment of the beam not being perfectly centered at the pupil plane. To remove this artifact, we performed retinal flattening. To flatten the retina, we computed the center of mass for each A-line to obtain the approximate center location of the retina. The center of mass position was used as an upper boundary to restrict a light-to-dark graph search for the RPE layer (see section 2.6). The position of the RPE was recorded and then fitted to a 3D polynomial [22]. Each A-line was then shifted to the fit to obtain a flattened volume. The flattening procedure reduced axial motion between B-scans and removed curvature from the circumpapillary scans.

2.6 Layer segmentation

We implemented the retinal layer segmentation algorithm outlined previously with slight modifications [17]. Briefly, a two-dimensional graph was constructed, where each B-scan pixel was represented by a node. Each node had a weight, which was calculated using the weight equation reported by Chiu et al. [17]. Connections between nodes were constructed in a directional pattern to save processing time [22]. Each node was connected to the node directly adjacent to it on the right, and to 2 nodes above and below in the adjacent column to the right. Boundaries for the retinal layers were searched from left to right using Dijkstra’s algorithm. The order of the retinal layers searched, the regional restrictions on the graph search, and the type of gradient used for the search (i.e. light-to-dark vs. dark-to-light) were modified from Srinivasan et al. for rat data [18]. To further reduce processing time, we downsampled each circumpapillary B-scan from 8192 A-lines to 512 A-lines by averaging laterally 8 times. After retinal layer segmentation, we upsampled the boundaries back to the original B-scan dimensions.

2.7 Vessel detection

Figure 2 illustrates the vessel detection procedure, which determined the vessel boundaries and vessel center positions in the circumpapillary scan. The coordinates of the vessel wall were determined in a later step (see section 2.9). Figure 2(A) shows the en face of the raster scan. Fourteen retinal vessels were marked (white numbers). A 100 circumpapillary scans were acquired (white dashed line). Figure 2(B) shows an en face of the circumpapillary scan volume. Each of the vertical dark bars is reflectance from a retinal vessel in Fig. 2(A).

Vessels were detected by creating a one-dimensional shadowgram from each B-scan. Figure 2(C) shows an average of the all the B-scans with the vessels numbered. First, A-line signals below the inner nuclear layer-outer plexiform layer (INL-OPL) boundary layer were averaged. Next, the shadowgram was then inverted and normalized (black line in Fig. 2D). To remove the baseline, the shadowgram was filtered with a moving average of 100 pixels, which gave a measure of the baseline (red line in Fig. 2D). Finally, a median filter was applied to reduce the noise, while preserving the shape of the peaks (black line in Fig. 2E). Peaks were detected in the shadowgram signal using the ‘findpeaks’ method in MATLAB (red crosses in Fig. 2E).

We generated shadowgrams for each B-scan and tracked the vessels using the peak-finding method. To find the boundaries of the vessel, we searched for the full-width at half-maximum to the left and right of each peak. The center of the vessel was determined by finding the center position of the full-width. The boundaries for the vessels identified in Fig. 2(A) are delineated by the red lines in Fig. 2(B).

2.8 Split-spectrum reconstruction

To perform spectroscopic OCT, we windowed the spectral interferogram in k-space and took the Fourier Transform. This procedure is often referred to as the short-time Fourier Transform, but a more appropriate name would be the short-k Fourier Transform. Here we simply refer to this procedure as spectral splitting. We applied 23 Gaussian windows with center wavelengths (${\lambda }_c$) ranging from 525 nm to 591 nm, equidistantly spaced by 3 nm. The FWHM in the $\lambda$-space was 13 nm (0.25 μm⁻¹ in k-space), which gave an axial resolution in air of 10.9 μm at 568 nm. These values were consistent with those used previously by Chen et al. [6].

To save on memory and computation time, we only performed spectral splitting on A-lines within the segmented vessels. After the spectral splitting procedure, each vessel was associated with a four-dimensional data set with dimensions of depth, radial position (angle), B-scan number, and ${\lambda }_c$. In order to reduce the dimensionality of the data and improve the signal-to-noise ratio, we compressed the data set along the radial position dimension by averaging the 6 center A-lines of a vessel. The final spectroscopic OCT image for each vessel has three dimensions: depth, B-scan number, and ${\lambda }_c$.

2.9 Cross-correlation

Even after retinal flattening, the spectroscopic OCT images had inter-B-scan motion. In addition, graph-search segmentation techniques are more biased towards straight paths [17]. Therefore, B-scans had to be aligned using a cross-correlation procedure. Unfortunately, vis-OCT images obtained with supercontinuum sources have a higher noise floor with a pink noise characteristic [6, 13]. We found that this noise floor can reduce the performance of cross-correlation. To solve this problem, we estimated the noise floor by fitting the first and last 50 pixels of an averaged A-line to a 2nd-degree polynomial. We then subtracted this fitted noise floor from each B-scan before cross-correlation. The cross-correlation step was performed using a sub-pixel shift registration algorithm [23].

2.10 Vessel wall segmentation with graph-search

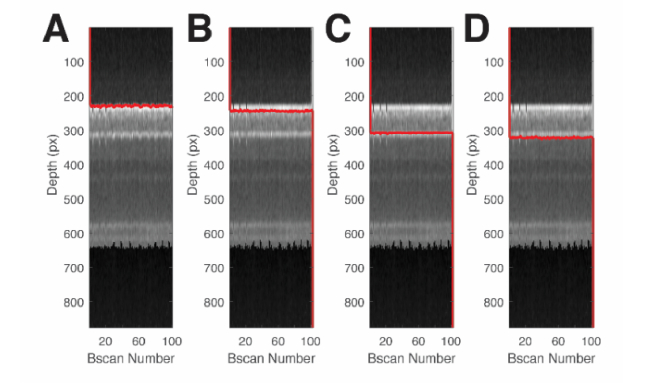
The same graph-search design and framework from section 2.6 was applied to segment the vessel walls. Figure 3 shows example of graph-search based segmentation of a vessel cross-section for a selected vessel. The images shown is the final spectroscopic OCT image for the vessel, but averaged over the ${\lambda }_c$ dimension. We searched for the vessel wall boundaries from the anterior portion of the retina towards the posterior. First, we found the top and bottom of the anterior wall (Fig. 3(A)-(B)). Next, we searched for the top and bottom of the posterior wall (Fig. 3(C)-(D)). Table 1 shows the search limits and weight type used for each graph cut.

Fig. 3.

Graph-search segmentation for the anterior and posterior vessel walls. (A) Segmentation of the top of the anterior wall. (B) Segmentation of the bottom of the anterior wall. (C) Segmentation of the top of the posterior wall. (D) Segmentation of the bottom of the posterior wall. Each column shows the vessel cross-section obtained from a circular B-scan. Pixel dimension in the depth direction was approximately 0.55 μm assuming a refractive index of retinal tissue, n = 1.35.

Table 1. Vessel wall segmentation parameters.

	Upper Limit	Lower limit	Weight Type
Top of anterior wall	0 μm from ILM	2 μm from ILM	Dark to Light
Bottom of anterior wall	1 μm from top of anterior wall	11 μm from top of anterior wall	Light to Dark
Top of posterior wall	10 μm from bottom of anterior wall	80 μm from bottom of anterior wall	Dark to Light
Bottom of posterior wall	1 μm from bottom of anterior wall	11 μm from bottom of posterior wall	Light to Dark

2.11 Spectral fitting

The OCT amplitude for the posterior wall was averaged between the segmented boundaries found using graph search. The averaged OCT amplitude was then fit to the oxygenated and deoxygenated hemoglobin attenuation coefficients, using the model originally proposed by Yi et al [10]. We set the W-factor to 0.2, consistent with Monte Carlo simulations performed by Chen et al. [11]. Attenuation coefficients were obtained from Faber et al. [24]. All twenty-three bands were used in the fitting process. For each fit, we calculated the coefficient of determination (R²) to measure the goodness-of-fit.

2.12 Accuracy, bias, and precision

The 100 B-scans in each circumpapillary scan are time consuming to acquire in practice. However, our goal was to use this large number of B-scans to study how the accuracy, bias, and precision of OCT amplitude extraction and sO₂ measurements vary with the number of B-scans used. To study this, we divided the 100 B-scans into N samples of M B-scans, where M ranged from 1 to 99. B-scans were selected for each sample in sequential order. For example, to study measurements from 2 B-scans, sample #1 would have B-scans #1 and #2. Sample #2 would have B-scans #2 and #3, and so on. Given M B-scans, N was equal to M-1. This method effectively simulates acquiring an image with M B-scans and using only that data to calculate sO₂.

Accuracy is the error of measurements compared to a gold standard (GS) reference measurement. Accuracy can be quantified by the root mean square error (RMSE) of N samples [25]. We chose our gold standard reference measurement to come from the best-case scenario from our data: the OCT amplitude and sO₂ measured with manual segmentation from 100 B-scans. The RMSE using M B-scans is defined as [25]:

$${\mathit{\text{RMSE}}}_M={\left[\frac{1}{N}{\displaystyle \sum }_{n=1}^N{\left(s{O}_{2;M,n}-s{O}_{2;GS}\right)}^2\right]}^{1/2},$$ (1)

where $s{O}_{2;GS}$ is the sO₂ measured from 100 B-scans with manual segmentation. $s{O}_{2;GS}$ is the sO₂ measured from n^th sample using M B-scans. Bias indicates whether the error is consistently negative or positive compared to the gold standard. The mean error (ME) defined in Eq. (2) gives a measure of the bias [25]

$$M{E}_M=\frac{1}{N}{\displaystyle \sum }_{n=1}^N(s{O}_{2;M,n}-s{O}_{2;GS}),$$ (2)

Precision is the spread of repeated measurements around their mean value. The standard. deviation (SD) of N samples gives a measure of the precision [25].

$$S{D}_M={\left[\frac{1}{N}{\displaystyle \sum }_{n=1}^N{(s{O}_{2;M,n}-\overline{s{O}_{2;M,N}})}^2\right]}^{1/2},$$ (3)

where $\overline{s{O}_{2;M,N}}$ denotes the average value of sO₂ obtained from N samples with M B-scans per sample. Note that sO₂ is a dimensionless value between 0 and 1, and the measures of accuracy, bias, and precision defined here are in the same units as the sO₂.

3. Results

3.1 Comparison of methods for OCT amplitude spectra extraction

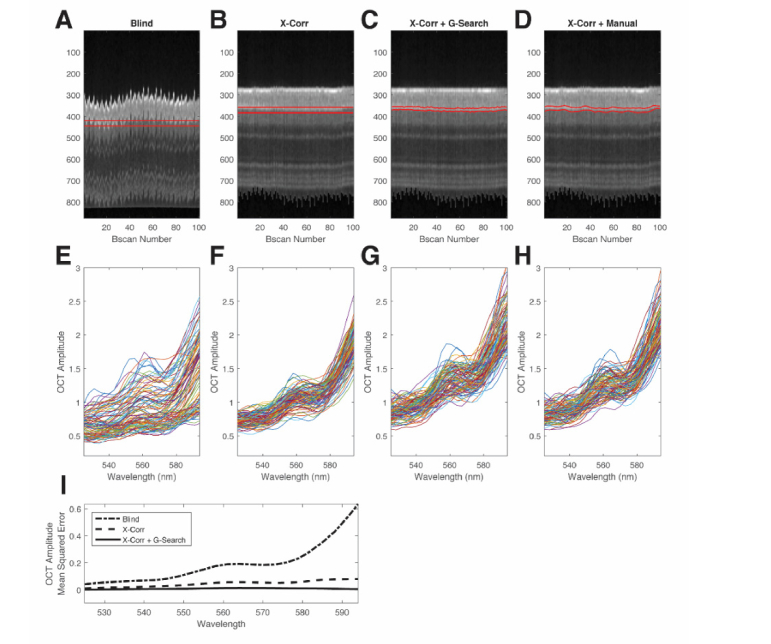
We compared four averaging methods to extract the spectrum from the posterior wall: (1) blind averaging with manually placed straight slab, (2) cross-correlation with manually placed manual straight slab (X-Corr), (3) cross-correlation with automatic graph-search (X-Corr + GS), and (4) cross-correlation with manual segmentation (X-Corr + Manual). In blind averaging, the extracted B-scans for each vessel were displayed and a slab was manually placed near the posterior vessel wall (slab width: 11 μm). For X-Corr, a slab was placed near the posterior wall after the cross-correlation step (slab width: 11 μm). For X-Corr + G-Search, the full method was performed. For X-Corr + Manual, cross-correlation was first performed, then each A-line was plotted and the peak location of the posterior wall was selected manually (slab width: 11 μm). This method was considered the “gold standard” for our measurements. Out of the four methods, only X-Corr + G-Search method was automatic and unsupervised.

Figure 4 shows results from a representative blood vessel acquired in an adult rat with significant motion. Figures 4(A)-4(D) show the vessel cross-sections, with the slabs indicated by the red lines. Figures 4(E)-4(H) show the spectra from each column. Spectra from the first three methods (Figs. 4E-4G) were compared with the spectra from the gold standard method (Fig. 4(H)) on a B-scan by B-scan basis. The mean squared error between the spectral results of each method and the gold standard was computed (Fig. 4(I)). Out of the three methods compared to the gold standard, the fully automatic method (X-Corr + G-Search) had the least OCT amplitude error across the spectrum (Fig. 4(I)).

Fig. 4.

Comparison of methods to extract the average OCT amplitude from the posterior wall for a single vessel. (A) Blind manual selection of straight manual slab for blind averaging. (B) Cross-correlation with manual selection of straight slab. (C) Cross-correlation with automatic graph-search segmentation for slab selection. (D) Cross-correlation with A-line by A-line manual selection of the peak signal from the posterior wall. Red lines in (A-D) denote the region of the slabs or segmentation. (E) Measured spectra from each B-scan for blind selection. (F) Measured spectra from each B-scan for cross-correlation alone. (G) Measured spectra from each B-scan for cross-correlation with graph-search segmentation. (H) Measured spectra from each B-scan for cross-correlation with manual selection. (I) Spectral OCT amplitude mean square error compared with the gold standard.

3.2 Comparison of accuracy, bias, and precision for OCT amplitude and sO₂

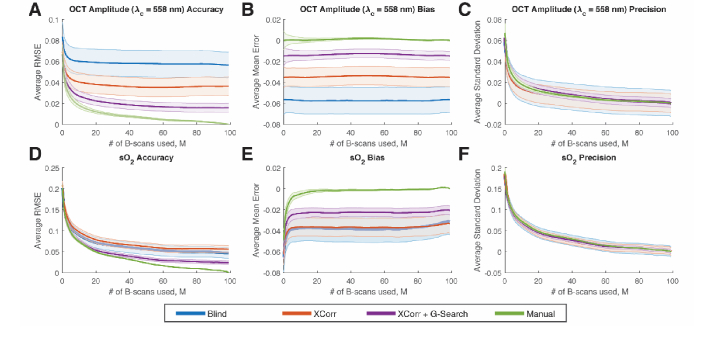
We studied the accuracy, bias, and precision for different numbers of B-scans used to compute the average OCT amplitude and sO₂. We chose a reasonable internal gold standard as the best possible scenario in our data set. This was the case of having 100 B-scans used for OCT amplitude averaging combined with manual peak selection of the vessel wall. Measurements of accuracy and bias used the gold standard measurement, while measurements of precision did not use the gold standard (see section 2.12).

Cross-correlation with graph-search segmentation was the most accurate technique for both OCT amplitude extraction and sO₂ measurements. The plots in Fig. 5(A) and Fig. 5(D) show the accuracy for the three methods. The gold standard (Manual) is shown as the green lines. As the number of B-scans (M) increases, the RMSE decreased for both OCT amplitude and sO₂. The X-Corr + G-Search line had the closest performance to Manual but did not completely overlap with the curve, suggesting residual error between the two methods. In addition, we also observed that the standard error of the mean (SEM) of the RMSE across vessels (see error bars in Fig. 5(A)) were the smallest with the X-Corr + G-Search method. This suggests that the X-Corr + G-Search method had more consistent RMSE values across different vessels.

Fig. 5.

Accuracy, bias, and precision for OCT amplitude (at ${\lambda }_c$ = 558 nm) and sO₂ for different number of B-scans used for averaging. (A-C) Accuracy, bias, and precision for OCT amplitude (at ${\lambda }_c$ = 558 nm) vs. number of B-scans used per sample. (D-F) Accuracy, bias, and precision for sO₂ vs. number of B-scans used per sample. Error bars indicate standard error of the mean across vessels.

We observed a negative bias for both OCT amplitude and sO₂. We attribute this to the fact that imperfect segmentation sometimes includes non-vessel wall signals, which tend to bias the OCT amplitude in the negative direction (Fig. 5(B)). This negative bias of the OCT amplitude further contributed towards biasing the sO₂ calculation in the negative direction (Fig. 5(E)). Out of all the methods, X-Corr + G-Search segmentation had the least amount of bias compared to the gold standard. Again, we also observed that the SEM of the ME was smallest with the X-Corr + G-Search method (error bars in Fig. 5(B), (E)), which means the bias is more consistent across vessels.

We also investigated the precision of the methods. We observed that the precision increased (average standard deviation decreased) as the number of samples increased; however, no method improved the mean precision over another (Fig. 5(C)&5(F)). The blind and X-Corr methods had larger variance in their precision measurements across the vessels (see error bars in Fig. 5(C)) compared with X-Corr + G-Search and Manual. Notably, the X-Corr + G-Search and Manual had similar precision mean values and similar variance in precision across vessels, which suggests that the X-Corr + G-Search method was close to the Manual method in terms of achieving high precision.

We were also interested in the number of averaged B-scans required to achieve accurate and precise sO₂ calculation. Based on the results in Fig. 5, we saw diminishing benefit in terms of accuracy, bias, and precision after ~20 averaging. Therefore, we believe that a reasonable number of averaged B-scans for our measurement method and imaging system would be between 20 and 40.

3.3 Automatic sO₂ measurements

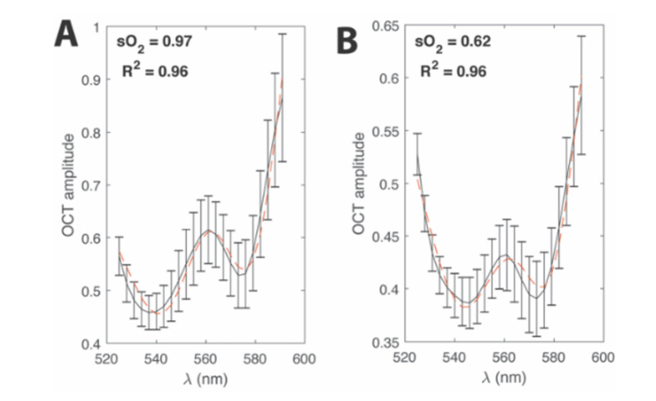
Figure 6(A) and Fig. 6(B) show representative vessel wall spectra from an artery (vessel #7 in Fig. 2) and vein (vessel #8 in Fig. 2), respectively (black lines). The error bars indicate the standard deviation of the OCT amplitude across the 100 B-scans used. The red dashed lines show the least-squares fits, which had good agreement to the data according to the R² values.

Fig. 6.

Spectral fitting. (A) Example of the least-squares spectral fit for an artery (vessel number 7 from Fig. 2). (B) Example of a least-squares spectral fit for a vein (vessel number 8 from Fig. 2). Black lines denote the measured average OCT amplitude after the graph-search algorithm. Error bars show the standard error of the mean of the OCT amplitude.

Table 2 shows the sO₂ values for the all the arteries and veins in Fig. 2. An alternating pattern of high-oxygenated and medium-oxygenated vessels is observed, which is consistent with the alternating pattern of arteries and veins in the rodent eye. The average arterial and venous sO₂ values (mean ± standard error of mean) were 0.96 ± 0.01 and 0.74 ± 0.03, respectively. These measurements are also consistent with previous studies using vis-OCT [10, 26]. The R² values were all above 0.8, with most being above 0.9, indicating that the regression predicts the measured data reasonably well.

Table 2. Automatic sO₂ measurements obtained with graph-search segmentation.

	1	2	3	4	5	6	7	8	9	10	11	12	13	14
sO2	0.99	0.75	0.99	0.64	0.99	0.85	0.97	0.62	0.88	0.79	0.96	0.66	0.97	0.85
R2	0.84	0.97	0.84	0.93	0.84	0.94	0.96	0.96	0.89	0.97	0.97	0.96	0.96	0.90

4. Discussion

We developed a method to solve the OCT amplitude extracting problem when performing vis-OCT oximetry. We combined circumpapillary scan (Fig. 2), cross-correlation, and graph-search segmentation of the vessel walls into an automatic method to calculate sO₂ (Fig. 3). Despite the lack of an external gold standard, we used an internal gold standard to investigate the accuracy, bias, and precision of our measurements (Figs. 4 & 5). This method achieves highly accurate measures of sO₂ with minimal bias compared to an internal gold standard. The variance in precision across vessels is also near-optimal. A similar analysis can be performed empirically on other vis-OCT systems, as results will vary based on the noise of the light source and performance of the spectrometer.

Our study evaluated the accuracy of X-Corr + G-Search compared with an internal gold standard. The accuracy depends mostly on the algorithm’s ability to correctly segment the signal from the posterior vessel wall. In addition, the accuracy will also be affected by motion, as moving subjects add an additional noise component to the measured spectra. This motion is also especially exacerbated when performing physiological studies of hypoxia, due to an increased respiratory rate when the amount of inhaled O₂ is reduced. We found that out of all the techniques in this study, X-Corr + G-Search performed the closest to manual peak selection of the vessel wall. Unfortunately, we still observed a bias in the measurement compared with the gold standard, which we attribute to the imperfect nature of automatic segmentation. Even with the techniques in this study, some background or non-vessel wall OCT signal was inevitably selected by the automatic segmentation algorithm, which led to negative bias in the OCT amplitude. This propagated to a negative bias in the sO₂. Despite this issue, we saw that the X-Corr + G-Search method had the smallest bias out of all the methods and the smallest variance of the bias across vessels. Future techniques will improve the segmentation to further minimize the error.

We are unaware of any current method that can serve as an independent gold standard for sO₂ measurements of individual vessels of the eye. Currently, the gold standard for retinal oxygen measurements is microelectrode-based measurement of oxygen partial pressure (pO₂) in the retina [27, 28]. Unfortunately, these measurements are highly invasive, laborious to perform, and difficult to directly correlate with sO₂ measurements from within blood vessels. We note that the model used to fit the spectrum is the same as that originally proposed by Yi et al. [10]. This model has been studied and verified in silico with Monte Carlo simulations and OCT reconstruction simulations [6, 11]. Studies have also shown good agreement for this model in vitro by vis-OCT of whole blood mixed with varied oxygenation levels [14, 26]. In addition, measurements of the retinal arteries in vivo corresponded well with the peripheral pulse oximetry measurements [26].

Our study also evaluated the precision of the amplitude and sO₂ measurements. We observed that the mean precision measures were similar between the methods. The precision includes the multiple sources of noise in OCT imaging. This includes noises from spectrometer camera, shot noise, and RIN noise. In addition, motion also adds a noise component to the OCT amplitude extraction. The variances of the precision across vessels were larger with the Blind method and X-Corr method, which signifies that some of the vessel measurements had more noise components. Since this variance decreased after adding G-Search to the X-Corr, the additional noise components likely came from motion. Future improvements in supercontinuum light sources with higher repetition rates and in spectrometers with better optical designs in the visible range, are expected to improve the precision further.

We found that averaging A-lines is important for calculating sO₂, even when manual peak segmentation was used. In this study, we found that there were diminishing benefit in OCT amplitude and sO₂ accuracy after ~20 B-scans (~120 A-lines). Results from <20 B-scans showed higher values of RMSE, ME, and SD for sO₂ measurements. Unfortunately, the exact number of averages to use cannot be directly transferred to all vis-OCT devices, since each has different light sources, camera integration times, and spectrometer designs. However, we can glean, as a general rule-of-thumb, that averaging >120 A-lines would provide accurate measurements of sO₂.

The method presented here for vessel wall segmentation is not limited to circumpapillary scans. To apply these methods to raster scans, vessel segmentation of the raster scans, akin to Fig. 2, would be required via either manual segmentation or automatic detection. Once these A-lines are collected, sections 2.9 to 2.11 could be applied. However, we caution that measuring sO₂ from along the length of a vessel combines different parts of the vessel for the measurement. Different parts of the retina receive different amounts of illumination, especially if there are cataracts or blood in the vitreous, which increases the variance of the collected spectra and biases the results. Moreover, different parts of the vessel may have different levels oxygenation, especially in disease states [29]. In this study, we sought to avoid this by using circumpapillary scans of the with fixed diameter, which repeatedly sampled vessels at the same retinal location.

Oxygenation measurements made with this method can be further extended to metabolic rate of oxygen measurements by combining sO₂ with retinal blood flow from Doppler OCT [5, 26]. In addition, retinal oximetry measurements may be applicable to different animal models of glaucoma [30], diabetic retinopathy [4], retinopathy of prematurity [5], vein occlusions, and age-related macular degeneration [31, 32].

Our algorithm is ultimately applicable to circumpapillary scan data from human patients. Although NIR OCT is well established for human retinal imaging, vis-OCT presents a set of new challenges for OCT researchers. Concerns about visible-light laser safety have limited the power for human imaging from 150 to 226 µW on the cornea [7, 33]. This limitation, coupled with the high RIN of supercontinuum light sources, can be a hurdle for achieving high signal-to-noise ratio images. In addition, due to the bright visible scanning pattern, patients’ eye fixation is more challenging, resulting in more motion artifacts. Finally, for large diameter vessels, the round-trip attenuation may prevent retrieval of the vessel wall signal. Despite these challenges, future studies will likely find innovative solutions to these technical issues to enable accurate human retinal oximetry.

5. Conclusion

In conclusion, we have shown automatic measurements of sO₂ from circumpapillary scans for the first time. We have used a unique approach involving graph-search segmentation to obtain the boundaries of the anterior and posterior vessel walls. Moreover, we have provided an in-depth analysis method to study the accuracy, bias, and precision for averaging using an internal gold standard. This study lays the foundation for future investigations, where large numbers of data sets must be analyzed automatically.

Funding

National Institutes of Health (NIH) (DP3DK108248, R01EY026078, R01EY029121, T32EY025202, T32GM008152, F30EY026472, and 1R21EY027502).

Disclosures

H.F.Z. has financial interests in Opticent Health, which did not support this work. Other authors declare that there are no conflicts of interest related to this article.