Accelerated RNA secondary structure design using preselected sequences for helices and loops

Abstract

Nucleic acids can be designed to be nano-machines, pharmaceuticals, or probes. RNA secondary structures can form the basis of self-assembling nanostructures. There are only four natural RNA bases, therefore it can be difficult to design sequences that fold to a single, specified structure because many other structures are often possible for a given sequence. One approach taken by state-of-the-art sequence design methods is to select sequences that fold to the specified structure using stochastic, iterative refinement. The goal of this work is to accelerate design. Many existing iterative methods select and refine sequences one base pair and one unpaired nucleotide at a time. Here, the hypothesis that sequences can be preselected in order to accelerate design was tested. To this aim, a database was built of helix sequences that demonstrate thermodynamic features found in natural sequences and that also have little tendency to cross-hybridize. Additionally, a database was assembled of RNA loop sequences with low helix-formation propensity and little tendency to cross-hybridize with either the helices or other loops. These databases of preselected sequences accelerate the selection of sequences that fold with minimal ensemble defect by replacing some of the trial and error of current refinement approaches. When using the database of preselected sequences as compared to randomly chosen sequences, sequences for natural structures are designed 36 times faster, and random structures are designed six times faster. The sequences selected with the aid of the database have similar ensemble defect as those sequences selected at random. The sequence database is part of RNAstructure package at http://rna.urmc.rochester.edu/RNAstructure.html.

INTRODUCTION

Fast and accurate nucleic acid design of sequences to adopt specified structures poses a challenge. One such design problem is secondary structure design, where the target structure is a set of canonical base pairs. One approach is to decompose the structure into regions, randomly or intelligently choose sequences that can fold to the desired structure in the region, and then refine the sequences by progressive refinement or exhaustive enumeration. The objective functions vary from folding free energy change to measures of ensemble folding behavior. Recent papers provide an overview of the objective functions and search routines of a number of available methods (Hofacker et al. 1994; Andronescu et al. 2004; Busch and Backofen 2006; Gao et al. 2010; Bindewald et al. 2011; Taneda 2011; Zadeh et al. 2011a; Lyngso et al. 2012; Garcia-Martin et al. 2013; Lee et al. 2014).

One algorithm for designing nucleic acids is NUPACK (Zadeh et al. 2011b), which minimizes ensemble defect, the sum of all nucleotide probabilities forming a desired structure subtracted from the number of nucleotides in that structure:

$$\text{Ensemble}\text{Defect}=N-\sum _{i=1}^N{P}_i,$$ (1)

where N is the total number of nucleotides, P_i is the probability of a nucleotide i forming the desired pair if it is paired in the target structure or the probability of nucleotide i being unpaired if it is unpaired in the target structure. Ensemble defect was introduced by Zadeh et al. (2011b) as a measure of the folding quality of the thermodynamic ensemble. NUPACK uses a tree decomposition scheme, and optimizes the sequences of fragments of the structure, where the sequences are chosen at random. Fragments are then assembled into the complete structure, and the fragments redesigned as necessary if they are found to cross-react instead of preferring to form the desired structures.

An alternative measure commonly used for sequence design is the folding free energy change of the sequence, specifically the design of sequences whose lowest folding free energy structure is the target structure. The rationale for this approach is that the lowest free energy structure is the most probable structure at equilibrium, and hence a sequence that folds with lowest folding free energy change to the target structure will fold to that structure with highest probability as compared to alternative structures. The drawback, however, is that, in spite of the probability of folding to the desired structure being the highest, the overall probability may in fact be low. This is because there can be alternative structures for the sequence with similarly low folding free energy change as the target structure.

Ensemble defect minimization, on the other hand, does guarantee that the target structure will be formed with high probability. Minimizing ensemble defect tends to minimize the folding free energy change because a low ensemble defect also requires the sequence to fold to the target structure with low folding free energy change relative to alternative structures. Minimizing ensemble defect also finds sequences for which there is low propensity to fold to alternative structures. It is worth noting, however, in spite of the shortcoming of free energy change as an objective function, a set of sequences designed by a program that optimizes folding free energy change could be subsequently filtered for low ensemble defect (or other measures) to also design sequences that fold with high probability to the desired target.

The current work aims to accelerate the rate of design by reducing the trial and error in refining sequences chosen at random. To do this, sequences are not generated at random, but instead loop and helix sequences are chosen from databases of sequences. The helix database contains helices composed of sets of complementary strands, with lengths from 1 to 10. The loop database contains single strands that are intended to not base pair. The helices and loops can be assembled to construct any valid secondary structure. Helices longer than 10 base pairs (bp), for example, can be constructed of multiple adjacent helices from the database. Internal loops, which contain two strands, are assembled from two separate strands sampled from the loop library. Multibranch loops, which are composed of any number of strands that do not pair, are constructed by sampling the number of needed strands from the loop database.

The databases were assembled to have the required features needed for sequence design. First, the thermodynamic features of helices in natural RNA structures were used to guide the selection of the set of helices in the database. As shown in the Results, RNA helices tend to have a specific range of folding stability, high probability of forming the exact helix, and low ensemble defect. Second, the helix and loop databases were screened for cross-hybridization with any other sequence in either database, and only those sequences with little propensity to interact with others were included in the final set.

The databases of helices and loops improve design by accelerating design and/or by improving the design quality, as estimated using ensemble defect, using the iterative design approach pioneered by NUPACK. There is a trade-off between design time and stringency of the design, and this trade-off was studied by varying the user-selected stringency parameters. By accelerating the design process, users are able to get designs faster with the same stringency or get improved design stringency with the same computer time.

The databases reported here can be used to design sequences that fold to natural RNA structures about 36 times faster than the conventional method, with similar ensemble defect as the conventional method. By reducing the trial and error component of the calculation, the databases facilitate the design of sequences by speeding the process. Design times range from less than a second to 5 min for sequences up to 451 nucleotides (nt) in length, without a strong correlation to sequence length. In comparison, the conventional method took up to 4 h to design a sequence.

RESULTS

Thermodynamic features of natural RNA structures

A list of all helices of lengths from 3 to 10 bp was extracted from a structure database (Bellaousov and Mathews 2010) that contains 1523 known structures from ten RNA families: small subunit rRNA (Gutell 1994), large subunit rRNA (Gutell et al. 1993; Schnare et al. 1996), 5S rRNA (Szymanski et al. 1998), group I introns (Waring and Davies 1984; Damberger and Gutell 1994), group II introns (Michel et al. 1989), RNase P RNA (Brown 1998), SRP RNA (Larsen et al. 1998), tRNA (Sprinzl et al. 1998), tmRNA (Zwieb et al. 1999), and telomerase RNA (Chen et al. 2000). This set of natural RNA sequences with known structures provides a wealth of information from which it can be deduced how evolution selects sequences that fold to a specific structure (Smit et al. 2006). An additional list of helices was created by keeping only unique sequences from the known structure database. The number of helices in the database for each helix length is shown in Table 1. Additionally, a list of all RNA helices, including G-U pairs, of lengths from 3 to 10 bp was generated (Table 1).

TABLE 1.

Counts for helices from known structure database and for all possible helices

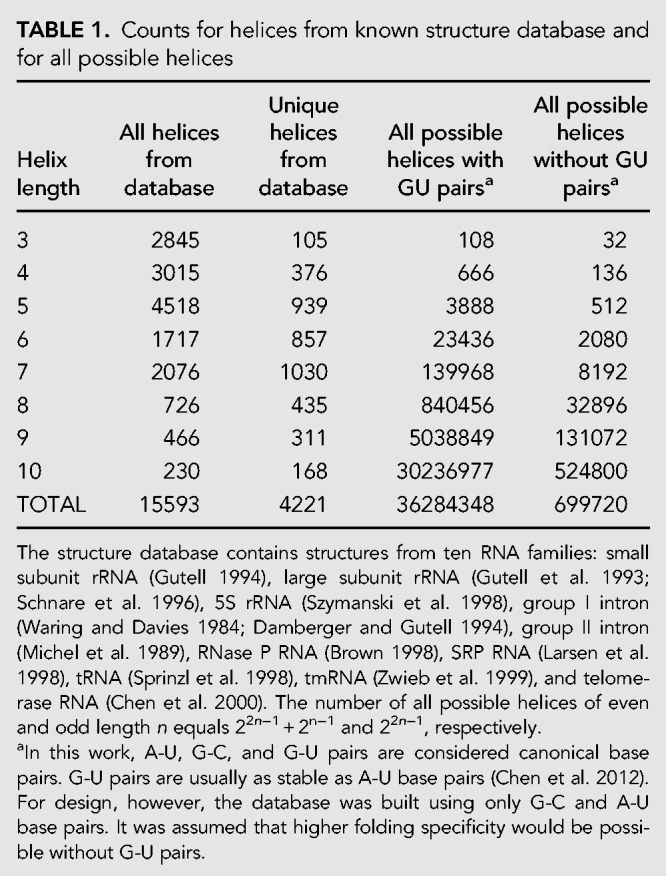
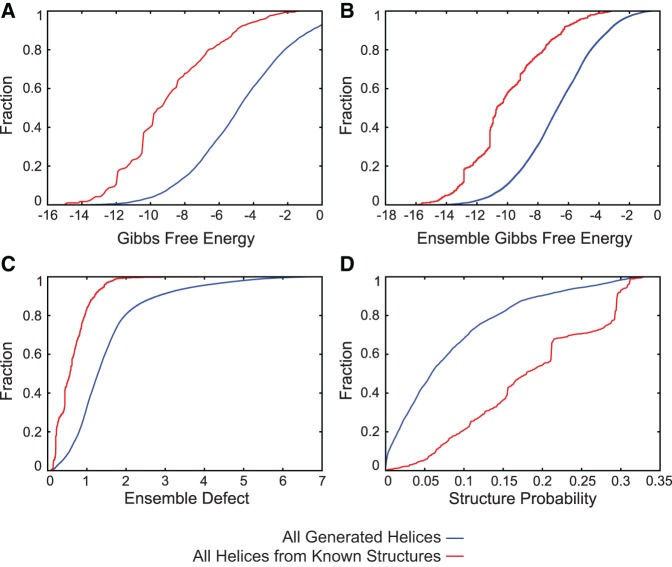
For each helix, the following parameters were calculated: bimolecular Gibbs free energy change of folding at 37°C (ΔG°₃₇) (Xia et al. 1998; Mathews et al. 1999); ensemble free energy change for folding of the helix, i.e., −RTln(Q_b), where R is a gas constant, T is the temperature of 310.15 K, and Q_b is the bimolecular partition function (Mathews 2004) for the helix; ensemble defect for the helix from the folding of two strands; and the probability of the helix forming from the two strands. Each of these parameters was calculated as though the two strands were interacting as separate sequences, i.e., as a bimolecular structure, and the extent of each sequence was the helix only. These data were calculated using the RNA folding nearest neighbor rules for free energies of folding at 37°C (Xia et al. 1998; Mathews et al. 1999, 2004). Prior work has shown that the melting temperature of sequences correlates with the optimal growth temperature of the organism from which the sequence was taken. The accuracy of free energy estimates, however, is poor for temperatures outside the range of 10°C to 60°C because of the heat capacity change of folding (Lu et al. 2006). Therefore, for this work, folding energies at 37°C were used. All the parameters were plotted using cumulative distribution plots for each helix length. Plots for each parameter for 7 bp helices are provided as Figure 1A–D, and the remaining plots are provided in the Supplemental Material as Supplemental Figures S1–S7.

FIGURE 1.

Trends in natural sequences. Distributions of folding free energy change, ensemble folding free energy change, ensemble defect, and structure probability for 7 bp helices. Cumulative distribution plots are provided in red for unique sequences observed in the database of RNA structures and in blue for all possible helices. Panel A is Gibbs free energy change, panel B is ensemble Gibbs free energy change, panel C is ensemble defect, and panel D is the probability of helix formation.

Figure 1A shows natural RNA helices tend to have a mid-range Gibbs free energy change of folding, e.g., a folding free energy change largely between −11 and −6 kcal/mol for 7 bp helices. Figure 1B shows natural helices tend to have mid-range ensemble free energy change, e.g., an ensemble folding free energy change largely between −12 and −7 kcal/mol for 7 bp helices. Figure 1C shows natural helices tend to minimize ensemble defect. Figure 1D shows natural helices tend to have higher structure probability when compared to all possible helices. This information suggests helix sequences have common features regardless of the structure in which they reside.

Creating a database of helices and single-stranded sequences

To build a database of helix sequences that have the desired properties, the database of all possible RNA helices of lengths from 3 to 10 bp (excluding GU pairs) was generated (Table 1) and sequences were removed that did not meet selection criteria. The set of helix sequences was trimmed in multiple steps to choose the best sequences: first, by choosing sequences with minimal ensemble defect; second, by choosing sequences with minimal sum of pairing probabilities for intramolecular base pairs; and third, choosing sequences with a minimal sum of base pair probabilities for forming intermolecular base pairs with other helix strands in the database. This was done to ensure helices have high propensity to form the expected structure, but low propensity to form undesired helices with other sequences in the database. The helix database has a total of 2000 sequences distributed from length 1 to 10 bp. The Materials and Methods section provides a detailed explanation.

A database of single-stranded sequences (to be used for loops) was also generated with all possible sequences and then trimmed for desired properties in multiple steps: first, by removing sequences that form intramolecular structures; second, by choosing sequences with minimal sum of pair probabilities for hybridization to each sequence in the helix database; and third, by choosing sequences with lowest sums of pair probabilities when hybridized to other sequences in the loop database. This ensured that single-stranded sequences have low propensity to form pairs with sequences in either database. These steps are detailed in Materials and Methods. The single-stranded sequence database has a total of 2075 RNA sequences from lengths 1 to 10 nt. This database was used for the design of hairpin loops, internal loops, bulge loops, and the unpaired regions in exterior and bulge loops.

Testing the databases of helices and single-stranded sequences

To test whether a preselected database of sequences could improve the speed of sequence design, a design software based on the NUPACK design algorithm (Zadeh et al. 2011b) was written. This software follows NUPACK closely, but differs from NUPACK in the decomposition of structures and energy model (see Design Algorithm section in Materials and Methods). The software runs in one of two modes: Design_Random uses random sequence selection as done in NUPACK (Zadeh et al. 2011b) to design the sequence, and Design_Preselected uses the database of preselected sequences to assemble the sequence. By implementing the Design_Random and Design_Preselected software, the effect of the databases on the speed and precision of design was specifically tested.

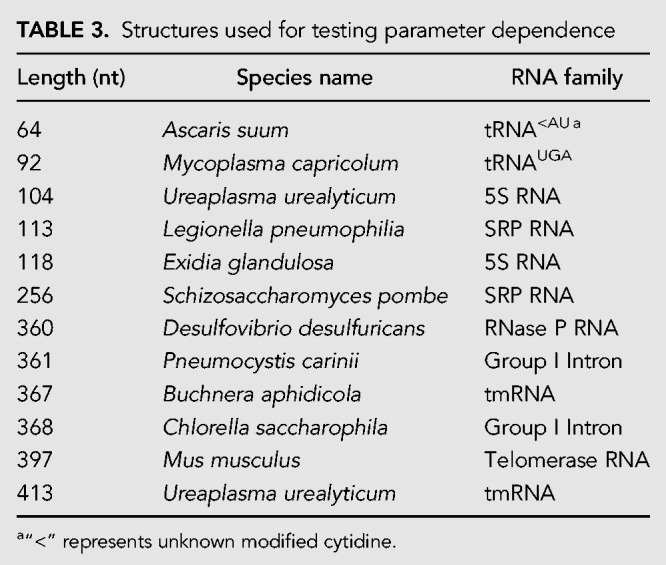
Design_Random and Design_Preselected have three adjustable parameters: length-normalized ensemble defect (NED) threshold, number of branch reoptimizations, and number of leaf optimizations (Zadeh et al. 2011b). The performance of both modes depends on these parameters, where lower NED threshold, higher branch reoptimizations, and higher leaf optimizations should result in more stringent designs at the cost of computer time (see Design Algorithm section in Materials and Methods). To evaluate the changes in performance, 72 and 192 combinations of the three adjustable parameters were used with Design_Random and Design_Preselected, respectively (Table 2). Both modes were evaluated by designing 24 structures, where twelve were selected from the set of RNA sequences with known structures (listed in Table 3) and twelve were minimum free energy RNA structures for random sequences (reported in Supplemental Table S1). The structures from random sequences contain helices, loops, multibranch loops, bulge loops, and internal loops and are hard to design because they may be difficult structures to fold to with fidelity. Structures like these have been used in prior work (Zadeh et al. 2011b).

TABLE 2.

Parameters used to evaluate performance of two design modes

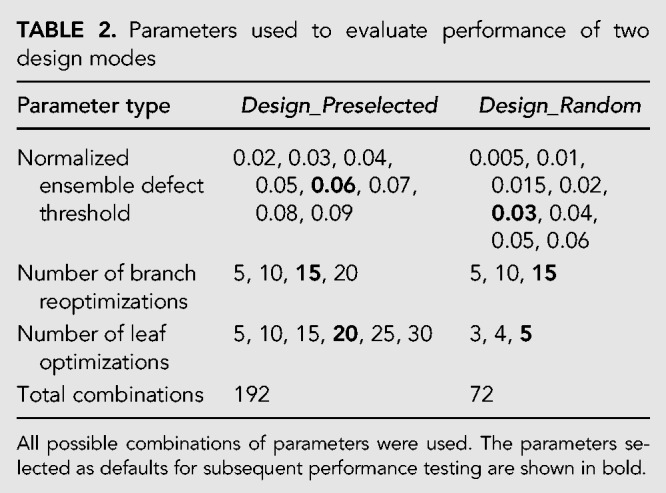
TABLE 3.

Structures used for testing parameter dependence

For each set of the three parameters, because time performance is stochastic, the calculations were repeated using five and ten random number seeds for Design_Random and Design_Preselected, respectively. The number of trials for Design_Random was fewer because these calculations require more computer time. Mean NED and mean design time in seconds were calculated for each designed sequence and these were averaged over all sequences within the same parameter sets. The results were plotted as a scatter plot (Fig. 2), demonstrating that there is a clear tradeoff between selection time and the quality of the selected sequence for either Design_Random or Design_Preselected. For a given time cost, Design_Preselected produces sequences with lower ensemble defect than Design_Random. Conversely, for a given ensemble defect, Design_Preselected costs less time than Design_Random.

FIGURE 2.

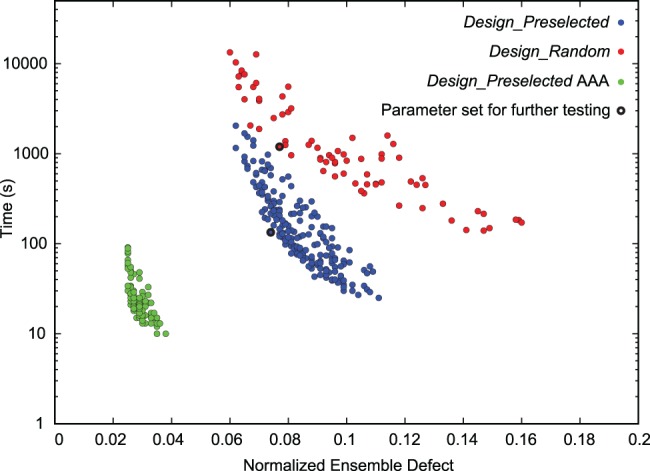
Algorithm performance distribution for sets of parameters. Blue and red dots represent performance of Design algorithm in Preselected and Random modes, respectively. Green shows the performance of the Design algorithm in Preselected mode using all adenines in place of single stranded regions. Each dot is the mean performance for a single set of parameters. Black outlines show the parameter sets that are used for further performance evaluation on a different set of structures. Performance is evaluated as mean time as function of mean NED.

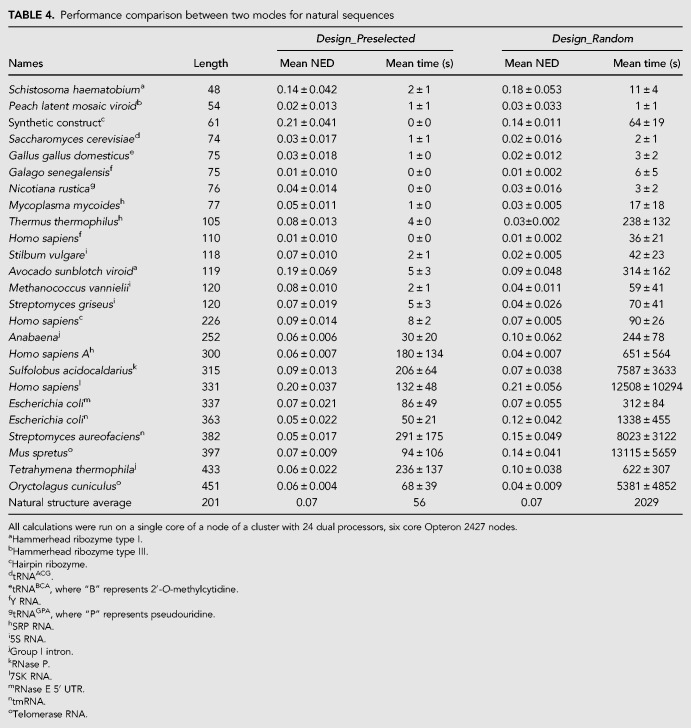
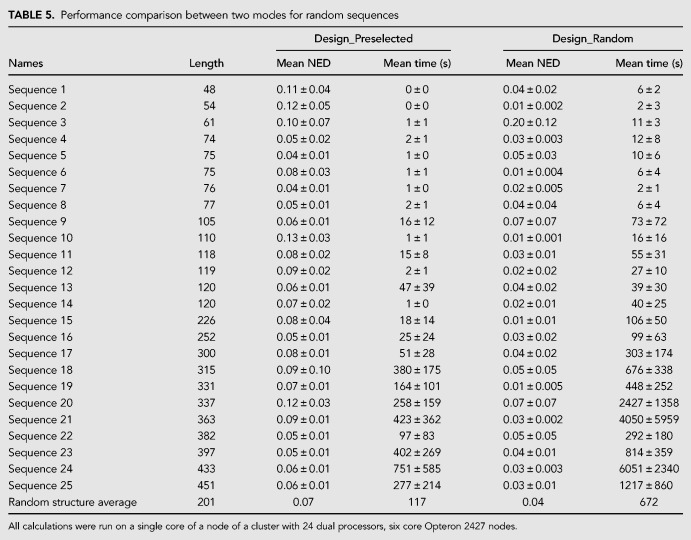
Both modes were then benchmarked on another set of 50 structures (listed in Tables 4 and 5) for a single set of parameters each. Twenty-five structures (Table 4) are known RNA structures for natural sequences. The RNA families include families not used in prior training (7SK RNA, hairpin ribozyme, hammerhead ribozyme type I, hammerhead ribozyme type III, RNase E 5′ UTR, and Y RNA). An additional 25 structures (Table 5) are lowest free energy structures for random RNA sequences of identical length as the 25 natural RNA structures. The parameters were chosen to balance time performance and NED (shown in bold in Table 2 and subsequently chosen as the default parameters for the software). The parameters were also chosen so that both programs would design sequences with similar NEDs. For Design_Random and Design_Preselected, respective NED thresholds were 0.03 and 0.06, respective numbers of leaf optimizations were 5 and 20, and number of branch reoptimizations was 15 for both algorithms (Table 2, shown in bold). The mean NEDs and mean design times are reported in Tables 4 and 5. The benchmarks were performed ten times for each sequence and averaged. The structures were both known RNA structures and structures found by minimizing RNA folding free energies for random sequences shown in Supplemental Table S2. Similar to the structures in the previous set, these structures contain helices, loops, multibranch loops, bulge loops, and internal loops.

TABLE 4.

Performance comparison between two modes for natural sequences

TABLE 5.

Performance comparison between two modes for random sequences

Mean time performance is the most important measure of design cost for large-scale projects, such as web servers, but mean performance can be distorted by outliers. Supplemental Table S3 provides median performance on natural structures for both time and NED for Design_Random and Design_Preselected. The NED performance is the same for mean and median values. The average time performance (mean across structures) is 9% shorter for median compared to mean for Design_Random and it is 4% shorter for Design_Preselected. Supplemental Table S4 provides the median performance on random structures. The median performance is lower than the mean performance for NED for Design_Random. Evidently, outliers have a large influence on NED. For Design_Preselected, the median NED is the same as the mean. The average time performance is 20% shorter for median compared to mean for Design_Random and 15% shorter for Design_Preselected.

To demonstrate that the speed improvement is tangible compared to other sequence design programs, NUPACK was also benchmarked for time and quality performance. Supplemental Tables S5 and S6 show the performance on natural structures and random structures, respectively. NUPACK and Design_Random performed similarly, although the comparison is not exact because NUPACK and Design_Random use different sets of thermodynamic parameters, the 1999 (Mathews et al. 1999) and 2004 (Mathews et al. 2004) sets, respectively. It is not clear how differences in parameter sets might affect the time performance of these algorithms.

Based on Tables 4 and 5, the databases of preselected sequences improve the speed of nucleic acid design by a factor of 36 and six for natural and random structures, respectively. At the same time, the NED remains comparable.

Simplification of loop model

As an additional test, structures were designed using only adenines in the loops to test the hypothesis that this would result in lower ensemble defect and faster design time. For many applications, this may not be desirable because the loop sequences lack the complexity required, for example, to functionalize the structure. This approach, however, further decreases both the design time and the NED of the designed sequence (Fig. 2) as compared to Design_Preselected with loops of heterogeneous composition. When testing this, the helix sequences were selected from the database of selected helices, as is done in Design_Preselected.

Asymptotic behavior

To study the difference in algorithm behavior on longer structures, the benchmarks were extended to include structures with up to 1995 nt in length using structures drawn from the RNA STRAND database (Supplemental Table S7; Andronescu et al. 2008). The gap in the time performance of Design_Preselected widens considerably for longer structures (>600 nt) as compared to NUPACK and Design_Random (Fig. 3), with Design_Preselected running over an order of magnitude faster and two orders of magnitude faster for many cases. For the two longest structures (1793 and 1995 nt), Design_Random and NUPACK did not complete all ten calculations within the allowed time of 75 d. Additionally, for NUPACK, the 697 nt structure did not complete all ten calculations. The NED was more consistently close to the threshold of 0.10 for NUPACK (Supplemental Fig. S8). The NED for Design_Preselected tended to have lower values than NUPACK for structures shorter than 600 nt, but was consistently higher for structures longer than 1000 nt.

FIGURE 3.

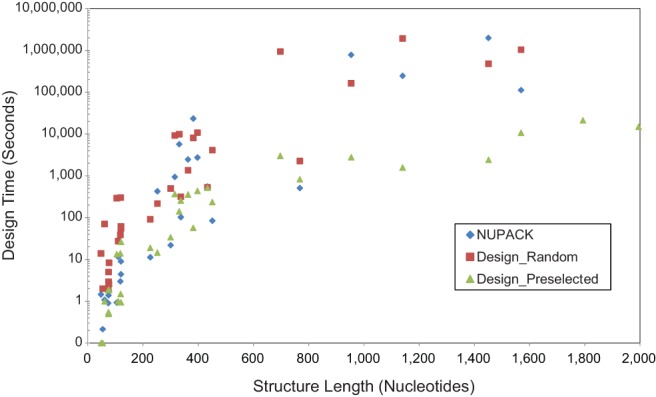
Time performance for long sequences. Designs were made for sequences of up to 1995 nt (Supplemental Table S7). Mean time performance is shown for ten calculations for each target structure. Design times were capped at 75 d of running time (6,480,000 sec). Points missing for NUPACK (697, 1793, and 1995 nt) and Design_Random (1793 and 1995 nt) had one or more designs that reached the maximum runtime and were terminated, so the mean could not be calculated. Design_Random and Design_Preselected were run with default parameters. NUPACK was run using rna99 thermodynamic parameters at 37°C, the NED threshold was set to 0.1 so that NUPACK produced structures of similar NED as Design_Random, and other parameters were set to defaults. Designs were performed on a single core of an Opteron 2427 processor.

As the length (in nucleotides) of a designed structure was increased, NUPACK was previously found to converge on a fixed ratio of total design cost (in time) to the cost of the evaluation metric (in time) (Zadeh et al. 2011b). The evaluation metric requires a cubic-scaling partition function calculation, but this observation demonstrates that sequences can be designed with a bound to the total cost that related to simply the evaluation. This finding is reproducible for the two types of structures studied in the paper reporting NUPACK (engineered structures and random structures; Supplemental Fig. S9). It appears, however, for structures from biologically relevant RNA sequences, that the cost either does not asymptotically converge or it converges much farther out in length (Supplemental Fig. S10). Additionally, we observe similar behavior for Design_Random and for Design_Preselected on the design of natural structures (Supplemental Fig. S11). In contrast to NUPACK, Design_Random and Design_Preselected do not asymptotically converge for engineered structures (Supplemental Fig. S12). This difference is likely the consequence of the alternative decomposition strategy used by Design (which decomposes by dividing structures at unpaired nucleotides in exterior and multibranch loops) as compared to NUPACK (which decomposes by dividing structures within helices). NUPACK by default will decompose structures down to 20 nt. Design, in contrast, performs up to five binary decompositions by default. The NUPACK strategy is specifically chosen for engineered structures that might contain fewer multibranch loops (Zadeh et al. 2011b).

DISCUSSION

Helix sequences derived from RNA sequences with known secondary structure showed clear trends in folding free energy change distribution, ensemble defect distribution, and structure probability distribution when compared to all possible helix sequences. This suggests a selection by evolution at the level of sequence components, and also suggests that sequences can be optimized to better design structures.

Using the observed biases for helix sequences, a database of sequences was assembled for RNA structure design. In addition to having features that mimic the RNA structure database, the sequences were selected to minimize cross-reactivity. This type of approach was previously used for DNA word design for the field of DNA computing (Shortreed et al. 2005). The database composition selections were costly in terms of total computer time, but this needed to be done only once and then the databases were ready for design of arbitrary structures.

For this work, NUPACK was reproduced so that random selection and selection from the database could be directly compared, controlling for other variables in the design process, such as energy function and decomposition scheme. The design software implemented here is not a replacement for NUPACK, which has a much richer set of features, such as the ability to constrain sequences and to design multimolecular complexes. On average, Design_Random and NUPACK have similar performance. For the natural structures, the mean time for Design_Random was 2029 sec and the mean NED was 0.07; the mean time for NUPACK was 1806 sec and the mean NED was 0.09. The comparison, however, is not exact because NUPACK used the 1999 thermodynamic parameters (Mathews et al. 1999), and Design_Random uses the 2004 thermodynamic parameters including coaxial stacking (Mathews et al. 2004). There are likely differences in performance that relate to the set of thermodynamic parameters that are used.

Another important aspect of this work is that it focuses on designs of sequences that fold into natural biological structures. The fact that the asymptotic convergence to a fixed cost ratio of design to evaluation is not reached for these structures, running out to 1995 nt in length, suggests there are some important differences compared to random structures and also engineered structures. First, natural structures probably rely more on noncanonical interactions to stabilize the overall structure. The focus of these designs is just on canonical pairs. The thermodynamic parameters include some of the sequence dependence of noncanonical interactions in loops, but there are many more sequence-specific interactions that are not included. Future work might focus on also including noncanonical pairs, perhaps using the MC-Fold approach (Parisien and Major 2008; Honer zu Siederdissen et al. 2011; Sloma and Mathews 2017). A second difference is that natural structures contain pseudoknots, which are neglected here. Accurate modeling of pseudoknots without sequence comparison or experimental mapping data remains an important challenge (Bellaousov and Mathews 2010; Hajdin et al. 2013).

To test the importance of selecting the database sequences against cross-hybridization, a second database was assembled without selecting against cross-hybridization. This database has the same selections based on the thermodynamic qualities, but instead of removing sequences that cross-hybridize, sequences were removed at random to yield a database of identical size to that benchmarked above. The results of parameter selection are provided in Supplemental Figure S13. For relatively high ensemble defect, this database can accomplish designs faster than Design_Random, but relatively low ensemble defects cannot be achieved. This is likely because the limited size of the database does not allow the Design_Preselected program to find a combination of sequences that do not cross-hybridize, and highlights the importance of selecting sequences for the database with little propensity to interact in undesired ways.

Figure 2 demonstrates a clear tradeoff in design time and the quality of the designed structure. The trend of this tradeoff is better when using the database of preselected sequences than when using random sequences. With constant ensemble defect, the preselected sequence databases improved design time for natural structures by a factor of 36 (Table 4) and, for structures generated by folding random sequences, by a factor of six (Table 5). Much of the improvement is observed to be in the longer structures. For structures composed of fewer than 100 nt, generally the design time is short with either random or preselected sequences. For the 300 and 400-mers, the gap in performance is considerable. Using the preselected sequence database, design of RNA sequences to fold into natural RNA structures performed about equally in terms of NED as compared to the conventional, random, method. These are important considerations for future work in RNA sequence design. As designed structures get longer, the databases of preselected sequences will become increasingly important to both limit overall design time and to reduce ensemble defect. This is supported by Figure 3, where a comparison of design times was made out to sequences of lengths of 1995 nt.

Previously, an approach for sequence design, informed by natural sequences, was reported (Esmaili-Taheri et al. 2014). This work differs in several significant ways. Esmaili-Taheri et al. (2014) first predicted structures by free energy minimization for the natural sequences. Then, they assembled a database of loops and helix sequences from the predicted structures. The database of natural sequences was then used as sequence components, i.e., helices or loops, of the target structure, and the ability of the designed sequence to fold to the desired structure was assessed by free energy minimization. Portions of the structure that did not fold into the desired structure were swapped for other sequences in the database. In this work, the natural sequences are shown to have specific properties, and then a database of other sequences was generated de novo to mimic those features. The database assembled here has little overlap with natural sequences, as shown by Supplemental Table S8 for helices. Only 8.2% of helices in the database are found in natural RNA sequences. For the longer helices, where the number of possible helices is relatively large, a smaller fraction of the database helices are found in nature, with none of the 10 bp helices appearing in natural sequences. Additionally, the database used here was selected for sequences that should not cross-hybridize in undesired ways, and the database speeds the design of sequences with low ensemble defect. This is important for the design of long sequences, but it is also important for the design of short sequences because, for example, it could facilitate the design of a large set of sequences that are elements of a larger complex.

The database was used here for designing sequences with low ensemble defect, pioneered by the NUPACK algorithm (Zadeh et al. 2011b), but the approach would be useful with other nucleic acid design approaches. This work and the work of Esmaili-Taheri et al. (2014) provide a new strategy for iterative refinement that should lead to a new generation of tools. The sequence database and design software are part of RNAstructure software package and can be downloaded at http://rna.urmc.rochester.edu/RNAstructure.html (Reuter and Mathews 2010).

MATERIALS AND METHODS

Helix database selection procedure

To start, all possible helices containing GC and AU base pairs were generated (Table 1 shows the number of helices by helix length). This database was then trimmed using multiple criteria to result in the helix database. Figure 4 shows an overview of the design procedure.

FIGURE 4.

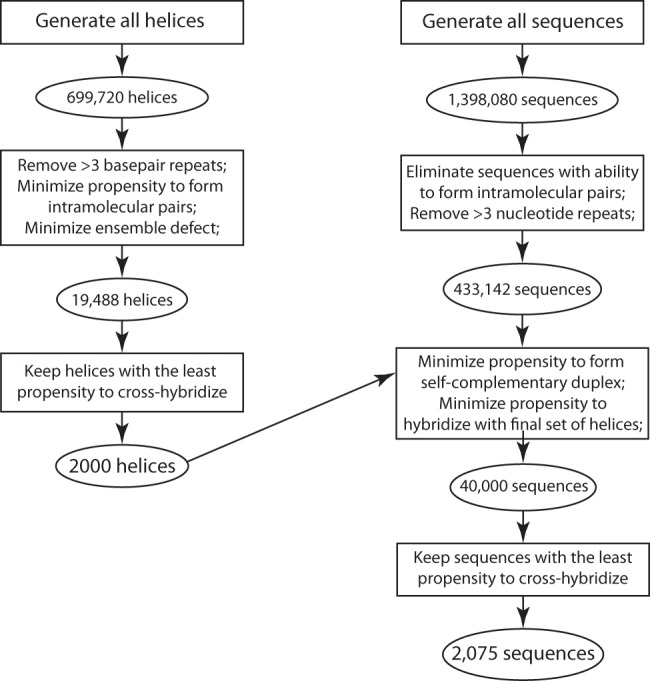
Generating the databases of RNA helices and loops. A list of all possible helices of lengths from 3 to 10 bp, composed of only canonical A-U and G-C base pairs, was trimmed by removing helices with more than three consecutive base pair repeats, by removing helices with strands that form intramolecular pairs, and by removing helices with high ensemble defect. The list was trimmed further by removing helices with high propensity to cross-hybridize with other helices in the list. To generate a list of sequences to use as loops, a list of all possible sequences of lengths from 3 to 10 nt was trimmed by removing sequences with more than three consecutive repeating nucleotides, and by removing sequences that can form intramolecular pairs. The list was trimmed further by removing sequences with high propensity of forming pairs with the final helix list and by removing sequences that can form self-complementary duplexes. The list was trimmed further by removing sequences with high propensity to cross-hybridize.

Step 1: This step ensured that only helices that fold precisely are included. NED was calculated for each helix in the database of all possible sequences. 25,854 total helices below a NED threshold, chosen specifically for each helix length (Table 6) were kept in the database while the other helices were discarded. NED thresholds were chosen based on helix yield. The target yield was 26,000 helices.

TABLE 6.

NED inclusion threshold

Step 2: Helices with more than three repeating consecutive nucleotides were omitted to prevent a possibility of forming quadruplex structures or other higher-order motifs.

Step 3: This step ensured that helix sequences do not fold back on themselves to form undesired structures, rather than interacting with the other strand of the same helix. Intramolecular ensemble pair probabilities (EPP), the sum of probabilities for every possible pair in the sequence, were calculated for each sequence:

$$EP{P}_{\mathrm{intramolecular}}=\sum _{i=1}^N\sum _{j=i}^N{P}_{i-j},$$ (2)

where N is the length of the sequence, and P_i−j is the probability of pair i-j in the sequence. P_i−j was calculated using a partition function calculation (Mathews 2004). It measures a propensity to form intramolecular structure.

Strands with ≥7 nt can form stacked base pairs. To make sure that the strands in the helix have low propensity to form intramolecular pairs, only helices with low EPP_{intramolecular} were kept. Helix EPPs were normalized to the length of the helix and the maximum EPP_{intramolecular} was capped as shown in Table 7. The cutoffs were chosen to provide sufficient remaining sequences for each length helix.

TABLE 7.

Normalized EPP cutoffs

Step 4: Each remaining helix was then tested for cross-hybridization with each other helix in the database, and helices with the propensity to cross-react were eliminated. For each helix pair, sums of four intermolecular EPPs (two strands for each helix pairing in all combinations) were calculated. Intermolecular EPP is the sum of probabilities for every possible intermolecular pair. It measures the propensity of intermolecular structure to form:

$$EP{P}_{\mathrm{intermolecular}}=\sum _{i=1}^N\sum _{j=1}^M{P}_{i-j},$$ (3)

where N is the length of strand 1 and M is the length of strand 2 of the helix. P_i−j, the probability of nucleotide i in strand 1 pairing to nucleotide j in strand 2, was calculated using a partition function calculation (Mathews 2004).

Intermolecular EPPs were normalized by dividing by the length of the shortest strand in the helix. The normalized EPPs were summed for each helix across all other helices. An iterative refinement of the database was performed, where the helix with the highest sum was removed from the database and the sums were recalculated for each step. This procedure was repeated until the total number of helices reached 1988, as shown in Supplemental Table S8. The maximum number of removed helices was tailored for helix length to ensure that each helix length is not underrepresented (Table 8). Once trimming reached the specified limit for a given helix length, the iterative refinement process was no longer allowed to trim a helix of that length.

TABLE 8.

Minimum number of helices allowed as a function of helix length

Subsequently, all 1 and 2 bp helices were added to the database bringing the total number of helices to 2000. Supplemental Table S9 provides an overview of the number of helices remaining after each step of the trimming process.

Loop database selection procedure

Loop sequences were selected from all possible sequences in a similar fashion. First, all possible RNA loop sequences of length 3 to 10 nt were generated, and sequences were removed to leave a set with desired properties. Supplemental Table S10 provides an overview of the number of sequences remaining in the database after each step of the trimming procedure outlined below.

Step 1: This step ensured that loop sequences do not fold back to form base pairs. Sequences with the length of 7 nt and longer can potentially form intramolecular structures. Minimum free energy structures were predicted for these using the Fold program from RNAstructure (Mathews et al. 2004; Reuter and Mathews 2010). Sequences that formed stable structures, i.e., ΔG°₃₇ < 0, were removed from the database.

Step 2: Sequences with more than three repeating consecutive nucleotides were trimmed.

Step 3: This step ensured that the loop sequences do not form base pairs with helix sequences. The remaining 433,142 sequences were cross-hybridized with each of the two strands of each helix in the final helix database. EPP for each hybrid was calculated. EPPs for the two hybrids in each helix were summed and normalized by the length of the shortest strand in the hybrid. Loops with the lowest total normalized EPP were retained, leaving 50,000 loop sequences.

Step 4: This step ensured that loop sequences do not form self-complementary duplexes, which might happen in sequences designed with the same loop sequence appearing more than once. The loop database was reduced to 40,000 sequences by removing loop sequences with highest EPP to form self-complementary structures.

Step 5: This step ensured that loop sequences do not interact with other loop sequences to form base pairs. All remaining loop sequences were cross-hybridized with each other. EPP for each hybrid was calculated and normalized by the length of the shorter strand. Normalized EPP was summed for each sequence. An iterative refinement was performed where the sequence with the highest sum was removed, and the sums were recalculated omitting the removed sequences. This procedure was repeated until all sequences with nonzero EPP were removed. All 1 and 2 nt sequences were added to the database bringing the total number of loop sequences to 2075. The minimum number of sequences of each size was preset to prevent over-trimming and ensure diversity (Table 8).

Energy model

To calculate free energy changes, the RNA nearest neighbor parameters were used (Xia et al. 1998; Mathews et al. 2004). The only exception was that the per branching helix in a multibranch loop parameter was set to −0.6 kcal/mol, according to the experimental results (Diamond et al. 2001; Mathews and Turner 2002) as has been done in recent work (Lu et al. 2009; Bellaousov and Mathews 2010; Harmanci et al. 2011; Seetin and Mathews 2012). The partition function includes coaxial stacking interactions for multibranch loops and exterior loops.

Design algorithm

The Design software was based on the NUPACK design algorithm by Zadeh et al. (2011b), with modifications to the structure decomposition and the energy model. For the energy model, Design uses the latest Turner energy rules for loops (Mathews et al. 2004), including explicit coaxial stacking in the partition function calculation (Mathews 2004). NUPACK uses the previous set of loop rules for RNA design (Mathews et al. 1999).

Like NUPACK, Design is capable of sequence design for pseudoknot-free structures. The Design program is in C++, and was built using a design class that inherits the RNA class from RNAstructure (Reuter and Mathews 2010). The Design algorithm, however, does not implement all the features in the NUPACK software, such as multiple-sequence design and the ability to specify sequence constraints.

Design first decomposes the target structure with a binary tree decomposition. A sequence of nucleotides that can fold to the desired structure is assigned to each leaf at random, and the ensemble defect is calculated. Ensemble defect is normalized to the number of nucleotides in the leaf, and is evaluated against the default threshold (Table 2). For leaves with nucleotides missing from the backbone connections, i.e., with a discontinuous backbone because of the decomposition, 6 nt that neither pair nor stack are used to connect the two strands for the partition function calculation needed to determine the NED. If the NED is above the threshold, the leaf sequence is redesigned using the ensemble defect-weighted mutation sampling as described by Zadeh et al. (2011b). The process terminates successfully when the NED of the leaf is below the threshold. In the case where every nucleotide has been mutated four times by default, leaf optimization terminates and restarts up to the default maximum number of times set by the “number of leaf optimizations” parameter (Table 2). If threshold NED is still not reached, the threshold NED is modified to reflect the lowest NED achieved (Zadeh et al. 2011b). This helps to minimize runtime for structures that are difficult to design.

Once all leafs are designed, they are merged into branches and the NED is calculated for each branch. If the NED of every branch is below the NED threshold, branches are merged to form branches of longer structures. If the NED of a branch is above the target threshold, NEDs of the current and nearest sub-branch are multiplied by randomly generated number from 0 to 1 and the sub-branch with the highest product is reoptimized and merged back. This involves traversing the tree back to the level of the leaf. This branch reoptimization step repeats up to the default maximum number of times set by the “number of branch reoptimizations” parameter (Table 2), at which point the threshold NED is modified to reflect the lowest NED achieved so far. This process is repeated at every merging step until the full sequence is reached. The random number generator algorithm (ran2) from “Numerical Recipes” was used (Press et al. 1992).

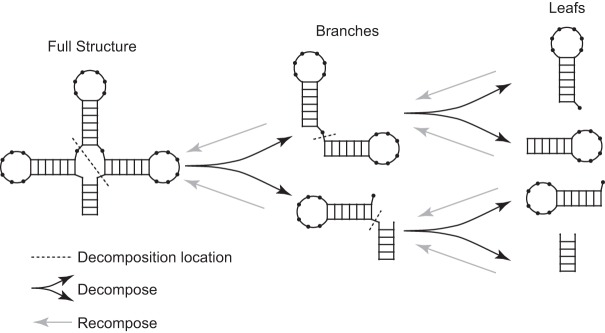
Hierarchical structure decomposition: The structure is recursively decomposed into two fragments at multibranch loops and exterior loops to a user-specified maximum depth (Fig. 5, black arrows). This is in contrast to NUPACK, which decomposes structures by dividing within helices. For Design, the default maximum depth is five decompositions, and this default was used for all the designs reported here. For each decomposition, the goal is to divide the sequence into two fragments of equal length as closely as possible. The sequence can be cut either one or two times to the 5′ side of unpaired nucleotides or a helical branch from an exterior or multibranch loop. Additionally, a valid fragment (branch or leaf) can have only one consecutive set of nucleotides missing, i.e., one interruption in the backbone. For example, the first cut in Figure 5 leaves the lower-left fragment with one consecutive set of missing nucleotides. Also, the minimum length of a fragment is 6 nt. The fragmentation at multibranch loops was chosen because the Design software was tested by designing sequences that will fold to natural structures. NUPACK fragments at structures helices, and this design choice was motivated because the authors of NUPACK were considering engineered structures that would typically have longer helices.

FIGURE 5.

Hierarchical structure decomposition. Black arrows show the structure decomposition into branches and leafs. Gray arrows show the merging of leafs or branches. Dotted line shows the location of structure decomposition.

Mode—Design_Random

The Design_Random mode closely follows the Zadeh et al. (2011b) NUPACK algorithm but with the revised hierarchical structure decomposition. In this mode, leaf redesign step mutates one unpaired nucleotide or base pair at a time. The goal of the algorithm is to generate the sequence with NED lower than a user-defined threshold.

Mode—Design_Preselected

Design_Preselected mode was modified from Design_Random. The initial leaf sequence is filled with sequences (blocks) from the preselected sequence databases instead of random sequences. Helix sequences are drawn from the helix database and loop sequences are drawn from the loop database. For sequences up to and including 20 bp (for helices) or nucleotides (for loops), two blocks are used, with their lengths divided into equal, or roughly equal portions with the length of the first portion rounded down, and blocks of those lengths are chosen. Sequences longer that 20 bp or nucleotides are assembled with blocks of size 10 until 20 or fewer base-pairs or nucleotides are remaining.

In this mode, the leaf redesign step is skipped. When the NED of the designed leaf is above the threshold, the algorithm advances to the leaf reoptimization step by selecting all new blocks. Otherwise assembled leaves are merged together into branches (Fig. 5, gray arrows) and the whole tree goes through the subsequence merging and reoptimization process to design the sequence with the optimal NED.

Structure sets

Parameter dependence of both modes was evaluated using 24 structures: 12 known RNA structures and 12 predicted lowest free energy RNA structures for random sequences (Table 3; Supplemental Table S1). Subsequent performance testing for one set of parameters for each mode was done using 50 structures: 25 lowest free energy structures for random RNA sequences and 25 known RNA structures (Tables 4, 5; Supplemental Table S2). The known structures were chosen to ensure diversity. They come from thirteen RNA families: 5S rRNA (Szymanski et al. 1998), Group I intron (Waring and Davies 1984), 7SK RNA (Andronescu et al. 2008; Nawrocki et al. 2015), hairpin ribozyme (Andronescu et al. 2008; Nawrocki et al. 2015), hammerhead ribozyme type I (Andronescu et al. 2008; Nawrocki et al. 2015), hammerhead ribozyme type II (Andronescu et al. 2008; Nawrocki et al. 2015), RNase E 5′ UTR (Andronescu et al. 2008; Nawrocki et al. 2015), RNase P RNA (Brown 1998), SRP RNA (Larsen et al. 1998), telomerase RNA (Chen et al. 2000), tRNA (Sprinzl et al. 1998), tmRNA (Zwieb et al. 1999), and Y RNA (Andronescu et al. 2008; Nawrocki et al. 2015), and span lengths from 48 to 451 nt. All pseudoknots were removed before designing structures by removing the fewest pairs needed to break a pseudoknot (Smit et al. 2008; Reuter and Mathews 2010). The random sequences mimic the length of known structures.

Lowest free energy structures for random sequences were generated using the Fold program from RNA structure and RNA folding parameters (Supplemental Tables S1, S2; Reuter and Mathews 2010). The sequences were generated using equal probability of nucleotides A, C, G, and U.

SUPPLEMENTAL MATERIAL

Supplemental material is available for this article.