Time at Risk and Intention-to-treat Analyses

Abstract

Although the standard recommendation is to exclude person-time not at risk (ie, time during which the outcome could not have occurred) from the denominators of disease rates, there are scenarios where person-time not at risk should be included. In particular, we draw an analogy between including person-time not at risk and intention-to-treat (ITT) analyses of randomized trials, and excluding person-time not at risk and compliance-corrected analysis of these same trials. Excluding person-time not at risk is appropriate when addressing questions of the biologic or mechanistic effects of an exposure, whereas the ITT-type approach typically addresses questions regarding the effect of an exposure under observed compliance patterns. The choice of approach directly affects the causal question being addressed and subsequent inference, with potential implications for public health. When interested in estimating treatment effects that allow and account for potential noncompliance, or where the exposure may be associated with the time at risk, we argue that person-time not at risk should be included. In the case of time to pregnancy, although the ITT-type analysis may underestimate the biological fecundity of the population, it may also yield an answer to a question that is of more interest to couples trying to become pregnant.

Exposure misclassification is common in epidemiologic data. In randomized trials, treatment noncompliance may be viewed as a type of exposure misclassification. However, this type of misclassification is often ignored in the randomized trial setting under the rationale of an intention-to-treat (ITT) analysis. An ITT approach estimates the causal effect of the assigned treatment plan, regardless of compliance with the component(s) of the assigned plan.^1,2 In this way, the ITT analysis answers questions regarding effectiveness of treatment under realistic scenarios that include noncompliers and cross-overs, and yet is a biased estimate of the biologic effect of exposure to the extent that there is noncompliance.

The portability of this ITT/effectiveness estimate depends on the assumption that the noncompliance in the target population will be the same as seen in the trial population.³ Thus, the ITT approach, while yielding a biased estimate of the biologic exposure effect, may come closer to estimating effects relevant in practice.⁴ However, exclusion of noncom-pliant individuals means that we are no longer studying treatment assignment per se, and accounting/adjusting for any post-treatment variables (eg, compliance) may lead to bias of the ITT effect.^5,6 On the other hand, appropriate compliance-corrected approaches can be used to estimate the biological effect for would-be compliers⁴ (ie, the complier-average causal effect) under additional and untestable assumptions using the principal stratification framework^7,8 or g-methods.^9–11

In an analogous fashion, it is important to consider how potential misclassification of the time at risk is handled in observational studies, as there are direct consequences on the questions that can be answered. Because it is acknowledged that a person must be at risk of the outcome for an exposure to have an effect, person-time when the outcome could not have occurred is generally excluded from the denominator of rates (or the risk set for hazards) to obtain unbiased effect estimates.¹² This person-time is commonly thought of as “immortal person-time” when this time not at risk occurs before study entry, and failure to account for person-time not at risk leads to bias that may be either toward or away from the null.^12–15 The direction of bias depends on whether the person-time not at risk is differential with respect to exposure, and what effect measure is of interest. The approach of excluding person-time not at risk is typically aimed at estimating the biologic or mechanistic effects of exposure, though other effects more relevant in practice may be of more interest.

The potential for this “immortal time bias” is not only theoretical, but also has been observed in practice. In fact, issues of accounting for person-time not at risk and the potential for immortal time bias have received considerable attention in the recent literature, as it has been observed that erroneous findings have been published owing to improper accounting for person-time not at risk.^14–22 Specifically, it was reported that sun exposure was associated with longevity,¹⁷ a finding that was later attributed to immortal time bias.^18–20 This bias has also been observed in the pharmacoepidemiology literature, most recently in the evaluation of statin use and progression of diabetes.¹⁶ These issues are not specific to a single substantive area of epidemiology (or the field of epidemiology itself), and recent errors highlight the need to carefully evaluate time at risk in epidemiologic analyses.

In each of the recent examples, the general recommendation to always exclude person-time not at risk has been maintained.²³ However, we argue that there are cases when the exposure is associated with being at risk, where exclusion may lead to bias, and that it may be advantageous to include person-time not at risk. In deciding whether to include or exclude person-time not at risk one must consider not only the question of interest but the underlying causal structure, as well. In these ways, the inclusion or exclusion of person­time not at risk can be thought of analogous to the ITT versus compliance-corrected analytic approaches to randomized trials. We consider the example of estimation of time to pregnancy below and argue that person-time not at risk should be included in effect estimation for a key question of most interest to couples trying to become pregnant.

TIME-TO-PREGNANCY APPLICATION

To illustrate these concepts, we consider estimation of time to pregnancy, the time it takes for a couple to conceive (or the number of noncontracepting menstrual cycles to conception). Time to pregnancy is often used to estimate a couple’s fecundability,^25,26 or the probability of conception per menstrual cycle for a sexually active couple not using contraception.²⁷ Time to pregnancy is of particular interest to couples planning pregnancy and to reproductive epidemiologists studying factors associated with fecundity.

To assess potential lifestyle, behavioral, or environmental impacts on time to pregnancy, epidemiologists typically limit evaluation to women “at risk” for pregnancy; this approach was employed by Baird and Wilcox.²⁸ Specifically, investigators typically argue that analysis should be limited to menstrual cycles at risk of pregnancy (ie, menstrual cycles where sexual intercourse occurred during the fertile window with no use of any contraception), and that including cycles not at risk would bias estimates of time to pregnancy, as well as associations with exposures of interest. When using only cycles at risk (that is, under “full compliance”), a study of time to pregnancy estimates the average number of cycles it takes a couple to become pregnant, which can be interpreted as an estimate of biologic fecundity. By excluding any menstrual cycle in which a couple did not have intercourse during the fertile window (and were thus “noncompliant,” and therefore immune/immortal to pregnancy, in the sense of being structurally not at risk of pregnancy), we are implicitly seeking to address the more biological hypothesis regarding a couple’s underlying fecundity.

However, suppose we chose to include the not-at-risk cycles: for example, cycles in which a couple does not have unprotected sex during a fertile period. In this case, we are estimating the number of cycles it takes a couple to become pregnant, with the understanding that during some cycles the couple may not be “actively trying” to conceive and thus are immune to pregnancy. This parameter may be of more interest to couples who are trying to become pregnant, especially those who are not timing intercourse. Therefore the choice to include or exclude cycles not at risk (that is, immortal person­time) depends strongly on the effect measure (or parameter) of interest. Of course, in reality, defining at-risk cycles depends on our ability to accurately define the fertile window, and to assess a couple’s intercourse behavior during that time. Thus, imperfect assessment of cycles at risk impacts our ability to answer questions regarding a couple’s underlying biologic fecundity.

These issues have also been explored in the statistical literature. Using a simple modeling approach, Zhou and Weinberg have formalized fecundability as the probability of conception, Y, for a given couple i in menstrual cycle j as:

$$P\left(Y_{ij}=1|X_{ijk}\right)=A_{ij}\left\{1-\underset{k}{\mathbf{\Pi }}{\left(1-p_{ijk}\right)}^{x_{ijk}}\right\}$$

where X_ijk is an indicator for intercourse on day k, with k centered on the day of ovulation, where A_ij is an indicator representing whether the cycle was “viable” or at risk.²⁷ Using this modeling approach, any cycle that is not at risk is not included in the estimation of fecundability (in line with the exclusion of person-time not at risk). However, the original model of fecundability developed by Barrett and Marshall did not include A_ij, and thus ignored whether cycles were “at risk,” and follows what we have been describing as an ITT-type of approach for modeling fecundability.²⁹

TIME-TO-PREGNANCY EXAMPLE

To illustrate this phenomenon, we used data from a study of the effects of smoking on time to pregnancy among 678 pregnant women who were interviewed to determine the time it took them to become pregnant.^28,30 Our goal was to show potential impacts of including and excluding person-time not at risk on time-to-pregnancy estimation. In the original analysis of these data,^28,30 the authors excluded cycles in which women reported sexual abstinence owing to travel, sickness, or other reasons; cycles with sporadic use of birth control were counted as half cycles. However, detailed information regarding intercourse patterns was not available in this study, and so we were not able tofurther refine and determine at-risk status for all cycles. Therefore, we simulated the immortal cycles using six probability distributions to set approximately 15% of cycles to be not at risk across the total number of cycles it took couples to become pregnant (Table 1). This estimate is based on prior reports from this study that showed that 9% of women had at least one cycle excluded for the reasons listed above, and 11% of women reported sporadic use of birth control for two or more cycles.^28,30 Probability distributions were chosen to cover scenarios where cycles not at risk were evenly distributed (using a uniform distribution of not-at-risk cycles), more likely to occur at the beginning of follow-up (such as situations where study participants were not familiar with the protocol, or did not have knowledge regarding the fertile window) (using a Poisson or exponential distribution), and more likely to occur later on in situations where couples become tired of “trying” consistently (using a growth curve model as described in the eAppendix, http://links.lww.com/EDE/A836). Couples who were administratively censored at 13 menstrual cycles in the original study were not included in this analysis. Kaplan-Meier curves (with number of menstrual cycles as the time scale) were plotted for both the original data (including the appended immortal person-time), and the data that excluded the cycles not at risk (Figure 1). In the latter case, active cycles were counted consecutively: for example, if a subject was at risk for cycles 1–5, absent for 6, and present for 7–13, then cycles 7–13 would be “left-justified” and counted as cycles 6–12. This approach is an approximation that is appropriate under a constant hazard of pregnancy. We also estimated the hazard ratios (HRs) for the association between smoking and time to pregnancy, and compared estimates between the original data, with person-time excluded using the six different probability distributions, with person-time excluded for smokers only, and with person-time excluded for non­smokers only. Further details are included in the eAppendix (http://links.lww.com/EDE/A836).

TABLE 1.

Original Time-to-pregnancy Data and Results After Exclusion of Simulated Cycles Not-at-risk, Based on Six Probability Distributions

		Cycle												% Person-time Included
		1	2	3	4	5	6	7	8	9	10	11	12
Original		227	123	72	42	21	31	11	14	6	4	7	9	100
Poisson (λ = 1)	e−1 / i!	288	113	53	31	23	19	11	8	5	4	9	3	81
Poisson (λ = 2)	e−2 2i / i!	291	128	58	30	19	13	9	6	4	3	4	2	72
Exponential (β = 0.9)	e−0.9i / 0.9	286	112	56	31	22	19	11	8	4	4	11	3	84
Uniform	(1/13)	255	131	72	40	21	22	9	8	4	2	3	0	77
Growth curve type 1	$\frac{1-e^{-ai}}{13-1/a},a=1$	251	131	73	41	21	24	8	9	3	2	2	2	77
Growth curve type 2	$\frac{1-e^{-ai}}{13-1/a},a=0.2$	245	131	75	42	20	25	9	9	4	3	2	2	78

FIGURE 1.

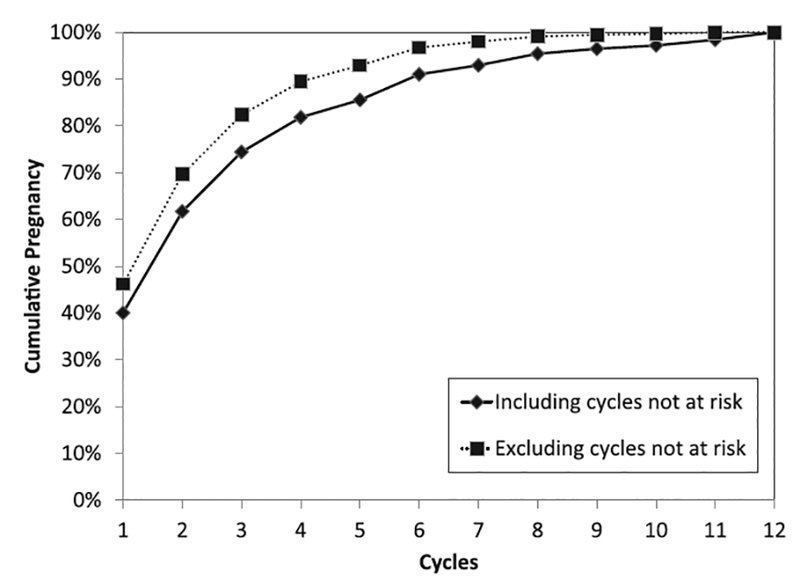
Complement of the Kaplan-Meier curves for 586 women followed for 12 months, both including and excluding not-at-risk cycles, based on a uniform distribution.

As expected, when cycles not at risk were excluded, the average time to pregnancy was shorter (Figure 1). For example, when excluded cycles followed a uniform distribution, 62% of women were pregnant after the second cycle (median time to pregnancy = 2) when including the cycles not at risk, compared with 70% of women when excluding the cycles not at risk (median time to pregnancy = 2). In other words, for couples in the general population with the same behavioral patterns as our cohort, the estimated percentage of women who are pregnant by the second cycle is 62%, though the true biological fecundability by the second cycle is 70%. To evaluate the effect of time not at risk on time to pregnancy, we estimated the HR for time to pregnancy comparing exclusion of time not at risk with inclusion of time not at risk. We observed an HR of 1.24 (95% confidence interval [CI] = 1.10–1.40), which indicates that the biological effect resulted in a time to pregnancy that was 25% shorter than the time to pregnancy for the public health effect after removal of only 15% cycles not at risk. Similar results were observed for all probability distribution assumptions for excluding person-time: in short, excluding the not-at-risk cycles has the effect of shifting the time-to- pregnancy distribution to the left. For couples who reported three menstrual cycles to become pregnant, the effect of excluding any not-at-risk cycles yields the true number of at-risk menstrual cycles it took them to become pregnant, which would be between 1 and 3. Though this analysis is based on several assumptions, this example illustrates that the estimated time to pregnancy depends on how not-at-risk cycles are handled.

We further evaluated the impact of excluding not-at-risk cycles when assessing the impact of smoking status on time to pregnancy (Table 2). In the data with the added cycles not at risk, the overall HR for the effect of smoking on time to pregnancy was 0.72 (95% CI = 0.58–0.90). Thus, including person-time not at risk here addresses what may be considered the more relevant public health question of the effect of smoking on time to pregnancy; that is, to estimate how long it would take a couple to achieve pregnancy under normal daily circumstances when some of cycles the couple may not be “actively trying” to conceive. When not-at-risk cycles were excluded, this association was attenuated, and estimates were less precise. Estimates of the HR ranged between 0.79 and 0.81 depending on how the not-at-risk cycles were generated, though the association was no longer always statistically significant, as there was a loss in power owing to excluding the cycles not at risk. Excluding these cycles not at risk seeks to address the more biological hypotheses regarding the effect of smoking on a couple’s underlying fecundity. The choice of distribution for excluding cycles not at risk had little impact on the results overall. Although these illustrations are contrived, they are meant to demonstrate that even modest amounts of time not at risk can have sizable impacts on epidemiologic results.

TABLE 2.

Association Between Smoking and Time-to-pregnancy Comparing All Cycles to Not-at-risk Cycles Excluded Overall, Excluded for Smokers Only, and Excluded for Non-smokers Only

	Original Data		With Not-at-risk Cycles Excluded
			Excluded for Everyone		Exclude for Smokers Only		Exclude for Nonsmokers Only
	HR	(95% CI)	HR	(95% CI)	HR	(95% CI)	HR	(95% CI)
Poisson λ = 1	0.78	(0.62–0.97)	0.80	(0.64–1.00)	0.90	(0.72–1.13)	0.69	(0.55–0.86)
Poisson λ = 2			0.79	(0.64–0.99)	0.99	(0.79–1.23)	0.62	(0.50–0.78)
Exponential β = 0.9			0.81	(0.65–1.02)	0.91	(0.73–1.14)	0.70	(0.56–0.87)
Uniform			0.81	(0.65–1.01)	0.97	(0.77–1.21)	0.64	(0.51–0.80)
Growth curve A = 1			0.81	(0.64–1.01)	0.94	(0.75–1.18)	0.65	(0.52–0.82)
Growth curve A = 0.2			0.80	(0.64–1.00)	0.92	(0.74–1.15)	0.66	(0.53–0.83)

Furthermore, one must also consider the underlying causal structure. Here we were interested in the effect of smoking on time to pregnancy, though these issues are gen- eralizable to any exposure of interest. If the time at risk is a function of acute exposure (eg, if smoking is associated with probability of intercourse during the fertile window), and there exists an unmeasured factor that is associated with being at risk and the outcome, then stratifying by exclusion on time at risk may lead to collider stratification bias (Figure 2A). Removing cycles that are not at risk, and therefore stratifying on being at risk (analogous to the bias induced by proportional hazards models),^30,31 could also be a source of collider-stratification bias. In our data example, we differentially excluded not-at-risk cycles for smokers and nonsmokers to simulate the scenario of an unmeasured factor that resulted in the removal of more cycles for smokers than nonsmokers (and vice versa). If person-time not at risk was excluded only for the smokers in this study (ie, differential, as shown in DAG 1), then the HRs became null. However, when not-at-risk person-time was excluded only for nonsmokers, the association between smoking and time to pregnancy was strengthened (HRs of 0.60–0.70). We observed that this differential exclusion of time not at risk had a strong effect on estimates and accompanying inference. In the analogous clinical trial setting, the ITT approach would be unbiased regardless of whether or not treatment assignment is associated with compliance when addressing the public health effect (Figure 2B). However, any compliance-adjusted analysis should consider whether or not treatment assignment is associated with compliance and employ methods that provide consistent estimators of the parameter of interest to avoid bias.

FIGURE 2.

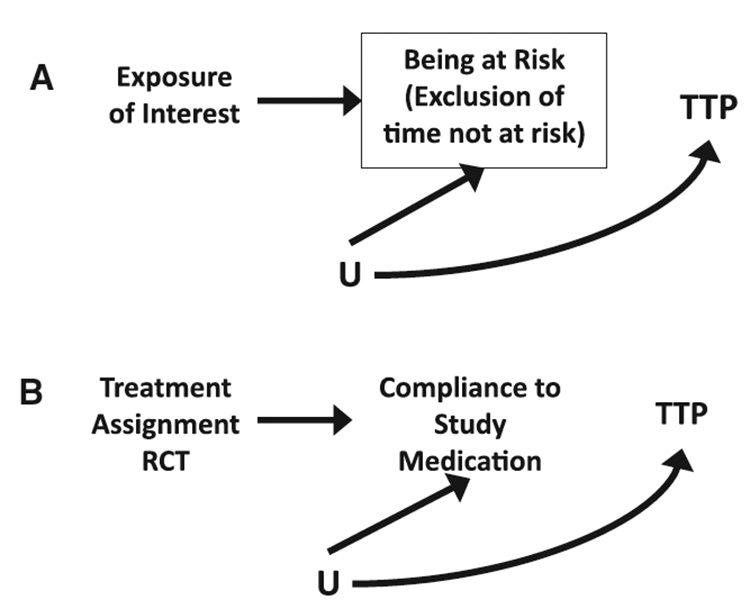
Directed acyclic graphs under the null demonstrating (A) exclusion of not-at-risk person-time in observational studies (box signifies conditioning on being at risk), and (B) The intent-to-treat approach. RCT indicates randomized controlled trial; TTP, time-to-pregnancy.

DISCUSSION

A standard recommendation is to exclude person-time not at risk for the outcome.²³ This recommendation may be the most appropriate strategy in many settings. For example, in studies of drug safety, when mechanistic effects of treatment on adverse events are of primary interest, exclusion of person-time not at risk is usually warranted.^13,14 However, there are settings, such as when studying the effect of exposures on time to pregnancy, where inclusion of person-time not at risk is an appropriate choice for estimation of the effect of interest, particularly in cases where the exposure of interest may be associated with being at risk. Exclusion of person­time not at risk and the ITT approach both inherently deal with issues of noncompliance or misclassification, though with compliance to different time scales: the time at risk and the time exposed. Though the ITT and person-time not-at-risk scenarios have an important difference in that the ITT is based on randomization, the question of how to deal with this mis- classification or noncompliance (whether for at-risk periods, or for time not exposed) is a critical issue in both situations because these issues affect interpretation of research findings and questions that are addressed. Excluding not-at-risk person-time addresses questions regarding biologic effects of an exposure, whereas the ITT-like approach of including the not-at-risk person-time addresses questions regarding effects of an exposure under the compliance observed. The effect of interest should thus be clearly stated; the appropriate design and analytic approach should follow accordingly and take the question of interest— and therefore the underlying causal structure— into account. We expect that in many cases estimates of both parameters will be desirable.

In the time-to-pregnancy example, including not-at-risk cycles (similar to the ITT-type approach) would provide an unbiased estimate of the population average time to pregnancy under the compliance observed (or the average number of cycles it takes a couple that behaves like the couples in our study to become pregnant). This is an underestimation of the biological fecundity of the population to the extent that there are cycles where the couples cannot conceive. We would expect the average time to pregnancy to differ across populations with different compliance if the not-at-risk person-time were not excluded, but to be more similar when not-at-risk person-time is excluded (although of course other differences, such as age distributions, coitus frequency, etc., will lead to heterogeneity across populations). Differences in the latter case are more likely owing to differences in biological fecundity. Practical considerations also come into play, as in many cases it may be difficult to accurately classify at-risk and nonat-risk periods. For example, in the case of determining at-risk menstrual cycles it is necessary to have daily information on intercourse to appropriately classify cycles with intercourse during the fertile window as the only at-risk cycles. Though such data are available in some studies, it is not always feasible to collect, or of the highest quality. Thus, even when attempting to exclude cycles that are not at risk, it may be difficult to reliably capture this information. Investigators are encouraged to use all of the available data to classify this person-time to the best extent possible, with appropriate sensitivity analyses to assess potential misclassification. Though we may not be able to answer questions regarding a couple’s biologic fecundity well, this may not be the question of central interest to couples. As previously stated, what may be of most interest to couples trying to become pregnant is the average number of months, including potential cycles not at risk, it will take them to conceive. To estimate this parameter, notat-risk person-time m ust be included, which goes against the standard recommended analytic approach.²³ It is important to note that in the example of time to pregnancy we have focused our attention on the aspect of classification of time at risk, and recognize that the different study designs used for time-to-pregnancy studies have critical impacts on inference and that studies are complicated by nuances that are not addressed in this example.^32,33

As pointed out, one must consider the underlying causal structure. We observed that when an exposure was associated with being at risk, removing cycles not at risk can lead to collider stratification bias. Here we limited our discussion of “cycles at risk” to cycles where intercourse occurred during the fertile window, though some have also considered restricting to ovulatory cycles. In the example of the effects of smoking on time to pregnancy, it is plausible that smoking may affect ovulation, and thus restricting to ovulatory cycles would be akin to adjusting for a mediator, which may also result in collider-stratification bias. Buck Louis et al³⁴ used a similar rationale for not adjusting for sexual intercourse in their analyses. These findings underscore the need to evaluate the underlying causal structure when assessing the impact of excluding time not at risk.

The decision to include or exclude time not at risk generalizes to several other settings. For example, in studies of effects of ski helmet use on head injuries, researchers often select head-injury cases and compare to controls with other injuries, to control for factors related to risk-taking behavior.^35,36 This approach considers only time at risk for an injury (ie, person-moments in which a fall occurs), and considers all other time (eg, time not on the slopes) as not at risk, which can (under certain assumptions) be used to estimate the effect of helmet use on head injury. Alternatively, investigators might include all person-time for helmet users and non-users and ignore the potential misclassification of time in which helmet users did not ski, which is analogous to the ITT approach and more closely addresses public health questions of interest regarding helmet use policies.

Likewise, some studies of HIV transmission focus on HIV-negative individuals in a committed partnership with an HIV-positive partner (that is, serodiscordant couples), whereas other studies focus on sexually active HIV-negative individuals with partners of unknown status. Considering only coital acts unprotected by condoms, all sex acts among the former couples are at risk, whereas in the latter case only those acts with an HIV-positive partner are truly at risk of HIV. Because the majority of studies are of the latter form, most analyses are ITT estimates of effect and may generalize poorly to serodiscordant couples.

Of note is the considerable body of work evaluating time not-at-risk (or immortal time) and classification of exposure in the context of inhaled corticosteroid use and chronic obstructive pulmonary disease in trying to understand differences in results between clinical trials and observational studies.^37,38 How person-time was handled in the design and analysis of these studies proved critical, as it led to differing recommendations for clinical practice. Observational studies that employed the conventional ITT approach were considered as suffering from immortal time bias.³⁶ These results highlight the importance of clearly stating the question of interest and handling person-time accordingly.

Investigators often have strong feelings regarding either the ITT approach or the exclusion of person-time not at risk. For example, some investigators are adamantly in favor of the ITT approach and simultaneously adamantly opposed to the inclusion of not-at-risk person-time; however, as we have described, these beliefs are in opposition in some cases. We have shown how these approaches are related, and how the arguments underlying each approach are parallel, but we do not argue that one approach is superior. The choice of whether to include or exclude not-at-risk person-time depends primarily on the underlying causal structure and whether one is interested in the more biologic-related or policy-related research questions. When interested in estimating treatment effects that allow, and account for potential misclassification or “noncompliance,” we argue that not-at-risk person-time should be included (but must be accounted for, perhaps using inverse-probability weights, where a positivity assumption is crucial). Moreover, in cases where being at risk and the outcome of interest share common causes, the general approach to exclude this person-time would be biased. In the case of time to pregnancy, though the ITT analysis may underestimate the biological fecundity of the population, it yields a more generalizable or population effect that answers the question of most interest to couples trying to become pregnant. Indeed, the ITT-like approach, including person-time not at risk, may be preferable for many questions in population health.