Radiotherapy of lung cancers: FFF beams improve dose coverage at tumor periphery compromised by electronic disequilibrium

Abstract

The purpose of this work was to investigate radiotherapy underdosing at the periphery of lung tumors, and differences in dose for treatments delivered with flattening filter-free (FFF) beams and with conventional flattened (FF) beams. The true differences between these delivery approaches, as assessed with Monte Carlo simulations, were compared to the apparent differences seen with clinical treatment planning algorithms AAA and Acuros XB.

Dose was calculated in a phantom comprised of a chest wall, lung parenchyma, and a spherical tumor (tested diameters: 1, 3, and 5 cm). Three lung densities were considered: 0.26, 0.2, and 0.1 g/cm³, representing normal lung, lung at full inspiration, and emphysematous lung, respectively. The dose was normalized to 50 Gy to the tumor center and delivered with 7 coplanar, unmodulated 6 MV FFF or FF beams. Monte Carlo calculations used EGSnrc and phase space files for the TrueBeam accelerator provided by Varian Medical Systems. Voxel sizes were 0.5 mm for the 1-cm tumor and 1 mm for the larger tumors. AAA and Acuros XB dose calculations were performed in Eclipse™ with a 2.5-mm dose grid, the resolution normally used clinically.

Monte Carlo dose distributions showed that traditional FF beams underdosed the periphery of the tumor by up to ~2 Gy as compared to FFF beams; the latter provided a more uniform dose throughout the tumor. In all cases, the underdosed region was a spherical shell about 5 mm thick around the tumor and extending into the tumor by 2–3 mm. The effect was most pronounced for smaller tumors and lower lung densities. The underdosing observed with conventional FF beams was not captured by the clinical treatment planning systems.

We concluded that FFF beams mitigate dose loss at tumor periphery and current clinical practice fails to capture tumor periphery underdosing and possible ways to mitigate it.

Introduction

When radiation travels from a region of low density into one of high density (e.g., air to tissue), there is a well-known buildup of secondary electrons corresponding to a buildup of dose. In this superficial region there is, in essence, an underdose compared to deeper depths where transient electronic equilibrium is established. This issue is clinically relevant and in some situations explicitly managed. For example, when the goal is to treat surgical scars to the surface, they are covered with bolus to ensure the surgical bed is not underdosed. In contrast, this issue is not managed (substantially because it cannot readily be managed) for lung tumors. When a radiotherapy beam passes through lung and then enters tumor, there is a buildup of dose in the periphery of the tumor, corresponding to an underdose of the tumor periphery compared to the bulk of the tumor volume. If this underdose is accounted for by the treatment planning system, the issue can at least be known in clinical practice. However, planning systems are notoriously poor at calculating dose in the buildup region as explained below, which raises serious concerns about how well this underdosing is actually identified in clinical practice. For example, an underdosing of the lung tumor periphery was concluded by Chetty et al. (2013) when reviewing a cohort of 133 patients treated with lung stereotactic body radiation therapy on the basis of different dose calculation algorithms. They estimated the underdose caused by electronic disequilibrium and found that it reduced the tumor control probability by up to 9% for some patients.

Mitigating the risk is difficult because it arises from basic interactions of x-rays in the media. However, in this study we consider a possible solution: the use of flattening filter-free (FFF) x-ray beams. For the Varian implementation of FFF beams, where energy is not raised (Xiao et al. 2015), the 6 MV FFF energy spectrum is considerably softer than that of the corresponding flattened beam, with average photon energies of 1.28 MeV and 1.75 MeV, respectively (Vassiliev et al. 2006b). We hypothesize that in the case of lung tumors, this effect will help to mitigate the underdosage caused by electronic disequilibrium because the range of secondary electrons, and therefore the range and magnitude of the underdose, will be less.

While the issues of electronic disequilibrium and the accuracy of the treatment planning system have been raised, a detailed study of these issues is actually even more complex because of the numerous factors that make dose calculations for lung radiotherapy particularly difficult (Chetty et al. 2007). Ranges of delta electrons in the low-density lung parenchyma are larger by a factor of about four than those in soft tissue, resulting in penumbra widening and necessitating more accurate models of electron transport, especially in high-dose-gradient areas and where the lung is adjacent to tissues of higher densities. Accurate radiation transport under these conditions is a serious challenge, and even contemporary dose calculation algorithms (e.g., analytical anisotropic algorithm; AAA) have shown substantial errors (Kry 2013, Dunn 2015). In addition to the challenges of radiation transport, the accuracy of dose calculations in interface regions is limited by the quality of computed tomography (CT) image sets used for treatment planning. Four-dimensional CT images are presently taken for most patients, but they are usually used only to determine the extent of tumor motion. Dose calculations most commonly are performed on the average CT image. Because of tumor motion, such averaging misrepresents densities near the interface - it replaces the very sharp density gradient truly present at the lung-tumor surface with a rather wide shell around the tumor where the density changes much more gradually. More specifically, Knybel et al. (2016) reported the mean tumor motion amplitude of 6.0 ± 2.2 mm in the superior-inferior direction for a cohort of 145 patients treated with stereotactic ablative therapy. This means that in the average CT image the mean width of the transition region from tumor to lung density expands by 6 mm. This exceeds the range of a 1 MeV electron in water. This indicates that in calculations of dose distributions near the lung-tumor interface, motion artifacts in the CT image often contribute more to the uncertainties than do the inaccuracies of electron transport algorithms. It is therefore unlikely that a treatment planning system even with advanced dose algorithms can fully capture underdosage caused by disequilibrium. In that case, the effect manifests as an underdosing in a treatment actually delivered.

The underdosing of lung tumor surface caused by electronic disequilibrium has not been well studied, nor are there any clinical solutions designed specifically to boost the dose at tumor surface so as to compensate for the dose lost due to the lack of equilibrium. The purpose of this study was therefore threefold. First, we assessed the degree of lung-tumor underdose caused by electronic disequilibrium. This was done in this study using high-resolution Monte Carlo simulations in a phantom with different sizes of tumor and different densities of lung tissue. Unlike previous studies, this approach provides a clear and isolated assessment of the underdose effect from electronic disequilibrium. Second, to mitigate this effect and the risk associated with it, we evaluated the impact of using FFF beams for radiotherapy instead of traditional flattened beams. Third, to understand how the use of FFF beams to mitigate the underdosing may be evaluated in a commercial treatment planning system, we repeated all of our calculations using two dose algorithms widely used in clinical practice: AAA and Acuros XB (Varian Medical Systems, Palo Alto, CA).

Methods and materials

Phantom

Dose calculations were done in a phantom that was spherically symmetric (see Figure 1). A spherical “tumor” (Gross Tumor Volume, GTV) was placed at its center. We considered three tumor diameters: 1, 3, and 5 cm. The tumor was surrounded by lung tissue (ICRU 46, 1992). For each tumor size, we considered three lung densities: 0.26, 0.2, and 0.1 g/cm³. These values correspond to the average density for a healthy adult (ICRU 46, 1992), density at full inspiration (Hanley et al, 1999), and density of an emphysematous lung (Schwarz et al, 2017), respectively. The lung tissue was bounded by a 3-cm-thick spherical shell representing the chest wall. The material of the tumor and the chest wall was water. The material outside the phantom was air. We chose to use a phantom for our analysis instead of a patient CT image to eliminate uncertainties associated with image artifacts, most importantly the blurring of tumor edge caused by respiratory motion described above.

Figure 1.

The phantom irradiated by seven coplanar beams.

Beams

The tumor was irradiated by seven coplanar beams collimated to the tumor with a Millennium 120 multileaf collimator (Varian Medical Systems). The leaves were positioned so as to create a 5-mm gap around the tumor. The isocenter for all beams was at the tumor center, and the source-to-axis distance was 1 m. For the FF beams, the beam energy was set at 6 MV because this is the most common energy used for treating lung tumors. For FFF beams, we also chose 6 MV because two recent studies have shown better sparing of organs at risk with 6 MV FFF beams than with 10 MV FFF beams (Lu et al. 2015; Tambe et al. 2016). All dose distributions were normalized to deliver 50 Gy (prescription dose, Dx) to the isocenter. We used this point normalization, rather than a planning target volume (PTV) coverage-based normalization, to remove the impact of dose calculation uncertainties in the transition region between the tumor and the lung, as that region was the focus of our study. The impact of electronic disequilibrium at the edge of the tumor was evaluated by comparing the dose calculated in the phantom as described above (for each lung density and tumor volume) versus the dose calculated in the phantom where the lung tissue was replaced with water.

Monte Carlo dose calculation

Our most accurate dose calculation method, used to define the actual dosimetry for the lung tumor, was full Monte Carlo. We used the BEAMnrc / DOSXYZnrc system (Rogers et al. 1995; Walters et al. 2005) to model the Varian TrueBeam accelerator. Initial particle characteristics were read from phase space files provided by the manufacturer (www.myvarian.com/montecarlo) that have been validated for both FF and FFF beams (Constantin et al. 2011; Gete et al. 2013; Belosi et al. 2014). All particle trajectories started in a plane located immediately above the jaws. Particle transport in the accelerator beamline below the phase space plane was done with a previously validated model of the Varian 2100 accelerator (Cho et al. 2005) and an in-house Monte Carlo model of the Millennium 120 multileaf collimator (Jang et al. 2006). Particle trajectories were terminated when they reached a plane immediately below the multileaf collimator, and their phase coordinates were saved in a second phase space file. Dose distributions were calculated in the phantom using these second phase space files, 1.7 billion histories per beam, and the DOSXYZnrc code. The phantom was voxelized with a voxel size of 1 mm for the 3-cm and 5-cm tumors and a voxel size of 0.5 mm for the 1-cm tumor. Particles from the second phase space file were reused (“recycled”) up to 20 times. The electron tracking cut-off energy was 521 keV, which includes the rest energy and corresponds to a residual range of ~10 µm in water (Francis et al. 2011). To reduce statistical uncertainties, we used the reflectional symmetry of individual beams with respect to the diametric line parallel to the direction of leaf motion and with respect to the diametric line normal to the direction of leaf motion. To do so, we added doses from the original beam and from two beams each flipped with respect to one of the two diametric lines, plus from a beam flipped twice, first against the first line and then against the second line. Statistical uncertainties in the target volume (1 standard deviation) were in the range of 0.1–0.4 Gy.

Clinical dose calculation

Clinical dose calculations are rarely based on Monte Carlo. Therefore, for comparison we also calculated dose distributions with two of the most advanced dose algorithms used commonly in the clinic, AAA and Acuros XB (AXB). Both algorithms belong to the category of model-based algorithms (Chetty et al. 2013). AXB is a grid-based Boltzmann equation solver (Vassiliev et al. 2010) and has been shown to consistently perform better than the AAA (Bush et al. 2011; Kroon et al. 2013; Dunn et al. 2015; Liang et al. 2016). In both cases, we used a 2.5 mm dose grid because it is the one usually used clinically, but we also calculated the Acuros XB results using a 1 mm dose grid. Both algorithms were configured using Varian’s TrueBeam representative beam data.

Analysis

The focus of this study was on the region near the tumor-lung interface. We compared the dose distribution at and around this tissue interface for FFF versus FF beams for each of the three different lung densities, tumor volumes, and calculation algorithms.

Results and discussion

The ring of underdosage

We first investigated the degree of tumor periphery underdosage caused by electronic disequilibrium. This disequilibrium is caused by the sharp density gradient between a lung tumor and the lung tissue surrounding it. To explain this effect, let us consider a small volume within the tumor. When photons interact with tissue in a volume, they transfer energy to delta electrons that carry out of the volume some of the energy they received (energy loss). This is offset by receipt of some energy from electrons produced outside the volume (energy gain), mostly from nearby regions located upstream with respect to the incident photon beam. In electronic equilibrium, the average energy loss is equal to the average energy gain.

Two main factors affect this energy balance. The first is the rate of electron production inside and outside the volume. This rate is determined by the photon collision density, which is the product of photon interaction cross section (electron production cross section) and photon fluence (Vassiliev, 2017). This cross section is approximately proportional to the number of electrons per unit volume (number density). Therefore, the electron production rate within the tumor is much higher than in the lung. Hence, if the volume is at the tumor surface, where the beam enters the tumor, nearby upstream regions of the lung will not produce a sufficient influx of electrons to compensate for the energy loss. This will result in disequilibrium and in underdosage of surface regions of the tumor. Chetty et al. (2013) described the effect as a “ring of underdosage”.

The second factor affecting the energy balance is geometrical. Because of the low lung density, electrons have a relatively large range. Therefore, reaching the tumor surface are not only electrons produced in the regions immediately adjacent to the tumor but also electrons produced farther upstream. These long-range electrons partially compensate for the low electron production rate. The compensation is partial because the number of electrons reaching the tumor surface is reduced by lateral scattering. This loss is greater for narrow beams than for wide beams, because in the latter case more scattered electrons remain within the beam boundaries. Accordingly, the impact of electronic disequilibrium on dose distributions is more apparent for small field sizes (Vassiliev et al. 2010). There is also a reduced dose region at the tumor surface where the beam exits. The reasons are similar, except in this case the influx of electrons backscattered from the lung towards the tumor is reduced for surface regions, as compared to volumes away from the surface.

Figure 2 shows the range of this ring of underdosage for a tumor of 3 cm in diameter irradiated by 7 standard flattened beams (FF). These Monte Carlo calculations show dose deficit in the tumor periphery for lung densities of 0.26 g/cm³ and 0.1 g/cm³ compared to the dose in a homogeneous phantom, in which the lung volume was assigned the same material as the tumor, density of 1 g/cm³. For this homogeneous phantom case using the flattened beam, the dose to the tumor edge was within 1% of the mean tumor dose, indicating that the tumor was geometrically covered by the treatment fields and that underdosing was due to electronic disequilibrium at the heterogeneous interfaces. Dose distributions in all cases were normalized to 50 Gy at the isocenter. It can be seen that at a lower lung density, the underdosage was more severe.

Figure 2.

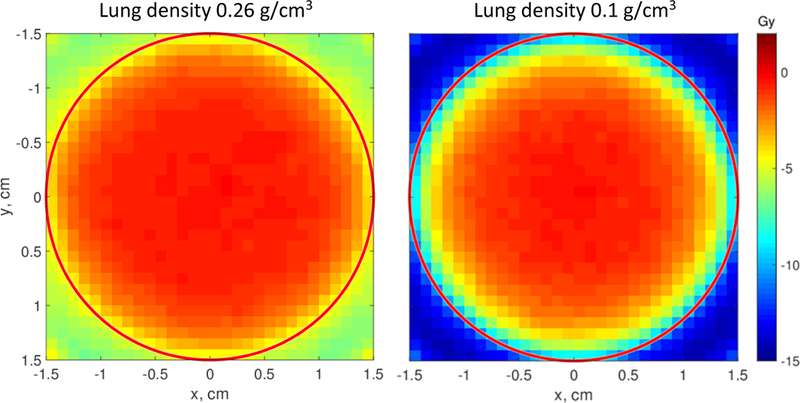
Dose differences ΔD=D(0.26) − D(1) (left) and D(0.1) − D(1) (right) for a 3-cm tumor irradiated with 6 MV FF beams. The numbers in parentheses are densities of the material surrounding the tumor: 0.26 g/cm³ is the average lung density, 0.1 g/cm³ represents a low-density emphysematous lung, 1 g/cm³ is water. Doses for each density were calculated with Monte Carlo and normalized to 50 Gy at the isocenter. Substantial dose deficit at the tumor periphery is seen in both cases. It is particularly severe for the low-density lung.

FFF beams versus FF beams

Previous studies have reported higher skin or surface doses with FFF beams than with FF beams (Vassiliev et al. 2006a, Wang et al. 2012) because of the softer spectrum of the FFF beams. The impact of this softer spectrum is seen in Fig. 3, where we show two-dimensional distributions of the difference between FFF and FF doses, ΔD = D(FFF) − D(FF), for the three tumor diameters (1, 3, and 5 cm) for the lung density of 0.26 g/cm³. In all three cases, FFF beams improved the dose by up to 2 Gy (4% of Dx) in a spherical shell approximately 5 mm thick, covering the tumor surface and extending into the lung. The additional dose to the lung is beneficial, because this region, close to the tumor, is usually a part of the clinical target volume (CTV). Mitigation of the dose loss was most pronounced for the smallest tumor volume and was relatively small for the 5-cm tumor. This latter result arises because non-modulated fields were used to irradiate the phantom, but these are non-flat for FFF beams (Vassiliev et al. 2006a), resulting in FFF beams delivering a lower dose near the beam edges. This effect is more pronounced for larger fields, but could be offset in clinical practice by modulating the treatment fields for larger tumor volumes.

Figure 3.

Dose difference ΔD = D(FFF) - D(FF) for three tumor diameters (1, 3, and 5 cm) and lung density of 0.26 g/cm³. Monte Carlo calculations.

Clinical dose calculation

Using the same lung density of 0.26 g/cm³ and commercial algorithms AAA and AXB, with clinical settings, the dose differences between FF and FFF distributions were calculated. The results are shown in Fig. 4. For all three tumor diameters, both the AAA and AXB underestimated the dose difference, sometimes by more than a factor of two. The AXB results were better than the AAA results but, nevertheless, did not match the Monte Carlo data. Of note, these calculations were performed using a geometrically cleanly defined phantom. In clinical treatment planning, distortion of the CT image by respiratory motion will further compromise the accuracy of calculated doses.

Figure 4.

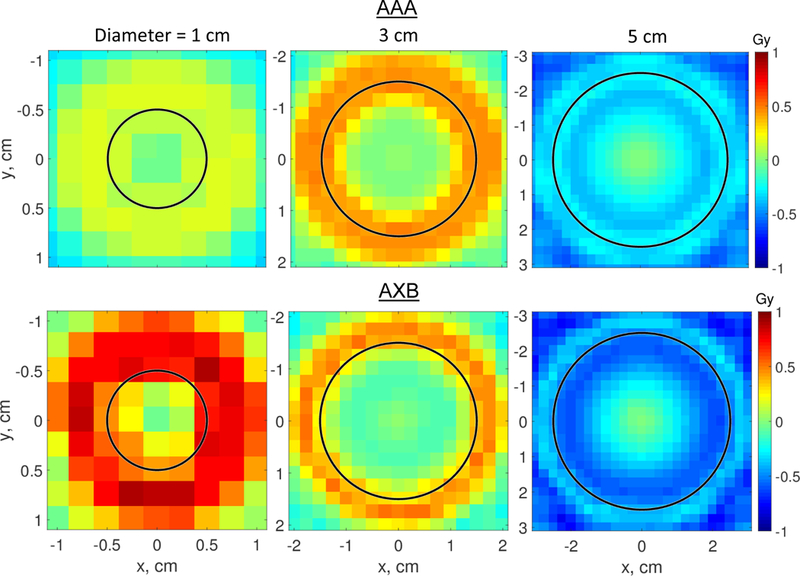
Dose difference ΔD = D(FFF) - D(FF) for three tumor diameters (1, 3, and 5 cm) and lung density of 0.26 g/cm³. The doses were calculated with the AAA algorithm (top row) and AXB (bottom row). Note that color scales in Figures 3 and 4 are different.

In Table 1, for a 3 cm tumor, we compare the minimum tumor doses, D95, and the doses at 2.5 mm from the surface calculated with Monte Carlo, AAA and Acuros XB. The Monte Carlo data show that the FFF provided a more uniform dose to the target for all scenarios examined. The AAA algorithm consistently underestimated all three dosimetric indices. It was previously reported (Ong et al., 2011) that the AAA algorithm has a voxel-size dependent artifact in low density tissue and recommended using 1 mm calculation grid resolution if a large area of such tissue is present. Acuros XB is, again, in a better agreement with Monte Carlo. Both algorithms, however, considerably underestimate the differences between FF and FFF beams. In this very idealized setup, the commercial algorithms partially detect underdosage at tumor surface, but with errors of up to 4–5%. For the lung density of 0.26 g/cm³, we additionally calculated doses with the Acuros XB algorithm with 1 mm calculation grid size. In this case dose differences between FF and FFF slightly improved as compared with the standard grid size of 2.5 mm. The differences, however, remain about a factor of two lower than the Monte Carlo results.

Table 1.

Dosimetric indices for a 3 cm tumor. Monte Carlo results are compared with calculations using two commercial algorithms, AAA and Acuros XB.

		GTV, Dmin, Gy		GTV, D95, Gy		Dose at 2.5 mm from tumor surface, Gy
Algorithm	Lung density, g/cm3	FF	FFF	FF	FFF	FF	FFF
Monte Carlo	0.10	37.2	39.2	39.4	41.1	33.3	35.7
	0.20	41.7	43.1	43.7	44.7	39.7	41.3
	0.26	44.1	45.0	45.0	45.7	41.8	42.9
AAA	0.10	35.5	36.6	39.1	40.0	34.7	35.4
	0.20	40.0	40.8	42.6	43.2	39.0	39.8
	0.26	41.7	42.4	43.9	44.4	40.7	41.3
Acuros XB, 2.5 mm grid	0.10	37.0	38.2	40.4	41.3	34.6	36.0
	0.20	41.2	41.9	43.8	44.1	39.9	40.6
	0.26	42.8	43.2	44.9	45.1	41.8	42.1
Acuros XB, 1 mm grid	0.26	42.6	43.1	45.0	45.2	42.0	42.6

The dose distributions in Figs. 3 and 4 were approximately radially symmetric. We calculated the dose as a function of the distance from the isocenter (radial distance), D(r), and Figures 5 and 6 show the results for 1-cm and 3-cm tumors for all three lung densities that we investigated. Data for the 5-cm tumor are not shown because the differences between FFF and FF dose distributions were small. Figures 5 and 6 show clearly that the underdosage depends on the lung density. Even the small density reduction at inspiration (0.2 versus 0.26 g/cm³) reduced the dose to the tumor edge by about 1.5 Gy (3% of Dx). This reduction should be taken into consideration when full-inspiration breath-hold treatments are planned.

Figure 5.

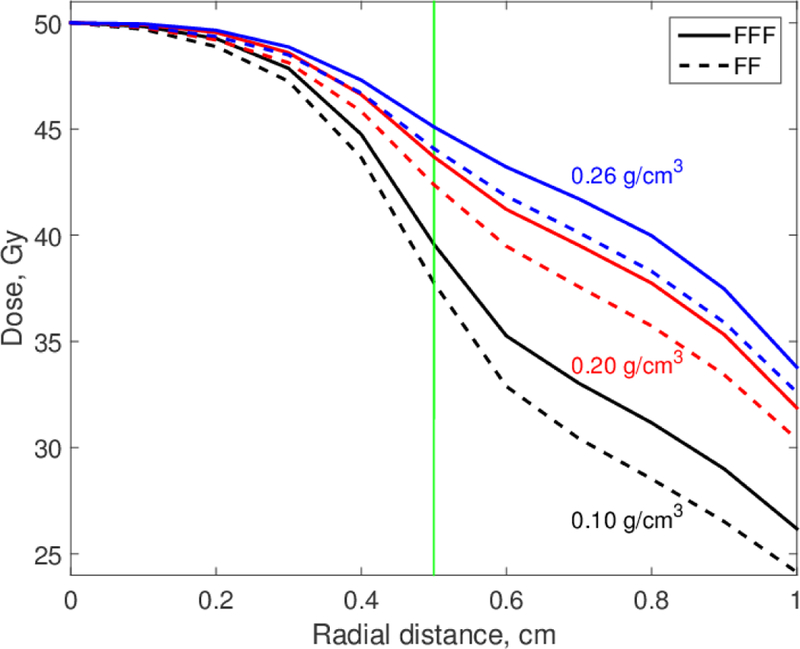
Radial dose distributions for 6 MV FF and FFF beams. Tumor diameter is 1 cm; lung densities are as shown.

Figure 6.

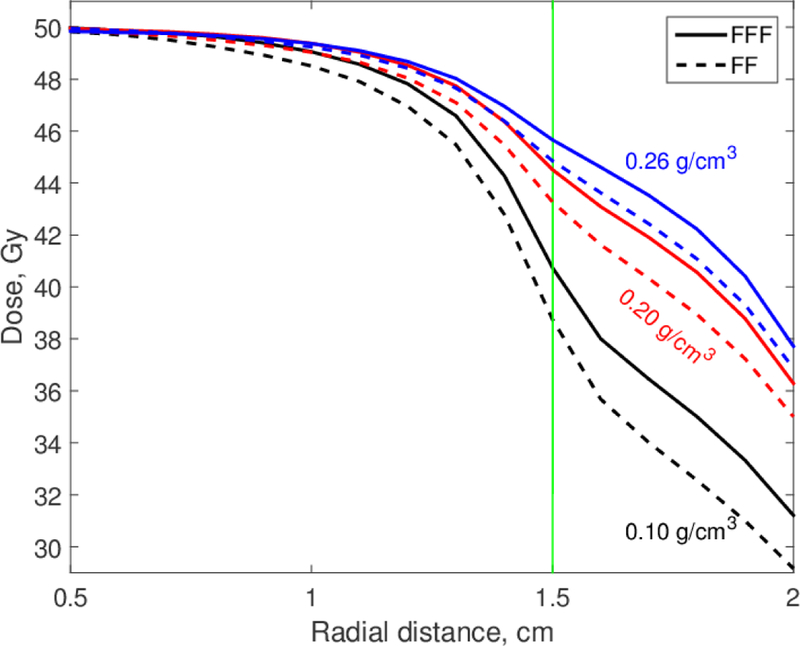
Radial dose distributions for 6 MV FF and FFF beams. Tumor diameter is 3 cm; lung densities are as shown.

Lung density depends on several other factors. In patients treated in a supine position, the anterior lung has a lower density than does the posterior lung because the gravity pulls blood in the posterior direction. The density may also be affected by disease, such as emphysema. A particularly severe underdosage is expected when the tumor is adjacent to an air cavity such as the bronchus.

In our study, FFF beams provided only a modest, 1–2 Gy (2–4% of Dx), dose improvement over FF beams. This dose improvement appears particularly small compared to the heterogeneity seen within the center of the tumor in SBRT treatments: the isocenter dose can be many tens of percent higher than the prescription dose. It must be noted that the heterogeneity near the center of the target generally reflects doses that are all above the prescription dose, meaning that they are all up on the shoulder of the sigmoid dose response curve and therefore these variations (at least in theory) have little impact in tumor response. In contrast, in this study FFF beams increased doses that were dropping below the prescription dose, where the tumor control response begins to rapidly decrease. Moreover, the improvement achieved with the FFF beams was observed in all cases and covered relatively large volumes extending deep into the tumor. The underlying reason for the improvement is in the physics of radiation transport at interfaces between different materials and will therefore be observed for most patients. Furthermore, FFF beams offer other benefits, including better sparing of normal tissues (Lu et al. 2015, Tambe et al. 2016) and faster treatment deliveries (Fu et al. 2004, Vassiliev et al. 2009, Xiao et al. 2015).

All numerical results reported in this study are for the Varian TrueBeam accelerator operated at 6 MV. Our data and conclusions are not directly applicable to other accelerator models because of considerable design differences between different accelerator models and in implementation of the FFF technology.

Conclusions

We carried out a systematic investigation of dose distributions near the interface between a tumor and lung parenchyma. We considered three factors affecting these distributions: tumor size, lung density, and modality: FFF versus FF. We confirmed the existence of a previously reported ring of underdosage at the tumor surface. We observed it in all cases that we considered and quantified the effect for various conditions; the underdosing was most pronounced for smaller tumors and lower lung density. The underdosage is clearly not negligible, easily reaching 10% of the prescription dose and, in some cases, more. It is, however, difficult to detect or correctly estimate the dose deficit using conventional treatment planning systems, substantially because of CT image motion artifacts and dose calculation limitations.

This underdosage cannot be completely eliminated. However, this study shows that a modest dose enhancement in the underdosed regions can be achieved by replacing FF beams with FFF beams. This enhancement was seen in all cases that we considered and spanned considerable volumes on both sides of the tumor surface. Given that FFF beams are already widely available in the clinic, implementing this technique for treating lung tumors is straightforward and inexpensive.