Bayesian Monte Carlo and Maximum Likelihood Approach for Uncertainty Estimation and Risk Management: Application to Lake Oxygen Recovery Model

Abstract

Model uncertainty estimation and risk assessment is essential to environmental management and informed decision making on pollution mitigation strategies. In this study, we apply a probabilistic methodology, which combines Bayesian Monte Carlo simulation and Maximum Likelihood estimation (BMCML) to calibrate a lake oxygen recovery model. We first derive an analytical solution of the differential equation governing lake-averaged oxygen dynamics as a function of time-variable wind speed. Statistical inferences on model parameters and predictive uncertainty are then drawn by Bayesian conditioning of the analytical solution on observed daily wind speed and oxygen concentration data obtained from an earlier study during two recovery periods on a eutrophic lake in upper state New York. The model is calibrated using oxygen recovery data for one year and statistical inferences were validated using recovery data for another year. Compared with essentially two-step, regression and optimization approach, the BMCML results are more comprehensive and performed relatively better in predicting the observed temporal dissolved oxygen levels (DO) in the lake. BMCML also produced comparable calibration and validation results with those obtained using popular Markov Chain Monte Carlo technique (MCMC) and is computationally simpler and easier to implement than the MCMC. Next, using the calibrated model, we derive an optimal relationship between liquid film-transfer coefficient for oxygen and wind speed and associated 95% confidence band, which are shown to be consistent with reported measured values at five different lakes. Finally, we illustrate the robustness of the BMCML to solve risk-based water quality management problems, showing that neglecting cross-correlations between parameters could lead to improper required BOD load reduction to achieve the compliance criteria of 5 mg/L.

1. Introduction

The use of hydrologic and water quality models are indispensable to water resource planning and environmental management. In Europe, the EC-Water Framework Directive (WFD) is the most important driving force to improve water quality (Hering et al., 2010). In the United States, Total Maximum Daily Load (TMDL) is the most important watershed based regulatory program (US EPA, 2011). In both of these programs, models have played and will continue to play a key role in their implementation and success. However, the simulations from these models are subject to significant uncertainty.

Quantifying uncertainty associated with water quality model predictions is imperative for risk-based environmental decision making and when significant public resources are at stake (Borsuk et al., 2002; Liu et al., 2008; Shen and Zhao, 2010; Patil and Deng, 2011). Errors in the input data, observations, parameters, and model structure are inevitable and bound to contribute to model uncertainty. An ideal methodology therefore should account for all sources of modeling errors and firmly integrate model uncertainty with risk-based management solutions for water quality problems (Wellen et al., 2015).

Previous efforts linking model calibration and uncertainty estimation to water quality risk assessment have used first-order variance analysis (FOVA) by focusing exclusively on parametric uncertainty and often requiring numerical approximation of first-order and second-order derivatives (e.g., Melching and Bauwen,s 2001; Zhang and Yu, 2004). While computationally frugal, FOVA methods limit uncertainty quantification to the first-two moments and are constrained by the requirement of relatively small coefficient of determination of the parameters.

Bayesian frameworks have been increasingly used to link model calibration and uncertainty estimation to water quality risk assessment. While Bayesian methods produce more comprehensive statistical inferences and have fewer restrictive assumptions, they are often computationally demanding (Lu et al., 2014). Bayesian Monte Carlo (BMC) (Camacho et al., 2015; Qian et al., 2003), Markov chain Monte Carlo (MCMC, Zheng and Han, 2015; Wellen et al., 2014; Lu et al., 2014; Cheng et al., 2014; Liu et al., 2008), and the Generalized Likelihood Uncertainty Estimation method (GLUE, Beven, 2006; Zheng and Keller, 2007; Vrugt et al., 2009) are most common approaches employed to compute the distribution of the model predictions and obtain uncertainty estimates such as the 95% confidence bounds.

An historical roadblock in the application of Bayesian approaches was that, for many model forms, using the posterior parameter distribution required solving highly complex analytically intractable integrals. To overcome this, the MCMC algorithms create a random walk, or a Markov process, that has the posterior probability mass of parameter set, as its stationary distribution (Gelman, 2004). The procedure is adaptive, so that starting from an initial point, it runs the process long enough so that the resulting sample closely approximates a sample from posterior probability mass of parameter set (Congdon, 2006). However being an iterative scheme, MCMC implementation remains challenging, with factors such as selection of sampler, burn-in period, the proposal distributions and their scale factors – all of which greatly affect the convergence and the efficiency of sampling from the target distribution (Camacho et al., 2015; Samanta et al., 2007).

The BMC on the other hand is essentially non-iterative and much simpler to implement but can be inefficient because the region of the posterior distribution may never be sampled (Qian et al., 2003). This view point is partly attributed to lack of a proper strategy for estimating the variance of residual error in the likelihood function and overlooks the fact that probabilities are calculated in terms of the basis of parameter sets and corresponding likelihoods (Hantush and Chaudhary, 2014).

Within BMC or MCMC, the likelihood function quantifying the probability that the observed values of a modeled variable correspond to a particular parameter set is constructed using ‘formal’ statistical models based on the temporal structure of the residuals between the model predictions and observations. Here the functional form of the likelihood function can be generalized to depend on the level of bias, heteroscedasticity and correlation of the residuals (Camacho et al., 2015). The main point of criticism in BMC and MCMC are the assumptions regarding the structure of the residual errors that may not be accurate in real modeling applications (although the modeler can evaluate the validity of their assumptions a posteriori).

On the other hand, GLUE generates ‘informal’ likelihood measures using common goodness of fit measures such as Nash-Sutcliffe coefficient (Beven, 2006) and often relies on subjectively selected threshold values for the likelihoods to separate Behavioral from non-Behavioral parameter sets. In a sense, it lacks rigorous statistical assumptions and uncertainty therefore is no longer expressed in terms of probabilities. While the informal likelihood measures in GLUE eliminate the need for assumptions on residual error models through a pragmatic approach, they neither ensure the convergence to the posterior probability distribution which is a fundamental property of the Bayesian approach (Vrugt et al., 2009) nor produce reliable estimates of prediction probabilities (Camacho et al., 2015).

Recently, Hantush and Chaudhary (2014) presented a novel approach (BMCML) that combines Bayesian Monte Carlo (BMC) simulation with maximum likelihood estimation (MLE). BMCML also borrows from the GLUE methodology the concept of “equifinality”, i.e. the emphasis is placed on the generated parameter sets (i.e., covariation among the parameters) and corresponding likelihoods as opposed to the posterior parameter distribution as the case in MCMC. This is also different from casual ensemble forecast approaches where after model calibration uncertain parameters are arbitrarily perturbed to generate the ensemble forecast. As with the GLUE, covariation among parameters in any Monte Carlo simulation are implicitly reflected by the likelihood weight associated with each randomly drawn parameter set. Within BMCML, the variance $,$ bias and lag-one autocorrelation coefficient of model residual errors are determined for each randomly drawn parameter set by maximizing the joint likelihood function.

Hantush and Chaudhary (2014) showed through several example applications that neglecting covariation among model parameters can have significant effect on computed risk-based management actions. Given a suite of above Bayesian methods, it is imperative to investigate the effectiveness and efficiency of these methods to guide strategies for uncertainty analyses in future water quality modeling and risk assessments.

The main objective of this paper is to characterize the uncertainty of a lake oxygen recovery model (Gelda et al., 1996) using the BMCML (Hantush and Chaudhary, 2014) and MCMC methods and demonstrated robustness of BMCML to risk management. The manuscript is organized as follows. First, we derive a new analytical solution for lake-reaeration dynamics by solving the differential equation that governs the mass balance of oxygen in the lake. Second, results derived are compared using the BMCML with the results obtained by Gelda et al. (1996) deterministically and the Markov Chain Monte Carlo (MCMC) method. Third, we construct a relationship between reaeration coefficient and wind speed along with 95% confidence band and evaluate its performance by comparison with observed data from five other lakes and similar relationships reported in the literature. Finally, we describe how BMCML can be used to estimate risk of violating lake water quality standard as a function of pollutant loading.

2. Methods

2.1. Lake Reaeration Process

The dissolved oxygen (DO) concentration is a critical factor for aquatic biodiversity and in regulating various biogeochemical processes. Depletion of DO in lakes is a common phenomenon that occurs in some lakes every year due to accumulation and oxidation of chemically reduced substances in lake’s hypolimnion over the summer. Maximum depletion occurs at turnover. This period is followed by a recovery period during the autumn whereby oxygen levels bounce back due to diffusive transfer of oxygen across the lake surface (i.e., reaeration) exceeding the rate of oxygen removal by plant uptake and oxidation processes. A return to near-saturated conditions takes 3–4 weeks (Gelda et al., 1996).

The atmospheric inputs of oxygen into the lakes depend on the reaeration coefficient which is a function of wind speed (surface turbulence). The recovery period thus offer a rare opportunity to identify the factors mediating the reaeration process and to evaluate the predictive expressions of reaeration coefficient based on wind speed.

Using the field monitored data on mean daily wind speed and dissolved oxygen in the hypereutrophic Onondaga Lake in Syracuse, New York over two post turnover recovery periods, Gelda et al. (1996) calibrated a typical lake oxygen recovery model and estimated the reaeration coefficient through essentially a mixed graphical and optimization approach. The lake is oriented along a NNW-SSE axis, and is 7.2 km long, 1.6 km wide (i.e. surface area =11.7 km²), with mean and maximum depths of 12 m and 20.5 m respectively. Gelda et al. (1996) collected a time series of DO measurements at 1-m intervals at two stations in the north and south basins of Onondaga Lake in late summer and fall of 1989 and 1990. However because their approach is deterministic, it neither lends itself to uncertainty estimation nor suited for probabilistic risk assessment.

The mass balance of lake-wide oxygen during the post turnover recovery period, assuming the gains of oxygen through tributary inflow and losses to lake outflow are negligible, is given by following differential equation (see Gelda et al. 1996 for details):

$$V\frac{dC}{dt}=V.K_a\left(C_s- C\right)+ V.S$$ (1)

where $K_a$ is the reaeration coefficient (d⁻¹); $C_S$ = saturation concentration of dissolved oxygen (g/m³); and C = lake-averaged oxygen concentration in the water (g/m³) at time t and V = lake volume (m³). $S$ is the net sum of all oxygen sources and sinks in the lake in g.m⁻³d⁻¹ (i.e. photosynthesis minus algal respiration and biochemical, sediment oxygen demand). In the short-term, over the recovery period, the reaeration coefficient displays significant temporal variations as a function of wind speed (surface turbulence) typically represented by:

$$K_a=\alpha U^{\beta }/H$$ (2)

where α and β are empirical constants; and U = wind speed (m/s) at a standard height above the water (=10 m) and H is the average depth of the lake.

Gelda et al. (1996) implemented a two-step procedure, whereby S and period-averaged $K_a$ were first obtained using the oxygen recovery data and solution of Eq. 1 based on constant $K_a$. They then solved the differential equation (Eq. 1) numerically, by seeking a value for α that minimizes the root mean square error (RMSE) between model-predicted DO and field observed DO. The value of β was fixed to be equal to 1.0 for U ≤ 3.5 m/s and 2.0 for U > 3.5 m/s. The observed values for $C_s$ were 11.67 and 11.27 g/m³ for the year 1989 and 1990, respectively. The net source term S was −0.289 and −0.151 g.m⁻³/d for the two years (from Gelda et al. 1996). Negative S implies net sink and that oxygen removal by algal respiration, BOD and SOD exceeded oxygen sources like photosynthesis and reaeration, averaged over the recovery periods. Once $\alpha$ was determined by optimization, Gelda et al. (1996) constructed a predictive relationship between liquid film-transfer coefficient for oxygen ($K_L= K_a\bullet H$) and wind speed ($U$).

2.2. Analytical Solution

We obtain the solution of the differential equation (Eq. 1) using the integration factor:

$$C\left(t_1\right)=C\left(t_0\right)e^{-{\displaystyle {\int }_{t_0}^{t_1}{K}_a\left(\tau \right)d\tau }}+ {\displaystyle {\int }_{t_0}^{t_1}\left[\left\{K_a\left(\phi \right)C_s+S\right\}{e}^{-\underset{\phi }{\overset{t_1}{{\displaystyle \int }}}{K}_a\left(\tau \right)d\tau }\right]d\phi }$$ (3)

where $C\left(t_1\right),\mathrm{ }C\left(t_0\right)$ are the concentration of dissolved oxygen (DO) in the lake at time $t_1$ and $t_0$ respectively (g/m³). We refer to Eq. (3) as the exact analytical solution. If the time interval $t_1-t_0$ is sufficiently small such that variation of the reaeration coefficient is negligible, the integral appearing in the exponential term in the integrand can be approximated in terms of the average value of K_a, $\overline{K_a}$, over the time interval [t₀, t₁], by virtue of the Mean Value Theorem for integrals, $\underset{\phi }{\overset{t}{{\displaystyle \int }}}{K}_a\left(\tau \right)d\tau \approx \overline{K_a}\left(t-\phi \right)$. Substituting this and carrying on the integration, the following expression is obtained (referred to approximate analytical solution):

$$C\left(t_1\right)= C\left(t_0\right)\cdot e^{-\overline{K_a}\left(t_1-t_0\right)}+ \left(C_s+S/\overline{K_a}\right)\cdot \left(1-e^{-\overline{K_a}\left(t_1-t_0\right)}\right)$$ (4)

where $\stackrel{-}{K_a}\approx \alpha {\stackrel{-}{U}}^{\beta }/H$ and $\stackrel{-}{U}$ is the average wind speed for the time interval [t₀, t₁]. In terms of $\stackrel{-}{U}$, Eq. (4) can be rewritten as:

$$C\left(t_1\right)= C\left(t_0\right)\cdot e^{-\frac{\alpha {\overline{U}}^{\beta }}{H}\left(t_1-t_0\right)}+ \left(C_s+S\cdot H/\left(\alpha {\overline{U}}^{\beta }\right)\right)\cdot \left(1-e^{-\frac{\alpha {\overline{U}}^{\beta }}{H}\left(t_1-t_0\right)}\right)$$ (5)

2.3. BMCML methodology for model calibration and uncertainty estimation

In the model described in Eq. (5) above, we considered the parameters $\mathrm{\alpha },\mathrm{ }\mathrm{\beta }$, S and $C_S$ to be unknown but random variables and generated 100,000 Monte Carlo samples from the following prior, uniform distributions: S ~ U (−3, 1), $C_S$ ~ U (8, 15), α ~ U (0.01, 2) and β ~ U (0.1, 4). Unlike the deterministic modeling approach taken by Gelda et al. (1996), we consider α, $\mathrm{\beta }$, S and $C_S$ to be uncertain parameters in the model to demonstrate that the analysis can be applied to oxygen lake recovery modeling for a region where the measured values of S and $C_S$ are not available.

The daily average (i.e. $t_1-t_0=1$ in Eq. 5 above) wind speed $\stackrel{-}{U}$ and dissolved oxygen ($\mathit{O}$) observations in Onondaga Lake were obtained from Gelda et al. (1996). For year 1990, 36 wind speed measurements were available along with 13 measurements of dissolved oxygen (DO). For 1989 wind speed was monitored for 20 days following the turnover event and DO levels monitored on 7 of those 20 days. The mean lake depth (H) was equal to 12 m (Gelda et al., 1996).

The relationship between DO observations ($\mathit{O}$) and the corresponding model simulated output ($C\left(\mathit{\theta }\right)$) can be expressed as: $\mathit{O}=C\left(\mathit{\theta }\right)+\mathit{\epsilon }$, where $\mathit{\epsilon }=\left({\epsilon }_1,{\epsilon }_2,\dots ,{\epsilon }_m\right),$${\epsilon }_i~N\left(0,{\sigma }_{\epsilon }^2\right)$ is zero-mean, independent and normally-distributed residual error; m is number of observations; and $\mathit{\theta }={(\alpha , \beta , C_S, S)}^{\mathrm{T}}$ is vector of model parameters. The error ε accounts for all sources of modeling errors (observational, structural, inputs and loadings).

In the context of the BMCML and according to Bayes theorem (see also Hantush and Chaudhary 2014):

$$P\left({\theta }_i\text{|}O\right)=k l\left({\theta }_i\right)P\left({\theta }_i\right)$$ (6)

where $P\left({\theta }_i\text{|}O\right)$ is the posterior probability mass of parameter set ${\theta }_i={\left({\alpha }^i, {\beta }^i,C_S{}^i,S^i\right)}^T$; i = 1,2,…,n, where n is number of randomly sampled parameter sets (n = 100,000); $l\left({\theta }_i\right)=P\left(O\text{|}{\theta }_i\right)$ is the likelihood of observations given ${\mathit{\theta }}_i;\mathbf{ }P\left({\mathit{\theta }}_i\right)$ is the prior probability mass of parameter set ${\mathit{\theta }}_i$; k is a normalizing factor such that ${\displaystyle {\sum }_{i=1}^{n}P\left({\theta }_i\text{|}O\right)}=1$; that is,$k={\left[{\displaystyle {\sum }_{i=1}^{n}l\left({\theta }_i\right)P\left({\theta }_i\right)}\right]}^{-1}$. We also assume equally likely parameter sets prior to the introduction of measurements, i.e., $P\left({\theta }_i\right)=1/n$.

Assuming independent, zero-mean and normally distributed model residual errors, the log-likelihood function given a set of m independent DO observations o₁,o₂,…,o_m and a parameter set ${\mathit{\theta }}_i$ is (Qian et al. 2003; Gelman et al. 2004):

$$\ln l\left({\theta }_i\right)=-\frac{m}{2}ln\left(2\pi \right)-m\ln {\sigma }_{\epsilon }-\frac{1}{2} {\displaystyle {\sum }_{k=1}^m{\left(\frac{O_k-C_k\left({\theta }_i\right)}{{\sigma }_{\epsilon }}\right)}^2}$$ (7)

Next, for each BMCML sampling step i, the value of ${\sigma }_{\epsilon }^2$ corresponding to parameter set ${\mathit{\theta }}_i$ is the maximum likelihood estimate. In other words, for each ${\mathit{\theta }}_i$, there corresponds a maximum likelihood estimator ${\widehat{\sigma }}_{\epsilon i}^2$ which maximizes the log-likelihood function (see also Stedinger et al. 2008). By setting $\partial ln l\left({\theta }_i\right)/\partial {\sigma }_{\epsilon i}^2=0$ one obtains:

$${\widehat{\sigma }}_{\epsilon i}^2=\frac{1}{m}{\displaystyle \sum }_{k=1}^m{\left[O_k-C_k\left({\theta }_i\right)\right]}^2$$ (8)

where subscript i denotes the dependence of the maximum likelihood estimators on the parameter set ${\mathit{\theta }}_i$. In this framework,${\sigma }_{\epsilon }^2$ is described by a probability distribution: $P\left({\widehat{\sigma }}_{\epsilon i}^2\text{|}O\right)=l\left({\theta }_i\right)$. The maximum likelihood estimate ${\widehat{\sigma }}_{\epsilon i}^2$ is expected to be close to the actual value of ${\sigma }_{\epsilon }^2$, which is jointly distributed with $\mathit{\theta }$ in a full Bayesian analysis (Stedinger et al., 2008).

Substituting ${\widehat{\sigma }}_{\epsilon i}^2$ into Eq. (7) and adjusting the terms, gives the maximum likelihood value $\widehat{l}\left({\theta }_i\right)$ :

$$\widehat{l}\left({\theta }_i\right)={\left(2\pi e {\widehat{\sigma }}_{\epsilon i}^2\right)}^{-\frac{m}{2}}$$ (9)

Eq. (9) and the probability distribution of ${\sigma }_{\epsilon }^2$ hence form the basis of BMCML methodology and sets it apart from BMC. The posterior probability mass of parameter set $P\left({\theta }_i\text{|}O\right)$ is then computed by simply substituting $\widehat{l}\left({\theta }_i\right)$ for $l\left({\mathit{\theta }}_i\right)$ in Eq. (6) and noting that $k={\left[{\displaystyle {\sum }_{i=1}^n\widehat{l}\left({\theta }_i\right)P\left({\theta }_i\right)}\right]}^{-1}$ and $P({\theta }_i) =1/n$ :

$$P\left({\theta }_i\text{|}O\right)=\frac{\widehat{l}\left({\theta }_i\right)}{{{\displaystyle \sum }}_{i=1}^n\widehat{l}\left({\theta }_i\right)}$$ (10)

Using $P\left({\mathit{\theta }}_i|\mathit{O}\right)$ values, likelihood-weighted (Bayesian estimate) and 95% confidence interval for each of the four model parameters can be computed.

The Bayesian estimate of the variance of residual errors can be calculated as (Hantush and Chaudhary, 2014):

$${\widehat{\sigma }}_{\epsilon }^2={\displaystyle {\sum }_{i=1}^n{\widehat{\sigma }}_{\epsilon i}^{2}P\left({\theta }_i\text{|}O\right)}$$ (11)

The Bayesian estimate of lake-averaged dissolved oxygen concentration Y at any point in time is the conditional mean of Y given the observation $O,\mathrm{ }E\left(Y|O\right)$, which in the discrete form can be approximated (assuming uniformly sampled parameter space) as (Hantush and Chaudhary, 2014):

$$E\left(Y\text{|}O\right)\approx {\displaystyle {\sum }_{i=1}^{n}E\left(Y\text{|}{\theta }_i\right) P\left({\theta }_i\text{|}o\right)}= {\displaystyle {\sum }_{i=1}^{n}E\left[C\left({\theta }_i\right)\right] P\left({\theta }_i\text{|}o\right)}$$ (12)

The explicit expression for the posterior CDF of the model parameters and the expressions used to construct predictions (i.e., median, confidence limits) for future observed values of Y given the observed record, O, is (Hantush and Chaudhary 2014):

$$F\left(y\text{|}O\right)\approx \frac{1}{2}+\frac{1}{2} {\displaystyle {\sum }_{i=1}^{n}erf\left(\frac{y-C\left({\theta }_i\right)]}{\sqrt{2} {\widehat{\sigma }}_{\epsilon }}\right) P\left({\theta }_i\text{|}O\right)}$$ (13)

2.4. The case of biased and auto correlated residual errors

Apart from the above case assuming independent, zero-mean and normally distributed model residual errors, we also considered the more general case of biased and auto correlated residual errors (first-order Markov process): ${\epsilon }_k-\mu =\rho \left[{\epsilon }_{k-1}-\mu \right]+{\omega }_k$,${\omega }_k~N\left(0,{\sigma }_{\omega }^2\right)$, in which $\mu$ is bias of the overall error; $\rho$ is lag-one autocorrelation of the overall error; ${\omega }_k$ is zero-mean, independent and normally-distributed residual error; and ${\sigma }_{\omega }^2$ is variance of residual errors (Hantush and Chaudhary, 2014) This residual error equation can be rewritten as:

$${\epsilon }_k=\rho {\epsilon }_{k-1}+\mu \left(1-\rho \right)+{\omega }_k= O_k-C_k\left({\theta }_i\right)$$ (14)

The log-likelihood function is

$$\ln l\left({\theta }_i\right)=-\frac{m}{2}ln\left(2\pi \right)-mln{\sigma }_{\omega }-\frac{1}{2} {\displaystyle {\sum }_{k=1}^m{\left(\frac{{\epsilon }_k-\rho {\epsilon }_{k-1}-\left(1-\rho \right)\mu }{{\sigma }_{\omega }}\right)}^2}$$ (15)

Minimizing ln l with respect to ${\sigma }_{\omega }^2$ $$ yields

$${\widehat{\sigma }}_{\omega }^2=\frac{1}{m}{\displaystyle {\sum }_{k=1}^m{\left[\left({\epsilon }_k-\widehat{\mu }\right)-\widehat{\rho }\left({\epsilon }_{k-1}-\widehat{\mu }\right)\right]}^2}$$ (16)

Note that minimizing ln l is identical to minimizing the sum of squares of residual errors of $y_t=a{x}_t+b+{\omega }_t$, where $y_t=$ ${\epsilon }_t,\mathrm{ }{x}_t=$ ${\epsilon }_{t-1},\mathrm{ }a=\rho$, and $b=\left(1-\rho \right)\mu$ and therefore the least-square estimates are (see Ang and Tang, 2007):

$$\left(1-\widehat{\rho }\right)\widehat{\mu }=\frac{1}{m}{\displaystyle {\sum }_{k=1}^m{\epsilon }_k-\frac{\widehat{\rho }}{m}{\displaystyle {\sum }_{k=1}^m{\epsilon }_{k-1}=\overline{{\epsilon }_k}-\widehat{\rho } {\overline{\epsilon }}_{k-1}}}$$ (17)

$$\widehat{\rho }=\frac{{{\displaystyle \sum }}_{k=1}^m\left({\epsilon }_{k-1}-{\overline{\epsilon }}_{k-1}\right)\left({\epsilon }_k-\overline{{\epsilon }_k}\right)}{{{\displaystyle \sum }}_{k=1}^m{\left({\epsilon }_{k-1}-{\overline{\epsilon }}_{k-1}\right)}^2}$$ (18)

in which $\overline{{\epsilon }_k}=\frac{1}{m}{\displaystyle {\sum }_{k=1}^m{\epsilon }_k}$, and ${\overline{\epsilon }}_{k-1}=\frac{1}{m}{\displaystyle {\sum }_{k=1}^m{\epsilon }_{k-1}}$

Evaluating (18) for $\widehat{\rho }$, then $\widehat{\mu }$ from (17) and finally (16) for ${\widehat{\sigma }}_{\omega }^2$ gives the residual error estimates. Substituting $\widehat{\rho }$,$\widehat{\mu }$ and ${\widehat{\sigma }}_{\omega }^2$ into Eq,(15) provides the maximum likelihood value $\widehat{l}\left({\theta }_i\right)$ $\mathit{ }$ for each parameter set that can be used to calculate the posterior probability mass of parameter set (through Eq. 10) as well as the Bayesian estimate of lake-averaged dissolved oxygen concentration (through Eq. 12).

2.5. Model performance evaluation

To evaluate the model performance, we calculate coefficient of determination (R²) and the Nash Sutcliff efficiency (E_NS; Nash and Sutcliff, 1970). With both metrics, higher values indicate better fit and 1.0 indicates perfect fit. An E_NS value of 0 indicates that the model predicts as well as the average of the observations, while negative E_NS value indicate a model that predicts more poorly than the average of the observations. The E_NS penalizes for linear bias, whereas the R² metric does not (Krause et al., 2005). R² describes the proportion of the variance in the observed data that can be explained by the model. Another performance metric is the root mean square error,$RMSE={(m-p)}^{-1}{\displaystyle {\sum }_{t=1}^m{({\widehat{L}}_t-O_t)}^2)}$, where m is the number of DO measurements (and m = 7 for 1989 and m = 13 for 1990); $p$ = 4, is the number of model parameters; $O_t$ is observed concentration of DO on any day t and ${\widehat{L}}_t$ is Bayesian estimate of measurement on day t. All the programming and statistical analysis were performed in MATLAB software (Mathworks, 2011).

2.6. Model Validation - Split Data Set Approach

In order to further explore the robustness of BMCML methodology, we used split dataset approach with the first time series of dissolved oxygen (DO) recovery observation from the year 1989 for model calibration and likelihood estimation while the second from the year 1990 is retained for methodology validation and uncertainty estimation (Oberkampf and Trucano, 2008). During the model validation part, the prior vectors of all 4 parameters along with their corresponding likelihoods (Eq. 10) are fed back into lake oxygen recovery model, with the mean daily wind speed observations from the year 1990. The objective is to check if the calibrated model is capable of predicting the lake oxygen recovery for future years. This is different from the approach by Gelda et al. (1996) where the model was calibrated for both years but never validated.

2.7. Comparison with regression and MCMC approaches

We compare the BMCML calibration results with those obtained by Gelda et al. (1996) and with those using Markov Chain Monte Carlo (MCMC). We performed MCMC sampling on the lake recovery model using the publicly available program WinBUGS, (Bayesian inference Using Gibbs Sampling; Lunn et al., 2009), to obtain inferences for all four model parameters α, β, C_s, S and the model error variance ${\sigma }_{\epsilon }^2$. A typical WinBUGS session starts with the user specifying the model to run in the form of the likelihood function and prior distributions for all parameters to be estimated (Spiegelhalter et al., 2003). Observations and initial values must also be specified.

We used the same prior distributions for all four model parameters as in BMCML above, while for model error variance ${\sigma }_{\epsilon }^2$, we defined a uniformly distributed prior,${\sigma }_{\epsilon }$~U (0.01, 1). We performed 50000 iterations on three separate chains with 1000 burn-in period and selecting every 5^th value. Through WinBUGS, we then generated MCMC simulations using Gibbs sampling algorithm such that the stationary distribution of the Markov chain is the posterior distribution of interest, with the process eventually providing posterior samples of size 10,000 for each of the five unknown variables from which summary statistics such as mean or 95% confidence intervals can be calculated.

For model validation, these posterior vectors were fed into the aeration model of Eq. 5 along with the mean daily wind speed observations from the year 1990 to obtain the MCMC estimate and 95% confidence intervals of lake oxygen levels.

2.8. Risk Assessment

In order to demonstrate the application of BMCML technique to water quality management, we use the calibrated model above to examine the general hypoxic state of the lake under study. The objective is to know on any day following the recovery, what is the maximum allowable BOD loading (CBOD and NBOD portion of S term in Eq. 5) in the lake such that the DO levels do not drop below the ambient water quality criterion (Y^*) of 5 mg/L (with 90% confidence). We used the following expression from Hantush and Chaudhary (2014) to compute the risk of violating Y^* at a particular loading S:

$$Risk=P[Y<Y^{*}|O]\approx \frac{1}{2}+\frac{1}{2}{\displaystyle {\sum }_{i=1}^{n}erf\left(\frac{Y^{*}-C({\theta }_i)]}{\sqrt{2}{\widehat{\sigma }}_{\epsilon }}\right)P({\theta }_i/O)}$$ (19)

where erf is error function. Starting with the Bayesian estimate of the net source term (S), we first compute the risk of violating Y^* at a current loading levels and then successively reduce the magnitude of S and calculated the risk according to Eq. (14) to obtain a functional relationship between S and risk. We refer to the above evaluation of risk as the formal approach since it follows from the firm application of laws of probability (total probability and Bayes theorems).

We also carried out the risk management analysis using the more commonly used informal approach, whereby parameter values are sampled independently from their posterior marginal distributions and then used to compute probability of violation. This approach does not consider potential parameter interactions as reflected by the corresponding likelihood function estimates. To compute the risk of violating Y* using informal approach, we computed the fraction of times the following inequality holds,$[P[C({{\theta }^{\prime }}_i)+{\epsilon }_i<Y^{*}]$, where ${\epsilon }_i~N\left(0,{\widehat{\sigma }}_{\epsilon }{}^2\right)$ is sampled independently. Here ${{\theta }^{\prime }}_i$ is a particular parameter set drawn from posterior marginal probability distributions of model parameters $\mathit{\theta }$ without due consideration of corresponding likelihoods. This is to distinguish ${{\theta }^{\prime }}_i$ from parameter set ${\mathit{\theta }}_i$ that is sampled from prior parameter distributions and has corresponding likelihood $\widehat{l}\left({\theta }_i\right)$. The latter contains potentially correlated parameter values.

3. Results and Discussion

3.1. Model Calibration and validation using BMCML

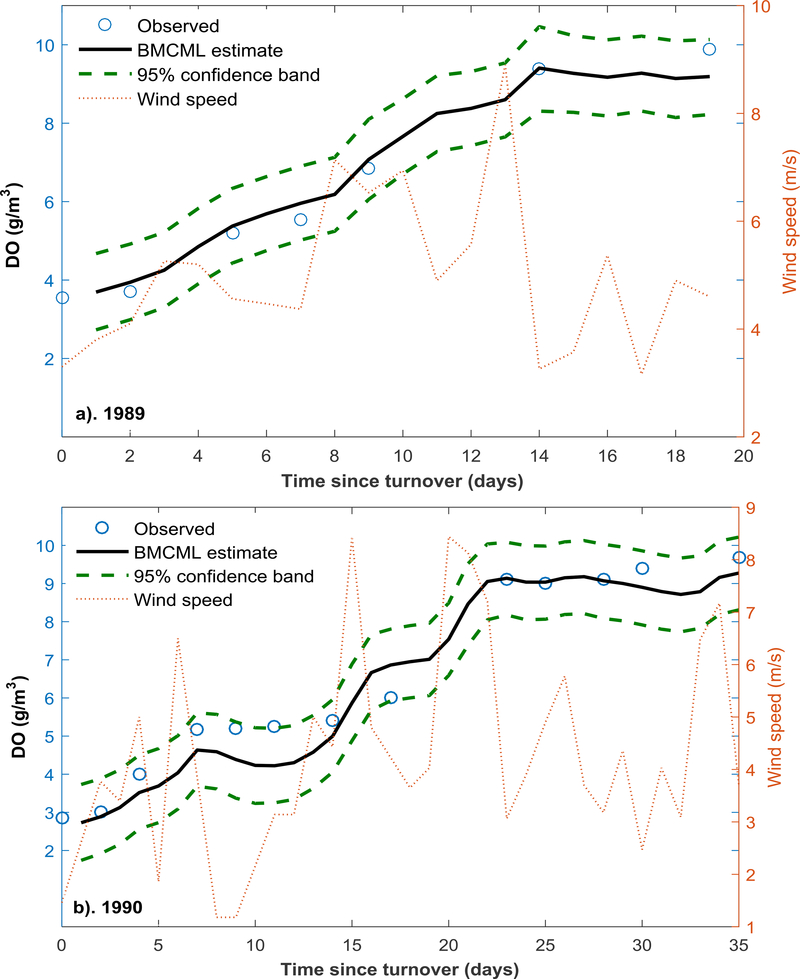
Fig. 1(a) shows the BMCML estimates and observed dissolved oxygen concentration values in lake Onondaga, New York for the recovery period of 1989. It can be seen that DO levels increased from 3.5 g/m³ on day 0 to 9.9 g/m³ over a period of 20 days. The estimated DO values fit very well to the observed trend in the increase of DO levels in the lake.

Fig. 1.

a) BMCML predicted and observed dissolved oxygen concentrations and 95% confidence limits following the 1989 turnover event at Lake Onondaga., b). Model validation showing the BMCML predicted and observed dissolved oxygen concentration and 95% confidence limits for the year 1990. Observed mean daily wind speed is also shown for both years as dotted line.

RMSE was found to be 0.21 g/m³, while the Nash-Sutcliff efficiency coefficient (E_NS) and coefficient of determination (R²) of the Bayesian estimates were both equal to 0.98. BMCML estimate of model error variance ${\sigma }_{\epsilon }^2$ is 0.22 (g²/m⁶). The observed values fell within the computed 95% confidence limits.

Fig. 1(b) shows the resulting fit between predicted and observed dissolved oxygen (DO) levels for the validation period 1990. We found RMSE to be 1.15 g/m³, whereas the E_NS and R² are 0.95 and 0.97 respectively. As shown in the Fig. 1(b), the variability and magnitude of the observed DO values are adequately reflected by the BMCML estimate. Moreover, the observed DO time series is contained by the estimated 95% confidence band, thus validating the model.

Table 1 shows the Bayesian estimates and 95% confidence intervals of all four model parameters (α, β, Cs, S) obtained using the BMCML and MCMC with the lake recovery analytical model of Eq. 5 and the 1989 daily average wind speed data.

Table 1.

Estimated parameter values and confidence intervals for lake aeration model (Eq. 5) using 1989 oxygen recovery data and comparison with Gelda et al. (1996) estimates.

Parameter	Method	2.5 percentile	Median	97.5 percentile	Bayesian estimate	Gelda et al.
α	BMCML	0.023	0.029	0.67	0.10	0.057 – 2
	MCMC	0.014	0.084	0.29	0.10
β	BMCML	0.44	2.29	2.50	1.90	1 – 2
	MCMC	0.26	1.28	2.35	1.30
S	BMCML	−0.80	−0.25	−0.065	−0.30	−0.289
	MCMC	−0.39	−0.075	0.201	−0.08
CS	BMCML	10.22	12.20	14.86	12.94	11.67
	MCMC	7.79	12.87	14.91	12.54

Table 2 lists a matrix of likelihood-weighted cross-correlations between the 4 model parameters (α, β, S, C_s) corresponding to likelihood values greater than 10⁻⁴. Highest correlation exists between α and β, followed by β and C_s. Parameters S and C_s and are also moderately correlated.

Table 2.

Likelihood-weighted cross correlation coefficients between model parameters values using 1989 data.

Parameters	α	β	S	Cs
α	1	−0.85	−0.037	0.24
β	−0.85	1	−0.05	−0.50
S (g.m−3d−1)	−0.037	−0.05	1	−0.37
Cs (g/m3)	0.24	−0.50	−0.37	1

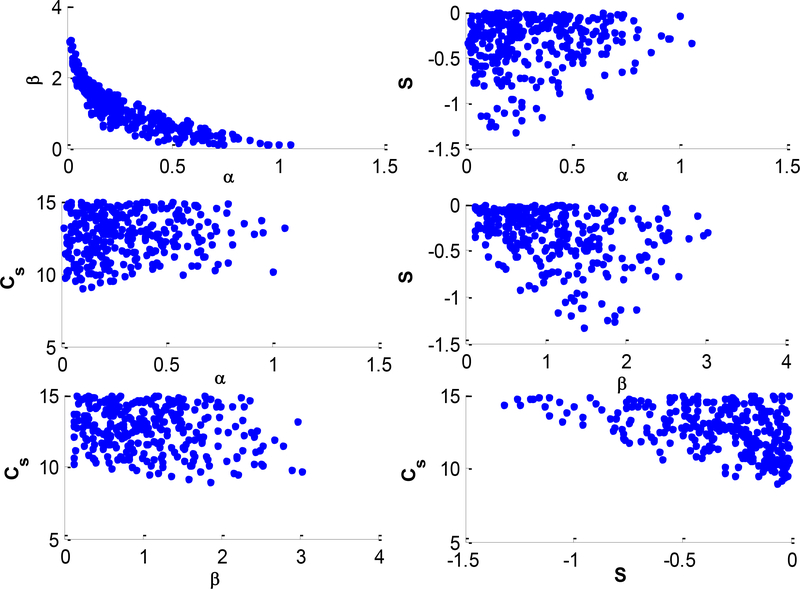
Dotty plots of paired parameter values with likelihoods greater than 10⁻⁴ are depicted in Fig. 2.

Fig. 2.

Dotty plots of paired parameter values with likelihood values greater than 10⁻⁴.

Interestingly, a discernable exponential relationship can be observed between α and β, which signifies a functional relationship between the two parameters. The similar plots for other parameter combinations are more scattered, thus, revealing weaker functional associations.

In order to test the sensitivity of the results to the assumption that reaeration coefficient is constant over daily time period, we also applied BMCML methodology to the exact analytical solution (Eq. 3) in order to compare the results with approximate analytical solution of Eq. 5. The daily observed values of $\stackrel{-}{U}$ were linearly interpolated to obtain hourly data. The results compare well with those obtained using Eq. 5, indicating that daily time resolution is sufficient to model short term lake dynamics for the current lake in question along with the added benefit of being computationally faster. The E_NS and R² of the Bayesian estimates both were close to 0.95 for both years and RMSE was equal to 0.38 g/m³.

It’s worth emphasizing that the length of the averaging period used for lake recovery model input is consistent with the response time of the system. For example, some simulation studies in the past have found that winds must persist over a period of >2 hours to stimulate any response in lake DO concentration. Thus wind speed data reported at intervals of less than 2 hours are of a finer scale than is necessary for these calculations. On the other extreme, the averaging period should not be so long as to obscure the impact of short-term high-wind events on reaeration phenomena. Our results agree with Gelda et al. (1996), who also found that the daily averaging period utilized in the Onondaga Lake analysis is consistent with the time scale of interest for the recovery of the lake’s oxygen resources.

In an additional run, we also applied the BMCML method assuming biased and auto-correlated residual errors (Eqs. 14–18, section 2.4). We found that in this case both the bias and lag-one autocorrelation coefficient for model residual errors came out negligibly small. The normality assumption for residual errors was also confirmed by Kolmogorov-Smirnov test for normal distribution (at α = 5% significance level).

3.2. Comparison with regression and MCMC approaches

The model fit obtained using BMCML is much improved compared with those obtained by regression technique of Gelda et al. (1996). For the calibration year 1989, the RMSE value is lower using BMCML (0.21 g/m³), compared to 0.77 g/m³ obtained by Gelda et al. (1996). The S values computed by Gelda et al. (1996), −0.289 g.m⁻³d⁻¹ for 1989 and −0.151 g.m⁻³d⁻¹ for 1990 are well within the 95% confidence interval generated by BMCML (Table 1). Period-averaged C_s values used by these authors - 11.67 and 11.27gm⁻³ for 1989 and 1990, respectively, are also within the 95% confidence limits obtained by the BMCML method (Table 1). Similarly, the 95% confidence limits for β encompasses the two values of 1 and 2 m/s for U below and above threshold value of 3.5 m/s proposed by Gelda et al. (1996). The corresponding optimized values obtained by the same authors for α below and above the threshold velocity, 0.2 and 0.057, respectively, are within the BMCML 95% confidence limits (Table 1). The BMCML estimates for β and α were 1.9 and 0.1, respectively.

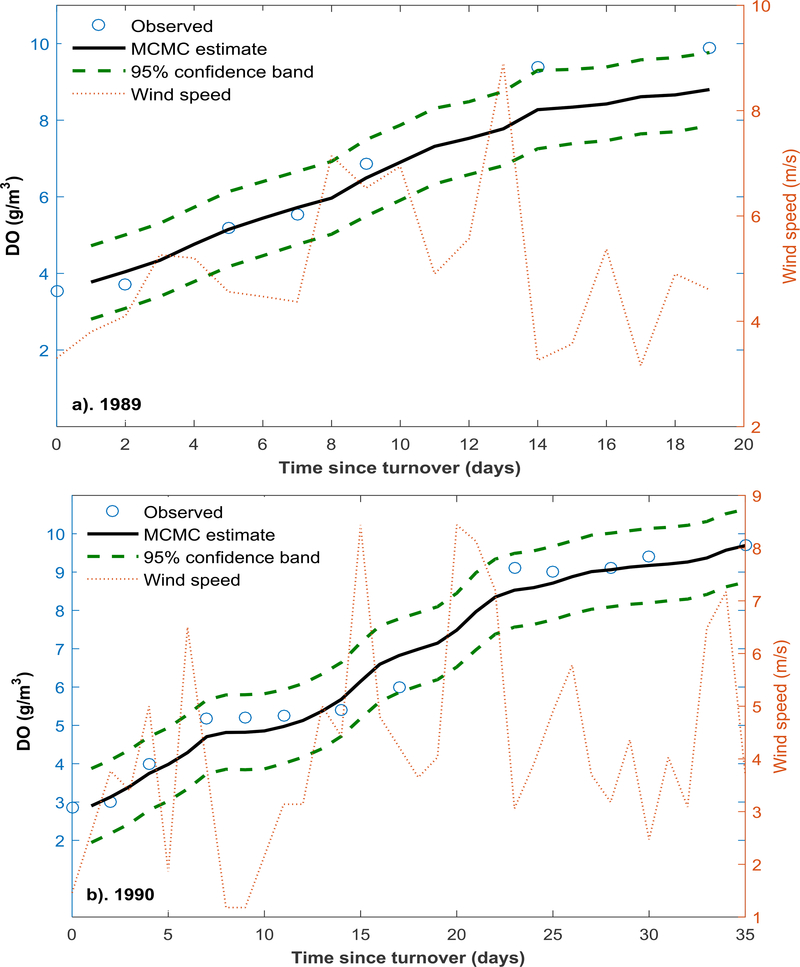
The predicted DO results obtained using MCMC were more or less similar to those obtained by BMCML. Fig. 3(a) presents the model calibration results obtained using MCMC. For the 1989 DO data, the E_NS and R² of the MCMC estimates were 0.98 and 0.93 respectively as compared to 0.98 for BMCML estimates. MCMC estimate of model error variance ${\sigma }_{\epsilon }^2$ was 0.24 g²/m⁶ compared to 0.22 for the BMCML, while the RMSE was 1.16 g/m³ for the calibration year 1989 which are higher than BMCML and Gelda et. al. (1996) estimates.

Fig. 3.

a). MCMC predicted and observed dissolved oxygen concentrations and 95% confidence limits following the 1989 turnover event at Lake Onondaga, b). Model validation showing the MCMC predicted and observed dissolved oxygen concentration and 95% confidence limits for the year 1990. Observed mean daily wind speed is also shown for both years as dotted line.

For the validation year 1990, MCMC estimates along with 95% confidence intervals are shown in Fig. 3(b). The E_NS and R² of the MCMC estimates were both 0.98 compared to 0.95 and 0.97 for the BMCML, while the RMSE between observed DO concentrations and MCMC predicted concentrations was 0.41 g/m³ compared to 1.15 g/m³ for the BMCML and 0.68 g/m³ reported by Gelda et al. (1996). The MCMC marginally outperformed the BMCML for the validation period.

Table 1 shows that BMCML and MCMC yielded comparable estimates of the parameters as depicted in the last column (Bayesian Estimate) except for S, −0.3 g.m⁻³d⁻¹ by the former and −0.08 g.m⁻³d⁻¹ by the latter. The value computed by the BMCML was almost similar to the rounded value of −0.3 g.m⁻³d⁻¹obtained by Gelda et al. (1996). The MCMC value of S was much smaller in absolute value.

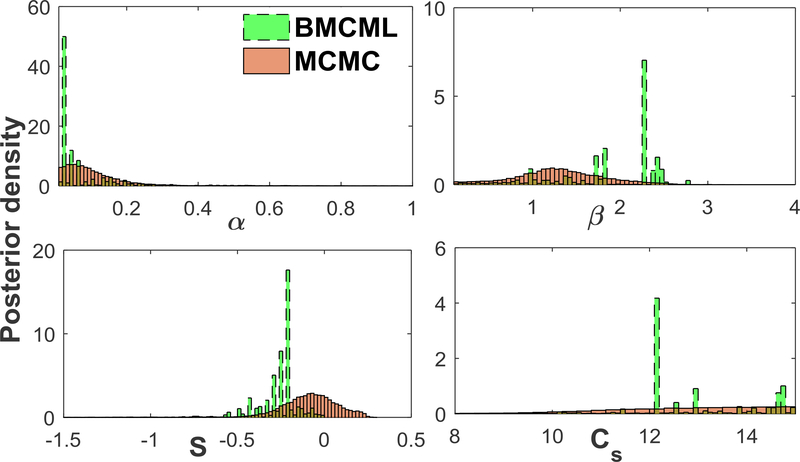
Fig. 4 shows the posterior probability distribution of all four model parameters generated using MCMC and the comparison with BMCML. Consistent with what was reported by Qian et al. (2003), the marginal posterior parameter distributions appear irregular and the corresponding 95% confidence limits were different between the two methods (Table 1). However, statistical inferences in the BMCML method are based on the parameter sets and corresponding likelihoods as opposed to sampling parameter values from their posterior marginal distributions (recall, the significant correlation and functional association between α and β).

Fig. 4.

Posterior probability distribution functions (PDFs) of lake oxygen recovery model parameters obtained using BMCML and MCMC for the year 1989.

We found that the computational cost of BMCML was comparable to that by the MCMC. Just like other Monte Carlo based methods, the BMCML is inherently computationally intensive especially in highly parameterized distributed hydrologic models where large number of model simulations are required to obtain relatively accurate probabilistic inferences. However, in such cases, this problem might be alleviated by limiting the analysis to most sensitive model parameters and implementing the Latin-Hypercube sampling approach.

3.3. Liquid film-transfer coefficient vs. wind speed relationship

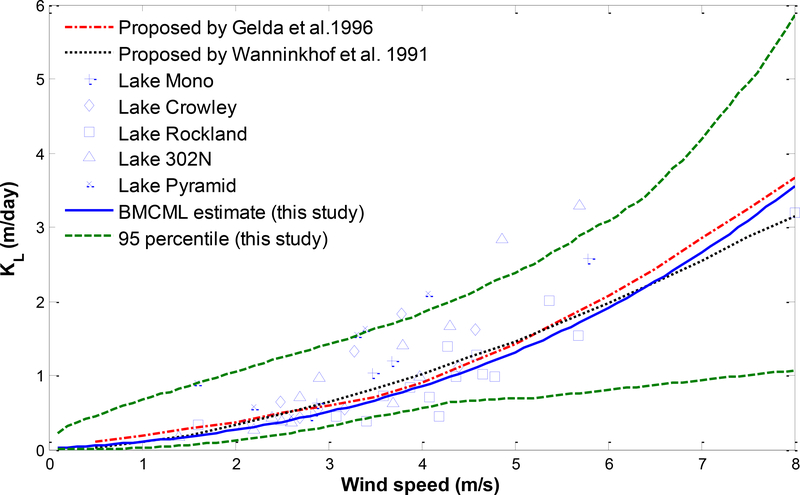
The paired α and β values and corresponding likelihoods allow the construction of the CDF for the liquid film-transfer coefficient (K_L) as a function of wind speed (U). For each U, statistical inferences including percentiles of K_L can be obtained. Fig. 5 shows the predicted liquid film-transfer coefficient ($K_L=\alpha U^{\beta }$) values at different wind speed ($U$) levels: $K_L\left(U\right)={\displaystyle {\sum }_{i=1}^n{\alpha }_i{U}^{{\beta }_i}\cdot P\left({\theta }_i\text{|}O\right)}$. It can be seen that observed values for all five lakes mostly fall within 95% confidence interval generated by us. The predicted (Likelihood-weighted) expression slightly underestimates the expression proposed by Gelda et al. (1996) and slightly underestimates/overestimates that by Wanninkhof et al. (1991) for wind speed less/greater than about 6.5 m/s. Note that uncertainty of K_L increases with wind speed as reflected by the increasingly thicker 95% confidence band. This is consistent with the observed data for the five lakes as scatter of the data appears to magnify with wind speed and can be attributed to the mathematic form (modeling error) and uncertainty in the observational data used. Overall, the BMCML estimates and uncertainty band were able to capture the K_L-wind speed and interpret the variability in the observed data. The Bayesian estimates of the K_L-wind speed were comparable to the models proposed by Gelda et al. (1996) and Wanninkhof et al. (1991).

Fig. 5.

Performance of K_L-Wind speed expression developed in this study in predicting measured values for five lakes and comparison with expressions proposed by Gelda et al. (1996) and Wanninkhof et al. (1991).

3.4. Risk Assessment

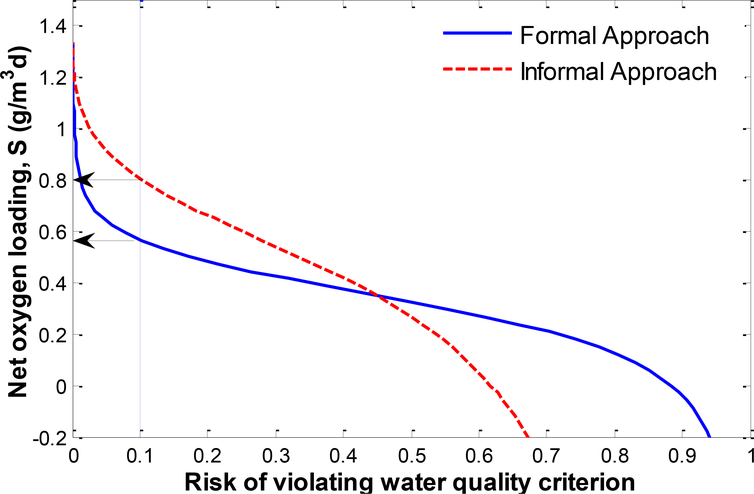
Fig. 6 shows the functional relationship between the net oxygen source S and risk of violating water quality criteria derived using the formal approach (Eq. 14). As S decreases, the risk of violating the WQ standard (5 mg/L) increases. S is positive when oxygen sources, such as aeration and photosynthesis exceed the sinks (BOD, SOD, and algal respiration) in the lake. As an example, for day 3, we obtained risk = $P\left[\left.Y<5\right|\right.O]$ = 0.97. It implies that at the current mean S = −0.3 g.m⁻³/d in the lake, the probability of violation of WQ criteria of 5 mg/L is 0.97 and thus it can be inferred that the current state of lake is hypoxic. It can be seen from the figure that a mean S of 0.58 g.m⁻³/d (bottom arrow) will reduce the risk of violation to 0.1 (solid line). In this example, we required P[Y< 5] > 0.1 (akin to 10^th percentile approach by the U.S. EPA for meeting water quality standards).

Fig. 6.

Allowable net oxygen loading (S) in the lake as a function of risk calculated using BMCML with both formal and informal approaches. Arrows indicate the allowable loading that ensures that dissolved oxygen water quality standard of 5 mg/L is met within the lake with 90% confidence.

The risk of violation calculated using informal approach is 0.68 which is significantly less than that calculated using the formal approach (0.97), but still implies prevalence of hypoxic conditions in the lake at current loading levels. Here again after successively reducing S and computing corresponding risk, we obtained the functional relationship shown in Fig. 6 (dashed line). It can be inferred from the figure that S = 0.81 g.m⁻³/d (upper arrow) would be required in order to ensure with 90% confidence that the lake is compliant with ambient water quality criteria for dissolved oxygen. This value is about 40% higher than that obtained by the formal approach, and requires more stringent control of BOD loading to the lake.

The information contained in Fig. 6 can be utilized for decision making in water quality management efforts such as TMDL analysis where hitherto an arbitrary margin of safety (MOS) is proposed either implicitly by means of conservative assumptions (e.g. by assuming conservative WQ standard) or explicitly by assigning a fraction of the computed load reduction as a protective cushion so that uncertainty in the analysis is accounted for. BMCML methodology as described in Sect. 2.6 furnishes an alternative but more objective probabilistic approach that can be used to compute the required load reduction and corresponding MOS as a function of risk (Hantush and Chaudhary, 2014).

Finally, we could only plot the risk of violating water quality criteria as a function of ‘net’ oxygen loading other than by aeration (S). This is because data on magnitude of individual sources and sinks that make up S was not available from Gelda et al. (1996). Ideally a functional relationship between risk and external BOD loading to the lake will be more useful from management point of view as the external loading can then be controlled through human intervention and actions. Therefore, for a more realistic application of water quality modeling for practical management purposes or regulatory programs such as TMDL, future studies should explore applying BMCML methodology to models depicting causal relationship between contaminant load and the water quality of the lake such as expanded Streeter-Phelps model including a sink of DO such as BOD, SOD or a more advanced model to include the impacts of Nitrification on DO.

The difference in the functional relationship obtained between net oxygen loading S and risk from formal and informal approaches shows the impact of potential parameters interactions on risk management. Both can lead to different management solutions of the water quality problem. In this example, it is shown that overlooking cross-correlations among parameters by sampling values from their posterior marginal distributions could lead to costlier management measures for relatively small risk values. From Fig. 6, one can see that for risk values greater than 0.45, greater BOD loading would be tolerated when parameter interactions are neglected (informal approach). For risk values less than 0.45 the opposite is true, and less BOD loading is tolerated by the informal approach, which entails costlier control measures to be implemented in the watershed leading to the lake. These findings are consistent with the results obtained by Hantush and Chaudhary (2014) for a BOD TMDL case-study in the state of Kansas.

4. Conclusions

We presented a probabilistic framework for integrated model calibration and risk-based water quality management, which relies on Bayesian Monte Carlo method and Maximum Likelihood estimation (BMCML). The probabilistic framework was demonstrated through a lake oxygen recovery example presented and modeled by previous investigators for eutrophic lake in upper state New York. The impact of observational, input, and model structure errors on uncertainty quantification, parameter identification and risk-based water quality management was systematically investigated. Major conclusions include the following.

• The BMCML performed well in drawing statistical inferences for lake recovery model parameters. The computational time of BMCML was comparable to that of MCMC with marginal differences in the results between the two methods.

• By comparing formal and informal approaches, we showed that neglecting covariation among parameters, which is reflected by significant cross-correlations computed from corresponding likelihoods, could lead to the over or under estimation of compliance load reductions and, consequently, costly/risky management decisions. Results thus emphasize the importance of parameter sets as opposed to simply sampling of parameter values from posterior marginal PDFs.

• No significant difference was found in the performance of the lake oxygen recovery model utilizing hourly wind speed data (exact solution, Eq. 4) and the one using daily average wind speed data (approximate solution, Eq. 5). This underscores the fact that, if properly calibrated, relatively simpler models could be as effective in interpreting observable data as more complex and computationally exhaustive models.

• A CDF for the liquid film-transfer coefficient is obtained as a function of wind speed. The predicted relationship between liquid film-transfer coefficient for oxygen and wind speed and the computed 95% confidence band were successful in interpreting observed values at five different lakes (Fig. 5), implying that such generic function may be used in lake oxygen modeling efforts where whole-lake measurements cannot be made.