Biophysical analysis of fluid shear stress induced cellular deformation in a microfluidic device

Abstract

Even though the majority of breast cancers respond well to primary therapy, a large percentage of patients relapse with metastatic disease, for which there is no treatment. In metastasis, a tumor sheds a small number of cancerous cells, termed circulating tumor cells (CTCs), into the local vasculature, from where they spread throughout the body to form new tumors. As CTCs move through the circulatory system, they experience physiological forces not present in the initial tumor environment, namely, fluid shear stress (FSS). Evidence suggests that CTCs respond to FSS by adopting a more aggressive phenotype; however, to date single-cell morphological changes have not been quantified to support this observation. Furthermore, the methodology of previous studies involves inducing FSS by flowing cells through the tubing, which lacks a precise and tunable control of FSS. Here, a microfluidic approach is used for isolating and characterizing the biophysical response of single breast cancer cells to conditions experienced in the circulatory system during metastasis. To evaluate the single-cell response of multiple breast cancer types, two model circulating tumor cell lines, MDA-MB-231 and MCF7, were challenged with FSS at precise magnitudes and durations. As expected, both MDA-MB-231 and MCF7 cells exhibited greater deformability due to increasing duration and magnitudes of FSS. However, wide variations in single-cell responses were observed. MCF7 cells were found to rapidly deform but reach a threshold value after 5 min of FSS, while MDA-MB-231 cells were observed to deform at a slower rate but with a larger threshold of deformation. This behavioral diversity suggests the presence of distinct cell subpopulations with different phenotypes.

I. INTRODUCTION

Metastatic cancer is the leading cause of cancer related deaths.¹ As such, an understanding of the biophysics of metastasizing cancer cells is necessary to develop new treatment strategies and therapies against secondary metastasis. Tumor cells can metastasize via several different routes, such as lymphatic and hematogenous spread. Hematogenous spreading can be simplified into a coordinated series of steps: detachment from a primary tumor, intravasation into the circulatory system, movement of the cells through the circulatory system, adhesion and extravasation, and, finally, growth of a secondary tumor.² While inside the circulatory system, the cancer cells are called circulating tumor cells (CTCs). The role of CTCs is particularly important in cancer metastasis as they constitute the intermediate state between the primary and secondary tumors.^3,4 One unique aspect of hematogenous spread is that the fluid flow in the circulatory system constantly exerts fluid shear stress (FSS) on the cells. In the human circulatory system, FSS can range from as low as 0.1 dyn/cm² in interstitial flow to as high as 3000 dyn/cm² around the heart.⁵ However, the average FSS that CTCs experience ranges from 0.5 to 30 dyn/cm² for several minutes, until their arrest in the vasculature.^6,7

Despite the importance of CTCs, the effect of FSS on CTC phenotype is not fully understood. Previous studies have tried to replicate the hemodynamic environment of the circulatory system in vitro by injecting cells through the tubing and utilizing the Hagen-Poiseuille Equation to approximate shear stress magnitudes.^5,8,9 These studies suggested that FSS elicits a strong response in CTCs, such as an acquisition of cancer stem cell (CSC)-like properties.⁹ CSCs are a specialized sub-population of tumors that have the ability to self-renew and differentiate much like healthy stem cells and progenitor cells, but also more poignantly, have tumor initiating characteristics.^2,10 Therefore, they are thought to be the “root cause” of tumor relapse, especially in patients with metastatic tumors. In breast tumors, the CSC population can be prospectively isolated using CD44⁺/CD24⁻ surface markers and/or by aldehyde dehydrogenase (ALDH) activity, and CTCs of metastatic breast cancer patients were previously observed to have a correlated overexpression of stem cell markers.^11–13

CTCs are also commonly characterized by their expression of the epithelial cell adhesion molecule (EpCAM). EpCAM is an important marker as it is commonly used in CTC detection devices.^14–16 EpCAM is also a marker for epithelial to mesenchymal transition (EMT), which allows for cell motility and detachment from the primary tumor. Prior studies have shown that FSS can induce EMT-like characteristics under constant flow.¹⁷ During EMT, epithelial marker expression can be downregulated, which is a challenge for CTC detection devices reliant on EPCAM.⁹ As a result, physical properties such as morphology and stiffness are also used as a CTC phenotype. For example, EMT causes morphological changes resulting in a cellular phenotype that is more elongated, less stiff, and highly motile. A decrease in cellular stiffness has been correlated with increased invasiveness in several studies.^18–20

While previous research confirms that FSS plays a role in cancer metastasis, many studies are limited by the methods used to challenge cells with FSS. The most common approach to shear cells involves flowing cells through micro-tubing using a peristaltic pump.^8,21 While effective, this approach is limited to constant values of fluid shear stress (e.g., a single flow rate and single FSS value) and is not capable of dynamic imaging techniques and relies solely on end-point analysis. Moreover, since cancer cells are intrinsically heterogeneous populations, technologies permitting single-cell analysis are necessary to obtain a better understanding of how FSS influences CTC phenotype.²²

Microfluidic devices have been found to be an effective method for trapping and studying single CTCs isolated from a mixed population as they can be easily tailored to take advantage of physical and/or biological differences between CTCs and surrounding blood cells. This cell capture is gentle enough to allow for further analysis of live cells while isolated inside the device with the tradeoff of lower sample volumes and cell counts compared to traditional assays. However, these devices largely focus on isolating CTCs from blood samples and are utilized as diagnostic tools.²³ Some devices perform biophysical manipulation of CTCs to aid in enrichment and capture, as studies have indicated, that CTCs exhibit greater deformability than other types of cells including immune cells and red blood cells.^24–26 While biophysical manipulation is utilized for CTC isolation, very few microfluidic systems have been designed and employed to examine precisely how fluid shear stress influences CTC phenotype. To address this limitation, this study presents the characterization and use of a microfluidic device capable of trapping single cancer cells and challenging them with precisely controlled and physically relevant magnitudes and durations of FSS. The device allows for both end-point and dynamic single cell analysis of how FSS exposure alters the biophysical properties of cancer cells by shear-induced deformation. This study finds that two different models circulating tumor cell lines (MCF7 and MDA-MB-231) respond differently to increasing magnitudes and durations of FSS. Population-based studies show that the extent of cellular deformation does not depend on the initial size of the cell and that different cells respond differently to increasing values of FSS. Single cell analyses identified distinct subpopulations that emerged to increasing durations and magnitudes of FSS. Finally, time-dependent studies identified two different subpopulations of cells that are ejected versus retained in the traps, suggesting that small populations of breast cancer cells are highly inclined to FSS-induced deformation.

II. MATERIALS AND METHODS

A. Computational simulations of fluid flow in the microfluidic device

The microfluidic device was designed using the simulation software COMSOL Multiphysics v4.3 (COMSOL, Burlington, MA). COMSOL was utilized to optimize cell trapping efficiency, visualize stream-lines, and quantify shear stress levels. For these simulations, water-fluidic properties, no-slip boundary conditions, and a two-dimensional device profile were assumed.

B. Microfluidic device design and fabrication

The microfluidic devices were developed by a combination of soft lithography and PDMS (polydimethylsiloxane) replication. The geometry was designed in AutoCAD software (Autodesk, USA) based on the COMSOL simulation specifications prior to fabrication. A silicon master was fabricated using a negative photoresist polymer, SU-8 2025 (MicroChem). The SU-8 was deposited on a clean 3″ silicon wafer and baked at 65 °C for 15 min followed by a second bake at 95 °C for 30 min. After cooling down, the wafer was exposed to UV light with 1.2 mW/cm² power intensity for 40 s using an iron oxide/chrome photo mask (Front Range) to create the fluidic channels. The wafer was baked again at 65 °C for 15 min and at 95 °C for 30 min, post UV exposure. The silicon wafer was developed with an SU-8 developer solution (Microchem) to remove the uncrosslinked SU-8 to produce the microfluidic patterns. The wafer was hard baked at 150 °C for 30 min to increase wafer durability. PDMS replicas (Sylgard 184, Ellsworth Adhesives) were generated by mixing the base agent in a 10:1 ratio with the curing agent, followed by degassing in a vacuum chamber to create a bubble-free mixture. This PDMS was poured on the silicon master and was cured for at least 6 h at 65 °C. Once cured, the PDMS was removed from the wafer, and the inlet and outlet ports were punched using a blunted 18-gauge needle. The PDMS replicas were permanently bonded to 25 × 75 mm glass slides (Corning) using an O₂ Harrick Plasma PDC-32G basic plasma cleaner with a 30 s exposure to plasma. The devices were left overnight to ensure proper bonding between the PDMS and the glass. To initiate cell trapping, Tygon tubing (Cole Palmer) was directly connected to the cell and media syringes fixed on two dual infusion syringe pumps (Harvard apparatus) and were inserted into the device inlet ports.

C. Cell culture and reagents

MDA-MB-231 and MCF7 cell lines were maintained with Dulbecco’s modified Eagle medium (DMEM) (Corning) supplemented with 10% v/v HyClone Cosmic Calf Serum (VWR Life Sciences Seradigm), 1% MEM Essential Amino Acids (Quality Biological Inc.), 1% MEM Non-Essential Amino Acids (Quality Biological Inc.), 1 mM Sodium Pyruvate (Thermo Fisher Scientific), and 6 μl insulin/500 ml media (Insulin, Human Recombinant dry powder, Sigma Aldrich). During preparation, cells were washed with 1X phosphate-buffered saline (PBS): 137 mM NaCl, 10 mM Na₂HPO₄, 27 mM KCl, and 1.75 mM KH₂PO₄ at pH 7.4. During experimentation, cells were suspended in extracellular buffer (ECB): 20 mM HEPES, 140 mM NaCl, 5 mM KCl, 1 mM MgCl₂·6H₂O, 1 mM CaCl₂·2H₂O, and 5 mM D-Glucose at pH 7.4.

D. FSS-induced cellular deformation studies

Prior to experimentation, the fluidic channels in the device were washed by injecting ECB into the media inlet of the device at 20 μl/min to remove trapped air bubbles. Once all air bubbles were removed, a cellular suspension (3 × 10⁵ cells/ml) in a l ml syringe (BD Biosciences) was connected to the cell inlet of the device by Tygon tubing. The cell and media solutions were infused into the device at rates of 0.2 μl/min and 1.6 μl/min based on the COMSOL simulations. The flow was terminated once the majority (∼75-90%) of traps contained cells. Prior to FSS exposure, images were collected across the entire trapping array to determine the number of traps occupied, cell area, and cell circularity. The media flow rate was then restored and increased to challenge isolated cells with defined magnitudes of fluid shear stress (5-15 dyn/cm²). During exposure to shear, a small region of the device with ∼6-8 cells was imaged via time lapse to analyze dynamic changes in cellular deformation. After the designated FSS duration, the media flow was halted, and the entire trapping array was imaged again. Imaging was performed using a Leica DMi8 inverted microscope outfitted with a fluorescein isothiocyanate (FITC) filter cube, 10X objective (Leica HC PL FL L, 0.4X correction), and phase contrast and bright-field applications. Digital images were acquired using the Flash 4.0 high speed camera (Hamamatsu) with a fixed exposure time of 10 ms. Image acquisition was controlled using the Leica Application Suite software. All images were recorded by using the same parameters. For time lapse experiments, images were captured every 10 s for the 15-min duration.

E. Cell viability assay

Cellular viability was performed on cells after being trapped in the device and exposed to an FSS magnitude of 15 dyn/cm² for a duration of 10 min. MDA-MB-231 cells were trapped and challenged with FSS as described above. After FSS exposure, a 1 ml syringe containing 3 μM Calcein AM was connected to the media inlet and infused into the device at a rate of 2 μl/min for 30 min. No flow was initiated through the cell inlet during this step. Images were collected using the FITC filter set with a fixed exposure time of 500 ms.

F. Image analysis and processing

All images were processed and analyzed using ImageJ software (National of Institutes of Health). The area and circularity were manually determined for each captured cell (pre- and post-exposure to FSS) in the device using defined parameters in ImageJ. Only single isolated cells were considered for analysis; traps containing more than one cell were excluded from the analysis. A comparison across the device using the pre-exposure and post-exposure images allowed for the determination of the ejection percentage by counting the cells in the traps before and after FSS exposure. If a cell was found to “move” from a filled trap to empty trap during FSS exposure, it was neglected from the analysis. All biophysical analyses presented in Figs. 2–6 are for cells that were retained in the traps for the duration of FSS exposure. The analysis of ejected cells is described below using the transient analysis. Two values were calculated for all cells challenged with FSS: the normalized area (NA) and the normalized circularity (NC) which are defined by Eqs. (1) and (2). A value of one for NA or NC indicates no change in area or circularity, respectively, due to FSS exposure. A value greater than one represented an increase in area or circularity, while a value less than one corresponds to a decrease in area or circularity:

$$\mathrm{NA}=\frac{\mathrm{Final}\mathrm{area}\mathrm{after}\mathrm{shear}}{\mathrm{Initial}\mathrm{area}\mathrm{before}\mathrm{shear}},$$ (1)

$$\mathrm{NC}=\frac{\mathrm{Final}\mathrm{circularity}\mathrm{after}\mathrm{shear}}{\mathrm{Initial}\mathrm{circularity}\mathrm{before}\mathrm{shear}}.$$ (2)

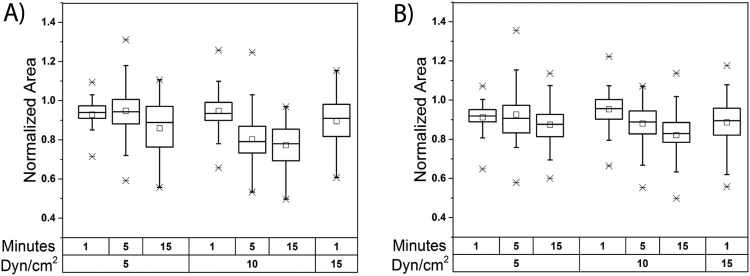
FIG. 2.

Effect of fluid shear stress magnitude and duration on cellular deformation as quantified by the normalized area. The normalized area was calculated for both MCF7 cells (a) and MDA-MB-231 cells (b) at increasing magnitudes and duration of fluid shear stress. Population statistics include the mean (open square), median (horizontal line), and the maximum and minimum outlier values denoted by an “X” in the box and whisker plots. For every condition, a minimum of 40 single cells were analyzed.

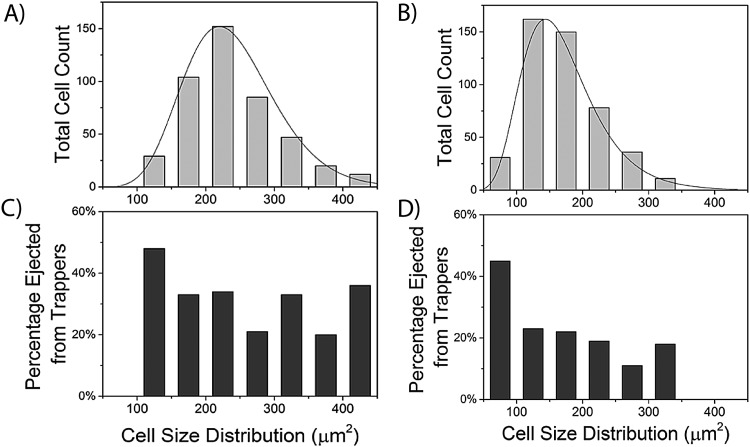
FIG. 3.

Size distribution and ejection percentages for cancer cells trapped in the microfluidic device. (a) The size distribution of all MCF7 cells was compared and found to follow a gamma distribution with a larger variation across cell size. (b) The size distribution of all MDA-MB-231 cells was compared and found to follow a log-normal distribution with a smaller variation across cell size. The ejection percentage of both MCF7 cells (c) and MDA-MB-231 cells (d) did not have a strong correlation to cell size above a threshold value of 150 μm². MCF7 (n = 460 cells) and MDA-MB-231 (n = 458 cells) cells from every experimental condition were analyzed as a single population, with bins representing a size distribution of 50 μm².

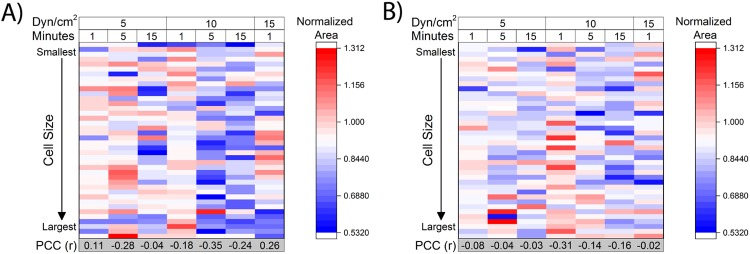
FIG. 4.

Initial cell size does not influence cellular deformation due to fluid shear stress. The initial area of both MCF7 cells (a) and MDA-MB-231 cells (b) showed no statistically significant correlation to the degree of deformation due to fluid shear stress as calculated by the normalized area. Pearson’s correlation coefficient (PCC) was calculated for seven conditions of increasing FSS duration and FSS magnitude for both cell lines to evaluate the relationship between cell size and deformation, as visualized by a heatmap. For a 0.98 level of significance (n = 40 cells), a coefficient between ±0.358 indicates no linear relationship between variables.

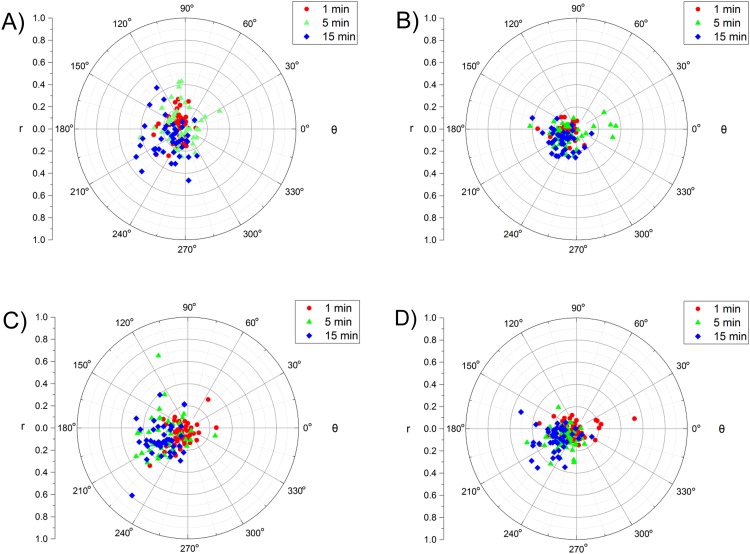
FIG. 5.

Single cell analysis of changes in cellular area and circularity due to increasing durations of fluid shear stress duration and magnitude. The normalized area and normalized circularity were converted to polar coordinates to bin subpopulations into four regions of increased circularity and area (0°-90°), increased circularity and decreased area (91°-180°), decreased circularity and area (181°-270°), and decreased circularity and increased area (271°-359°) for both MCF7 [(a) and (b)] and MDA-MB-231 cells [(c) and (d)] exposed to FSS magnitudes of 5 dyn/cm² [(a) and (c)] and 10 dyn/cm² [(b) and (d)]. For each condition, a minimum of 40 cells were analyzed at the durations listed in the legends.

FIG. 6.

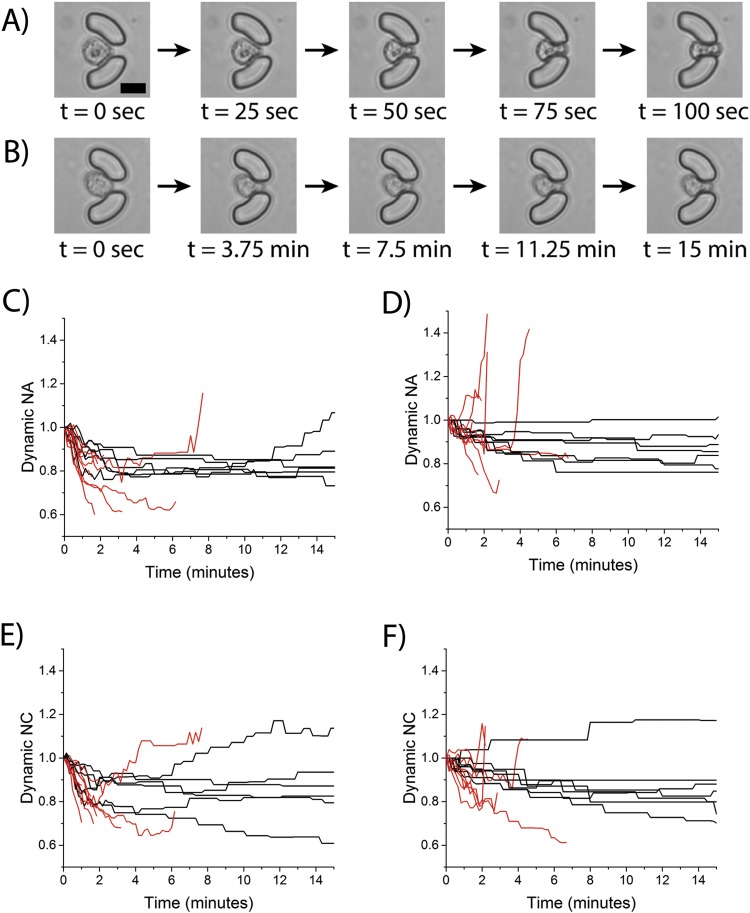
Time-dependent deformation of cancer cells due to fluid shear stress. Images of FSS-induced deformation of single MCF7 cells that were ejected from a trap (a) or retained in a trap (b). Scale bar is 20 μm. Time-dependent change in the area of MCF7 cells (c) and MDA-MB-231 cells (d) was quantified every 10 s. A similar analysis for change in circularity for MCF7 cells (e) and MDA-MB-231 cells (f). Black lines indicate cells that were retained in traps, and red lines indicate cells that were ejected from traps.

G. Conversion of rectangular NA and NC values to polar values

The values for NA and NC, as described above, were translated to better visualize the change in cellular area and circularity at the single cell level due to exposure to fluid shear stress (Fig. 5). The rectangular values were converted to polar values to create two new metrics of deformation: r and θ. The r value was a metric of how deformed the cell became due to FSS, and the θ value allowed for the binning of the cells into four distinct groups. A value of 0°-90° corresponded to an increase in area and circularity, a value of 91°-180° corresponded to an increase in circularity and a decrease in area, a value of 181°-270° corresponded to a decrease in both area and circularity, and a value of 271°-359° corresponded to a decrease in circularity and an increase in area. As defined, a value of one for NA and one for NC corresponded to a cell that showed no signs of deformation due to FSS exposure; however, the conversion to polar coordinates required a translation of the origin from (1,1) to (0,0). This was accomplished by subtracting one from each value. The values for r and θ were calculated using the standard conversions from rectangular to polar coordinates following the Pythagorean Theorem.

H. Time-dependent analysis of cellular deformation

For the time-dependent experiments, the definitions of normalized area (NA) and normalized circularity (NC) were adjusted. Here, the time-dependent dynamic NA was calculated at each time point (in 10 s intervals) by dividing the cellular area by the initial area of the cell at t = 0 min to normalize all cells. A similar approach was used to calculate the dynamic NC. Thus, every cell starts with dynamic NA and dynamic NC values of 1. An increase in dynamic NA corresponds to an increase in cell area over time, while a decrease in dynamic NA corresponds to a decrease in cell area over time. A similar trend is observed for dynamic NC. Mean dynamic NA and mean dynamic NC values were calculated for each cell by averaging all of the dynamic NA and NC values collected during the 15 min time course. Mean values for cells that were ejected in the middle of the time course were only calculated up until the point of ejection. A range was then calculated for the dynamic NA and the dynamic NC for each cell by subtracting the minimum value from the maximum value observed during the time course to determine how each cell deformed in terms of area and circularity. A coefficient of variance (COV) was calculated for each cell by dividing the range for dynamic NA by the mean dynamic NA value. A similar calculation was performed to determine a COV for dynamic circularity for each cell. Finally, population averages were calculated by averaging all the mean dynamic NA values for each group of cells (MCF7 retained, MCF7 ejected, MDA-MB-231 retained, and MDA-MB-231 ejected). A similar calculation was performed to get an average range value for each population.

III. RESULTS AND DISCUSSION

A. Determination of device parameters and fluid shear stress magnitudes using COMSOL simulations

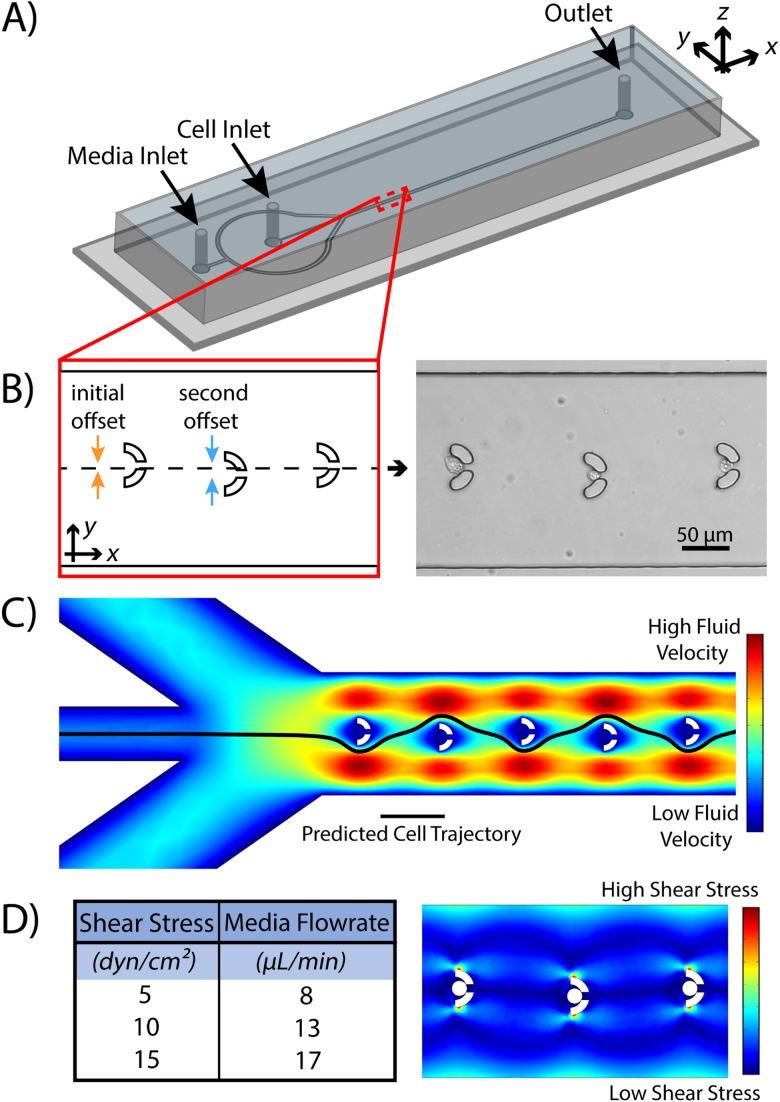
The design of the microfluidic device is based on a similar geometry previously described by Tran et al. which was used for the isolation of CTCs from a blood sample.²⁷ The device consists of a linear array of 100 semi-circular microsieves (herein referred to as traps) capable of trapping single cancer cells [Fig. 1(a)]. The traps were designed with an opening width of 30 μm (outer diameter of 50 μm) and a gap at the center of the semi-circle with a width of 10 μm [Fig. 1(b)]. Here, the traps serve a dual function of trapping the cells and serving as a location for controlled shearing and deformation analysis of single cells. The traps were designed to accommodate cell sizes ranging from 15 to 30 μm in diameter, the range associated with most CTCs.²⁸ To facilitate single cell trapping, the device took advantage of sheath flow induced by flow originating from two inlet ports: the cell inlet and media inlet (Fig. 1). The media flow inlet is split and then converges on the cell flow inlet to focus the suspension of cells in the center axis of the device to direct the cells into the array of traps. The array of cell traps was designed by taking three parameters into account: initial trapper offset in the positive y-direction, secondary trapper offset in the negative y-direction, and lateral trapper spacing in the positive x-direction. Similar to the work by Tran et al., the traps were offset with the first trap shifted 4 μm in the positive y-direction and the second trap offset 6 μm in the negative y-direction to allow for optimal cell flow [Fig. 1(b)]. This orientation was repeated every two traps through the entire array. The result was a weaving streamline motion between traps while maintaining an overall central axial position within the sheath flow [Fig. 1(c)]. As such, once a cell is trapped, the fluid flow through that gap is subsequently diminished, inhibiting further cell capture in that specific trap and promoting the following cell to the next trap. The traps were positioned 150 μm apart to allow for the cell suspension streamline to regain a central axial position after encountering a trap, like what was shown by Tran et al. A ratio of 8:1 of media inlet flow rate to cell inlet flow rate provided ideal streamlines for the device, which had a total width of 225 μm (y-axis).

FIG. 1.

The microfluidic device utilizes an array of traps to isolate and capture single CTCs and then challenges them with precise magnitudes of fluid shear stress. (a) A complete schematic of the entire microfluidic device. (b) Traps were offset to optimize the ability to capture and isolate single cells. (c) COMSOL Multiphysics simulations of the velocity profile of the device with the estimated path of cells depicted by the black stream line. (d) Calculation of FSS magnitudes dependent on the media flow rate into the device as calculated by the COMSOL point of the evaluation method.

Once the cellular trajectories and trapping potential were confirmed, the next step was to determine the relationship between media flow rate and FSS magnitude in trapped cells. Using the point of an evaluation method in COMSOL and the relationship spf.mu(vx + uy), the average fluid shear stress magnitude was calculated on simulated cells with a diameter of 20 μm [Fig. 1(d)]. The point of evaluation method was used to calculate FSS at the point on the cell closest to the direction of fluid flow. At this point, the change in velocity of the media, and therefore FSS, is highest. Since the surface of the cells experiences various levels of shear (similar to how they would in the circulatory system), the highest value was used. For these calculations, flow in the cell inlet was halted so that the only flow came from the media inlet to obtain greater control over the system. The simulation also revealed that a low-velocity region surrounded individual traps containing cells. Because the fluid is relatively stagnant around these microstructures, cells isolated within the traps do not experience a pressure gradient as they would in other areas of the device. Based on these findings, it is assumed that cellular deformation results from induced FSS and not from hydrodynamic pressure gradients within the array. To insure trapping and FSS did not cause cell death, a total of 55 cells were screened after shearing and 47 were found to be alive. The extreme duration of 10 min at 15 dyn/cm² is rare physiologically and was therefore a longer duration than examined at this shear magnitude. As such, a 90% cell viability is acceptable. Cell exposure to FSS inside of the tubing during the trapping phase was quantified with the Hagen-Poiseuille equation for fluid flow in a cylindrical vessel. A tubing diameter of 0.022 in. and a media dynamic viscosity of 1.0 × 10⁻³ kg/m/s correspond to a wall shear stress value of approximately 0.002 dyn/cm², which was considered to be negligible. The effects of FSS in the z-direction were also considered to be negligible due to the similar dimensions of the height of the microfluidic channels (20 μm) and the average diameter of the cells (∼15-20 μm). The most often case would be for the cells to perfectly occlude the outlet port of the trap; however, if the cells do not occlude the outlet port, the much slower fluid flow above or below the cell would not generate a high value of FSS to be detrimental to the predicted value. To further ensure that the fluid shear stresses as calculated were the dominant forces causing cellular deformation, the pressure drop across individual trapped cells was quantified using COMSOL simulations and were found to be approximately 10 and 21 Pa for 5 and 15 dyn/cm², respectively. These magnitudes are fractional when compared to established studies that look at pressure induced cell deformation, which can use pressure gradients in the range of 1500–20 265 Pa.^29,30

B. Increasing fluid shear stress magnitude and duration results in a greater extent of cellular deformation

The microfluidic device was utilized to analyze the deformation of individual cells challenged with increasing durations and magnitudes of fluid shear stress followed by population-based analysis on two model circulating tumor cell lines (MCF7 and MDA-MB-231). These two cell lines were selected due to their difference in metastatic potential with the MCF7 having been shown to be less invasive, while the MDA-MB-231 cells were found to be highly invasive.³¹ Once single cells were trapped and isolated in the device they were exposed to three magnitudes of FSS (5, 10, and 15 dyn/cm²) for three durations (1, 5, and 15 min) which induced cellular deformation as the cells entered the gap. Cellular deformation was quantified using the normalized area (as defined in the methods section) which allowed for a comparison across the physiologically relevant FSS conditions used to challenge the cells (Fig. 2). To maintain statistical relevance, a minimum number of 40 cells were analyzed per condition. No data are presented for the 5 and 15 min durations for cells exposed to 15 dyn/cm² because this high combination of FSS magnitude and duration resulted in the majority of cells being ejected from the trapper. As cells are unlikely to encounter these combinations of magnitude and duration in vivo, they were ignored from the subsequent analysis. Additional control experiments were performed to confirm that the observed changes in area and circularity were due to exposure to fluid shear stress and not due to exerting pressure on cells in close proximity to a narrow pore. As seen in Fig. S2A in the supplementary material, the absence of flow resulted in negligible changes in cellular area confirming that the observed deformation of the cells is due to fluid shear stress induced by flow into the device and not by an inherent pressure gradient within the device. To further confirm that cellular deformation was caused by exposure to FSS and not pressure, cell deformation after exposure to FSS and when flow was halted was examined [Fig. S2(B) in the supplementary material]. No significant change in the normalized area was observed in any of the cells during these time periods after fluid flow (and FSS exposure) was stopped. This strongly indicates that FSS is the driving force for cellular deformation, as it is well documented that cell shape will recover after deformation caused by pressure forces at similar time scales.³²

Two important statistical metrics, the mean and the interquartile range (IQR), were calculated to assess the population response of MCF7 and MDA-MB-231 cells exposed to different durations and magnitudes of FSS to demonstrate the sensitivity and variety of the response. IQR is a measure of spread that contains the middle 50% of data around the median and is represented by the width of the box in the box-and-whisker plot. As seen in Fig. 2, there is a positive relationship between IQR and both FSS magnitude and duration for both cell lines. For example, the IQR increases three-fold from 0.059 to 0.186 for MCF7 cells and two-fold from 0.057 to 0.112 for MDA-MB-231 cells as duration increases from 1 to 15 min at 5 dyn/cm² of FSS. This observation highlights the heterogeneity of cells within the same population, as the variety in their responses increases with increasing magnitude and duration. Both cell lines were found to exhibit outlier values approximately four times greater than the mean of the population which confirms the heterogeneity of the population and suggests that certain cells exhibit a much greater deformability potential than others. As cells must deform and extravasate to exit the bloodstream, and only a few cells must complete the metastatic process to form secondary tumors,⁶ these highly deformable cells are of extreme importance. Interestingly, both MCF7 and MDA-MB-231 cells were found to follow similar trends with respect to response sensitivity. It was observed that increasing FSS magnitude and duration caused a consistent decrease in the mean and median values for the normalized area with the exception of the 5 min/5 dyn/cm² condition for both cell lines. At this condition, some cells began to partially emerge from the trap, expanding in the area as they did so. These enlarged cells were ejected at greater FSS durations, possibly explaining this deviation. Despite the similar trends between the two different cell types at certain conditions, important differences were observed. The foremost distinction between the two cell lines was that MCF7 cells [Fig. 2(a)] exhibited the capability for faster deformation when compared to MDA-MB-231 cells [Fig. 2(b)], as MCF7 cells have a lower mean normalized area after a 15 min duration for 5 and 10 dyn/cm². Conversely, MCF7 cells appeared to reach a deformation limit as can be seen by the similarities between normalized area distributions at 5 and 15 min for 10 dyn/cm². This was not the case for MDA-MB-231 cells, which continue to deform at these conditions. This indicates that MDA-MB-231 cells appear to be initially more resistant to FSS-induced deformation than MCF7 cells; however, they will continue to deform to a large extent.

C. FSS-induced cellular deformation does not depend on the initial cell area

Once it was determined that FSS magnitude and duration affected cellular deformation as a population, the next step was to identify what factors in individual cells influenced the extent of FSS-induced deformation. During experimentation, it was observed that when cells reach a high enough extent of deformation due to a combination of decreased area and circularity, they can squeeze through the 10 μm gap and get ejected from the trap. Initially, it was hypothesized that the extent of cellular deformation and ejection from the device was due to the initial size of the cell. As previously stated, an important step in the metastatic cascade involves CTCs deforming and extravasating through the vasculature.⁶ To investigate this, the relationship between cell size and ejection was examined to link extravasation capability to cell size. A comprehensive cell population was formed by combining the initial cell area and ejection data for all FSS duration and magnitudes studied for MCF7 cells (n = 460) and MDA-MB-231 cells (n = 458). Cell size distribution of both the entire population and cells ejected was visualized with the use of a histogram with a bin size of 50 μm² (Fig. 3). When comparing the population distributions, MCF7 cells [Fig. 3(a)] were found to have a larger average initial area and variance when compared to MDA-MB-231 cells [Fig. 3(b)], with the most numerous cell sizes being 200-250 μm² and 100-150 μm², respectively. Interestingly, this analysis found that the two cell lines have different population distributions. MCF7 cells follow a gamma distribution, while MDA-MB-231 cells follow a log-normal distribution [Figs. 3(a) and 3(b)]. Individual Distribution Identification was performed using Minitab to identify the best fit distribution, which evaluates fits based on P-values and the Anderson-Darling statistic. These trends indicated that the MDA-MB-231 population is more heavily skewed to smaller cell sizes, reiterating the size differences of cells trapped between the two cell lines. Even though differences were observed for average cell size and distribution, both cell lines exhibited similar behavior when comparing initial cell size and ejection. The analysis of the entire population of MCF7 and MDA-MB-231 cells found that beyond a threshold value, cellular ejection from the traps does not depend on initial cell size. This threshold value was the smallest bin of cells for both cell lines, which encompasses cell sizes below 150 μm² for MCF7 cells and 100 μm² for MDA-MB-231 cells [Figs. 3(c) and 3(d)]. This disparity between threshold areas further suggests that MCF7 cells are capable of a greater extent of deformation when compared to MDA-MB-231 cells. Interestingly, MCF7 cells were found to have a higher ejection percentage than MDA-MB-231 cells for similar size distributions (e.g., 200-250 μm²) as well as the overall population, despite being the larger cell line. For the overall population, 30% of MCF7 cells were ejected, while only 22.6% of MDA-MB-231 cells were. Even though cell size was determined to not correlate to ejection, cell type influences ejection to a large extent.

To further study the effect of cell size on deformation, a comparison was performed between the initial cell area and the normalized area for both MCF7 cells and MDA-MB-231 cells at the single cell level. Heatmaps were generated to visualize this relationship by organizing 40 cells from smallest to largest for every tested condition and then using the color range to denote the change in the normalized area (Fig. 4). The warmer colors represent an increase normalized area, while the cooler colors denote a decrease in normalized area. For both MCF7 cells [Fig. 4(a)] and MDA-MB-231 cells [Fig. 4(b)], this analysis revealed no vertical color trend suggesting that no relationship existed between initial cell size and deformation. The linearity of this relationship was quantified using Pearson’s correlation coefficient (PCC) for each of the combinations of FSS magnitude and duration. For a 0.98 level of significance (n = 40), no linear relationship existed between variables for a PCC between −0.358 and +0.358. The results of the heatmap agree with the calculated PCC, which confirms no statistically significant linear relationship between cell size and normalized area. Interestingly, a horizontal color change was observed on the heatmaps implying that increasing the duration and magnitude of FSS results in a decrease in cellular area as denoted by a normalized area less than one. These findings correlate with the previous analysis for the entire population presented in Fig. 2. The lack of a vertical trend with respect to the color in the heatmap coupled with the presence of a horizontal trend indicates that cell deformation only depends on fluid shear stress magnitude and duration.

D. Heterogeneity of single cell deformation due to different magnitudes and durations of fluid shear stress

While performing population-based analysis on the effects of fluid shear stress magnitude and duration are enlightening, a strength of the microfluidic approach is the ability to perform single cell analysis on how FSS affects cellular deformation. To visualize how exposure to FSS affected cellular deformation, the values of NA and NC were converted to polar coordinates where the r value corresponded to the extent in which a cell deformed due to the FSS and the θ value allowed for the binning of the cells into four distinct subpopulations based on their changes in normalized area and normalized circularity (Fig. 5). This analysis found that the extent to which a cell deformed was dependent on both FSS magnitude and duration. As shown in Table I, the average r value increased from FSS durations of 1-15 min and FSS magnitude of 5-10 dyn/cm². Additionally, the extent of cellular deformation was found to strongly depend on the cell line. The average r value for MCF7 cells increased by 67% and 125% when exposed to 5 dyn/cm² and 10 dyn/cm², respectively, for a duration of 15 min compared to the 1-min duration. An increase of 80% and 95% was observed for MDA-MB-231 cells under similar conditions. Interestingly, the r value for MCF7 cells only increased by 5% when increasing the duration from 5 to 15 min at 10 dyn/cm². This suggested that while MCF7 cells can deform to a greater extent when exposed to increasing durations and magnitudes of shear stress, this deformation reaches a maximum level by ∼5 min. Conversely, the extent of deformation of MDA-MB-231 cells increased by 30% under similar conditions. This suggests that while MDA-MB-231 cells are more resistant to FSS-induced deformation, they will continue to deform at increasing durations of high shear stress magnitudes.

TABLE I.

Binning of heterogeneous subpopulations of MCF7 and MDA-MD-231 cells exposed to increasing values of FSS magnitude and duration.

Duration (dyn/cm2)	MCF7 cells						MDA-MB-231 cells
	5			10			5			10
Magnitude (min)	1	5	15	1	5	15	1	5	15	1	5	15
0°-90°	13.636	14.815	2.326	7.407	0	0	1.695	7.843	0	8.696	1.786	0
91°-180°	59.091	31.481	23.256	22.222	26.829	22.727	33.898	19.608	10	23.188	12.5	15.909
181°-270°	25.000	40.741	60.465	55.556	65.854	77.273	64.407	62.745	82.5	50.725	80.357	77.273
271°-360°	2.273	12.963	13.953	14.815	7.317	0	1.695	9.804	7.5	17.391	5.357	6.818
Avg r	0.140	0.178	0.235	0.129	0.275	0.290	0.108	0.171	0.196	0.118	0.175	0.230
SD r	0.0793	0.0997	0.1341	0.0873	0.1410	0.1240	0.0537	0.0847	0.0793	0.0871	0.0921	0.1199

The single cell biophysical analysis also provided insight into how the cells deform when exposed to increased FSS magnitude and duration. The majority of both MCF7 and MDA-MB-231 cells exhibited a decrease in both circularity and area when exposed to the 10 dyn/cm² FSS for 15 min (Fig. 5, Table I). The largest percentage of θ values shown in Table I falls between 181° and 270° for both MCF7 and MDA-MB-231 cells at increasing FSS magnitude and duration, displaying that FSS elicits a decrease in cellular area and circularity. However, the largest population of MCF7 cells was found to exhibit a decrease in the area yet an increase in circularity, corresponding to θ values between 91° and 180°, when exposed to the lowest magnitude (5 dyn/cm²) for the shortest duration (1 min). The majority of MDA-MB-231 cells experienced a decrease in both area and circulatory under similar conditions. This suggests that MCF7 cells have a different initial response to FSS than MDA-MB-231 cells. Differences in cellular responses, as given by Fig. 5 and Table I, support the claim that subpopulations in a tumor have distinct phenotypical features that induce cells to act a certain way. As shown in Table I, as the FSS duration increases, both MCF7 cells and MDA-MB-231 cells begin to act increasingly similar to one another. Approximately 55% of MCF7 cells show a decrease in both circularity and area when exposed to FSS at 10 dyn/cm² for 1 min (θ values of 181°-270°). When the FSS duration is increased to 15 min, MCF7 cells are only present in two regions with 22% having θ values of 91°-180° and 77% having θ values of 181°-270°. A similar response is observed in MDA-MB-231 cells (Table I). The bottleneck effect observed in these cell populations suggests that FSS alters the phenotype of cells in such a way that cells begin to act similar to other cells under more intense magnitudes and durations of fluid shear stress.

E. Time-dependent deformation in single cancer cells due to fluid shear stress

Another advantage of the microfluidic approach is the ability to measure dynamic changes in single cell area and circularity under different FSS magnitudes and durations, including cells that were ejected from traps. As described above, a subset of the total number of cells trapped in the device was ejected during exposure to FSS due to their high extent of deformation. The time-dependent studies here were able to visualize this rapid extent of deformation of a single MCF7 that was ejected [Fig. 6(a)] compared to an MCF7 that was retained [Fig. 6(b)]. The ejected cell was able to rapidly deform under 10 dyn/cm² FSS in less than 2 min, which resulted in it squeezing between the gap in the trap and getting ejected. To expand upon this analysis and explore differences between ejected and retained cells from both MCF7 and MDA-MB-231 cells, two new metrics were calculated: the dynamic NA and dynamic NC. The values normalize cellular area and circularity by dividing each time-dependent value by the value at the t = 0 min time point. The dynamic NA and dynamic NC values were then calculated for both MCF7 cells [Figs. 6(c) and 6(e)] and MDA-MB-231 cells [Figs. 6(d) and 6(f)]. Furthermore, this allowed for a comparison between cells that were ejected [red lines, Figs. 6(c)–6(f)] and cells there were retained [black lines, Figs. 6(c)–6(f)]. As expected, the degree of deformation of the ejected cells was much more pronounced than retained cells. The time-dependent analysis also demonstrated the rate in which the cells deformed and how this affected cellular retention. Ejected MCF7 cells had a rapid decrease in normalized area with some cells reaching values of dynamic NA of ∼0.6 in 2-6 min followed by ejection. Conversely, retained MCF7 cells had a slower deformation which ultimately stabilized at an average dynamic NA value of ∼0.8 within 5 min. These results correspond with those presented above (Fig. 5, Table I) for MCF7 cells that show the cells reaching a deformation threshold by ∼5 min. Interestingly, MDA-MB-231 cells that were ejected demonstrated an even greater rate of deformation reaching upper and lower dynamic NA values from 1.5 to 0.6 within 2-3 min; conversely, the retained cells followed a similar pattern as described above reaching a threshold dynamic NA value of ∼0.9 within ∼6-8 min. This confirms the above findings that the rate of deformation of retained MDA-MB-231 cells is slower than MCF7 cells, but that they can deform to a greater extent given a longer duration.

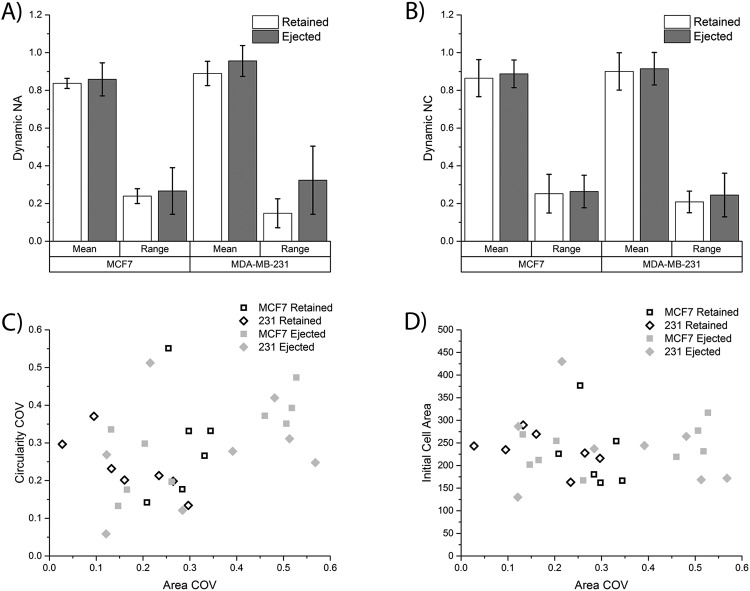
Based on the observed differences between the ejected and retained cells, it was decided to further investigate the population behavior of these two different types of cells. New metrics were calculated to describe the population of MCF7 cells that were ejected (n = 6) versus retained (n = 9) and MDA-MB-231 cells that were ejected (n = 7) versus retained (n = 8). The mean dynamic NA and mean dynamic NC were calculated as described in the methods section to identify a lifetime average of deformation for all cells challenged with 10 dyn/cm² FSS. Interestingly, there was no statistically significant difference between the mean dynamic NA and mean dynamic NC values for the retained versus ejected cells for both cell lines [Figs. 7(a) and 7(b)]. The second metric calculated was the mean population range which measured how far the cell deformed with respect to normalized area and normalized circularity during time-dependent deformation. These ranges can be visualized in Figs. 6(c)–6(f) by looking at the path the dynamic NA and dynamic NC values take as a function of time. As seen in Figs. 6(c) and 6(d), the ejected cells have much larger ranges than retained cells (compare red lines to black lines). When looking at the average population range for dynamic NA, there is a significant difference between ejected and retained cells for the MDA-MB-231 cells (p = 0.034), but not for the MCF7 cells (p = 0.554) [Figs. 7(a) and 7(b)]. Interestingly, this trend was not observed with the average population range values for normalized NC for both MCF7 cells (p = 0.451) and MDA-MB-231 cells (p = 0.821), suggesting that cell size and not cell circularity has a greater distinction for ejected versus retained cells. This analysis suggests that a subpopulation of MDA-MB-231 cells are so deformable that they are ejected very quickly in the device when exposed to higher magnitudes and durations of FSS which excludes from the pre- and post-FSS analysis. This also suggests that MCF7 cells as a population may deform more; however, MDA-MB-231 cells are more heterogeneous with subpopulations that are very susceptible to deformation and others that are less susceptible to deformation.

FIG. 7.

Comparison of cellular deformation between retained and ejected cells. (a) The population averages for both the mean dynamic NA and the dynamic NA range were calculated for both MCF7 cells (n = 6 retained cells and n = 9 ejected cells) and MDA-MD-231 cells (n = 7 retained cells and n = 8 ejected cells). (b) A similar calculation was performed to get the population averages for the mean dynamic NC and the dynamic NC range. (c) The area COV and circularity COV were plotted for all MCF7 and MDA-MB-231 cells that were retained in traps and ejected from traps. (d) The area COV was plotted against the initial cell area for MCF7 and MDA-MB-231 cells.

To expand on this at the single cell level and elucidate potential subpopulations, a final metric, the coefficient of variance (COV), was calculated for both area and circularity as described in the methods. A high COV value corresponds to either a large range or small mean dynamic value, both of which indicate a high extent of deformation. When comparing the area COV to the circularity COV, an ejection threshold value emerges of ∼0.4 for the area COV. As shown in Fig. 7(c), both MCF7 and MDA-MB-231 cells above this value are ejected from the traps. Conversely, there exists another subpopulation of both cell lines that are ejected with lower area COV values, suggesting that something other than biophysical deformation results in cellular ejection. Interestingly, the circularity COV does not play an important role in distinguishing ejected versus retained cells further emphasizing the role of decreasing cell size, and not circularity, as the more important metric of deformation. Additionally, the effect of initial cell area was examined as a cause for ejection over retention. Similar to as described above, cell size does not play a role in ejection over retention [Fig. 7(d)] as all four categories of ejected versus retained for both cell lines fall within the normal distributions of each cell line.

IV. CONCLUSIONS

In order to gain a deeper understanding of the role of the hemodynamic environment in metastasis, a microfluidic device was used that was capable of trapping and isolating single model CTC cell lines and exposing them to physiologically relevant and precisely controlled values of fluid shear stress. The two model breast cancer cell lines, MCF7 and MDA-MB-231, were exposed to 5, 10, and 15 dyn/cm² of shear stress for durations of 1, 5, and 15 min. Both cell lines exhibited area deformation and an increasingly heterogeneous response when challenged with increasing magnitudes or durations of FSS. MCF7 cells were found to deform quicker and to a greater extent, as determined by population and single cell dynamic analyses. The effect of pre-shear cell size on deformation was investigated and shown to have no correlation to the amount of deformation; yet, distinct subpopulations were identified in both cell lines. A subpopulation was identified in both cell lines that exhibited the ability for rapid and extreme area deformation, enough to become ejected completely from the traps. Conversely, another subpopulation of ejected cells was observed that did not undergo a large area change. As size was determined to be irrelevant in deformation, innate differences, such as cytoskeleton rigidity or gene expression, must be present and causing these observed biophysical differences. These results highlight the importance of performing single cell studies on heterogeneous populations of cancer cells, as a population study would silence these outliers and subpopulations that contain properties that could be crucial to the completion of the metastatic cascade.

SUPPLEMENTARY MATERIAL

See supplementary material for images associated with the live stain of MDA-MB-231 cells trapped and sheared in the device.