Many listeners cannot discriminate major vs minor tone-scrambles regardless of presentation rate

Abstract

A tone-scramble is a random sequence of pure tones. Previous studies have found that most listeners (≈ 70%) perform near chance in classifying rapid tone-scrambles composed of multiple copies of notes in G-major vs G-minor triads; the remaining listeners perform nearly perfectly [Chubb, Dickson, Dean, Fagan, Mann, Wright, Guan, Silva, Gregersen, and Kowalski (2013). J. Acoust. Soc. Am. 134(4), 3067–3078; Dean and Chubb (2017). J. Acoust. Soc. Am. 142(3), 1432–1440]. This study tested whether low-performing listeners might improve with slower stimuli. In separate tasks, stimuli were tone-scrambles presented at 115, 231, 462, and 923 notes per min. In each task, the listener classified (with feedback) stimuli as major vs minor. Listeners who performed poorly in any of these tasks performed poorly in all of them. Strikingly, performance was worst in the task with the slowest stimuli. In all tasks, most listeners were biased to respond “major” (“minor”) if the stimulus ended on a note high (low) in pitch. Dean and Chubb introduced the name “scale-sensitivity” for the cognitive resource that separates high- from low-performing listeners in tone-scramble classification tasks, suggesting that this resource confers sensitivity to the full gamut of qualities that music can attain by being in a scale. In ruling out the possibility that performance in these tasks depends on speed of presentation, the current results bolster this interpretation.

I. INTRODUCTION

Music in the major diatonic scale sounds “happy” to many listeners whereas music in the minor scale sounds “sad” (Blechner, 1977; Crowder, 1984, 1985a,b; Gagnon and Peretz, 2003; Gerardi and Gerken, 1995; Heinlein, 1928; Hevner, 1935; Kastner and Crowder, 1990; Temperley and Tan, 2013). Because of this striking qualitative difference, the major and minor scales have come to play a central role in western music. Surprisingly, however, many listeners seem to have difficulty discriminating major vs minor melodies (Halpern, 1984; Halpern et al., 1998; Leaver and Halpern, 2004).

Chubb et al. (2013) investigated sensitivity to major vs minor musical modes using a new class of stimuli, called tone-scrambles, specifically designed to isolate perceptual differences due to variations in musical scale from other aspects of music structure. These stimuli comprised 32 tones from the Western diatonic scales, each 65 ms in duration presented in a random sequence. The major and minor tone-scrambles used in the first experiment reported by Chubb et al. (2013) all contained eight each of the notes G₅, D₆, and G₆ (which established G as the tonic center of each stimulus); in addition, major tone-scrambles contained eight B₅'s (the third degree of the G major scale) whereas minor tone-scrambles contained eight $B{♭}_5$'s (the third degree of the G minor scale). (The stimuli used in the “8-task” in the current study are identical to these.) On each trial, the listener heard either a major or a minor tone-scramble and strove (with trial-by-trial feedback) to classify it as major vs minor. The results revealed a bimodal distribution of performance: approximately 70% of listeners performed near chance, whereas the other 30% performed nearly perfectly.

These results make it clear that high-performers possess auditory processing capabilities that low-performers do not. Dean and Chubb (2017) explored the nature of these processing capabilities. Specifically, they tested listeners in five tasks similar to the major-vs-minor tone-scramble task used by Chubb et al. (2013). In each task, the stimuli were tone-scrambles that contained 32, randomly sequenced, 65 ms tones; like the tone-scrambles used by Chubb et al. (2013), all of the stimuli of Dean and Chubb (2017) contained eight each of the notes G₅, D₆, and G₆ (to establish G as the tonic center of every stimulus in all conditions). In addition, each stimulus contained eight identical target notes. In the “2” task, the target notes were either $A{♭}_5$'s or A₅'s (diminished second or second scale degree); in the “3” task, the target tones were either $B{♭}_5$'s or B₅'s [minor or major third scale degree, replicating Chubb et al. (2013)]; in the “4” task, the target tones were either C₆'s or $D{♭}_6$'s (fourth scale degree or tritone); in the “6” task, the target tones were either $E{♭}_6$'s or E₆'s (minor or major sixth scale degree); and in the “7” task, the target tones were either F₆'s or $G{♭}_6$'s (minor or major seventh scale degree).

The results were well-described by a “bilinear” model proposing that performance in all five tasks is determined predominantly by a single computational resource R. Specifically, for any listener k and any task t, let R_k be the amount of R possessed by listener k, and let F_t be the strength with which R facilitates task t. Then the bilinear model asserts that the sensitivity (as reflected by $d\prime$) of listener k to the difference between the two types of stimuli in task t is

$$d_{k,t}^{\prime }=R_k{F}_t.$$ (1)

This model accounted for 79% of the variance in $d_{k,t}^{\prime }$ across 139 listeners and the five tasks. Consonant with the results of Chubb et al. (2013), most listeners (around 70%) had levels of R near zero, yielding near-chance performance in all five tasks; the other roughly 30% of listeners had levels of R that enabled substantially better performance. However, some tasks were facilitated more strongly than others by R; in particular, the highest levels of performance were achieved in the 2, 3, and 6 tasks; the 4 task was harder, and the 7 task was harder still. Thus F₂ ≈ F₃ ≈ F₆ > F₄ > F₇.

What do these findings suggest about the nature of the resource R? The 3, 6, and possibly the 7 tasks require differential sensitivity to the major vs the minor scale. In each of these tasks, one target note belongs to the major but not the minor diatonic scale, and the other target note belongs to the minor but not the major scale. However, this is not true of the 2 and 4 tasks. In each of these tasks, one target note belongs to both the major and minor scales, and the other target note belongs to neither scale. Dean and Chubb (2017) concluded that the resource R implicated by the study of Chubb et al. (2013) is not specific to the difference between the major vs minor scales; rather, they proposed that R confers sensitivity more generally to the spectrum of qualities that music can achieve by creating a scale through establishing a tonic and selecting a subset of notes relative to that tonic. Accordingly, Dean and Chubb (2017) called R “scale-sensitivity.”

A. Musical training and scale-sensitivity

On average, trained musicians have higher scale-sensitivity than non-musicians. In particular, both Chubb et al. (2013) and Dean and Chubb (2017) observed fairly strong correlations between years of musical training and performance in the tone-scramble task. However, a plausible hypothesis is that these correlations are driven primarily by a self-selection bias: listeners with high levels of scale-sensitivity tend to seek out musical training whereas listeners with low levels of scale-sensitivity do not. This interpretation is supported by the following observations. In each of Chubb et al. (2013) and Dean and Chubb (2017), the positive correlation between years of musical training and scale-sensitivity was driven primarily by a large group of listeners with no musical training who had very little scale-sensitivity as well as a smaller group with many years of musical training who had high scale-sensitivity. Strikingly, however, Chubb et al. (2013) and Dean and Chubb (2017) also observed moderate numbers of listeners with many years of musical training with little or no scale-sensitivity as well as other listeners with little or no musical training who had high scale-sensitivity, suggesting that musical training is neither necessary nor sufficient to attain high levels of scale-sensitivity. It should be noted, however, that in the study of Dean and Chubb (2017), the highest levels of scale-sensitivity were achieved only by listeners with at least four years of musical training. Thus, although musical experience is not sufficient for scale-sensitivity, it may be necessary to attain the highest levels of scale-sensitivity.

B. The current study

Is “scale-sensitivity” really an appropriate name for R? In the studies of both Chubb et al. (2013) and Dean and Chubb (2017), all of the tone-scrambles comprised rapid, random sequences of 65 ms tones; i.e., tones were presented at the rate of 15.38/s. As shown by Viemeister (1979), listeners are maximally sensitive to temporal amplitude modulations (of a white noise carrier) from 2 Hz up to 16 Hz with gradually decreasing sensitivity to temporal frequencies above 16 Hz. These results suggest that listeners should be very sensitive to the temporal modulations of amplitude in the tone-scrambles used by Chubb et al. (2013) and Dean and Chubb (2017).

However, other research has documented strong individual differences in the performance of various temporal-sequence-discrimination tasks (Johnson et al., 1987; Kidd et al., 2007). This raises the possibility that high-performers in tone-scramble tasks differ from low-performers solely in being able to extract scale-generated qualities from these rapid, musically degenerate stimuli. If so, then if the stimuli are presented more slowly, the gap in sensitivity separating high and low performers should disappear. The main purpose of the current study was to investigate this possibility.

II. METHODS

All methods were approved by the UCI Institutional Review Board.

A. Participants

Seventy-three listeners participated in this study. All were undergraduates from the University of California, Irvine, with self-reported normal hearing. Forty-five listeners reported having at least one year of musical training. Across all 73 listeners, the mean number of years of training was 3.1 (standard deviation: 3.94). Participants were compensated with course credit.

B. Stimuli

The stimuli in this experiment were tone-scrambles. These stimuli were originally introduced by Chubb et al. (2013) to isolate effects due to variation in scale from other sorts of musical structure, e.g., timbre, loudness, interval sequence, etc. All tones were pure tones windowed by a raised cosine function with a 22.5 ms rise time. Five different notes were used, all from the standard equal-tempered chromatic scale: G₅ (783.99 Hz), $B{♭}_5$ (932.33 Hz), B₅ (987.77 Hz), D₆ (1174.66 Hz), and G₆ (1567.98 Hz).

The current study used tone-scrambles of eight different types listed in Table I. For n = 1, 2, 4, 8, the n-each stimuli included n each of the notes G₅, D₆, and G₆ as well as n copies of a target note T which was B₅ in n-each major stimuli vs $B{♭}_5$ in n-each minor stimuli. Each tone in an n-each stimulus lasted $520/n\hspace{0.17em}\text{ms}$. For example, a four-each-major tone-scramble consisted of a random sequence of 16 tones, each 130 ms in duration; four of these tones were G₅'s, four were B₅'s, four were D₆'s, and four were G₆'s. Note that each of the eight different types of tone-scramble had a total duration of 2.08 s.

TABLE I.

The eight different types of tone-scramble used in the current experiment. For n = 1, 2, 4, 8, in the “n-task” on each trial the listener heard either a n-each-major or a n-each-minor tone-scramble and strove to judge which type she had heard. Feedback was given after each trial.

Task	Stimulus type	Tone duration	# G5's	# $B_5♭$'s	# B5's	# D6's	# G6's
1-task	1-each-major	520 ms	1	0	1	1	1
	1-each-minor	520 ms	1	1	0	1	1
2-task	2-each-major	260 ms	2	0	2	2	2
	2-each-minor	260 ms	2	2	0	2	2
4-task	4-each-major	130 ms	4	0	4	4	4
	4-each-minor	130 ms	4	4	0	4	4
8-task	8-each-major	65 ms	8	0	8	8	8
	8-each-minor	65 ms	8	8	0	8	8

C. Design

Each listener was tested in four different, separately blocked tasks: the 1-task, the 2-task, the 4-task, and the 8-task. On each trial in the n-task (for n = 1, 2, 4, 8), the listener heard either an n-each-major or an n-each-minor tone-scramble and strove to judge which type she had heard. In the visual prompt provided for the listener to enter each response, the two types of stimuli were identified as “HAPPY (major)” and “SAD (minor)”; the listener entered a “1” on the keyboard for “major,” or “2” for “minor.” Correctness feedback was given after each trial, and proportion correct was presented visually at the end of each block. In each task, the listener performed two blocks of 50 trials, the second block following after the first with a brief break in between. Each block contained 25 “major” stimuli and 25 “minor” stimuli. Task order was counterbalanced across listeners a using Latin square design. For the basic analysis reported in Sec. III, we followed the procedure of the previous tone-scramble studies and treated the first block of trials as practice and used $d\prime$ for the second block of 50 trials as our basic dependent measure (Chubb et al., 2013; Dean and Chubb, 2017). (We note, however, that the pattern of results would be very similar if we computed $d\prime$ using all 100 trials.) In the task-specific analyses reported in Sec. V, to increase statistical power, we used all 100 trials from each listener.

At the start of the experiment, each listener filled out a brief questionnaire. The only information from this questionnaire that is used in the analysis below is the number of years of musical training reported by the listener. Testing was done in a quiet lab on a Windows Dell computer with a standard Realtek audio/sound card using matlab. Stimuli were presented at the rate of 50 000 samples/s. During testing, the listener wore JBL Elite 300 noise-cancelling headphones with volume adjusted to his or her comfort level. Prior to the first block of trials in the n-task (for n = 1, 2, 4, 8), the listener was presented with eight, visually identified, example stimuli alternating between n-each-major and n-each-minor tone-scrambles.

D. Can we account for performance in the 1-, 2-, 4- and 8-tasks in terms of a single cognitive resource?

It is possible that the slower major and minor tone-scrambles used in the 1-, 2-, and/or 4-tasks may be discriminable by neural systems other than the system used by high-performing listeners in the 8-task. If so, then multiple cognitive resources may be required to account for variations in performance across all four tasks. In this case, the bilinear model is likely to provide a poor description of the data.

Conversely, if performance is well-described by the bilinear model, then plausibly the same cognitive resource that underlies performance in the 8-task also controls performance in the 1-, 2-, and 4-tasks. Note that in this case, if the results for the 8-task replicate the findings of Chubb et al. (2013) and Dean and Chubb (2017), then the majority of listeners k will perform poorly in the 8-task, implying that they have levels of R_k near 0, implying in turn that they will also perform poorly in the 1-, 2-, and 4-tasks.

In the current context, the bilinear model proposes that the values $d_{k,t}^{\prime }$ of $d\prime$ achieved by our 73 listeners k in all four of our tasks t are captured by Eq. (1), where [as in Dean and Chubb (2017)] R_k is the amount of R possessed by listener k and F_t is the strength with which task t is facilitated by R.

It should be noted that the model of Eq. (1) is underconstrained. We get exactly the same predictions from a model in which (1) R_k is rescaled by an arbitrary factor A and (2) F_t is rescaled by A⁻¹. To avoid this problem, we impose the constraint that

$$\sum _{\text{tasks}\hspace{0.17em}t}{F}_t=4\hspace{0.17em}(\text{where}\hspace{0.17em}4\hspace{0.17em}\text{is}\hspace{0.17em}\text{the}\hspace{0.17em}\text{number}\hspace{0.17em}\text{of}\hspace{0.17em}\text{tasks}).$$ (2)

Equation (2) makes it easy to interpret the results. If all four tasks are equally facilitated by R, then F_t will be 1 for all tasks. Deviations from 1 directly indicate deviations of relative facilitation strength. In addition, imposing this constraint also makes R_k a prediction of the average value of $d_{k,t}^{\prime }$ achieved by listener k across the four tasks. [It should be noted, however, that Dean and Chubb (2017) imposed a different constraint; specifically, they forced the sum of squared F_t values to be 1.]

III. RESULTS

In computing $d\prime$ values for the analyses reported in this section, we used only the last 50 trials in each task (treating the first 50 as practice). If a listener responded correctly on all 25 “major” (or “minor”) stimuli, the probability of a correct “major” (“minor”) response was adjusted to $24.5/25=0.98$ [as suggested by Macmillan and Kaplan (1985)]. This leads to $d\prime$ values of 4.1075 for listeners who perform perfectly across all 50 trials.

For each pair of tasks, Fig. 1 plots the $d\prime$ values achieved (by all listeners) in one task against those achieved in the other. Note first that in each scatterplot, there is (1) a large group of listeners for whom $d\prime$ is near 0 in both tasks and (2) a smaller group of listeners who achieve levels of $d\prime$ near 4.1075 (the value corresponding to perfect performance) in both tasks. In addition, there are other listeners intermediate between these two extreme groups. The relative difficulty of the two tasks being compared in a given scatterplot is evident in the distribution of $d\prime$ values for this intermediate group.

FIG. 1.

Scatterplots of $d\prime$ achieved by all listeners in each pair of tasks. $d\prime$ estimates are based on the last 50 trials in each task. Associated with each scatterplot are a t-statistic and the corresponding p-value derived from a paired samples t-test of the null hypothesis that the mean value of $d\prime$ is equal for the two tasks. Note that the 1-task yields lower values of $d\prime$ than the all of the other tasks.

Inspection of the scatterplots in the left column of Fig. 1 reveals that these intermediate listeners tend to achieve higher levels of $d\prime$ in each of the 2-, 4-, and 8-tasks than they do in the 1-task. Specifically, in each of these three plots, most of the points corresponding to these intermediate listeners fall above the main diagonal. That these differences in task difficulty are significant is confirmed by paired-samples t-tests of the null hypothesis that the mean values of $d\prime$ for the tasks being compared are equal; the p-values comparing the 1-task to the 2-, 4-, and 8-tasks are all highly significant. By contrast, none of the tests comparing the mean $d\prime$ values between the 2-, 4-, and 8-tasks reach significance. We conclude that the 1-task is more difficult than the other three tasks, which are roughly equal in difficulty.

A. The bilinear model results

The estimated values of F_t are shown in Fig. 2. Note that F_1-task is lower than all of F_2-task, F_4-task, and F_8-task. This is to be expected in light of Fig. 1 which shows that listeners found the 1-task more challenging than the other three tasks. Below we address the question of why this is.

FIG. 2.

Estimated values of F_t for the four tasks. As suggested by Fig. 1, F_1-task is lower than all of F_2-task, F_4-task, and F_8-task, reflecting the fact that performance in the 1-task is facilitated less strongly by the cognitive resource R than are the other three tasks. Error bars are 95% Bayesian credible intervals.

The left panel of Fig. 3 shows the histogram of R levels estimated for our 73 listeners. This histogram is very similar to the histogram of R values observed by Dean and Chubb (2017); once again, the histogram is positively skewed with a large number of listeners with R values near 0 but does not appear bimodal. However, when we plot the histogram of proportion correct that our listeners would be predicted to achieve in the 8-task (assuming they all used optimal criteria), we obtain a bimodal distribution very similar to the distribution of performance observed in experiment 1 of Chubb et al. (2013).

FIG. 3.

Left panel: Histogram of estimated R levels for all listeners. This histogram shows high skew, with a large number of listeners with R values near 0 and a long positive tail. Right panel: the histogram of predicted proportions correct in the 8-task corresponding to the R levels in the left panel. This histogram appears bimodal even though the histogram of R levels does not.

The bilinear model provides an excellent description of the results. This is shown by Fig. 4 which plots the estimates of $d_{k,t}^{\prime }$ derived individually from the data for each listener k in each task t against the values predicted by the bilinear model. The bilinear model accounts for 84% of the variance in the values of $d_{k,t}^{\prime }$ for our 73 listeners across the 1-, 2-, 4-, and 8-tasks, reflecting the strong relationship visible in Fig. 4.

FIG. 4.

The description provided by the bilinear model. This scatterplot contains a point for each listener k in each task t. The abscissa is the value of $d_{k,t}^{\prime }$ predicted by the bilinear model, and the ordinate is the corresponding maximum likelihood estimate of $d_{k,t}^{\prime }$ derived independently from the data for listener k in task t. As indicated by the legend, points derived from different tasks t are plotted in different gray-scales.

It should be noted, however, that the bilinear model does not account for all of the structure in the data. In the Appendix, we use nested F-tests to compare the fit provided by the bilinear model with fits provided by generalizations of the bilinear model that allow $d_{k,t}^{\prime }$ to depend on more than one cognitive resource. The results reported there suggest that performance is influenced slightly but significantly by variations in a single cognitive resource in addition to R.

B. The effect of music training

Figure 5 plots the levels of R possessed by the listeners as a function of their self-reported years of musical training. The correlation of 0.50 is due mainly to the large number of listeners with no musical training who have low levels of R. Of the 25 listeners k in our sample who had five or more years of musical training, 13 had R_k < 1 (corresponding to an average of <70% correct across all four tasks). Note in particular the lone listener in our sample who had 18 years of musical experience had scale-sensitivity 0.32. A larger number of such listeners were also reported by Chubb et al. (2013) and also by Dean and Chubb (2017).

FIG. 5.

The relation between years of musical training and R.

Strikingly, however, in both Dean and Chubb (2017) and the current study, listeners with few years of musical training invariably possess lower levels of R than do the most sensitive listeners with five or more years of musical training. Out of all of the 43 listeners, k, in the current sample with two or fewer years of musical training, none achieved levels of R_k higher than around 2 (corresponding to an average proportion correct around 86% across all four tasks). By contrast, four of the 25 listeners with 5 or more years of musical training had levels of R_k near 4 (corresponding to near perfect performance across all four tasks).

IV. DISCUSSION OF THE PRESENT STUDY

The current study is focused on the following general question: What is the nature of the skill that separates high- from low-performers in the major-vs-minor tone-scramble classification task (Chubb et al., 2013) and other tone-scramble tasks (Dean and Chubb, 2017)? All of the stimuli used in Chubb et al. (2013) and Dean and Chubb (2017) were very rapid tone-scrambles (presented at the same rate as the stimuli in the 8-task of the current study). This raises the possibility that the high-performing listeners differ from low-performing listeners solely in being able to extract scale-generated qualities from very rapid stimuli. If so, then many listeners who perform poorly in the 8-task [identical to the major-vs-minor tone-scramble classification task of Chubb et al. (2013)] might be expected show improvement on the 4-, 2-, and perhaps especially the 1-task. As our results reveal, however, the major-vs-minor tone-scramble classification task becomes no easier for listeners if the stimuli are presented more slowly. In particular, the 1-task—in which each note was presented for more than half a second—proved to be the most difficult.

Moreover, performance across all of the 1-, 2-, 4-, and 8-tasks is well-described by the bilinear model of Eq. (1) suggesting that performance in these four tasks depends predominantly on a single cognitive resource. Given that the 8-task was one of the five tasks included in the study of Dean and Chubb (2017), it is likely that the cognitive resource controlling performance in the 1-, 2-, 4-, and 8-tasks is identical to the cognitive resource R that was found to control performance across the five semitone tasks studied by Dean and Chubb (2017). In ruling out the possibility that high-performers in the 8-task differ from low-performers merely in their ability to extract scale-defined qualities from very rapid note sequences, the current findings bolster the interpretation of R suggested by the name “scale-sensitivity” introduced by Dean and Chubb (2017), i.e., that R confers general sensitivity to the range of qualities that music can achieve by being in a scale.

A final question remains from the current study: What makes the 1-task more difficult than the 2-, 4-, and 8-tasks? Section V explores this issue.

V. WHAT MAKES THE 1-TASK HARDER THAN THE 2-, 4- AND 8-TASKS?

A. Some notation

It will be convenient to indicate the notes G₅, $B{♭}_5$, B₅, D₆, and G₆ by the integers 1, 4, 5, 8, and 13, reflecting their locations in the chromatic scale starting at G₅. We will refer to these numbers as the “pitch-heights” of notes. We shall also use the symbol “T” to refer to the “target” note (4 or 5) in a given stimulus. Thus, if a stimulus S has T = 4, then S is minor; if S has T = 5, then S is major. A “note-order” is a permutation of the four symbols, “1”, “8”, “13,” and “T”; by substituting “4” for T, we obtain a symbol string corresponding in an obvious way to a minor stimulus; by substituting “5” for T, we obtain a symbol string corresponding to a major stimulus. Finally, for a given note-order Q, we will write $S_Q^{+}$ for the stimulus with note-order Q that has T = 5 and $S_Q^{-}$ for the stimulus with note-order Q that has T = 4.

B. The order of the tones in a stimulus affects responding

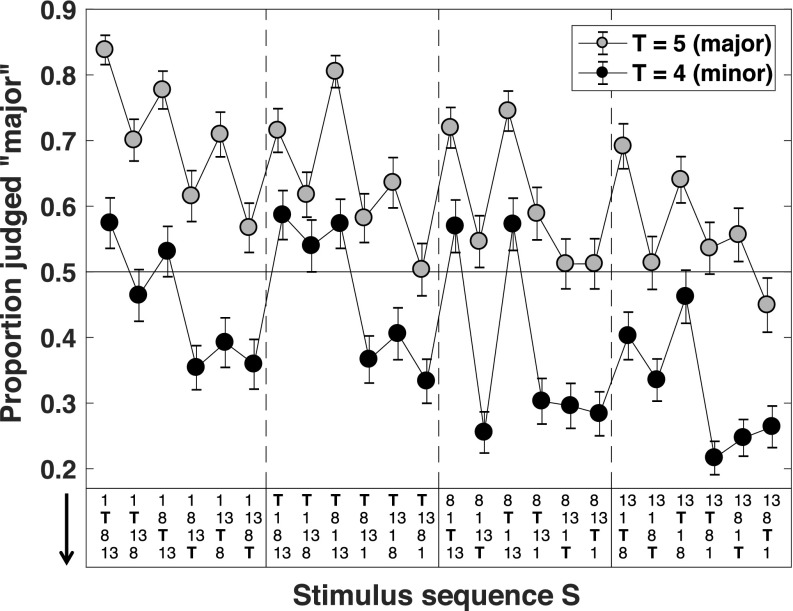
As revealed by Fig. 6, the results from the 1-task show unanticipated structure. This figure presents results averaged across all 100 trials performed by each of our 73 listeners. For each stimulus S, Fig. 6 plots the proportion of all of the trials on which S was presented that the response was “major.” If the judgments of our listeners depended only on whether S has T = 4 or T = 5, then across the 24 different note-orders on the horizontal axis, each of the plots for S with T = 5 and T = 4 would be flat. On the contrary, we see dramatic and roughly parallel variations in the two curves suggesting that, irrespective of whether the stimulus is major or minor, the specific order of the notes in the sequence exerts significant influence on the responses of our listeners.

FIG. 6.

The proportion of “major” responses to all 48 task-1 stimuli S. The plot pools the data across all 100 trials performed by all 73 listeners. The gray markers show the proportion of “major” responses for major stimuli (target note T = 5); the black markers show the proportion of “major” responses for the corresponding minor stimuli (target note T = 4). The note-order of a given stimulus S is shown (running downward) at the bottom of the figure; $1=G_5,\hspace{0.17em}4=B{♭}_5,\hspace{0.17em}5=B_5,\hspace{0.17em}8=D_6,\hspace{0.17em}13=G_6$. Error bars are 95% confidence intervals for the mean proportion.

C. Modeling note-order effects

Note that listeners k whose levels of R_k are very high are likely to perform perfectly in the 1-task; because the responses of such listeners depend only on whether T = 4 or T = 5, they will necessarily be invariant with respect to the order of the notes in the stimulus. Conversely, the responses of any listeners whose level of R_k is insufficient to support perfect performance may show dependencies on the order of notes in the stimulus. It is difficult, however, to anticipate the pattern of such dependencies. For this reason, both of the models described below allow the strength of note-order effects to vary freely as a function of R_k.

1. The general modeling framework

Both of the models we consider assume that on a trial in which listener k is presented with stimulus S, the listener computes a noisy internal statistic and compares it to a criterion η_k that is fixed across all trials performed in the 1-task by listener k. If this internal statistic is larger than η_k, the listener responds “major”; otherwise, the listener responds “minor.” We use the symbol “M_k,S” to denote the expectation of this internal statistic, and we assume that the noise is Gaussian with standard deviation 1. Formally,

$$\text{Response}\hspace{0.17em}\text{of}\hspace{0.17em}\text{listener}\hspace{0.17em}k\hspace{0.17em}\text{to}\hspace{0.17em}\text{stimulus}\hspace{0.17em}S=\{\begin{array}{cc}"\text{Major}"& \text{if}\hspace{0.17em}{M}_{k,S}+X>{\eta }_k,\hfill \\ "\text{Minor}"\hfill & \text{if}\hspace{0.17em}{M}_{k,S}+X<{\eta }_k,\hfill \end{array}$$ (3)

where X is a standard normal random variable.

The fullest model of the form expressed by Eq. (3) allows M_k,S to be a free parameter for each listener k and each task S. However, this model provides no traction in understanding the effects revealed by Fig. 6. Instead, we consider two nested models below, each of which is nested within the fullest model.

The first model we consider is called the “descriptive” model because its purpose is to describe with full freedom the variations in the stimulus-specific biases present in the data. Accordingly, the descriptive model includes free parameters for all of these biases. The “pitch-height-biased” model described below will attempt to capture with fewer parameters the pattern of the biases revealed by the descriptive model.

D. Fitting procedures

Below we describe two models, called the “descriptive model,” and the “pitch-height-biased model.” To estimate parameter values for each of these models, we use a Bayesian fitting procedure. Specifically, we assume a jointly uniform prior distribution with wide bounds on all model parameters. We then use Markov chain Monte Carlo simulation to extract a sample of vectors from the posterior joint density characterizing the parameters. All of the error bars in figures plotting parameter values give the 0.025 and 0.975 quantiles of the marginal density for the given parameter.

E. The descriptive model

For any stimulus S, let

$${\tau }_S=\{\begin{array}{cc}\hfill 1& \hfill \text{if}\hspace{0.17em}\text{stimulus}\hspace{0.17em}S\hspace{0.17em}\text{has}\hspace{0.17em}\mathbf{T}=5,\\ \hfill -1& \hfill \text{if}\hspace{0.17em}\text{stimulus}\hspace{0.17em}S\hspace{0.17em}\text{has}\hspace{0.17em}\mathbf{T}=4.\end{array}$$ (4)

Thus, τ_S is the variable that the listener should be using to make her judgment on each trial. However, Fig. 6 suggests that different stimuli S inject stimulus-specific biases into the judgments of many listeners k. For any stimulus S, we write β_S for the bias associated with S. We assume that the influence on M_k,S both of τ_S and also of β_S depends on R_k. Specifically, the descriptive model assumes that

$$M_{k,S}=f_{\tau }(R_k){\tau }_S+f_{\beta }(R_k){\beta }_S,$$ (5)

where the function f_τ(R) reflects the strength with which the response of a listener with scale-sensitivity R is influenced by τ_S (i.e., whether S has T = 4 or T = 5), and the function f_β(R) reflects the strength with which the response of a listener with scale-sensitivity R is influenced by the stimulus-specific bias β_S.

To limit the number of parameters contributed to the model by f_τ(R) and f_β(R), we force each of these functions to assign a fixed value to all R_k in a given sextile of the distribution of scale-sensitivities observed across all listeners k in the current study.

In order for the descriptive model [Eq. (5)] to be uniquely specified, additional constraints need to be imposed on the stimulus-specific biases β_S. Specifically, we require that

$$\sum _S{\beta }_S=0\hspace{1em}\text{and}\hspace{1em}\frac{1}{48}\sum _S{\beta }_S^2=1,$$ (6)

where each sum is over all 48 stimuli S. The first constraint insures that the β_S values cannot trade off with the threshold values η_k. The second constraint insures that the β_S values cannot trade off with f_β. The specific form of this second constraint on the β_S values is chosen to make their magnitudes comparable to those of the τ_S values (which also satisfy $\frac{1}{48}{\Sigma }_S{\tau }_S^2=1$).

The parameters of the descriptive model are the 48 β_S values, the six values of each of f_τ and f_β and the 73 values of η_k. Therefore, taking into account the two degrees of freedom sacrificed by imposing the constraints of Eq. (6) on the β_S values, the model has 73 + 48 + 12 − 2 = 131 degrees of freedom.

The main aim of this model is to derive estimates of the stimulus-specific biases, β_S, that are cleanly dissociated from the powerful influences that we know are exerted by τ_S on the responses of listeners high in scale-sensitivity. We naturally expect f_τ(R) to increase strongly with R. We also know that for very high values of R, f_β(R) must tend to 0; however, we have no strong a priori expectations concerning the form of f_τ(R) for lower values of R.

F. Results from the descriptive model

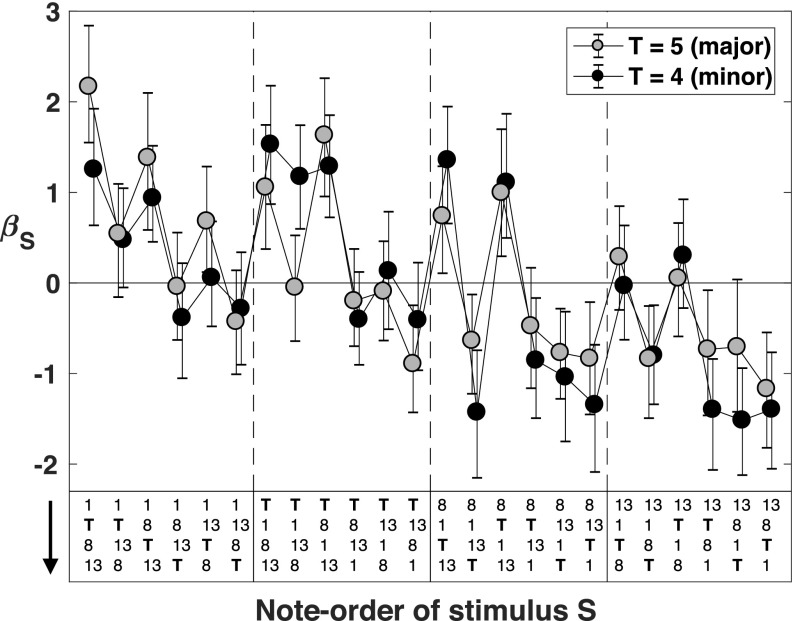
The stimulus-specific biases β_S for all 48 stimuli S are shown in Fig. 7. Across the 24 note-orders on the horizontal axis, the gray markers show the results for stimuli S with T = 5, and the black markers show the results for S with T = 4. The main thing to note is that there are dramatic differences between the stimulus-specific biases for different stimuli, and these biases appear similar for major and minor stimuli with the same note-order.

FIG. 7.

The stimulus-specific biases β_S for the 48 1-task stimuli S. The gray markers show the stimulus-specific biases for stimuli S with T = 5; the black markers show the stimulus-specific biases for stimuli S with T = 4. The note-order of a given stimulus S is shown (running downward) at the bottom of the figure. Error bars are 95% Bayesian credible intervals.

It is useful to replot the data in terms of the following two statistics:

$${\delta }_Q=\frac{{\beta }_{S_Q^{+}}-{\beta }_{S_Q^{-}}}{2}$$ (7)

and

$${\mu }_Q=\frac{{\beta }_{S_Q^{+}}+{\beta }_{S_Q^{-}}}{2}.$$ (8)

Thus δ_Q reflects sensitivity to the difference between target notes 5 vs 4 in the context of note-order Q, and μ_Q reflects the bias injected by note-order Q regardless of the target note.

The black disks in the left (right) panel of Fig. 8 plot μ_Q (δ_Q) for all 24 note-orders. The gray triangles in the left panel plot the fit provided by the nested “pitch-height-biased” model described below. The fact that nearly all of the credible intervals in the right panel contain 0 shows that note-order exerts little or no influence on sensitivity to the difference between target notes 5 vs 4. By contrast, as shown by the black disks in the left panel, the note-order-specific bias μ_Q depends strongly on Q.

FIG. 8.

The note-order-specific biases μ_Q (left panel) and note-order-specific sensitivities δ_Q (right panel) for the 24 note-orders Q. The note-orders on the horizontal axis run downward. The black circles show the estimates derived from the descriptive model in which all stimulus-specific biases are free parameters. The gray triangles show the predictions of the pitch-height-biased model. Error bars are 95% Bayesian credible intervals.

The upper left panel of Fig. 10 plots the functions f_τ (black) and f_β (gray) in the 1-task. As expected, f_τ increases with R_k. By contrast, f_β remains flat (and significantly greater than 0) across all 6 sextiles of the distribution of R_k (with a 50% drop-off for the last sextile). This implies that whatever factors are operating to produce the note-order-specific biases μ_Q are largely invariant with respect to R_k.

FIG. 10.

The functions f_τ and f_β in all four tasks. The values of R_k plotted on the horizontal axis are the mean values of the six sextiles of R_k observed across the 73 listeners k tested. The black (gray) plot shows f_τ(R_k) [f_β(R_k)]. Error bars are 95% Bayesian credible intervals.

G. The pitch-height-biased model

Chubb et al. (2013) noted that mean pitch-height exerted strong influence on performance in classifying major vs minor tone-scrambles, especially on the performance of low-performing listeners. In particular, tone-scrambles that included more high tonics (G₆'s) than low tonics (G₅'s) were more likely to be judged major. This finding suggests that the variations in μ_Q (the black disks in the left panel of Fig. 8) might have to do with the variations in pitch-height across different notes in the stimulus.

The pitch-height-biased model expresses this intuition. Writing S(t) for the pitch-height of the note in temporal location t = 1, 2, 3, 4, we estimate the stimulus-specific bias β_S of a given stimulus S as follows:

$${\beta }_S=\sum _{t=1}^4{w}_t(S(t)-6.625),$$ (9)

where the w_t's are model parameters called “sequential pitch-height weights,” and the constant 6.625 is the expected pitch-height of the note occurring on any given trial at any one of the four sequence locations in the 1-task. The four sequential pitch-height weights actually use only two degrees of freedom because, in order for the model to be uniquely determined, the w_t's must (1) sum to 0 and (2) be chosen so that the resulting β_S's satisfy the right side of Eq. (6). The total number of degrees of freedom in the pitch-height-biased model is 87: 2 degrees of freedom for the 48 β_S parameters, 73 for the η_k's, and 6 for each of the functions f_J and f_β.

H. Results from the pitch-height-biased model: The importance of ending on a high note

The data are captured very cleanly by the pitch-height-biased model. This is shown by Fig. 8. The left (right) panel of Fig. 8 plots the μ_Q (δ_Q) values given by the descriptive model (black disks) along with the estimates given by the pitch-height-biased model (gray triangles). The patterns are strikingly similar even though the pitch-height-biased model uses only two degrees of freedom to estimate all of the μ_Q and δ_Q values of the descriptive model (48 parameters that take 46 degrees of freedom).

The four pitch-height weights used in Eq. (9) to estimate the β_S values predicted by the pitch-height-biased model (and consequently also the μ_Q and δ_Q values plotted by the gray triangles in Fig. 8) are plotted in the upper left panel of Fig. 9. This panel shows that the bias injected by a particular note-order Q in the 1-task depends primarily on the pitch-height of the last note (although the weights of the first three notes also significantly influence mean bias). If the note-order ends on a high note, then the bias will be toward a “major” response.

FIG. 9.

The pitch-height weights for all four tasks. The sequential pitch-height weights w_t, for all locations t in the stimulus in each of the four tasks. These weights are used in the pitch-height-biased model [Eq. (9)] to estimate the values β_S for all 48 stimuli S, and consequently also the values μ_Q and δ_Q for all note-orders Q. Error bars are 95% Bayesian credible intervals.

I. Do the 2-, 4-, and 8-tasks also show the ending-on-a-high-note effect?

Although the 2-, 4-, and 8-tasks include too many possible stimuli to allow us to fit the descriptive model in which the influence of each note-order is reflected by a free parameter, we can easily fit the pitch-height-biased model to the data from each of these conditions. The resulting sequential pitch-height weights w_t for the 2-, 4-, and 8-tasks are shown in the upper right, lower left, and lower right panels of Fig. 9. Each of these functions shows that ending on a high note introduces a bias to respond “major.” The upper right, lower left and lower right panels of Fig. 10 show the f_τ and f_β functions for these three tasks. The relative influence of note-order is lower for the 2-, 4-, and 8-tasks than it is for the 1-task. However, note-order exerts a significant influence on the responses of all listeners k other than those with levels of R_k in highest sextile (who perform nearly perfectly in each of the 2-, 4-, and 8-tasks).

J. Discussion of the note-order effects

The note-order effects revealed by the analysis are unanticipated. Note-order is entirely irrelevant to the task the listeners are striving to perform; moreover, the trial-by-trial feedback that listeners received throughout this experiment might be expected to suppress effects of this sort. Nonetheless, as our results make clear, a powerful bias to respond “major” to stimuli that end on a high note is prominent across the listeners tested in this study in all task conditions.

The ending-on-a-high-note bias seems to be unrelated to scale sensitivity. The flatness of the gray curve in the upper left panel of Fig. 10 shows that this bias operates in the 1-task with nearly equal effectiveness across all listeners irrespective of their levels of scale-sensitivity. Similar effects are seen in the other panels of Fig. 10, except that in the 2-, 4-, and 8-tasks listeners k with R_k values in the highest sextile are largely immune to the ending-on-a-high-note bias.

We speculate that our instructions to classify stimuli as “HAPPY (major)” or “SAD (minor)” may have produced the ending-on-a-high-note effects. Although the current study sheds no light on exactly why ending on high (low) note has the effect of making a tone-scramble sound “HAPPY” (“SAD”), theories about the relationship between music and speech may shed some light into this effect (Patel, 2005; Patel et al., 2006). In particular, when a speaker asks a question, or is excited, elated, or happy, the intonation of the voice is steered toward ending on a high pitch (Juslin and Laukka, 2003; Swaminathan and Schellenberg, 2015; Curtis and Bharucha, 2010). Thus, if music inherits some of its emotional expressiveness from our sensitivity to speech variations, then we might expect the ending-on-a-high-note effect. Evidence supporting this idea is presented in Romano (2002).

VI. GENERAL DISCUSSION

This study was designed to investigate the nature of the cognitive resource R that separates high- from low-performing listeners in the task of classifying major vs minor tone-scrambles (Chubb et al., 2013; Dean and Chubb, 2017). Dean and Chubb (2017) hypothesized that R confers general sensitivity to variations in scale relative to a fixed tonic; accordingly, they called R “scale-sensitivity.” However, all of the tone-scrambles used in the experiments of Chubb et al. (2013) and Dean and Chubb (2017) used very rapid stimuli (32 tones in 2.08 s); this raises the possibility that high-performing listeners differ from low-performing listeners merely in being able to extract scale-generated qualities from very rapid stimuli. If so, then the difference between high- vs low-performing listeners should disappear if stimuli are presented more slowly.

The current results decisively reject this possibility. First, the results for the 8-task replicate those from previous studies (Chubb et al., 2013; Dean and Chubb, 2017); i.e., the 8-task yielded a strongly bimodal distribution in performance with ≈ 70% of listeners performing near chance and the remaining listeners performing near perfect. In addition, the bilinear model [Eq. (1)] provides a good description of the results for 73 listeners across all of the 1-, 2-, 4-, and 8-tasks (accounting for 84% of the variance). As implied by Eq. (1), the many listeners who performed poorly in the 8-task possess levels of R near 0 and therefore (also as implied by Eq. 1) performed poorly in all of the 1-, 2-, and 4-tasks as well.

The main findings thus support the idea proposed by Dean and Chubb (2017) that the resource R confers general sensitivity to the qualities that music can achieve by varying the scale in the presence of a fixed tonic. This confirms the appropriateness of the term “scale-sensitivity” introduced by Dean and Chubb (2017) to refer to R.

A. How should we think about scale-defined qualities?: The analogy to color

The main purpose of this section is to clarify what we take to be the central open questions concerning scale-sensitivity. We will first describe a working hypothesis concerning the nature of scale-sensitivity. We will then state the main questions raised in light of this hypothesis. Finally, we will discuss possible methods for addressing these questions.

The qualities of many auditory textures seem to be represented by additive summary statistics (McDermott and Simoncelli, 2011; McDermott et al., 2013), i.e., by neural processes that compute the average of some temporally local statistic over an extended time window. Plausibly, this is the case for the qualities that tone-scrambles can evoke. Moreover, the fact that the performance of listeners with high levels of scale-sensitivity is unperturbed by the random sequencing of tone-scrambles suggests that the summary statistics corresponding to scale-defined qualities do not depend on note-order but only on the proportions of different notes in the stimulus—i.e., on the scale of the stimulus, where the term “scale” refers to the histogram of notes in the stimulus.

These observations suggest that the way in which scale-defined musical qualities are encoded by the auditory system may be analogous to the way colors are encoded by the visual system. Note in particular that just as the scale-defined quality evoked by a tone-scramble is determined by the proportions of different notes the tone-scramble contains (i.e., by the scale of the tone-scramble), the color of a light of some fixed quantal flux is similarly determined by the proportions of different-wavelength quanta the light contains (i.e., by the spectrum of the light).

The color of a light for photopic vision is determined by three summary statistics: the activations produced by the light in the L-, M-, and S-cone classes (i.e., the long-, medium-, and short-wavelength sensitive cone classes). For example,

$$L–\text{cone}\hspace{0.17em}\text{activation}\hspace{0.17em}\text{produced}\hspace{0.17em}\text{by}\hspace{0.17em}\text{light}\hspace{0.17em}H=K_H\sum f_L(\lambda )P_H(\lambda ),$$ (10)

where the sum is over all wavelengths λ that occur in the light, K_H is a constant that depends on the quantal flux of H, P_H(λ) gives the proportion of quanta in H that have wavelength λ, and the function f_L(λ) gives the sensitivity of L-cones to quanta of wavelength λ.

If scale-defined qualities are analogous to colors, then for some set of scale-sensitive neuron classes $C_1,C_2,\dots ,C_N$, the scale-defined quality evoked by a tone-scramble is determined by the activations that the tone-scramble produces in these N neuron classes. For a given neuron class, C_i,

$$\text{Time}–\text{averaged}\hspace{0.17em}\hspace{0.17em}\text{activation}\hspace{0.17em}\hspace{0.17em}\text{produced}\hspace{0.17em}\text{in}\hspace{0.17em}{C}_i\hspace{0.17em}\text{by}\hspace{0.17em}\text{a}\hspace{0.17em}\hspace{0.17em}\text{tone}–\text{scramble}\hspace{0.17em}S=K_S\sum f_i(d)P_S(d),$$ (11)

where:

• (1)the sum is over all scale-degrees d (relative to whichever note has been established as the tonic) that occur in the tone-scramble S,
• (2)K_S is a constant that depends on the rate of presentation of the tones in S,
• (3)P_S(d) gives the proportion of tones in S that have scale-degree d, and
• (4)f_i(d) gives the influence exerted on the activation of neurons in class C_i by an instance of a tone with scale-degree d.

Of course actual melodies differ from tone-scrambles in that the notes they contain may vary in such ancillary qualities as attack, timbre, duration, loudness and rhythmic context. Plausibly, however, these complexities can be handled with a simple modification of Eq. (11). Let S(t) be the scale degree of the tth tone in tone-scramble S, and let N_S be the total number of tones in S. Then we can rewrite Eq. (11) as follows:

$$\text{Time}–\text{averaged}\hspace{0.17em}\text{activation}\hspace{0.17em}\text{produced}\hspace{0.17em}\text{in}\hspace{0.17em}{C}_i\hspace{0.17em}\text{by}\hspace{0.17em}\text{a}\hspace{0.17em}\hspace{0.17em}\text{tone}–\text{scramble}\hspace{0.17em}S=\frac{1}{N_S}\sum _{t=1}^{N_S}{f}_i\left(S\right(t\left)\right).$$ (12)

If we suppose that the ancillary features of a given note in a melody M collectively operate only to modify the weight exerted by that note in activating a given neuron class C_i, then we can generalize Eq. (12) as follows:

$$\begin{array}{c}\text{Time}–\text{averaged}\hspace{0.17em}\text{activation}\hspace{0.17em}\text{produced}\hspace{0.17em}\text{in}\hspace{0.17em}{C}_i\hspace{0.17em}\text{by}\hspace{0.17em}\text{melody}\hspace{0.17em}M=\frac{1}{\text{Total}\hspace{0.17em}M–\text{weight}}\sum _{t=1}^{N_M}{f}_i\left(M\right(t\left)\right)W_M\left(t\right),\end{array}$$ (13)

where M(t) is the scale-degree of the tth note of M, N_M is the number of notes in M, and W_M(t) is the weight (determined by the ancillary features of the tth note of M) exerted by the tth note in M, and

$$\text{Total}\hspace{0.17em}M–\text{weight}=\sum _{t=1}^{N_M}{W}_M(t).$$ (14)

In summary:

• (1)If the auditory system represents scale-defined qualities analogously to the way in which the visual system represents colors, then (for listeners with non-zero scale-sensitivity) the auditory system will contain neuron classes C_i, $i=1,2,\dots ,N$, each of which confers sensitivity to a different dimension of scale-defined quality. Each of these dimensions should be characterized by a sensitivity function f_i(d) that reflects the influence exerted on the activation of neurons in class C_i by tones of scale degree d (relative to whichever note has been established as the tonic), and the time-averaged activation produced in neuron class C_i by a tone-scramble S and should be given by Eq. (12).
• (2)Under the assumption that the ancillary qualities of a note (e.g., its attack, timbre, loudness, and duration) in an actual melody operate only to modify the weight that the note exerts in activating neurons in class C_i, the time-averaged activation produced by any melody M in C_i should be given by Eq. (13).

This model may well prove to be false, in which case future experiments are likely to reject it; however, from our current vantage point, it provides a useful working hypothesis. Under the tentative assumption that the model is true, several important questions leap out:

• •How many distinct neuron classes C_i exist in the auditory systems of listeners with high scale-sensitivity?
• •What do the different classes C_i sense? I.e., what are the sensitivity functions f_i(d) characterizing the different neuron classes C_i?
• •How do the different ancillary properties of a note (attack, timbre, loudness, rhythmic context) operate to modify the weight exerted by the note in Eq. (13)?

Various psychophysical methods can be used to attack these questions. By testing the relative discriminability of a sufficiently large number of tone-scrambles with different note-histograms, it is possible to determine the space spanned by the sensitivity functions f_i, $i=1,2,\dots ,N$. The dimensionality of this space is a lower bound on the number of neuron classes C_i that are sensitive to scale-defined qualities. [This was essentially the method used by Maxwell (1855) to show that human color perception is 3-dimensional.] It is more challenging to determine the actual sensitivity functions f_i characterizing individual classes C_i of scale-sensitive neurons. A method for addressing this problem has recently been developed and applied in the domain of visual perception to analyze the mechanisms sensitive to spatially random mixtures of small squares varying in gray-scale (Silva and Chubb, 2014; Victor et al., 2017).

In order to investigate the influence of the ancillary properties of a note on the weight it exerts in activating a give scale-sensitive neuron class, C_i, it is first necessary to construct tone-scrambles whose note-histogram “isolates” the neuron class C_i. In order to construct such tone-scrambles, one must first determine the sensitivity functions f_j characterizing all of the neuron classes C_j. Then one must derive the component ${\tilde{f}}_i$ of f_i that is orthogonal to the space spanned by all of the other f_j's (e.g., by using Gram-Schmidt orthogonalization). Then in the context of a task requiring the participant to classify tone-scrambles whose histograms differ by ${\tilde{f}}_i$, one can vary the ancillary properties of the notes in the stimulus to measure the influence that these changes exert on performance.

B. Melodic contour and the ending-on-a-high-note bias

The contour of a melody (the rising and falling pattern of pitch in the melody) is an important aspect of melodic structure and has long been a focus of research in music perception [for reviews see Justice and Bharucha (2002); Quinn (1999); Schmuckler (1999, 2016)]. In the current context, if we define the pitch-height of a tone as 1, 4, 5, 8, or 13 depending on whether the tone is a G₅, $B{♭}_5$, B₅, D₆, or G₆, then for n = 1, 2, 4, 8, the pitch contour of a stimulus in the n-task is the vector S of length n whose tth entry is the pitch-height of the tth tone in the stimulus. As revealed by the analysis of the 1-task in Sec. V, the randomly varying pitch contours of the stimuli in all of the 1-, 2-, 4-, and 8-tasks exerted a strong influence on the judgments of most listeners. This influence obeys a simple rule. For the n-task, there exists a vector $w=(w_1,w_2,\dots ,w_n)$ of pitch-height weights that we can think of as a pitch-contour sensitivity profile that is fixed across all listeners. Then the additive bias exerted on the decision statistic used by any listener to make his or her judgment is $w•S$ (the inner product of the pitch-contour sensitivity profile with the stimulus pitch-contour).

Strikingly, this effect operates as strongly in listeners with low scale-sensitivity as it does in those with high scale-sensitivity. This suggests that sensitivity to this feature of the stimulus is independent of scale-sensitivity.

This observation raises the possibility that, in general, sensitivity to melodic contour is independent of scale-sensitivity. To investigate this issue, one would need to devise new tasks to measure sensitivity to melodic contour. For this purpose, one could use tone-scramble-like stimuli. However, to assess sensitivity to melodic contour, one would want to use the same note histogram across all trials while varying the temporal order of the notes in the stimulus. For example, one might use stimuli comprising random permutations of 13, 65 ms tones, one each of the 13 notes in the chromatic scale from G₅ to G₆. In a given task condition, the listener would strive, on each trial, to judge (with feedback) whether the pitch contour of the stimulus correlated positively vs negatively with a particular “target” contour that was fixed across all trials in the condition. This target contour might resemble the contours shown in Fig. 9 or it might take a different form.

Contour-sensitivity tasks of this sort can be used to probe the question of whether or not sensitivity to melodic contour is independent of scale-sensitivity. A natural approach is to measure performance in both the 8-task (to gauge scale-sensitivity) and in a contour-sensitivity task across a large sample of listeners. If the correlations between performance in the two tasks are low, this would lend support to the claim that contour-sensitivity is independent of scale-sensitivity.

If the experiment is expanded so that each listener is tested on several scale-sensitivity tasks [e.g., several of the tasks used by Dean and Chubb (2017)] as well as several contour-sensitivity tasks using different target contours, then the case for the independence of scale-sensitivity and contour-sensitivity would be strengthened if it were found that two distinct factors were required to account for performance of all subjects across all tasks, one that accounts for performance across the scale-sensitivity tasks and another that accounts for performance across the contour-sensitivity tasks.

C. Does musical training increase scale-sensitivity?

The current results echo those of Dean and Chubb (2017) in suggesting that musical training may heighten scale-sensitivity in some listeners but not in others (Fig. 5). The claim that scale-sensitivity can be heightened in some listeners is supported by the observation that the highest levels of scale-sensitivity observed across the subjects we tested were achieved only by listeners with at least 5 years of musical training. Our sample contained four such listeners with levels of scale-sensitivity near (or above) 4, implying that they achieved nearly perfect performance in all four tasks. By contrast, across the 43 listeners in our sample with 2 or fewer years of musical training, the highest levels of scale-sensitivity were only slightly above 2 (corresponding to an average percent correct around 86% across the four tasks). On the other hand, the evidence supporting the claim that musical training fails to heighten scale-sensitivity in other listeners is supported by the observation that among our 25 listeners with 5 or more years of experience, 13 had levels of scale-sensitivity less than 1 (corresponding to an average percent correct less than 70% across all four tasks) including one listener with 18 years of musical training who had scale-sensitivity 0.36 (which corresponds to an average percent correct of at most 57% across all four tasks).

The current results thus suggest the following picture: some listeners possess the potential to attain high levels of scale-sensitivity whereas others do not. Musical training can heighten scale-sensitivity in listeners who possess this potential; however, no amount of musical training can heighten scale-sensitivity in listeners who lack this potential.

D. The importance of measuring scale-sensitivity in assessing the effects of musical training

Trained musicians have been shown to perform better than non-musicians on a wide range of auditory tasks. For example, musicians are better than non-musicians at discriminating simple tones (Buss et al., 2014; Fujioka et al., 2004, 2005; Micheyl et al., 2006) and complex melodic stimuli (Pantev et al., 1998). They also perform better than non-musicians in tasks requiring sound segregation (Parbery-Clark et al., 2009), auditory attention (Strait et al., 2010), speech-processing (Besson et al., 2011a,b; Marie et al., 2010; Marie et al., 2011; Morrill et al., 2015; Parbery-Clark et al., 2011) as well as executive control (Bialystok and DePape, 2009; Zuk et al., 2014).

If it is found that musicians perform better than non-musicians in a given task, it is tempting to leap to the conclusion that musical training improves performance in the task; however, another possibility is that the task in question requires resources that are inherited or acquired through early experience, and people who possess those resources are more likely to become musicians than people who do not. It has proven challenging to decide between these alternatives in many cases.

In any study investigating the relationship between musical training and performance in some perceptual or cognitive task, we propose that the scale-sensitivity of all listeners should be measured as a matter of standard practice for the following reasons:

• (1)If performance in the target task is correlated positively with musical training, this may be due to the fact that task performance depends on scale-sensitivity.
• (2)Although scale-sensitivity and years of musical training are correlated, the two variables can be readily dissociated due to the existence of listeners with little or no musical training but high scale-sensitivity and other listeners with many years of musical training but very low scale-sensitivity.
• (3)It is easy to measure a variable that reflects scale-sensitivity by testing a listener in 100 trials of the 8-task and estimating $d\prime$ from the last 50 trials.
• (4)Only by including scale-sensitivity in one's model can one determine whether musical training accounts for any additional variance in predicting task performance.

APPENDIX

This appendix shows that the bilinear model does not capture all of the structure in the current data. We use F-tests to compare the fits provided by several nested models of the following form:

$$d_{k,t}^{\prime }=\sum _{i=1}^n{R}_{i,k}{F}_{i,t}+\text{measurement}\hspace{0.17em}\text{noise},$$ (A1)

where R_i,k and F_i,t are real numbers, and n can be any of 1, 2, or 3. (The case of n = 4 is equivalent to the unconstrained model in which $d_{k,t}^{\prime }$ is estimated separately for each listener k in each task t.) For n = 1, Eq. (A1) is equivalent to the bilinear model.

If we think of each of our listeners k as providing a four-dimensional vector ${\overrightarrow{d}}_k=({d^{\prime }}_{k,1},{d^{\prime }}_{k,2},{d^{\prime }}_{k,4},{d^{\prime }}_{k,8})$, then for a given n, the model of Eq. (A1) proposes that the vectors ${\overrightarrow{d}}_k$ produced by our listeners reside (except for measurement noise) in a subspace of dimension n.

We compare the fits provided by:

• (1)The bilinear model with the model of Eq. (A1) with n = 2; this test yields F(74, 142) = 1.93, p = 0.0004 implying that the vectors ${\overrightarrow{d}}_k$ are not confined to a line.
• (2)The model of Eq. (A1) with n = 2 to the model with n = 3; this test yields F(72, 70) = 1.17, p = 0.25. This test thus fails to reject the null hypothesis that that the vectors ${\overrightarrow{d}}_k$ are confined to a plane.

The number of free parameters in the bilinear model is 76 = 73 + 3 [the number of listeners plus the number of tasks minus 1 (because of Eq. (2))]. The number of free parameters in the model of Eq. (A1) is 76 + 74 = 150 for n = 2; 222 = 76 + 74 + 72 for n = 3. For each of these models, the number of degrees of freedom is equal to $d{f}_{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l}}-\#freeparameters$, where df_total = 73 × 4 (the number of listeners times the number of tasks).

For a given comparison between a nested vs a fuller model, we first derive the residual sums of squared deviations RSS_nested and RSS_fuller of the model predictions from unconstrained values of $d_{k,t}^{\prime }$ (across all listeners k and all semitone tasks t). Then under the null hypothesis that the constrained model captures the true state of the world, the random variable

$$Q=\frac{(RS{S}_{\mathit{n}\mathit{e}\mathit{s}\mathit{t}\mathit{e}\mathit{d}}-RS{S}_{\mathit{f}\mathit{u}\mathit{l}\mathit{l}\mathit{e}\mathit{r}})/(d{f}_{\mathit{n}\mathit{e}\mathit{s}\mathit{t}\mathit{e}\mathit{d}}-d{f}_{\mathit{f}\mathit{u}\mathit{l}\mathit{l}\mathit{e}\mathit{r}})}{RS{S}_{\mathit{f}\mathit{u}\mathit{l}\mathit{l}\mathit{e}\mathit{r}}/d{f}_{\mathit{f}\mathit{u}\mathit{l}\mathit{l}\mathit{e}\mathit{r}}}$$ (A2)

has an F distribution with degrees of freedom df_fuller − df_nested in the numerator and df_fuller in the denominator.