Guidelines on constructing funnel plots for quality indicators: A case study on mortality in intensive care unit patients

Abstract

Funnel plots are graphical tools to assess and compare clinical performance of a group of care professionals or care institutions on a quality indicator against a benchmark. Incorrect construction of funnel plots may lead to erroneous assessment and incorrect decisions potentially with severe consequences. We provide workflow-based guidance for data analysts on constructing funnel plots for the evaluation of binary quality indicators, expressed as proportions, risk-adjusted rates or standardised rates. Our guidelines assume the following steps: (1) defining policy level input; (2) checking the quality of models used for case-mix correction; (3) examining whether the number of observations per hospital is sufficient; (4) testing for overdispersion of the values of the quality indicator; (5) testing whether the values of quality indicators are associated with institutional characteristics; and (6) specifying how the funnel plot should be constructed. We illustrate our guidelines using data from the Dutch National Intensive Care Evaluation registry. We expect that our guidelines will be useful to data analysts preparing funnel plots and to registries, or other organisations publishing quality indicators. This is particularly true if these people and organisations wish to use standard operating procedures when constructing funnel plots, perhaps to comply with the demands of certification.

1 Introduction

A range of audiences, including hospital staff and directors, insurance companies, politicians and patients, are interested in quantifying, assessing, comparing and improving the quality of care using quality indicators.^1,2 Currently, a huge amount of clinical data is routinely collected. These data enable researchers to routinely measure and compare clinical performance of institutions or professional and use these results to support or critique policy decisions. Among other institutions, hospitals are increasingly publicly compared in benchmarking publications. The benchmark may be defined externally, such as a government target to reduce the standardised rate of teenage pregnancies.³ However, most often no external value is available and hospitals are compared to an internal summary, such as the average of the quality indicator across participating hospitals.⁴

Funnel plots can be used to present the values of a quality indicator associated with individual hospitals and compare these values to the benchmark. The value of the quality indicator for each hospital is plotted against a measure of its precision, often the number of patients or cases used to calculate the quality indicator. Control limits indicate a range, in which the values of the quality indicator would, statistically speaking, be expected to fall. The control limits form a “funnel” shape around the external or internal benchmark, which is presented as a horizontal line. If a hospital falls outside the control limits, it is seen as performing differently than is to be expected, given the value of the benchmark.^3,5,6 Incorrectly constructed funnel plots could lead to incorrect judgements being made about hospitals. This potentially has severe consequences, especially if a range of audiences use them to judge or choose hospitals.

When looking at a funnel plot, it is important to be able to assume that hospitals falling outside the control limits indeed performed in the statistical sense significantly differently than would be expected, given the benchmark. It is also important to be able to assume that there is no reason to suspect that hospitals falling inside the control limits are not preforming according to the benchmark. Hence, the methods used to construct funnel plots, including obtaining control limits, need to have a solid justification in statistical theory and accepted good practice. Most published literature on comparing hospital performance^6–12 and registry reporting^13–17 using funnel plots refer to a single seminal paper on funnel plot methodology.³ However, this paper describes multiple methods to construct control limits and it does not provide explicit guidance. Furthermore, it is not always clear which method is used in applied studies. Various choices in obtaining control limits may lead to different results. Some papers describe exactly which method of this paper was used,^8,11,14,15 while others provide a reference but it remains unclear which method was used.^10,12,16,17 We found no publications describing a guideline for producing funnel plots, in which all steps required when producing a funnel plot are described.

The aim of this paper is to provide guidance, accompanied by a workflow diagram, for data analysts on constructing funnel plots for quality assessment not only in hospitals, but also in other healthcare institutions or individual care professionals.

As (hospital) quality indicators are often binary at the patient level, we focus on this type of indicators, presented as proportions, risk-adjusted rates and standardised rates^18–20 and funnel plots with 95% and 99% control limits. We use the Dutch National Intensive Care Evaluation (NICE) registry²¹ as a motivating example. This registry enables participating intensive care units (ICUs) to quantify and improve the quality of care they offer.²¹ Since 2013, the NICE registry has published funnel plots for the standardised mortality rate for all and for subgroups of ICU admissions.⁴

Section 2 of this paper describes the motivating example of this study, and section 3 describes theoretical considerations in funnel plot development. We described the methodological choices we made for the motivating example in section 4 and the results in section 5.

2 Motivating example: The Dutch National Intensive Care Evaluation (NICE) registry

2.1 The NICE registry

The NICE registry²¹ receives demographical, physiological and diagnostic data from the first 24 hours of all patients admitted to participating ICUs. These data include all variables used in the Acute Physiology and Chronic Health Evaluation (APACHE) IV patient correction model,²⁰ used to adjust in-hospital mortality of ICU patients for differences in patient characteristics. Patients are followed until death before hospital discharge or until hospital discharge. Registry staff check the data they receive for internal consistency, perform onsite data quality audits and train local data collectors. The NICE registry has been active since 1996 and, in 2014, 85 (95%) of Dutch ICUs participated in it. The NICE registry presents a portfolio of quality indicators to the staff of participating ICUs in a secure dashboard environment. Since 2013, the NICE registry has made the outcomes of some of these quality indicators publicly available as funnel plots.²¹

We obtained permission from the secretary of the NICE board (Email: info@stichting-nice.nl), to use data from the NICE registry at the time of the study. The NICE board assesses each application to use the data on the feasibility of the analysis and whether or not the confidentiality of patients and ICUs will be protected. To protect confidentiality, raw data from ICUs are never provided to third parties. For the analyses described in this paper, we used an anonymised dataset. The use of anonymised data does not require informed consent in the Netherlands. The data are officially registered in accordance with the Dutch Personal Data Protection Act.The data collected by the registry are officially registered in accordance with the Dutch Personal Data Protection Act. The medical ethics committee of the Academic Medical Center stated that medical ethics approval for this study was not required under Dutch national law (registration number W16_191).

2.2 Funnel plots for the NICE registry

In this paper, we describe constructing funnel plots for three ICU quality indicators based on in-hospital mortality. The first quality indicator is the crude proportion of initial ICU admissions resulting in in-hospital death. This quality indicator is not formally used by the NICE foundation, but is included in this study as an extra example to describe the guidelines on how to deal with proportions. The second quality indicator is the standardised in-hospital mortality rate and only includes patients fulfilling the APACHE IV inclusion criteria.²⁰ We calculated the standardised in-hospital mortality rates per hospital by dividing the observed number of deaths by the APACHE IV predicted number of deaths. The third quality indicator is the risk adjusted in-hospital mortality rate. This quality indicator can be calculated by multiplying the standardised in-hospital mortality rates per hospital by the crude proportion of in-hospital mortality over all national ICU admissions. Since the NICE registry does not use funnel plots for standardised mortality rates, we do not give an example for risk-adjusted rates. However, these measures are similar and test outcomes do not differ. Control limits for funnel plots for standardised mortality rates are examined by first examining control limits for risk-adjusted rates and dividing them by the overall crude proportion of mortality.

In addition, we examined funnel plots for the standardised in-hospital mortality rate for three subgroups of ICU admissions based on the type of ICU admission.⁴ In keeping with the definitions in the APACHE IV model,²⁰ we defined an ICU admission as ‘medical’ if a patient was not admitted to the ICU directly from an operating theater or recovery room, as ‘emergency surgery’ if the patient had undergone surgery immediately prior to ICU admission and where resuscitation, stabilisation, and physiological optimisation are performed simultaneously, and as ‘elective surgery’ otherwise. In-hospital mortality generally differs substantially between these three groups.

As the APACHE IV model was constructed based on data collected in 2002 and 2003 in the USA, the quality of case-mix correction is suboptimal for current NICE registry data. From 2016, the NICE registry recalibrates the APACHE IV probability of in-hospital mortality using a logistic regression model with the in-hospital mortality as a dependent variable. The logit-transformed original APACHE IV probability and the interaction between type of ICU admission and APACHE II score transformed using a restricted cubic spline function (4 knots) were included as independent variables.

3 Guidelines on producing funnel plots

In this section, we describe our guidelines on producing funnel plots. We developed these guidelines following a focussed literature search, in which we identified six conceptual steps in constructing a funnel plot. These are: (1) defining policy level input; (2) checking the quality of models used for case-mix correction; (3) examining whether the number of observations per hospital is sufficient to fulfill the assumptions upon which the control limits are based; (4) testing for overdispersion of the values of the quality indicator; (5) testing whether the values of the quality indicators are associated with institutional characteristics; and (6) specifying how the funnel plot should be constructed.

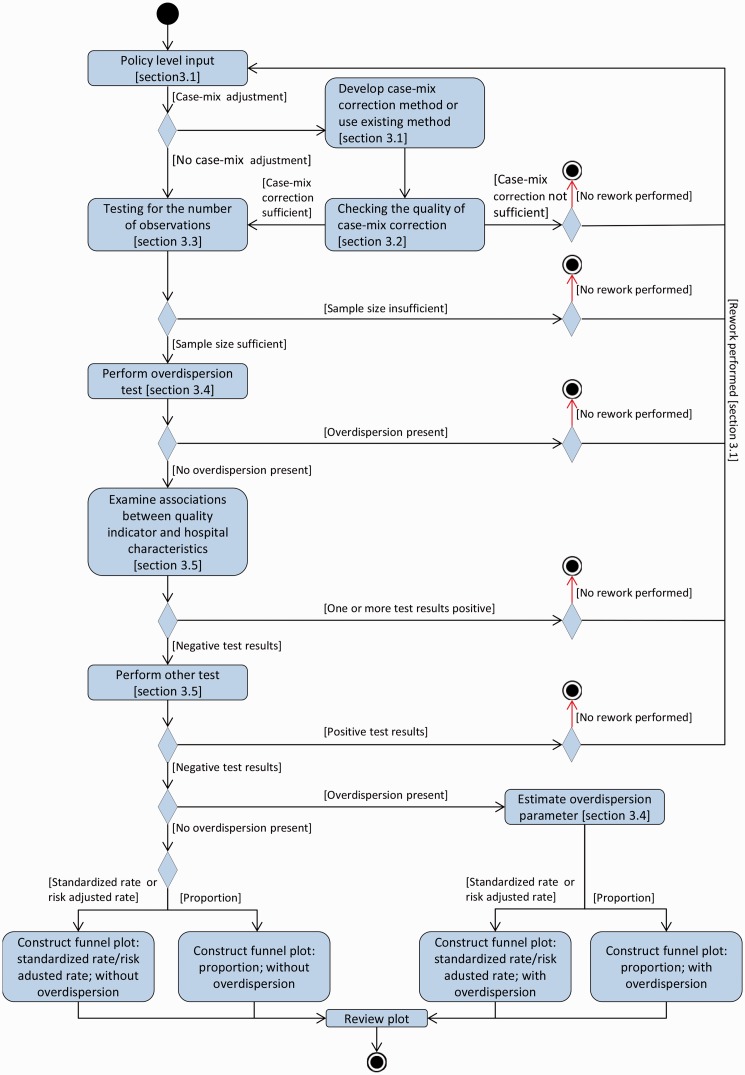
We describe the six steps in the text as well as in a unified modelling language activity diagram, Figure 1. Unified modelling language is used in the field of software engineering to standardise the meaning when communicating about a system.²² We recommend that data analysts prepare a statistical analysis plan before performing the analysis needed for each step. In this plan, they should specify which statistical tests they will use in each step and for which outcomes of these tests they will decide that presenting a quality indicator by means of a funnel plot is acceptable.

Figure 1.

Workflow diagram as UML activity diagram: funnel plots for proportions, risk-adjusted rates and standard rates.

This section describes the theoretical considerations of the six steps in funnel plot development.

3.1 Step one: defining policy level input

The first step consists of obtaining policy level decisions from the institution that is responsible for calculating and publishing the quality indicators. The policy-level decisions are choices on: (a) the quality indicator and associated external or internal benchmark; (b) the data source, or registry, and patient population, including inclusion and exclusion criteria; (c) the reporting period; (d) control limits and whether data analysts are allowed to inflate them to correct for overdispersion. Overdispersion occurs when there is true heterogeneity between institutions, over and above the expected level of variation due to randomness.^23–31 Overdispersion is discussed in depth in section 3.4 of this paper.

The choice of the quality indicator will dictate whether and how the indicator will be corrected for differences in patient characteristics between institutions and the statistical methods for constructing the control limits. The value of the benchmark, against which hospitals are judged, may be externally provided³ or derived from the data.¹⁰ If the value of the benchmark is obtained from the data, we recommend using the average value of the quality indicator over all included patients, rather than an ‘average’ over hospitals. This choice gives equal weight to each patient’s data and reflects how the values of the quality indicator are calculated for each hospital. Disadvantages of this choice are that it ignores intra-hospital correlation. Correlated data and very large hospitals may have very large influence on the value of the benchmark.

We recommend using exact binomial methods to construct control limits for quality indicators, which are binary at the patient level and presented as proportions, risk-adjusted rates and standardised rates. Most of the literature^6–17 on funnel plots lean on one study, the background of funnel plots.³ Two studies^23,32 compared different methods to construct control limits and concluded that care should be taken to understand the properties of the limits constructed before using them to identify outliers;²³ and control limits obtained using probability-based prediction limits have the most logical and intuitive interpretation.³² Several other methods to construct control limits have been proposed for binary data. These include assuming that proportions or standardised rates, or risk-adjusted rates follow a normal or log-normal distribution or assuming that the number of patients, who die, follows a Poisson distribution. However, these assumptions may not be valid, especially if mortality rates are very low or hospitals are small.²⁵

3.2 Step two: checking the quality of prediction models used for case-mix correction

In this paper, we present guidelines on producing funnel plots for quality indicators, presented as proportions, risk-adjusted rates or standardised rates. Quality indicators presented as proportions do not use prediction models used for case-mix correction. Hence, for these quality indicators, step two is omitted.

Ideally, differences between hospitals only represent true differences in the quality of care and random variation.²⁶ However, there may also be additional variation due to differences in patient level variables between hospitals, also known as case-mix. Prediction models can be used to correct for differences in case-mix between hospitals. If differences in case-mix are not accounted for, these can unfairly influence the positions of hospitals in the funnel plot. This can occur if there is a complete lack of case-mix correction, if clinically important patient characteristics are excluded from the case-mix correction, or if there are biases in the parameters of the case-mix correction model. These biases can occur if the model was developed in another setting or time period.

A range of methods for assessing the performance of prediction models for binary outcomes has been proposed. We recommend using goodness-of-fit statistics for calibration, the Brier score to indicate overall model performance, and the concordance (or C) statistic for discriminative ability.²⁷ However, no consensus exists on the values of these performance measures that indicate that a prediction model is of ‘sufficient’ quality for the purpose of benchmarking.

In a recent study, four levels (mean; weak; moderate and strong) of calibration were described. The authors recommend to perform moderate calibration including 95% confidence intervals when externally validating prediction models, to avoid distortion of benchmarking. Moderate calibration is achieved if the mean observed values equal the mean predicted values for groups of patients with similar prediction. Furthermore, they recommend to provide summary statistics for weak calibration, i.e. the calibration slope for the overall effect of the predictors and the calibration intercept.²⁸

Second, the accuracy of a prediction model could be verified by the Brier score

$$\frac{1}{N}\sum _{i=1}^N(p_i-o_i{)}^2$$

where the observed mortality (o_i) is 0 or 1 and the predicted mortality probability (p_i) ranges between 0 and 1 for all patients from 1 to N. The Brier score is a mixture between discrimination and calibration and can range from 0 for a perfect model to 0.25 for a non-informative model with a 50% incidence of the outcome. The Brier score could be scaled by its maximum score, which is lower if the incidence is lower.²⁷ The scaled Brier score was determined by one minus the ratio between the Brier score and the maximum Brier score. This scaled Brier score is defined by

$$\begin{array}{c}1-\frac{1}{N}\sum _{i=1}^N((\frac{1}{N}\sum _{i=1}^N{o}_i)-o_i{)}^2\end{array}$$

where p_i is replaced by the average observed value. This scaled Brier score ranges between 0 and 1, with higher values indicating better predictions and has a similar interpretation to R² in linear regression. Hence, values less than 0.04 can be interpreted as very weak; between 0.04 and 0.15 as weak; between 0.16 and 0.35 as moderate; between 0.36 and 0.62 as strong; and values greater than 0.63 as very strong.²⁹

Third, to describe the discriminative ability of the model, the C-statistic could be used, which describes the ability to provide higher probabilities to those with the event compared to those without the event. For binary outcomes, the C-statistic is equal to the area under the receiver operating characteristic (ROC) curve (AUC), which is a plot of sensitivity versus one minus specificity. A C-statistic of 1.0 means a model with perfect discrimination and a C-statistic of 0.5 means no discrimination ability. Whether discriminative ability is sufficient enough depends on the quality indicator and clinical relevance of the quality indicator used. For judgement, often the following scale is used: values between 0.9 and 1.0 are interpreted as excellent; between 0.8 and 0.9 as good; between 0.7 and 0.8 as fair and between 0.6 and 0.7 as poor and between 0.5 and 0.6 as fail.³⁰ However, Austin et al.³¹ caution against only using the accuracy of a model, especially for benchmarking, since they found only a modest relationship between the C-statistic for discrimination of the risk-adjustment model and the accuracy of the model.

If a quality indicator is corrected for differences in patient characteristics using a prediction model, it is important to assess the performance of the prediction model. If the performance of the prediction model is not sufficient, we recommend not constructing a funnel plot for the quality indicator and instigating policy-level discussion on recalibrating the existing²⁸ or developing a new prediction model.

3.3 Step three: examining whether the number of observations per hospital is sufficient

It is important to be able to reliably assume that institutions falling outside the control limits in a funnel plot deviate from the value of the benchmark and that there is no reason to suspect that institutions falling inside the control limits are not performing according to the benchmark. For institutions with a small number of admissions, control limits are essentially meaningless. In a recent study, Seaton et al. concluded that for a small expected number of deaths, an institution had to perform very differently from that expected number to have a high probability that the observed SMR would fall above the control limits.³² Furthermore, they examined the statistical power of an observed standardised mortality ratio falling above the upper 95% or 99.8% control limits of a funnel plot compared to the true SMR and expected number of events. The number of observed events in this study was assumed to follow a Poisson distribution.³²

Similar to Seaton et al.,²³ we suggest using a three-stage method to estimate the statistical power for each number of admissions to detect a defined true quality indicator (proportion or risk-adjusted rate), assuming the quality indicator could be interpreted as a probability and is binomially distributed. If the quality indicator is a standardised rate, the risk-adjusted rate can be used for this test. In the first stage, the upper control limit for probabilities (p_i) from 0 to 1 and sample size n_j from 1 to 10,000 (O_u,pi,nj) is calculated: the smallest value O_u for which P(X ≤ O_u | p_i,n_j) is greater than 0.975 (for 95% control limits) or 0.995 (for 99% control limits). In the second stage, for each p_i and n_j, the probability that the number of observations is larger than the estimated upper control limit (O_u,pi,nj), given the true probability (p_true,_i =1.5p_i), has to be calculated: P(X > O_u,pi,nj | p_true,i,n_j). In the third stage, the smallest number of observations, n_j, for which this probability was greater than the chosen statistical power for each probability p_i has to be extracted_. The quality indicator used determines which outcome values are clinically relevant. Figure S1 present the number of admissions required to get 80% power to detect an increase of 1.5 times the benchmark value for different benchmark probabilities.

If the sample size is not sufficient enough, the sample size could be either redefined or the analyses could be discontinued. Ways to redefine the sample size are (1) make record selection more general (redefine in- and exclusion criteria, back to beginning); (2) extend the period of reporting (back to beginning); (3) consider exact methods to predict control limits (discussed in this paper); (4) group similar ICUs into clusters; (5) continue but only display control limits for clusters fulfilling test; or (6) describe the sample size issue in the figure’s legend and document text. If the sample size is decided to be sufficient enough, we suggest performing explorative analyses by constructing funnel plot(s) using the exact binomial method to calculate control limits (without overdispersion) as a first attempt to examine the funnel plot for the chosen outcome measure and to apply other reliability tests.

3.4 Step four: testing for overdispersion of the values of the indicator

Ideally, differences between hospitals only represent true differences in the quality of care and random variations.³³ However, overdispersion occurs when there is true heterogeneity between hospitals, over and above that expected due to random variation.^33–41 If overdispersion occurs, one needs to be careful to draw conclusions from the funnel plot, since the assumptions with respect to the distribution of the quality indicator are violated.

Often the cause of overdispersion is not clear, but heterogeneity may arise when hospitals serve patients with different characteristics for which the model does not sufficiently correct; due to registration bias or errors; or policy choices or variability in the actual quality of care offered.³⁹

We shortly discuss frequently used tests for the existence, the degree of overdispersion and how to correct for overdispersion. A frequently used test is the Q-test, described by DerSimonian and Laird.⁴² A visual way to detect overdispersion is by inspection of the deviance residual plots.⁴³ Several methods are discussed to correct for overdispersion by the random effect approach.^{36,38,40,41,44–46} The most used method is the DerSimonian–Laird (methods of moment estimator) (DL [MM]) method.⁴² The random effect approach could be easily applied when using a normal approximation of the binomial distribution to construct control limits. However, this approach could not be implemented using exact binomial control limits. In addition to the random effect method, a multiplicative approach could be used to detect overdispersion.³ This method could be implemented for exact binomial control limit. However, using a multiplicative approach can lead to control limits that are overly inflated near the origin, which could be avoided by Winsorising the estimate. In the multiplicative method, the overdispersion factor $(\varphi )$ is estimated by the mean standardised Pearson residuals (z-scores): $\hat{\varphi }=\frac{1}{k}\sum _{i=1}^N{z}_i^2$, with z_i the standard Pearson residuals $z_i=\frac{y_i-{\theta }_0}{\sqrt{V(Y|{\theta }_0)}}$, Y the outcome measure and y_i the outcome for patient i, ${\theta }_0$ the benchmark value and k the number of hospitals.³ These values are winsorized, the 10% largest z-scores are set to the 90% percentile and the 10% lowest z-scores are set to the 10% percentile. This approach estimates an overdispersion factor, $\stackrel{⌢}{\varphi }$. If there is no overdispersion, the value of $\stackrel{⌢}{\varphi }$ is close to one and the variable $k\stackrel{⌢}{\varphi }$ follows a chi-squared distribution with k degrees of freedom, where k is the number of hospitals.

If a quality indicator demonstrates overdispersion in a particular reporting period, we advise to take steps to improve correction for differences in patient characteristics and hospital policy choices and reduce registration errors and bias before the next reporting period,³ even if they have approved inflating the control limits in the current reporting period.

3.5 Step five: testing whether the values of quality indicators are associated with institutional characteristics

A funnel plot is constructed based on the assumption that the benchmark and dispersion displayed by the control limits hold for the whole sample of the population. A funnel plot can be used as a tool to identify a small percentage of deviating institutions. It is not meant to be used to judge whether different groups of institutions perform differently. For this reason, quality indicators can only be validly presented in funnel plots if there is no association between the values of the quality indicator and hospital characteristics.³

As examples, we assume no association between outcome and volume, i.e. for small institutions a specific quality indicator shows the same expectation and dispersion as for larger institutions. Furthermore, we assume no association between outcome and predicted probability of mortality, i.e. institutions with more severely ill patients. We therefore advise to test for an association between the values of the quality indicator and the number of admissions qualifying for inclusion in the quality indicator, i.e. assuming that for small institutions a specific quality indicator shows the same expectation and dispersion as for larger institutions. Furthermore, we advise to test for an association between the values of the quality indicator and, if case-mix correction is used, the average predicted probability of mortality. In addition, we advise to discuss the need for other tests internally, on policy level, before constructing funnel plots for a particular reporting period.

These associations could be examined using binomial regression between the values of the quality indicator and continuous or discrete hospital characteristics, with the quality indicator as dependent variable and the hospital characteristic as independent variable. The Spearman’s rho test could also be used to examine associations for continuous variables and the Kruskal–Wallis test could also be used to examine associations between the quality indicator and categorical variables. However, these tests do not account for differences in size of the institutions.

If there is a significant association between the values of the quality indicator and hospital characteristics, we advise to reconsider funnel plot construction and to consider case-mix correction improvement or commissioning separate funnel plots for different subgroups of hospitals, following the same distribution.

3.6 Step six: specifying how the funnel plot should be constructed

When constructing a funnel plot, the ways to present the measure of precision on the horizontal axis, the benchmark, the control limits, and the shape between the control limits need to be specified. For the measure of precision, the number of cases (say patients or admissions) or the standard error of the estimate of the quality indicator can be used. The benchmark value can be presented as a solid horizontal line. Control limits could be presented by solid or dashed lines or coloured areas. Furthermore, horizontal or vertical gridlines or an inconclusive zone could be added to the funnel plot.⁴⁷

4 Statistical analysis plan for NICE quality indicators

In this section, we present our statistical analysis plan for producing funnel plots for the quality indicators for the NICE registry. The structure of the plan is based on the six steps presented in section 3. Section 5 describes the results of the analyses. In all of analyses, we viewed p < 0.05 as statistically significant. We performed the analyses and produced the funnel plots using R statistical software, version 3.3.1 (R Foundation for Statistical Computing, Vienna, Austria).⁴⁸ We present the R code used in each step in the supplemental R markdown file.

4.1 Step one: defining policy level input

We produce funnel plots for two quality indicators, crude proportion of in-hospital mortality and standardised in-hospital mortality rate for all ICU admissions; medical admissions; admissions following elective surgery; and admissions following emergency surgery. The associated benchmarks were obtained from the empirical data (internal) and equal to the value of the quality indicator over all included patients. These quality indicators were based on data from the NICE registry for initial admissions for the crude proportion of in-hospital mortality and admissions fulfilling the APACHE IV criteria²⁰ for the standardised in-hospital mortality rate of participating ICUs between 1 January and 31 December 2014. The funnel plots were to contain the 95% and 99% control limits constructed using exact binomial methods.³ These control limits reflect ‘moderate’ and ‘moderate to strong evidence’ against the null-hypothesis that the hospitals are performing as expected given the value of the benchmark.⁴⁹ We have permission from the board of directors to correct for overdispersion.

4.2 Step two: checking the quality of models used for case-mix correction

We evaluated the performance of the recalibration of the APACHE IV prediction model for in-hospital mortality, described in section 2, by obtaining the calibration, accuracy and discrimination of the model. First, we derived weak calibration by examining the regression curve of the plot between the observed mortality and the predicted mortality. Furthermore, we examined moderate calibration not entirely, but for 50 subgroups of predicted values. We accept calibration as good enough, if there is no significant difference between the mean predicted and observed probability of the event of interest or a calibration plot with an intercept of zero and slope of one.²⁷ Second, we calculated the scaled Brier score. We decide to only use the quality indicator for presentation in a funnel plot if the scaled Brier score is at least moderate, equal or larger than 0.16.²⁸ For the discriminative ability, we used the AUC curve and regarded values larger than 0.7 as acceptable.

If the prediction model does not show satisfactory performance according to the measures described above, we did not construct the funnel plot for the quality indicator and first discuss the results and consequences with the board of directors.

4.3 Step three: examining whether the number of observations per hospital is sufficient

We plotted control limits for hospitals with enough admissions to provide at least 80% power⁵⁰ to detect an increase in proportion or standardised rate from the benchmark value to 1.5 times this value for an alpha of 0.05 (95% control limits) or 0.01 (99% control limits). If fewer than half of hospitals have enough admissions to fulfil this criterion, we did not construct the funnel plot and first discuss the results and consequences with the board of directors.

4.4 Step four: testing for overdispersion of the values of the indicator

We tested the values of quality indicators and inflated control limits for proportions and standardised rates for overdispersion using the multiplicative approach with a Winsorised estimate of $(\hat{\varphi })$.^3,51 If the value of the overdispersion factor was significantly greater than one, control limits were inflated by a factor of $\sqrt{\hat{\varphi }}$ around the benchmark value.³ We did not shrink the control limits towards the benchmark value if the value of the overdispersion factor was less than one.³

4.5 Step five: testing whether the values of quality indicators are associated with institutional characteristics

We used binomial regression with the quality indicator as the dependent variable and the hospital characteristics as the independent variable to test whether the values of the quality indicators were associated with institutional characteristics. We examined associations between the values of the quality indicators and the number of admissions, the mean probability of mortality, and whether a hospital was university affiliated; a teaching hospital or a general hospital. If we find a significant association between the values of the quality indicator and hospital characteristics, we do not present the funnel plot and first discuss the results and consequences with the board of directors.

4.6 Step six: specifying how the funnel plot should be constructed

We placed the value of the quality indicator on the vertical axis and the number of ICU admissions included when calculating the quality indicator on the horizontal axis. We presented each hospital as a small dot and the benchmark value as a solid horizontal line. We present the control limits as dashed lines drawn from the appropriate lower limit of number of admissions, as calculated in section 4.3 of this paper, to a value slightly larger than the number of patients used to calculate the value of the quality indicator for the largest hospital. We used different types of dashed line to differentiate between the 95% and 99% control limits.

5 Funnel plots for NICE registry quality indicators

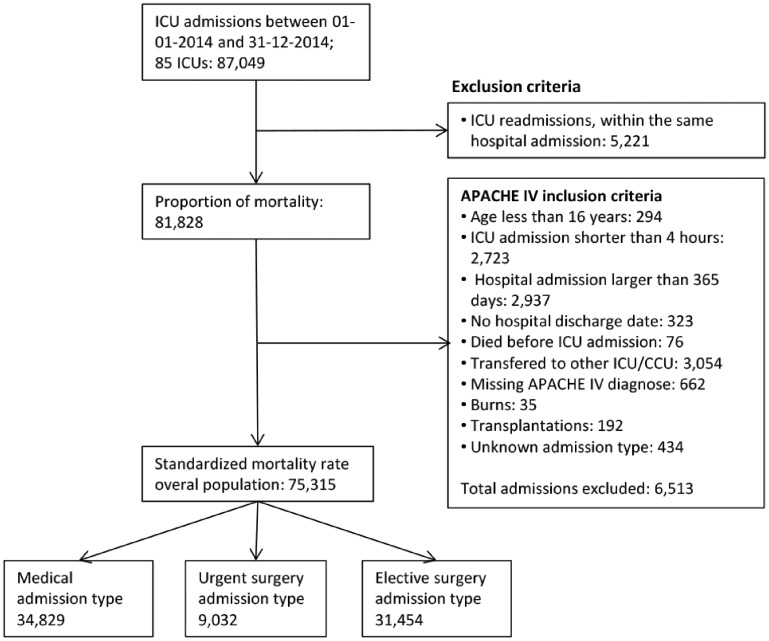
In this section, we describe the results of the analysis plan described in section 4. For the motivating example, the policy-level decisions of step 1 are described in section 4.1. Between 1 January and 31 December 2014, the NICE registry contains 87,049 admissions to 85 hospitals for this period. We present a flow chart of exclusion criteria and number of admissions used for each indicator in Figure 2. Table 1 describes the results of the different steps in the process of funnel plot construction for each of the quality indicators and subgroups used in the motivating example. The parameters for the recalibration used in this paper are presented in Table S1.

Figure 2.

Flowchart illustrating the inclusion and exclusion criteria for entry into the study for proportion of mortality, standardised mortality rate and standardised readmission rate.

Table 1.

The results of the first five steps when producing a funnel plot for the NICE quality indicators.

Step in the process	Outcome or test	Proportion mortality full population	SMR full population	SMR medical admissions	SMR emergency surgery	SMR elective surgery
Step 1	Total admissions	81,828	75,315	34,829	9,032	31,454
	Median admissions (range ICUs	684 (222–3,546)	643 (214–3,425)	352 (76–1,179)	75 (22–362)	182 (13–2253)
	Overall percentage of deaths (range ICUs)	11.9 (3.6–21.4)	11 (3.7–20.6)	17.7 (7.7–28.9)	14.4 (4.4–28.6)	27.2 (0.0–10.7)
	Overall number of deaths (range ICUs)	9,705 (11–337)	8,265 (11–310)	6,178 (8–206)	1,300 (2–69)	787 (0–63)
	Overall standardised rate (range ICUs)	–	1.00 (0.51–1.51)	1.00 (0.50–1.62)	1.00 (0.25–1.99)	0.99 (0–3.32)
	Overall risk adjusted rate (range ICUs)	–	0.11 (0.02–0.27)	0.18 (0.04–0.38)	0.14 (0.01–0.54)	0.02 (0–0.27)
Step2	Moderate calibrationb (95% CI)	–	α = 0.00 (−0.00 to 0.01); β= 0.99 (0.97–1.01)	α = −0.00 (−0.06 to 0.00); β = 1.00 (0.98–1.02)	α = 0.01 (−0.00 to 0.01); β = 0.96 (0.94–0.99)h	α = 0.02 (−0.00 to 0.05); β = 0.77 (0.68–0.86)h
	Center-based calibrationc (95% CI)	–	α = 0.01 (−0.00 to 0.03); β = 0.87 (0.72–1.03)	α = 0.04 (0.02–0.07); β = 0.74 (0.60–0.88)h	α = 0.04 (0.00–0.07); β = 0.75 (0.51–0.98)h	α = 0.01 (0.00–0.02); β = 0.75 (0.51–0.98)h
	Patient level scaled brier score	–	0.33	0.32	0.27	0.12i
	Concordance statistic	–	0.90	0.87	0.85	0.85
Step 3a	Required sample size for 95% control (number and percentage ICUs with insufficient sample size)	274 (4; 5%)	304 (8; 9%)	181 (9; 11%)	168 (68; 80%)j	1,359 (79; 93%)j
	Required sample size for 99% control limits (number and percentage ICUs with insufficient sample size)	410 (16; 19%)	445 (24; 28%)	269 (20; 24%)	251 (74; 87%)j	2,028 (84; 99%)j
Step 4a	Winsorised estimate φ (p-value)	5.50 (p < 0.01)f	2.45 (p < 0.01)f	1.71 (p < 0.01)f	1.03 (p = 0.41)	1.10 (p = 0.24)
Step 5	Number of admissions (divided by 100): relative odds ratio (exp(β (CI))d	1.00 (1.00–1.00)e	1.00 (1.00–1.00)	1.00 (0.99–1.01)	0.96 (0.90–1.01)	1.00 (0.99–1.01)
	Average predicted probability: relative odds ratio (exp(β (CI))d	–	0.64 (0.29–1.40)	0.23 (0.12–0.42)g	0.25 (0.06–1.10)	0.00 (0.00–0.06)g
	Hospital type: specialised academic, teaching or general hospital: relative odds ratio (exp(β (CI))e	0.95 (0.93–0.98)g	0.99 (0.96–1.02)	1.01 (0.97–1.05)	0.96 (0.89–1.03)	0.94 (0.85–1.03)

SMR: standardised mortality rate; ICU: intensive care unit; CI: confidence interval.

^aStep 3 and 4 are examined using risk adjusted rates in state of standardised rates.

^bOrdinary least square regression for 50 subgroups of predicted mortality (x = mean predicted and y = mean observed).

^cOrdinary least square regression for 85 ICUs (x = mean predicted and y = mean observed).

^dH₀:there is no significant relationship between outcome measure and number of admissions or average predicted probability.

^eH₀:distribution of the outcome measure is identical for each hospital type.

^fSignificant p-value < 0.05.

^gRelative odds ratio significant different from 1, i.e. the confidence interval of relative odds ratios does not contain 1.

^hThe confidence interval around α does not contain 0 or the confidence interval around β does not contain 1.

ⁱThe scaled brier score < 0.16.

^jSample size not sufficient enough for more than 50% of the hospitals.

Grey cells: stop the process, results are not satisfactory according to the statistical analyses plan in chapter 4

5.1 Quality indicator: crude proportion of in-hospital mortality

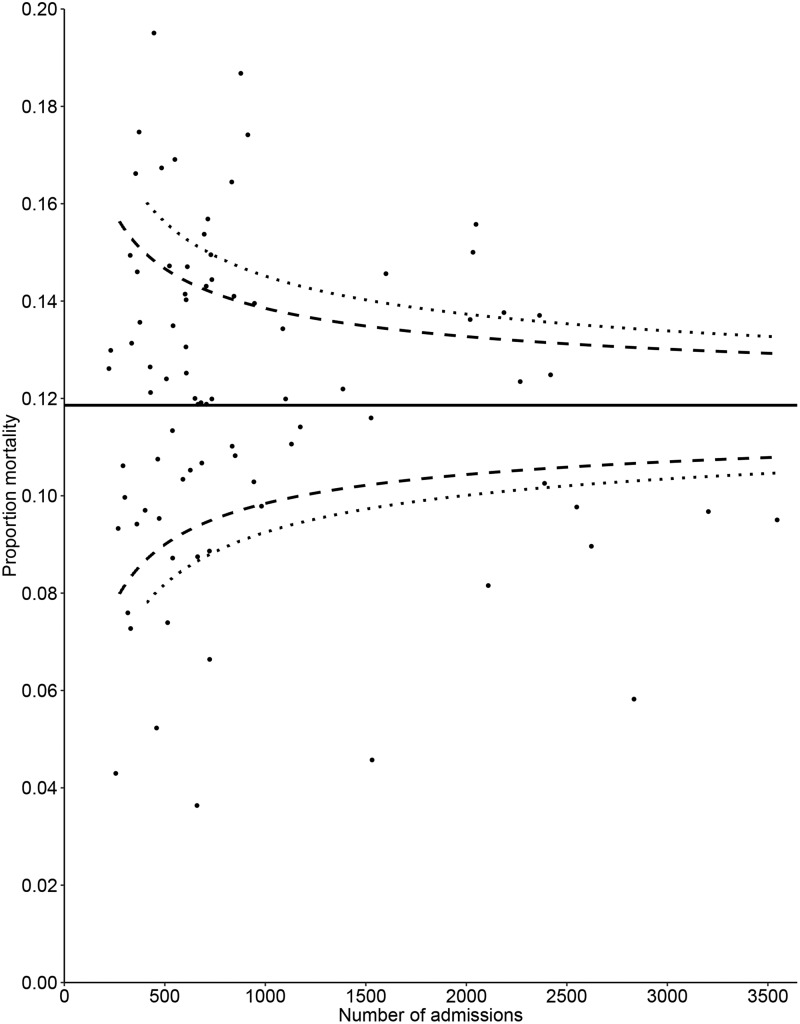
We included 81,828 ICU admissions, and the overall proportion of in-hospital mortality was 11.9% (range 3.6% to 21.4%). For the purpose of this example, we omit the step of case-mix correction for crude hospital mortality. There was significant overdispersion, (parameter 5.50; p < 0.01), which indicates that the control limits of the funnel plot will need to be corrected for overdispersion. There was indication that the proportion of in-hospital mortality was associated with the number of admissions (p < 0.01) and hospital type (p = 0.03). These results were not satisfactory, and we do not recommend presenting the resulting funnel plot. However, to demonstrate the need to correct for differences in patient characteristics of in-hospital mortality as outcome indicator, the funnel plot is presented in Figure 3.

Figure 3.

Funnel plot for the crude proportion of in-hospital mortality. The value of the quality indicator is presented on the vertical axis and the number of ICU admissions included when calculating the quality indicator is presented on the horizontal axis. Small dots represent ICUs and the solid line represent the benchmark value. Dashed lines represent control limits, different types of dashed line are used to differentiate between the 95% and 99% control limits.

5.2 Quality indicator: standardised in-hospital mortality rate for all ICU admissions

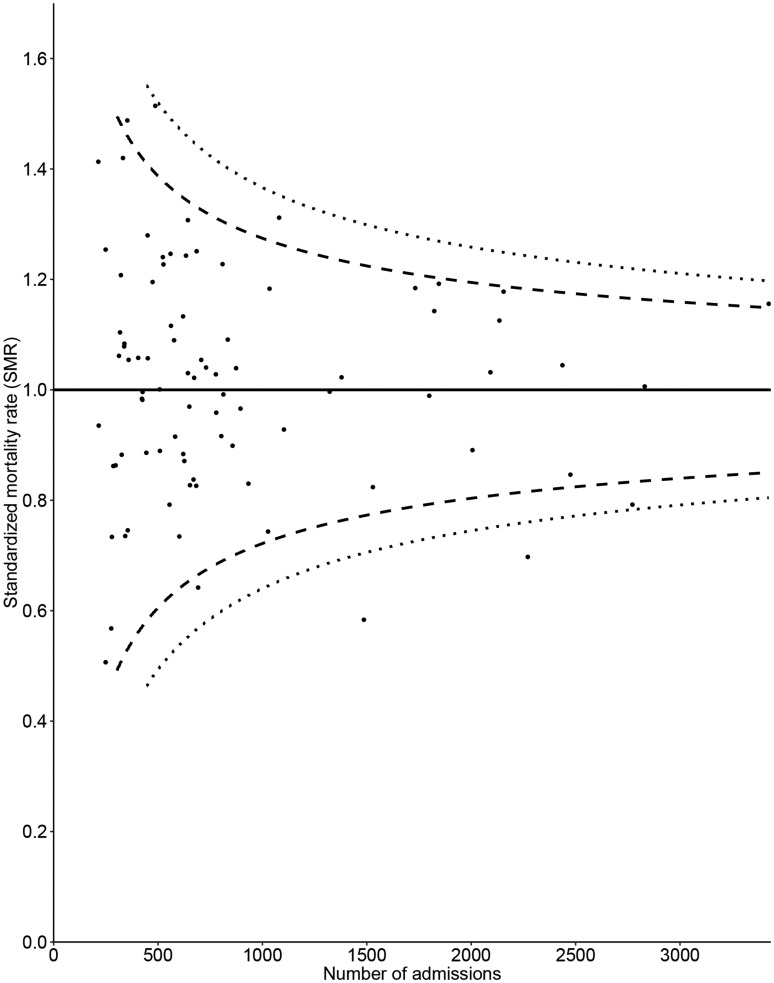
We included 75,315 ICU admissions fulfilling the APACHE IV inclusion criteria. By definition, the overall recalibrated standardised rate was 1.00 (range over hospitals 0.51–1.51). According to the criteria defined at section 4.2, the quality of the case-mix correction was satisfactory. Supplemental figure S2 present calibration plots based on ICUs, for different subgroups. The 95% control limits could not be presented for 8 (9%) hospitals for the 95% control limits and 24 (28%) hospitals for 99% control limits, due to small sample size. There was significant overdispersion (parameter 2.45; p < 0.01), meaning the control limits of the funnel plot need to be corrected for overdispersion. There was no association between the standardised mortality rate and the number of admissions; the average predicted probability of mortality; or hospital type. These results are satisfactory and we present the resulting funnel plot in Figure 4. The funnel plot for this indicator shows that eight hospitals (9.5%) fall outside the 95% control limits (expected for Poisson distribution: 0.05 × 84 = 4.2) and two hospitals (2.3%) fall outside the 99% control limits (expected for Poisson distribution: 0.01 × 84 = 0.84).

Figure 4.

Funnel plot for the APACHE IV standardised in-hospital mortality rate for all ICU admissions, control limits inflated for overdispersion. The value of the quality indicator is presented on the vertical axis and the number of ICU admissions included when calculating the quality indicator is presented on the horizontal axis. Small dots represent ICUs and the solid line represents the benchmark value. Dashed lines represent control limits, different types of dashed lines are used to differentiate between the 95% and 99% control limits.

5.3 Quality indicator: standardised in-hospital mortality rate for medical admissions

We included 34,829 ICU admissions fulfilling the APACHE IV inclusion criteria and are medical admissions. The overall recalibrated standardised rate was 1.00 (range 0.50–1.62) For step 2, the coefficients of the regression line through the calibration curve were not satisfactory, α = 0.04 (0.02–0.07) and β = 0.74 (0.60–0.88) across ICUs. The overdispersion parameter was significant (parameter 1.71; p < 0.01). Testing whether the values of quality indicators are associated with institutional characteristics the standardised mortality rate was associated with the average predicted probability of mortality (relative odds ratio 0.23; p < 0.01), see Figure S3. Based on the strict requirements defined in steps 2 and 5 in section 4, we recommend to not present the funnel plot for this indicator and first discuss the results and consequences with the board of directors.

5.4 Quality indicator: standardised in-hospital mortality rate for admissions following emergency surgery

We included 9,032 ICU admissions fulfilling the APACHE IV inclusion criteria following emergency surgery. The overall recalibrated standardised rate was 1.00 (range 0.25–1.99). For step 2, the coefficients of the regression line through the calibration curve across ICUs (α = 0.04 (0.00–0.07) and β = 0.75 (0.51–0.98)) and across 50 subgroups of predicted mortality (α = 0.04 (0.00–0.07) and β = 0.75 (0.51–0.98)) were not satisfactory. The number of admissions was not satisfactory for, respectively, 68 (80%) ICUs for 95% control limits and for 74 (87%) ICUs for 99% control limits. Furthermore, the overdispersion parameter was not significant and we did not find significant associations between the value of the quality indicator and hospital characteristics. Since the quality of the case-mix correction and the number of admissions per ICU was not satisfactory, we do not present the funnel plot.

5.5 Quality indicator: standardised in-hospital mortality rate for admissions following elective surgery

We included 31,454 ICU admissions following elective surgery fulfilling the APACHE IV inclusion criteria. The overall standardised rate was 0.99 (range 0.00–3.32). For step 2, the coefficients of the regression line through the calibration curve across ICUs (α = 0.01 (0.00–0.02) and β = 0.75 (0.51–0.98)) and across 50 subgroups of predicted mortality (α = 0.02 (−0.00–0.05) and β = 0.77 (0.68–0.86)) were not satisfactory. The number of admissions was not satisfactory for, respectively, 79 (93%) ICUs for 95% control limits and for 84 (99%) ICUs for 99% control limits. The scaled brier score was 0.12, weak, and concordance statistic was 0.85. The overdispersion parameter was not significant. We did find a significant relationship between the quality indicator and the average predicted probability (relative odds ratio 0.00; p = 0.01). We do not present the funnel plot, since the prediction model did not satisfy our requirement and the number of admissions per ICU was not satisfactory.

6 Discussion and concluding remarks

We have presented guidelines for producing funnel plots for the evaluation of binary quality indicators, such as proportions, risk-adjusted rates and standardised rates, in hospitals and other healthcare institutions. Our guidelines focused on six steps: (1) policy (board of directors) level input; (2) checking the quality of prediction models used for case-mix correction; (3) ensuring that the number of observations per hospital is sufficient; (4) overdispersion of quality indicators; (5) examining associations between the values of quality indicators and hospital characteristics; and (6) funnel plot construction. We expect that our guidelines will be useful to data analysts and registry employees preparing funnel plots and striving to achieve consistency in funnel plot construction over projects, employees and time.

We illustrated these six steps using data from ICU admissions recorded in the NICE registry. We performed all of the steps for two quality indicators: crude proportion of in-hospital mortality; and standardised in-hospital mortality rate for four subgroups of patients all ICU admissions; medical admissions; admissions following elective surgery; and admissions following emergency surgery. Our results showed that it was appropriate to develop funnel plots for standardised in-hospital mortality rate for all ICU admissions, but not for the other three subgroups based on admission type.

There are three main strengths of our work. First, we provide a framework, in which standard operating procedures involving the construction of funnel plots are described. These standard operating procedures are important, for example, for certification of a registration. Second, although previous studies on funnel plots have been published,^3,23,32 we brought together literature on many aspects of the development of funnel plots. Third, we used a large-scale real life data problem as a motivating example. This means that we have encountered and considered practical, rather than just theoretical, aspects of funnel plot production.

Our study also has three main limitations. First, we only considered funnel plots for binary quality indicators and not for other types of data, such as normally and non-normally distributed continuous quality indicators. Second, we preformed no internal or external tests to assess the usability of our approach. Future research should use data from another registry to conduct external usability tests on our guidelines.

Data analysts presenting funnel plots should be aware of small number of events and of small hospitals when presenting binary quality indicators. We based our choice on the number of admissions needed to provide enough power (80%) to detect an increase in proportion or standardised rate from the benchmark value to 1.5 times this value. In this choice, we were relatively conservative. Furthermore, we recommended the use of binary control limits compared to examining control limits using an approximation to the binomial distribution, such as the normal distribution. Literature shows that the normal approximation to the binomial distribution is good for np(1 − p) ≥ 5 if |z| ≤ 2.5, with n the overall sample size, p the proportion of events and z the z-score of the normal distribution (|z| = 2.5 for two-sided 95% control limits),³⁷ which lead to lower values of number of sample size for our example. This study does not contain guidelines for funnel plots for quality indicators based on other types of data, including normally and non-normally distributed continuous data. Control limits for normally distributed outcomes can be derived analytically, but control limits for non-normally distributed outcomes, such as ICU length of stay,⁵² can be difficult to derive analytically. Hence, the potential role of alternative methods, such as resampling,⁵³ in obtaining control limits needs to be developed further. In addition, data visualisation researchers should investigate the optimal way to present the information, including control limits, in funnel plots. Although this study presents guidance on constructing funnel plots for quality assessment in hospitals and other healthcare institutions or individual care professionals, we expect that this guidelines could also be used for institutions outside the healthcare settings.

Declaration of conflicting interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Funding

The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: Drs. Verburg, Dr de Keizer and Dr Holman’s institutions received grant support and support for participation in review activities from the National Intensive Care Evaluation (NICE) Foundation (The NICE Foundation pays the department of Medical Informatics for maintaining the national database, providing feedback reports, and doing analyses; Drs Verburg, de Keizer, and Holman are employees of the Department of Medical Informatics). de Keizer is a member of the board of the NICE Foundation.

Supplemental material

Supplemental material is available for this article online.