Evaluating Amber force fields using computed NMR chemical shifts

Abstract

NMR chemical shifts can be computed from molecular dynamics (MD) simulations using a template matching approach and a library of conformers containing chemical shifts generated from ab initio quantum calculations. This approach has potential utility for evaluating the force fields that underlie these simulations. Imperfections in force fields generate flawed atomic coordinates. Chemical shifts obtained from flawed coordinates have errors that can be traced back to these imperfections. We use this approach to evaluate a series of AMBER force fields that have been refined over the course of two decades (ff94, ff96, ff99SB, ff14SB, ff14ipq and ff15ipq). For each force field a series of MD simulations are carried out for eight model proteins. The calculated chemical shifts for the ¹H, ¹⁵N and ¹³C^a atoms are compared with experimental values. Initial evaluations are based on root mean squared (RMS) errors at the protein level. These results are further refined based on secondary structure and the types of atoms involved in non-bonded interactions. The best chemical shift for identifying force field differences is the shift associated with peptide protons. Examination of the model proteins on a residue by residue basis reveals that force field performance is highly dependent on residue position. Examination of the time course of non-bonded interactions at these sites provides explanations for chemical shift differences at the atomic coordinate level. Results show that the newer ff14ipq and ff15ipq force fields developed with the implicitly polarized charge method perform better than the older force fields.

Introduction

Empirical force fields are used to model the atomic interactions in molecular dynamics (MD) simulations.¹ These force fields are based on classical mechanics and electrostatics. Ideally, these interactions should be characterized by quantum mechanical (QM) wave functions, but this is not computationally feasible for large biomolecules. The MD simulations supported by these force fields have provided unique insights into structure and function at the atomic level,² but they also have a long list of shortcomings. This list includes inadequate treatment of polarization, problematic aromatic interactions, inconsistent treatment of higher order relationships, and a bewildering array of water models with different bulk properties.^3–13 The accuracy of MD simulations is also a function of the similarity between the interactions being studied and the data sets used for parameter fitting. Progressive refinement of force fields over the past several decades has steadily improved the accuracy and general applicability of MD simulation, but much work remains to be done.¹⁴ Developing and refining force fields is tedious and time consuming. Comparing force fields and testing their efficacy is also a challenging task. Modern force fields contain hundreds of parameters and different force fields are usually optimized against different data sets. The ultimate test for a force field is the ability to reproduce experimentally accessible properties in MD simulations. One potentially useful property for this purpose is the NMR chemical shift.

We recently introduced a new approach for calculating NMR chemical shifts (¹H, ¹³C^a and ¹⁵N) from molecular dynamics (MD) simulations.¹⁵ The key insight of the approach is that the magnetic field influencing an atom, and, correspondingly, the chemical shift, is a highly local property that can be well characterized by the immediately adjacent polar and aromatic atoms. As illustrated by Fig. 1, we construct templates that describe this local environment through a set of pairwise distances. The local environment of a residue (including nearby water molecules) is matched using these distances to the closest template in a library of conformers with known chemical shifts. Matching is performed across the MD simulation to compute an ensemble average that takes into account the dynamic conformational sampling of the simulation. The chemical shifts for library template conformers are obtained by ab initio quantum chemical (QM) calculations using density functional theory at the B3LYP level combined with a 6–311+G(2d,p) basis set.^16–19 The previously described library contained 169,499 members and was evaluated and its errors characterized using a single force field on six proteins. Here we expand the library to 258,428 templates that cover the conformational sampling needed for eight proteins simulated using six force fields.

Fig. 1.

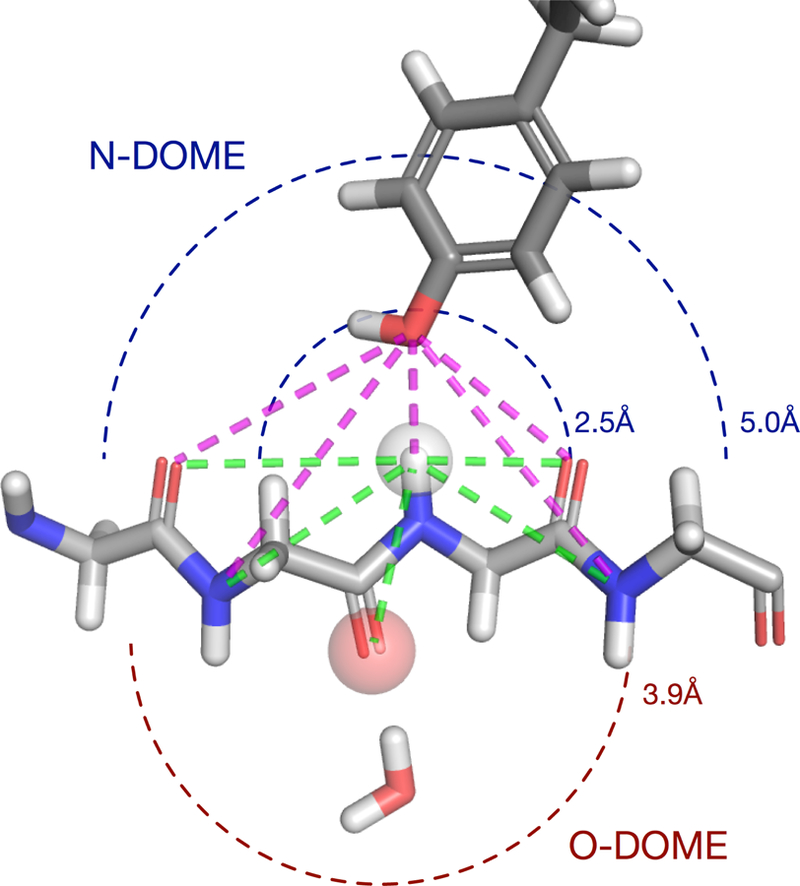
The local environment used for template matching. Templates are identified by the non-bonded polar and aromatic atoms contained in hemispheres surrounding each peptide bond. These atoms have the largest effect on the local magnetic field and resulting chemical shift. The hemisphere centered on the peptide proton is the NDOME. The hemisphere centered on the peptide oxygen is the ODOME. The NDOME contains all polar atoms within 2.5 Å and all aromatic atoms within 5.0 Å of the peptide proton. The ODOME contains all polar and aromatic atoms within 3.9 Å of the peptide oxygen. Templates are defined in terms of distances from the atom of interest (N or O) that fully define the local conformation of the protein (green) and nearby polar and aromatic atoms (magenta).

The original goal of our approach was to generate accurate NMR chemical shifts from MD simulation trajectories. Comparisons with experimental values, however, revealed significant errors. These errors arise because the QM calculations are carried out on the raw coordinates from the MD simulation frames without further optimization.²³ These errors are solely dependent on the level of QM theory and the spatial relationships defined by these coordinates. The overall RMS errors for the ¹H, ¹³C^a and ¹⁵N atoms in the protein backbones of the original model proteins were 1.575 ppm, 3.194 ppm, and 5.479 ppm, respectively. The ¹H chemical shift values were also significantly lower than the observed values in almost all cases. These characteristics suggest that calculated chemical shifts might be useful for evaluating force fields. A force field with fewer imperfections should generate atomic coordinates that are more realistic. This should result in a reduction of computed chemical shift error. NMR chemical shift error could supplement other comparison approaches from NMR spectroscopy such as order parameters, relaxation times and scalar J couplings.^24–30

New approaches for comparing force fields should be validated on force fields that are well documented. The force fields in the AMBER family fulfill this requirement. They have been widely used and progressively refined over the course of two decades. Important milestones in development include the ff94, ff96, ff99SB, ff14SB, ff14ipq and ff15ipq releases. These force fields are in rough chronological order and the deficiencies in each member of this series are well known. The oldest member of this series is ff94.²⁰ This force field was a successor to the Wiener et al force field.³¹ It was based on the same diagonal potential function with electrostatic potentials based on atom centered charges. New charges were introduced based on quantum calculations using the 6–31G* basis set and the restricted electrostatic potential (RESP) charge fitting protocol. Improved van der Waals parameters also led to the elimination of the polar hydrogen model and the need for a 10–12 function to represent hydrogen bonds. Finally, the φ and ψ angle parameters were refined using quantum calculations on a set of glycyl and alanyl dipeptides. Although this force field has been widely used for over a decade, flaws such as over-stabilization of α-helices and underrepresentation of β-hairpins in regions with helical transitions led to new attempts at parameterization.^32–34

The ff96 and the ff99 force fields introduced tetrapeptide glycine and alanine conformers in an attempt to deal with electronic structure contributions from larger fragments as well as polarization effects.^35–36 These force fields improved the inadequate balance with respect to secondary structure, but did not eliminate it. The largest problem was a strong conformational preference for glycine. This was partially corrected in the ff99SB force field which identified a flaw in the treatment of dihedrals involving non-glycine backbone atoms.³⁷ The flaw involved improper treatment of the second set of dihedrals associated with the β-carbons in the torsional parameters. Parameterization was also carried out using a larger set of tetrapeptides treated at the MP2 level of QM theory. Unfortunately, backbone secondary structure preferences were not eliminated and weaknesses in sidechain rotamer conformations persisted. This was addressed in the ff14SB force field which performed a complete refit of all side chain dihedral parameters and included new dihedral parameters for the different protonation states of ionizable side chains.³⁸ These new parameter sets improved the secondary structure content for short peptides and more closely reproduced the NMR scalar coupling measurements for proteins in solution.

In 2014, significant modifications were made to the ff14SB force field.³⁹ New charges were assigned based on the implicitly polarized charge model (IpolQ).⁴⁰ In this model, the partial atomic charges are represented by values that are halfway between the charges on dipeptides in the gas phase and dipeptides in a solvent reaction field. Torsion parameters were assigned based on the single point energies at the MP2/cc-pVTZ level of QM theory carried out on structures optimized by the force field itself. Minor adjustments to the van der Waals parameters were also incorporated. Performance with respect to α-helical and β-sheet oligopeptides was significantly improved over ff99SB. In 2016, ff15ipq, a second generation force field based on the IpolQ charge model was released.⁴¹ This force field included a new derivation of more that 300 atomic charges, 900 torsions terms and 60 new angle parameters along with new atomic radii for polar hydrogens. Atomic charges were obtained using the SPC/E_b water model. The new force field appeared to improve the accuracy of salt bridge interactions over ff14SB while maintaining expected conformational propensities. It also reproduced penta-alanine scalar J-coupling constants with high accuracy and gave satisfactory agreement with NMR relaxation parameters.

In the present study, a series of 30 MD simulations are carried out on 8 model proteins for each of these AMBER force fields. The force fields associated with these simulations are compared at increasing levels of detail based on the differences between calculated and observed chemical shifts. Initial evaluations are based on root mean squared (RMS) error at the protein level. These results are further refined based on secondary structure and the types of atoms involved in non-bonded interactions. We find that the best chemical shift for identifying force field differences is the shift associated with peptide protons. Examination of the model proteins on a residue by residue basis reveals that force field performance is highly dependent on residue position. Examination of the time course of non-bonded interactions at these sites provides explanations for chemical shift differences at the atomic coordinate level. Improvements in chemical shift error mirror the improvements made to these force fields over the last two decades. Overall, we find that the ff14ipq and ff15ipq force fields developed with the implicitly polarized charge method perform better than the older force fields.

Methods

Molecular dynamics simulations

Eight proteins from the Protein Data Bank (PDB) were selected as model proteins for force field comparison. These proteins are listed in Table I. The list includes the 6 proteins that were used to create the original library of conformers for the template matching approach.¹⁵ This set was augmented with two proteins (PDB 1L2Y and 2A3D) used in folding studies. The proteins in this list contain a broad cross-section of structural motifs and amino acid distributions.

TABLE I.

Model proteins used for force field comparison

PDB ID	Name	Class	Architecture	Function	Residues
1ENH	Engrailed homeodomain	Mostly Alpha	Orthogonal bundle	DNA binding	54
1IGD	Protein G	Alpha Beta	Roll	Cell wall component	61
1HIK	Interleukine-4	Mainly Alpha	Up-down bundle	Cytokine activity	129
1L2Y	Trpcage	Mainly Alpha	Trp-cage motif	Rapidly folding synthetic	20
1QZM	ATP dependent protease	Mainly alpha	Orthogonal bundle	ATP dependent protease	94
1UBQ	Ubiquitin	Alpha Beta	Roll	Regulatory protein	76
2A3D	Three-helix synthetic	Mostly Alpha	Three-helix bundle	Large folding synthetic	73
3OBL	Cyanobacterial lectin	Mostly Beta	Beta barrel	Carbohydrate binding	132

MD simulations using 6 different AMBER force fields were carried out on each of these proteins using GPU accelerated AMBER version 16 and the ff94, ff96, ff99SB, ff14SB, ff14ipq and ff15ipq force fields.^{20,32,35,37,40,41} All protein structures were solvated to form an octahedral TIP3P water box that extended 12 Å beyond the protein. Each system was neutralized with Na+ or Cl- ions as needed. Each system underwent two rounds of minimization with the first round minimizing the solvent and the second round minimizing the full system. A 100 ps constant volume equilibration was performed with weak positional restraints on the protein during which the temperature was warmed from 0 K to 300 K followed by another 100 ps equilibration at constant pressure. Simulations were performed using the particle mesh Ewald (PME) method with a non-bonded cutoff of 10 Å. For production runs, constant pressure periodic boundaries and isotropic position scaling were used to maintain a pressure of 1 atmosphere. Langevin dynamics were used for temperature control. Complete simulation parameters are provided in the Supplement.

We evaluated two protocols for production simulations. The protocol consisted of 3 runs with a duration of 100 nanoseconds (ns) each. The second consisted of 30 runs with a duration of 10ns each. All runs were started from a different set of initial velocities. The coordinates for all trajectories were saved at picosecond (ps) intervals (N=300,000).

The original library of template conformers provided high quality matches for 89.3% of the conformations in 1L2Y and 94.1% in 2A3D, two proteins that were not used during the construction of the library. The library was further augmented by performing additional QM calculations as necessary to a total of 258,428 template conformations. More templates were required to adequately match the 30 10ns trajectories than the 3 100ns trajectories, indicating that, for the same amount of simulation, using multiple, smaller simulations resulted in greater conformational sampling. This led us to use the 30 10ns simulations protocol for the remainder of our evaluations. Our results are qualitatively similar if the longer simulations are used (data not shown).

Chemical shift calculations and RMS error measurements

Chemical shifts are assigned to the ¹H, ¹⁵N and ¹³C^a backbone atoms of the 8 model proteins listed in Table I using our template matching approach. ¹⁵ These assignments are made for every residue position in each simulation frame. The chemical shifts assigned to the residues in each frame are averaged over the course of each trajectory to yield ensemble averages. Experimentally observed chemical shifts for these same residues are obtained from the Biological Magnetic Resonance Bank (BMRB).⁴² For 1L2Y, only the ¹H chemical shift data is available, so this protein is excluded from error analysis involving ¹⁵N and ¹³C^a chemical shifts. The global RMS error for each protein is calculated from the difference between computed and observed chemical shifts at each residue position. This provides the initial basis for force field comparison.

The influence of secondary structure on chemical shift error is determined by analyzing trajectory subsets containing α-helical, β-sheet or coil architecture. These subsets are identified by residue position using information obtained from an analysis of the PDB coordinates of each model protein with the Stride program.⁴³ The RMS error for each subset is calculated for each of the 6 AMBER force fields.

Non-bonded interactions with peptide protons

Examination of the NDOME patterns at each residue position over all the simulation frames in this study (N=1.36 × 10⁹) shows that the majority of non-bonded interactions with the peptide proton involve one or more of the 6 atom types {O, W, A, L, R, and Z} that are described in Table II. The four initial members of this list are hydrogen bonding partners. The R type represents aromatic ring atoms close enough to influence the chemical shift of the peptide proton. The Z pattern is a null pattern where no polar or aromatic atoms are close enough to influence the peptide proton. Hydrogen bonding influence extends to a distance of ~2.5 Å. Aromatic influence extends to ~5–6 Å. The presence or absence of these atoms in the NDOME patterns used for template matching provides useful information about the chemical environment surrounding peptide protons and its evolution over time. For each atom type we calculate a number called the “pattern fraction” that represents the count of NDOME patterns containing that atom type divided by the total number of NDOME patterns in the trajectory. Pattern fractions are also calculated for selected subsets drawn from full trajectories. Large O fractions occur when hydrogen bonding to backbone oxygen atoms form α-helices, β-sheets or hairpin turns. Large W fractions are correlated with solvent access. Large A fractions indicate hydrogen bonding with acidic oxygens. Large L fractions indicate hydrogen bonding to hydroxyl oxygens. Both A and L fractions may contain information about the rotameric preference of their respective sidechains. Large R fractions indicate interaction with aromatic ring currents which may be positive or negative depending on ring orientation. Finally, a large Z fraction is usually associated with a temporary unwinding of secondary structure in regions with limited solvent access.

TABLE II.

Common NDOME atoms interacting with peptide protons

Atom Type	Description
O	Oxygen in a backbone peptide (part of an α-helix, β-sheet, or hairpin turn)
W	Oxygen in a water molecule
A	Oxygen in an aspartic or glutamic acid sidechain or a C-terminus
L	Oxygen in a serine, threonine or tyrosine sidechain
R	Carbon or nitrogen atom in an aromatic ring
Z	No polar or aromatic atom within the NDOME cutoff ranges

Pairwise Comparison on a Residue by Residue Basis

Pairwise force field comparisons are carried out on selected proteins and force fields on a residue by residue basis. In these comparisons, the absolute value of the chemical shift error at each residue position for the first force field is subtracted from the absolute value of the error for the second force field. A similar process is applied to the pattern fractions associated with these pairwise comparisons. The values of the pattern fractions for the second force field are subtracted from the values for the first force field.

Detailed Analysis of Individual Residue Positions

Residues of interest are identified from the largest positive or negative values in pairwise force field comparisons. Selected residue positions are examined in greater detail in individual proteins by following the time course of chemical shift and pattern fraction changes. This is accomplished by averaging the chemical shifts assigned to the selected residue in windows of 1ns duration (N=1000) over the entire trajectory. The average pattern fraction for each of the O, W, A, L, and R fractions is also calculated for this interval. Changes in pattern fraction correlate with changes in chemical shift.

Error Analysis based on Empirically Derived Chemical Shifts

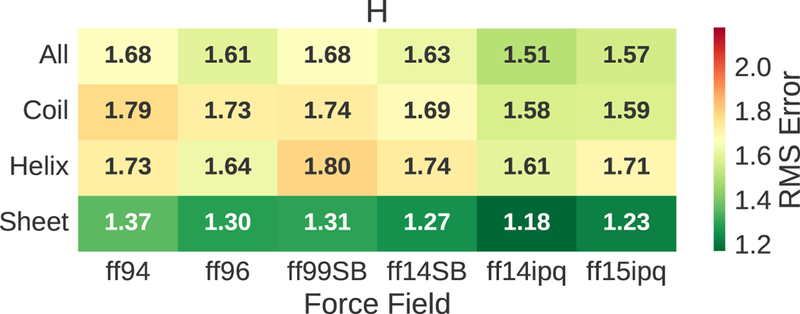
The RMS error measurements for the 6 AMBER force fields are repeated for the 8 model proteins listed in Table I using empirical chemical shifts obtained from the SHIFTX2 program.⁴⁴ Chemical shifts for all the backbone atoms in each frame of each trajectory (300,000 frames x 8 proteins x 6 force fields) are calculated. RMS errors are generated from ensemble averages using the same approach employed in template matching. These errors are normalized with respect to the values for the ff94 AMBER force field and displayed in the same fashion. The results are compared with the results obtained from template matching.

Results and Discussion

Average RMS Error for 6 AMBER Force fields

MD simulations were carried out as described in the methods section for each model protein using the ff94, ff96, ff99SB, ff14SB, ff14ipq and ff15ipq AMBER force fields. The average RMS chemical shift error is determined for each protein and each force field using the squared difference between the calculated ensemble average and the observed values at each residue position. The results for the ¹H, ¹⁵N and ¹³C^a chemical shift errors are presented in Fig. 2–4.

Fig. 2.

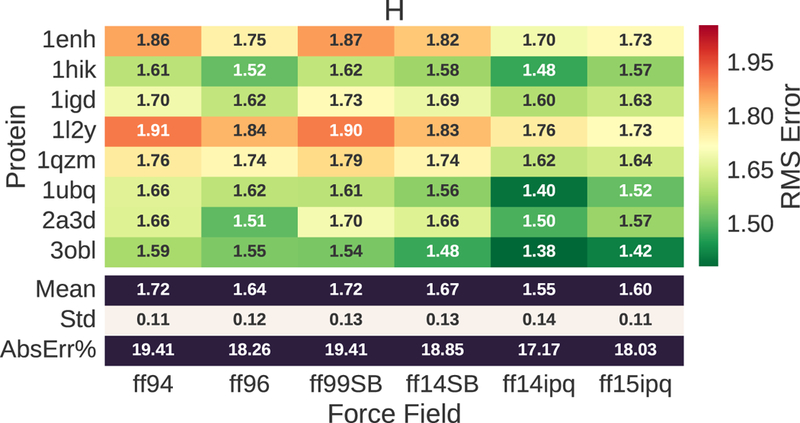
¹H chemical shift error for evaluated proteins and force fields. The RMS error ranges from 1.55 to 1.72. This corresponds to 19–21% of the mean value (8.280) for the observed chemical shifts.

Fig. 4.

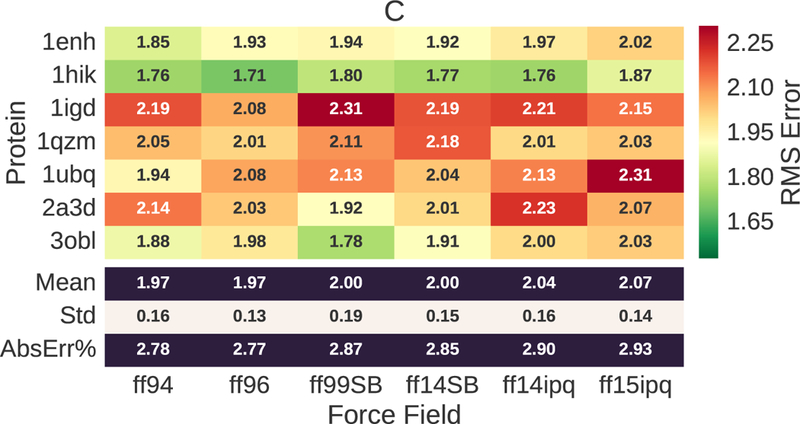
¹³C^a chemical shift error for evaluated proteins and force fields. The RMS error ranges from 1.97–2.07 ppm. This corresponds to ~3% of the mean value (56.652) for observed chemical shifts.

The ¹H chemical shift errors (Fig. 2) show that the ff14ipq force field generally yields a lower RMS error than the other force fields. The error ranges from 1.55 ppm to 1.72 ppm. This represents 19–21% of the mean of the observed values (AbsErr%). The next best performance is provided by ff15ipq which outperforms ff94, ff96, ff99SB and ff14SB. On average, ff15ipq has a greater error than ff14ipq, but it outperforms ff14ipq for the 20-residue synthetic protein 1L2Y. Different proteins have significantly different RMS errors for the same force field. This suggests that the results are dependent on differences in the secondary structure or the chemical environment associated with each protein.

The ¹⁵N chemical shift errors (Fig. 3) show that ff14ipq and ff15ipq outperform the other force fields, with ff15ipq exhibiting lower error. The ¹⁵N chemical shift errors ranges from 5.61 ppm to 6.14 ppm. This error, however, only represents ~4% of the mean for the observed values. In this case, the chemical shift error is close to the noise level resulting from the template matching process and the underlying errors in the experimental observations.¹⁵ This is even more evident for the ¹³C^a chemical shift errors (Fig. 4) which range from 1.97–2.07 ppm. Here, the magnitude of the errors is less than 3% of the mean for the observed values. The ¹³C^a chemical errors exhibit no significant difference between the different force fields.

Fig. 3.

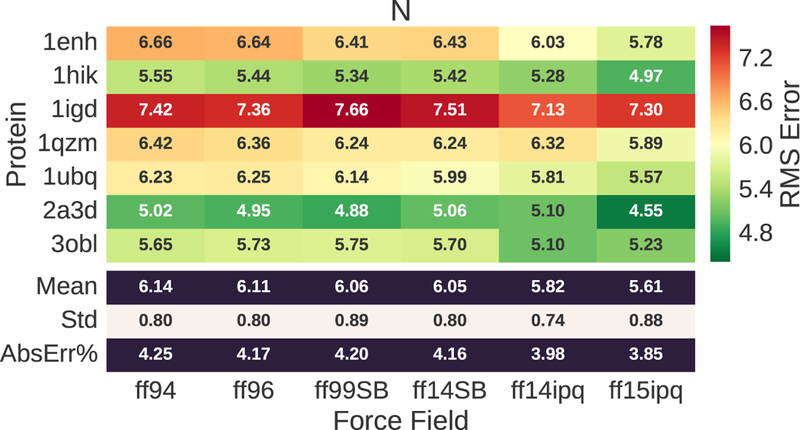
¹⁵N chemical shift error for evaluated proteins and force fields. The RMS error ranges from 5.61–6.14 ppm. This corresponds to ~4% of the mean value (118.646) for observed chemical shifts.

The reference values for calculating chemical shifts were obtained from regression analysis on a large series of representative organic compounds as previously described.¹⁵ The ¹H RMS error is much more significant than the ¹³C^a or ¹⁵N errors when the range of each chemical shift is considered. Using the mean value of the different chemical shifts over the model proteins as denominators, the respective magnitude of these errors is 18.9%, 5.61% and 4.61%. The larger error associated with ¹H chemical shifts may be related to a flawed representation of hydrogen bonds. In the original series, analyses of subsets of conformations centered on the observed ¹H chemical shift values show distances between hydrogen bonding partners that are consistently 0.2–0.3 Å less than chemical shifts from ensemble averages. These ¹H chemical shifts are also sensitive to manipulations of local electrostatic, van der Waals and dielectric parameters. Simulations that strengthen the interactions of local hydrogen bonding pairs result in ¹H chemical shifts that are closer to observed values. Ensemble averages in these simulations show similar shortenings of the distances between hydrogen bonding pairs of 0.2–0.3 Å. Correlation studies using the observed chemical shifts for the original model proteins also demonstrate that the ¹H chemical shift values are not correlated with the ¹³C^a chemical shifts. The dominant factors influencing ¹³C^a chemical shifts are residue type and local ϕ, ψ and χ angles.²³ By contrast, the ¹H chemical shifts are mainly influenced by non-bonded inter-residue contacts. The ¹⁵N chemical shifts are influenced by both sets of factors. The correlation factors for the ¹H-¹³C^a, ¹H-¹⁵N and ¹³C^a-¹⁵N relationships are 0.068, 0.256, and 0.279. The corresponding p-values are 0.12, 3.9e-⁰⁹ and 1.3e-¹⁰.

The ¹H chemical shift errors have a greater utility for comparing force fields than errors in ¹⁵N or ¹³C^a chemical shifts because they are far above the underlying noise level. It is also important to note that the ¹H chemical shift errors are strongly dependent on the non-bonded interactions that occur at each residue site which complements other measurements for comparing force fields involving NMR spectroscopy.^24–30 The ¹³C^a chemical shift error primarily reflects the ϕ, ψ and χ angular relationships in the protein backbone which can be determined easily from scalar J couplings.^23,45 The ¹⁵N chemical shift errors are a function of the angular relationships as well as the surrounding electrostatic environment which made them difficult to interpret. For these reasons, we base all further force field comparisons on the ¹H chemical shifts.

To better visualize force field differences and minimize systematic errors common to all force fields, the ¹H chemical shift errors normalized with respect to the oldest force field, ff94, are shown in Fig. 5. This further emphasizes the reduction in error achieved by ff14ipq and ff15ipq. It is also apparent that the same force field produces different results for different proteins. To explain these differences, it is necessary to break down the RMS results by secondary structure and chemical environment.

Fig. 5.

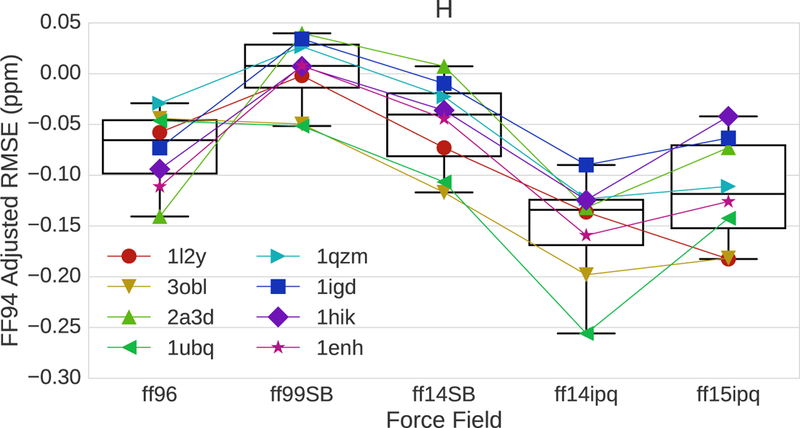
Chemical shift error adjusted on a residue level by subtracting the ff94 error. More negative values indicate a reduction of error.

Influence of Structural Differences on ¹H Chemical Shift Error

The trajectories for the 8 model proteins associated with each force field were divided by residue into subsets containing α-helical, β-sheet or coil secondary structures based on the structure assignment of the initial structure. Fig. 6 shows that the ¹H chemical shift error for α-helices is much larger than the error associated with β-sheets. This is true for all six force fields. Interestingly, the RMS errors associated with coil regions are similar to, and in some cases better than, the errors associated with α-helical regions. The best overall performance belongs to ff14ipq followed by ff15ipq. The difference in RMS error between the β-sheet subset and the other two subsets provides a partial explanation for the differences in chemical shift error seen in Fig. 2 as the best performance belongs to the proteins with the highest β-sheet content (1UBQ, 3OBL). The fact that ¹H Chemical shift error is heavily influenced by secondary structure underlines the importance of comparing force fields on a residue by residue basis.

Fig. 6.

The ¹H chemical shift error for the different force fields broken out by secondary structure. Squared errors are averaged across all residues of a given secondary structure (unlike Fig. 2 where errors are averaged across proteins).

Pairwise Residue by Residue Comparison of Force Field Performance

We compare different force fields on a residue by residue basis using ¹H chemical shift error and NDOME pattern fractions. The accuracy of the atomic interactions simulated by different force fields depends on the type of interaction. Since inaccurate representations lead to chemical shift errors, residue by residue comparisons provide an opportunity to identify interaction-specific shortcomings in force fields. Correlation of the chemical shift error with pattern fractions provides insight into the reasons for chemical shift error differences.

An example of a residue by residue comparison involving the ff94 and ff14ipq force fields is presented in Fig. 7 (top). This example is drawn from the trajectories for ubiquitin (PDB 1UBQ). The positive bars mean that the ff14ipq force field outperforms the ff94 force field at that residue position with respect to ¹H chemical shift error. The negative bars mean that ff94 outperforms ff14ipq. The ff14ipq force field outperforms ff94 at the majority of positions. It is also clear that the magnitude of the error has a large variance. This is consistent with previous observations about the variability of chemical shift error with respect to secondary structure and local chemical environment. At a few positions, ff94 performs better than ff14ipq, but the differences are small. This is expected because ff94 represents the state of the art two decades ago. The regions with the smallest improvements are associated with the presence of helical secondary structure (23–40, 56–59). The pattern fractions for this example are presented in Fig. 7 (bottom). Six of the residue sites improved their error performance by 1.0–1.5 ppm using the ff14ipq force field (18, 39, 53, 55, 69, 72). For the first four members of this series, the improvement was related to an increase in the number of hydrogen bonds between the peptide proton and the acidic oxygen of aspartate or glutamate side chains. This increase for ff14ipq appeared as a negative peak (green). By contrast, ff94 had an increase in hydrogen bonds related to water molecules (blue). Examination of individual frames drawn from these residue sites reveals rotameric changes involving aspartate or glutamate sidechains that are responsible for the changes seen in chemical shift errors. The large changes in the final two sites are related to changes in backbone hydrogen bonding, aromatic interaction and solvent access.

Fig. 7.

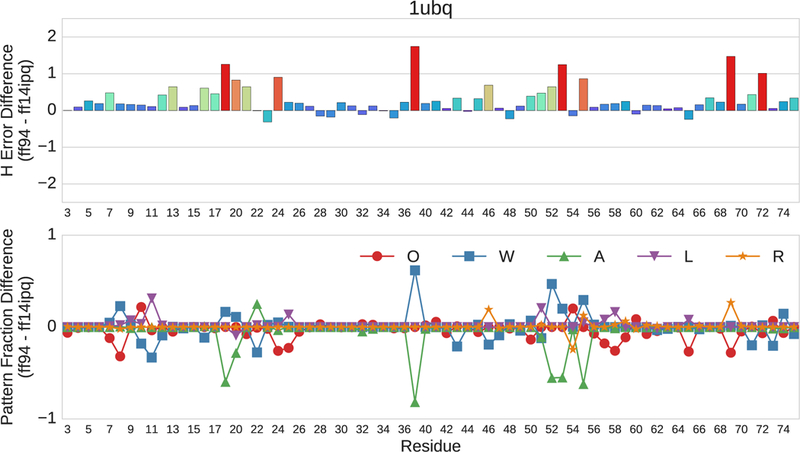
Pairwise residue by residue comparison of the error differences in ¹H chemical shifts between the ff94 and ff14ipq force fields for ubiquitin (1UBQ). The horizontal axis depicts residue position. The upper vertical axis represents ppm. The lower vertical axis represents the fractional difference of each pattern.

The changes seen in the residue by residue pairwise comparison of the ff94 and ff14ipq force fields in Fig. 7 are typical of the changes seen for all 8 model proteins. Pairwise comparisons between ff94 and ff14ipq for all eight proteins are shown in Fig. 8. In the majority of cases, the chemical shift errors recorded for the ff14ipq force field are much less than the errors recorded for ff94. The magnitude of the error also varies from residue to residue similar to the ubiquitin example. However, at isolated positions the ff14ipq force field performs poorly. These sites include position 29 in 1IGD, position 54 in 1QZM and positions 52, 99, 110 and 119 in 3OBL. At most of these sites, examination of pattern fractions shows differences in hydrogen bonding similar to those described for ubiquitin (1UBQ).

Fig. 8.

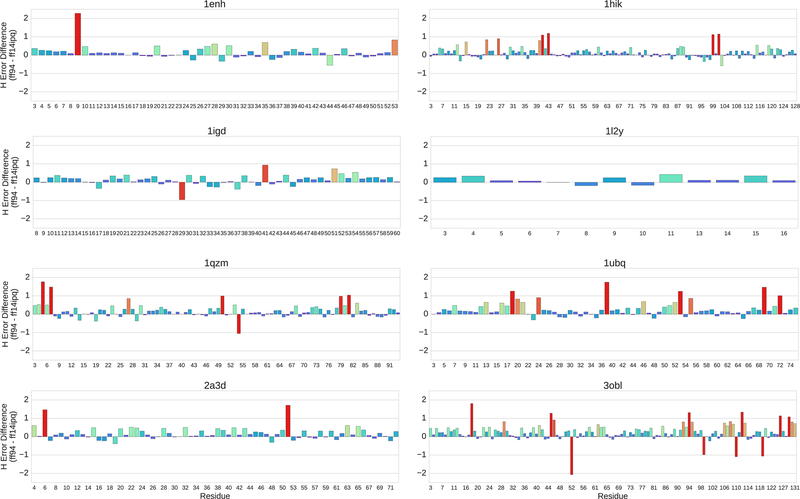
Residue by residue comparison of the ff94 and ff14ipq force fields for all 8 model proteins.

Comparison of force fields that are closely related is more challenging as the error differences are less consistent. This tends to obscure the RMS error differences seen in overall RMS comparisons or the differences seen in comparing error contributions for individual NDOME atoms. The error delta between ff14ipq and ff15ipq at different residues of 3OBL is shown in Fig. 9. At approximately 75% of the residue positions, ff14ipq outperforms ff15ipq with respect to chemical shift error (negative bars). The error differences are small, however, averaging less than 0.50 ppm. At approximately 25% of residue positions, ff15ipq outperforms ff14ipq (positive bars). At four of these sites (52, 95, 99, 119) the error differences are on the order of 0.75–1.50 ppm. Closer examination of these large differences using pattern fractions shows that positions 52, 99 and 119 in ff15ipq experience an increase in solvent access and a decrease in aromatic interaction. Each of these sites is located at the transition zone between a β-sheet and a coil segment. At position 95, the large difference in favor of ff15ipq is related to a switch from the W fraction to the A fraction. There is also a large switch in pattern from the O fraction to the W fraction at position 68 that is only associated with a small change in favor of the ff14ipq force field. Most large changes in chemical shift error are associated with changes in pattern fractions, but large changes in pattern fractions are not necessarily associated with changes in chemical shift error. Similar variances in error differences are seen for all pairwise comparisons of closely related force fields. In most cases, there are instances of positive and negative differences on the order of 1.0–1.5 ppm at selected sites that correspond to marked differences in conformational sampling.

Fig 9.

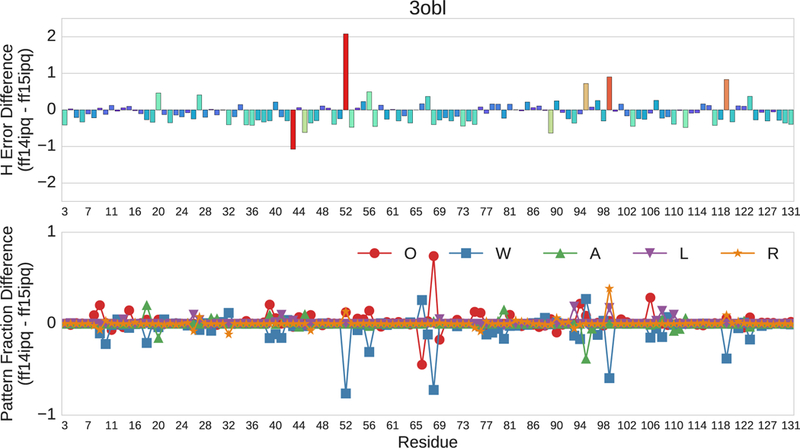
Pairwise residue by residue comparison of the ff14ipq and ff15ipq force fields with respect to ¹H chemical shift error of 3OBL. The horizontal axis depicts residue position. The upper vertical axis represents ppm. The lower vertical axis represents the fractional difference of each pattern.

Drilling Down on Error Differences at Individual Residue Sites

Insights into the reasons for a residue’s chemical shift error can be obtained by correlating changes in chemical shift over time with changes in pattern fractions and inspecting the corresponding structures. We use the term “drilling down” to characterize this process. The results of applying this process to simulation trajectories for 1UBQ are shown in Fig. 10–12. In this example, the ff94 and ff14ipq force fields are compared. Drilling down takes place at the glutamic acid at position 39 where ff14ipq exhibits ~1.5ppm less error than ff94. Fig. 10 shows the change in the ¹H chemical shift over time relative to the overall average (top) and the change in pattern fractions (bottom) over time for ff94. The pattern fraction traces show that the backbone proton alternates between a predominant water interaction (W) and an occasional acidic side chain interaction (A). These transitions are tightly correlated with changes in the chemical shift. In contrast, ff14ipq, shown in Fig. 11, exhibits the opposite interaction preference with almost no sampling of the water interaction and a dominant interaction with the acidic side chain of the residue. Representative conformations for GLU39 are shown in Fig. 12. In ff14ipq the intra-residue hydrogen bond between the backbone proton and the carboxyl group is stable and results in a computed chemical shift that is ~1.5ppm closer to the experimental value than the water interaction exhibited in ff94 simulation.

Fig. 10.

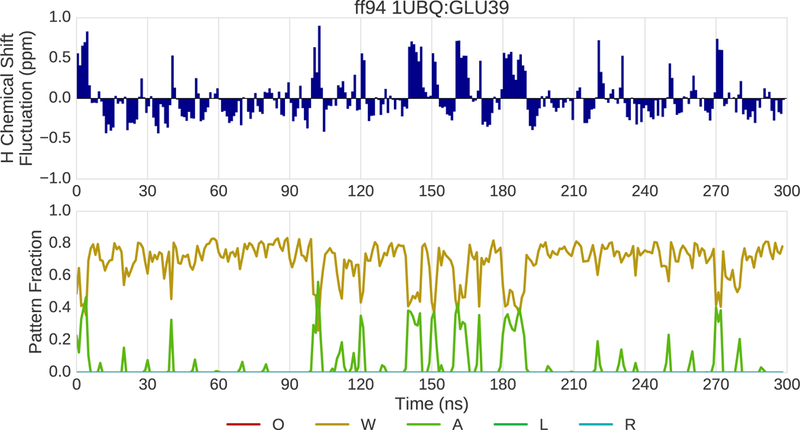
(top) Fluctuation of the ¹H chemical shift around the mean over the course of 300 ns of MD simulation for residue 39 of 1UBQ simulated with the ff94 force field. (bottom) Fraction of various interaction patterns over the course of the simulation.

Fig. 12.

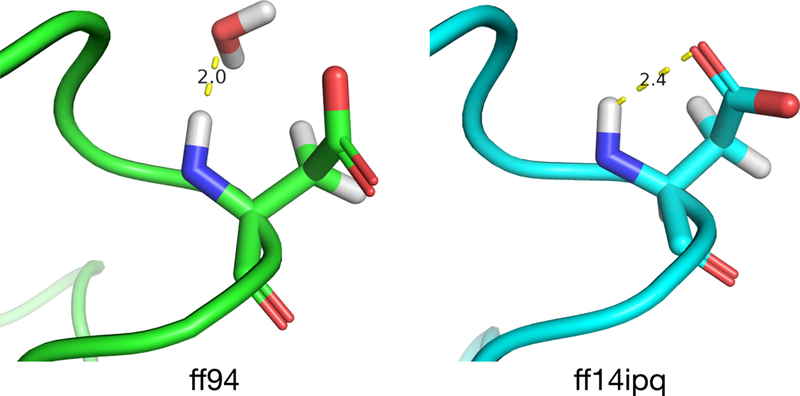
Representative conformations of GLU39 in 1UBQ extracted from ff94 (left) and ff14ipq (right) simulations.

Fig. 11.

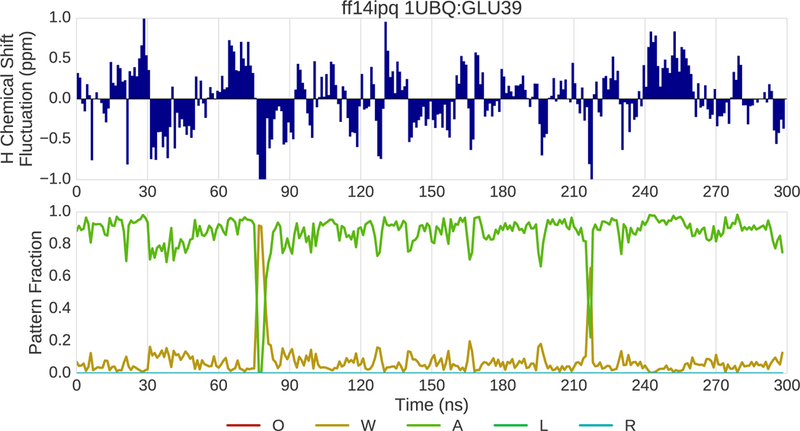
(top) Fluctuation of the ¹H chemical shift around the mean over the course of 300 ns of MD simulation for residue 39 of 1UBQ simulated with the ff14ipq force field. (bottom) Fraction of various interaction patterns over the course of the simulation.

An additional example of drilling down is provided in Fig. 13–15. In this example, the ff14ipq and ff15ipq force fields are compared in simulations of 3OBL. Drilling down takes place at the tyrosine residue at position 52. Fig. 13 shows the change in the ¹H chemical shift (top) and in pattern fractions (bottom) over time for ff14ipq. The pattern trace shows two alternating patterns. The first pattern is characterized by water interactions (W) and the second by O and R fractions indicating the presence of a hydrogen bond with a backbone oxygen and the proximity of an aromatic ring. Not shown cases where no polar or aromatic interactions are present within the distance cutoffs. Changes in chemical shift are correlated with transitions between these two patterns. The fluctuations in the chemical shift are large with a range of nearly 3.5 ppm. Figure 14 shows dramatically different changes for the chemical shift and the pattern fractions for the ff15ipq force field. Interactions with water dominate with a corresponding stability in the chemical shift. Representative conformations of TYR52 are shown in Fig. 15. The ff14ipq simulations maintain a backbone hydrogen bond with GLY56 and the aromatic ring of the tyrosine sometimes intrudes on the NDOME hemisphere. These interactions stabilize a tight turn that excludes water. In contrast, the looser structure associated with the ff15ipq force field favors solvent access. Greater solvent access improves the chemical shift error by almost 1.5ppm at this position. Eight additional examples involving different proteins and different force field comparisons are included in the Supplement.

Fig. 13.

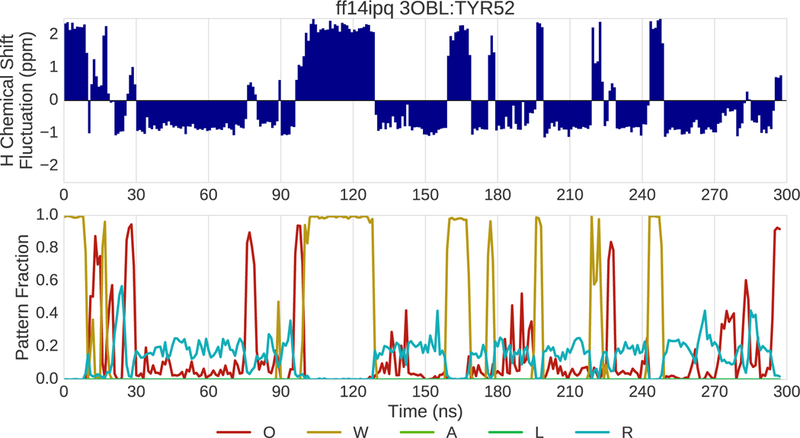
(top) Fluctuation of the ¹H chemical shift around the mean over the course of 300 ns of MD simulation for residue 52 of 3OBL simulated with the ff14ipq force field. (bottom) Fraction of various interaction patterns over the course of the simulation.

Fig. 15.

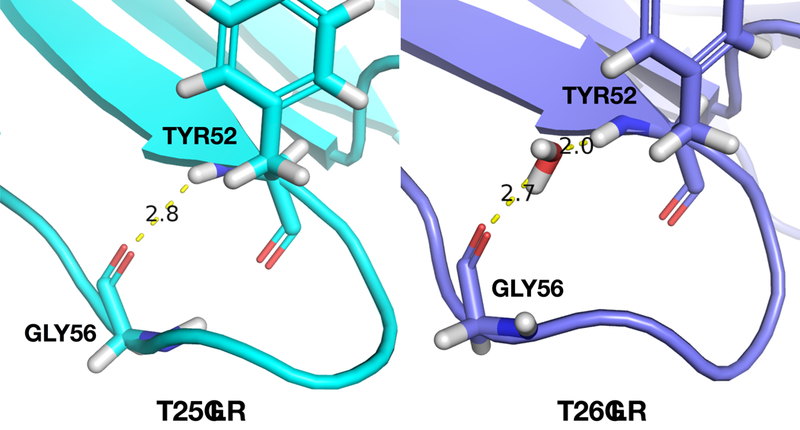
Representative conformations of TYR52 in 3OBL extracted from ff14ipq (left) and ff15ipq (right) simulations.

Fig. 14.

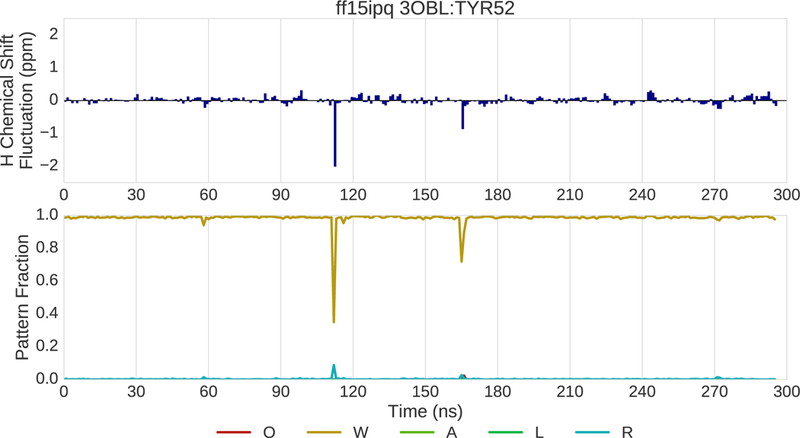
(top) Fluctuation of the ¹H chemical shift around the mean over the course of 300ns of MD simulation for residue 52 of 3OBL simulated with the ff15ipq force field. (bottom) Fraction of various interaction patterns over the course of the simulation.

Conclusions

We show that the error between computed and observed NMR chemical shifts is useful for force field evaluation. If one force field outperforms another, it generates atomic coordinates that are more realistic from a chemical standpoint. Since calculated chemical shifts for a given level of QM theory are only dependent on atomic coordinates, the best performing force field will produce the lowest error. On a global scale, force field differences are reflected in the overall RMS error. The best performing force fields in this study are the ff14ipq and ff15ipq force fields which are based on the implicitly polarized charge method. The differences are best reflected in the ¹H chemical shift errors. Smaller improvements are seen in the ¹⁵N chemical shift errors. The ¹³C^a chemical shift errors by contrast are unchanged. Correlation studies of observed chemical shifts indicate that ¹H chemical shifts are largely independent from ¹³C^a chemical shifts. The ¹H chemical shifts are heavily influenced by the electrostatic and van der Waals interactions associated with local non-bonded interactions, so the improvements seen with ff14ipq and ff15ipq can probably be attributed to the new charge model. The ¹³C^a chemical shift errors, on the other hand, are mainly dependent on localized ϕ, ψ and χ angular relationships. Since the differences in angular parameters between the 6 AMBER force fields are less dramatic, the ¹³C^a chemical shift error differences are small. The ¹⁵N chemical shifts depend on both sets of factors.

We show that the ¹H chemical shift errors associated with the hydrogen bonds in α-helices are significantly larger than the ¹H chemical shift errors in β-sheets for all model proteins. The reason for this is not completely clear. It may relate to the fact that electrostatic interactions are turned off for 1–3 and reduced for 1–4 bonded atoms in α-helices. An examination of the distance between the peptide protein and its carbonyl oxygen partner shows that the bonding distance is smaller on average for β-sheets by 0.5–0.8 Å. Analysis of data contained in the Supplement of a previous paper shows that shorter hydrogen bond distances are associated with lower chemical shift errors.¹⁵ The stronger electrical field associated with the implicitly polarized charge model may be responsible for the improvement in error seen with the ff14ipq and ff15ipq force fields.

We also show the importance of comparing force fields on a residue by residue basis using a set of model proteins. Different force fields show significant differences in chemical shift error at specific residue sites. We show it is possible to examine the template matching pattern at these sites to derive important information about hydrogen bonding patterns, solvent access and aromaticity. It is also possible to examine the time course of these parameters to gain insight into the dynamic differences associated with difference force fields. The use of chemical shift error for evaluating force fields supplements previously used NMR methods for force field comparison.

This approach provides a straight-forward means for comparing force fields on a residue by residue basis. The best way to compare two force fields with this approach starts with the selection of a set of model proteins that contains multiple examples of features of interest. The next step involves conducting a residue by residue comparison of ¹H chemical shift error (and possibly ¹⁵N and ¹³C^a) on trajectories simulated with these force fields. The final step involves drilling down at every residue position that has a difference in chemical shift error. Our source code and template database are freely available under a permissive open source license at https://github.com/dkoes/MD2NMR.

Conclusions

We evaluate the ff94, ff96, ff99SB, ff14SB, ff14ipq and ff15ipq AMBER molecular dynamics force fields using the error between computed and observed NMR chemical shifts. These force fields represent progressive refinements over the course of two decades. Chemical shifts are assigned to the ¹H, ¹⁵N and ¹³C^a backbone using a library of conformers and a template matching approach. The chemical shifts for the library conformers are obtained from quantum chemical calculations. Chemical shift errors are calculated by comparing values obtained from ensemble averages to observed values. These chemical shift errors have a systematic component that results from imperfections in the atomic coordinates generated by the simulation algorithms. These imperfections in turn are a function of the particular force field. If one force field performs better than another, it generates atomic coordinates that are more realistic from a chemical standpoint. When this occurs, the chemical shift error decreases. The use of chemical shift error for evaluating force fields supplements previously used NMR methods for force field comparison. This approach also provides a straight-forward means for comparing force fields on a residue by residue basis.

These studies show that chemical shift error can be used to compare and evaluate force fields. The ¹H chemical shift error associated with the peptide proton is particularly useful. General comparisons between force fields can be made using global RMS error differences. The real utility of the approach, however, lies in the ability to drill down at individual residue sites. This provides information about performance differences at the atomic coordinate level. The best way to compare two force fields with this approach starts with the selection of a set of model proteins that contains multiple examples of features of interest. The next step involves conducting a residue by residue comparison of ¹H chemical shift error on trajectories simulated with these force fields. The final step involves drilling down at every residue position that has a difference in chemical shift error. Our source code and template database are freely available under a permissive open source license at https://github.com/dkoes/MD2NMR.