Constructing Multi-frequency High-Order Functional Connectivity Network for Diagnosis of Mild Cognitive Impairment

Abstract

Human brain functional connectivity (FC) networks, estimated based on resting-state functional magnetic resonance imaging (rs-fMRI), has become a promising tool for imaging-based brain disease diagnosis. Conventional low-order FC network (LON) usually characterizes pairwise temporal correlation of rs-fMRI signals between any pair of brain regions. Meanwhile, high-order FC network (HON) has provided an alternative brain network modeling strategy, characterizing more complex interactions among low-order FC sub-networks that involve multiple brain regions. However, both LON and HON are usually constructed within a fixed and relatively wide frequency band, which may fail in capturing (sensitive) frequency-specific FC changes caused by pathological attacks. To address this issue, we propose a novel “multi-frequency HON construction” method. Specifically, we construct not only multiple frequency-specific HONs (intra-spectrum HONs), but also a series of cross-frequency interaction-based HONs (inter-spectrum HONs) based on the low-order FC sub-networks constructed at different frequency bands. Both types of these HONs, together with the frequency-specific LONs, are used for the complex network analysis-based feature extraction, followed by sparse regression-based feature selection and the classification between mild cognitive impairment (MCI) patients and normal aging subjects using a support vector machine. Compared with the previous methods, our proposed method achieves the best diagnosis accuracy in early diagnosis of Alzheimer’s disease.

1 Introduction

As an irreversible, severe degenerative neurological disease, Alzheimer’s disease (AD) is notorious for progressive perceptive and cognitive deficits. Mild cognitive impairment (MCI) is known as an intermediate stage between normal aging and AD. Although some individuals with MCI remain stable over time, more than half of MCI subjects progress to dementia within ~5 years, at a ratio of about 10–15% per year [1]. Such a high conversion rate could possibly be reduced if receiving proper treatments in this “early AD” stage. Thus, early detection of MCI is significantly important and clinically valuable for delaying AD progression. However, accurate MCI diagnosis based on brain imaging is still challenging, since brain anatomical and functional changes at this stage are considerably subtle [2, 3].

Resting-state functional magnetic resonance imaging (rs-fMRI), which measures the blood oxygenation level-dependent (BOLD) signals as a neurophysiological index of neural activity, has been successfully applied to identify functional pathological biomarkers for MCI diagnosis [4]. Functional connectivity (FC), defined as the temporal correlation of BOLD signals between any pair of brain regions, has been widely applied to explore brain intrinsic functional architectures, with which a whole-brain FC network can be constructed; such connectomics information has contributed considerably to brain disease diagnosis [5, 6]. While promising, the previous mostly-adopted FC network is a typical low-order network (LON), since it usually characterizes the pairwise relationship between brain regions by using the temporal synchronization of BOLD signals. As a result, this type of network can hardly reveal the potentially complex relationship and high-level interactions among multiple brain regions, which may be more sensitive to the subtle MCI-related changes.

One of recent promising technique advances on brain network modeling is called high-order FC network (HON), which quantifies high-level inter-regional interactions by using topographical resemblance information between low-order sub-networks [7, 8]. However, both LON and HON are constructed at a fixed and relatively wide frequency band, which may be insensitive and insufficient to capture the frequency-specific changes caused by early pathological attacks. Actually, it has been suggested that the neuronal oscillations at distinct frequency bands have different biophysiological meanings and may contribute differently to FC [9]. Thus, the frequency-specific FC as well as the cross-frequency interaction analysis have opened up a new effective way for exploring basic neuroscience problems on high-level cognitive functions [10], and could be used for revealing subtle pathological variations in a scenario where the traditional LON is less effective to detect [11].

In this study, we propose a novel brain connectomics-based disease diagnosis frame-work based on frequency-specific HONs from rs-fMRI. Specifically, we construct multiple frequency-specific HONs and multiple cross-frequency interaction-based HONs (based on the LONs calculated at each frequency band). The frequency-specific HONs (namely, intra-spectrum HONs) are constructed based on the topographical similarity between low-order sub-networks for each sub-frequency band, which characterize the intra-spectrum high-level interactions. On the other hand, the cross-frequency interaction-based HONs (namely, inter-spectrum HONs) are constructed by quantifying cross-frequency-band topographical similarity between low-order sub-networks derived from different frequency bands. Since different frequency bands carry different neurobiological functions, such inter-spectrum HONs are able to measure high-level modulations among brain functional systems. To evaluate the effectiveness of these new network modeling metrics, we use both types of these HONs, along with frequency-specific LONs, for classification between MCI patients and normal controls (NC). We conduct extensive comparisons between our framework and other state-of-the-art methods in MCI diagnosis. The results show our framework can significantly outperform comparison methods.

2 Methods

Our proposed framework consists of the following 6 steps. (1) For each subject, the regional mean time series of BOLD signals in each ROI are decomposed into multiple frequency sub-bands. (2) Within each sub-band, one LON is constructed by calculating Pearson’s correlation between each pair of the frequency-specific regional mean time series. (3) An intra-spectrum HON is thus estimated based on the topographical similarity between each pair of the low-order FC sub-networks constructed from the same frequency sub-band. (4) An inter-spectrum HON is further estimated based on the topographical similarity between each pair of the low-order FC sub-networks that are constructed from two different frequency sub-bands. (5) From each of the constructed FC networks, the complex network property-related features are extracted using weighted clustering coefficients for each “node” [12]; among them, the discriminative features are selected using sparse regression-based feature selection. (6) Support vector machine (SVM) with a linear kernel is trained on the selected features for MCI classification. Figure 1 illustrates the main flowchart of our proposed multi-frequency HONs construction approach.

Fig. 1.

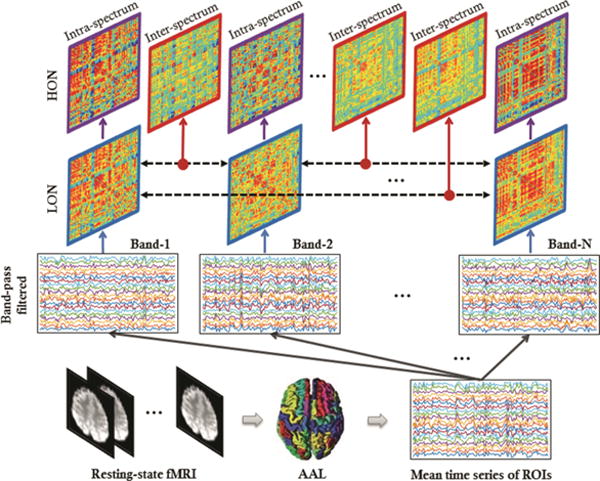
Illustration on how to construct intra-spectrum low-order and high-order FC networks, as well as inter-spectrum high-order FC networks.

2.1 Multi-frequency High-Order FC Networks

Suppose that X ∈ ℝ^P×R denotes regional mean time series with P time points from a total of R regions-of-interest (ROIs), where each mean time series has been band-pass filtered at a relatively wide frequency band. A full-spectrum FC is derived by computing the Pearson’s correlation C_ij between the mean time series of the i-th and the j-th ROIs. By estimating the FC between each possible pair of ROIs, a FC network can be constructed as a symmetric matrix C = [C_ij] ∈ ℝ^R×R. Without loss of generality, we assume each column of X has been de-meaned and also variance-normalized by dividing by the standard deviation. The FC network can thus be equivalently computed by C = X^TX. This defines one LON by simply calculating temporal correlation between mean time series from any pair of brain ROIs. In addition, this LON is a full-spectrum FC network (i.e., 0.015–0.15 Hz in this study), which could be incapable to capture the subtle pathological changes particularly at specific frequency spectrum.

In this study, we address the above issue by the construction of multi-frequency HONs. By fast Fourier transformation, the mean time series X can be decomposed into frequency-band-specific time series X^k ∈ ℝ^P×R (k = 1, 2, 3 and 4) at four different sub-bands: SB₁ = 0.015–0.0488 Hz, SB₂ = 0.0488–0.0825 Hz, SB₃ = 0.0825–0.1163 Hz, SB₄ = 0.1163–0.15 Hz (through equal separation of 0.015–0.15 Hz). Within the k-th sub-band, one LON can be constructed as C^k = (X^k)^TX^k, and thus totally four frequency-specific LONs can be obtained. Different from full-spectrum analysis, these frequency-specific LONs (constructed at their respective sub-frequency bands) are able to reveal those frequency-specific pathological variations.

Alternatively, each frequency-specific LON C^k can also be rewritten as ${\mathbf{C}}^k=\left[{\mathbf{c}}_1^k,{\mathbf{c}}_1^k,\dots ,{\mathbf{c}}_R^k\right]\in {\mathrm{ℝ}}^{R\times R}$, where the i-th column ${\mathbf{c}}_i^k$ (or the i-th row due to the symmetry of C^k) delineates the connectivity pattern between the i-th ROI and all other ROIs and can be regarded as a low-order “sub-network”. Thus, a high-order FC can further be defined as pair-wise topographical similarity between low-order sub-networks. Similar to the frequency-specific LONs, the intra-spectrum HON at the k-th sub-band can be constructed by calculating the high-order FC between every pair of low-order sub-networks as H^k = (C^k)^TC^k. The difference between the frequency-specific LONs and the intra-spectrum HON is that the latter characterizes high-level interactions among brain regions in each frequency sub-band, and totally there are four intra-spectrum HONs.

To comprehensively explore high-level FC, we further construct an inter-spectrum HON which is calculated based on the correlation of low-order sub-networks defined at two different sub-bands. Specifically, the inter-spectrum high-order FC between two different frequency sub-bands, i.e., SB_k and SB_l, is estimated by computing Pearson’s correlation between ${\mathbf{c}}_i^k$ and ${\mathbf{c}}_j^l\left(k,l=1,\dots ,4,k\ne l;i,j=1,\dots ,R,i\ne j\right)$. With a unified form, an inter-spectrum HON between two different sub-bands can be constructed by H^kl = (C^k)^TC^l. Such inter-spectrum HON provides a straightforward way to characterize the high-level cross-frequency modulations among brain regions. For the four sub-frequency bands, we have totally $C_4^2=6$ inter-spectrum HONs.

2.2 Feature Extraction and Classification

For each subject, a total of 14 FC networks are constructed, including (1) four frequency-specific LONs, (2) four intra-spectrum HONs, and (3) six inter-spectrum HONs. But, the feature dimensionality will be rather high, if directly using the connectivity strengths from these 14 networks as features. An effective alternative is using complex network properties, extracted by graph theoretic analysis, as high-level features. To this end, we compute a weighted local clustering coefficient [12, 13] for each node (for reflecting the efficiency of information transferring in a local range) in each network as a feature, and then concatenate all these features to form a long feature vector with the length of 14 × R. Since there could be some redundant features which may affect classification, we conduct feature selection based on sparse regression [14, 15] to derive a subset of features with best discriminability. Finally, the SVM with a linear kernel is trained on the selected feature subset for MCI classification.

3 Experiments

3.1 Data

We use the Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset (http://adni.loni.usc.edu/) for validation of the proposed multi-frequency HONs in MCI classification. Totally, 59 NC subjects and 53 MCI patients (consisting of both early and late MCIs) are selected from ADNI-2 for our experiments. Subjects from both classes are age- and gender-matched, and they were all scanned using 3.0T Philips scanners. The rs-fMRI data are preprocessed using SPM8 software (http://www.fil.ion.ucl.ac.uk/spm/software/spm8/) according to the well-accepted pipeline. Specifically, the first three volumes of each subject are discarded before preprocessing for magnetization equilibrium. Then, rigid-body registration is used to correct head motion. The rs-fMRI data are normalized to Montreal Neurological Institute (MNI) space, and further spatially smoothed by a Gaussian kernel with full-width-at-half-maximum (FWHM) of 6 × 6×6 mm³. Of note, we do not perform scrubbing to the data with large (i.e., >0.5 mm) frame-wise displacement. However, the subjects who have more than 2.5 min rs-fMRI data with large frame-wise displacement are excluded for further analysis. Head motion parameters and also the mean BOLD time series of white matter and cerebrospinal fluid are regressed out to further remove artifacts that may interfere with FC estimation. According to the Automated Anatomical Labeling (AAL) atlas, the rs-fMRI data are parcellated into 116 ROIs. Regional mean rs-fMRI time series of each ROI is band-pass filtered between 0.015 and 0.15 Hz.

3.2 Performance Evaluation

The leave-one-out cross-validation (LOOCV) scheme is adopted to evaluate the diagnosis performance of the proposed method. Specifically, in each fold of LOOCV procedure, an additional inner LOOCV is carried out on the training data to determine the optimal hyper-parameters for both sparse regression (used for feature selection) and SVM (used for classification). The classification performance is measured based on classification accuracy (ACC), area under ROC curve (AUC), sensitivity (SEN), and specificity (SPE). To fairly evaluate the effectiveness of our proposed framework, extensive experimental comparisons are carried out based on the following 9 methods (1) LON^F: Low-order FC networks constructed using full-spectrum BOLD signals; this is the most widely used method. (2) HON^F: High-order FC networks constructed based on the LON^F. (3) LON^F+HON^F: Combination of the full-spectrum low- and high-order FC networks. (4) LON^IA: Intra-spectrum low-order FC networks, which were previously used mainly for group-level analysis. (5) HON^IA: Intra-spectrum high-order FC networks, newly proposed by us. (6) Inter-spectrum high-order FC networks, newly proposed. (7) LON^IA+HON^IA: Combination of the intra-spectrum low- and high-order FC networks. (8) HON^IA+HON^IE: Combination of the intra-spectrum and inter-spectrum high-order FC networks. (9) LON^IA+HON^IA+HON^IE: Combination of intra-spectrum low- and high-order FC networks as well as inter-spectrum high-order FC networks, i.e., our full method.

Table 1 summarizes the classification performance on MCI diagnosis for all of the 9 aforementioned methods. Compared with LONs, HONs achieved better classification performance in either full-spectrum or multi-spectrum FC analysis. From another aspect, multiple-spectrum FC analysis outperformed full-spectrum FC analysis for either LONs or HONs. By exploiting the high-level interactions among brain regions across different frequency spectrums, the HON^IE produced the best performance among all comparison methods using a single type of the FC networks. On the other hand, integrating different types of FC networks further improved the classification results. The combination of LON^IA, HON^IA and HON^IE yielded the best classification performance (i.e., 83.9% in accuracy). This indicates that all the three types of FC networks, characterizing brain functional organizations from different aspects, provide complementary information to each other for MCI diagnosis.

Table 1.

Performance comparison of different methods in MCI classification.

Method	ACC (%)	AUC	SEN (%)	SPE (%)
LONF	61.6	0.648	56.6	66.1
HONF	65.2	0.658	56.6	72.9
LONF + HONF	67.9	0.698	60.4	74.6
LONIA	70.5	0.746	66.0	74.6
HONIA	73.2	0.747	71.7	74.6
HONIE	75.0	0.757	71.7	78.0
LONIA + HONIA	75.9	0.798	73.6	78.0
HONIA + HONIE	79.5	0.833	77.4	81.4
LONIA + HONIA + HONIE	83.9	0.908	79.3	88.1

3.3 Intra-spectrum and Inter-spectrum HONs

Figure 2 presents the group-averaged HON^IA (0.015–0.0488 Hz), HON^IA (0.0488–0.0825 Hz), and HON^IE (across two sub-bands) for NC and MCI groups as an example. The discriminability index [16], calculated as an r²-value for each connection in each type of the FC network, is also shown. Larger r²-value indicates higher separability of the feature distribution patterns between two classes. From these results, we can see that the three HONs identified several different discriminative FC links, indicating that they may serve as complementary features for MCI diagnosis. This also offers an additional evidence for the highest classification performance achieved by the combination of three types of networks.

Fig. 2.

Group-averaged FC networks of HON^IA (0.015–0.0488 Hz), HON^IA (0.0488–0.0825 Hz), and HON^IE (across two sub-bands) for NC and MCI groups, as well as the separability matrices between two groups for each type of the networks.

4 Conclusion

In this paper, we have presented a novel framework based on multi-frequency high-order FC networks for MCI diagnosis. Rather than using the full-spectrum FC, we construct both intra-spectrum HONs and inter-spectrum HONs to capture those previously ignored frequency-dependent high-order FC and cross-frequency modulation-related high-order FC. Both multi-frequency LONs and HONs are jointly used for MCI diagnosis. Experimental results show that different brain networks do provide valuable complementary information for MCI classification, and our full method achieves the best performance. This indicates the promise of the proposed brain network modeling method for brain connectomics-orientated studies.