Disordered linkers in multidomain allosteric proteins: Entropic effect to favor the open state or enhanced local concentration to favor the closed state?

Abstract

There are many multidomain allosteric proteins where an allosteric signal at the allosteric domain modifies the activity of the functional domain. Intrinsically disordered regions (linkers) are widely involved in this kind of regulation process, but the essential role they play therein is not well understood. Here, we investigated the effect of linkers in stabilizing the open or the closed states of multidomain proteins using combined thermodynamic deduction and coarse‐grained molecular dynamics simulations. We revealed that the influence of linker can be fully characterized by an effective local concentration [B]₀. When K _d is smaller than [B]₀, the closed state would be favored; while the open state would be preferred when K _d is larger than [B]₀. We used four protein systems with markedly different domain–domain binding affinity and structural order/disorder as model systems to understand the relationship between [B]₀ and the linker length as well as its flexibility. The linker length is the main practical determinant of [B]₀. [B]₀ of a flexible linker with 40–60 residues was determined to be in a narrow range of 0.2–0.6 mM, while a too short or too long length would dramatically decrease [B]₀. With the revealed [B]₀ range, the introduction of a flexible linker makes the regulation of weakly interacting partners possible.

Short statement

In this study, coarse‐grained molecular dynamics simulations were combined with thermodynamic deduction to reveal the role of disordered linker in multidomain allosteric proteins. It was shown that the influence of linker can be fully characterized by an effective local concentration, which was determined to be as high as 0.2–0.6 mM in four markedly different protein systems, making the regulation of weakly interacting partners possible.

Abbreviations

IDRs

intrinsically disordered regions

Introduction

Protein allostery is common in biological processes, where a signal at “another site” modifies the activity/function of a protein. It was originally defined as cooperation between different chains, and its underlying molecular mechanisms in oligomeric proteins are well known as the Monod–Wyman–Changeux (MWC) model1 and the Koshland–Nemethy–Filmer (KNF) model2 in terms of a transition between two conformations. Later, it was recognized that conformational changes in a monomeric protein also result in allosteric regulation.3, 4, 5 Actually, allosteric communication not only occurs via structural transition, but also comes from changes in protein dynamics.6, 7 Theoretically speaking, all nonfibrous proteins are potentially allosteric when the conformational redistribution is not due to direct binding to the functional sites.8, 9, 10 In this sense, it is not surprising that intrinsically disordered regions (IDRs), which lack ordered structures but still possess important biological functions in cell signaling and gene transcription,11, 12 were found to be widely involved in allosteric regulation.13, 14, 15, 16 Some IDRs show disorder‐to‐order transitions when they bind with their targets, and the allosteric mechanism can be described with the ensemble allostery model (EAM).17 However, if IDRs are not induced to transform into ordered structures, can they regulate the allosteric process and what is the underlying mechanism?

Actually, IDRs exist in many multidomain allosteric proteins without a disorder‐to‐order transition. For example, Polo‐like kinase1 (PLK1), a serine/threonine kinase controlling cell signaling through phosphorylation, contains a long disordered linker of 51 residues between the kinase domain and the polo‐box domain.18, 19, 20 Similarly, PIN1,21, 22 CaN,23 PKA,24 PCK,25 SRC,26, and CDK227 are auto‐inhibited allosteric kinases with different length of inter‐domain linkers. Generally, the basic architecture of most multidomain allosteric proteins is composed of two domains connected by a disordered linker, and the two domains can adopt a closed (bound) or open (unbound) state, where the equilibrium is affected by the allosteric ligand. The closed‐to‐open transition enables the protein function, which has been described as a “Bi‐stable Switch.”10 A general analysis of the stability difference between the open and closed states, and the influence of ligand binding is plotted in Figure 1. The central quantity is the free energy difference between the open and closed states written as

$$\Delta G_{\text{Closed}-\text{Open}}=-\mathit{RT}ln\frac{P_{\text{Open}}}{P_{\text{Closed}}},$$ (1)

where, R is the gas constant, T is the temperature, and P _Closed and P _Open are the percentage of the closed and open states. ΔG _{Closed–Open} > 0 for the auto‐inhibited kinases (left panels in Fig. 1), where the closed state is more stable than the open state without the allosteric ligand (or covalent modifications), and both the substrate and allosteric ligand bind to the open state, but not to the closed state (e.g., the binding pockets are buried in the closed state at the interdomain interface). The binding of an allosteric ligand shifts the equilibrium to the open state, and thus favors substrate binding (activation), resulting in the observed allosteric effect. The disordered linker plays an essential role in ensuring an adequate range of stability for the open/closed state (Supporting Information Fig. S1). Recently, Tompa has proposed a novel entropic model to explain the role of IDRs in allosteric effects, where it was emphasized that a disordered linker contributes an entropic effect to the free energy distribution of a multidomain system, preferring an open state.13 On the other hand, there exists an opposite case (right panels in Fig. 1), where the open state is more stable without an allosteric ligand, and the allosteric ligand binds to the closed state to shift the open/closed equilibrium. For the latter case, the disorder linker is often thought to increase the local concentration of different domains and enhance the binding affinity of domains, preferring a closed state.28, 29, 30 Here it seems confusing whether the added disordered linker prefers the open or closed state. The allosteric effect occurred only in the left and right panels in Figure 1, but not in the weak‐binding pathway.

Figure 1.

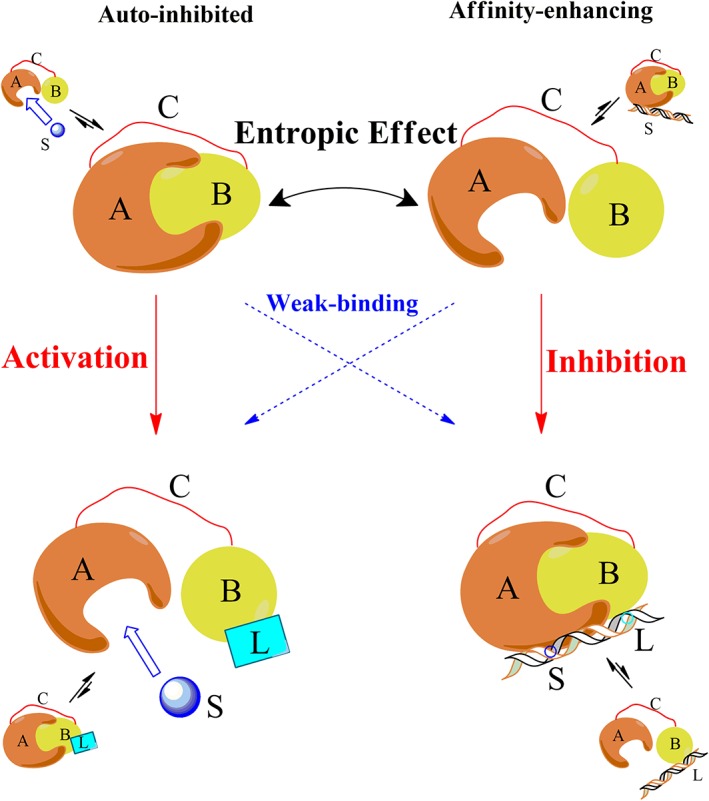
Schematic diagram illustrating the allosteric effects in multidomain proteins with a disordered linker. A protein is composed of two domains (A, the functional domain, and B, the allosteric domain) with mutual attraction, connected by a disordered linker C. The top panels represent the cases without an allosteric ligand, while the bottom panels represent the cases in which an allosteric ligand (L) is added to bind domain B. The left panels represent auto‐inhibited systems such as kinase‐like proteins, where the ensemble without a ligand is dominated by the closed state, so that its active site in domain A is inaccessible to the substrate S, and the addition of allosteric ligand L changes it to the open state. The right panels represent affinity‐enhancing systems such as the DNA‐binding proteins, where the ensemble without a ligand is dominated by the open state. The entropic effect of linker C influences the equilibrium between the open and closed states. Adding L leads to four possible pathways (indicated by red and blue arrows) from the initial ensemble to the final ensemble. The allosteric process only exists in the red pathways.

In this article, we combined coarse‐grained molecular dynamics simulations and thermodynamic deduction to clarify the role of a disordered linker in ΔG _{Closed–Open} of multidomain allosteric proteins. We will show that the role of linker can be fully measured by a characteristic concentration [B]₀, which interplays with the domain–domain binding affinity K _d to enable different allosteric pathways: when [B]₀ > K _d, the closed state is preferred with ΔG _{Closed–Open} > 0 where a mechanism described in the left panels in Figure 1 is applicable; when [B]₀ < K _d, the open state is preferred with ΔG _{Closed–Open} < 0 to enable the pathway in the right panels in Figure 1.

Methods

Coarse‐grained simulation

Coarse‐grained models have been widely used in protein studies,31, 32, 33, 34, 35 especially for large conformation movements.36, 37, 38 We adopt a coarse‐grained native‐centric Gō‐like model,39, 40, 41, 42 to calculate the free energy profile of a protein with two domains connected with a disordered linker. Non‐bonded interactions were defined with different adjustable strengths for intradomain interaction, interdomain interaction,39, 43, 44 and an extra nonspecific interaction within a disordered chain.45 As shown in our previous studies, a disordered protein chain can be treated as an isotactic polymer in an equivalent field‐effect solution both in the theoretical model 46 and molecular dynamics simulations.37 The potential energy of the continuum C _α coordinates of the amino acid residues is written as:

$$\begin{array}{c}{V}_{\text{total}}=V_{\text{streching}}+V_{\text{bending}}+V_{\text{torsion}}+V_{\text{non}-\text{bonded}}^{\text{intra}-\text{domain}}+V_{\text{non}-\text{bonded}}^{\text{inter}-\text{domain}}+V_{\text{non}-\text{bonded}}^{\text{with}-\text{linker}}=\sum _{i,\text{bonds}}{K}_r{\left(r_i-r_i^{\left(0\right)}\right)}^2+\alpha {\sum }_{i,\text{angles}}{K}_{\theta }{\left({\theta }_i-{\theta }_i^{\left(0\right)}\right)}^2+\alpha {\sum }_{i,\text{dihedrals}}\left\{K_{\phi ,1}\left[1-cos\left({\phi }_i-{\phi }_i^{\left(0\right)}\right)\right]+K_{\phi ,3}\left[1-cos3\left({\phi }_i-{\phi }_i^{\left(0\right)}\right)\right]\right\}+\alpha \left\{\sum \begin{array}{c}\text{intra}‐\text{domain}\\ i<j-3\\ \text{native}\end{array}\epsilon \left[5{\left(\frac{r_{\mathit{ij}}^{\left(0\right)}}{r_{\mathit{ij}}}\right)}^{12}-6{\left(\frac{r_{\mathit{ij}}^{\left(0\right)}}{r_{\mathit{ij}}}\right)}^{10}\right]+\sum \begin{array}{c}\text{intra}‐\text{domain}\\ i<j-3\\ \text{non}‐\text{native}\end{array}\epsilon {\left(\frac{r_{\mathrm{rep}}}{r_{\mathit{ij}}}\right)}^{12}\right\}+\beta \left\{\sum \begin{array}{c}\text{inter}‐\text{domain}\\ i<j-3\\ \text{native}\end{array}\epsilon \left[5{\left(\frac{r_{\mathit{ij}}^{\left(0\right)}}{r_{\mathit{ij}}}\right)}^{12}-6{\left(\frac{r_{\mathit{ij}}^{\left(0\right)}}{r_{\mathit{ij}}}\right)}^{10}\right]+\sum \begin{array}{c}\text{inter}‐\text{domain}\\ i<j-3\\ \text{native}\end{array}\epsilon {\left(\frac{r_{\mathrm{rep}}}{r_{\mathit{ij}}}\right)}^{12}\right\}+\left\{\delta {\sum }_{i<j-3}^{\text{with}-\text{linker}}\epsilon exp\left[-\frac{{\left(r_{\mathit{ij}}-\sigma \right)}^2}{2}\right]+\alpha {\sum }_{i<j-3}^{\text{with}-\text{linker}}\epsilon {\left(\frac{r_{\mathrm{wl}}}{r_{\mathit{ij}}}\right)}^{12}+\alpha {\sum }_{i<j-3}^{\text{linker}-\text{domain}}\epsilon {\left(\frac{r_{\mathrm{rep}}}{r_{\mathit{ij}}}\right)}^{12}\right\}\end{array},$$ (2)

where, r _i, θ _i, φ _i, and r _ij are the virtual bond length, bond angle, torsion angle and non‐bonded spatial distance defined by C _α coordinates, respectively; r _i ⁽⁰⁾, θ _i ⁽⁰⁾, φ _i ⁽⁰⁾, and r _ij ⁽⁰⁾ are the corresponding native values taken from the PDB structure. Strength parameters were set as K _r = 100ε, K _θ = 20ε, K _φ,1 = ε, and K _φ,3 = 0.5ε, with ε = 1.0, as described in previous studies.39, 40, 41 The distance parameters were set as r _rep = 4.0 Å, r _wl = 9.0 Å, and σ = 11.2 Å to describe nonspecific interactions (Supporting Information Fig. S2).

Non‐bonded parameters are vital for simulating conformation changes. Intra‐domain interaction parameter α was set to 1.2 as an implicit‐water system as mentioned before.39 Inter‐domain interaction parameter β was fixed in simulations according to the experimental binding constant K _d between domains, or alternatively, simply fixed at β = 1.0. In either case, a reweighting method (as described below) was used to extract the properties of the system under any other β or K _d values.39 The remaining with‐linker interaction parameter δ was the only variable to control linker flexibility, which is affected by the solvent condition.45, 46 A larger β results in tighter domain binding, whereas larger δ results in more collapsed linker conformations and a shorter persistence length (Supporting Information Fig. S3). The flexibility and chain dimension of the linker can be determined by experiments such as small‐angle X‐ray scattering (SAXS)37, 47 and smFRET.48, 49

The closed–open transition equilibrium was simulated in the form of Langevin dynamics with the same integration time‐step and identical parameterization of mass, viscosity, and the random force as specified in our previous studies.36, 39

Accelerating method

The free energy profiles were obtained by the umbrella sampling method which contains bias potentials and histogram techniques.43 We adopt a modified reaction coordinate Q _w to reflect the free energy information.39 Q _w for a given conformation is defined as:

$$Q_{\mathrm{w}}\left(\left\{r_i\right\},\left\{r_j\right\}\right)=Q_{\mathrm{b}}^{\left(\mathrm{N}\right)}{Q}_{\mathrm{b}}\left(\left\{r_i\right\},\left\{r_j\right\}\right)-w\sum _{i\in \mathrm{A},i\in \mathrm{B}}^{\mathrm{NCS}}\left(r_{\mathit{ij}}-r_{\mathit{ij}}^{\left(\mathrm{N}\right)}\right),$$ (3)

where, Q _b ^(N) is the number of inter‐domain contacts between domain A and B in the native structure. r _ij and r _ij ^(N) are the distances between residues i and j in the given conformation and in the PDB, respectively. The constant w was set to 0.02 Å⁻¹. When Q _w is positive, it approximately equals to the native contact number of the given conformation; otherwise, the absolute value of negative Q _w is approximately proportional to the mass center distance between the two domains.

About 24 parallel trajectories were performed under a harmonic bias potential of:

$$V_{\text{bias}}=a_{\text{bias}}{\left(Q_{\mathrm{w}}-Q_{\mathrm{w},\text{bias}}\right)}^2,$$ (4)

where, a _bias was set to 0.02 and Q _w,bias is the harmonic minimum position that varies with different trajectories. For each trajectory, the system is equilibrated in 10⁷ steps and the total step is 10⁸. The convergence of simulation is fast (see Supporting Information Fig. S4). According to the principle of statistical mechanics, we assembled population distributions to give the overall distribution and free energy of the original system (without the bias potential).43 A typical free energy profile has two valleys (see Fig. 2), corresponding to the open and the closed states, respectively.

Figure 2.

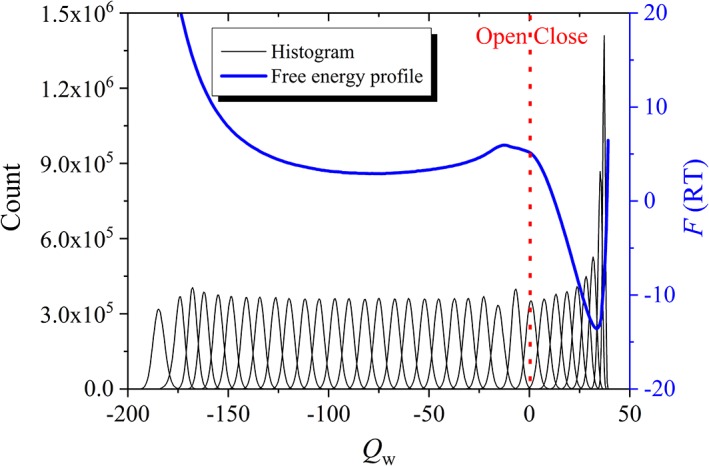
Umbrella sampling method used in this study, taking a linker (N = 60, δ = 0.2) for example: partial histogram results of different bias potentials are shown as black peaks, and the free energy profile is represented in a blue curve as a function of Q _w. Q _w > 0 for the closed state, with its value approximately corresponding to the inter‐domain contact number; Q _w < 0 for the open state, with –Q _w approximately proportional to the domain separation distance. The red dotted line is the boundary between the open and closed states.

After the free energy profile at one inter‐domain interaction strength β value was achieved, the profiles under other β values can be obtained efficiently using a reweighting method based on the principle of statistical mechanics.39 The population distribution is given as:

$$p\left(x,U\right)\propto f\left(x\right)exp\left(-\frac{U}{\mathit{RT}}\right),$$ (5)

where, x is any conformational property we want to calculate (namely Q _b and Q _w here) and U is the conformational energy. Therefore, the population distribution under a different interaction strength β′ value can be calculated as:

$$p\left(x,U\left({\beta }^{\prime }\right)\right)=p\left(x,U\left(\beta \right)\right)exp\left(-\frac{U\left({\beta }^{\prime }\right)-U\left(\beta \right)}{\mathit{RT}}\right).$$ (6)

Protein systems

In order to differentiate the influence of linker from that of domains, we considered four groups of protein pairs from the literature,39 namely, Barnase/Barstar (PDB code: http://bioinformatics.org/firstglance/fgij//fg.htm?mol=1BRS),50 BMP/BMP‐receptor (PDB code: http://bioinformatics.org/firstglance/fgij//fg.htm?mol=2QJ9),51 CheY/CheA (PDB code: http://bioinformatics.org/firstglance/fgij//fg.htm?mol=1A0O),52 S‐protein/S‐peptide (PDB code:http://bioinformatics.org/firstglance/fgij//fg.htm?mol=1D5E),53 with some of their experimental facts listed in Table 1. Two of them are order–order protein pairs, and others are order–disorder protein pairs, considering both strong and weak binding affinity for possible situations. A disordered linker with various lengths and flexibility was added to connect two domains in simulations. For the sake of contrast, the systems without added linker were also simulated, and the simulated K _d was determined as described previously.39

Table 1.

Summary of the Considered Protein Systems ^a

PDB	Domain A (length)	Domain B (length)	Structure	K d (M)	R ee (Å)	Ref.
http://bioinformatics.org/firstglance/fgij//fg.htm?mol=1BRS	Barnase (87)	Barstar (108)	Order–order	1.3E‐14	48	50
http://bioinformatics.org/firstglance/fgij//fg.htm?mol=2QJ9	BMP (93)	BMP‐receptor (103)	Order–disorder	1.0E‐8	30	51
http://bioinformatics.org/firstglance/fgij//fg.htm?mol=1A0O	CheY (70)	CheA (128)	Order–order	3.0E‐7	49	52
http://bioinformatics.org/firstglance/fgij//fg.htm?mol=1D5E	S‐protein (14)	S‐peptide (101)	Order–disorder	6.0E‐12	15	53

^a The data is for domain–domain complexes before a disordered linker is added to connect two domains. The chain length listed in brackets is measured as the number of residues in the PDB file. R _ee is the distance between the C‐terminal residue of domain A and the N‐terminal residue of domain B in the PDB structure, which sets the constraint for the end‐to‐end distance of the linker in the closed state.

Results and Discussion

Determinants of ΔG _{closed–open} in multidomain proteins with a disordered linker

The calculated ΔG _{Closed–Open} under various conditions for http://bioinformatics.org/firstglance/fgij//fg.htm?mol=1BRS is summarized in Figure 3. For usual linkers in a coiled state with δ = 0.2, a linker length of N = 60 rendered the closed state the most stable for the wild‐type case (β = 1.35), while the stabilization effect was weakened by shorter or longer linkers. The variation in the range of ΔG _{Closed–Open} caused by N changing [indicated by black arrows in Fig. 3(a)] between 30 and 120 residues was about 1.2 RT, which is not sensitive enough to change the pathway of the regulation process in the wild‐type case with ΔG _{Closed–Open} ≈ 13 RT. However, a very short linker (N = 19) caused a significant stability loss in the closed state of about 5.0 RT compared with the most stable case of N = 60 [Fig. 3(c)]. In contrast, the variation in β [indicated by blue arrows in Fig. 3(a)] was more efficient in changing the pathway of the regulation process, which can be implemented by mutation or allosteric ligand binding at the domain–domain interface. If an adding allosteric activating ligand (probably together with interface mutation) is able to decrease the binding affinity by 9.0 RT, the system with a rigid linker would switch from the closed state to the open state for a kinase‐like function, as indicated by the blue arrow on the left in Figure 3(a), and a typical pathway‐shift was observed.

Figure 3.

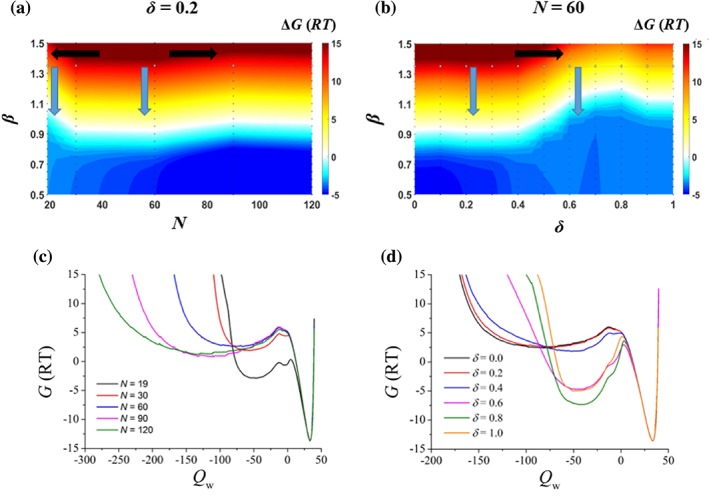
The effect of disordered linkers, taking http://bioinformatics.org/firstglance/fgij//fg.htm?mol=1BRS as an example. (a) The color map of the free energy change, ΔG _{Closed–Open}, as a function of the disordered linker's length, N, and the domain–domain attraction, β, when the linker was in a coiled state (δ = 0.2). The white color represents ΔG _{Closed–Open} = 0 and the boundary of the closed‐open transition. The black arrows show the effect due to the linker's length, N, while the blue arrows show the effect of decreasing β or allosteric binding affinity. β was equal to 1.35 for wild type Barnase/Barstar. (b) ΔG _{Closed–Open} as a function of the linker's flexibility parameter, δ, and the domain–domain attraction, β, while the linker length was fixed at N = 60. The coil‐globule transition of the linker occurred in a rough range of δ ∈ [0.4, 0.6]. (c, d) The free energy profiles as a function of the binding reaction coordinate, Q _w (positive for the bound state and negative for the unbound state with –Q _w approximately proportional to the domain separation distance), at β = 1.35.

A disordered linker mainly plays its entropic effect on allosteric regulation when it is expanded, but only contributes to conformation restriction when it is collapsed. When the linker flexibility parameter, δ, (which is related to the nonspecific attraction and can be modified by a denaturant,46 for instance) increased, a coil‐globule transition of the linker occurred at a rough range of δ ∈ [0.4, 0.6] [Fig. 3(d)]. This lead to a notable decrease in ΔG _{Closed–Open} of over 6 RT [Fig. 3(b) and Supporting Information Fig. S5]. Therefore, the linker flexibility is a sensitive parameter in the regulation process [indicated by black arrows in Fig. 3(b)].

Characterization of the linker's influence: the effective local concentration [B]₀

The contribution of the linker to ΔG _{Closed–Open} can be deduced based on a thermodynamic analysis as follows. We consider the transition equilibriums in both the without‐linker protein pair and the with‐linker system:

$$\begin{array}{c}\mathrm{AB}\stackrel{K_{\mathrm{d}}}{\leftrightarrow }\mathrm{A}+\mathrm{B}\widehat{\mathrm{AB}}\stackrel{{\mathrm{\Delta }G}_{\text{Closed}-\text{open}}}{\leftrightarrow }\mathrm{A}\sim \mathrm{B}\end{array}$$ (7)

Here A, B, AB, A~B, and $\widehat{\mathrm{AB}}$ represents the dissociated protein domain A, the dissociated protein domain B, the protein complex AB, the open state of with‐linker system, and the closed state of with‐linker system, respectively. The equilibriums are determined by

$$K_{\mathrm{d}}=\frac{\left[\mathrm{A}\right]\left[\mathrm{B}\right]}{\left[\mathrm{AB}\right]}$$ (8)

$${\mathrm{\Delta }G}_{\text{Closed}-\text{open}}=-\mathit{RT}ln\frac{\left[\mathrm{A}\sim \mathrm{B}\right]}{\left[\widehat{\mathrm{AB}}\right]}$$ (9)

Here [.] represents the equilibrium concentration of the corresponding species. From Equation (9), it can be seen that the open‐closed ratio of the with‐linker system is independent of the total protein concentration $c_{\text{total}}=\left[\mathrm{A}\sim \mathrm{B}\right]+\left[\widehat{\mathrm{AB}}\right]$. However, for the without‐linker system, the open–closed (unbound/bound) ratio of the domain A or B, that is, [A]/[AB] or [B]/[AB], is influenced by the total protein concentrations [A]_total = [A] + [AB] and [B]_total = [B] + [AB] in the system. To measure the effect of disordered linker in terms of the characteristic concentration of the without‐linker system where the open–closed ratios in two systems are equal, that is, the induced local concentration by the linker, we consider a simplified situation where B is excess over A. Under such a case, [B] ≈ [B]_total and Equation (8) is simplified into a first‐order reaction for A to give

$$\frac{\left[\mathrm{A}\right]}{\left[\mathrm{AB}\right]}=\frac{K_{\mathrm{d}}}{{\left[\mathrm{B}\right]}_{\text{total}}}$$ (10)

Now, the open–closed ratio of domain A is not influenced by its total concentration, [A]_total, being similar to the with‐linker system. It is noted that the ratio is dependent on [B]_total. When the open–closed ratios of the without‐linker and with‐linker systems equal to each other, that is,

$$\frac{\left[\mathrm{A}\right]}{\left[\mathrm{AB}\right]}=\frac{\left[\mathrm{A}\sim \mathrm{B}\right]}{\left[\widehat{\mathrm{AB}}\right]}$$ (11)

[B]_total is solved to be

$${\left[\mathrm{B}\right]}_{\text{total}}={\left[\mathrm{B}\right]}_0\equiv K_{\mathrm{d}}exp\left(\frac{\mathrm{\Delta }{G}_{\text{closed}-\text{open}}}{\mathit{RT}}\right).$$ (12)

Here we use a different symbol [B]₀ to emphasize that it is the [B]_total value at which the open‐closed ratios of the two systems are same while [B]_total is generally regarded as a free variable of the system.

K _d in the without‐linker system is mainly determined by the protein–protein interaction. When a flexible linker is added to connect two domains, the same protein–protein (domain–domain) interaction contributes to ΔG _{Closed–Open} of the with‐linker system together with the influence from the linker. Interestingly, the contribution of the domain–domain interaction to K _d cancels out its contribution to ΔG _{Closed–Open} in Equation (12), resulting in a characteristic concentration [B]₀ nearly independent on the interaction strength. For example, with our reweighting method, when tuning protein–protein interaction strength β, the curves of ΔG _{Closed–Open} and −lnK _d as a function of β experience the same tendency, see Figure 4.

Figure 4.

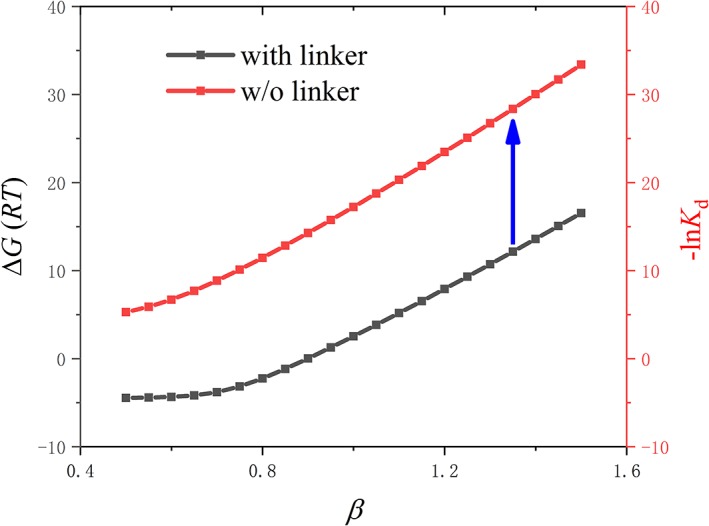
Reweighting curves of ΔG _{Closed–Open} and − lnK _d as a function of β, taking http://bioinformatics.org/firstglance/fgij//fg.htm?mol=1BRS for example. In the without‐linker system, −lnK _d as a function of protein–protein interaction strength β is shown as red curve. In the with‐linker system, ΔG _{Closed–Open} as a function of β is shown as black curve. For the wild type, Barnase/Barstar, β = 1.35. The blue arrow indicates the stable intercept difference between them.

In the applicable range of binding affinity, lnK _d is linear to β:39

$$-ln{K}_{\mathrm{d}}=\mathit{k\beta }+a_1.$$ (13)

For the with‐linker system, a similar linear relationship is also found:

$$\frac{\mathrm{\Delta }{G}_{\text{closed}-\text{open}}}{\mathit{RT}}=\mathit{k\beta }+a_2.$$ (14)

The kβ term in Equations (13) and (14) comes from the domain–domain interaction energy.39 Then [B]₀ defined in Equation (12) can be expressed as:

$${\left[B\right]}_0=exp\left(a_2-a_1\right),$$ (15)

which is independent on β.

Therefore, [B]₀ can be used to quantitatively measure the effect of the linker in connecting two domains, which can be readily determined from simulated results. [B]₀ interplays with the domain–domain interaction (characterized by the binding affinity K _d of the without‐linker system) to determine ΔG _{Closed–Open} of the with‐linker system and the allosteric pathways: when K _d < [B]₀, ΔG _{Closed–Open} > 0 and the closed state is preferred, so an auto‐inhibition mechanism described in the left panels in Figure 1 is applicable for allosteric regulation; when K _d > [B]₀, ΔG _{Closed–Open} < 0 and the open state is preferred to enable an affinity‐enhancing mechanism for allosteric regulation in the right panels in Figure 1.

An alternative way to consider the local concentration

There is an alternative way to analyze the local concentration caused by adding the linker (Fig. 5). The introduction of a linker had little influence on the bound (closed) state, so the basins at Q _w > 0 in the free energy profile could be aligned to be well overlapped with that without a linker [Fig. 5(a)]. However, it had a marked effect on the unbound (open) state with Q _w < 0 [Fig. 5(a)]: with the linker, the two domains were restricted to be near each other; without the linker, the two domains could separate at any distance, and the free energy decreases with the distance because of the increased space volume. The difference is demonstrated more clearly when we plotted the population distribution of the unbound (open) state as a function of the mass‐center distance between two domains (ΔR) [Fig. 5(b)]. Based on the P(ΔR) curves for the systems with and without a linker, a characteristic distances (R ₀), is defined as the distance where the cumulative population ${\int }_0^{R_0}P\left(\mathrm{\Delta }R\right)\mathrm{d\Delta }R$ of the system with and without a linker is equal [Fig. 5(b)]. In other words, if one protein A molecule and one protein B molecule were put into a spherical volume with a radius of R ₀ and A (or B) was fixed at the sphere center, the resulting unbound–bound ratio would be equal to the open–closed ratio when a linker is added. The determined vale of R ₀ does not depend on the domain–domain attraction strength since the relative population between the unbound state and the open is note affected by the potential‐well depth of the bound and the closed states. R ₀ can be further converted into the corresponding characteristic concentration as

$$c_{R_0}=\frac{1}{N_{\mathrm{A}}*\frac{4}{3}\pi R_0^3},$$ (16)

where N _A is Avogadro's number.

Figure 5.

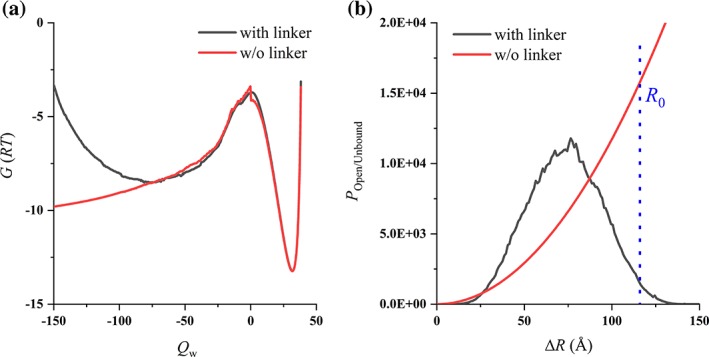
An alternative way to analyze the local concentration, taking http://bioinformatics.org/firstglance/fgij//fg.htm?mol=1BRS for example. (a) The free energy profiles: with (black) and without (red) the linker. (b) The population distribution as a function of the mass‐center distance between two domains (ΔR): the open (black) and unbound (red) state. β = 1.0 was used in simulation.

Numerical results on local concentration

To measure the effect of disordered linker, the characteristic local concentration [B]₀ and c _R0 were determined from simulations for all four protein systems listed in Table 1, and the results were shown in Figure 6 and Table 2 when the linker length is N = 60. Although defined in different ways, [B]₀ and c _R0 show no significant difference. The four protein systems are markedly different in structure order/disorder, binding affinity, surface/interface and the end‐to‐end distance R _ee in the complex, but the resulting characteristic local concentrations lie in a narrow range of 0.2–0.6 mM. It indicated that the introduction of a disordered linker would fix the effective concentration at an order of magnitude of mM. As a comparison, the values of [B]₀ evaluated from the experimental29, 54, 55, 56, 57 K _d and ΔG _{Closed–Open} were among 0.2–5.3 mM, for different linker length among 8–44 residues. When the linker‐domain excluded volume interaction is increased, [B]₀ would decreases slightly due to the enhanced entropic effect (Supporting Information Fig. S6).

Figure 6.

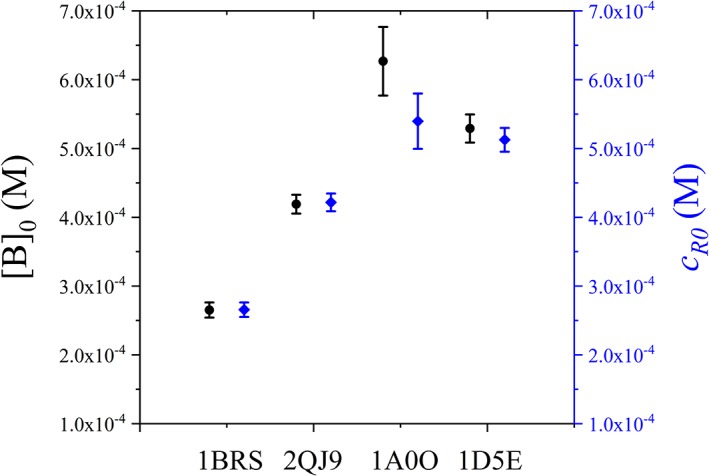
Characteristic concentration of disordered linker (N = 60 with δ = 0.2) in four protein systems. The effective local concentration [B]₀ and c _R0 were shown as black circles and blue diamonds, respectively.

Table 2.

Summary of Free Energy and Effective Concentration Results ^a

PDB	β	K d (M)	ΔG (RT)	[B]0 (M)	c R0 (M)
http://bioinformatics.org/firstglance/fgij//fg.htm?mol=1BRS	1.0	2.10E‐5 ± 8.69E‐7	2.54	2.65E‐4 ± 1.10E‐5	2.66E‐4 ± 1.06E‐5
http://bioinformatics.org/firstglance/fgij//fg.htm?mol=2QJ9	1.0	4.11E‐8 ± 1.34E‐9	9.23	4.19E‐4 ± 1.37E‐5	4.22E‐4 ± 1.29E‐5
http://bioinformatics.org/firstglance/fgij//fg.htm?mol=1A0O	1.0	6.71E‐3 ± 5.34E‐4	−2.37	5.09E‐3 ± 2.79E‐4	5.40E‐4 ± 4.02E‐5
http://bioinformatics.org/firstglance/fgij//fg.htm?mol=1D5E	1.0	8.10E‐4 ± 3.13E‐5	−0.43	5.29E‐4 ± 2.04E‐5	5.13E‐4 ± 1.73E‐5

^a The data were derived from simulation of disordered linker (N = 60 with δ = 0.2) in four protein systems. The domain–domain binding affinity parameter β was set to 1.0 to align different protein systems. K _d and ΔG were calculated by free energy profiles as Figure 2. [B]₀ and c _R0 was calculated as Figures 4 and 5, and plotted in Figure 6.

This provides a clue in understanding the benefit of disordered linker in allosteric regulation. If a pair of protein domains have a low expression level, for example 10 nM, the binding probability is very small if K _d = 10 μM. Introducing a flexible linker will significantly enhance the local concentration and greatly promote the binding probability, making the regulation of weakly interacting possible.

The largest [B]₀ difference in Figure 6 occurs between http://bioinformatics.org/firstglance/fgij//fg.htm?mol=1BRS (0.265 mM) and 1A0O (0.509 mM), giving a ratio of 2.4, although their R _ee is almost identical (48 Å vs. 49 Å). It suggested that the end‐to‐end distance in native structure was not so important as the protein scaffold. To investigate the influence of other factors, [B]₀ of http://bioinformatics.org/firstglance/fgij//fg.htm?mol=1BRS was determined under various linker length (N) and flexibility (δ), see Figure 7. Remarkably, a coil‐to‐globule transition of a N = 60 disordered linker brought 3 order of magnitude of decreasing to [B]₀, from mM to μM, see Figure 7(a). Highly collapsed conformations of linker severely prevented the domains from binding, resulting in the weakening of local concentration increasing effect. In realistic conditions, such a coil‐to‐globule transition is difficult to achieve.46 On the other hand, the linker length is a more realistic parameter to control, which caused 2 order of magnitude to the variation of [B]₀ in our simulations, see Figure 7(b). When the linker is too short, elastic stress is induced in the closed state to reduce its stability and to decrease the effective [B]₀. When the linker is too long, the open state has much more allowed conformations, leading to the decreasing of [B]₀. For example, when N increases from 60 to 120, [B]₀ decreases with almost one order of magnitude. Therefore, [B]₀ is mainly determined by the linker while little affected by the domains.

Figure 7.

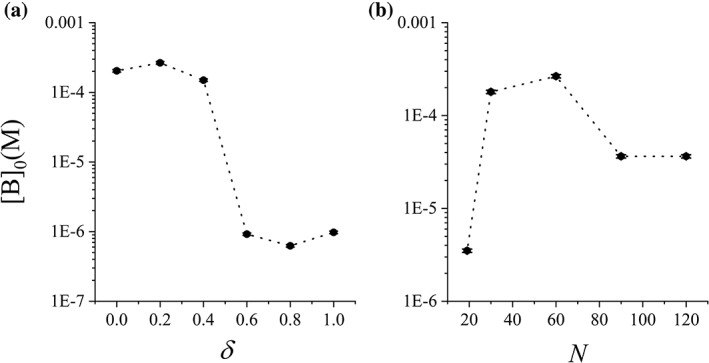
Characteristic concentration [B]₀ of disordered linker in http://bioinformatics.org/firstglance/fgij//fg.htm?mol=1BRS as a function of (a) the linker flexibility δ and (b) the linker length N. N = 60 in (a) and δ = 0.2 in (B).

[B]₀ is a bridge in relating K _d of the without‐linker protein system to ΔG _{Closed–Open} of the with‐linker system, which would be useful in experimental study. Experimentally, usually only K _d or ΔG _{Closed–Open} was measured, while it is very rare to obtain both K _d and ΔG _{Closed–Open} for the same domain pairs probably due to experimental obstacle. For example, the most favorable ΔG _{Closed–Open} range to be directly measured is around ΔG _{Closed–Open} = 0, but this would correspond to K _d at an order of magnitude near mM, which is difficult to be measured in many usual techniques. With the approximate value [B]₀ from simulations, it is thus straightforward to measure ΔG _{Closed–Open} and convert it into K _d based on Equation (15), or vice versa. It would be helpful in evaluate the potential of engineering an existing protein system by removing or adding the connecting disorder linker.

Comment on possible improvement on the model

The open/close equilibrium of multidomain proteins is determined by the competition between the entropic stabilization of open state (destabilization of closed state) and the enhancement of local effective concentration to favor the closed state. In our study, we adopted a Gō‐like coarse‐grained model considering only C_α coordinates, which is both concise and computationally efficient. This may underestimate the entropic contribution and is worthy of further study, for example, using atomic models. Furthermore, to establish a conceptual model, we did not consider specific intralinker or linker–domain interaction which involved sequence specificity. In realistic situations, the physical properties of disordered linker were not limited to the chain length and flexibility. Many other specific properties are also important. For example, positively and negatively charge residues of disordered linkers were shown to be important to the conformation distributions.58, 59 Asphericity was also used as another important factor of IDRs.60 Moreover, phosphorylation sites, polar or hydrophobic residues, even directed‐proline residues could affect the dimension of IDRs.61 The attracting interaction between domains and linker may stabilize the closed state and increase [B]₀, while the enhanced excluded‐volume (repulsive) interaction between domains and linker would decrease [B]₀. The incorporation of these effects is straightforward by adopting other more delicate coarse‐grained models, for example, the modified Gō‐like model with sequence‐dependent hydrophobic interaction,45, 62 the SIRAH model with incorporated ion and coulomb interaction,63, 64 or Miyazawa–Jernigan‐type contact potentials.65, 66

Conclusion

In summary, we investigated the role of a disordered linker in stabilizing the open or the closed states of multidomain allosteric proteins. Coarse‐grained molecular dynamics simulation was performed to determine the free energy profile of the system under various conditions. Deduction based on a thermodynamic analysis was conducted to reveal that the influence of linker can be fully characterized by an effective local concentration [B]₀. When K _d < [B]₀, the closed state would be favored to enable an auto‐inhibition mechanism for allosteric regulation; while the open state would be preferred to enable an affinity‐enhancing mechanism for allosteric regulation when K _d > [B]₀. We used four protein systems with markedly different domain–domain binding affinity and structural order/disorder as model systems to investigate the relationship between [B]₀ and its various determinants. [B]₀ is nearly independent of K _d, while the linker length N is its main practical determinant. [B]₀ of a linker with N = 40–60 was determined to be in a narrow range of 0.2–0.6 mM, while a too short or too long length would dramatically decrease [B]₀. Overall, the introduction of a flexible linker significantly increases the possibility of the closed state, making the regulation of weakly interacting partners possible.

Supporting information

Supporting Information.