 Energy transfer between FRET pairs is employed herein to reveal novel intermolecular interactions between self-assembled macrocycles, built via Watson–Crick pairing between complementary dinucleosides, and mononucleoside competitors.
Energy transfer between FRET pairs is employed herein to reveal novel intermolecular interactions between self-assembled macrocycles, built via Watson–Crick pairing between complementary dinucleosides, and mononucleoside competitors.
Abstract
As molecular self-assembled systems increase in complexity, due to a large number of participating entities and/or the establishment of multiple competing equilibria, their full understanding becomes likewise more complicated, and the use of diverse analytical techniques that can afford complementary information is required. We demonstrate in this work that resonance excitation energy transfer phenomena, measured by fluorescence spectroscopy in combination with other optical spectroscopies, can be a valuable tool to obtain supplementary thermodynamic data about complex supramolecular landscapes that other methods fail to provide. In particular, noncovalent macrocyclization processes of lipophilic dinucleosides are studied here by setting up a competition between intra- and intermolecular association processes of Watson–Crick H-bonding pairs. Multiwavelength analysis of the monomer emission changes allowed us to determine cyclotetramerization constants and to quantify chelate cooperativity, which was confirmed to be substantially larger for the G-C than for the A-U pair. Furthermore, when bithiophene-BODIPY donor–acceptor energy transfer probes are employed in these competition experiments, fluorescence and circular dichroism spectroscopy measurements in different regions of the visible spectrum additionally reveal intermolecular interactions occurring simultaneously at both sides of the macrocyclization reaction: the cyclic product, acting as a host for the competitor, and the monomer reactant, ultimately leading to macrocycle denaturation.
Introduction
Modern analytical chemistry offers a wide plethora of tools and techniques to study the structure and function of self-assembled systems and to measure diverse thermodynamic and kinetic parameters controlling their equilibria with other bound and unbound species.1 However, as the system's complexity increases, the combination of multiple techniques that can provide complementary information on different concurrently competing equilibria is often required. Among them, fluorescence emission spectroscopy stands out as a very convenient technique that is non-invasive, provides high sensitivity and a short timescale, employs low analyte concentrations, and can be additionally implemented in microscopy and imaging. Fluorescence spectroscopy also allows for real-time monitoring of energy transfer events between photoexcited units. In this context, Förster resonance energy transfer (FRET) is a widely employed phenomenon in which the energy of a photoexcited donor fluorophore (d) is transferred to an energy-accepting unit (a) through long-range dipole–dipole interactions.2 Such excitation transference depends on the relative orientation and distance between the donor and the acceptor, as well as on the spectral overlap of donor emission and acceptor absorption.
The study of FRET phenomena is thus considered as a potent tool to detect and monitor molecular interactions and dynamic changes.3 The benefits of FRET have been exploited in polymer chemistry, as a method for the determination of polymer morphology,3a,4 and in chemical biology, for the analysis of protein/DNA conformational changes5 and for monitoring enzyme activity and intracellular molecular dynamics.6 The area of supramolecular chemistry is also increasingly employing energy transfer events between donors and acceptors to unveil the thermodynamic and kinetic aspects of self-assembled synthetic systems. The groups of Rebek7 and Diederich8 were pioneers in the use of FRET to study the exchange kinetics and conformational switching events in supramolecular complexes. Supramolecular FRET probes have also been useful for investigating diverse characteristics of discrete self-assembled systems, such as isomer distribution of dimeric cyclic peptides;9 guest inclusion in G-quadruplexes;10 protein interactions with synthetic supramolecular elements;11 or the dynamics in rotaxane,12 foldaxane13 and metal–ligand assemblies.14 On the other hand, FRET phenomena are also helpful in polymeric noncovalent systems, for instance, to study the structure, thermodynamic stability, and cargo release mechanisms of vesicles and nanospheres;15 to construct light-harvesting photosynthetic mimics;10b,16 or to monitor monomer rearrangements or self-sorting events in supramolecular polymers.17
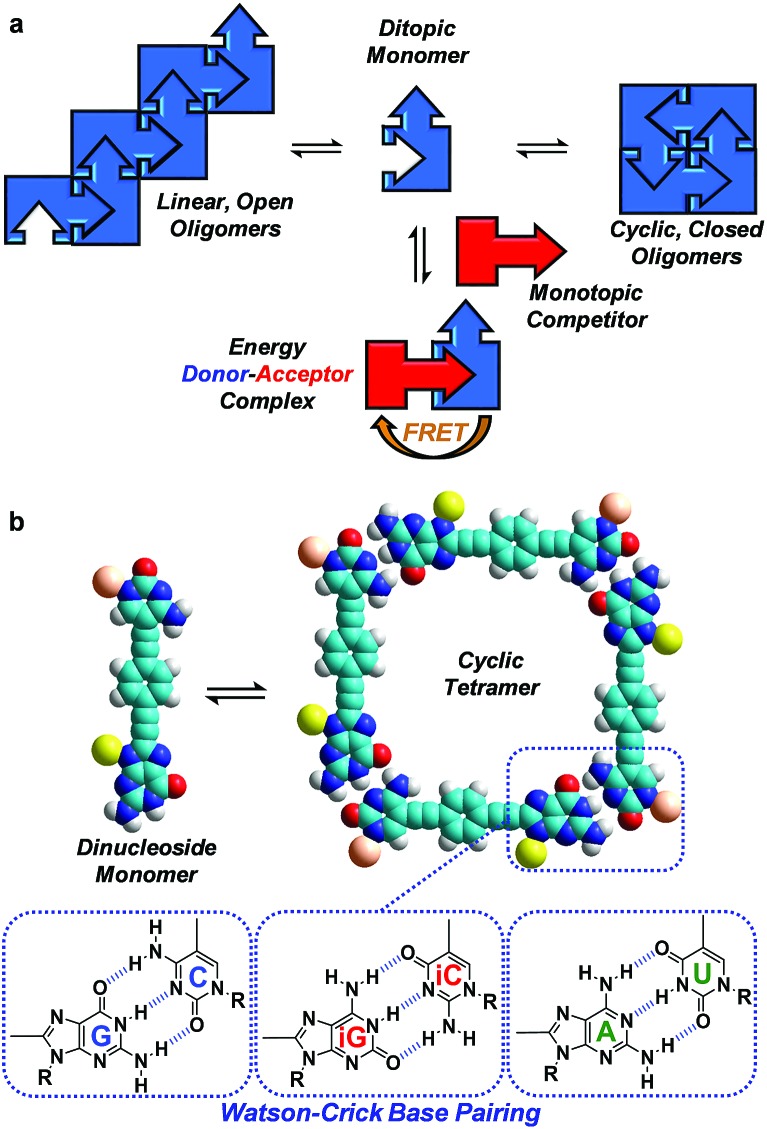
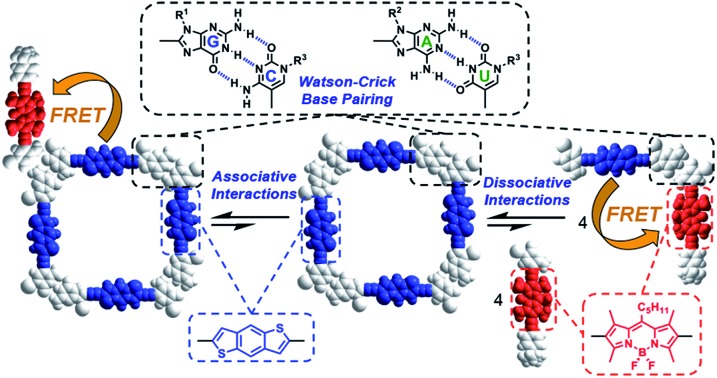
Here, we evaluate FRET processes as a tool to obtain thermodynamic information on noncovalent ring-chain equilibrium processes and, more concretely, on the case where the formation of ring assemblies is strongly favoured. When a molecule is endowed with (at least) two complementary binding sites, noncovalent association in solution may lead to competing equilibria between linear oligomers and cyclic assemblies (Fig. 1a).18 A key parameter arises in the analysis of such systems: the effective molarity (EM), which affords an estimate of the propensity of the system to cyclize by comparing intra- and intermolecular association constants for a given binding event (EM = Kintra/Kinter), and therefore quantifies the chelate effect.19 If the EM values are high and the overall concentration is maintained within certain limits, ring-chain equilibria may shift to the formation of a particular closed species, which is commonly the smallest, non-strained macrocycle. This is actually the basic principle used by supramolecular chemists to produce a wide variety of well-defined discrete architectures that often mimic those found in the natural world: helicates, ladders, grids, macrocycles, cubes, prisms, capsules, etc.
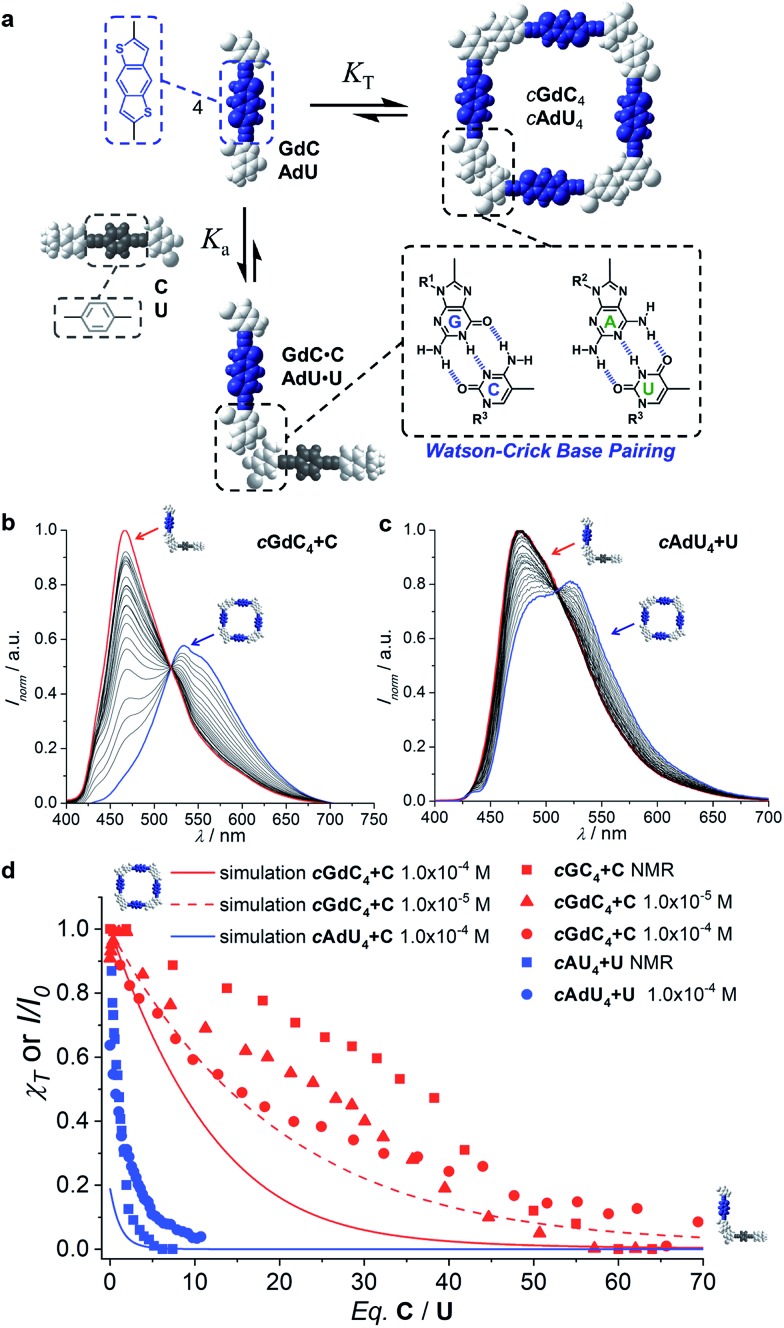
Fig. 1. (a) Scheme showing a competition between a ditopic FRET-donor molecule (in blue), able to establish an equilibrium between open linear oligomers and closed cyclic assemblies by complementary self-association, and a monotopic FRET-acceptor competitor (in red) equipped with the same binding motif. (b) Cyclic tetramer self-assembly through Watson–Crick G-C, iG-iC or A-U H-bonding interactions between dinucleoside monomers.
The determination of self-association equilibrium constants and the dissection of EM values from the overall free energy of the system are, however, not always simple practices. The approach we propose here is to set up a competition between a ditopic FRET-donor molecule, able to form closed cyclic assemblies by complementary self-association, and a mono-topic FRET-acceptor competitor equipped with the same binding motif (Fig. 1a). Upon addition of increasing amounts of the competitor, the closed ensemble will progressively dissociate because this new species competes for the binding sites at the constituent molecules. Actually, in these experiments the intramolecular and intermolecular binding events are made to compete and constitute a very appropriate way to detach the intrinsic contribution of chelate cooperativity from the overall free energy of the system.
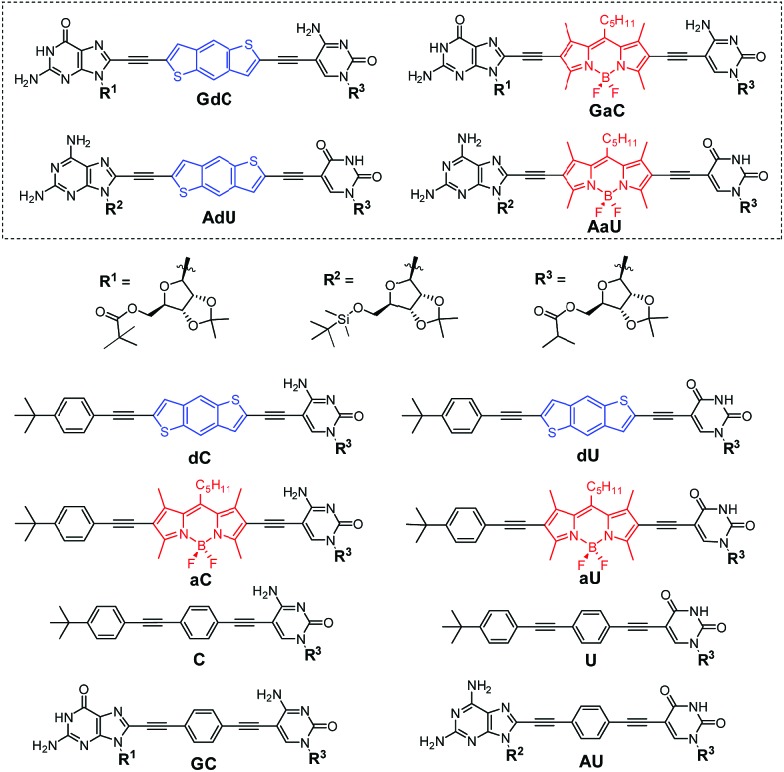
Our supramolecular case study involves dinucleoside monomers that self-assemble into H-bonded cyclic tetramers (Fig. 1b),20 as recently demonstrated by us with molecules that comprised a p-diethynylbenzene central block substituted at the edges with the following lipophilic complementary nucleobases:21 guanosine (G)-cytidine (C), 2-aminoadenosine (A)-uridine (U) or isoguanosine (iG)-isocytosine (iC).22 The cyclotetramerization constants (KT) were determined by diverse NMR and optical spectroscopy methods in different solvents and, from them, EMs were calculated and found to range between 102 and 103 M for the G-C (GC, Fig. 2) and iG-iC cyclic tetramers, a record value for this kind of cycle,19e and between 10–2 and 10–1 M for the A-U (AU, Fig. 2) macrocycle. This significant difference was ascribed to the unsymmetric nature of the ADD-DAA H-bonding pattern in the G-C and iG-iC monomers, as opposed to the symmetric ADA-DAD pattern of the A-U monomer, which largely contributes to the preorganization of the system toward cyclization.21c
Fig. 2. Structure of mononucleosides C, U, dC, dU, aC and aU, dinucleosides GC and AU, and novel dye-labelled dinucleosides GdC, AdU, GaC and AaU.
In this work, with the aim of using FRET as an instrument to report intermolecular association, we designed and prepared a novel family of dinucleosides equipped with complementary G-C or A-U bases (GdC, AdU, GaC and AaU; Fig. 2). The ribose units were substituted with bulky lipophilic groups so as to increase solubility and prevent stacking interactions. As an energy donor (d), a benzo[1,2-b:4,5-b′]dithiophene unit, widely used in organic photovoltaics,23 was employed. As an energy acceptor (a), a BODIPY24 moiety was installed as a central block. This donor–acceptor pair displays absorption and emission maxima that are separated by about 200 nm and the donor emission partially overlaps with acceptor absorption in the 450–550 nm region, which is a requirement for achieving high FRET efficiencies. Since optical spectroscopy measurements require low concentrations, an apolar aromatic solvent (toluene) was selected to maintain high association constants between nucleobases.25 The most important photophysical parameters of these dye-conjugated molecules measured in toluene can be found in the ESI† accompanying this paper.
With this set of molecular probes, we demonstrate in this work that the combination of fluorescence spectroscopy and energy transfer phenomena, together with complementary tools such as circular dichroism (CD), can be a highly valuable strategy to extract supplementary thermodynamic information on complex supramolecular systems in which several equilibria participate concurrently. Here, the use of fluorescence spectroscopy not only allowed us to quantify chelate cooperativity, but also and for the first time, to discern and analyse simultaneously intermolecular interactions between FRET pairs occurring at the product (cyclic tetramer) and reactant (monomer) sides of a noncovalent reaction.
Results and discussion
Synthesis of dinucleoside monomers GdC, AdU, GaC and AaU
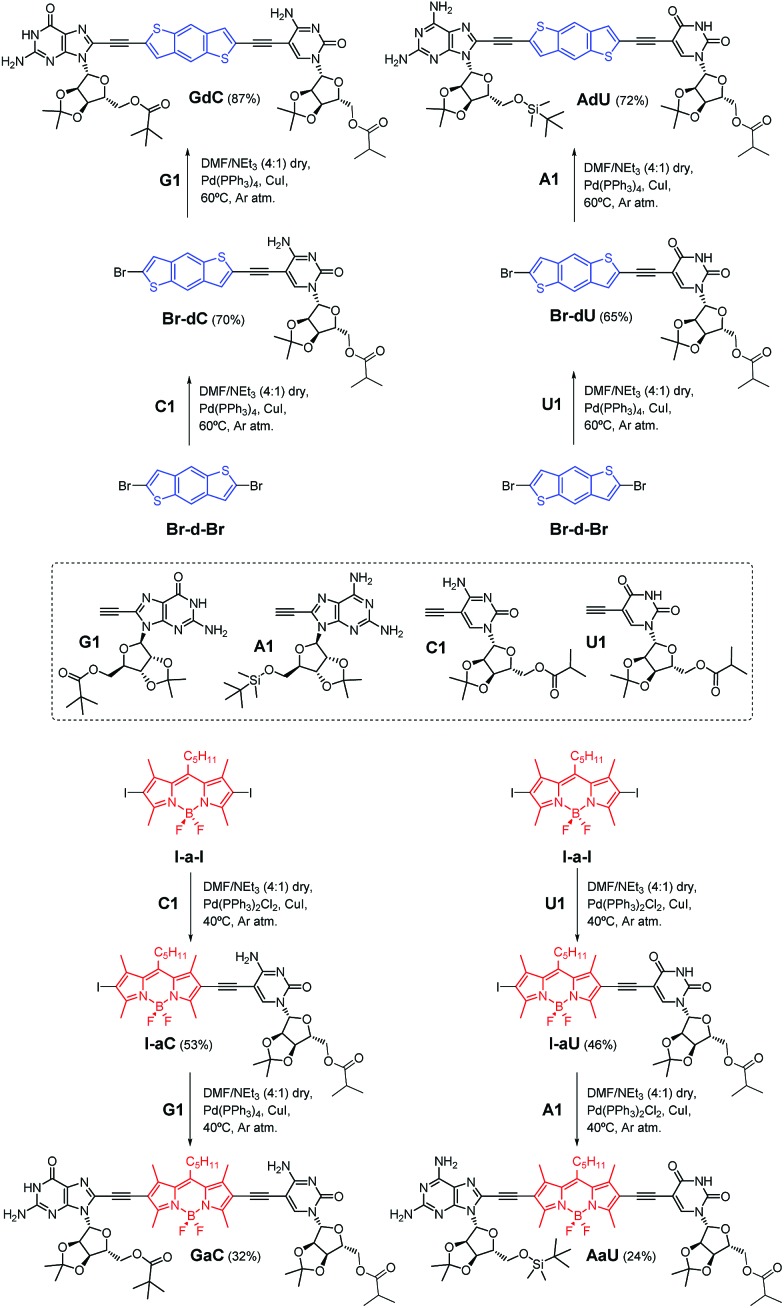
The dye-conjugated mononucleosides (dC, dU, aC and aU)25 as well as the reference mono- (C and U)26 and dinucleosides (GC and AU)21a,c shown in Fig. 2 have been previously described by us. Here, we report the synthesis and full characterization of novel donor (GdC and AdU) and acceptor (GaC and AaU) dinucleosides, which required two consecutive Pd-catalyzed couplings. In the first one, we connected 5-ethynylpyrimidine (C1 and U1)26 to the dibromobithiophene (Br-d-Br) or diiodoBODIPY (I-a-I) blocks and, subsequently, the corresponding 8-ethynylpurine (G1 and A1)26 was coupled (Scheme 1).
Scheme 1. Synthesis of dinucleosides GdC and AdU from dibromobithiophene Br-d-Br and GaC and AaU from diiodoBODIPY I-a-I via two consecutive Sonogashira coupling reactions.
Analysis of the macrocyclization process. Determination of the degree of cyclotetramerization (χT)
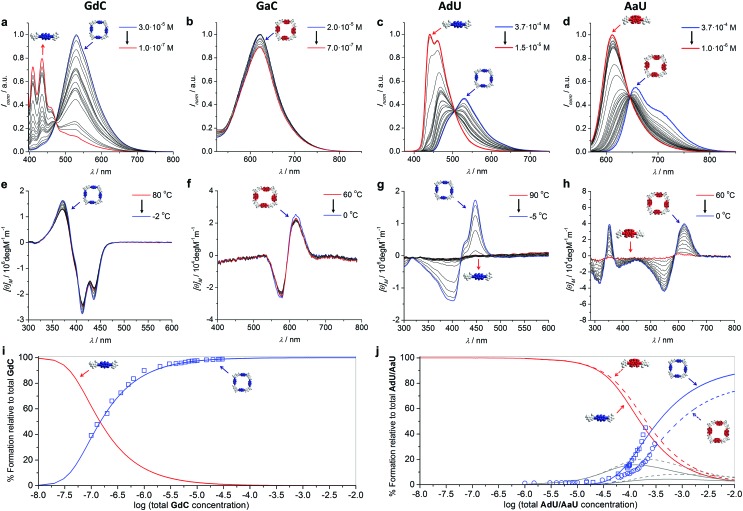
Prior to performing the key competition experiments, we wanted to gain a clear insight into the initial situation, that is, the degree of self-association of our chromophore-dinucleoside monomers (GdC, AdU, GaC and AaU) into cyclic tetramers at different concentrations in toluene. In previous work we demonstrated by 1H NMR experiments that GC (Fig. 2) displayed extremely high EMs, which resulted in strong all-or-nothing monomer-cycle equilibria. In contrast, EM values decreased dramatically for AU (Fig. 2), which resulted in a lower cyclic tetramer stability and, depending on the experimental conditions, the additional formation of small amounts of short open H-bonded oligomers (dimers, trimers,…).21a,c Unfortunately, 1H NMR analysis cannot be employed here because (1) the concentration range required is much higher than the one used in fluorescence spectroscopy, and (2) these compounds with large π-conjugated central blocks displayed poorly resolved 1H signals in toluene-D8 at such high concentrations.27
However, absorption and especially CD and emission spectroscopy experiments are also suitable tools to determine the degree of cyclotetramerization.21 When the chiral monomers associate in cyclic species, fluorescence emission is appreciably quenched and red-shifted, and a Cotton CD effect arises. More concretely, GdC or AdU monomer emission exhibits two maxima below 460 nm (see, as representative examples, the red spectra in Fig. 3a and c), while the corresponding cyclic tetramers (cGdC4 and cAdU4) show a single maximum at around 530 nm (see, for instance, the blue spectra in Fig. 3a or 3c). For GaC and AaU, monomer and cyclic tetramer maxima in the BODIPY emission region show smaller but still measurable shifts (620 and 623 nm for GaC and 612 and 656 nm for AaU; see the red and blue spectra in Fig. 3d). On the other hand, the cyclic tetramers display Cotton effects at the bithiophene/BODIPY dye absorption maxima (negative for cGdC4 and positive for cAdU4, cGaC4 and cAaU4; see Fig. 3e–h) that vanish at high temperatures or low concentrations as a result of cyclic tetramer dissociation.21
Fig. 3. (a–d) Concentration-dependent emission experiments (T = 298 K; toluene) of (a) GdC (λexc = 385 nm), (b) GaC (λexc = 545 nm), (c) AdU (λexc = 365 nm) and (d) AaU (λexc = 555 nm). (e–h) Temperature-dependent CD experiments of (e) GdC at 1.0 × 10–5 M, (f) GaC at 1.0 × 10–5 M, (g) AdU at 1.4 × 10–5 M and (h) AaU at 1.0 × 10–4 M in toluene. (i–j) Simulated speciation curves (lines) and experimental dilution data (squares for GdC/AdU and circles for AaU; calculated by using the areas within the measurement range) indicating the molar fraction of each species (cyclic tetramer: blue; monomer: red; open dimers and trimers: grey) as a function of the total concentration of (i) GdC and (j) AdU (solid lines)/AaU (dashed lines) in toluene. The dissociation of cGaC4 could not be analysed in the same way, but a comparison of (for instance) the CD spectra as a function of concentration/temperature (see Fig. 3e and f) suggests a similar stability to cGdC4.
These spectral changes in toluene can be monitored as a function of concentration (Fig. 3a–d) to evaluate quantitatively the molar fraction of molecules associated as cyclic tetramers (χT) in solution, and therefore the main equilibrium parameters associated with the macrocyclization process.21a We also performed temperature-dependent emission experiments at different concentrations within the 10–4 to 10–6 M range (Fig. S2A–D†) that support quantitatively the results obtained from the dilution measurements. Cyclic tetramer dissociation could be complementarily evaluated by monitoring the disappearance of the CD features with concentration and temperature (Fig. 3e–h). In all cases, an excellent correlation between CD and emission data was noted. In order to fit the experimental data, the following equilibria were considered that, in the case of the G-C couple, can be expressed as
| 2GdC ↔ GdC2 (K = Ka) | 1 |
| 3GdC ↔ GdC3 (K2 = Ka2) | 2 |
| 4GdC ↔ GdC4 (K3 = Ka3) | 3 |
| 4GdC ↔ cGdC4 (K4 EM = Ka4 EM = KT) | 4 |
| 5GdC ↔ GdC5 (K4 = Ka4) | 5 |
| 6GdC ↔ GdC6 (K5 = Ka5) | 6 |
where K is the equilibrium constant between Watson–Crick H-bonding pairs, and can be approximated using the reference association constant (Ka), previously determined from titration experiments in toluene with the corresponding mononucleoside combinations.25 The only variable is hence KT, which was calculated by multiwavelength analysis (see the ESI† for further details).28 EM values for each dinucleoside cyclotetramerization process were then calculated using the relationship EM = KT/Ka4. These thermodynamic parameters are displayed in the first three entries in Table 1 and show a good agreement with our previous work.21c They suggest that neither the presence of the rigid bithiophene/BODIPY unit as a central block instead of a p-phenylene group (compare GC/AU with GdC/AdU in Fig. 2) nor the change of the solvent medium to toluene has a profound influence on the chelate cooperativity of the system. Previously published work also supported the notion that EM values are typically not much impacted by the solvent nature,29a,21a unless specific solvation generates strain/steric effects between closely spaced binding sites, as determined recently.29b
Table 1. Cyclotetramerization (KT), peripheral binding (Kp) equilibrium constants and effective molarity (EM) calculated from the data obtained in different experiments in toluene.
| K a c [M–1] | C d [M] | K T [M–3] | K p [M–1] | EM e [M] | |
| GdC a | 5.0 × 105 | 6.3 × 1024 | 1.0 × 102 | ||
| AdU a | 2.0 × 103 | 3.2 × 1011 | 2.0 × 10–2 | ||
| AaU a | 2.0 × 103 | 1.0 × 1011 | 6.3 × 10–3 | ||
| GdC + aC b | 5.0 × 105 | 1.0 × 10–4 | — f | — f | — f |
| 2.0 × 10–5 | 8.9 × 1024 | 1.4 × 104 | 1.4 × 102 | ||
| 1.0 × 10–5 | 8.3 × 1024 | 1.1 × 104 | 1.3 × 102 | ||
| 5.0 × 10–6 | 2.5 × 1025 | 1.7 × 104 | 4.0 × 102 | ||
| Dilution g | 6.3 × 1024 | 8.5 × 104 | 1.0 × 102 | ||
| AdU + aU b | 2.0 × 103 | 1.1 × 10–4 | 3.5 × 1011 | 1.0 × 103 | 2.2 × 10–2 |
aData obtained from concentration-dependent experiments (Fig. 3).
bData obtained from competition experiments (Fig. 5).
cReference association constant between complementary nucleosides in toluene.25
dDinucleoside (GdC or AdU) concentration used in the competition experiment.
eEffective molarities were calculated as EM = KT/Ka4.
fNot fitted.
gFitting of the dilution experiment at a constant [GdC]/[aC] 1 : 1 ratio (see Fig. 8).
Speciation curves, which reproduce the relative abundance of species as a function of overall concentration, were then simulated using the equilibrium parameters extracted from these dilution experiments.30 In addition to monomer and cyclic tetramer species, short linear H-bonded oligomers (from dimers to hexamers; see eqn (1)–(6)) were included in these simulations. As shown in Fig. 3i and j, there exists a good correlation between simulated (solid lines) and experimental data (circles/squares) when representing the molar fraction of cyclic tetramers in solution.
All these results clearly indicate that the macrocycles formed by the G-C couple are far more robust than those associated with the A-U couple. For instance, under the conditions at which the competition experiments were carried out (298 K and 10–4 to 10–5 M range), cGdC4 and cGaC4 are associated almost quantitatively. As shown in Fig. 3i, S2A and S2B,† GdC and GaC fluorescence and CD spectra are virtually invariable under these conditions, and only start to display the typical monomer features at high temperatures and/or concentrations below 5 × 10–6 M. In sharp contrast, the molar fraction of AdU and AaU molecules associated as cyclic tetramers is just below 0.5 at the highest concentration measured, and decreases rapidly with temperature or concentration in the 5 × 10–4–10–5 M concentration range (see Fig. 3j, S2C and S2D†). These results additionally confirm that the superior stability of the macrocycles assembled via G:C versus A:U base pair is not only due to the higher H-bonding strength of the G:C couple, but also due to the stronger chelate effect that this unsymmetric ADD-DAA binding interaction supplies when compared to the symmetric DAD-ADA pattern (see our previous work).21c The lower EM of AdU or AaU is reflected in the significant participation of small open oligomers, mainly dimers and trimers, in equilibrium at concentrations between 10–5 M and 10–2 M (see grey curves in Fig. 3j). GdC/GaC, in sharp contrast, display strong all-or-none features and cyclic tetramer and monomer species are seen as the only competing species in solution.
Analysis of the macrocyclization process by competition experiments with complementary mononucleosides
Once we gained a clear insight into the self-assembly of our dinucleoside molecules in toluene solutions, we set up competition experiments between the ditopic donor molecule (GdC or AdU) and a monotopic pyrimidine acceptor that does not bear the energy-accepting functionality (C or U, respectively; see Fig. 2), and that will compete for binding to the purines (see Fig. 4a for a schematic representation). In order to start from a situation where the maximum number of molecules are associated as cyclic species, the total donor dinucleoside concentration in toluene was kept constant throughout the titration experiment above 10–5 M for GdC and just over 10–4 M for AdU. According to the previous results, these concentrations afford cyclic tetramer molar fractions of χT ∼1.0 for GdC, which is the ideal situation, and χT ∼0.25 for AdU. Fluorescence spectroscopy can be used here due to the different emission features of the dinucleoside monomers as a function of the association state: either as a cyclic tetramer at the beginning of the titration, or as a bimolecular GdC·C/AdU·U complex at the end of the titration (see Fig. 4a). The excitation wavelength was set at 385 nm, a region where the reference C or U mononucleosides do not absorb, so only the GdC/AdU dinucleoside chromophores are excited. Fig. 4b and c show, as an example, the evolution of the fluorescence spectrum of GdC/AdU upon gradual addition of C/U, respectively.
Fig. 4. (a) Schematic representation of the competition experiment between GdC/AdU dinucleosides and C/U mononucleosides. Cyclic tetramers are in equilibrium with monomers (KT) and, under the conditions at which the competition experiments were carried out, such equilibrium is strongly (GdC) or moderately (AdU) shifted to the macrocycle side. Upon addition of the complementary C/U mononucleoside, a competing equilibrium is established in which the free dinucleoside monomer binds to the mononucleoside stopper (Ka), which shifts the cyclotetramerization equilibrium toward the formation of GdC·C/AdU·U pairs. (b and c) Normalized fluorescence emission changes (λexc = 385 nm, T = 298 K, toluene) observed in the titration of (b) GdC with increasing amounts of C ([GdC] = 1.0 × 10–4 M, [C] = 1.4 × 10–2 M) and (c) AdU with increasing amounts of U ([AdU] = 1.4 × 10–4 M, [U] = 3.0 × 10–3 M). (d) Representation of the degree of cyclic tetramer association (χT) or emission changes (I/I0) as a function of the equivalents of complementary pyrimidine mononucleoside added for GdC + C ([GdC] = 1.0 × 10–4 M (red circles) or 1.0 × 10–5 M (red squares; see Fig. S3A†)) and for AdU + U ([AdU] = 1.4 × 10–4 M (blue circles)). For the sake of comparison, we also include previous results obtained in competition experiments between GC/AU and C/U measured by 1H NMR at 10–2 M concentration in CDCl3 (red and blue squares).21c Speciation curves were simulated using the previously calculated Ka and KT values (Table 1).
The changes observed resemble those obtained in concentration- or temperature-dependent experiments (see Fig. 3a–d and S2†): as the cyclic tetramer dissociates, a blue-shift in emission maxima and a moderate intensity enhancement are noted. However, the final spectra (in red) obtained in these titrations, with maxima at 464 nm for GdC + C and 477 for AdU + U are not exactly the same as in the dilution measurements, since the final species (i.e. the GdC·C/AdU·U complex or GdC/AdU dinucleoside, respectively) is also different (please compare Fig. 4b and c with Fig. 3a and c).
While the emission changes in the course of these titrations are similar for GdC and AdU, the number of equivalents of complementary pyrimidine mononucleoside required to reach saturation is very different for each base pair (please compare the red and blue solid circles in Fig. 4d). Whereas more than ca. 60 equivalents of C are required to denature the cyclic cGdC4 assemblies, less than ca. 10 equivalents of U are needed to fully dissociate cAdU4. The trends recorded also show a reasonable match with those obtained through previously reported competition experiments with dinucleosides GC and AU (also included in Fig. 4d for comparison),21c despite the fact that different molecules (GdC/AdUvs.GC/AU), solvents (toluene vs. CDCl3), concentration ranges (10–2–10–3 M vs. 10–4–10–5 M), techniques (emission vs.1H NMR spectroscopy) and physical observables were employed.
Using the previously calculated Ka and KT values (Table 1), we built speciation curves and compared them with the molar fraction of molecules associated as cyclic tetramers (χT) obtained at each titration point for all GdC + C (at 10–4 and 10–5 M; see Fig. S3A†) and AdU + U (at 10–4 M) competition experiments. An additional equilibrium was considered that, in the case of the G-C couple, can be expressed as
| GdC + C ↔ GdC·C (K′ = Ka) | 7 |
where, again, we made the approximation that Watson–Crick binding in the GdC·C/AdU·U species (K′) is equal to the one calculated for the corresponding mononucleoside mixtures in toluene (Ka; see Table 1).25 As can be noted in Fig. 4d, the simulations show only a modest agreement with the experimental results for AdU + U at 10–4 M (blue curve) and for GdC + C at 10–5 M (red dashed curve), but they deviate substantially from the trends obtained for GdC + C at 10–4 M (red solid curve). As a matter of fact, the overall competition equilibrium we are consideringcGdC4 + 4C ↔ 4GdC·C (KC)should be concentration-dependent, since the number of species at the product side is lower than that at the reagent side, and should shift to the formation of GdC·C at higher concentrations. This means that, for a given set of Ka and KT values, the denaturation trends obtained in these competition titrations should decay more abruptly as the concentration is increased, just as the simulations show (see also Fig. S3B,† where we simulate denaturation at different concentrations within the 10–2–10–6 M range). In contrast, our experiments revealed quite similar denaturation curves for the titration of GdC with C at both concentrations. However, as we found out in the next set of experiments (see below), in these competition experiments we do not consider a relevant additional equilibrium taking place in solution between GdC/AdU dinucleosides and C/U mononucleosides.
Analysis of the macrocyclization process by competition experiments with FRET-dye-labelled complementary mononucleosides
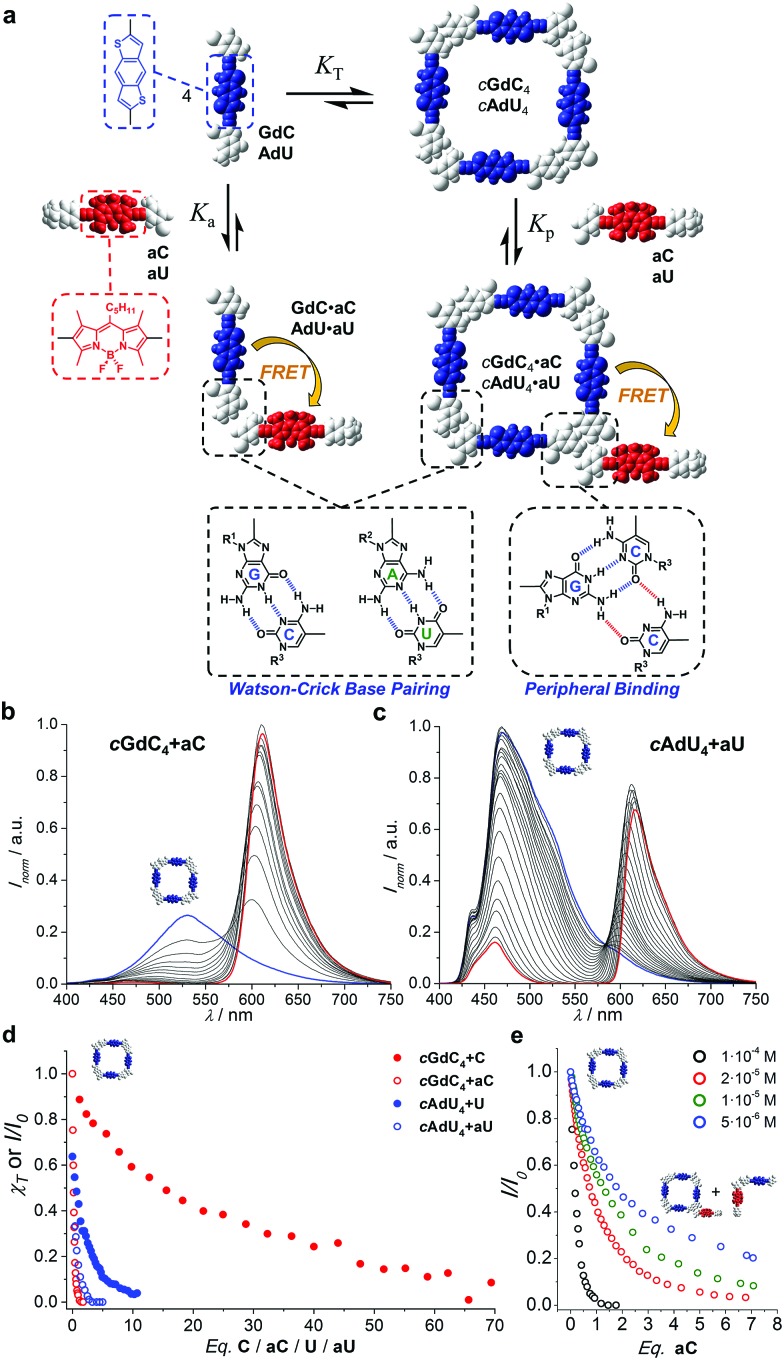
One of the aims of this work is to address and report supramolecular interactions by utilizing energy transfer processes with FRET couples. Thus, we carried out the same kind of denaturation experiments of cGdC4 and cAdU4 now in the presence of increasing amounts of the corresponding mononucleosides bearing the complementary energy-acceptor dye aC or aU (see Fig. 5a).
Fig. 5. (a) Schematic representation of the competition experiment between GdC/AdU dinucleosides and aC/aU mononucleosides. Cyclic tetramers are in equilibrium with monomers (KT) and, under the conditions at which the competition experiments were carried out, such equilibrium is strongly (GdC) or moderately (AdU) shifted to the tetramer side. Upon addition of the complementary mononucleoside, two competing equilibria, both of them resulting in donor emission quenching due to energy transfer, would be established: (1) peripheral binding (Kp) to external sites of the cyclic tetramer (a hypothetical binding mode of aC to cGdC4 is shown) and (2) binding to the free dinucleoside monomer (Ka), which will shift the cyclotetramerization equilibrium toward the formation of GdC·aC/AdU·aU FRET pairs. (b and c) Normalized fluorescence emission changes (I/I0; λexc = 385 nm, T = 298 K, toluene) observed in the titration of (b) GdC with increasing amounts of aC ([GdC] = 1.0 × 10–4 M, [aC] = 2.0 × 10–4 M) and (c) AdU with increasing amounts of aU ([AdU] = 1.1 × 10–4 M, [aU] = 4.7 × 10–4 M). (d) Representation of the degree of cyclic tetramer association (χT) or emission changes (I/I0), as a function of the equivalents of complementary pyrimidine mononucleoside added for GdC + C (Fig. 4b; [GdC] = 1.0 × 10–4 M; red solid circles), AdU + U (Fig. 4c; [AdU] = 1.4 × 10–4 M; blue solid circles), GdC + aC (Fig. 5b; [GdC] = 1.0 × 10–4 M; red open circles), and AdU + aU (Fig. 5c; [AdU] = 1.1 × 10–4 M; blue open circles). (e) Normalized emission changes of GdC as a function of the equivalents of aC added at different GdC concentrations (see also Fig. S3C†).
An example of the fluorescence spectral changes recorded in these titrations with GdC and AdU is shown in Fig. 5b and c, respectively. In order to maximize the FRET effect, the excitation wavelength was set at 385 nm, where the donor/acceptor absorption ratio reaches a maximum. As expected, donor emission is gradually quenched as increasing amounts of aC or aU are added. This is supposedly due to the formation of the corresponding donor–acceptor complex (GdC·aC and AdU·aU, as shown in Fig. 5a), in which the donor bithiophene emission is strongly quenched by energy transfer to the BODIPY acceptor. At the same time, acceptor emission is enhanced in the course of the titrations, which is partly due to the energy transfer event, but mainly due to the fact that the concentration of acceptor molecules is increased constantly in the experiment.
The fluorescence intensity within the donor emission range (450–560 nm) was then plotted as a function of the equivalents of mononucleoside acceptor added (Fig. 5d; red and blue open circles). It is clearly evident that donor emission, either GdC or AdU, is virtually fully quenched (>95%) after the addition of a few equivalents (i.e. <4 eq.) of complementary acceptor. These results strongly contrast with the trends previously obtained for cAdU4 and cGdC4 denaturation, respectively, using the changes in emission maxima (see Fig. 4), which are also reproduced in Fig. 5d for the sake of comparison (red and blue closed circles).
We believe that the most reasonable explanation for such a significant deviation comes from the fact that we must now take into account other competing equilibria, as is shown schematically in Fig. 5a: the binding of the mononucleoside acceptor (aC or aU) to external sites at the cyclic tetramer periphery, without actually causing macrocycle dissociation. Such peripherally bound cGdC4·aC/cAdU4·aU species also combines FRET donor and acceptor molecules, and therefore its formation should contribute as well to the gradual GdC/AdU emission quenching observed. The participation of this species should be mostly manifested at the beginning of the titrations, where only a few equivalents of acceptor quencher are added, and for the stronger cGdC4 assembly, which can withstand a higher amount of mononucleoside competitor. A tentative association mode for cGdC4·aC, where the C pyrimidine forms two H-bonds with the G-amine proton and the C-carbonyl lone pair that are not participating in Watson–Crick interactions, is shown in Fig. 5a. Other binding modes or binding of more than one energy-accepting unit to the cyclic tetramers are, of course, also plausible, but cannot be assessed through the spectroscopic techniques employed in this work.
In order to corroborate the presence of this additional equilibrium and prove the formation of cGdC4·aC and cAdU4·aU species, where the competitor binds to non-dissociated macrocycles, we performed different sets of complementary experiments.
First, we reasoned that the formation of the cGdC4·aC assemblies should be favoured at higher concentrations. Therefore, supplementary competition experiments were carried out at different initial GdC concentrations: 1.0 × 10–4, 2.0 × 10–5, 1.0 × 10–5 and 5.0 × 10–6 M (see Fig. S3C†). As can be observed in Fig. 5e, at the beginning of the titrations, when only a few equivalents of aC are added, the original GdC fluorescence is quenched to a higher extent at higher concentrations. In other words, the relative amount of aC required to achieve a given quenching factor is lower as the overall concentration increases. This trend supports the hypothesis of an associative process where aC would bind to cGdC4 and activate energy transfer between bithiophene and BODIPY units.
On the other hand, despite the strong quenching and very low GdC residual emission, it is interesting to note that the characteristic blue emission shift from ca. 530 to 460 nm (as noted in the transformation of cGdC4 to GdC·C; Fig. 4b) was also detected in the course of the titrations of cGdC4 with up to 100 equivalents of aC (see Fig. S3D†). This observation confirms that the GdC·aC/AdU·aU species, resulting from cyclic tetramer dissociation at high aC/aU relative concentrations, are still the main products at the end of these titrations.
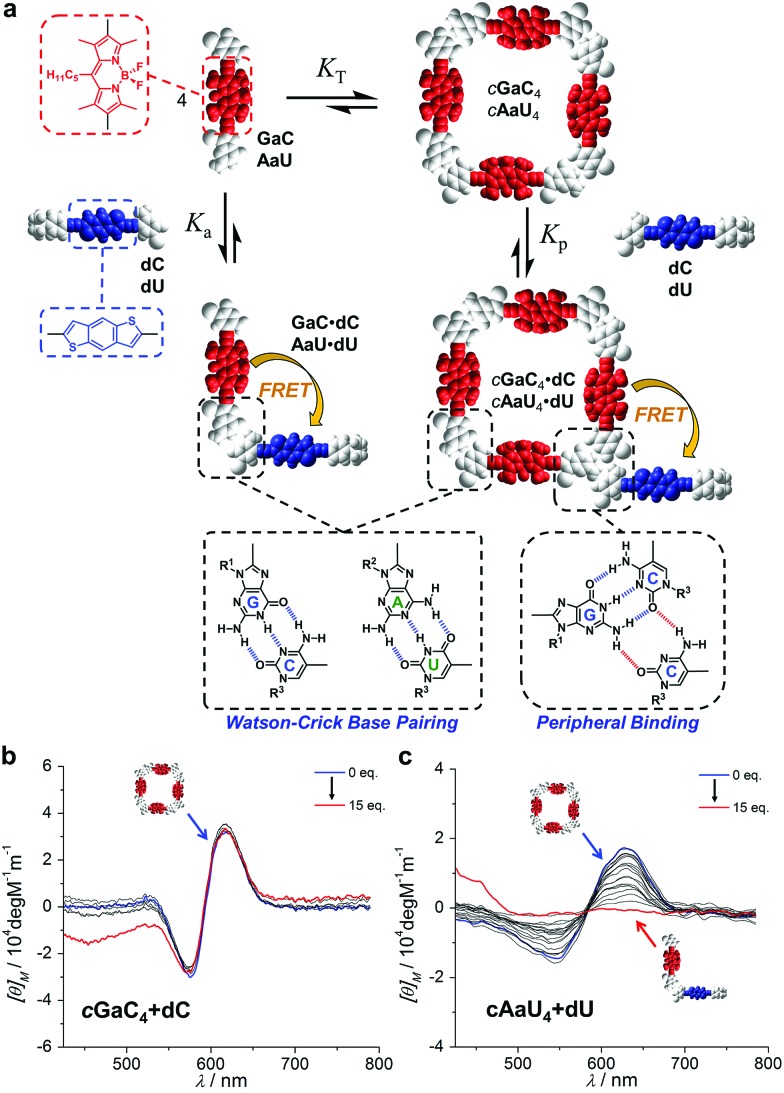
Additionally, monitoring these competition experiments by CD spectroscopy proved to be a helpful source of complementary information that confirmed that the cyclic tetramers are not dissociated at the beginning of the titrations with aC, despite the strong quenching recorded. The bithiophene and BODIPY dinucleosides, besides being complementary FRET pairs, absorb in different regions of the visible spectrum. Thus, swapping the energy donor and acceptor functionalities in the dinucleoside and mononucleoside molecules (that is, using GaC + dC and AaU + dU combinations) allowed us to isolate and record the CD spectra of the cGaC4 and cAaU4 cyclic tetramers (between 500 and 700 nm) without contamination due to the strong absorption of the excess of dC/dU competitor (at ca. 400 nm) (Fig. 6a).31 The opposite combination, that is, cGdC4 + aC or cAdU4 + aU, used in the fluorescence quenching experiments, was also tested with similar results, but suffers from absorption saturation from the excess of aC/aU molecules in the GdC/adU absorption region, which produces a considerable distortion of the CD spectra, as shown as an example in Fig. S3E.† Therefore, another type of competition experiment was performed in which cyclic tetramer denaturation in the presence of increasing amounts of dC/dU was monitored by the disappearance of the characteristic cGaC4/cAaU4 CD signals at around 600 nm. The results are shown in Fig. 6b and c, respectively.
Fig. 6. (a) Schematic representation of the competition experiment between GaC/AaU dinucleosides and dC/dU mononucleosides (see also Fig. 4). CD signal changes (λexc = 385 nm, T = 298 K, toluene) observed in the titration of (b) GaC with increasing amounts of dC ([GaC] = 1.0 × 10–4 M, [dC] = 7.0 × 10–3 M) and (c) AaU with increasing amounts of dU ([AaU] = 1.0 × 10–4 M, [dU] = 2.8 × 10–3 M).
It is evident that the addition of dC does not produce major changes in the CD spectrum of cGaC4, indicating that, at least up to 15 equivalents of competitor, this cyclic species does not suffer from significant denaturation at 1.0 × 10–4 M (see also Fig. S3F,† in which the same experiment was performed at a concentration one order of magnitude lower). Further addition, up to 72 eq. of dC, led to the disappearance of this CD signal, but it could not be properly monitored because the huge excess of donor began to interfere in this absorption region as well. In sharp contrast, the characteristic cAaU4 CD signal is gradually lost with the addition of up to ca. 10 eq. of dU. These results are in good agreement with the trends shown in Fig. 4d and substantiate the idea that, due to the large differences in EM, the cGdC4/cGaC4 and cAdU4/cAaU4 cyclic systems are insignificantly and totally dissociated, respectively, upon addition of a small excess of the complementary mononucleoside. These CD titrations also verify the hypothesis that the strong GdC emission quenching observed after the addition of the first aC equivalents (Fig. 5b) is caused by the interaction between cGdC4 and aC in a way that must be different to ring-opening via Watson–Crick competition.
Analysis of the peripheral association between mononucleosides and dinucleoside macrocycles
In short, it is evident that the use of FRET pairs, where energy donors and acceptors communicate with each other, has the advantage of reporting additional binding events occurring in solution, namely the interactions between non-dissociated cyclic tetramers and mononucleoside molecules, which is especially clear in the case of GdC when compared to AdU. Therefore, in order to fit the GdC/AdU donor emission deactivation trends in the presence of aC/aU, a supplementary process (see also Fig. 5a) was now considered in addition to equilibria (1)–(7) that takes into account peripheral binding, which, for the G-C couple, can be expressed as
| cGdC4 + aC ↔ cGdC4·aC (Kp) | 8 |
Both KT and Kp were calculated simultaneously and the results are shown in Table 1 (see Fig. S3G and S3H† for further details). The term Kp should be regarded as an apparent association constant that describes the binding of quencher molecules to the macrocycle, resulting in donor emission deactivation, and was calculated to be Kp = 104–105 M–1 for cGdC4·aC and Kp = 103 M–1 for cAdU4·aU in toluene. Unfortunately, from all the data collected we cannot determine the number of quencher molecules that can bind to the cyclic tetramers, or if subsequent binding events quench donor fluorescence in the macrocycle to the same extent as the first one.
This model comprising multiple competing equilibria provides an insight into the relative population of the different supramolecular species during the titrations. New speciation curves30 were simulated including the peripheral binding equilibrium (8) and they are now able to reproduce rather satisfactorily both the donor emission quenching behaviour observed for our cGdC4/cAdU4 macrocycles in the course of the titration experiments with aC/aU (Fig. 5) and the emission changes recorded in the titrations with C/U (Fig. 4).
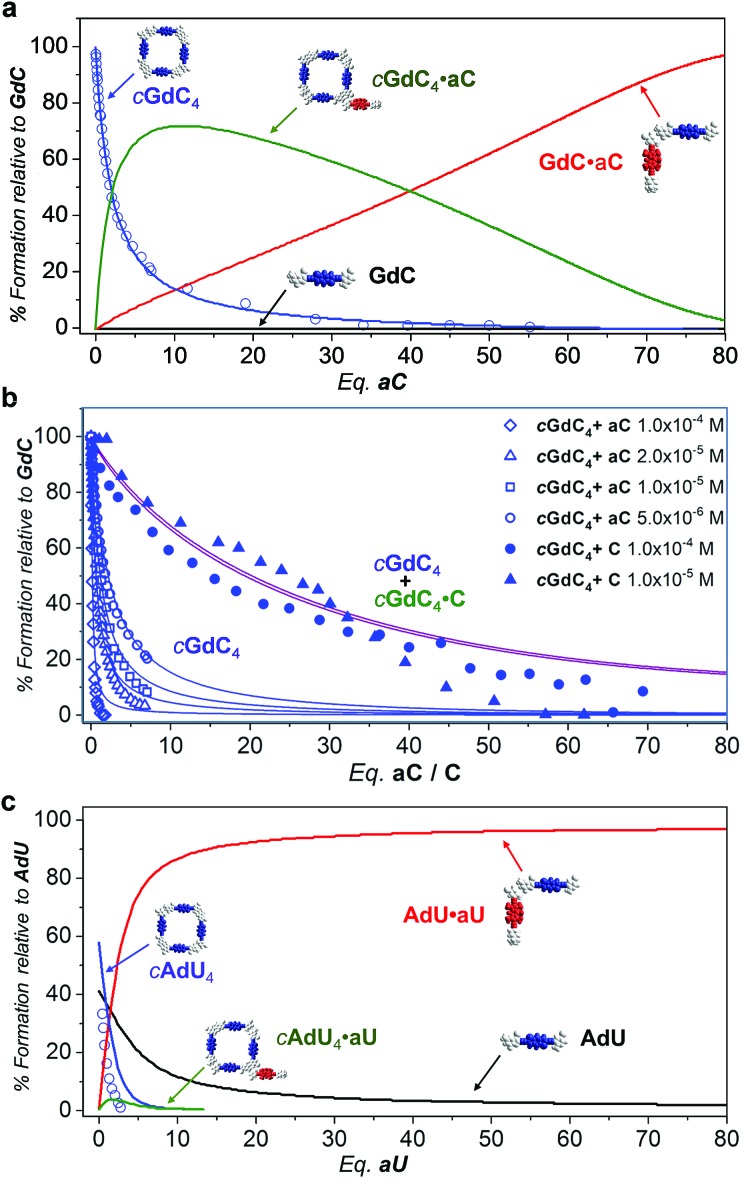
Fig. 7a thus provides an accurate picture of the distribution of species that coexist at different [aC] (or [C])/[GdC] ratios. At low [aC]/[GdC] ratios, the cGdC4·aC assembly is formed in significant amounts (green curve), but its concentration then decreases at higher aC equivalents in favour of the bimolecular GdC·aC complex (red curve). Both of these complexes, where energy donors and acceptors are non-covalently bound, contribute to the emission quenching observed for the GdC molecule (open blue circles; see Fig. 5), which fits quite well with the disappearance of cGdC4 to yield cGdC4·aC and GdC·aC (blue line).
Fig. 7. Simulated speciation profiles (lines; using the Ka, EM and Kp values displayed in Table 1) and experimental titration data obtained from the donor emission quenching trends (open shapes; see Fig. 5) or emission shifts (solid shapes; see Fig. 4) for the competition experiments of (a and b) cGdC4 + aC (or C) at (a) a single (b) or different concentrations (see Fig. 4d and 5e), or (c) cAdU4 + aU (or U) in toluene.
Furthermore, the introduction of equilibrium (8) in the simulations leads to comparable KT and Kp values when employing different GdC concentrations, and reproduces the concentration-dependent behaviour observed in the cGdC4 fluorescence deactivation trends in the presence of aC (Fig. 5e). The relative abundance of this cyclic species (blue curves in Fig. 7b) is seen to decrease more abruptly at higher concentrations, which is mostly due to an equilibrium shift toward the formation of peripherally bound cGdC4·aC.
However, the peripherally bound cGdC4·C species cannot be detected without the assistance of FRET events. Even if it is presumably being formed in the course of the titration experiments with C, monitored by changes in the emission spectra (Fig. 4), it must exhibit very similar emission (and CD) features to cGdC4. Nonetheless, its formation does affect the overall equilibrium by sequestering C competitor molecules, so equilibrium (8) should be additionally taken into account when simulating the cyclic tetramer denaturation curves shown in Fig. 4d. Therefore, in this case the combined cGdC4 and cGdC4·C relative abundances must be considered, which results in the purple curves in Fig. 7b. These “addition” curves now reproduce reasonably well the changes observed in the emission spectra as the number of C competitor equivalents increases (Fig. 4). Moreover, the combined model predicts a very weak dependence on the total concentration, which suggests that the presence of equilibrium (8) introduces a “buffering” effect by diminishing the relative amount of competitor molecules available for the denaturation equilibrium. This is in line with our experimental observation that cyclic tetramer denaturation, monitored with different techniques at different concentrations (as shown in Fig. 4d), is not extraordinarily sensitive to the overall concentration (please also see Fig. S3B†).
Similarly, Fig. 7c describes the picture obtained in the simulations of the competition titrations of AdU with U or aU. This system is far less interesting in the context of the results described in this work, since the binding constant between complementary nucleobases and the EM values are significantly lower. This makes the cAdU4 macrocycle much weaker, and its formation was far from quantitative under the initial conditions of our competition experiments. Moreover, as a consequence of a much lower chelate cooperativity, cAdU4 (blue curve) dissociates abruptly at low [U]/[AdU] ratios to yield the AdU·U species (red curve) in equilibrium with the AdU monomer (black curve), and the participation of peripherally bound cAdU4·U species (green curve) becomes insignificant and cannot be properly monitored.
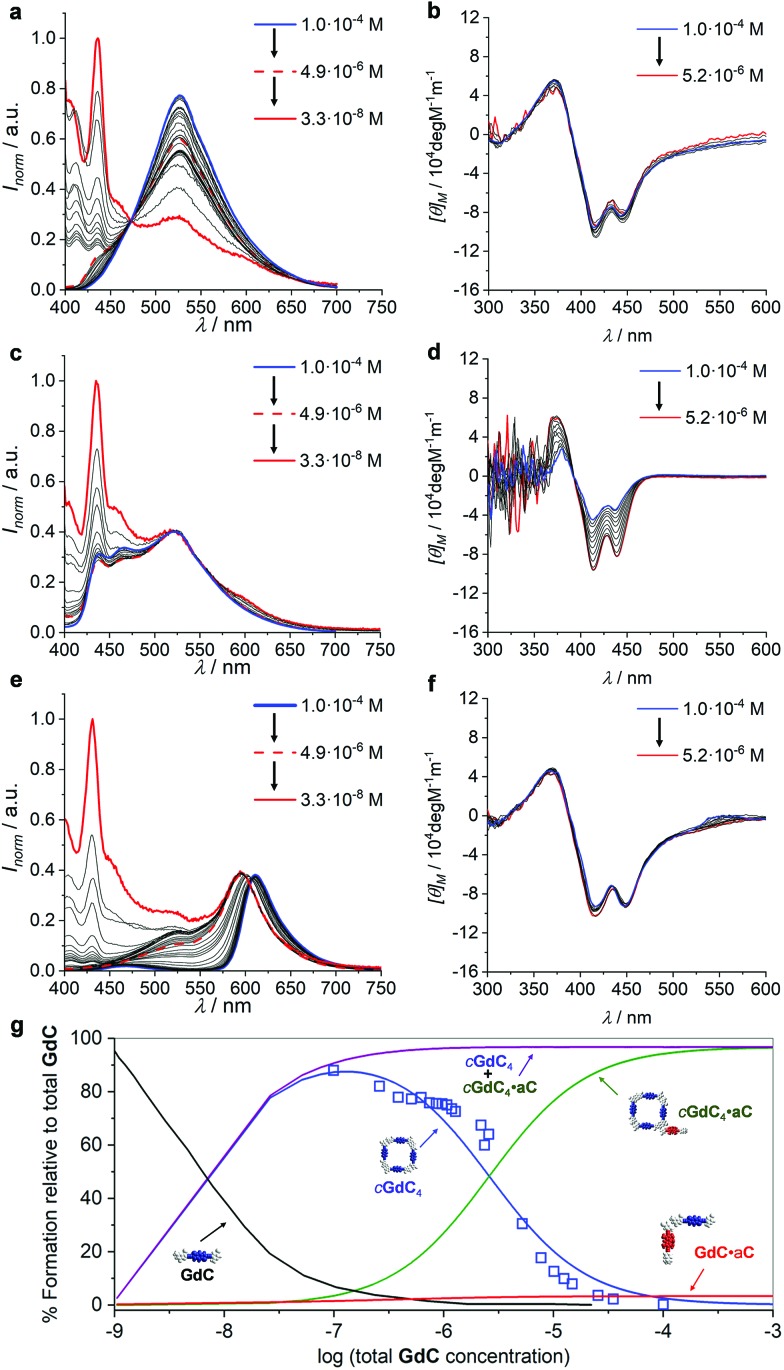
Finally, in view of the results obtained, we were intrigued to examine the effect of changing the overall concentration on the different competition equilibria between GdC and C or aC at constant [C] (or [aC])/[GdC] ratios. For such a goal, we performed dilution experiments (Fig. 8) monitored by emission (in the 1.0 × 10–4–3.3 × 10–8 M range) and CD spectroscopy (in the 1.0 × 10–4–5.2 × 10–6 M range) of three different samples: (1) GdC, (2) GdC with 10 equivalents of C, and (3) GdC with 1 equivalent of aC.
Fig. 8. (a, c, and e) Normalized emission spectra at different concentrations within the 1.0 × 10–4–3.3 × 10–8 M range and (b, d, and f) CD spectra at different concentrations within the 1.0 × 10–4–5.2 × 10–6 M range of (a and b) GdC, (c and d) a 1 : 10 GdC + C mixture or (e and f) a 1 : 1 GdC + aC mixture. (g) Speciation profiles (lines; simulated using the values shown in Table 1) and calculated EFRET values at different concentrations (blue open squares) within the 10–2–10–9 M range.
As already shown in Fig. 3, within this concentration range the cGdC4 macrocycle is not significantly dissociated in toluene and the normalized GdC emission, with a maximum at 530 nm, and CD spectra remain virtually unaltered (see Fig. 8a and b). Only at the lowest concentrations, which could only be studied by fluorescence spectroscopy, do the monomer emission bands start to rise below 450 nm.
We then compared these results with the dilution of GdC in the presence of the competitor. In the case of the 1 : 10 GdC + C mixture (Fig. 8c and d), no significant changes were noted within the 10–4–5 × 10–6 M range. According to our model, the most abundant species under these conditions should be cGdC4·C, in equilibrium with small amounts of GdC·C. The emission maxima found at 525 nm can be attributed to the first cyclic species (please compare them with the emission maxima of the pristine cGdC4 macrocycle in Fig. 8a), while the smaller bands at 470 and 435 nm seem to indicate the presence of the latter non-cyclic species. If the concentration is reduced to 10–8 M, the typical GdC monomer emission bands below 450 nm progressively become more abundant. Likewise, the CD spectra recorded between 10–4 and 5 × 10–6 M are similar to those recorded for cGdC4, confirming the presence of cyclic species, though it is slightly perturbed by the presence of a large excess of C, especially at high concentrations.
Finally, for the 1 : 1 GdC + aC combination (Fig. 8e and f), the emission spectra revealed a considerably quenched GdC emission at high concentrations, as expected in view of the previous results. However, as the concentration decreases at a constant GdC : aC 1 : 1 ratio, the cGdC4 emission features, with a maximum at 530 nm, are gradually recovered, which is in agreement with the dissociation of the peripherally bound cGdC4·aC complex and in line with the titrations at different concentrations shown in Fig. 5e. The degree of emission quenching (or FRET efficiency) was then calculated as EFRET = 1 – (IDA/ID), where ID and IDA are the fluorescence emission intensities under the same experimental conditions of the donor molecule in the absence (Fig. 8a) or presence (Fig. 8e) of the corresponding acceptor, respectively, at the 530 nm emission maximum, where the aC molecule does not emit. The calculated EFRET can be related to the molar fraction of emitting GdC molecules, which are mostly associated as cyclic tetramers above 5 × 10–6 M, and is represented in Fig. 8g as open blue squares. Again, the CD spectra recorded in this concentration range do not change and exhibit comparable intensity to the one obtained for GdC alone (compare Fig. 8b and f), thus confirming the persistence of cyclic species, either cGdC4 or cGdC4·aC.
The quantitative analysis of these dilution experiments, using again the previously calculated Ka, EM and Kp values (Table 1), provided an accurate picture of the relative distribution of species as a function of concentration, which is represented in Fig. 8g for the GdC : aC 1 : 1 mixture within the 10–2–10–9 M range. The cGdC4·aC species dominate at high concentrations, competing with a small amount of GdC·aC. As shown in Fig. S4,† where similar speciation profiles were generated by changing Ka, EM and Kp values, the degree of participation of the bimolecular GdC·aC species depends on the magnitude of EM and Kp, but not on Ka. Both species are responsible for the quantitative GdC emission quenching observed under these conditions. Dilution down to 5 × 10–6 M leads primarily to the dissociation of aC from the macrocycle periphery and to the gradual release of emissive cGdC4 cyclic tetramers. It is important to note that the evolution of cGdC4 is in reasonable agreement with the calculated EFRET values at each concentration point. Therefore, within this 10–2–10–6 M range peripherally bound cGdC4·aC and unbound cGdC4 macrocycles are the main species in solution, and the equilibrium between them depends exclusively on Kp, but not on EM or Ka (see Fig. S4†). Interestingly, the sum of the relative abundances of these two cyclic species (purple curve in Fig. 8g) is almost constant within this concentration window, which is in agreement with the trends observed in Fig. 8c, where the shape of the emission spectra did not display important changes down to 10–6 M. Hence, these dilution experiments supported the notion that, if peripheral binding comes into play, a “buffering” effect is introduced and the overall equilibrium in the presence of a competitor is not strongly dependent on concentration. Finally, decreasing the concentration below 10–6 M produces the dissociation of both cyclic and non-cyclic species, and the GdC monomer, characterized in the emission experiments by two maxima at 435 and 415 nm, dominates in the low concentration regime. As shown in Fig. S4,† the concentration at which this species comes into play depends on Ka and EM, but not on Kp.
Conclusions
This whole analysis led us to conclude that the measurement of FRET phenomena, which basically report the proximity of donor and acceptor pairs and therefore the presence of specific binding interactions, can be very useful to obtain supplementary information from a supramolecular association landscape that other techniques, such as NMR or absorption/CD spectroscopy, fail to disclose. In particular, a noncovalent macrocyclization process has been studied here by means of fluorescence emission spectroscopy by setting up a competition between a ditopic monomer, which bears complementary purine–pyrimidine bases at the edges and self-associates in cyclic tetramers in solution, and a monotopic pyrimidine molecule that is gradually added to the solution and that will compete for binding to the purine units. Multiwavelength fitting of the emission changes experienced by the monomer chromophore during these titrations allowed us to determine the KT and EM values. Furthermore, when this mononucleoside competitor is equipped with the BODIPY energy acceptor pair, fluorescence spectroscopy analysis additionally allowed us to monitor and quantify peripheral interactions between intact macrocycles and mononucleosides. Our results indicate that donor fluorescence deactivation during the competition titrations is due to binding of the complementary acceptor to both the product (cyclic tetramer) and reactant (monomer) sides of the macrocyclization reaction. These effects are more clearly discerned and quantified in the case of cGdC4, due to its higher stability and stronger chelate cooperativity when compared to cAdU4. At a moderate competitor content, associative processes may become dominant and the macrocycle acts as a host for the competitor. As the competitor ratio increases, the cyclic species is however forced to dissociate.
We deem that the outcome and conclusions of our work can be very interesting for the study of host–guest ensembles in which the host is a self-assembled system that can either dissociate or accommodate the guest molecule. Future work involving related complementary donor–acceptor FRET pairs will be focused on selecting guests with H-bonding motifs that can bind to specific sites of the macrocycle's periphery with high Kp association constants, and on utilizing the exceptional time resolution of fluorescence spectroscopy to monitor exchange kinetics between diverse components in these H-bonded macrocycles.
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
Funding from the European Research Council (ERC-Starting Grant 279548 PROGRAM-NANO) and MINECO (CTQ2014-57729 P and CTQ2017-84727 P) is gratefully acknowledged. E. F. would like to thank Sharif University of Technology of Iran for financial support. D. S.-M. would like to acknowledge Comunidad de Madrid for financial support through contract PEJ16/IND/AI-0849.
Footnotes
†Electronic supplementary information (ESI) available: Synthetic details, compound characterization, DOSY experiments, emission and CD measurements and analysis of the titration and competition experiments. See DOI: 10.1039/c8sc03229g
References
- Schalley C. A., Analytical Methods in Supramolecular Chemistry, Wiley-VCH, Weinheim, 2012. [Google Scholar]
- (a) Sapsford K. E., Berti L., Medintz I. L. Angew. Chem., Int. Ed. 2006;45:4562–4588. doi: 10.1002/anie.200503873. [DOI] [PubMed] [Google Scholar]; (b) FRET - Förster Resonance Energy Transfer: From Theory to Applications, ed. I. Medintz and N. Hildebrandt, Wiley-VCH, Weinheim, 2014. [Google Scholar]
- (a) Saini S., Srinivas G., Bagchi B. J. Phys. Chem. B. 2009;113:1817–1832. doi: 10.1021/jp806536w. [DOI] [PubMed] [Google Scholar]; (b) Sahoo H. J. Photochem. Photobiol., C. 2011;12:20–30. [Google Scholar]
- Jares-Erijman E. A., Jovin T. M. Nat. Biotechnol. 2003;21:1387–1395. doi: 10.1038/nbt896. [DOI] [PubMed] [Google Scholar]
- Preus S., Wilhelmsson L. M. ChemBioChem. 2012;13:1990–2001. doi: 10.1002/cbic.201200400. [DOI] [PubMed] [Google Scholar]
- (a) Farinha J. P. S., Spiro J. G., Winnik M. A. J. Phys. Chem. B. 2001;105:4879–4888. [Google Scholar]; (b) Sustarsic M., Kapanidis A. N. Curr. Opin. Struct. Biol. 2015;34:52–59. doi: 10.1016/j.sbi.2015.07.001. [DOI] [PubMed] [Google Scholar]; (c) Shrestha D., Jenei A., Nagy P., Vereb G., Szöllősi J. Int. J. Mol. Sci. 2015;16:6718–6756. doi: 10.3390/ijms16046718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (a) Castellano R. K., Craig S. L., Nuckolls C., Rebek Jr J. J. Am. Chem. Soc. 2000;122:7876–7882. [Google Scholar]; (b) Barrett E. S., Dale T. J., Rebek Jr J. J. Am. Chem. Soc. 2007;129:3818–3819. doi: 10.1021/ja0700956. [DOI] [PubMed] [Google Scholar]; (c) Barrett E. S., Dale T. J., Rebek Jr J. J. Am. Chem. Soc. 2007;129:8818–8824. doi: 10.1021/ja071774j. [DOI] [PubMed] [Google Scholar]
- Azov V. A., Schlegel A., Diederich F. Angew. Chem., Int. Ed. 2005;44:4635–4638. doi: 10.1002/anie.200500970. [DOI] [PubMed] [Google Scholar]
- Brea R. J., Vázquez M. E., Mosquera M., Castedo L., Granja J. R. J. Am. Chem. Soc. 2007;129:1653–1657. doi: 10.1021/ja066885h. [DOI] [PubMed] [Google Scholar]
- (a) Rivera J. M., Martín-Hidalgo M., Rivera-Ríos J. C. Org. Biomol. Chem. 2012;10:7562–7565. doi: 10.1039/c2ob25913c. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Pu F., Wu L., Ran X., Ren J., Qu X. Angew. Chem., Int. Ed. 2015;54:892–896. doi: 10.1002/anie.201409832. [DOI] [PubMed] [Google Scholar]
- (a) Zhang L., Wu Y., Brunsveld L. Angew. Chem., Int. Ed. 2007;46:1798–1802. doi: 10.1002/anie.200604222. [DOI] [PubMed] [Google Scholar]; (b) Bill A., Blockus H., Stumpfe D., Bajorath J., Schmitz A., Famulok M. J. Am. Chem. Soc. 2011;133:8372–8379. doi: 10.1021/ja202513s. [DOI] [PubMed] [Google Scholar]
- (a) Suresh M., Mandal A. K., Suresh E., Das A. Chem. Sci. 2013;4:2380–2386. [Google Scholar]; (b) Mandal A. K., Gangopadhyay M., Das A. Chem. Soc. Rev. 2015;44:663–676. doi: 10.1039/c4cs00295d. [DOI] [PubMed] [Google Scholar]; (c) Gangopadhyay M., Maity A., Dey A., Das A. J. Org. Chem. 2016;81:8977–8987. doi: 10.1021/acs.joc.6b01631. [DOI] [PubMed] [Google Scholar]
- Denisov S. A., Gan Q., Wang X., Scarpantonio L., Ferrand Y., Kauffmann B., Jonusauskas G., Huc I., McClenaghan N. D. Angew. Chem., Int. Ed. 2016;55:1328–1333. doi: 10.1002/anie.201508611. [DOI] [PubMed] [Google Scholar]
- Huang C.-B., Xu L., Zhu J.-L., Wang Y.-X., Sun B., Li X., Yang H.-B. J. Am. Chem. Soc. 2017;139:9459–9462. doi: 10.1021/jacs.7b04659. [DOI] [PubMed] [Google Scholar]
- (a) Jiwpanich S., Ryu J.-H., Bickerton S., Thayumanavan S. J. Am. Chem. Soc. 2010;132:10683–10685. doi: 10.1021/ja105059g. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Li L., Thayumanavan S. Langmuir. 2014;30:12384–12390. doi: 10.1021/la502760c. [DOI] [PMC free article] [PubMed] [Google Scholar]; (c) Gong B., Choi B.-K., Kim J.-Y., Shetty D., Ko Y. H., Selvapalam N., Lee N. K., Kim K. J. Am. Chem. Soc. 2015;137:8908–8911. doi: 10.1021/jacs.5b05385. [DOI] [PubMed] [Google Scholar]; (d) Zhang M., Yin X., Tian T., Liang Y., Li W., Lan Y., Li J., Zhou M., Ju Y., Li G. Chem. Commun. 2015;51:10210–10213. doi: 10.1039/c5cc02377g. [DOI] [PubMed] [Google Scholar]
- Meng L.-B., Li D., Xiong S., Hu X.-Y., Wang L., Li G. Chem. Commun. 2015;51:4643–4646. doi: 10.1039/c5cc00398a. [DOI] [PubMed] [Google Scholar]
- (a) Petkau-Milroy K., Uhlenheuer D. A., Spiering A. J. H., Vekemans J. A. J. M., Brunsveld L. Chem. Sci. 2013;4:2886–2891. [Google Scholar]; (b) Sendai T., Biswas S., Aida T. J. Am. Chem. Soc. 2013;135:11509–11512. doi: 10.1021/ja4060146. [DOI] [PubMed] [Google Scholar]; (c) Albertazzi L., van der Veeken N., Baker M. B., Palmans A. R. A., Meijer E. W. Chem. Commun. 2015;51:16166–16168. doi: 10.1039/c5cc06951c. [DOI] [PMC free article] [PubMed] [Google Scholar]; (d) Baker M. B., Gosens R. P. J., Albertazzi L., Matsumoto N. M., Palmans A. R. A., Meijer E. W. ChemBioChem. 2016;17:207–213. doi: 10.1002/cbic.201500606. [DOI] [PubMed] [Google Scholar]; (e) Sarkar A., Dhiman S., Chalishazar A., George S. J. Angew. Chem., Int. Ed. 2017;56:13767–13771. doi: 10.1002/anie.201708267. [DOI] [PubMed] [Google Scholar]
- (a) De Greef T. F. A., Smulders M. M. J., Wolffs M., Schenning A. P. H. J., Sijbesma R. P., Meijer E. W. Chem. Rev. 2009;109:5687–5754. doi: 10.1021/cr900181u. [DOI] [PubMed] [Google Scholar]; (b) Fox J. D., Rowan S. J. Macromolecules. 2009;42:6823–6835. [Google Scholar]; (c) Kulkarni C., Balasubramanian S., George S. J. ChemPhysChem. 2013;14:661–673. doi: 10.1002/cphc.201200801. [DOI] [PubMed] [Google Scholar]; (d) Aparicio F., Garcia F. and Sanchez L., Supramolecular Polymers in Encyclopedia of Polymer Science and Technology, John Wiley & Sons, Inc., 2012, ISBN 9780471440260. [Google Scholar]
- (a) Hunter C. A., Anderson H. L. Angew. Chem., Int. Ed. 2009;48:7488–7499. doi: 10.1002/anie.200902490. [DOI] [PubMed] [Google Scholar]; (b) Ercolani G., Schiaffino L. Angew. Chem., Int. Ed. 2011;50:1762–1768. doi: 10.1002/anie.201004201. [DOI] [PubMed] [Google Scholar]; (c) Mayoral M. J., Bilbao N., González-Rodríguez D. ChemistryOpen. 2016;5:10–32. doi: 10.1002/open.201500171. [DOI] [PMC free article] [PubMed] [Google Scholar]; (d) Di Stefano S. and Ercolani G., Equilibrium Effective Molarity as a Key Concept in Ring-Chain Equilibria, Dynamic Combinatorial Chemistry, Cooperativity and Self-assembly in Advances in Physical Organic Chemistry, ed. I. H. Williams and N. H. Williams, Elsevier Ltd., 2016, vol. 50, ch. 1, pp. 1–77. [Google Scholar]; (e) Motloch P. and Hunter C. A., Thermodynamic Effective Molarities for Supramolecular Complexes in Advances in Physical Organic Chemistry, ed. I. H. Williams and N. H. Williams, Elsevier Ltd., 2016, vol. 50, ch. 2, pp. 77–118. [Google Scholar]
- Bilbao N., Destoop I., De Feyter S., González-Rodríguez D. Angew. Chem., Int. Ed. 2016;55:659–663. doi: 10.1002/anie.201509233. [DOI] [PubMed] [Google Scholar]
- (a) Montoro-García C., Camacho-García J., López-Pérez A. M., Bilbao N., Romero-Pérez S., Mayoral M. J., González-Rodríguez D. Angew. Chem., Int. Ed. 2015;54:6780–6784. doi: 10.1002/anie.201501321. [DOI] [PubMed] [Google Scholar]; (b) Romero-Pérez S., Camacho-García J., Montoro-García C., López-Pérez A. M., Sanz A., Mayoral M. J., González-Rodríguez D. Org. Lett. 2015;17:2664–2667. doi: 10.1021/acs.orglett.5b01042. [DOI] [PubMed] [Google Scholar]; (c) Montoro-García C., Camacho-García J., López-Pérez A. M., Mayoral M. J., Bilbao N., González-Rodríguez D. Angew. Chem., Int. Ed. 2016;55:223–227. doi: 10.1002/anie.201508854. [DOI] [PubMed] [Google Scholar]; (d) Montoro-García C., Mayoral M. J., Chamorro R., González-Rodríguez D. Angew. Chem., Int. Ed. 2017;56:15649–15653. doi: 10.1002/anie.201709563. [DOI] [PubMed] [Google Scholar]; (e) Montoro-García C., Bilbao N., Tsagri I. M., Zaccaria F., Mayoral M. J., Fonseca Guerra C., González-Rodríguez D. Chem.–Eur. J. 2018;24:11983–11991. doi: 10.1002/chem.201801704. [DOI] [PubMed] [Google Scholar]
- Mayoral M. J., Montoro-García C. and González-Rodríguez D., Self-assembled Systems via Nucleobase Pairing in Reference Module in Chemistry, Molecular Sciences and Chemical Engineering, Comprehensive Supramolecular Chemistry II, ed. J. Atwood, Elsevier Ltd., 2017, pp. 191–257. [Google Scholar]
- Yao H., Ye L., Zhang H., Li S., Zhang S., Hou J. Chem. Rev. 2016;116:7397–7457. doi: 10.1021/acs.chemrev.6b00176. [DOI] [PubMed] [Google Scholar]
- (a) Loudet A., Burgess K. Chem. Rev. 2007;107:4891–4932. doi: 10.1021/cr078381n. [DOI] [PubMed] [Google Scholar]; (b) Ulrich G., Ziessel R., Harriman A. Angew. Chem., Int. Ed. 2008;47:1184–1201. doi: 10.1002/anie.200702070. [DOI] [PubMed] [Google Scholar]; (c) Frath D., Massue J., Ulrich G., Ziessel R. Angew. Chem., Int. Ed. 2014;53:2290–2310. doi: 10.1002/anie.201305554. [DOI] [PubMed] [Google Scholar]
- Mayoral M. J., Camacho-García J., Magdalena-Estirado E., Blanco-Lomas M., Fadaei F., Montoro-García C., Serrano-Molina D., González-Rodríguez D. Org. Biomol. Chem. 2017;15:7558–7565. doi: 10.1039/c7ob01930k. [DOI] [PubMed] [Google Scholar]
- Camacho-García J., Montoro-García C., López-Pérez A. M., Bilbao N., Romero-Pérez S., González-Rodríguez D. Org. Biomol. Chem. 2015;13:4506–4513. doi: 10.1039/c5ob00098j. [DOI] [PubMed] [Google Scholar]
- These dye-conjugated molecules could be instead dissolved in CDCl3, revealing relatively sharp peaks, and subjected to DOSY experiments in this solvent (see Fig. S1). The diffusion coefficients obtained were used to estimate the cyclic tetramer size, which is in agreement with computational models. The gradual addition of DMSO-d6 to these solutions resulted in cyclic tetramer dissociation, and the monomer could be detected in slow exchange with the cycle both in 1H NMR and DOSY measurements (see Fig. S1 and our previous work)
- Calculated using ReactLab™ EQUILIBRIA (Jplus Consulting Pty Ltd). This software offers the possibility of global fitting, meaning that all wavelengths in the whole spectra are fitted simultaneously (see the ESI)
- (a) Sun H., Hunter C. A., Navarro C., Turega S. J. Am. Chem. Soc. 2013;135:13129–13141. doi: 10.1021/ja406235d. [DOI] [PubMed] [Google Scholar]; (b) Henkel S., Misuraca M. C., Ding Y., Guitet M., Hunter C. A. J. Am. Chem. Soc. 2017;139:6675–6681. doi: 10.1021/jacs.7b01765. [DOI] [PubMed] [Google Scholar]
- Alderighi L., Gans P., Lenco A., Peters D., Sabatini A., Vacca A. Coord. Chem. Rev. 1999;184:311–318. [Google Scholar]
- This is not the ideal situation for the titration experiments monitored by fluorescence spectroscopy, since it is preferable to excite the donor and monitor its emission quenching at a constant donor concentration, while using the acceptor as the titration agent added in excess (that is, the GdC + aC and AdU + aU combination detailed in the manuscript). In the alternative titration (GaC + dC or AaU + dU), in contrast, the donor concentration is constantly increasing), in contrast, the donor concentration is constantly increasing and this brings about several practical inconveniences. However, the opposite occurs when considering CD spectroscopy. In the regular titration (and this brings about several practical inconveniences. However, the opposite occurs when considering CD spectroscopy. In the regular titration (GdC + aC and AdU + aU), the absorbance of excess aC/aU in the 300–500 nm region quickly saturates the absorption spectrum and hampers a correct monitoring of the cGdC4/cAdU4 CD signal (see Fig. S3E). Instead, cGaC4 and cAaU4 macrocycles show isolated CD signals between 500 and 700 nm, a region where the absorption of the donor molecules does not interfere (or at least not up to a reasonable excess, see Fig. 6 and S3F)
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.