Statistical Methods for Conditional Survival Analysis

SUMMARY

We investigate the survival distribution of the patients who have survived over a certain time period. This is called a conditional survival distribution. In this paper, we show that one-sample estimation, two-sample comparison and regression analysis of conditional survival distributions can be conducted using the regular methods for unconditional survival distributions that are provided by the standard statistical software, such as SAS and SPSS. We conduct extensive simulations to evaluate the finite sample property of these conditional survival analysis methods. We illustrate these methods with real clinical data.

1. Introduction

Traditionally, survival analysis in clinical researches has been to investigate the distribution of patients’ survival times measured from the diagnosis of a disease or the start of a treatment (i.e., baseline). This type of analysis provides the survival probability of patients expected at the start of treatment that will be useful to predict their prognosis before starting the treatment. However, the survival probability evolves over time and usually decrease with increased survivorship, so that both patients and clinicians are interested in the change in survival probability over the progress of treatment and disease. Residual lifetime of individuals when they have survived over a relevant landmark of time can serve towards this end. For example, when comparing the efficacy of an intensive treatment with a standard treatment, patients receiving the prior may have a higher risk due to treatment-related mortality during treatment period, but may have a much lower risk once they survive over the treatment period with the disease cured.

While researches on residual lifetime theory have been very active in reliability area (e.g. Bryson and Siddiqui, 1969; Hollander and Proschan, 1975; Muth, 1977; Ruiz and Navarro, 1994), those in biostatistics field have been sparse. Among some biostatistical examples are Jeong and Jung (2008) on two-sample comparison of median residual lifetime, and Jung, Jeong and Bandos (2009) extending the two-sample problem to regression analysis. More recently, residual lifetime analysis has been very popularly used in clinical trials to analyze the change in survival distribution of patients as a progress of disease (e.g. Zamboni et al. 2010; Zabor et al. 2013; Bischof et al. 2015; Mertens et al. 2015) under the name of conditional survival analysis. Let T be the survival variable of a population with survivor function S(t) = P (T ≥ t). The t-year conditional survival distribution for patients who have survived for t₀ years, P (T ≥ t + t₀|T ≥ t₀), is denoted as S(t|t₀) = S(t + t₀)/S(t₀) for t ≥ 0. In the clinical literatures (e.g. Zabor et al. 2013; Mertens et al. 2015), investigators estimate the conditional survival distributions by replacing the survivor functions with their Kaplan-Meier (1958) estimates, but they do not provide a formal statistical testing to compare them between patient groups.

This paper can be regarded as a review paper supporting the analysis methods that are popularly used in medical field without theoretical justification. In this paper, we present analysis methods for conditional survival distributions including confidence interval of conditional survivor function for 1-sample problem, the conditional log-rank test for 2-sample test, and the conditional Cox (1972) proportional hazards model for regression analysis. We present simulation results to evaluate the performance of these methods. The proposed methods are demonstrated with real clinical data.

2. Analysis of Conditional Survival Distributions

2.1. One-Sample Problem

Suppose the lifetimes from n patients T₁, …,T_n are independent and identically distributed with survivor function S(t) = P(T_i ≥ t) and cumulative hazard function ⋀(t) = — log S(t). From patient i, we observe (X_i,δ_i), where X_i is the minimum of T_i and censoring time C_i, and δi is an event indicator taking 1 if patient i had an event and 0 otherwise. We assume that censoring times are independent of the survival times.

For patients who have survived for at least t₀(≥ 0) years, the probability that they live additional t years, S(t|t₀) = P(T_i ≥ t + t₀|T_i ≥ t₀), is given as

$$S\left(t|t_0\right)=S\left(t+t_0\right)/S\left(t_0\right)\text{for}t\ge 0$$ (1)

by the definition of conditional probabilities. S(t|t₀) is called the conditional survivor function for patients who have survived for t₀ years.

The conditional cumulative hazard function ⋀(t|t₀) = – log S(t|t₀) is given as ⋀(t|t₀) = ⋀(t + t₀) – ⋀(t₀) from (1). Hence, for t ≥ 0, the conditional hazard function λ(t|t₀) = ∂⋀(t|t₀)/∂t is identical to the unconditional (or marginal) hazard function λ(t + t₀) = ∂⋀(t + t₀)/∂t. Jeong, Jung and Costantino (2008) propose a nonparametric inference method on conditional median residual lifetime θ that satisfies S(θ|t₀) = 1/2.

Let $\widehat{S}\left(t\right)$ denote the Kaplan-Meier estimator of S(t). Then, S(t|t₀) is consistently estimated by

$$\widehat{S}\left(t|t_0\right)=\widehat{S}\left(t+t_0\right)/\widehat{S}\left(t_0\right)\text{for}t\ge 0.$$

From Corollary 3.2.1 of Fleming and Harrington (1991), we have

$$\sqrt{n}\left[\begin{array}{c}\widehat{S}\left(t+t_0\right)-S\left(t+t_0\right)\\ \widehat{S}\left(t_0\right)-S\left(t_0\right)\end{array}\right]=-\sqrt{n}\left[\begin{array}{c}S\left(t+t_0\right){\displaystyle {\int }_0^{t+t_0}Y{\left(s\right)}^{-1}dM\left(s\right)}\\ S\left(t_0\right){\displaystyle {\int }_0^{t_0}Y{\left(s\right)}^{-1}dM\left(s\right)}\end{array}\right]+o_p\left(1\right)$$ (2)

where $M\left(t\right)={\displaystyle {\int }_0^t\left\{dN\left(s\right)-Y\left(s\right)d\Lambda \left(s\right)\right\}}$ is a 0-mean martingale, and $N\left(t\right)={\displaystyle {\sum }_{i=1}^n{\delta }_{i}I\left(X_i\le t\right)}$ and $Y\left(t\right)={\displaystyle {\sum }_{i=1}^{n}I\left(X_i\ge t\right)}$ denote the event and the at-risk processes, respectively. Let y(t) denote the uniform limit of n⁻¹Y (t) for t ≤ τ, where τ denotes the minimum of the upper limits of the supports of censoring and survival distributions. By the martingale central limit theorem, $\sqrt{n}\left\{\widehat{S}\left(t+t_0\right)-S\left(t+t_0\right),\widehat{S}\left(t_0\right)-S\left(t_0\right)\right\}$ converges to N (0, Σ) in distribution, where

$$\Sigma =\left[\begin{array}{cc}S{\left(t+t_0\right)}^2{\displaystyle {\int }_0^{t+t_0}y{\left(s\right)}^{-1}d\Lambda \left(s\right)}& S\left(t_0\right)S\left(t+t_0\right){\displaystyle {\int }_0^{t_0}y{\left(s\right)}^{-1}d\Lambda \left(s\right)}\\ S\left(t_0\right)S\left(t+t_0\right){\displaystyle {\int }_0^{t_0}y{\left(s\right)}^{-1}d\Lambda \left(s\right)}& S{\left(t_0\right)}^2{\displaystyle {\int }_0^{t_0}y{\left(s\right)}^{-1}d\Lambda \left(s\right)}\end{array}\right],$$

which can be consistently estimated by replacing y(t), S(t) and d⋀(t) with their consistent estimators Y(t)/n, $\widehat{S}\left(t\right)$ and Y(t)⁻¹dN(t), respectively. That is, a consistent estimator of Σ is given as

$$\widehat{\Sigma }=n\left[\begin{array}{cc}\widehat{S}{\left(t+t_0\right)}^2\widehat{a}\left(t+t_0\right)& \widehat{S}\left(t_0\right)\widehat{S}\left(t+t_0\right)\widehat{a}\left(t_0\right)\\ \widehat{S}\left(t_0\right)\widehat{S}\left(t+t_0\right)\widehat{a}\left(t_0\right)& \widehat{S}{\left(t_0\right)}^2\widehat{a}\left(t_0\right)\end{array}\right],$$

where $n\widehat{a}\left(t\right)$ is a consistent estimator of ${\displaystyle {\int }_0^{t}y{\left(s\right)}^{-1}d\Lambda \left(s\right)}$ that is given as

$$\widehat{a}\left(t\right)={\displaystyle {\int }_0^{t}Y{\left(s\right)}^{-1}d\widehat{\Lambda }\left(s\right)}={\displaystyle \sum _{i=1}^n\frac{{\delta }_{i}I\left(0\le X_i\le t\right)}{{\left\{{\displaystyle {\sum }_{j=1}^{n}I\left(X_j\ge X_i\right)}\right\}}^2}}$$

by using the Nelson-Aalen (Nelson, 1969; Aalen, 1978) estimator $\widehat{\Lambda }\left(s\right)={\displaystyle {\int }_0^{t}Y{\left(s\right)}^{-1}dN\left(s\right)}$

The partial differentiation of θ₁/θ₂ with θ₁ = S(t + t₀) and θ₂ = S(t₀) is given as

$$\nabla ={\left[\frac{1}{S\left(t_0\right)},-\frac{S\left(t+t_0\right)}{S{\left(t_0\right)}^2}\right]}^T.$$

Hence, by the delta-method, $\sqrt{n}\left\{\widehat{S}\left(t|t_0\right)-S\left(t|t_0\right)\right\}$ converges to N (0,σ²) in distribution, where

$${\sigma }^2={\nabla }^T\Sigma \nabla ={\left\{S\left(t|t_0\right)\right\}}^2{\displaystyle {\int }_{t_0}^{t+t_0}y{\left(s\right)}^{-1}d\Lambda \left(s\right)}.$$

A consistent estimator ${\widehat{\sigma }}^2$ can be estimated by replacing S(t), y(t) and d⋀(t) with their consistent estimators $\widehat{S}\left(t\right)$, n⁻¹Y(t) and Y(t)⁻¹dN(t), respectively. That is,

$${\widehat{\sigma }}^2=n\widehat{S}{\left(t|t_0\right)}^2{\displaystyle \sum _{i=1}^n\frac{{\delta }_{i}I\left(t_0\le X_i\le t+t_0\right)}{{\left\{{\displaystyle {\sum }_{j=1}^{n}I\left(X_j\ge X_i\right)}\right\}}^2}}.$$

A 100(1 — α)% confidence interval for the conditional survival probability S(t|t₀) can be calculated using this asymptotic result, i.e.

$$\widehat{S}\left(t+t_0\right)/\widehat{S}\left(t_0\right)\pm z_{1-\alpha /2}\widehat{\sigma },$$

where z_1-α denote the 100(1 — α) percentile of the standard normal distribution.

These inferences are available only when there are patients who are at risk at t0 in the data set. In fact, these inferences can be much simplified. Suppose that P(T_i ≥ t₀)P (C ≥ t₀) > 0, i.e. the maximum survival time is longer than t₀ and some patients are followed for longer than t₀. Then, for t > 0, we have

$$P\left(T_i\ge t+t_0|X_i\ge t_0\right)=\frac{P\left(T_i\ge t+t_0,X_i\ge t_0\right)}{P\left(X_i\ge t_0\right)}.$$ (3)

The right hand side of (3) equals

$$\frac{P\left(T_i\ge t+t_0,T_i\ge t_0,C_i\ge t_0\right)}{P\left(T_i\ge t_0,C_i\ge t_0\right)}=\frac{P\left(T_i\ge t+t_0,C_i\ge t_0\right)}{P\left(T_i\ge t_0,C_i\ge t_0\right)}=\frac{P\left(T_i\ge t+t_0\right)}{P\left(T_i\ge t_0\right)}$$

since X_i = min(T_i,C_i), and T_i and C_i are independent. Hence, we have S(t|t₀) = P(T_i ≥ t + t₀|X_i ≥ t₀), denoting the survival probability at t + t₀ for patients who are at risk at t₀. This implies that the conditional survival probability S(t|t₀) can be estimated by calculating the Kaplan-Meier estimator at t + t₀ from the patients who are at risk at t₀.

This relationship becomes clearer by the definition of Kaplan-Meier estimator. For simplicity of notation, suppose that there are no ties among X_i, …,X_n. Then, by the definition of Kaplan-Meier estimator, (2) is expressed as

$$\begin{array}{c}\widehat{S}\left(t|t_0\right)=\frac{{{\displaystyle \prod }}_{i:X_i\le t+t_0}\left\{1-{\delta }_i/Y\left(X_i\right)\right\}}{{{\displaystyle \prod }}_{i:X_i\le t_0}\left\{1-{\delta }_i/Y\left(X_i\right)\right\}}\\ \text{}={\displaystyle \prod }_{i:t_0<X_i\le t+t_0}\left\{1-{\delta }_i/Y\left(X_i\right)\right\},\end{array}$$

which is the Kaplan-Meier estimator at t + t₀ calculated from the data set consisting of patients who are at risk at time t₀, and its variance is consistently estimated by $n^{-1}{\widehat{\sigma }}^2$. Hence, one-sample inference of conditional survival distribution using the delta-method will be identical to that based on the standard (or, unconditional) survival distribution using Kaplan-Meier estimator to the subset of data consisting of the patients who are at risk at t0. These results hold with tied survival data too.

An alternative confidence interval for S(t|t₀) can be obtained using the Fieller’s (1954) method. Let $\rho =\widehat{S}\left(t_0\right)/\widehat{S}\left(t+t_0\right)$. By using the asymptotic result for Kaplan-Meier estimator, $\sqrt{n}\left\{\rho \widehat{S}\left(t+t_0\right)-\widehat{S}\left(t_0\right)\right\}$ is asymptotically normal with mean 0, and its variance can be consistently estimated by $n\left({\rho }^2{\widehat{\sigma }}_{22}-2\rho {\widehat{\sigma }}_{12}+{\sigma }_{11}\right)$, where ${\widehat{\sigma }}_{ij}$ is the (i, j)-component of $n^{-1}\widehat{\Sigma }$. Hence, we have

$$P\left(-z_{1-\alpha /2}<\frac{\rho \widehat{S}\left(t+t_0\right)-\widehat{S}\left(t_0\right)}{\sqrt{\rho {\sigma }_{11}-2\rho {\sigma }_{12}+{\sigma }_{22}}}<z_{1-\alpha /2}\right)=1-\alpha .$$ (4)

We can obtain a 100(1 – α)% confidence interval of S(t|t₀) by solving the equation within the probability of (4) with respect to p, i.e.

$$\frac{f_1\pm \sqrt{f_1^2-f_0{f}_2}}{f_2},$$

where $f_0=\widehat{S}{\left(t+t_0\right)}^2-{\widehat{\sigma }}_{11}{z}_{1-\alpha /2}^2$, $f_1=\widehat{S}\left(t+t_0\right)\widehat{S}\left(t_0\right)-{\widehat{\sigma }}_{12}{z}_{1-\alpha /2}^2$ and $f_2=\widehat{S}{\left(t_0\right)}^2-{\widehat{\sigma }}_{22}{z}_{1-\alpha /2}^2$. This formula gives an appropriate confidence interval when $f_1^2>f_0{f}_2$

2.2. Two-Sample Log-Rank Test

Suppose that n_k patients are randomized to arm k(= 1, 2), and the survival time $T_{k1},\dots ,T_{k{n}_k}$ from the n_k patients of arm k are independent and identically distributed with survivor function Sk(t) = P(T_ki ≥ t) and cumulative hazard function Λ_k(t) = – log S_k(t). From patient i(= 1,–, n_k) in arm k(= 1, 2), we observe (X_ki, δ_ki), where X_ki is the minimum of T_ki and censoring time C_ki, and δ_ki is an event indicator taking 1 if the patient had an event and 0 otherwise. We assume that the censoring times are independent of the survival times within each arm. Let $N_k\left(t\right)={\displaystyle {\sum }_{i=1}^{n_k}{\delta }_{ki}I\left(X_{ki}\le t\right)}$ and $Y_k\left(t\right)={\displaystyle {\sum }_{i=1}^{n_k}I\left(X_{ki}\ge t\right)}$ denote the event and the at-risk processes for arm k, respectively. Also, let n = n₁ + n₂, N(t) = N₁(t) + N₂(t) and Y(t) = Y₁ (t) + Y₂ (t).

For conditional survivor function S_k(t|t₀) = S_k (t + t₀)/S_k (t₀), we want to derive a log-rank test to test H₀ : S₁(t|t₀) = S₂(t|t₀) for all t ≥ 0 against H₁ : S₁(t|t₀) ≠ S₂(t|t₀) for some t ≥ 0. From the previous section, d⋀(t|t₀) = d⋀(t + t₀) for t ≥ 0, so that we can consider a log-rank test for comparing conditional survival distributions for patients who have survived over t₀,

$$W_{t_0}=\sqrt{n}{\displaystyle {\int }_0^{\infty }H\left(t+t_0\right)}\left\{d{\widehat{\Lambda }}_1\left(t|t_0\right)-d{\widehat{\Lambda }}_2\left(t|t_0\right)\right\}=\sqrt{n}{\displaystyle {\int }_0^{\infty }H\left(t+t_0\right)}\left\{d{\widehat{\Lambda }}_1\left(t+t_0\right)-d{\widehat{\Lambda }}_2\left(t+t_0\right)\right\},$$

which is identical to

$$W_{t_0}=\sqrt{n}{\displaystyle {\int }_{t_0}^{\infty }H\left(t\right)}\left\{d{\widehat{\Lambda }}_1\left(t\right)-d{\widehat{\Lambda }}_2\left(t\right)\right\}$$

where H(t) is a predictable function that is uniformly convergent to h(t) over [t₀,τ] and τ is the minimum of the supports of the censoring and survival distributions. The logrank statistic (Peto and Peto, 1972) uses H(t) = n⁻¹Y₁(t)Y₂(t)/Y(t), the Gehan-Wilcoxon test (Gehan, 1965) uses H(t) = n⁻²Y₁(t)Y₂(t), and the Prentice-Wilcoxon test (Prentice, 1978) uses $H\left(t\right)=n^{-1}{\widehat{S}}^{-}\left(t\right)Y_1\left(t\right)Y_2\left(t\right)/Y\left(t\right)$, where ${\widehat{S}}^{-}$ is the left-continuous version of the Kaplan-Meier (1958) estimate from the pooled data.

Note that $W_{t_0}$ has the same expression as the standard rank tests W₀ except that the range of the integration is restricted to [t₀, ∞). Using the same arguments as those used for the standard rank tests (e.g. Gill, 1980; Fleming and Harrington, 1991), we can show that $W_{t_0}/{\widehat{\sigma }}_{t_0}$ is asymptotically standard normal with

$${\widehat{\sigma }}_{t_0}^2=n{\displaystyle {\int }_{t_0}^{\infty }\frac{H{\left(t\right)}^2}{Y_1\left(t\right)Y_2\left(t\right)}}dN\left(t\right)$$

under H₀. Hence, we reject H₀ in favor of H₁, if $\left|W_{t_0}/{\widehat{\sigma }}_{t_0}\right|>z_{1-\alpha /2}$ with two-sided type I error rate α.

For example, for the conditional log-rank test, we have

$$\begin{array}{c}{W}_{t_0}=\frac{1}{\sqrt{n}}{\displaystyle {\int }_{t_0}^{\infty }\frac{Y_1\left(t\right)Y_2\left(t\right)}{Y\left(t\right)}}\left\{d{\widehat{\Lambda }}_1\left(t\right)-d{\widehat{\Lambda }}_2\left(t\right)\right\}\\ =\frac{1}{\sqrt{n}}\left\{{\displaystyle \sum _{i=1}^{n_1}{\delta }_{1i}I\left(X_{1i}\ge t_0\right)}\frac{{\displaystyle {\sum }_{i^{\prime }=1}^{n_2}I\left(X_{2i^{\prime }}\ge X_{1i}\right)}}{{\displaystyle {\sum }_{k=1}^2{\displaystyle {\sum }_{i^{\prime }=1}^{n_k}I\left(X_{k{i}^{\prime }}\ge X_{1i}\right)}}}-{\displaystyle \sum _{i=1}^{n_2}{\delta }_{2i}I\left(X_{2i}\ge t_0\right)}\frac{{\displaystyle {\sum }_{i^{\prime }=1}^{n_1}I\left(X_{1i^{\prime }}\ge X_{2i}\right)}}{{\displaystyle {\sum }_{k=1}^2{\displaystyle {\sum }_{i^{\prime }=1}^{n_k}I\left(X_{k{i}^{\prime }}\ge X_{2i}\right)}}}\right\}\end{array}$$

and

$$\begin{array}{c}{\widehat{\sigma }}_{t_0}^2=\frac{1}{n}{\displaystyle {\int }_{t_0}^{\infty }\frac{Y_1\left(t\right)Y_2\left(t\right)}{Y{\left(t\right)}^2}}dN\left(t\right)\text{}\\ =\frac{1}{n}{\displaystyle \sum _{k=1}^2{\displaystyle \sum _{i=1}^{n_k}{\delta }_{ki}I\left(X_{ki}\ge t_0\right)}}\frac{\left\{{\displaystyle {\sum }_{i^{\prime }=1}^{n_1}I\left(X_{1i^{\prime }}\ge X_{ki}\right)}\right\}\left\{{\displaystyle {\sum }_{i^{\prime }=1}^{n_2}I\left(X_{2i^{\prime }}\ge X_{ki}\right)}\right\}}{{\left\{{\displaystyle {\sum }_{k^{\prime }=1}^2{\displaystyle {\sum }_{i^{\prime }=1}^{n_{k^{\prime }}}I\left(X_{k^{\prime }{i}^{\prime }}\ge X_{ki}\right)}}\right\}}^2}.\end{array}$$

From the expression of $W_{t_0}$ and ${\widehat{\sigma }}_{t_0}^2$, it is obvious that the conditional log-rank test at t₀ can be carried out by applying the standard log-rank test to the data set consisting of patients who are at risk at t₀, $\mathcal{D}\left(t_0\right)=\left\{\left(X_{ki},{\delta }_{ki}\right):X_{ki}\ge t_0,k=1,2,i=,\dots ,n_k\right\}$. The 2-sample conditional log-rank test can be easily extended to the log-rank test for K-sample cases with K > 2. These results holds for other types of conditional rank tests.

2.3. Regression Method

From patient i = 1,…, n, we observe covariates z_i = (z_1i, …, z_mi)^T together with the minimum of the survival and censoring times X_i and event indicator δ_i. We assume that, given z_i, the survival and censoring times are independent. Suppose that the conditional survival distribution for patients who have survived over t₀ has a proportional hazards model

$${\lambda }_i\left(t|t_0\right)={\lambda }_0\left(t|t_0\right)\exp \left({\beta }^T{z}_i\right)$$ (5)

for t ≥ 0, where λ_i(t|t₀) denotes the baseline conditional hazard function. As was shown in the previous sections, the conditional hazard function λ_i(t|t₀) is identical to the unconditional hazard function λ_i(t + t₀), so that (5) can be expressed as the regular proportional hazards model

$${\lambda }_i\left(t\right)={\lambda }_0\left(t\right)\exp \left({\beta }^T{z}_i\right)$$

for t ≥ t₀. Hence, if the (unconditional) survival distribution has a proportional hazards model with constant covariate effect over the whole time span, then the conditional survival distribution for any t₀(> 0) has the same proportional hazards model. However, if the covariate effect changes over time, then the regression model for conditional survival distribution changes in t₀.

The partial score and information matrix (Cox 1972) are given as

$$U_{t_0}\left(\beta \right)={\displaystyle \sum _{i=1}^n{\displaystyle {\int }_{t_0}^{\infty }\left(Z_i-\frac{{\displaystyle {\sum }_{j=1}^n{Z}_j{Y}_j\left(t\right)e^{{\beta }^T{Z}_j}}}{{\displaystyle {\sum }_{j=1}^n{Y}_j\left(t\right)e^{{\beta }^T{Z}_j}}}\right)}}{Y}_i\left(t\right)d{N}_i\left(t\right)$$

and

$$A_{t_0}\left(\beta \right)={\displaystyle \sum _{i=1}^n{\displaystyle {\int }_{t_0}^{\infty }\left\{\frac{{\displaystyle {\sum }_{j=1}^n{Z}_j^{\otimes 2}{Y}_j\left(t\right)e^{{\beta }^T{Z}_j}}}{{\displaystyle {\sum }_{j=1}^n{Y}_j\left(t\right)e^{{\beta }^T{Z}_j}}}-{\left(\frac{{\displaystyle {\sum }_{j=1}^n{Z}_j{Y}_j\left(t\right)e^{{\beta }^T{Z}_j}}}{{\displaystyle {\sum }_{j=1}^n{Y}_j\left(t\right)e^{{\beta }^T{Z}_j}}}\right)}^{\otimes 2}\right\}}}{Y}_i\left(t\right)d{N}_i\left(t\right)$$

respectively, where z^⊗2 = zz^T for a column vector z. Using the same asymptotic theory for the Cox regression method, we can show that $\sqrt{n}\left(\widehat{\beta }-\beta \right)$ is approximately normal with mean 0 and its variance-covariance matrix can be consistently approximated by $n{A}_{t_0}^{-1}\left(\widehat{\beta }\right)$.

For a univariate proportional hazards model with a dichotomous covariate, it is easy to show that the partial score test under $\beta =0,U_{t_0}\left(0\right)/\sqrt{A_{t_0}\left(0\right)}$, is identical to the conditional log-rank test, $W_{t_0}/{\widehat{\sigma }}_{t_0}$, that was discussed in the previous section. From the expression of the partial score and information, it is obvious that the conditional Cox regression model (5) can be fitted by applying the standard Cox regression method to the data set consisting of the patients who are at risk at t0, i.e. D (t₀) = {(X_i,δ_i,z_i) : X_i ≥ t₀,i = 1, …,n}. Kurta et al. (2014) proposed this analysis method without any theoretical justification.

3. Numerical Studies

3.1. Simulations

We want to show that the standard inference methods using the subset of data appropriately reflect the conditional survival distribution concept. At first, we conduct simulations on one-sample problems using a piecewise exponential distribution with survivor function

$$S\left(t\right)=\{\begin{array}{ll}\exp \left(–{\lambda }_{1}t\right)\hfill & \text{if}\text{0}\le t<2\hfill \\ \exp \left\{–{\lambda }_{2}t-2\left({\lambda }_1-{\lambda }_2\right)\right\}\hfill & \text{if}t\ge 2\hfill \end{array}$$

This distribution has a hazard function of λ₁ for 0 ≤ t ≤ 2 and λ₂ for t ≥ 2. By choosing λ₁ = 0.3466 and λ₂ = λ₁/2, the median survival for the whole patients is 2 years at the baseline, while that for those who have survived the first t₀ = 2 years is 4 years starting from the 2-year time point. Survival times are generated from S(t) and censoring times from U(0,a), where a is chosen for 30% of censoring rate. With a fixed at this value, we consider censoring distribution U(b, a + b) with b chosen for 15% of censoring. We generate 10,000 simulation samples of size n = 200. From each sample, we estimate S(t|t₀) and its 95% confidence interval by the delta-method and Fieller’s method for t₀ = 1, 2, 3, and 4, and t = 1, 2,…, 5 – t₀.

Table 1 reports mean bias and the sample standard deviation over the simulation samples (SSD) of the estimator, $\widehat{S}\left(t|t_0\right)$, and empirical coverage probabilities of the two confidence interval methods. Table 1 also reports the mean of the standard deviation (MSD) of $\widehat{S}\left(t|t_0\right)$ estimated by the delta method over the simulation samples. We observe that the estimated conditional probabilities have very small bias and the bias tends to increase in censoring proportion. As expected, SSD and MSD tend to increase in censoring proportion. They are very close for each simulation setting, but MSD is slightly smaller than SSD. This may result in slightly anti-conservative empirical coverage probability of the confidence intervals by the delta method. As t₀ and t increase, the number of subjects at risk decreases and the bias tends to be negative. The two confidence interval methods have empirical coverage probabilities close to the nominal 95% overall, but Fieller’s method always have slightly larger average length and more accurate coverage probability than the delta method. It is known that Fieller’s method usually provides better large sample approximation for a ratio of parameters than the delta method, e.g. Herson (1975). For each method, the average length increases in censoring proportion.

Table 1.

Bias, SSD, and MSD of $\widehat{S}\left(t|t_0\right)$, and average length and empirical coverage probability of 95% confidence intervals by Delta and Fieller methods

					Delta Method		Fieller Method
t0	t	Bias	SSD	MSD	ECP	Length	ECP	Length
			Under 15% Censoring
1	1	0.0004	0.0308	0.0299	0.9407	0.1096	0.9411	0.1098
	2	0.0005	0.0381	0.0379	0.9471	0.1486	0.9476	0.1489
	3	0.0001	0.0396	0.0390	0.9465	0.1528	0.9468	0.1530
	4	0.0000	0.0379	0.0371	0.9430	0.1453	0.9434	0.1456
2	1	0.0003	0.0386	0.0384	0.9470	0.1505	0.9477	0.1511
	2	−0.0001	0.0440	0.0432	0.9442	0.1694	0.9451	0.1701
	3	−0.0001	0.0434	0.0425	0.9433	0.1665	0.9435	0.1672
3	1	−0.0004	0.0487	0.0475	0.9387	0.1860	0.9425	0.1879
	2	−0.0004	0.0548	0.0536	0.9404	0.2099	0.9433	0.2120
4	1	−0.0002	0.0607	0.0589	0.9350	0.2307	0.9399	0.2352
			Under 30% Censoring
1	1	0.0003	0.0308	0.0299	0.9457	0.1170	0.9460	0.1172
	2	0.0006	0.0425	0.0416	0.9458	0.1631	0.9462	0.1634
	3	0.0000	0.0438	0.0432	0.9427	0.1696	0.9428	0.1699
	4	−0.0001	0.0422	0.0415	0.9398	0.1629	0.9402	0.1632
2	1	0.0004	0.0434	0.0425	0.9438	0.1668	0.9451	0.1875
	2	−0.0002	0.0488	0.0482	0.9420	0.1891	0.9433	0.1899
	3	−0.0002	0.0486	0.0477	0.9398	0.1872	0.9406	0.1881
3	1	−0.0006	0.0542	0.0531	0.9349	0.2085	0.9388	0.2109
	2	−0.0007	0.0620	0.0604	0.9376	0.2369	0.9418	0.2397
4	1	−0.0003	0.0686	0.0666	0.9320	0.2614	0.9374	0.2677

Now, we investigate the finite sample properties of the two-sample log-rank test on conditional distributions. Suppose that arm 1 has an exponential distribution with S_i (t) = exp(–λ₁t) for t ≥ 0, and arm 2 has a piecewise exponential distribution with survivor function

$$S_2\left(t\right)=\{\begin{array}{ll}\exp \left(–{\lambda }_{2}t\right)\hfill & \text{if}\text{0}\le t<2\hfill \\ \exp \left\{–{\lambda }_{1}t-2\left({\lambda }_2-{\lambda }_1\right)\right\}\hfill & \text{if}t\ge 2\hfill \end{array}$$

Note that, if λ₁ ≠ λ₂, then the two arms have different survival distributions, but with t₀ ≥ 2, their conditional distributions are identical with S_k(t|t₀) = exp(–λ₁t) and λ_k(t|t₀) = λ_k(t + t₀) = λ₁ for t ≥ 0. So, the log-rank test will have some power for t₀ < 2, but not for t₀ ≥ 2. We set λ₁ = 0.3466, λ₂ = λ₁/2, and n₁ = n₂ = 100, 150 or 200. We consider 15% and 30% censoring by uniform censoring variables as in the previous simulations. We generate 10,000 samples, apply the 2-sample log-rank test with 2-sided α = 0.05 for t₀ = 0,1, 2, 3, 4 to each sample, and estimate the empirical power as the proportion of samples that the log-rank test rejects the null hypothesis that two arms have the same conditional survival distributions. Note that the test with t₀ = 0 corresponds to the standard log-rank test to compare two unconditional distributions.

Table 2 reports the empirical power of the log-rank tests. As expected, the empirical power of the conditional log-rank test is close to the nominal level α = 0.05 with t₀ ≥ 2, for which two conditional distributions are identical. However, with t₀ = 0 and 1, it has some power, and the power becomes higher with a smaller t₀(= 0) since the time interval over which the two conditional distributions are different is wider in this case. The empirical power for t₀ = 0 and 1 also increases in n(= n₁ + n₂), while that for t₀ ≥ 2 is close to the nominal α = 5% regardless of the sample size. We observe that the power with t₀ < 2 does not much depend on the censoring proportion under the simulation setting.

Table 2.

Empirical power of the conditional log-rank tests between S₁(t) and S₂(t) for t₀ = 0,1, 2, 3, 4

n	Censoring	t0 = 0	1	2	3	4
200	15%	0.5490	0.1971	0.0522	0.0510	0.0558
	30%	0.5608	0.1853	0.0476	0.0549	0.0551
300	15%	0.7202	0.2601	0.0508	0.0480	0.0485
	30%	0.7324	0.2597	0.0515	0.0509	0.0516
400	15%	0.8451	0.3345	0.0501	0.0535	0.0546
	30%	0.8490	0.3206	0.0504	0.0502	0.0505

We consider two regression models for simulations on Cox regression analysis of conditional survival distributions. In Model 1, given covariate value z_i, the hazard function is given as

$${\lambda }_i\left(t\right)=\{\begin{array}{ll}{\lambda }_0\exp \left(\beta z_i\right)\hfill & \text{if}\text{0}\le t<2\hfill \\ {\lambda }_0\hfill & \text{if}t\ge 2\hfill \end{array}$$

Since the hazard function for t ≥ 2 does not depend on z_i, the conditional Cox regression with t₀ > 2 will be free of the covariate. The cumulative hazard function is given as

$${\Lambda }_i\left(t\right)=\{\begin{array}{ll}{\lambda }_{0}t\exp \left(\beta z_i\right)\hfill & \text{if}\text{0}\le t<2\hfill \\ {2\lambda }_0\exp \left(\beta z_i\right)+{\lambda }_0\left(t-2\right)\hfill & \text{if}t\ge 2\hfill \end{array}$$

and the survivor function is given as

$$S_i\left(t\right)=e^{-{\Lambda }_i\left(t\right)}=\{\begin{array}{ll}\exp \left\{-{\lambda }_{0}t\exp \left(\beta z_i\right)\right\}\hfill & \text{if}\text{0}\le t<2\hfill \\ \exp \left\{-{2\lambda }_0\exp \left(\beta z_i\right)-{\lambda }_0\left(t-2\right)\right\}\hfill & \text{if}t\ge 2\hfill \end{array}$$

For a U(0,1) random variable U_i, we generate T_i by solving S_i(T_i) = U_i. We set β= 0.3 and λ₀ = 0.3 for Model 1.

In Model 2, we consider a piecewise exponential distribution with a time-dependent covariate effect: for patient i with covariate value z_i, λ_i(0) = 0,

$${\lambda }_i\left(t\right)={\lambda }_0\exp \left(\beta /j{z}_i\right)\text{if}j-1<t\le j$$

for j = 1, 2,.… For this model, the covariate effect β/j decreases in t. The cumulative hazard function given z_i is,

$${\Lambda }_i\left(t\right)={\lambda }_0{\displaystyle \sum _{j=1}^k\exp \left(\beta /j{z}_i\right)}-\left(k-t\right){\lambda }_0\exp \left(\beta /k{z}_i\right)\text{if}k-1<t\le k.$$

Since ⋀_i(t) = – log S_i(t) and S_i(T_i) ~ U(0,1) for T_i with cumulative survivor function S_i(t), we generate T_i by solving equation ⋀_i(T_i) = – log U_i for U_i ~ U(0,1), i.e.

$$T_i=k-\frac{{\lambda }_0{\displaystyle {\sum }_{j=1}^k\exp \left(\beta /j{z}_i\right)+\log U_i}}{{\lambda }_0\exp \left(\beta /k{z}_i\right)}\text{if}{\lambda }_0{\displaystyle \sum _{j=1}^{k-1}\exp \left(\beta /j{z}_i\right)}<-\log U_i\le {\lambda }_0{\displaystyle \sum _{j=1}^k\exp \left(\beta /j{z}_i\right)}.$$

We set λ₀ = 0.3 and β = 0.4 for Model 2.

For each of the survival models, we generate 10,000 simulation samples of size n = 500 and generate 15% and 30% censoring from uniform distributions U(b, a + b) as in the previous simulations. For each subject, covariate z_i is generated from the standard normal distribution. From each sample, conditioning on (T_i ≥ t₀) with t₀ = 0, 1, 2, 3, or 4, we fit a proportional hazards model with a time-independent regression coefficient, estimate the regression coefficient, and test on H₀ : β= 0 with 2-sided α = 0.05.

Table 3 report the mean regression estimate and empirical power under the two models. For Model 1, with t₀ ≥ 2, the mean regression estimate is close to 0 and the empirical power is close to the nominal 0.05 level as expected. But, for t₀ < 2, the regression estimate is smaller than β= 0.3 since the covariate effect is diluted over the time interval t ≥ 2 which has no covariate effect. The regression estimate is smaller with t₀ = 1 than with t₀ = 0 since the former case has a narrower time interval with non-zero regression coefficient. With 30% of censoring, the regression estimate is larger since the additional censoring over 15% censoring occurs over t ≥ 2 (b = 2.2 for Model 1) for which the covariate has no effect. For Model 2, we observe that the regression estimate decays in t₀. And the decaying trend is more prominent with 30% censoring since the additional censoring occurs after b = 2.1 where the covariate effect is smaller than that over the earlier time interval. The empirical power quickly decreases in t₀ since both the mean covariate effect and the number of observations used in analysis decrease. However, the decrease of power in censoring proportion is smaller since the additional censoring occurs over the time interval with smaller covariate effect.

Table 3.

Mean regression estimate and empirical power of the conditional regression method

		Model 1		Model 2
Censoring	t0	Mean Est	Power	Mean Est	Power
15%	0	0.2022	0.8866	0.2610	0.9817
	1	0.1327	0.3706	0.1456	0.3912
	2	0.0036	0.0522	0.1076	0.1724
	3	0.0035	0.0530	0.0862	0.1043
	4	0.0026	0.0565	0.0717	0.0768
30%	0	0.2191	0.8824	0.2787	0.9793
	1	0.1470	0.3538	0.1514	0.3409
	2	0.0021	0.0545	0.1102	0.1475
	3	0.0004	0.0560	0.0869	0.0951
	4	−0.0033	0.0553	0.0692	0.0741

3.2. Real Data Analysis

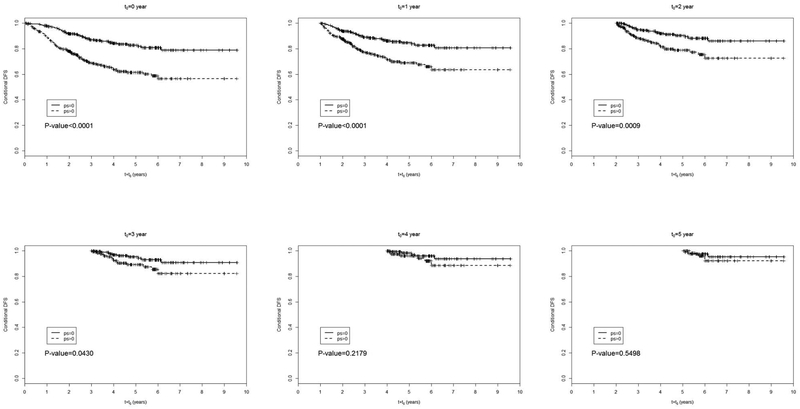
Kim et al. (2016) report analysis results of a retrospective record study on 723 lung adeno­carcinoma patients. All the patients underwent complete resection and mediastinal lymph node dissection with or without postsurgical adjuvant therapy. From each patient, overall survival (OS), time to death of any cause from surgery for tumor resection, and progression-free survival (PFS), time to tumor progression, were observed as outcomes together with risk factors including ECOG performance score (PS), with or without adjuvant chemotherapy (adj), tumor-shadow disappearance ratio (TDR) on CT value, and maximum standardized uptake value (SUV) on 18F-uoro-2-deoxyglucose (FDG)-PET/CT. SUV is log-transformed to lower the effect of outliers. The objectives of the study is to associate OS and PFS with the latter four clinical and image predictors using conditional survival analysis. We report the analysis results on OS to illustrate the conditional survival analysis methods. At first, patients are partitioned into two groups by PS = 0 and PS ≥ 1. Figure 1 displays the conditional survivor functions of the two PS groups and conditional log-rank p-value for t0 = 0,1,…, 6. We observe that the effect of PS decays as time passes from surgery and becomes insignificant for patients who have survived for t₀ = 4 years or longer. For each t₀ value, we regress the conditional survival at t₀ = 0, 1, …, 6 on these four covariates using a multivariate proportional hazards model. Figure 2 displays the regression estimate of each covariate and its 95% confidence interval against t₀. The covariate effect diminishes for longer survivors except history of adjuvant therapy which has a strong and consistent negative effect on OS. A high log-SUV tends to be associated with shorter OS, but it is not so significant for the t₀ values considered. Poor PS is significantly associated with poor OS until t₀ = 2 years and its effect becomes weak after t₀ = 4 years. High TDR is associated with longer until about t₀ = 4 years, but its effect diminishes among survivors over t₀ = 5 years.

Figure 1:

Conditional survivor functions for t₀ = 0,1, 2, 3, 4, 5. The p-values are from the conditional log-rank test between PS=0 and PS> 0 groups

Figure 2:

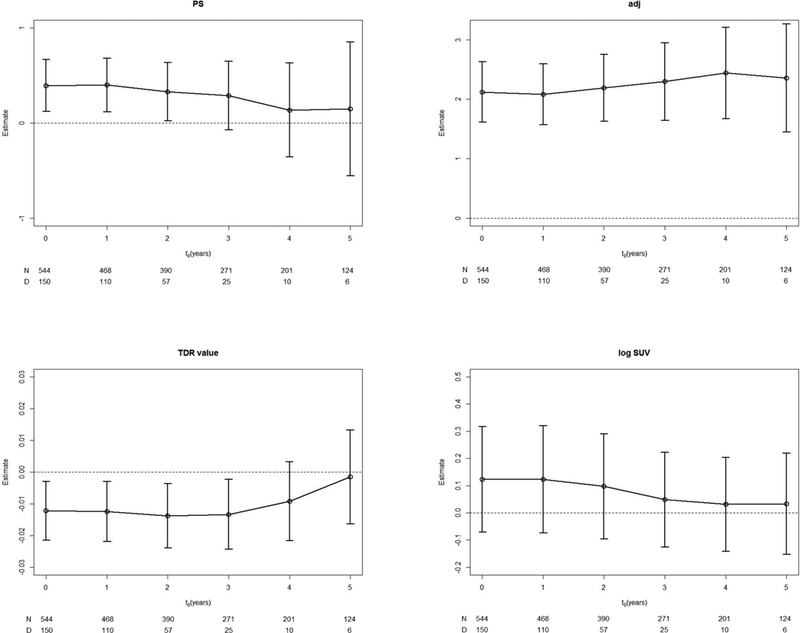
Regression estimate of each covariate and its 95% confidence interval against t₀

4. Conclusions

Conditional survival analysis has been popularly used to investigate the long term effect of treatment and baseline characteristics on the prognosis in clinical researches. As a reviewer points out, this analysis provides some new insight on the difference and effect of non-proportional hazards, early and late treatment and baseline patient characteristics. One meaningful scenario is that an aggressive surgical treatment may have a high early mortality, but leads to much higher survival or even cure after the treatment period, while a chemotherapy does not have a severe treatment-related mortality, but leads to a moderate treatment effect over a long time span. The conditional survival analysis would be particularly useful to compare this kind of early and late survival benefit between treatments.

Without any theoretical justification, investigators have applied the standard survival analysis methods, such as log-rank test and Cox regression, to the data removing the patients whose censoring or event times are shorter than t₀ claiming that this results in the survival distributions of the survivors over t₀. This paper is to theoretically justify this claim. We have reviewed inference methods of one-sample, two-sample and regression analysis for conditional survival distributions. For a reliable estimation of S(t|t₀), we need enough number of patients who are at risk at t₀ and enough number of patients followed for at least t + t₀ unless all patients have events before this time point. Hence, a conditional survival analysis will not be available unless the follow-up period is long enough. Since the conditional survival analyses among the patients who survived over t₀ are identical to the standard survival analyses using the data set consisting of patients who are at risk at time t₀. Hence, we can conduct any conditional survival analysis using existing statistical softwares, such as SAS or SPSS, with the standard survival analysis procedures. These methods are based on large sample theory. Through simulations, we find that these methods accurately reflect the change in risk function over time and have good finite sample properties.

If the marginal survival distribution satisfies a proportional hazards model (PHM) assumption with time-fixed covariate effect, then the regression estimates from conditional survival analysis will give similar regression estimates for various t₀ values. We may be able to develop a goodness of fit test for PHM assumption of a marginal survival distribution using this concept. Jung and Wieand (1999) propose a goodness of fit test for PHM using a similar approach. By plotting the trend of regression estimates of conditional survival analysis over t₀, we can also model the time trend of covariates with time-varying effect, refer to Therneau and Grambsch (2000).