Recommendations for Simulating Microparticle Deposition at Conditions Similar to the Upper Airways with Two-Equation Turbulence Models

Abstract

The development of a CFD model, from initial geometry to experimentally validated result with engineering insight, can be a time-consuming process that often requires several iterations of meshing and solver set-up. Applying a set of guidelines in the early stages can help to streamline the process and improve consistency between different models. The objective of this study was to determine both mesh and CFD solution parameters that enable the accurate simulation of microparticle deposition under flow conditions consistent with the upper respiratory airways including turbulent flow. A 90° bend geometry was used as a characteristic model that occurs throughout the airways and for which high-quality experimental aerosol deposition data is available in the transitional and turbulent flow regimes. Four meshes with varying degrees of near-wall resolution were compared, and key solver settings were applied to determine the parameters that minimize sensitivity to the near-wall (NW) mesh. The Low Reynolds number (LRN) k-ω model was used to resolve the turbulence field, which is a numerically efficient two-equation turbulence model, but has recently been considered overly simplistic. Some recent studies have used more complex turbulence models, such as Large Eddy Simulation (LES), to overcome the perceived weaknesses of two-equation models. Therefore, the secondary objective was to determine whether the more computationally efficient LRN k-ω model was capable of providing deposition results that were comparable to LES. Results show how NW mesh sensitivity is reduced through application of the Green-Gauss Node-based gradient discretization scheme and physically realistic near-wall corrections. Using the newly recommended meshing parameters and solution guidelines gives an excellent match to experimental data. Furthermore, deposition data from the LRN k-ω model compares favorably with LES results for the same characteristic geometry. In summary, this study provides a set of meshing and solution guidelines for simulating aerosol deposition in transitional and turbulent flows found in the upper respiratory airways using the numerically efficient LRN k-ω approach.

1 INTRODUCTION

Laminar, transitional and fully turbulent flows are all expected to occur in the upper respiratory airways. Transitional and turbulent flow as well as the process of flow regime change from laminar to turbulent flow is notoriously difficult to predict and can be influenced by upstream conditions, wall surface roughness and even environmental noise (Schlichting, 1987; Tennekes & Lumley, 1972; Wilcox, 1998). Transitional and turbulent flows are known to have a significant impact on particle deposition through the interaction of turbulent eddies and discrete elements, which typically increases deposition compared with the laminar flow case (Crowe, Troutt, & Chung, 1996). Therefore, accurate predictions of lung doses arising from either inhaled pollutant particulate matter or pharmaceutical aerosols requires reasonable approximations of both the turbulent flow field and the interaction of turbulent eddies with particles.

The upper airways consist of the oral and/or nasal geometry, trachea and approximately the first six airway bifurcations. Jets of airflow with flow detachment and recirculation are formed in the nasal valve and larynx (Xi, Longest, & Martonen, 2008; J. Xi, Berlinski, Zhou, Greenberg, & Ou, 2012). As described in previous experimental and numerical results (Ahmed & Giddens, 1983a, 1983b; Ghalichi et al., 1998), transition to turbulence in flow constrictions of 50 and 75% area reductions occurs at Reynolds numbers of approximately 1,100 and 400, respectively, which are significantly lower than the typical value of 2,300 for a straight cylindrical conduit. Considering a mean inhalation flow rate of 60 L/min (LPM), upper-airway Reynolds number values for an adult range from approximately 10,620 (larynx) to 553 (bifurcation B6). Peak inhalation flow rate with a dry powder inhaler (DPI) can reach 160 LPM (Delvadia, Wei, Longest, Venitz, & Byron, 2016), significantly multiplying these Reynolds number estimates at the point in time when the largest concentration of an inhaled pharmaceutical aerosol is entering the lungs. Furthermore, inhalers introduce air jets or sprays in the mouth-throat (MT) geometry, which are frequently turbulent and significantly impact MT depositional loss of the aerosol (DeHaan & Finlay, 2004; Longest, Hindle, Das Choudhuri, & Xi, 2008). In a previous study of the laryngeal jet, Xi et al. (2008) showed that the turbulent viscosity ratio maintained a value of at least 2 through bifurcation B6 at an inhalation flow rate of 30 LPM. The study of Lin et al. (2007) also showed turbulence intensity values of 20% extending from the laryngeal jet into the lungs. A number of studies have demonstrated the importance of turbulence on deposition throughout the upper airways (Ball, Uddin, & Pollard, 2008; Jayaraju, Brouns, Lacor, Belkassem, & Verbanck, 2008; Lambert, O'Shaughnessy, Tawhai, Hoffman, & Lin, 2011; Longest, Tian, Delvadia, & Hindle, 2012; Matida, Finlay, Breuer, & Lange, 2006; Xi et al., 2008; J. Xi & Longest, 2007; Zhang & Kleinstreuer, 2011). Surprisingly, some of these studies have shown that turbulence can increase or decrease depositional loss (Longest & Vinchurkar, 2007b; Xi et al., 2008). While eddy interaction serves to increase depositional particle losses, the more blunt turbulent velocity profiles can actually reduce impaction at carinal ridges. Furthermore, increased eddy viscosity can reduce secondary flows and associated particle impaction on bifurcation sidewalls.

Turbulence has been captured in respiratory airway geometries with models that range in complexity from the one-equation Spalart-Allmaras model (Wilcox, 1998) to full resolution of all turbulence scales with direct numerical simulation (DNS) (Lin et al., 2007). Specific examples include two-equation turbulence models such as the k-ε (Stapleton, Guentsch, Hoskinson, & Finlay, 2000) and k-ω (Xi et al., 2008; Zhang & Kleinstreuer, 2011), detached eddy simulation (Jayaraju et al., 2008), large eddy simulation (LES) (Jayaraju et al., 2008; Jin, Fan, Zeng, & Cen, 2007; Matida et al., 2006) and DNS (Lin et al., 2007). In general, studies that compare results from multiple models typically find that the simpler model is inadequate compared with the more complex model. This move to more complex turbulence models makes the simulation of large airway regions including the influence of transient inhalation over a 5 s period impractical due to the time and computational power that is required to run the simulations. Critical questions that are often overlooked in turbulence model comparison studies include: (i) what impact will discrepancies in velocity and turbulence parameters have on particle deposition, (ii) are the simpler models being properly applied, and (iii) is the most developed version of each simpler model being applied. For example, Ball et al. (2008) compared experimental results with predictions of two-equation turbulence models and found discrepancies in the velocity and turbulent kinetic energy (TKE) results. However, particle deposition was not considered and the more recent Low Reynolds Number (LRN) k-ω model was not included. Matida et al. (2006) compared aerosol deposition between LES and shear stress transport (SST) k-ω turbulence models and found significantly better predictions with the LES model compared to in vitro experiments. While these results were based on particle deposition, they did not include LRN k-ω predictions and neglected near-wall (NW) corrections, which were previously shown to be important (Matida, Finlay, & Grgic, 2004). Similar findings of superior performance with a LES model compared with a standard k-ω model without NW corrections were reported by Jayaraju et al. (2007). Furthermore, while LES has been found to be more accurate than two-equations models based on the predictions of turbulence properties, the increase in computational cost is very large. In a simple representative geometry of a curved pipe at Re = 10,000, Breuer et al. (2006) reported that grid convergent results required approximately 2.3 million control volumes. In a constricted pipe test geometry, Zhang and Kleinstreuer (2011) reported that LES simulations required approximately 100-fold more computer power than using a two-equation turbulence model.

Two-equation turbulence models implement the Reynolds Averaged Navier Stokes (RANS) equations and simulate turbulent effects typically with a kinetic energy (k) and dissipation (ε or ω) term. Transport equations are formed for the two turbulence terms, which are then combined into a turbulent viscosity scalar that is present in the RANS equation and functions as an added viscosity on the flow field (Wilcox, 1998). The effect of turbulence on particle dispersion is then approximated through the use of an eddy interaction model, which implements the turbulence terms to stochastically recreate eddy structures and predict associated chaotic motion of particles as a random walk (Crowe et al., 1996). A primary shortcoming of all two-equation turbulence models is the assumption of isotropic (direction independent) turbulent fluctuations near wall boundaries (Wilcox, 1998). Matida et al. (2004) provided a NW correction for anisotropic turbulence effects, which has frequently been applied (Longest & Hindle, 2009; Longest, Hindle, Das Choudhuri, & Byron, 2007; Longest et al., 2008). Longest and Xi (2007) reported that improved NW interpolation of the velocity field was also needed in turbulent simulations using two-equation models. Of the available two-equation models, the LRN k-ω model has been most successful in predicting transitional and turbulent flows including reasonable predictions of particle deposition (Kleinstreuer & Zhang, 2003; Longest & Hindle, 2009; Longest et al., 2007; Longest et al., 2008; Longest, Tian, Delvadia et al., 2012; Longest, Tian, Walenga, & Hindle, 2012; Longest & Xi, 2007; Tian, Longest, Su, Walenga, & Hindle, 2011; Zhang & Kleinstreuer, 2003, 2011). Low Reynolds number refers to the fact that the model simulates the flow field all the way through the viscous sub-layer, i.e., the low Reynolds number region, and can be successfully applied to both low and high Reynolds number flows (Wilcox, 1998). The primary advantage of two-equation models is high efficiency approximation of very complex transitional and turbulent flow phenomena. However, questions remain if these models can successfully be applied to predict particle deposition in the upper respiratory airways (Ball et al., 2008; Matida et al., 2006).

Studies that have used the LRN k-ω model with NW anisotropic and sometimes velocity interpolations have reported reasonable agreement with experimental results of turbulence metrics and particle deposition. Zhang and Kleinstreuer (2003) compared the performance of two-equation turbulence models in a constricted flow geometry and showed that the LRN k-ω model reproduced laminar, transitional and turbulent flow characteristics comparable with the experimental measurements of Ahmed and Giddens (1983a; 1983b; 1984). Other studies also using the constricted tube geometry have reached similar conclusions (Ryval, Straatman, & Steinman, 2004; Varghese & Frankel, 2003). The more recent study of Zhang and Kleinstreuer (2011) considered a series of two-equation turbulence models compared with LES in constricted tube and MT geometries. The LRN k-ω model was again shown to perform well and predictions of nanoparticle deposition in the MT were similar to LES. Our group has successfully applied the LRN k-ω model to predict particle deposition in the upper respiratory airways with good agreement to in vitro (Longest & Hindle, 2009; Longest, Tian, Walenga et al., 2012; Longest & Vinchurkar, 2007b; Longest & Xi, 2007) and in vivo (Longest, Tian, Khajeh-Hosseini-Dalasm, & Hindle, 2016; Tian, Hindle, Lee, & Longest, 2015) studies. These simulations have considered pharmaceutical aerosols including jet and spray effects from DPIs (Longest, Tian, Delvadia et al., 2012; Longest, Tian, Walenga et al., 2012; Tian et al., 2011), metered dose inhalers (MDI) (Longest, Tian, Walenga et al., 2012; Walenga & Longest, 2016; Walenga, Tian, & Longest, 2013), and soft mist inhalers (Delvadia, Longest, Hindle, & Byron, 2013; Longest & Hindle, 2009; Longest, Hindle, & Das Choudhuri, 2009). For example, Longest et al. (2012) showed that the MT deposition predicted by the LRN k-ω model with NW corrections was within 10% of in vitro experimental data for complex pharmaceutical aerosols including the effect of polydisperse aerosol size, transient inhalation over an approximately 5 s period and turbulence for MDI and DPI devices.

Based on successful applications of the LRN k-ω model with NW corrections in predicting aerosol deposition in upper airway geometries, it appears that this model provides a good compromise between accuracy and efficiency. However, in other studies we have shown that computational mesh structure and type can have a dramatic effect on solution accuracy (Longest & Vinchurkar, 2007a; Vinchurkar & Longest, 2008). Guidelines for the use of the LRN k-ω model and for two-equation models in general are not well defined for applications to the respiratory airways. The current specification of 20 layers of computational cells through the turbulent wall region including the buffer layer (ANSYS, 2012) may be computational prohibitive for large complete-airway simulations (Longest, Tian, Delvadia et al., 2012), and not necessary. Current recommendations may also be difficult to implement in complex geometries such as the nasal valve and larynx where flow passages are very narrow (Subramaniam, Richardson, Morgan, Kimbell, & Guilmette, 1998). For example, Walenga et al (2014) reported excellent agreement with experimental results of particle deposition in the nose with a nasal cannula interface using only 5 NW cell layers. Furthermore, no recommendations are currently available for overall layer-to-layer (L2L) thickness of the NW mesh, or recommendations on the method used to calculate gradients within control volumes, which interact with mesh type and resolution to influence the solution accuracy. Finally, mesh style in conjunction with turbulence modeling has previously not been considered in respiratory airway geometries.

The objective of this study is to determine both mesh and CFD solution parameters that enable the accurate simulation of microparticle deposition under flow conditions consistent with the upper respiratory airways including turbulent flow. To represent conditions similar to the upper respiratory airways, a simple 90^o curved tube is selected as a characteristic geometry. This geometry provides a different test scenario than the constricted tube model that is typically used to represent turbulence in the upper airways. Both the nasal and MT airways contain curved tube features that are associated with high particle deposition. Furthermore, deposition in bifurcations is often approximated with correlations for deposition in curved tubes (Martonen et al., 2000). The comparison metric considered will be total microparticle deposition, based on the well documented experimental results of Pui et al. (1987) with Re = 6,000 and Re = 10,000. For comparison, Breuer et al. (2006) previously published LES in curved tubes with excellent agreement when compared with Pui et al. (1987). In addition to an evaluation of mesh and solution parameters, a key questions to be addressed is whether the LES agreement with experiments (Breuer et al., 2006) can be matched with the correct use of a much simpler and computationally efficient two-equation turbulence approach.

2 METHODS

2.1 STUDY DESIGN

For the selected 90° bend geometry and a regular hexahedral core mesh, turbulent kinetic energy and particle deposition are first compared across four NW mesh resolutions (namely Recommended, Intermediate, Targeted, and Poor Ratio). Both the effects of the first NW cell layer height and the discretization schemes (Least Squares Cell Based vs. Green Gauss Node Based) are considered. The analysis is then extended to evaluate the effects of meshes with irregular tetrahedral elements having prismatic triangular NW cell layers. The utility of anisotropic turbulence corrections and NW velocity interpolations are demonstrated. Finally, recommended solution parameters are defined and applied to make best-case predictions, which are then compared to experimental results at two Reynolds numbers and previously published LES results.

2.2 EXPERIMENTAL MODEL AND RESULTS

For a curved tube geometry, the Pui et al. (1987) data was collected by measuring the deposition of monodisperse aerosols with Stokes numbers from 0.1 to 1.4 through glass and stainless steel 90° bends with internal diameters (ID) of 0.93, 3.95, 5.03, and 8.51 mm and Reynolds numbers (Re) of 100, 1,000, 6,000, and 10,000. In this study, CFD-predicted aerosol deposition results are compared with the following Pui et al. (1987) experimental data sets: Re = 6,000 with ID = 5.03 mm; and Re = 10,000 with ID = 8.51 mm, which were both evaluated with stainless steel tubes. This covers a range of turbulent conditions and changes in the geometry by increasing the tube diameter. The correlation from the experimental study gives aerosol deposition efficiency (η) as a function of particle Stokes number (St), as:

$$\eta =1-{10}^{-0.963\text{St}}$$ (1)

The deposition efficiency and correlation results for the selected experimental models are given in Table 1.

Table 1.

Experimental results and correlation predictions for selected Pui et al. models

Reynolds Number [−]	Tube ID [mm]	Stokes Number [−]	Particle Diameter [μm]	Experimental DE [%]	Correlation Prediction [%]
6,000	5.03	0.03	1.10	6.1	6.4
		0.13	2.38	13.4	25.0
		0.19	2.89	29.6	34.4
		0.36	4.01	55.0	55.0
		0.60	5.20	76.0	73.6
		0.72	5.70	80.6	79.7
		1.00	6.74	88.4	89.1
10,000	8.51	0.03	1.50	N/A	6.4
		0.13	3.10	N/A	18.5
		0.19	3.80	N/A	28.3
		0.27	4.56	48.4	45.0
		0.29	4.73	50.3	47.4
		0.46	5.98	65.6	63.9
		0.75	7.66	82.7	81.0

2.3 NUMERICAL GEOMETRY AND MESHES

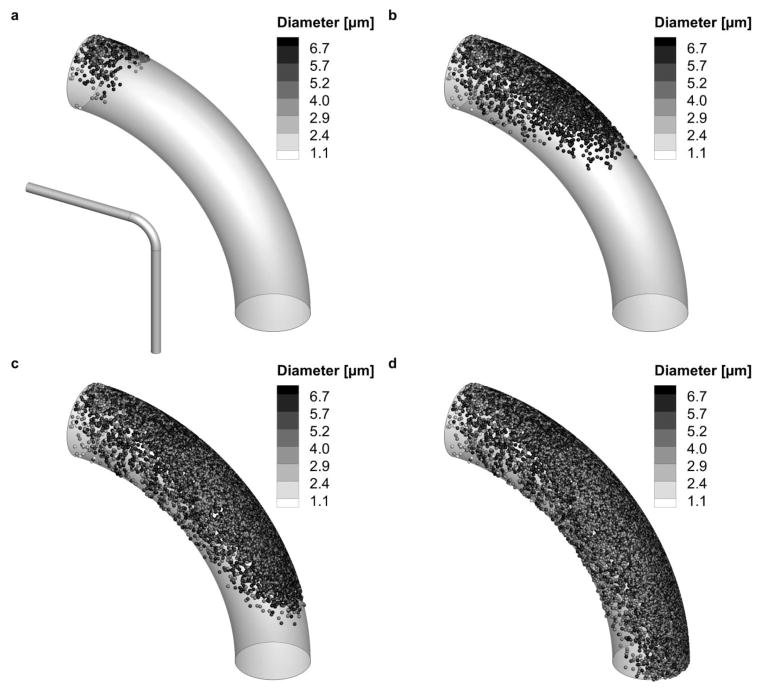
The inset in Figure 1a shows the full computational domain that matches the experimental setup of the Pui et al. (1987) geometry. The straight entry and exit sections of the tube were included to ensure that the flow is fully developed at the 90° bend inlet and smoothly exits the geometry, as was the case with the experiemental model. The curvature ratio (bend radius over tube radius) also matches the original setup, with ratios of 5.7 and 5.6 for the Re = 6,000 and 10,000 cases, respectfully.

Figure 1.

Overview of geometry and particle deposition locations on the 90-degree bend at deposition times of (a) 0.003 s, (b) 0.006 s, (c) 0.009 s, and (d) 0.012 s. Results shown are for the Re = 6,000 case that follows the CFD guidelines recommended at the conclusion of this study.

2.3.1 Mesh Dependency

Preliminary results compared five meshes to evaluate the dependency of results on mesh resolution. The 90° bend section for each case had approximately 1,400,000, 672,000, 368,000, 208,000, and 83,000 hexahedral cells, inclusive of the NW layers. Consistency between deposition profiles (deposition fraction vs. particle diameter), velocity profiles at the inlet and outlets, and pressure drop across the tube were considered. Sensitivity of the turbulent flow to mesh resolution was also assessed by comparing u⁺ vs. y⁺ plots between the five meshes and to Spalding’s equation (1961). These u⁺ vs. y⁺ plots were generated from data in the region of fully developed flow within the turbulent buffer and sub-layer near the wall.

The mesh dependency evaluation concluded that the coarse (368,000 cells) case gave the best compromise of small numerical error and reduced cell count. In several of the meshes that are evaluated in subsequent sections of this study, the resolution of the mesh in the NW region is adjusted to determine the influence on results. In all cases, the core mesh (covering the bulk flow) for the grid independent case was retained, and different NW mesh resolution parameters are then applied.

2.3.2 Near-wall Mesh Resolution

Traditionally, there are two approaches to modelling the NW region when using two-equation RANS turbulence models. The wall function method uses an empirical formulation to model the flow in the inner and outer layer with a relatively large NW cell height. Wall y⁺ values should ideally be greater than 30, with 15 as an acceptable minimum. For low to medium Reynolds number flow, such as the respiratory airways, the ANSYS FLUENT Theory Manual (2012) advises against using the wall function approach as the assumptions that the method uses are not applicable to this flow regime. The other approach is to use the enhanced wall treatment (EWT) method where the mesh aims to fully resolve the NW turbulent layers. This method is considered to be y⁺ independent, but wall values of one are recommended . The main concern when using the EWT method is that there are an adequate number of cell layers to resolve the flow in the NW region. When using the k-ω turbulence model in ANSYS FLUENT, the EWT method is implemented by default.

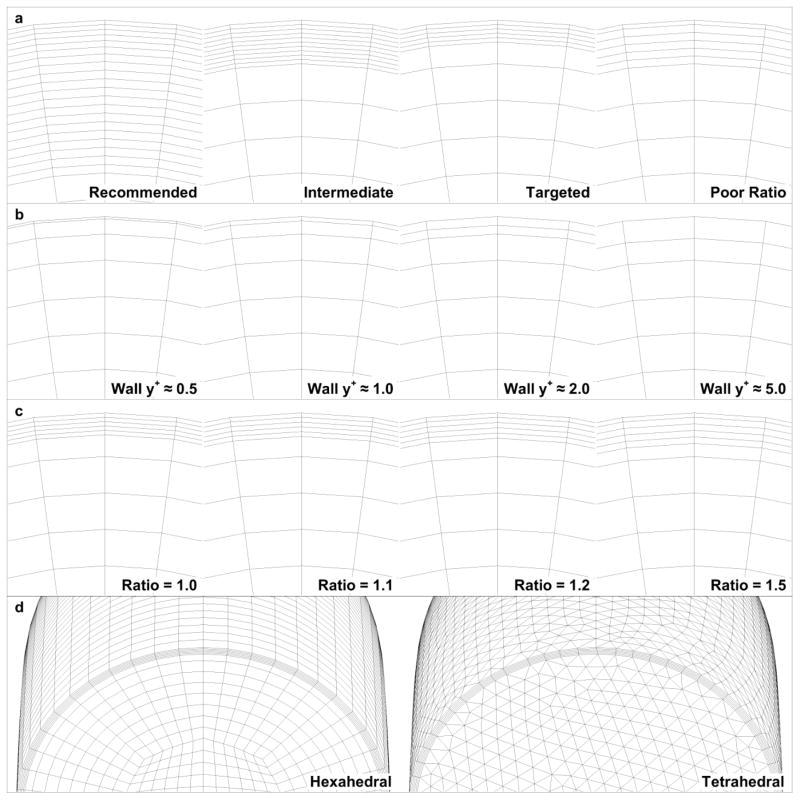
Initially four meshes are compared that each have varying degrees of NW mesh resolution and are suitable for the EWT method. These meshes are referred to as the Recommended, Intermediate, Targeted, and Poor Ratio cases, and are presented in Figure 2a. The Recommended mesh follows the NW mesh resolution guidelines in the ANSYS FLUENT Theory Guide (2012), with 20 cell layers that cover the region from the wall up to a y⁺ value of approximately 60 and a first layer thickness that gives a wall y⁺ of approximately one. These recommended guidelines aim to model the flow in the sublayer and buffer region accurately when using the EWT option by using a high fidelity mesh in the NW region. However, there are several close proximity surfaces in the nasal cavity, especially the meatuses, where such a high level of mesh resolution is not feasible. Ideally, the NW mesh in an upper airway model would be similar to the Targeted mesh, with five equally spaced NW cell layers and a first layer height that gives a wall y⁺ of approximately one. Here the resolution is fine enough to capture the large flow field gradients near the wall, but the overall cell layer height is thin enough to be included between close proximity surfaces. Fewer cell layers also drastically reduces the total cell count, so accurate results from the Targeted mesh would provide a more computationally efficient model. The Intermediate model uses 10 equally spaced NW cell layers with a wall y⁺ of approximately one. This provides a level of mesh resolution that falls within the Recommended and Target models. Finally, the Poor Ratio mesh is similar to the Targeted case, with the exception that the L2L ratio from Layer 1 to 2 is 1.8, and the layers are then equally spaced from Layer 2 to 5. This mesh is included in the evaluation to determine how poorly defined L2L thicknesses can influence the results. In complex geometries, the meshing software can stretch and shrink cell layers in order to conform to the surface. Therefore, it is possible to have large increases in the L2L ratio such as the Poor Ratio case, which may not accurately capture high gradients in the flow field.

Figure 2.

Summary of meshes used to evaluate the sensitivity of the TKE field and particle deposition related to near-wall resolution and cell type.

After evaluating the four NW mesh conditions described above, both first cell layer height and L2L ratio are considered. The effect of increasing the thickness of the first NW layer is evaluated using the meshes shown in Figure 2b. The definition of these Wall y⁺ meshes uses only one NW layer to neglect the influence of L2L ratio on results. Consistency in deposition profiles between cases will indicate that first layer thickness does not influence results within the range considered. The effect of L2L ratio between Layer 1 and 2 is explored further with the meshes in Figure 2c. The Ratio meshes determine at what point the ratio between Layer 1 and 2 becomes excessive and begins to influence results. The NW layer thickness in Figure 2c is consistent between each of the Ratio meshes and gives a wall y⁺ of approximately one. The NW cell layer height that gives the required wall y⁺ is estimated by using Blasius’ equation for turbulent flow in a circular pipe (Blasius, 1913) to approximate the skin friction and subsequently the wall shear stress. This is then used in the standard y⁺ equation to obtain an estimation of the distance from the NW cell centroid to the wall boundary. Table 2 summarizes each of the meshes described here and includes the meshing parameters that are used to generate the required NW cell layers.

Table 2.

Summary of near-wall meshes and parameters

Name	# NW Layers	First Layer Thickness (y+)	Layer-to-Layer Ratio	Total NW Thickness
Recommended	20	0.02 (≈1.0)	Layers 1–8: 1.1	0.7
			Layers 8–20: 1.0
Intermediate	10	0.02 (≈1.0)	1.0	0.20
Targeted	5	0.02 (≈1.0)	1.0	0.10
Poor Ratio	5	0.02 (≈1.0)	Layer 1–2: 1.8	0.20
			Layers 2–5: 1.0
Wall y+ ≈ 0.5	1	0.01 (≈0.5)	N/A	0.01
Wall y+ ≈ 1.0	1	0.02 (≈1.0)	N/A	0.02
Wall y+ ≈ 2.0	1	0.04 (≈2.0)	N/A	0.04
Wall y+ ≈ 5.0	1	0.10 (≈5.0)	N/A	0.10
Ratio = 1.0	5	0.02 (≈1.0)	1.0	0.10
Ratio = 1.1	5	0.02 (≈1.0)	Layer 1–2: 1.1	0.12
			Layers 2–5: 1.0
Ratio = 1.2	5	0.02 (≈1.0)	Layer 1–2: 1.2	0.15
			Layers 2–5: 1.0
Ratio = 1.5	5	0.02 (≈1.0)	Layer 1–2: 1.5	0.26
			Layers 2–5: 1.0

2.3.3 Mesh Construction and Cell Types

The meshes shown in Figure 2 where generated by the ICEM CFD 14.5 meshing package (ANSYS, Inc., Canonsburg, PA, USA). The effects of the NW cell layer parameters were initially explored using hexahedral cells, as shown in Figure 2d for the Targeted case. This mesh type was constructed using the block mesh approach available in ICEM CFD 14.5, which allows the user to create a regular, mapped, hexahedral mesh.

Regular hexahedral meshes are ideal for CFD analysis in airway type systems, as they generally give the best accuracy when applied to the finite volume method (Vinchurkar & Longest, 2008). However, this type of mesh construction is not possible when developing models of nasal anatomy and potentially the MT, as the geometry is often too complex. Irregular tetrahedral meshes are employed in such cases, as they are able to conform to intricate surfaces, but numerical accuracy and robustness is sacrificed to some degree (Vinchurkar & Longest, 2008). Therefore, this study will compare the results of hexahedral and tetrahedral meshes directly to determine if there are substantial drawbacks associated with using tetrahedral meshes when modelling aerosol deposition. The mesh on the right side of Figure 2d is an example of the tetrahedral meshes used in the evaluation, specifically the Targeted NW cell layer case. These meshes were also generated with ICEM CFD 14.5 using the Tetra meshing capabilities.

2.4 PHYSICS MODEL AND SOLVER SETTINGS

The ANSYS FLUENT 14.5 CFD software package (ANSYS, Inc., Canonsburg, PA, USA) solves the transport equations that describe the flow field and particle trajectories through the numerical models. Initially, existing best practices developed by our group for modelling aerosol deposition in the extrathroacic region were applied to the Recommended, Intermediate, Targeted, and Poor Ratio meshes. The k-ω model solves the TKE and specific dissipation rate (SDR) fields, as is generally recommended for internal flows. The LRN correction uses a coefficient to dampen the turbulent viscosity that is determined when the TKE and SDR transport equations are combined. This coefficient is calculated from the material properties, turbulent field quantities, and model constants; the details of which are given by Wilcox (1998). The LRN correction should be applied when flow is close to the transition regime. In this study, the solver uses the SIMPLEC scheme for Pressure-Velocity coupling, with Least Squares Cell Based (LSQ) gradient discretization and second-order upwind schemes for flow variables. Particle trajectories through the domain are modeled using Lagrangian tracking with the Runge-Kutta scheme (Longest & Hindle, 2009; Longest et al., 2007; Longest, Tian, Delvadia et al., 2012; Longest et al., 2016; Longest, Tian, Walenga et al., 2012; Longest & Vinchurkar, 2007b; Tian et al., 2015; Tian et al., 2011). The particle drag, turbulent dispersion, and eddy interaction model are modified with NW correction user-defined functions (UDFs), which correct for turbulent anisotropy near wall boundaries (Longest et al., 2008; Matida et al., 2004) and perform NW velocity interpolation (Longest & Xi, 2007). These UDFs are described in greater detail in Section 2.4.3.

2.4.1 Turbulence

To date, LRN k-ω turbulence has been the two-equation model of choice for CFD particle deposition studies from our group. It has been extensively validated against in vitro (Longest & Hindle, 2009; Longest et al., 2007; Longest, Tian, Delvadia et al., 2012; Longest, Tian, Walenga et al., 2012; Longest & Vinchurkar, 2007b; Tian et al., 2011) and in vivo (Longest et al., 2016; Tian et al., 2015) experimental data, and provided accurate results in these studies. Advanced models, specifically the k-ω SST and Reynolds Stress Model (RSM), are available that aim to model turbulence with greater accuracy and detail. The SST k-ω model combines the free-stream advantages of the k-ε model with the NW benefits of k-ω. It is the recommended RANS turbulence model in the ANSYS FLUENT User Guide (2012), and includes a LRN option for modeling flow that is close to transition. Chen et al. (2009) used the SST k-ω model for a CFD assessment of flow through the nasal cavity in patients with septal deviations, although their study did not include particle deposition. The RSM has both ε and ω formulations, and solves seven additional transport equations for each of the Reynolds stresses. Rygg and Longest (2016) applied RSM to model pharmaceutical aerosol deposition in the adult nasal cavity, as its formulation includes turbulence anisotropy near walls without additional UDFs.

Despite the advanced formulation of SST and RSM k-ω, preliminary work for this study showed that these models increased processing times by approximately 30% and did not show substantially different results in terms of NW mesh sensitivity compared with the LRN k-ω model. In addition, RSM gave a very unusual velocity profile at the inlet and outlet of the 90° bend when compared to the other turbulence formulations. Therefore, the remainder of this investigation will use the LRN k-ω model, based on its previous successful use.

2.4.2 Gradient and Spatial Discretization Schemes

The default gradient discretization scheme available in ANSYS FLUENT is the LSQ scheme developed by Anderson and Bonhaus (1994). This method computes the cell gradient by using a weighting that is based on the distance from the cell centroid to its adjacent cells. The two other options available for gradient discretization are the Green-Gauss Node-based (GGN) and Green-Gauss Cell-based (GGC) methods. Equation (2) describes the Green-Gauss Theorem , which defines the gradient of any field variable at the cell centroid (∇ϕ) by using the cell volume (V), number of cell faces (N_f), field variable value at the face centroid (ϕf), and the face area vector ( $\overrightarrow{A_f}$):

$$\nabla \varphi =\frac{1}{V}\sum _{f=0}^{N_f}({\varphi }_f\overrightarrow{A_f}).$$ (2)

In the CFD solution, everything in Equation (2) is known except for ϕ_f, which is where the GGN and GGC methods are applied. The GGN method approximates ϕ_f by taking it as the average of the face node values, as given by:

$${\varphi }_f=\frac{{\varphi }_0+{\varphi }_1+\cdots +{\varphi }_n}{N_n}.$$ (3)

As the GGN method requires calculation of nodal values, it is generally more computationally expensive than other methods. Note that, N_n is eight for a hexahedral cell, four for a tetrahedral cell, and six for a prismatic cell. The GGC method approximates the field variable value at the cell face by taking it as the average of the current cell (ϕ₀ ) and the other cell that is attached to the face (ϕ₁), as given by:

$${\varphi }_f=\frac{{\varphi }_0+{\varphi }_1}{2}.$$ (4)

Preliminary results showed that switching from the LSQ to GGC method had little influence on the flow field and deposition results. Therefore, the Results section will only focus on how the model behaves when the LSQ vs. GGN methods are applied. The disadvantage of the GGN method being more computationally expensive will be acceptable if it is capable of providing consistent results between the different NW meshes.

It is noted that preliminary work also evaluated spatial discretization methods that are alternatives to second-order upwind in ANSYS FLUENT, including the third-order MUSCL scheme. These schemes were all excluded from further evaluation as they either did not apply to tetrahedral meshes, or did not have a positive effect on results at the Reynolds numbers considered in this study.

2.4.3 Near-wall Correction

The NW correction UDFs developed by Longest and Xi (2007) have been used extensively by our group when validating numerical results against in vitro (Longest & Hindle, 2009; Longest et al., 2007; Longest, Tian, Delvadia et al., 2012; Longest, Tian, Walenga et al., 2012; Longest & Vinchurkar, 2007b; Tian et al., 2011) and in vivo data (Longest et al., 2016; Tian et al., 2015). These UDFs perform two corrections: (i) anisotropic velocity fluctuations are introduced, and (ii) the wall-normal velocity is damped in the NW region, which is consistent with particle-wall hydrodynamic interactions. Furthermore, whenever velocity and turbulence field quantities are required for a calculation, they are interpolated at the particle location instead of using cell centroid values. Including anisotropic turbulence and damping velocity fluctuations in the NW region for pharmaceutical aerosols was originally implemented by our group in a study by Longest et al. (2008). This method built upon anisotropic turbulence work reported by Matida et al. (2004), which in turn was based on DNS data from Wang and James (1999).

Two control parameters are used to determine at what point each correction is applied to the particle. If the normal distance from the particle to the wall is less than the NW limit parameter, the UDFs use linear interpolation (based on the particle distance to the wall) to approximate the velocity and TKE values at the particles current location, and the wall-normal velocity component of the continuous phase is zeroed. The NW limit parameter is typically mesh, flow, and particle size dependent, and as such, can be modified during the model development stage to match experimental data.

If the non-dimensional particle y⁺ is below the y⁺ limit, the eddy lifetime is calculated based on the interpolated TKE value, and an anisotropic fluctuating velocity is defined with the new TKE value and random numbers from a Gaussian distribution. The eddy lifetime and fluctuating velocity are then updated each time the particle enters a new eddy. Unlike the NW limit, the y⁺ limit parameter is not case dependent and set to a value of 60, as this has given good results in a numerous previous studies (Longest & Hindle, 2009; Longest et al., 2007; Longest, Tian, Delvadia et al., 2012; Longest et al., 2016; Longest, Tian, Walenga et al., 2012; Longest & Vinchurkar, 2007b; Matida et al., 2004; Tian et al., 2015; Tian et al., 2011; Walenga & Longest, 2016).

In previous work, the linear method for NW interpolation that the NW correction UDFs use is best described by Walenga and Longest (2016). For this project, interpolation of the velocity and TKE fields was modified in an effort to make the NW correction less mesh dependent, as the objective is to improve consistency in results for different NW meshes. The modified approach first uses an inverse-distance weighted method to calculate all nodal velocity and TKE values in the domain, based on the cell centroid values to which each node is connected. Next, the cell in which the particle is currently located is identified, and the same inverse-distance weighted method is used to interpolate the velocity and TKE values at the particle location from the nodes that define the cell. In order to minimize computational effort, Shephard’s method for interpolating irregularly-spaced data is employed (1968), and extended for use in 3D space. Computation time is also reduced by storing all nodal values in memory, and retrieving the data as needed when interpolating to the particle location. In all, processing times for this modified method are negligible when compared to the time taken to reach a converged solution for the flow and turbulence transport equations.

2.5 BOUNDARY CONDITIONS

At the inlet, a uniform velocity magnitude was specified and the flow reached a fully developed state before it entered the 90° bend section. Default values for Turbulence Intensity (5%) and Turbulent Viscosity Ratio (10) are applied, as the length of the straight section should minimize the effects of inlet conditions on the turbulence field in the 90° bend. The outlet from the domain simply uses the outflow condition, whereby all mass that enters though the inlet also leaves through the outlet. All walls on the straight and 90° bend sections use a no-slip condition, and particles are trapped upon wall contact with the particle center of mass.

2.6 PARTICLE INJECTION

Particles are introduced into the domain with a blunt, random spatial distribution, as recommended by Longest and Vinchurkar (2007b). The blunt profile defines a uniform proportion of particles throughout the bulk flow, and then rapidly decreases the proportion as the particles near the wall. This realistic distribution is used as more particles enter along higher flux rings of flow. For the circular tube, a center point, normal vector, and radius define the random inject coordinates. The center point is selected so that particles are injected into the tube where the straight entry section of the tube ends and the 90° bend starts.

For the Re = 6,000 case, the injected particle size distribution uses seven bins with particle diameters that match the Pui et al. experimental data as described in Table 1. The size distribution for the Re = 10,000 CFD case also uses seven bins, with the 4.56–7.66 μm particles matching the sizes in the Re = 10,000 experimental data, and the 1.50–3.80 μm selected to match the Stokes numbers in the Re = 6,000 case. No experimental data is available for these three smaller bin sizes, and these particles are included to compare against the correlation at the lower end of the size range. The CFD model injects 5,000 particle for each bin size, as previous validation of steady-state models by our group have shown that tracking this number of particles per bin gives good particle convergence (Longest, Tian, Walenga et al., 2012).

2.7 COMPARISON CRITERIA

2.7.1 Deposition Fraction

The deposition fraction (DF) is defined as the ratio of the deposited particle mass to the injected particle mass and is expressed as a percentage:

$$\text{DF}=\frac{\text{Particle}\text{Mass}\text{Deposited}}{\text{Particle}\text{Mass}\text{Injected}}\times 100$$ (5)

2.7.2 Continuous Phase Velocity

As mentioned previously, preliminary results showed that the differences in the NW mesh layers are most sensitive to the effects of the turbulent dispersion model. This model uses the combination of the mean (ū) and fluctuating (u′) parts of the flow velocity, which is hereafter referred to as the continuous phase velocity (u) where:

$$u=\overline{u}+u^{\prime }$$ (6)

The fluctuating velocity used by the turbulent dispersion model is defined by a random number from a Gaussian distribution (ζ) and the TKE (k), given by:

$$u^{\prime }=\zeta \sqrt{\frac{2}{3}k}$$ (7)

3 RESULTS

3.1 SENSITIVITY STUDY

3.1.1 Application of Current Best Practices

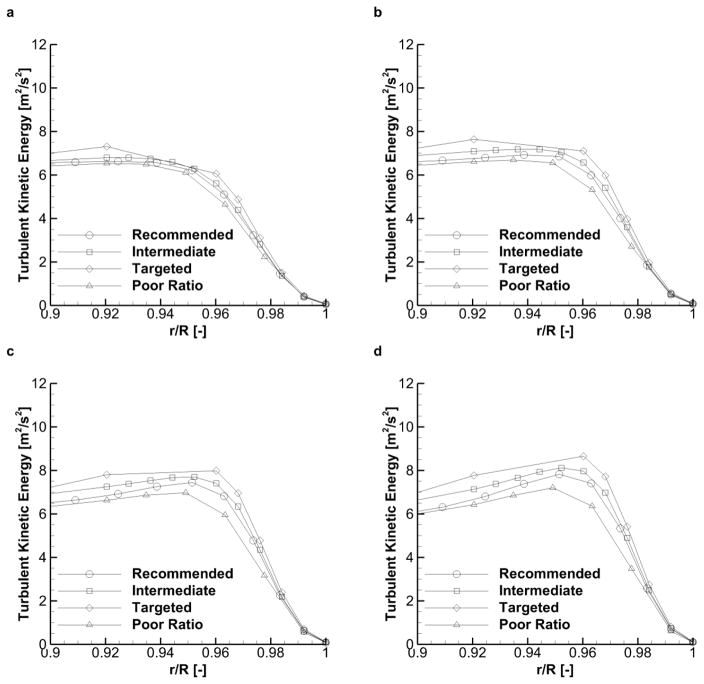
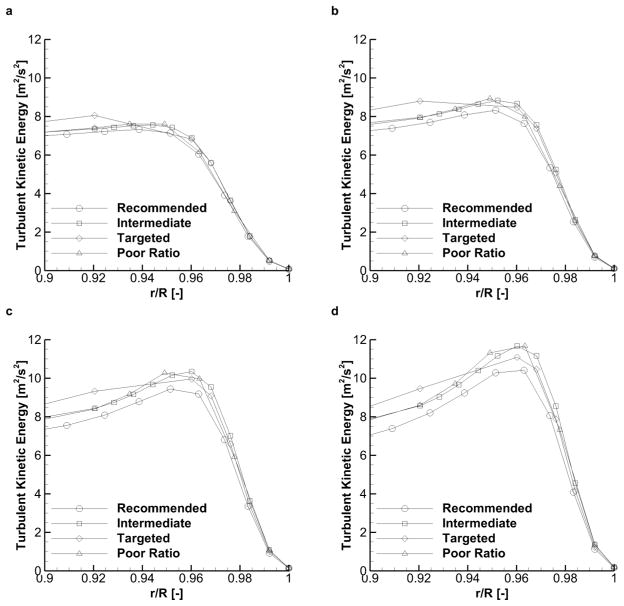
Figure 3 shows the TKE profile at 20°, 40°, 60°, and 80° around the 90° bend for the Recommended, Intermediate, Targeted, and Poor Ratio meshes. The plot shows a steep gradient near the wall, with a profile shape that is consistent with the DNS results from Wang and James (1999). In Figure 3a, the results for each mesh are all similar, as the flow is relatively uniform as it leaves the straight entry section of the tube. However, as the flow becomes more disturbed moving through the bend from Figure 3a to d, the profiles show more variability between the four meshes. Variability between each of the TKE profiles in Figure 3 can be evaluated by applying a 6^th-order polynomial line of best fit (R² > 0.999) and taking 30 equally-spaced sample points throughout the NW region. Moving from a location of 20° to 80° in the bend, the average and maximum standard deviation increases from 0.20 to 0.46 m²/s² and 0.41 to 0.90 m²/s² respectively. Qualitatively, both the peak TKE value near the wall and incline of the NW gradient vary considerably in each case. In order to achieve accurate and consistent results from the turbulent dispersion model, the TKE field in this NW region must be well resolved.

Figure 3.

Initial near-wall TKE profiles for each of the four meshes at angles around the 90-degree bend of (a) 20 degrees, (b) 40 degrees, (c) 60 degrees, and (d) 80 degrees

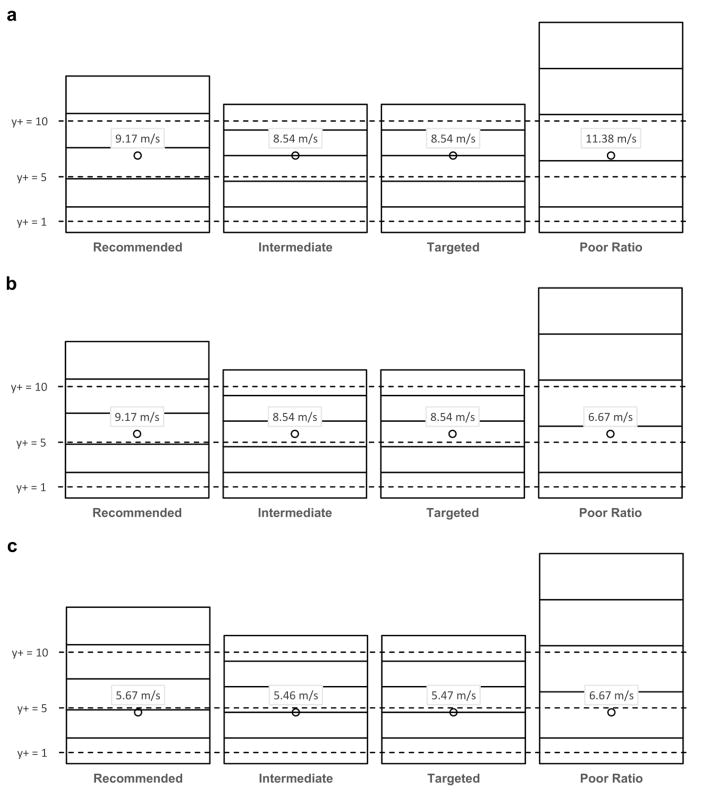
The continuous phase velocity, which the particles experience near the wall in each of the four meshes, is shown graphically in Figure 4. The continuous phase velocity is calculated from Equations (6) and (7), with the random number assumed to have a value of one for the purpose of comparison between different CFD models. This assumption is necessary, as the random number that the commercial code uses is not known.

Figure 4.

Continuous phase velocity (combined mean and fluctuating parts) to which the particle is exposed at wall-normal distances of (a) 60 μm, (b) 50 μm, and (c) 40 μm, for several mesh configurations

The values are sampled at the outlet of the 90° bend on the outer edge of the curved tube radius, as this location has the most variability and clearly deomonstrates the difference between each NW mesh. The mean velocity profiles for each case are very similar (not shown), but Figure 4 demonstrates how different the flow field can be when the fluctuating velocity is included. From Figure 4a to c, a sample particle moves through the NW cell layers of each mesh at a wall-normal distance of 60, 50, and 40 μm, respectively. The y⁺ values are included to indicate the non-dimensional wall distance for reference, with the average value for all four cases used, as the flow field varies for each mesh. From this figure it is clear that the particles are exposed to very different continuous phase velocities between each mesh. As the continuous phase velocity varies for each mesh, the particle trajectories through each computational domain are also different.

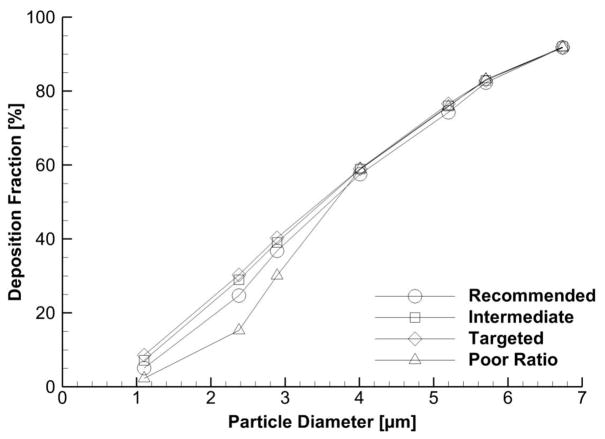
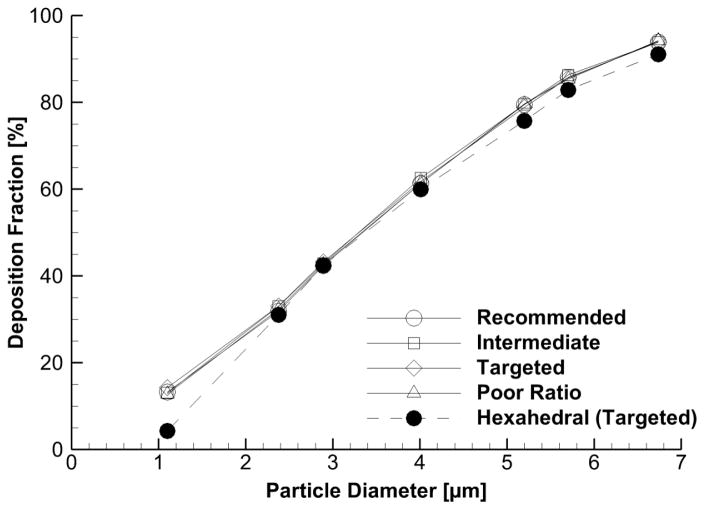
The variability in the TKE field close to the wall in turn affects the particle deposition profile between each of the four meshes, as seen in Figure 5. At the smaller end of the microparticle size range, particles are more susceptible to turbulent dispersion (Hjelmfelt & Mockros, 1966; Lee & Durst, 1982; Sommerfeld, 1990) and as such, show more variation in DF for each mesh. As diameters move towards the nanoparticle size range, the particle momentum becomes too low to be influenced by dispersion or pass though the viscous sublayer. Between the Targeted and Poor Ratio mesh, the DF decreases by about 25% for 2.89 μm particles (40.32% vs. 30.10%), 50% for 2.38 μm particles (30.30% vs. 15.28%), and 73% for 1.10 μm particles (2.28% vs. 8.58%). Note that meshes in Figure 3 that gave lower peak TKE values and a shallower gradient also gave less particle deposition. That is, lower TKE provides less turbulent dispersion, which results in lower DFs for particles less than 4 μm, as expected.

Figure 5.

Comparison of particle deposition profiles between the four meshes

3.1.2 Including the Green-Gauss Node-based Discretization Scheme

Using the GGN method for gradient discretization greatly reduces the sensitivity of the TKE field to the NW mesh resolution, as shown in Figure 6. As before, the differences between the four meshes become more varied as the flow progresses through the 90° bend. However, there is less overall variability between each case. Using the same method as before, GGN decreases the average and maximum standard deviation by 40% and 45% respectively for the 20° profile (0.20 vs. 0.12 m²/s² and 0.41 vs. 0.23 m²/s²), 33% and 40% for the 40° profile (0.29 vs. 0.20 m²/s² and 0.60 vs. 0.36 m²/s²), 22% and 32% for the 60° profile (0.38 vs. 0.29 m²/s² and 0.75 vs. 0.51 m²/s²), and 13% and 25% for the 80° profile (0.46 vs. 0.40 m²/s² and 0.89 vs. 0.67 m²/s²). Furthermore, the peak TKE values compare closely with one another, and the incline of the gradient near the wall is similar for all four meshes. Removal of the Poor Ratio mesh from this comparison would further improve agreement in the TKE field.

Figure 6.

Reduced sensitivity of TKE to the mesh when using Green-Gauss node-based discretization scheme at angles around the 90-degree bend of (a) 20 degrees, (b) 40 degrees, (c) 60 degrees, and (d) 80 degree

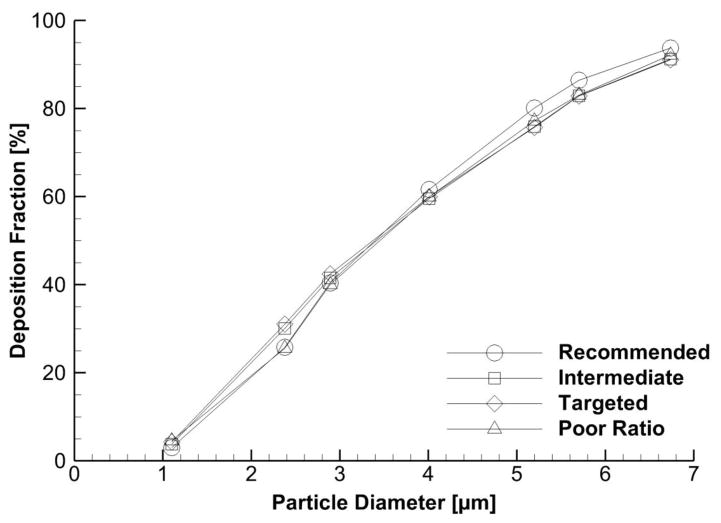
As a result of less variability in the TKE values, there is much better consistency in the deposition profiles for each mesh, as shown by Figure 7, especially for particles less than 4 μm in diameter. Now, between the Targeted and Poor Ratio mesh, the DF decreases by about 5% for 2.89 μm particles (42.46% vs. 40.06%), 18% for 2.38 μm particles (31.06% vs. 25.58%), and increased by 6% for 1.10 μm particles (4.30% vs. 4.54%). Table 3 summarizes the mean and standard deviation for the DF across all four meshes and compares the LSQ and GGN methods. This confirms that less variability in the TKE field gives less variability in particle deposition results. More importantly, these results show that application of the GGN method greatly reduces the sensitivity of the flow field and particle trajectories to the NW mesh resolution.

Figure 7.

Reduced sensitivity of deposition when using G-G node-based method

Table 3.

Mean and standard deviations of the deposition fraction for the Recommended, Intermediate, Targeted, and Poor Ratio meshes when using the Least Squares Cell-based (LSQ) and Green-Gauss Node-based (GGN) gradient discretization methods

Particle Diameter [μm]	LSQ Mean (SD) DF [%]	GGN Mean (SD) DF [%]
1.10	5.77 (2.37)	3.91 (0.59)
2.38	24.82 (5.88)	28.12 (2.47)
2.89	36.57 (3.94)	41.11 (0.95)
4.01	58.58 (0.60)	60.29 (0.80)
5.20	75.67 (0.85)	77.24 (1.77)
5.70	82.83 (0.32)	83.81 (1.52)
6.74	91.87 (0.10)	92.05 (1.06)

3.1.3 Near-wall Mesh Resolution

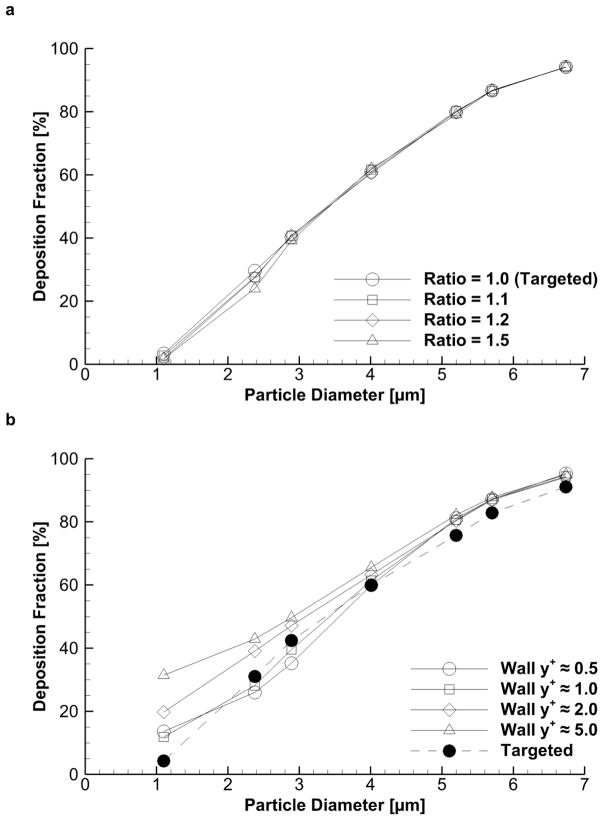
Figure 8a shows that increasing the L2L ratio for Layer 1 to 2 from a value of 1.0 (i.e. the same mesh as the Targeted case) to 1.1, 1.2, and 1.5 (as shown in Figure 2c) does not appreciably influence the particle deposition profile when using the GGN method. This is consistent with the reduced variability between results, especially the Poor Ratio case, which was presented in Figure 7. This means the variable L2L ratio capabilities that are available in meshing software can be employed without negatively affecting the aerosol deposition results. These meshing features allow the thickness of NW cell layers to be reduced when the surface-to-surface proximity decreases, which maintains the required mesh resolution near the wall.

Figure 8.

Comparison of results when varying the (a) layer to layer ratio and (b) target wall y⁺ value

Figure 8b demonstrates how increasing the thickness of the first NW layer from an approximate wall y⁺ of 0.5, 1.0, 2.0, and 5.0 affects the deposition profile. Note that these meshes use only one NW layer so the L2L ratio does not mask the sensitivity of results to the target wall y⁺. For comparison, the Targeted mesh, with a wall y⁺ of one and five equally-spaced layers, is also included in this figure. From this plot it is clear that increasing the thickness of the first NW cell layer, and associated wall y⁺ value, rapidly increases the DF for small (<4 μm) particles. Convergence of the deposition profiles occurs when using a first layer height that gives an approximate wall y⁺ of 1.0.

In summary, the results from this section and Section 3.1.2 show that the Targeted NW mesh, which is desirable for infant nasal models, is capable of producing deposition results that are comparable with the Recommended NW mesh in a simplified model, when suitable best practices are applied.

3.1.4 Tetrahedral Mesh Type

Using a tetrahedral mesh, as depicted in Figure 2d, and the GGN method gives a very consistent deposition profile across the four NW meshes considered, as shown in Figure 9. This draws parallels to the behavior seen when activating the GGN method in Figure 7. Table 4 summarizes the mean and standard deviation across all four meshes, and shows that the variability between each case is much less than the hexahedral meshes (see Table 3). Therefore, highly mesh independent results can be produced with tetrahedral meshes and the GGN method, which are desirable for the complex surfaces.

Figure 9.

Deposition comparison when using a mesh with a triangular surface, prismatic near-wall layers, and tetrahedral core. Each of the near-wall mesh resolutions presented use the same parameters as the hexahedral cases.

Table 4.

Mean and standard deviations of the deposition fraction for the Recommended, Intermediate, Targeted, and Poor Ratio meshes when using a tetrahedral volume mesh, prismatic near-wall cell layers, and the Green-Gauss Node-based (GGN) gradient discretization method

Particle Diameter [μm]	Tetrahedral Mesh Mean (SD) DF [%]
1.10	13.35 (0.55)
2.38	32.58 (0.50)
2.89	42.78 (0.32)
4.01	61.76 (0.51)
5.20	79.38 (0.31)
5.70	85.78 (0.34)
6.74	94.02 (0.15)

Figure 9 also includes the deposition profile for the hexahedral mesh that uses the Targeted NW mesh parameters from Figure 7. Interestingly, the DF of the 1.10 μm particles for the tetrahedral meshes is much greater than the hexahedral results (14.26% vs. 4.30%). The fact that smaller particles are more influenced by subtle changes in the velocity and TKE field is the likely cause of this discrepancy between results. Recall that the NW correction UDFs also influence DFs for the smaller particles, and have not been applied at this stage in the study.

3.2 NEAR-WALL CORRECTION

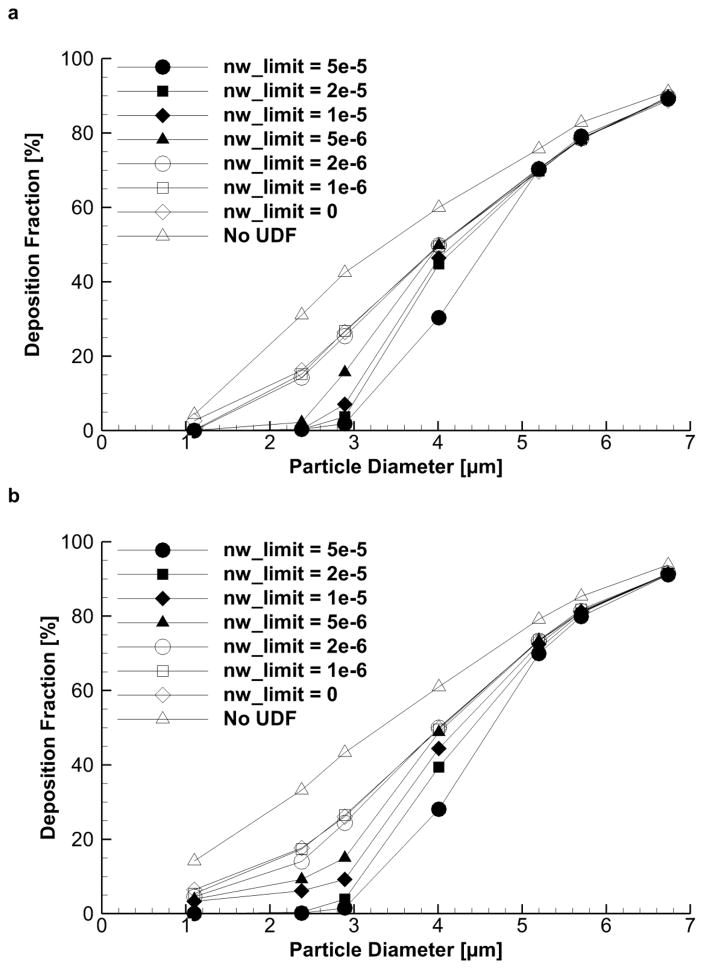
Figure 10a and b present the effects of applying the NW correction UDFs to the hexahedral and tetrahedral mesh with targeted NW cell layers respectively. For reference, the No UDF lines in each plot are the deposition profiles for the Targeted hexahedral and tetrahedral meshes from Figure 7 and Figure 9 respectively. As expected, increasing the NW limit parameter decreases the DF for particles less than 4 μm, as the UDF begins zeroing the wall-normal flow velocity further away from the wall. The plots also show that setting the NW limit to zero, effectively disabling the zeroing of wall-normal velocity, still influences the results as the particle drag force and turbulence anisotropy correction are applied outside of this limit.

Figure 10.

Adjustment of near-wall UDF parameters to tune deposition results and match experimental data for the (a) hexahedral and (b) tetrahedral mesh with targeted NW parameters

Adjusting the NW limit parameter allows the computational results to be tuned to match experimental data. The results from the tetrahedral mesh in Figure 10b show that increasing the NW limit leads to a gradual decrease in DF for small particles, which makes it easier to fine-tune the results. Figure 10a shows that the hexahedral mesh gives a very abrupt change in DF when adjusting the NW limit parameter beyond 2 μm. This is most apparent when looking at the results when changing from a NW limit of 2 to 5 μm for the 2.38 μm particles, as the DF drops from 14.28% to 2.24%. Generally, setting the NW limit parameter to a value of approximately 1 to 2 μm gave consistent results between mesh types, and compares well with experimental data (as detailed in the following section).

3.3 COMPARISONS WITH EXPERIMENTAL DATA

Figure 11a and b compares the CFD deposition profile for the 90° bend hexahedral and tetrahedral models, with the Re = 6,000 experimental data and correlation from Pui et al. (1987). From this comparison, it is clear that applying the best-case mesh and solver parameters, with the NW correction UDFs, gives a very good match between experimental and numerical results. To provide the best match to the Pui et al. data, the hexahedral case uses a NW limit value of 1.0 μm, and the tetrahedral case uses 2.0 μm. Note that the CFD results also exhibit the characteristic S-curve that is common for deposition profiles in the pharmaceutical aerosol size range. This profile shape is not represented by the correlation, but is apparent in the experimental data points. It is noted that the CFD predictions match the experimental data points better than the algebraic correlation at a majority of the points considered.

Figure 11.

Comparison to Pui et al. data when all CFD recommendations are applied for (a) Re = 6,000 with the hexahedral mesh, (b) Re = 6,000 with the tetrahedral mesh, (c) Re = 10,000 with the hexahedral mesh, and (d) Re = 10,000 with the tetrahedral mesh

Figure 11c and d show the comparison between a hexahedral and tetrahedral CFD model that also adheres to the recommended guidelines developed by this study, and the Re = 10,000 experimental model. The experimental and numerical data also match well, which suggests that the CFD meshing and solver guidelines that are recommended by this work are applicable to a range of flow characteristics. Interestingly, both of these cases gave the best match to the Pui et al. data with NW limit values of zero; hence, the wall-normal fluctuating velocity does not need to be damp for these models. This may be a specific characteristic of high Reynolds number cases. Recall that the Re = 10,000 case uses both a larger diameter tube and higher inlet flow rate, so the recommended CFD guidelines are independent of model geometry and inlet conditions.

4 DISCUSSION

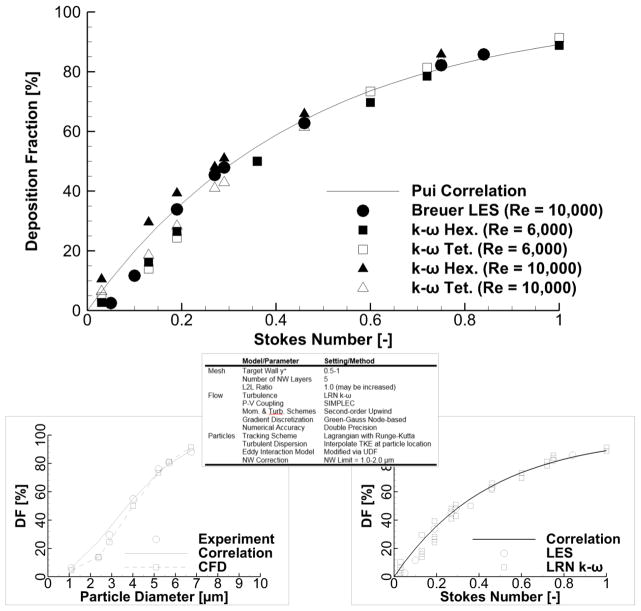
This study determines a set of meshing and solver guidelines that provide consistent results across several different NW meshes, and have been validated against experiments of aerosol deposition. The selected meshes have evaluated the effects of the number of cell layers, wall y⁺, L2L ratio, and cell type (hexahedral or tetrahedral) on the flow field and particle trajectories, in order to determine the most efficient use of NW cell layers for aerosol deposition models. The investigation explored different discretization schemes and control parameters for anisotropic turbulence correction, with final results showing a reliable match with the Pui et al. data. The guidelines are applicable across a range of flow Reynolds numbers and particle sizes. Table 5 summarizes the recommended guidelines at the conclusion of this study.

Table 5.

Summary of recommended mesh and solver parameters

	Model/Parameter	Setting/Method
Mesh	Target Wall y+	0.5–1
	Number of NW Layers	5
	L2L Ratio	1.0 (may be increased with no negative effects)
Flow	Turbulence	LRN k-ω
	P-V Coupling	SIMPLEC
	Mom. & Turb. Schemes	Second-order Upwind
	Gradient Discretization	Green-Gauss Node-based
	Numerical Accuracy	Double Precision
Particles	Tracking Scheme	Lagrangian with Runge-Kutta
	Turbulent Dispersion	Interpolate TKE at particle location from nodes
	Eddy Interaction Model	Modified via UDF
	NW Correction	NW Limit = 1.0–2.0 μm

As expected, the DF of particles less than 4 μm is most sensitive to the NW TKE field, because particles in this size range are largely influenced by eddy motion and have sufficient momentum to maintain an eddy dispersion velocity. Lower TKE in the NW region leads to less deposition of these smaller particles, and as such, one should strive for CFD models that give a reliable TKE field before having confidence in deposition results. Application of the GGN discretization scheme greatly reduced the variability of the TKE and particle deposition results across all the evaluated NW meshes with the small expense of an 11% increase in computational time (over 5,000 iterations). Therefore, the reasonable upper airway meshes, with five equally-spaced layers, can be applied to future work in contrast with the previously recommended NW mesh with 10–20 layers. Further exploration of the NW mesh parameters with the GGN scheme showed that it is important to aim for a wall y⁺ of approximately 1.0, and that varying the L2L ratio did not drastically influence the variability of results between cases. This means that should the meshing software increase or decrease layer thickness to confirm to the model geometry, the results should not be significantly affected.

Use of the NW correction UDFs allows the numerical results to be tuned to match experimental data. As with previous studies (Longest & Hindle, 2009; Longest et al., 2007; Longest, Tian, Delvadia et al., 2012; Longest et al., 2016; Longest, Tian, Walenga et al., 2012; Longest & Vinchurkar, 2007b; Matida et al., 2004; Tian et al., 2015; Tian et al., 2011; Walenga & Longest, 2016), a y⁺ limit of 60 was suitable for the anisotropic turbulence correction. For the Re = 6,000 case, a NW limit of 1–2 μm was required to match experimental data for the hexahedral and tetrahedral cases, below which the wall-normal velocity is damped. For the Re = 10,000, a NW limit of zero was used, which means that the velocity damping correction was not required in the more turbulent case.

Preliminary work considered the use of the wall roughness model to provide a more realistic representation of the wall boundary surface. However, activating the wall roughness model, with parameters that are consistent with the tube materials used in the Pui et al. (1987) experiments, had a negligible effect on the CFD deposition profiles (changed by <1%). This is most likely because the tubes were made from stainless steel and glass, which are relatively smooth materials, hence the associated wall roughness height was very small (<2 μm). However, the layered additive manufacturing process of common 3D printers often leads to rough surfaces and should be considered when evaluating regional and highly localized deposition (Holbrook & Longest, 2013).

Generally, CFD results tend to over-predict deposition, especially for smaller particle diameters. The UDFs correct this over-prediction by introducing anisotropic fluctuating velocity components with random numbers from a Gaussian distribution, and zeros the wall-normal velocity component as the particle approaches the wall. The current study improved the UDFs by introducing an inverse-distance weighted interpolation method to approximate velocity and TKE values at the particle location, based on cell centroid values. This modification aims to make the correction less mesh dependent. Results show how the NW limit parameter adjusts the deposition profile for hexahedral and tetrahedral meshes. Based on the results of this study with the recommended meshing guidelines, we recommend NW limit values of 1–2 μm for transitional flows with Reynolds number below 10,000, and removing the NW limit correction when the Reynolds number exceeds 10,000. In summary, use of the aforementioned guidelines and anisotropic turbulence correction leads to a very good match between the numerical and experimental data for this 90° bend model.

The findings from this study are consistent with previous work that has evaluated the LRN k-ω model in simplified models of biological internal flow. Studies by Varghese and Frankel (2003) and Ryval et al. (2004) both concluded that the LRN k-ω model gave a good match to experimental data when modeling flow through a stenosed tube, which is similar to constrictions in blood vessels or the respiratory airways. These models have similar flow conditions to the 90° bend model presented in this article, as they all experience laminar, transitional, and turbulent flow. Matida et al. (2004) demonstrated realistic NW corrections are required in order to match deposition results from the k-ω model to experiments. The same conclusions are drawn from the current study, as application of the NW correction UDFs, which were in part (anisotropy but not NW interpolation) based upon the findings of Matida et al. (2004), allows the deposition profile to be tuned to match the Pui et al. data (1987). Specific to modelling pharmaceutical aerosol deposition in the lungs with LRN k-ω, Xi and Longest (2007) reported good comparisons between numerical models, of both realistic and simplified geometries, and experimental data. The meshing and solution parameter recommendations presented in this paper add to the research field by providing clear guidelines for using the LRN k-ω model. This will streamline the CFD model development process for future work that plans to take advantage of the efficiency and accuracy that the LRN k-ω turbulence model provides for microparticle deposition.

Recently in the literature, there has been a shift towards using more complex turbulence models in CFD studies. The LES model resolves the turbulence field in greater detail than two-equation RANS models. Its formulation is also capable of overcoming some of the inherent NW issues with the k-ω model, which are outlined by this study, without the need for corrections. However, LES models demand much longer meshing and solver processing times, as very small cell sizes are necessary to resolve the required length scales, which in turn gives high cell counts. Zhang and Kleinstreuer (2011) compared the LRN k-ω, SST transition, and LES models for nanoparticle deposition in a constricted tube and idealized human airway model. They observed negligible differences between the three turbulence models for predicting laminar, transition and turbulent flow. They also report that the more complex LES model required 100-fold more computational resources than the two-equation RANS model. Conversely, Jayaraju et al. (2008) concluded that LES/DES provided a better agreement with experimental data for a MT model than k-ω. However, their study used the standard implementation of the k-ω model, which does not include the LRN correction. It is noted that the two-equation RANS CFD models that are discussed here and have successfully matched experimental data (Ryval et al., 2004; Varghese & Frankel, 2003; J. Xi & Longest, 2007; Zhang & Kleinstreuer, 2011), including the present study, have used the k-ω model with LRN correction.

Similar to how this study compared the LRN k-ω CFD results to the Pui et al. model (1987), Breuer et al. (2006) provided a comparison between LES results and the same experimental data set. They showed a good match between the DF from their computational model and the curve fitted correlation. Figure 12 reproduces the deposition profile for the Re = 10,000 model from Breuer et al. (2006), and includes the results from this study for the Re = 6,000 and 10,000 cases, and both hexahedral and tetrahedral meshes. This comparison across different Reynolds numbers is reasonable as the Pui et al. correlation is only a function of Stokes number, and hence is independent of Reynolds number. Figure 12 shows that the LRN k-ω models gives similar deposition results to the LES model across a range of particle diameters (Stokes number). Therefore, we believe that the LRN k-ω model, with the guidelines and NW corrections defined by this study, is capable of modeling aerosol deposition under conditions consistent with the upper respiratory airways. Advanced turbulence models are invaluable for modeling complex phenomena and aiding the development and validation of two-equation RANS models. For example, the NW correction UDFs utilized by this work rely on findings from the DNS data from Wang and James (1999). However, the LRN k-ω model provides a more computationally efficient method that can resolve the flow field in sufficient detail to capture microparticle deposition with the same degree of accuracy as LES models.

Figure 12.

Comparison of LRN k-ω results using the best practices from this study with LES data from Breuer et al. Particle diameters converted to Stokes number to be consistent with the LES study and across different tube diameters

Future work will apply these guidelines to upper airway geometries and aim to provide the same reliable and validated results that are presented here. This investigation showed that both hexahedral and tetrahedral meshes can be used with little drawbacks for either cell type. Using tetrahedral meshing capabilities makes the modelling of complex airways like the nasal cavity much easier, where using a regular hexahedral mesh on complex geometries is not possible. Cut-cell meshing technologies should be explored, where a Cartesian grid is fitted to the geometry by excluding and cutting cells outside of the domain. This method results in a mesh that is mostly regular and hexahedral in the core, with some tetrahedral, pyramid, and other polyhedra near the surface. The core mesh would provide the robust and computationally efficient benefits that are common with regular hexahedral, but it is unclear at this stage how the cut cells near the surface affect turbulence properties and aerosol deposition in airway CFD models.

In conclusion, this study has provided a set of recommendations for mesh and solver settings that give consistent and validated results for a characteristic geometry. It is expected that application of these guidelines to more complex geometries will improve the model development process and provide more reliable aerosol deposition results in the upper respiratory airways.

Highlights.

• Development and validation of CFD meshing/solution guidelines for aerosol deposition

• Sensitivity to near-wall mesh resolution is reduced with newly recommended parameters

• Numerical results compare well with experimental data for a characteristic geometry

• Computationally efficient LRN k-ω compares well with LES data for the same model