Computational Anatomy and Diffeomorphometry: A Dynamical Systems Model of Neuroanatomy in the Soft Condensed Matter Continuum

Abstract

The non-linear systems models of Computational Anatomy that have emerged over the past several decades are a synthesis of three significant areas of computational science and biological modeling. First is the algebraic model of biological shape as a Riemannian orbit, a set of objects under diffeomorphic action. Second is the embedding of anatomical shapes into the soft condensed matter physics continuum via the extension of the Euler equations to geodesic, smooth flows with inverses, encoding divergence for the compressibility of atrophy and expansion of growth. Third, is making human shape and form a metrizable space via geodesic connections of coordinate systems. These three themes place our formalism into the modern data science world of personalized medicine supporting inference of high-dimensional anatomical phenotypes for studying neurodegeneration and neurodevelopment. The dynamical systems model of growth and atrophy that emerges is one which is organized in terms of forces, accelerations, velocities, and displacements, with the associated Hamiltonian momentum and the diffeomorphic flow acting as the state, and the smooth vector field the control. The forces that enter the model derive from external measurements through which the dynamical system must flow, and the internal potential energies of structures making up the soft condensed matter. We examine numerous examples on growth and atrophy.

INTRODUCTION

Computational Anatomy (CA) in its earliest articulation^{10, 11, 35, 52, 54, 63, 70}, has been an attempt at formalizing Medical Imaging in the sense of Shannon theory⁶⁷ by modeling the human anatomy being imaged separately from the medical imaging devices themselves. At the heart of CA is the comparison of human shape, morphology, as pioneered by D’Arcy Thompson⁶⁹, focusing on shapes formed by the submanifolds of the human body in ℝ³. The models in CA describe cross-sectional variation of anatomical coordinate systems and dynamical change of growth and atrophy via equations of motions associated to flows of the Lie groups of diffeomorphisms. Spatial smoothness through differentiability is at the base of the representation, therefore limiting our models to the morphome scales of the anatomical Physiome^{22, 39}, 50–100µm and above where continuity and advection equations hold.

Our models in CA are constructed via the Theory of Transformations as formalized in Metric Pattern theory³² as deformable templates, in which the objects being studied are subordinated to groups of transformations which are rich enough to generate the space of observables. This abstraction models biological form as a Riemannian orbit, a set of objects and manifolds under group action. For deformable and biological shapes in CA the diffeomorphism group, one-to-one and onto smooth transformations with smooth inverses, plays the central role as the group of transformations. The group properties and their empirical statistics play the central role in the modeling, and are therefore well aligned with the modern empirical approaches of data-science.

The approaches of the CA community have to a great extent examined shape by focusing on the transformations, rather than explicit modeling of the constitutive laws of the tissues. This viewpoint connects to classical continuum mechanics models through Hamilton’s variational principles from which we derive geodesic flows interpretable in momentum and force equations. The geodesics through the group make anatomical shape and form a metrizable space. The associated Euler-Lagrange equation on the geodesics encode the evolution in time of the shape momentum as internal forces created as flows representing atrophy and growth. For biological shape such as neuroanatomy that is highly condensed, the internal body forces encoding the diffeomorphic constraint implies the geodesics are highly curved by other particles in the dense continuum.

These shape geodesics are derivative of Euler’s original 1755 treasure, generalized to the divergence-full case to accommodate growth and atrophy and derived from a Sobolev metric controlling continuous spatial derivatives of the vector fields of the flows. This ensures smooth flows of diffeomorphic motion which form the basis for CA. This strongly links our field to V. I. Arnold’s^6–8 pioneering work demonstrating that the subgroup of diffeomorphisms with vector fields which are divergence-free has geodesics which correspond to the Euler equation. The CA community’s focus on growth and atrophy requires the release of the incompressibility constraint of divergence free vector fields. Local in space compressibility and expandability places us firmly at the soft active matter^{49, 68} spectrum of the condensed matter continuum being studied extensively in the emerging fields of systems biology and tissue engineering.

We also summarize the dynamical systems models organized in terms of forces, accelerations, velocity and displacements in order to understand the soft matter continuum of biological shape, studied in CA for cross-sectional variation as well as for growth and atrophy. The model has several blocks. The state of the dynamical systems model is the flow coordinates and Hamiltonian momentum. The dynamical control is the Eulerian velocities of flow, related to the state through the Green’s kernel of a linear system applied to the Hamiltonian momentum. The dynamical state equations are the differential equation relating Eulerian velocity and the instantaneous change in the flow, and a non-linear Euler-Lagrange force equation satisfying conservation of momentum describing geodesic flows with spatially localized expansion and compression. For this non-linear dynamical system, force is quadratic in velocity. The observables, the medical images, are the outputs of a non-linear observer equation which models the magnetic resonance images as an orbit under group action. We show how the dynamical systems model relates to growth, atrophy, and metric space structures for manifolds of shapes.

The Algebraic Orbit Model of Shapes and Forms

Computational anatomy (CA) of shape examines the interplay between the imaged anatomical structures and the underlying or latent, implicitly or explicitly indexed coordinate systems. Hereafter we call the objects being imaged a shape or form; the two principal shapes that are studied in CA are substructures in the human body (collections of 0, 1, 2, 3 dimensional submanifolds), and dense scalar and tensor imagery of functions in the human body. As we are interested in human shape and form at the morphome scale, visible anatomy, exemplars are always taken as anatomical coordinate systems, atlases, the Mai-Paxinos⁴⁸ or Mori atlases^{21, 59, 60} for brains are examples.

We follow the basic approach of D’Arcy Thompson⁶⁹ which is to recognize in one shape another, the starting point being the template or exemplar, and the class of shapes understood relative to the template. This is the basic deformable template model of Grenander’s Pattern theory³². The act of comparison to the basic forms are understood topologically via bijective correspondences, 1-1 and onto dense mappings between the coordinates. Figure 1 depicts the link to image analysis. To understand every point in the target, there should be a unique label. At the same time, we want to be able to understand the target completely, thus the notion of onto. The label maps are carried by the arrows. Notice in the bottom row the crunched face is immediately defined through the correspondences depicted via the arrows which are parts of the vector field defining the bijection.

Figure 1.

Showing space of face with bijective, 1-1, onto correspondence between them carrying the label maps. There is one face which is not bijective to others.

The Deformable Template Model

The transformations, denoted as φ : X ⊂ ℝ³ → X, are densely defined such that they act on all of 3D space, rather than a set of feature points. These transformations have inverses, defining 1-1 correspondences on the background space. To be able to compose these bijections, we define them to be in a group φ ∈ 𝒢, with law of composition of functions, φ ◦ φ′(·) ≔ (φ(φ′(·)) and inverses as functions φ⁻¹; denote the identity in the group id ∈ 𝒢. These transformations are continuous and differentiable in space with differentiable inverse so that we can calculate arc-length, curvature, surface area and volumes. We call them difeomorphisms.

The algebraic, orbit model of CA represents the shapes as points in a set m ∈ ℳ, I ∈ ℐ, the sets called the orbits. The shapes are both manifolds and images. The manifolds have smooth coordinates through the mapping m : 𝒮 ↦ ℝ³; for curves then m : 𝒮 ⊂ ℝ¹, for surfaces and triangulated meshes 𝒮 ⊂ ℝ². The diffeomorphisms φ ∈ 𝒢 transform the shapes via group action, denoted algebraically (φ, m) ↦ φ(m) ∈ ℳ, (φ, I) ↦ φ · I ∈ ℐ.

The theory of shapes is an infinite dimensional one, with both the transformations and the shapes functions of infinite dimension. The group moves the coordinates directly as function composition^{1, 4, 23, 37, 43, 64–66, 78, 82}, or for images the action is as the inverse acting on the right:

$$m:𝒮\to {ℝ}^3,(\phi ,m)\mapsto \phi ·m≔\phi ◦m$$ (1a)

$$I:{ℝ}^3\to {ℝ}^{+},(\phi ,I)\mapsto \phi ·I≔I◦{\phi }^{-1}.$$ (1b)

The group actions satisfy the property φ · (φ′ · m) = (φ ◦ φ′) · m, φ · (φ′ · I) = (φ ◦ φ′) · I. There are group actions for vector fields¹⁸, DTI¹⁷ and images mixed with submanifolds⁷⁵. We use the notation m instead of I for manifolds, because a curve or surface has an infinity of parametrizations. When defining an action (or another operation) through a transformation of m, it is important to ensure that the resulting transformation of I does not depend on the chosen parametrization (which is true for the just-defined action).

Figure 1 shows a family of shape elements of the orbit I ∈ ℐ. One of the examples, the not-face, is not bijective to the others and not in the orbit. Given a single exemplar - the face - and the orbit of all faces generated by transformations of the exemplar, the action of the group moves between all the faces in the orbit. In mathematical terms the orbit is homogeneous and the action is transitive. Of course different exemplars can have different topologies, implying collections of homogeneous shape space orbits are required to understand the richer set of anatomical configurations. The inverse property implies the orbit can be moved redvia transformations which can be composed as often as required as in the linear algebra case of invertible matrices.

The Theory of Smooth Transformation via Flows of Diffeomorphisms

Quoting from D’Arcy Thompson’s classic work on Growth and Form⁶⁹: In a very large part of morphology, our essential task lies in the comparison of related forms rather in the precise definition of each; […] This process of comparison, of recognizing in one form a definite permutation or deformation of another, […] is the Method of Coordinates, on which is based the Theory of Transformations.

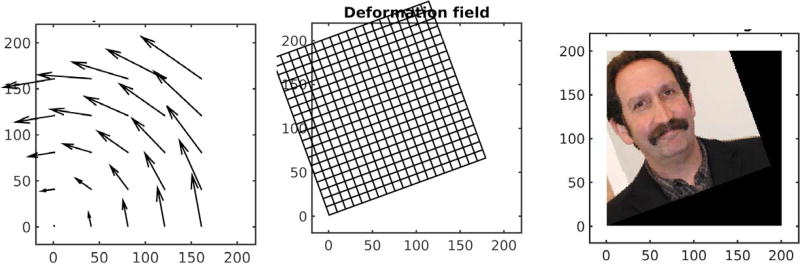
A familiar use of the theory of transformations is the study of the kinematics of rigid bodies⁵⁰ and more recently computer vision⁴⁶ which builds naturally on the generalized linear group of matrices with inverses and subgroups of rotations and scales. Figure 2 shows the action by rotations. Panel 1 shows the displacement vector field Ox − x for x a 2D spatial coordinate and O a rotation matrix, with panels 2 and 3 showing the action on the grid and via the inverse on the image.

Figure 2.

Example of rotation displacement vector field Ox − x (panel 1) applied to q =grid, φ_O ◦ grid, (panel 2) and MIM face φ_O · I(x) ≔ I(O⁻¹x).

The theory of transformation of shape is dual to image understanding and close to the ideas of Chomsky^{3, 20} on labelling and parsing via the theory of transformations for language understanding. Rather than parsing linguistic structure via grammatical transformations building correspondences between the variations in the phrases representing word strings, shape transformation builds correspondences between the variations between coordinate systems. The correspondences are the parsing engine.

Compositions of Flows

For deformable models in Pattern Theory, the dimension of transformation increases^31–34. There are many choices for defining bijective correspondences on ℝ³, generalizing away from the finite, low dimensionality of the rotations, scales and skews. Each point in ℝ^m can move by m-dimensions, implying it is natural to define the transformations via vector fields in ℝ^m. We construct the transformations to be diffeomorphisms using Lagrangian and Eulerian flows of vector fields from classical mechanics. For a time-dependent vector field υ_t ∈ ℝ³, the flow φ_t for differential equation ẏ = υ_t(y) with φ₀ = id, is given by,

$${\dot{\phi }}_t={\upsilon }_t◦{\phi }_t,t\in [0,1],$$ (2)

with φ̇_t ∈ ℝ³ and υ_t ∈ ℝ³ the so called Lagrangian and Eulerian vector fields. (Here and in the following φ̇_t refers to the time derivative $\frac{\partial {\phi }_t}{\partial t}$. The inverse follows, ${\phi }_0^{-1}=\text{id}$,

$$\frac{\partial }{\partial t}({\phi }_t^{-1})=-(d{\phi }_t^{-1}){\upsilon }_t,t\in [0,1],$$ (3)

with 3 × 3 Jacobian matrix ${[\mathit{\text{df}}]}_{i,j}≔\left(\frac{\partial f_i}{\partial x_j}\right)$ of f : ℝ³ → ℝ³. For shape diffeomorphometry we ensure smooth flows of diffeomorphisms associated to (2) by controlling the vector field to be once continuously differentiable in each spatial derivative of the Jacobian matrix υ ↦ (dυ)^{24, 71}. The Sobolev embedding theorem provides the important link of modeling continuously differentiable functions with quadratic energies represented via the Hilbert spaces of functions, denoted H^k which have generalized square-integrable derivatives of order k. In 3-dimensions, X = ℝ³, $k>\frac{3}{2}+1$ generalized derivatives in square-integral ‖υ‖_H^k < ∞ are required to imply one continuous derivative²⁴. The norm for H^k is defined by

$${\Vert \upsilon \Vert }_{H^k}^2≔\sum _{|h|\le k}{\int }_X{\partial }_h\upsilon (x)·{\partial }_h\upsilon (x)\mathit{\text{dx}},$$ (4)

where the sum is made over all partial derivatives with multi-index h of total order less than or equal to k. The vector fields υ ∈ H^k are smooth, since they have k square-integrable derivatives.

The Diffeomorphism Group

The group used for Computational Anatomy G_H^k are solutions of the flows ${\phi }_1^{\upsilon }$ of Eqn. (2) φ̇^υ = υ ◦ φ^υ, with vector fields absolutely integrable under the norm :

$$G_{H^k}≔\{{\phi }^{\upsilon }:{\int }_0^1{\Vert {\upsilon }_t\Vert }_{H^k}\mathit{\text{ dt}}<\infty \}.$$ (5)

Importantly for Computational Anatomy, our group of diffeomorphisms G_H^k allows the Jacobian determinant of the flows corresponding to expansions and or compressions to vary locally in order to support growth and atrophy and local size variation in the population. In this sense, the CA model of diffeomorphisms departs from the incompressible flows characterized by Arnold⁵ corresponding to the divergence-free vector fields (see the discussion of hydrodynamics below).

Transformation of Shape is Composition

Composition of functions, not addition, is at the heart of shape theory. For the integrated flow ${\phi }_t:x\mapsto {\int }_0^t{\upsilon }_s◦{\phi }_s(x)\mathit{\text{ds}}$, the flows can be decomposed illustrating the role of the nonlinearity of the compositions of small motions.

Statement 1

For mappings ${\phi }_{t_0,t}≔{\phi }_t◦{\phi }_{t_0}^{-1}=\text{id}+{\int }_{t_0}^t{\upsilon }_s◦{\phi }_s\mathit{\text{ds}}$, deformations decompose, implying control of the definiteness of the Jacobian as a product of determinants, and the nonlinear composition of small motions; for all t₀ ≤ t₁ ≤ ⋯ ≤ t_i = t,

$${\phi }_{t_0,t}={\phi }_{t_{i-1},t_i}◦\cdots ◦{\phi }_{t_0,t_1},\simeq (\text{id}+(t_i-t_{i-1}){\upsilon }_{t_{i-1}})◦\cdots ◦(\text{id}+(t_1-t_0){\upsilon }_{t_0})$$ (6)

Transformations are Smooth in a Reproducing Kernel Hilbert Space

For modeling purposes, we make the Hilbert space into a reproducing kernel Hilbert space (r.k.h.s.) by specifying the k-derivative norm via an equivalent one determined by a one-to-one, differential operator L or self-adjoint operator A,

$${\Vert \upsilon \Vert }_L^2≔{\int }_{X}L\upsilon (x)·L\upsilon (x)\mathit{\text{dx}}={\int }_{X}A\upsilon (x)·\upsilon (x)\mathit{\text{dx}},$$ (7)

where the operator A = L^†L, † the adjoint. This definition of the norm links us to the Green’s kernel and r.k.h.s.’s. The norm (7) is equivalent to the H^k norm in that for some constants 0 < c₁ ≤ c₂, $c_1{\Vert \upsilon \Vert }_{H^k}^2\le {\Vert \upsilon \Vert }_L^2\le c_2{\Vert \upsilon \Vert }_{H^k}^2$, and therefore the group does not depend on L because of this equivalence.

Now for k > d/2, H^k is an r.k.h.s. where the kernel K is smooth given by the inverse K = A⁻¹ expressed as a matrix operator. The vector fields form smooth transformations of shape in terms of the kernel superpositions weighted by the dual elements σ ∈ H^k*, i.e. the generalized functions or linear forms that act on H^k:

$$\upsilon (x)={\int }_{X}K(x,y)\sigma (\mathit{\text{dy}})\in H^k.$$ (8)

The interpretation of (8) is that, for a given x, the jth coordinate of υ(x) is obtained by evaluation of σ against the jth column of K(x, ·). We will refer to υ formed as in (8) as “r.k.h.s. splines.” We assume that the L is chosen in what follows to satisfy the smoothness condition of 1, continuous derivative, for example L = (−∇² + 1)² where ∇² is the Laplacian operator, and work with the associated norm ‖υ‖_L. In the Appendix A we show the explicit Green’s kernels for different differential operators. The Gaussian kernel is an example which is not a finite order differential operator.

Vector Fields are Smooth, Momentum is a Generalized Function

While the vector fields are smooth υ ∈ H^k with k-generalized square-integrable derivatives, the momentum Aυ ∈ H^k* of (7) are dual elements in the dual space σ ≔ Aυ ∈ H^k*, and not necessarily functions in the classical pointwise sense. In order to build forces on pointsets and curves or surfaces in ℝ³ that can push anatomical coordinates via vector fields, we need momentum to be Dirac-charges and generalized functions, just like in Maxwell’s equations. The dual element momenta can be generalized functions, so the norm product (7) specifying 2k derivatives must be interpreted via integration by parts. Since we shall focus on Green’s kernels which are shift-invariant, it is very natural to interpet the dual space through the Fourier spectral domain; see Appendix B.

Dynamical Systems Model of Shape and Form

Our model of cross-sectional shapes in populations and growth and atrophy takes a standardized optimization and control-theory form.^{16, 24, 28, 29, 55–57, 73–77, 80} The model is a dynamical system with the state t ↦ q_t, and the controls t ↦ υ_t satisfying general dynamics

$${\dot{q}}_t=f(q_t,{\upsilon }_t),q_0=q_{\text{init}}.$$ (9)

In optimal control the pair (q_t, υ_t), t ∈ [0, 1] minimizes some running or integrated cost.

The model for growth, atrophy or cross-sectional study corresponds to modeling submanifolds m : 𝒮 → ℝ³ as the flowing shape φ_t ◦ m(s), s ∈ 𝒮, 𝒮 of 0, 1, 2, 3 dimensions of landmarks, curves, surfaces, and subvolumes. For dense images, then 𝒮 = X = ℝ³ and φ_t(x), x ∈ ℝ³, with the image moved under diffeomorphic flow according to $I◦{\phi }_t^{-1}$. The observations are modeled as noisy measurements of elements within the orbit, m ∈ ℳ, I ∈ ℐ. The measurements are introduced as penalty or cost terms which the dynamical systems must align or register to as the coordinates flow.

There are many flows; diffeomorphism space is big. For matching in CA, geodesic solutions through the group of diffeomorphic flows are optimized over by introducing the Lagrangian determined by kinetic energy of the flow and minimizing via Hamilton’s principle the action integral. This determines the dynamics of the solutions associated to (9).

Hamiltonian Geodesics on Anatomical Submanifolds

To accommodate the submanifolds, we link to the Hamiltonian, modeling the deformations directly indexed to the state defined as the flowing submanifold q_t(s) = φ_t ◦ m(s), s ∈ 𝒮, q_t(x) = φ_t(x), x ∈ X. Under suitable assumptions, the Hamiltonian adds a Lagrange multiplier t → p_t, also called the co-state which controls the state dynamics q̇_t = υ_t ◦ φ_t(m), and is indexed over the submanifold ∫_𝒮 p_t(s) · (υ_t ◦ q_t(s))ds. Adding the kinetic energy gives

$$H(p,q,\upsilon )={\int }_{𝒮}p(s)·(\upsilon \circ q(s))\mathit{\text{ds}}-\frac{1}{2}{\int }_{X}A\upsilon ·\upsilon \mathit{\text{dx}}.$$

Along geodesics, the Hamiltonian is constant H(p_t, q_t) = constant, given by

$$H(p_t,q_t)=\underset{\upsilon }{\text{max}}H(p_t,q_t,\upsilon )=\frac{1}{2}{\int }_{𝒮}{\int }_{𝒮}{p}_t(s)·K(q_t(s),q_t(s\prime ))p_t(s\prime )\mathit{\text{dsds}}\prime ,$$ (10)

$$\{\begin{array}{c}{\dot{q}}_t=\frac{\partial }{\partial p_t}H(p_t,q_t,{\upsilon }_t)={\upsilon }_t◦q_t\hfill \\ {\dot{p}}_t=\frac{\partial }{\partial q_t}H(p_t,q_t,{\upsilon }_t)=-{(d{\upsilon }_t)}_{q_t}^T{p}_t\hfill \\ {\upsilon }_t=\text{arg }\underset{\upsilon }{\text{max}}H(p_t,q_t,{\upsilon }_t)={\int }_{𝒮}K(·,q_t(s))p_t(s)\mathit{\text{ds}}\hfill \end{array}.$$ (11)

For volumes 𝒮 = X = ℝ³, q_t(x) = φ_t(x), x ∈ X, geodesics υ(·) = ∫_X K(·, q_t(x))p_t(x)dx with

$$H(p_t,q_t)=\frac{1}{2}{\int }_X{\int }_X{p}_t(x)·K(q_t(x),q_t(x\prime ))p_t(y)\mathit{\text{dxdx}}\prime .$$

For pointsets, 𝒮 = 1, …, n, q_t(i) = φ_t(x_i), geodesics υ(·) = Σ_iK(·, q_t(i))p_t(i) with

$$H(p_t,q_t)=\frac{1}{2}\sum _i\sum _{i\prime }{p}_t(i)·K(q_t(i),q_t(i\prime ))p_t(i\prime ).$$

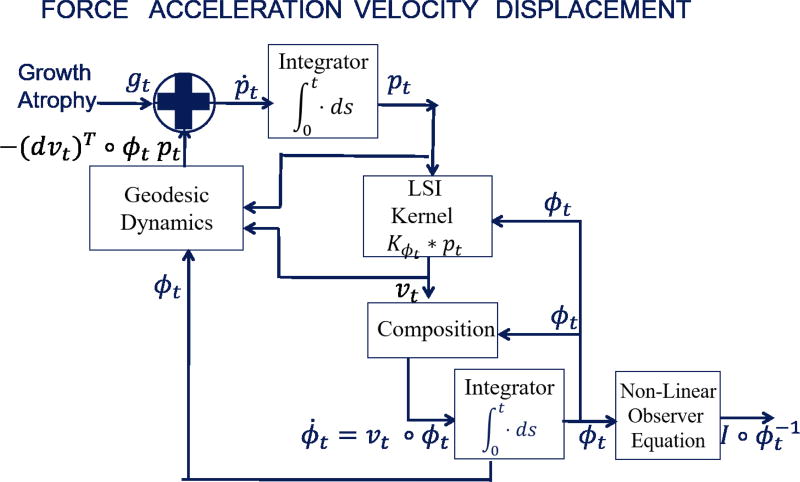
The Hamiltonian momentum evolution for landmarks appeared in^{25, 55–57}; the surface cases in^{56, 57, 74, 75}. Figure 3 shows the systems diagram representation of the dynamical system.

Figure 3.

Dynamics model in CA organized by force, acceleration, velocity, and displacement. Input term $g_t=\frac{\partial U}{\partial q}$ (see (17)) represents energy derived forces from external measurements or internal energies of substructures. Images enter via the non-linear observer I ◦ φ⁻¹.

Diffeomorphometry: The Riemannian Metric and GPS

Diffeomorphometry constructs the metric between diffeomorphic transformations via the geodesic flows between diffeomorphisms. The metric minimizes the integrated lengths over flows connecting group elements, with flows having tangent length at each point of the manifold of diffeomorphisms with norm ‖φ̇‖_φ giving

$$\rho (\phi ,\phi \prime )≔\underset{{\phi }_t,t\in [0,1],{\phi }_0=\phi ,{\phi }_1=\phi \prime }{\text{inf}}{\int }_0^1{\Vert {\dot{\phi }}_t\Vert }_{{\phi }_t}\mathit{\text{dt}}.$$ (12)

The metric was first characterized in⁵³, with many extensions discussed in⁵⁷. The metric determines the shape of the space. The geodesics of the metric positions shape information between the objects and provides coordinates of the objects in the orbit. Solving the geodesic equations for fixed initial conditions υ₀ ∈ H^k is positioning, which is why we call this system a Geodesic Positioning System (GPS), and termed the Riemannian exponential; solving for the initial υ₀ that generates a specific diffeomorphism φ ∈ G_H^k are the coordinates and is termed Riemannian logarithm which is only well defined when the geodesic distance has a unique minimum:

$${\text{Exp}}_{\text{id}}:\upsilon \in H^k\mapsto {\text{Exp}}_{\text{id }}(\upsilon )\in G_{H^k},$$ (13a)

$${\text{Log}}_{\text{id}}:\phi \in G_{H^k}\mapsto {\text{Log}}_{\text{id }}(\phi )={\upsilon }_0\in H^k.$$ (13b)

Extending to the group, Exp_φ(υ₀ ◦ φ) ≔ Exp_id(υ₀) ◦ φ, with Log_φ(φ) = Log_id (φ ◦ φ⁻¹) ◦ φ.

Invariance of the Diffeomorphometry

Metric Metrics often have invariance to basic motion through the space. The Euclidean metric is invariant to rigid translation or rotation. The diffeomorphism metric gives invariance to reparameterization by a diffeomorphism of the background space, and extends to a metric on the orbit of images⁵³.

Statement 2

For ${\Vert {\dot{\phi }}_t\Vert }_{{\phi }_t}≔{\Vert {\dot{\phi }}_t◦{\phi }_t^{-1}\Vert }_L$ ρ is right-invariant, transforming the background coordinates by g ∈ G_H gives the same:

$$\rho (\phi ,\phi \prime )=\rho (\phi ◦g,\phi \prime ◦g),g\in G_H.$$

This implies that distance can be measured from the identity: ρ(φ, φ′) = ρ(id, φ′ ◦ φ⁻¹), and it also implies that this induces a metric on the orbit of images:

$$\rho (I,I\prime )≔\underset{{\phi }_t,t\in [0,1]:{\phi }_0=\mathit{\text{id}},{\phi }_1=\phi ,\phi ·I=I\prime }{\text{inf}}{\int }_0^1{\Vert {\dot{\phi }}_t\Vert }_{{\phi }_t}\mathit{\text{dt}}.$$ (14)

The Appendix E shows the proof for right invariance, which follows from ${\Vert \frac{d\phi }{\mathit{\text{dt}}}\Vert }_{{\phi }_t}={\Vert \frac{d\phi }{\mathit{\text{dt}}}◦g\Vert }_{{\phi }_t◦g}$. It also does the regular exponential/logarithm for scalars as another example of a metric with invariance to demonstrate that this is a ubiquitous concept; in logarithm you can multiply each by the same scalar.

Inference in the Random Orbit Model, A Generative Theory of Shape

The random orbit model provides the prior distribution for solving for the geodesic positioning of shapes and images in CA associated to cross-sectional, growth and atrophy. The inference problem is to estimate the unknown hidden elements in the orbit and their flow of coordinates associated to the diffeomorphism. Our generative theory constructs the orbit of shapes as a random spray, with random flows acting on the templates to generate the space of random shapes inducing the probability law. For this we induce a Gaussian random field on the vectors at the identity of the group υ ∈ H^k, running the geodesic equations Exp_id (υ) ∈ G_H, which in turn induce the laws on shape and form Exp_id (υ) · m ∈ ℳ, Exp_id (υ) · I ∈ ℐ.

In the random orbit model, statistical variation is always indexed relative to template coordinates, so shape theory is local to the exemplar or template. Templates are generally estimated using template estimation procedures^{2, 40, 44, 45}.

The observables are modeled as noisy observations from the orbit. Maximum a-posteriori (MAP) and conditional mean estimation are the classic tools of choice. Since the flows are high-dimensional (infinite), we use optimization algorithms designed to estimate the unknown diffeomorphisms in the orbit. These correspond to MAP estimators for finite dimensional approximations of the parameter space.

Inference via Inexact Matching onto Observable Targets

The state of the dynamical system is the pair (φ_t, p_t) with control the flow of vector fields with dynamics given by (11). The targets enter as input data, with matching terms given by some smooth energy terms U : q_t → ℝ⁺, t ∈ [0, 1] driving the state towards the targets. For cross-sectional inference,^{10, 35, 55, 63} the matching term appears only as a single endpoint at time t = 1. For longitudinal time series^{52, 57, 72}, the data enters along the path on discrete times t_i ∈ [0, 1].

We write the matching term as a density in time, entering along the path. For the endpoint and or longitudinal time-series on discrete time, then U_t carries delta-Diracs.

Variational Problem

$${\dot{\phi }}_t={\upsilon }_t◦{\phi }_t,q_t={\phi }_t◦m,q_0=m,{\phi }_t·I=I◦{\phi }_t^{-1},{\phi }_0·I=I$$

$$\underset{{\upsilon }_t,t\in [0,1]}{\text{min}}C(\upsilon )≔\frac{1}{2}{\int }_0^1{\Vert {\upsilon }_t\Vert }_L^2\mathit{\text{ dt}}+{\int }_0^1{U}_t(q_t)\mathit{\text{dt}}$$ (15)

Statement 3

For state t → q_t, q̇ = υ ◦ q with velocity υ_t = ∫_𝒮K(·, q(s))p_t(s)ds minimizes

$$-{\int }_0^1{\int }_{𝒮}{p}_t·({\dot{q}}_t-{\upsilon }_t◦q_t)\mathit{\text{dsdt}}+\frac{1}{2}{\int }_0^1{\int }_{X}A{\upsilon }_t·{\upsilon }_t\mathit{\text{dxdt}}+{\int }_0^1{U}_t(q_t)\mathit{\text{dt}},$$ (16)

has Hamiltonian momentum satisfying

$$-{\dot{p}}_t-{(d{\upsilon }_t)}_{q_t}^T{p}_t-\frac{\partial U_t}{\partial q}(q_t)=0.$$ (17)

This shows the explicit role of the data in generating the g-function of Figure 3, i.e. $g=-\frac{\partial U}{\partial q}$. Measured data in cross-sectional and growth and atrophy problems provide exogenous g-inputs. The setting where the body itself has other structures internal to it, this can also create potential energy forces and therefore non-exogenous g-functions. For cross-sectional matching and for longitiudinal time-series the measurements are on discrete times, the external forces of the measurements enter on discrete times.

Statement 4

For landmark matching^{16, 41}, q_t(i) = φ_t(x_i), $U_t(q_t)=\delta (t-1)\frac{1}{2}{\sum }_{i=1}^n|y_i-q_1(i){|}^2$ giving

$$\frac{\partial U_t}{\partial q(i)}(q_1)=-\delta (t-1)(y_i-q_1(i)),i=1,\dots ,n.$$ (18)

For dense image matching LDDMM¹⁵, q_t = φ_t, and $U_t({\phi }_1)=\delta (t-1){\int }_X{(J-I\circ {\phi }_1^{-1})}^2\mathit{\text{dx}}$ giving

$$\frac{\partial U_t}{\partial \phi }({\phi }_1)=\delta (t-1)(J◦{\phi }_1-I){(d{\phi }_1)}^{-1T}\nabla I|d{\phi }_1|.$$ (19)

These problems for image matching via (15) have been used extensively via LDDMM¹⁵ for dense image matching and dense tensor matching^{17, 18}, optimizing over the vector fields υ_t, t ∈ [0, 1]. The proof of the variation of Eqn. (19) is derived in the Appendix D. Several important methods have emerged as well solving this problem efficiently including Advanced Normalization Toolkit (ANTS)¹² and Ashburner’s fast LDDMM⁹.

Alternatively shooting methods by shooting the atlas onto the target using the Riemannian exponential, finding an initial vector field to minimize the matching cost, have been used extensively as well. The shooting approach for images was championed originally by^{62, 81} by using shooting to match images, redefining the state from the diffeomorphism to the image-flow itself q_t ≔ φ_t · I. One efficient implementation is that by Zhang and Fletcher⁸³. This is much akin to the Stationary-LDDMM methods^{38, 79} which have seen wide adoption, although not identical because the Riemannian exponential departs from the stationary LDDMM solution where υ_t is chosen to be constant in time.

Forces associated to Internal Potential Energy

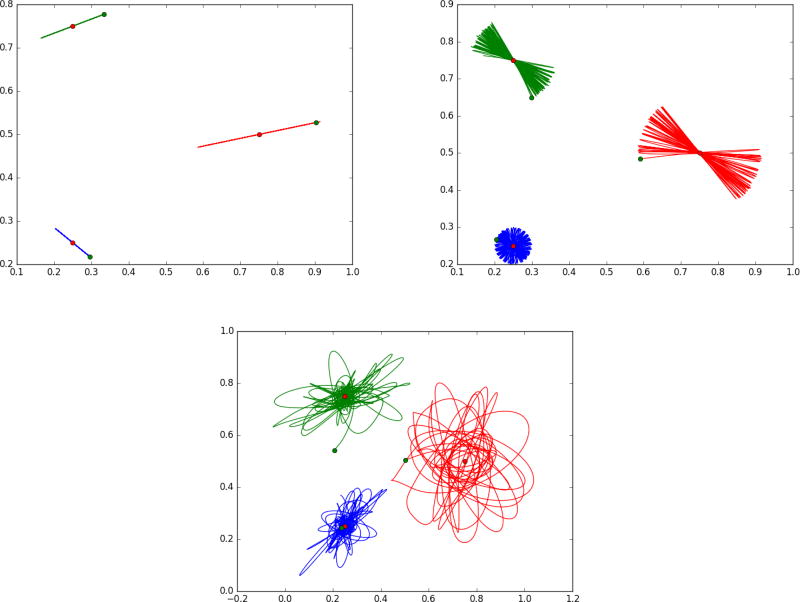
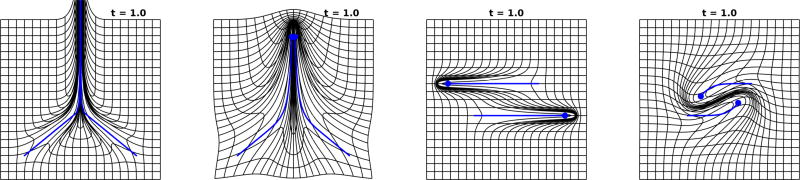
The g−forces arise as boundary conditions in matching problems which have been studied extensively. But in growth and atrophy we should expect that both internal potential energies of structures as well as external exogenous forces (like the wind) should provide continuous forces g_t(·), t ∈ [0, 1]. Shown in Figure 4 are results from shooting single landmarks with added potential energy function U(q) making it reminiscent of harmonic oscillators and pendulum mechanics. To illustrate we show three landmarks (green) as they move with potential energy given by their distance from the targets shown in red. We vary the kernel size so that at the smallest size the particles are independent (following straight lines), while at the largest kernel size they interact with each other because they can feel the force fields of other landmarks through their kernels.

Figure 4.

Showing landmark flowing with potential energy giving inputs $g(·)=\frac{\partial }{\partial q}U(q)$ that enters continuously along the path of the flow ṗ + g = −(dυ)^T ◦ φp. Potential energy term U giving the g terms expressed by the distance squared between the green landmark and the target red landmark. Panel 1 is for a small kernel (0.01); panel 2 is for a larger kernel .05, notice the trajectory slowly rotates, panel 3 shows large chaotic motions for kernel 0.1. See text in “Forces associated to Internal Potential Energy” section for more detail.

The attached figures show the trajectories of three landmarks (initialized at the green dots) and three attractors (visualized as red dots). The Hamiltonian momentum satisfies (17) with potential energy $U_t(q_t)=\frac{1}{2}|q^{\mathit{\text{red}}}-q_t^{\mathit{\text{greed}}}{|}^2$, the squared distance between each landmark and its attractor, and dynamical system

$$-{\dot{p}}_t-{(d{\upsilon }_t)}_{q_t}^T{p}_t-\frac{\partial U}{\partial q}(q_t)=0.$$ (20)

Panel 1 shows a small kernel size (0.01) and the resulting motion is similar to a pendulaum mechanical model as it overshoots and builds up potential energy, with trajectories that are straight line segments. With a larger kernel size (0.05), panel 2 shows the oscillations slowly rotate with a constant rate amplitude giving these flower-like images. With the largest kernel size (0.1), panel 3 shows the trajectories becoming chaotic. The computation uses a symplectic Euler method.

Shape Diffeomorphometry as Soft Condensed Matter: H^k, H⁰ Metrics

In placing our modeling of the brain in the soft condensed matter continuum^{26, 30, 42, 49, 68} we are taken centrally to equations that have much in common with classical equations of hydrodynamic flows and soft, active-matter physics. We rewrite the geodesic equations in terms of Eulerian momentum evolution, introducing the Riemannian metric ${\Vert \dot{\phi }\Vert }_{\phi }^2={\Vert \dot{\phi }◦{\phi }^{-1}\Vert }_L^2$. We establish the geodesic equations characterizing our diffeomorphism group with the H^k-equivalent metric as shown in MTY⁵⁴. This allows us to contrast our group G_H^k to the alternative group of volume preserving diffeomorphisms, |dφ_t| = 1 first studied by Arnold⁵. For comparison we add incompressibility to obtain a direct link to Euler’s equation of 1755²⁷. The relationship between geodesics associated to diffeomorphisms and Euler’s equation has been examined in⁶¹.

The H_k Shape Metric for Soft Matter

The derivation of the Euler-Lagrange equation takes variations in the group of flows of path integrals of the Riemannian metric. For generalized coordinates φ, φ̇, take as Lagrangian the Riemannian metric:

$$ℒ(\phi ,\dot{\phi })≔\frac{1}{2}{\Vert \dot{\phi }◦{\phi }^{-1}\Vert }_L^2=\frac{1}{2}{\int }_{X}A(\dot{\phi }◦{\phi }^{-1})·(\dot{\phi }◦{\phi }^{-1})\mathit{\text{dx}}.$$ (21)

The action integral and Euler-Lagrange equations are given as

$$J(\phi )={\int }_0^1ℒ({\phi }_t,{\dot{\phi }}_t)\mathit{\text{dt}}\text{with}$$ (22a)

$$-\frac{d}{\mathit{\text{dt}}}\underset{\text{Hamiltonian momentum}}{\underbrace{\frac{\partial ℒ(\phi ,\dot{\phi })}{\partial {\dot{\phi }}_t}}}+\frac{\partial ℒ(\phi ,\dot{\phi })}{\partial {\phi }_t}=0.$$ (22b)

Notice, $p≔\frac{\partial }{\partial \dot{\phi }}ℒ(\phi ,\dot{\phi })$ in (22b) is the Hamiltonian momentum of equation (11), the Lagrange multiplier. We call the generalized function Aυ ∈ H^k*, υ = φ̇ ◦ φ⁻¹ the Eulerian shape momentum for the operator A, which is termed the inertial operator. Eulerian momentum acting on the Eulerian vector field gives energy density. In this section we assume that Eulerian momentum Aυ is a classical vector function with respect to dx the volume measure in X = ℝ³. The section on geodesics of submanifolds emphasizes the singular case for the case when Aυ is a generalized function.

Statement 5

Lagrangian ℒ(φ, φ̇) of Eqn. (21) gives Euler-Lagrange equation

$$\frac{d}{\mathit{\text{dt}}}A{\upsilon }_t+(\mathit{\text{dA}}{\upsilon }_t){\upsilon }_t=-{(d{\upsilon }_t)}^{T}A{\upsilon }_t-\underset{\mathit{\text{local scale}}}{\underbrace{(\nabla ·{\upsilon }_t)A{\upsilon }_t}}.$$ (23)

Equation (23) was derived in MTY⁵⁴ for the Eulerian-momentum density; see Appendix (G) for its derivation. The left hand of (23) corresponds to ṗ for $p=\frac{\partial ℒ}{\partial \dot{\phi }}=A\upsilon ◦\phi |d\phi |$ as derived in Appendix section C equation (33) below, and is the advective non-linearity of the Navier-Stokes equation. Similarly for the first term on the right-hand side it is (dυ)^T p. The second term on the right hand side arises from the derivative of the Jacobian scale (d/dt)|dφ_t| in equation (35) of Appendix F giving the divergence term (∇·υ)Aυ which enters as an additional force balance in the Euler-Lagrange equations since the local determinant of Jacobian is not controlled. For incompressibility, this is replaced by pressure corresponding to constancy of local scale.

Arnold and the H⁰ Hydrodynamic Metric

Arnold using this action demonstrated that geodesics of square-integrable, divergence-free vector fields υ ∈ H⁰ (A = id, ∇ · υ = 0) retrieve Euler’s 1755²⁷ equation for inviscid, incompressible, conservative (no gravity) uniform density fluids. Adding incompressibility associates the constraint ∇ · υ = 0, requiring Lagrange multiplier λ in the action:

$${ℒ}^{\lambda }(\phi ,\dot{\phi })≔\frac{1}{2}{\int }_{X}A(\dot{\phi }◦{\phi }^{-1})·(\dot{\phi }◦{\phi }^{-1})\mathit{\text{dx}}+{\int }_X\lambda \nabla ·(\dot{\phi }◦{\phi }^{-1})\mathit{\text{dx}}.$$ (24)

To link to classical inviscid Navier-Stokes and the Euler equation, we write the solution for both the H⁰ and H^k metric reducing to Euler’s equation and use the fact that

$$(\mathit{\text{dA}}{\upsilon }_t){\upsilon }_t=({\upsilon }_t·\nabla )A{\upsilon }_t.$$

Statement 6

For incompressibility, ∇ · υ_t = 0, then the pressure P_t replaces the divergence:

$$H^k\mathit{\text{metric}}\frac{\partial }{\partial t}A{\upsilon }_t+({\upsilon }_t·\nabla )A{\upsilon }_t=\frac{1}{2}{(\mathit{\text{dA}}{\upsilon }_t)}^T{\upsilon }_t-\frac{1}{2}{(d{\upsilon }_t)}^{T}A{\upsilon }_t+\nabla \underset{\mathit{\text{pressure}}}{\underbrace{P_t}};$$ (25)

$$H^0\mathit{\text{metric }}(A=\mathit{\text{id}})\frac{\partial }{\partial t}{\upsilon }_t+({\upsilon }_t·\nabla ){\upsilon }_t=\nabla P_t.$$ (26)

Interestingly, the Lagrange multiplier dependent Pressure evolves according to the Laplacian:

$${\nabla }^2{P}_t=\nabla ·({\upsilon }_t·\nabla ){\upsilon }_t\underset{=0\mathit{\text{ for }}{H}^0(A=\mathit{\text{id}})}{\underbrace{-\frac{1}{2}({\upsilon }_t·({\nabla }^{2}A{\upsilon }_t)-A{\upsilon }_t·({\nabla }^2{\upsilon }_t))}}.$$ (27)

The proof of (25) is derived in Appendix G.

Fundamental questions about these equations with the H⁰ square integral metric remain since Euler’s original formulation. It remains an open Clay Millennium Problem associated to singularity arising in finite time from smooth initial conditions. In the 1-D case this is a form of inviscid Burger’s equation¹⁴ known to shock. The importance of the H^k metric in Computational Anatomy is that the vector fields satisfying the finite Sobolev norm condition υ ∈ H^k have guaranteed solutions of the forward and inverse maps of (2), (3)²⁴. The examination of the divergence-free case has been examined associated to specific matrix valued Green’s kernels⁵¹. Note that Equation (26) can also be formulated without a Lagrange multiplier by directly reasoning on the group of measure-preserving diffeomorphisms⁵⁸.

Dense Geodesic Brain Shape Space is Curved

The brain is a dense computing continuum. Geodesic flows through brain space are curved by the interaction between neighboring particles. Particle geodesics of (18) corresponding to φ_t(x_i), i = 1, 2, …, n of (11) have velocity ${\upsilon }_t(·)={\sum }_{i=1}^{n}K(·,{\phi }_t(x_i))p_t(i)$ with acceleration which is quadratic in velocity

$${\dot{p}}_t(i)=-{(d{\upsilon }_t)}_{{\phi }_t(x_i)}^T{p}_t(i).$$

Figure 5 (panels 1,2) shows particles following straight line paths as they come together at which point they curve each other “hooking up” traveling north at 0°. Figure 5 (panels 3,4) shows two particles which are “passing in the night.” The kernel has been selected σ = 3.5 so that the particles are in the range of attraction, ultimately joining hands as they go by and curving each other’s motion.

Figure 5.

Shows the two particle curving solution φ̇_t = υ_t ◦ φ_t, υ_t(·) = Σ_i=1,2 k(·, φ_t(x_i))p_t(i). Left two panels show particles coming together along geodesics they turn “north” together; kernel σ = 3.5. Right two panels show two particles passing each other along geodesics are attracted within the zone of attraction of the kernel width, curving the trajectories; kernel σ = 3.5

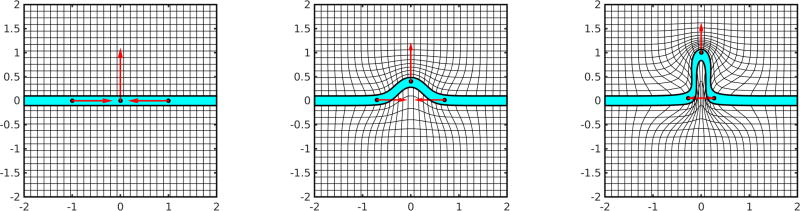
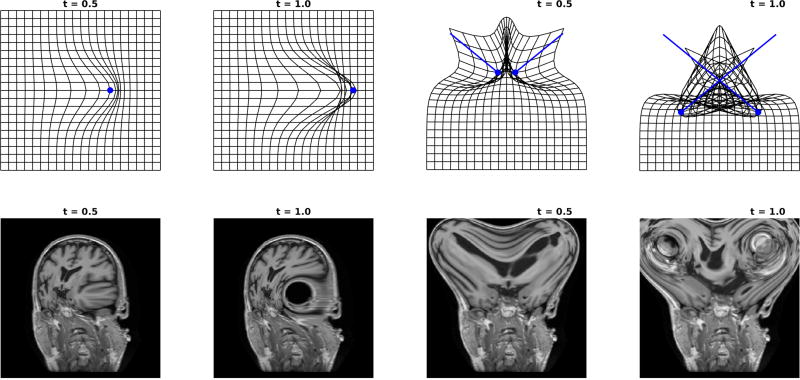
Shown in Figure 6 is the folding of a cortical simulation associated to three landmarks flowing. Figure 6 shows an example of 3 particle momentum representing large deformation kinematics. The flow was generated via 3 momenta in the plane p(1), p(2), p(3) giving initial vector field ${\upsilon }_0={\sum }_{s=1}^{3}K(x,x_i)p_0(i)$. Figure 6 was simulated to correspond to the depth of a large deformation kinematic fold, showing the geodesics (11) flow φ applied to the cyan region corresponding to three initial momenta forces p₀.

Figure 6.

Shows folding of a thin layer modeling cortical gray matter, for three particle momentum flow.

Figure 7 shows the effect of kernel scale. The two particle dynamics shown in Figure 7 has a significantly smaller kernel size, panels one and three σ = 1, with panels two and four σ = 2.5. The particles as they flow do not interact and literally pass by each other, which can be compared to Figure 5 which has σ = 3.5. Particles are attracted and curve their trajectories.

Figure 7.

Showing the effect of kernel size determining the scale of shape. Two particle “waltzing” solutions φ̇_t = υ_t ◦ φ_t, υ_t(·) = Σ_i=1,2 k(·, φ_t(x_i))p_t(i) for kernel scales 1.0 (panels 1,3) and 2.5 (panels 2,4).

Sparse single particle brain space is flat

Dense brain space is highly curved, the curving of space coming from other particles which form interactions. Only in the limit of single particles are geodesics straight lines in space.

Statement 7

For υ smooth C^∞ with Gaussian kernel on ℝ³, sparse single particle geodesics φ_t(x₁) are straight lines with constant speed ${\dot{p}}_t(1)=-{(d{\upsilon }_t)}_{{\phi }_t(x_1)}^T{p}_t(1)=0$, p_t(1) = p₀(1):

$${\upsilon }_t(·)=K(·,{\phi }_t(x_1))p_0(1).$$ (28)

For a single particle ∇K(x, φ_t(x₁))|_x=φt(x1) = 0 implying dυ_|φ(x1) = 0 of (28). Figure 8 shows the flows of a single particle in the sparse limit. Notice the linear motion of the particle. Importantly the grids flow diffeomorphically. The r.k.h.s. gives smooth flow of coordinates; the invertibility results from the Eulerian reindexing. The second and fourth panels show the carry of the image by the coordinates φ · I ≔ I ◦ φ⁻¹.

Figure 8.

Shows single particle flow ${\phi }_t:x\mapsto x+{\int }_0^t{\upsilon }_s◦{\phi }_s(x)\mathit{\text{ds}}$ for straight line, constant speed motion, p_t = p₀, υ_s(·) = k(·, φ_s(x₁))p₀, and action on the image, φ_t · I = I ◦ φ_t.

The Inverse Dilemma of Linear Motions

Smoothness of the vector fields alone is not enough to give inverses to form the basis for our theory of shape and form. Even for single particles, for sufficiently large motion, smooth linear splines have no general inverse even within the r.k.h.s. C¹, C², C^∞ smoothness setup. The Eulerian definition of the reindexed vector field to the flow coordinates is required. Define linear splines for smooth vector fields:

$${\psi }_t:x\mapsto x+{\int }_0^t{\upsilon }_{\tau }(x)d\tau .$$ (29)

Top row of Figure 9 shows examples for the single particle spline (panels 1,2) ψ_t(x) = x + tυ₀(x) for υ_t(x) = k(x − x₁)p₀(1), and two particle (panels 3,4) spline. Neither have an inverse. Panels one and three shows the grid close to crossing; panels two and four shows large deformation causing the grid to cross corresponding to singularity of the Jacobian. Bottom row of Figure 9 shows the action on the image I ◦ ψ_t. The singularity results in the large hole seen in the left 4 panels, and the crossing of the two particles shows complete scrambling seen in the right 4 panels.

Figure 9.

Top row: Single particle linear spline ψ_t : x ↦ x + tυ₀(x) (panels 1,2) and two particle spline (panels 3,4) with the grid crossing implying no inverse. Bottom row: Application of linear transformation splines to the images with the inverse catastrophe ψ_t · I = I ◦ ψ_t. kernel σ = 3.5; panels 1,3 shows t=0.5, panels 2,4 shows t=1.

Statement 8

For coordinates (ψ_t, ψ̇_t = υ_t), acting linearly with r.k.h.s. spline

$${\psi }_t:x\mapsto x+t{\upsilon }_0(x)\mathit{\text{ with constant }}{\upsilon }_0(·)=\int K(·,y)p_0(y)\mathit{\text{dy}}.$$ (30)

The inverse map ${\psi }_t^{-1}$ does not in general exist.

Take single particle motion in ℝ² from the origin (0, 0) for Gaussian kernel giving velocity $\upsilon (x)=e^{-\frac{1}{2}{|x|}^2}p$, and spline ψ⁽¹⁾(x) = x⁽¹⁾ + k(x)p⁽¹⁾, ψ⁽²⁾(x) = x⁽²⁾ + k(x)p⁽²⁾, with Jacobian

$$d\psi (x)=\left(\begin{array}{cc}\hfill 1-x^{(1)}{e}^{-{|x|}^2}{p}^{(1)}\hfill & \hfill -x^{(2)}{e}^{-{|x|}^2}{p}^{(1)}\hfill \\ \hfill -x^{(1)}{e}^{-{|x|}^2}{p}^{(2)}\hfill & \hfill 1-x^{(2)}{e}^{-{|x|}^2}{p}^{(2)}\hfill \end{array}\right).$$

For singularity take p⁽²⁾ = 0 for a particle moving along the x-axis, determinant goes through zero and changes sign for x⁽¹⁾e^−|x|2 p⁽¹⁾ ≥ 1 implying degeneracy for

$$\{(x^{(1)},x^{(2)}):{|x^{(1)}|}^2-\text{ln }{x}^{(1)}+{|x^{(2)}|}^2\le \text{ln }{p}^{(1)}\}.$$

Growth

Landmark and Curve Matching

In a typical landmark matching example, the template would include n labeled points q_t(i) = φ_t(x_i), and the cost function would be sum of square error,

$$U^{\text{landmark}}(q_1)=\frac{1}{2{\sigma }^2}\sum _{i=1}^n{|q_1(i)-l^{\text{target}}(i)|}^2,$$

with U_t(q_t) = δ(t − 1)U^landmark(q₁). In a typical curve matching example a template sulcal groove (for example) would be represented by a discrete curve, an ordered set of n points. To be invariant to the sampling of the curve, the cost function is generally curve-based current matching²⁸, which is minimized when curves and their tangent vectors are close. We define a center c(i) = (q₁(i + 1) + q₁(i))/2 and a length weighted tangent vector τ (i) = q₁(i + 1) − q₁(i) for i ∈ {1, …, n − 1} for each segment in the curve. The same notation is used for target curves, which may have a different number of segments, and are denoted by the superscript “target”.

$$U^{\text{curve}}(q_1)=\frac{1}{2{\sigma }^2}(\sum _{i,j=1}^{n-1}{\tau }^T(i)K^{\text{curve}}(c(i)-c(j))\tau (j)-2\sum _{i=1}^{n-1}\sum _{j=1}^{n^{\text{target}}-1}{\tau }^T(i)K^{\text{curve}}(c(i)-c^{\text{target}}(j)){\tau }^{\text{target}}(j)+\sum _{i,j=1}^{n^{\text{target}}-1}{\tau }^{\text{target}T}(i)K^{\text{curve}}(c^{\text{target}}(i)-c^{\text{target}}(j)){\tau }^{\text{target}}(j))$$

with U_t(q_t) = δ(t − 1)U^curve(q₁). Here |·|² denotes the vector norm in ℝ³, and σ² is a parameter controlling the importance of matching accuracy as compared to regularity of the solution. Here K^curve is a kernel function, in general matrix valued but often of the form k(·)Id, which defines a neighborhood around which points and tangent vectors should match closely on average.

Algorithm 1

These geodesic shooting problems can be solved with a gradient descent approach using an adjoint method^{13, 36, 47, 57}. Using the current guess for υ₀ the variables q, p are flowed forward in time from t = 0 to t = 1. The gradient of U^{landmark/curve} is calculated and this information is backpropagated by flowing a dual system of variables λ^q, λ^p from t = 1 to t = 0 according to an adjoint system of equations. The system is initialized with ${\lambda }_1^q=-\nabla U^{\text{landmark}/\text{curve}}(q_1),{\lambda }_1^p=0$, and is linear in the λ. The variable p₀ is updated according to the rule $p_0\mapsto p_0-\epsilon (p_0-K^{-1}·{\lambda }_0^p)$ for some small positive step size ε. By K⁻¹ · y we mean the solution to the linear equation K · x = y. We include here the landmark solution.

$${\lambda }_1^q(i)=-\frac{1}{{\sigma }^2}(q_1(i)-l^{\mathit{\text{target}}}(i)),{\lambda }_1^p(i)=0$$

$${\dot{\lambda }}_t^q(i)=\sum _{j=1}^n-[{\lambda }^{\mathit{\text{qT}}}(i)p(j)+{\lambda }^{\mathit{\text{qT}}}(j)p(i)]{\mathit{\text{DK}}}^T(q(i)-q(j))+p^T(i)p^T(j)D\nabla K(q(i)-q(j))[{\lambda }^p(i)-{\lambda }^p(j)]$$

$${\dot{\lambda }}_t^p(i)=\sum _{j=1}^n-K(q(i)-q(j)){\lambda }^q(j)+p(j)\mathit{\text{DK}}(q(i)-q(j))[{\lambda }^p(i)-{\lambda }^p(j)]$$

here ∇ places partial derivatives down a row, D places partial derivatives across a column.

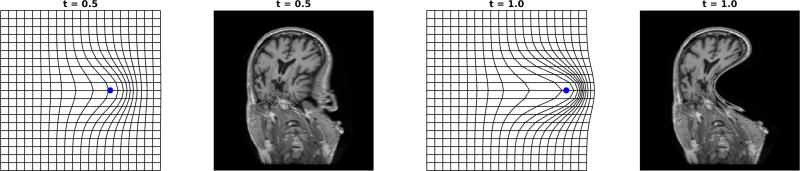
Figure 10 shows an example of growth in the medial temporal lobe associated to a 36 week MRI of a 2D-section through the medial temporal lobe showing the closed curve contour representing the entorhinal cortex and the collateral sulcus folding into the perirhinal sulcus. Panels 1–5 show sections depicting the evolution of the flow carrying the baby fold onto the adult. Panel 6 shows the spline solution of matching the cyan baby onto the target red adult. The target is an adult target section medial temporal lobe. The initial section shows the baby section in cyan, and the target adult in red. Notice the adult has a complete, tight fold that is typical of medial temporal lobe. Compare panels 5 and 6. Notice both map the baby onto the target, but the spline solution must fold the grid corresponding to the Jacobian of the map flipping sign and going through 0.

Figure 10.

Panels show folding of the closed curve contour of entorhinal cortex boundary associated to a 2-D cortical section through the medial temporal lobe of a 36 week old (cyan) folding onto the target (red). Blue line shows the cyan map BLUE ≔ φ · CY AN. Panel 6 shows the spline.

Cortical Curve and Surface Folding

A typical surface matching example, a template subcortical gray matter structure (for example) would be represented by a discrete triangulated surface, a set of n points and a triangulation of n^f faces. The j-th face consists of three ordered points from q₁ whose indices are denoted f(j, 1), f(j, 2), f(j, 3). To be invariant to the sampling of the surface, the cost function is generally surface based current matching⁷⁶, which is minimized when surfaces and their normal vectors are close. We define face centers c(j) = [q₁(f(j, 1)), q₁(f(j, 2)), q₁(f(j, 3))]/3 and area weighted normals A(j) = [q₁(f(j, 2)) − q₁(f(j, 1))] × [q₁(f(j, 3)) − q₁(f(j, 1))]/2 for × the cross product in ℝ³ and j ∈ {1, …, n^f}. The same notation is used for target surfaces, which may have a different number of faces or vertices, and are denoted by the superscript “target”

$$U^{\text{surface}}(q_1)=\frac{1}{2{\sigma }^2}(\sum _{i,j=1}^{n^f}{A}^T(i)K^{\text{surface}}(c(i),c(j))A(j)-2\sum _{i=1}^n\sum _{j=1}^{n^{\mathrm{f}\text{ target}}}{A}^T(i)K^{\text{surface}}(c(i),c^{\text{target}}(j))A^{\text{target}}(j)+\sum _{i,j=1}^{n^{\mathrm{f}\text{ target}}}{A}^{\text{target}T}(i)K^{\text{surface}}(c^{\text{target}}(i),c^{\text{target}}(j))A^{\text{target}}(j))$$

with U_t(q_t) = δ(t − 1)U^surface(q₁). Here K^surface is a kernel defined similarly to that above.

The ideas behind current matching have been expanded into a more general framework called varifold matching¹⁹. One advantage of this framework is that it can match curves and surfaces by considering the direction of tangents and normals, while ignoring their sign. In some situations this is more desirable than modeling anatomy with oriented curves and surfaces.

Atrophy via Image Matching

Image matching cost function U(q)

For image matching, the simplest and most commonly used cost function is the L² norm

$$U^{\text{image}}(I_1)=\frac{1}{2{\sigma }^2}{\int }_{{ℝ}^3}{(I_1-I^{\text{target}})}^2\mathit{\text{dx}}$$ (31)

with U_t(I_t) = δ(t − 1)U^image(I₁), in which we make the assumption that images are compactly supported to ensure the finiteness of the integral. The integral is discretized over a regular grid for numerical computation. The L² norm can also be useful for closed curve or surface matching problems, especially when the target is represented as an image I^target obtained from segmentation, typically equal to 1 inside the manifold and 0 outside, assuming however a continuous transition at the boundary to ensure differentiability of the norm. If q is the parametrization of a closed curve or surface, and Ω_q denote its interior, the L² norm between the indicator function of Ω_q and I^target can then be expressed as

$$U(q)=\frac{1}{2{\sigma }^2}{\int }_{{\mathrm{\Omega }}_q}(1-2I^{\text{target}})\mathit{\text{ dx}}+\frac{1}{2{\sigma }^2}{\int }_{{ℝ}^d}{(I^{\text{target}})}^2\mathit{\text{dx}}$$

with d = 2 or 3. The first integral can conveniently be expressed as a curve or surface integral using the divergence theorem by introducing a function h^target such that ∇ · h^target = I^target, giving

$$U(q)=\frac{1}{2{\sigma }^2}{\int }_{\partial {\mathrm{\Omega }}_q}(x/d-2h^{\text{target}}(x))N_q(x){\sigma }_q(\mathit{\text{dx}})+\frac{1}{2{\sigma }^2}{\int }_{{ℝ}^d}{(I^{\text{target}})}^2\mathit{\text{dx}}$$ (32)

where σ_q is the line or surface area measure on ∂Ω_q and N_q the unit normal. The vector field h^target can be computed as h^target = ∇H^target, with ∇²H^target = I^target with H compactly supported, which is easy to solve numerically. Once done, the first integral in (32) can be discretized over a triangulation of q, namely (using the notation above)

$$U(q)=\frac{1}{2{\sigma }^2}\sum _{i=1}^{n^f}(c(i)/d-2h^{\text{target}}(c(i)))A(i).$$

Medial Temporal Lobe in Alzheimer’s

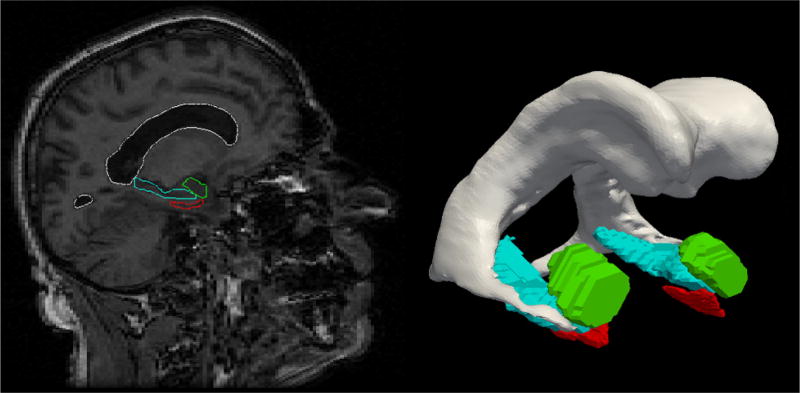
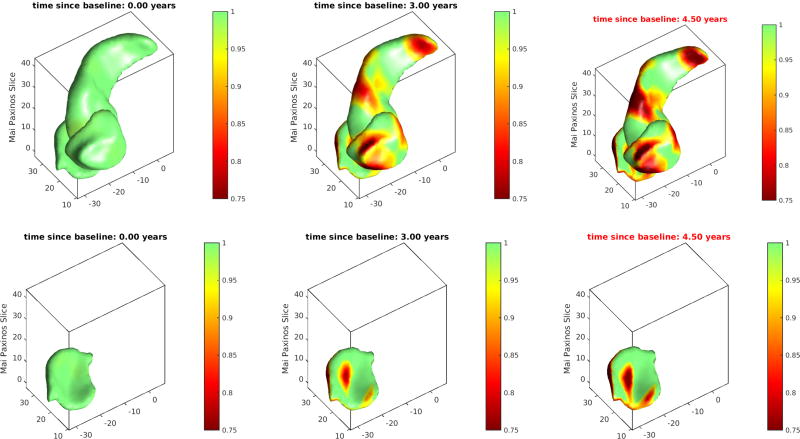
Shown in Figure 11 are an example of a template medial temporal lobe and a section through an MRI of a particular individual associated to a large study called the BIOCARD study of Alzheimer’s disease. The three structures are the amygdala, entorhinal cortex, and hippocampus. Shown in Figure 12 are depictions of two subjects (top and bottom rows) in the BIOCARD study showing the atrophy spreading across the entorhinal cortex of the individuals. This is a subject suffering from Alzheimer’s disease and atrophying in the entorhinal cortex at an averaged rate of 25% and half that (bottom row) year over year. Diffeomorphometry has been used to map the first timepoint through the time series of the individual’s four MRI timepoints. Shown superimposed via the color scale is the atrophy (red colors) and expansions (blue colors) as the individual atrophies. Notice there is only atrophy in the entorhinal cortex in this case. The yellow color in the bottom row implies 20% total loss from the first scan time localized from vertex to vertex across the surface.

Figure 11.

Showing medial temporal lobe structures with both the MRI section and the solid models segmentations.

Figure 12.

Showing atrophy in the medial temporal lobe. The series of sections show the entorhinal cortex from two idividual (top and bottom rows), with the geodesic flow depicted across the four time points. Top row shows clear spread of disease as neutral green (no change) spreads to red (decrease) of localized volume indexed to the surfaces. The top subjects shows significantly more year over year loss than bottom.

Shown in Figure 13 are the three structures amygdala, entorhinal cortex and hippocampus. The entorhinal cortex is hidden in the top row view by amygdala and hippocampus. The bottom row shows the entorhinal cortex which is hidden in the top row view. The color bar red show 25 percent loss relative to the first timepoint, with green showing no change relative to the first time point in the time series of scans. Notice that the color bar red implies 25% atrophy, whereas yellow implies 5% localized loss.

Figure 13.

Showing atrophy in the medial temporal lobe. The top row shows all three structures: amygdala, hippocampus and hidden below is entorhinal cortex. The bottom row shows the entorhinal cortex which is hidden in the top row. The color bar red show 25 percent loss, with green showing no change relative to the first time point in the time series of scans.

CONCLUSIONS

The growth and atrophy model from Computational Anatomy is constructed around the analogues of force, momentum, velocity and position. The medical images are transformed by the vector fields of positions, encoded as a flow of diffeomorphisms, which act on the images as group actions.

Interestingly, one of the most important results from the CA project has been the development of the smoothness condition constraint on the vector fields, placing them into a reproducing kernel Hilbert space with kernel which is at least one time continuously differentiable. For this setting there are no shocks, and the metric between elements in the orbit of images under the action of the group is well defined. This smoothness condition forces particles to interact, so that neighboring particles within the scale of the smoothness constraint bond in the sense of metric pattern theory, which is manifest by the Eulerian and Hamiltonian momentum being differential combinations of adjacent particles. This also results in the fact that the space of human anatomies is a curved space. Only in the sparse limit of single particles are geodesic trajectories between configurations straight lines. The curved nature of the flows is implied by dense neighboring particles interacting. Geodesics associated to least-action of the reproducing kernel Hilbert space have trajectories which are therefore highly curved in the dense limit.

The Euler-equation encoding the geodesics under the least-action principle are an extension of the inviscid equation of the classic divergence-free case. This is the dense active tissue model which includes local scale implying divergence-full vector fields. This gives a force-balance Euler equation on the geodesics which includes an adjustment from the classical inviscid equations by the divergence weighted by the Eulerian-momentum. In some sense this replaces the usual pressure terms that arises in the divergence free case.

Numerous examples are shown exhibiting both growth as well as atrophy associated to neurodegeneration. In the growth case, the example is included to demonstrate the smooth folding of tissue suggesting that the metric associated to the dense active-tissue model naturally supports smooth folding rather than crumpling which likely explains in some part the observations of the deep cortical folds.

A Green’s Kernel examples

Green’s kernels are used throughout engineering for which shift invariant differential operators appear in the energy. Define the 3 × 3 identity operator Id, with K(x, y) ≔ κ(x − y)Id. For continuity H², let L = (−∇² + 1)Id with A = (−∇² + 1)²Id, kernel κ(x) = e^−|x|; for 1 continuous derivative, H³ satisfies the k > 2.5 square-integrable condition, then L = (−∇² + 1)^1.5Id with A = (−∇² + 1)³Id giving kernel κ(x) = (1 + |x|)e^−|x|; for 2 continuous derivatives, H⁴ with A = (−∇² + 1)⁴Id gives kernel κ(x) = 4(3 + 3|x| + |x|²)e^−|x|.

The Green’s kernel is smooth, for all α = (α₁, α₂, α₃) ∈ ℝ³, then K(·, x_i)α ∈ H^k and it evaluates for the inner-product, $w\in H^k:{\langle K(·,x_i)\alpha ,w(·)\rangle }_L={\sum }_{j=1}^3{\alpha }_j{w}_j(x_i)$. The reproducing property follows, α, β ∈ ℝ³,

$${\langle K(·,x)\alpha ,K(·,y)\beta \rangle }_L=\alpha ·K(x,y)\beta .$$

B Spectral interpretation of the Dual Space

We restrict ourselves to shift-invariant kernels, so K(x, y) = K(x − y) implying there is a natural interpretation through the spectrum of the dual. To understand the dual space spectrally, then H^k is the space of functions υ = (υ₁, υ₂, υ₃), with Fourier transforms υ̂_i (ω), i = 1, 2, 3 that have a spectrum which fall at a polynomial rate in high frequencies. So they are square-integrable when weighted by a degree 2k polynomial emphasizing the high frequencies. The dual on the other hand H^k*, has elements σ = (σ₁, σ₂, σ₃) ∈ H^k* with each component a generalized function with Fourier transforms σ̂_i (ω), i = 1, 2, 3 with a square-integrable spectrum only when down-weighted by the inverse of a degree 2k polynomial:

$${\int }_{{ℝ}^3}\frac{{|{\hat{\sigma }}_i(\omega )|}^2}{1+{|\omega |}^{2k}}d\omega <\infty .$$

The integral notation used to represent the evaluation of σ ∈ H^k* at some w ∈ H^k is

$$\sigma (w)=\int w·\sigma (\mathit{\text{dx}}),$$

which does not necessarily correspond to a usual integral with respect to a measure, with some properties (such as the change of variable formula) not always holding.

C Euler-Lagrange Derivation

For Aυ a classical function having density, to derive the Euler-Lagrange of equation (23) for compressibility with the H^k metric we take the variation of the kinetic energy

$$ℒ(\phi ,\dot{\phi })=\frac{1}{2}{\int }_{X}A(\dot{\phi }◦{\phi }^{-1})·\dot{\phi }◦{\phi }^{-1}\mathit{\text{dx}},$$

with respect to Lagrangian velocity φ̇ → φ̇^ε = φ̇ + εδφ̇ giving terms

$$\frac{d}{d\epsilon }ℒ(\phi ,{\dot{\phi }}^{\epsilon })=\frac{1}{2}{\int }_X\frac{d}{d\epsilon }(A({\dot{\phi }}^{\epsilon }◦{\phi }^{-1}))·{\dot{\phi }}^{\epsilon }◦{\phi }^{-1}\mathit{\text{dx}}+\frac{1}{2}{\int }_{X}A({\dot{\phi }}^{\epsilon }◦{\phi }^{-1})·\frac{d}{d\epsilon }({\dot{\phi }}^{\epsilon }◦{\phi }^{-1})\mathit{\text{dx}}$$

Operator A is self-adjiont giving identical terms; at ε = 0 gives Hamiltonian momentum:

$${\int }_X{(A({\dot{\phi }}^{\epsilon }◦{\phi }^{-1}))·\frac{d}{d\epsilon }(\dot{\phi }+\epsilon \delta \dot{\phi })◦{\phi }^{-1}\mathit{\text{dx}}|}_{\epsilon =0}={\int }_X\underset{\partial ℒ/\partial \dot{\phi }\text{Ham}.\text{ mom}.}{\underbrace{A\upsilon ◦\phi |d\phi |}}·\delta \dot{\phi }\mathit{\text{dx}}.$$ (33)

This is the Hamiltonian expression in

The variation φ → φ^ε = φ + εδφ, requires the inverse according to the first order perturbation:

$${({\phi }^{-1}+\epsilon \delta {\phi }^{-1})◦(\phi +\epsilon \delta \phi )\simeq \text{id}+\epsilon (d{\phi }^{-1})|}_{\phi }{\delta \phi +\epsilon \delta {\phi }^{-1}|}_{\phi }$$

$$\text{implying}\delta {\phi }^{-1}={-(d{\phi }^{-1})\delta \phi |}_{{\phi }^{-1}}={-{(d\phi )}_{{\phi }^{-1}}^{-1}\delta \phi |}_{{\phi }^{-1}}.$$

Taking a similar variation of the Lagrangian as above gives

$$\int {(A({\dot{\phi }}^{\epsilon }◦{\phi }^{-1}))·\frac{d}{d\epsilon }(\dot{\phi }◦({{\phi }^{-1}-{(d\phi )}_{{\phi }^{-1}}^{-1}\delta \phi |}_{{\phi }^{-1}}))|}_{\epsilon =0}\mathit{\text{dx}}=-\int {A\upsilon ◦(d\upsilon )(d\phi )|}_{{\phi }^{-1}}{{(d\phi )}_{{\phi }^{-1}}^{-1}\delta \phi |}_{{\phi }^{-1}}\mathit{\text{dx}}=-\int \underset{\partial ℒ/\partial \phi }{\underbrace{{(d\upsilon )}_{\phi }^{T}A\upsilon ◦\phi |d\phi |}}·\delta \phi \mathit{\text{dx}}.$$ (34)

D Variation of the Image Matching Term

To prove the variation in the dense image matching term of Eqn. (19), take the variation of ∫(J − I ◦ φ⁻¹)²dx via perturbation φ → φ^ε = φ + εδφ requires the inverse perturbation $\delta {\phi }^{-1}={-{(d\phi )}_{{\phi }^{-1}}^{-1}\delta \phi |}_{{\phi }^{-1}}$. Then we have

$$\frac{d}{d\epsilon }\frac{1}{2}{\int }_X{{(J-I◦{\phi }^{\epsilon -1})}^2\mathit{\text{dx}}|}_{\epsilon =0}={\int }_X{(J-I◦{\phi }^{-1})\nabla I_{{\phi }^{-1}}·{(d\phi )}_{{\phi }^{-1}}^{-1}\delta \phi |}_{{\phi }^{-1}})\mathit{\text{dx}}={\int }_X(J◦\phi -I){(d\phi )}^{-1T}\nabla I|d\phi |·\delta \phi \mathit{\text{dx}}.$$

E Right-invariant Metric and Logarithm-Exponential Example

The right-invariance follows from ${\Vert \frac{d\phi }{\mathit{\text{dt}}}\Vert }_{{\phi }_t}={\Vert \frac{d\phi }{\mathit{\text{dt}}}◦g\Vert }_{{\phi }_t◦g}$. Substituting into ρ(φ, φ′) gives

$$\underset{{\phi }_t:{\phi }_0=\phi ,{\phi }_1=\phi \prime }{\text{inf}}{\int }_0^1{\Vert \frac{d{\phi }_t}{\mathit{\text{dt}}}◦g\Vert }_{{\phi }_t◦g}^2\mathit{\text{dt}}\stackrel{({\phi }_t={\phi }_t◦g)}{=}\underset{{\phi }_0=\phi ◦g,{\phi }_1=\phi \prime ◦g}{\text{inf}}{\int }_0^1{\Vert \frac{d{\phi }_t}{\mathit{\text{dt}}}\Vert }_{{\phi }_t}^2\mathit{\text{dt}}=\rho (\phi ◦g,\phi \prime ◦g).$$

E.0.1 Logarithm-exponential

A familiar example for the group of multiplicative reals are natural logarithm and the inverse the exponential. For x, y ∈ (0, ∞), multiplication x◦y = xy, the metric d(x, y), x, y ∈ (0, ∞) is the geodesic curve x_t, t ∈ [0, 1] satisfying

$$d(x,y)≔\underset{x_t:x_0=x,x_1=y}{\text{inf}}{\int }_0^1\frac{|{\dot{x}}_t|}{x_t}\mathit{\text{dt}}=|\text{log}(y/x)|.$$

The invariance for the log-distance is d(x, y) = d(xz, yz), z ∈ (0, ∞).

F Lemma: Constant scale and divergence free vector fields

This Lemma links divergence of the vector fields generating the transformations to the volume preservation of incompressibility as expressed via the Jacobian of the transformation.

Lemma 1

$$\frac{d}{\mathit{\text{dt}}}|d{\phi }_t|=(\nabla ·{\upsilon }_t)◦{\phi }_t|d{\phi }_t|.$$ (35)

For all w(·), examine the differential equation:

$$\frac{d}{\mathit{\text{dt}}}\int w|d({\phi }_t)|\mathit{\text{dy}}=\frac{d}{\mathit{\text{dt}}}\int w◦{\phi }_t^{-1}\mathit{\text{dx}}.$$

Using the transport equation $\frac{d}{\mathit{\text{dt}}}{\phi }^{-1}=-d({\phi }^{-1})\upsilon$ gives

$$\int w\frac{d}{\mathit{\text{dt}}}|d({\phi }_t)|\mathit{\text{dy}}=\int \frac{d}{\mathit{\text{dt}}}w({\phi }_t^{-1})\mathit{\text{dx}}=-\int d(w◦{\phi }^{-1}){\upsilon }_t\mathit{\text{dx}}=\int w◦{\phi }_t^{-1}(\nabla ·{\upsilon }_t)\mathit{\text{dx}}.$$

The last equality is the divergence theorem. Substituting variables gives the equality for all functions w:

$$\int w\frac{d}{\mathit{\text{dt}}}|d({\phi }_t)|\mathit{\text{dy}}=\int w(\nabla ·{\upsilon }_t)◦{\phi }_t|d{\phi }_t|\mathit{\text{dx}}.$$

G Euler-Lagrange Equation for Eulerian Momentum Density: Diffeomorphometry and Incompressible Hydrodynamics

As shown in Eqn. (11) with state q_t = φ_t, the time derivative of the Hamiltonian momentum density can be expressed as $0={\dot{p}}_t+(d{\upsilon }_t^T)◦{\phi }_t{p}_t$. Using this relationship and substituting in terms of the Eulerian momentum density p_t = Aυ_t ◦ φ_t|dφ_t|, this equation can be written

$$\frac{d}{\mathit{\text{dt}}}{p}_t+{(d{\upsilon }_t)}^T◦{\phi }_t{p}_t=\frac{\partial }{\partial t}A{\upsilon }_t◦{\phi }_t|d{\phi }_t|+(\mathit{\text{dA}}{\upsilon }_t)◦{\phi }_t{\upsilon }_t◦{\phi }_t|d{\phi }_t|+A{\upsilon }_t◦{\phi }_t|d{\phi }_t|\nabla ·{\upsilon }_t◦{\phi }_t+{(d{\upsilon }_t)}^T◦{\phi }_{t}A{\upsilon }_t◦{\phi }_t|d{\phi }_t|.$$

Seeting this to 0 and evaluating at φ⁻¹ gives the result of the Euler-Lagrange Eqn. (23). For the incompressible case, the requirement ∇ · υ = 0 constrains the kinetic energy according to

$${ℒ}^{\lambda }=ℒ(\phi ,\dot{\phi })+\int \lambda (x)\nabla ·(\dot{\phi }◦{\phi }^{-1}(x))\mathit{\text{dx}}.$$

Hamiltonian momentum adjusted by the gradient of the Lagrange multiplier

$$\frac{\partial {ℒ}^{\lambda }}{\partial \dot{\phi }}=p_t=(A{\upsilon }_t-\nabla {\lambda }_t)◦{\phi }_t|d\phi |,$$

with Jacobian |dφ_t| = 1 and identical dynamics ṗ_t = −(dυ_t)^T ◦ φ_t p_t: Differentiating Hamiltonian momentum and applying φ⁻¹ gives

$$\frac{d}{\mathit{\text{dt}}}{p}_t+{(d{\upsilon }_t)}^T◦{\phi }_t{p}_t=\frac{d}{\mathit{\text{dt}}}A{\upsilon }_t+(\mathit{\text{dA}}{\upsilon }_t){\upsilon }_t+{(d{\upsilon }_t)}^{T}A{\upsilon }_t-\nabla \frac{d}{\mathit{\text{dt}}}{\lambda }_t-d{(\nabla {\lambda }_t)}^T{\upsilon }_t-{(d{\upsilon }_t)}^T\nabla {\lambda }_t$$

The gradient pressure term ∇P_t follows from these equalities:

$$\nabla (\frac{d}{\mathit{\text{dt}}}{\lambda }_t\nabla {\lambda }_t·{\upsilon }_t)=\nabla \frac{d}{\mathit{\text{dt}}}{\lambda }_t+d{(\nabla {\lambda }_t)}^T{\upsilon }_t+{(d{\upsilon }_t)}^T\nabla {\lambda }_t{(d{\upsilon }_t)}^{T}A{\upsilon }_t=\frac{1}{2}{(d{\upsilon }_t)}^{T}A{\upsilon }_t-\frac{1}{2}d{(A{\upsilon }_t)}^T{\upsilon }_t+\frac{1}{2}\nabla ({\upsilon }_t^{T}A{\upsilon }_t).$$

implying

$$\nabla P_t=\nabla (\frac{d}{\mathit{\text{dt}}}{\lambda }_t+\nabla {\lambda }_t·{\upsilon }_t-\frac{1}{2}{\upsilon }_t^{T}A{\upsilon }_t),$$

so that

$$\frac{d}{\mathit{\text{dt}}}(A{\upsilon }_t)+(\mathit{\text{dA}}{\upsilon }_t){\upsilon }_t=\frac{1}{2}(d{(A{\upsilon }_t)}^T{\upsilon }_t-{(d{\upsilon }_t)}^{T}A{\upsilon }_t)+\nabla P_t.$$

Taking the divergence, one can check directly that for any vector fileds u and w,

$$\nabla ·(w·{\mathit{\text{du}}}^T)=\mathit{\text{Tr}}(\mathit{\text{dw}}.{\mathit{\text{du}}}^T)+w·{\nabla }^{2}u,$$

yielding the Laplacian equation for computing the pressure:

$${\nabla }^{2}P=\nabla ·(\nabla ·{\upsilon }_t)A{\upsilon }_t+\frac{1}{2}{\nabla }^2{\upsilon }_t·A{\upsilon }_t-\frac{1}{2}{\nabla }^{2}A{\upsilon }_t·{\upsilon }_t.$$