Abstract
It is now common to record dozens to hundreds or more neurons simultaneously, and to ask how the network activity changes across experimental conditions. A natural framework for addressing questions of functional connectivity is to apply Gaussian graphical modeling to neural data, where each edge in the graph corresponds to a non-zero partial correlation between neurons. Because the number of possible edges is large, one strategy for estimating the graph has been to apply methods that aim to identify large sparse effects using an L1 penalty. However, the partial correlations found in neural spike count data are neither large nor sparse, so techniques that perform well in sparse settings will typically perform poorly in the context of neural spike count data. Fortunately, the correlated firing for any pair of cortical neurons depends strongly on both their distance apart and the features for which they are tuned. We introduce a method that takes advantage of these known, strong effects by allowing the penalty to depend on them: thus, for example, the connection between pairs of neurons that are close together will be penalized less than pairs that are far apart. We show through simulations that this physiologically-motivated procedure performs substantially better than off-the-shelf generic tools, and we illustrate by applying the methodology to populations of neurons recorded with multielectrode arrays implanted in macaque visual cortex areas V1 and V4.
Keywords: Bayesian inference, False discovery rate, Functional connectivity, Gaussian graphical model, Graphical lasso, High-dimensional estimation, Macaque visual cortex, Penalized maximum likelihood estimation
1. Introduction
The rapid growth in the number of neurons being recorded simultaneously (Ahrens et al., 2015; Alivisatos et al., 2013; Kerr and Denk, 2008; Kipke et al., 2008) creates an urgent need for statistical procedures that can identify the structure of covariation in neural network activity (Shadlen and Newsome, 1998; Brown et al., 2004; Cunningham and Yu, 2014; Stevenson and Kording, 2011; Song et al., 2013; Yatsenko et al., 2015; Cohen and Maunsell, 2009; Cohen and Kohn, 2011; Efron et al., 2001; Kelly and Kass, 2012; Mitchell et al., 2009; Vinci et al., 2016). An appealing approach to network analysis begins by representing multivariate activity as a graph, that is, a set of nodes together with a specification of which nodes are connected by edges (Bassett and Sporns, 2017). In the case of multi-neuron recordings, each node would correspond to a neuron. Because these recordings are typically noisy, capturing in full detail the interactions among neurons, which can occur at multiple timescales, is very difficult. An initial simplification is to consider the vector of spike counts, within a time interval of several hundred milliseconds, to be a Gaussian random vector X whose covariance matrix Σ defines a graph based on the inverse matrix Ω = Σ−1 (assuming Σ is invertible). Specifically, the edges in the graph correspond to the non-zero off-diagonal elements of Ω = [ωij], that is, an edge between nodes i and j is absent if and only if ωij·= 0. Furthermore, ωij= 0 if and only if the corresponding partial correlation satisfies ρij = 0, and ρij = 0 if and only if the i and j nodes are independent conditionally on all the other nodes, that is in our case, an edge exists between pairs of neurons that have a unique component of covariation that is not associated with all the other neurons. The time-scale, imposed by the scientific questions of interest or by objective choice of bin size, such as experimental task durations, affects the elements of Σ and hence the conclusions one might draw from the graph.
Such Gaussian graphical models are widely applied and studied (Murphy, 2012). However, even this simple case becomes challenging as the number of neurons grows: although, for typical spike count data, estimation of any single correlation coefficient may incur a relatively small error, compounding thousands of such small errors produces an unstable estimate of the matrix Σ. Thus, some form of regularization in the estimation of Σ is usually applied. In recent years, the most commonly-applied form of covariance regularization has been the Graphical lasso (Glasso) (Yuan and Lin, 2007; Friedman et al., 2008; Banerjee et al., 2008; Rothman et al., 2008; Mazumder and Hastie, 2012). To define it, we write the Gaussian likelihood function as, where with X(r) representing the Gaussian random vector of spike counts of d neurons on trial r, for r = 1,... ,n, we assume the number of non-zero elements of Ω is comparatively small (so the matrix is sparse), and we maximize the penalized log likelihood function
| (1) |
where is the L1 matrix norm of Ω (with or without the diagonal entries) (Yuan and Lin, 2007; Friedman et al., 2008; D’Aspremont et al., 2008; Rothman et al., 2008; Mazumder and Hastie, 2012) and Ω is assumed to be positive definite. The magnitude of the regularization parameter λ > 0 controls the degree of sparsity.
Glasso performs well in the presence of a small number of large effects, i.e., a small number of large non-zero offdiagonal elements of Ω, which corresponds to large signals relative to noise. In microelectrode array recordings, however, we expect instead to find a large number of small and noisy effects. Indeed, using realistic settings for a numerical simulation (spike counts on coarse time scales 300 ~ 1000ms) we found that Glasso and existing variants perform poorly (see Fig. 1 and the simulation section). We therefore sought to enhance off-the-shelf regularization by including information that is specific to the neural setting. In this paper we introduce a variant of Glasso that takes advantage of known neurophysiology: the covariation of pairs of neurons’ spike counts depends on their distance apart and their tuning curve correlation (Smith and Kohn, 2008; Smith and Sommer, 2013; Goris et al., 2014; Vinci et al., 2016). We use a Bayesian formulation of the problem to allow the penalty to vary with each neuron pair, separately, so that edges can become less likely to be placed between neurons as their distance apart increases or their tuning curve correlation decreases - the relationship of the penalty to these two covariates is learned from the data. We call the method Graphical lasso with Adjusted Regularization (GAR). Fig. 1 illustrates the typical benefit of applying GAR in comparison with Glasso. We provide an extensive simulation study to compare GAR with several variants of Glasso that have appeared in the literature. We also show how the Bayesian approach provides an elegant framework to construct the graph, in a manner similar to false discovery rate regression (Scott et al., 2015). Finally, we apply the method to populations of neurons recorded with multielectrode arrays implanted in macaque visual cortex areas V1 and V4 to illustrate aspects of network behavior that can be discovered with this approach.
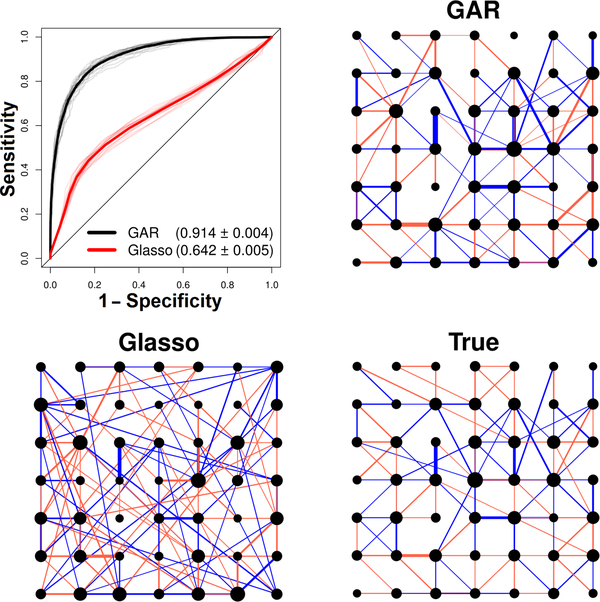
Fig. 1.
Glasso and GAR graph estimation performances for a simulated network. The true graph contains d = 49 neurons and 118 edges, and is based on parameter settings derived from cortical data. Blue and red edges denote positive and negative partial correlations and the size of each node is proportional to the number of its connections. The GAR and Glasso estimates displayed are based on a sample size of n = 200 (see simulation Section 2.4 for details). For clarity, we show only the 118 strongest estimated connections (Glasso estimated 642 edges and GAR 204). ROC curves were obtained for 50 repeat simulated data; all 50 curves are plotted as thin lines and their averages as thick lines. The average area under the curves (AUC) is written in parentheses ± 2 simulation standard error: GAR is more accurate than Glasso.
2. Results
We first describe several penalized likelihood methods for estimating Ω, including GAR (Sections 2.1 and 2.2). We then explain how to infer a neuronal network connectivity graph from the estimate of Ω (Section 2.3). Finally, we illustrate the properties of these methods in an extensive simulation study (Section 2.4), and we estimate the connectivity graphs of populations of neurons recorded with multielectrode arrays implanted in macaque visual cortex areas V1 and V4 (Section 2.5).
2.1. Estimating the precision matrix Ω
The Glasso estimate of Ω is obtained in Eq. (1) where
| (2) |
is the sample covariance matrix of, and λ > 0 is chosen according to one of several possible criteria (Yuan and Lin, 2007; Liu et al., 2010; Foygel and Drton, 2010). Here we use the criterion of Fan et al. (2009), taking λ to minimize the cross-validated risk of estimating Ω with, calculated as the average loss, , across 500 random (90%, 10%) splits of the data where is the estimate in Eq. (1) based on.
A variant is the adaptive Glasso (AGlasso) (Fan et al., 2009) given by
| (3) |
that is Eq. (1) but with the penalty ‖Ω‖1 replaced by ‖Q⊙Ω‖1, where ⊙ denotes the entry-wise matrix multiplication and Q is a matrix containing values inversely related to the absolute values of an initial estimate , for example with the inverse of the sample covariance matrix (Fan et al., 2009). Hence, the AGlasso aims to penalize less/more the large/small entries of Ω. However, a reliable initial estimate of Ω is not always available; for instance, when the number of neurons d is greater than the number of trials n, requires modifications to be inverted, such as adding a small constant to its diagonal to make it positive definite. Because the AGlasso estimate depends on the quality of the initial estimate of Ω, it does not necessarily outperform the Glasso estimate.
The Bayesian Adaptive Glasso (BAGlasso; Wang (2012)) supplements the Gaussian likelihood with a prior distribution for Ω
| (4) |
where Λ = [λij] is a symmetric matrix that contains a different penalty for each wij, to make it possible to penalize less/more the large/small wij. The data automatically tunes the penalties if we assume a sufficiently flexible hyperprior for Λ, for example independent Gamma distributions for each λij (Wang, 2012). The BAGlasso estimate of Ω is taken to be the mean (posterior expectation) or the mode (maximum a posteriori, a.k.a. MAP) of , the posterior distribution of Ω. The BAGlasso estimator is not necessarily better than the Glasso or the AGlasso estimator because the added model flexibility also induces more variability. Note that the simple case where λij· = λ for all (i, j) is known as the Bayesian Glasso (BGlasso; Wang (2012)); furthermore the BGlasso MAP estimate of Ω for a fixed λ is the Glasso estimate in Eq. (1).
The Glasso framework in Eq. (1) can also be extended into the Sparse-Low rank model (SPL)
| (5) |
where Ω = S — L ≻ 0 is assumed to be the combination of a sparse component S representing the dependence structure of the recorded neurons conditionally on all other recorded and latent neurons in the network, and a low-rank component aimed at capturing the network effect of latent neurons on the recorded ones (Chandrasekaran et al., 2012; Giraud and Tsybakov, 2012; Yuan, 2012; Yatsenko et al., 2015). The parameters λ and q in Eq. (5) may be selected via cross-validation, analogously to Glasso. If L is set to zero, then Eq. (5) is equivalent to Glasso in Eq. (1). Partial correlations based on the component S alone would represent the conditional dependence structure of the observed neurons in an unknown larger network containing a set of unobserved units of intrisic dimensionality assumed to be smaller than q. However, for small sample sizes n and large numbers of neurons d, the sparse and low-rank components may become too expensive to estimate accurately so that SPL might perform no better than other methods (Giraud and Tsybakov, 2012; Yatsenko et al., 2015).
Proposed methods
The AGlasso and BAGlasso penalize less the Ω matrix entries that are anticipated to be larger, where the “anticipation” is explicitly garnered from an initial estimate of Ω for AGlasso, or implicitly data driven in the BAGlasso. Sometimes we have available additional variables that carry information about the strength of the dependence between neurons, for example inter-neuron distance and tuning curve correlation, which have been observed to regulate the shared activity of neuron pairs (Smith and Kohn, 2008; Smith and Sommer, 2013; Goris et al., 2014; Yatsenko et al., 2015; Vinci et al., 2016). Our proposed methods take advantage of these known, strong effects by allowing the penalties to depend on them: for example, pairs of neurons that are close together will be penalized less than pairs that are far apart (see data analysis, Section 2.5).
Let be a vector of m auxiliary quantities that carry information about the strength of the dependence between neurons i and j. The Smooth Adaptive Glasso (SAGlasso) is a “smooth” variant of the AGlasso, where the entries qij of the weight matrix Q in Eq. (3) are taken to be smooth functions of Wij. This smoothing will both reduce the noise in Q and introduce the information carried by Wij.into the regularized estimation of Ω. To proceed, we regress on Wij using a local smoother such as smoothing splines or local polynomials, where we divide the qij by so that they are on the scale of the partial correlations
| (6) |
To ensure that the resulting weights qij are positive, we either perform a Gamma regression (Algorithm 1, Appendix), or log transform first if a Gaussian regression is used.
The Graphical lasso with Adjusted Regularization (GAR) is a variant of the BAGlasso, where we impose additional structure on λij in Eq. (4). Specifically, we assume that the penalties are functions of the auxiliary variables Wij according to:
| (7) |
where the function g(Wij) is fitted to the data rather than pre-specified, and the ai ‘s are positive parameters that mimic the scaling components in Eq. (6), so that g(Wij) is on the scale of the partial correlation 𝜌ij. We render g identifiable by setting , which is reasonable since αi mimics , and the mean parameter of in Eq. (4) is . Then, while the BAGlasso postulates a hyperprior for Λ in Eq. (4), here we assume a hyperprior on the parameters of Λ in Eq. (7), that is on Θ = {α, g}, where α = (α1,…,αd), and g is the m-variate function of the auxiliary variables W. The GAR full Bayes estimate of Ω is taken to be the mean or the mode of, the posterior distribution of Ω given the data and auxiliary covariates W = {Wij}. Ideally, g should be as general a function as possible. However, the model is complex enough to make the posterior difficult to calculate or simulate from so we opted to use the simplest of non-parametric functions: a step function. In Section 2.2.2 we describe a Gibbs sampler to simulate from, and thus obtain sample mean or mode estimates of Ω. An alternative that allows a general form of g is to take an empirical Bayes approach to obtain a point estimate of Θ as the maximizer of the likelihood of Θ given and W, and calculate the posterior distribution of Ω conditional on that estimate, that is, instead of calculating the full Bayes posterior. We implement this approach in Section 2.2.3 and apply it to our data in Section 2.5, taking 9 to be a regression spline with knots at the quartiles of the auxiliary variables. In the end, we have the full Bayes and the empirical Bayes GAR variants, and we can take the estimate of Ω to be either the mean or the mode of the corresponding posterior distribution. In our simulations (Section 2.4) we show that the improvement provided by GAR can be substantial compared to the competing methods, especially for values of d and n typically found in experimental neural data.
The proposed and existing methods considered here are similarly scalable. All methods aim to estimate the d(d + 1)/2 parameters of the precision matrix Ω, but their regularizations have different complexities: Glasso uses a single regularization parameter, λ in Eq. 1, and SPL uses two, λ and q in Eq. 5, while AGlasso and BAGlasso allow d(d + 1)/2 different penalties across the entries of Ω. SAGlasso and GAR also allow a different penalty for each entry of Ω, but their effective number is smaller than d(d + 1)/2. Indeed, the SAGlasso penalties all depend on W through a regression function that depends only on a limited number of regression coefficients. For GAR, all penalties are functions only of g and the d parameters αi (Eq. 7), where g is a regression function with a few degrees of freedom, e.g. splines with 3 or 4 knots. Morever, SAGlasso and GAR gain statistical efficiency when the auxiliary variables W are informative.
Finally, we note that a simple way to combine GAR with SPL (GAR-SPL) consists of replacing the penalty λ‖S‖1 in Eq. (5) by, where is a GAR estimate of, and ξ and q are selected via cross-validation. In our simulations, GAR-SPL outperformed SPL but not GAR. A full Bayesian treatment of GAR-SPL, where the penalty matrix is estimated in direct combination with S rather than Ω, might provide a better performance; this is a topic of future research.
2.2. GAR estimation
In Sections 2.2.2 and 2.2.3 we describe Full and Empirical Bayes implementations of GAR, which both involve a data augmentation sampler that we present in Section 2.2.1. Algorithms and details are in Appendix.
2.2.1. Data augmentation
Both Full and Empirical Bayes implementations of GAR involve drawing samples from the posterior distribution
| (8) |
where the likelihood and the prior π(Ω | Λ) are defined in Eqs. (2) and (4). We proceed using a data augmentation strategy (Wang, 2012) where we introduce the nuisance random quantity, and jointly sample from
| (9) |
using the block Gibbs Sampler in Appendix, Algorithm 2, where
| (10) |
| (11) |
| (12) |
φ(u | μ,σ2) is the Gaussian p.d.f. with mean μ and variance σ2, γ(z|a,b) is the Gamma p.d.f. with shape and rate parameters a and b, and is the finite normalizing constant of Eq. (11). Then, because the Laplace distribution is a Gaussian scale mixture (Andrews and Mallows, 1974; West, 1987), we can write Eq. 8 as the integral of Eq. 9:
so that the matrix Ω in a samp le drawn from Eq. (9) is a sample from the posterior distribution in Eq. 8.
2.2.2. Full Bayes estimation
Let g in Eq. (7) be a step function with K steps and value βk > 0 in step k, that is:
| (13) |
where I is the indicator function, ∀h ≠ l, Ah ⋂ Al = ∅, and . Let α = (α1,…,αd), β = (β1,…,βK) and Θ = {α,β}, where. Following the augmentation strategy in Section 2.2.1, Eq. (10) reduces to
| (14) |
where G(Θ) is the finite normalizing constant. We further assume the hyperprior density on Θ
| (15) |
with r = s = 1, r′ = 0.01, and s′ = 0.00001; results were not sensitive to the choice of these parameters. We use the Gibbs sampler in Appendix, Algorithm 3, to sample from the full joint posterior distribution
| (16) |
where the likelihood is defined in Eq. (2), and the prior joint distribution is the product of Eqs. (14) and (15).
In practice, we take the number of steps K in Eq. (13) to be relatively small, e.g. 4 or 5, if we expect the penalties to change relatively slowly with W. Otherwise, to increase the flexibility of g while ensuring that enough data points contribute to estimating each βk, we can afford of take since d(d + 1)/2 values of W are available. We further locate the steps at evenly spaced empirical quantiles of the W’s, using a hierarchical quantile splitting when W is multi-dimensional, so that each step contains approximately the same number of W’s. If no auxiliary quantity W is available, full Bayes GAR can still be applied by setting K = 1. If we wanted to constrain g to be monotonic increasing, we could enrich the prior in Eq. (15) with the factor , which requires βk to be sampled from the same distribution at step 2 of Algorithm 3, but truncated to be within the interval (βk-1, βk+1), where β0 = 0 and βK+1 = ∞. Different features of g may be imposed in similar ways.
2.2.3. Empirical Bayes estimation
By assuming Eq. (7) and, Eq. (4) reduces to
| (17) |
where Θ = {α, g}, g is a positive function of any form estimable in a Gamma regression, and G(Θ) is the normalizing constant. We further assume the prior density
| (18) |
where p (Θ) is a density on Θ. We estimate Θ by maximizing the posterior density
| (19) |
using an Expectation-Maximization algorithm (Dempster, 1977; Gelman et al., 2004):
-
–E-step: Given the current estimate Θold, we compute the expectation
with respect to , which reduces to c + Q(Θ | Θold), where c is a constant of Θ and(20)
where can be approximated using the Gibbs sampler (Section 2.2.1). -
–M-STEP: Q(Θ | Θold) is concave with respect to g and αi, i = 1,…,n, so we can maximize it with respect to Θ by circularly optimizing with respect to α and g until convergence, as follows: assuming p(Θ) ∝ 1 in Eq. (18), subject to αi > 0 yields the maximizer
where , and the maximizing function g is obtained by regressing on Wij, i < j in a Gamma regression model.(21)
We summarize the procedure for the case p(Θ) ∝ 1 in Appendix, Algorithm 4.
2.3. Estimating a connectivity graph
Here, we explain how to estimate graphs based on partial correlation estimates, so as to control the edge false discovery and false nondiscovery rates.
Let E = {eij} be a true graph, where eij = 1 when nodes i and j are connected by an edge, and eij = 0 otherwise. We build graph estimators of two kinds:
- A δ-graph has edges such that, for a threshold δ ∈ [0,1),
where is a point estimate of the partial correlation in Eq. (6). That is, an edge is present in the graph estimate if the corresponding estimated absolute partial correlation exceeds some threshold δ.(22) - A (p, δ)-graph has edges such that, for thresholds p, δ ∈ [0,1),
where(23)
is the edge posterior probability, that is the posterior probability that the magnitude of the partial correlation ρ- exceeds δ. The (p, δ)-graph uses the full posterior probability of the partial correlations rather than the point estimates , setting an edge to zero if the edge posterior probability (Eq. 24) is smaller than p. In our simulations, (p, δ)-graphs were often more precise than δ-graphs.(24)
One must choose values for δ and p. Using δ = 0 in Eq. (22) could produce a completely dense graph, while using a large value would only identify strong edges, which is not sensible for neural networks since connections can be small and numerous. Ideally, δ should be as close as possible to the minimum magnitude of the true non-zero partial correlations; we take a robust estimate of that minimum to be the 5-th quantile of the magnitudes of the non-zero MAP partial correlation estimates. We use the same δ in Eq. (23), and choose p to control the false discovery and non-discovery rates of the graph edges (FDR and FNR, respectively), that is the rate of false detected edges (number of (i, j) such that but eij = 0) out of all detections (number of ) and the rate of true missed connections (number of (i, j) such that but eij = 1) out of all non-detections (number of):
| (25) |
and
| (26) |
where the expectations are taken with respect to the data . Then for a fixed δ, a (p, δ)-graph can be selected by choosing either
for some desired upper bound C, depending on whether we want to control the FDR or the FNR, or choose p to balance the FDR and FNR, that is FDR ≈ FNR (the intersection of the green and red curves in Fig. 2). However, the FDR and FNR are easy to approximate in simulations when the true graph E is known, but not otherwise. An alternative is to calculate their Bayesian counterparts, obtained by Eqs. (25) and (26) but with expectation taken conditionally on the data , which yields
| (27) |
and
| (28) |
where πij (δ) is the edge posterior probability defined in Eq. (24). Equation (27) has the same form as the Bayesian FDR in multiple hypothesis testing (Efron et al., 2001; Efron, 2007) and FDR-regression (Scott et al., 2015), obtained as the average of the local FDRs, i.e. posterior probabilities that the hypotheses are null, across the rejections. In our framework (1 — πij (δ)) is the local FDR for the pair (i,j). In Fig. 2 we show by simulation that bounding FDRII or FNRII also appears to bound their frequentist counterparts. This result is not surprising because empirical estimates of the Bayesian FDR are typically upward biased estimates of the frequentist FDR (Efron and Tibshirani, 2002).
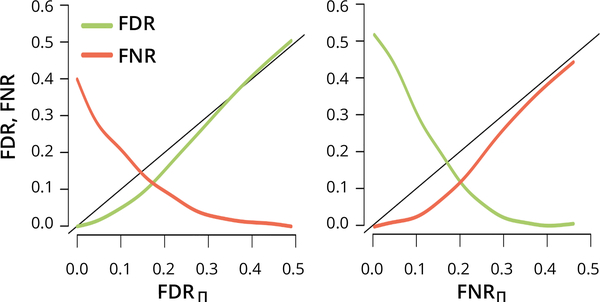
Fig. 2.
Bayesian FDR and FNR, FDRII and FNRII, plotted on the x- axes, control their frequentist counterparts FDR and FNR, plotted on the y-axes, in a simulation based on d = 100 neurons and sample size n = 500 (Section 2.4). The black lines are the first bisectors x = y.
ROC curves summarize graph estimation performance
Other useful measures of detection error are sensitivity and specificity
| (29) |
and
| (30) |
which give the proportions of true edges correctly identified and of missing edges correctly omitted, respectively. By tuning the parameters defining the estimated edges ’s, for example λ in Eq. (1) and p in Eq. (23), we can obtain the curve of SENS versus 1 — SPEC, known as Receiver Operating Characteristic (ROC) curve (see Figs. 1 and 3). A point above the ROC curve denotes an edge detection performance that cannot be achieved by the estimator, i.e. no values of the tuning parameters could make the estimator produce that outcome. Therefore, a larger area under a ROC curve (AUC) indicates a better edge detection performance; we use this metric to compare graph estimators in our simulations (Figs. 1 and 3).
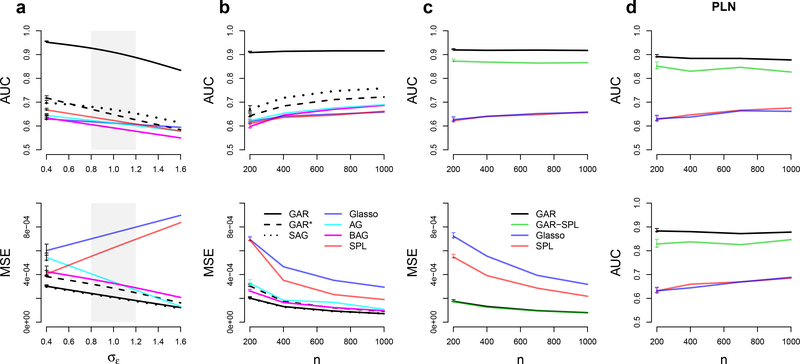
Fig. 3.
Performance of graph estimates, measured by areas under ROC curves (AUC), and of partial correlation estimates, measured by MSEs, for d = 50 neurons simulated according to Eq. (31) as functions of σϵ in (a), where σϵ ≈ 1 (shaded grey area) represents a real data scenario, and as functions of the sample size n in (b). (c) AUC and MSE for d = 50 observed neurons conditionally on q = 20 latent ones as functions of n. (d) AUC when methods are applied to non-Gaussian Poisson-lognormal (PLN) data without (top) and with (bottom) latent neurons, as functions of n. The horizontal intevals on the left of ah curves are 95% simulation intervals.
2.4. Statistical properties of the estimates of Ω in simulated data
We compared the performance of the various estimators of Ω in an extensive simulation study. We simulated data sets of n d-dimensional Gaussian vectors , with μ chosen to match typical values found in experimental data, and with Ω = [ωij] generated as follows: for i < j,
| (31) |
where I (A) = 1 if A is true and I (A) = 0 otherwise, so that Zij ∈ {—1,1} makes ωij negative with probability η and positive with probability 1 — η. We use a simple auxiliary variable Wij, which we take to be the physical distance between neurons i and j on a 4mm × 4mm Utah electrode array, and used b = –2, η = 0.75, and σ𝜖 = 1 to generate values of ωij that are consistent with the experimental data analyzed in Section 2.5. We then symmetrized Ω by setting ωji = ωij, and set the diagonal entries ωii to the smallest positive ω* that rendered Ω positive definite. We achieved sparsity by resetting to zero the smallest half of the partial correlations so that half of the graph edges were null, and rescaled Σ = Ω−1 so its diagonal elements would have magnitude similar to the experimental data analyzed in Section 2.5.
Fig. 1 shows a simulated network of d = 49 neurons with dependence structure in Eq. (31), the Glasso graph estimate, and the empirical Bayes GAR estimate (Algorithm 4) with g (Eq. 7) taken to be a regression spline: GAR uses the spatial information of the inter-neuron distances and yields more accurate connectivity graph estimates. Here and in the rest of the paper, all GAR parameters, including the penalty parameters, are assigned a prior distribution and are thus selected implicitly. Similarly for the other Bayesian methods. For the non-Bayesian methods, Glasso, AGlasso, and SPL, the penalty parameters are selected by cross validation (Fan et al., 2009).
Fig. 3a shows the AUC and mean squared error (MSE) of the partial correlation matrix estimate for a simulated network of d =50 neurons and sample size n = 200, for moderate deviations from 𝜎𝜖 = 1 in Eq. (31), where the MSE is the average of the squared error, , across repeat simulations. We show only the performance of the full Bayes GAR estimate; it is comparable to that of the empirical Bayes GAR estimate but faster to compute. Fig. 3b shows how AUC and MSE vary with the sample size n for fixed 𝜎𝜖 = 1 and d = 50. GAR outperforms all other methods in Figs. 3a and 3b. The SAGlasso is the next best method. It is easier to implement than GAR but provides only a modest improvement over other methods.
Figs. 3a and 3b also show the performance of GAR*, the full Bayes estimate that uses a constant g(w) in Eq. (7). Comparing GAR and GAR* shows the added benefit of including auxiliary information within our novel Bayesian framework. Note that GAR* appears to outperform the Glasso and its variants even without adapting the regularization to the covariate. This may be due to the parameters αi (Eq. 7) forcing the penalty to be on the standardized scale of the partial correlations rather than on the scale of the precision matrix entries, which are known to be highly sensitive to the variance of the Gaussian vectors X (Yuan and Lin, 2007). It is also possible that, while the Glasso variants AGlasso and BAGlasso also attempt to attenuate the data scaling effect on the regularization, they involve d(d +1) /2 regularization parameters (the entries of Q in Eq. 3 and the λij ‘s in Ea. 4), whereas GAR* achieves the same goal with only d +1 parameters (the αi’s and the constant g), which might reduce the variance of the partial correlation estimates.
The problem of estimating pairwise dependences conditionally on both observed and latent units (here neurons) has been dealt with previously by applying SPL in Eq. (5). In Fig. 3c we compare the performances of GAR, Glasso, SPL, and GAR-SPL to estimate the dependence structure of d =50 recorded neurons when an additional q = 20 neurons belong to the network but their activity is not observed. GAR outperformed SPL, likely because the information extracted from the inter-neuron distance overcompensated the missed information about the activity of the latent variables. SPL outperformed Glasso only in terms of MSE. The variant GAR-SPL outperformed SPL but not GAR, likely because of the additional variance due to the estimation of the low-rank component. However, a full Bayesian treatment of GAR-SPL might provide a better performance; this is a topic of future research.
Fig. 3d repeats the AUC curves of Figs. 3bc but with non-Gaussian data generated from the multivariate Poisson- lognormal distribution (Vinci et al., 2016)
| (32) |
where the spike counts on trial r are independent given their latent log-rates, and μ and Σ were set to match typical values found in experimental spike count data (μi ≈ 2, Σii ≈ 0.25, implying about 8.37 spikes/s on average). Under this model, dependences between spike counts are weaker than those of their latent rates due to Poisson-noise corruption (Vinci et al., 2016; Behseta et al., 2009). Since the dependences between the log-rates likely provide a better representation of input correlation (Vinci et al., 2016), we estimate the neuronal graph based on the partial correlations Ω = Σ−1 of the latent rates, applying first the square root transformation to the spike counts to improve their fit to a Gaussian distribution (Kass et al., 2014; Georgopoulos and Ashe, 2000; Yu et al., 2009). Fig. 3d shows that GAR outperformed all other methods, presumably because it successfully extracted the connectivity information carried by inter-neuron distance despite the Poisson noise. Also as in Fig. 3c, GAR-SPL outperformed SPL but not GAR. We repeated the simulation of Fig. 3d with values of μi small enough to induce neurons’ firing rates of about 0.1 spikes/s and, compared to Fig. 3d, noted a loss of AUC of about 5% for GAR and GAR-SPL, and about 20% for all other methods that do not use auxiliary information.
2.5. Estimating neural connectivity in macaque visual cortex
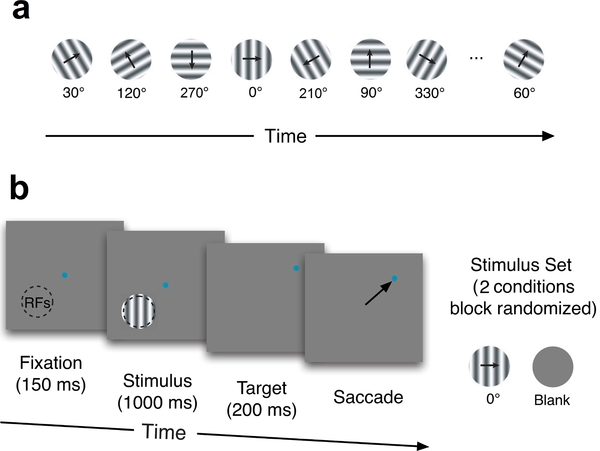
Spike data were recorded from the V1 and V4 visual cortex of two rhesus macaque monkeys using 100-electrode Utah arrays. For the V1 data (Kelly et al., 2010; Scott et al., 2015; Cowley et al., 2016), visual stimuli were presented to an anesthetized animal. The stimuli were either a 30s sequence of drifting sinusoidal gratings (98 different orientations and two blanks, 300ms each), or blank gray screen (Fig. 4a). The 30s stimuli sequence was randomly ordered, and then repeated in that same order 120 times. For the V4 data, the visual stimuli were either vertical drifting sinusoidal gratings or a blank gray screen (Fig. 4b). Each trial began with the animal fixating a small dot for 150ms before the grating or blank screen was presented for 1000ms. Then the stimulus and fixation point were extinguished and the animal received a liquid reward for making an eye movement to a target 8 degrees from fixation in a random direction. Each stimulus (the vertical grating or the blank) was repeated 126 times. All procedures were approved by the Institutional Animal Care and Use Committee of the University of Pittsburgh and Albert Einstein College of Medicine, and were in compliance with the guidelines set forth in the National Institutes of Health’s Guide for the Care and Use of Laboratory Animals.
Fig. 4.
Experiments. (a) The V1 stimuli consist of 30 second sequences of 98 randomly ordered oriented drifting gratings, or a blank gray screen. (b) The V4 stimuli consist of a blank gray screen or a vertical drifting sinusoidal grating appearing in the aggregate receptive field of the V4 neurons (RFs, indicated by the dashed circle).
We applied GAR to the neurons’ spike counts in repeated trials of duration 300ms and 1000ms in the V1 and V4 experiments, respectively, to estimate the connectivity at the trial time scale. We square-root transformed the spike counts to mitigate the dependence between variance and mean and thus improve their fit to Gaussian distribution we assume in this paper.
V1 data
We obtained recordings for 128 candidate neuronal units by sorting the voltage signals of the 76 electrodes with the best signal to noise ratio (Kelly et al., 2007), in response to a sequence of 98 drifting sinusoidal gratings and blank screen (Fig. 4a). Previous analyses of these data have been published (Kelly et al., 2010; Scott et al., 2015; Cowley et al., 2016). To produce easily readable graphs, we analysed only 100 neurons, selected as follows: we first retained the highest spiking neuron on each of the 76 electrodes that had identifiable action potentials, and then added the 24 highest spiking remaining neurons. The firing rates of these 100 neurons ranged from 0.61 to 31.97 spikes/s, with mean 6.27, and 2.5th and 97.5th percentiles 1.12 and 16.20.
Neurons in V1 are driven by drifting gratings of orientation θ ∈ (0, 360] (Scott et al., 2015), and their average firing rates are usually described by sinusoidal tuning functions of θ, with similar tuning in diametrically opposite orientations θ and θ + 180 degrees (Butts and Goldman, 2006; Smith and Kohn, 2008; Scott et al., 2015; Vinci et al., 2016). Hence maximal firing rates occur at θ* and θ * + 180, for some θ*, and minimal firing rates occur in the orthogonal orientations, θ* ± 90. The tuning similarity of two neurons can be quantified by their tuning curve correlation (TCC), computed as the Pearson’s correlation of the two neurons’ tuning curves across stimuli (Smith and Kohn, 2008; Smith and Sommer, 2013; Ecker et al., 2014; Kass et al., 2014; Vinci et al., 2016). The strength of the dependence between two neurons’ activities has been observed to increase with TCC and decrease with inter-neuron distance (DIST) (Smith and Kohn, 2008; Smith and Sommer, 2013; Goris et al., 2014; Vinci et al., 2016), so we considered these two auxiliary quantities for our GAR connectivity graph estimation.
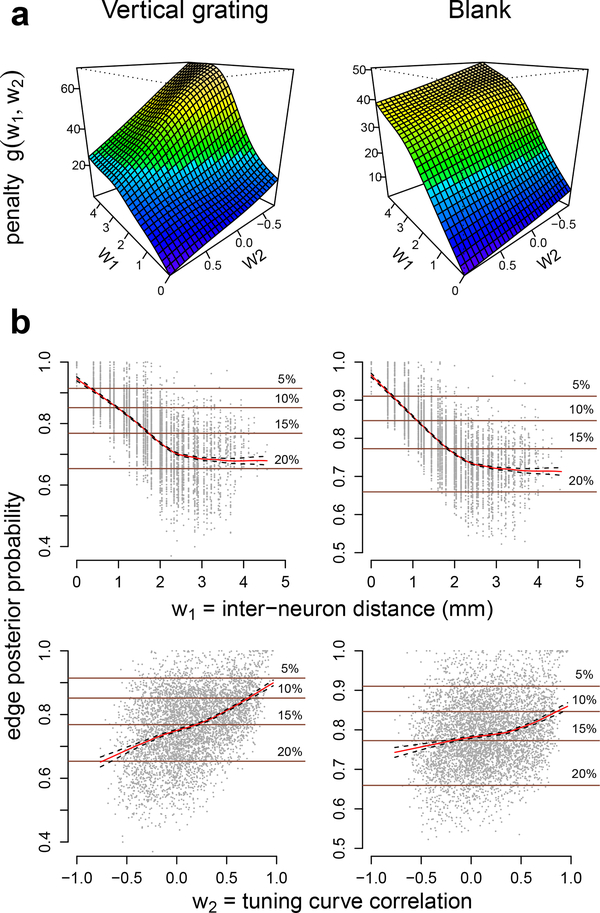
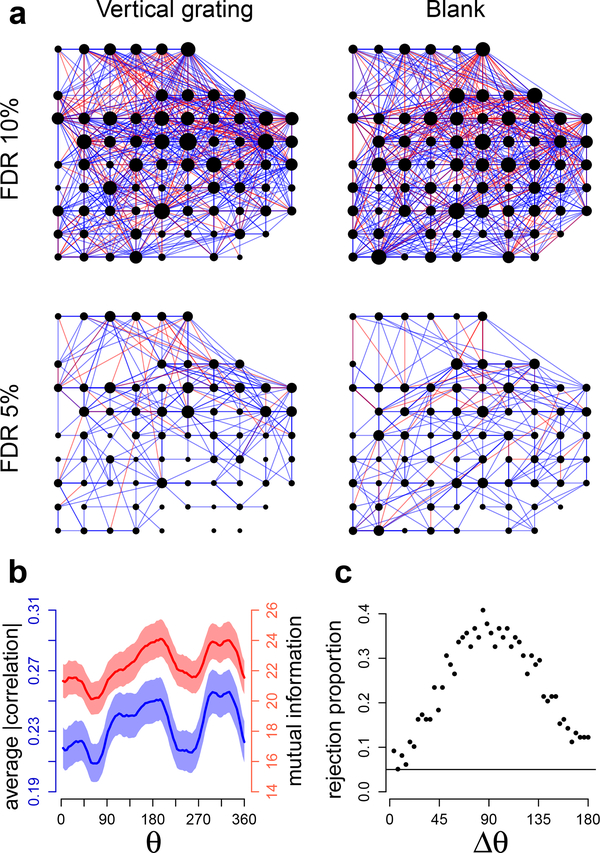
Fig. 5 shows the results of GAR applied to 300 ms square root transformed spike counts for the vertical grating (θ = 0) and blank screen conditions. The estimated penalty functions g(W1,W2) in Eq. (7) (fitted using Algorithm 4, with g a bivariate regression splines) are plotted in Fig. 5a: they increase with W1 = DIST and decrease with W2 = TCC, which is consistent with previous analyses of V1 macaque data (Goris et al., 2014; Smith and Kohn, 2008; Scott et al., 2015) where neurons dependences in macaque V1 were observed to decrease with inter-neuron distance and increase with tuning curve similarity. Fig. 5b shows that the corresponding edge posterior probabilities (Eq. (24)) decrease with DIST and increase with TCC, on average; the horizontal lines denote probability thresholds that lead to different graph FDRII controls (Eqs. (23), (25), and (27)). We obtained similar results for all grating orientations. Finally, Fig. 6a displays the estimated (p, δ)-graphs (Eq. (23)): the graph for the vertical grating contains 1160 edges (859 positive and 301 negative connections) with 10% FDRn, and 350 edges (307 positive, 43 negative) with 5% FDRII; the graph under blank screen contains 1246 edges (937 positive, 309 negative) with 10% FDRn, and 405 edges (362 positive, 43 negative) with 5% FDRII.
Fig. 5.
(a) Estimated penalty functions (Eq. 7) and (b) edge posterior probabilities (Eq. (24)) for ad pairs of V1 neurons, with average plotted in red, under vertical grating and blank conditions. The penalty g(W1, W2) increases with W1 = inter-neuron distance and decreases with W2 = tuning curve correlation. The average edge posterior probability decreases with W1 and increases with W2. The horizontal Lines are the probability thresholds that lead to the corresponding 5, 10, 15, or 20% FDRII controls in (p, δ)-graphs (Eqs. (23), (25), and (27)).
Fig. 6.
Connectivity of V1 neurons. (a) Estimated connectivity (ρ,δ)-graphs under vertical grating and blank conditions, with respective number of edges 1160 ± 87 and 1246 ± 87 (95% bootstrap intervals) at 10% FDRII, and 350 ± 29 and 405 ± 30 at 5% FDRII. The node positions represent the individual active channels on the 4×4 mm electrode array, blue and red edges denote positive and negative partial correlations, and a node size is proportional to the number of its connections. (b) Average across neuron pairs of absolute correlation (blue, Eq. 33) and mutual information (red, Eq. 34) with 95% posterior probability bands, as function of grating orientation θ. Larger values imply stronger connectivity. Both measures show maximal values about 20% above their minimum values. (c) Proportions of rejections across θ values of the 5%-level permutation tests that compare connectivities between orientations Δθ apart. Connectivity changes smoothly as a function of Δθ, and the connectivity at an arbitrary orientation θ differs maximally from the connectivity at the orthogonal orientations θ ± Δθ with Δθ = 90.
To investigate the extent to which covariation is tuned to orientation we computed the average absolute correlation
| (33) |
and the multivariate Gaussian Mutual Information (Shannon, 1964; Guerrero, 1994; Cover and Thomas, 2012)
| (34) |
where C(θ) = diag(Σ(θ))−1/2 × Σ(θ) × diag(Σ(θ))−1/2 = [cij(θ)] is the correlation matrix of the square-rooted spike counts at orientation θ, and Σ(θ) = Ω(θ)-1. Larger AC(θ) and MI(θ) imply stronger connectivity. Fig. 6b shows the posterior means of AC(θ) and MI(θ) as functions of θ, with 95% posterior probability bands; both measures display similar variations in connectivity and it appears that grating orientations θ and θ + 180 yield graphs with similar connectivity. To confirm this, we considered the network connectivity at orientations Δθ apart: given some orientation θ and some Δθ, we (i) calculated
| (35) |
(ii) obtained a permutation test p-value (Kass et al., 2014) of the null hypothesis that the connectivity is the same at θ and θ + Δθ, i.e. D(Δθ) = 0, and repeated (i) and (ii) for all 98 values of θ ∈ [0,360]. Fig. 6c shows how the proportion of 5%-level test rejections varies with Δθ: the connectivity changes smoothly as a function of Δθ, and the connectivity at an arbitrary orientation θ differs maximally from the connectivity at the orthogonal orientations θ ± 90, and minimally at orientation θ + 180.
We applied GAR to estimate the V1 neuron network because our simulation study suggests it is the most accurate method. For comparison’s sake, we also applied AGlasso (Eq. 3) and drew qualitatively similar conclusions: 681 edges were identified for vertical grating and more, specifically 945, for blank screen (although the resulting graphs look quite different since only about 50% of these edges were also identified by GAR at 10% FDRn within each condition) and the mutual information and average absolute correlation showed variations with orientation that were similar to, but more volatile than in Fig. 6b.
V4 data
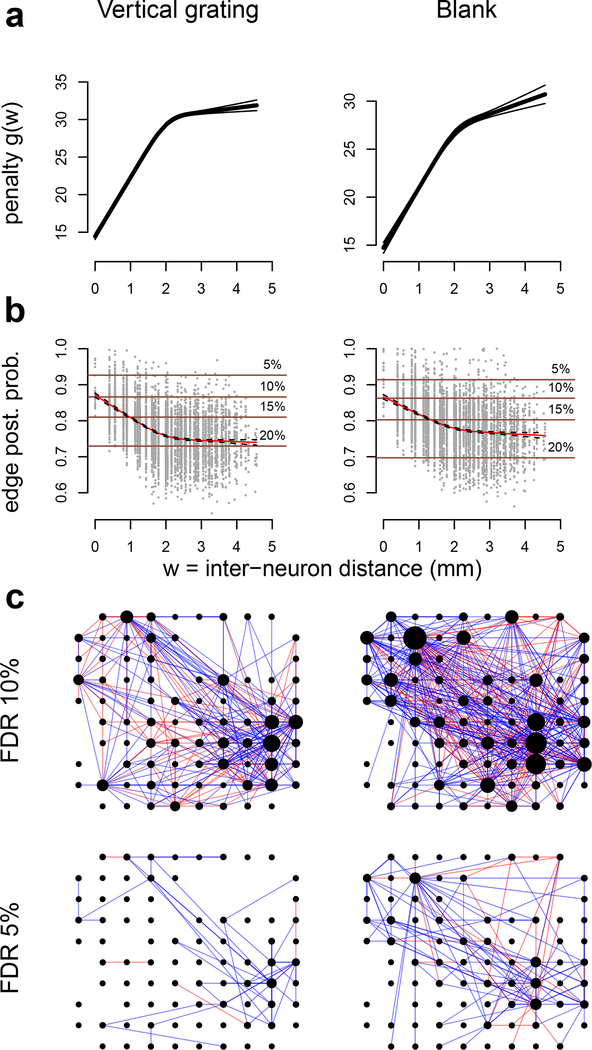
V4 data were recorded in response to a vertical grating (θ = 0) and a blank screen (Fig. 4b). We selected 100 out of the 152 available candidate neuronal units, according to the same criteria used for the V1 data. The firing rates of these 100 neurons ranged from 0.04 to 38.54 spikes/s, with mean 6.64, and 2.5th and 97.5th percentiles 0.09 and 27.33. We applied GAR (Algorithm 4 with a univariate regression spline) to the 1000 ms square root transformed spike counts with inter-neuron distance (DIST) as an auxiliary quantity, and estimated the connectivity in the two conditions. The estimated penalty function g(W) (Eq. (7), Fig. 7a) increases with W = DIST and the edge posterior probability (Eq. (24), Fig. 7b) decreases with DIST, which is consistent with the previous analyses in Smith and Sommer (2013) and Vinci et al. (2016). Note that the posterior probability of non-zero partial correlations (|ρ| > δ = .005) remains substantial at 70–75% between neurons that are over 2mm apart, but because these correlations have magnitude (absolute value of posterior mean) close to the threshold δ (not shown), they do not appear in the (p, δ)-graphs displayed in Fig. 7c, at 10% and 5% FDRII. The graph under vertical grating contains 333 edges (229 positive and 104 negative) with 10% FDRII, and 59 edges (53 positive and 6 negative) with 5% FDRII the graph under blank screen contains 573 edges (400 positive and 173 negative) with 10% FDRII, and 143 edges (115 positive and 28 negative) with 5% FDRII. These results suggest that neural connectivity is denser in the spontaneous activity induced by the blank screen. This was confirmed by a permutation test (Kass et al., 2014) based on the statistic , analogous to Eq. (35), with null hypothesis D(a, b) = 0: the p-value was smaller than 10-8.
Fig. 7.
(a) Estimated penalty functions (Eq. 7) and (b) edge posterior probabilities (Eq. (24)) for all pairs of V4 neurons, with average plotted in red, under vertical grating and blank conditions. The penalty g(W) increases with W = inter-neuron distance. The average edge posterior probability decreases with W. The horizontal lines are the probability thresholds that lead to the corresponding 5, 10, 15, or 20% FDRII controls in (p,d)-graphs (Eqs. (23), (25), and (27)). (c) Estimated connectivity (p, δ)-graphs under the two conditions, with respective number of edges 333 ± 79 and 573 ± 89 (95% bootstrap intervals) at 10% FDRII, and 59 ± 19 and 143 ± 21 at 5% FDRII. The node positions represent the individual active channels on the 4 × 4 mm electrode array, blue and red edges denote positive and negative partial correlations, and a node size is proportional to the number of its connections.
For comparison sake, we also estimated the V4 neuron network using the AGlasso (Eq. 3) and found 297 and 492 edges for vertical grating and blank screen, respectively; about 42% of AGlasso’s edges were also discovered by GAR at 10% FDRII in the vertical grating condition, and about 44% in the blank screen condition.
Remarks
In the two datasets we analysed here, the estimated function g (Eq. (7)) increased with inter-neuron distance and decreased with tuning curve correlation; conversely, the edge posterior probabilities (Eq. (24) decreased and increased with inter-neuron distance and tuning curve correlation, respectively (Figs 5 and 7). Because g was fitted using splines, the dependence of the regularization on the auxiliary variables was estimated from the data rather than prespecified. Hence, GAR automatically extracted the neurons functional connectivity information carried by the auxiliary variables and incorporated it into the estimation of the partial correlations and dependence graphs. These are the main results of our data analyses. Note that the penalty function g is not constrained to be monotonic. While lateral connectivity in a region or within a single cortical area decreases with distance, which was encoded in our two data examples by g increasing with distance, there are many long neural pathways in the brain (see Van Den Heuvel and Sporns (2011)). If these also induce functional connectivity, GAR will extract that information and fit a penalty function g that varies accordingly.
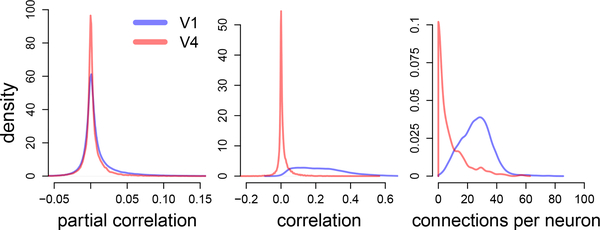
We further note that in both analyses reported here, the number of positive connections were approximately two to four times the number of negative ones. This result is consistent with previous analyses in macaque visual cortex where the majority of pairwise correlations were positive (Smith and Kohn, 2008; Smith and Sommer, 2013), which in turn suggests that finding a majority of positive partial correlations is reasonable (if a positive-definite covariance matrix has mostly positive entries, then its inverse has mostly negative entries, and consequently partial correlations are mostly positive according to Eq. (6)); a majority of positive partial correlations has also been observed in mouse visual cortex (Yatsenko et al., 2015). Moreover, it is also known that in macaque visual cortex the ratio of excitatory to inhibitory neurons is about 80/20 (Markram et al., 2004), which, depending on the relative proportion of inhibitory to excitatory neurons recorded and their connection strengths and probabilities, might favors positive functional connections. We also found that the partial correlations in areas V1 and V4 had similar magnitudes (Fig. 8a), but that the correlations were larger and the connectivity denser in V1 (Figs. 8b and 8c), which is consistent with previous findings in V1 (Smith and Kohn, 2008) and V4 (Smith and Sommer, 2013; Vinci et al., 2016). Denser connectivity and higher correlations in V1 may be due to differences in time-scales and correlation between cortical layers (Smith et al., 2013), since the V1 data were targeted at more superficial layers than V4, as well as other differences in connectivity structure between the two cortical regions. In addition, slow fluctuations in activity due to anesthesia may have played a role in the higher correlation values in V1 (Ecker et al., 2014), although the values present in the data analyzed here are similar to other V1 reports in awake animals (Gutnisky and Dragoi, 2008; Poort and Roelfsema, 2009; Samonds et al., 2009; Rasch et al., 2011).
Fig. 8.
Distributions of partial correlations, correlations, and number of connections per neuron in areas V1 and V4. Partial correlations in areas V1 and V4 have similar magnitudes. Correlations and number of connections per neuron are larger in area V1.
3. Discussion
We have derived and implemented a method for pairwise covariate adjustment of the regularization penalty in the Graphical lasso, and have shown that it can greatly improve identification of the functional connectivity graph in high - dimensional neural spike count data. We have also illustrated the use of this technique in studying network activity by analyzing data from cortical areas V1 and V4, where the covariates were distance between neurons and tuning curve correlation. We expect this approach to be applicable to neural activity throughout cortex, and in subcortical areas as well. At the very least, partial correlation may be expected to change with inter-neuron distance, regardless of where these neurons are located, although cell-type shape specific information may also be useful to include, for example through a group-lasso type regularization (Yuan and Lin, 2006), to adjust for anisotropies of neurons’ axonal projections (Sin- cich and Blasdel, 2001). In addition, even in the absence of a well-defined tuning curve, it is reasonable to expect partial correlation to depend on other characterizations of trial- averaged responses across experimental conditions (based, for example, on the PSTH), or anatomical connectivity and genetic information about neurons. Thus, we suggest the incorporation of this kind of covariate information is likely to be helpful in a wide range of problems involving neural functional connectivity.
While we are inclined, based on the research reported here, to think that the general idea of incorporating covariate information into regularization is a good one, there are many different ways to carry it out. These could involve alternative forms of regularization (e.g. an elastic net may be better suited than an L1 penalty to regularize a large number of small effects), within both Bayesian and nonBayesian frameworks, as well as regularization combined with dimensionality reduction (Chandrasekaran et al., 2012; Yuan, 2012; Yatsenko et al., 2015). These are topics for future research. Also, in previous work we noted that when spike count correlation is viewed as resulting from underlying firing-rate correlation after corruption by Poisson-like noise (Vinci et al., 2016; Behseta et al., 2009), the firing- rate correlation can be much larger than spike count correlation, and may be expected to be more sensitive to experimental manipulation because it likely provides a better representation of input correlation (Vinci et al., 2016). A natural next step, therefore, is to nest GAR within the hierarchical model of Vinci et al. (2016). We are currently working on that extension to the method developed here. In addition, covariate-adapted regularization may be applied to high-dimensional point process models of neural spike trains (Kass et al., 2014) and time series models for local field potentials and other continuous-time neural signals. We hope to investigate the utility of the general idea in these diverse neural contexts.
Acknowledgments
Data from visual area V1 were collected by Matthew A. Smith, Adam Kohn, and Ryan Kelly in the Kohn laboratory at Albert Einstein College of Medicine, and are available from CRCNS at http://crcns.org/data-sets/vc/pvc-11. We are grateful to Adam Kohn and Tai Sing Lee for research support. Data from visual area V4 were collected in the Smith laboratory at the University of Pittsburgh. We are grateful to Samantha Schmitt for assistance with data collection. Giuseppe Vinci was supported by the National Institute of Health (NIH 5R90DA023426–10). Robert E. Kass and Valerie Ventura were supported by the National Institute of Mental Health. Matthew A. Smith was supported by the National Institute of Health (NIH EY022928 and P30EY008098), the Research to Prevent Blindness, and the Eye and Ear Foundation of Pittsburgh. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
4. Appendix
4.1. SAGlasso algorithm
There are several ways to build the weight matrix Q of SAGlasso. We used Gamma regression, as described in Algorithm 1, which can be implemented efficiently with standard statistical software, e.g. R packages glm (Dobson and Barnett, 2008; Hastie and Pregibon, 1992; McCullagh and Nelder, 1989; Venables and Ripley, 2002), mgcv (Wood, 2011), and gam (Hastie and Tibshirani, 1990). Note that in Eq. (3), Q is typically estimated by the square rooted absolute entries of the inverse sample covariance matrix. In SAGlasso, we observed a slightly better performance without applying any transformation.
Algorithm 1.
SAGlasso
| Input: , W, λ > 0, and , preliminary estimate of Ω. |
| 1. Obtain {Yij}i<j, where . |
| 2. Fit Gamma regression of Yij on Wij with rate g(Wij). |
| 3.Obtain where , for i ≠ j, and , for i = 1,..., d. |
| 4. Solve Eq. (3) with Q = and λ. |
| Output: Estimate. |
4.2. GAR algorithms
GAR Algorithms 2–4 are derived in Section 2.2, and implemented in our R package “GARggm” available in ModelDB.
In Algorithm 2, U ~ InvGaussian(a, b) has p.d.f. . Moreover, given a matrix M, Mij is the i-th row and j-th column entry of M; M-ij is the j-th column of M without the i-th entry; Mi-j is the i-th row of M without the j-th entry; and M-i-j is the submatrix obtained by removing the i-th row and the j - th column from M. Algorithms 3 and 4 both produce posterior samples of Ω whose average approximates the posterior mean of Ω. The posterior mode of Ω can be obtained by solving Eq. (1) with λ||Ω|| replaced by , where is the estimated penalty matrix from either Algorithm 3 or 4, and ⊙ denotes the entry-wise matrix multiplication. This optimization can be performed using R functions such as glasso (package glasso, Friedman et al. (2008)) with argument rho set equal to ; see also the R package QUIC, Hsieh et al. (2011). We solve the SPL problem in Eq. (5) by the EM algorithm of Yuan (2012) involving Glasso, and we impose the GAR penalty matrix on S in the Maximization step to obtain the GAR-SPL estimate. For d ~ 100, we suggest to run the Gibbs samplers for at least B = 2000 iterations, including a burn-in period of 300 iterations. The Gamma regression in step 2b of Algorithm 4 can be implemented either parametrically or nonparametrically by using standard statistical software (e.g. R packages glm (Dobson and Barnett, 2008; Hastie and Pregibon, 1992; McCullagh and Nelder, 1989; Venables and Ripley, 2002) and mgcv (Wood, 2011)); in the data analyses we used splines (Kass et al., 2014).
Algorithm 2.
Block Gibbs sampler for .
| Input: and Λ; start value of Ω; number of iterations B. |
| For b =1,..., B : |
| 1. For i < j: sample . |
| 2. For i = 1, ...,d: compute and |
| , where |
| ξ ~ Γ(n/2 + 1, Sii/2 + λii), and η ~ N(−AS−ii,A), with |
| and |
| . |
| 3. Set Ω(b) = Ω. |
| Output: Sequence Ω(1),..., Ω(B). |
Algorithm 3.
GAR - Full Bayes
| Input: and W; parameters r,r’, s, s’, K; sets; start values of Ω,α, and β; number of iterations B. |
| For b = 1,..., B: |
| 1. For i = 1, ...,d: |
| , |
| where . |
| 2. For k = 1,..., K: |
| , |
| where , and |
| . |
| 3. Do steps 1–2 of Algorithm 2 with current Λ. |
| 4. Set Ω(b) = Ω and Θ(b) = {α, β}. |
| Output: Sequences {Ω(1),Θ(1)},…, {Ω(B),Θ(B)}. |
Algorithm 4.
GAR - Empirical Bayes
| Input: and W; start values of Ω and Θ. |
| 1. E-step: For i < j, approximate by Algorithm 2. |
| 2. M-STEP: Iterate a)-b) until convergence: |
| a) For i = 1,..., d, update αi according to Eq. (21). |
| b) Obtain g as the rate function of the Gamma regression of on Wij, i < j. |
| 3. Iterate 1–2 until convergence. |
| Output: Estimate of Θ. |
4.3. Computational efficiency of estimators
Table 1 contains the computation times of the graph estimators considered for d = 50,100 and n = 200,500, using the programming language R, CPU Quad-core 2.6 GHz Intel Core i7, and RAM 16 GB 2133 MHz DDR4. These times could be improved substantially by using a lower level language such as C++. Glasso, AGlasso, SPL, and SAGlasso are fitted with tuning parameter optimization based on tenfold cross-validation involving 500 random splits over a fine grid of 20 values of the tuning parameter about its optimal value. GAR full Bayes (Algorithm 3; K = []) involved B = 2000 iterations, where the Gibbs sampler converged after about 300 iterations. GAR empirical Bayes (Algorithm 4; splines with 3 knots) involved 30 EM iterations, each including 500 iterations of Gibbs sampler for the E-step; the efficiency of this method may be improved by replacing the Gibbs sampler with some alternate faster approximation of Eq (20)
Table 1.
Computational time in seconds with 95% confidence intervals for d = 50,100 and n = 200,500.
| Method | d = 50 | d = 100 | ||
|---|---|---|---|---|
| n = 200 | n = 500 | n = 200 | n = 500 | |
| Glasso | 150 ± 1 | 160 ± 1 | 1198 ± 6 | 1057 ± 10 |
| AGlasso | 65 ± 1 | 87 ± 1 | 410 ± 3 | 501 ± 7 |
| SPL | 541 ± 19 | 641 ± 12 | 4626 ± 41 | 2709 ± 23 |
| BAGlasso | 96 ± 3 | 97 ± 2 | 825 ± 5 | 824 ± 5 |
| SAGlasso | 91 ± 1 | 116 ± 2 | 550 ± 18 | 626 ± 8 |
| GAR-FB | 92 ± 1 | 92 ± 1 | 827 ± 11 | 823 ± 3 |
| GAR-EB | 654 ± 22 | 724 ± 5 | 4163 ± 38 | 4337 ± 40 |
Contributor Information
Giuseppe Vinci, Department of Statistics Rice University, 6100 Main St, Houston, TX 77005, USA, Tel.: +1-713-348-6032, Fax: +1-713-348-5476.
Valerie Ventura, Department of Statistics, Carnegie Mellon University, 5000 Forbes Avenue, Pittsburgh, PA 15213, USA, Tel.: +1-412-268-2717, Fax: +1-412-268-7828.
Matthew A. Smith, Department of Ophthalmology, University of Pittsburgh, Eye and Ear Institute, Room 914, 203 Lothrop St., Pittsburgh, PA 15213, USA, Tel.: +1-412-647-2313
Robert E. Kass, Department of Statistics, Carnegie Mellon University, 5000 Forbes Avenue, Pittsburgh, PA 15213, USA, Tel.: +1-412-268-2717, Fax: +1-412-268-7828
References
- Ahrens MB, Orger MB, Robson DN, Li JM, & Keller PJ (2013). Whole-brain functional imaging at cellular resolution using light-sheet microscopy. Nature methods, 10(5), 413–420. [DOI] [PubMed] [Google Scholar]
- Alivisatos AP, Andrews AM, Boyden ES, Chun M, Church GM, Deisseroth K, et al. (2013). Nanotools for neuroscience and brain activity mapping. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrews DF, Mallows CL (1974). Scale mixtures of normal distributions. Journal of the Royal Statistical Society. Series B (Methodological), 1, 99–102. [Google Scholar]
- Banerjee O, Ghaoui LE, & d’Aspremont A (2008). Model selection through sparse maximum likelihood estimation for multivariate gaussian or binary data. Journal of Machine learning research, 9(March), 485–516. [Google Scholar]
- Bassett DS, & Sporns O (2017). Network neuroscience. Nature Neuroscience, 20(3), 353–364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behseta S, Berdyyeva T, Olson CR, & Kass RE (2009). Bayesian correction for attenuation of correlation in multi-trial spike count data. Journal of neurophysiology, 101(4), 2186–2193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown EN, Kass RE, & Mitra PP (2004). Multiple neural spike train data analysis: state-of-the-art and future challenges. Nature neuroscience, 7(5), 456–461. [DOI] [PubMed] [Google Scholar]
- Butts DA, & Goldman MS (2006). Tuning curves, neuronal variability, and sensory coding. PLoS Biol, 4(4), e92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chandrasekaran V, Parrilo PA, and Willsky AS (2012). Latent variable graphical model selection via convex optimization. Annals of Statistics. Volume 40, Number 4 (2012), 1935–1967. [Google Scholar]
- Cohen MR, & Kohn A (2011). Measuring and interpreting neuronal correlations. Nature neuroscience, 14(7), 811–819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MR, & Maunsell JH (2009). Attention improves performance primarily by reducing interneuronal correlations. Nature neuroscience, 12(12), 1594–1600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cover TM, & Thomas JA (2012). Elements of information theory. John Wiley & Sons. [Google Scholar]
- Cowley BR, Smith MA, Kohn A, & Yu BM (2016). Stimulus-Driven Population Activity Patterns in Macaque Primary Visual Cortex. PLOS Computational Biology, 12(12), e1005185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cunningham JP, & Yu BM (2014). Dimensionality reduction for large-scale neural recordings. Nature neuroscience, 17(11), 1500–1509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- d’Aspremont A, Banerjee O, & El Ghaoui L (2008). First-order methods for sparse covariance selection. SIAM Journal on Matrix Analysis and Applications, 30(1), 56–66. [Google Scholar]
- Dempster AP, Laird NM, & Rubin DB (1977). Maximum likelihood from incomplete data via the EM algorithm. Journal of the royal statistical society. Series B (methodological), 1–38. [Google Scholar]
- Dobson AJ, & Barnett A (2008). An introduction to generalized linear models. CRC press. [Google Scholar]
- Ecker AS, Berens P, Cotton RJ, Subramaniyan M, Denfield GH, Cadwell CR, et al. (2014). State dependence of noise correlations in macaque primary visual cortex. Neuron, 82(1), 235–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron B, Tibshirani R, Storey JD, & Tusher V (2001). Empirical Bayes analysis of a microarray experiment. Journal of the American statistical association, 96(456), 1151–1160. [Google Scholar]
- Efron B, & Tibshirani R (2002). Empirical Bayes methods and false discovery rates for microarrays. Genetic epidemiology, 23(1), 70–86. [DOI] [PubMed] [Google Scholar]
- Efron B (2007). Size, power and false discovery rates. The Annals of Statistics, 1351–1377. [Google Scholar]
- Fan J, Feng Y, & Wu Y (2009). Network exploration via the adaptive LASSO and SCAD penalties. The annals of applied statistics, 3(2), 521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foygel R, & Drton M (2010). Extended Bayesian information criteria for Gaussian graphical models. In Advances in neural information processing systems (pp. 604612). [Google Scholar]
- Friedman J, Hastie T, & Tibshirani R (2008). Sparse inverse covariance estimation with the graphical lasso. Biostatistics, 9(3), 432–441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman A, Carlin J, Stern HS, & Rubin DB (2004). Bayesian Data Analysis CRC Press; New York. [Google Scholar]
- Georgopoulos AP, & Ashe J (2000). One motor cortex, two different views. Nature Neuroscience, 3(10), 963. [DOI] [PubMed] [Google Scholar]
- Giraud C, & Tsybakov A (2012). Discussion: Latent variable graphical model selection via convex optimization. Annals of Statistics, 40(4), 1984–1988. [Google Scholar]
- Goris RL, Movshon JA, & Simoncelli EP (2014). Partitioning neuronal variability. Nature neuroscience, 17(6), 858–865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guerrero JL (1994). Multivariate mutual information: Sampling distribution with applications. Communications in Statistics-Theory and Methods, 23(5), 1319–1339. [Google Scholar]
- Gutnisky DA, & Dragoi V (2008). Adaptive coding of visual information in neural populations. Nature, 452(7184), 220–224. [DOI] [PubMed] [Google Scholar]
- Hastie TJ, & Pregibon D (1992). Generalized linear models. In: Chambers JM, Hastie TJ, editors. Wadsworth & Brooks/Cole. [Google Scholar]
- Hastie TJ, & Tibshirani RJ (1990). Generalized additive models (Vol. 43). CRC press. [Google Scholar]
- Hsieh CJ, Dhillon IS, Ravikumar PK, & Sustik MA (2011). Sparse inverse covariance matrix estimation using quadratic approximation. In Advances in neural information processing systems (pp. 2330–2338). [Google Scholar]
- Kass RE, Eden UT, & Brown EN (2014). Analysis of variance In Analysis of Neural Data (pp. 361–389). Springer; New York. [Google Scholar]
- Kelly RC, Smith MA, Samonds JM, Kohn A, Bonds AB, Movshon JA, & Lee TS (2007). Comparison of recordings from microelectrode arrays and single electrodes in the visual cortex. Journal of Neuroscience, 27(2), 261–264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly RC, Smith MA, Kass RE, & Lee TS (2010). Local field potentials indicate network state and account for neuronal response variability. Journal of computational neuroscience, 29(3), 567–579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly RC, & Kass RE (2012). A framework for evaluating pairwise and multiway synchrony among stimulus- driven neurons. Neural computation, 24(8), 2007–2032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerr JN, & Denk W (2008). Imaging in vivo: watching the brain in action. Nature Reviews Neuroscience, 9(3), 195–205. [DOI] [PubMed] [Google Scholar]
- Kipke DR, Shain W, Buzski G, Fetz E, Henderson JM, Hetke JF, & Schalk G (2008). Advanced neurotechnologies for chronic neural interfaces: new horizons and clinical opportunities. Journal of Neuroscience, 28(46), 11830–11838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu H, Roeder K, & Wasserman L (2010). Stability approach to regularization selection (stars) for high dimensional graphical models. In Advances in neural information processing systems (pp. 1432–1440). [PMC free article] [PubMed] [Google Scholar]
- Markram H, Toledo-Rodriguez M, Wang Y, Gupta A, Silberberg G, & Wu C (2004). Interneurons of the neocortical inhibitory system. Nature Reviews Neuroscience, 5(10), 793. [DOI] [PubMed] [Google Scholar]
- Mazumder R, & Hastie T (2012). The graphical lasso: New insights and alternatives. Electronic journal of statistics, 6, 2125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCullagh P, & Nelder JA (1989). Generalised linear models II.
- Mitchell JF, Sundberg KA, & Reynolds JH (2009). Spatial attention decorrelates intrinsic activity fluctuations in macaque area V4. Neuron, 63(6), 879–888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy KP (2012). Machine learning: a probabilistic perspective. MIT press. [Google Scholar]
- Poort J, & Roelfsema PR (2009). Noise correlations have little influence on the coding of selective attention in area V1. Cerebral Cortex, 19(3), 543–553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasch MJ, Schuch K, Logothetis NK, & Maass W (2011). Statistical comparison of spike responses to natural stimuli in monkey area V1 with simulated responses of a detailed laminar network model for a patch of V1. Journal of neurophysiology, 105(2), 757–778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rothman AJ, Bickel PJ, Levina E, & Zhu J (2008). Sparse permutation invariant covariance estimation. Electronic Journal of Statistics, 2, 494–515. [Google Scholar]
- Samonds JM, Potetz BR, & Lee TS (2009). Cooperative and competitive interactions facilitate stereo computations in macaque primary visual cortex. Journal of Neuroscience, 29(50), 15780–15795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scott JG, Kelly RC, Smith MA, Zhou P, & Kass RE (2015). False discovery rate regression: an application to neural synchrony detection in primary visual cortex. Journal of the American Statistical Association, 110(510), 459–471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadlen MN, & Newsome WT (1998). The variable discharge of cortical neurons: implications for connectivity, computation, and information coding. Journal of neuroscience, 18(10), 3870–3896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shannon CE (1964). Mathematical Theory of Communications. Urbana, University of Illinois Press. [Google Scholar]
- Sincich LC, & Blasdel GG (2001). Oriented axon projections in primary visual cortex of the monkey. Journal of Neuroscience, 21(12), 4416–4426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith MA, & Kohn A (2008). Spatial and temporal scales of neuronal correlation in primary visual cortex. Journal of Neuroscience, 28(48), 12591–12603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith MA, & Sommer MA (2013). Spatial and temporal scales of neuronal correlation in visual area V4. Journal of Neuroscience, 33(12), 5422–5432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith MA, Jia X, Zandvakili A, & Kohn A (2013). Laminar dependence of neuronal correlations in visual cortex. Journal of neurophysiology, 109(4), 940–947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song D, Wang H, Tu CY, Marmarelis VZ, Hampson RE, Deadwyler SA, & Berger TW (2013). Identification of sparse neural functional connectivity using penalized likelihood estimation and basis functions. Journal of computational neuroscience, 35(3), 335–357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stevenson IH, & Kording KP (2011). How advances in neural recording affect data analysis. Nature neuroscience, 14(2), 139–142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Den Heuvel MP, & Sporns O (2011). Rich-club organization of the human connectome. Journal of Neuroscience, 31(44), 15775–15786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venables WN, & Ripley BD (2002). Modern Applied Statistics with S. New York: Springer. [Google Scholar]
- Vinci G, Ventura V, Smith MA, & Kass RE (2016). Separating spike count correlation from firing rate correlation. Neural computation, 28(5), 849–881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H (2012). Bayesian graphical lasso models and efficient posterior computation. Bayesian Analysis, 7(4), 867–886. [Google Scholar]
- West M (1987). On scale mixtures of normal distributions. Biometrika, 1, 646–8. [Google Scholar]
- Wood SN (2011). Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 73(1), 3–36. [Google Scholar]
- Yatsenko D, Josi K, Ecker AS, Froudarakis E, Cotton RJ, & Tolias AS (2015). Improved estimation and interpretation of correlations in neural circuits. PLoS ComputBiol, 11(3), e1004083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu BM, Cunningham JP, Santhanam G, Ryu SI, Shenoy KV, & Sahani M (2009). Gaussian-process factor analysis for low-dimensional single-trial analysis of neural population activity. In Advances in neural information processing systems, 1881–1888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan M, & Lin Y (2006). Model selection and estimation in regression with grouped variables. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 68(1), 49–67. [Google Scholar]
- Yuan M, & Lin Y (2007). Model selection and estimation in the Gaussian graphical model. Biometrika, 19–35. [Google Scholar]
- Yuan M (2012). Discussion: Latent variable graphical model selection via convex optimization. Annals of Statistics, 40(4), 1968–1972. [Google Scholar]