Geometric distortion of panoramic reconstruction in third molar tilting assessments: a comprehensive evaluation

Abstract

Objectives:

To evaluate the geometric distortion of tilting of mandibular third molars with respect to second molars on panoramic reconstruction.

Methods:

Cone-beam CT (CBCT) reconstructions of 160 third molars, obtained due to an indication of risk of inferior alveolar nerve damage during surgery, were used. CBCT-reconstructed panoramic images were used as bi-dimensional (2D) images, to avoid distortions other than geometric distortions. The angle between the second and the third molar was measured in 2D and three-dimensional (3D) images. Student’s t-test was used to assess the null-hypothesis of no difference between 2D and 3D measurements.

Results:

A significant mean difference (−2.3° ± 6.3°) between 2D and 3D measurements was found, with an absolute error of 3.6° ± 5.7° and a relative error of 10%. These findings comprehensively explain the geometric distortion on panoramic radiographs.

Conclusions:

Although a widely used and undoubtedly useful tool for diagnosis and surgical planning of mandibular third molar extractions, panoramic reconstruction are biased from geometric distortion that may influence surgical planning.

Introduction

The partial or complete impaction rate of third molars is reported to range from 18 to 73%.^1–3 Removal of the third molars is the most commonly performed oral surgery,⁴ but may have numerous complications. Among those that occur more frequently are pain, root apex fracture, transitory or permanent inferior alveolar nerve injury, lingual nerve injury, temporomandibular joint discomfort, alveolar osteitis, and mandibular fracture.⁵ The onset of complications can expose the surgeon to malpractice litigation, with consequent request for compensation.^{6, 7}

Accurate surgical planning is therefore crucial, and is most frequently based on panoramic X-rays,^8–10 although it is difficult to evaluate third molars using this examination.¹¹ Parameters indicating surgical risks are inferior alveolar nerve/root tip relation, the level of impaction, root/tooth morphology, angulation and relation to second molars, loss of the mandibular canal (MC) border, change in MC direction, MC narrowing, and superimposition of the nerve and tooth.^{11, 12} In more complex cases, evaluation using cone-beam CT (CBCT) can provide additional information, at a reasonably low radiation dose, and therefore seems important for proper risk assessment.¹²

The angulation of impacted third molars is a variable known to influence the difficulty and duration of surgery.¹¹ Currently, diagnostic software allows three-dimensional (3D) reconstruction and measurement of the angle and length of the tooth root.^{13, 14} However, a number of studies have reported an error in evaluating third molar angulation with respect to second molars when using panoramic X-rays.^{3, 15,16} This distortion has been ascribed to projection geometry as well as to tomographic movement. Moreover, such studies have compared the panoramic angle to the angle as measured on a bi-dimensional (2D) plane, reconstructed from CBCT or CT scans, or casts, parallel to the molar region and perpendicular to the occlusal plane. Thus, such studies suffer from the same bias that afflicts panoramic radiographic images, i.e. the flattening of angles during the transition from 3D to 2D.

In the present study, we evaluated the amount of distortion due to projection geometry, i.e. the distortion caused by flattening of 3D objects to 2D images. To do this, we compared the CBCT-generated panoramic angle between the axes of the second and third molars and the true 3D CBCT angle. The null hypothesis of the study was that there would be no difference between the angle of the long axis of second and third mandibular molars as measured in CBCT-generated panoramic images and as measured in 3D reconstruction.

Methods and Materials

In this study, CBCT of patients referred to the Dental School of the University of Pavia, over a 24-month period (from May 2015 to May 2017) were analyzed. CBCT was performed only in cases where a very close relationship between the inferior dental canal and the root of the mandibular third molar was suspected, as identified in panoramic radiographs. Thus, the CBCT images were originally obtained because of a suspected risk of injury to the inferior alveolar nerve, rather than for assessing the orientation of the third molar. The presence of severe metal artifact was an exclusion criteria. CBCT scans were de-identified and duplicated for analysis in this study.

All of the CBCT radiographs were taken by the same operator with a Soredex SCANORA™ 3D device (Soredex, Helsinki, Finland; Receptor type: CMOS flat panel 124 × 124 mm; fixed anode tube; focal spot 0.5 mm IEC 60336; 85 kV; 4.0–12.5 mA; voxel sizes 0.25 mm; scan time 13 s). All scans were acquired in the axial plane, without gantry tilt.

CBCT DICOM files were analyzed with Simplant® 17 Pro software (DENTSPLY SIRONA Inc., York, PA). The software allows to obtain CBCT-generated panoramic images, and to measure the 3D angle using the “Implant relations calculator” tool (Figure 1). To use this software, that is originally designed to measure relations between implants, we drew a 0.5 mm diameter personalized implant and we positioned it as long axis of the tooth. A line passing through the upper point of the floor of the pulpar chamber and the root apex (for mono-radicular teeth) or through the middle of the line joining the two root apexes (for bi-radicular teeth) was used to define the long axes of the molars. The angle between the long axes of the second and third molars was recorded from the CBCT-generated panoramic radiographs (2D angle) and the CBCT reconstruction (3D angle) by means of Simplant® 17 Pro software tools.

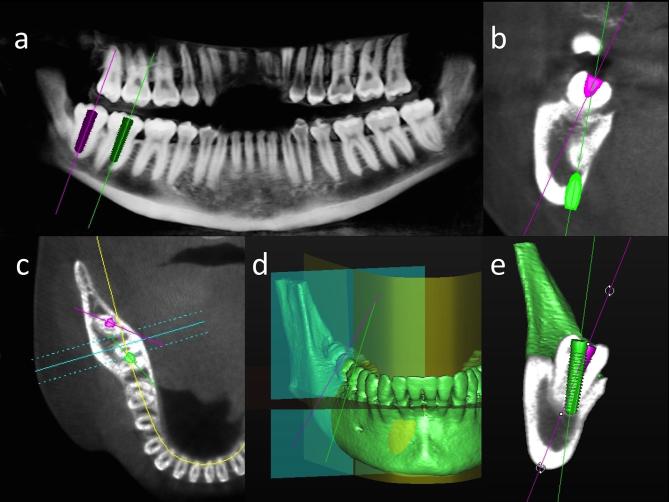
Figure 1.

For data collection, as mentioned in Methods and Materials section, personalized implants with a 0.5 mm diameter were used to not confuse the examiner. Because 0.5 mm implants are visible only as a line (or as a dot in a section view), to clearly identify the implants to the reader, in Figure 1 3.8 × 16 mm implants were represented. (a) CT-generated panoramic images of a mandible. The long axes of the second (green line) and third (fuchsia line) molars appear nearly parallel. (b) Cross-sectional CBCT view, showing the axes of the third (fuchsia line) and second (green line) molars in the buccal−lingual direction. In this projection, the axes of the second and third molars form an acute angle. (c) CBCT image of a mandible, showing the transverse plane view. Yellow line: CBCT-generated panoramic curve; fuchsia line: third molar axis; green line: second molar axis; cyan lines: cross-sectional planes. (d) 3D reconstruction. All the planes are shown: the transverse plane is shown in red, the panoramic plane is shown in yellow, and the cross-sectional plane is shown in cyan. The actual angle between the second and third molar can be evaluated accurately. (e) 3D clipping view. The actual angle between the second and third molar can be evaluated accurately. 3D, three-dimensional; CBCT, cone-beam CT.

The difference between the 2D and the 3D angles was evaluated with Student’s t-test for paired samples.

Results

In total, 104 patient scans, including images of 160 mandibular third molars, were collected. There were 67 female and 37 male patients; 56 patients had both third mandibular molars, while 48 patients had only one mandibular third molar. The mean age of patients was 33 years; the youngest patient was 18 years and the oldest was 65 years.

According to Winter’s classification, 16 of these teeth (10%) were horizontal, 57 (35.6%) were mesio-angular, 47 (29.4%) were vertical, and 40 (25%) were disto-angular. According to Pell and Gregory’s classification, the following distribution was observed: IA: 48 (30%), IIA: 12 (7.5%), IIIA: 3 (1.9%), IB: 20 (12.5%), IIB: 10 (6.25%), IIIB: 14 (8.8%), IC: 26 (16.3%), IIC: 20 (12.5%), IIIC: 7 (4.4%).

The mean angle between the second and third molar axes was 33.7° ± 26.2°, as measured on CBCT-generated panoramic images, and 35.9° ± 24.5° as measured on CBCT reconstruction images. The difference was significant (p < 0.0001). The mean difference between the long axis angles as measured on 2D and 3D reconstruction was −2.3° ± 6.3°, and the mean absolute error was 3.6° ± 5.7°. These results are summarized in Table 1.

Table 1. .

Main results

Patients	104
Male	37
Female	67
Total number of teeth	160
Right	82
Left	78
Monolateral	48
Bilateral	112
Classification according to Winter
Horizontal	16
Mesioangular	57
Vertical	47
Distoangular	40
Mean panoramic reconstruction angle	33.7° ± 26.2°
Mean CBCT angle	35.9° ± 24.5°
p (Student’s t test)	<0.00001
Difference panoramic reconstruction-CBCT angle, min value	–27.3
Difference panoramic reconstruction-CBCT angle, max value	9.12
Difference panoramic reconstruction-CBCT angle, mean value	–2.3° ± 6.3°
Difference panoramic reconstruction-CBCT angle, mean absolute error	3.6° ± 5.7°
Pearson's correlation coefficient panoramic reconstruction angle-CBCT angle	0.971018726
Pearson's correlation coefficient panoramic reconstruction angle-(difference panoramic and CBCT angle)	0.381001776
Pearson's correlation coefficient panoramic reconstruction angle-absolute error	–0.299575081

CBCT, cone-beam CT.

Discussion

Dental panoramic images are commonly used as the first-level imaging for evaluation of mandibular third molars prior to their surgical removal.^{9, 12,17,18} An important factor in the assessment of surgical difficulty is the inclination of the third molar with respect to the second molar.¹¹ The inclination of the third molar indicates the direction in which the tooth should be discharged from its alveolus; if there are some obstacles, such as bone or the second molar, in this direction, the surgery may also require osteotomy and/or tooth sectioning, which prolongs surgical time and increases the possibility of post-operative complications. Hence, correct pre-surgical evaluation of third molar tilting, with respect to the second molar, is very important.

Previous studies that evaluated third molar tilting with respect to the second molar have focused on unequal magnification, tomographic movement, and geometric distortion of the panoramic radiograph,^{3, 15,16} but they did not quantify each of these components that give rise to the final distortion. Moreover, measurements in those studies were prone to the same bias that creates geometric distortion in panoramic imaging, i.e. measuring of the angle between the second and third molars on a 2D plane. In this study, we evaluated the geometric component of distortion that is caused by the flattening of the 3D angle to a 2D plane, and measured the actual angle between the two axes in 3D space, which has not been reported to date. To quantify the error of panoramic evaluations due to geometric projection, we reconstructed 2D panoramic images from CBCT scans in this study. The software used to flatten 3D reconstruction allows to obtain a simil-panoramic reconstruction; the final 2D image is the flat reconstruction obtained by the sum of numerous layers parallel to the chosen panoramic line and is not a single layer corresponding to the panoramic line. This tool allows to obtain a final panoramic reconstruction more similar to a panoramic radiography, in which only objects in the focal layer appear in the final image. In this way, magnifications or distortion due to tomographic movement were avoided. At the same time, the panoramic reconstruction shows a complete image of teeth, and not only the portion of them passing throughout the panoramic line. We found a difference caused by the projection of 3D objects to a 2D plane, and thus the null-hypothesis was rejected.

The mean difference between 2D and 3D inclination was −2.3° ± 6.3°, indicating that the geometric distortion results in underestimation of the tilting of the third molars. This finding is in accordance with that of a previous study,³ but is in contrast to previous studies that indicated an overestimation of about 5°.^{15, 16} Moreover, in the present study, the mean absolute error between 2D and 3D evaluation was 3.6° ± 5.7°, which represents a relative error of 10%. Pearson’s correlation coefficients indicated a strong positive correlation between the 2D and 3D angles, but a loose correlation of the difference between the 2D and 3D angles with the 2D angle, as well as a loose correlation of the difference between the 2D and 3D angles and the absolute error. These results indicate that 2D measurements correlate well with the actual 3D parameter, but that 2D angulation cannot predict geometric distortion. The results of the present study can be explained theoretically, as follows.

It is well known that different geometrical properties of a 3D object are not invariant during projection. In particular, parallelism, orthogonality, and length and angle measurements change when a 3D object is projected onto a 2D plane. Let us consider a Cartesian system (x, y, z), with the long axis of the first tooth placed on a plane parallel to the projection plane, i.e. the x-z plane resulting from the 3D→2D projection. Let us now consider the long axis of the second tooth, displaying a misalignment θ with respect to the first tooth. If the plane defined by these two axes is parallel to the projection plane, the angle θ measured in the projection is exactly the real angle θ. In contrast, any rotation of the plane on which the axes of the teeth are placed would affect the projected angle. Indeed, in an extreme case, if we consider that the axes of the teeth are placed on a plane parallel to the (y-z) plane, the projected angle would be equal to 0, irrespective of the degree of misalignment between the two axes.

A more subtle situation is created when the misalignment not only occurs in the plane formed by the two axes, and is still represented by θ, but when it is also out of the plane. In such a case, the plane parallel to the projection plane is formed by the first axis and the line connecting the bases of the two axes, but the axis of the second tooth points out of the plane. The out-of-plane misalignment is represented by the angle φ formed by the projection of the out-of-plane axes onto the (x-y) plane and the x axis (or x-z plane). When this situation is projected onto the (x-z) plane, the misalignment θ is under/over estimated, and the error must be evaluated.

The problem can be managed in projecting geometry,¹⁹ using the well-known Euler angles, which allow a description of the position of a point in the (x,y,z) Cartesian system using spherical coordinates. If we consider a vector r(x,y,z) in the (x,y,z) system, a description of the polar system is obtained by applying the following transformations:

$${\displaystyle \mathrm{x}=\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{n}\theta \mathrm{c}\mathrm{o}\mathrm{s}\phi }$$

$${\displaystyle \mathrm{y}=\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{n}\theta \mathrm{s}\mathrm{i}\mathrm{n}\phi }$$

$${\displaystyle \mathrm{z}=\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\theta }$$

With this description, the φ angle is formed by the projection of the out-of-plane axes onto the (x-y) plane and the x axis or (x-z) plane. It is easy to verify that the error in the estimation of angle θ is equal to |1-cosφ|.²⁰

For small angles we can use the Taylor series terminated at the second order term; thus we obtain:

$${\displaystyle |1-\mathrm{c}\mathrm{o}\mathrm{s}\phi |\approx |1-1+{\phi }^2/6|={\phi }^2/6}$$

If we imagine an out-of-plane misalignment between 10° and 15° the error in the estimation of θ is ranging between 0.5 and 1.1%. These values are smaller than those experimentally derived by us but we have to underline that the error estimation has been made under a very strict assumption. Indeed, if the plane formed by the first tooth axis and the line connecting the two bases of the two axes is not strictly parallel to the projection plane, angle estimation error increases rapidly.

A licit criticism to the present study is that CBCT data is theorically distorted in the first place compared to real situation and MDCT. To reply to this criticism, some consideration must be taken into account. First of all, CBCT distortion has been proved over linear measurements,^21–23 but until this moment the authors are not aware of studies demonstrating a distortion in angle CBCT measurement. On the contrary, CBCT data is considered more reliable than 2D X-rays for orthodontic evaluation.²⁴ Moreover, MDCT itself suffers of linear measurement distortion, although it is considered more reliable than CBCT for linear measurement.²⁵ By contrast, it has been previously proved that CBCT does not present a geometric distortion of the scanned object, excepted that which is below the resolution power of the volume tomograph.²⁶ The last, but more appropriate, consideration is the following: in the present study was not evaluated the difference between second and third molar axis comparing CBCT and traditional panoramic imaging. The main theme is to quantify the error due to flattening of an angle between two axes in the space into a 2D projection plane. Thus, also considering that CBCT data (minimally) distorts geometric relationship between objects (and currently the contrary has been proven), the distortion between a real object and its CBCT reconstruction is not the point of the present study. For this reason we decided to compare the 3D CBCT angle to the 2D simil-panoramic reconstruction, and not to the traditional panoramic X-rays. In this study we assessed only the geometric distortion and not the distortion due to tomographic movement or magnification. The geometric distortion due to flattening of a 3D object to a 2D plane is present both in CBCT panoramic reconstruction and in traditional panoramic X-rays, and in the latter it is only a fraction of the total distortion. The results of the present study show that the pre-evaluation of the surgical difficulty of third molars extraction, due to inclination with respect to the second molars, suffers of a certain geometric distortion. The results of the present study are theoretically applicable also for MDCT.

Panoramic reconstruction is limited because it provides a 2D image of 3D structures, with distortion of the linear measures and a loss of definition due to the superimposition of underlying structures.^{27, 28} The present study evaluated only the geometric distortion due to 3D to 2D flattening in panoramic reconstruction, but the final distortion in panoramic radiography also entails other errors, such as magnification or tomographic movement. While the latter can be theorically improved with technical advances, the first cannot be avoided. Therefore, the possibility of distortion in panoramic radiographic images must always be considered.

Conclusions

Panoramic reconstruction of third molar tilting is representative of the actual inclination of these teeth, but the possibility of geometric distortion due to misalignment of second and third molars axes on different planes should always be kept in mind. Geometric distortion is the only source of distortion in CBCT-generated panoramic images, but is only a part of total distortion in panoramic X-rays. Geometric distortion can entail a relative error up to 10%.