An anatomically constrained model for path integration in the bee brain

Summary

Path integration is a widespread navigational strategy in which directional changes and distance covered are continuously integrated on an outward journey, enabling a straight-line return to home. Bees use vision for this task – a celestial-cue based visual compass, and an optic-flow based visual odometer – but the underlying neural integration mechanisms are unknown. Using intracellular electrophysiology, we show that polarized-light based compass-neurons and optic-flow-based speed-encoding neurons converge in the central complex of the bee brain, and through block-face electron microscopy we identify potential integrator cells. Based on plausible output targets for these cells, we propose a complete circuit for path integration and steering in the central complex, with anatomically-identified neurons suggested for each processing step. The resulting model-circuit is thus fully constrained biologically and provides a functional interpretation for many previously unexplained architectural features of the central complex. Moreover, we show that the receptive fields of the newly discovered speed neurons can support path integration for the holonomic motion (i.e. a ground velocity that is not precisely aligned with body orientation) typical of bee-flight, a feature not captured in any previously proposed model of path integration. In a broader context, the model-circuit presented provides a general mechanism for producing steering signals by comparing current and desired headings – suggesting a more basic function for central-complex connectivity from which path integration may have evolved.

Introduction

Animals with a fixed nest use diverse sensory cues to ensure that they can return home after extended foraging trips. One widespread yet sophisticated strategy for carrying out this task is path integration [1,2]: the animal continuously integrates the distance covered in each direction over the duration of the outbound foraging trip to generate a homeward-pointing vector that allows a straight-line return to the nest. This ‘allothetic’ path integration, i.e., maintenance of an estimate of location relative to a world-based frame of reference (hereafter referred to as path integration for brevity), uses a combination of different self-generated motion cues in most animals. In bees however, visual information alone is key to this task [1], making them uniquely accessible for identifying the neural components involved. Celestial skylight cues, such as polarized light, are used as a compass reference [3], while image-motion across the retina (optic flow), caused by the movement of the bee through its environment, is used for estimating distance (visual odometer) [1,4]. Across the planet, bee species perform this behavior in a large variety of sensory environments, suggesting that the underlying neural mechanisms are both robust and conserved. However, despite rich behavioral data, the neural basis of path integration in bees, or insects in general, is unknown, although several hypothetical circuits have been proposed (reviewed and compared in [5]). One region of the insect brain that plays a prominent role in orientation behaviors is the central complex (CX), a conglomerate of highly conserved brain compartments [6]. In migratory locusts and fruit flies this region houses an ordered array of compass neurons, which encode heading based on celestial visual cues in the locust [7] and based on a combination of visual and self-motion cues in Drosophila [8]. Additionally, the activity of individual CX-neurons can reliably predict intended movement directions in freely walking cockroaches, indicating direct involvement in steering [9]. These and similar findings place the CX on the boundary between higher-order sensory processing and behavioral planning. We here provide a biologically constrained, computational model of the CX that combines novel physiological findings with highly conserved anatomical properties of CX-neurons found across insects to provide a coherent account of how path integration and homeward steering could be implemented in this neuropil.

Results

Visual compass sensing in the bee CX

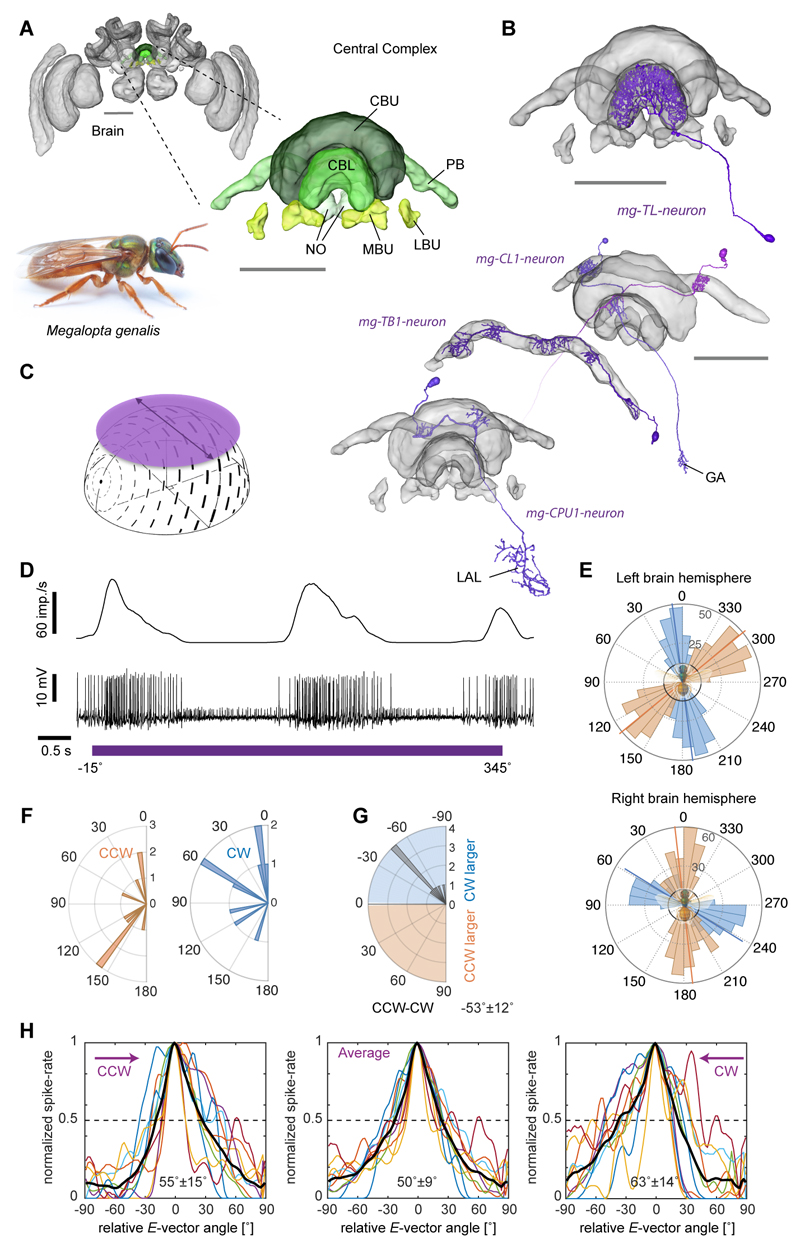
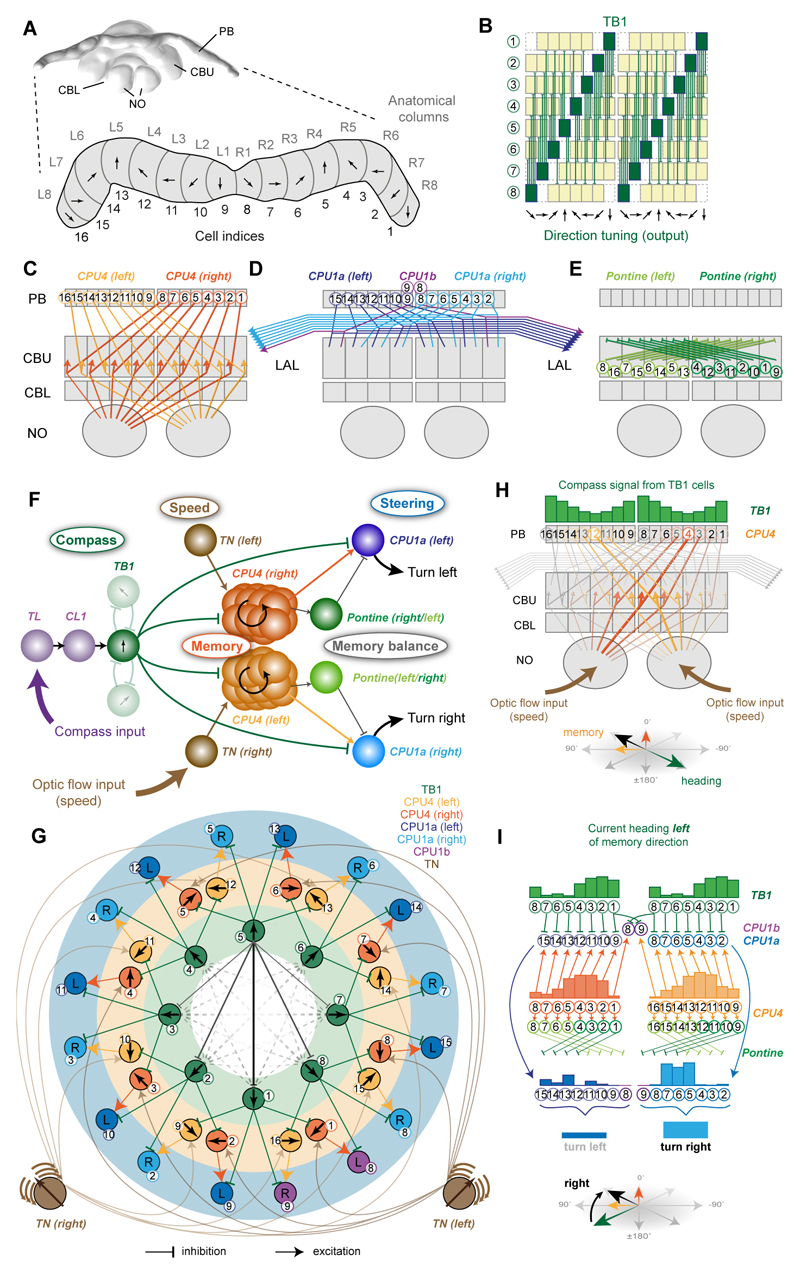
Integrating an outbound foraging path requires sensing of direction and speed, and in most arthropods the directional information is obtained from external celestial compass cues. To build a realistic model of path integration based on the bee CX, we thus first needed to identify visual compass neurons in bees. In locusts and butterflies polarized-light information is relayed to the CX via a highly conserved neural pathway [10,11], which, in locusts, has been shown to produce an ordered array of compass neurons, suited to encode heading in a global reference frame due to the fixed relation between E-vector angle and solar azimuth [7]. In flies, homologous cells also encode head direction, suggesting that mapping of directional space in the CX is a shared feature across insects [8,12]. These cells encode head-direction based on visual landmark cues, but are also updated by self-motion cues in the absence of vision [8], a finding recently confirmed in cockroach head-direction cells [13]. As bees possess specialized eye regions for perceiving polarized light [14,15] and use a polarized-light based compass during foraging, we first ask whether polarized-light based compass neurons also exist in the bee CX (Figure 1). For physiological recordings, we focused on the CX of the tropical nocturnal bee Megalopta genalis [16] (Figure 1A). These bees forage at times of the day when polarized skylight provides the single most reliable directional cue in their rainforest habitat and they possess all optical specializations typical for polarized-light perception [15]. Bees were captured with light traps directly from their natural habitat in Panama during foraging flights and tested within two weeks of capture. We successfully recorded from 160 Megalopta bees to test responses of CX-neurons to linearly polarized light (Figure 1B-H) by continuously rotating an artificial sky above the animal (Figure 1C-E). We found strong sinusoidal modulations of firing frequency in response to this stimulus (i.e. polarized-light tuning) in ten neurons. The neurons showed an average tuning width of 50° and a difference in tuning between clockwise and counter-clockwise rotations of 53° on average, with anticipatory tuning optima, i.e., during clockwise rotations the optimum was shifted counter-clockwise with respect to the average tuning and vice versa for counter-clockwise rotations (Figure 1E-H). This phenomenon has been found in compass neurons of other species and, in locusts, has been proposed to aid correct compass encoding during fast body rotations [17]. None of the cells tested (5 out of 10 cells) responded strongly to large-field motion cues presented in a 360° LED arena and showed no or only weak responses to a bright bar moving around the bee (tested in 9 out of 10 cells), demonstrating that the recorded neurons are selectively encoding polarized-light based compass cues (Figure S1). Seven compass neurons were analyzed anatomically. All arborized in the lower division of the central body (ellipsoid body in flies; Figure 1B), a part of the CX tightly associated with compass encoding in migratory insects and a key component of the Drosophila head direction network [8,10,11]. Indeed, both identified neuron types with compass-like activity in Megalopta (6x TL, and 1x CL1-neurons) are either homologous to the GABAergic (inhibitory) ring-neurons or to the E-PG-neurons that comprise the head direction system of the Drosophila CX. These cells make up an estimated 5-10% of all CX-neurons and identical neurons have been described in detail in locusts [18,19], monarch butterflies [10] and dung beetles [20] with physiological responses to polarized light that are highly similar to those in Megalopta. Additionally, we identified bee-counterparts of all remaining locust compass neurons, occupying the protocerebral bridge (PB) (TB1-neurons; anatomically identified) and the upper division of the central body (CBU, fan-shaped body in flies) (CPU1-neurons; anatomy and physiology) (Figure 1B, S4). Together these findings strongly suggest that the CX serves as an internal compass in bees as well.

Figure 1. Compass-neurons of the bee central complex.

(A) Brain of the sweat bee Megalopta genalis (body-length: 1-2 cm; photo: A. Narendra). Highlight/inset: compass regions. (B) 3D-reconstructions of polarized-light-sensitive compass-neurons based on intracellular injections. (C) Schematic stimulus: rotating, large polarizer, illuminated with an array of UV LEDs (artificial sky). (D) Recording trace from individual TL-neuron during polarizer-rotation (bottom: membrane voltage; top: sliding-average mean activity). (E) Tuning of two TL-neurons (one on each brain hemisphere) to polarized-light angle for clockwise (blue; 360°-0°) and counter-clockwise (orange; 0°-360°) filter rotations (binned mean activity, individual rotations). Black circles: background firing rate. (F) Distribution of tuning angles for clockwise rotations (CW) and counter-clockwise (CCW) rotations. (G) Distribution of difference angles between CW and CCW tunings (mean ± SD is indicated numerically). (H) Tuning curves of all recorded compass neurons (n=10); normalized to peak activity, minimum activity set to zero, peak activity shifted to 0°, tuning width measured at half-maximal excitation. Black curves: population mean. Mean width ± SD indicated for each graph. Abbreviations: CBL, lower division of the central body; CBU, upper division of the central body; PB, protocerebral bridge; NO, noduli; MBU, medial bulb; LBU, lateral bulb; LAL, lateral accessory lobes; GA, gall. Scale bars: 100 μm; brain in (A), 200μm. See also Figure S4.

Optic flow sensing in the bee CX

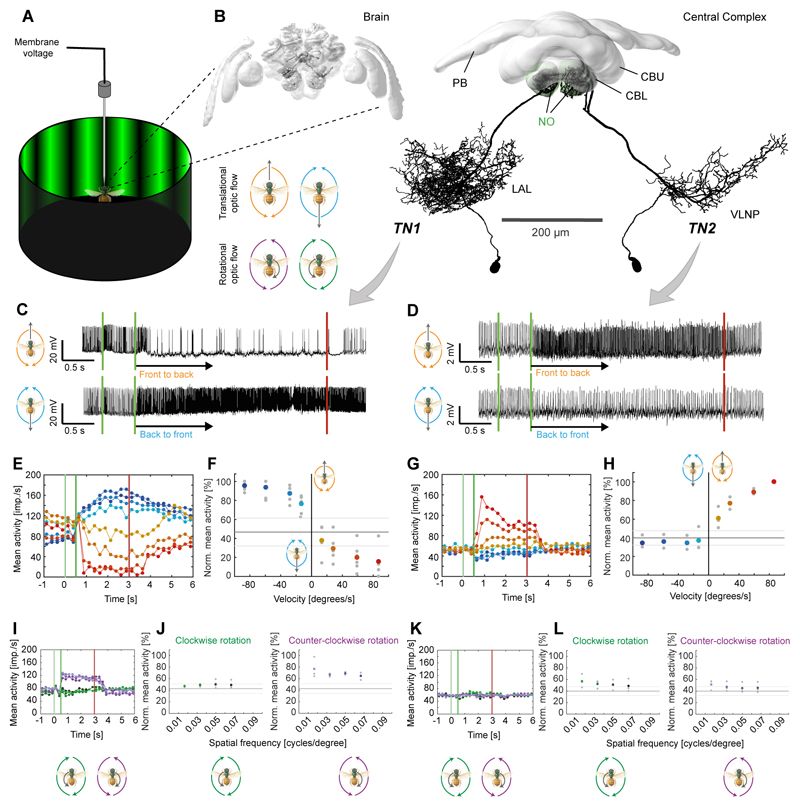
The second requirement for path integration is an odometer, which for the bee requires neurons that encode translational information from optic flow to converge with visual compass information [4]. Recent evidence from Drosophila and cockroaches shows that the CX houses neurons sensitive to large-field motion cues [21–23]. During intracellular recordings from CX-neurons we presented large-field optic flow stimuli (high-contrast sinewave gratings moving at different speeds) to bees located in the center of a 360° LED arena (Figure 2A). Two types of CX-neurons responded strongly to translational optic flow, whereas they were invariant to compass stimuli (tested in 5 of 14 recordings; Figure S1). Both selectively provided input to two CX compartments called the noduli and were named noduli tangential neurons (TN-neurons). They had extensive input branches in the lateral regions of the central brain in one brain hemisphere and innervated large parts of the ipsilateral nodulus with dense, blebbed fibers (Figures 2B, S2; Movie S1). The two types differed in the location, extent and shape of their input fiber projection fields (Figures 2B, S2; Movie S1). Physiologically, TN2-cells were excited by simulated forward flight (Figure 2D,G/H) increasing firing approximately linearly with stimulus velocity, up to a sustained peak activity of approximately 150 impulses/s at a stimulus velocity of 90°/s. This grating velocity matches the preferred optic flow of Megalopta in flight tunnels and their ground speed of 20 cm/s [24], which is significantly slower than that of other bees [24]. This cell type could thus serve as a neural speed indicator, and may correspond to cockroach neurons that increase activity with increasing walking speed of the animal [9,25], resembling speed-cells in the rat entorhinal cortex [26]. In contrast, TN1-cells were inhibited by simulated forward flight but were strongly excited by simulated backwards flight (peak activities of up to 200 impulses/s; Figure 2C,E/F). In approximately half the neurons of that type the neural response outlasted the stimulus by a few seconds (Figure 2C,E), a characteristic that could constitute a low pass filter providing the bee’s odometer with a smooth optic-flow based speed signal in a discontinuous, complex environment of fast changing spatial density (e.g. forests).

Figure 2. Neurons of the bee central complex are sensitive to translational optic flow.

(A) Schematic illustration of recording setup. The bee was placed inside a 360° LED arena that was used to display rotational (clockwise and counter-clockwise) and translational (forward and backward) optic flow. (B) 3D-reconstructions of TN1 (left) and TN2-neurons (right) registered into a common reference brain (additional morphologies in Fig. S2). Left: neurons embedded in whole brain; right: neurons with central complex only. Note that both cell types exist in both brain hemispheres. VLNP, ventrolateral neuropils; remaining abbreviations see Figure 1. (C,D) Voltage traces from intracellularly recorded cells responding to front-to-back (top) and back-to-front (bottom) translational optic flow. First green line: grating presented; second green line: motion onset; red line: motion stop. TN1-neuron (C), TN-2 neuron (D). (E,G) Activity of the same neurons to different stimulus velocities (–90°/s to 90°/s (blue to red); values: ±10, ±30, ±60, ±90°/s). Vertical lines as in (C,D). (F,H) Normalized mean activity during the final 2 s of each stimulus bout of TN1-neurons (F; n = 5) and TN2-neurons (H; n = 3). Colored circles: mean; grey circles: individual data-points; solid line: background activity (± SD, grey lines). (I/K) Responses to rotational optic flow at different spatial frequencies of the same neurons as (E/G). (J/L) Mean responses to rotational optic flow of the same neurons as (F/H). In (J) responses were tested only in four out of five cells from (F); shown only for cells located in the right brain hemisphere (n = 3), as preferences for clockwise and counter-clockwise rotations were inverted for left-side cells. See also Figure S1,S2,S3.

Both cell types responded more weakly or not at all to rotational optic flow (Figure 2I-L), even at higher velocities up to 160°/s, despite identical grating parameters (contrast, velocity, spatial frequency), suggesting that the response must be determined by antagonistic directional tuning within different regions of the neuron’s receptive fields. By mapping receptive fields with a narrow, bright bar moving around the bee, we thus analyzed the local directional tuning preferences of each cell (Figure 3A). TN-neurons responded strongly to this stimulus and received information from the entire panorama (Figure 3B). Like many optic lobe cells (e.g. [27,28]), the neurons possess preferred and anti-preferred motion directions within their receptive fields, and several of these regions with opposite directional tuning tiled the visual space around the animal (Figure 3C-F). Four different receptive field signatures could be distinguished. Each of them had a characteristic pattern of local tuning preferences that allowed us to predict four different optimal expansion points for translational optic flow that were offset from the body axis between 25° and 75° either to the right or to the left (average behind the bee: 135°, average in front of the bee: 48°; Figure 3C-G). The preference in optic-flow expansion direction towards either the right or the left side of the body axis was determined by the hemisphere in which each TN-cell was located. As only a subset of the recorded optic-flow processing neurons could be characterized anatomically (7 out of 14), we used these characteristic receptive field structures to infer neural identity of the non-dye injected recordings.

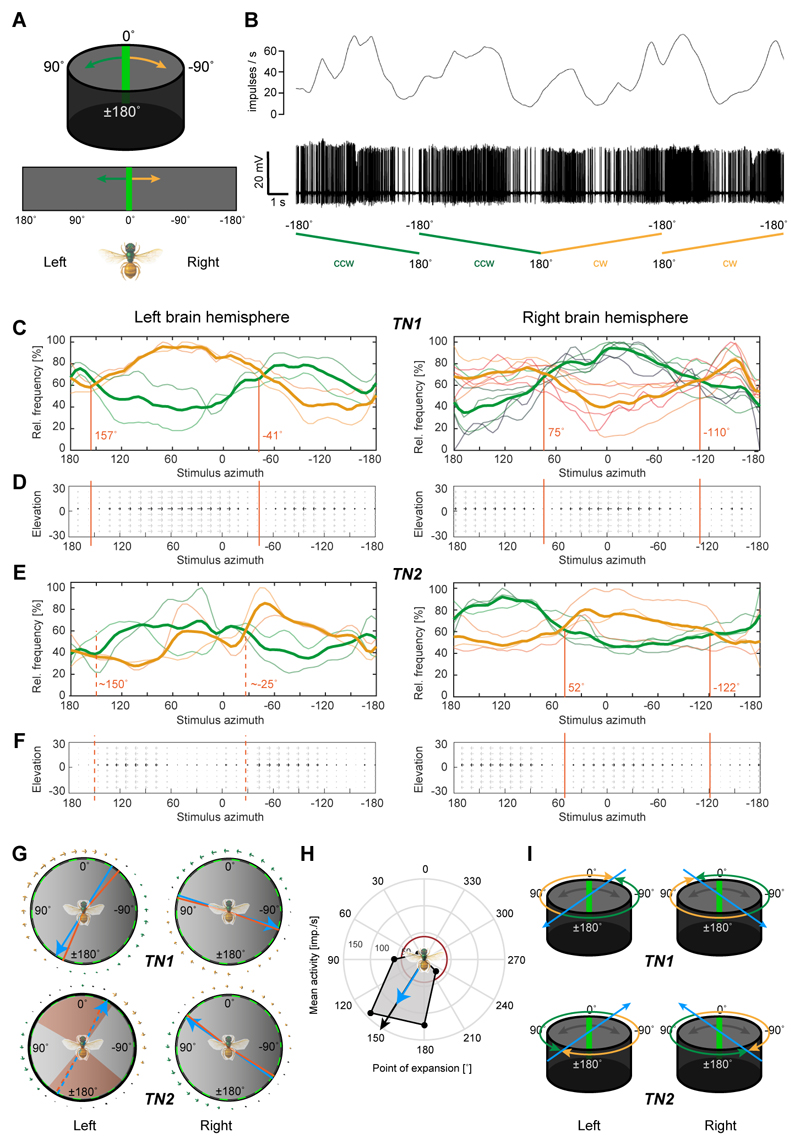
Figure 3. Receptive fields of optic-flow-sensitive neurons define encoded movement space.

(A) Top: stimulus for receptive-field mapping was a green bar moving around the bee at constant speed. Bottom: schematic display of flattened arena used for graphs in (C-F). (B) Typical neural response to a moving bar of a TN1-neuron. Top: gliding average of spike rate; bottom: spike train. Ramps indicate movement of bar, either clockwise (cw) or counter-clockwise (ccw). (C) Mean normalized activity (thick curve) during receptive field mapping of TN1-neurons shown with individual response curves. Yellow traces: cw movement; green traces: ccw movement. Responses of neurons in right (n=6) and left brain hemispheres (n=2) are approximately mirror-symmetric, but directionally inverted (e.g. green curve on the right mirrors yellow curve on the left). Different parts of the receptive fields are preferentially tuned to cw or ccw movement, with null-points with no observable tuning indicated by red lines. (D) Flow-fields indicating local directional tuning preferences of TN1 neurons, mapped onto spatial extent of the LED arena. Grey arrows indicate that the tuning could result from any position along the vertical axis of the arena (elevation range covered by the bar stimulus). (E,F) As in (C,D), but for TN2-neurons. Responses are inverted compared to TN1-neurons (left: n=2; right: n=3). (G) Calculated null-points (red) without directional tunings displayed in a circular diagram for both cell-types and both brain hemispheres. Blue lines: Average null-point assuming axial symmetry of responses (i.e. frontal null-point is opposite of posterior one), predicting an optimal point of optic-flow expansion. Arrows around the circle are based on flow fields in D/F. In TN2-cells of the left brain hemisphere a range of angles without clear tuning preference occurred and is indicated in red, with null-crossings of tuning preferences shown as dotted lines. (H) Responses to translational optic flow with different expansion-points (45° intervals) of one of the neurons in C (from left brain-hemisphere). Resulting preferred expansion point (black arrow) matches predictions from G (blue arrow). Red circle: background activity. I, Idealized preferred expansion points of TN-neurons from both brain hemispheres, which were used as a basis for modeling. See also Figure S2,S3.

The predicted point of expansion for translational optic flow based on local tuning preferences was directly tested and confirmed in one recording (Figure 3H). Based on the average values resulting from the receptive field analysis, we thus extrapolated that this set of cells likely encodes four cardinal directions of movement (Figure 3I), thereby forming a basis for encoding holonomic movements (i.e. movements during which the body axis is not aligned with the movement direction) in the bee’s flightpath.

We additionally recorded and characterized an example of a TN2-neuron in the bumblebee Bombus terrestris (Figure S3). The detailed morphology of bumblebee TN-cells in the noduli was examined by block-face electron microscopy, which revealed that indeed there are only two large tangential input neurons per nodulus (i.e. four individual neurons per brain) that resembled Megalopta TN1- and TN2-neurons. Each of them possessed many hundreds of synaptic outputs (active zones) associated with large pools of synaptic vesicles (Figure 4I,J), showing that TN-neurons provide input to the noduli. The identical morphology in two distantly related species suggests that these cells have evolved more than 100 million years ago [29] and might be part of the core network of the bee CX.

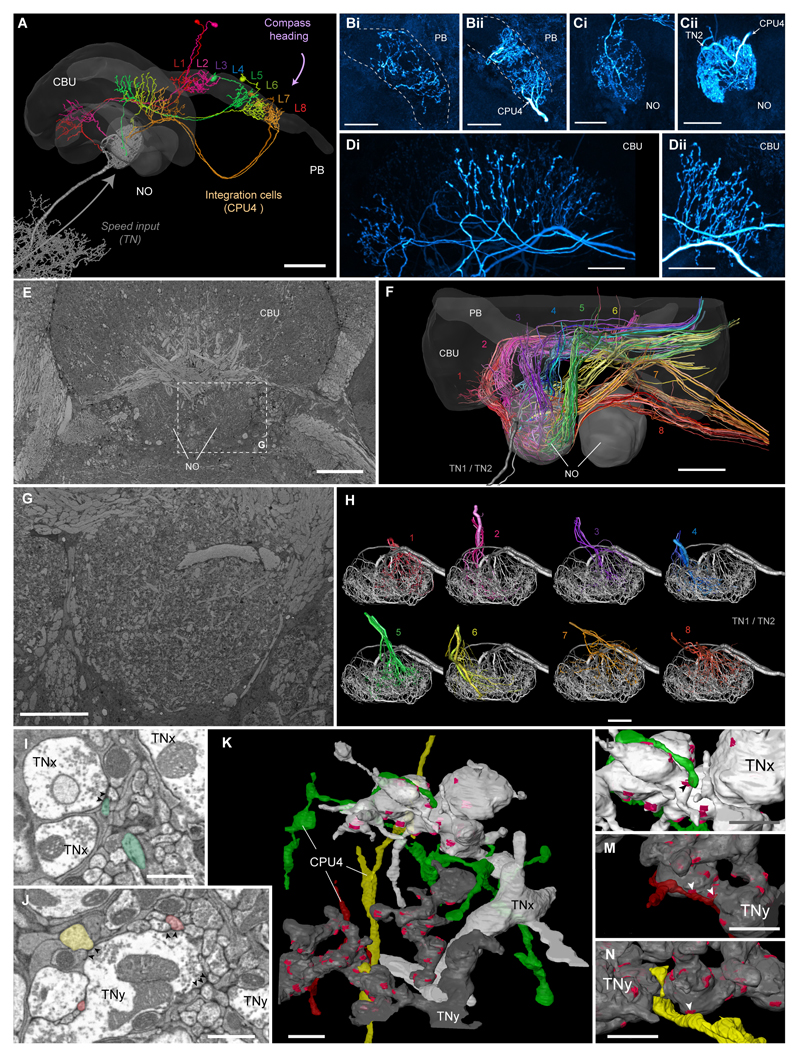
Figure 4. Speed neurons are presynaptic to proposed integrator cells.

(A) 3D-reconstruction of six CPU4-cells (colored) simultaneously stained with a single TN1-neurons (grey) from Megalopta genalis. Shown together with 3D surface reconstruction of central-complex (CX) neuropils (CBU, upper division of the central body; PB, protocerebral bridge; NO, noduli). The eight central-complex columns are numbered in the PB. (B-D) Maximal intensity projections of intracellularly filled CPU4-neuron arborizations in the PB (Bi, Bii), noduli (Ci,Cii), and the CBU (Di,Dii); two examples shown for each neuropil. Polarity of cells is clearly presynaptic in CBU, but inconclusive in PB and noduli, suggesting mixed terminals. (E) Single section from low-resolution (voxel size: 100x100x100 nm) block-face electron-microscopical image-stack of the bumblebee CX. (F) 3D tracing of all neurons innervating the right nodulus (based on image stack in E). Colors correspond to confocal data in A and indicate columnar identity. Fiber trajectories and arborizations in the CBU match the confocal data and allow identification of all 16-19 traceable cells per column as likely CPU4-cells. (G) Single section from medium-resolution (voxel size: 23x23x50 nm) data stack from the bumblebee. (H) CPU4-neurons from each CX-column possess overlapping projection fields within one nodulus, a prerequisite for possible microcircuits within the noduli. Shown are three to five cells from each bundle. (I,J) Single sections from high-resolution image stack (voxel-size: 11.5x11.5x50 nm) revealing synaptic vesicles associated with active zones (arrowheads) within TN-cells directly opposite of likely CPU4-cells (colored as in (H)). (K) Surface reconstruction of one terminal branch of each TN-neuron (grey; TNx and TNy, as identity cannot be established as TN1 or TN2 based solely on noduli fibers). Clearly identifiable active zones are highlighted in magenta. Three columnar neurons postsynaptic to TN-cells (colors according to bundle identity) are also reconstructed and were traced to their bundle of origin. (L-M) Detailed 3D-views of contact points of three CPU4- and TN-cells (arrowheads) shown in (I,J). Scale bars: A/E/F, 50 μm; B-D,G/H, 20 μm; K, 2 μm; I/J/L-N, 1 μm.

A plausible substrate for integration of speed and direction

To reveal the postsynaptic partners of the speed cells, we carried out additional block-face electron microscopy of the bumblebee noduli. Through tracing neurites in low and medium resolution images (Figure 4E,G) we found between 16 and 19 columnar neurons for each of the 8 CX bundles (per hemisphere) that showed overlapping arborization domains with TN-cells (Figure 4F,H). These fibers follow an identical trajectory as columnar CPU4-neurons that were co-stained with TN-cells recorded in Megalopta (Figure 4A), closely resembling identical cells from other species [30–33]. These cells are characterized by three arborization regions, one in the PB, one in the contralateral nodulus, and a third branch in the upper division of the central body (CBU, fan-shaped body in flies). As only the most medial parts of the PB were included in even the largest image stack (low resolution stack), we were only able to trace 19 out of 141 neurons to their origin in the PB (19 of 35 in the medial two bundles). Whereas the fine branches in the PB were either below the resolution of the data or outside the imaged region, we identified fibers in the CBU in most cells (122 of 141; 18 of 18 for two bundles), while all cells innervated the noduli. With the exception of two CL2-neurons per bundle, which project to the CBL instead of the CBU and originate in a different part of the noduli, all cells in the traced CX bundles are thus most likely CPU4-neurons. Using this reasoning for the higher resolution datasets (only covering one nodulus) to infer CPU4-neuron identity, we found strong evidence that TN-cells and CPU4-cells are not only in close proximity, but indeed form synaptic contacts (Figure S4I-N).

As CPU4-cells have input terminals in the noduli as well as in the PB they are ideally suited to integrate speed signals from the noduli with compass signals from the PB. Unfortunately, not much is known about the function of these cells in any species: preliminary recordings in Megalopta have revealed responses to translational optic flow in CPU4-cells (data not shown), while in locusts these cells show context dependent responses to compass stimuli [19].

Crucially, the third projection area of CPU4-neurons provides output to the CBU, which houses the dendrites of the columnar CPU1-neurons. These cells are the largest columnar neurons of the CX and have been described anatomically in many species [20,30–35] (they comprise the ‘horizontal fiber system’ in Drosophila [31,35]). Functionally, they have been studied in locusts, butterflies and dung beetles, and consistently respond to visual compass stimuli. The latter was confirmed in Megalopta by preliminary recordings (Figure S3). Based on their anatomical and physiological properties [7,20,30,33] CPU1-cells have been suggested to be postsynaptic to neurons of the PB and likely to provide a main output pathway from the insect CX.

Across all species examined to date, CPU1-cells converge in a premotor control region, the lateral accessory lobe (LAL) [7,20,30–33]. This brain region contains neurons descending to the thoracic motor centers and detailed work in the moth Bombyx mori has shown that it is involved in generating steering commands in response to pheromone pulses [36,37]. This potential direct role of CX output cells in initiating steering responses was recently confirmed in cockroaches, in which neural activity in the CX directly influences reflex circuits in the thorax for steering [9]. Thus, in principle, the bee CX contains all elements for a path integration circuit that has the potential to integrate speed and compass signals and relays this information to motor control centers. We now present a detailed proposal for how this computation could take place.

A proposed circuit for path integration

The model presented in Figure 5 combines data from the current study with anatomical constraints based on the assumptions that, first, input and output regions of CX-cell types (cell polarity) can be reliably inferred from morphologically distinct fiber terminals (smooth versus blebbed) (compare e.g. [7,30,33] with [31,32]) and second, that overlapping fibers with opposite polarity are synaptically connected. Effectively, this excludes impossible connections and assumes all other connections exist, which is likely an over simplification, but, in the absence of sufficient direct connectivity data, allows us to generate systematic, plausible connections between all major CX cell-types. These are dictated directly by their interhemispheric projection patterns (Figures 5B-E, S4E), which have been observed consistently across a range of insects [30,31,33] (see below and Methods for further details of the evidence for each assumed circuit element). In the following we propose a functional interpretation of these data that constitutes a complete model for path integration.

Figure 5. Deduction of circuit-model from anatomically plausible connections in the central complex.

(A) 3D reconstruction of the Megalopta genalis central complex (CX); posterior view. Enlargement: Schematic protocerebral bridge (PB) with columnar organization highlighted. Proposed head-direction tuning of direction cells indicated for each column (based on data from flies [8]. (B) Projection pattern of TB1-neurons in the PB; direction tuning indicated as arrows; green columns: output fibers; yellow columns: input fibers. (C-E) Schematic interhemispheric projection patterns of CPU4-neurons (C), CPU1-neurons (D), and pontine neurons (E). (F) Principal connections of all cell-types included in the proposed path integration circuit. Shown are all connections of one TB1 direction cell irrespective of columnar identity of individual cells (only two out of six connections to other TB1-cells are shown). (G) Ring-like topology of proposed path integration circuit, obtained using a force-directed graph. Neurons are arranged in three layers: Direction cells (TB1), memory cells (CPU4), and steering cells (CPU1), with connections matching the interhemispheric projection patterns in B-E. Only one CPU4 cell per column is drawn (representing the entire columnar population). Connections between TB1-neurons form a ring attractor network (solid lines: connections of one cell; dashed lines: remaining cells; line thickness: connection strength). CPU1-neurons receive inputs from CPU4-neurons with a rightwards (yellow) or leftwards (orange) shift relative to their TB1-input. Arrows: directional tuning (TB-neurons), integrated direction preference (CPU4-cells). Pontine neurons were omitted for clarity. (H) Illustration for memory acquisition during outbound journey. Width of lines indicates activation strength. Memory accumulates opposite to outbound heading direction and is encoded as two partial vectors (each generated by the CPU4-cell population on one brain hemisphere). (I) Illustration of how memory is combined with current heading to generate an imbalance between the right and left CPU1-neuron population activity. The activity in each cell is indicated by the height of the bars above the cell-indices. Current heading: green arrow (bottom); target direction encoded by memory (black arrow). Activity of TB1 (inhibitory) and CPU4-cells (excitatory) are compared by CPU1-cells. Due to the one-column shift between CPU1 and CPU4 projections, this results an imbalance in the combined CPU1 output that initiates turning towards the target. Pontine neurons have the identical activity as CPU4 cells (not shown) and normalize the memory output from each CPU4 population by subtractive inhibition of neurons with opposite directional tunings. For a more mathematical explanation of how the steering signal in generated see Figure S6B-D. Abbreviations see Figure 1. See also Figure S4,S5,S6.

The PB (Figure 5A) receives input from columnar cells of the ellipsoid body/lower division of the central body (CL1, Figure 5F) [38,39], characterized as compass neurons in flies [8], locusts [19], butterflies [10], beetles [20] and bees (this work). Our model assumes that each of the eight multiglomerular TB1-neurons in the PB directly receives this input and, in accordance with data from flies [8,38–40], is tuned to one specific azimuth direction and together they tile the azimuth around the animal with a resolution of 45° (Figure 5A,B). The proposed mutual connections of TB1-neurons onto one another follow a specific pattern suggested by the distribution of their dendrites (Figure 5B), which is conserved at least across locusts, butterflies, beetles and bees [7,20,33]: TB1-cells have no input fibers in PB-columns that neighbor their output fibers, while the density of input fibers is highest in columns most distant from output fibers. TB1-cells are likely inhibitory [7], and thus their cross-connectivity could form a ring attractor [41], which allows potentially noisy directional inputs to produce a stable single ‘bump’ of activity - more explicitly, we propose the circuit stabilizes as a sinusoidal activity pattern with its peak in the direction of strongest directional input. The ring attractor hypothesis is consistent with both recent observations and recent models of PB activity in Drosophila [38–40,42]. Thus, in our model, the activity of the TB1-neurons represents the current head direction of the bee.

Through their output fibers each TB1-neuron is proposed to inhibit two types of columnar neurons, CPU4- and CPU1-cells (Figure 5C,E). As described earlier in this paper, CPU4-cells, occurring in 18 copies per CX-column, also receive input from TN ‘speed’ neurons in the noduli. We hypothesize that all CPU4-neurons of each columnar bundle form recurrent microcircuits between the PB and the noduli to provide a basis for an activity-based memory, in a manner similar to that theorized in e.g. [43,44]. The possibility of a recurrent circuit is supported by the mixed appearance (combined input and output regions) of terminals of CPU4-neurons in both the noduli and the PB in confocal images (Figure 4B,C) and EM data that confirm both types of synapses in these neurons in the noduli, including synapses interconnecting likely CPU4-cells. Nevertheless, given the lack of substantial physiological data from CPU4-neurons in any species, we emphasize that this role as memory units is purely speculative, but generates a concrete prediction: by continuously integrating the speed information from optic flow in proportion to the input from TB1-neurons, these units could encode the distance travelled in each compass direction, i.e., serve as direction-locked odometers.

Note that by combining excitatory TN-speed input with inhibitory TB1-direction signals, the proposed CPU4-memory will increase proportionally to the bee’s speed in columns opposite to the current flight heading (Figure 5H), and moreover will be shifted by +45° in one hemisphere, and -45° in the other, corresponding to the offset in optimal optical flow expansion observed in left and right TN-cells (Figure 3I) with which they overlap (the noduli connections are contralateral only; Figure 4A,F). If the animal’s motion is not directly aligned with its head direction, the rate of accumulation in each hemisphere will differ, but will, in a distributed form, represent the inverse of the actual motion, i.e., the correct home vector (Figure S6).

In the CBU, the anatomy suggests that the CPU4-cells connect to CPU1-cells both directly (Figure 5C,D) and indirectly via pontine cells (Figures 5E, S4E,F). Pontine cells have been found in the CX across many species, and connect single columns of the CBU between the right and left brain hemispheres [30,33–35,45–47]. CPU1-cells also appear to get direct input from TB1-cells in the PB (Figure 5F). Importantly, CPU4- and CPU1-neurons do not follow the same projection pattern: neurons of both types originating in one PB column make connections in different columns of the CBU, offset by one column to either the right or the left [30,31,33]. We propose that this allows CPU1-neurons to effectively compare the current heading (inhibitory TB1-activity) and the desired heading (CPU4-encoded home vector) and thereby generate a steering command (Figure 5I).

The functional principle of the model-circuit can be best understood by using a force-directed graph layout to reveal the underlying logic of the complex cross-hemisphere and column-shifted connections between TB1-, CPU4- and CPU1-neurons (Figure 5G). We emphasize that this connectivity pattern was entirely derived from anatomy and not proposed specifically to support the function we now suggest. All right hemisphere CPU1-cells (light blue) will be activated by the difference between the current heading (green TB1-input) and the home vector (yellow CPU4-input) shifted leftwards by 90° relative to the TB1-input. This shift is due to the 45° columnar offset of CPU4- to CPU1-projections, plus the 45° offset (relative to zero) of the preferred expansion point of TN-neuron input to CPU4-cells in that hemisphere. Similarly, the left hemisphere CPU1-cells (dark blue) will be activated by the difference between the current heading (green TB1) and a 90° rightwards shifted home vector (orange CPU4). Thus, the circuit as a whole ‘evaluates’ whether a left or right rotation would produce a better match between the current heading and the memory (Figure S6). Due to the separate path integration in each hemisphere, it would be possible for the output amplitude of one hemisphere to exceed the other as a result of non-symmetric holonomic flight, rather than a better directional match to memory. However, the two outputs for corresponding directions are normalized by subtractive inhibition from the cross-connecting pontine neurons (Figures 5I, S4E,F). Thus the relative output of left and right CPU1-cells provides the steering signal needed to align the animal with its home vector. As path integration is assumed to be always operating, during a return route the memory in CPU4-cells will gradually become equal in all directions and when the home location is reached, there will no longer be a difference in output from the steering cells.

We note here that the steering principle we have described, a consequence of the CPU4-CPU1 columnar offset, could be a general purpose mechanism by which the CX compares an animal’s current heading to its desired heading to generate an appropriate correction. We return to this point in the discussion.

Demonstrating the robustness of the model through simulation

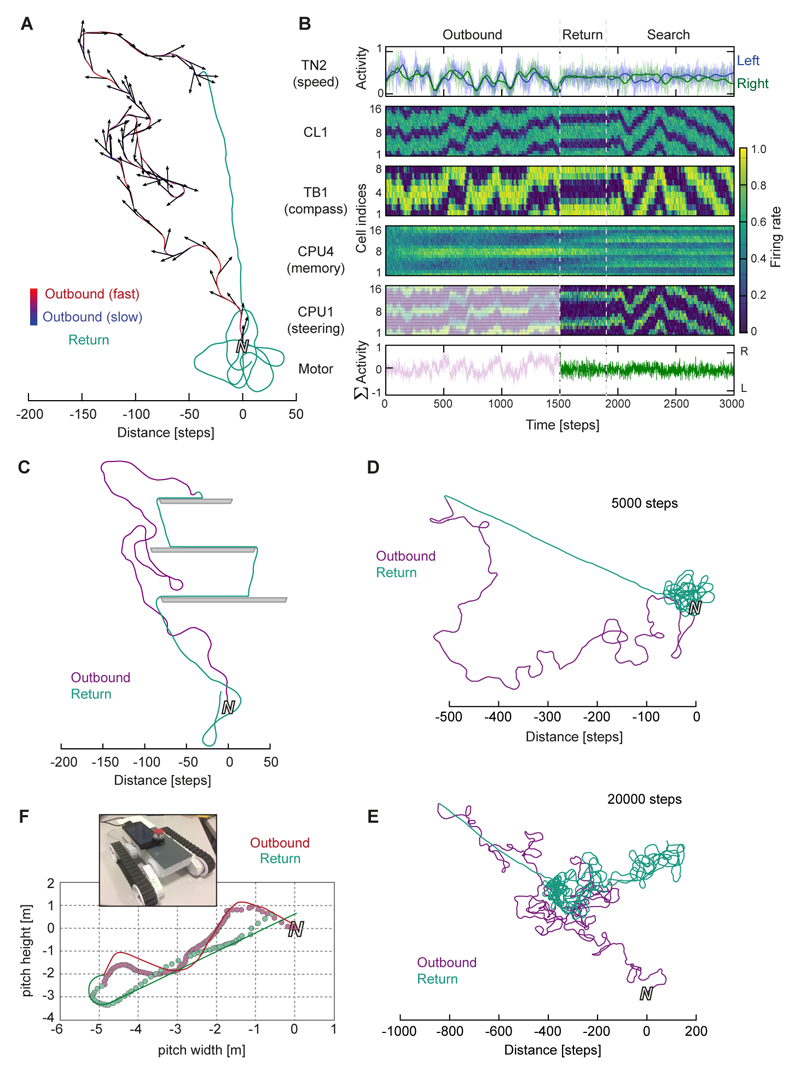
We implemented a computational model of this anatomically plausible circuit using rate-based neurons and tested it in an agent simulation (Figures 6,7; Movie S2; in the Methods and Figure S6 we also mathematically demonstrate the function by adapting a known algorithmic framework [48]). Tested with random outbound routes, the agent homes directly to within a few steps of its starting location, where it automatically produces an emergent search pattern (Figure 6A; Movie S2). The homing ability is not affected by biologically relevant amounts of holonomic movements that are typically produced during bee flight (±45°) [49,50]. These simulation results match the theoretical expectations. During the outbound route, the shifting head-direction bump of TB1-activity leads to accumulation of two sinusoidal activity patterns in the CPU4-neuron populations in each brain hemisphere (Figure 6B), which then control steering in the correct direction on the return trip. While homing, the continuously operating integrator rebalances the memory activity, and in the absence of a stopping criterion, produces the observed search patterns. Due to the continuous memory update the agent can also deal with forced deviations on its homeward path (Figure 6C). The search patterns and response to deviations resemble behavioral data from ants [51]. The memory capacity depends on assumptions about the rate of accumulation and decay, but for the settings used here, routes of up to 5000 steps still produce accurate return paths (Figure 6D), whereas very long routes (>20,000 steps) start to saturate the memory, although this still allows recovery of a correct heading direction while undershooting in distance (Figure 6E).

Figure 6. The biologically constrained circuit successfully performs path integration.

(A) Example trace: The agent is driven on a random outbound journey (variable speed, 1500 steps), during which the circuit accumulates memory. For return, the steering cells guide the agent back to its origin. Close to the nest, the agent automatically initiates searching behavior, similar to path-integrating insects. (B) Activity of all neurons in the circuit over time during the trial in A. Each cell is represented by one line over time. Cells of the same type are arranged according to columnar identity, revealing activity bumps within the protocerebral bridge (PB). Neural noise: 10%; firing rate normalized to peak rate within each cell-type. Cell indices correspond to columns of the PB according to Figure 5A. (C) Same outbound route as in A, but obstacles present during homing. (D,E) Performance of the circuit during longer outbound journeys. After correct homing for up to 5000 step long outbound routes (D), the agent begins to undershoot during the inbound journey, while maintaining the correct heading, during longer runs (E). This indicates that memory capacity is exceeded during the outbound journey. (F) Example trace of robot path integration trial. Line: trajectory of the robot; circles: position estimate based on CPU4 neuron readout. Inset: Robotic platform for circuit implementation. See also Figure S6,S7.

Figure 7. The proposed path integration circuit is resilient to disturbance.

(A) Performance during increasingly longer outbound journeys and increasing neural noise. Closest distance to nest during homing (mean ± SD from 1000 runs) plotted against length of outbound journey. (B) Distribution of angular deviations from true home after initiation of steering (10° bins, 1000 trials) for different noise levels (colors as in A). (C) Deviation from the best possible route (straight line) during homing (10% noise). C: distance covered towards the nest after L steps, (L = straight-line distance to nest); L/C = path tortuosity (average: 1.150). (D-H,I) Responses to disturbances reveal the robustness of the circuit. Plotted is the closest distance to home during homing after a 1500 step random outbound route against different types of disturbances (mean ± SD). Dashed grey line: 20 step home range used to illustrate successful homing. (D) stochastic noise in the sigmoids of each neuron. The 0.1 level was also used for all remaining trials (blue curves; green curves are without sigmoid noise). (E) Effect of randomly varying synaptic weights. (F) Effect of shifting clockwise and counter-clockwise preference angles of compass signal. Orange line: Value found for Megalopta compass neurons (Figure 1). (G) Effect of deviation of translational optic-flow preference axis from the bee’s body axis in TN2-neurons. Orange line: Average value obtained in Megalopta TN-neurons (Figure 3). (H) Effect of actual speed exceeding capacity of speed neuron (TN2) coding range. Right: Example routes show that the agent undershoots, but maintains the correct heading, when speed neurons saturate during outbound route. (I) Effect of low-pass filtering of the speed signal (as found for TN1-neurons). Right: Example of how a smoothed speed signal affects homing.

To test whether the presented circuit can function in a real-world environment we implemented the same model on a robotic platform (Figure 6F, Movie S3), using camera-perceived optic flow and inertial-rotation based compass estimation as inputs. The robot successfully performs path integration under these realistic conditions: after a random outbound journey taking the robot 6-12 m away from the origin, the CX circuit guided it back to within an average of 16 cm of home (SD 11.1 cm; n=10).

In repeated tests, the network is robust to added noise of 10-20%, generating highly accurate homing until the outbound route extends beyond the capacity of the memory cells (Figure 7A). Using a criterion from bee experiments, the ‘disappearance direction’, we see that the direction in which the agent sets out for home is tightly constrained around 0° (Figure 7B), and the route taken is quite direct (Figure 7C). In addition to varying the neural activity noise and the route distance (Figure 7A,D), we tested how robust the model is to perturbations of several model parameters. For each test, N=2000 homing tasks were completed for each parameter value: 1000 trials at default neural activity noise (10%) and 1000 at no noise. The homing accuracy was assessed by the minimum distance from home achieved by the agent.

First, we tested the effects of varying the connection weights between cells (Figure 7E). Fixed noise on the weights is less likely to balance out over time than additive noise at each time step, causing an intrinsic bias and making it more detrimental to the system. However, despite a weight-noise variance of up to 5%, the network was still able to achieve good homing behavior. To test whether the rotation-dependent offset in the preference angle of the compass input neurons (TL and CL; Figure 1G) affects the circuit, we mimicked the experimental data in the model by gradually increasing the difference angle between rotation directions. As in the experimental results, peak activity would always pre-empt the preference angle. In these tests, there was not a strong effect over the range tested, although performance improved somewhat with a small tuning shift (compared to no shift), similar to the one observed in the bee neurons (Figure 7F). This could be due to counteracting lag from the signal propagating through the model, especially due to the dynamics of the TB1 ring attractor.

As we have used idealized values of lateral offset in the preferred angle of optic flow expansion for the model speed neurons (TN) (Figure 3I), we tested the effects of perturbations in the angular offsets by systematically changing the preference angle of optic flow expansion. An angle of 0 is equivalent to assuming that the speed cells in each brain hemispheres respond optimally to a point of expansion directly in front, which would result in the two CPU4-neuron populations integrating the path identically. For noise-free experiments, the agent homed with similarly good performance at all preference angles smaller than 45°. For trials with neural noise, the best angle was around 45°, corresponding to the experimentally measured average value in bee TN-neurons (Figure 3G). In both tests, as angles exceeded 60° homing ability decreased smoothly (Figure 7G). For paths with random holonomic motion, the inaccuracy this introduces tends to cancel out and we do not see a substantial difference in results (Figure 7G). However, if we force the agent to move continuously in one direction while facing another direction, this encoding produces predictable and substantial error in the home vector, which does not occur for the (biologically observed) 90° separation of expansion preference direction (Figure S7D-F).

Next, we increased the speed of the agent, so that the TN-neurons would reach saturation, i.e., be unable to correctly represent the highest speeds. Acceleration was increased up to three times the default value, which had been set to provide a full range of neural activity. Initially, barely any drop in path integration performance was noticeable, because only a small proportion of motion occurs at the highest speeds. As speed increased beyond 1.5× we saw a degradation of performance and the agent undershoots during homing (Figure 7H). Finally, TN-input was smoothed to mimic the sustained responses shown in Figure 2E, which also lead to a gradual decline in homing precision (Figure 7I).

The main conclusion from these tests is that the properties of the model are robust. Failure can arise if the limits of the network are exceeded in terms of noise tolerance and memory or if cell tuning-curves are shifted too far from their ideal preference angles, but small changes of any parameter do not cause catastrophic failures of the model. The use of rate-based neurons, and the assumption that CPU4 activity can simply accumulate, are clearly abstractions; in future work we need to verify that use of spiking neurons does not limit the practical performance (e.g. accuracy, memory limit), although we are confident that the basic principle of operation will carry over.

Discussion

We have presented a biologically constrained circuit model for path integration that combines a previously well-described compass network with speed-sensing neurons reported here for the first time, and which makes concrete predictions about synaptic connectivity consistent with all available functional and anatomical data across insect species.

Several highly conserved structural features of the insect CX gain relevance through our model. The anatomically-inspired eight-fold encoding of compass directions has the advantage that geometric operations such as taking sine and cosine can be obtained by making a single column shift of activity in opposite directions, providing a first suggestion as to why the CX across most insects consists of 2x8 vertical slices. The distinct sensory pathway transmitting translational optic flow information to the CX reveals a function for the CX-noduli, a region present in all flying insects, but of hitherto unknown function. The conserved complex pattern of dendritic and axonal fibers in the multiglomerular TB1-neurons is the core of the ring attractor circuit. The characteristic connectivity schemes of different types of columnar neurons (CPU4, CPU1) fully account for the functions necessary for memory and steering. Finally, the functionally undescribed CX-pontine cells, the last remaining cell-class of the CX that is also present in all species examined [30,33–35,45–47], are crucial in maintaining the balance between outputs of the two hemispheres.

Furthermore, with the TN-speed neurons we have functionally characterized a new component of the CX-circuitry. The identical morphology of these cells in two distantly related species suggests that these cells have evolved more than 100 million years ago [29] and might be part of the core network of the bee CX. As both species inhabit vastly different sensory environments, our recordings from Megalopta provide the basis for future investigations comparing multiple species physiologically. These will be able to address how the CX-circuitry has adapted to the demands of specific habitats and illuminate quantitative differences in the sensory encoding of information underlying navigation behavior.

Head direction encoding has been firmly established as a functional feature of the Drosophila PB [8,38–40] and ring attractor dynamics have been experimentally demonstrated to underlie this direction code [38–40]. Our model of a TB1-neuron based ring attractor complements these recent models of Drosophila ring attractors, which are based on recurrent connections between the CBL and the PB (via E-PG- and P-EN-neurons [39,52]). Specifically, it suggests a basis for the global inhibition across the PB that was postulated in those models. Whether the ring attractor circuit in the bee also includes homologous counterparts of the recurrent E-PG- and P-EN-neurons from Drosophila (called CL1 and CL2 neurons in other insects), remains to be shown, but circuitry to maintain the bump in the temporary absence of external input, and to shift it according to cues for self-rotation, would be fully consistent with our model. We simply assume that external compass input dominates when available, as it is not subject to cumulative drift. More importantly, our model circuit provides a first account of how the head-direction code present in the PB can be used to drive behavior. Nevertheless, as this recent work shows, there is still much to be discovered about the functional capacities of this circuit.

The proposed model of path integration relates to several previous hypothetical neural models. The concept of a head direction circuit controlling (speed-dependent) accumulation of activity on a circular array of units, producing a ‘distributed’ home vector, has been used in several computational models, utilizing vastly different numbers of directional memory units (from 3-100) [53–58]. As discussed in [5] this encoding can be considered a redundant or generalized form of Cartesian encoding (i.e., using more than 2 axes), particularly if the head direction encoding used across the units is a cosine function of direction. Cartesian encoding (taking the sine and cosine of the movement vector, and keeping a running sum of each) was first suggested theoretically as a ‘bi-component’ model [59] and implemented in a neural model three decades later [60]. All these models differ in how the homing control is achieved. Most similar to the mechanism proposed here is that described in [53] which also activates sets of left and right steering cells by the combination of the current direction and a right or left shifted memory, to determine if right or left rotation by the agent will improve the match between the current heading and the home vector. However, conceptually, our circuit can be better interpreted in the terms proposed in [48]. In that model, the current direction is represented as a sinusoidal activity pattern across an array of neurons. A corresponding memory array accumulates these inputs, at a rate corresponding to speed. The resulting memory activity is thus also a sinusoid, with the home vector direction represented by the phase, and home vector length by the amplitude. The readout for steering in that model involves cells that “have receptive fields on both neuron arrays [current direction and memory] that are displaced relative to one another” [48] to detect deviation to the left or right. Strikingly, our model, which was derived from anatomical considerations, essentially differs from this model only in its use of two memory arrays, receiving orthogonal speed inputs, which enables holonomic path integration as described above.

Besides suggesting functional relevance for anatomical features of the insect CX and implementing a model for path integration completely constrained by CX anatomy, our model produces a range of concrete predictions that open up multiple new lines of structural, physiological and behavioral research. Firstly, since the CPU4 columnar cells are the proposed physical substrate for path integration memory, this suggests memory capacity is linked to the number of parallel CPU4-neurons per CX-column. Thus, path-integrating insects should in principle have more CPU4-cells compared to species with different navigational strategies. This is also applicable if males and females of the same species differ in their behavioral strategy, as is frequently the case in bees. Second, as the homing vector is hypothesized to be represented by ongoing recurrent neural activity, the path integration memory should be less stable compared to memory laid down by synaptic remodeling (e.g. in the mushroom body) and thus be more prone to experimental disturbance, e.g. via brain cooling at the beginning of a homing flight. Third, physiologically, our network predicts that during path integration the activities of CPU4-cells and pontine cells should increase over time and that specific patterns of activity across the CX result from specific outbound flights. Although it would not be trivial to generate the right motivational and behavioral conditions, these patterns, and the accumulation of activity, are in principle observable by electrophysiology or functional imaging. Finally, our model can also be tested in behavioral experiments. Manipulating optic flow to introduce controlled biases during outbound routes (e.g. generating the impression of continuous backwards flight, or excessive flight speed) as well as direct manipulations of neuronal activity, e.g. via current injection, can be used to mimic conditions that break our model in simulations in predictable ways (Figure S7).

In a broader context, the proposed circuit compares the animal’s current heading with its desired heading and initiates compensatory steering commands in case of a mismatch. The same model circuit, with fewer recurrent CPU4-neurons per CX-column, could store an ongoing direction of movement, allowing steering back to the desired direction in case of disturbance [61,62]. Alternatively, CPU4-neurons could permanently encode the migratory heading of long distance navigators, such as the monarch butterfly. Furthermore, during all behavioral episodes where CPU4 neuron activity (e.g., encoding path integration memory) does not drive behavior (e.g., on the outward exploratory route) it is necessary that memory and steering are decoupled. Our proposed steering mechanism could meanwhile compare the current heading encoded in the PB with other information arriving at the dendritic trees of CPU1 neurons in the CBU. In line with this idea, the CBU receives input from many areas of the insect brain [33,35,63], which could deliver information about the animal’s desired heading in different sensory/motivational contexts. Our model circuit could therefore support any situation in which the animal needs to adjust its current direction to match some ‘desired’ direction, e.g., alignment with a landmark, through the same ‘compare the match for left and right rotation’ principle. This implies that the input to CPU1 from CPU4 can be switched off (gating the use of the home vector) or is affected by other contextual, motivational or sensory information, most likely within the CBU. While there is no direct evidence for this state-dependent (exploring vs. homing) switch in active synaptic transmission, there is strong evidence for state-dependent change in neural signaling in the CX in general [19,64], combined with a rich variety of neuromodulator expression in this region [65,66]. This simple expansion of our model could thus also explain behaviors such as steering towards landmarks, choosing between targets, and following routes; and may additionally provide a basis for combining diverse directional cues into a single coherent action.

STAR Methods

Contact for Reagent and Resource Sharing

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Stanley Heinze (stanley.heinze@biol.lu.se).

Experimental Model and Subject Details

Adult bees of the genus Megalopta (species M. genalis and M. centralis) were caught from the wild using light traps (white sheets illuminated by a bright light source containing UV wavelengths). Traps were placed ca. 2 m above ground within small canopy openings of the tropical forest on Barro Colorado Island (field station of the Smithsonian Tropical Research Institute), located in the Panama Canal, Panama. Trappings were carried out during the activity phase of the bees between 4:30 am and 5:30 am in the morning, i.e. during early morning twilight. Caught bees were kept individually in 50 ml plastic vials, equipped with two cotton balls, one soaked in honey solution as well as one soaked in water. Vials were kept at room temperature in a dark secondary container (small amounts of natural light were allowed to reach the bees to ensure continuous circadian entrainment). Bees were used for experiments within two weeks after capture to ensure healthy condition. With few exceptions used bee were large to medium sized females.

Female bumblebees (Bombus terrestris) were obtained from a commercial supplier (Koppert, Berkel en Rodenrijs, The Netherlands) and kept at room temperature in a room sized flight cage at Lund University, Sweden. Feeders with honey solution were available at all times.

Method Details

Visual stimulation

For visual stimulation, we developed a new virtual reality environment combining a 360° panoramic LED arena (consisting of 96 LED-arrays of 8x8 570 nm LEDs, mounted on FlyPanels-G3, controlled by a panels display control unit; IO-Rodeo, Pasadena, USA) with an artificial sky. The arena had an angular resolution of 1.5° and covered 55° of vertical space (equal parts above and below the horizon). The artificial sky consisted of a planar array of UV LEDs (365 nm) illuminating a large polarizer (BVO-UV, Boldervision; 88° of dorsal space) mounted on a custom-built rotation stage (Prototypverkstaden, Lund, Sweden) driven by a Micos DT-50 rotation stage (controlled via MoCo controller; Micos). All LED panels as well as the rotation stage were controlled via an integrated, custom designed MATLAB-based software.

Polarized-light stimuli were applied by switching the LED illumination of the sky on and rotating the polarizer through 360° at constant speed (60°/s or 30°/s) clockwise and counter-clockwise (as seen from the animal’s point of view).

Optic-flow stimuli were shown in stereotypical series of individual stimulus bouts separated by darkness. Each bout consisted of 0.5 s stationary display of the stimulus pattern followed by 3 s of movement at constant velocity, followed by 3 s of darkness. As patterns, we used sinus-gratings of different spatial frequencies (ranging from 0.017 cycles/° to 0.067 cycles/°) at maximal contrast, moving at velocities between 10°/s to 160°/s. For translational optic flow, the stimulus moved clockwise in one hemisphere and counter-clockwise in the other hemisphere, while the entire panorama moved in one coherent direction during rotational optic flow.

Receptive fields were mapped using a narrow vertical stripe (width: 7.5°) that moved around the entire panorama at constant speed (60°/s) either clockwise or counter-clockwise. Each stimulus consisted of two clockwise rotations followed by two counter-clockwise rotations. The bar was introduced into the arena behind the bee and remained stationary for 0.5 s before movement commenced. Control voltages were recorded for all stimuli, indicating the timing of displayed frames in the virtual reality arena and the angular position of the rotation stage controlling the polarizer.

Electrophysiology

Intracellular recordings were carried out with sharp-tipped electrodes (resistance 50-150 M) drawn from borosilicate glass capillaries (Sutter P-97 puller). Bees were cooled on ice (bumblebees in freezer) until immobile and waxed to a plastic holder. Legs and wings were removed for increased stability of the preparation. The head capsule was opened frontally between the antennal base and the ocelli, and air-sacks and fat tissue were pushed aside or removed if necessary. The brain surface was shortly exposed to Pronase (crystals applied directly), after which the neural sheath was removed with tweezers. A silver wire was placed in the ventral part of the head (near mandibles) as reference electrode. After placing the preparation in the center of our virtual reality arena (vertical orientation), the recording electrode (tip filled with 4% neurobiotin (Vector Laboratories) in 1M potassium chloride, backed up with 1M potassium chloride) was frontally inserted into the brain using the antennal lobes and the vertical lobes of the mushroom body as landmarks (Sensapex micromanipulator, stepping mode). Target areas were the noduli and the central body of the central complex (CX). Once cells were impaled and the stimulation protocol was successfully tested, a depolarizing current (1-3 nA) was applied to iontophoretically inject neurobiotin into the recorded neuron in most experiments.

Recordings were performed throughout the day on 160 female worker bees (with the exception of very few male Megalopta). With few exceptions, only one cell was recorded and analyzed per bee to ensure a clear correspondence between anatomy and physiology. Whenever the recording was lost before dye injection, the physiology of more than one cell was recorded, but never were two cells of the exact same type encountered within the same bee in these cases. Therefore, for physiological data the number of cells always equals the number of bees used for the displayed cell population. Signals were amplified with a BA-03X amplifier (NPI) (Panama setup) or a SEC05-LX amplifier (NPI) (Sweden setup), digitized using CED-1401 micro (Cambridge Electronics Design), and recorded with Spike2 software (Cambridge Electronics Design). All recordings were performed at room temperature (20-25°C).

Histology for light microscopy

Neurobiotin injected brains were processed as follows. Injected brains were removed from the head capsule and fixed in neurobiotin fixative (4% paraformaldehyde, 2% saturated picric acid, 0.25% glutaraldehyde) over night at 4°C. Brains were transferred to 0.1M PBS until further processing. After rinsing the brains for 4x15min in PBS, they were incubated with Streptavidin conjugated to Cy3 (1:1000, in 0.1M PBT (PBS plus 0.3% TritonX-100)) for 3 days. The brains were then washed (4x20 min PBT, 2x 20 min PBS) and dehydrated in an increasing ethanol series. Finally, they were cleared in Methyl salicylate and mounted in Permount (between two coverslips, separated by spacers).

Immunohistochemical stainings were performed to visualize the boundaries of brain regions, in particular the CX. Antibodies against the synaptic protein Synapsin (monoclonal, mouse antibodies; obtained from Drs. Erich Buchner and Christian Wegener) were used for this purpose [68]. Brains were dissected and fixed in Zinc-Formaldehyde fixative [69] (overnight at 4°C). After washing in Hepes-buffered saline (HBS, 8x30 min; [69]), the brains were subjected to a permeabilization step (85 min incubation with a fresh mixture of DMSO and Methanol (20:80)) and washed 3x 10 min in Tris-HCL buffer. After pre-incubation in normal goat serum (NGS, 5% in PBT), the brains were incubated with the primary antibody solution (anti-Synapsin, 1:25, in PBT with 1% NGS) for 5-6 days at 4°C. The brains were washed in PBT (8x 30 min) and incubated with the secondary antibody solution (goat-anti-mouse antibody conjugated to Cy5, 1:300, in PBT with 1% NGS) for 4-5 days at 4°C. After washing (4x 30 min PBT, 2x 30 min PBS) the brains were dehydrated, cleared and mounted as described above.

Block-face electron microscopy

Bumblebee brains were dissected in fixative (4% paraformaldehyde, 2% glutaraldehyde, in Cacodylate-buffer) overnight at 4°C. After washing 4x 15 min in 0.1M PBS, the brains were embedded in albumin/gelatin and postfixed overnight in 4% paraformaldehyde. To cut out the region of interest (central-complex noduli), a single thick section (200 μm) was cut from each brain using a vibrating blade microtome. These sections were stored in PBS until further processing.

Samples were then rinsed in PBS buffer for 5 min, before osmification (in 2% osmium tetroxide and 1.5% potassium ferricyanide, aqueous solution) for 1 h at room temperature. Then, samples were washed in pure water (3 x 5 min) and incubated for 20 min in thiocarbohydrazide solution (1% aqueous), washed in pure water (3 x 5 min) and incubated for another 30 min in osmium tetroxide (2% aqueous; room temperature). After more rinsing (3 x 5 min) in pure water, samples were transferred into 1% uranyl acetate for overnight incubation at 4°C. Finally, the samples were incubated with lead aspartate (after 3 x 5 min washing in pure water) for 60 min at 60°C (oven). After more washing (3 x 5 min pure water), the samples were dehydrated in an increasing ethanol series (20%, 50%, 70% 90%, 2x 100%; 5 min each). Next, the samples were slowly infiltrated with a mixture of Durcupan and ethanol (25%, 50%, 75%, 2 h each), before transferring them to 100% Durcupan overnight. After transferring to fresh Durcupan for 2 h, samples were embedded in fresh resin for 48 h at 60°C. Samples were embedded in a thin layer of resin (just enough to cover the sample). They were trimmed and mounted onto aluminum stubs using 2 part conductive silver epoxy.

Imaging and image processing

Electron-microscopical imaging was carried out using a Zeiss Sigma VP scanning electron microscope equipped with a Gatan 3view. Low resolution scans were obtained with a voxel size of 100 x 100 nm (field of view: 400 x 400 μm) in 100 nm steps at 2 kV, medium resolution scans were done with a voxel size of 23 x 23 nm (field of view: 95 x 95 μm) in 50 nm steps and at an energy of 2 kV, while high-resolution scans were carried out with a voxel-size of 11.5 x 11.5 nm at an energy of 2 kV (field of view: 46 x 46 μm) in 50 nm steps. Acquired images of each stack were aligned and several consecutive imaging runs were merged into one continuous stack using Amira 5.3 software. After contrast optimization, the image stack was down-sampled to 8 bit image depth. This enabled use of the Skeletonize plugin for Amira [50] to perform neuron tracing, as well as to perform image segmentation (Amira segmentation editor).

Neuron profiles were traced manually by adding short, straight skeleton segments linked by branchpoints. The midline of large branches was automatically fitted to match the image information. The same tracing was carried out in both the high-, medium- and low-resolution stacks. For low-resolution stacks only the main neurite and the largest branches of cells were traceable, albeit over longer distances. Neuropil boundaries of the noduli were generated after down-sampling the image stack to 1x1x1 μm voxel size. We used the segmentation editor of Amira to manually segment key cross sections of the noduli in all three spatial planes. This provided a 3D scaffold of the noduli that was then used as the basis for generating a surface model of this brain region using the Amira wrapping algorithm. Volumetric reconstruction of selected neuronal fibers was also carried out with the Amira segmentation editor. For this purpose, cross sections of neuronal profiles were traced in the highest resolution image-plane (x-y plane) for each section until the 3D shape of the neurite of interest became apparent. The resulting label field was used to generate a surface model of the neurite. Active zones were identified by aggregations of synaptic vesicles adjacent to an electron-dense part of the neuronal membrane. Profiles directly opposite of the active zone were identified as postsynaptic.

Confocal imaging was carried out with a Zeiss LSM 510 equipped with a 10x objective (Plan Apochromat 10x/0.45, water immersion, Zeiss) for imaging large neuropil structures and whole brains, as well as a 25x long distance objective (LD LCI Plan-Apochromat 25×/0.8 Imm Corr DIC, Zeiss) for obtaining single-neuron morphologies and high-resolution neuropil dJacata. Neurons were imaged at a voxel size of 0.3x0.3x0.88 μm. All image stacks together covering the full extent of one cell were aligned to a common reference frame (using Amira) and used as input to the skeletonize plugin [70]. Neurons were traced manually and the resulting skeletons were finalized by automatic midline fitting and diameter adjustment (using local brightness information of the image data). Neuropils were reconstructed by manual image segmentation of key cross-sections of each structure combined with automatic surface wrapping in Amira. This was carried out for neuropils innervated by each neuron (based on background staining) as well as from anti-Synapsin antibody labeled preparations.

Reconstructions based on antibody labelling were used to generate a representative reference brain, which then served as a shared frame of reference for individual neuron data (neuron atlas). Individual neuron data were registered into this reference brain via manual affine registration (nine degrees of freedom). Registration parameters were obtained by registration of individual neuropil models to their counterparts in the reference brain. For TN-neurons we used the compartments of the CX, as well as the lateral antennal lobe tract as reference structures.

Simulation Methods

The proposed path integration network was implemented in Python 2.7 (Including scipy, numpy and matplotlib external libraries). Animation of the model used the following javascript libraries: jQuery, tinycolor, tinygradient. All simulations were carried out on a standard PC (Dell Precision 7610). We used a simple firing rate model for each neuron [71], in which the output firing rate r is a sigmoid function of the input I:

$$r=\frac{1}{\left(1+e^{-\left(aI-b\right)}\right)}$$

where parameters a and b control the slope and offset of the sigmoid (see Figure S5 for parameter values and curve shapes). Optional Gaussian noise ${ϵ}_r\sim 𝒩\left(0,{\sigma }_r^2\right)$ can be added to the output, which is then clipped to fall between 0 and 1. The input I is given by the weighted sum of activity of neurons that synapse onto neuron j:

$$I_j={\displaystyle \sum _i{w}_{ij}{r}_i}$$

In the current simulation, these weights only take values of 0 (no connection), 1 (excitation) or -1 (inhibition) with optional added Gaussian noise ${ϵ}_w\sim 𝒩\left(0,{\sigma }_w^2\right).$ In the case of added noise, the sign of weights is preserved by clipping any values that fall outside this range, i.e. excitatory connections cannot become inhibitory and vice versa. Rather than tuning the weights, we tune the sigmoid function parameters for each neuron type to balance the number and scale of the inputs to each layer (see Figure S5A). Tuning was carried out visually, by attempting to ensure that each layer would cover a full range of firing rates during a batch of typical runs. Due to the robust nature of this network, many combinations of parameters work and there was no need to carry out extensive parameter tuning, e.g. through a grid search.

The model consists of six layers of neurons, some of which have additional properties to those above (described in more detail below): the TN and TL (input) layers receive direct sensory input from the agent; the TB1 (compass) layer has self-connection weights with values that can fall between -1 and 0; the CPU4 (proposed memory) layer has additional synaptic accumulation; and the CPU1 (output) layer connects to the agent's motor system. In the following description of the individual layers of our model, we use θ for allocentric and φ for egocentric angles. A superscript in parentheses is used to represent values at a particular time step, and subscripts are used to differentiate parameters by layer and cell index.

Speed Layer 1 – TN-neurons: In our simulation the speed estimate, in terms of forward-to-backward optic flow originating from the diagonally offset preference angles of TN-cells on each hemisphere, is calculated by

$$\begin{array}{l}{I}_{{\text{TN}}_L}=\left[\mathit{\text{sin}}\left({\theta }_h+{\varphi }_{\text{TN}}\right)\mathit{\text{cos}}\left({\theta }_h+{\varphi }_{\text{TN}}\right)\right]\mathbf{\text{v}}\\ I_{{\text{TN}}_R}=\left[\mathit{\text{sin}}\left({\theta }_h-{\varphi }_{\text{TN}}\right)\mathit{\text{cos}}\left({\theta }_h-{\varphi }_{\text{TN}}\right)\right]\mathbf{\text{v}}\end{array}$$

where v is the velocity of the agent in Cartesian coordinates, θ_h ∈ [0, 2π) is the current heading of the agent and φ_TN is the preference angle of a TN-neuron, i.e. the point of expansion of optic flow that evokes the biggest response. For our model, a default preference angle of ${\varphi }_{\text{TN}}=\frac{\pi }{4}$ was used. TN2-neurons act as a rectified linear function, meaning they respond in a positive linearly proportional manner to I_TN, but have no response to negative flow (backwards motion) (Figure S5A).

$$r_{\text{TN2}}=\max \left(0,2I_{\text{TN}}-1\right)$$

Optional Gaussian noise ε_r can be added to the output, after which activity is clipped to fall between 0 and 1, as above.

Heading Layer 1 – TL-neurons: The first direction-related layer consists of 16 inhibitory TL-neurons, which have been shown to be polarization sensitive across a range of insect species [13,21,23] and to encode visual landmarks used to compute heading direction in flies (ring neurons [11]). Each TL neuron has a preferred direction θ_TL, with the 16 neurons representing 8 cardinal directions θ_TL ∈ {0, π/4, π/2, 3π/4, π, 5π/4 3π/2 7π/4} twice over. Collectively they encode the heading of the agent at every time step, by each receiving input activation corresponding to the cosine of the angular difference between the current and their preferred heading:

$$I_{\text{TL}}=\text{cos}\left({\theta }_{\text{TL}}-{\theta }_{\text{h}}\right)$$

Heading Layer 2 - CL1-neurons: The 16 CL1-neurons have a response as described in [72], i.e., they are inhibited by TL-neuron activity, effectively inverting the polarization response. This is included for completeness but makes no functional difference in our current model.

Heading Layer 3 – TB1-neurons: The 8 TB1-neurons receive excitatory input from each pair of CL1-neurons that share same directional preference, θ_TB1. The TB1-layer also contains mutually inhibitory connections (Figure S5B), with a weighting that reflects stronger inhibition for greater difference in their preferred directions [6,7,11]:

$$w_{ij}=\frac{\text{cos}\left({\theta }_{\text{TB1},i}-{\theta }_{\text{TB1},j}\right)-1}{2}$$

Where θ_TB1,i and θ_TB1,j are the preferred directions of their respective CL1 inputs. The total input for each TB1 neuron is:

$$I_{{\text{TB}}_{1,j}}^{\left(\text{t}\right)}=\left(1-c\right)r_{{\text{CL}}_{1,j}}^{\left(\text{t}\right)}+c{\displaystyle \sum _{i=1}^8{W}_{ij}{r}_{{\text{TB}}_{1,i}}^{\left(t-1\right)}}$$

where c = 0.33 is a scaling factor for the relative effect of lateral TB1 inhibition compared to the direct CL1 excitation. This layer thus acts as a ring attractor [41], which creates a stable sinusoidal encoding of the heading direction, reducing noise from the previous layers, and forming the underpinning for the accurate memory and steering functions in subsequent layers.

Layer 4 - CPU4-neurons: The CPU4-layer consists of 16 neurons. The input for these neurons is an accumulation of heading θ_h^(t) of the agent represented by the sinusoidal TB1-response, modulating the speed signal from the TN2-neurons in the noduli, as reported in the current paper. In addition, there is a constant memory decay to all CPU4-cells:

$$I_{\text{CPU}4}^{\left(t\right)}=I_{\text{CPU}4}^{\left(t-1\right)}+h\left(r_{\text{TN}2}^{\left(t\right)}-r_{\text{TB}1}^{\left(t\right)}-k\right)$$

where h = 0.0025 determines the rate of memory accumulation and k = 0.1 the uniform rate of memory loss. All memory cells are initialized with a charge of I⁽⁰⁾ = 0.5 and as they accumulate are clipped on each time step to fall between 0 and 1. The eight TB1-neurons each provide input to two CPU4-neurons, each of which also receives input from a single TN2-cell, from the opposite hemisphere. As these neurons integrate the velocity (speed and direction) of the agent, activity across this layer at any point in time provides a population encoding of the home vector.

Layer 5 - Pontine neurons: 16 pontine neurons project contralaterally and connect two CBU columns eight columns apart from one another [30,33,35,45] (see Figures S4E,F; S5B). Each cell receives input from one CPU4-column:

$$I_{\text{Pontin}}^{\left(t\right)}=r_{\text{CPU}4}^{\left(t\right)}$$

Layer 6 - CPU1-neurons: The CPU1-layer has 16 neurons. It consists of two subtypes of neurons, CPU1a and CPU1b that exhibit distinct projection patterns between the PB and the CBU and are conserved across insect species [30,31,33]. Each TB1-neuron provides inhibitory inputs (weight = -1) to two CPU1-neurons, in the same pattern as TB1-CPU4 connections. Additionally, each CPU4-neuron provides input to a CPU1-neuron, but with the offset connectivity pattern shown in Figure 5, which produces the connectivity matrix shown in Figure S5B. As TB1-input is inhibitory and CPU4-input excitatory, the effective input to CPU1-cells is the difference of the activity in these units, representing the difference between the integrated path and the current heading direction. Finally, CPU1-cells also receive inhibitory input from contralateral pontine neurons so their total input is:

$$I_{\text{CPU}1}^{\left(t\right)}=r_{\text{CPU}4}^{\left(t\right)}-r_{\text{Pontin}}^{\left(t\right)}-r_{\text{TB}1}^{\left(t\right)}$$

The CPU1-neurons form two sets, connecting to either the right or left motor units (postulated to be located in the lateral accessory lobes, the anatomical convergence site of CPU1-neurons). The activation of each set is summed, and the difference determines the turning direction and angle of the agent. Currently this is done by multiplying the difference in summed activity by a constant m = 0.5, which is used to change the heading of the agent by that number of radians:

$${\theta }_h^{\left(t\right)}={\theta }_h^{\left(t-1\right)}+m\left({\displaystyle \sum _{i=1}^8{r}_{\text{CPU1R},i}}-{\displaystyle \sum _{i=1}^8{r}_{\text{CPU1L},i}}\right)$$

All connection weight matrices and other model parameters can be seen in Figure S5. In our model, the unit of distance is arbitrary, so we describe everything here in terms of steps in x and y and time steps t, which provides a meaningful measure of accuracy on a homing task by examining the tortuosity of a homing route, the angular errors, and errors relative to the distance of the outbound path. Outbound routes were generated by a filtered noise process, approximating a second order stochastic differential equation (SDE):

$$\begin{array}{l}{\omega }^{\left(t\right)}=\lambda {\omega }^{\left(t-1\right)}+{ϵ}_{\omega }\\ {\theta }_{\text{h}}^{\left(t\right)}={\theta }_{\text{h}}^{\left(t-1\right)}+{\omega }^{\left(t\right)}\end{array}$$

where for each time step the change in angular velocity ε_ω was generated by drawing from a von Mises distribution with zero mean:

$${ϵ}_{\omega }\sim \mathit{\text{VonMises}}\left(\mu =0,\kappa \right)$$

where μ measures the location and κ is the concentration. For our simulations κ = 100, with smaller values increasing the tortuosity of the outbound route. We used λ = 0.4, to minimize excessive spiraling motion. Acceleration for outbound routes is generated by drawing $\frac{T}{50}$ evenly spaced values from a uniform distribution:

$$a\sim U\left(a_{\text{min}},a_{\text{max}}\right)$$

and setting the acceleration between those points using third order spline interpolation, causing the agent to speed up and slow down in a smooth manner, thus imitating natural flight behavior. Velocity of the agent is determined at each time step by a linear drag model:

$${\mathbf{\text{v}}}^{\left(t\right)}={\mathbf{\text{v}}}^{\left(t-1\right)}+\left[\begin{array}{l}\begin{array}{l}\text{sin}\left({\theta }_{\text{h}}^{\left(t\right)}\right)\hfill \\ \text{cos}\left({\theta }_{\text{h}}^{\left(t\right)}\right)\hfill \end{array}\hfill \end{array}\right]\cdot a^{\left(t\right)}\left(1-F_D\right)$$

where F_D=0.15 is the default drag. For regular trials a_min = 0 and a_max = 0.15 were tuned to cause v to mostly fall below 0 and 1, allowing the TN cells to capture all speeds without their activity saturating, whereas for inbound paths a constant a = 0.1 was used. The agent’s starting position on each simulation is x⁽⁰⁾ = 0, y⁽⁰⁾ = 0. These are updated iteratively depending on the velocity.

$$\begin{array}{l}{x}^{\left(t\right)}=x^{\left(t-1\right)}+v_0^{\left(t\right)}\\ y^{\left(t\right)}=y^{\left(t-1\right)}+v_1^{\left(t\right)}\end{array}$$

Detailed model assumptions

Beyond the experimental data, two fundamental assumptions underlie the model: 1) Input and output regions of CX-cell types (cell polarity) can be reliably inferred from morphologically distinct fiber terminals (smooth versus blebbed). 2) Overlapping fibers with opposite polarity are synaptically connected. Combined, this generates systematic connections between all major CX cell-types that are dictated directly by their interhemispheric projection patterns. Each of those connections is detailed below together with the evidence that directly supports these connections. Assumptions strongly supported by evidence are marked with ***, assumptions with weaker support are marked with **, while assumptions with little support (i.e. predictions) are marked with *.

***Connectivity – assumption 1: TB1-neurons form a ring attractor network by mutually inhibitory connections onto one another, whose synaptic weights increase with distance of each TB-neuron pair. Evidence: TB1-cells have no input fibers in PB-columns that neighbor their output fibers, i.e. neighboring TB1-cells cannot connect to one another. Second, density of input fibers is highest in columns most distant from output fibers. Third, in locusts, responses of CPU1-cells (likely postsynaptic to TB1) are maximally out of phase with TB1-cells, indicating that TB1-cells are likely inhibitory. Also, locust TB1-cells contain the neuropeptide Allatostatin [7], that has been shown to possess inhibitory receptors.

***Connectivity – assumption 2: TB1-cells synapse onto CPU1 and CPU4-cells in regions of overlapping arborizations. Evidence: Both TB1- and CPU1-cells contribute to the mapping of polarized light tunings in locusts, with CPU1-cells out of phase from TB1-cell output columns [7]. Additionally, anatomical polarities of CPU1- and TB1-cells are very pronounced and CPU1-cells additionally show clear postsynaptic potentials when recorded from the PB [73]. Moreover, the TB1-output fibers are the most prominent columnar output arborizations of the PB conserved across insects [7,20,31–33]. This leaves these cells as the most likely presynaptic cells to all columnar cells with input in the PB, including CPU4-cells. In locusts, CPU4-cells are conditionally polarization sensitive, with the PB being the most likely source of this information [19]. The only other cell type with major outputs in the PB (likely presynaptic to TB1) are CL1a-neurons [19,20,30,33]. While a network involving CL1a to CPU1 and CPU4 connections with similar overall properties is thinkable, it would be more complex and require more subsequent assumptions

**Connectivity – assumption 3: CPU4-cells synapse onto CPU1-cells in a way that is reflected in their arborization patterns. Evidence: In the CBU the polarity of CPU1-cells is postsynaptic, while CPU4 anatomy clearly indicates presynaptic terminals [30–33]. Polarity predicted by anatomical means (clear varicose versus smooth terminals) in locust and monarch butterfly CX has proven correct across species in all cases by mapping of presynaptic marker proteins in Drosophila (compare e.g. [30] and [32]). This makes the CPU1-cells (together with the highly similar CPU2 cells) the only potential target cells for CPU4-outputs that exist across all species. The only cell type that is equally likely to receive input from the CPU4-cells are pontine cells, which provide direct connections between ipsi- and contralateral columns within the CBU [30,33–35,45]. As these cells likely also target the CPU1-neurons, there is either a direct connection between CPU4- and CPU1-cells, an indirect connection between them, or a combination. In fact, our model becomes most robust, if both of these connections are used, which also represents the most parsimonious interpretation of the anatomical data: All overlapping arborizations with the correct polarity are equally likely to correspond to synaptic connections.

*Memory – assumption 1: CPU4-columns have a mechanism to integrate activity, and thus motion. Evidence: Neuronal terminals of Megalopta CPU4-cells in the PB and the noduli appear of mixed type, indicating both input and output. In the noduli, our EM-work in bumblebees shows that arborization patterns of CPU4-cells are highly overlapping, in particular between the 19 cells from the same fiber bundle (corresponding to one PB-column), generating a sufficiently large population of cells for memory formation and the spatial proximity needed for column-intrinsic circuits. Furthermore, synaptic connections exist between small EM-profiles within the noduli, most likely corresponding to CPU4-cells, while individual CPU4-cells contain both input and output synapses in the noduli. Finally, preliminary recordings in Megalopta have shown responses to translational optic flow in CPU4-cells (data not shown), while in locusts these cells show context dependent responses to compass stimuli [19].

*Memory – assumption 2: Pontine cells of the CX use inhibition to balance the memory in the CPU4 populations, causing the overall activity on the right brain hemisphere and the left brain hemisphere to remain the same. Evidence: Pontine cells are highly conserved and are found across all species examined [34,35,45–47]. They have a pattern of midline crossing connectivity uniquely suited to bridge output regions of CPU4-cells and contralateral input regions of CPU1-cells. These cells have been shown to contain neuromodulators in locusts (CCAP (crustacean cardioactive peptide) [47] and nitric oxide [45,46]) and thus could act through inhibitory metabotropic receptors. Finally, preliminary intracellular recordings from Megalopta pontine cells have revealed pronounced, yet non-stereotypical responses to translational optic flow (data not shown).

**Steering – assumption 1: Activity is summed for CPU1 on each hemisphere to drive steering. Evidence: Anatomically, CPU1-neurons converge in highly overlapping regions of the LAL in all species examined [30–33]. Furthermore, in Monarch butterflies and locusts, neurons potentially postsynaptic to CPU1-cells occupy identical regions of the LAL and connect to posterior regions of the brain that provide input to descending pathways [10,19]. Additionally, polarized-light tuning has been found in locust neurons interconnecting the LALs of the right and left brain hemisphere [19]. Highly similar cells are involved in generating steering in response to pheromone pulses in the moth Bombyx mori [36,37].

*Steering – assumption 2: CPU4-cells have no influence on steering when the animal is not in a homing state. Evidence: The decoupling of memory and steering is necessary during behavioral episodes where memory does not drive behavior. This occurs either at the output or input of CPU1-neurons, thus disabling memory to either reach CPU1-cells or the motor circuit of the LAL. Even though there is no direct evidence for this strong state-dependent switch in active synaptic transmission, there is strong evidence for state-dependent change in neural signaling in the CX in general [19,64], combined with a rich variety of neuromodulator expression in this region [65,66].

Probing the limits of the path integration circuit

To explore the effects of altering different model parameters on the path integration performance, a set of values were chosen for each parameter and N=2000 homing tasks were completed for each value: 1000 trials at default neural activity noise variance σ_r²=0.1 and 1000 at no noise. Small changes to weight matrices between cells were tested by modifying σ_w² ∈ {0, 0.01, 0.02, 0.05, 0.1, 0.2}. Perturbations to the angular offset of the speed neurons were made by changing the preference angle between 0 and $\frac{\pi }{2}$ so that ${\varphi }_{\text{TN}}=\frac{x\pi }{16}$ where x ∈ {0,…,8}. Experiments were carried out with a rotation-dependent offset to the preference angle of the compass input neurons (TL and CL). Peak activity would pre-empt the preference angle, similar to the tuning found in real recordings as shown in Figure 1G. A gradually increasing angle of perturbation was used:

$${\theta }_{{\text{CL}}_{\text{offset}}}={\theta }_{\text{CL}}+\mathrm{sgn}({\theta }_{\text{h}}^{(t)}-{\theta }_{\text{h}}^{(t-1)})\frac{x\pi }{32}$$

where x ∈ {0,…,8}. Finally, TN input was smoothed to mimic delayed responses seen in Figure 2D. An exponential moving average was used so that:

$$I_{{\text{TN}}_{\text{smooth}}}^{(t)}=n{I}_{\text{TN}}^{(t)}+(1-n)I_{{\text{TN}}_{\text{smooth}}}^{(t-1)}$$

where $n\in \left\{\frac{1}{1},\frac{1}{2},\frac{1}{5},\frac{1}{10},\frac{1}{20},\frac{1}{50}\right\}.$

Furthermore, to test the effects of saturated speed signals, we increased the speed of the agent, with the intention of saturating the activity of TN neurons. Acceleration was increased in 5 equal increments up to three times the amount in our default settings, which was initially set to provide a full range of neural activity.

Testing of the model in an agent simulation

Each trial was evaluated at five values of noise: σ_r² ∈ {0, 0.1, 0.2, 0.3, 0.4}. The effect of these noise levels on the sigmoid I/O functions for all neurons is illustrated in Figure S5A. As a control, attempting to find home using a random walk with similar parameters to the outbound route generation mechanism was also included. N=100 trials were run at twenty distances ranging between 10 and 10,000 steps. The trials distances were equally spaced on a logarithmic scale:

$$d_x={10}^{1+\frac{3x}{20}}$$

where x ∈ {0,1, …, 20}. In each trial a unique route was generated up to a turning point. For each route the agent was given the same number of return steps as the outbound steps. The closest distance (in steps) that the agent obtained from the nest during this length-limited return path was used to quantify the homing success (Figure 7A). Accuracy can also be evaluated by whether the agent was heading the right way towards the nest shortly after it began homing, a commonly used technique when conducting field experiments with homing insects [74]. Homing direction was determined by measuring the angle when the agent exited a perimeter with 20 step radius around the turning point. The homing angle and correct angle between the nest and the turning point was compared (Figure 7B). Location estimate was decoded directly from the built-up memory representation of CPU4-neurons (before the addition of output noise) by summing the two CPU4 subpopulations as shown in Figure S6. Finally, to show that the agent was moving towards the nest in a relatively straight manner we measured the tortuosity of the return route, using the formula:

$$\tau =\frac{L}{C}$$

where L is the straight distance to the nest, and C is the distance towards the nest that the agent has covered after L steps, i.e., C = L – d_L, where d_L is the distance of the agent from the nest after L steps (Figure 7C).

Testing of the model in a robotic implementation

We have implemented the CX model on a custom robot platform which combines a Dangu Rover 5 chassis with a motorboard, Arduino Mega 2560 and a Nexus 5 Android smart-phone. Visual input is obtained from the front camera of the phone with a 360° lens attachment, and preprocessed to produce a 10x90 pixel image capturing approximately ±20° elevation around the horizon.

Speed input is calculated using optic flow on the low-resolution greyscale image obtained from the phone. We apply the dense optic flow 'Farneback' algorithm using the OpenCV calcOpticFlowFarneback function, which produces a motion vector for every pixel. We create two filters for the preferred optic flow for each pixel column, corresponding to the preferences observed in the data for left and right TN-neurons, i.e., the horizontal flow expected from translation in the direction ± π/4 respectively. These filters are multiplied with the observed vector for each pixel and the sum taken over the whole image to obtain the speed. In testing, this speed measure is noisy and dependent on the distance of objects from the robot, but on average scales linearly with the speed of the robot and proved sufficient for path integration.

Compass information is taken from the phone's GAME_ROTATION_VECTOR which uses a combination of gyroscope and accelerometer to estimate the phone's yaw, pitch and roll. Mounted flat on the robot and operating on a flat floor, the yaw output provided a reliable heading direction with negligible drift or cumulative error over the run lengths used to test the system, although in future a compass sense with an absolute external reference would be needed to emulate the celestial compass used by bees.

The computational CX model described above was re-coded in Java to run on the phone, using the sensory inputs as described, but with no other modifications. A preprogrammed random path drives the robot on its outbound route, while the home vector accumulates in CPU4 memory neurons. To return home, the motor output (the difference in activity of left and right CPU1 steering neurons) is translated into action by veering left or right (setting wheel speeds in the ratio 1:10) if the respective activity difference exceeds a threshold, and otherwise driving straight.

Mathematical framework

An intuitive way to understand how our CX model achieves path integration is to think in terms of the addition of sinusoids at the fundamental frequency, i.e. with a period of 2π, similar to a theoretical solution to path integration proposed by [48]. Due to the lateral inhibition of the TB1 (compass) cells, the activity bump across these neurons in the protocerebral bridge is roughly sinusoidal and can be used to encode an allocentric heading. We propose that the amplitude of this activity bump is scaled in a speed dependent manner by TN (speed) neurons and is repeatedly added at the CPU4 (memory) neurons where these two signals converge. A theoretical outline of why this works is given below, before elaborating on how this fits in with the architecture of the CX.

Any point in R2 (standard vector space of real numbers in two dimensions) can be expressed as a sinusoid representing polar coordinates, where the amplitude captures the radial coordinate and the phase shift captures the angular coordinate. A population of cells using a sinusoid to encode a location could be described as:

$$A\cos (\theta +\alpha )$$

where A represents the distance travelled, α represents the heading and each cell has its own preference angle θ. A property of this representation is that any linear combination of two sinusoids with the same period results in another sinusoid with same period, but different amplitude and phase shift:

$$\begin{array}{l}A\cos (\theta +\alpha )+B\cos (\theta +\beta )=A[\cos (\theta )\cos (\alpha )-\sin (\theta )\sin (\alpha )]+B[\cos (\theta )\cos (\beta )-\sin (\theta )\sin (\beta )]\\ =\underset{x}{\underbrace{[A\cos (\alpha )+B\cos (\beta )]}}\cos (\theta )-\underset{y}{\underbrace{[A\sin (\alpha )+B\sin (\beta )]}}\sin (\theta )\\ =x\cos (\theta )-y\sin (\theta )\end{array}$$

For any x,y ∈ R we can write x = R cos(ψ) and y = R sin(ψ) with ψ ∈ [0, 2π) and R>0.

$$\begin{array}{l}A\text{cos}(\theta +\alpha )+B\text{cos}(\theta +\beta )=R[\cos (\psi )\cos (\theta )-\sin (\psi )\sin (\theta )]\\ =R\cos (\theta +\psi )\end{array}$$

To find R and ψ we can use the Pythagorean identity:

$$\begin{array}{l}{R}^2=R^2{\text{cos}}^2\left(\varphi \right)+R^2{\text{sin}}^2\left(\varphi \right)\\ ={\left[A\text{cos}\left(\alpha \right)+B\text{cos}\left(\beta \right)\right]}^2+{\left[A\text{sin}\left(\alpha \right)+B\text{sin}\left(\beta \right)\right]}^2\\ R=\sqrt{{\left[A\text{cos}\left(\alpha \right)+B\text{cos}\left(\beta \right)\right]}^2+{\left[A\text{sin}\left(\alpha \right)+B\text{sin}\left(\beta \right)\right]}^2}\\ \psi =\text{atan}2\left(R\text{sin}\left(\psi \right),R\text{cos}\left(\psi \right)\right)\\ =\text{atan}2\left(A\text{sin}\left(\alpha \right)+B\text{sin}\left(\beta \right),A\text{cos}\left(\alpha \right)+B\text{cos}\left(\beta \right)\right)\end{array}$$

$$\begin{array}{l}A\text{cos}\left(\theta +\alpha \right)+B\text{cos}\left(\theta +\beta \right)=\sqrt{{\left[A\text{cos}\left(\alpha \right)+B\text{cos}\left(\beta \right)\right]}^2+{\left[A\text{sin}\left(\alpha \right)+B\text{sin}\left(\beta \right)\right]}^2}\\ \cdot \text{cos}\left(\theta +\text{atan}2\left[A\text{sin}\left(\alpha \right)+B\text{sin}\left(\beta \right),A\text{cos}\left(\alpha \right)+B\text{cos}\left(\beta \right)\right]\right)\end{array}$$

After summing two sinusoids representing consecutive movement vectors the resulting amplitude and phase shift correspond to a sinusoid matching a vector that is the sum of both (Figure S6C). Therefore, by summing the corresponding activity of both cell groups we retain a population code that remains accurately pointing to the new location.

These properties prove to be useful in several ways for the CX. A single sinusoid (TB1) is repeatedly subtracted (due to inhibition) to form a consistent memory representing a home vector (CPU4). Different speeds can also be captured by modulating the amplitude of the sinusoid (TN).

Motion on a plane can be tracked by measuring the velocity component (speed) along vectors at two offset angles (θh ± φTN), forming a basis. In general, the motion may be holonomic, that is the head direction (origin of egocentric coordinate system) and direction of motion may not be aligned. The two velocity components are stored in two separate memories, the two duplicate populations of CPU4, and could be summed and decoded by re-aligning the sinusoids correctly. In our case, we propose the modulation of the sinusoid happens by inhibition, meaning that the shape of the compass (TB) cannot be inverted (multiplied by a negative constant). Because of this only partial holonomic motion can be accurately integrated, with a direction of motion between ${\varphi }_{\text{TN}}-\frac{\pi }{4}$ and ${\varphi }_{\text{TN}}+\frac{\pi }{4}$ as defined in the Methods section when describing the Speed Layer 1. Another way to think about this circuit is as a re-projection from an egocentric basis defined with respect to the heading angle at θh±φTN to an allocentric one defined with respect to the angle of the sun at θTB1±φTN, where all CPU4 cells with input from the same TB1 cell store motion projected on to their basis vector, at $\frac{\pi }{4}$ intervals (8 columns) creating a redundant memory.

By element-wise multiplying two discrete sinusoids and summing the output, you can determine how much their phase is aligned. The offset between current heading (TB1) and desired heading (CPU4) is estimated through inhibition of the CPU4 activity from connecting TB1 cells.

As the animal rotates, the TB1 sinusoid is shifted with respect to the memory. A low response indicates high overlap as all highly active cells are suppressed by the TB1 inhibition, meaning current and desired heading are similar. However, due to the CPU4-TB1-CPU1 connectivity pattern, when comparing CPU4 to the TB1 signal, the two populations that make up the composite memory are each shifted by one column, increasing the existing offset of both memories caused by the TN cell preferences to approximately $\pm \frac{\pi }{2}$. Therefore, a strong alignment with one CPU4 sub-population means the desired heading is approximately $\frac{\pi }{2}$ to the left, and with the other $\frac{\pi }{2}$ to the right. These two values are combined to drive steering as can be seen in Figure S6D-F. In the case of ${\varphi }_{\text{TN}}=\frac{\pi }{4}$ we can prove that the circuit steers correctly. The compound memory can be expressed as a function f(θ), the sum of two memory sinusoids in the same coordinate space (Figure S6E), where the peak indicates the desired heading:

$$f\left(\theta \right)=A\text{cos}\left(\theta +\alpha \right)+B\text{cos}\left(\theta +\beta \right)$$

To find the stationary points which implicitly defines the θ corresponding to the desired heading:

$$\begin{array}{l}{f}^{\prime }\left(\theta \right)=-A\text{sin}\left(\theta +\alpha \right)-B\text{sin}\left(\theta +\beta \right)=0\\ -A\text{sin}\left(\theta +\alpha \right)=B\text{sin}\left(\theta +\beta \right)\\ A\text{cos}\left(\theta +\alpha +\frac{\pi }{2}\right)=B\text{cos}\left(\theta +\beta -\frac{\pi }{2}\right)\\ \text{or}\\ A\text{cos}\left(\theta +\alpha -\frac{\pi }{2}\right)=B\text{cos}\left(\theta +\beta +\frac{\pi }{2}\right)\end{array}$$

The correct heading is found when both sinusoids are offset by ± π/2 and are equal. This is the case due to the combined ${\varphi }_{\text{TN}}=\frac{\pi }{4}$ and the additional π/4 columnar offset. However, the circuit still operates robustly with different φTN values (See results below). At a cellular scale, the steering mechanism can also be understood by observing the activity of a single TB1 compass cell, the corresponding pairs of CPU1 steering cells, and both CPU4 memory cells that connect to them, (Figure S6B). When TB1i= θh-π , it is most inactive, so the CPU4 synapsing on to the corresponding CPU1 will be least suppressed. As the two CPU4 are ±π/2 offset from the TB1 cell, the memory cells that capture the portion of the home vector pointing in θh±π/2 will be weighted the most when steering. If the CPU4 with a preference angle of θh-π/2 is higher than that of the with preference θh+π/2, the agent will turn to the left to head home and vice versa. The pontine cells projecting from CPU4 to CPU1 act as an inhibitory stabilizer. In effect this normalizes both memory sinusoids, ensuring they have the same mean activity, meaning one will not dominate due to unbalanced charging by different TN neurons.

A useful side-effect of this representation is that it becomes trivial to extract a polar coordinate from the population code, e.g. for a waggle dance, by finding the cells with peak activity, while retaining many of the attractive properties of a Cartesian coordinate system [75]. For species that migrate or just want to move in a fixed direction for a while, a permanent or semi-permanent bump in the CPU4 cells would cause them to move consistently in that direction. If retrieving previously visited locations and putting them to CPU4 memory is possible, then this could be done as either a homebound or outward vector, depending on whether the stored memory is added or subtracted from a zero-state memory. In addition, a sequence of known paths that link together known landmarks could be sequentially added to memory, resulting in a total home vector, similarly to the addition during normal path integration, meaning the animal could perform shortcuts over previously unvisited terrain. The state of the home vector upon return to the nest could potentially also be used as an error signal. By inhibiting a stored vector with the remaining home vector, both the outbound and inbound PI estimates could be combined in a weighted manner to provide a more accurate waggle dance.

A fully holonomic path integrator

The described model can successfully capture holonomic movements in a range of ± π/2 deviation of body axis and movement direction. This is in line with the observation that honey bees maintain a steady head direction aligned with their average flight direction during behavioral experiments. However, bees also perform hovering flights when close to food sources as well as orientation flights when leaving the nest. During those flight segments, no significant distances are covered. Even though these flight segments are not perfectly captured, our model performs with only minor errors when including them in the outbound trajectory. Nevertheless, given that bees perform fully holonomic flight maneuvers, we deemed it desirable to explore the possibility of expanding our model to enable integration of those flight segments. In fact, only a single additional assumption must be made to transform our partial holonomic model into a fully holonomic model, without contradicting anatomical and physiological data. To achieve this, the TB1 activity bump, indicating compass direction, must be able to affect CPU4 memory in either an additive or subtractive manner (in the current model it is purely additive) using the input of all four TN neurons identified in this study (i.e. speed neurons and inverted speed neurons; Figures 2,3). This could be done by the activation from TB1 cells effectively acting as a gating mechanism to either positive or negative effects on the memory from opposing TN cells. The implemented results are shown in Figure S7.

Quantification and Statistical Analysis

Action potentials were extracted from the recorded voltage traces using threshold based event detection in MATLAB. Only recordings with stable baseline were evaluated. Timing of events was then correlated to the recorded stimulus traces by custom designed analysis scripts.

For all presented neuron types, numbers of recorded cells can be found in the results section as well as in the figure legends. Within each cell type the number of cells always equals the number of bees used.

For optic-flow stimuli each stimulus bout was analyzed independently. Spikes were counted in bins of 0.25 s during stimulation intervals and the resulting mean frequencies were plotted for display of individual stimulus responses. To calculate tuning curves, the last 2 s of each stimulus interval was used to compute the mean response frequency for the analyzed condition and plotted against either stimulus velocity or spatial frequency. Background activity of a neuron was calculated as the mean activity during 2 s before onset of the first stimulus. For averaging tuning curves, we normalized each individual tuning curve to its maximal value and then calculated the mean and standard deviation of each stimulus condition across all recorded neurons of the same type. Mean normalized background activity was calculated accordingly.

Receptive field mapping was analyzed by finding the number of events during each frame of the display of the moving bar (192 frames per rotations; 6 s per rotation) and averaging the resulting frequencies over three neighboring frames (resulting bin duration: ca. 0.1 s). The mean across the two stimulations with identical movement direction was calculated for each bin and the result was low pass filtered (window-size: 3 bins) to display receptive field responses of individual cells. Filtered data were normalized to peak frequency and averaged across neurons of the same type. Directional preference was calculated for each azimuth bin by vector addition of clockwise and counter-clockwise response strength. The resulting vector was displayed as an arrow, whose length and direction correspond to the local tuning preference. Mean and individual receptive fields were displayed either as vector maps of local tuning preferences projected onto a 32x192 matrix (dimension of LED arena) or as line plots (mean ±SD).

Translational optic flow with different expansion points was analyzed as for tuning curve analysis of other optic flow stimuli. The resulting mean frequencies during each stimulation interval were then displayed in a circular plot against the azimuth of expansion of the optic flow. The maximally effective stimulus was calculated by converting the mean spike frequencies of each response to a distribution of azimuth angles (spike frequency = frequency of corresponding azimuth angle in the distribution). The circular mean of this distribution was calculated with the circular statistics package for MATLAB [67].

Polarized-light stimuli were analyzed by assigning angles (position of the polarizer) to each spike-event. This list of angles was used to display data in circular plots (bin size 10°, converted from spike count to frequency by dividing by bin duration) and to perform statistical analysis in MATLAB. A cell was rated polarization sensitive if the distribution of action potentials during a rotation of the polarizer was significantly different from a uniform distribution (Rayleigh test for axial data; alpha level 0.05). Clockwise and counter-clockwise rotations of the polarizer were analyzed separately. Tuning curves were calculated by normalizing each response to its peak firing rate, adjusting the minimum firing rate during stimulation to zero, and shifting the curve, so that peak activity coincided with 0° E-vector angle. The width of the tuning curve at half-maximal excitation was taken as the tuning width.

Data and Software Availability

All code used for the described simulation is available at https://github.com/InsectRobotics/path-integration. For most cell types, 3D neuronal anatomies based on confocal microscopy can be found in the InsectBrainDatabase (www.insectbraindb.org). The neurons have been deposited in the InsectBrainDatabase under the following neuron identification numbers (NINs): NIN-0000061 (TN1-cells left; https://www.insectbraindb.org/neurons/61/), NIN-0000062 (TN1-cells right; https://www.insectbraindb.org/neurons/62/), NIN-0000121 (TN2-cells, left; https://www.insectbraindb.org/neurons/121/), NIN-0000222 (TN2-cells, right; https://www.insectbraindb.org/neurons/222/), NIN-0000100 (TL-cells left; https://www.insectbraindb.org/neurons/100/), NIN-0000221(CPU4-cell; https://www.insectbraindb.org/neurons/221/), NIN-0000198 and NIN-0000200 (Pontine cell-types: https://www.insectbraindb.org/neurons/198/; https://www.insectbraindb.org/neurons/200/).

Supplementary Material

Movie S1. TN-cell morphology; related to Figure 2.

3D reconstruction of TN1 (blue) and TN2 (orange) cells shown with and without neuropils (grey) of the Megalopta reference brain.

Movie S2. Model animation; related to Figure 5.

Top left: Top-down view of the agent in a simulated environment. Purple: Foraging with randomly varying acceleration and heading. Green: The agent homes towards the nest and begins a systematic search. Right: Corresponding activity in the neural circuit (top: arranged by a force directed graph; bottom: layered arrangement resembling anatomy more closely). Green: TB1-cells (compass). Orange: CPU4-columns (memory). Brown: TN-cells (speed). Blue: CPU1-cells (steering). The summed CPU1 activity drives left and right steering during homing. Bottom left: Simulated Calcium imaging experiment for CL1, TB1, CPU4 and CPU1 populations.

Movie S3. Robot implementation of the bee CX path integration circuit; related to Figure 6.

A wheeled robotic platform was equipped with the circuit derived from the bee CX and successfully performed homing behavior.