Global Assessment of the SMAP Level-4 Surface and Root-Zone Soil Moisture Product Using Assimilation Diagnostics

Abstract

The Soil Moisture Active Passive (SMAP) mission Level-4 Soil Moisture (L4_SM) product provides 3-hourly, 9-km resolution, global estimates of surface (0-5 cm) and root-zone (0-100 cm) soil moisture and related land surface variables from 31 March 2015 to present with ~2.5day latency. The ensemble-based L4_SM algorithm assimilates SMAP brightness temperature (Tb) observations into the Catchment land surface model. This study describes the spatially distributed L4_SM analysis and assesses the observation-minus-forecast (O-F) Tb residuals and the soil moisture and temperature analysis increments. Owing to the climatological rescaling of the Tb observations prior to assimilation, the analysis is essentially unbiased, with global mean values of ~0.37 K for the O-F Tb residuals and practically zero for the soil moisture and temperature increments. There are, however, modest regional (absolute) biases in the O-F residuals (under ~3 K), the soil moisture increments (under ~0.01 m³ m⁻³), and the surface soil temperature increments (under ~1 K). Typical instantaneous values are ~6 K for O-F residuals, ~0.01 (~0.003) m³ m⁻³ for surface (root-zone) soil moisture increments, and ~0.6 K for surface soil temperature increments. The O-F diagnostics indicate that the actual errors in the system are overestimated in deserts and densely vegetated regions and underestimated in agricultural regions and transition zones between dry and wet climates. The O-F auto-correlations suggest that the SMAP observations are used efficiently in western North America, the Sahel, and Australia, but not in many forested regions and the high northern latitudes. A case study in Australia demonstrates that assimilating SMAP observations successfully corrects short-term errors in the L4_SM rainfall forcing.

1. Introduction

Soil moisture plays an important role in the water, energy and carbon cycles (e.g., Seneviratne et al. 2010) and is considered an essential climate variable by the World Meteorological Organization (WMO 2006). The radiometer instrument onboard the NASA Soil Moisture Active Passive (SMAP) satellite mission (Entekhabi et al. 2010; Piepmeier et al. 2017) observes the Lband (1.4 GHz) microwave radiation emitted from the Earth’s surface. Over land, the observed radiances (or brightness temperatures; or Tbs) are sensitive to the moisture in the top few centimeters of the soil, provided the overlying vegetation is not too dense (Jackson and Schmugge 1991; Entekhabi et al. 2014). This sensitivity is exploited in the SMAP Level-4 Soil Moisture (L4_SM) algorithm to obtain estimates of surface (0-5 cm) and root-zone (0-100 cm) soil moisture (Reichle et al. 2014b, 2017b). Specifically, the ensemble-based L4_SM algorithm assimilates the SMAP Tb observations into the NASA Catchment land surface model (Koster et al. 2000), and the resulting L4_SM product consists of 3-hourly, 9-km resolution, global estimates of soil moisture and related land surface variables with complete coverage. These estimates are available from 31 March 2015 to present with a mean latency of ~2.5 days from the time of the SMAP observations.

Reichle et al. (2017b) validated the L4_SM soil moisture estimates against in situ measurements from SMAP core validation sites, which provide spatially averaged soil moisture measurements (at the grid-cell scale of the model and of the satellite estimates) for about a dozen distinct watersheds. They determined that the unbiased RMSE (ubRMSE, or standard deviation of the error) for L4_SM surface (root-zone) soil moisture estimates is 0.038 m³ m⁻³ (0.030 m³ m⁻³) at the 9-km scale and 0.035 m³ m⁻³ (0.026 m³ m⁻³) at the 36-km scale. The L4_SM product thus meets its soil moisture accuracy requirement, which was specified prior to launch as an ubRMSE of 0.04 m³ m⁻³ or better (excluding regions of snow and ice, frozen ground, mountainous topography, open water, urban areas, and vegetation with water content greater than 5 kg m⁻²). Moreover, the L4_SM estimates improve (significantly at the 5% level for surface soil moisture) over model-only estimates, which do not benefit from the assimilation of SMAP Tb observations and have a 9-km surface (root-zone) ubRMSE of 0.042 m³ m⁻³ (0.032 m³ m⁻³) (Reichle et al. 2017b). Furthermore, Reichle et al. (2017b) corroborated these results with other metrics, including time series correlations, and through validation against point-scale in situ measurements from ~400 sparse network sites, which represent a greater variety of climate and land cover conditions. Moreover, Crow et al. (2017) demonstrated for the south-central US that the assimilation-based L4_SM soil moisture estimates have significantly improved utility for forecasting the streamflow response to future rainfall events (relative to that of soil moisture retrievals from L-band and higher-frequency Tb observations).

Validation versus in situ measurements is an important step in the assessment of any data product that is based on satellite measurements and numerical modeling. For soil moisture, however, the available in situ measurements are limited to a relatively small number of locations (compared to the ~1.6 million land grid cells of the L4_SM product) and do not fully represent the tremendous variety of land cover, soil, and climate conditions encountered across the global land area. It is therefore important to supplement the in situ validation of the L4_SM product with additional assessments that provide a more global perspective. The key objective of the present paper is to offer this global evaluation perspective for the L4_SM product. This is accomplished by investigating a variety of this product’s data assimilation diagnostics, including statistics of the observation-minus-forecast (O-F) Tb residuals, the observation-minus-analysis (O-A) Tb residuals, and the analysis-minus-forecast soil moisture differences (or increments). These diagnostics provide important information about the internal consistency of the assimilation system and the impact of the assimilated observations (Gelb 1974). Perhaps most importantly, the assimilation diagnostics are available wherever and whenever SMAP observations are assimilated and therefore have a much greater coverage in space and time than in situ soil moisture measurements.

There is a long history of using assimilation diagnostics to assess the performance of atmospheric assimilation systems (Hollingsworth and Lönnberg 1989; Daley 1992; Desroziers et al. 2005; Todling 2013). Assimilation diagnostics have also been used extensively in land data assimilation. For example, O-F residuals were used to assess whether the assumed error characteristics are consistent with actual errors (e.g., Reichle et al. 2002a; De Lannoy and Reichle 2016a,b), construct adaptive filtering approaches (Crow and Reichle 2008; Reichle et al. 2008), tune the input error parameters (Crow and van den Berg 2010), and dynamically estimate and correct for bias (Draper et al. 2015). Furthermore, an investigation of the analysis increments demonstrated the progress made in revising the soil moisture analysis of the Integrated Forecasting System at the European Centre for Medium-Range Weather Forecasts (Drusch et al. 2009; de Rosnay et al. 2013).

This paper is organized as follows. Following a brief overview of the L4_SM system and data product (section 2a), we describe the ensemble-based data assimilation algorithm (section 2b) and assimilation diagnostics (section 2c). Thereafter, our results address the global climatology of the L4_SM soil moisture estimates (section 3a) and illustrate the L4_SM analysis with a case study in Australia (section 3b). Next, we investigate the observation counts (section 3c), the OF Tb residuals (section 3d), and the soil moisture and temperature increments (section 3e). A summary and conclusions are provided in section 4.

2. L4_SM Data Product and Algorithm

A short overview of the Version 2 L4_SM product and algorithm is provided in Reichle et al. (2017b). In this section, we briefly summarize the key aspects of the L4_SM modeling system and data product following their text. Thereafter, we provide a more detailed discussion than Reichle et al. (2017b) of the L4_SM analysis and assimilation diagnostics. This more detailed discussion is adapted from Reichle et al. (2014b) and De Lannoy and Reichle (2016a,b).

a. Overview

The L4_SM algorithm, shown schematically in Figure 1 of Reichle et al. (2017b), is a customized version of the ensemble-based land data assimilation component of the Goddard Earth Observing System, version 5 (GEOS-5), modeling and assimilation system. This component is built around the Catchment land surface model (hereinafter “Catchment model”; Koster et al. 2000; Ducharne et al. 2000). Besides the surface meteorological forcing data (see below), the key drivers of the L4_SM system are the 36-km resolution SMAP Level-1C Tb observations (Chan et al. 2016). The assimilated SMAP observations include horizontal-polarization (H-pol) and vertical-polarization (V-pol) Tbs from ascending and descending half-orbits (after first averaging over fore- and aft-looking Tbs). These observations are merged every three hours with the model estimates in a soil moisture and temperature analysis that uses a spatially distributed ensemble Kalman filter (EnKF; section 2b).

Fig. 1.

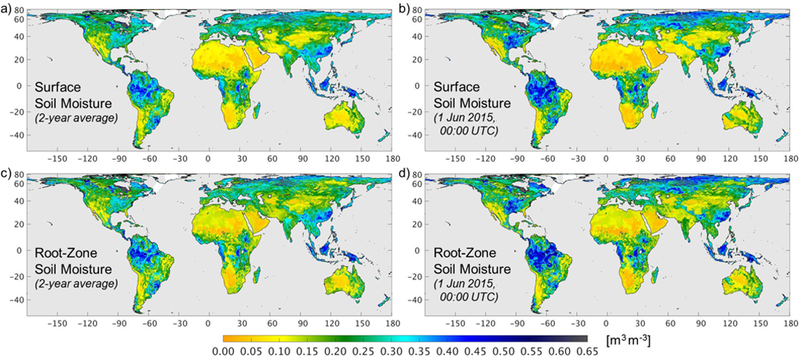
(a) Two-year average (April 2015 to March 2017) L4_SM surface soil moisture. (b) Snapshot of L4_SM surface soil moisture on 1 June 2015 at 00:00 UTC. (c) As in (a) but for root-zone soil moisture. (d) As in (b) but for root-zone soil moisture.

The Catchment model used in the L4_SM algorithm includes an explicit treatment of the spatial variation of soil water and water table depth within each 9-km grid cell based on the statistics of the watershed topography. Furthermore, the snow pack is simulated in a three-layer snow model component that tracks the evolution of the snow water equivalent, snow depth, and snow heat content (Stieglitz et al. 2001). The surface meteorological forcing data used in the L4_SM algorithm are from the GEOS-5 operational forward-processing (FP) system at 0.25°×0.3125° (latitude × longitude) resolution (Lucchesi 2013a). The GEOS-5 precipitation data are corrected using daily, gauge-based precipitation observations from the NOAA Climate Prediction Center Unified (CPCU) product (Reichle and Liu 2014; Reichle et al. 2017b). These precipitation corrections are applied globally except in Africa, where no corrections are applied, and in the high latitudes, where corrections are linearly tapered between 42.5° and 62.5° latitude (in both Hemispheres) and no corrections are applied poleward of 62.5° latitude. The Catchment model is supplemented with a zero-order “tau-omega” radiative transfer model (De Lannoy et al. 2013, 2014) that converts the Catchment model soil moisture and temperature estimates into estimates of L-band Tbs, which are required for the radiance-based L4_SM soil moisture analysis. See Reichle et al. (2017b) and references therein for details about the Catchment and radiative transfer model configuration, parameters, and forcing data.

The L4_SM data are generated and distributed on the global, cylindrical, 9-km Equal-Area Scalable Earth, version 2 (EASEv2), grid (Brodzik et al. 2012). The L4_SM outputs include soil moisture estimates for the “surface” (0-5 cm), “root-zone” (0-100 cm) and “profile” (0 cm to depth of bedrock) layers, along with a large number of related land surface variables, including surface (skin) temperature, soil temperature (in 6 layers down to ~13 m depth), snow mass, land surface fluxes, surface meteorological forcing data, assimilation diagnostics, land model parameters, and error estimates for soil moisture and surface temperature (Reichle et al. 2015a). The L4_SM surface (layer-1) soil temperature estimates are for the 0-10 cm layer except for tropical (broadleaf evergreen) forests, where the surface soil temperature is for the 5-15 cm layer. The layer thickness associated with the overlying land skin temperature is thus negligible except for tropical forests, where the L4_SM skin temperature represents the average temperature of the canopy and the 0-5 cm soil layer.

In this paper we use L4_SM Version 2 data (Science Version ID: Vv2030) for the 2-year period from April 2015 to March 2017. Specifically, we use 3-hourly, instantaneous “forecast” and “analysis” soil moisture and temperature fields along with the corresponding Tb observations, forecasts, analysis, and error estimates from the “analysis update” files (Reichle et al. 2016a). We further use surface soil moisture, root-zone soil moisture, snow mass and precipitation estimates from the 3-hourly time-average “geophysical” files (Reichle et al. 2016b). Note that the latter files also provide many other land surface fields. Finally, time-invariant land model parameters (including soil porosity and wilting point) are available in the “land-model-constants” file (Reichle et al. 2016c). See Reichle et al. (2015a) for additional details about data product specifications.

b. Assimilation algorithm

The L4_SM algorithm is built on the EnKF - a Monte-Carlo variant of the Kalman filter (Evensen 2003). The idea behind the EnKF is that a small ensemble of model trajectories captures the relevant parts of the model forecast error structure. Each member of the ensemble experiences perturbed instances of the surface meteorological forcing fields (representing errors in the forcing data) and/or randomly generated noise that is added to the model parameters and prognostic variables (representing errors in model physics and parameters). The error covariance matrices that are required for the filter update can then be diagnosed from the spread of the ensemble at the update time. Its relative ease of implementation made the EnKF a popular choice for land data assimilation (Reichle et al. 2002a,b; Andreadis and Lettenmaier 2006; Pan and Wood 2006; Zhou et al. 2006; Durand and Margulis 2008; Hendricks Franssen et al. 2008; Kumar et al. 2008; Lahoz and De Lannoy 2014; Carrera et al. 2015; Reichle et al. 2014a; Kurtz et al. 2016).

The EnKF works sequentially by performing in turn a model forecast and a filter update. Its implementation for the L4_SM algorithm is shown schematically in Figure 1 of De Lannoy and Reichle (2016b), except that - for the L4_SM system discussed here - the model is on the 9-km grid and the assimilated SMAP observations are only available for a single, 40° incidence angle.

Formally, the forecast step using the land surface model f(•) can be written as

$$x_t{ }^{j-}=f(x_{t-1}{ }^{j+},w_t{ }^j),$$ 1

where x_t ^j− and x_t-1 ^j+ are the forecast (denoted with ^- ) and analysis (denoted with ⁺) state vectors at times t and t-1, respectively, of the j-th ensemble member. The model error (or perturbation vector) is denoted with w_t ^j. Each ensemble member represents a particular realization of the possible model trajectories with perturbations in model prognostic and forcing variables. The EnKF state vector is at 9-km resolution and consists of the Catchment model prognostic variables for soil moisture (surface excess, root-zone excess, and catchment deficit), skin temperature, and surface (layer-1) soil heat content. The latter is the Catchment model prognostic variable from which the surface soil temperature is diagnosed.

With the observations available at time t, the state vector of each ensemble member is updated to new values. To this end, the filter update produces increments Δx_t ^j at time t that can be written as

$$\Delta x_t{ }^j={\text{K}}_t\left(y_t{ }^j-h\left(x_t{ }^{j-}\right)\right)$$ 2

where $y_t{}^j$ denotes the (suitably perturbed) vector of Tb observations (Burgers et al. 1998) and h(•) is the observation operator that converts the 9-km soil moisture and temperature state estimates into model estimates of Tb at the coarser resolution of the SMAP observations. The analyzed state vector is obtained as $x_t{{}^j}^{+}=x_t{{}^j}^{-}+\Delta x_t{}^j$. As expressed in equation (2), the Kalman gain matrix K_t maps the coarser-resolution observational information, expressed in the O-F residuals, $(\text{i}.\text{e}.,y_t{}^j\text{- h}\left(x_t{}^{j-}\right))$onto the model state increments $\Delta x_t{}^j$ at 9-km resolution. The Kalman gain is given by

$${\text{K}}_t=\text{Cov}\left(x_t^{-},h\left(x_t^{-}\right)\right){\left[\text{Cov}\left(h\left(x_t^{-}\right),h\left(x_t^{-}\right)\right)+{\text{R}}_t\right]}^{-1}$$ 3

where the forecast error (cross-)covariances Cov(•) are diagnosed from the ensemble, and R_t is the observation error covariance (including contributions from instrument errors and errors of representativeness). Simply put, the Kalman gain represents the relative weights given to the model forecast and the observations based on their respective uncertainties and based on the modeled error correlations between different elements of the state vector and the corresponding Tbs. Finally, the EnKF state estimate is given by the ensemble mean, and the reduction of the uncertainty resulting from the analysis update is reflected in the reduction of the ensemble spread.

The EnKF updates in the L4_SM algorithm are spatially distributed in the sense that all observations within a radius of 1.25° impact the analysis at a given 9-km grid cell (De Lannoy et al. 2016b; their section 3.1). The weight of an O-F residual towards the soil moisture (temperature) increments at a given 9-km grid cell is proportional to the modeled error correlations between the Tb at the observation location and the soil moisture (temperature) at the location of the increment (equation 3). Since this error correlation typically decays with increasing distance of the observation from the location of the increment, its sample-based estimate becomes noisier with increasing distance, which is addressed through a distance-based covariance localization approach using a Gaspari-Cohn function (Gaspari and Cohn 1999; De Lannoy and Reichle 2016a) with the above-mentioned compact support radius of 1.25°. The L4_SM system uses 24 ensemble members. The perturbation parameters for the model forcing and prognostic variables match those of De Lannoy and Reichle (2016a; their Table 2) except that the spatial correlation scale for the perturbations of the model prognostic variables is set to 0.3° (instead of 0.5°) in the L4_SM system. The observation error standard deviation is set to 4 K, which includes ~1.3 K instrument error and ~3.8 K representativeness error (that is, error in the radiative transfer model and remapping associated with the observation operator h(•)) (Reichle et al. 2017b).

The Kalman gain of equation (3) is optimal (in the sense of minimum estimation error variance) only if the dynamic system (equation 1) is linear, if its model and observation error characteristics satisfy certain assumptions (including white and uncorrelated noise), and if the input error parameters are correctly specified (Gelb 1974). In this case, the EnKF estimate is mathematically the best possible estimate of the true state given the observations, the model prediction, and the estimated errors of both. But the L4_SM land model and observation operator are not linear (Koster et al. 2000; De Lannoy et al. 2013), and the L4_SM error characteristics further violate the above-mentioned assumptions. The L4_SM analysis is therefore not optimal. Nevertheless, as mentioned above, the analysis estimates have proven superior to model-only estimates when both are validated against in situ measurements (Reichle et al. 2017b).

To address seasonally varying bias in the modeled Tbs, the observations (y_t ^j) and model forecast (h(x_t ⁻)) of equation (2) are taken to be the anomalies of the SMAP and modeled Tbs from their respective long-term mean seasonal cycles. The seasonal cycle of the SMAP Tbs was estimated from SMOS (version-5) Tb observations for the period July 2010 to June 2014. The seasonal cycle of the modeled Tbs was estimated from a model-only simulation of the L4_SM system for the same period. For details of this rescaling procedure, see section 3b and Figures 1 and 2 of (De Lannoy and Reichle 2016a) and section 2d of (Reichle et al. 2017b).

Fig. 2.

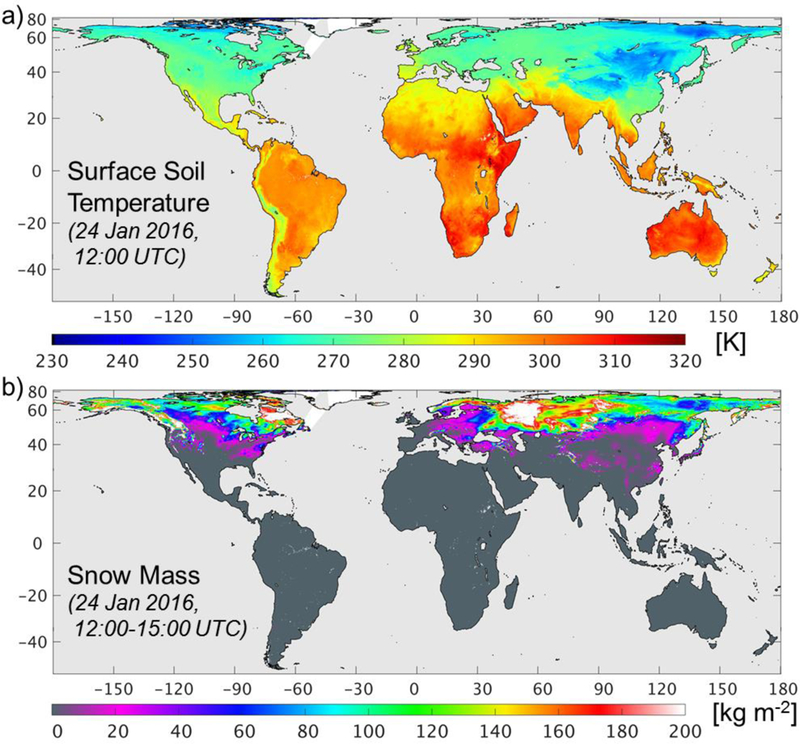
L4_SM (a) surface soil temperature analysis for 24 January 2016, 12:00 UTC and (b) snow mass for 24 January 2016, 12:00-15:00 UTC.

c. Assimilation diagnostics

The L4_SM system generates a variety of useful internal algorithm diagnostics that are available wherever and whenever SMAP observations are assimilated (see also Reichle et al. 2015b; their Appendix B). Most importantly, the Tb forecasts generated by the model within the cycling assimilation system are repeatedly confronted with the assimilated observations as part of the analysis (equation 2). This routine evaluation of model estimates against the assimilated observations is primarily reflected in the ensemble mean O-F Tb residuals (i.e., y_t - h(x_t⁻)).

In an optimally calibrated, linear system that satisfies the usual error assumptions (section 2b), the (ensemble mean) O-F residuals are a zero-mean, white noise sequence, thereby reflecting an unbiased analysis that extracts all of the information from the observations (Gelb 1974). As already mentioned above (section 2b), the L4_SM analysis is not strictly optimal, but it is still interesting to know how close to optimal the system operates in any given region. When the lagged auto-correlations of the O-F residuals are small and consistent with white noise, the system is nearly optimal and has extracted most of the available information from the observations (Daley 1992). Conversely, when the lagged auto-correlations are not small, then the observations are not being used efficiently (Daley 1992). The sample auto-correlation estimates presented below are based on the asymptotically unbiased estimator (Jenkins and Watts 1968; their equation 5.3.25). Four sets of sample auto-correlations were computed, separately for H-pol and V-pol O-F residuals from ascending and descending half-orbits, and then averaged across the four sets. Auto-correlations were computed at a given location only if a total of at least 80 lagged data pairs were available.

Moreover, the standard deviation of the O-F residuals is a measure of the typical (absolute) difference between a model forecast Tb and the corresponding (rescaled) SMAP observation. In an optimally calibrated system, the covariance of the O-F residuals should thus equal the sum of the covariances of the model forecast and observation errors (Reichle et al. 2002a; Desroziers et al. 2005), that is,

$$\text{Cov}\left(y_t-h\left(x_t^{-}\right)\right)=\text{Cov}\left(h\left(x_t^{-}\right),h\left(x_t^{-}\right)\right)+{\text{R}}_t$$ 4

In this expression, the left-hand-side represents the actual errors encountered in the system, and the right-hand-side represents the assumed errors. The latter are prescribed through the specification of the observation error covariance and through the specification of the model and forcing perturbations, which are key inputs to the ensemble-based L4_SM assimilation algorithm (section 2b). Assuming that the off-diagonal elements of the O-F covariance (equation 4) are small, a useful assimilation diagnostic is the standard deviation of the normalized O-F residuals. This diagnostic is readily obtained from the published L4_SM output by normalizing each O-F residual with its ensemble-diagnosed assumed error standard deviation, and then taking the time series standard deviation of these normalized O-F residuals. In an optimally calibrated system, this diagnostic ought to be unity. Values greater than one for this diagnostic indicate that the actual errors in the system are underestimated (that is, the actual errors are greater than the assumed errors). Similarly, values less than one indicate that the actual errors are overestimated (that is, the actual errors are less than the assumed errors). Note that the diagnostic only addresses the total error and does not distinguish between observation and forecast errors.

Another useful diagnostic is provided by the ensemble mean O-A Tb residuals (i.e., y_t - h(x_t⁺)), which are the differences between the (rescaled) SMAP Tb observations and the analyzed Tbs. (In the L4_SM system, the latter are diagnosed from the analyzed soil moisture and temperature fields.) As for the O-F residuals, the mean value for the O-A residuals should be zero in an optimally calibrated system. The standard deviation of the O-A residuals should be less than that of the O-F residuals, with the difference reflecting the reduction in the uncertainty of the estimated Tbs obtained through the analysis. Finally, the (time series) mean of the (ensemble mean) soil moisture and temperature increments (Δx_t) should be zero in an optimally calibrated system, and the standard deviation of the increments is a measure of a typical analysis-based adjustment to the model forecast.

3. Results

Results are discussed in five subsections. First, we present global maps of L4_SM soil moisture estimates (section 3a). Next, we briefly illustrate the impact of the SMAP observations in the L4_SM analysis by investigating a particular rain event in Australia in May 2016 (section 3b). Finally, an assessment of the internal diagnostics of the L4_SM assimilation system offers useful insights at the global scale into the quality of the L4_SM product (section 3c-e). This evaluation focuses on the counts of the assimilated Tb observations, on the statistics of the O-F and O-A Tb residuals, and on the statistics of the soil moisture and temperature analysis increments. Some of the text in this section is adapted from two non-peer reviewed project reports (Reichle et al. 2015b, 2016d) and has been updated to reflect the results obtained for the Version 2 L4_SM product and the longer validation period used here.

a. Global soil moisture

We start with a discussion of global maps of time-averaged L4_SM surface soil moisture (Figure 1a) and root-zone soil moisture (Figure 1c) for the 2-year period from April 2015 to March 2017. The global patterns are as expected - arid regions such as the southwestern US, the Sahara desert, the Arabian Peninsula, southern Africa, and central Australia exhibit generally dry surface and root-zone soil moisture conditions, whereas the tropics (Amazon, central Africa, and Indonesia) and high-latitude regions show wetter conditions. One notable exception is that a portion of the Democratic Republic of Congo and adjacent areas appear unexpectedly dry. This is because over Africa, the Version 2 L4_SM algorithm uses precipitation forcing directly from the GEOS-5 FP system, which has a known dry bias in central Africa similar to that of the model-generated precipitation from the Modern-Era Retrospective Analysis for Research and Applications, version 2 (MERRA-2), reanalysis product (Reichle et al. 2017a; their Figure 3b).

Fig. 3.

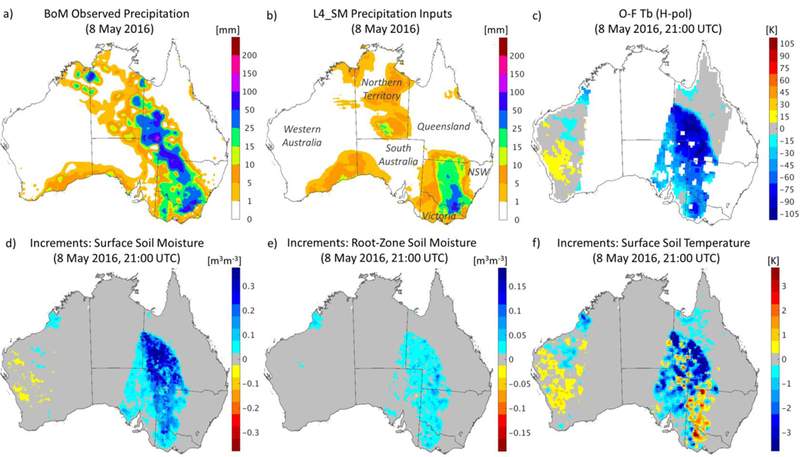
Cumulative precipitation for 8 May 2016 (00:00 UTC to 00:00 UTC) indicated by (a) measurements from the Australian Bureau of Meteorology (BoM) and (b) the L4_SM precipitation inputs. (c) O-F residuals for H-pol Tb on 8 May 2016, 21:00 UTC. Analysis increments of (d) surface soil moisture, (e) root-zone soil moisture, and (f) surface soil temperature on 8 May 2016, 21:00 UTC. Australian states and territories are labeled in (b).

Generally, the global patterns of absolute soil moisture values are dominated by soil parameters and climatological factors, which is reflected in the similar patterns of the long-term average surface and root-zone soil moisture maps. The influence of soil texture is noticeable in the coarse-scale patterns in the Sahara desert, where little is known about the spatial distribution of mineral soil fractions. In the land model, areas with high values of soil organic carbon (including, for example, the region along the southern edge of Hudson Bay and portions of Alaska) are assigned a high porosity value and show persistently wetter conditions than other areas.

The strong impact of climate on global soil moisture patterns is also reflected in the overall similarity between the time-averaged fields (Figure 1a and 1c) and the corresponding instantaneous fields for 1 June 2015 at 00:00 UTC, shown in Figure 1b and 1d, respectively, for surface and root-zone soil moisture. In the latter maps, however, some regions do exhibit strong differences in soil moisture conditions from the long-term average values. For example, the very wet conditions on 1 June 2015 in Texas, Oklahoma, and Kansas and extending into the US Midwest (Figure 1b and 1d) resulted from extreme rainfall events throughout May 2015. Another notable feature is the strong spatial contrast in dry and wet soil moisture conditions in western Australia on 1 June 2015. This contrast resulted from parts of the region having seen unseasonably high rainfall conditions in May 2015, with a few locations recording their wettest May on record, and with many locations recording their wettest May for over twenty years. In contrast, the rest of Western Australia recorded rainfall that was below to very much below average (Bureau of Meteorology 2017). Also visible in Figure 1b and 1d are the dry conditions on 1 June 2015 in Spain, which in this year experienced its driest May on record, followed by an extraordinarily long, intense summer heat wave (Blunden and Arndt 2016).

The L4_SM product also includes a large number of output fields that are not subject to formal validation requirements. Such “research” outputs include the surface meteorological forcing fields, land surface fluxes, soil temperature, and snow. Figure 2 illustrates two of these fields for 24 January 2016, the surface soil temperature (at 12:00 UTC) and the snow mass (3-hour average for 12:00-15:00 UTC). Again, the global patterns are consistent with expectation. The hottest surface soil temperatures are in equatorial eastern Africa, where the local time is around 3pm and the diurnal cycle of the surface soil temperature is at or near its peak. The soil is frozen in large portions of the mid and high northern latitudes. The snow mass distribution is also consistent with expectation, with nearly continuous snow cover in the northern high latitudes and in the northern hemisphere high mountain ranges. Also visible is the snow accumulation from the severe blizzard that hit the eastern US on January 22-24, 2016 (Greybush et al. 2017). Snow is all but absent in the southern hemisphere in the middle of the austral summer. The L4_SM snow mass estimates are, by construction, similar to those from MERRA-2, which were found to have reasonable skill when compared to independent data (Reichle et al. 2017c).

It should be noted that the L4_SM temperature and snow fields are largely determined by the forcing data and the Catchment model physics. The L4_SM temperature fields are also impacted by the SMAP observations (directly through the soil temperature increments, and indirectly through the effect of soil moisture on the surface energy balance via the latent heat flux). But this impact is relatively minor (Reichle et al. 2017b; their Figure 6). In any case, though, the L4_SM temperature and snow estimates are consistent with the L4_SM soil moisture estimates and may be useful for studies that require land surface data beyond soil moisture. For example, the surface soil temperature and snow fields can be used to identify frozen or snow-covered conditions. Unlike the SMAP Level 2 and 3 retrieval products, the L4_SM product does not provide binary flags to classify the conditions at the time for which the soil moisture estimates are valid. Rather, the L4_SM product provides quantitative estimates of skin and soil temperatures, snow mass, precipitation, etc. (section 2a) that contain far more complete information than binary flags. Users can readily convert this quantitative information into binary flags should the need arise.

Fig. 6.

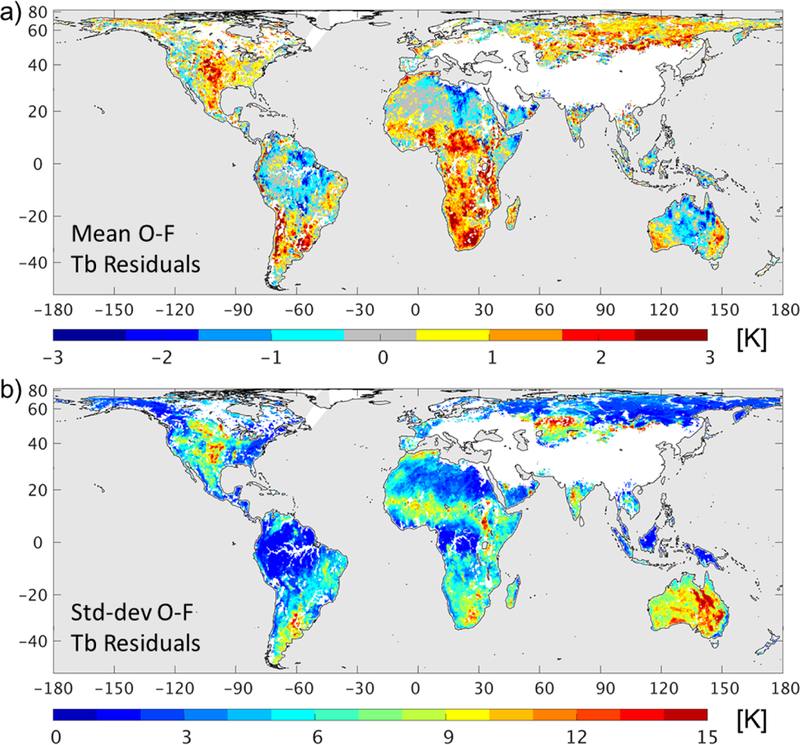
(a) Mean and (b) standard deviation of the O-F Tb residuals from the L4_SM algorithm for April 2015 to March 2017.

b. Illustration of the L4_SM analysis

A key element of the L4_SM analysis update (section 2b) is the downscaling and inversion of the coarse-scale observational information of the assimilated Tbs into the modeled geophysical variables on the 9-km grid, a calculation that is based on modeled error characteristics, which vary dynamically and spatially. In this section we provide an example and illustration of a single analysis update.

Routine monitoring of the L4_SM analysis diagnostics (section 2c) revealed a large spike in the (spatial) standard deviation of the H-pol and V-pol O-F Tb residuals on 8 May 2016 at 21:00 UTC (see also section 3d). A closer investigation revealed that a major rain event occurred in the interior of Australia on this day (Figure 3a), according to observations from the Australian Bureau of Meteorology (2017), and that this rain event was very poorly represented in the L4_SM forcing data (Figure 3b). The L4_SM system relies on the daily, global, 0.5°, gaugebased CPCU product (section 2a), which does not include many of the high-quality, local measurements available to the Bureau of Meteorology. As a consequence, the precipitation used in the L4_SM system missed most of the rainfall that occurred in southeastern Queensland and northeastern South Australia. The L4_SM precipitation further underestimated the rainfall in northern New South Wales. Therefore, the soil moisture in the model forecast for 21:00 UTC was too dry, and the model forecast Tb was too high compared to the SMAP observations, resulting in very large negative O-F Tb residuals (Figure 3c). Consequently, the L4_SM analysis of the SMAP Tb observations resulted in substantial corrections (or increments) to the modeled surface soil moisture (Figure 3d), root-zone soil moisture (Figure 3e), and surface soil temperature (Figure 3f).

The example in Figure 3 clearly illustrates the difficulties of modeling soil moisture at the global scale using standard meteorological forcing datasets and the benefits to this modeling of assimilating SMAP Tb observations. The quality of the global precipitation products that meet the L4_SM latency requirement is uneven at best. The accuracy of the gauge-based CPCU product - the product selected for the L4_SM system - in a given region obviously depends on the density of gauges in that region, and few gauges are available in the interior of Australia (Reichle et al. 2017a; their Figure 8e). Note also that over land, satellite-based precipitation products are not necessarily better on average than gauge-based products, and global combined satellite-gauge products are not available with the required latency (for L4_SM operational production) and length of record (to calibrate the L4_SM system). In this particular case, the SMAP Tb observations are clearly inconsistent with the precipitation estimates from the CPCU product but are consistent with the more accurate regional precipitation measurements from the Australian Bureau of Meteorology. The analysis of SMAP Tb observations was able to correct short-term errors in the L4_SM CPCU-based precipitation forcing and thereby improve the L4_SM soil moisture estimates.

Fig. 8.

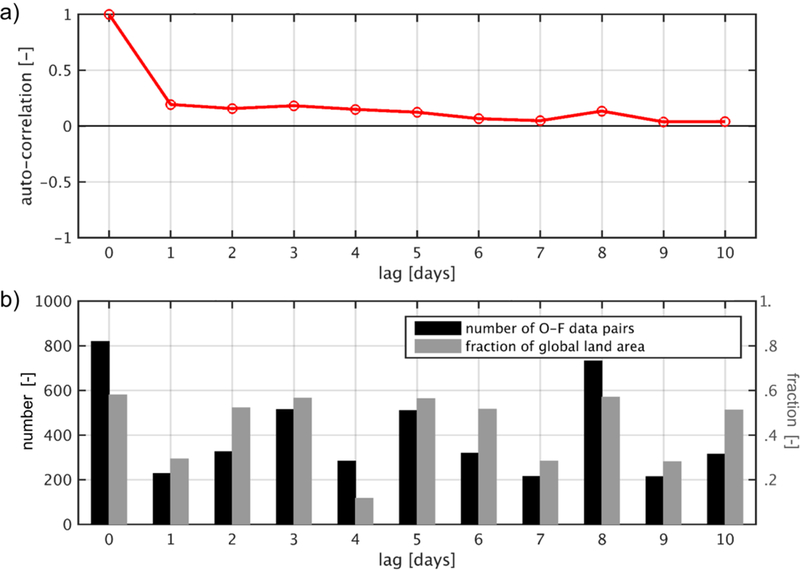
(a) Spatially averaged, lagged sample auto-correlation of the O-F Tb residuals. (b) Average number of O-F data pairs at each grid cell (black; left axis) and fractional area coverage (gray; right axis) contributing to the sample auto-correlation values.

c. Observation counts

In this section we investigate the number of assimilated SMAP Tb observations. Figure 4 shows the total number of Tb observations that were assimilated during the assessment period (April 2015 to March 2017). This count includes H-pol and V-pol observations from ascending and descending half-orbits (after first averaging over fore- and aft-looking Tbs). The average data count across the globe is ~804 for the 731-day period (excluding areas where observations were never assimilated, see below), which implies that one pair of H-pol and V-pol Tb observations was assimilated approximately every other day on average. Few or no SMAP Tbs were assimilated (1) in some mountainous areas, including portions of the Rocky Mountains and the Andes, (2) along coastlines and next to major rivers and lakes, including the Amazon, the Congo, and the Great Lakes, and (3) in regions with many small lakes, such as in northern Canada. Generally, SMAP Tb observations within 40 km of major water bodies and for grid cells with water fraction exceeding 5% are excluded because the L4_SM model cannot predict the mixed (land and water) signal that is present in these observations and would thus yield an incompatible (land-only) Tb forecast. Despite the much shorter warm (unfrozen) season at high-latitudes, far northern areas exhibit relatively high counts of assimilated Tb observations because of SMAP’s polar orbit, which results in more frequent revisit times there.

Fig. 4.

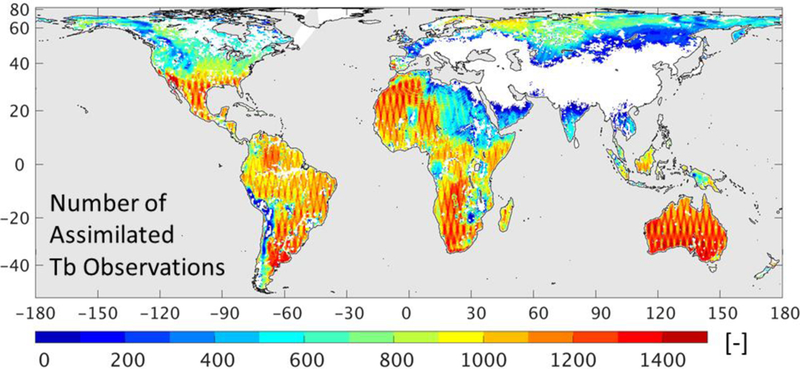
Number of SMAP Tb observations used in the L4_SM algorithm during April 2015 to March 2017. Data counts include H-pol and V-pol data from ascending and descending half-orbits.

SMAP Tb observations were also never assimilated across large areas in eastern Europe and the southern half of continental Asia (Figure 4) because in this region L-band radio-frequency interference (RFI) is common (Oliva et al. 2012). To the extent possible, SMAP is equipped with a variety of hardware and software tools that detect and mitigate RFI, which allows SMAP to provide science-quality observations of the naturally emitted Tb with near-global coverage (Piepmeier et al. 2014, 2017). However, the L4_SM algorithm also requires knowledge of the climatological seasonal cycle of the L-band Tb observations to address the bias in the corresponding Tb model forecasts (section 2b). This (seasonally varying) L-band climatology is derived from observations provided by the Soil Moisture Ocean Salinity (SMOS) mission. In the RFI-affected areas, SMOS does not provide Tb observations of sufficient quality and quantity to derive the climatology. The resulting spatial (and temporal) gaps in the climatology thus constrain the coverage of SMAP assimilation in Version 2 of the L4_SM algorithm. (These gaps are largely closed in the recently released Version 3 L4_SM system because its Tb rescaling parameters are based on SMOS and SMAP observations.) It is important to note, though, that the L4_SM product provides soil moisture estimates everywhere, even if in some regions the L4_SM estimates are not based on the assimilation of SMAP observations and thus rely solely on the information in the model and forcing data.

Next, Figure 5a shows a daily time series of the global observation counts for April 2015 to March 2017, again including H-pol and V-pol observations from ascending and descending halforbits. The data counts clearly vary with season. They also vary with time of day (not shown); there are 8 analysis times per day (at 0z, 3z, …, 18z, and 21z), and the counts vary according to the amount of land surface area at those times having a local time close to 6am or 6pm, when SMAP crosses the Equator. Each day the L4_SM analysis typically ingests between 40,000 and 100,000 SMAP Tb observations (Figure 5a), with a mean of about 65,300 observations.

Fig. 5.

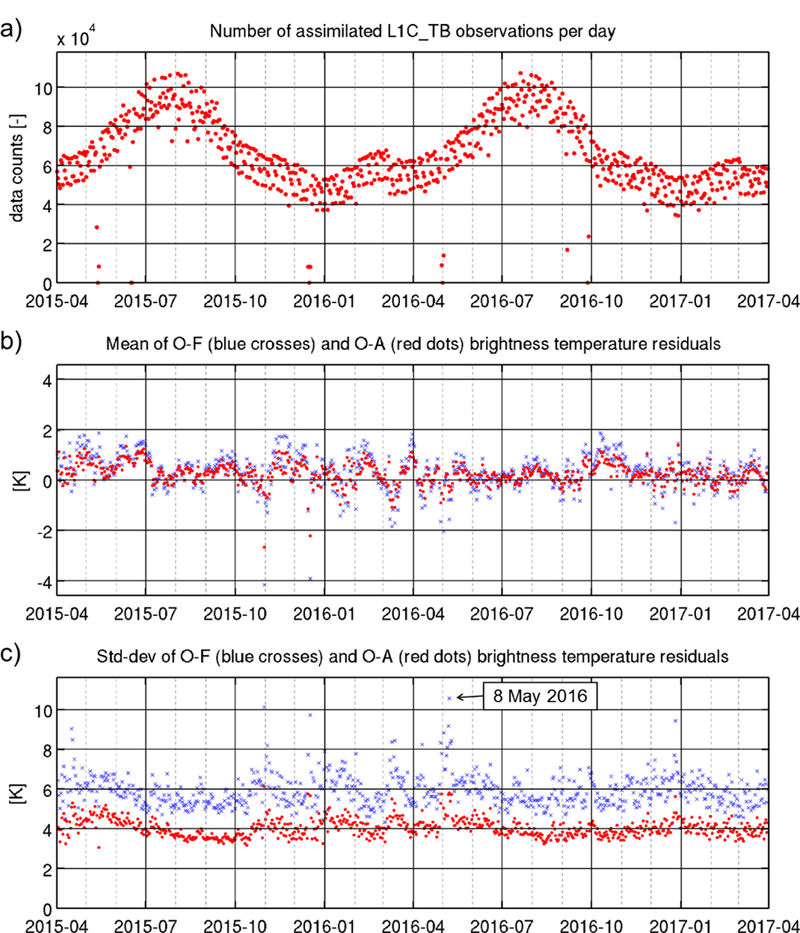
(a) Daily counts of SMAP Tb observations assimilated into L4_SM during April 2015 to March 2017, including H-pol and V-pol data from ascending and descending orbits. (b) Mean of the corresponding O-F and O-A Tb residuals, where the mean values are computed separately for each 3-hourly analysis by averaging across the global land domain (where SMAP observations are assimilated) and then averaging the resulting values over the 8 analysis times for each day. (c) As in (b) but for the standard deviation. Vertical grid lines indicate the first day of each month.

Occasionally, few or no observations were assimilated (e.g., 13 May 2015, 16 Dec 2015, 1 May 2016) because of short gaps in the SMAP observation record when the spacecraft was in safe mode.

d. Brightness temperature residuals

In this section we investigate the O-F and O-A Tb residuals (section 2c). Figure 5b shows the daily time series of the spatially averaged O-F and O-A residuals. Global mean O-F values typically range from −2 K to 2 K, with a long-term average value of just 0.34 K. Typical mean O-A values are slightly smaller than mean O-F values and have a long-term average value of 0.25 K. Overall, the relatively small mean O-F and O-A values suggest that the assimilation system is reasonably bias-free, at least in a global average sense.

Typical magnitudes of the O-F Tb residuals, indicated by the values of their daily (spatial) standard deviation, range between 4 K and 10 K (Figure 5c). The standard deviations of the O-A residuals range from 3 K to 6 K and are generally lower than those of the O-F residuals (Figure 5c). The long-term average of 4.0 K for the O-A standard deviation, compared to 5.9 K for the O-F residuals, reflects the reduction in uncertainty obtained from the analysis. The values of the O-F spatial standard deviation show occasional spikes of around 8-10 K. Some of the spikes occur simply because few observations were assimilated on the days in question (Figure 5a). The 8 May 2016 spike, however, as well as several others (e.g., 1 January 2016, 2 Feb 2016, and 10 March 2016), can be traced back to extreme O-F values in the corresponding 21z analysis over Australia, which has very large negative O-F values reaching −90 K across a large region (e.g., Figure 3c). That is, these spikes correspond to major rain events in Australia during an unusually wet period, rain events that were missed in the CPCU-based precipitation forcing data used for L4_SM (section 3b). This again highlights the potential for SMAP to provide valuable information about soil moisture and rainfall in areas where precipitation estimates are most impacted by errors.

Next, Figure 6 shows the global distributions of the time series mean and standard deviation of the O-F residuals. The time mean values of the O-F residuals are typically small and mostly range from −3 K to 3 K (Figure 6a). Overall, there is a positive bias of 0.37 K, with fewer areas exhibiting negative mean O-F values. The largest values of around 3 K are found in the Sahel and in central and southern Africa. Note that over Africa (and in the high latitudes), the L4_SM precipitation forcing is not corrected to the gauge-based product (section 2a; Reichle and Liu 2014). Consequently, the L4_SM algorithm is somewhat biased where the climatology of the present forcing data (from the ~¼° GEOS-5.13 FP system; Lucchesi 2013a) is inconsistent with that of the historic forcing data (from the ~½° GEOS-5.9 reprocessing “FP-IT” system; Lucchesi 2013b), which was used to derive the Tb rescaling parameters in the pre-launch algorithm calibration (section 2b). Relatively high mean O-F values are also seen in the center of the United States, Argentina, Uruguay, Australia, and portions of Siberia, which indicates that the L4_SM system would benefit from further calibration of the Tb rescaling parameters or, preferably, from reducing the bias in the modeling system.

The time series standard deviation of the O-F residuals ranges from a few Kelvin to around 15 K, with a global (spatial) average of about 6.0 K (Figure 6b). High values are found, for example, in central North America, the Sahel, central Asia, and Australia. These regions have sparse or modest vegetation cover and typically exhibit strong variability in soil moisture conditions. The O-F residuals are generally smallest in more densely vegetated regions, including the eastern United States, the Amazon basin, and tropical Africa. Small values are also found in the highlatitudes, including Alaska and Siberia, and in the Sahara desert. The spatially averaged time series standard deviation of the O-A residuals is 4.0 K (not shown), which again reflects the impact of the SMAP observations on the L4_SM system. (Note that the spatio-temporal average statistics reported for Figure 5 are slightly different from those of Figure 6 because they are derived in different ways: by temporally averaging spatial statistics and by spatially averaging temporal statistics, respectively.)

Next, Figure 7 shows the standard deviation of the normalized O-F residuals, which measures the consistency between the assumed (modeled) errors and the actual errors in the observations and the model forecasts (section 2c). The global average of the metric is indeed 1.0 (Figure 7), which would suggest that, on average, the assumed errors are consistent with the actual errors. The metric, however, varies greatly across the globe. Typical values are either too low or too high. In densely vegetated regions (Amazon basin, eastern US, tropical Africa, Indonesia), deserts (Sahara, Arabian Peninsula), and the high northern latitudes, values range from 0.25 to 0.5, and thus the actual errors there are considerably overestimated. In these regions, the total actual Tb errors (Figure 6b) are smaller than the assumed observation error standard deviation of 4 K, suggesting that the error of representativeness (which dominates the assumed observation error; section 2b) is too large. Conversely, in agricultural regions, including irrigated areas, and in transition zones between dry and wet climates (including central North America, portions of Brazil and Argentina, the Sahel, and India), values range from 1.5 to 4, meaning that the actual errors in these regions are considerably underestimated. Large values are also found in most of Australia, where errors in the precipitation forcing are particularly pronounced (section 3b) and presumably underestimated. In these regions, it is thus likely that the model forecast error is underestimated.

Fig. 7.

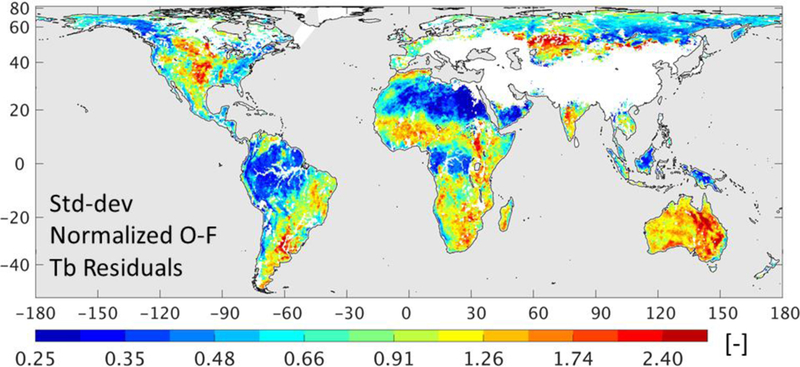
Standard deviation of the normalized O-F Tb residuals from the L4_SM algorithm for April 2015 to March 2017.

The standard deviation of the normalized O-F residuals (Figure 7) only evaluates the total error covariance (equation 4), whereas the Kalman gain (equation 3), and thus the weights given to the observations in the analysis, depend on the relative magnitude of the observation and model forecast errors. That is, the algorithm may well be using near-optimal weights even as the total error covariance is poorly specified. How efficiently the algorithm uses the observations is measured, at least for a linear system, by the lagged auto-correlation of the O-F residuals (section 2c). The global average of this metric is shown in Figure 8a for lags from 1 day to 10 days. The auto-correlations are always positive, which is not consistent with the white noise characteristics expected from an optimal (linear) system.

The average number of data pairs that contribute to the auto-correlation estimate at a given location is shown in Figure 8b, along with the corresponding fraction of the global land area for which auto-correlation estimates were computed. These statistics vary with lag according to the characteristics of the SMAP orbit (Figure 8b). Statistics with at least 50% coverage are available for lags of 2, 3, 5, 6, 8 and 10 days. The maximum number of data pairs and coverage is obtained for a lag of 8 days, which matches the exact repeat interval for the SMAP orbit. (Note that the number of data pairs and coverage is very similar for lags separated by 8 days, e.g., for lags of 2 and 10 days.)

The spatial distributions of the auto-correlations for lags of 2, 3, 5, 6, 8 and 10 days are shown in Figure 9. Auto-correlation values that are within the 95% confidence intervals for white noise are shown in gray. When interpreting Figure 9, it is important to keep in mind that the width of the 95% confidence intervals, and thus the area showing significant auto-correlations, changes with lag partly because the number of data points changes with lag (Figure 8b) owing to the SMAP orbital characteristics. Notably, the 95% confidence intervals are smaller at 3-day lag than at 2-day lag, and they are smallest at 8-day lag. Across the lags shown in Figure 9, the autocorrelations are consistent with white noise (that is, not significantly different from zero at the 5% level) in several regions, including most of western North America, the Sahel, southern Africa, and central Australia, suggesting that in these regions the L4_SM algorithm makes efficient use of the observations.

Fig. 9.

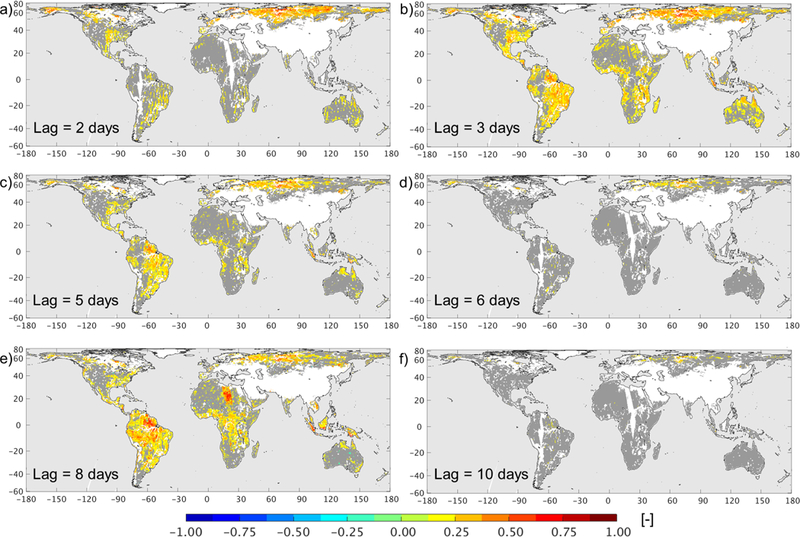
Sample auto-correlation of the O-F Tb residuals at (a) 2-day, (b) 3-day, (c) 5-day, (d) 6-day, (e) 8-day, and (f) 10-day lag. Values that are not significantly different from zero (at the 5% level) are shown in gray.

The auto-correlations are significant, however, for some lags across the eastern US, most of South America, central Africa, and in the northern high latitudes (Figure 9), suggesting that in these regions the SMAP observations are not used efficiently in the current version of the L4_SM algorithm. A closer inspection of the results reveals that the regions with significant O-F auto-correlations (Figure 9) tend to have relatively small (typical) O-F values (Figure 6b) that are dominated by seasonally varying bias (not shown), resulting in high auto-correlation values. Somewhat fortuitously, many regions of sub-optimal algorithm performance thus largely coincide with regions where SMAP Tb observations are not expected to have much influence on the L4_SM estimates, including the forested regions of the eastern US and the tropics, where there is relatively little sensitivity of L-band Tbs to soil moisture.

Furthermore, the high auto-correlation at 8-day lag in Libya (Figure 9e) can be traced back to the 6pm (ascending) SMAP overpass time and is probably related to errors caused by residual RFI in the 6pm (descending) SMOS observations used to derive the Tb rescaling parameters (section 2b). Moreover, the high auto-correlation values at lags up to 8 days in the northern high latitudes and in the non-forested regions of Africa (Figure 9) may be related to seasonally varying bias caused by the above-mentioned inconsistencies between the current (GEOS-5 FP) and historic (GEOS-5 FP-IT) model forcing data. Finally, there is a relative maximum in the O-F autocorrelations at 8-day lag (Figures 8 and 9), which may reflect the periodicity in the spatial representativeness errors caused by the 8-day exact repeat interval of the SMAP viewing geometry. A similar connection between errors in gridded soil moisture retrieval products and orbit repeat cycles was tentatively established by Su et al. (2013) and Lei et al. (2017).

The auto-correlations reveal potential avenues for improving the L4_SM algorithm, but it is important to keep in mind that the inferences offered above are uncertain. For example, serially correlated model or observation errors, if present, result in non-zero values of the lagged O-F auto-correlations, even if the weights assigned to the observations are nearly optimal, which compromises the use of the O-F auto-correlations as a diagnostic for optimality (Daley 1992; Crow and van den Berg 2010). In the L4_SM system, errors in the parameters of the radiative transfer model (required for the observation operator) likely result in serially correlated observation errors, and the ensemble perturbations approach likely results in serially correlated model errors. Moreover, the L4_SM land surface model dynamics are non-linear. The O-F auto-correlations results must therefore be interpreted carefully.

e. Soil moisture and temperature increments

Finally, we evaluate the statistics of the soil moisture and temperature analysis increments (section 2c). Strictly speaking, the increments are in the space of the Catchment model prognostic variables that make up the EnKF state vector, including the “catchment deficit”, “root-zone excess”, “surface excess”, and “top-layer ground heat content” (section 2b; Reichle et al. 2017b). For the discussion below, the increments were expressed in the equivalent soil moisture and temperature terms.

Figure 10 shows the average number of increments that the L4_SM algorithm generated per day during the assessment period (April 2015 to March 2017). The global mean is 0.70 (excluding areas where increments were never computed), which means that for a given location, there are approximately two increments applied every three days on average, either from an ascending or a descending overpass. The overall pattern of the increments count follows that of the count of the assimilated observations (Figure 4). The coverage of the increments, however, is somewhat greater than that of the observations due to the spatial interpolation and extrapolation of the observational information in the distributed analysis update of the L4_SM algorithm. The figure also reveals the diamond patterns resulting from SMAP’s regular 8-day repeat orbit.

Fig. 10.

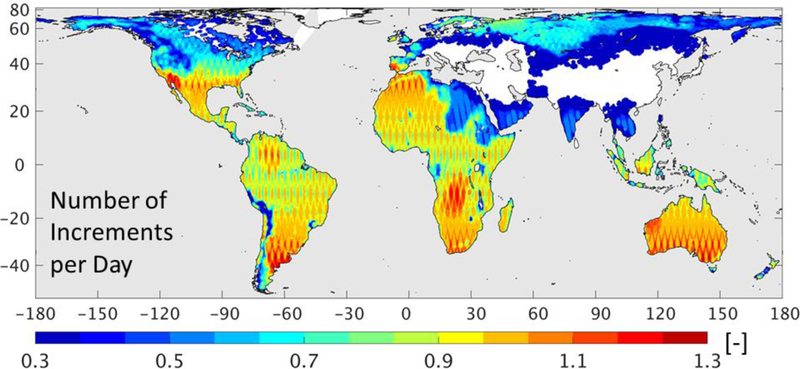
Average number of increments per day generated by the L4_SM algorithm during April 2015 to March 2017. The result applies equally to all elements of the control vector, including the model prognostic variables related to surface soil moisture, root-zone soil moisture, skin temperature, and surface (layer-1) soil temperature.

Next, Figure 11 shows the time mean values of the analysis increments for surface and root-zone soil moisture as well as for the surface (layer-1) soil temperature. In the long-term average, the increments for root-zone soil moisture and surface soil temperature vanish nearly everywhere. Only the increments in surface soil moisture exhibit a bias in some regions, including the US Great Plains, the Sahel, southern Africa, and Australia, with occasional values of around −0.01 m³ m^-3. These mean drying increments are a reflection of the warm bias in the O-F residuals (Figure 6a). Nevertheless, Figure 11 suggests that the analysis system is very nearly unbiased in the global mean sense.

Fig. 11.

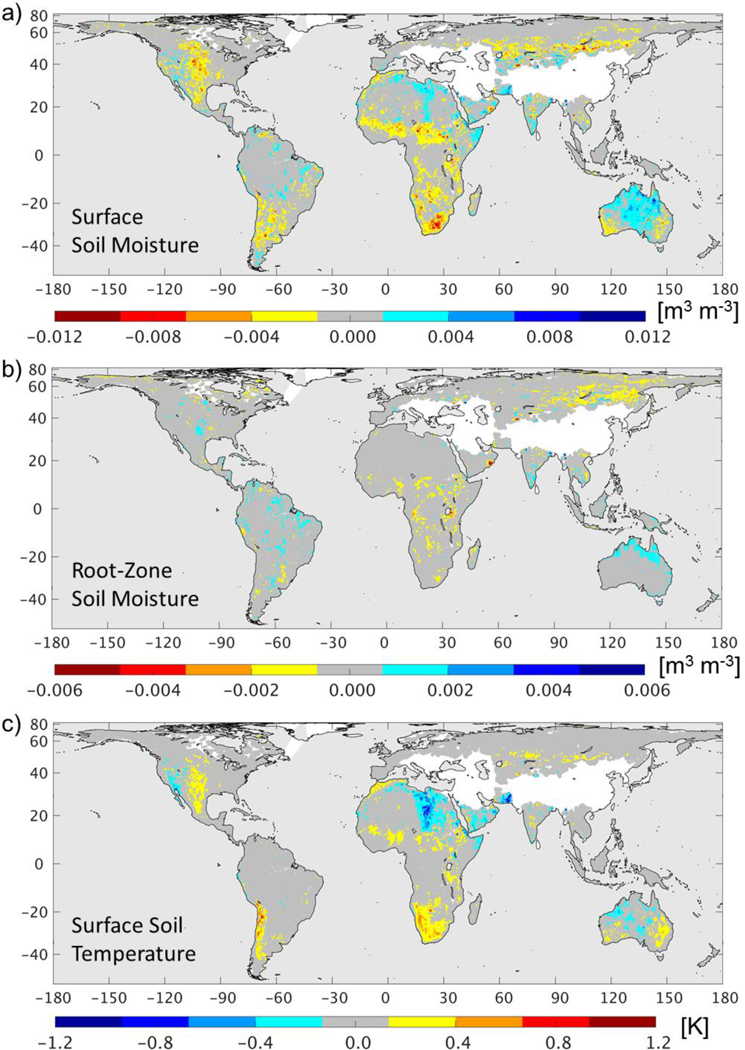
Time series mean of the increments for (a) surface soil moisture, (b) root-zone soil moisture, and (c) surface (layer-1) soil temperature from the L4_SM algorithm for April 2015 to March 2017.

Finally, Figure 12 shows the time series standard deviation of the increments in surface and rootzone soil moisture as well as surface soil temperature. This metric measures the typical magnitude of instantaneous increments. Typical increments in surface soil moisture (Figure 12a) are on the order of 0.01-0.02 m³ m⁻³ in the western US, central Mexico, southern Argentina, the Sahel, southern Africa, central Asia, and southern India. Typical increments are somewhat larger (0.02-0.03 m³ m⁻³) in most of Australia and smaller (0.005 m³ m⁻³) in the eastern US, eastern Brazil, and the high northern latitudes. Over the tropical forests, surface soil moisture increments are generally negligible, reflecting the fact that in those areas the measured SMAP Tbs are mostly sensitive to the dense vegetation and are only marginally sensitive to soil moisture and soil temperature.

Fig. 12.

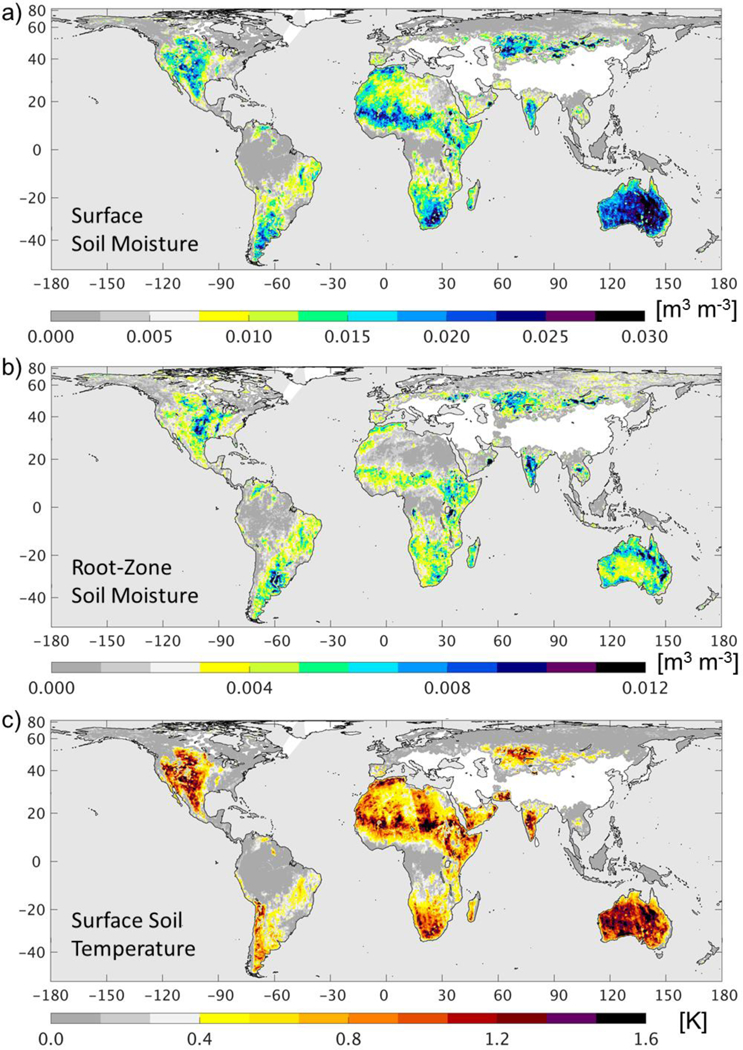
Same as Figure 10 but for time series standard deviation of the increments.

Typical increments in root-zone soil moisture (Figure 12b) show a global pattern that is very similar to that of the surface soil moisture increments, albeit with smaller magnitudes that again reflect the weaker error correlations between the Tb observations and the deeper layer soil moisture. The magnitude of the average root-zone soil moisture increments rarely exceeds 0.01 m³ m⁻³, with a global average value of about 0.003 m³ m⁻³ (excluding areas where increments were never computed). Finally, typical increments for the surface soil temperature (Figure 12c) and the skin temperature (not shown) also exhibit a pattern similar to that of the surface soil moisture increments, with typical (absolute) surface soil temperature increments in dry regions ranging between 0.5 K and 1.5 K. The relatively small magnitude of the temperature increments reflects the fact that the L4_SM Tb analysis has been calibrated primarily for updating the model soil moisture (De Lannoy and Reichle 2016a; Reichle et al. 2017b).

5. Summary and Conclusions

The SMAP L4_SM algorithm assimilates SMAP Tb observations into the NASA Catchment model and thereby interpolates and extrapolates the information from the SMAP observations in time and in space by combining them with the model estimates, taking into consideration the relative uncertainties of each. The resulting L4_SM data product represents this merged information and consists of global, 3-hourly, 9-km resolution estimates of surface and root-zone soil moisture conditions, along with a number of related land surface fields such as soil temperatures and snow mass. The L4_SM product is available from 31 March 2015 to present, with a latency of 2-3 days from the time of observation.

The 2-year climatology of the L4_SM surface and root-zone soil moisture estimates captures the expected global patterns of arid and humid regions (Figure 1). Moreover, we investigated the 8 May 2016, 21:00 UTC analysis over Australia, which exhibited very large negative O-F Tb residuals, suggesting that the model forecast soil moisture was much too dry at the time in question (Figure 3). The reason for the lack of soil moisture prior to the analysis turned out to be a large underestimation in the rainfall used to force the model over the course of the preceding day. The assimilation of SMAP observations resulted in a considerable correction of the model forecast soil moisture towards wetter conditions, thereby compensating for the short-term deficit in the L4_SM rainfall forcing. This case study clearly demonstrates that the assimilation of SMAP Tb observations can correct for such transient errors in the L4_SM modeling system. The L4_SM system is not designed, however, to correct for bias in the forcing data, such as the dry precipitation bias in the GEOS-5 forcing in central Africa (section 3a).

By validating the L4_SM product against in situ measurements, Reichle et al. (2017b) demonstrated that the L4_SM soil moisture estimates meet their accuracy requirement and are better than estimates from a model-only simulation that does not benefit from the assimilation of SMAP observations. The number of locations with suitable in situ measurements, however, is very limited. The present paper supplements the in situ validation results of Reichle et al. (2017b) with an evaluation of the internal diagnostics of the L4_SM assimilation algorithm, which are available quasi-globally, wherever and whenever SMAP observations are assimilated. The assimilation diagnostics include the statistics of the observation counts, the O-F and O-A Tb residuals, and the soil moisture and temperature increments.

The Version 2 L4_SM system assimilates between 40,000 and 100,000 SMAP Tb observations each day (Figure 5a), or about one pair of H-pol and V-pol Tb observations every other day, on average, over land where SMAP data are assimilated. SMAP observations are not assimilated over land that is permanently glaciated, close to open water or major rivers, or affected by RFI, where the necessary L-band climatology cannot be obtained from SMOS, including large portions of Europe, the Arabian Peninsula, and southern continental Asia (Figure 4). Because the impact of the assimilated SMAP Tb observations in the spatially distributed analysis update is non-local, soil moisture and temperature increments are applied over a somewhat larger area, which includes land close to major rivers and shorelines (Figure 10).

The instantaneous soil moisture and temperature analysis increments are within a reasonable range and, as expected, small over densely vegetated regions (Figure 12). The distributed filtering approach results in spatially smooth soil moisture increments (Figure 3). Moreover, the time-average increments are well below 0.01 m³ m⁻³ for soil moisture and less than 1 K for surface soil temperature nearly everywhere (in terms of magnitude), suggesting that the L4_SM system is reasonably unbiased (Figure 11). Similarly, the O-F Tb residuals exhibit only small (absolute) biases on the order of 1-3 K between the (rescaled) SMAP observations and the corresponding L4_SM model forecasts (Figure 6a). This further indicates that the assimilation system is essentially unbiased owing to the rescaling of the Tb observations prior to assimilation. The spatially averaged time series standard deviation of the O-F Tb residuals is 5.9 K (Figure 6b), which reduces to 4.0 K for the O-A residuals. This decrease reflects the reduction of the uncertainty following the assimilation of the SMAP observations. Averaged globally, the time series standard deviation of the normalized O-F residuals is close to unity (Figure 7), which would suggest that the magnitude of the assumed errors in the model and the observations approximately reflects that of the actual O-F errors.

The results, however, also reveal several limitations of the Version 2 L4_SM data product and science algorithm calibration that will need to be addressed in future releases. Regionally, the time series standard deviation of the normalized O-F residuals deviates considerably from unity (Figure 7), which indicates that the L4_SM assimilation algorithm either over- or underestimates the actual errors that are present in the system. This pattern is caused, at least in part, by the use of a spatially constant Tb observation error variance that does not capture the spatially variable representativeness errors associated with the radiative transfer model. Additionally, the spatially constant perturbation parameters do not account for spatially varying model error characteristics, including errors associated with the lack of irrigation in the modeling system.

Furthermore, non-zero and generally positive values of the lagged auto-correlations of the O-F residuals suggest that the SMAP Tb observations are not used efficiently in many forested regions (including the eastern US and the tropics), in most of the northern high latitudes, and in portions of South America and Africa (Figures 8 and 9). The lack of efficiency may be caused by seasonally varying bias, auto-correlated model and/or observation errors, and/or nonlinearities in the land model and observation operator. In many of these regions, SMAP has only a small impact on the L4_SM soil moisture estimates (that is, typically small O-F residuals and soil moisture increments), which is, at least for the forested regions, as expected. Finally, the adverse impact of RFI on the SMOS Tb observations in large portions of Europe, the Middle East, and East Asia made it impossible to calibrate the L4_SM algorithm and assimilate SMAP observations in these regions in the Version 2 L4_SM release (Figure 4).

Future improvements of the L4_SM algorithm should focus on mitigating the over- and underestimation of the actual errors, which will likely require the specification of spatially variable inputs for the observation and model error characteristics. Additional revisions should focus on the structure and parameters of the Catchment model to reduce the bias in the L4_SM soil moisture and temperature (Reichle et al. 2017b). This bias in the L4_SM product is primarily driven by the bias in the Catchment model because the Tb rescaling yields, by construction, a reasonably unbiased L4_SM analysis. Furthermore, the radiative transfer model and its parameters should be improved to reduce the Tb bias in the modeling system and thus minimize the need for Tb rescaling. These biases could be reduced prior to data assimilation (through model calibration) or dynamically within the assimilation system (through augmentation of the state vector).

Eliminating the seasonally varying bias in the modeled Tb and soil moisture, however, is difficult and likely requires a few more years of SMAP observations. In the meantime, the recently released Version 3 L4_SM product employs improved Tb rescaling parameters that are based on (1) a longer period (and newer version) of SMOS observations where available and the shorter record of SMAP observations elsewhere (in particular, in regions where RFI prevents the use of SMOS data) and (2) a model Tb climatology constructed using retrospective surface meteorological forcing data that are more consistent with the forcing data used during the SMAP period. In this way, SMAP observations are now assimilated almost everywhere and with improved bias correction. In summary, the present paper and its companion (Reichle et al. 2017b) demonstrate that the L4_SM product is sufficiently mature and of adequate quality for distribution to and use by the larger science and application communities.