Neutral and selective dynamics in a synthetic microbial community

Significance

We created a synthetic microbial community to help understand how evolution and selection pressure change the species diversity of an ecosystem. Our results show that there is a clear transition between neutral and selective regimes that depends on the rate of immigration as well as the fitness differences.

Abstract

Ecologists debate the relative importance of selective vs. neutral processes in understanding biodiversity. This debate is especially pertinent to microbial communities, which play crucial roles in areas such as health, disease, industry, and the environment. Here, we created a synthetic microbial community using heritable genetic barcodes and tracked community composition over repeated rounds of subculture with immigration. Consistent with theory, we find a transition exists between neutral and selective regimes, and the crossover point depends on the fraction of immigrants and the magnitude of fitness differences. Neutral models predict an increase in diversity with increased carrying capacity, while our selective model predicts a decrease in diversity. The community here lost diversity with an increase in carrying capacity, highlighting that using the correct model is essential for predicting community response to change. Together, these results emphasize the importance of including selection to obtain realistic models of even simple systems.

Microorganisms are essential players in biogeochemical cycling (1, 2), food production (3), industrial processes (4, 5), and human health and disease (6). Furthermore, it is often the community that gives rise to the output or property of interest (7), rather than any individual organism. Understanding microbial communities is therefore important in a wide variety of systems for predicting responses to anthropogenic (2) and natural perturbations, engineering desired outputs (8, 9), and understanding native functions. The study of microbial communities has been aided by increasing quantities of data as sequencing technologies have rapidly advanced, but to move from taxonomic descriptions to deeper understanding, there have been calls for placing these results in the context of a theoretical framework (10–16).

There exist myriad ecological theories and numerous ways of classifying them. In the framework of Vellend (17), theories can be classified by their inclusion of four classes of process: selection, drift, dispersal, and speciation. Theories that do not include selective effects are considered neutral, and much debate in ecology has focused on the importance of including selection vs. considering only the neutral processes in understanding biodiversity (18–20). Models incorporating selection take a wide variety of forms but critically differ from neutral theories in that they specify explicit differences between community members. For instance, one species may grow faster in certain abiotic conditions or might be killed as prey to feed another species (21). These models can make detailed predictions but often necessitate measurements or estimates of many parameters (22, 23). Conversely, neutral models take into account only random mechanisms. In ecology, they draw no distinction between individuals, even across different species that act in competition for a single limiting resource. Each species has the same fitness, and each species’ relative abundance changes only due to random processes such as immigration and drift from random sampling (18). Despite obvious species differences documented by decades of observation, neutral models under certain assumptions can, perhaps surprisingly, recapture frequently observed patterns of natural communities, such as lognormal-like species relative abundance distributions (24) and power law-like species area relationships (25). Neutral models are thus a potentially enticing way to understand communities by abstracting away complicated differences between species, but a natural question arises about their applicability under varying balances between selective and random processes.

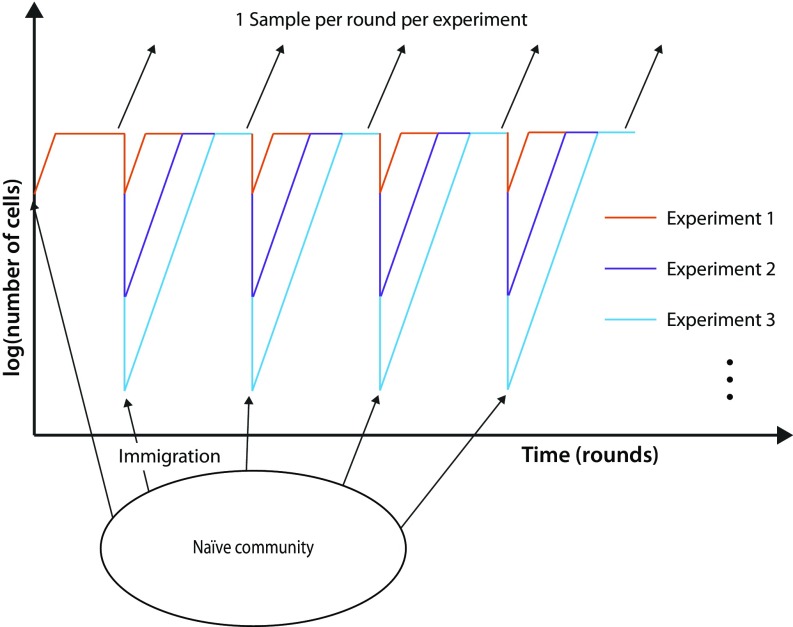
As in macroscopic ecology, both selective and neutral theories have been discussed in microbial ecology, and studies have reached a wide range of conclusions about the relative contributions of selective and neutral processes to community assembly and structure (26–37). As a result, researchers have emphasized the need for controlled time-course experiments to explore how the balance among different processes such as selection, drift, and immigration compels the application of different models (12, 38). Toward this end, we created a synthetic microbial “community” to emulate an ecological community. In this community, “species” are represented by unique heritable DNA barcodes (39, 40) that distinguish otherwise clonal Escherichia coli bacterial cells. We created and validated a library of 456 different strains with Sanger sequencing to become the different species in our community. Starting with all species present, we grew this community to saturation then passaged it through a bottleneck once per day in 2 mL of shaken rich media using a wide range of bottleneck sizes (∼10⁰ to 10⁷ cells from the smallest to largest bottlenecks, respectively). After each bottleneck event, we immigrated a controlled number of cells from the naïve barcoded “metacommunity” (average of 55 cells per round). We took samples from the saturated growth at each time point and used high-throughput amplicon sequencing of the inserted barcodes to measure the abundance of each species present in each experimental community every round for 25 days (Fig. 1). Our approach had a detection limit for species down to abundances of 1/1,000. Details of the experimental methods can be found in SI Appendix, Methods.

Fig. 1.

Experimental setup. A total of 456 genetically barcoded E. coli strains were serially propagated at a variety of dilutions with an influx of immigrant cells after each dilution.

We note, of course, that this simplified system far from captures the complexity present in natural microbial communities. The species exist in a well-mixed environment and, since they started as clones, they share similar fitness and the same nutrient requirements. Therefore, interactions between species are essentially a zero-sum competition for a limiting resource and do not include other types of interactions such as mutualism or predation. Recall, however, that neutral models only account for competitive interactions between species and do not account for fitness differences. In fact, deviations from these conditions might be expected to drive the system away from neutral dynamics, so the experiments here might be expected to be even more neutral than higher-complexity natural communities.

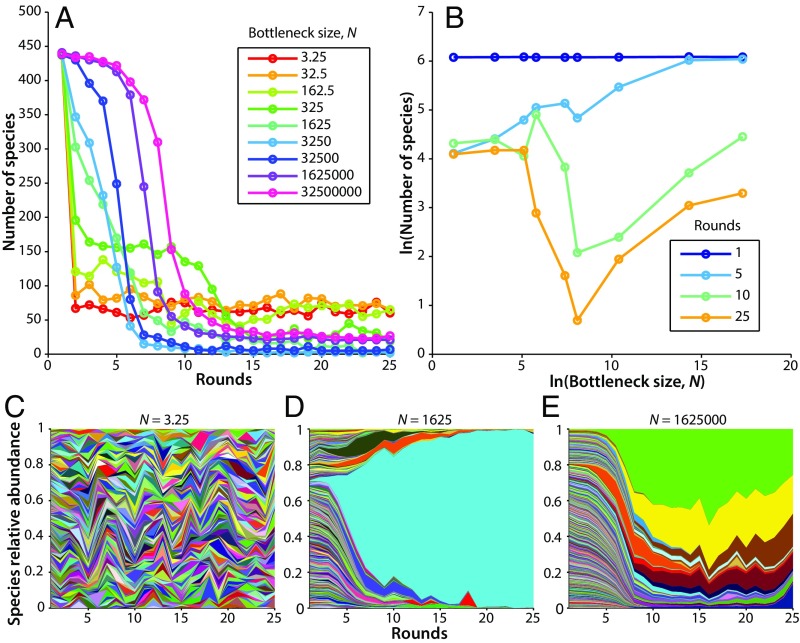
Fig. 2A shows the number of species present over time in nine different experiments as the bottleneck size was varied. We found that the number of species present in each condition declined from the initial state, with a variety of dynamics depending on bottleneck size. For each experiment, we also visualized the relative abundance of all 456 species over time with Muller plots (Fig. 2 C–E and SI Appendix, Fig. S12), which show differences in dynamics between different species within a single experiment and different patterns of dynamics across bottleneck sizes. In analogy to classic species area curves (41, 42) in which area is often assumed to be proportional to the number of individuals (42), we also created log–log plots of the number of species present as a function of number of individuals passing through the bottleneck. These plots change with time and do not appear to reach an equilibrium (Fig. 2B). We also visualized the data with residence time histograms, rank abundance plots, and species relative abundance histograms (SI Appendix, Figs. S15, S18, and S21). For a simple case with no immigration, see SI Appendix, Fig. S8.

Fig. 2.

Experimental time dynamics. Immigration is ∼55 cells per round for each experiment. (A) Number of species detected over time for a range of dilutions. (B) Species area curves over time. (C–E) Muller plots showing the relative abundance of all 456 strains over time in three different experiments. Each species is represented by a different color, whereby the proportion of each color represents the relative abundance of that species. Color/species pairings are consistent from plot to plot. Bottleneck was 3.25 cells per round in C; 1,625 cells per round in D; and 1,625,000 cells per round in E.

We constructed and simulated a simple neutral model in an attempt to capture the system dynamics. The simulation has 25 rounds for each time point of the experiment. Each round, the new community is chosen from the old community by Poisson sampling to account for the bottleneck size, N. After the bottlenecking event, a mean number of cells, M, are immigrated from the original naïve population to the community, also by a Poisson process. When there is no immigration, this neutral model predicts that the community will eventually contain only one species (SI Appendix, Fig. S8). When immigration is included, the number of species present eventually reaches a stable equilibrium (Fig. 3A and SI Appendix, Fig. S10), independent of starting conditions (SI Appendix, Fig. S9). Like other neutral models (25), this model predicts a power law relationship with an exponent near ¼ when the number of species present is plotted against the bottleneck size for simulations that reach equilibrium (Fig. 3I). Characteristic species relative abundance plots are also predicted (SI Appendix, Fig. S22). Details of the model and expanded results can be found in SI Appendix, Models and Data and Comparisons.

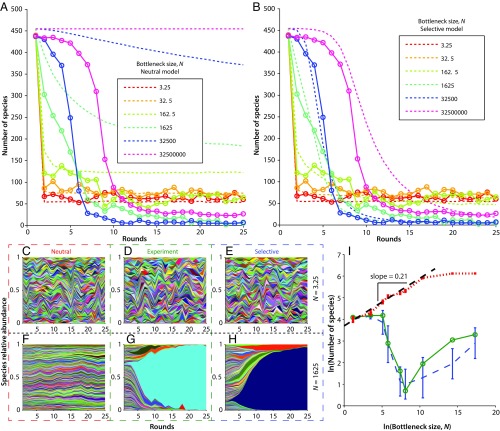
Fig. 3.

Comparison of neutral (A) and selective (B) models to the experimental data. (A and B) Number of species detected over time for a range of bottleneck sizes. Solid lines are experimental data, dashed lines are model data (means of 100 simulations). Note that for ease of visualization, not all bottleneck sizes are displayed. For the remaining bottleneck sizes, see SI Appendix, Data and Comparisons. (C–H) Muller plots showing the relative abundance of all 456 strains over time for two different bottleneck sizes (representative trials picked for simulations). Bottleneck was 3.25 cells per round in C–E and 1,625 cells per round in F–H for neutral (C and F) and selective (E and H) models compared with experiment (D and G). (I) End point (round 25) species area curves for neutral (red dashed line) and selective (blue dashed line) models compared with experiment (solid green line). Note that the neutral model predicts a power law relationship for the smaller bottleneck sizes. Error bars denote 1 SD from 100 simulated trials and are negligible for larger bottleneck neutral simulations.

Community dynamics in many experiments begin to differ drastically from the predictions of the neutral model (Fig. 3A). During the early time points (rounds 1 to 5) experiments with larger bottlenecks lost diversity slower relative to those with smaller bottlenecks as predicted by the neutral model, but experiments with medium and large bottlenecks lost diversity at much faster absolute rates than predicted. At later time points, the experiments with the two smallest bottlenecks continued to match the neutral predictions well, but experiments with medium-sized bottlenecks had the lowest diversity and those with large bottlenecks lost an intermediate amount of diversity. This resulted in an experimental species-vs.-area plot that does not follow a monotonic trend or stabilize over the duration of the experiment and rapidly develops a pronounced minimum at medium bottleneck sizes, contrasting sharply with the neutral prediction (Fig. 3I). Although a neutral model with additional stochasticity (such as a very large variance in growth) could lead to a fast loss of diversity as seen in the experiments, our experimentally extracted estimates of the growth variance in individual lineages show that this variance is far too small to explain the loss of diversity at large bottleneck sizes (SI Appendix, Stochasticity).

A comparison of the Muller plots between the experiment and the neutral model illuminates the cause of the discrepancy. Muller plots from the neutral model matched the experiments with the smallest two bottlenecks reasonably well (Fig. 3C vs. Fig. 3D). However, in all experiments with larger bottlenecks, the neutral model predicted relatively uniform and consistent relative abundances between species through the simulated time, compared with the experiments in which one or more species began to take over the population (Fig. 3F vs. Fig. 3G and SI Appendix, Figs. S12 and S13). As these species became dominant, the community rapidly lost diversity. The dominant species seemed to rise in prevalence exponentially over time (Fig. 3G), typical of a fitness advantage instead of a random process. For species that appeared to grow adaptively, we extracted their relative fitnesses from the relative abundance-vs.-time data, correcting for immigration. We obtained maximum per-round Malthusian relative fitnesses, R, of 100 to 180%, translating to maximum per-replication Malthusian relative fitnesses, r, of 5 to 15%, a similar order of magnitude to per-replication fitness differences measured in experimental evolution experiments starting with clonal microbes (40, 43). Here, R = xr, where x is the number of replication cycles required to grow to N_ƒ, the final population size, given by $x={\log }_2\frac{N_f}{N+M}$. R decreased approximately linearly with log N, consistent with constant r across experiments due to an advantage in the exponential phase of growth. We noticed overlap in the identities of the fit species across experiments, suggesting the presence of preexisting fitness differences. Regardless of the underlying source of these fitness differences (for a discussion of these, see SI Appendix, Distribution and Nature of Selective Advantage and Table S1), they appear to cause deviations from the neutral predictions for larger bottleneck sizes.

A more complex model that captures the dynamics over a larger range of bottleneck sizes might then depart from neutrality and include selection in the form of fitness differences between species. We changed the model to include preexisting fitness differences by assigning each species a per-replication relative fitness, constant across experiments, selected randomly from an exponential distribution (44, 45). We then scaled this fitness by the number of replication rounds per experiment to obtain a per-round fitness for each species, consistent with advantages in the exponential growth phase (SI Appendix, Distribution and Nature of Selective Advantage). Simulations including this modification captured many more features over a larger range of the parameter space (Fig. 3B), including species relative abundance trajectories in which one or more species come to dominate (Fig. 3H), as well as nonmonotonic species area curves that do not stabilize over the experiment (Fig. 3I). Further additions to the model, such as including the chance for mutations to arise during the course of the experiment, may lead to a more complete picture, especially at timescales beyond those investigated here. Noting the success of the neutral model at small bottlenecks, we next assessed under what conditions additional complexities departing from neutrality become necessary.

The fact that small fitness differences can lead to nonneutral dynamics has been understood in the population genetics literature (46) for some time and has more recently been studied in the context of neutral ecology models (26, 47–49). Transitions from neutrality have been proposed along speciation (50) and immigration (26) gradients and with different interplays between species interactions and stochasticity (38, 51–53). In our experiment, the different bottleneck sizes have different proportions of immigrants, $m\equiv \frac{M}{M+N}$, allowing us to explore the transition from neutral to selective along an immigration gradient in a well-controlled experiment. In addition to the simulated models, below we discuss and compare our results to the theoretical predictions for the simple scenario of a single species with a fitness advantage, R, over a neutral background, following the derivation by Sloan et al. (26), which can be found in SI Appendix, Models.

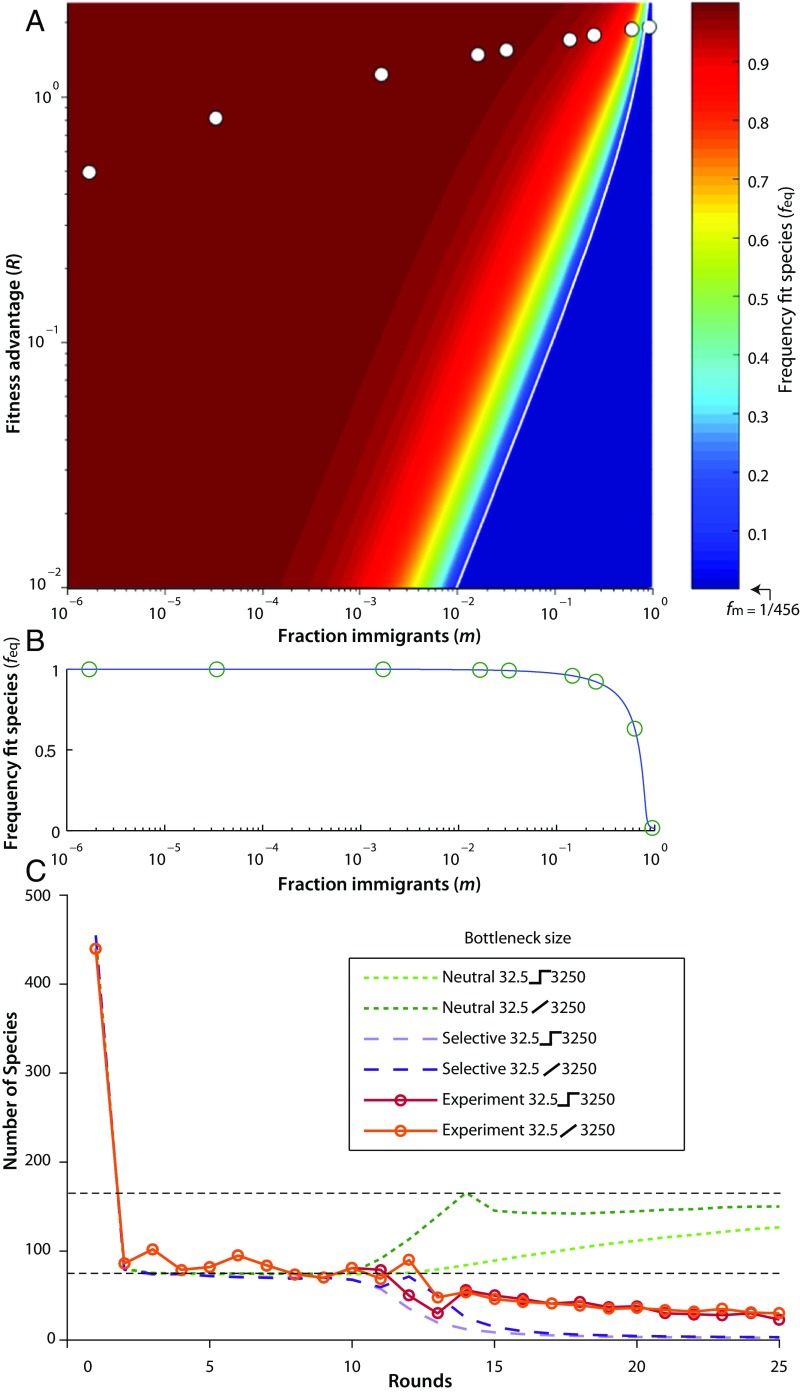
For the neutral case, any given species’ mean frequency is simply equal to that species’ frequency in the incoming immigrant pool, f_m. When there is a selective advantage, the probability distribution of the fit species, P(f), is shifted toward higher frequencies. This effect is most noticeable when selection is stronger than stochastic effects—that is, $R\gg \frac{1}{N_e}$, where N_e is the effective population size, which is on the order of the harmonic mean of the population size as it grows, starting at the total population size after immigration, N + M, and ending at the population size after saturated growth. Even if selection is strong, the distribution can appear neutral if immigration is strong enough to compensate. For strong selection and strong immigration, the equilibrium frequency, f_eq, of the fit species given by the deterministic dynamics is a good measure for determining whether the distribution appears neutral or not. Fig. 4A shows f_eq as a function of the selective advantage, R, and immigration proportion, m, with the experimentally investigated points noted. The f_eq transitions from f_m when neutral, up to 1 (indicating near-fixation) when nonneutral.

Fig. 4.

Transition from selective to neutral. (A) Phase space of equilibrium frequency (f_eq) of a single-fit clone in a neutral background as a function of per-round relative fitness (R) vs. fraction of immigrants (m). Points indicate the experimentally investigated region, and bottleneck size decreases from left to right (assuming a maximum per-replication relative fitness of 8.5%). The immigration fraction of any species is, $f_m\approx 1/456$. The white line indicates the R = δ threshold. (B) A slice through the phase space along the experimentally tested conditions. A transition is predicted: At high immigrant fraction, fit clones do not rise to high abundance and the system is neutral; and at the low immigration fraction, the fit species dominates the population and causes departure from neutrality. Each circle indicates the theoretical prediction for f_eq. (C) Community recovery. Here, a community is maintained at a bottleneck size of 32.5 for 10 rounds and then the bottleneck is allowed to expand to 3,250. The recovery took the form of either a step function or a gradual expansion. Although both models predict a similar number of species to the experimental community before recovery (lower horizontal dashed line), the neutral model (green lines) makes drastically different predictions than a selective model (purple lines) after recovery. The neutral model predicts that the number of species in the community will increase to the new equilibrium level (upper horizontal dashed line), with the recovery happening much slower for the step function (light-green dashed line) than the gradual increase (dark-green dashed line). The selective model predicts that the community will lose diversity independent of step (lavender dashed line) or gradual recovery (purple dashed line). In both the step (solid red line) and gradual recovery (solid orange line) the experimental communities lost diversity.

The transition from neutral to selective happens when selection and immigration are the same scale. It can be understood heuristically by considering the effective growth rate of cells already in the population. Immigration exerts an effective negative fitness effect because cells are replaced by new immigrants. Starting at initial frequency, f₁, the frequency would drop to $\stackrel{\sim }{f}=\left(1-m\right)f_1=\frac{N}{N+M}{f}_1$ because the fraction m is replaced. It is convenient to define a negative fitness, δ, such that $\frac{N}{N+M}=e^{-\delta }$. After immigration, the population grows again until the end of the cycle. The fit species’ frequency is then $f_2=e^R\stackrel{\sim }{f}=e^{R-\delta }{f}_1$, so R − δ acts as an effective fitness. If $R-\delta \mathrm{\gtrsim }0$, then the frequency of cells in the population increases despite replacement by immigration, defining the conditions for the transition from a neutral to a selective regime. If we assume that the fitness advantage is an increase in the bacterial doubling rate by r such that the fitness per cycle, R, scales with the number of doublings, then we can predict when the transition occurs for our experiments by solving R = δ . For $r\approx$ 8.5% (and using M = 55 and a final cell count of 6.5 × 10⁹), the transition is predicted when $m\approx$ 0.89. This matches well the results in Fig. 3I (comparing number of species between the experiment and each simulated model), whereby the smallest bottleneck (m = 0.94) appears neutral while the second-smallest bottleneck (m = 0.63) departs from neutrality and all larger bottlenecks appear nonneutral (m ≤ 0.25). Note that the maintenance of diversity by migration is reminiscent of the rescue effect (54) or mass effects (55) from classical ecology.

An interesting feature of the experiments is that the fastest exponential takeover and loss of diversity in the population happens at an intermediate bottleneck size, leading to, at least transiently, nonmonotonic species area curves. This feature is not directly predicted by existing theory and, if bottlenecking events are understood as a disturbance, our results over this range of bottleneck sizes stand in contrast to the intermediate disturbance hypothesis, which suggests that diversity is maximized at intermediate levels of disturbance (56, 57), likely due to lack of a competition-colonization trade-off in this system. The concept of an effective fitness, R ‒ δ, is useful in explaining this feature of the data; as the bottleneck size increases, the chance of being replaced by an immigrant (negative fitness effect, δ) decreases, but the growth phase advantage (positive fitness effect, R) also decreases. This results in a trade-off in which the effective fitness is maximized when $N=\frac{M}{r}\ln 2$, as found in SI Appendix, Models. With the same M and r as before, this gives N = 450, in agreement with the observation that a species in the N = 325 bottleneck had the largest effective fitness extracted from the experiments.

In our final experiment, we addressed whether knowing which model to apply has practical implications for understanding and managing how a community responds to change. Communities that have been restricted by severe bottlenecks lose diversity—for example, the human gut microbiome after antibiotic treatment (58). To investigate recovery from severe bottleneck, we maintained a community with a bottleneck size of 32 for 10 rounds and then increased the bottleneck size to 3,250 with immigration of 55 individuals per round. Neutral models predict that as the bottleneck size is increased, the diversity of the community will also increase. Furthermore, under these conditions, a neutral model predicts that diversity is actually predicted to recover faster from a slow, rather than an abrupt, increase in the bottleneck size, prescribing a strategy in which the bottleneck size is gradually increased to maximize the rate at which diversity is recovered (Fig. 4C). To test this in the experiment, we carried out both gradual and step increases to the bottleneck size. Opposite the neutral predictions, a selective model predicts that diversity would only continue to decay as bottleneck size is increased, regardless of the dynamics of the increase, since increasing the bottleneck size decreases the immigration fraction, thereby increasing the effective fitness and only helping the fit species to outcompete. Both models captured the experimental results at the initial smaller bottleneck size, but as the bottleneck was increased, regardless of increase dynamics, diversity was lost, which was in far better agreement with the model incorporating fitness differences because the system transitioned well out of the regime in which a neutral model was appropriate. (Fig. 4C) This illustrates that using the correct model is important to predicting the outcomes of change and that management strategies based on incorrect models can have unintended consequences.

Perhaps the most surprising aspect of this work is that despite the construction of initial conditions in our system with minimal differences between species and a relatively homogenous environment, a neutral model failed at all but the highest immigration fractions to capture the community dynamics. However, as shown in Fig. 4A, if fitness differences had been an order of magnitude or more smaller, a neutral model would have captured communities with much more reasonable immigration fractions. Classic population genetics predicts that if we were to continue running the experiment, as the population approached optimal fitness, the fitness differences between individuals would decrease (59). Could this effect redeem a neutral model for capturing longer-term communities? On the surface, systems such as the long-term evolution experiment show diminishing population-level fitness gains over time (60), suggesting smaller fitness differences between individuals. However, beneath the surface of the population, clear niche differentiation (61–63) and definitively selective changes in allele frequency are occurring, even after 60,000 generations (63), making increased duration unlikely to redeem a purely neutral framework. Similar emergent niche effects have also been observed in other simple systems (64, 65), athough we did not observe them in this experiment, potentially due to the duration and the decreased ability to resolve community members as species were lost and barcode pools became more homogenous. Given the poor performance of a neutral framework in simple systems, we suspect that selective effects cannot typically be neglected in microbial communities, even after long amounts of time.

These results show a transition between selective and neutral regimes, providing an experimental case in which the general R − δ guideline balancing fitness differences and immigration proportion successfully predicts whether the system can be treated as neutral (only if R − δ < 0). If these conditions are not met, then nonneutral explanations are required to understand the community. These results also show that using the correct model is essential when predicting community response to change and can impact management strategies. Lastly, we note that athough these results were obtained using a synthetic microbial community, the framework, models, and analytical results may be useful in other ecological systems involving fitness differences and immigration.

Materials and Methods

Random DNA barcodes were cloned into plasmids and transformed into otherwise clonal E. coli bacteria. A total of 456 strains that passed validation by Sanger sequencing were grown to saturation and combined in an equal volume ratio to create a strain library that was manipulated as a mock ecological community in these experiments. This community was propagated in 2 mL of shaken LB Lennox media at 37 °C via serial passaging once per day across a broad range of dilutions such that different numbers of cells passed from one time point to the next across different experiments. After each dilution, a mean of ∼55 cells from the original (complete) community was added to each experimental condition.

Samples from the saturated growth after each time point were extracted by Miniprep Kit (Qiagen), and amplicon libraries were generated and sequenced on an Illumina MiSeq using a two-stage PCR that introduced unique molecular indices. After demultiplexing, reads were assigned to particular strains from the initial library, and the fraction of reads above a noise threshold of 1/1,000 was taken to be proportional to the fraction of the community made up by each labeled strain. Additional experiments were run in which the dilution factor was changed across rounds to explore the effect of changing population size on community dynamics.

Stochastic simulations were set up and run in MATLAB to model community dynamics, using Poisson sampling to mimic the dilution and immigration steps of each experimental condition. The neutral versions of these simulations did not contain fitness differences between community members, whereas the selective versions incorporated fitness differences. Full details on materials and methods appear in SI Appendix.