Active apolar doping determines routes to colloidal clusters and gels

Significance

Collections of polar active particles have been unable to form stable and long-living structures due to the presence of self-propulsion. We solve this timely issue by introducing the concept of “active doping” and show that a few light-activated apolar, i.e., non–self-propelling, units can be used to rapidly trigger the formation of solid clusters and gels composed of passive colloidal particles. Our active doping can be used to assemble disparate microscopic objects, including synthetic or biological ones, paving the way toward the extension of fundamental concepts of gel and glass formation to active out-of-equilibrium systems.

Abstract

Collections of interacting active particles, self-propelling or not, have shown remarkable phenomena including the emergence of dynamic patterns across different length scales, from animal groups to vibrated grains, microtubules, bacteria, and chemical- or field-driven colloids. Burgeoning experimental and simulation activities are now exploring the possibility of realizing solid and stable structures from passive elements that are assembled by a few active dopants. Here we show that such an elusive task may be accomplished by using a small amount of apolar dopants, namely synthetic active but not self-propelling units. We use blue light to rapidly assemble 2D colloidal clusters and gels via nonequilibrium diffusiophoresis, where microscopic hematite dockers form long-living interstitial bonds that strongly glue passive silica microspheres. By varying the relative fraction of doping, we uncover a rich phase diagram including ordered and disordered clusters, space-filling gels, and bicontinuous structures formed by filamentary dockers percolating through a solid network of silica spheres. We characterize the slow relaxation and dynamic arrest of the different phases via correlation and scattering functions. Our findings provide a pathway toward the rapid engineering of mesoscopic gels and clusters via active colloidal doping.

Active colloids constitute an emergent class of autonomous, motile elements that display fascinating collective behavior evoking that of active biological systems (1–8). Given the experimental accessible time/length scales, these artificial prototypes represent a laboratory-scale model system for self-organization under out-of-equilibrium conditions with the possibility of describing them in terms of simplified potentials and interactions. While densely packed passive colloids have been used as a reference system to analyze the formation of gels (9), glasses (10), or jammed phases (11), active systems may provide a faster route toward their formation, and richer phenomenologies, due to the emergent dynamics intrinsic to their nonequilibrium nature. However, at low or moderate concentrations, active particles displaying self-propulsion have been unable to form stable and long-living structures due to the presence of a net drift velocity that gives rise to collisional dynamics. Recent experiments (12–15) and simulations (16–22) have reported the formation of clusters from mixtures of active–passive systems, but at moderate concentrations such structures were found to be dynamic in nature, i.e., continuously breaking and reforming over time.

We show here that more routes toward the formation of 2D clusters and gels may be uncovered by using a few active apolar colloidal dopants that are dispersed in a population of inert passive particles. The activity and interactions between the synthetic dopants are controlled by light, and the absence of self-propulsion makes them ideal dockers for the formation of stable and strong bonds that chemophoretically glue different inert particles, creating solid, space-filling networks. This contrasts with previous works based on active polar, i.e., self-propelling, units that were activated by external fields or chemical reactions. By varying the fraction of doping, we show different types of gels where either the active particles localize in the interstitial regions of large clusters or they assemble into percolating structures that surround the passive spheres, forming a protective, structural scaffold. Computer simulations complement our experiments and allow us to explore in depth the structural relaxation of the identified phases.

To realize gels and clusters via external command, we use a mixture of passive and apolar colloidal particles. The former are silica microspheres (diameter ${\sigma }_p=4\hspace{0.17em}\mathrm{\mu }\mathrm{m}$) that present simple Brownian fluctuations in the dispersing medium, here presented by a mixture of water and $9\%$ hydrogen peroxide (${\text{H}}_2{\text{O}}_2$). The apolar particles are ferromagnetic hematite ellipsoids with a long (short) axis equal to $a=1.8\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ ($b=1.3\hspace{0.17em}\mathrm{\mu }\mathrm{m}$) (Fig. 1A). The particles are characterized by a small, permanent dipole moment $m=2\times 10^{-16}{\mathrm{A}\mathrm{m}}^2$ in the direction of the particle short axis (23). The presence of this moment adds a further degree of functionality to the system, since external magnetic fields can be used as an independent tool to manipulate the inclusions outside or within the formed clusters. The hematite magnetic dipole can also be used as an additional means to manipulate the morphology of the emerging structures, since the magnetic anisotropy favors the initial chaining of the hematite ellipsoids. Hence, both the hematite chain orientation and the associated structure kinetics may be controlled by an external field.

Fig. 1.

(A) Scanning electron microscopy (SEM) image of one hematite ellipsoid ($\alpha -{\mathrm{F}\mathrm{e}}_2{\mathrm{O}}_3$). (Scale bar, $500\hspace{0.17em}\mathrm{n}\mathrm{m}$.) (B and C) Colloidal gel assembled from doping a bath of silica spheres (${\mathrm{S}\mathrm{i}\mathrm{O}}_2$) with a few hematite ellipsoids in a water solution containing ${\mathrm{H}}_2{\mathrm{O}}_2$ ($9\%$ vol). The time $t=0\hspace{0.17em}\mathrm{s}$ (C) corresponds to the application of blue light ($\lambda =450-490\hspace{0.17em}\mathrm{n}\mathrm{m}$, $P=1.04\hspace{0.17em}\mathrm{m}\mathrm{W}$) that triggers the phoretic attraction, and C shows the stationary structure observed after $t=2.7\hspace{0.17em}\mathrm{m}\mathrm{i}\mathrm{n}$. (D) Enlargement of the central region shown in the box in C. (Scale bars, $50\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ for all images.) See corresponding video (Movie S1). (E) Schematic showing the assembly of ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ particles due to photoactivated dopants. (F) Formation of one colloidal cluster composed of $4-\mathrm{\mu }\mathrm{m}$ silica particles, when light is applied at $t=0\hspace{0.17em}\mathrm{s}$. (Scale bar, $10\hspace{0.17em}\mathrm{\mu }\mathrm{m}$.)

Once dispersed in water and sedimented above the surface, the system is globally in a liquid phase, with both types of particles performing simple Brownian diffusion (Fig. 1B). Illumination with blue light activates only the hematite ellipsoids that start the decomposition of hydrogen peroxide (${\mathrm{H}}_2{\mathrm{O}}_2$) in solution, 2${\mathrm{H}}_2{\mathrm{O}}_{2\left(aq\right)}\to {\text{O}}_{2\left(g\right)}$ + 2${\mathrm{H}}_2{\mathrm{O}}_{\left(l\right)}$. This reaction produces a gradient in the chemical concentration around the particle, inducing diffusiophoretic flows (24). These flows push hematite particles toward the bottom surface, slightly reducing their diffusivity and promoting the capture of neighboring particles (Fig. 1E). As a result, strong, long-range effective attractive interactions arise between the particles, leading to a fast aggregation process: The hematite dopants attract both neighboring silica colloids and other hematite ellipsoids. On the contrary, under the same illumination a suspension of passive silica spheres does not induce any interaction in the same medium. Already a small number of hematite colloids are able to promote the rapid formation of large clusters of silica particles that, once merged at high concentration, form an extended network covering the entire observation area (Fig. 1 C and D). The assembly process is relatively fast, as after a few minutes of light exposure a stable colloidal structure is formed. The activated inclusions locate in the interstitial space between the silica particles (Fig. 1 E and F), aligning their long axis parallel to the passive colloids. This geometric arrangement favors close packing and maximizes order, avoiding the frustration observed in other binary mixtures where active and passive colloids are located on the same plane (25). The cluster formation over a long time results from the absence of self-propulsion. Indeed, isolated hematite ellipsoids, when illuminated by light, do not show any drift motion due the symmetry of the generated flow around their surface. Even when this symmetry is broken by the presence of the silica sphere as shown in Fig. 2A, we did not observe any propulsive behavior that can be distinguished from thermal fluctuations. We also note that similar hematite dockers were observed to propel in an aqueous ${\mathrm{H}}_2{\mathrm{O}}_2$ solution after being etched with hydrochloric acid (26). The etching process increased the particle porosity and thus the generated chemical field (26, 27).

Fig. 2.

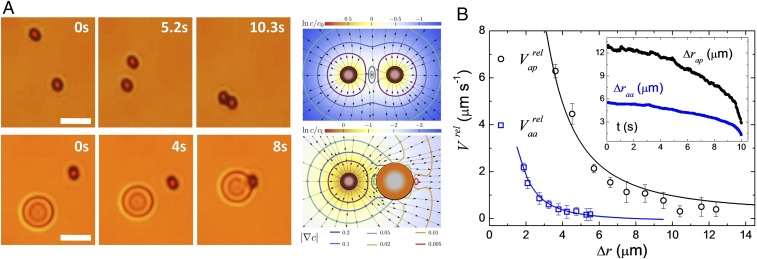
(A, Left) Microscope images showing the light-induced attraction between two active–active (aa) particles (Top) and an active–passive (ap) pair (Bottom). A, Right shows the color-coded logarithm of the chemical-field concentration around the aa (Top) and ap (Bottom) pair. The vector field denotes at each point the direction of the diffusiophoretic speed, while the level curves are the absolute value of the velocity-field module. (B) Relative particle speed $V^{rel}$ of an ap pair (black circles) and of an aa pair (blue squares) vs. relative distance $\mathrm{\Delta }r$. Solid lines are fitted to the data following the model in the main text. B, Inset shows the corresponding distances $\mathrm{\Delta }r$ vs. time.

The phoretic attraction between the hematite–silica particles, here named active–passive (ap), and the hematite–hematite particles, active–active (aa), can be described by considering the chemical field $c\left(\mathbf{r}\right)$, generated by a hematite colloid at position $\mathbf{r}$. In a first approximation, an active spherical particle of diameter ${\sigma }_a$, acting as a source, generates an isotropic, monopolar, chemical field, $c\left(r\right)=c_0+\alpha {\sigma }_a^2/\left(4D_{c}r\right)$, where $D_c$ is the diffusion constant of the chemical product, and $\alpha$ is the production/consumption rate of the chemical per unit area (28, 29). A probe particle of diameter $\sigma$ at a distance $d$ from the source experiences a concentration difference $\delta$ across its size of magnitude proportional to $\delta \propto \sigma c\prime \left(d\right)\propto \sigma /d^2$. To the lowest order, this concentration gradient on the probe particle can be described by a dipolar chemical field. This chemical gradient induces a diffusiophoretic velocity of the probe particle, $\mathit{v}=\mu {\nabla }_{\parallel }c$, where $\mu$ is a mobility, and forces motion of the embedding fluid (Fig. 2A). Integration of the surface velocity over the surface of the probe particle results in a net diffusiophoretic velocity with dominant magnitude $v\propto d^{-2}$. Specifically, the relative speed between pairs of active and passive particles of radii, ${\sigma }_a$ and ${\sigma }_p$, respectively, reads as

$$V_{ap}^{rel}=V_0\left[\overline{\mu }{\left(\frac{{\sigma }_a}{d}\right)}^2+\frac{1}{4}{\left(\frac{{\sigma }_p}{{\sigma }_a}\right)}^3{\left(\frac{{\sigma }_a}{d}\right)}^5\right],$$ [1]

$$V_{aa}^{rel}=2V_0\left[{\left(\frac{{\sigma }_a}{d}\right)}^2+\frac{1}{4}{\left(\frac{{\sigma }_a}{d}\right)}^5\right],$$ [2]

where $V_0={\mu }_a{\sigma }_a^2/\left(12D_c\right)$ is the characteristic chemical diffusiophoretic velocity for an active pair, and $\overline{\mu }={\mu }_p/{\mu }_a$ is the ratio between mobilities of the two types of particles (Materials and Methods). The first terms on the right-hand side of Eqs. 1 and 2 describe the direct interaction between two particles, while the second terms result from the reflection of the chemical concentration produced by an active particle on the receptor one.

Due to their permanent magnetic moment, the hematite ellipsoids will attract magnetically at short distances, forming ribbon-like structures where they assemble side by side to minimize their magnetic energy. For parallel aligned magnetic particles, such interactions contribute to the relative speed with a term of smaller magnitude, $2V_m{\left(d_a/r\right)}^4$. Here $V_m=3{\mu }_0{m}^2/\left(4{\pi }^2\eta d_p^5\right)$, with ${\mu }_0$ the permittivity of vacuum and $\eta$ the kinematic viscosity of the dispersing medium. Thus, two apolar particles will approach with a total relative velocity $V_{aa}=V_{aa}^{rel}+V_m$. As shown in Fig. 2B, we validate the derived functional dependence of the interaction velocity for a pair of particles vs. $\mathrm{\Delta }r$ by fitting Eqs. 1 and 2 to the experimental data. We then use the result to calibrate the magnitudes of $V_0$ and $\overline{\mu }$ for the numerical simulation. At parity of light power and ${\mathrm{H}}_2{\mathrm{O}}_2$ concentration, we find a stronger attraction between ap particles than between two active ones. The attractive phoretic flow generated by one active particle can easily drag a passive sphere nearby, while two activated dopants have to adjust their relative orientation to assemble side by side (Fig. 2A). When in close contact, the magnetic dipolar interaction becomes dominant and promotes chain formation. We note that the magnetic interactions are shorter range compared with the phoretic ones. In fact, for distances of $r\sim 1\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ they become of the order of thermal energy $U_m\sim k_{B}T$, being $T=293\hspace{0.17em}\mathrm{K}$, the ambient temperature.

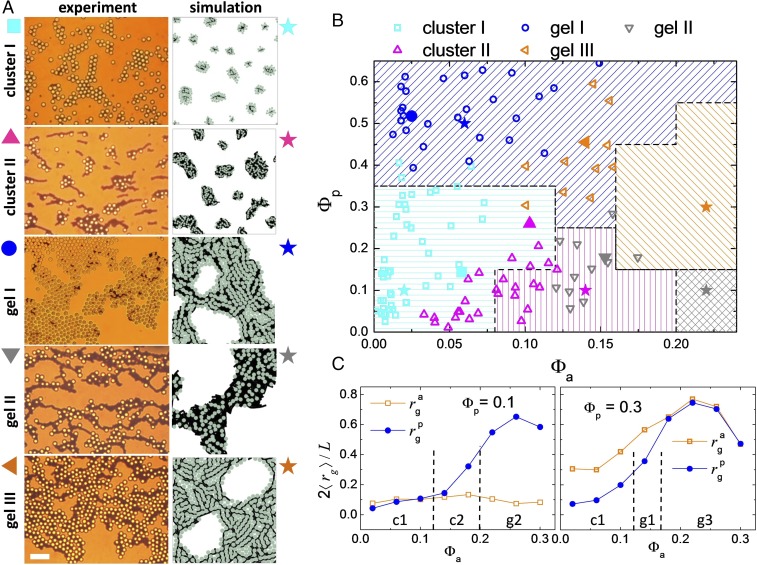
We next characterize the assembly process in a mixture of hematite and silica particles, by varying the relative surface fraction covered by the two active and passive particles, quantified by ${\mathrm{\Phi }}_a=N_a\pi ab/\left(4L^2\right)$ and ${\mathrm{\Phi }}_p=N_p\pi {\sigma }_p^2/\left(4L^2\right)$, respectively. Here $L$ is the lateral size of the observation area and $N_a,N_p$ the number of particles of a given type. The emerging stationary phases are shown in Fig. 3A, while the diagram in Fig. 3B reports their location in the (${\mathrm{\Phi }}_a,{\mathrm{\Phi }}_p$) plane. The system is activity quenched from a homogeneous distribution of silica particles and hematite ellipsoids. We observe the appearance of a rich phase behavior after a fast aggregation process, with different types of clusters and space-filling structures. In the first case, the clusters may be either composed of a triangular lattice of silica colloids glued together by a few interstitial dopants (${\mathrm{\Phi }}_a\le 0.06,{\mathrm{\Phi }}_p<0.4$, cluster I) or composed of a more disordered morphology ($0.09<{\mathrm{\Phi }}_a<0.2$ and ${\mathrm{\Phi }}_p<0.25$, cluster II). Here an entangled cluster-percolating network of active particles destroys the hexagonal structure of the silica clusters and slows down its dynamics, as shown in Fig. 4. At a larger surface fraction of ellipsoidal particles, ${\mathrm{\Phi }}_a>0.2$, chains of active particles completely surround the silica clusters, forming a continuous gel-like structure (gel II). Another way to create an arrested gel is by increasing the concentration of silica particles ${\mathrm{\Phi }}_a$. Above ${\mathrm{\Phi }}_p=0.35$ ($0<{\mathrm{\Phi }}_a<0.15$), only the silica particles form a percolating network, while few ellipsoids that assemble the structure remain separated within its interstitial region (gel I). In contrast, for ${\mathrm{\Phi }}_a>0.15$ the active colloids form a percolating network that now completely scaffolds the silica spheres (gel III), preventing the collapse into a compact aggregate. Here the percolation of hematite particles is different from that of the silica ones, as their dipolar attraction leads to a preferential linear growth, giving a certain degree of directionality in the formed structures. The emergence of gel structures is also seen in the low-$q$ divergence of the structure factors $S\left(q\right)\sim q^{-D}$, as shown in SI Appendix, Fig. S1.

Fig. 3.

(A) Sequence of images showing the five different morphologies observed. Left column displays experimental images. (Scale bar, $20\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ for all images.) Right column shows small snapshots from numerical simulations. See corresponding videos (Movies S2–S6). (B) Phase diagram in the $\left({\mathrm{\Phi }}_a,{\mathrm{\Phi }}_p\right)$ plane combining experimental points (open symbols) and simulation results (regions with solid lines). Solid symbols indicate the location of the experimental (symbols) and simulation (stars) images shown in A. (C) Normalized average radius of gyration $⟨r_g⟩$ vs. fraction ${\mathrm{\Phi }}_a$ for different densities of passive particles, ${\mathrm{\Phi }}_p=0.1$ (Left graph) and ${\mathrm{\Phi }}_p=0.3$ (Right graph). Here we define $⟨r_g⟩=1/N{\sum }_k{n}_k{\left[{1/n}_k{\sum }_j\left({\mathbf{r}}_j^k-{\mathbf{r}}_{cm}^k\right)\right]}^{1/2}$, with $N$ the total number of particles, $n_k$ the number of particles that belong to the $k$th cluster, and ${\mathbf{r}}_j^k$ the position of the $j$th particle in the $k$th cluster with center of mass located at position ${\mathbf{r}}_{cm}^k$.

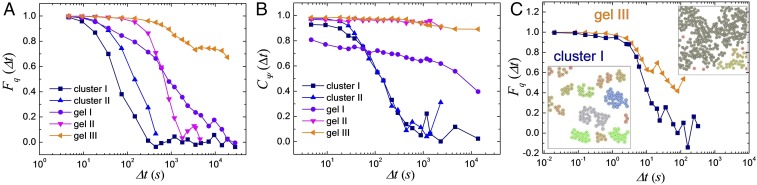
Fig. 4.

Numerical simulations. (A and B) Dynamic scattering function $F_q\left(t\right)$ (A) and self-correlation function of the bond orientational order $C_{\mathrm{\Psi }}\left(t\right)$ (B) vs. time calculated for the different assembled structures. Here the wave vector is $\left|q\right|=2\pi /{\sigma }_p$, being ${\sigma }_p=4\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ the diameter of the passive spheres. Experiments in C show scattering function from the experimental data obtained for the cluster I (${\mathrm{\Phi }}_p=0.22,{\mathrm{\Phi }}_a=0.03$) and gel III phases (${\mathrm{\Phi }}_p=0.421,{\mathrm{\Phi }}_a=0.105$). C, Insets show color-coded clusters analyzed from the particle position in the experimental system.

To reproduce numerically the main features observed in the experimental system, we have set up a simulation code based on the pair interactions between the different colloidal units (SI Appendix). The phase diagram summarized in Fig. 3B and the snapshots of the different morphologies in Fig. 3A, Right column show that the computational model captures satisfactorily the experimentally observed self-assembled structures. To classify them we calculate the radius of gyration $⟨r_g⟩$ form the particle positions (30) (Fig. 3C). From these measurements we distinguish between cluster and percolating structures by identifying a relative percolation threshold for the passive particles, $r_p^{*}\sim 0.5$, and active inclusions, $r_a^{*}\sim 0.4$. Cluster phases occur when the emerging structures stay below the percolation thresholds, $⟨r_g^p⟩<r_p^{*}$ and $⟨r_g^a⟩<r_a^{*}$, and thus type I (II) occurs for $⟨r_g^a⟩<⟨r_g^p⟩$ ($⟨r_g^p⟩<⟨r_g^a⟩$). We note here that the observed clusters represent a stable stationary phase, as they were found to not coalesce over the whole experimental/simulation time. Further, above the respective percolation thresholds gels I ($⟨r_g^a⟩<r_a^{*}$, $⟨r_g^p⟩>r_p^{*}$), II ($⟨r_g^a⟩>r_a^{*}$, $⟨r_g^p⟩<r_p^{*}$), and III ($⟨r_g^a⟩>r_a^{*}$, $⟨r_g^p⟩>r_p^{*}$) were observed. The presence of a magnetic interaction competing against the attractive interaction of chemical origin gives an internal structure and slows the size growth of the system below $R\sim t^{1/4}$ and arrests the structures in the gel phases. When comparing the images in Fig. 3, one can note a more anisotropic shape for the clusters obtained in the experiments than the one from the simulations. While it could be considered an effect of hydrodynamic interactions (31), it arises from the presence of a small bias field that results from an imperfect balance of the Earth’s magnetic field. This field induces initial particle chaining and a more anisotropic growth of the structures.

We characterize the structural arrest of the observed gels both through the dynamic scattering function $F_q\left(t_0,\mathrm{\Delta }t\right)$ that describes the relaxation of the density field $\rho \left(\mathbf{r}\right)$ and through the bond-orientational correlation function $C_{\mathrm{\Psi }}\left(t_0,\mathrm{\Delta }t\right)$, which quantifies the evolution of the local hexatic ordering in the system. Both quantities, defined in SI Appendix, are shown in Fig. 4 A and B for the different phases obtained from the computational model. In all cases, we find that the slow dynamics of our systems do not display any intermediate plateaus and thus particle localization, in agreement with what is theoretically predicted for 2D systems (32). While cluster phases rapidly relax toward equilibrium, where $F_q$ vanishes, gel phases display a very slow decay of $F_q$ over all time scales, corresponding to a long subdiffusive regime of the passive particles, as also confirmed by measuring their mean-square displacement. The decay of the bond orientational correlation function identifies more clearly the slow relaxation associated to the gels in contrast with a fast relaxation process for cluster phases. Despite the difficulties in maintaining stable experimental conditions over sufficiently long times for large concentrations of chemically reacting hematite particles, we succeeded in measuring the intermediate dynamic scattering function for the cluster I and gel III phases (Fig. 4C). In agreement with the computational predictions, in the cluster I phase $F_q$ shows a smooth decay for large values of the wave vector $q$. As we move to small wave vectors, the system decorrelates at longer time scales, while for gel III we observe an initial decay that subsequently slows down.

In conclusion, we have shown that a few active apolar dopands are enough to rapidly engineer large-scale space-filling 2D gels or clusters composed of passive microscopic particles. Thus, we have demonstrated how active doping may be used for the realization of amorphous soft–solid materials. Moreover, we also uncovered a rich scenario for arrested systems that may have distinctive properties emerging from their intrinsic nonequilibrium nature, tunable upon external command. We note that our structures are the result of nonequilibrium interactions that arise solely from the activated hematite particles. Thus, in contrast to clusters and gels realized via attractive interactions such as polymer depletion (9, 10, 33), our particles are subjected to interactions that favor the formation of anisotropic clusters of bicontinuous structures (gel II and gel III). This is not possible via simple attractive interactions such as the ones in a polymer–colloidal mixture (34). It would be interesting to explore how the reported structure changes upon further variation of the density and size of the colloidal dopants. In the first case, we limit to a maximum density of active particles ${\mathrm{\Phi }}_a=0.17$, to avoid bubble generation and the appearance of artifacts in the experimental system. In the second case, increasing the size of the hematite ellipsoids would favor disorder, as the active particles would not be able to fit within the interstitial region of the passive spheres. Thus, we expect that this could produce a change in the phase diagram in Fig. 3A, with the appearance of more disordered clusters. Our colloidal model system bridges gels and glass formation with active systems allowing us to investigate on exceptionally short time scales exciting scenarios when driven by nonequilibrium forces. All in all our findings may be extended to other arrested systems and states or more complex environments spanning living and nonliving artificial systems.

Materials and Methods

Experimental Details.

Monodisperse hematite ellipsoids are synthesized following the “gel-sol” technique (35). Typically, an iron chloride hexahydrate solution ($54.00\hspace{0.17em}\mathrm{g}\hspace{0.17em}{\mathrm{F}\mathrm{e}\mathrm{C}\mathrm{l}}_3-6{\mathrm{H}}_2$O in $100\hspace{0.17em}\mathrm{m}\mathrm{L}$ of high deionized ${\mathrm{H}}_2$O) is gradually added to a sodium hydroxide mixture ($19.48\hspace{0.17em}\mathrm{g}$ of NaOH in $90\hspace{0.17em}\mathrm{m}\mathrm{L}$ of ${\mathrm{H}}_2$O) and stirred at room temperature. After $5\hspace{0.17em}\mathrm{m}\mathrm{i}\mathrm{n}$, we add to the stirring solution $10\hspace{0.17em}\mathrm{m}\mathrm{L}$ of ${\mathrm{H}}_2$O containing $0.29\hspace{0.17em}\mathrm{g}$ of potassium sulfate (${\mathrm{K}}_2{\mathrm{S}\mathrm{O}}_4$). The resulting mixture, after being stirred for $5\hspace{0.17em}\mathrm{m}\mathrm{i}\mathrm{n}$, is hermetically sealed and left to age at $100\hspace{0.17em}°\mathrm{C}$ for 8 d. After synthesis, the ellipsoids are stabilized with SDS in a highly deionized ${\mathrm{H}}_2$O (milliQ; Millipore) solution containing also hydrogen peroxide (${\mathrm{H}}_2{\mathrm{O}}_2$). We add $0.11\hspace{0.17em}\mathrm{g}$ of SDS and $11\hspace{0.17em}\mathrm{g}$ of ${\mathrm{H}}_2{\mathrm{O}}_2$ for $80\hspace{0.17em}\mathrm{m}\mathrm{L}$ of ${\mathrm{H}}_2{\mathrm{O}}_2$. The pH is adjusted to 9.5 by adding tetramethylammonium hydroxide. As passive microspheres we use monodisperse particles of $4\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ based on silicon dioxide (44054; Sigma-Micro). Particle size and shape were analyzed by SEM (Quanta 200 FEI, XTE 325/D8395).

The solution containing the magnetic ellipsoids and the ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ particles is introduced by capillarity in a rectangular microtube made of borosilicate glass (inner dimensions $0.1\times 2.0\hspace{0.17em}\mathrm{m}\mathrm{m}$; CMC Scientific) that is immediately sealed. The particles sediment close to a glass plate, where they remain quasi-2D confined due to gravity, displaying a small thermal motion. The illumination is provided via a commercial mercury fiber illuminator system (C-HGFI Intensilight; Nikon) connected to an upright optical microscope via an epifluorescent tower. Blue light is obtained via a fluorescent filter cube with excitation wavelength between $450\hspace{0.17em}\mathrm{n}\mathrm{m}$ and $490\hspace{0.17em}\mathrm{n}\mathrm{m}$. The optical power is measured at the sample plane with a power meter (PM200; Thorlabs) equipped with a photodiode sensor (S121C; Thorlabs). We irradiated at a power $P=1.04\hspace{0.17em}\mathrm{m}\mathrm{W}$. The dynamics of the particles are monitored with a CCD camera (Basler Scout scA640-74f), at a frame rate of $50\hspace{0.17em}\mathrm{f}\mathrm{p}\mathrm{s}$, mounted on top of a light microscope (Eclipse Ni; Nikon) equipped with high-magnification objectives.

Theoretical Model.

We model active and passive particles as spheres of size ${\sigma }_a$ and ${\sigma }_p$, respectively, immersed in a concentration field with Neumann boundary conditions $D_c{\partial }_{r}c\left(r\right){|}_{\sigma }\propto \alpha$ on each particle, where $\alpha$ is the production/consumption rate of the chemical, and $D_c$ its diffusion constant; for passive particles $\alpha =0$. We consider the production and consumption to be small compared with the provided reactant and hence disregard fuel depletion.

The concentration field around an active particle, $i$, located in the origin in the presence of a second one, $j$, a distance $d=\left|{\mathit{r}}_i-{\mathit{r}}_j\right|$ away from each other, with the center-to-center direction parallel to $\widehat{\mathit{z}}$, can be expressed as

$$c_i\left(r,d,\theta \right)=\frac{{\alpha }_i{\sigma }_i^2}{4D_c}\frac{1}{r}+c_{i,j}\hspace{0.17em}\left(r,d,\theta \right),$$ [3]

where the first term on the right-hand side corresponds to the corresponding production of chemicals, and the second term gives the disturbance of the chemical concentration produced by the $j$th particle to guarantee the boundary condition in the $i$th particle. The disturbance term $c_{ij}$ can be expanded as a multipolar series with the axis of symmetry along $\widehat{\mathit{z}}$.

The first contribution on particle $i$ created by a particle $j$, $c_{i,j}^{\left(1\right)}\left(r,d,\theta \right)$, corresponds to a dipole and depends on the activity ${\alpha }_j$ of the $j$th particle, and the distance between the pair,

$$c_{i,j}^{\left(1\right)}\left(r,d,\theta \right)=-\frac{1}{2}{\left(\frac{{\sigma }_i}{2}\right)}^3\frac{1}{d^2}\frac{{\alpha }_j{\sigma }_j^2}{4D_c}\frac{\cos \theta }{r^2}.$$ [4]

The second dipolar contribution on particle $i$ appears only on active particles. The monopolar field generated by $i$ is reflected on particle $j$ and gives, on $i$ the dipolar term, $c_{i,j}^{\left(2\right)}$. As expected it depends on ${\alpha }_i$ as

$$c_{i,j}^{\left(2\right)}\left(r,d,\theta \right)=-\frac{1}{2}{\left(\frac{{\sigma }_i}{2}\right)}^3{\left(\frac{{\sigma }_j}{2}\right)}^3\frac{1}{d^5}\frac{{\alpha }_i{\sigma }_i^2}{4D_c}\frac{\cos \theta }{r^2}.$$ [5]

The gradient of the chemical concentration on the surface of a sphere generates a tangential diffusiophoretic velocity, $\mathit{v}={\mu }_d{\nabla }_{\parallel }c\left(\mathit{r}\right)$, of the fluid at the particle interface. Momentum conservation leads to a particle velocity,

$$\mathit{V}=\frac{-1}{\pi {\sigma }^2}\int d\mathrm{\Omega }\mathit{v}\left(r,\theta \right)={\left(\pi {\sigma }^2\right)}^{-1}{\mu }_d\int d\mathrm{\Omega }{\nabla }_{\parallel }c\left(r,\theta \right).$$ [6]

The integration of ${\nabla }_{\parallel }c$ for a multipolar expansion of the form $c\left(\theta ,r\right)={\sum }_l{B}_l{P}_l\left(\cos \theta \right)r^{-\left(l+1\right)}$ on a spherical shell of diameter $\sigma$ results in a velocity in $\widehat{\mathit{z}}$, the symmetry axis of the system:

$$\mathit{V}=\frac{2}{3}{\mu }_d{\left(\frac{2}{\sigma }\right)}^3{B}_1\widehat{\mathit{z}}.$$ [7]

Introducing Eqs. 4 and 5 into Eq. 7, we recover the relative velocities Eqs. 1 and 2, with a characteristic velocity $V_0=\alpha {\sigma }_a^2/\left(12D_c\right)$. We have taken into account that active and passive particles have different diffusophoretic mobilities, ${\mu }_d^{\left(a\right)}$, ${\mu }_d^{\left(p\right)}$, and have introduced their ratio, $\mu ={\mu }_d^{\left(p\right)}/{\mu }_d^{\left(a\right)}$.