Application of Graph Theory to Assess Static and Dynamic Brain Connectivity: Approaches for Building Brain Graphs

Abstract

Human brain connectivity is complex. Graph theory based analysis has become a powerful and popular approach for analyzing brain imaging data, largely because of its potential to quantitatively illuminate the networks, the static architecture in structure and function, the organization of dynamic behavior over time, and disease related brain changes. The first step in creating brain graphs is to define the nodes and edges connecting them. We review a number of approaches for defining brain nodes including fixed versus data-driven nodes. Expanding the narrow view of most studies which focus on static and/or single modality brain connectivity, we also survey advanced approaches and their performances in building dynamic and multi-modal brain graphs. We show results from both simulated and real data from healthy controls and patients with mental illnesse. We outline the advantages and challenges of these various techniques. By summarizing and inspecting recent studies which analyzed brain imaging data based on graph theory, this article provides a guide for developing new powerful tools to explore complex brain networks.

I. Introduction

Brain performance has been characterized and quantitatively studied using state of the art noninvasive brain imaging techniques [1–3]. For example, magnetic resonance imaging (MRI) studies have shown that brain regions are not only structurally connected [4–6] but also functionally associated when performing cognitive tasks or even in resting state [7–9]. In the last decade, graph theory based analysis has become a powerful and popular approach for assessing brain networks [10–41], largely because of its potential to quantitatively illuminate the static architecture in structure and function [42–60], the organization of dynamic behavior over time in resting state or during different cognitive tasks [61–83], the development across the lifespan [84–103], and changes in mental disorders [104–161].

Technically, when building a brain graph using imaging data, the first step is typically to define the nodes, and then build edges between them [162]. The use of fixed spatial regions of interest (ROIs) assessed by anatomical atlases based on brain structure is one of the popular methods for defining brain nodes [163]. This approach is appropriate for structural brain imaging data. However, the selected ROIs do not necessarily respect the functional boundaries of the brain [164]. Thus, more approaches have been developed for defining the nodes when building brain graphs using functional magnetic resonance imaging (fMRI) data [165], such as independent component analysis (ICA) which is adopted to decompose the whole-brain fMRI into independent spatial components (called ICA nodes) [129, 166]. Briefly, both fixed (including ROIs, voxels) and data-driven (such as ICA) methods are widely used to define the nodes in brain graph studies using fMRI data [167].

While the dynamics of both structural and functional brain connectivity across different age stages have been investigated, most previous studies hypothesize that the functional brain connectivity is static over a scanning time. However, recent fMRI experiments have shown that functional brain connectivity is dynamic on the scale of tens of seconds even during the resting state [168, 169]. Currently, more studies are investigating time varying brain graph performance [82]. While structural brain graphs can be built across different ages, functional brain graphs are built not only across the life span, but also on short time scales such as across different cognitive tasks, or even across a few minutes of the resting state [170–172].

In addition to dynamic analysis, techniques to perform multimodal fusion analysis of brain imaging data are required, because collecting multiple types of brain data from the same individual using various non-invasive imaging techniques has become a common practice [173]. A key motivation for jointly analyzing multimodal data is to take advantage of the cross-information of the existing data, thereby potentially revealing important variations that may only be partially detected by a single modality [174–176]. Recent studies have developed powerful methods to build multimodal brain graphs.

In this article, we briefly review and compare the research findings in static and dynamic (across the life span, at different ages, during various cognitive tasks, or during the resting state), structural (gray matter and diffusion image data) and functional brain graphs with nodes defined by different methods in not only healthy controls, but also patients with mental disorder. We survey advanced techniques for defining the brain nodes, building dynamic and multimodal brain graphs, and point out potential directions for developing new tools to build and characterize brain graphs. The rest of this paper is organized as follows: In Section II, we review and compare research results from static structural and functional brain graphs. In Section III, we focus on dynamic brain graphs. In Section IV, we survey studies creating brain graphs with multimodal data. Finally, we discuss the limitations of existing methods and suggest possible directions for developing new approaches in investigating different brain graphs.

II. STATIC STRUCTURAL AND FUNCTIONAL BRAIN GRAPHS

In gray matter and diffusion image structural brain graph studies, nodes are typically defined using ROIs though at multiple spatial scales. Edges are usually defined using correlation of gray matter volume or thickness, or fiber tracks (connections) between pairs of ROIs in gray matter and diffusion magnetic resonance imaging (dMRI) data respectively.

When building brain graphs in fMRI data, spatial brain components evaluated by group ICA have been used to define data-driven nodes, as opposed to fixed atlas-based ROI nodes. Edges are defined using a variety of metrics including Pearson correlation, partial correlation, or wavelet-based frequency dependent correlation between the time courses of any pair of nodes.

A. Structural Brain Graphs Built with ROIs

A main finding of gray matter structural brain graph studies is that the topology of structural brain networks shows “small world” properties rather than random. Previous studies have defined the nodes in ROIs from different ways, such as using 3 × 3 × 3 voxel cubes (size corresponding to 6 × 6 × 6 mm³) as nodes [177], or using 104 ROIs defined by atlas images as nodes [115]. It has also been shown that different cortical scales lead to cortical networks with different values of small-worldness when building brain graphs at 23 cortical scales (number of nodes varied from 66 to 1494) based on the Desikan-Killiany atlas [178].

Consistent with gray matter structural brain graphs, diffusion brain image-based graphs are also not random. When using 78 cortical ROIs from the automated anatomical labeling (AAL) atlas [179] as nodes, the topology of the diffusion brain image-based graph resembled a small-world architecture characterized by an exponentially truncated power-law distribution. In addition, the diffusion brain image-based graph was characterized by major hub regions in association cortices that were connected by bridge connections following long-range white matter pathways [180]. Importantly, the observed inter-scan reproducibility of the graph measures was high [181].

Diffusion brain image-based graphs have also been built at multiple scales. In a diffusion spectrum imaging (DSI) and diffusion tensor imaging (DTI) study, 90, 180, 360, 720 ROIs defined by AAL atlas, 110, 220, 440, and 880 ROIs defined by the Harvard-Oxford Atlas (HO), and 54, 108, 216 and 432 ROIs defined by the LONI Probabilistic Brain Atlas (LPBA40) were used as nodes respectively. Basic connectivity properties and several graph metrics displayed high reproducibility and low variability in both DSI and DTI networks [182].

An impressive property of previous diffusion brain image-based graphs is the so-called “rich club” organization initially identified by a study using 82 ROIs defined by Freesurfer suite as nodes. A rich club organization is characterized by a tendency for high-degree nodes to be more densely connected among themselves than nodes of a lower degree in the graph [183]. A following study which used 1170 ROIs as nodes showed that the set of pathways linking rich club regions formed a central high-cost, high-capacity backbone for global brain communication [184].

A wide application of brain graph analysis is for the detection of potential biomarkers of mental illness such as schizophrenia. Altered brain graph properties have been revealed in schizophrenia using DTI data with different nodes. When using 82 ROIs [104] and 108 ROIs [185] as nodes to build the graphs respectively, it was shown that though small-world attributes were conserved in schizophrenia, the cortex was interconnected more sparsely and up to 20% less efficiently [104], and node specific path lengths were longer in patients [185]. Another DTI study which used 90 ROIs defined by AAL as nodes discovered decreased global efficiency in schizophrenia [186].

In summary, structural brain graphs have been extensively studied using multi scale ROIs as nodes. Structural brain graphs show small-world properties with hub nodes, modular, and rich club organization, and graph measures are robust across scans. Nodes with different cortical scales may lead to different levels of small-world organization. Graph metrics including path length and global efficiency have been shown to be disrupted in schizophrenia [185, 186].

B. Functional Brain Graphs Built with ROIs

In line with structural graphs, the functional brain graphs also show small world rather than random topology. This topological property has been consistently revealed by graphs with different nodes such as the 90 ROIs come from AAL atlas [47, 105, 179, 187], and single voxels [188, 189]. For a review of the small world topology of functional brain networks see [190]. In addition to small-world property, functional brain graph show scale-free topology when using single voxels as nodes [188, 189], and significantly non-random modular organization when using AAL-based 90 ROIs as nodes [84]. Modules have been found to be consistent with cognitive function when using five different node definitions, in which each module was associated with a discrete cognitive function [191]. Moreover, functional brain graph studies strongly suggested that brain hubs play important roles in information integration underpinning numerous aspects of complex cognitive function [192].

The reliability of graph measures in functional brain connectivity has also been studied. A test-retest study of graphs with 90 ROIs defined by AAL as nodes estimated the reliability of various graph measures including clustering coefficient, characteristic path length, local and global efficiency, assortativity, modularity, hierarchy and small-worldness. Results showed that the second order metrics (small-worldness, hierarchy, assortativity) tended to be more robust than first order metrics (clustering coefficient, characteristic path length, modularity, global and local efficiency) [193].

Similar to structural brain graphs, functional brain graphs have been built with ROIs in multiple spatial resolutions as well. It was found that the graphs with nodes of higher resolution exhibited the small-world properties more prominently. And region-based graphs fragmented more at high thresholds than voxel-based graphs, suggesting region-based graphs are less robust [194]. Although the degree distributions of all graphs followed an exponentially truncated power law rather than a true power law, the higher the resolution, the closer the distribution was to a power law. Furthermore, voxel-based analyses enhanced visualization of the results in the 3D brain space. These results demonstrated benefits of constructing the brain graph at the finest scale [194]. Another study built functional brain graphs with seven different parcellation resolutions (84, 91, 230, 438, 890, 1314, and 4320 regions) based on the AAL atlas. Results showed that gross inferences regarding graph topology, such as whether the brain was small-world or scale-free, were robust. But both absolute values of, and individual differences in, specific parameters such as path length, clustering, small-worldness, and degree distribution descriptors varied considerably across the resolutions [49]. Brain graphs with 90 (AAL) or 70 (Automated Nonlinear Imaging Matching and Anatomical Labelling [ANIMAL-atlas] [195]) ROIs as nodes were found to show robust small world properties and truncated power-law connectivity degree distribution. However, significant differences in multiple topological parameters (e.g., small-worldness and degree distribution) between the two graphs were revealed [196].

Functional brain graphs have been extensively investigated in brain disorders. Using AAL-based 90 ROIs as nodes, pairwise functional connectivity was found to be decreased and the variance was increased in schizophrenia [124]. Graph measures including degree, clustering coefficient, global efficiency, and local efficiency were decreased and path length was increased in patients with schizophrenia [122]. These findings were repeated in another fMRI study which used 72 ROIs defined by AAL as nodes [107]. Altered community structure was also reported in schizophrenia in graphs with 278 ROIs nodes defined with FSL’s cortical and subcortical Harvard-Oxford probabilistic atlas [197].

In addition to schizophrenia, disruptions of functional brain graphs have also been studied in other brain disorders including Alzheimer’s disease [198, 199], amnestic mild cognitive impairment (aMCI) – the prodromal stage of Alzheimer’s disease [200], major depressive disorder [201], children with frontal lobe epilepsy (FLE) [202], children with attention-deficit/hyperactivity disorder (ADHD) [203], and mesial temporal lobe epilepsy (mTLE) patients [204] using different ROI nodes.

In summary, functional brain graphs with high resolution voxel level rather than low resolution brain region level nodes showed less fragmentation. The higher resolution graphs exhibited more prominent small-world properties, and the higher the resolution, the closer the degree distribution was to a power law [194]. However, there were some disadvantages when defining the nodes at voxel level. For example, some voxels may be located completely in white matter, thus it was difficult to remove the effects of white matter signal fluctuations [49]. In addition, computational burden was high for calculating graph metrics in weighted voxel-based brain graphs. Optimization of these computational algorithms is an important goal [194]. Notably, graph measures were largely disrupted in brain disorders.

C. Functional Brain Graphs Built with ICA Nodes

There are some limitations when defining the ROI nodes in functional MRI data based on anatomical brain atlases. For example, The ROIs may not correspond well to real functional boundaries [167] in the brain or fully capture individual subject variability [179, 205–207]. Although functional connectivity-based data-driven methods for brain parcellation have been developed both at the group [208–212] and individual level [213, 214], no study to our knowledge has used these approaches to define brain nodes for building graphs. In contrast, ICA is a popular data-driven method for defining the nodes to mitigate these limitations of ROI-based nodes in building functional brain graphs using fMRI data. In this approach, the fMRI data of a group subjects are firstly decomposed into a number of spatial components. Then single subject components and their associated time courses are back-reconstructed [215–218]. The graph nodes of spatial brain components evaluated by ICA are functionally homogeneous and may capture individual differences better than anatomical atlas-based ROI nodes [166, 215, 216, 219]. Using this node definition approach, the topology of brain graphs has also been revealed to be small world and modular with hub nodes. Moreover, alterations of graph measures including connectivity strength, clustering coefficient, local efficiency, characteristic path length, global efficiency, modularity, and rich club parameters were discovered in schizophrenia [55, 127–129]. However, limitations of defining nodes using ICA include spatial overlap of some of the nodes (though this can potentially be an advantage as well [220]), and the number of nodes/components need to be selected [129, 220].

D. Comparing ROI and ICA Methods for Building Functional Brain Graphs using Simulations

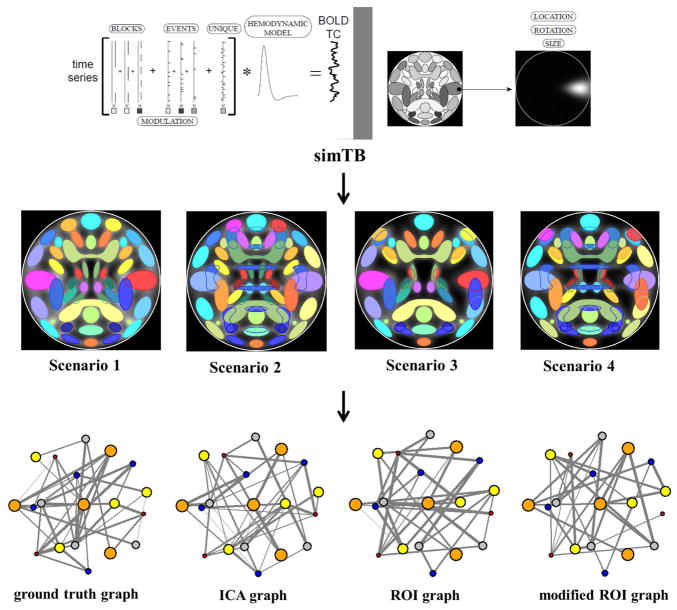
An important and open question is that which method (atlas-based ROI vs data-driven ICA) can better define the nodes of brain graph in fMRI data. Using simulated data to evaluate the node definition methods may be promising, because different scenarios can be estimated and graph measures computed with different nodes can be compared to a known ground truth. In one recent study [221], simulated data was generated using SimTB (http://mialab.mrn.org/software/simtb/), a MATLAB toolbox which implements a data generation model consistent with spatiotemporal separability, that is, data can be expressed as the product of time courses (TCs) and spatial maps (SMs) (for details of the data generation model in SimTB see Erhardt et al 2012 [222]). Four scenarios involving different SM configurations were analyzed. In scenario 1, spatial maps (SMs) were created with little overlap. In scenario 2, twenty-nine SMs were with little overlap plus three artificial SMs. In scenario 3, SMs were with large overlapping. In scenario 4, SMs were with large overlapping and included 3 “artefactual” SMs.

Four kinds of undirected weighted graphs were built based on the simulated data in each scenario. The number of nodes (N) was same in all graphs (N = 29). In scenarios 2 and 4, three artefactual SMs associated nodes were excluded when building the four types of graphs.

1. Ground truth graph. In this graph, the nodes were SMs (excluding artifacts if any) in the simulation. Edges were the Pearson correlation between each pair of simulated time courses of the SMs.

2. ICA graph. In this graph, the nodes were spatial independent components obtained by group ICA performed on the simulated data. Edges were the Pearson correlation between each pair of ICA time courses of the components.

3. ROI graph. In this graph, the nodes were ROIs which were defined base on the SMs of the simulation using a threshold of 0.8. Time series of voxels within each ROI were averaged into one representative time course. Edge weights of the graph were the Pearson correlation between each pair of representative time courses of the ROIs.

4. Modified ROI graph (MROI-graph). When using ROIs as graph nodes, the ROIs are usually defined base on a brain atlas which will not perfectly match the variation in an individual subject. To simulate the effects of individual subject variability in brain shape and functional domains, and compare with the ideal ROI scenario, a MROI-graph (in which nodes deviate from the ground truth ROIs to reflect subject variability) was built and examined. In this graph, the nodes were spatially moved up to 15% of the area of the ROI. See Yu et al. [221] for details of the method. See figure 1 for a pipeline of the analysis in that study.

Fig. 1.

An analysis pipeline of the simulation study which compared graphs with ROI nodes and ICA nodes [221]. Simulated fMRI data were generated in four scenarios using SimTB. Group ICA was performed on the simulated data. Graphs with different nodes (ground truth nodes, ICA nodes, ROI nodes, and modified ROI nodes) were then built. Graph metrics between the ground truth graph and any other graph were compared. (The figure was reproduced with permission from both author and journal of Yu et al. 2017 [221].)

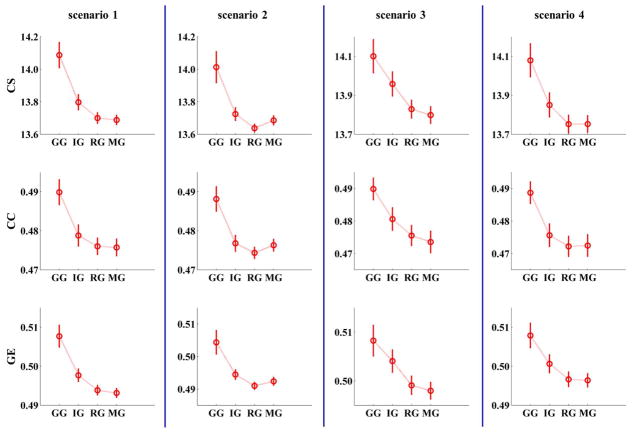
When comparing the measures including connectivity strength, clustering coefficient, and global efficiency of graphs with ROI nodes and ICA nodes with ground truth, results showed that in all scenarios, values of all graph metrics for the data-driven ICA graph (compared to the ROI and MROI graphs) were closer to the ground truth graph. In the cases with no artifacts (scenarios 1 and 3), graph measures in the MROI graph were far away from ground truth compared to the ROI graph. However, in cases with artifacts (scenarios 2 and 4), graph measures of the MROI graph were closer to ground truth than the ROI graph (see Figure 2). Since ROIs are typically defined using anatomical atlases which may not correspond well to real functional boundaries in the brain or to individual subject variability, these findings suggest that a data-driven ICA method is more accurate compared to a fixed ROI method for defining graph nodes in functional brain network studies. Similar conclusions have also been shown in another study [223].

Fig. 2.

Results of a simulation study which compared graphs with ROI nodes and ICA nodes (Yu et al. [221]). The measures of graphs with different nodes (GG: ground truth graph; IG: ICA graph; RG: ROI graph; MG: modified ROI graph) in all four scenarios. All measures of ICA graphs are closer to ground truth than ROI graphs and MROI graphs. (CS: connectivity strength; CC: clustering coefficient; GE: global efficiency). (The figure was reused with permission from both author and journal of Yu et al. 2017 [221].)

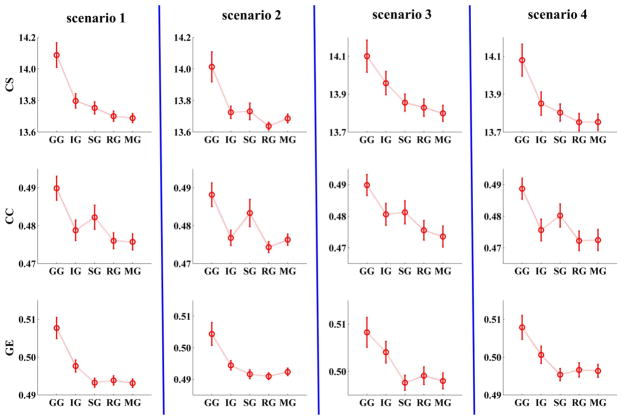
Since previous studies have shown some benefits of using single voxel than ROI with a group of voxels as graph node, a voxel level graph was also estimated in that simulation study. In this graph, each node was the voxel with the highest intensity value in each of the 29 SMs. Results were mixed. The clustering coefficient for the voxel level graph was closer to ground truth than the ICA graph, the ROI graph, and the MROI graph. Connectivity strength of voxel level graph was closer to ground truth then the ICA graph in scenario 2. Global efficiency of voxel level graph was further from the ground truth than the ICA graph (see Figure 3). These findings suggest that graph metrics of voxel level graphs do not consistently reflect ground truth better than ICA graph.

Fig. 3.

Measures of graphs built with different node definition methods in simulated data. Clustering coefficient of voxel level graph is closer to ground truth than ICA graph, ROI graph, and MROI graph. Connectivity strength of voxel level graph is closer to ground truth then ICA graph in scenario 2. Global efficiency of voxel level graph is further to ground truth than ICA graph. (GG: ground truth graph; IG: ICA graph; SG: single voxel level graph; RG: ROI graph; MG: modified ROI graph; CS: connectivity strength; CC: clustering coefficient; GE: global efficiency). (The figure was reproduced with permission from both author and journal of Yu et al. 2017 [221].).

However, there are limitations of the simulation findings. The simulated data were generated using a linear model (the product of time courses and spatial maps). While ICA, which is based on a linear model, has revealed robust brain networks in both resting state and task fMRI data, it is not clear whether the linear model is a perfect match for real fMRI data. In addition, the conclusions are limited to the four scenarios considered here. Future studies may simulate more scenarios for generating the ROIs such as functional connectivity based pacellation methods [208–214].

E. Comparing graphs with ROI nodes and ICA nodes to differentiate schizophrenia patients from controls

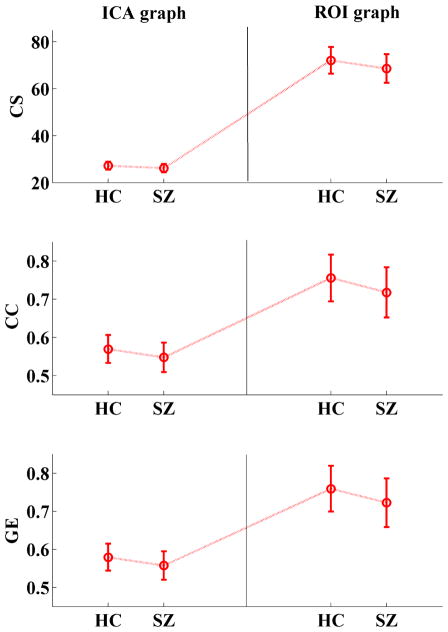
To evaluate the ability of differentiating patients from controls using graphs with different nodes, we build both an ROI graph (in which nodes are 96 ROIs selected from AAL such that each ROI has more than one gray matter voxel) and an ICA graph (in which nodes are 48 spatial brain components) in resting state fMRI data of 164 (82 controls vs 82 patients with schizophrenia) subjects. This work has not been reported before. However, for details on data collection and preprocessing see Yu et al. [172]. Results show that though two sample t-tests (controls vs patients) of graph measures (including connectivity strength, clustering coefficient, and global efficiency) are significant in both ICA and ROI graphs, p-values are lower and effect sizes (Hedges’ g) [224] are higher in the ICA graph compared to the ROI graph (see Table 1). Thus, the ICA nodes outperform the ROI nodes for differentiating patients from controls. Group mean values for the graph measures are reported in Figure 4. In order to provide a statistical view and to eliminate the possibility that the findings may due to the different number of nodes between the two types of graphs, we perform 1000 permutation analysis by randomly selecting 48 ROIs from the 96 ROIs to build ROI graphs and perform t-tests between HCs and SZs on graph measures. Results show that the p values and (Hedges’ g) effect sizes of the ICA graphs listed in Table 1 are located at about the 10^th percentile of the corresponding 1000 permutated values.

TABLE I.

P values and effect sizes (Hedges’ g) of two sample t-tests (controls vs patients) on graph measures in ICA graph, ROI graph, and voxel level graph. (CS: connectivity strength; CC: clustering coefficient; GE: global efficiency)

		CS	CC	GE
P value	ICA graph	7.73 × 10 (-5)	1.13 × 10 (-4)	7.12 × 10 (-5)
	ROI graph	1.89 × 10 (-4)	1.91 × 10 (-4)	1.91 × 10 (-4)
	Voxel level graph	5.15 × 10 (-5)	5.09 × 10 (-5)	5.24 × 10 (-5)
Effect size	ICA graph	0.63	0.62	0.63
	ROI graph	0.59	0.59	0.59
	Voxel level graph	0.65	0.65	0.65

Fig. 4.

Group mean of graph measures in controls and patients with schizophrenia in graph with ICA nodes and ROIs. Error bars correspond to standard deviation. Two sample t-tests show that graph measures are significantly (p < 0.001) lower in patients than controls in both ICA graph and ROI graph. However, p values are lower and effect sizes (Hedges’ g) are higher in ICA graph then ROI graph (see Table 1). (HC: healthy controls; SZ: patients with schizophrenia; CS: connectivity strength; CC: clustering coefficient; GE; global efficiency)

A voxel level graph (with 96 nodes) is also constructed to estimate the ability of single voxel graphs in differentiating the two groups. In this graph, each of 96 nodes is a gray matter voxel randomly selected in each of the 96 AAL ROIs. Two sample t-tests of graph measures in the two groups of subjects show that p values are a little lower than those of the ICA graph and the ROI graph, and effect sizes (Hedges’ g) are a little higher than the results of those two graphs (see Table 1). Again, we perform 1000 permutation analyses by randomly selecting 48 ROIs from the 96 ROIs and build voxel level graphs with 48 single voxels from these 48 ROIs. T-tests (HCs vs SZs) are performed in each permutation. This time, the p values and (Hedges’ g) effect sizes of the ICA graphs listed in Table 1 are located at about the 40^th percentile of the corresponding 1000 permutated values. Due to computational load for calculating graph measures of large weighted graphs [194], we do not run the tests with all voxels in this study.

III. Dynamic BRAIN graphs

Recent brain imaging studies have shown that brain connectivity is dynamic rather than static over time [169]. The dynamics of brain connectivity have been studied at different age stages (life span), during different cognitive tasks, and during the resting state. Dynamic graph analysis is a powerful tool to quantitatively characterize the time evolving brain performance in a system level.

A. Development of Structural and Functional Brain Graphs with ROI Nodes

Using 82 ROIs as graph nodes, a DTI study investigated the development throughout childhood and adolescence (7 –23 years). Results showed a simultaneous age-related decrease in average path length and increase in node strength and network clustering, which may reflect fine-tuning of topological organization in brain development [95]. When assessing the developmental changes of diffusion brain image-based graph in an age range (19 – 85 years) using 78 cortical ROIs from AAL as graph nodes, a reduction in overall cortical connectivity with age, and decreased local efficiency in older brains were revealed [225]. Another DTI brain graph study which involved 882 participants (ages 8 – 22) showed that structural modules became more segregated with age. Evolving modular topology facilitated global efficiency and was driven by age-related strengthening of hub edges. In addition, both modular segregation and graph efficiency were associated with enhanced executive performance and mediated the improvement of executive functioning with age. These results delineated a process of structural network maturation that supports executive function in youth [75]. Another more recent brain graph study also used DTI data of 882 participants (ages 8 – 22) to investigate how structural connectivity facilitates changes and constrains patterns of dynamics in the developing brain. That work draw on the computational tools and conceptual frameworks of theoretical physics and engineering to study two complementary predictors of brain dynamics, controllability and synchronizability, which separately predict the brain’s ability to transition to nearby vs. distant states, or to maintain a single state characterized by a stable temporal dynamic. Results showed that white matter connectivity becomes increasingly optimized for a diverse range of predicted dynamics in development. Notably, stable controllers in subcortical areas were negatively related to cognitive performance. These findings suggested that the brain optimizes the controllability at the expense of the synchronizability. That optimization occurred during development in youth aged 8 – 22 years, and individual differences in control architecture of white matter were correlated with individual differences in cognitive performance. Impressively, that work used forward-modeling computational approaches to identify constrained evolutionary trajectories which provided evidence that network control is a key mechanism in development [226].

Functional brain graphs in resting state fMRI data were studied using 264 ROIs which were identified by meta-analyses in task fMRI data and connectivity mapping of resting state fMRI data [227–229] as nodes to quantify the formation of graph modules across age 8 – 22 years. It was shown that functional graph organization changes in youth through a process of modular evolution that was governed by the specific cognitive roles of each system, as defined by the balance of within- vs. between-module connectivity, which suggested that dynamic maturation of network modules in youth may be a critical driver for the development of cognition [68]. Another study used the same 264 ROIs as nodes and revealed that brain networks in the elderly (older: 59 – 74 years; younger: 18 –26 years) showed decreased modularity and decreased local efficiency [230].

Using task fMRI data, a study investigated age-related change of brain connectivity during memory encoding and recognition. Ninety ROIs from AAL atlas were used as nodes. It was found that age-related changes mainly occurred in long-range connections with widespread reductions. The older adults (75 – 87 years) had longer path lengths linking different regions in the functional brain networks as compared to the younger adults (20 – 27 years). The increases in shortest path length in the networks were combined with the loss of long-range connections. These findings suggest that normal aging was associated with disruption of large-scale brain systems during the performance of memory tasks [231].

Development of functional brain graphs have also been examined with nodes at multiple scales. One study in which subjects were 10 – 20 years old used two methods to define nodes: 1. voxel-wise approach in which each 4 mm³ gray matter voxel as a node; 2. 160 ROIs defined based on a meta-analysis of fMRI activation. Results showed that hub architecture was evident in late childhood and was stable from adolescence to early adulthood. Connectivity between hub and non-hub regions changed with development from childhood to adolescence [232].

When examining the developmental changes in graph organization, connectivity strength, and integration to inhibitory control development across four stages, childhood (10 – 12 y olds), early adolescence (13 –15 y olds), late adolescence (16 – 19 y olds), and adulthood (20 – 26 y olds), using 264 ROIs which were identified by meta-analyses in task fMRI data and connectivity mapping of resting state fMRI data [227–229] as nodes, results indicated that network organization was stable throughout adolescence. However, cross-network integration increased with age. Those findings provided compelling evidence that the transition to adult-level inhibitory control was dependent upon the refinement and strengthening of integration between specialized networks, and supported a novel, two-stage model of neural development, in which networks stabilize prior to adolescence and subsequently increase their integration to support the cross-domain incorporation of information processing critical for mature cognitive control [170].

In summary, brain graphs with ROI nodes initially change with age by decreasing path length, and increasing connectivity strength, clustering coefficient, local efficiency, and modularity for enhancing the integration of information processing from childhood to adolescence (young adult). The change of these graph measures was reversed from young adults to elder adults.

B. Functional Brain Graphs across Cognitive Tasks

When using single voxels as nodes to build brain graphs using fMRI data of different tasks or cognitive states including resting state, visual stimulation, and multisensory (auditory and visual stimulation) conditions, results showed that despite stability of graph measures at global level, brain graphs exhibited considerable task-induced changes in connectivity, efficiency, and community structure at the nodal level [171].

Another task fMRI study used 264 ROIs which were identified by meta-analyses in task fMRI data and connectivity mapping of resting state fMRI data [227–229] as nodes, and found that the frontoparietal brain network (FPN)’s brain-wide functional connectivity pattern shifted more than those of other networks across a variety of task states. These connectivity patterns could be used to identify the current task which supported a central role for frontoparietal flexible hubs in cognitive control and adaptive implementation of task demands [233].

C. Sliding Window Based Functional Dynamic Brain Graphs

Sliding window is a popular method for assessing dynamic functional connectivity in fMRI data across a short time (a few minutes to a few hours) [169, 234]. When using the sliding window method to build a dynamic resting state fMRI graphs with 264 ROIs, which were identified by meta-analyses in task fMRI data and connectivity mapping of resting state fMRI data [227–229] as nodes, it has been shown that brain regions spontaneously changed their module affiliations on a temporal scale of seconds. These dynamics were highly reproducible across repeated scanning sessions [82]. Another sliding window graph study which used ROIs with multiple scales as nodes discovered that the most dynamic connections were inter-module, and localize to known hubs of default mode and frontoparietal systems. In addition, spatially distributed regions spontaneously increased the efficiency with which they can transfer information, producing temporary, globally efficient network states, which suggested that brain dynamics give rise to variations in complex network properties over time, possibly achieving a balance between efficient information-processing and metabolic expenditure [83].

However, some properties have been found to be static across sliding window graphs. For example, when using 90 ROIs from AAL atlas and a random parcellation of 1024 ROIs as nodes, dynamic functional graphs exhibited evident small-world and assortativity architecture, with several regions (e.g., insula, sensorimotor cortex and medial prefrontal cortex) emerging as functionally persistent hubs though possessing large temporal variability in their degree centrality [235].

Another interesting dynamic graph called a hypergraph [236] can be built based on time-varying graphs. For example, a study firstly established sliding window graphs using 194 ROIs as nodes in fMRI data from a task-free resting state, an attention-demanding state, and two memory-demanding states. Then hypergraphs in which nodes were the edges in the graph of 194 ROIs were constructed. Results identified the presence of groups of functional interactions that fluctuated coherently in strength over time both within (task-specific) and across (task-general) brain states, demonstrating that brain adaptability can be described by common processes that drive the dynamic integration of cognitive systems [67]. Another study used a hypergraph approach in fMRI data of 780 participants (ages 8 – 22) to investigate the development of functional brain connectivity. Three distinct classes of subnetworks (hyperedges) including clusters, bridges, and stars were revealed. Cluster hyperedges showed a strong resemblance to previously described functional modules of the brain including somatomotor, visual, default mode, and salience systems. In contrast, star hyperedges represented highly localized subnetworks centered on a small set of regions, and were distributed across the entire cortex. Finally, bridge hyperedges linked clusters and stars in a core-periphery fashion, with the greatest developmental effects occurring in networked hyperedges within the functional core [89]. The hypergraph method has also been used to evaluate individual differences in dynamic functional brain connectivity across the human lifespan [88].

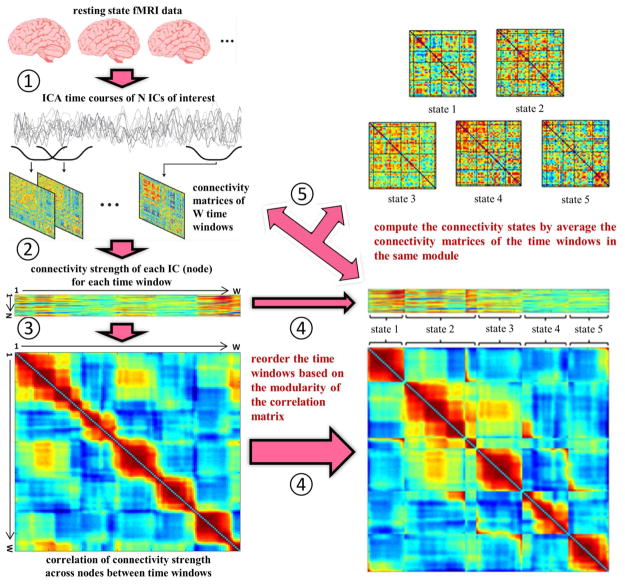
When assessing dynamic functional brain connectivity using the sliding window approach, brain states with different connectivity patterns can be detected by k-means clustering or decomposition methods [237]. Both k-means and decomposition methods require selecting the number of states [168]. One can also use time-varying graph measures to examine the brain states during the resting state using ICA nodes. This method was developed by a study which firstly constructed time-varying dynamic graphs with ICA nodes using sliding windows. Then connectivity states were detected based on the correlation of nodal connectivity strength between time-varying brain graphs. Results show that patients with schizophrenia exhibit decreased variance in the dynamic graph metrics [172]. For a pipeline of this approach see Figure 5.

Fig. 5.

The flowchart of the algorithmic pipeline for a method of evaluating connectivity states base on graph analysis of ICA nodes developed in one of our studies [172]. Five steps were labeled as follows. ➀ do group ICA, segment ICA time courses, and calculate the correlation between any pair of (N = 48) independent components (ICs) for each time-window; ➁ compute nodal connectivity strength of the weighted brain graph for each time-window; ➂ calculate the correlation of nodal connectivity strength between any pair of time-windows (W = 131) across (N = 48) ICs; ➃ reorder the time-windows based on the modular organization of the correlation matrix; ➄ compute the brain connectivity states by averaging the connectivity matrices of the time windows belonging to the same module. (The figure was reused with permission from both author and journal of Yu et al. 2015 [172].)

In summary, functional brain graphs are indeed dynamic across different time scales. Sliding window is the most popular method to build dynamic brain graphs across a relatively short time (a few minutes to a few hours), though there are many other approaches which are adapted as well [238].

IV. Multimodal graphs

As there has been increasing interest in performing multimodal analysis of brain imaging data, more approaches are being developed to build multi-modal brain graphs which may be helpful to understand the physiological, electrophysiological, or even genetic basis of the topological properties in brain connectivity.

A. Associate Single Modal Brain Graph with Other Modalities

Combing functional and structural brain data may reveal the structural basis of the functional brain graphs. To this end, one study built functional brain graphs with nodes defined by ROIs of AAL atlas using fMRI data acquired during an episodic memory-for-context task in both healthy controls and patients with schizophrenia, and performed a morphometric analysis to investigate schizophrenia-related deficits. Functional graphs showed significant reductions in local efficiency in schizophrenia. Structural data showed several key network “hub” regions including bilateral dorsal anterior cingulate gyrus with reduced gray matter volume in schizophrenia patients. These findings suggest that loss of gray matter volume may contribute to local inefficiencies in the architecture of the functional graph underlying memory-for-context in schizophrenia [239]. Another study combined high-resolution diffusion weighted imaging (DWI) with resting-state fMRI. DWI data were used to build structural graph with 1170 ROIs segmented by Freesurfer as nodes, and eleven resting state brain networks were detected by ICA in fMRI data. By associating structural graphs with functional networks, new evidence suggesting that the brain’s rich club serves as a macroscopic anatomical substrate to cross-link functional networks was provided. Such links likely play an important role in the integration of information between segregated functional domains of the human cortex [240].

The relationship of functional hubs to measures of brain physiology (regional cerebral blood flow, rCBF) had been studied using fMRI data and arterial-spin-labeling (ASL) perfusion data during resting state and an N-back working-memory task. During the resting state, functional graphs were built at the voxel-level and hubs with higher functional connectivity strength (FCS) were identified. The FCS showed a striking spatial correlation with rCBF. During the working memory task, task-induced changes of FCS and rCBF in the lateral-parietal lobe positively correlated with behavioral performance. Together, these findings suggest a tight coupling between blood supply and brain functional topology during rest and its modulation in response to task demands [241].

B. Associate Graphs Built in Different Modalities

Building graphs with same nodes using different datasets is powerful, because the graphs may be directly compared. A life span study built fMRI and diffusion brain image-based graphs using 114 ROIs which demonstrated that both whole brain functional and structural connectivity exhibit reorganization with age. Components of the control, default mode, saliency/ventral attention, dorsal attention, and visual networks became less functionally cohesive, as evidenced by decreased component modularity. Paralleling this functional reorganization was a decrease in the density and weight of anatomical white-matter connections. Hub regions were affected by these changes, and the capacity of those regions to communicate with other regions exhibits a lifelong pattern of decline. Functional connectivity along multi-step structural paths tends to be stronger in older subjects than in younger subjects [85].

Associations between sMRI (gray matter) graphs and magnetoencephalography (MEG) graphs were also investigated. One study used 78 AAL cortical ROIs as nodes in both sMRI and MEG data to build structural and functional brain networks respectively in both healthy controls and multiple sclerosis (MS) patients. A beamformer approach was adopted to map the MEG data from sensor level to source space within the cortical ROIs. In MS patients, a more regular network organization for structural covariance graphs and for functional graphs in the theta band and a more random network organization for functional graphs in the alpha2 band were revealed. By computing the correlation coefficient between structural and functional connectivity measures across the nodes, a positive association between covariation in thickness and functional connectivity in especially the theta band in MS patients was revealed [242]. Another work studied the association among three graphs (fMRI, MEG, and structural MRI). FMRI and MEG graphs were built using the 78 AAL ROIs as well. By computing an overlap metric, a high overlap of nodes with high degree in these two resting-state functional graphs was found in fMRI and especially alpha band in MEG. This overlap was characterized by a strongly interconnected functional core network in temporo-posterior brain regions. After combining with structural data, by building a distance vs degree reconfiguration model, it was discovered that this functional core network could be explained by a trade-off between the product of the degrees of structurally-connected regions and the Euclidean distance between them. For both fMRI and MEG, the product of the degrees of connected regions was the most important predictor for functional network connectivity. Together, these results indicate that, irrespective of the modality, a functional core network in the human brain is especially shaped by communication between high degree nodes of the structural network [243].

C. Graphs with Multimodal Nodes

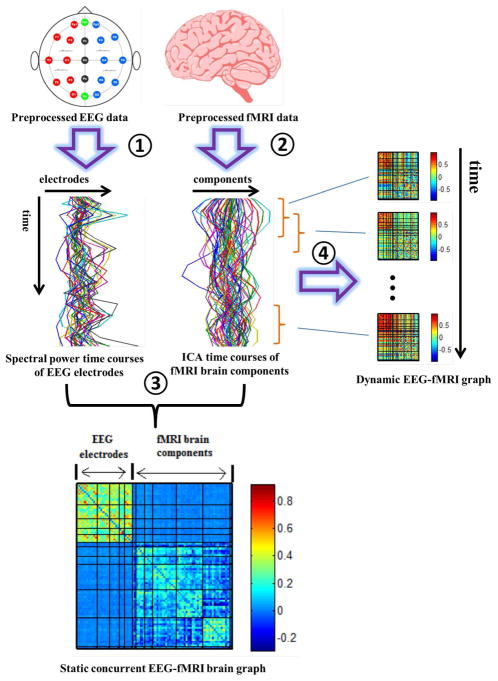
Another interesting approach for analyzing multimodal graph is to build a graph with nodes from multi-modalities. For example, an approach for building concurrent EEG-fMRI multi-modal brain graphs has been developed in which nodes are fMRI ICA spatial maps and EEG electrodes [244]. In that study, both static and dynamic EEG-fMRI graphs were estimated. Concurrent EEG-fMRI data were simultaneously collected during eyes open (EO) and eyes closed (EC) resting states. EEG time series were segmented into time windows with 2 seconds length (which was the TR of the fMRI data), and then spectral power of 5 frequency bands (delta; theta; alpha; beta; low gamma) of each time window was computed. Thus, the temporal resolution of EEG spectral power time courses was matched to that of the fMRI time series. At the global level, static graph measures and properties of dynamic graph measures were different across frequency bands and were mainly showing higher values in eyes closed than eyes open. Nodal level graph measures of a few brain components were also showing higher values during eyes closed in specific frequency bands. Overall, these findings incorporated fMRI spatial localization and EEG frequency information which could not be obtained by examining only one modality [244]. However, graph metrics were computed based on the formula defined for a single-modal (classical) graph. It is unclear how global level graph measures within a multi-modal graph are affected by the distribution of edges and nodes from different modalities. Thus, future studies should define new methods for computing topological measures in graphs with multimodal nodes. See Figure 6 for a pipe line of this method.

Fig. 6.

Pipeline for building concurrent EEG-fMRI multi-modal brain graphs (from Yu et al. [244]). ➀ Segment EEG signal into 2s time windows, and compute the average spectral power within a selected frequency window. ➁ Perform group ICA on fMRI data. ➂ Compute the correlation coefficient within and across the EEG spectral power’s and fMRI ICA’s full time courses, generating one EEG-fMRI static connectivity matrix for each frequency band. ➃ Segment EEG spectral power and fMRI ICA time courses into time windows, then compute the correlation between each pair of time windowed time courses to get dynamic EEG-fMRI brain graphs. (The figure was reused with permission from both author and journal of Yu et al. 2016 [244].)

Another work constructed graphs with multi-modality nodes and investigated how different brain areas were associated to genetic disorders and risk genes. In particular, a tripartite graph with genes, genetic diseases, and brain areas as nodes was constructed based on the associations among them reported in the literature through text mining. In the resulting graph, a disproportionately large number of gene-disease and disease-brain associations were attributed to a small subset of genes, disease, and brain areas. Furthermore, a small number of brain areas were found to be associated with a large number of the same genes and diseases. These core brain regions encompassed the areas identified by the previous genome-wide association studies, and suggest potential areas of focus in the future imaging genetics research [245].

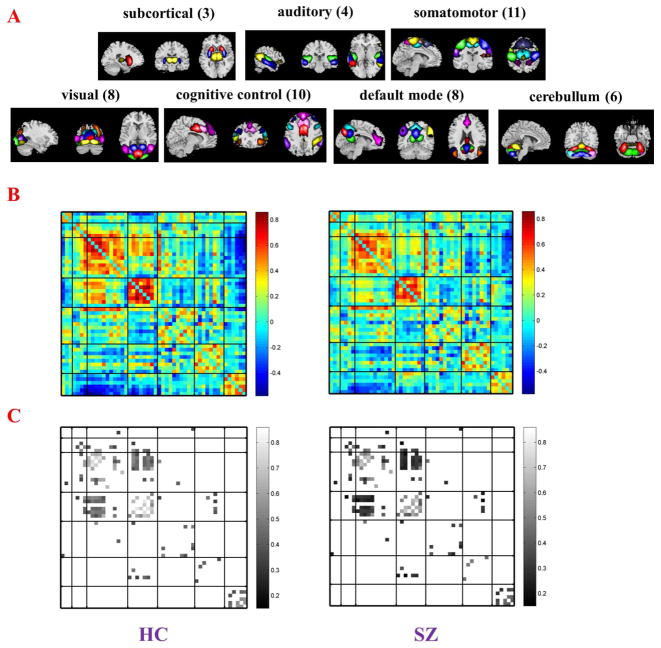
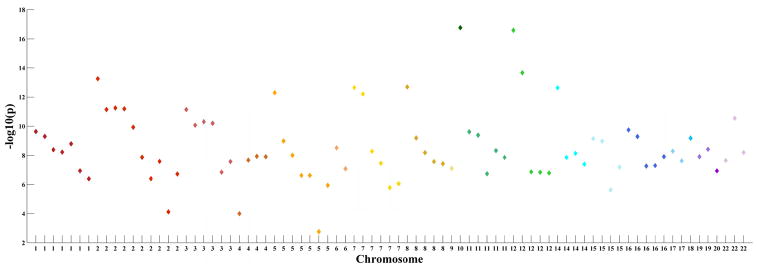
To explore genetic basis of functional brain connectivity, we build a bipartite graph which includes fMRI nodes and genetic nodes using a cohort consisted of 97 healthy controls and 70 patients with schizophrenia for which good-quality resting state fMRI and single nucleotide polymorphism (SNP) data have been collected. This analysis has not been reported before. However, for details on recruiting information and data processing see Damaraju et al. [246] and Chen et al. [247]. To define the brain nodes, fMRI are firstly decomposed into spatial components by group ICA. Then functional network connectivity (FNC) [248, 249] is estimated using the correlation between time courses of 50 brain components (Figure 7AB). In the bipartite graph which is built, fMRI nodes are not brain components. Instead, each fMRI node is a connection in the FNC. A total of 83 connections (Figure 7C) of the FNC show significant group difference (p < 0.05, FDR correction) are selected as the fMRI nodes. The genetic nodes in the bipartite graph are 81 schizophrenia associated SNPs selected base on the Psychiatric Genomics Consortium (PGC) study [250]. See Figure 8 for a Manhattan plot of these 81 SNPs. To define edges in the bipartite graph, the association between each pair of nodes (one from fMRI and the other from SNPs) is assessed across all 167 subjects using a multivariate regression model (http://mialab.mrn.org/software/mancovan) in which fMRI connectivity (correlation values of FNC connections) is the dependent variable, SNP allele (0, 1, or 2) is the independent variable, and data sites, diagnosis groups, and race are covariates. If the p value of any pair of fMRI node and SNP node is smaller than 0.05 (uncorrected), there is a link between them. Thus, the bipartite graph is a binary network. For the structure of this bipartite graph see Figure 9. Degree of each node is computed. SNPs with high degree in this SNP-FNC bipartite graph may modulate more functional brain connectivity. See Table 2 for the name of 81 SNP nodes and their degree. This analysis provides a new model to examine brain imaging and genetic associations. It can be adopted to investigate genetic basis of functional brain connectivity that is further related to mental illnesses.

Fig. 7.

Spatial maps (A) of 50 brain components which are selected to compute the functional network connectivity (FNC). Brain components are divided into groups and arranged based on their anatomical and functional properties. Structure of group mean FNC (B; HC: healthy controls; SZ: patients with schizophrenia) shows that brain connectivity is lower in SZ. Eighty three connections (C) in the FNC are selected to be nodes for constructing the SNP-FNC bipartite graph.

Fig. 8.

Scatter plots which showing schizophrenia associations of the selected 81 SNPs as genetic nodes and the distribution of them across chromosomes. The x axis is chromosomal position and the y axis is the significance (−log10(p)) of association as reported by the PGC study [250].

Fig. 9.

Structure of the genetic-fMRI bipartite graph. Some SNP nodes are showing high degree.

TABLE II.

Eighty one SNP nodes and degree of them in the fMRI-genetic bipartite graph.

SNP	degree	SNP	degree	SNP	degree
‘rs10503253’	31	‘rs778341’	5	‘rs9906500’	2
‘rs4674917’	24	‘rs2068012’	5	‘rs12903146’	2
‘rs7201930’	21	‘rs12129573’	4	‘rs4648845’	2
‘rs79235996’	15	‘rs9611520’	4	‘rs67401222’	2
‘rs604362’	14	‘rs4481150’	4	‘rs1209749’	2
‘rs3784399’	14	‘rs5995756’	4	‘rs12446487’	2
‘rs12623667’	14	‘rs1501362’	4	‘rs7722581’	2
‘rs7267348’	13	‘rs10206411’	4	‘rs10860955’	2
‘rs4908939’	12	‘rs7197756’	4	‘rs6867549’	2
‘rs11693094’	11	‘rs12939020’	4	‘rs2007044’	1
‘rs1009080’	9	‘rs2789605’	4	‘rs7108770’	1
‘rs34026011’	8	‘rs215411’	4	‘rs2973155’	1
‘rs11210892’	8	‘rs4129585’	3	‘rs34538000’	1
‘rs12132780’	8	‘rs11688767’	3	‘rs217326’	1
‘rs7896519’	7	‘rs16880919’	3	‘rs7438’	1
‘rs7240986’	7	‘rs2053079’	3	‘rs134900’	1
‘rs67733815’	7	‘rs11956240’	3	‘rs2693698’	1
‘rs4788190’	7	‘rs6846161’	3	‘rs17149781’	1
‘rs6670165’	7	‘rs7838490’	3	‘rs211792’	1
‘rs2851447’	6	‘rs1355585’	3	‘rs4546329’	0
‘rs9876421’	6	‘rs2300990’	3	‘rs12705304’	0
‘rs1076884’	6	‘rs10745572’	3	‘rs68002929’	0
‘rs4728408’	6	‘rs8039305’	2	‘rs11229116’	0
‘rs7018304’	6	‘rs13240464’	2	‘rs1470276’	0
‘rs7927176’	6	‘rs787983’	2	‘rs832190’	0
‘rs13227554’	5	‘rs2514218’	2	‘rs302321’	0
‘rs11693528’	5	‘rs66691851’	2	‘rs2909456’	0

In summary, there are three main ways to perform graph analysis in multimodal data. 1. Graphs built in one modality and then are associated with information from other modalities. 2. Graphs built in different modalities with the same nodes so that they are comparable. 3. A single multimodal graph in which nodes are formed using multi-modality data. Such approaches can expand our knowledge of the brain by linking together various complementary modalities.

V. Conclusion and perspective

In this article, we briefly review the findings of brain graphs in which nodes are defined using different methods. While structural (gray matter and diffusion image-based) brain graphs can be constructed using ROI nodes at different spatial resolutions, functional brain graphs may be built using either ROI or ICA nodes. Generally, both structural and functional brain graphs show features of complex networks, such as small world and scale free topology, rich club and modular organization with highly connected hubs. Moreover, those graph properties and some other measures such as clustering coefficient, local efficiency, global efficiency, path length show changes in patients with brain disorders in both graphs with ROI nodes and ICA nodes. These brain graph features have been studied at different time scales (across the life span, in different cognitive states, or moment to moment) as well as in multi-modality data.

When building brain graphs with ROI nodes at different spatial resolutions, it has been shown that the higher the resolution the more prominent is small-world properties. Region-based graphs fragmented more tremendously at high thresholds than voxel-based graphs, implying more robust graphs with high resolution nodes. ICA is a data-driven method for defining brain nodes in fMRI data that may mitigate some of the limitations of anatomical atlas-based nodes by providing regions that are temporally coherent and also adaptive to individual subjects. Graphs with different numbers of ICA spatial components have not been fully investigated. ROI and ICA-based methods for defining the graph nodes were compared in a simulation study, which revealed that graphs built with ICA nodes were closer to the ground truth than graphs built with ROI nodes, though this conclusion is limited to the scenarios that were simulated. More comparisons among graphs with nodes defined by different methods using real fMRI data are required in future studies. A potential direction is to perform data mining methods including deep learning, support vector machine classification, or clustering on topological measures of the brain graphs built with different nodes to evaluate which method performs better for classifying healthy controls and patients. Such approaches may have some clinical utility in the future; though it is also important to recognize that classification accuracy does not equate to advances in understanding the mechanisms of brain disease. For this, it is important to evaluate the predictive features in order to build new models of disease that can be tested in future work. Future studies may also try to define nodes using ICA or source based morphometry (SBM) [251] in structural MRI data.

In terms of dynamic brain graph, nodes with different resolutions within and/or between methods (ROI vs ICA) have rarely been compared. Future studies may build multi-layered brain graphs by incorporating both spatial-varying and time-varying information to investigate the development, growth, and state changes of the human brain [252].

Although multimodal graphs are helpful to better understand the topological properties of the brain by combining information from different modalities, and multi-modal parcellation of the human brain methods have also been developed [253], how to define the nodes is still a challenge when building a multimodal graph. Because different modalities provide different spatial or temporal information of the brain, it is hard to define comparable nodes across modalities. However, a promising way may be to build bipartite or tripartite graphs in which edges may only present within modality nodes not between modality nodes. In addition, network control theory may be adopted to investigate the relationship among modalities [254, 255]. Building multilayer brain graphs is another approach for performing multimodal data analysis [256–260].

Biographies

Qingbao Yu Dr. Yu received his B.S. degree in physics and PhD. degree in biomedical engineering: neuroinformatics from Dalian University of Technology in 2003 and 2009 respectively. Then he worked at the Mind Research Network, NM, USA as a postdoctoral fellow and got promoted to Research Scientist in 2013. His research topics include ICA and graph theory analysis in human brain neuroimaging data (fMRI, EEG) and their applications in brain diseases. His ongoing work is trying to build multimodal brain graphs and to combine with deep learning methods to classify patients with mental illness from healthy controls. He has published more than 50 peer-reviewed journal papers. He also serves as reviewers for more than 20 peer-reviewed journals.

Yuhui Du Dr. Du is currently a Research Scientist at the Mind Research Network. She aims to develop new methods to accurately estimate brain functional networks and identify biomarkers from brain images. She also focuses on distinguishing different mental disorders using advanced machine learning methods, in order to achieve a biologically meaningful nosology and benefit individual diagnosis. She has published about 50 publications and won Trainee Abstract Travel Awards from the Organization for Human Brain Mapping in 2011 and 2016. She successfully obtained a patent and software for brain image analysis. As PI or co-investigator on several grants, she laid the groundwork by developing novel methods for brain network estimation and disease classification. She also serves as a reviewer for more than 20 journals in the neuroimaing field.

Jiayu Chen Dr. Chen received the Ph.D. degree in electrical engineering and is currently a research scientist at The Mind Research Network, Albuquerque, NM, USA. Her research is focused on developing computational algorithms for integrating multi-modal imaging, genetic and phenotypic data to better understand psychiatric disorders including but not limited to schizophrenia, bipolar disorder and attention deficit/hyperactivity disorder. She has published more than 40 peer-reviewed papers in this interdisciplinary field involving engineering, neuroscience, genetics and psychiatry.

Jing Sui (Senior Member, IEEE) received her B.S. and PhD. Degree in optical engineering with honors from Beijing Institute of Technology in 2002 and 2007 respectively. Then she worked at the Mind Research Network, NM, USA as a postdoctor fellow and got promoted to Research Scientist in 2010 and Assistant Professor of Translational Neuroscience in 2012. She is currently a full professor at the National Laboratory of Pattern Recognition & Brainnetome Center, Institute of Automation, Chinese Academy of Science (CAS). Her research interests include machine learning in neuroimaging, multi-modal brain imaging data fusion (fMRI, sMRI, dMRI, EEG, genetics), pattern recognition and their applications in mental illnesses. Her ongoing work in predictive data mining attempts to meet clinical challenges of making early and optimal intervention possible based on fundamental neuroimaging data. She is a recipient of One Hundred Talents plan of CAS in 2013. Now she has published 70 peer-reviewed journal articles and over 60 technical reports, abstracts and conference proceedings. She also serves as grant reviewer for China Natural Science Foundation, China Overseas Scholarship Council, Ministry of Science and Technology etc. and regular reviewers for more than 40 peer-reviewed journals.

Tülay Adali (S’89–M’92–SM’98–F’09) received the Ph.D. degree in Electrical Engineering from North Carolina State University, Raleigh, NC, USA, in 1992 and joined the faculty at the University of Maryland Baltimore County (UMBC), Baltimore, MD, the same year. She is currently a Distinguished University Professor in the Department of Computer Science and Electrical Engineering at UMBC. She has been active in conference and workshop organizations. She was the general or technical co-chair of the IEEE Machine Learning for Signal Processing (MLSP) and Neural Networks for Signal Processing Workshops 2001−2008, and helped organize a number of conferences including the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP). She has served or currently serving on numerous editorial boards and technical committees of the IEEE Signal Processing Society. She was the chair of the technical committee on MLSP, 2003−2005 and 2011−2013, and the Technical Program Co-Chair for ICASSP 2017. She is the Special Sessions Chair for ICASSP 2018. Prof. Adali is a Fellow of the IEEE and the AIMBE, a Fulbright Scholar, and an IEEE Signal Processing Society Distinguished Lecturer. She was the recipient of a 2010 IEEE Signal Processing Society Best Paper Award, 2013 University System of Maryland Regents’ Award for Research, and an NSF CAREER Award. Her current research interests are in the areas of statistical signal processing, machine learning, and applications in medical image analysis and fusion.

Godfrey D. Pearlson Dr. Pearlson is currently Professor of Psychiatry & Neuroscience at Yale University Medical School, founding director of the Olin Neuropsychiatry Research Center (www.NRC-IOL.org) at the Institute of Living (IOL)/Hartford Hospital in Hartford CT and IOL Research Director. Dr. Pearlson’s research uses neuroimaging as a tool to address a broad array of questions regarding the neurobiology of major mental disorders, primarily psychosis (e.g. the NIMH-funded B-SNIP Consortium) and drug abuse (primarily alcohol & marijuana). He has received an NIMH MERIT award, a NARSAD Distinguished Investigator Award, the Ziskind-Sommerfeld Research Award from the Society of Biological Psychiatry, the Stanley Dean Award in Schizophrenia Research from the American College of Psychiatry, is a member of the Johns Hopkins Society of Scholars (for distinguished alumni) and was awarded the Albert M. Biele Lectureship from Jefferson Medical College, a Michael Visiting Professorship from the Weizmann Institute & is on the editorial board of several neuroimaging in psychiatric journals. He has published over 650 peer-reviewed research articles. He is also co-founder of the annual BrainDance Competition, which is open to high school and college students across New England. The BrainDance Awards encourage students to gain knowledge about psychiatric diseases and to develop a more tolerant and realistic perspective toward people with severe psychiatric problems.

Vince D. Calhoun, biography not available at the time of publication.