Theoretical Models of Neural Development

Abstract

Constructing a functioning nervous system requires the precise orchestration of a vast array of mechanical, molecular, and neural-activity-dependent cues. Theoretical models can play a vital role in helping to frame quantitative issues, reveal mathematical commonalities between apparently diverse systems, identify what is and what is not possible in principle, and test the abilities of specific mechanisms to explain the data. This review focuses on the progress that has been made over the last decade in our theoretical understanding of neural development.

Graphical Abstract

Biological Sciences; Neuroscience; Developmental Neuroscience; Theoretical Neuroscience; In Silico Biology

Introduction

As you seamlessly interact with the world around you, reliably perceiving the subtlest of cues and generating incredibly precise motor actions, it is easy to forget that you built the neural hardware needed to perform these amazing feats of computation from scratch. Each of your 10¹¹ neurons had to be born, specified as a particular initial phenotype, migrate to an appropriate location, make appropriate connections with potentially thousands of other neurons, sculpt those connections in response to early experience, and then continue to refine those connections throughout life. Given the complexity of these processes it is not surprising that we still have a long way to go to understand how the adult brain comes to be.

There are many reasons that it is important to improve this understanding. Since altered neurodevelopment underlies many common neurological disorders (Rubenstein, 2011, Homberg et al., 2016), the design of therapies depends on understanding the developmental processes that have gone awry. A related aspect is the high sensitivity of the developing nervous system to the environment: how can the deleterious effects of exposure to harmful drugs or altered sensory experience during early life be minimized or reversed? The developing brain is far more plastic (has a greater ability to change) than the adult brain and so provides an excellent system for studying plasticity more generally, and also how greater plasticity might be encouraged in adults. From a technological perspective, some of the biggest breakthroughs in artificial intelligence (AI) have taken inspiration from neuroscience (Hassabis et al., 2017), and yet these algorithms all generally assume the necessary hardware has already been built (apart from optimizing the strengths of pre-existing synaptic connections), and the potential for using insights from neural development to drive new forms of self-organizing AI remains largely unexplored.

Mathematical models have an important role to play in improving our understanding of neural development. A general definition we will follow is “a mathematical model is an abstract, simplified mathematical construct related to a part of reality and created for a particular purpose” (Bender, 2000). The significance of mathematical models in biology has been extensively discussed elsewhere (Edelstein-Keshet, 1988, Murray, 2002). Briefly, mathematics forces hypotheses to be formulated with a precision that means that implicit assumptions are less likely to slip by; mathematics provides a concise language that encourages manipulation and a large number of potentially useful theorems derived from hundreds of years of research; the consequences of a set of assumptions can be far more rigorously explored than descriptions based on words, and as a consequence quantitative models often have greater predictive power than qualitative models.

Of course, modeling can also have pitfalls. Perhaps the most significant of these is a potential reliance on large numbers of parameters that are not directly available from experimental data. In such cases, it is often hard to draw robust insights into the key mechanisms underlying experimental data, and such models may not generalize well to cases they were not specifically designed to reproduce. Models that have relatively few free parameters, even if these parameters are somewhat abstract, are therefore often most prized. On the other hand, however, sometimes emphasizing elegance can lead one down the wrong path. One example in the context of developmental biology is the specification of stripes of gene expression in the developing Drosophila embryo: although initially a Turing-like reaction diffusion mechanism seemed an appealing theoretical explanation, it turned out that less elegantly general (but still theoretically interesting) mechanisms were at work (Akam, 1989, Jaeger et al., 2004, Green and Sharpe, 2015).

The mathematical modeling of neural development has been characterized by a dynamic tension between the consideration of processes dependent on molecular processes, such as the initial targeting of neural connections, versus those dependent on neural activity, such as receptive field development. The field of artificial neural networks has exerted a strong influence in favor of activity-dependent processes, by demonstrating the great computational effectiveness of activity-dependent learning rules for adjusting synaptic strengths. On the other hand, modeling activity-independent processes in neural development has instead usually followed more in the tradition of classical mathematical biology (Edelstein-Keshet, 1988, Murray, 2002). It has often taken inspiration from better-understood aspects of non-neural tissue development, such as the roles of molecular gradients and interacting networks of gene expression in determining regional identity. Here we will review some models in both of these camps, but a goal for future work is to develop models that better integrate these two perspectives.

In the limited space available it is not possible to be comprehensive, and so we will consider some illustrative examples of how theory has been used to illuminate processes of neural development, with a bias toward more recent work (last 10 years or so). Excellent reviews of older work can be found in van Ooyen, 2003, van Ooyen, 2011. Modeling neural development is of course a special case of modeling biological development in general (Tomlin and Axelrod, 2007), and sometimes tools well developed in areas for which more data are available (e.g., modeling gene regulatory networks) (Smolen et al., 2000) can be applied directly to the particular case of the nervous system. However, in many cases, more bespoke models are required to address the often astonishing complexity of the developing nervous system and to take into account the relative paucity of data available relative to non-neural systems.

Mechanical Forces in Neurulation and Cortical Folding

Although molecularly based explanations of development have been largely dominant for the past several decades, there is now an increasing appreciation that mechanical forces can play a critical role in shaping the geometry of developing tissue (Heller and Fuchs, 2015), and in particular the nervous system (Franze, 2013). One of the earliest events is neurulation, whereby the flat sheet of cells destined to become the nervous system forms a fold and then rolls up to form the neural tube (Vijayraghavan and Davidson, 2016). Some early insights into such physical events in tissue development such as this were obtained from models that were themselves physical, involving, e.g., rubber bands (Lewis, 1947), but more recently computational models have been employed. A good example is the multi-scale finite element modeling approach of Chen and Brodland (2008) (Figure 1A). Using parameters tightly constrained from experimental data, the model helped delineate the relative importance of different mechanisms and showed that time-dependent mechanical properties are not required to produce the tissue motions seen experimentally.

Figure 1.

Models of Neurulation and Cortical Folding

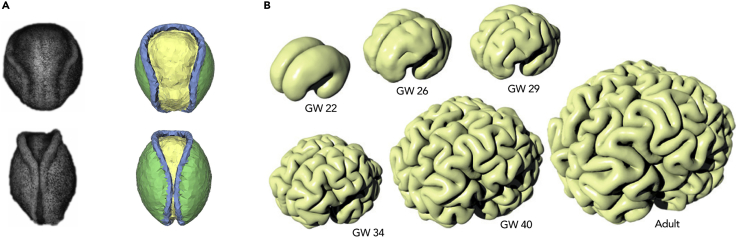
(A) Experimental data (left column) and simulation results (right column) from stages 14 (top row) and 17 (bottom row) of axolotl neurulation (adapted with permission from Chen and Brodland (2008)). For the right column, yellow represents neural plate tissue, green represents non-neural ectoderm, and blue represents the neural ridges. The height of each image represents approximately 2 mm.

(B) A simulation of cortical folding in humans where the brain is treated as a soft elastic solid and the cortex expands tangentially. GW, gestational weeks. Adapted with permission from Tallinen et al. (2016).

A folding event that occurs much later in neural development is the formation of sulci and gyri in the surface of the expanding cortex, at least in some species, including humans. In principle, many factors could play a role in this, including molecular specification, precise patterns of neural proliferation and migration, and axonal tension (Striedter et al., 2015). However, several computational models have explored the hypothesis that the mechanical forces generated by the expanding outer layer of tissue are all that are required (Bayly et al., 2013). Geng et al. (2009) investigated models involving pulling by white matter tension and growth of the cortical sheet modeled as osmotic expansion, based on magnetic resonance imaging of the sheep brain. Tallinen et al. (2016) developed a literal instantiation of the osmosis idea by presenting a gel model of a human brain at an early stage of development, with dimensions determined from magnetic resonance imaging, and then coated it with a thin layer of elastomer gel. Immersing the brain in a solvent caused expansion initially just in the outer layer, which generated patterns of folding bearing a strong similarity to those seen in the human brain (Figure 1B). Following this proof of principle, the authors then built a computational model of the forces involved and suggested that the three-dimensional geometry of cortical folds are a consequence of mechanical instability rather than molecular cues.

Specifying Regions and Areas

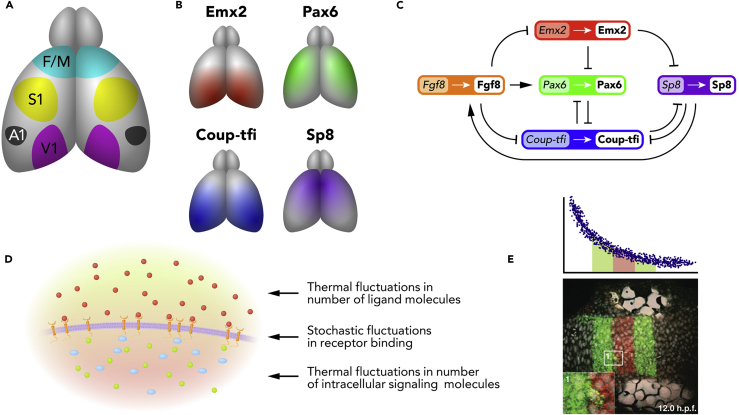
Nervous system development is characterized by increasingly detailed specification of different groups of neurons to perform different functions. Although later reprogramming by activity-dependent cues is sometimes possible, it is certainly the case that initial regionalization is driven by molecular cues (Sur and Rubenstein, 2005). One prominent example is the segregation of the cerebral cortex into distinct areas (Figure 2A). Although spatial gradients of several genes have been implicated in this process (Figure 2B), the complex network of potential interactions between these genes and their products makes purely intuitive reasoning challenging. Given the paucity of quantitative information available from experiments about expression levels, Giacomantonio and Goodhill (2010) formulated this as a Boolean model, where expression levels were considered to be purely binary (on or off). This model made testable predictions by determining the constraints on the network interactions necessary to reproduce the experimentally observed gradients (Figure 2C). Subsequent work transformed the Boolean model into a system of differential equations for continuous-valued expression levels and showed that the existing experimental data was not sufficient to uniquely specify the network (Giacomantonio and Goodhill, 2014). This is one example of a much more general research program using mathematical models to understand the properties of gene networks (Smolen et al., 2000, Jaeger et al., 2004).

Figure 2.

Regional Specification and the Role of Noise

(A) Layout of key functional areas in the mouse cortex (O'Leary et al., 2007). V1, primary visual cortex; A1, primary auditory cortex; S1, primary somatosensory cortex; F/M, frontal/motor cortex.

(B) Some of the molecular gradients that play a role in specifying areal identity in mouse cortex during development.

(C) One of the networks of interactions between signaling molecules in the model of Giacomantonio and Goodhill (2010) that generated arealization patterns most consistent with the experimental data. Shaded and unshaded labels indicate genes and proteins, respectively.

(D) Schematic of three sources of noise that constrain concentration measurement by a cell.

(E) Specification of boundaries in the developing zebrafish hindbrain by a gradient of retinoic acid. Top: schematic representation of the retinoid acid gradient. Any such gradient can only provide noisy information. Bottom: experimental image showing that by 12 hr postfertilization this gradient has nevertheless helped to specify sharply defined borders of the expression of krox20 (green) and hoxb1a (red). Adapted from Zhang et al. (2012).

Spatial gradients of morphogens or gene expression are a key mechanism for embryonic patterning in developmental biology in general and the subject of much theoretical attention (Lander, 2011, Lander, 2013). The model of Saha and Schaffer (2006) explored how different transport mechanisms affect the dynamics of gradient formation and thus pattern formation of Sonic hedgehog (Shh), a critical molecule patterning the neural tube (Cohen et al., 2013). A key finding was that the gradient could be dynamically patterned by combining different modular elements (such as binding to the extracellular matrix) to produce outcomes appropriate for different tissues. A model focusing instead on the transcriptional circuit downstream of Shh showed that its design confers robustness to fluctuations in Shh signaling (Balaskas et al., 2012).

A critical issue in measuring concentration, for instance, for a cell to determine its position from a morphogen gradient, is that of noise (Gregor et al., 2007, Lander, 2011). Even a gradient that is established completely reliably (i.e., has exactly the shape it is supposed to have) provides unreliable information, because (1) it is made up of individual molecules whose local concentration fluctuates as a result of Brownian motion, (2) it is read by a cell through stochastic receptor binding, and (3) this binding is interpreted via computations based on finite numbers of signaling molecules (Figure 2D). These sources of noise mean there are fundamental physical limits to the spatial accuracy with which a particular gradient cue can specify tissue identity (Bialek and Setayeshgar, 2005, Hironaka and Morishita, 2012, Lander, 2013, Bicknell et al., 2015). A striking application of this concept showed that the precision with which the Bicoid gradient in the Drosophila embryo is read out is close to the physical limits (Gregor et al., 2007). Although these ideas have not yet been extensively applied to gradients patterning the nervous system, a relevant example is the specification by a retinoic acid gradient of the boundaries between rhombomeres in the developing hindbrain. In particular, it has been argued that noise in the expression of two genes downstream of retinoic acid can combine to sharpen initially rough borders via a novel noise attenuation mechanism (Zhang et al., 2012) (Figure 2E).

Neurogenesis and Building the Cerebral Cortex

A fascinating quantitative problem in neural development is building the layers of the cerebral cortex. Progenitor cells in the ventricular zone just below the cortical plate divide symmetrically, forming two new progenitor cells, or asymmetrically, forming one progenitor cell and one postmitotic neuron. The latter then migrate to their appropriate cortical layer, building the cortex in an inside-out fashion, and some of these neurons later die (Dehay and Kennedy, 2007) (Figure 3A). A mathematical challenge is to understand how the extraordinarily large variation in cortical area (1,000 times larger in humans than mice) and duration of construction (about 84 days in humans compared with 6 days in mice) arise from variations in underlying parameters of the system, including variations in the length of the cell cycle (Gohlke et al., 2007).

Figure 3.

Neural Migration and Polarization

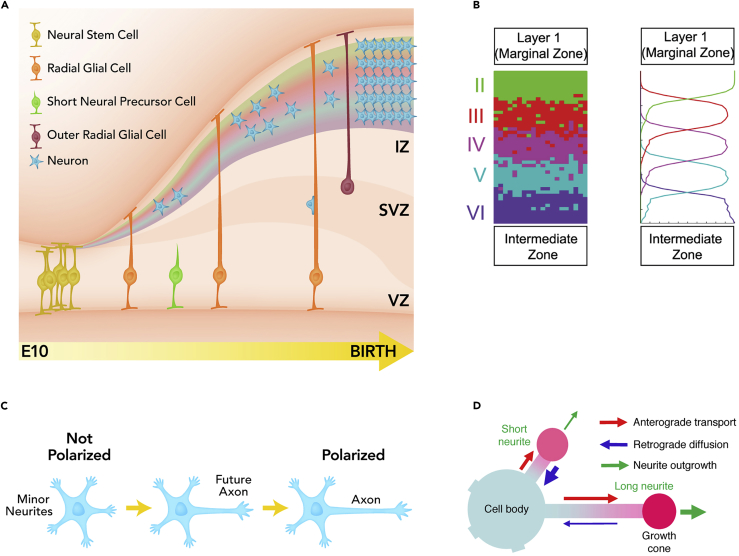
(A) In the developing cortex neurons migrate from their place of birth along radial glia, forming the layers of the cortex in an inside-out fashion. IZ, intermediate zone; VZ, ventricular zone; SVZ, subventricular zone. Time axis is for mouse (E10; embryonic day 10).

(B) Left: the results of a single simulation of cortical layer formation in the model of Caffrey et al. (2014). Right: average of 50 simulations, where the vertical axis is distance and horizontal axis is agent density. Reproduced from Caffrey et al. (2014).

(C) In general, several neurites sprout from a neuron, and then the longest becomes the axon, whereas the others become dendrites.

(D) The mechanism of polarization modeled in Toriyama et al. (2010): accumulation of shootin1 in the growth cone provides a positive feedback loop.

Using partial differential equations to represent the time evolution of the transition probabilities, Gohlke et al. (2007) compared several scenarios and analyzed parameter sensitivity. One prediction was that cell death may be more important for correct cortical development in primates than rodents. In contrast, Cahalane et al. (2014) considered ordinary differential equations for the rates of change of the number of precursor and differentiated neurons. The model predicted that increases in the number of neurons per cortical column, within an individual or over evolution, are accommodated primarily in superficial cortical layers, which develop later. A similar model system was recently analyzed by Picco et al. (2018), who argued that such modeling can help to identify which new experimental measurements will be most informative.

Neuronal Migration and Polarization

Once born, neurons must migrate to their appropriate locations in the brain. Focusing on the cortex, excitatory projection neurons generally migrate radially to their appropriate cortical layer along glial cells, whereas inhibitory interneurons are born outside the cortex and migrate using biochemical cues (Marín et al., 2010). Neurons migrate by first extending a leading process, into which the nucleus then translocates via “nucleokinesis,” and the trailing process is then eliminated. Britto et al. (2009) showed that this could be well modeled as a critically damped spring-dashpot system. Furthermore, they found that the estimated parameters for the system were unchanged by biochemically perturbing branching of the leading process, suggesting that nucleokinesis is a quantitatively stereotyped event.

Two types of approaches to modeling the migration of populations of neurons are as a continuum, usually using partial differential equations, or as a set of individual agents following simple rules of interaction with their environment and other agents. A common form of the latter is a cellular automata model, where the agents reside on a lattice. Often these rules are stochastic, but general principles can emerge from averaging over many simulations. For instance, Caffrey et al. (2014) used a cellular automata to test hypotheses regarding the role of Reelin in cortical layer formation (Figure 3B). The results suggested that Reelin acts as a chemoattractant rather than a stop signal for neurons, and that loss of neuron motility is affected by other nearby neurons. Setty et al. (2011) also used an agent-based model to investigate the role of Reelin in cortical migration but broadened the discussion to investigate its interplay with the molecules Lis1, DCX, and GABA, predicting how changes in expression levels in these molecules should affect migration. An unexpected result was that reduced expression of Lis1 could give rise to an oscillatory neuron-glial interaction.

Although cortical migration has been a popular target for agent-based modeling, there are also other important areas of application in neural development. For instance, Newgreen et al. (2013) reviewed both agent-based and continuum (partial differential equation-based) models for the development of the enteric nervous system, which controls gastrointestinal function. These models suggested that Hirschsprung disease (a loss of nerve innervation to parts of the intestine) is most likely a defect of cell proliferation rather than cell motility, contrary to initial expectations. A non-mammalian example is provided by a detailed model of cell migration in the zebrafish posterior lateral line system (Knutsdottir et al., 2017). This model included Wnt-FGF signaling, chemical gradients, mechanical forces, and also changes in cell shape and addressed behavior in both normal and mutant fish.

Neuronal migration is a special case of the wider field of cell migration in general. Modeling in much of the latter has focused on experimental systems that are more robust than notoriously delicate neurons, such as fish keratocytes or cancer cell lines. Masuzzo et al. (2016) reviewed computational issues in studying cell migration in general, including image processing and metrics for quantifying cell movement. Recent reviews providing more mathematical details include Carlsson and Sept (2008) and Holmes and Edelstein-Keshet (2012). In this context, a specific focus is often how the forces needed for motility are generated within the cell, e.g., by actin-myosin contractility (for a recent example see Nickaeen et al. (2017)).

After they are born neurons acquire a polarization, such that one process becomes the axon, whereas other processes become dendrites (Figure 3C). This polarization could potentially be influenced by a variety of factors, including spontaneous symmetry breaking (perhaps by a Turing-like mechanism [Turing, 1952] and/or based on the relative lengths of the different processes), intrinsic asymmetries arising from the last mitotic event, non-uniform distributions of molecules or substrate stiffness in the extracellular environment, and the position of the centrosome (Cheng and Poo, 2012). In a combined experimental and theoretical study, Toriyama et al. (2010) showed that shootin1 accumulates in neurite tips in a length-dependent manner and regulates axon growth, therefore possibly providing a positive feedback loop amplifying random fluctuations in shootin1 concentration (Figure 3D). Naoki and Ishii (2014) investigated a related but more abstract model in which a factor X (possibly a phosphatidylinositol (3,4,5)-trisphosphate [PIP3] inducer) is generated in the soma and then transported to the tips of the neurites. There it activates a factor Y (possibly PIP3) via a bistable switch, causing rapid extension of the first neurite to reach threshold. This increased total volume causes the overall concentration of X to drop, making it unlikely that any other neurites will be able to reach threshold.

Axon and Dendrite Growth, Guidance, and Branching

Once neurons have reached their destinations and become polarized, their axons grow over often long distances to find their appropriate targets (Dickson, 2002, Chédotal and Richards, 2010) and their dendrites often branch into highly elaborate tree structures (Jan and Jan, 2010). Growing neurites are led by growth cones at their tips, sensory-motile structures that can operate semi-autonomously. This stage of neural development has been examined theoretically from a number of different perspectives, and some reviews of older work can be found in Maskery and Shinbrot, 2005, Simpson et al., 2009, and Mortimer et al. (2012). One class of models proposes stochastic rules governing axon and dendrite growth and branching and applies those to generate neuronal morphologies and neural network structures capturing some of the statistics of real neurons and networks (Eberhard et al., 2006, Donohue and Ascoli, 2008, Koene et al., 2009, Cuntz et al., 2010, van Ooyen et al., 2014, Torben-Nielsen and De Schutter, 2014) (Figure 4A). These models are often proposed as overall simulation frameworks for investigating neural development and may also include processes such as neurogenesis (Zubler and Douglas, 2009) (Figure 4B). In such models the focus is usually phenomonological rather than mechanistic.

Figure 4.

Axon and Dendrite Growth and Guidance

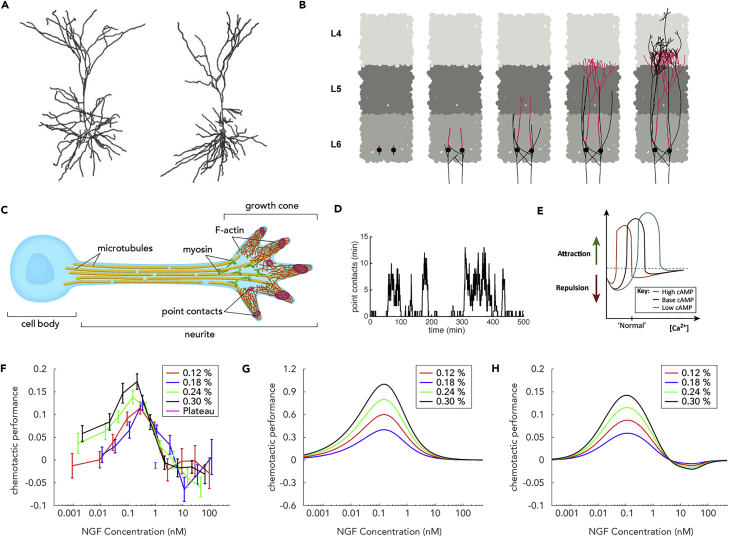
(A) Left: Reconstruction of a typical rat cortical pyramidal neuron. Right: A neuron generated with NETMORPH using appropriately tuned model parameters (reproduced with permission from Koene et al. (2009)).

(B) Example of simulated growth of axons (black) and dendrites (red) across three cortical layers (reproduced from Zubler and Douglas (2009)).

(C) Some key structures and molecules involved in neurite growth and guidance.

(D) Number of growth cone point contacts as a function of time from the model of Padmanabhan and Goodhill (2018), corresponding to stochastic oscillations between growth and paused states.

(E) Model predictions for whether axons are attracted or repelled in response to a molecular gradient as a function of levels of calcium and cAMP (Forbes et al., 2012) (reproduced with permission from Sutherland et al. (2014)).

(F) Measured chemotactic sensitivity as a function of concentration and steepness of dorsal root ganglion explants grown in gradients of nerve growth factor (Mortimer et al., 2009).

(G) Chemotactic sensitivity predicted by the Bayesian model of Mortimer et al. (2009) (different y axis units from F).

(H) Chemotactic sensitivity predicted by the model of Bicknell et al. (2018a), which addresses signaling pathways shared between growth and guidance (same y axis units as F).

Other models have examined more closely the biophysical mechanisms driving neurite elongation (Kiddie et al., 2005, Graham and van Ooyen, 2006, O’Toole et al., 2008, Franze and Guc, 2010) (Figure 4C). Graham et al. (2006) proposed a continuum model of neurite growth describing the diffusion of tubulin and construction of the microtubule cytoskeleton as a set of partial differential equations. A key idea was that neurite growth is rate limited by tubulin supply. Building on this work, the same concept was used in the model of Hjorth et al. (2014) to explain the apparent competition sometimes observed between neurite branches, whereby outgrowth of a branch can lead to the retraction of neighboring branches. Linking to a lower level of biophysical detail, Tsaneva-Atanasova et al. (2009) proposed a model linking neurite outgrowth to secretory vesicle dynamics. A prediction of this model was that vesicular delivery without cytoskeletal dynamics can generate only small neurites.

Another property of growing axons is that their movement often alternates between growth and paused states, even in vitro in the absence of spatially patterned environmental cues. Padmanabhan and Goodhill (2018) proposed a model of the Rac1-and point contact-dependent signaling network in the tip of the axon that exhibits bistability. Owing to random fluctuations, this bistability causes a switching between growth and paused states, with temporal dynamics similar to that seen experimentally (Figure 4D). The actin treadmill was modeled by Craig et al. (2012), who showed that this can be driven by both myosin contractile forces and membrane tension. Including more biophysical detail, Zeitz and Kierfeld (2014) and Xu and Bressloff (2015) considered the effect of Rac1 and stathmin on the growth and catastrophe rates of microtubules and thus growth cone membrane polarization. The model of Goodhill et al. (2015) explained spatiotemporal patterns of shape changes in growth cones in terms of competition of microtubules for limited supplies of tubulin (Janulevicius et al., 2006). Addressing the forces involved in growth cone movement, Chan and Odde (2008) modeled the molecular clutch mechanism that links F-actin to the substrate, predicted different behavior on stiff and soft substrates, and confirmed the model predictions experimentally.

However, none of these models directly address chemotaxis, an area of very broad interest in mathematical biology. Since the mid-1990s numerous molecules that have a chemotactic effect on growing neurites have been discovered, and this has been believed to be a critical mechanism by which axons are guided to their targets in the developing nervous system (Mortimer et al., 2008). Although recent results have begun to question how ubiquitous this mechanism might be in early development in vivo (Goodhill, 2016, Dominici et al., 2017, Varadarajan et al., 2017), it is certainly true that neurites can show robust chemotactic responses to graded cues in vitro. Several models have examined the molecular signaling pathways inside growth cones by which small changes in ligand concentration across their width might be amplified to produce turning (Meinhardt, 1999, Sakumura et al., 2005, Causin and Facchetti, 2009, Bouzigues et al., 2010). Guidance of axons in vivo in the model system of the developing tadpole has been addressed in Borisyuk et al., 2014, Roberts et al., 2014, and Davis et al. (2017), and a general simulation tool for modeling the trajectories of axons in gradients applicable to a variety of situations was presented in Krottje and van Ooyen (2007).

A surprising experimental finding is that axonal responses to gradients can switch from attraction to repulsion depending on the levels of both calcium and cAMP in the growth cone (reviewed in Song and Poo (2001) and Sutherland et al. (2014)). Intriguingly the signaling pathways underlying this switch bear strong similarity with the pathways involved in switching between long-term potentiation and long-term depression at a synapse (Graupner and Brunel, 2010). Building on models proposed in that domain, Forbes et al. (2012) proposed that growth cone attraction vs repulsion depends on the ratio between the two sides of the growth cone of the ratio of CAMII to calcineurin, induced by differing upstream calcium levels caused by the external gradient (Figure 4E). Experiments confirmed some surprising predictions of this model (Forbes et al., 2012). In an alternative approach to attractive-repulsive switching, Naoki et al. (2016) proposed a model based on more general activator-inhibitor dynamics and used this to explain why such switching in response to gradients is seen in growth cones but not generally in non-neural cells. An activator-inhibitor system was also investigated by Roccasalvo et al. (2015), who combined this with the neurite growth simulation framework of Zubler and Douglas (2009) to generate neurite trajectories.

One interesting theoretical question is how fundamental physical constraints on concentration measurement might limit the chemotactic responses of growth cones (Goodhill, 1998). Mortimer et al. (2009) and Mortimer et al. (2011) proposed a Bayesian model for how a gradient sensing device such as a growth cone could optimally determine gradient direction given stochastic fluctuations in receptor binding. The predicted chemotactic sensitivity curves closely matched the results of a large-scale experimental characterization of neurite sensitivity to nerve growth factor as gradient steepness and concentration were varied (Mortimer et al., 2009) (the data from this study are now publicly available, Bicknell et al., 2018b) (Figures 4F and 4G). This predicted sensitivity was then used to understand the results of a different experimental situation in Catig et al. (2015). Within a similar framework to Mortimer et al. (2009) but using information-theoretic arguments, Nguyen et al. (2015) investigated how concentration (and thus gradient) measurements are degraded by receptor diffusion, and Nguyen et al. (2014) determined the theoretically optimal spatial distribution of receptors to avoid bias in estimating gradient direction, which turned out to be non-uniform. To explain growth biased by the gradient but not involving biased growth cone turning, Mortimer et al. (2010) proposed a model whereby concentrations could be compared along a neurite, rather than across the tip, and then influence outgrowth speed. A recent model showed how this form of chemotactic response could be realized by shared signaling mechanisms that couple growth and guidance and provided the first explanation of experimentally observed differences in behavior between neurites growing from dissociated neurons versus from tissue explants (Bicknell et al., 2018a) (Figure 4H).

Retinotectal Map Formation

A well-established model system for studying the collective behavior of growing axons is the formation of topographic projections between brain areas. Although the later refinement of these maps is dependent on neural activity, their initial formation appears to depend on molecular guidance of axons to topographically appropriate positions in the map, primarily involving Eph receptors and ephrin ligands (Cang and Feldheim, 2013, Weth et al., 2014). Many different mathematical models of this process have been proposed, usually based on an interplay of the key components of chemotactic guidance, neural activity, and competition between axons. Starting with Sperry's chemospecificity hypothesis (Sperry, 1963) and the resulting search for molecules that might implement this, retinotectal map formation is an area where theoretical ideas have been unusually influential on experimental work. Rather than there being one “correct” model, competing theoretical hypotheses have all helped guide and clarify experimental results.

Older models have already been extensively reviewed in, e.g., Goodhill and Xu, 2005, Simpson et al., 2009, and van Ooyen (2011). Recent work has often focused on intriguing experimental results from mice with different combinations of Ephs, ephrins, or other molecules knocked in and/or out (Reber et al., 2004, Simpson and Goodhill, 2011, Triplett et al., 2011, Grimbert and Cang, 2012, Godfrey and Swindale, 2014, Owens et al., 2015, Tikidji-Hamburyan et al., 2016, Savier et al., 2017). Although often these models are built on different theoretical frameworks and are thus difficult to succinctly compare, a systematic comparison of several different models in terms of their ability to account for a particular set of experimental findings was presented by Hjorth et al. (2015). They found that only one of the models they investigated could explain all these data. However, all models required an additional as yet undiscovered guidance cue to explain one of the observed phenotypes, thus presenting a new challenge for experimental work.

Activity-Dependent Development

Once initial wiring patterns have been established, there is a long period of refinement of these connections that is dependent on neural activity. This can involve both pruning and addition of connections and also adjustment of the strength of existing connections via synaptic plasticity. Although this plasticity is most profound during development, it continues throughout life as the basis for adult learning. Abstract models of activity-dependent synaptic plasticity form the basis of most learning algorithms for artificial neural networks, and a productive conversation between these two fields extends back many decades (Cox and Dean, 2014). For instance, the recent dramatic success of deep learning (LeCun et al., 2015) has prompted renewed interest in how the back-propagation algorithm (on which deep learning is based) might be implemented in the real brain (Lillicrap et al., 2016, Guerguiev et al., 2017), and the same is true for long short-term memory networks (e.g., Costa et al., 2018). However, here we will focus on models more directly motivated by nervous system development.

The most important theoretical concept in activity-dependent development is Hebbian learning, which has many different mathematical instantiations (Dayan and Abbott, 2001). Foundational work in the 1970s and 1980s showed that Hebbian rules could generate maps in the brain representing variables such as topography (Willshaw and von der Malsburg, 1976), preference for the orientation of visual stimuli (von der Malsburg, 1973, Linsker, 1986), and preference for input from one eye versus the other (ocular dominance) (von der Malsburg and Willshaw, 1976, Swindale, 1980, Miller et al., 1989). A proliferation of Hebbian-based models for visual maps was highly successful at explaining the receptive field and map structures formed during normal development and their plasticity in response to altered visual input (reviewed in Swindale, 1996, Swindale, 2003, Miikkulainen et al., 2005, Goodhill, 2007). Some recent successful experimental tests of the predictions of these models provide examples of their continued relevance. First, orientation pinwheel density in the visual cortex was found to be very close to π, as predicted (Kaschube et al., 2010) (Figures 5A and 5B). Second, the bandedness of ocular dominance columns was observed to change over development, as predicted (Keil et al., 2010). Third, raising animals seeing mostly vertical contours in one eye and mostly horizontal in the other caused a shift in the position of pinwheels relative to ocular dominance column borders (Cloherty et al., 2016), as predicted (Giacomantonio et al., 2010) (Figure 5C). A key component of all these models is some form of competition for resources, so that as some inputs grow others must shrink. Competitive processes during neural development in general have been examined in a number of different models (van Ooyen, 2001, van Ooyen, 2011), for instance, how competition for neurotrophic factors affects cell survival (van Ooyen and Willshaw, 1999, Deppmann et al., 2008).

Figure 5.

Activity-Dependent Development

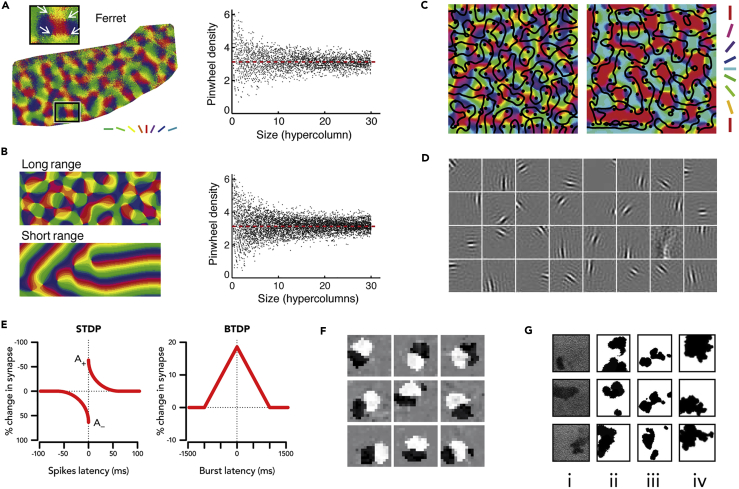
(A) Left: Orientation selectivity map in the visual cortex of a ferret (Kaschube et al., 2010). The colors represent the orientations in the visual field to which each point in the cortex is most responsive; the white arrows in the inset highlight pinwheels, where all orientations are represented around a point. The map wavelength is about 1 mm. Right: Average pinwheel density from several animals is close to π.

(B) Left: Maps formed in models with and without long-range connections: only the former produce maps resembling those seen experimentally (cf A). Right: Pinwheel density for the simulated maps is remarkably similar to that seen experimentally (Kaschube et al., 2010). (A and B) reproduced with permission from Kaschube et al. (2010).

(C) Left: Simulated orientation maps with overlaid pinwheels (black dots) and ocular dominance column borders (black lines) for a normally reared animal from the model of Cloherty et al. (2016). Right: Predicted map for an animal seeing horizontal contours in one eye and vertical contours in the other during development. Reproduced from Cloherty et al. (2016).

(D) Sample of oriented receptive fields produced by applying independent components analysis to natural scenes. Each gray square represents one neuron's receptive field, and the weights in that receptive field are represented by the gray scale with most weights being zero. Reproduced from Hyvärinen et al. (2009).

(E) Dependence of change in synaptic strength with time Δt between pre- and post-synaptic spikes for STDP and BTDP.

(F) Examples of oriented receptive fields produced by a model using an STDP learning rule. Gray scale is similar to (D). Reproduced with permission from Clopath et al. (2010).

(G) (i) Retinal waves observed experimentally in ferrets at three different time points; each panel corresponds to an approximately 2 by 2-mm patch of retina. (ii) Simulated retinal waves from the model of Butts et al. (1999). (iii) Simulated retinal waves from the model of Godfrey and Swindale (2007). (iv) Simulated retinal waves from the model of Albert et al. (2008). Reproduced from Albert et al. (2008).

The development of ocular dominance and orientation selectivity has provided a test case for more abstract top-down principles of neural coding, such as the closely related concepts of sparse coding and efficient coding (Olshausen and Field, 1996, Olshausen and Field, 2004). Sparse coding applied to natural scenes produces oriented receptive fields that are appropriately spatially localized (Olshausen and Field, 1996, Bell and Sejnowski, 1997), as does independent components analysis (Hyvärinen et al., 2009) (Figure 5D). Several suggestions have been made for how such computational principles might be implemented biologically, for instance, using local learning rules (Isomura and Toyoizumi, 2016, Pehlevan et al., 2017) and spiking neurons (Savin et al., 2010, Zylberberg et al., 2011). Sparse coding can also account for the plasticity of receptive fields under conditions of altered visual input such as monocular deprivation or restricted orientation rearing (Hsu and Dayan, 2007, Hunt et al., 2013). In active efficient coding, the role of behavior (e.g., eye movements) in optimizing coding has also been considered (Lonini et al., 2013). Recent work has argued that top-down and bottom-up explanations for receptive field development can be unified by a principle of non-linear Hebbian learning (Brito and Gerstner, 2016).

The properties of learning rules based on spike-timing-dependent plasticity (STDP; Dan and Poo (2006) and Markram et al. (2012)) have been extensively investigated (Morrison et al., 2008), including their potential role in visual map development (Song and Abbott, 2001, Wenisch et al., 2005) (Figures 5E and 5F). A voltage-based STDP rule (Clopath et al., 2010) was used to model the development of local recurrent connections in mouse visual cortex (Ko et al., 2013), and initial gap junctional-coupling between clonally related neurons was found to be an important component for explaining how recurrent connections tend to form between neurons with similar receptive fields. Many recent models have also advanced our general understanding of self-organization in networks based on STDP rules without specifically focusing on neural development (e.g., Litwin-Kumar and Doiron, 2014, Zenke et al., 2015). However, neural activity is often less temporally refined during early stages of development and ill-matched to the millisecond precision required for STDP rules (Butts and Kanold, 2010). One alternative is burst-time-dependent plasticity (BTDP) (Butts et al., 2007), which integrates over hundreds of milliseconds, and has been used to explain, for instance, segregation of ON/OFF pathways in the lateral geniculate nucleus (Gjorgjieva et al., 2009). Modeling has also addressed the development of gain-scaling in cortical neurons during mouse early development (Mease et al., 2013) and shown that intrinsically driven changes in ion channel composition can cause the observed change from early sluggish responses to faster and more temporally refined responses (Gjorgjieva et al., 2014).

A limitation of simple Hebbian plasticity alone is that it can cause unbounded increases in synaptic strengths and thus also cell activity. There is therefore much interest in how Hebbian learning combines with mechanisms of homeostatic plasticity to maintain roughly constant average cell activity (Bienenstock et al., 1982, Clopath et al., 2010, Tetzlaff et al., 2011, Gjorgjieva et al., 2011, Yger and Gilson, 2015, Gjorgjieva et al., 2016, Keck et al., 2017). For instance, Toyoizumi et al. (2014) argued that a specific type of interaction between Hebbian and homeostatic plasticity is required to produce the ocular dominance plasticity dynamics seen experimentally. Modeling has also examined the role of inhibitory plasticity (Vogels et al., 2011) and how changes in inhibition in the cortex during development can cause the opening of the critical period for ocular dominance plasticity (Toyoizumi et al., 2013). One problem for integrating Hebbian and homeostatic plasticity is that, to achieve stability, many models have had to assume a timescale for homeostatic processes that is much faster than that observed in real data; however, several possible solutions have been suggested (Zenke et al., 2017, Zenke and Gerstner, 2017).

Spontaneous activity plays a critical role in establishing circuit connectivity (Kirkby et al., 2013), and this has been addressed by a variety of models (Gjorgjieva and Eglen, 2011, Richter and Gjorgjieva, 2017). A popular target for theoretical work has been the retinal waves that sweep across the eye before visual experience (Godfrey et al., 2009, Hennig, 2014). Spontaneous firing of individual cholinergic amacrine cells spreads to neighboring neurons, and a directed wave is created owing to refractory suppression of further activity once a neuron has fired (Feller et al., 1997, Butts et al., 1999). Relatively simple cell automata models can produce a good match to the overall statistics of these waves (Godfrey and Swindale, 2007, Albert et al., 2008), as do models based on more biophysically realistic neurons (Hennig et al., 2009, Ford et al., 2012) (Figure 5G). An interesting finding from both types of models is that the retinal network may be operating close to the point of a percolation phase transition, providing statistics similar to those of natural images (Albert et al., 2008, Hennig et al., 2009). Theoretical analyses have provided precise predictions for the dependence of wave behavior on model parameters (e.g., Lansdell et al., 2014, Karvouniari et al., 2017).

Structures downstream of the retina also show spontaneous activity, which can be endogenously generated besides being driven by retinal activity (Weliky and Katz, 1999, Luczak et al., 2009). Several models address how sensory inputs can organize cortical activity into neural assemblies via STDP-like learning rules (e.g., Lazar et al., 2009, Litwin-Kumar and Doiron, 2014, Miconi et al., 2016), although some of these address more generic adult plasticity mechanisms rather than specifically developmental processes. Using a learning rule with a timescale consistent with BTDP, Triplett et al. (2018) showed that neural assemblies can arise even without afferent input. Modeling has also emphasized the importance of gap junctions in cortical waves during development and suggested an increasing gradient of intrinsic excitability across the cortex (Barnett et al., 2014). Taking a more normative theoretical perspective, the statistics of spontaneous activity become more similar to those evoked by natural input during development, suggesting that spontaneous activity could act as a Bayesian prior for evoked activity (Berkes et al., 2011).

Discussion

It is apparent from the earlier discussion that there is a conceptual division between modeling activity-dependent and activity-independent components of neural development. The latter generally involves special cases of mechanisms that also apply more generally in biological development, such as specifying cell identity or deciding in which direction to grow. Here models can leverage data and theories derived from non-neuronal systems, which are often easier to study. However, it is sometimes the case that there is a high “entry fee” for such work, in terms of a large amount of system-specific jargon (such as lists of gene names) that must be mastered to develop models that make direct contact with the biology. By contrast, activity-dependent neural development has far fewer counterparts in non-neural development and thus requires different theoretical thinking. However, it is still the case that theoretical ideas developed in a broader context can still be relevant, for instance, general ideas of pattern formation (Cross and Greenside, 2009) applied to the activity-dependent development of visual maps (Reichl et al., 2012).

Experimental techniques across both activity-dependent and activity-independent domains are rapidly improving. Technologies such as CRISPR are opening up new opportunities for understanding the roles of specific genes during development (Harrison et al., 2014). Fluorescent calcium (Chen et al., 2013) and voltage (Yang and St-Pierre, 2016) indicators now allow the activity of large neural populations to be observed and manipulated using optogenetics (Yizhar et al., 2011). Imaging technologies such as brain clearing (Vigouroux et al., 2017) and light sheet microscopy offer unprecedented opportunities for visualizing neuron structure, cell movements (Keller et al., 2008), and activity at single-neuron resolution but whole-brain scale during development (Ahrens et al., 2013). Each new experimental finding has the potential to prompt new questions amenable to theoretical analysis. Conversely, these technologies allow quantitative theories to be tested with a precision hitherto unavailable.

A particularly exciting area related to modeling neural development is the success of artificial neural networks, particularly deep learning, for solving real-world problems (LeCun et al., 2015, Schmidhuber, 2015). Originally inspired by neuroscientific findings about brain development and plasticity (Hassabis et al., 2017), these algorithms are now able for the first time to rival (or sometimes improve upon, e.g., Silver et al. (2017)) human performance in tasks such as image and speech recognition. Although there are long-standing controversies about how “biological” these algorithms actually are, there have been a number of recent suggestions for ways around these issues (e.g., Bengio et al., 2015, Lillicrap et al., 2016). However, despite various attempts to incorporate network growth (for an early example see Frean (1990)), current algorithms generally rely on a designer to exactly specify the system's neural architecture and wiring pattern. In effect, the biological inspiration has come entirely from the very last stages of development reviewed in this article, with little or no consideration of earlier stages. One might argue that this is justified because perhaps these earlier stages do nothing but set the scene for the real action regarding information processing, which is adjusting patterns of synaptic strengths. However, it is certainly the case that the computational potential of a more holistic view of neural development has been far less explored. An important part of the future of artificial intelligence lies in neuromorphic computing (Indiveri et al., 2011, Neftci, 2018), yet despite many recent advances we are still far from neuromorphic chips that build themselves. Therefore, it is possible that inspiration from neural development still has much to offer for the future of artificial intelligence.