Multiscale analysis of architecture, cell size and the cell cortex reveals cortical F-actin density and composition are major contributors to mechanical properties during convergent extension

ABSTRACT

The large-scale movements that construct complex three-dimensional tissues during development are governed by universal physical principles. Fine-grained control of both mechanical properties and force production is crucial to the successful placement of tissues and shaping of organs. Embryos of the frog Xenopus laevis provide a dramatic example of these physical processes, as dorsal tissues increase in Young's modulus by six-fold to 80 Pascal over 8 h as germ layers and the central nervous system are formed. These physical changes coincide with emergence of complex anatomical structures, rounds of cell division, and cytoskeletal remodeling. To understand the contribution of these diverse structures, we adopt the cellular solids model to relate bulk stiffness of a solid foam to the unit size of individual cells, their microstructural organization, and their material properties. Our results indicate that large-scale tissue architecture and cell size are not likely to influence the bulk mechanical properties of early embryonic or progenitor tissues but that F-actin cortical density and composition of the F-actin cortex play major roles in regulating the physical mechanics of embryonic multicellular tissues.

Highlighted Article: Application of the cellular solids model to Xenopus dorsal isolates reveals that F-actin cortex composition, in the form of F-actin cross-linking, plays a major role in bulk mechanics during neurulation.

INTRODUCTION

Tissue movements during development depend on mechanics. Early movements facilitate the formation of complex tissue architectures that establish the vertebrate body plan. Here, we define architecture as the geometrical organization of cellularized tissue structures with surrounding extracellular matrix. Precise control of mechanical properties and force production during early development is required for successful generation of complex architectures. During gastrulation, embryos of the frog Xenopus laevis undergo dramatic changes in architecture as germ layers are reshaped through bottle cell contraction, mediolateral and radial cell intercalation, and tissue thickening (Davidson, 2008; Keller et al., 2003). The forces generated by these cellular behaviors are integrated mechanically to drive tissue movements, such as ectoderm epiboly, involution and convergent extension, that build the dorsal domain of the embryo, which is composed of the neural plate ectoderm along the outer surface of the embryo, the mesoderm consisting of a central notochord flanked by presomitic mesoderm (PSM), and the endoderm facing the archenteron (Fig. 1A). The relative positions of germ layers are preserved as neurulation progresses, but each layer, particularly the neural plate ectoderm and PSM, are reshaped into new tissue architectures with distinctive cell shapes.

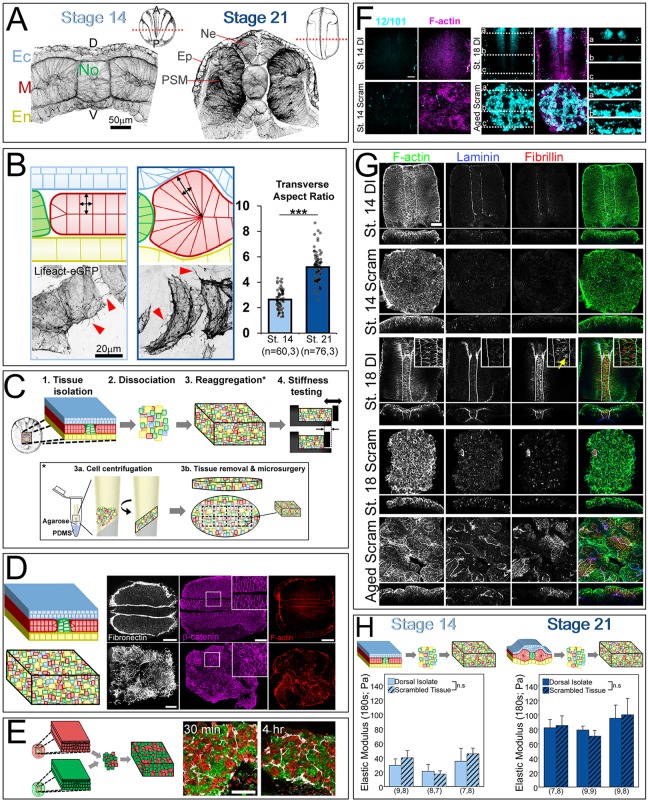
Fig. 1.

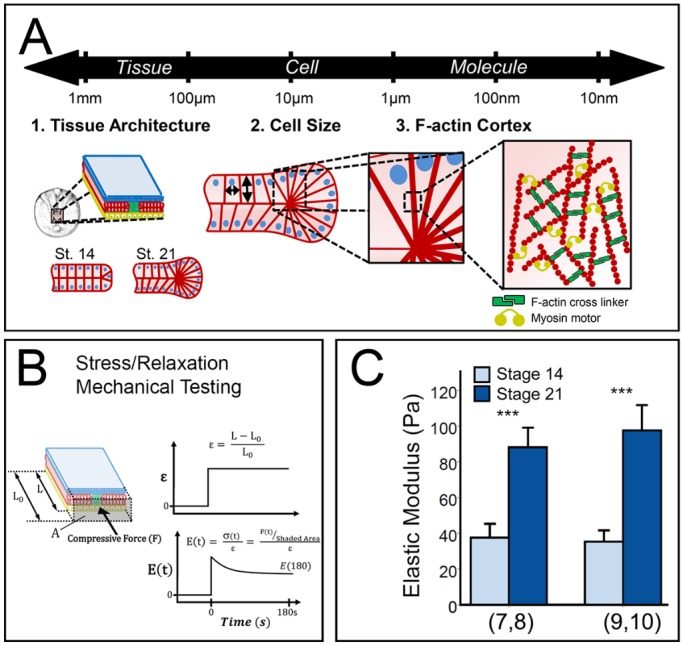
Multiscale contributors to tissue mechanical properties. (A) Structural elements at the tissue, cell and molecular scale may contribute to bulk tissue mechanical properties. Germ layers in the dorsal axis are depicted in different colors: ectoderm (blue), mesoderm (red) and endoderm (yellow). (B) Time-dependent Young's modulus [E(t)] of dorsal tissues measured by uniaxial stress relaxation. Dorsal tissues from Xenopus laevis embryos are microsurgically isolated and loaded into the nanoNewton force measurement device (nNFMD). Tissues are compressed to a fixed strain (ε) and the compressive force is measured using a calibrated force transducer. Modulus is calculated from strain, force and the cross-sectional area measured after fixation (Zhou et al., 2009). (C) Residual elastic modulus [E(180)] determined from testing shows that dorsal tissues stiffen ∼150% between stages 14 and 21. Two clutches were tested (number of explants in each set indicated in parentheses below the plot). ***P<0.001 by Mann–Whitney U test. Error bars represent s.d. Note: explants were treated with 0.5% DMSO.

Regulation of tissue mechanical properties and force production during embryonic development have been studied in many organisms. Studies in Drosophila have demonstrated that mechanical properties play key roles in early processes, such as mesoderm invagination, germ band elongation and dorsal closure, as well as a diverse set of epithelial morphogenetic movements at later stages (Rauzi et al., 2015). Direct mechanical measurements of the epithelial blastula wall in sea urchin revealed that apical extracellular matrix (ECM) can also be a major contributor to Young's modulus (Davidson et al., 1999) and places severe physical constraints on the contribution of otherwise plausible cellular mechanisms to invagination (Davidson et al., 1995). Studies using zebrafish induced embryonic cell aggregates have implicated cell-cell adhesion interactions in positioning of germ layers (Maitre et al., 2012). Perturbing cell-cell adhesion can also disrupt the normal sorting processes that position epidermal cells on the outer surface of the zebrafish embryo (Manning et al., 2010).

Embryos of the African claw-toed frog Xenopus laevis have been extensively studied with respect to the mechanics involved in gastrulation, neurulation, heart formation and tailbud elongation stages. Tissue fragments from these stages, known as explants or isolates, can be microsurgically excised and develop normally in culture. Mechanical studies of explants have revealed that early dorsal tissues are extremely soft compared with adult tissues, display anisotropic Young's modulus (different mechanical properties in each direction) (Moore et al., 1995), and exhibit a six-fold increase in Young's modulus from early gastrula to tailbud stages (Zhou et al., 2009). Ectoderm isolates and aggregates can appear fluid-like, but exhibit elastic behaviors to guide tissue morphogenesis (Luu et al., 2011). The modulus of ventral tissues also increases after neurulation, as the heart and other ventral organs form (Jackson et al., 2017). At later stages, large-scale structures such as the notochord also play a role; for instance, the tailbud embryo straightens and lengthens as vacuoles within the collagen sheathed notochord swell (Adams et al., 1990). Thus, changes in both material composition, e.g. cytoskeleton, and large-scale multicellular structures, such as the notochord, can contribute to both the Young's modulus, and morphogenesis of the Xenopus embryo. Thus far, several mechanical features of Xenopus embryonic development, such as ultra-soft material properties, stage- and germ-layer dependence of mechanical properties, and force production have been confirmed in other vertebrates, such as zebrafish (Krieg et al., 2008; Puech et al., 2005), avian species (Agero et al., 2010; Zamir and Taber, 2004) and mouse (Lau et al., 2015).

Although our understanding of the mechanical patterning of the embryo during development is improving, little is known about the tissue-, cell- and molecular-scale mechanisms that regulate these cell- and tissue-mechanical properties. Such regulators may be categorized by their impact on three different scales (Fig. 1A): (1) at the finest scale, changes in composition of materials, such as newly assembled extracellular matrix or intracellular F-actin cortex, (2) at an intermediate scale, changes in cellular architecture, such as the size and shape of cells, and (3) at the largest scale, changes in tissue microanatomy, such as assembly of laminar cell sheets, or the ECM-wrapped notochord. In Xenopus, studies have focused primarily on composition by perturbation of ECM, F-actin, microtubules and myosin contractility; for instance, F-actin and contractile myosin II account for approximately 60% of the Young's modulus at the end of gastrulation (Zhou et al., 2009; Zhou et al., 2010). These studies have consistently found that embryos exhibiting higher than normal Young's modulus are increasingly liable to developmental defects. Beyond these studies, little is known about the role of cell- or tissue-scale features that may establish the Young's modulus or how these features might be regulated to contribute to stage-to-stage or tissue-to-tissue level variation.

In this study, we test the contribution of tissue-, cellular- and subcellular-scale structures to the changing Young's modulus of the Xenopus embryonic dorsal axis during neural elongation (Fig. 1A). We adapt a formal theoretical framework known as the cellular solids model (CSM) (Gibson and Ashby, 1997) to Xenopus embryonic tissues. CSM was developed to characterize the bulk mechanical properties of open- and closed-cell materials, both synthetic and biological in origin, based on microstructure of the cells making up the material. The term ‘cell’ in this context refers to three-dimensional, repeating units that form the materials, such as cork or a honey bee's comb. For our purposes the ‘cell’ in CSM will refer to embryonic cells. After describing this model, we test its core assumption that a material's bulk property can be captured by the unit mechanics of its component cells. Next, we test the role of cell size, cell cortex thickness, and cortex composition on the mechanics of dorsal tissues. We find that dorsal tissues with lower and higher cell density correlate with predictions of the CSM but that cell density changes contribute less than a 20% increase in stiffness from early to late neurulation. To modulate the thickness and material stiffness of the ‘cell wall’, here defined as the cell cortex directly beneath the cell plasma membrane, we modulated cortical F-actin cross-linking and found that F-actin cortex composition, in the form of F-actin cross-linking, plays a major role in bulk mechanics during neurulation. In this study, we leverage several aspects of Xenopus laevis embryology that make it an ideal model to test the contribution of structures at multiple scales to the mechanics of the embryo.

RESULTS

Embryonic dorsal tissues stiffen 150% during neurulation

Following gastrulation, the Xenopus dorsal axis is composed of three germ layers that can be microsurgically isolated and cultured for more than 24 h. This isolated tissue, known as the dorsal isolate, undergoes convergent extension similar to the analogous tissues in the intact embryo. The dorsal isolate retains a consistent cross-sectional composition along its anterior to posterior axis and allows the use of unconfined compression testing to measure its mechanical properties. Previous studies demonstrated the dorsal isolate stiffens more than six-fold over the course of gastrulation and neurulation (Zhou et al., 2009). Applying a ∼20% strain along the anterior-posterior axis yields a time-dependent Young's modulus calculated from the plateau compressive force, strain during testing and cross-sectional area (Fig. 1B). Dorsal isolates stiffen 150% in 5 h from early neural plate to post neural tube formation stages (stage 14 to stage 21; Fig. 1C) in agreement with previous measurements (Zhou et al., 2009).

Cellular solids model

We adopted the cellular solids model (Gibson and Ashby, 1997) to evaluate the contribution of structures, ranging in scale from millimeters to nanometers, to the mesoscopic mechanical properties of the Xenopus dorsal isolate. CSM is a formal theoretical framework that represents the Young's modulus of cellular materials as a foam the function of which depends on component structures ranging from cell size, or cellular density, to the thickness of cell walls, to the mechanical material properties of the wall material. A foam contains a solid or liquid phase surrounding pockets of gas or fluid and can be categorized as either open, with material able to move from one cell to another, or closed, with solid membranes over the faces of the cells that prevent movement of material. Solid closed-cell foams differ from liquid closed-cell foams by their structure, mode of deformation and viscous dissipation. Solid foams bear loads through cell wall bending and stretching whereas liquid foams are governed by their surface tension. Like solid foams, liquid foams behave elastically under small deformations but behave plastically under larger deformations that induce topological changes, e.g. cell rearrangement (Weaire and Hutzler, 2001), and are often used to describe cell shapes and rearrangement within two-dimensional epithelia (e.g. Farhadifar et al., 2007; Hayashi and Carthew, 2004). During morphogenesis, Xenopus tissues can generate significant anisotropic stresses and sustain loads (Lau et al., 2015; Zhou et al., 2015). Thus, we propose that embryonic tissues can be described as solid closed-cell foams and that their mechanical properties depend on microstructures similar to those that underlie the mechanical properties of solid closed-cell foams. Here, we utilize the CSM for its dimensional analysis of closed-cell foams to test the proportionalities between cell size, cell wall thickness and Young's modulus in embryonic tissues.

A central assumption of the CSM in relating the Young's modulus to the structure and materials of its constituent parts is that physical properties depend only on the structure of repeating unitary cells and do not depend on larger multicellular structures such as embedded truss-like or fiber-wound hydrostat elements. However, bulk mechanical properties of biological tissues, like manufactured materials, may depend on embedded coherent three-dimensional tissues or anatomical architectures (e.g. Fung, 1981; Vincent, 2012), such as those found in laminar germ layers, grooved neural ectoderm, or columns of PSM.

Architecture changes in dorsal isolates are concurrent with tissue stiffening

Like all vertebrates, the process of neurulation involves both formation of the neural tube and convergence of PSM (Keller, 2000; Vijayraghavan and Davidson, 2016). These morphological changes rely on coordinated large-scale movements of laminar cell sheets and result in dorso-ventrally thicker, anterio-posteriorly longer and medio-laterally narrower tissue (Fig. 2A). We examined the morphological changes that occur during neurulation by bisecting dorsal tissues at stages 14 and 21. At stage 14, the dorsal axis is 128±13 μm (mean±s.d.) in thickness and contains a flat neural plate and brick-shaped PSM. By stage 21, the dorsal axis is 228±14 μm in thickness and has undergone major architectural changes, specifically neural plate folding and mesoderm reshaping. The two-cell-layered neural plate thickens significantly between stages 14 and 21 from 29±4 to 75±8 μm and forms the neural tube. Cell shapes within the PSM change significantly between stage 14 and stage 21. The transverse aspect ratio of PSM cells increases two-fold between stages 14 and 21 (P<0.001; Mann–Whitney U test; 2.6±0.8 at stage 14, 5.2±1.2 at stage 21; Fig. 2B). Mosaic labeling also revealed that PSM cells extend numerous filopodia-like protrusions, often more than 10 µm (Fig. 2B, red arrowheads; Movie 1). Thus, neurulation is accompanied by the generation of large coherent structures from originally planar neural ectoderm and PSM. In this study, we began by testing the assumption of the CSM that tissue architecture does not contribute to Young's modulus by generating, characterizing and mechanically testing disordered, or scrambled, tissues.

Fig. 2.

Young's modulus depends on stage, not architecture. (A) Transverse sections of stage 14 and stage 21 dorsal tissues stained for F-actin (phallacidin). Note the large-scale tissue architecture change between stages. A, anterior; D, dorsal; Ec, ectoderm; En, endoderm; Ep, prospective epidermis; M, mesoderm; Ne, neural ectoderm; No, notochord; P, posterior; V, ventral. The flat neural plate (Ec; stage 14) bends, folds and internalizes to form the neural tube (Ne). (B) Cell shapes in PSM tissues in dorsal isolates mosaically injected with the F-actin reporter Lifeact-eGFP. By stage 21, mesoderm cells lengthen dorso-ventrally (as revealed by the transverse aspect ratio), reflecting tissue-level mesoderm thickening (***P<0.001; Mann–Whitney U test; n=cells, explants). Arrowheads indicate filopodia-like protrusions from the lateral surface of the cells. Schematics depict the morphological changes in cell shape in the PSM during neurulation. (C) Schematic of tissue architecture disruption. Tissues were isolated at neurula stage, dissociated, and re-aggregated into ‘scrambled’ tissues. Mechanical properties and extracellular matrix organization within scrambled tissues were compared with native tissues. The re-aggregation process is detailed in the inset beneath the summary schematics. Dissociated cells were loaded into custom-made chambers and centrifuged to generate single ∼0.8×1 mm elliptical sheets of tissue that were dissected into regular dorsal isolate-shaped blocks. (D) Fibronectin and β-catenin staining reveal loss of bulk architecture, stereotypic fibronectin organization and cell shape in scrambled tissues. (E) Cross-explant mixing occurs within ECM encapsulated clusters as seen in scrambled tissues made from half rhodamine dextran (red)-injected embryos and half FITC-dextran (green)-injected embryos. (F) En face z-slices of dorsal isolate and scrambled tissues stained for the somite marker 12/101 and F-actin (phallacidin). Dashed white lines indicate optical sections at three points along the dorsal axis from anterior (a) to posterior (c). Cells within aged scrambled tissues (to the equivalent of stage 18) express 12/101, indicating differentiation to somitic tissue. (G) En face z-slices of dorsal isolate and scrambled tissues stained for F-actin, laminin and fibrillin. Insets reveal high levels of fibrillin between notochord cells (yellow arrow). Aged scrambled tissues (to the equivalent of stage 18) reveal de novo synthesis of laminin and fibrillin. (H) Scrambled tissues (hashed bars) have the same Young's modulus as native control tissues (unhashed bars) in early and late neurula tissues (stage 14: 27.9 Pa versus 33.8 Pa; two-way ANOVA, P=0.371; stage 21: 85.5 Pa versus 85.1 Pa; two-way ANOVA, P=0.971). Each cluster represents one experiment and n value (beneath the bars) represents number of explants tested per group. Error bars represent s.d. Xenopus stage schematics adapted from Nieuwkoop and Faber (1967). n.s., not significant. Scale bars: 100 μm.

Architecture of the dorsal isolate is disrupted after ‘scrambling’

To construct a tissue that was devoid of large coherent three-dimensional structures, we microsurgically isolated dorsal tissues, scrambled the tissues by gentle cell dissociation, and regenerated dorsal isolate-shaped tissue blocks (Fig. 2C). Brief incubation in Ca²⁺- and Mg²⁺-free media disrupted laminar tissue structures and dissociated cells. After restoring Ca²⁺ and Mg²⁺, dissociated cells can be repacked into large flat elliptical-shaped tissue ‘cakes’ by centrifugation (8 min at 2000 g). Up to 14 dorsal isolates were dissociated and combined to generate single ∼0.8×1 mm elliptical sheets of tissue that were dissected into regular dorsal isolate-shaped blocks. Scrambled tissue blocks remain viable and maintain a similar cell density as intact tissue (U.L.B., unpublished data).

To assess how well scrambling disrupted architecture, we fixed and stained both stage-matched dorsal isolates, and scrambled tissues for fibronectin, the dominant extracellular matrix protein at this stage that marks interfaces between all germ layers (Davidson et al., 2004). As suspected, fibronectin distribution revealed a complete loss of bulk tissue architecture (Fig. 2D); however, local tissue microdomains comprising small clusters of two to 20 cells can be found surrounded by fibronectin fibrils. Scrambled tissues retain their shape but do not undergo convergent-extension movements, or neural fold formation as observed in control tissues (Fig. S1; Movie 2).

To test whether microdomains reflect residual connections between cells from a single dorsal isolate, or if mixing occurs, we prepared dorsal isolates from embryos injected with the lineage tracers FITC-dextran and TRITC-dextran. If cells from single isolates retained their neighbors, we would expect only single colors within fibronectin-bounded microdomains. However, cells from different embryos mixed within microdomains in as little as 30 min, and persisted at least 4 h after aggregation (Fig. 2E). Thus, cells from different embryos were able to join into single microdomains during the aggregation process. We also note that cell shapes within scrambled tissues are irregular compared with stereotypical cell shapes within germ layers in intact dorsal isolates (Fig. 2D). Over the time course of convergent extension we did not observe reassembly of large-scale structures reminiscent of the laminar germ-layers of intact dorsal isolates.

Differentiation and assembly of laminin and fibrillin fibrils in scrambled tissues parallels development of native tissue

To determine whether scrambled tissues continued to develop as intact dorsal tissues, we checked whether scrambled tissues expressed stage-appropriate markers. To assess maturation of PSM, we tested whether scrambling inhibited somitic cell differentiation. The immunomarker 12/101 stains myofibers (Kintner and Brockes, 1984), appears during neurula stages, and appears in scrambled tissues over the same stages (Fig. 2F). Laminin and fibrillin are two ECM proteins that are present at low levels during early neurulation (stage 14), and form dense arrays by deep neural groove stage (stage 18) (Fey and Hausen, 1990; Skoglund et al., 2006); we confirmed their assembly at the notochord, at mesoderm-ectoderm, and at mesoderm-endoderm interfaces by deep neural groove stage (Fig. 2G). Fibrillin is also present between notochord cells (Fig. 2G, red arrows). In scrambled tissues, both fibrillin and laminin organization is disrupted (Fig. 2G); however, like intact tissues, scrambled tissues assemble fibrillin and laminin arrays, and form fibrillin fibers between cells in a subpopulation of cell clusters (Fig. 2G). Thus, cells within scrambled tissues maintain stage-dependent developmental programs of ECM assembly.

To assess F-actin cytoskeletal dynamics in cells within scrambled tissues, we imaged mesoderm cells expressing Lifeact-GFP (Riedl et al., 2008). Scrambled tissues containing scattered F-actin labeled mesoderm cells were then cultured on a fibronectin-coated substrate. Intercalating mesoderm cells normally exhibit bipolar protrusions along the mediolateral axis (Shih and Keller, 1992a,b). In scrambled tissues, protrusive activity was maintained but was no longer oriented (Fig. S2).

Next, we compared the mechanical properties of scrambled tissues with those of intact dorsal isolates. Surprisingly, the Young's modulus of early neural plate stage (stage 14) scrambled tissues subjected to an unconfined compression test were not significantly different from stage-matched dorsal isolates (Fig. 2H). Similarly, post-neurulation (stage 21) scrambled tissues showed no difference from stage-matched dorsal isolates. Thus, the Young's modulus of scrambled tissues was indistinguishable from dorsal isolates with native architecture. Next, we investigated whether stage 14 scrambled tissues would mimic native tissue stiffening when cultured to stage 21. We created scrambled tissues at just after blastopore closure (late stage 13) and aged them to the equivalent of stage 14 and stage 21. Aged scrambled tissues stiffened to a limited degree (P=0.001; two-way ANOVA; Fig. S3), but did not attain the full stiffness of scrambled tissues created at stage 21. Thus, tissue architecture does not contribute to Young's modulus in early- and late-stage dorsal isolate tissues; however, scrambling limits the capacity of aging tissues to stiffen at the same rate as dorsal isolates.

CSM relates cell size to Young's modulus

Because the Young's modulus of the dorsal isolate is independent of the complex architecture of the germ layers and neural ectoderm, we turned to testing predictions of the CSM. The first of these predictions suggests that decreases in cell size would produce tissues with greater Young's modulus. The CSM predicts a relatively minor contribution of cell size to Young's modulus even though cell cycle, and thus cell size, is tightly regulated during animal morphogenesis. As the Xenopus embryo undergoes cycles of reductive cleavage coincident with developmental phases of rapid stiffening, we sought to understand the contribution of decreasing cell size on tissue stiffness.

The second of these predictions is based on the thickness and composition of the cell wall, or cell cortex. From a materials perspective, F-actin gels are more solid than liquid (Gardel et al., 2004), and we propose that Xenopus embryonic tissues can be described as solid closed-cell foams, the mechanical properties of which can be predicted by the CSM. The mechanical function of the cell wall depends on F-actin and myosin II contractility in the cell cortex (Zhou et al., 2009; Heisenberg and Bellaiche, 2013). Considering cell size and the cell cortex, the Young's modulus of a closed-cell foam filled with an incompressible fluid is given by:

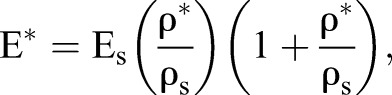(1)

where E* is the tissue Young's modulus, E_s is the Young's modulus of the solid material, ρ* is the density of the cellular solid (mass of solid fraction divided by total tissue volume) and ρ_s is the density of the solid it is made from (mass of solid fraction divided by volume of solid fraction). The most important feature is the relative density, ρ*/ρ_s, which simplifies to the volume fraction of cortex to total cell volume:

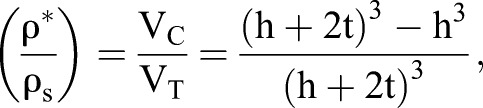(2)

where V_C is total cortex volume, V_T is total cell volume, t is the cell wall thickness, approximated to be 150 nm, and h is the length of the cell, excluding cell wall thickness. In our case, we relate changes in ρ*/ρ_s to changes in the number of cells per unit volume, assuming constant t. We calculate the resulting change in h after estimating the change in cell volume from changes in nuclear density. For instance, if 56 nuclei are found in a 0.2 nl volume (Fig. 3D) we calculate that each cell length, h, is 15.3 µm and the volume fraction of the cell cortex, ρ*/ρ_s, is 5.7%. The CSM then predicts a change E* based on the change in ρ*/ρ_s between control and experimental tissues and assuming that E_s is unchanged (Fig. S4).

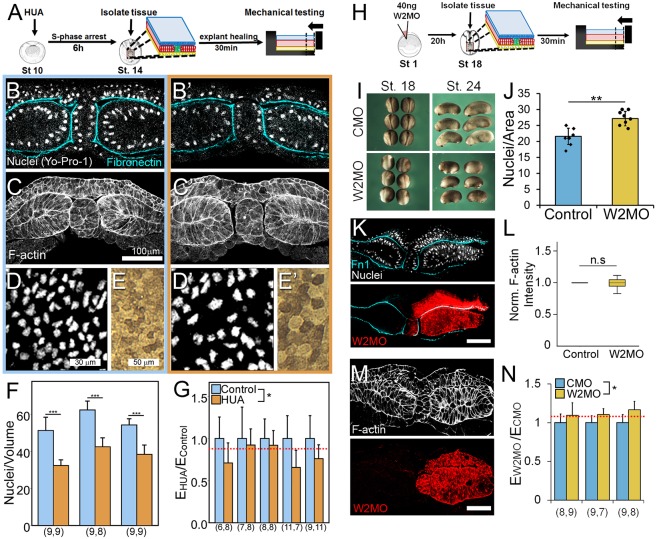
Fig. 3.

Testing predictions of the cellular solids model: cell size correlates with stiffness. (A) To generate large cells in tissue explants, we arrested the cell cycle using a combination of cell cycle inhibitors, hydroxyurea and aphidicolin (HUA). Tissues were microsurgically isolated at stage 14 and mechanically tested. (B-E′) Representative images of control (B-E) and HUA-treated (B′-E′) tissues stained for nuclei (Yo-Pro-1), fibronectin (4H2) and F-actin (phallacidin). (F,G) Tissues treated with HUA show reduced nuclei/volume (***P=0.01; Mann–Whitney U test; F) and a 25% decrease in Young's modulus (two-way ANOVA, P=0.04; G). Dashed red line indicates CSM prediction. (H) To generate small cells in tissue explants, we induced a cell division in the PSM by inhibiting a developmentally regulated cell cycle inhibitor, Wee2, using anti-sense morpholino knockdown. Tissues were microsurgically isolated at stage 18 and mechanically tested. (I) Depletion of Wee2 in whole embryos compared with control morpholino (CMO). Note reduced convergence of neural folds at stage 18 and shortened axis at stage 24. (J) Increased nuclear density within Wee2-depleted mesoderm tissue (morpholino co-injected with rhodamine dextran; n=8; **P<0.002, Student's t-test). (K) Transverse sections of stage 18 unilaterally Wee2-depleted tissues stained for nuclei (DAPI) and fibronectin (Fn1). Note increased nuclear density within Wee2-depleted tissues. (L) Normalized F-actin is unperturbed in Wee2-depleted tissues compared with control morpholino. (M) Transverse sections of stage 18 unilaterally Wee2-depleted tissues stained for F-actin (phallacidin). (N) Tissues depleted of Wee2 show 12% increase in Young's modulus (two-way ANOVA, P=0.038). Young's modulus is normalized to control morpholino (CMO)-injected tissues. Dashed red line indicates CSM prediction. Each cluster represents one experiment and n value (beneath the bars in F,G,N) represents number of explants tested per group. Error bars represent s.d. Xenopus stage schematics adapted from Nieuwkoop and Faber (1967). n.s., not significant. Scale bars: 100 μm.

Lower cell density reduces the Young's modulus of dorsal isolates

As the mesoderm is the stiffest of the germ layers in the developing neurula, we focused on cell size in the mesoderm (Zhou et al., 2009). To increase cell size, we inhibited cell cycle progression through S phase with a combination of 20 mM hydroxyurea and 150 µM aphidicolin (HUA). HUA induces cell-cycle growth arrest in various cell types in the Xenopus neurula (Harris and Hartenstein, 1991). Dorsal structures, such as the neural tube, can develop normally without cell division (Harris and Hartenstein, 1991). Because rates of cell division slow by the mid-gastrula stage (Saka and Smith, 2001), we apply HUA at the start of gastrulation to produce embryos with larger cells by stage 14 (Fig. 3A). To ensure that HUA did not perturb large-scale tissue organization or F-actin cortex, whole embryos treated with HUA were stained for fibronectin and nuclei (Fig. 3B,B′), or F-actin (Fig. 3C,C′), revealing qualitatively unchanged tissue and F-actin organization throughout all three germ layers compared with control embryos. En face confocal sections of dorsal isolate explants (Fig. 3D,D′) revealed that HUA decreased nuclear density by 34% (Fig. 3F), resulting in a 52% increase in cell volume. Surface epithelial cells also exhibited an increase in apical area (Fig. 3E,E′). The CSM predicts a 13% decrease in tissue stiffness for a 52% increase in cell volume. We found that tissue explants with larger cells exhibited a 25% decrease in Young's modulus compared with control tissues (Fig. 3G). Thus, the CSM predicts the decrease in Young's modulus that accompanies an increase in cell sizes within dorsal isolates.

Increased cell density increases the Young's modulus of dorsal isolates

Next, we tested whether the CSM could accurately predict the Young's modulus of denser dorsal isolates. To reduce cell size, we inhibited the developmentally regulated cell cycle inhibitor Wee2 (Fig. 3H,I). Wee2 is a tyrosine kinase expressed in the paraxial mesoderm during gastrulation that inhibits cell cycle progression by phosphorylating Cdk1 (Leise and Mueller, 2002) and blocking mitosis in paraxial mesoderm (Leise and Mueller, 2004). To test the effects of Wee2 on cell density we co-injected 20 ng Wee2 morpholino (Wee2-MO) with rhodamine dextran amine (RDA) into one blastomere at the two-cell stage. By stage 16, we confirmed a 26% increase in mesoderm cell density (Fig. 3J,K), amounting to a 21% decrease in cell volume. To ensure that Wee2 depletion did not grossly alter the actin cytoskeleton, we compared the Wee2-MO injected side with the contralateral uninjected side, and found no difference in F-actin intensity (Fig. 3L,M).

Having confirmed increased cell density in Wee2-MO injected embryos, we tested the role of increased cellular density on bulk mechanical properties. The CSM predicts an 8% increase in tissue stiffness after a 21% decrease in cell volume. Wee2-MO-injected tissues exhibited a small, yet significant, 12% increase in Young's modulus compared with control morpholino (CMO)-injected dorsal isolates (Fig. 3N), consistent with the CSM prediction. Mechanical testing of dorsal isolates with lower and higher cell density confirmed the predictions of the CSM; however, the limited increases observed in cell density cannot account for the much larger increase in Young's modulus over the same time frame.

Testing predictions of the CSM relating cell cortex composition to Young's modulus

Additional factors contributing to bulk stiffness in solid foams include the thickness and material properties of the ‘cell wall’ that serve as the major load-bearing elements within a foam. In predicting the role of the cell wall on Young's modulus, CSM includes effects of cell-wall thickness (t), density (ρ_s) and modulus (E_s) (Eqns 1 and 2). The distinction between ρ_s and ρ* is that ρ_s is the density of the material in the wall of the foam, i.e. mass of the wall over the volume of the wall, whereas ρ* is the density of the cellular material, i.e. mass of the solid, ‘wall’ parts over the total volume of the foam. In the derivation of the CSM, thickness is independent of material properties; however, in practice ρ_s and E_s may be coupled. For instance, the Young's modulus of reconstituted F-actin gels depend not only on the concentration of F-actin but also on filament length and on association of F-actin with actin-binding proteins, including F-actin motor proteins such as myosins and F-actin cross-linkers such as α-actinin (Claessens et al., 2006; Grooman et al., 2012; Xu et al., 1998). To understand the relationship between ρ_s and E_s, we refer to computational models of actomyosin arrays (Kim et al., 2009; Gong et al., 2013) and experimental studies of reconstituted F-actin gels (Gardel et al., 2004; Shin et al., 2004; Tseng et al., 2002; Wagner et al., 2006).

To understand how the physical properties of the actin cortex might regulate bulk physical properties, we measured cortical F-actin intensity between stages 14 and 21. To quantify F-actin density, we took two approaches, first measuring mean intensity within the entire cross-sectional area of mesoderm tissue (Fig. 4A,A′, dashed white ROI). As this approach may not distinguish F-actin in the cortex from other pools of F-actin within the cytoplasm, we adopted a second approach, collecting higher resolution confocal z-slices and measuring intensity across the cell cortex. Between stage 14 and stage 21, mesoderm F-actin density is enhanced by 70% according to bulk intensities (Fig. 4A-B) and increased 85% across cell-cell borders (Fig. 4C-D). Additionally, F-actin networks become polarized and oriented towards the midline by stage 21 (Fig. 4E,E′).

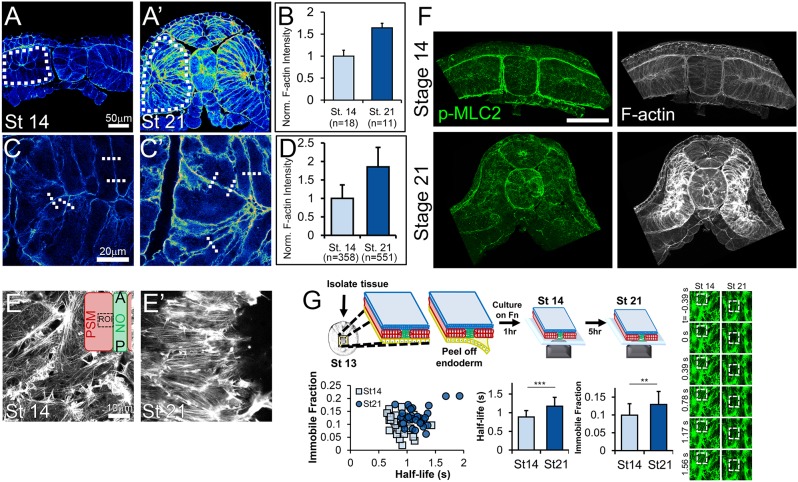
Fig. 4.

F-actin is enhanced and stabilized in mesoderm during neurulation. (A-D) Transverse sections of stage 14 (A,C) and stage 21 (A′,C′) dorsal tissues stained for F-actin reveal an increase in mesodermal F-actin abundance. Bulk measurements of mean phalloidin intensity within mesoderm cells (dotted white ROIs) reveals a 70% increase in intensity (A-B; Mann–Whitney U test, P<0.01). Phalloidin intensity was also measured by comparing max intensities across lines drawn perpendicular to cortex (dashed white lines), revealing an 85% increase (C-D; Mann–Whitney U test, P<0.001). F-actin intensity plots are normalized to mean stage 14 intensity. (E,E′) High-resolution confocal images of the endoderm-side mesodermal F-actin network at stage 14 (E) and stage 21 (E′) reveal alignment and polarization of F-actin network by stage 21. Inset in E illustrates the location of the ROI within the presomitic mesoderm and adjacent to the notochord. (F) Transverse sections of stage 14 and 21 dorsal isolates stained for p-MLC2 and F-actin. Scale bar: 100 µm. (G) Top: Schematic of F-actin FRAP experiment. Dorsal isolate tissues were isolated from stage 13 embryos injected with an F-actin live reporter (LifeAct-GFP), and the endoderm was peeled off and cultured on fibronectin to stage 14. Right: FRAP experiments were performed on stage 14 (n=32 cells) and stage 21 (n=30 cells) tissues. Representative FRAP experiment showing ∼50% bleach at 0 s with full recovery by 1.5 s. Dashed boxes indicate bleached area. Bottom: Stage 21 mesoderm tissues had higher immobile fraction and half-life (**P<0.002, ***P<0.0001; Student's t-test) compared with stage 14 tissues. Error bars represent s.d.

Because myosin II can also regulate the mechanics of actin gels, we investigated changes in activation of myosin light chain and dependence of Young's modulus on Rho kinase activation. Although both bulk and junctional F-actin is greatly enhanced between stages 14 and 21, no gross increase in myosin II activation (p-MLC2) was observed (Fig. 4F). A previous study showed that myosin II contractility contributes significantly to the Young's modulus at stage 16 (Zhou et al., 2009). To extend this analysis, we treated both stage 14 and stage 21 dorsal explants with the Rho kinase (ROCK) inhibitor Y-27632 (50 µM) and found that ROCK inhibition reduced stiffness by 52% in stage 14 explants (36.3±6.8 Pa versus 17.6±7.8 Pa; two-way ANOVA P=0.017) and 39% in stage 21 explants (93.3±13.4 Pa versus 56.5±10.3 Pa; two-way ANOVA P=0.019), indicating that myosin contractility contributes less to the Young's modulus after closure of the neural tube than at early neural plate stages (Fig. S5). Thus, both tissue scale and cortical F-actin density increase significantly in the dorsal isolates at the same time as Young's modulus increases.

As F-actin contribution to Young's modulus depends on its stability, we assessed F-actin stability using fluorescence recovery after photo-bleaching (FRAP) experiments on mesodermal cells exposed in stage 13 dorsal isolates. FRAP analysis reveals how F-actin is partitioned between static and dynamic pools. F-actin in the cortex is significantly more stable at stage 21 (as revealed by half-life and immobile fraction, P<0.05; Fig. 4G). Thus, changes to the cell wall material can explain a portion of the change in Young's modulus observed in developing embryos, and the changes we observe for the F-actin cortex suggest that additional molecular processes are responsible for changes in cell wall material.

F-actin cortex thickness is unchanged during neurulation

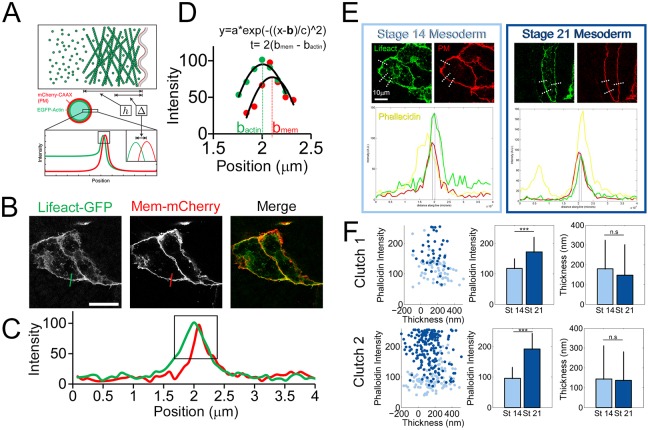
The enhancement of F-actin cortex intensity could be due to increased cortex thickness or an increase in cortex density. The CSM predicts that cortex thickness can be a strong contributor to Young's modulus; for instance, a 150% increase during neurulation would require a 79% increase in cortex thickness. To quantify cortex thickness, we adapted a super-resolution approach used to measure F-actin cortex thickness in single cells (Fig. 5A-D) (Clark et al., 2013). Because F-actin cortex thickness is below the light resolution limit, it is impossible to measure thickness directly by conventional confocal microscopy; however, cortex thickness can be calculated, independently of intensity, using a theoretical description of cortex geometry that relates the distance between the centers of the plasma membrane and actin cortex obtained from confocal sections. The F-actin cortex is assumed to be uniformly dense, to decay abruptly at the cytoplasm interface and to be in direct contact with the negligibly thin plasma membrane. Thus, the distance between the center of the actin cortex and center of the plasma membrane is half the cortex thickness.

Fig. 5.

F-actin cortex thickness is unchanged during neurulation. (A) Schematic from Clark et al. (2013) showing method of measuring cortex thickness in single isolated HeLa cells. (B) A similar approach was applied in Xenopus mesoderm cells expressing both a membrane label (Mem-mCherry) and an F-actin label (Lifeact-GFP). Scale bar: 20 μm. (C,D) The intensity profile across a junction between a cell expressing membrane/actin markers and a non-expressing cell (C) is obtained followed by Gaussian fitting around peaks in each channel (D). From the Gaussian fit parameters, the separation between the positions of the actin and membrane linescan peaks (b_actin and b_mem, respectively) is obtained and related to cortex thickness (t). The x-axis in C and D is distance along line profile. (E) Representative z-slices of mosaically labeled cells with example lines profiles (dotted white lines) drawn across junctions. Plots represent intensity values versus position on line profile (red, Mem-mCherry; green, Lifeact-GFP; yellow, BODIPY FL Phallacidin). (F) No relationship was revealed between cortex intensity (phalloidin intensity) and cortex thickness. Cortex intensity increases significantly between stages 14 and 21 (*** P<0.001; Mann–Whitney U test), but cortex thickness does not (clutch 1: P=0.29; clutch 2: P=0.27; Mann–Whitney U test). n.s., not significant. Error bars represent s.d. Super-resolution schematics (A) adapted from Clark et al. (2013).

Measuring cortical thickness in a compact tissue requires optical isolation of single cells for which the membrane and F-actin cortex are simultaneously labeled. To obtain single labeled cells, we injected mRNAs encoding actin and membrane reporters into single blastomeres at the 16-cell stage (Fig. 5E). Once fixed, tissues were also labeled with phalloidin, to assess F-actin intensity independently of Lifeact expression levels to compare F-actin intensity and cortex thickness for each line scan. Cortex thickness is calculated using the intensity profile across a junction between a cell expressing fluorescent proteins for both membrane and F-actin and a non-expressing cell followed by Gaussian fitting around peaks in each channel (Fig. 5D). Interestingly, we saw no change in cortex thickness in mesoderm cells between stages 14 and 21 (Fig. 5F) nor did we observe a relationship between cortex intensity and thickness. From this analysis, we suggest that F-actin enrichment from early to late neural stages is due to increased cortex density rather than increased cortex thickness.

Mechanical properties of the cell wall: Actn1 cross-linking regulates dorsal axis stiffness

In order to test mechanical contributions of the cell wall, we sought to modulate the stiffness of the cell cortex. Rheological studies have shown that pure actin filaments form relatively weak gels at physiological concentrations and thus require auxiliary F-actin binding proteins to cross-link and bundle actin filaments into stiffer arrays (Xu et al., 2000). In vitro studies of reconstituted actin gels have shown that increased cross-linking of F-actin results in stiffer gels (Esue et al., 2009; Gardel et al., 2004; Luan et al., 2008; Wachsstock et al., 1994; Xu et al., 1998) and stiffer cell aggregates (Cunningham et al., 1992). As F-actin is enriched in the cortex in the mesoderm during neurulation and is known to contribute to the bulk mechanics of dorsal tissues (Zhou et al., 2009), we investigated whether the degree of cross-linking can control mechanics of the dorsal axis.

To test the potential role of F-actin cross-linking in stage-dependent stiffening, we modulated α-actinin-1 (Actn1) function by overexpression of wild-type protein and expression of a dominant-negative, actin-binding domain-deleted form (Fig. 6A,B). We chose α-actinin-1 because its expression increases sharply during neurulation (Session et al., 2016) (Fig. S6) and it is expressed at relatively high levels in the dorsal marginal zone (Popov et al., 2017). Moderate to high levels of α-actinin-1 overexpression strongly disrupted normal development by inhibiting blastopore closure (Fig. S7). Reduced levels of overexpression allowed embryos to complete gastrulation and still exhibit increased F-actin intensity (Fig. 6C,D; P<0.001; paired sample t-test), and a 39% increase in stiffness (Fig. 6E; P<0.001) in stage 16 dorsal isolates. Previous cell culture studies have shown that α-actinin-1 overexpression can increase density and reduce turnover of actin filaments during cytokinesis (Mukhina et al., 2007), indicating that overexpression may inhibit F-actin depolymerization. To test whether overexpression of α-actinin-1 alters turnover at these stages we carried out FRAP analysis in animal cap epithelial cells and found increased F-actin immobile fraction and half-life in the apical cortical domain of overexpressing cells (Fig. S8) consistent with a role for α-actinin-1 in stabilizing as well as cross-linking the cortical F-actin network. To reduce F-actin cross-linking, we expressed a dominant-negative α-actinin mutant with the actin-binding domain deleted (ACTN1-ΔABD). ACTN1-ΔABD can form heterodimers with endogenous α-actinin-1 and -4, inhibiting their F-actin cross-linking activity (Low et al., 2010). To confirm the function of ACTN1-ΔABD, we tested its ability to rescue a blastopore closure defect observed with overexpression of α-actinin-1. Overexpression of ACTN1-ΔABD with α-actinin-1 rescued the blastopore closure defect accompanying α-actinin-1 expression alone (Fig. S7). Interestingly, overexpression of ACTN1-ΔABD alone resulted in no detectable change in F-actin intensity (Fig. 6C,D; P<0.15; paired sample t-test), but slightly delayed normal development (Fig. S9). After confirming the function of ACTN1-ΔABD we found that it induced a 27% reduction in stiffness (Fig. 6E; P<0.005) in stage 21 dorsal isolates, indicating that F-actin cross-linking can control mechanical properties independently of cortical F-actin density. Thus, α-actinin-1 cross-linking can regulate the stability and density, but not thickness, of cortical F-actin and can regulate Young's modulus of dorsal tissues in the late neurula.

Fig. 6.

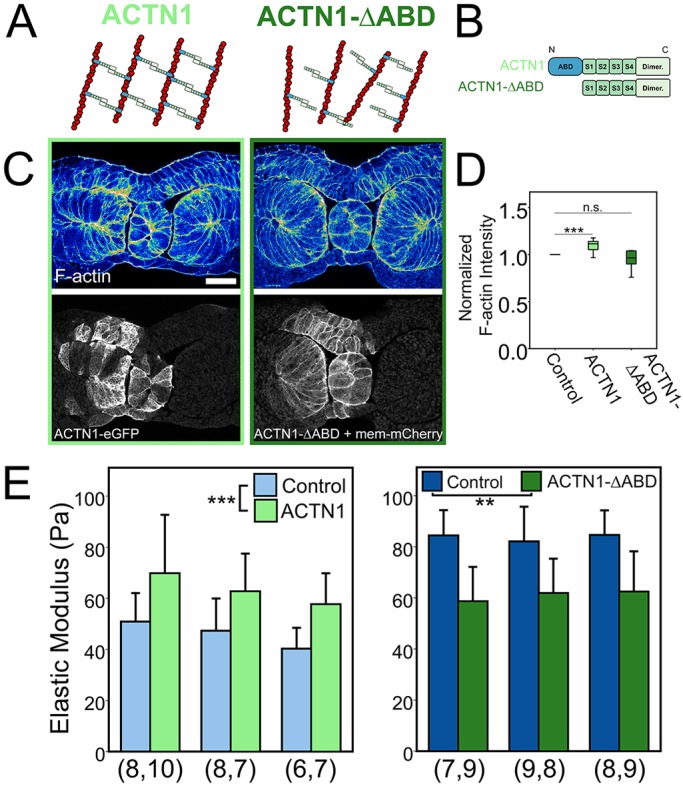
α-actinin-1 cross-linking regulates both F-actin intensity and Young's modulus. (A,B) Diagrams of the interactions between wild-type and mutant α-actinin and F-actin filaments (A) and the specific α-actinin constructs used, showing the N-terminal actin binding domain (ABD), C-terminal calmodulun-like dimerization domain (Dimer) and four spectrin repeats (S1-S4) (B). For the ACTN1 construct, eGFP was at the N terminus. (C) Transverse sections of stage 16 dorsal tissues contralaterally injected with ACTN1 or ACTN1-ΔABD and stained for F-actin (phallacidin). ACTN1-ΔABD was co-injected with Mem-mCherry. Scale bar: 100 µm. (D) F-actin intensity levels of injected cells were compared with contralateral, uninjected cells within mesoderm tissues. F-actin was significantly enhanced in cells injected with ACTN1 (***P<0.001; paired sample t-test), but not ACTN1-ΔABD (P=0.15; paired sample t-test). The box represents the 25th-75th percentiles surrounding the median (indicated by the line within the box) and whiskers represent the upper and lower quartiles. (E) Stage 16 dorsal isolates overexpressing ACTN1 were 39% stiffer than controls (***P<0.001; two-way ANOVA). Stage 21 dorsal isolates overexpressing ACTN1-ΔABD had a 27% reduction in stiffness (**P<0.005; two-way ANOVA). Each cluster represents one experiment and n value (beneath the bars) represents number of explants tested per group. n.s., not significant. Error bars represent s.d.

DISCUSSION

In this study, we investigated the structural origin of mechanical properties and sources of stiffening of dorsal embryonic tissues in the frog embryo. We confirmed a 150% stiffening during neurulation and compared the mechanics of dorsal embryonic tissues with those of solid closed-cell foams. We used predictions of the CSM of solid closed-cell foams to guide our biomechanical analysis of the different ways that features at various size scales contribute to the bulk mechanical properties of dorsal tissues. Before we could use CSM predictions, we ruled out a major role for tissue architecture in establishing mechanical properties by scrambling native architecture. In testing predictions of the CSM on the role of cell size in foam mechanics, we determined that stiffening during neurulation cannot be explained by decreasing cell size; however, we cannot formally rule out possible changes to cell cortex induced by HUA or Wee2 perturbations that alter cell size. We concluded our study by testing the contribution of cortical F-actin density and cross-linking to embryonic tissue mechanical properties as the ‘cell wall’ is predicted by the CSM to be a major contributor to Young's modulus. Also, from earlier studies we have found that the majority of forces and contributors to the modulus arise from the actomyosin cytoskeleton (Zhou et al., 2009). In Xenopus embryos, most of the actomyosin cytoskeleton is found at the cell cortex rather than the cell-spanning stress fibers so often found in cultured fibroblast cells. Additionally, studies have revealed that cycles of F-actin assembly and myosin II-mediated contraction of the cortex are highly correlated with cell shape change and morphogenesis (Kim and Davidson, 2011; Köppen et al., 2006). We found a substantial increase in the abundance and stability of mesodermal F-actin between stages 14 and 21. We chose to investigate the role of the actin-binding protein α-actinin-1 because of its expression profile and well-characterized contribution to the Young's modulus of reconstituted F-actin gels. Full-length and mutant forms of α-actinin-1 can alter F-actin cortex composition and produce significant increases in bulk stiffness with increasing levels of cross-linking. The enhancement of F-actin is likely to be regulated by several, potentially overlapping, molecular mechanisms. Each of these different molecular mechanisms may be independently regulated through expression or activity in different germ layers. Cortical actin cross-linking is likely to be one of many mechanisms responsible for increasing bulk modulus. Further studies will be needed to explore the role of other actin-binding proteins, including alternative cross-linkers, such as fascin-1, filamin B, α-actinin-4, end-cappers, polymerizing factors, etc., and their effects on tissue- and stage-dependent changes in Young's modulus of embryonic tissues.

Embryonic tissues behave like solid closed-cell cellular solids

Although the CSM has been useful in predicting how structural features might influence bulk mechanical properties, the basic equations of the CSM do not capture the contribution of fine-scale structures within the cortex. For instance, measures of cortex thickness do not incorporate information on F-actin cortex organization, density, or the degree of cross-linking. Interestingly, a recent study using cultured HeLa cells showed that depletion of four different F-actin cross-linkers known to mediate F-actin gel mechanics similarly did not affect cortex thickness (Chugh et al., 2017). Furthermore, although cortex thickness and cross-linking can regulate mechanical properties of the tissue they are not the only factors that can contribute. Changes in myosin II contractility also play a key role. For instance, even though the F-actin cortex of mouse oocytes thickens during meiosis I, reduced myosin II contractility drives increased compliance (Chaigne et al., 2013). Similarly, depletion of F-actin in human fibroblasts has no effect on cortex mechanics yet increased myosin II contractility does (Cartagena-Rivera et al., 2016). Cortex mechanics may be further regulated by the different morphologies of F-actin networks (Claessens et al., 2006; Grooman et al., 2012; Xu et al., 1998). Future biophysical studies using complex reconstituted gels or synthetic membrane-associated F-actin arrays may provide considerable insights into the mechanisms cells use to tune cortex mechanics (Shin et al., 2004).

The mechanism of F-actin enhancement in the dorsal axis may involve multiple factors operating simultaneously. The degree to which cortical F-actin networks are shaped in vivo will be challenging to assess. Future studies, combining theoretical and experimental tests will be needed to challenge the specific roles of F-actin regulators on cortical F-actin dynamics, mesoscale mechanical properties such as tissue viscosity, and their roles in the mechanics of morphogenesis.

Scrambled tissues are stable and undergo normal differentiation, but do not mature mechanically

For many years, biologists have dissociated cells from their native architectures to investigate regeneration (Wilson, 1907), how positional information is stored in early embryos (Kuroda et al., 2005) and how different cell types within tissues sort to position specific cells in their correct location (Townes and Holtfreter, 1955). Contrary to our expectations, cells in scrambled tissues did not self-assemble the large-scale coherent structures of the dorsal isolate. Prior studies at earlier stages than we investigate here have found that Xenopus tissues are stiffer in one direction than another (Moore et al., 1995). The origins of these early mechanical anisotropies are unknown but may relate to the distinctive planar polarized cell shapes, polarized cytoskeletal structures, or as yet undescribed factors that generate cortex-intrinsic anisotropic mechanical properties. Surprisingly, we found that tissues scrambled at stage 14 and aged to stage 21 did not increase their Young's modulus as much as aged dorsal isolates or freshly excised isolates (compare Fig. 2H with Fig. S3). We suspect this failure to mechanically ‘mature’ depends on cues from tissue architecture that are lost after dissociation and re-aggregation. As scrambled tissues do not undergo large-scale morphogenetic movements, they may be deprived of native stresses that serve to stiffen the tissues. The inability of scrambled tissues to mature their mechanical properties fully may parallel similar deficits observed in engineered cells and tissues, such as induced cardiomyocytes that fail to generate the levels of force seen in natively isolated cardiomyocytes (Yang et al., 2014).

MATERIALS AND METHODS

Embryos and microsurgery

Xenopus laevis embryos were obtained by standard methods (Kay and Peng, 1991), fertilized in vitro, de-jellied in 2% (w/v) cysteine and cultured in 1/3× modified Barth's saline at 22°C. Staging of embryos was performed according to the table of Nieuwkoop and Faber (Nieuwkoop and Faber, 1967). To isolate dorsal tissues, early neurula embryos were selected and transferred to culture media, Danilchik's for Amy (DFA). Vitelline membranes were removed with forceps and dorsal isolate explants were microsurgically isolated using hair tools. Dorsal isolates were allowed to heal for 20-30 min under a small cover glass before mechanical testing. Staging of explants was carried out by comparison with co-cultured whole embryos.

Cell cycle inhibition to generate larger cells

A combination of cycle inhibitors, 20 mM hydroxyurea and 150 μM aphidicolin (HUA) was used at the start of gastrulation (stage 10) and embryos were cultured to stage 14 for mechanical testing. Drugs used in cell cycle manipulation experiments were introduced at their respective doses in sealed acrylic chambers mounted on glass. The drugs were reconstituted in DFA.

Microinjection of morpholino

In Wee2 depletion experiments, 20 ng Wee2 morpholino (W2MO; Gene Tools, LLC) was injected into two dorsal blastomeres (for stiffness testing) or one dorsal blastomere (for F-actin and nuclei characterization) at the four-cell stage (Leise and Mueller, 2004). For microinjection of W2MO, embryos were placed in 1× MBS containing 3% Ficoll (Sigma-Aldrich). For contralateral injections, W2MO was co-injected with RDA to identify the injected side. Morpholino-injected embryos were cultured to stage 18 and selected based on the whole embryo mutant phenotype, which is characterized by a reduced somitic ridge and reduced convergence of dorsal tissues.

Actinin mRNA constructs

α-actinin-1-eGFP (hsACTN1 splice variant 2) was generously provided by Carol Otey (Edlund et al., 2001). The dominant-negative mutant lacking the actin binding domain (ACTN1-ΔABD; amino acids 251-892) was amplified using PCR using α-actinin-1 as a template. ACTN1-ΔABD has been shown to form heterodimers with endogenous α-actinin and act as a dominant negative in NRK cells (Low et al., 2010). For overexpression studies, 2 ng of α-actinin-1 mRNA or 4 ng of ACTN1-ΔABD mRNA was injected into the equator of the two dorsal blastomeres at the four-cell stage. Total volumes of injected mRNA were 4-10 nl per blastomere at the four-cell stage.

Fluorescence recovery after photobleaching

FRAP experiments were performed on a laser scanning confocal microscope (SP5; Leica Microsystems) with a 63× oil objective and 3× optical zoom using the FRAP wizard with LASAF software package. A square ROI (5 µm×5 µm) was manually selected within the F-actin cortex of either animal cap epithelium or mesoderm for bleaching (Kim and Davidson, 2011). To maximize frame rate, 256×256-pixel images were acquired at 700 Hz (∼0.37 s/frame). Bleaching was achieved by zooming in to the square ROI (‘zoom-in’ feature on software) and exposing the 488 nm argon laser for two time steps (∼0.74 s). The laser power was set to 25% and the ND filter setting to 100% for bleaching. Five frames were collected before bleaching and 30 frames after at the same frame rate. After acquisition, intensity profiles were analyzed using custom Matlab software to calculate half-life and immobile fraction.

F-actin cortex thickness measurement

To quantify ‘cell-wall’ thickness, we adapted a method used in single cells to measure F-actin cortex thickness (Clark et al., 2013). Cell cortex thickness measurements within a tissue require mosaic labeling of membrane and actin reporters. Membrane and actin mRNA reporters are co-injected in one dorsal blastomere at the 16-cell stage to achieve scatter throughout the axis. Regions of cortex within mesoderm tissue were manually selected through confocal stacks of transverse tissue sections. A custom program was used to create perpendicular lines (across the junction) using 5 μm thickness and 5 μm spacing and collect intensity along each line scan. Peak positions and intensities were determined by fitting a Gaussian function to the seven points surrounding and including the pixel with highest intensity. Line scans were filtered to ensure a peak was detected in each channel (peak intensity >4× baseline, where baseline is identified as all points excluding the seven points surrounding and including the pixel with highest intensity) and goodness of Gaussian fit (r²>80%). Using parameters from the Gaussian fit, we determined the separation between the positions of the actin cortex and membrane, Δ. We assumed that the membrane is negligibly thin; therefore, cortex thickness was calculated as 2*Δ.

Limitations of cortex thickness measurement and the CSM

Our super-resolution methods assume the cell cortex is flat and fully perpendicular to the plane of the confocal image. The degree of curvature in the out-of-plane direction may confound results, increasing the apparent thickness of the cortex. Cells in the mesoderm range in shape from nearly cuboidal at stage 14 to highly elongated ‘banana’-shaped cells at stage 21 (Fig. 2B). Angle skew in the xz or yz plane would likely result in an underestimation of the relative distance between cortex and membrane positions, and thus an underestimation in thickness. Additionally, sub-resolvable intracellular vesicles involved in transport, endocytosis or exocytosis may confound thickness measurements. Another limitation of measuring cortex thickness in mosaically labeled cells is that it is assumed adjacent cells do not receive any injected mRNA. Low levels of Lifeact mRNA in ‘unlabeled’ cells sharing a junction with ‘labeled’ cells can result in a skewing of the relative position of the cortex towards the membrane and thus an underestimation of cortex thickness. We have attempted to minimize the influence of geometric variations but cannot rule out the influence of intracellular vesicles on cortex thickness measurements.

Nuclear density measurements

Because it is difficult to accurately measure cell volumes, we instead measured nuclear density within a confined volume or area of tissue and correlated that with cell size. As the nuclear density decreases within a confined volume, cell size is increased. Nuclear densities were measured by manually counting nuclei within the given volume or area of mesoderm in each tissue sample. Cell shape was assumed to be cuboidal for simplicity.

Tissue dissociation and re-aggregation

Dorsal tissues were dissociated in Ca²⁺⁺- and Mg²⁺-free DFA for 5-7 min and superficial epithelium was discarded. Dissociated cells were transferred to custom wells. To enable tissue re-aggregation without attachment, 50 µl agarose was pipetted into each well. Cells were centrifuged for 8 min at 2000 g to create disc-shaped tissues and confirmed the top and bottom surfaces of the scrambled tissues were flat. After centrifugation, scrambled tissues were removed from the chamber and cultured in DFA for 30 min before microsurgery. Scrambled tissues were cut into regular-shaped ‘bricks’ approximately 200×400×600 µm for mechanical testing.

Mechanical testing

Time-dependent viscoelastic properties of embryonic tissues were measured using an unconfined uniaxial compressive stress-relaxation test that has been described in detail previously (Davidson and Keller, 2007). In brief, the tissue sample is compressed ∼20% along its anterior-posterior axis and the resistive force is measured by the deflection of the optical fiber force transducer. The tissue samples are visualized by stereomicroscopy during compression to obtain length measurements throughout testing. Immediately after testing, samples are fixed in 4% paraformaldehyde, bisected and imaged to obtain cross-sectional areas. Young's modulus after 180 s of compression, E(180), is then calculated using measured resistive force, cross-sectional area and strain measurements as shown below:

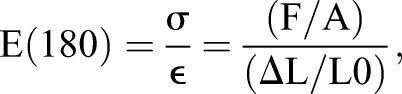(3)

where E is the time-dependent Young's modulus, F is the resistive force measured during the stress-relaxation test, A is the cross-sectional area, L0 is the length of samples before compression and ΔL is the change in length before and after compression. Statistical significance of treatments on E(180) over a set of different clutches was analyzed with two-way ANOVAs using commercial statistical software (IBM SPSS).

Confocal microscopy and immunohistochemistry

To assess structure, dorsal isolates and scrambled tissues were fixed with 4% paraformaldehyde for 3 h at room temperature or overnight at 4°C or Dent's fixative overnight at 4°C. Immediately after fixation in paraformaldehyde or after rehydration from Dent's fixative, explants were bisected and blocked in 10% goat serum prior to antibody staining. Immunofluorescence staining was carried out with primary antibodies against fibrillin-2 (JB3, Developmental Studies Hybridoma Bank; 1:200), laminin (L9393, Sigma-Aldrich; 1:500), fibronectin (4H2, courtesy of Douglas DeSimone, University of Virginia, Charlottesville, VA, USA; 1:500), β-catenin (C2206, Sigma-Aldrich; 1:500), muscle marker (12/101; Developmental Studies Hybridoma Bank) and pMRLC (ser19; Cell Signaling, 3671). We additionally used fluorophore-conjugated primary antibodies against EGFP (Alexa Fluor 647; ThermoFisher, A-31852) and mCherry (Alexa Fluor 488; ThermoFisher, M-11239). Appropriate secondary antibodies included goat anti-rabbit IgG H+L (Jackson ImmunoResearch, 111-003) and goat anti-mouse IgG H+L (Jackson ImmunoResearch,115-003). Laser scanning confocal microscopy was used to acquire high-resolution image stacks of scrambled and native tissues. Stacks were collected using a confocal laser scan head (SP5 Leica Microsystems) mounted on an inverted compound microscope (DMI6000, Leica Microsystems) using acquisition software (LASAF, Leica Microsystems).