Forecasting the new case detection rate of leprosy in four states of Brazil: A comparison of modelling approaches

Abstract

Background:

Brazil has the second highest annual number of new leprosy cases. The aim of this study is to formally compare predictions of future new case detection rate (NCDR) trends and the annual probability of NCDR falling below 10/100,000 of four different modelling approaches in four states of Brazil: Rio Grande do Norte, Amazonas, Ceará, Tocantins.

Methods:

A linear mixed model, a back-calculation approach, a deterministic compartmental model and an individual-based model were used. All models were fitted to leprosy data obtained from the Brazilian national database (SINAN). First, models were fitted to the data up to 2011, and predictions were made for NCDR for 2012–2014. Second, data up to 2014 were considered and forecasts of NCDR were generated for each year from 2015 to 2040. The resulting distributions of NCDR and the probability of NCDR being below 10/100,000 of the population for each year were then compared between approaches.

Results:

Each model performed well in model fitting and the short-term forecasting of future NCDR. Long-term forecasting of NCDR and the probability of NCDR falling below 10/100,000 differed between models. All agree that the trend of NCDR will continue to decrease in all states until 2040. Reaching a NCDR of less than 10/100,000 by 2020 was only likely in Rio Grande do Norte. Prediction until 2040 showed that the target was also achieved in Amazonas, while in Ceará and Tocantins the NCDR most likely remain (far) above 10/100,000.

Conclusions:

All models agree that, while incidence is likely to decline, achieving a NCDR below 10/100,000 by 2020 is unlikely in some states. Long-term prediction showed a downward trend with more variation between models, but highlights the need for further control measures to reduce the incidence of new infections if leprosy is to be eliminated.

1. Introduction

Leprosy, or Hansen’s disease, is an infectious disease caused primarily by Mycobacterium leprae. It affects the skin, peripheral nerves, the mucosa of the upper respiratory tract and the eyes (Leprosy, 1982). Most people are able to clear the bacterium before disease occurs, or are resistant to the leprosy infection. The most likely route of transmission of leprosy is through aerosols (Hatta et al., 1995), with contacts closest to a patient with leprosy, in particular within household contacts, having the highest risk of acquiring the infection (Fine et al., 1997; Moet et al., 2006). Detection of leprosy is based on clinical signs and classified into paucibacillary (PB; ≤5 skin lesions) and multibacillary (MB; >5 skin lesions) leprosy. Currently, the main strategies to control leprosy are early detection of cases, and treatment with multidrug therapy (Global leprosy update, 2015). Chemoprophylaxis and immune-prophylaxis are both potential interventions but are not yet routinely available.

Global elimination of leprosy has been a target for many years. In 1991, the World Health Assembly set a goal for “elimination of leprosy as a public health problem”, defined as a prevalence of less than 1 per 10,000, by the year 2000 (WHO, 1991). More recently, the World Health Organization (WHO) has formulated new targets for leprosy, which include global interruption of transmission or elimination by 2020, and reduction of grade-2 disabilities in newly detected cases to below 1 per million population at global level by 2020 (WHO, 2012). Currently, worldwide, more than 200,000 new cases of leprosy are detected annually, with India, Brazil and Indonesia accounting for around 80% of all new cases (Global leprosy update, 2015). This incidence has remained fairly stable over the past decade. Brazil has the second highest annual incidence with approximately 31,000 new cases and annual new case detection rate (NCDR) of 15.32 per 100,000 population in 2014 (Ministry of health, 2015). Brazil was one of the countries that did not achieve elimination by 2000 (Castro et al., 2016). In 2011, the Ministry of Health defined an integrated action plan to reduce the burden of leprosy and to eliminate leprosy as a public health problem by 2015. This plan includes active case finding and timely provision of treatment in prioritized municipalities, primarily located in the Amazon region (Ministry of Health, 2012).

The spatial distribution of leprosy in Brazil is known to be heterogeneous with the highest number of cases in the Northern, North-Eastern and Central-Western regions. Most high-risk states or districts are part of the Brazilian Amazon (Penna et al., 2009; Penna et al., 2013). In 2014, ten states (37%) had a NCDR of more than 20 per 100,000, eight states (30%) a NCDR between 10 and 20 per 100,000, and nine states (33%) with a NCDR of less than 10 per 100,000 (Ministry of health, 2015). The highest rates can be found in the hyperendemic states of Mato Grosso and Tocantins with NCDR of 82.03 and 69.88 per 100,000, respectively. Also, within each state, leprosy is known to be unevenly distributed (Alencar et al., 2012; Kerr-Pontes et al., 2004). Although recent numbers show a slight declining trend in most states, more than two thirds of the states in Brazil can be regarded as highly endemic.

Although the WHO target is the interruption of leprosy transmission globally by 2020, it is clear that this will not be feasible due, for example, to the long incubation time of leprosy. We therefore focus on the feasibility of reducing the NCDR to low levels, which is likely to result in a reduced transmission. The aim of this study is to compare four modelling approaches being applied to leprosy in the context of assessing whether a NCDR of less than 10 per 100,000 can be met by 2020 and predicting the annual probability of NCDR being below 10 per 100,000 in four states of Brazil: Rio Grande Do Norte (low endemic), Amazonas (medium-high endemic), Ceará (high endemic), and Tocantins (hyper endemic state). These states were purposively selected based on differences in levels of endemicity and historic patterns of leprosy NCDR.

Prediction of infectious disease patterns is complicated by the intrinsic non-linearity in the transmission process: more transmission leads to more infection which leads to more disease which leads to more transmission. Models are, by definition, abstract simplifications of reality, and in order to have confidence in their results, need to be challenged and validated. The best way to develop consensus advice is through comparison of outputs of different models. Consequently, we applied two statistical models and two mathematical transmission models to estimate future NCDR of leprosy from the same data, including: a linear mixed model, a Bayesian back-calculation approach, a deterministic compartmental model and the individual-based stochastic model SIMCOLEP. Back-calculation has shown potential to estimate numbers of newly infected individuals in Thailand (Crump and Medley, 2015). SIMCOLEP, which models the transmission and control of leprosy in a population structured by households, has been used to estimate future NCDR trends in Bangladesh, India, Brazil, and Indonesia, and to explore the potential impact of various interventions targeting household contacts (Blok et al., 2015a; de Matos et al., 2016; Fischer et al., 2011). In this study, we will explore the levels of agreement between these methods on future projections of the NCDR in the four chosen states. Model results are discussed to understand factors contributing to similarities and differences between methods.

2. Materials and methods

2.1. Data

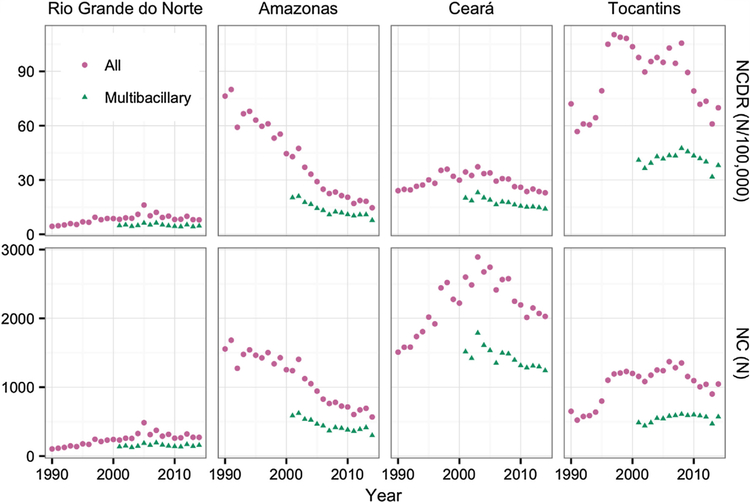
Annual summary data by state were extracted via the SINAN database’s web interface (SINAN, 2016) for the years 1990–2012. The SINAN database is the Brazilian government’s repository for information on communicable diseases. The data retained for use in this study consisted of the annual number of new cases diagnosed (NC) and the annual new case discovery rate (NCDR) for MB and PB diagnoses combined, for 1990–2012, and for MB cases separately, from 2000 to 2012, along with the population size. Equivalent data for 2013 and 2014 were retrieved from documents on the Brazilian government’s health portal (Ministry of health, 2015; Ministry of health, 2014). Population size and NCDR for MB diagnoses were not reported in the 2013 and 2014 data tables. However, the NCDR for total diagnoses and the number of total diagnoses and MB diagnoses were still included. Using the NCDR for total diagnoses and the number of total diagnoses, we calculated the population size and finally generated the NCDR for MB diagnoses for 2013 and 2014. Four states were chosen for inclusion in the study using NCDR to indicate the level of endemicity in the state. The states selected were Tocantins (NCDR in 2014 69.9 per 100,000), Ceará (22.9), Amazonas (14.6) and Rio Grande do Norte (8.0) (Ministry of health, 2015). The data for the four states are presented in Fig. 1.

Fig. 1.

Observed new case detection rates (NCDR) and numbers of new cases (NC) for four Brazilian states. Data for combined paucibacillary and multibacillary diagnosis types from 1990 to 2014 and for multibacillary diagnoses separately since 2001.

2.2. Estimation approaches

The fundamental purpose is to compare four different methods for probabilistic forecasting of leprosy. Each method (whether Bayesian or frequentist) yields the probability distribution of future outcomes, i.e. results not used for training the model. Four approaches were used: a linear mixed model, a Bayesian back-calculation approach, a deterministic compartmental model, and the individual-based stochastic model SIMCOLEP. In no case did we use data used for fitting or training as part of the test or evaluation set. By bringing these models together, we can evaluate to what extent predictions of NCDR are similar or different in order to validate and to improve predictive quality. The next sections provide a brief description of each approach with further details provided in the supplementary materials S1–S3. The model code of the linear mixed model, back-calculation approach and deterministic compartmental model are provided in supplementary material S5. The model code of the individual-based model SIMCOLEP can be found in Blok et al. (Blok et al., 2015a).

2.3. Linear mixed models

A standard linear mixed effects regression was fitted to the data, as in Brook et al. (Brook et al., 2015). Specifically, we modelled the log of the annual new case detection rate as a linear function of time, with a random slope and intercept. We used only years 2001–2011 for the fitting. To model the uncertainty, we used the Metropolis algorithm (a Markov chain Monte Carlo (MCMC) procedure) to estimate the posterior joint distribution of the fixed effect estimates (overall slope and intercept), the variance of the random intercept and slope, and the residual error. Our method corresponds to a Bayesian analysis with noninformative priors; the maximum posterior density occurs at the maximum likelihood estimate. More specifically, we have assumed a random effect for the slope and intercept for each state; all states were included in common statistical model, though forecasts were only generated for the four states under consideration. Finally, conditional on these estimates, we simulated from the joint distribution of random effects to project forward.

2.4. Back-calculation

Back-calculation utilises information on diagnoses and the time between infection and diagnosis to make inferences about the infection dynamics of infectious diseases. For discrete time periods the number of diagnoses in any given period is the sum of the number of infections in the previous periods multiplied by the probability of diagnosis in the current period given the infection period. Leprosy can only be diagnosed in clinical cases, therefore the time from infection to diagnosis can be subdivided into the period from infection to onset of clinical symptoms (the incubation period) and from onset of clinical symptoms to diagnosis (the detection delay). Crump and Medley (Crump and Medley, 2015) applied back-calculation to the national annual summary data for leprosy in Thailand. Here we use a similar model, with a two-stage time between infection and diagnosis where the hazard of being diagnosed in any year i given onset of symptoms in year j (j < i) is scaled by a parameter which might be interpreted as diagnostic effort or success within a period.

Parameters of the incubation period distribution (IPD) and detection delay distribution (DDD) were estimated from a small dataset with known, relatively short periods of exposure to leprosy infection (Crump and Medley, 2015). A Bayesian MCMC procedure was used to generate samples from the joint posterior probability distributions of these parameters which were subsequently used in the back-calculation.

The back-calculation model was implemented in the Stan probabilistic programming language (Stan Development Team, 2015) and run in the R statistical environment (R Core Team, 2016) via the rstan package (Stan Development Team, 2016). Details of the model are given in the Supplementary Material (S1). The model was similar to that of Crump and Medley (Crump and Medley, 2015) with some methodological changes, including having the expected number of new subclinical cases in a year be proportional to the number of extant undiagnosed clinical cases and the lack of data in the present study to inform the timing of changes in diagnostic effort and absence of data on grade 2 disability diagnoses. Changes in diagnostic effort were assumed to occur at the end of 1995, 2000 and 2007 for all analyses.

Resistance or susceptibility to leprosy and self-healing are not accounted for in the back-calculation model. The data analysed are the annual number of new cases diagnosed. As a result, the numbers of subclinical and clinical cases inferred by the model refer specifically to those as-yet asymptomatic and symptomatic cases that will result in diagnosed cases in the future.

For each sample from the joint posterior distribution of parameters included in the back-calculation model (diagnostic effort parameters, the annual proportion of infective individuals giving rise to a new subclinical case, the proportion of new diagnoses which are MB and the expected number of new diagnoses at equilibrium) observed values were simulated across the time period. New subclinical cases in each year were sampled from a negative binomial distribution with expectation proportional to the size of the infective pool and variance equal to the expectation squared. Binomial sampling was used to decide the year in which subclinical cases became clinical (based on the hazard function of the IPD) and clinical cases were diagnosed (based on the hazard function of the DDD and the diagnostic effort parameters). More information is provided in the Supplementary Material (S1).

To incorporate the uncertainty about the IPD and DDD parameters, multiple inference was used. The model was run repeatedly for any dataset with a randomly selected set of IPD and DDD parameters used in each run. Each of 1000 back-calculation runs were used to generate 25 samples from the posterior probability distributions of values associated with the infection process. The outputs from these runs were combined post-analysis to give 25,000 samples for each state-analysis combination. Estimates of NCDR were generated from the posterior samples of the numbers of new cases using the same predictions of population size as used in the SIMCOLEP simulations. Summary statistics of these 25,000 samples from the posterior probability distributions form the primary results for this model reported here: means, 2.5th and 97.5th percentiles and the proportion of NCDR samples which less than 10/100,000.

2.5. Compartmental model

We used a deterministic compartmental model similar to previously published models (Lechat et al., 1974; Lietman et al., 1997), which includes compartments for susceptible non-infected individuals (whether Bacillus Calmette–Guérin (BCG) vaccinated or not), latent infected individuals, symptomatic infected individuals, and individuals who are both diagnosed and treated. The compartments for infected individuals are stratified into paucibacillary and multibacillary leprosy infections (S2 Table 1). Flow from one compartment to another is defined by a directed acyclic graph (S2 Fig. 1), and the dynamics of flow from one compartment to another is defined by a set of differential equations (S2 Table 2) that describe the change in size of these compartments over time. These equations model the factors that affect flow into and out of each compartment.

A set of initial values for the state variables of these equations and a set of values for the parameters (S2 Table 3) in these equations is necessary and sufficient to calculate model forecasts for a given time period. In order to calculate these initial values and parameter values, the following approach was used: some values were modelled as fixed-values that were derived from relevant literature (S2 Table 4), and some values were calculated using Markov Chain Monte Carlo (MCMC) sampling from prior distributions derived from relevant literature (S2 Table 5). This MCMC process calculates maximum-likelihood parameter values based on leprosy incidence data for the years 2001–2011. Gelman-Rubin statistics were used to evaluate chain convergence. The model is equivalent to a Bayesian analysis with noninformative priors.

Once calculated, these initial values and parameter values were used to generate a distribution of model forecasts. Residual variance from the training data was then applied to the model forecasts, to more accurately capture the uncertainty in the data. This distribution of forecasts was then used to calculate a mean, 2.5th percentile and 97.5th percentile model forecast for each forecast year, in order to generate credible intervals for the model forecasts.

2.6. SIMCOLEP

The individual-based model SIMCOLEP simulates the spread of M. leprae in a population structured in households. Dynamics of the population are described by births, movements between households, and deaths. Births are determined by birth rates and new-borns are placed in the household of their mother. Movements of individuals to another newly created or existing household occur after marriage, during adolescence or after becoming a widow(er). Deaths are determined by death rates (Blok et al., 2015b; Fischer et al., 2010).

In the model, transmission of M. leprae occurs after direct contact of a susceptible individual with an infectious individual. We assumed that 20% of the population is susceptible (i.e. 80% will not develop leprosy), based on the results of a previous modelling study (Fischer et al., 2010). Since the mechanism that underlies susceptibility is still unknown, susceptibility of an individual is randomly determined at birth. Two transmission processes are modelled separately: transmission in the general population and within-household transmission. Infectivity is determined by the product of the contact rate and the probability of infection during a contact. Each transmission process has its own contact rate. An infected individual will develop either PB or MB leprosy, which is randomly determined based on the distribution of the type of leprosy in each state. In the model, both types can be detected, treated and cured, but only MB leprosy is considered infectious. The natural history of leprosy is modelled following Meima et al. (Meima et al., 1999).

Leprosy control includes treatment with multidrug therapy (MDT), passive case detection, and active case finding. Passive case detection is reflected by estimated annual detection delays (Gamma distributed). Active case finding or household contact tracing are based on annual coverage rates (Ministry of health, 2015). After detection the patient is given MDT treatment and considered not to be infectious from then on. The model further assumes a protective effect of 60% of BCG vaccination prior to the infection (Schuring et al., 2009). Each state was modelled separately using SIMCOLEP. First the distribution of household sizes was fitted to the data in each state. Afterwards, leprosy NCDR trends were fitted to the data by calibrating contact rates and detection delays. Based on previous work, the contact rate within households was fixed at 0.98 (Fischer et al., 2010). The coverage of active case finding was set to 43% since 2003 in all states (Ministry of Health, 2011). For the long-term predictions, coverage rates were increased from 2014 onwards based on data (Ministry of health, 2015). The contact rate in the general population and annual detection delays were estimated for each state separately. Simulated new case detection rates were compared to the data using a log-likelihood function assuming a Poisson distribution. Using fitted values future predictions were made for 2012–2014 and finally 2015–2040. Final results were based on 1000 runs, which were used to calculate the mean and the 2.5th and 97.5th percentile. The probability of future NCDR being below 10 per 100,000 was calculated as the proportion of runs in which the target was achieved. More information is provided in the Supplementary Material (S3).

2.7. Analyses

Two sets of analyses were performed with each approach. In the first, the ability of the models to forecast was evaluated by omitting data from 2012 to 2014 and the models fitted to the remaining data. Short-term forecasts of NC and NCDR for the omitted data, for all diagnoses and MB diagnoses, were then compared between the approaches and the data.

Each of the analyses gave a probability distribution for NC and NCDR in the forecast years, for all and MB diagnoses. An approximate density function was fitted to each of these using the logspline package in R (Kooperberg, 2016) and the probability of the observed data points for 2012–2014 were calculated from these densities. The log likelihood of each observed value was computed based on the forecasted distribution (Bröcker and Smith, 2007), and the sums of the log likelihood over the years 2012–2014 by state, variable (NC and NCDR) and analysis for each diagnosis type (all or MB diagnoses) were calculated as indicators of which analysis gave the better short-term forecasts in these data sets.

Following this evaluation of the short-term model forecasts using observed data, the models were used to forecast trends. All of the data were included in the second analyses and forecasts of NCDR for combined paucibacillary and multibacillary diagnoses were generated for each year from 2015 to 2040. The resulting distributions of NCDR and probability of NCDR being below 10 per 100,000 of the population for each year were then compared between approaches.

3. Results

Figs. 2–5 show the major results for NCDR of all diagnosed leprosy cases. The figures relating to NC of all leprosy cases and both NC and NCDR for multibacillary diagnoses are provided in the Supplementary Material (S4).

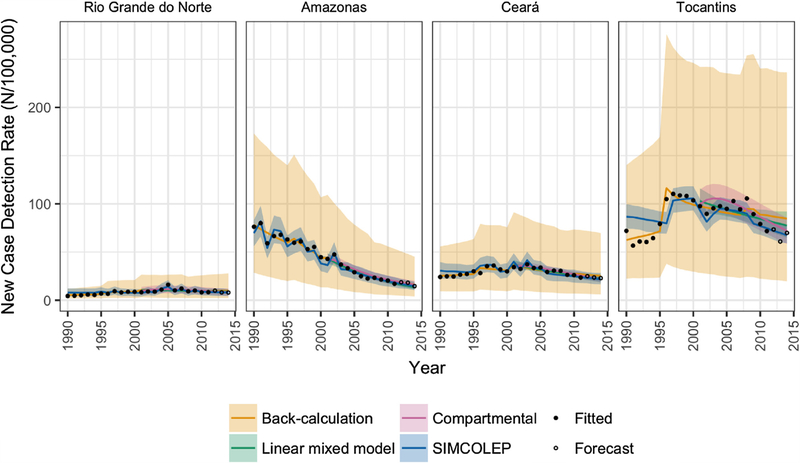
Fig. 2.

Comparison of predicted trends from four modelling approaches with the observed new case detection rates of leprosy in four states of Brazil. Model outcomes are represented by means (solid lines) and 95% prediction intervals (shaded areas).

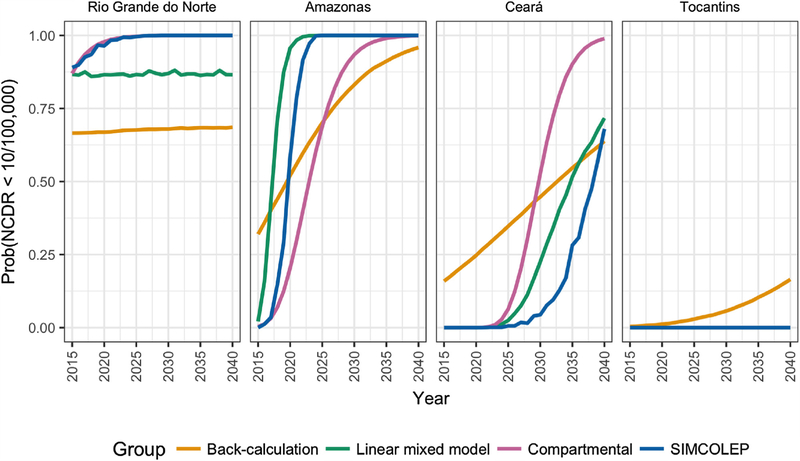
Fig. 5.

Probability of achieving a NCDR of less than 10 per 100,000 by year and state, as predicted by SIMCOLEP, compartmental, back-calculation and linear mixed models.

Fig. 2 shows the mean and 95% forecast interval of predicted NCDR values from analyses excluding 2012–2014 observations for the period 1990–2014 from each model overlaid with the observed data points. Generally, SIMCOLEP predictions appear to follow the data more closely than the smoother fit of the back-calculation and the compartmental model, however all models provide a good visual fit to the observed data. There is noticeably more variation in the predictions from the back-calculation but the difference in variability varies between the States. Similar results are found for the predicted NCDR of MB cases and NC of all and MB cases (See S4).

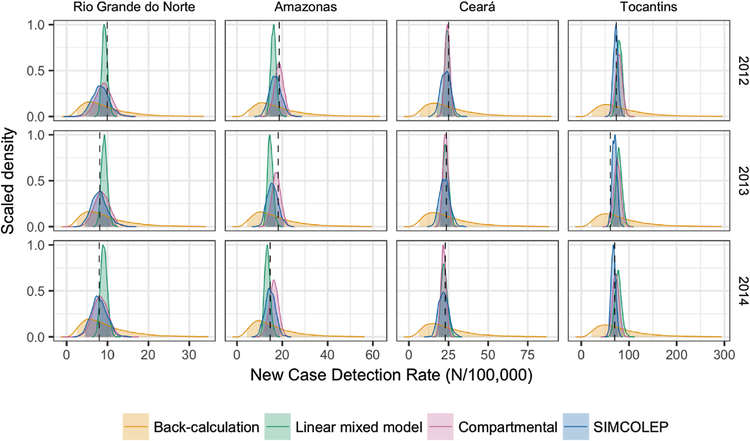
The distribution of short-term forecasted NCDR values are presented by State and year in Fig. 3, this figure providing a more detailed look at the forecast distributions included in Fig. 2 trends. Almost all data points lie within the distribution of predicted forecasts for all models. Table 1 contains sum of log likelihoods for the forecast data points for each analysis, with a higher (less negative) log likelihood indicating a better forecast. These values are relative to each other and do not have an independent interpretation. No model was clearly superior in terms of the sum of the log likelihoods of the forecast data, with the highest values for each analysis being shared evenly between SIMCOLEP, the compartmental model and the linear mixed model. The posterior densities for the back-calculation model were very broad, giving lower density at any given point.

Fig. 3.

Distribution of forecasted new case detection rates of leprosy in 2012–2014 by state, as predicted by four modelling approaches. The observed value for each state-year combination is indicated by a vertical black dashed line.

Table 1.

Sum of log likelihood of observed data from 2012 to 2014 conditional on the outcomes of analyses to forecast these data by state and model.

State	Variable	Model	Diagnoses
			All	MB
Rio Grande do Norte	NCa	SIMCOLEP	−15.56	−14.23
		Compartmental	−15.22	−12.55
		Back-calculation	−18.39	−16.63
		Linear mixed model	−14.06	−11.84
	NCDRb	SIMCOLEP	−5.11	−3.63
		Compartmental	−4.83	−1.89
		Back-calculation	−7.87	−6.12
		Linear mixed model	−4.53	−1.92
Amazonas	NCa	SIMCOLEP	−17.33	−16.48
		Compartmental	−17.74	−17.04
		Back-calculation	−20.73	−19.39
		Linear mixed model	−21.05	−20.83
	NCDRb	SIMCOLEP	−6.26	−5.50
		Compartmental	−5.27	−4.64
		Back-calculation	−9.86	−8.49
		Linear mixed model	−10.09	−9.76
Ceara	NCa	SIMCOLEP	−19.76	−18.83
		Compartmental	−18.53	−17.43
		Back-calculation	−24.23	−22.80
		Linear mixed model	−18.12	−16.38
	NCDRb	SIMCOLEP	−6.37	−5.39
		Compartmental	−4.61	−3.74
		Back-calculation	−10.83	−9.42
		Linear mixed model	−4.85	−3.05
Tocantins	NCa	SIMCOLEP	−17.33	−16.02
		Compartmental	−17.31	−18.01
		Back-calculation	−21.97	−20.17
		Linear mixed model	−20.42	−24.66
	NCDRb	SIMCOLEP	−9.52	−7.99
		Compartmental	−11.10	−15.64
		Back-calculation	−13.96	−12.11
		Linear mixed model	−14.27	−23.07

^aNumber of new cases.

^bNew case detection rate.

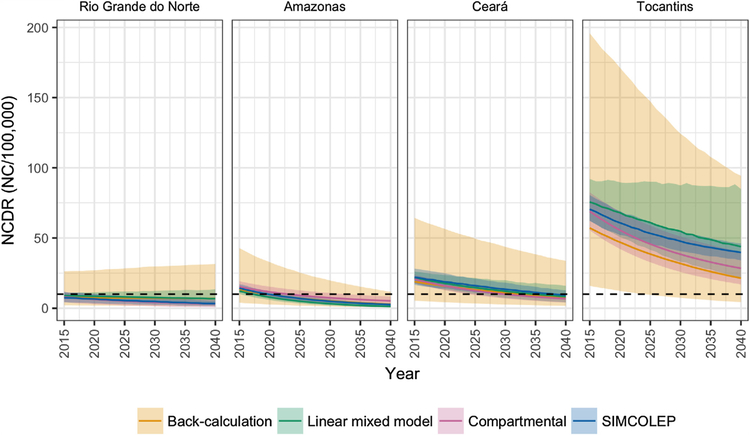
Fig. 4 shows the longer-term forecasts of NCDR by state and year. All modelling approaches predict a downward trend until 2040 in all four states. In 2020, the median NCDR is expected to remain above 10 per 100,000 in all states except for Rio Grande do Norte. In general, the compartmental model and SIMCOLEP are more optimistic than the back-calculation approach. This is also reflected in the annual probability of NCDR falling below 10 per 100,000 (Fig. 5). According to the compartmental model and SIMCOLEP, the probability of achieving the target increases to 100% in Rio Grande do Norte from 2024 and 2025 onwards, respectively, whereas the linear mixed model and the back-calculation predicts a steady probability of 87% and 67%, respectively. In Amazonas the target can be met with 80% probability in 2027, 2022, 2029, and 2019 according to the compartmental model, SIMCOLEP, back-calculation and the linear mixed model, respectively. The predictions for Ceará also show a discrepancy between the models. According to the linear-mixed model, the back-calculation and SIMCOLEP, a NCDR below 10 per 100,000 is very unlikely in Ceará before 2040, while the compartmental model predicts that it becomes more likely closer to the year 2040. All models predict that Tocantins will not achieve the target incidence within the modelled time span.

Fig. 4.

Predicted long-term NCDR trends from four modelling approaches by year and state. The horizontal black dashed line marks the elimination as a public health problem threshold of 10 new cases per 100,000. Model forecasts are represented by means (solid lines) and 95% prediction intervals (shaded areas).

4. Discussion

This paper compared the results of four approaches with the purpose to assess the feasibility of a NCDR below 10 per 100,000 by 2020 and to predict the annual probability of NCDR falling below 10 per 100,000 until 2040 in four states of Brazil. According to the prediction of our models, this is only feasible by 2020 in the state of Rio Grande do Norte. All models clearly showed that by 2020 the NCDR remains above 10 per 100,000 in Amazonas, Ceará and Tocantins, indicating that the target will not be met. Long-term predictions of the NCDR trend showed a downwards trend in all states, assuming that Brazil continues the current level of effort to control leprosy. Amazonas will likely achieve the target before 2040, while in Ceará and Tocantins the NCDR most likely remain (far) above 10 per 100,000 in the modelled time frame.

Our findings highlight the need for a shift in the current leprosy control strategy in order to achieve a NCDR of less than 10 per 100,000 in a reasonable time frame. Preventive interventions should be targeted on contacts of leprosy patients, since they have the highest risk of getting infected and developing clinical leprosy (Moet et al., 2004). Examples of such interventions include intensified contact tracing and providing chemoprophylaxis and/or immunoprophylaxis (vaccination) to contacts. Chemoprophylaxis with a single dose rifampicin is effective at preventing clinical leprosy (Moet et al., 2008). Recent modelling work showed that when provided in household contact only, it can speed up elimination (de Matos et al., 2016).

All models performed well in short-term forecasting of future diagnoses. Note that the performance of straightforward longitudinal analysis was comparable to the other procedures, with the exception of MB trends in Tocantins. Here, the regression continued to extrapolate a rising trend into the future, partially due to the use of a separate regression model for each outcome and to the use of a random effect for slope in the model. Other methods, such as the use of exponentially weighted smoothing, would be more influenced by the most recent data points than those further in the past, and may have improved performance. Similarly, regression models informed by prior distributions reflecting additional epidemiological information (e.g., a long term rising trend is less credible when all other regions are declining) may perform better.

There is a great difference between models for the longer-term forecasting of NCDR and the probability of NCDR falling below 10 per 100,000. The back-calculation does not include a mechanistic description of transmission but new subclinical cases arise at a rate proportional to the size of the infectious pool (with a naïve definition of the infectious pool as being all the existing undiagnosed clinical cases). The change in NCDR beyond 2014 in the back-calculation analysis is caused by a combination of the rate of incidence of new subclinical cases, the diagnostic effort (assumed to be the same as 2014) and population growth. The decline, as predicted by SIMCOLEP, can be attributed to leprosy control efforts. The model assumed a continuation of the leprosy control in 2014 in each state. This also includes household contact tracing with a coverage of 56%, 76%, 70%, and 85% in Rio Grande do Norte, Amazonas, Ceará and Tocantins, respectively (Ministry of health, 2015). Contact tracing and treatment further reduces transmission of leprosy.

There is greater variability in the predicted values from the back-calculation approach and this may be due to the simultaneous estimation of the associated parameters (diagnostic effort, multibacillary diagnosis proportion), the incorporation of uncertainty about these parameters into the outcomes and the assumed variation in simulating new subclinical infections. In contrast, predictions of SIMCOLEP were based on the best fit of estimated parameters, including the contact rate in the general population and detection delays. Other parameters, such as MDT treatment and household contact tracing were fixed to values obtained from data and literature, which also reduces variability. One of the benefits of multi-model comparisons is that they expose the variability due to model assumptions, but also exposes the differences in the way that uncertainty is handled. There is clearly a trade-off between models accurately reflecting uncertainty, and being sufficiently precise to be useful to programme managers and policy makers. The back-calculation approach has very few (model) assumptions, and no fixed parameters, and more accurately reflects the possibility that, for example, a large number of people were infected in 2015 and have yet to be diagnosed, i.e. there is no information on the most recent infection rates. SIMCOLEP more accurately reflects current understanding of infection and essentially rules out dramatic changes in infection rates. We do not believe that there is a formal solution to enable these differences to be reconciled.

In this study we assessed the feasibility of reducing the NCDR to lower levels as a first step to achieve the target of interruption of transmission. However, the NCDR is not a reliable indicator to assess reduction of transmission, because it is also very dependent on the control efforts in a state. A better benchmark for cutting transmission would be to achieve zero leprosy cases among children (Smith et al., 2014).

The quality of reported data remains a concern in this study. The modelled States are among the poorest in Brazil, and they tend to have long(er) detection delays, which results in a large number of undiagnosed leprosy cases. Thus the national leprosy database, SINAN, tends to underestimate the real numbers of cases (Kerr-Pontes et al., 2004; Salgado et al., 2016). Targeted field surveys in the Amazon regions have resulted in many new cases detected (Barreto et al., 2012; Salgado et al., 2012). These undiagnosed cases remain a threat for breaking transmission in general (Smith et al., 2015). Reported detection rates are known to reflect operational variation in time, of which some are known and others unknown (Penna et al., 2009). It is believed that migration, especially in Tocantins, might explain to some extent the fluctuation in NCDR trends (Monteiro et al., 2015; Nobre et al., 2015). None of the models includes specific assumptions about migration and the possibility that cases are diagnosed in a State different from that in which they were infected, and there is clearly a need for model development to include movement.

Another consideration is the uneven distribution of leprosy in each state (Alencar et al., 2012; Kerr-Pontes et al., 2004). A state such as Rio Grande do Norte has (historically) relatively low NCDR, but nevertheless contains hyper endemic municipalities (Nobre et al., 2015). Although our models predict that Rio Grande do Norte will very likely achieve the target of a NCDR below 10 per 100,000, continuous control efforts remain needed to bring down leprosy in high endemic municipalities.

5. Conclusions

The NCDR for leprosy is expected to continue to decline in Brazil, if it keeps the current level of efforts to control leprosy. However, these results show that the efforts made to achieve the gains to date are required for many years to come, due to the long incubation period of leprosy and hidden cases. By bringing together multiple models we have evaluated the trends using very different methods, to give more robust insight on the likely future trends of the NCDR. The model estimates suggest that there are high levels of ongoing transmission in some of these states, meaning that control efforts will need large increases in efficacy to reduce the NCDR to low levels over the next decade, and breaking transmission may require a shift in policy, such as providing post-exposure prophylaxis to contacts.